应力与应变间的关系
应力和应变之间的关系
即为平面应力状态,有
1
1 E
s 1 s 3
3
1 E
s 3 s 1
联立两式可解得:
s1
E 1
2
1 3
210 10 1 0 .3
2
9
240
0 . 3 160 10
6
s3
44 . 3 M Pa 9 E 210 10 3 1 160 0 . 3 240 10 2 2 1 1 0 .3
利用空间应力状态下最大切应力的计算式可得:
t max s1 s3
2 7.25MPa
§7-5 平面应力状态下的电测法
对各向同性材料图示平面应力状态,在线弹性、 小变形条件下,sx、sy与切应变无关,即有:
sy sx
x y
1 E 1 E
s s
E
x
s s s
y
y F a
sy sx sz
x
a
(a)
z
(b)
解:铜块应力状态如图b所示,横截面上的压应力为:
s
y
F A
30 MPa
受钢槽的限制,铜块在另两个方向的应变为零, 并产生压应力,即有:
x z
1 E 1 E
s s
x
s s
y
s s
z
0 0
所以,应变能密度为: v
d V dxdydz
1tx 2 G
而对纯剪应力状态,其主应力为:
s 1 tx
s2tx
s1 t
x
s
2
材料力学中的应力与应变关系

材料力学中的应力与应变关系材料力学是研究材料在受力作用下的力学行为和性能的学科,应力与应变关系是其中的核心内容之一。
本文将讨论材料力学中的应力与应变的概念及其数学表示,以及应力与应变之间的线性关系与非线性关系。
一、应力的概念及表示应力是指材料单位面积上的内部力,常用符号σ表示。
根据受力情况的不同,可以分为正应力、切应力和体积应力。
正应力是指与作用力方向垂直的内部力,常用符号σ表示;切应力是指与作用力方向平行的内部力,常用符号τ表示;体积应力是指作用在体积内的内部力,常用符号p表示。
正应力的数学表示为σ = F/A,其中F为作用力的大小,A为受力面积。
切应力的数学表示为τ = F/A,其中F为切力的大小,A为受力面积。
体积应力的数学表示为p = F/V,其中F为体积力的大小,V为受力体积。
二、应变的概念及表示应变是指材料在受力作用下产生的形变程度,常用符号ε表示。
根据变形方式的不同,可以分为线性应变和体积应变。
线性应变是指在受力作用下,材料产生的长度或角度发生变化,常用符号ε表示;体积应变是指在受力作用下,材料产生的体积发生变化,常用符号η表示。
线性应变的数学表示为ε = ΔL/L0,其中ΔL为长度变化量,L0为原始长度。
体积应变的数学表示为η = ΔV/V0,其中ΔV为体积变化量,V0为原始体积。
三、应力与应变的线性关系在一定范围内,应力与应变之间可以表现为线性关系。
根据胡克定律(Hooke's Law),线性弹性材料的应力与应变之间满足σ = Eε,其中E为弹性模量。
弹性模量是材料刚度的度量,表示材料单位应力产生的单位应变。
常见的弹性模量有杨氏模量、剪切模量和泊松比。
杨氏模量的数学表示为E = σ/ε,其中σ为应力,ε为线性应变。
剪切模量的数学表示为G = τ/γ,其中τ为切应力,γ为切应变。
泊松比的数学表示为ν = -εv/εh,其中εv为垂直方向的线性应变,εh为水平方向的线性应变。
应力与应变间的关系

22
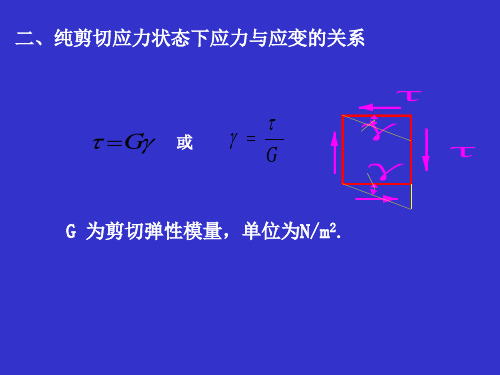
例题7-7 边长 a = 0.1m 的铜立方块, 无间隙地放入体积较
大, 变形可略去不计的钢凹槽中, 如图 所示。 已知铜的弹 性模量 E=100GPa, 泊松比 =0.34, 当受到P=300kN 的均布 压力作用时, 求该铜块的主应力. 体积应变以及最大剪应力。
P a
y
z
x
23
y
解:铜块上截面上的压应力为
9
3、 特例
(1)平面应力状态下(假设 Z = 0 )
x
1 E
(
x
y)
y
1 E
(
y
x)
z E ( x y)
xy
xy
G
10
(2) 广义胡克定律用主应力和主应变表示时 三向应力状态下:
1
1
E [ 1
(
2
3)]
2
1 E
[
2
(
3
1)]
3
1 E
[
3
( 1
2)]
(7-7-6)
11
平面应力状态下 设 3 = 0, 则
x y z x y y z z x
y
σy
上面
x y z x y y z z x
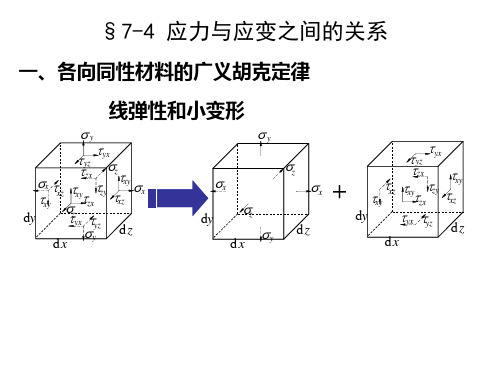
1、各向同性材料的广义胡克定律 (1)符号规定
τ yx
τ τ yz
xy
τ τ zy xz
τ zx
右侧面
σx
(a)三个正应力分量:拉应力为正
σz
x
o
压应力为负。 z
前面
3
(b)三个剪应力分量: 若正面(外法线与坐标轴
dxdydz
dxdydz(1 1 2 3) dxdydz
dxdydz
机械设计基础应力和应变的关系

机械设计基础应力和应变的关系应力和应变是机械设计中的重要概念,理解和分析应力和应变的关系对于工程师在机械设计过程中具有重要意义。
本文将介绍机械设计基础中应力和应变的概念,并探讨它们之间的关系。
一、应力的定义和分类应力是指物体内部由于外力作用而引起的单位面积上的力。
在机械设计中,常常根据作用点的不同方向和应力分布特点将应力分类。
主要有以下几种类型的应力:1. 拉应力(张应力):作用于物体的力使物体内部发生拉伸的应力。
2. 压应力:作用于物体的力使物体内部发生压缩的应力。
3. 剪应力:作用于物体平面内的力使物体内部发生切变的应力。
4. 弯曲应力:作用于物体梁状结构上的力使物体内部产生弯曲变形的应力。
二、应变的定义和分类应变是物体在受力作用下产生的形变量。
根据物体的不同变形方式和变形量的方向分,应变也可以进行分类。
主要有以下几种类型的应变:1. 纵向应变:在物体长度方向上的形变量。
2. 横向应变:在物体宽度或厚度方向上的形变量。
3. 剪应变:在物体平面内的形变量。
三、应力和应变的关系应力和应变之间存在一定的关系,即胡克定律。
胡克定律表明了应力和应变之间的线性关系,可以用以下公式表示:应力 = 弹性模量 ×应变其中,弹性模量是材料特性参数,被用来描述材料抵抗弹性变形的能力。
通过实验测试可以得到材料的弹性模量。
应力和应变的关系可以有两种形式,分别是拉伸形式和剪切形式。
1. 拉伸形式的应力和应变关系:拉伸形式下,材料在拉伸力作用下发生变形,初始长度增加,发生纵向应变,由此产生拉应力。
根据胡克定律,拉应力与纵向应变之间的关系是线性的,即应力和应变成正比。
这种关系可通过拉伸试验获得。
拉伸试验是一种常用的材料力学测试方法,通过加载不同的拉应力,测量相应的纵向应变,即可得到应力和应变之间的关系曲线。
从曲线上可以得到材料的拉伸强度和杨氏模量等重要机械性能参数。
2. 剪切形式的应力和应变关系:剪切形式下,材料受到切变力作用从而产生平面内形变,产生剪应变。
应变和应力关系

新能源技术:利用应变和应力原理,优化风力发电机叶片设计,提高风能 利用率和发电效率。
机器人技术:通过研究应变和应力与机器人关节运动的关系,提高机器人 的灵活性和稳定性,拓展机器人的应用领域。
应变和应力对未来科技发展的影响
增强材料性能:通过深入研究应变和应力,可以开发出性能更强的新型材 料,为未来的科技发展提供物质基础。
智能制造:利用应变和应力的知识,可以优化制造过程中的材料性能,提 高生产效率和产品质量,推动智能制造的发展。
生物医学应用:在生物医学领域,应变和应力的研究有助于更好地理解和 控制人体生理机制,为未来的生物医学应用提供支持。
压痕法:利用压痕仪在物体表面压出一定形状的压痕,通过测量压痕的尺寸来计算应力
应变和应力的相互影响
应变和应力之间的关系:应变是应力作用下的物体形状变化,应力是抵抗变形的力。
应变和应力的测量方法:通过应变计和应力计进行测量,应变计测量物体变形,应力计测量物 体受到的力。
应变和应力的相互影响:应变和应力之间存在相互影响,例如在材料屈服点附近,应变和应力 之间会发生突变。
应力的概念
分类:正应力、剪应力、弯 曲应力等
定义:物体受到外力作用时, 内部产生的反作用力
单位:帕斯卡(Pa) 作用效果:使物体产生形变
应变和应力的关系
应变是物体形状 的改变,应力是 物体内部抵抗变
形的力
应变和应力之间 存在线性关系, 即应变正比于应
力
应变和应力之间 的关系可以用胡 克定律表示,即 应力=弹性模量
应变和应力关系
汇报人:XX
应变和应力的定义 应变和应力的测量方法 应变和应力的应用领域 应变和应力的研究进展 应变和应力的未来展望
应变和应力的概念

应变和应力的概念一、引言应变和应力是材料力学中重要的概念,在工程和科学研究中有着广泛的应用。
应变是描述物体形变程度的物理量,而应力则是描述物体内部受力状态的物理量。
本文将详细介绍应变和应力的概念,并深入探讨两者之间的关系。
二、应变的概念2.1 应变的定义应变是描述物体形变程度的物理量,通常用符号ε表示。
应变可分为线性应变和非线性应变两种情况。
线性应变发生在物体受到小的力引起的形变情况下,其应变与受力成正比。
非线性应变则发生在物体受到大的力引起的形变情况下,其应变与受力不成正比。
2.2 应变的分类1.纵向应变2.横向应变3.剪切应变4.体积应变三、应力的概念3.1 应力的定义应力是描述物体内部受力状态的物理量,通常用符号σ表示。
应力分为正应力和剪应力两种情况。
正应力是指垂直于物体截面的力在单位面积上的分布情况,剪应力是指平行于物体截面的力在单位面积上的分布情况。
3.2 应力的分类1.纵向应力2.横向应力3.剪切应力4.欧拉应力四、应变与应力的关系应变与应力之间存在着密切的关系,可以由材料的应力-应变曲线来描述。
应力-应变曲线显示了材料在受力下的变形和应力的关系,以此来研究材料的力学性质。
4.1 弹性阶段在弹性阶段,材料受力后会发生一定程度的形变,但当去除外力时,材料可以恢复到原先的形状。
此时应力与应变呈线性关系,称为胡克定律。
4.2 屈服阶段当外力超过了材料的弹性极限时,材料会进入屈服阶段。
此时材料会产生更大的形变,但仍能回复到非常接近原来形状的状态。
4.3 塑性阶段当外力超过了材料的屈服极限时,材料将进入塑性阶段,并发生不可逆的形变。
在这个阶段,应力与应变之间的关系不再是线性的,材料会呈现出时间依赖性和屈服后的流变行为。
4.4 断裂阶段当外力继续增加,超过了材料的断裂强度,材料将发生断裂并失去原有的结构完整性。
五、总结应变和应力是描述材料力学性质的重要概念。
应变是描述物体形变程度的物理量,而应力是描述物体内部受力状态的物理量。
应力与应变间的关系

τ xy
右侧面
σx τ xz
x
γ xy
γ yz
γ zx
O
∠ xOy ∠ yOz
∠zox 。
z
σz
前面
2、各向同性材料的广义胡克定 、 律
(1)线应变的推导 线应变的推导 分别单独存在时, 在σx σy σz 分别单独存在时 x 方 依次为: 向的线应变 εx 依次为
x σ
z
x
x σ
εx ' =
σx
τ = Gγ
或
γ=
τ
G
τ γ γ τ
为剪切弹性模量,单位为N/m G 为剪切弹性模量,单位为N/m2.
三、复杂应力状态下应力与应变的关系 σx σy σz τ x y τ y z τ z x εx ε y ε z γ x y γ y z γ z x
1、各向同性材料的广义胡克定律 (1)符号规定 ) (a)三个正应力分量 拉应力为正 (a)三个正应力分量 三个正应力分量:拉应力为正
因此, 该圆筒变形后的厚度并无变化, 因此 该圆筒变形后的厚度并无变化 仍然为 t =10mm .
G G G
在线弹性范围内, 小变形条件下, 在线弹性范围内 小变形条件下 各向同性材料。 各向同性材料。
1 εx = σx ν (σ y +σz ) E 1 E
[
]
公式的适用范围 : 在线弹性范围内,小 在线弹性范围内 小 变形条件下, 变形条件下 各向同性材 料。
ε y = [σ y ν (σz +σx )]
ν ν ε z = (σ x + σ y ) = (τmax + τmax ) = 0 E E
同理可得,圆筒中任一点 该点到圆筒横截面中心的距离为 该点到圆筒横截面中心的距离为ρ 同理可得 圆筒中任一点 (该点到圆筒横截面中心的距离为ρ) 处 的径向应变为
应力与应变间的关系共31页
P a
y
z
x
y 解:铜块上截面上的压应力为
yP A30 0 .1 1 20 3 0
y x
3M 0 Pa
x
(b) Z z
1[ ( )]0
x Ex
y
z
由
1[ ( )]0
z Ez
x
y
解得
x
z
(1 1 2
)
y
0.314-(01.3042.34)(30)
-15.5MPa
铜块的主应力为
σ 1 σ 2 1 .5 M 5 σ P 3 3 a M 0 ,P
体积应变和最大剪应力分别为
1 E 2(123 ) 1 .9 5 1 4 0
max 1 2(13)7.25MPa
例题9-8 壁厚 t =10mm , 外径 D=60mm 的薄壁圆筒, 在表面上 k 点 处与其轴线成 45°和135° 角即 x, y 两方向分别贴上应变片,然后在 圆筒两端作用矩为 m 的扭转力偶,如图 所示已知圆筒材料的弹性模 量为 E = 200GPa 和 = 0.3 ,若该圆筒的变形在弹性范围内,且 max = 80MPa , 试求k点处的线应变 x ,y 以及变形后的筒壁厚度。
在x y z同时存在时, y,z方向的线应变为
y E 1[y (z x)] z E 1[z (x y)]
(2)剪应变的推导 剪应变 xy , yz ,zx与剪应力xy ,yz ,zx之间的关系为
xy
xy G
yz
yz G
zx
zx G
公式的适用范围 : 在线弹性范围内, 小变形条件下, 各向同性材料。
右侧面
σx
τ xz x
前面
2、各向同性材料的广义胡克定
应力应变之间的关系

应力与应变的关系
你想啊,咱们每天上班下班,跟个陀螺似的转个不停,这不就是生活中的“应力”嘛!有时候,老板给的任务多了点,压力山大啊,感觉就像是被压得喘不过气来。
这时候,咱们不能硬扛,得学会“应变”。
比如,合理安排时间,提高工作效率,或者偶尔偷个闲,跟同事开个玩笑,放松放松心情,这不就是咱们应对压力的“应变”小妙招嘛!
再瞅瞅咱们身边的朋友圈,有时候也会遇到点小摩擦,比如意见不合啦,误会啥的。
这时候,如果都死磕着不放,那友谊的小船说翻就翻。
所以啊,咱们得学会变通,学会理解,学会包容,就像弹簧一样,压一下,弹回来,还能更加紧密。
这就是友情里的“应力与应变”,相互磨合,才能更加坚固。
还有啊,咱们对待自己的身体也得这样。
工作再忙,也不能忽视了健康。
不然,身体一出问题,那可就是大问题了。
这时候,咱们得赶紧调整作息,均衡饮食,适当运动,给身体减减压,让它也能“应变”过来,继续活力满满地陪咱们闯荡江湖。
说到底,应力与应变,就像是生活中的一场场小考,考验着咱们的智慧和心态。
咱们不能一味地逃避,也不能硬碰硬,得学会灵活应对,找到最适合自己的方式去化解压力,享受生活的乐趣。
毕竟,人生嘛,就是一场修行,一场关于如何在压力中成长,在变化中前行的修行。
所以啊,下次当你觉得压力山大的时候,不妨换个角度想想,这也许是个机会,让你学会更多,变得更加强大。
毕竟,没有压力,哪来的动力呢?咱们啊,就在这应力与应变的交织中,一步步成长,一步步走向更加美好的未来!。
应力和应变关系

第四章应力和应变关系一. 内容介绍前两章分别从静力学和运动学的角度推导了静力平衡方程,几何方程和变形协调方程。
由于弹性体的静力平衡和几何变形是通过具体物体的材料性质相联系的,因此,必须建立了材料的应力和应变的内在联系。
应力和应变是相辅相成的,有应力就有应变;反之,有应变则必有应力。
对于每一种材料,在一定的温度下,应力和应变之间有着完全确定的关系。
这是材料的固有特性,因此称为物理方程或者本构关系。
对于复杂应力状态,应力应变关系的实验测试是有困难的,因此本章首先通过能量法讨论本构关系的一般形式。
分别讨论广义胡克定理;具有一个和两个弹性对称面的本构关系一般表达式;各向同性材料的本构关系等。
本章的任务就是建立弹性变形阶段的应力应变关系。
二. 重点1. 应变能函数和格林公式;2. 广义胡克定律的一般表达式;3. 具有一个和两个弹性对称面的本构关系;4. 各向同性材料的本构关系;3. 材料的弹性常数。
知识点应变能原理应力应变关系的一般表达式完全各向异性弹性体正交各向异性弹性体本构关系弹性常数各向同性弹性体应变能格林公式广义胡克定理一个弹性对称面的弹性体本构关系各向同性弹性体的应力和应变关系应变表示的各向同性本构关系§4.1 弹性体的应变能原理学习思路:弹性体在外力作用下产生变形,因此外力在变形过程中作功。
同时,弹性体内部的能量也要相应的发生变化。
借助于能量关系,可以使得弹性力学问题的求解方法和思路简化,因此能量原理是一个有效的分析工具。
本节根据热力学概念推导弹性体的应变能函数表达式,并且建立应变能函数表达的材料本构方程。
根据能量关系,容易得到由于变形而存储于物体内的单位体积的弹性势能,即应变能函数。
探讨应变能的全微分,可以得到格林公式,格林公式是以能量形式表达的本构关系。
如果材料的应力应变关系是线性弹性的,则单位体积的应变能必为应变分量的齐二次函数。
因此由齐次函数的欧拉定理,可以得到用应变或者应力表示的应变能函数。
应力和应变之间的关系

应力和应变的关系曲线
描述
应力和应变的关系曲线是描述应力与应变之间关系的图形表示。
形状
在弹性范围内,曲线呈直线上升;超过弹性极限后,曲线出现弯曲。
应用
通过应力和应变的关系曲线,可以确定材料的弹性模量、屈服点和 极限强度等机械性能参数。
04
应力和应变的应用
弹性力学
弹性力学是研究弹性物体在外力作用下 变形和内力的规律的科学。在弹性力学 中,应力和应变是描述物体变形和受力 状态的基本物理量。
公式
σ=Eεsigma = E varepsilonσ=Eε
解释
σ为应力,E为弹性模量,ε为应变。 当应力增加时,应变也相应增加, 且两者成正比关系。
非线性关系
描述
当材料受到超过其弹性极限的应力时 ,应力与应变之间的关系不再是线性 的,而是呈现非线性关系。
特征
在非线性阶段,应变随应力的增加而 急剧增加,可能导致材料发生屈服或 断裂。
设计优化
优化结构设计
通过对应力和应变的分析,优化结构设计,提高结构的承载能力 和稳定性。
考虑材料特性
在设计过程中,充分考虑材料的力学特性和性能,合理选择和使 用材料,以降低应力和应变对结构的影响。
引入减震和隔震措施
通过引入减震和隔震措施,降低地震等外部载荷对结构产生的应 力和应变,提高结构的抗震性能。
时间
蠕变
在长期恒定应力作用下,材料会发生 缓慢的塑性变形,即蠕变。蠕变会影 响材料的应力和应变关系,特别是在 高温和长期载荷作用下。
时间依赖性
某些材料的力学性能会随时间发生变 化,对应力和应变的关系产生影响。 例如,疲劳和时效等现象会导致材料 性能随时间发生变化。
07
应力和应变在工程实践中的 注意事项
应力与应变间的关系
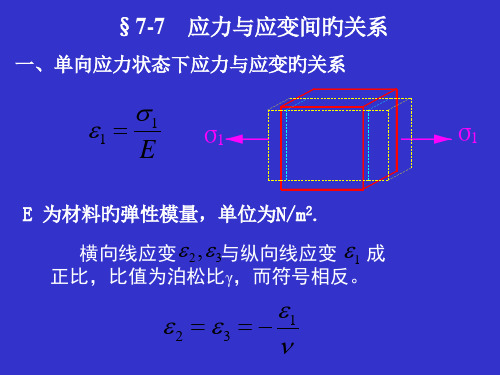
一、单向应力状态下应力与应变旳关系
1
1
E
σ1
σ1
E 为材料旳弹性模量,单位为N/m2.
横向线应变2,3与纵向线应变 1 成
正比,比值为泊松比γ,而符号相反。
2
3
1
二、纯剪切应力状态下应力与应变旳关系
G 或
G
τ γ γτ
G 为剪切弹性模量,单位为N/m2.
三、复杂应力状态下应力与应变旳关系
x y z x y y z z x
y
σy
上面
x y z x y y z z x
1、各向同性材料旳广义胡克定律 (1)符号要求
τ yx
τ τ yz
xy
τ τ zy xz
τ zx
右侧面
σx
(a)三个正应力分量:拉应力为正
σz
x
o
压应力为负。 z
前面
(b)三个剪应力分量: 若正面(外法线与坐标轴
P a
y
z
x
y 解:铜块上截面上旳压应力为
y
P A
300 103 0.12
y x
30MPa
x
(b) Z z
1 [ ( )] 0
xE x
y
z
由
1 [ ( )] 0
zE z
x
y
解得
x
z
(1 1 2
)
y
0.34(1 0.34) 1- 0.342
(30)
-15.5MPa
特例
在平面纯剪切应力状态下:σ 1 σ 3 τ xy
代入得
1 2
E
(1
2
3)
1 2
弹塑性力学 应力和应变之间的关系

我所认识的应力和应变之间的关系在单向应力状态下,理想弹性材料的应力和应变之间的关系是满足胡克定律的一一对应的关系。
在三维应力状态下描述一点处的应力状态需要9个分量,相应的应变状态也要用9个应变分量来表示。
对于一个具体的理想弹性体来讲,如果在三维应力状态下,应力与应变之间仍然有线性一一对应关系存在,则称这类弹性体为线性弹性体。
所谓各向弹性体,从力学意义上讲,就是弹性体内的每一点沿各个方向的力学性质都完全相同的。
这类线性弹性体独立的唐兴常数只有两个。
各向同性体本构关系特点:1.主应力与主应变方向重合。
2.体积应力与体积应变成比例。
3.应力强度与应变强度成比例。
4.应力偏量与应变偏量成比例。
工程应用中,常把各向同性弹性体的本构方程写下成11()11()11()x y z xy xy y x z yz yz z y x xz xz E G E G E G εσμσσγτεσμσσγτεσμσσγτ⎧⎡⎤=-+=⎣⎦⎪⎪⎪⎡⎤=-+=⎨⎣⎦⎪⎪⎡⎤=-+=⎪⎣⎦⎩,式中分别为弹性模量、泊松比和剪切模量。
在E G μ、、这三个参数之间,实际上独立的常量只有两个,它们之间存在关系为()21E G μ=+。
屈服条件:弹性和塑性的最主要区别在于变形是可以恢复。
习惯上,根据破坏时变形的大小把工程材料分为脆性材料和塑性材料两类。
对于加载过程如图1OA: 比例阶段;线性弹性阶段AB: 非弹性变形阶段 BC : 初始屈服阶段 s σσ≤ CDE :强化阶段;应变强化硬化阶段EF : 颈缩阶段;应变弱化,软化阶段s σσ≥ C 点为初始屈服点具有唯一性。
在应力超过屈服应力后,如果在曲线上任意一点D 处卸载,应力和应变之间将不再遵循原有的加载曲线规律,而是沿一条接近平行于OA 的直线DO ’变化,直到应力下降为零,这时应变并不为零,即有塑性应变产生。
如果用OD ’表示总应变ε,O ’D ’表示可以恢复的弹性应变eε,OO ’表示不能恢复的塑性应变p ε,则有e p εεε=+,即总应变等于弹性应变加上塑性应变。
应力与应变间的关系

压应力为负。 z
前面
(b)三个剪应力分量: 若正面(外法线与坐标轴
正向一致的平面)上剪应力矢 的指向与坐标轴正向一致, 或 负面(外法线与坐标轴负向一 致的平面)上剪应力矢的指向 与坐标轴负向一致,则该剪 应力为正, 反之为负。
y
o
z σz
σy
τ yx τ yz τ zy τ zx
上面
τ xy
右侧面
)
y
0.34(1 0.34) 1- 0.342
(30)
-15.5MPa
铜块的主应力为
σ1 σ2 15.5MPa , σ3 30MPa
体积应变和最大剪应力分别为
1 2
E
(1
2
3)
1.95 104
max
1 2
(1
3
)
7.25MPa
(1)概念:构件每单位体积的体积变化, 称为 体积应变用θ表示。
(2)各向同性材料在空间应力状态下的 体积应变
公式推导
2
设单元体的三对平面为主平面, 其 三个边长为d x, d y, d z 变形后的边 长分别为 d x(1+ , d y(1+2 , d z(1+3 , 因此变形后单元体的体 积为:
y
1 E
[ y
( z
x )]
z
1 E
[ z
( x
y )]
(2)剪应变的推导
剪应变 xy , yz ,zx与剪应力xy ,yz ,zx之间的关系为
xy
xy
G
yz
试说明弹性力学中应力,应变,位移三者之间的关系

试说明弹性力学中应力,应变,位移三者之间的关系.
应力和应变之间的关系是可以用弹性力学的材料模型来表示的,它们之间的关系可表示为受力的物体会产生一个应变,这个应变是受力强度和材料的模量来决定的,当应力变化时,物体产生的应变也会变化,关系可以用弹性力学方程来表示:应力= 应变× 模量。
另外,应力和位移之间也有关系,当施加力时,物体会产生一个位移,而位移又是一个受力强度和材料模量共同决定的参数,可用弹性力学方程来表示:应力 = 位移× 模量。
另外,弹性模量有时也称为弹性常数,它可用来衡量材料的弹性程度,以及材料在受力时所受到的影响,它是决定应力和应变、应力和位移关系的一个基本参数,物理现象中可以用来描述物体变形的程度,将应力与物体变形程度结合起来可以确定应力对物体变形的影响。
同时,这种参数也可以用来描述弹性体在受力作用下所产生的变形量。
由于弹性模量的作用,物体对于受力时大小的变形量可以用模量值来确定:弹性模量越大,物体几乎不变形,弹性模量越小,则物体的变形量越大;另外,弹性模量也能够描述物体在受力作用下所产生的力和位移关系,弹性模量越大,物体受到相同力量作用时,其所受到的变形量和位移量也会更小,反之,弹性模量越小,受到相同力量作用时,其所受到的变形量和位移量也会更大。
因此,弹性模量可以决定物体受力后的变形情况,以及材料的弹性程度。
应力与应变

应力与应变概念解释在物理学和材料科学领域中,应力(stress)和应变(strain)是两个重要的概念。
应力描述的是物体内部的力状态,而应变描述的是物体对于应力的响应。
理解应力和应变的关系对于材料强度和工程设计具有重要意义。
应力是指物体内部的力,可以描述为单位面积上施加的力。
它通常用符号σ(sigma)表示,单位为帕斯卡(Pa)。
应力可以分为正应力(tensile stress)和剪应力(shear stress)两种类型。
正应力指作用在物体上的拉伸或压缩力。
拉伸应力是指物体被拉伸的力,压缩应力是指物体被压缩的力。
正应力的大小等于作用力除以物体横截面的面积。
剪应力指作用在物体上的剪切力,是指物体内部各点上的两个互相垂直的力之间的比例。
剪应力的大小等于剪切力除以物体横截面的面积。
应变是指物体对于应力的响应,是单位长度的长度变化。
应变可以描述为物体在单位长度上的变形程度。
应变可以分为线性应变(linear strain)和剪应变(shear strain)两种类型。
线性应变指物体的长度变化与原始长度的比例。
它是一个无量纲的物理量,通常用符号ε(epsilon)表示。
线性应变可以是拉伸应变,也可以是压缩应变。
拉伸应变是指物体在拉伸力作用下产生的应变,压缩应变是指物体在压缩力作用下产生的应变。
剪应变指物体产生的平面变形,在受到平行力作用的情况下,物体的形状会发生变化。
剪应变可以通过一个无量纲数值来表示物体的错位程度。
应力-应变关系应力和应变之间存在一种关系,称为应力-应变关系。
它描述了物体在受到应力作用时的应变程度。
应力-应变关系可以是线性的,也可以是非线性的。
在线性应力-应变关系中,应力和应变之间存在简单的比例关系。
例如,在拉伸应力作用下,当应力增加时,应变也会以同样的比例增加。
这种关系可以由胡克定律(Hooke's law)来描述。
胡克定律是一种线性弹性模型,描述了应力和应变之间的关系。
根据胡克定律,应力与应变之间的比例常数被称为弹性模量(elastic modulus)。
应力应变关系

应力应变关系
应力应变关系是指在物体受到外力作用时,物体内部会产生应力,从而引起物体的变形,这种变形称为应变。
应力和应变之间的关系可以通过应力-应变曲线来描述。
在弹性区域内,应力和应变成正比,即应力与应变的比例关系为线性关系,弹性模量为比例系数。
弹性区域内,当外力去除后,物体能够恢复到原始形状和体积。
在超过弹性极限后,物体进入塑性变形区,此时应力和应变之间的关系不再是线性关系,物体会发生不可逆的塑性变形。
应力应变关系是材料力学的基本理论,对于材料的工程应用和设计具有重要的意义。
通过研究应力应变关系,可以了解材料的强度、刚度等力学性质,从而指导工程实践中的设计和施工。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
210 × 10 9 = ( − 160 + 0 .3 × 240 ) × 10 − 6 = − 20 .3MPa 1 − 0 .3 2 6
∴σ 1 =44 .3 MPa ;σ 2 =0;σ 3 = − 20 .3MPa ;
0.3 ε 3 = − (σ 3 + σ 1 ) = − ( − 22.3 + 44.3) × 10 6 = − 34.3 × 10 − 6 E 210 × 10 9 实 际上 从排 序的 角度 来 看是 求得 ε 2
µ
注意:主应力和主应变的方向是相同的 注意 主应力和主应变的方向是相同的. 主应力和主应变的方向是相同的
2011-11-30
7
§7-4 应力与应变间的关系
一、单拉下的应力--应变关系 单拉下的应力--应变关系 -y
σx
εx=
σx
E
ε y =− σ x
E
γ ij ≈ 0 (i,j = x,y,z )
µ
ε z =− σ x
E
µ
z
x
y
二、纯剪的应力--应变关系 纯剪的应力--应变关系 --
γ xy =
2011-11-30
τ xy
1 − 2µ θ = (σ 1 + σ 2 + σ 3 ) E 1 − 2µ = (σ x + σ y + σ z ) E
2011-11-30
3(1 − 2 µ ) (σ 1 + σ 2 + σ 3 ) σ m θ = = E 3 k 体积胡克定律, k 为体积弹性模量,
σ m 是三个主应力的平均值
所以, 所以,该点处为平面应力状态
′ σ2
E [ε 1 + µε 2 ] ∴σ 1 = 2 1− µ 210 × 10 9 = ( 240 − 0 .3 × 160 ) × 10 − 6 = 44 .3MPa 1 − 0 .3 2
E ∴σ 2 = [ε 2 + µε 1 ] 2 1− µ
2011-11-30
G
1 ε x = σ x − µ (σ y +σ z ) E 1 ε y = σ y − µ (σ z +σ x ) E 1 ε z = σ z − µ (σ x +σ y ) E
[
]
] ]
2011-11-30
2
主应力 --- 主应变关系
1 [σ 1 − µ (σ 2 +σ 3 )] E 1 ε 2 = [σ 2 − µ (σ 3 +σ 1 )] E
5
例1 已知一受力构件自由表面上某一点处的两个面内主应变分别 弹性模量E=210GPa,泊松比 为:ε1=240×10-6, ε2= -160×10-6,弹性模量 × × , 为 µ=0.3, 试求该点处的主应力及另一主应变。 , 试求该点处的主应力及另一主应变。
解 : 自由面上
σ3 = 0
′ σ1
2011-11-30
τ xy =Gγ xy
3
主应力与主应变方向一致 主应力与主应变方向一致? 方向一致
γ xy ′ tg 2α 0 = = =− =tg 2α 0 σ x −σ y E [(ε −ε )(1−µ )] (ε x −ε y ) x y 1−µ 2
主应力与主应变方向是重合的 主应力与主应变方向是重合的
ε1=
1 ε 3 = [σ 3 − µ (σ 2 +σ 1 )] E
方向一致
′ tg 2α 0 =
−γ xy
ε x −ε y
=−
2τ xy
σ x −σ y
=tg 2α 0
四、平面状态下的应力---应变关系: σ z =τ yz =τ zx =0 平面状态下的应力---应变关系: ---应变关系 E [ε x + µε y ] σ x= 2 1− µ E [ε y + µε x ] σ y= 2 1− µ
G
ε i ≈0 (i=x,y,z)
γ yz =γ zx ≈0
z
τxy
x
1
三、复杂状态下的应力 --- 应变关系
σy
y
依叠加原理, 依叠加原理,得:
σx σz
zτxyxFra bibliotekε x=
σx
E E E 1 = σ x − µ (σ y +σ z ) E
−µ
σy
−µ
σz
[
]
[ [ τ xy γ xy = G τ yz γ yz = G γ zx =τ zx
−2τ xy
−2γ xy G
2011-11-30
4
五、体积应变与应力分量间的关系
V = dxdydz V1 = dx (1 + ε 1 ) dy (1 + ε 2 ) dz (1 + ε 3 )
体积应变: 体积应变:
V1 − V θ = = ε1 + ε 2 + ε 3 V
体积应变与应力分量间的关系: 体积应变与应力分量间的关系:
