非稳态法测材料的导热性能实验报告
非稳态准稳态法测材料的导热性能实验

非稳态(准稳态)法测材料的导热性能实验非稳态(准稳态)法是一种测量材料导热性能的实验方法,它通过在材料的一侧施加热量,测量另一侧的热流量来计算材料的导热系数。
这种方法相对于稳态法,具有设备简单、操作方便、测量速度快等优点。
下面是关于非稳态(准稳态)法测材料的导热性能实验的详细描述。
一、实验目的本实验的目的是通过非稳态(准稳态)法测量材料的导热性能,包括导热系数、热扩散系数和比热容等参数。
这些参数对于材料的热设计、能源利用和工程应用具有重要意义。
二、实验原理非稳态(准稳态)法基于热传导的傅里叶定律,其基本公式为:q=-k AΔT/L,其中q为热流量,k为导热系数,A为传热面积,ΔT为两侧温度差,L为材料的厚度。
在实验中,通过测量材料的传热面积和两侧温度差,可以计算出材料的导热系数。
三、实验步骤1.准备材料:选择待测材料,并准备相应的支架、加热器和温度传感器等设备。
2.安装样品:将待测材料放置在支架上,将加热器和温度传感器分别与材料的两侧接触,并固定好。
3.开始测量:打开加热器,使加热器输出的热量均匀地施加到材料的左侧,同时使用温度传感器测量材料的右侧温度。
记录下加热时间和温度变化。
4.数据处理:根据测量的数据,绘制温度随时间变化的曲线。
通过曲线可以计算出材料的导热系数、热扩散系数和比热容等参数。
四、实验结果与分析通过实验测量和数据处理,我们可以得到待测材料的导热系数、热扩散系数和比热容等参数。
这些参数可以用来评估材料的导热性能和热特性。
例如,导热系数高的材料可以更好地传递热量,适用于需要高效散热的场合;比热容大的材料可以吸收更多的热量,适用于需要储存和释放热量的场合。
在分析实验结果时,需要注意以下几点:1.实验结果的准确性受到多种因素的影响,如测量设备的精度、环境温度和湿度等。
因此,需要对实验结果进行误差分析,以确定其可信度。
2.对于不同种类的材料,其导热性能和热特性可能存在差异。
因此,需要对不同种类的材料进行分别测量和分析。
非稳态法导热仪实验心得

非稳态法导热仪实验心得
非稳态法导热仪是一种常用的实验仪器,用于测量材料的导热性能。
下面是一些关于非稳态法导热仪实验的心得体会:
1. 实验准备:在进行实验前,需要详细了解实验仪器的操作原理和步骤。
同时,确保实验仪器的正常运行状态,并进行必要的校准。
2. 样品准备:将待测材料切割成适当的尺寸,并确保样品表面的光洁度和均匀性。
这有助于确保实验的准确性和可重复性。
3. 数据处理:在实验过程中,要记录实验环境的温度变化以及样品的温度变化。
根据采集到的数据,可以使用适当的数学模型进行数据处理和分析,计算样品的导热系数等参数。
4. 实验注意事项:在进行实验时,注意操作规范和安全操作。
避免在实验过程中产生其他热源,如阳光直射、电器设备加热等,以免干扰实验结果。
同时,保持实验环境的稳定性,避免风的干扰。
5. 实验结果与讨论:根据实验结果,可以对样品的导热性能做出评价和分析,并进行讨论。
如对比不同材料的导热性能、分析导热性能受温度、压力等因素的影响等。
需要注意的是,以上心得是基于一般的实验情况,实际实验操作还需要根据具体的实验设备和要测量的材料进行相应的调整和注意。
非稳态法导热仪实验是一项技术性较高的实验,所以在实验之前最好能与教师或专业人士进行咨询和指导,以确保实验的顺利进行。
非稳态(准稳态)法测材料导热性能实验

非稳态(准稳态)法测材料的导热性能实验一、实验目的一、本实验属于创新型实验,要求学生自己选择不同原料、依照不同配比进行加工出新型实验材料,并对该材料的热物性(密度、导热系数、比热容、导温系数)进行实验测量。
2.快速测量绝热材料(不良导体)的导热系数和比热,把握其测试原理和方式。
3、把握利用热电偶测量温差的方式。
二、实验测试原理本实验是依照第二类边界条件,无穷大平板的导热问题来设计的。
设平板厚度为2δ,初始温度为t 0,平板两面受恒定的热流密度q c 均匀加热(如以下图所示)。
依照导热微分方程式、初始条件和第二类边界条件,关于任一刹时沿平板厚度方向的温度散布t(x ,τ)可由下面方程组解得;方程组的解为:式中:τ——时刻;λ——平板的导热系数;α——平板的导温系数;t 0——初始温度; —傅立叶准那么;δβμn n = ,n=1,2,3…;q c ——沿X 方向从端面向平板加热的恒定热流密度。
0),0(0),()0,(),(),(022=∂∂=+∂∂=∂∂=∂∂xt q x t t x t x x t a x t cτλτδτττ)1()]exp()cos(2)1(63[),(2211220o n n n n n c F x x q t x t μδμμδδδδατλτ--+--=-+∞=∑2δατ=F随着时刻τ的延长,F 0数变大,式(1)中级数和项愈小。
当F 0>时,级数和项变得很小,能够忽略,式(1)变成(2)由此可见,当F 0>后,平板遍地温度和时刻成线性关系,温度随时刻转变的速度是常数,而且处处相同。
这种状态即为准稳态。
在准稳态时,平板中心面X=0处的温度为:平板加热面X=δ处为:此两面的温差为: (3) 已知q c 和δ,再测出△t ,就能够够由式(3)求出导热系数:(4)事实上,无穷大平板是无法实现的,实验老是用有限尺寸的试件,一样能够为,试件的横向尺寸为厚度的6倍以上时,双侧散热对试件中心的温度阻碍能够忽略不计。
传热学实验指导书---实验一(本部)
实验一 非稳态法测量材料的导热性能实验一、实验目的1. 快速测量绝热材料的导热系数和比热。
2. 掌握使用热电偶测量温差的方法。
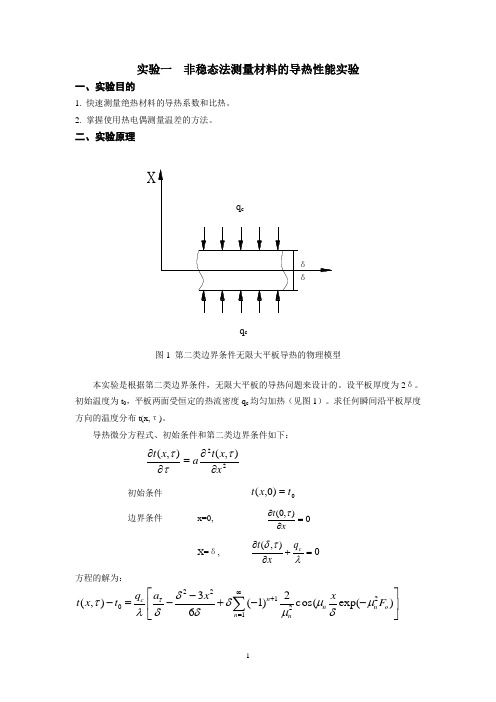
二、实验原理X图1 第二类边界条件无限大平板导热的物理模型本实验是根据第二类边界条件,无限大平板的导热问题来设计的。
设平板厚度为2δ。
初始温度为t 0,平板两面受恒定的热流密度q c 均匀加热(见图1)。
求任何瞬间沿平板厚度方向的温度分布t(x,τ)。
导热微分方程式、初始条件和第二类边界条件如下:22),(),(x x t a x t ∂∂=∂∂τττ初始条件 0)0,(t x t =边界条件x=0,0),0(=∂∂xt τX=δ,0),(=+∂∂λτδcq x t 方程的解为:⎥⎦⎤⎢⎣⎡--+--=-∑∞=+1221220)exp(cos(2)1(63),(n o n n n n c F x x a q t x t μδμμδδδδλττq c式中: t —温度; τ—时间; t 0 — 初始温度;ɑ — 平板的导温系数; μn — n π n=1,2,3,……2δτa Fo =— 傅立叶准则; q c— 沿方向从端面向平板加热的恒热流密度;随着时间t 的延长,Fo 数变大,上式中级数和项愈小。
当Fo>0.5时,级数和项变得很小,可以忽略,上式变成:)612(),(220-+-=-δτδτλδτa a q t x t c 由此可见,当Fo>0.5后,平板各处温度和时间成线性关系,温度随时间变化的速率是常数,并且到处相同。
这种状态称为准稳态。
在准稳态时,平板中心面x=0处的温度为:)61(),0(20-=-δτλδτa q t t c 平板加热面X=δ处为:)31(),(20+-=-δτλδτδa q t t c 此两面的温差为:λδττδcq t t t 21),0(),(=-=∆如已知q c 和δ,再测出t ∆,就可以由上式求出导热系数:tq c∆=2δλ式中,λ—平板的导热系数,oW /(m C)⋅ cq —沿x 方向给平板加热的恒定热流密度,2W /mδ—平板的厚度,mt ∆—平板中心面x=0处和平板加热面x=δ处两面的温差,o C又,根据热平衡原理,在准稳态有下列关系:式中,F —平板的横截面积ρ—试件材料的密度C —试件材料的比热—准稳态时的温升速率由上式可求得比热为:实验时, 以试件中心处为准。
传热学实验

《传热学》实验指导书与报告工程热物理教研室传热学实验室编班级:姓名:学号:华北电力大学能源与动力工程学院目录(一)非稳态(准稳态)法测材料的导热性能实验. . . . . . . . . . . . .2 (二)强迫对流单管管外放热系数测定实验. . . . . . . . . . . . . . . .9 (三)热管换热器实验. . . . . . . . . . . . . . . . . . . . . . . . .18 附:铜—康铜热电偶温度与毫伏对照表实验一非稳态(准稳态)法测材料的导热性能实验一.实验目的1.测量绝热材料(不良导体)的导热系数和比热、掌握其测试原理和方法;2.掌握使用热电偶测量温差的方法。
二.实验装置(图2和图3)按上述理论及物理模型设计的实验装置如图2所示,说明如下:(1)试件试件尺寸为100mm×100mm×δ,共四块,尺寸完全相同,δ=10~16mm。
每块试件上下面要平齐,表面要平整。
(2)加热器采用高电阻康铜箔平面加热器,康铜箔厚度仅为20μm,加上保护箔的绝缘薄膜,总共只有70μm。
其电阻值稳定,在0—100℃范围内几乎不变。
加热器的面积和试件的端面积相同,也是100㎜×100㎜的正方形。
两个加热器的电阻值应尽量相同,相差应在0.1%以内。
(3)绝热层用导热系数比试件小的材料作绝热层,力求减少热量通过,使试件1。
4与绝热层的接触面接近绝热。
这样,可假定式(4)中的热量q c等于加热器发出热量的0.5倍。
(4)热电偶利用热电偶测量试件2两面的温差及试件2、3接触面中心处的温生速率,热电偶由0.1㎜的康铜丝制成。
实验时,将四个试件齐迭放在一起,分别在试件1和2及试件3和4之间放入加热器1和2,试件和加热器要对齐。
热电偶的放置如图3,热电偶测温头要放在试件中心部位。
放好绝热层后,适当加以压力,以保持各试件之间接触良好。
三.实验原理本实验是根据第二类边界条件,无限大平板的导热问题来设计的。
导热系数的测量实验报告

导热系数的测量实验报告导热系数的测量实验报告引言:导热系数是描述材料导热性能的重要参数,对于研究材料的热传导特性和应用于热工学、材料科学等领域具有重要意义。
本实验旨在通过测量不同材料的导热系数,探究不同材料的导热性能差异,并对实验结果进行分析和讨论。
实验方法:1. 实验仪器和材料准备:本实验使用的仪器包括导热系数测量仪、热电偶、热电偶接线仪、数字温度计等。
实验所用材料包括铝、铜、铁、玻璃等。
2. 实验步骤:a. 将导热系数测量仪预热至一定温度,使其达到稳定状态。
b. 将待测材料样品放置在测量仪器的传热面上,并保持其表面平整。
c. 记录待测材料样品的初始温度,并启动测量仪器。
d. 根据测量仪器的指示,等待一段时间,直至待测材料样品达到热平衡状态。
e. 记录待测材料样品的最终温度,并停止测量仪器。
实验结果:通过实验测量得到的材料导热系数如下表所示:材料导热系数(W/m·K)铝 205铜 385铁 80玻璃 1.05实验讨论:从实验结果可以看出,不同材料的导热系数存在明显差异。
铜的导热系数最高,达到385 W/m·K,而玻璃的导热系数最低,仅为1.05 W/m·K。
这是因为不同材料的结构和化学成分决定了其导热性能。
对于金属材料,其导热性能优于非金属材料,因为金属的导热机制主要是通过自由电子的传导。
而非金属材料如玻璃,则主要通过分子之间的振动传递热量,导致其导热性能较差。
此外,实验结果还表明不同金属材料的导热系数也存在差异。
铜的导热系数明显高于铝和铁,这是因为铜具有更高的电导率和更低的电阻率,使得其导热性能更好。
铁的导热系数较低,这可能与其晶格结构和杂质含量有关。
实验的不确定性主要来自于测量仪器的精度和待测材料样品的表面状态。
如果样品表面不平整或存在氧化层等影响传热的因素,将会对实验结果产生一定影响。
因此,在进行导热系数测量实验时,需要注意样品的处理和仪器的校准,以提高实验的准确性和可靠性。
物体导热系数的测量实验报告

物体导热系数的测量实验报告物体导热系数的测量实验报告引言:导热系数是描述物体传导热量能力的一个重要物理参数,它对于热传导的研究和应用具有重要意义。
本实验旨在通过测量不同材料的导热系数,探究不同材料的导热性能差异,为实际应用提供参考依据。
实验方法:1. 实验器材准备:- 热导率仪:用于测量材料的导热系数。
- 不同材料样本:选取具有不同导热性能的材料,如金属、塑料、木材等。
- 温度计:用于测量样本的温度。
- 定时器:用于控制实验时间。
- 电源:为热导率仪提供电力支持。
2. 实验步骤:a. 将热导率仪连接至电源,并保证其正常工作。
b. 准备不同材料样本,确保其形状和大小相同,以消除外界因素的影响。
c. 将一个样本放置在热导率仪的测量区域,并记录下初始温度。
d. 启动定时器,开始测量。
e. 在一定时间间隔内,记录样本的温度变化情况。
f. 根据测量得到的温度数据,计算出样本的导热系数。
实验结果:通过多次实验,我们得到了不同材料样本的导热系数数据,并进行了整理和分析。
1. 金属材料:我们选取了铜、铝和铁作为金属材料的代表。
实验结果显示,铜的导热系数最高,其次是铝,铁的导热系数最低。
这是因为金属材料中的自由电子能够快速传递热量,导致其导热系数较高。
2. 塑料材料:我们选取了聚乙烯、聚丙烯和聚氯乙烯作为塑料材料的代表。
实验结果显示,聚乙烯的导热系数最低,聚丙烯次之,聚氯乙烯的导热系数最高。
这是因为塑料材料中的分子间相互作用较弱,导致其导热系数较低。
3. 木材:我们选取了松木、柚木和橡木作为木材的代表。
实验结果显示,橡木的导热系数最低,柚木次之,松木的导热系数最高。
这是因为木材中的纤维结构和孔隙结构会影响热量的传导,导致不同木材的导热系数差异较大。
讨论与结论:通过本实验,我们得到了不同材料的导热系数数据,并进行了分析。
实验结果表明,导热系数与材料的性质密切相关。
金属材料的导热系数较高,塑料材料的导热系数较低,而木材的导热系数则介于两者之间。
导热系数测量实验报告

导热系数测量实验报告导热系数测量实验报告导热系数是一个物质传导热量的能力指标,它描述了物质在温度梯度下传热的速率。
在工程和科学领域中,了解物质的导热性质对于设计和优化热传导设备以及预测材料的热行为至关重要。
本实验旨在通过测量不同材料的导热系数,探讨不同材料的热传导特性。
实验装置包括一个导热系数测量仪器和一系列不同材料的试样。
首先,我们选择了金属、陶瓷和塑料等常见材料作为研究对象。
这些材料具有不同的导热性质,将有助于我们对导热系数的测量和比较。
在实验过程中,我们首先将试样放置在导热系数测量仪器中,并确保试样与仪器接触良好。
然后,我们通过在试样的一侧施加恒定的热量,观察另一侧的温度变化。
通过测量温度的变化率,我们可以计算出试样的导热系数。
在测量过程中,我们发现金属类材料的导热系数要远高于陶瓷和塑料。
这是由于金属的电子结构和晶格结构使其具有更好的导热性能。
而陶瓷和塑料由于其分子结构的特殊性质,导热系数较低。
进一步的实验中,我们还研究了不同金属的导热系数差异。
我们选择了铜、铝和铁三种常见金属进行比较。
结果显示,铜具有最高的导热系数,而铝和铁的导热系数相对较低。
这与金属的晶格结构和电子迁移能力有关。
除了材料的选择外,我们还对试样的几何形状进行了研究。
我们制备了不同厚度的试样,并测量了它们的导热系数。
结果表明,试样的厚度对导热系数有一定影响。
较薄的试样具有更高的导热系数,而较厚的试样导热系数较低。
这是由于热量在较薄的试样中更容易传导。
此外,我们还研究了温度对导热系数的影响。
通过改变试样的温度,我们发现导热系数随温度的升高而增加。
这是由于温度升高会增加材料内部原子和分子的热运动,从而促进热量的传导。
综上所述,本实验通过测量不同材料的导热系数,探讨了不同材料的热传导特性。
我们发现金属类材料具有较高的导热系数,而陶瓷和塑料的导热系数较低。
此外,金属的导热系数还受到其晶格结构和电子迁移能力的影响。
试样的几何形状、厚度和温度也会对导热系数产生影响。
高温超导材料热导率实验测试

高温超导材料热导率实验测试为了将高温超导材料(SHTc )绕制成超导线圈以产生强磁场,SHTc带材的热导率的测量是必不可少的,除此之外外加磁场也将对其产生影响。
现代工艺技术为超导带材提供了各式各样的金属镀层,以加强其导热性能及电荷载能力。
本文通过稳态测量法,测量了在低温下含银覆盖层YBCO高温超导带材的热导率,以及外加磁场对其热导率的影响,并进行了比较。
实验表明,在环境温度为77K 时,外加磁场能增大银覆盖层YBCO带材的热导率。
关键词:高温超导带材;YBCO;热导率;磁场1 引言1.1 超导材料的发展自1908年荷兰莱顿大学的卡末林-昂内斯教授成功地实现了氦气的液化并于1911年在极低温度下发现汞的超导现象以来[1],由于超导体材料所具有零点组和抗磁性的优越特性,超导材料便一直受到强烈的关注,越来越多的超导元素和材料被发现,图1.1中标明了具有超导特性的元素。
在一些特定的技术条件下,如高压技术、薄膜技术、极快速冷却以及非晶无序技术等,另一些元素也能显示出超导特性,但这些并不能满足人类对超导材料的实际需求。
为获得具有实际应用价值的超导材料,研究者们将目光转向了合金和化合物。
低温超导材料在20世纪60年代被发现,一大批具有超导特性的合金材料相继被发现,其中具有代表性的有:NbTi 、N 3b Sn 、N 3b Al [2],它们有较高的临界温度,机械加工性能较好,这类合金超导体的临界温度在20K 左右,能在液氮温区内正常工作,但这些超导材料的临界温度太低,离不开液氦制冷设备,成本高而且不方便。
1986年,高温氧化物超导体La-Ba-Cu-O 的发现标志着人类进入了高温超导材料发展时期。
1987年2月,美国科研小组宣布合成了临界温度在液氮沸点以上的超导材料,同年2月24日中国科学院物理研究所宣布制成钇、钡、铜氧化合物超导体,其临界温度能达到92.8K ,后续大量高温超导材料相继被发现[3],这些氧化物中最低的临界温度在77K 以上,其中以具有实用性的Bi-2212和Bi-2223超导材料为代表,图1.1概述超导材料发现和超导材料临界温度提高的历史,每年高温超导材料的临界温度都在提高。
导热系数测定实验报告

导热系数测定实验报告导热系数,作为材料的一项重要物理性质,能够评估材料传导热量的能力。
通过测定导热系数,可以了解材料的导热性能以及在不同工况下的散热能力。
本实验旨在通过实际操作测定不同材料的导热系数,并分析结果对比。
一、实验目的本实验的主要目标是测定不同材料的导热系数,了解热量在材料之间的传导规律,并比较不同材料的导热性能。
通过实验数据的处理和分析,探究导热系数与材料性质之间的关系。
二、实验装置和方法实验所用的装置包括热导率仪和不同材料的试样。
热导率仪由热源、测温探头和显示器组成,用于测量不同材料在不同温度下的热传导情况。
实验的具体步骤如下:1. 准备试样:根据需要测量的材料种类和厚度,制备相应的试样切片。
2. 测量温度:先将测温探头放在设定温度的热源上,进行温度校准,确保准确测量。
3. 安装试样:将试样放置在热导率仪的传热平台上,保持试样与测温探头的接触完全。
4. 测量实验:通过控制热源的温度,使其保持在恒定状态。
记录热导率仪上显示的温度变化情况,并计算得出试样的导热系数。
三、实验数据处理和分析在实验中,我们选择了金属、塑料和木材作为不同材料的代表,分别测量了它们的导热系数,并进行对比分析。
通过实验数据的处理和分析,我们可以得到各材料的导热系数数值。
可以发现,金属材料的导热系数相对较高,这与金属的导电性质有关。
塑料材料的导热系数比金属低,这主要是由于塑料材料结构中有许多绝缘空隙的存在。
木材的导热系数相对较低,并且呈现出随纤维方向变化的趋势,这是因为木材的导热性能与其组织结构有着密切的关系。
导热系数除了与材料的物性有关外,还受到温度的影响。
在不同温度下,导热系数可能会发生变化。
实验中我们选择了不同温度下的测量点,以了解导热系数与温度之间的变化规律。
通过实验数据的分析,我们可以得出导热系数随温度的变化呈现出一定的规律性,不同材料的导热系数随温度变化的趋势可能不同。
四、实验结果与讨论根据实验数据的处理和分析,得出了不同材料在不同温度下的导热系数。
导热系数测试原理

导热系数测试原理导热系数是衡量物质导热性能的重要参数,其测试原理有多种。
本文将对其中常见的几种测试原理进行介绍,包括稳态法、非稳态法、热线法、保护热流法和瞬态热平面法。
一、稳态法稳态法是最经典的导热系数测试方法,其原理基于热传导的稳态条件。
在该条件下,物体的温度分布达到稳定状态,不再随时间变化。
测试时,将样品置于两个平行的加热元件之间,通过加热元件对样品进行加热。
当热量在样品内部传导达到稳态时,测量加热元件的温差和传热面积,并根据傅里叶定律计算导热系数。
稳态法的优点是原理简单、准确度高,适用于各种材料的导热系数测试。
二、非稳态法非稳态法与稳态法不同,其基于热传导的非稳态条件。
在非稳态条件下,物体的温度分布随时间变化。
非稳态法测试时,通过对样品进行快速加热或冷却,使样品内部的温度分布处于动态变化状态。
通过测量样品内部的温度随时间的变化规律,并根据相关公式计算导热系数。
非稳态法的优点是测试时间短、对样品尺寸要求低,适用于某些难以达到稳态条件的材料。
三、热线法热线法是一种特殊的导热系数测试方法,其原理基于一维导热模型。
测试时,将一根细长的热线(通常是镍或铂)置于待测样品中,并对其通电加热。
热线与样品之间发生热交换,导致热线温度发生变化。
通过测量热线的电阻变化和加热电流,结合热线的几何尺寸和材料属性,可以计算出待测样品的导热系数。
热线法的优点是测试精度高、对样品尺寸要求低,适用于薄膜和纤维等细小样品的导热系数测试。
四、保护热流法保护热流法是一种适用于测量松散颗粒材料导热系数的测试方法。
其原理是将待测样品填充在一个容器中,并在容器的底部放置加热元件。
通过测量加热元件的温差和传热面积,结合传热方程和已知的热物性参数(如颗粒密度和比热容),可以计算出样品的导热系数。
保护热流法的优点是可以测量松散颗粒材料的导热系数,且测试操作相对简单。
五、瞬态热平面法瞬态热平面法是一种利用激光脉冲瞬时加热样品的导热系数测试方法。
导热系数测定实验报告

导热系数测定实验报告导热系数测定实验报告导热系数是描述物质传导热量能力的物理量,对于研究材料的热传导性质具有重要意义。
本实验旨在通过测定不同材料的导热系数,探究材料的热传导特性,并分析实验结果的意义。
实验仪器与原理本实验使用的仪器主要包括导热系数测定仪、测温仪、样品夹和样品。
导热系数测定仪是一种常用的实验设备,可以测量材料的导热系数。
测温仪则用于测量样品的温度变化。
样品夹用于固定样品,保证测试的准确性。
实验步骤1. 首先,将待测材料切割成相同大小的样品,并清洁表面,确保样品的质量和纯度。
2. 将样品夹住,确保样品与夹具之间没有空隙,以免影响测量结果。
3. 将样品夹放入导热系数测定仪中,并调整仪器参数,确保实验的准确性。
4. 开始实验后,观察样品的温度变化,记录下每个时间点的温度数据。
5. 根据实验数据,计算出样品的导热系数,并进行分析和比较。
实验结果与分析通过实验测得的数据,我们可以计算出不同材料的导热系数,并进行比较。
导热系数的大小反映了材料的热传导能力,数值越大表示材料的热传导能力越强。
在实验中,我们选取了几种常见的材料进行测试,包括金属、塑料和绝缘材料。
结果显示,金属材料的导热系数通常较高,而塑料和绝缘材料的导热系数较低。
这一结果与我们的常识相符。
金属材料由于其内部电子的自由运动,具有较高的导热性能。
而塑料和绝缘材料由于其分子结构的特殊性,导热系数较低。
此外,通过实验还可以发现,导热系数与温度之间存在一定的关系。
随着温度的升高,导热系数通常会增大。
这是因为高温下,物质内部的分子运动加剧,热传导能力增强。
实验的局限性与改进尽管本实验得到了一些有意义的结果,但仍然存在一些局限性。
首先,实验中的样品大小和形状可能对测量结果产生影响。
因此,为了提高实验的准确性,可以选择更多的样品进行测试,并进行多次重复实验。
其次,实验中没有考虑到材料的厚度对导热系数的影响。
在实际应用中,材料的厚度也会对热传导性能产生影响。
导热系数的测定实验报告

导热系数的测定实验报告导热系数的测定实验报告引言:导热系数是衡量物体传热性能的重要参数,对于热工学、材料科学等领域具有重要意义。
本实验旨在通过测定不同材料的导热系数,探究不同材料的传热性能差异,并了解导热系数的测定方法。
实验装置与方法:实验装置包括导热仪、不同材料样品、温度计等。
首先,将导热仪预热至稳定状态,然后将不同材料样品放置在导热仪的测试台上。
接下来,将测试台加热到一定温度,同时记录下测试台和样品的温度变化情况。
根据测得的温度和时间数据,通过导热仪的计算软件计算出不同材料的导热系数。
实验结果与分析:我们选择了铜、铝和玻璃作为实验样品,分别进行了导热系数的测定。
实验结果显示,铜的导热系数最高,铝次之,玻璃的导热系数最低。
这与我们的预期相符,因为铜和铝是金属材料,具有良好的导热性能,而玻璃是非金属材料,导热性能较差。
进一步分析发现,导热系数与材料的物理性质密切相关。
铜和铝具有较高的电子迁移率和热导率,因此导热系数较高。
而玻璃由于其分子结构的特殊性,导致热传导受到限制,因此导热系数较低。
此外,我们还发现导热系数与温度的关系。
在实验中,我们分别在不同温度下测定了样品的导热系数。
结果显示,导热系数随温度的升高而增大。
这是因为随着温度升高,材料内部的分子振动增强,热传导更加迅速,导致导热系数的增加。
实验误差与改进:在实验过程中,我们注意到了一些误差来源。
首先,导热仪本身存在一定的测量误差,这可能会对实验结果产生影响。
其次,样品的几何形状和尺寸也会对测量结果产生一定的影响。
此外,实验中的温度测量也可能存在一定的误差。
为了减小误差,我们可以采取以下改进措施。
首先,选择更高精度的导热仪进行测量,以提高测量的准确性。
其次,对于样品的几何形状和尺寸,可以采用更加精确的测量方法,例如使用光学显微镜等。
此外,在温度测量方面,可以使用更加精确的温度计进行测量。
结论:通过本实验,我们成功测定了不同材料的导热系数,并了解了导热系数的测定方法。
导热系数的测量实验实训报告doc

导热系数的测量实验实训报告 .doc 导热系数测量实验实训报告一、实验目的本实验旨在通过测量物质的导热系数,深入理解导热系数的物理意义和影响因素,掌握导热系数测量的基本原理和方法,提高实验操作技能和数据处理能力。
二、实验原理导热系数是描述物质导热性能的重要参数,其大小反映了物质在单位时间内、单位温度差下通过单位面积的热流量。
根据傅里叶导热定律,稳态导热过程中,单位时间内通过单位面积的热流量Q与温度梯度ΔT成正比,与传热面积A和材料热阻R成反比,可用公式表示为:Q = -λAΔT/R其中,λ为导热系数,A为传热面积,R为材料热阻。
因此,通过测量热流量Q、温度梯度ΔT和传热面积A,可以计算出材料的导热系数λ。
三、实验步骤1.准备实验器材:导热系数测量仪、加热器、温度传感器、样品杯、天平、砝码、镊子、电源线等。
2.安装实验器材:将加热器放置在样品杯中央,将温度传感器插入加热器侧壁,将样品杯放置在导热系数测量仪平台上。
3.准备样品:选取具有不同导热系数的物质,如金属、陶瓷、塑料等,将其研磨成粉末,用天平称取一定质量,置于样品杯中。
4.开始测量:连接电源线,打开导热系数测量仪电源开关,设置加热器温度、测量时间等参数,启动测量程序。
5.记录数据:观察实验过程中温度变化情况,记录各个时间点的温度值。
6.数据处理:根据实验数据,计算导热系数,分析实验结果。
四、实验结果与分析1.数据记录:将各个时间点的温度值记录在表格中,计算温度梯度ΔT和热流量Q。
2.导热系数计算:根据公式λ = Q/(AΔT),计算物质的导热系数。
将计算结果记录在表格中。
3.结果分析:比较不同物质的导热系数大小,分析导热系数的影响因素。
可以从物质的结构、分子排列、分子量等方面进行讨论。
例如,金属的导热系数普遍较高,因为金属晶体中存在大量的自由电子,可以快速传递热量;而塑料和陶瓷的导热系数相对较低,因为它们存在大量的分子间空隙和缺陷,阻碍了热量的传递。
导热系数的测量实验报告

导热系数的测量实验报告导热系数是物质传导热量的性质,它是描述物质导热性能的一个重要参数。
在工程和科学研究中,准确测量物质的导热系数对于材料的选取和性能评价至关重要。
本实验旨在通过测量不同材料的导热系数,探究其导热性能的差异,为相关领域的研究和应用提供参考。
实验材料和仪器。
本实验选取了几种常见的材料,包括金属、塑料和绝缘材料,以便对比它们的导热系数。
实验中使用的仪器包括导热系数测量仪、热源、温度传感器等。
实验步骤。
1. 将待测材料切割成一定尺寸的样品,并对样品表面进行抛光处理,以确保表面平整。
2. 将热源与导热系数测量仪相连接,使热源能够持续向待测材料传递热量。
3. 将温度传感器与待测材料接触,实时监测样品表面的温度变化。
4. 记录不同时间点下样品表面的温度变化情况,以得出热量传导的速率。
5. 通过实验数据计算出各材料的导热系数,并进行对比分析。
实验结果。
经过实验测量和数据处理,我们得到了不同材料的导热系数。
结果表明,金属材料的导热系数普遍较高,而塑料和绝缘材料的导热系数相对较低。
这与我们对这些材料导热性能的直观认识相符合。
实验分析。
通过对不同材料导热系数的测量和对比分析,我们可以得出以下结论:1. 金属材料具有较高的导热系数,适合用于传热设备和导热结构的材料选择;2. 塑料和绝缘材料的导热系数较低,适合用于隔热材料和绝缘材料的选取。
3. 导热系数的大小与材料的热传导性能密切相关,对于工程应用具有重要意义。
实验总结。
本实验通过对不同材料导热系数的测量,探究了不同材料的导热性能差异。
实验结果对于材料的选取和工程设计具有一定的参考价值。
在今后的工程应用中,我们应该根据材料的导热性能特点,合理选择材料,以实现更好的热传导效果。
结语。
通过本次实验,我们对导热系数的测量方法和意义有了更深入的了解,也增加了对材料导热性能的认识。
在今后的工程实践中,我们将继续探究材料的热学性能,为工程设计和科学研究提供更准确的数据支持。
非稳态法测材料导热性能的实验

实验二 非稳态(准稳态)法测材料的导热性能实验一﹑实验目的1、测量绝热材料的导热系数和比热,掌握其测试原理和方法;2、掌握使用热电偶测量温差的方法。
二﹑实验装置实验装置见下图三﹑实验原理本实验是根据第二类边界条件, 无限大平板的导热问题来设计的设平板厚度为δ, 初始温度0t , 平板两面受恒定的热流密度c q 均匀加热求任何瞬间沿平板厚度方向的温度分布(,)t xτ导热微分方程式﹑初始条件和第二类边界条件如下:22),(),(xx t a x t ∂∂=∂∂τττ 0=τ时, 0t t = 0x =处, 0=∂∂xtδ±=x 处, cq xt =∂∂-λ方程的解为:2203(,)[6c q a x t x t τδτλδδ--=-120212(1)cos()exp()]n n n n xF δμμμδ∞+=+--∑ (1)式中: τ—时间(s );λ—平板的导热系数(0W m C ⋅); a —对流换热系数(2m ); n μ—πn (n=1,2,3,.....);0F —2δτa (傅立叶准则);0t —初始温度();c q —沿x 方向从端面向平板加热的恒定热流密度(2W m )。
随着时间τ的延长, 0F 数变大,式(1)中级数和项愈小 当0F >0.5时, 级数和项变得很小, 可以忽略, 式(1)变成:)612(),(220-+=-δδλδx at q t t x t c (2)由此可见, 当0F >0.5后, 平板各处温度和时间成线性关系, 温度随时间变化的速率是常数, 并且到处相同这种状态称为准稳态。
在准稳态时, 平板中心面0x =处的温度为:)61(),0(0-=-δτλδτa q t t c 平板加热面x δ=处为:)31(),(20+=-δτλδτδa q t t c (3) 此两面的温差为:1(,)(0,)2c q t t t δδττλ∆=-=⋅如已知c q 和δ, 再测出t ∆, 就可以由式(3)求出导热系数:tq c ∆=2δλ (4) 实际上,无限大平板是无法实现的,实验总是用有限尺寸的试件。
导热系数实验报告

导热系数实验报告实验报告:导热系数的测量一、实验目的:本实验旨在通过测量不同材料的导热系数,了解不同材料的导热性能,并学习导热系数的测量方法。
二、实验原理:导热系数是指单位时间内单位面积上的热量流过某一材料时,单位温度差的比值。
导热系数的单位是W/(m·K)。
使用导热系数可以衡量材料的导热性能,通常情况下,导热系数越大,材料的导热性能越好。
在本实验中,我们采用热传导实验方法来测量导热系数。
热传导实验方法主要是通过测量两个温度的差异,以及材料的厚度和面积来计算导热系数。
三、实验器材:1. 导热系数测量仪:用于测量不同材料的导热系数。
2. 不同材料样品:如金属、塑料等。
3. 温度计:用于测量样品的温度。
四、实验步骤:1. 准备不同材料的样品,并记录其厚度和面积。
2. 打开导热系数测量仪的电源,预热一段时间,使其达到稳定状态。
3. 将待测材料样品放置在测量仪的样品夹中,并将温度计插入样品内部。
4. 等待一段时间,直到样品的温度稳定在一个恒定值。
5. 记录样品的两个温度,并计算其温度差。
6. 根据测量仪的读数和样品的尺寸,计算样品的导热系数。
7. 重复以上步骤,对其他材料进行测量,得到它们的导热系数。
五、实验数据处理:根据实验测量的数据,我们可以计算得到每个材料的导热系数。
对于每个样品,我们可以分别计算其平均导热系数和标准偏差,以评估实验的准确性。
六、实验结果和分析:根据实验数据处理的结果,我们可以得到不同材料的导热系数,并进行比较分析。
通常情况下,金属材料的导热系数较大,而塑料等非金属材料的导热系数较小。
七、实验误差和改进方案:在实验过程中,可能存在一些误差,如温度测量误差、尺寸测量误差等。
为了减小误差,可以采取以下改进方案:1. 提高温度测量的准确性,使用更为精确的温度计。
2. 提高尺寸测量的准确性,使用更为精确的测量工具。
3. 减小环境温度对实验的影响,避免温度波动较大的情况发生。
八、实验心得:通过本次实验,我了解了导热系数的测量方法,并了解了不同材料的导热性能。
非稳态(准稳态)法测材料的导热性能实验

非稳态(准稳态)法测材料的导热性能实验非稳态(准稳态)法测材料的导热性能实验一、实验目的1、本实验属于创新型实验,要求学生自己选择不同原料、按照不同配比进行加工出新型实验材料,并对该材料的热物性(密度、导热系数、比热容、导温系数)进行实验测量。
2.快速测量绝热材料(不良导体)的导热系数和比热,掌握其测试原理和方法。
3、掌握使用热电偶测量温差的方法。
二、实验测试原理本实验是根据第二类边界条件,无限大平板的导热问题来设计的。
设平板厚度为2δ,初始温度为t 0,平板两面受恒定的热流密度q c 均匀加热(如下图所示)。
根据导热微分方程式、初始条件和第二类边界条件,对于任一瞬间沿平板厚度方向的温度分布t(x ,τ)可由下面方程组解得;方程组的解为:式中:τ——时间;λ——平板的导热系数;α——平板的导温系数;t 0——初始温度; —傅立叶准则;δβμn n = ,n=1,2,3…;q c ——沿X 方向从端面向平板加热的恒定热流密度。
随着时间τ的延长,F 0数变大,式(1)中级数和项愈小。
当F 0>0.5时,级数和项变得很小,可以忽略,式(1)变成(2) 0),0(0),()0,(),(),(022=∂∂=+∂∂=∂∂=∂∂xt q x t t x t x x t a x t cτλτδτττ)1()]exp()cos(2)1(63[),(2211220o n n nn n c F x x q t x t μδμμδδδδατλτ--+--=-+∞=∑)612(),(222-+=-δδατλδτx q t x t c o 2δατ=F由此可见,当F 0>0.5后,平板各处温度和时间成线性关系,温度随时间变化的速率是常数,并且到处相同。
这种状态即为准稳态。
在准稳态时,平板中心面X=0处的温度为:平板加热面X=δ处为:此两面的温差为: (3) 已知q c 和δ,再测出△t ,就可以由式(3)求出导热系数:(4)实际上,无限大平板是无法实现的,实验总是用有限尺寸的试件,一般可认为,试件的横向尺寸为厚度的6倍以上时,两侧散热对试件中心的温度影响可以忽略不计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.:x 2
x = 处,
q c
.x
方程的解为:
图1第二类边界条件无限大平板
导热的物理模型
t(x, ) -t
査2
c 2
q
c r
a …3x &5 66
od
:.(-护 1
n d 2 x
—^cosC l n-)exp^j 2F 0)]
J n :
(1)
式中:T —时间(S );
入一平板的导热系数(w/m ? °C ); 2
a —平板的导热系数(m /s )
J n
— n 二 n=1 ,2,3,
F0-
孑傅立叶准则;。
一初始温度(C );
非稳态(准稳态)法测材料的导热性能
、实验目的
测量绝热材料(不良导体)的导热系数和比热、掌握其测试原理和方法。
、实验原理
本实验是根据第二类边界条件,无限大平板的导热问题来设计的。
设平板厚度 为23,初始温度为
t 0,平板两面受恒定的热流密度qc 均匀加热(见图1) o 求任
何瞬间沿平板厚度方向的温度分布t (x ,■)。
导热微分方程式、初始条件和第二类 边界条件如下:
A
2
d(x, )
: t(x,) a CT
x=0 处,
q c —沿x 方向从端面向平板加热的恒定热流密度(w/m );
随着时间T 的延长,F 0数变大,式(1 )中级数和项愈小。
当F °>0.5时,级数和项变得很小,可以忽略,式(1)变成:
并且到处相同。
这种状态称为准稳态。
=亚(苓1)
(3)
q c F
由上式可得比热:
在准态时,平板中心面x=0处的温度为:
qg az 1 t(0, ) -t o
、 6
平板加热面x= S 处为:
此两面的温差为:
.:t =t (-, J -t (o,)= 1q
“
2 扎
如已知q c 和再测出△ t ,就可以由式(3)求出导热系数: (4)
实际上,无限大平板是无法实现的,实验总是用有限尺寸的试件。
一般可认为, 试件的横向尺寸为厚度的6倍以上时,两侧散热试件中心的温度影响可以忽略不 计。
试件两端面中心处的温度差就等于无限大平板两端面的温度差。
根据势平衡原理,在准态时,有下列关系:
dt d
式中:F 为试件的横截面(m 2);
C 为试件的比热(J/kg ? C );
P 为试件的密 度(kg/m 3
),1200 kg/m 3
;
鱼为准稳态时的温升速率「C /s );
d
q c c =
P6色
d
实验时,
dt
以试件中心处为准。
d
实验装置(图2)
按上述理论及物理模型设计的实验装置如图2所示,说明如下:
2t
测温装置1
测温装置2
加热器2
图2 实验装置图
1}试件
试件尺寸为200mm X 200mm X§,共四块,尺寸完全相同,8=10mm 每块试件上下面要平齐,表面要平整。
2)加热器
采用高电阻康铜箔平面加热器,康铜箔厚度仅为20卩m加上保护箔的绝缘薄膜,总共只有70卩m=其电阻值稳定,在0-100 C范围内几乎不变。
加热器的面积和试件的端面积相同,也是200mmX 200m m的正方形。
两个加热器的电阻值应尽量相同,相差应在0.1%以内。
3)绝热层
用导热系数比试件小的材料作绝热层,力求减少热量通过,使试件1、4与绝热层的接触面接近绝热。
这样,可假定式(4)中的热量q c等于加热器发出热量的 0.5 倍。
4)热电偶
利用热电偶测量试件2两面的温度及试件2、3接触面中心处的温升速率。
实验时,将四个试件齐迭放在一起,分别在试件1和2及试件3和4之间放入加热器1和2,试件和加热器要对齐,温度传感器的放置如图2。
四、实验步骤(见PC机界面说明)
1、用卡尺测量试件的尺寸:面积F和厚度8。
2、按图2放好试件、加热器和温度传感器,接通电源。
3、接通电源,给加热器通以恒定电流,(实验过程中,电流不允许变化),同时启动秒表,每隔一分钟记录试件2两侧热电势(由热电势查温度值),经一段时间后(随所测材料而不同,一般在10-20分钟)系统进入准稳态
4、第一次实验结束,将加热器开关K切断,取下试件及加热器,用电扇将加热器吹凉,待其和室温平衡后才能继续作下一次实验。
但试件不能连续做实验,必须经过四小时以上放置,使其冷却至与室温平衡后,才能再作下一次实验。
图15第二类边全条件束限大平板须切断电源,一切恢
复原状。
导热的物理模型
五、实验数据记录和处理
试件截面尺寸F: 0.2 X 0.2 [ m2] 试件厚度0.01 [m]
试件材料密度p =1200 [ kg/m3] 加热功率P: [w]
计算:计算热流密度q c[w/ m]
准稳态时的温差厶t (平均值)「C ]
准稳态时的温升速率世[C /S]
然后,即可计算出试件的导热系数入[w/m ? k ]和比热c[J/ kg ? C ]。
