图像拼接实验报告
图像拼接调研报告

图像拼接的调研报告1.图像拼接的意义和国内外研究现状1.1 意义图像拼接(image mosaic)技术是将一组相互间存在重叠部分的图像序列进行空间配准,经重采样融合后形成一幅包含各图像序列信息的宽视角场景的、完整的、高清晰的新图像的技术。
图像拼接是数字图像处理领域的一个重要的研究方向,在摄影测量学、计算机视觉、遥感图像分析、计算机图形等领域有着广泛的应用价值。
图像拼接技术一个日益流行的研究领域,是虚拟现实、计算机视觉、计算机图形学和图像处理等领域的重要研究课题,在宇宙空间探测、海底勘测、医学、气象、地质勘测、军事、视频压缩和传输、视频的索引和检索、物体的3D重建、军事侦察和公安取证、数码相机的超分辨率处理等领域都有广泛的应用。
因此,图像拼接技术的研究具有很好的应用前景和实际应用价值。
1.2 国内外研究现状。
关于图像拼接的方法国内外已有不少的论文发表,其算法大致可分为基于模型的方法,基于变换域的方法,基于灰度相关的方法和基于特征的方法,而如何提高图像拼接的效率,减少处理时间和增强拼接系统的适应性一直是研究的重点。
①基于模型:1996年,微软研究院的Richard Szeliski提出了一种2D空间八参数投影变换模型,采用Levenberg-Marquardt迭代非线性最小化方法(简称L-M算法)求出图像间的几何变换参数来进行图像配准。
这种方法在处理具有平移、旋转、仿射等多种变换的待拼接图像方面效果好,收敛速度快,因此成为图像拼接领域的经典算法,但是计算量大,拼接效果不稳定。
2000年,Shmuel Peleg等人在Richard Szeliski的基础上做了进一步的改进,提出了自适应图像拼接模型,根据相机的不同运动而自适应选择拼接模型,通过把图像分成狭条进行多重投影来完成图像的拼接。
这一研究成果推动了图像拼接技术的进一步的发展,从此自适应问题成为图像拼接领域新的研究热点。
匹兹堡大学的Sevket Gumustekin对消除在固定点旋转摄像机拍摄自然景物时形成的透视变形和全景图像的拼接进行了研究。
图像融合实验报告

图像融合实验报告图像融合实验报告引言图像融合是一种将多幅图像合并成一幅新图像的技术,广泛应用于计算机视觉、图像处理和模式识别等领域。
本实验旨在探究图像融合的原理和方法,并通过实验验证其效果。
一、图像融合的原理图像融合的原理是将多幅图像的信息融合到一幅图像中,使得新图像能够综合展示各幅图像的特点。
常见的图像融合方法包括像素级融合、特征级融合和决策级融合。
1. 像素级融合像素级融合是将多幅图像的像素按照一定规则进行融合,常用的方法有平均法、加权平均法和最大值法。
平均法将多幅图像对应像素的灰度值取平均,得到新图像的灰度值;加权平均法则根据不同图像的重要性给予不同权重;最大值法则选取多幅图像中灰度值最大的像素作为新图像的灰度值。
2. 特征级融合特征级融合是将多幅图像的特征进行融合,常用的特征包括纹理、边缘和颜色等。
通过提取多幅图像的特征并进行融合,可以得到具有更多信息的新图像。
3. 决策级融合决策级融合是将多幅图像的决策结果进行融合,常用的方法有逻辑运算、加权决策和模糊逻辑等。
通过对多幅图像的决策结果进行融合,可以得到更准确的决策结果。
二、实验过程本实验选取了两幅具有不同特征的图像进行融合,分别是一幅自然风景图和一幅抽象艺术图。
实验过程如下:1. 图像预处理首先对两幅图像进行预处理,包括图像的缩放、灰度化和边缘检测等。
通过预处理可以使得图像具有相似的特征,方便后续的融合操作。
2. 图像融合方法选择根据实验目的,选择合适的图像融合方法进行实验。
本实验选取了像素级融合和特征级融合两种方法进行对比。
3. 像素级融合实验首先对两幅图像进行像素级融合实验。
通过将两幅图像的对应像素进行平均或加权平均,得到新图像。
然后对新图像进行评估,包括灰度分布、对比度和清晰度等指标。
4. 特征级融合实验接着对两幅图像进行特征级融合实验。
通过提取两幅图像的纹理、边缘和颜色等特征,并进行融合,得到新图像。
然后同样对新图像进行评估。
5. 结果分析根据实验结果对比,分析不同融合方法的优劣。
创意拼贴的实验报告(3篇)

第1篇一、实验背景拼贴艺术作为一种独特的艺术形式,源于20世纪初的欧洲,它通过将不同材质、不同风格的元素组合在一起,创造出全新的视觉效果。
在我国,拼贴艺术也逐渐受到年轻人的喜爱,成为了一种流行的艺术创作方式。
本实验旨在通过创意拼贴,探索不同材质、色彩、图案的搭配,以实现独特的视觉效果。
二、实验目的1. 了解拼贴艺术的基本原理和技巧。
2. 掌握不同材质、色彩、图案的搭配方法。
3. 提高创意思维和审美能力。
4. 创作出具有个人特色的拼贴作品。
三、实验材料1. 背景纸:A4尺寸,颜色自选。
2. 彩色卡纸:不同颜色、不同纹理。
3. 剪刀、胶水、铅笔、橡皮等工具。
4. 主题素材:图片、照片、海报等。
四、实验步骤1. 确定主题:选择一个感兴趣的主题,如自然、城市、人物等。
2. 收集素材:根据主题收集相关图片、照片、海报等素材。
3. 设计草图:在纸上绘制出拼贴作品的草图,确定各个元素的布局。
4. 切割素材:按照草图,将素材剪切成所需形状。
5. 拼贴组合:将剪切的素材按照草图进行拼贴,调整位置和角度。
6. 调整细节:检查拼贴作品的整体效果,对细节进行调整。
7. 固定作品:使用胶水将拼贴作品固定在背景纸上。
五、实验结果与分析1. 创意拼贴作品的效果:本次实验创作的拼贴作品以自然为主题,通过将彩色卡纸、图片、照片等素材进行拼贴,形成了一幅富有创意和想象力的作品。
作品中的色彩搭配、图案布局以及素材选择都体现了个人的审美和创意。
2. 实验过程中遇到的问题及解决方法:(1)素材选择:在收集素材时,遇到了素材颜色不协调、图案过于复杂等问题。
解决方法是筛选出与主题相符、色彩搭配合理的素材。
(2)拼贴技巧:在拼贴过程中,遇到了素材边缘不整齐、拼接不牢固等问题。
解决方法是调整剪刀角度,确保切割整齐;使用胶水固定素材,增强拼接牢固度。
3. 实验结论:(1)创意拼贴是一种富有创造性的艺术形式,通过素材的选择、色彩搭配和图案布局,可以表现出独特的视觉效果。
全景图像拼接
实验目的:图像拼接的目的是将有衔接重叠的图像拼成一张高分辨率全景图像,它是计算机视觉、图像处理和计算机图形学等多学科的综合应用技术。
图像拼接技术是指将对同一场景、不同角度之间存在相互重叠的图像序列进行图像配准,然后再把图像融合成一张包含各图像信息的高清图像的技术。
本实验是根据输入的只有旋转的一系列图像序列,经过匹配,融合后生成一张360度的全景图像。
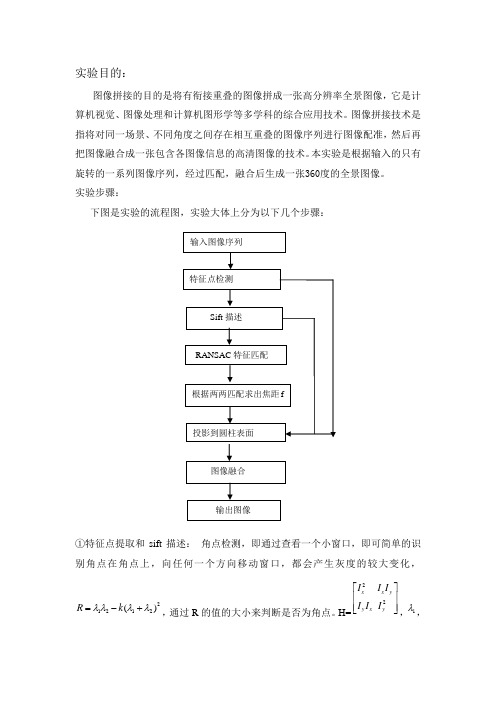
实验步骤:下图是实验的流程图,实验大体上分为以下几个步骤:①特征点提取和sift 描述: 角点检测,即通过查看一个小窗口,即可简单的识别角点在角点上,向任何一个方向移动窗口,都会产生灰度的较大变化,21212()R k λλλλ=-+,通过R 的值的大小来判断是否为角点。
H=22x x y y x y I I I I I I ⎡⎤⎢⎥⎢⎥⎣⎦,1λ,输入图像序列 特征点检测 Sift 描述RANSAC 特征匹配根据两两匹配求出焦距f投影到圆柱表面图像融合输出图像为矩阵的两个特征值。
实验中的SIFT描述子是对每个角点周围进行4个区域2进行描述,分别是上下左右四个区域,每个方块大小为5*5,然后对每个方块的每个点求其梯度方向。
SIFT方向共有8个方向,将每个点的梯度方向做统计,最后归为8个方向中的一个,得到分别得到sift(k,0),sift(k,1)···sift(k,8),k为方块序列,0-8为方向,共有四个方块,所以生成32维的向量,然后按幅值大小对这32维向量进行排序,并找出最大的作为主方向。
图为角点检测和sift描述后的图②.如果直接根据描述子32维向量进行匹配的话,因为噪声的影响,角点检测的不准确,会导致找出一些错误的匹配对,如何去掉这些错误的匹配呢?RANSAC算法是基于特征的图像配准算法中的典型算法,其优点是:可靠、稳定、精度高,对图像噪声和特征点提取不准确,有强健的承受能力,鲁棒性强,并且具有较好的剔出误匹配点的能力,经常被使用在图像特征匹配中。
图像拼接报告

图像拼接学习1为什么要进行图像拼接在很多研究领域需要一些分辨率很高的超高清、全景图像。
而现有的全景相机、广角镜头等设备不仅昂贵,而且存在失真的现象。
所以要使用图像无缝拼接技术将很多张具有部分重叠区域的图像进行拼接,从而得到一幅宽视角的全景图像,满足人们在各领域研究的需要。
2图像拼接的流程一、图像拼接的流程:大致可分为三部分:图像预处理,图像配准,图像融合。
详细分为:①预处理—>②特征点搜索—>③特征点筛选—>④两幅图像中的特征点配对—>⑤根据配对点找到不同图片之间的映射变换关系—>⑥图形融合3图像的预图处理图像预处理包括:噪声去除、灰度处理、几何畸变的校正等图像处理。
4图像配准提取参考图像和待拼接图像中的特征信息,然后在提取出的特征信息中寻找最佳的匹配。
图像配准算法主要包括三类:基于图像像素的方法、基于图像特征的配准算法和基于图像区域配准算法。
4.1基于特征的图像配准算法一、为什么选用这种方法:这种方法提取了图像的特征,压缩了图像信息的数据量,因此在匹配时计算量小,速度较快。
而且能保持图像位移、旋转、比例等方面的特征。
并且图像特征具有很好的独特性以相互区分,对位置变化敏感,匹配精度高。
二、算法介绍:首先对两幅待匹配的图像进行特征提取,将这些特征作为控制结构,然后利用提取到的特征结构来完成图像特征之间的匹配,通过控制结构的匹配关系建立图像之间的映射变换关系。
匹配的特征可以是边缘、轮廓、直线等。
常用的匹配特征主要有点特征、线特征和区域特征。
三、算法种类:常用的特征点提取算法有Susan算法、Harris算法、SIFT算法等。
4.2Harris角点检测算法4.2.1角点的数学定义:①角点是图像灰度一阶导数所对应的最大值的位置;②角点是图像中两条或两条以上边缘的交点;③角点是图像中灰度变化最大的位置;④角点位置的一阶导数最大,二阶导数为零;⑤角点是图像中物体边缘变换不连续的位置;⑥角点是二维图像亮度变化剧烈的位置。
小波变换图像拼接实验报告

图像拼接实验报告一、实验目的选用适当的拼接算法实现两幅图像的拼接。
二、实验原理图像拼接技术就是将数张有重叠部分的图像(可能是不同时间、不同视角或者不同传感器获得的)拼成一幅大型的无缝高分辨率图像的技术。
图像配准和图像融合是图像拼接的两个关键技术。
图像配准是图像融合的基础,而且图像配准算法的计算量一般非常大,因此图像拼接技术的发展很大程度上取决于图像配准技术的创新。
早期的图像配准技术主要采用点匹配法,这类方法速度慢、精度低,而且常常需要人工选取初始匹配点,无法适应大数据量图像的融合。
图像拼接的方法很多,不同的算法步骤会有一定差异,但大致的过程是相同的。
一般来说,图像拼接主要包括以下五步:(1)图像预处理:包括数字图像处理的基本操作(如去噪、边缘提取、直方图处理等)、建立图像的匹配模板以及对图像进行某种变换(如傅里叶变换、小波变换等)等操作。
(2)图像配准:就是采用一定的匹配策略,找出待拼接图像中的模板或特征点在参考图像中对应的位置,进而确定两幅图像之间的变换关系。
(3)建立变换模型:根据模板或者图像特征之间的对应关系,计算出数学模型中的各参数值,从而建立两幅图像的数学变换模型。
(4)统一坐标变换:根据建立的数学转换模型,将待拼接图像转换到参考图像的坐标系中,完成统一坐标变换。
(5)融合重构:将带拼接图像的重合区域进行融合得到拼接重构的平滑无缝全景图像。
图像拼接技术主要包括两个关键环节即图像配准和图像融合对于图像融合部分,由于其耗时不太大,且现有的几种主要方法效果差别也不多,所以总体来说算法上比较成熟。
而图像配准部分是整个图像拼接技术的核心部分,它直接关系到图像拼接算法的成功率和运行速度,因此配准算法的研究是多年来研究的重点。
目前的图像配准算法基本上可以分为两类:基于频域的方法(相位相关方法)和基于时域的方法。
相位相关法对拼接的图像进行快速傅立叶变换,将两幅待配准图像变换到频域,然后通过它们的互功率谱直接计算出两幅图像间的平移矢量,从而实现图像的配准。
实验5 图像拼接

二、图像拼接的前期处理工作
5.
色调调整
色调调整是遥感数字图像拼接技术的一个重要环节。不 同时相或成像条件存在差异的图像,由于要拼接的图像 辐射水平不一样,图像的亮度差异比较大,若不进行色 调调整,拼接后的图像,即使几何位置很精确,也会由 于色调不同,而不能很好的满足应用。因此,必须进行 色调调整这一步骤。
二、图像拼接的前期处理工作
2.
预处理工作
包括辐射校正、去条带和斑点、几何纠正。
3.
确定实施方案
在进行多幅图像拼接时,拼接方案的好坏直接影响着工 作时间和工作量。为此,需要首先确定标准像幅,一般 位于拼接区中央,其次决定拼接顺序,即以标准图幅为 中心,由中央向四周逐步散开。
4.
确定实施方案
包括遥感图像拼接工作的进行主要是基于相邻区域的重 叠区。无论是色调调整,还是几何拼接,都是将重叠区 作为基础进行的。
三、运用Erdas进行图像拼接
Mosaic Tool窗口有菜单条、工具条、图形 窗口和状态条4部分组成,其中菜单条中的 菜单命令及功能如表1所列,工具条中的图 标及其功能如表2所列。
表1.菜单条中的菜单命令及功能
三、运用Erdas进行图像拼接
表1.菜单条中的菜单命令及功能(接上)
三、运用Erdas进行图像拼接
调整完成后,在Mosaic Tool窗口单击,退出图像叠置 组合状态。
三、运用Erdas进行图像拼接
4.
图像匹配设置
在Mosaic Tool工具条单击Set Intersection Mode图标, 进入设置图像关系模式。单击Overlap Function图标,打开 Set Overlap Function对话框。 在Set Overlap Function对话框中设置一下参数:
实验2 图像的拼接和裁剪
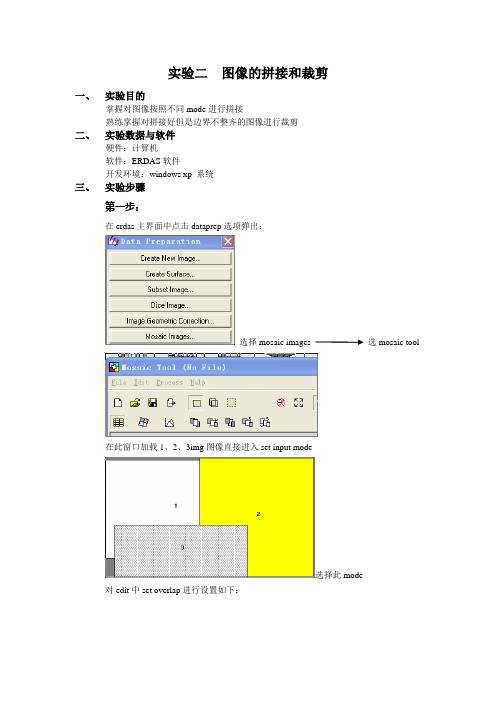
实验二图像的拼接和裁剪一、实验目的掌握对图像按照不同mode进行拼接熟练掌握对拼接好但是边界不整齐的图像进行裁剪二、实验数据与软件硬件:计算机软件:ERDAS软件开发环境:windows xp 系统三、实验步骤第一步:在erdas主界面中点击dataprep选项弹出:选择mosaic images 选mosaic tool在此窗口加载1、2、3img图像直接进入set input mode选择此mode 对edit中set overlap进行设置如下:并对color corrections 中设置为(use.histogram matching)至此对拼接的设置完成,Process preview mosaic 后直接保存为拼接1:在view#中打开拼接1:由于拼接的图像边界不是规则的,故进行第二步的裁剪第二步:打开第一步中拼接好的图像(拼接1),并在AOI下拉框中选择tools自动弹出工具,选择矩形裁剪框,任意调整想要裁剪的区域如下:接下来,把此视图保存为.aoi文件步骤为:file save 保存为c.aoi 回到erdas 主界面选择Dataprep 选subset然后引进拼接好的图,新建裁剪3点击AOI导入c.aoi文件进行最后的裁剪图像生成:单击OK后等候片刻,就会在存储路径下生成裁剪3.img,,并在view#中打开图像显示如下:四、实验结果与分析1、对比裁剪预览可知室所裁剪的结果2、拼接三幅图像可以采样不同的六种mode ,然后得到的拼接图像也不相同,比较后选择本实验的这种mode最佳3、可能室软件源或者安装等的问题出现有些功能和属性设置在本实验中问能按要求设置,如:在拼接未能找(edit下的overlap areas),但是设置了color corrections中use.histogram matching也能实现拼接。
图像的裁剪与拼接与实验心得体会

图像的裁剪与拼接与实验心得体会遥感图像拼接(镶嵌)与裁剪一、实验目的与要求图像镶嵌指在一定数学基础控制下,把多景相邻遥感图像拼接成一个大范围、无缝的图像的过程,在ENVI中提供了透明处理、匀色、羽化等功能。
实验要求可以用ENVI解决镶嵌颜色不一致、接边以及重叠区等问题。
图像裁剪的目的是将研究之外的区域去除。
常用的方法是按照行政区划边界或者自然区域边界进行图像裁剪;在基础数据生产中,经常还要进行标准分幅裁剪。
ENVI的图像裁剪过程,可分为规则裁剪和不规则裁剪。
实验要求学生们学会通过ENVI软件对下载的地区图像进行裁剪和拼接,将南京区域裁剪出来。
基于MATLAB的图像拼接技术

基于MATLAB的图像拼接技术实验报告学院:数信学院专业班级: 12级信息工程1班姓名学号:一、 实验名称:基于MATLAB 的图像拼接技术二、 实验目的:利用图像拼接技术得到超宽视角的图像,用来虚拟实际场景。
三、 实验原理:基于相位相关的图像拼接技术是一种基于频域的方法,通过求得图像在频域上是相位相关特点来找到特征位置,从而进行图像拼接。
其基本原理是基于傅氏功率谱的相关技术。
该方法仅利用互功率谱中的相位信息进行图像配准,对图像间的亮度变化不敏感,而且所获得的相关峰尖突出,具有一定的鲁棒性和较高的配准精度。
基于相位相关法进行图像拼接的基本原理如下:假设f (x ,y )表示尺寸 为M ⨯N 的图像,该函数的二维离散傅里叶变换(DFT )为:112(//)001(,)(,)M N j ux M vy N x y F u v f x y eM Nπ---+===⨯∑∑其中,F (u ,v )是复变函数;u 、v 是频率变量,u=0,1,…,M-1,v=0,1,…,N-1;x 、y 是空间或图像变量。
二维离散傅里叶逆变换(IDFT )为:112(//)0(,)(,)N M j ux M vy N y x f u v e F x y π---+===∑∑其中,x=0,1,…,M-1;y=0,1,…,N-1。
设两幅图像1I 、2I 的重叠位置为(0x ,0y ),则图像1I 、2I 的互功率谱为:00*2()1212(,)(,)(,)(,)j x y I I e I I πξηξηξηξηξη-+⨯=⨯其中,*为共轭符号,对上式两边进行傅里叶逆变换将在(0x ,0y )处产生一个 函数。
因此,只要检测上式傅里叶逆变换结果最大值的位置,就可以获得两幅图像间的评议量(0x ,0y 。
具体算法步骤如下: ①读入两幅图片1I 、2I (函数输入),并转换为灰度图像; ②分别对1I 、2I 做二维傅里叶变换,即: A=2fft (1I ) B=2fft (2I )则通过A 、B 的简单的矩阵运算得到另一矩阵3C ,即: 3C =B*.conj (A )/norm (B*.conj (A ),1)矩阵3C 的二维傅里叶逆变换C 在(0x ,0y )处取得最大,可通过遍历比较C (i ,j )大小即可找到该位置,并作为函数返回值。
图像融合的实验报告

图像融合的实验报告实验报告:图像融合一、实验目的本实验的目的是研究和实践图像融合的方法,探究图像融合在多种应用中的作用和效果。
二、实验原理图像融合是将两幅或多幅图像以某种方式进行合成,生成一幅新的图像,使之具有源图像的一些特征和信息。
在图像融合中,常使用的方法包括像素级融合和特征级融合。
像素级融合是将不同图像中的像素点通过某种算法进行融合,产生新的像素值;特征级融合则是将不同图像中的特征提取出来,然后进行融合得到新的特征。
三、实验步骤1. 收集源图像:从不同角度和距离拍摄相同目标的不同图像,作为源图像;2. 图像预处理:对源图像进行预处理,包括灰度化、图像增强、去噪等操作,以便提取和融合图像的特征;3. 特征提取:使用特征提取算法,如边缘检测、角点检测等,从源图像中提取出不同的特征;4. 图像融合:根据所选的融合方法,将不同图像的像素点或特征进行融合;5. 融合结果评估:对融合结果进行评估,包括图像质量评估、信息保留度评估等。
四、实验结果与分析经过以上步骤,我们将图像进行了融合,并得到了融合后的图像。
对融合后的图像进行质量评估发现,融合后的图像与原图相比,整体上有明显的信息保留,且清晰度较高,细节丰富。
这说明我们所选择的特征融合方法在一定程度上是有效的。
五、实验应用图像融合在多个领域有着广泛的应用。
在军事领域,图像融合可以用于红外图像和可见光图像的融合,以提高目标探测和识别的准确率。
在医学领域,图像融合可以将不同类型的医学图像进行融合,帮助医生更准确地进行诊断和治疗。
在遥感领域,图像融合可以将多源的遥感图像融合,提高地物的分类精度和信息提取能力。
六、实验总结本实验通过对图像融合的研究和实践,了解了图像融合的原理和方法,并在实验中得到了一定的实际经验。
图像融合在多个领域都有重要的应用,可以提高图像质量、增强图像信息特征、准确识别目标等。
未来,我们可以进一步研究更多的图像融合方法,优化融合结果,并在更多领域中应用图像融合技术。
图像融合实验报告心得

图像融合实验报告心得引言图像融合是指将多幅图像或图像序列中的信息合成为一副新的图像,以提取出更多的信息或增强原图像的视觉效果。
在本次实验中,我们学习了图像融合的基本概念和常用方法,并完成了一系列实验任务。
通过实验,我深刻理解了图像融合的原理与技术,并对图像处理领域有了更深入的认识。
实验过程实验环境搭建首先,我们需要搭建实验环境。
在本次实验中,我们选择使用Python语言进行图像融合实验。
我们通过安装OpenCV和NumPy等库来实现实验需求,并搭建了合适的开发环境。
这一步骤对实验的顺利进行起到了关键作用。
图像融合方法实现在实验中,我们学习了多种图像融合方法,并根据需求选择了合适的融合方法。
我们实现了以下几种融合方法:1. 像素级融合:将不同图像中相应像素点的数值进行加权平均,得到融合后的像素值。
这种方法简单直接,但对于不同图像的对齐要求较高。
2. 小波变换融合:利用小波变换将图像进行频域分解,然后再进行逆变换融合。
这种方法可以提取出不同图像的低频和高频信息,在保留细节的同时增强了图像的对比度。
3. 金字塔融合:利用金字塔法将图像进行多层分解,再将不同层次的图像进行加权合成。
这种方法可以在保留图像细节的同时,实现对整体图像的融合。
实验结果与讨论在实验中,我们将这些图像融合方法应用到实际图像上,并进行了多组实验。
通过比较不同融合方法的结果,我们发现不同方法对图像的处理效果有所不同,适用于不同的应用场景。
比如,在需要突出图像的细节和纹理时,小波变换融合方法表现出色,能够提取出图像的高频信息,使图像更加清晰。
而当需要保留整体图像结构和颜色信息时,金字塔融合方法则更为适用。
不同的融合方法可以互相补充,使得融合后的图像更加自然。
除了不同方法的比较,我们还测试了不同融合参数对结果的影响。
通过调整融合权重、金字塔层数、小波变换的尺度等参数,我们发现合适的参数选择可以显著改善融合结果。
因此,在实际应用中,我们需根据需求和图像特点来选择合适的融合方法和参数。
一种稳健快速的图像拼接的开题报告

一种稳健快速的图像拼接的开题报告引言随着计算机技术的发展,图像处理技术得到了广泛的应用,其中图像拼接是其中一项重要的技术。
图像拼接是将多幅图像拼接成一幅大的全景图像的处理过程,解决了原本单幅图像无法涵盖全部场景的问题。
图像拼接应用广泛,如卫星图像处理、遥感图像处理、医学图像处理等领域,因此图像拼接技术的研究和发展一直备受关注。
本文主要介绍一种稳健快速的图像拼接方法。
首先介绍了图像拼接的技术原理和现有的算法,然后针对现有算法存在的问题提出了改进方案,并给出了具体的实验结果。
技术原理图像拼接的技术原理主要包括两个步骤:特征点提取和图像变换。
特征点提取是指从图像中提取出一些具有代表性的特征点,例如角点、边缘等。
图像变换是指对图像进行变换,使得相邻两幅图像之间的特征点对应关系保持一致,从而实现拼接。
现有算法目前,图像拼接的主要算法有两种:基于特征点匹配和基于深度学习的方法。
基于特征点匹配的方法是比较传统的方法,它主要是通过在两幅图像中提取出一些特征点,然后通过特征点之间的匹配来实现拼接。
但是基于特征点匹配的方法存在诸多问题:第一,提取的特征点可能不准确;第二,匹配出的特征点可能存在误匹配,从而造成拼接的不准确性;第三,在多幅图像之间拼接时,匹配出的特征点之间不一定存在对应关系。
近年来,基于深度学习的方法在图像拼接领域也得到了广泛的应用。
这种方法通过卷积神经网络来学习图像的特征表示,并通过深度学习的方法来实现图像的拼接。
基于深度学习的方法相对于基于特征点匹配的方法具有更高的准确性和鲁棒性,但是它需要大量的数据集和计算资源。
改进方案针对现有算法存在的问题,本文提出了一种改进方案。
该方法主要分为三个步骤:图像预处理,特征提取,以及图像变换。
1. 图像预处理图像预处理是指在拼接之前通过一些处理手段,提高图像的特征信息,减少图像中的噪声,从而提高拼接的准确性。
常见的预处理方法有高斯滤波、边缘检测、直方图均衡化等。
图像融合实验报告

图像融合实验报告
《图像融合实验报告》
图像融合是一种将多幅图像融合为一幅图像的技术,它可以用于增强图像的质量、提取图像的信息以及实现图像的特定应用。
本实验报告将介绍图像融合的
基本原理和实验过程,并展示实验结果。
首先,我们选取了两幅不同类型的图像,一幅是自然风景图像,另一幅是人像
图像。
然后,我们利用图像融合算法,将这两幅图像进行融合。
在融合过程中,我们采用了多种融合策略,包括像素级融合、特征级融合和深度学习融合等。
通过比较不同融合策略的效果,我们得出了最佳的融合方法。
在实验过程中,我们发现图像融合可以有效地提取出图像的特征信息,使得融
合后的图像更加清晰、丰富。
同时,图像融合还可以实现不同类型图像的融合,从而创造出新的图像效果。
这些实验结果表明,图像融合技术具有广泛的应用
前景,可以在医学影像、遥感图像、安防监控等领域发挥重要作用。
总之,本实验报告通过图像融合实验展示了图像融合技术的基本原理和应用效果,为进一步研究和应用图像融合技术提供了重要参考。
希望通过本报告的介绍,能够引起更多人对图像融合技术的关注和研究。
基于特征点的图像拼接技术研究中期报告

基于特征点的图像拼接技术研究中期报告摘要:本文主要介绍基于特征点的图像拼接技术的研究进展,包括主流算法的原理、优缺点以及近年来的发展趋势。
该技术旨在将多个局部图像拼接成一个完整的全景图像,并且能够处理图像中的透视、畸变等问题。
本文提出了一种结合SIFT与SURF算法的特征点提取方法,同时引入了图像映射变换模型、多尺度拼接和图像融合等技术,增强了拼接效果和可靠性。
通过实验结果验证了该方法的有效性和可行性。
关键词:特征点;图像拼接;SIFT;SURF;映射变换;多尺度拼接;图像融合一、引言图像拼接技术是近年来计算机视觉研究的热点之一。
它可以将多个局部图像拼接成一个完整的全景图像,广泛应用于航拍、卫星影像、医学影像等领域,具有广阔的应用前景。
图像拼接涉及到多个技术领域,包括图像特征点提取与匹配、图像变换、图像融合等内容。
当前,基于特征点的图像拼接技术已经成为主流方法之一,它能够有效处理图像中的透视、畸变等问题,并且具有较高的拼接准确度和图像质量。
本文将主要介绍该领域的研究现状和发展趋势,并给出自己的研究思路和方法。
二、相关技术介绍1. 特征点提取图像拼接的第一步是对图像中的特征点进行提取和匹配。
当前常用的特征点提取算法主要有SIFT(Scale Invariant Feature Transform)和SURF(Speeded Up Robust Features)算法。
这些算法能够提取出尺度不变、旋转不变、光照不变等特征点,具有较高的特征匹配准确率。
2. 图像变换在进行图像拼接之前,需要将拼接图像进行变换和校正,以保证拼接后的图像具有较高的质量和准确度。
图像变换主要包括透视变换、仿射变换、相似变换等,其中透视变换是最常用的一种变换方法。
3. 图像融合图像拼接最后一步是进行图像融合,将拼接后的局部图像进行融合,以达到拼接后图像的平滑过渡和细节保持。
常用的图像融合算法主要包括像素平均、拉普拉斯金字塔等方法。
实验报告-3.图像合成

实验名称
ห้องสมุดไป่ตู้图像合成
实验类型
验证
演示
综合
设计
班级
B131008
学号
B13100809
姓名
何嘉文
指导教师
王琪
成绩
√
一、实验目的
要求使用几张素材合成一个带有乌云或者多云效果的图片。z
二、实验内容及结果分析
实验内容:使用Photoshop中的蒙板合成一张具有云彩效果的图片。
具体步骤:1.在Photoshop中打开一张天空灰暗的图片。
2.然后打开另外一张带有云彩的素材图。
3.把素材图复制到原图上,并建立一个图层蒙板,在蒙板中用渐变工具作出合适的蒙板渐变,即可得到最终合成图。
原图:
素材图:
合成图:
签名:何嘉文
日期:2013年12月5日
图像融合-图像拼接实习报告论文

图像融合——图像拼接1)综述图像融合的方法;2) 选择合适的目标(可以使风景、建筑、汽车等),自行用数码相机采集子图像;3)将子图像转换为灰度图像;4)设计图像算法并编写程序,实现两幅图像的拼接;提示:1)拍摄的左右子图像,必须是在相同距离、同等光照下拍摄的正面图像;2)要有一个明确的标识出现在左右图像中。
3)可以先用windows画图工具生成简单图像进行算法测试,然后在用真实图像。
1 引言 (3)2 图像融合—拼接的方法 (4)2.1 图像配准 (4)2.2 图像处理 (5)2.2.1中值滤波法消除拼接缝 (6)2.2.2利用小波变换的方法消除拼接缝 (6)2.2.3利用加权平滑的方法消除拼接缝 (6)3 图像拼接算法 (7)参考文献 (7)附件:程序 (7)图像融合——图像拼接摘要:选择图像拼接就是想两张图像拼接在一起是别人看不出来是两张图片,能完美的将两张图片拼接在一起。
图像拼接技术可以解决由于相机等成像仪器的视角和大小的限制,不能产生很大图片的问题。
所谓“图像拼接”就是将两幅或者两幅以上相邻间具有部分重叠的图像进行无缝拼接,生成一张具有较宽视角的高分辨率图像或者360度视角的全景的技术,涉及到计算机视觉,计算机图形学,图像处理以及一些数学工具等。
该技术为图像降运动物体去除,模糊消除噪,视场扩展,空间解析的提高,和动态范围增强提供了可能性。
对图像拼接的两个主要过程:图像配准和图像融合分别进行了详细介绍。
图像配准是图像拼接的核心技术,本文还对现有的图像配准方法进行归类总结,对每个配准算法进行优缺点描述。
对目前现有以及常用的图像融合方法也进行了详细的介绍。
最后提出了图像拼接技术不足。
关键词:图像拼接图像配准图像融合1 引言这个学期我们学习了图像处理这门课程,这么课程主要是讲解了对于图片的处理以及一下如何处理图片的方法。
图像拼接现在在我们的生活中越来越多的出现了,我们可以看到许多图像都是有图像融合、图像拼接技术做出来了。
图像的裁剪与拼接与实验心得体会

图像的裁剪与拼接与实验心得体会
图像拼接的含义:将多幅在不同时刻、从不同视角或者由不同传感器获得的图像经过对齐然后无缝地融合在一起,从而得到一幅大视场、高分辨率图像的处理过程。
图像拼接有两种类型,一种是传统全景图,没有或只有轻微的运动视差,另一种是多重投影拼接图,但存在较大的运动视差
利用MATLAB进行图像拼接时,要注意以下几点:
第一方面:在图像格式上,由于图像格式包括索引色和真彩色这两大类不同的类型,所以需要统一转换一下才能拼接。
这两类图像的判断根据是读入的数据是二维还是三维,对于二维的数据,如果调色板为空,则按照灰度图像处理。
第二方面:在数据格式上,由于具体的图像文件格式不同,读入的数据可能是logical、uint8、uint16、uint32、single、uint64、double等各种不同的格式,要想进行拼接,需要转换为同一种数据类型,这样在拼接的时候才不会出现错误。
在图像拼接过程中,要特别注意找出两幅图像之间最优的空间位置和色彩之间的变换关系,使一幅图像中的点最优地映射到另一幅图像中,也就是要让图像对齐好,这关系到图像的处理效果。
图像拼接的步骤如下:1选取拍摄位置以及图像获取方式;2获取图像;3图像预处理;4图像对齐;5图像合成;6输出拼接图像。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图像拼接一、实验原理及实验结果图像拼接就是将一系列针对同一场景的有重叠部分的图片拼接成整幅图像,使拼接后的图像最大程度地与原始场景接近,图像失真尽可能小。
基于SIFT算法则能够对图像旋转、尺度缩放、亮度变化保持不变性,对视角变化,仿射变换,噪声也能保持一定程度的稳定性。
本次实验运用SIFT匹配算法来提取图像的特征点,采用随机抽样一致性算法求解单应性矩阵并剔除错误的匹配对。
最后用加权平均融合法将两帧图像进行拼接。
具体过程为:首先选取具有重叠区域的两帧图像分别作为参考图像和待拼接图像,然后使用特征提取算法提取特征点,并计算特征点描述子,根据描述子的相似程度确定互相匹配的特征点对。
再根据特征点对计算出待拼接图像相对于参考图像的单应性矩阵,并运用该矩阵对待拼接图像进行变换,最后将两帧图像进行融合,得到拼接后的图像。
1.特征点检测与匹配特征点检测与匹配中的尺度空间理论的主要思想就是利用高斯核对原始图像进行尺度变换,获得图像多尺度下的尺度空间表示序列,再对这些序列就行尺度空间的特征提取。
二维的高斯核定义为:G(x,y,σ)=12πσ2e−(x2+y2)2σ2⁄对于二维图像I(x,y),在不同尺度σ下的尺度空间表示I(x,y,σ)可由图像I(x,y)与高斯核的卷积得到:L(x,y,σ)=G(x,y,σ)∗I(x,y)其中,*表示在x 和 y方向上的卷积,L表示尺度空间,(x,y)代表图像I上的点。
为了提高在尺度空间检测稳定特征点的效率,可以利用高斯差值方程同原图像进行卷积来求取尺度空间极值:D(x,y,σ)=(G(x,y,kσ)−G(x,y,σ))∗I(x,y)= L(x,y,kσ)−L(x,y,σ)其中k为常数,一般取k=√2。
SIFT算法将图像金字塔引入了尺度空间,首先采用不同尺度因子的高斯核对图像进行卷积以得到图像的不同尺度空间,将这一组图像作为金字塔图像的第一阶。
接着对其中的2倍尺度图像(相对于该阶第一幅图像的2倍尺度)以2倍像素距离进行下采样来得到金字塔图像第二阶的第一幅图像,对该图像采用不同尺度因子的高斯核进行卷积,以获得金字塔图像第二阶的一组图像。
再以金字塔图像第二阶中的2倍尺度图像以2倍像素距离进行下采样来得到金字塔图像第三阶的第一幅图像,对该图像采用不同尺度因子的高斯核进行卷积,以获得金字塔图像第三阶的一组图像。
这样依次类推,从而获得了高斯金字塔图像。
每一阶相邻的高斯图像相减,就得到了高斯差分图像,即DOG图像。
对DOG尺度空间每个点与相邻尺度和相邻位置的点逐个进行比较,得到的局部极值位置即为特征点所处的位置和对应的尺度。
为了寻找尺度空间的极值点,DOG尺度空间中中间层的每个像素点都需要跟同一层的相邻8个像素点以及它上一层和下一层的9个相邻像素点总共26个相邻像素点进行比较,以确保在尺度空间和二维图像空间都检测到局部极值。
图像的高斯滤波保证了特征点不受噪声影响,DOG图像保证了特征点不受亮度差的影响,在高斯差分图像空间提取极值点保证了尺度不变性。
剔除不好特征点时,利用高斯差分算子检测到的特征点中,含有一些低对比度的特征点和不稳定的边缘特征点,需要进行剔除。
使用泰勒级数将尺度空间方程D(x,y,σ)展开:D(X)=D+∂D T∂XX+12X T∂2D∂X2X其中X=(x,y,σ)T,∂D∂X和∂2D∂X2分别为一阶和二级偏导数矩阵。
式中的一阶和二阶导数可以通过附近区域的差分近似求得,求导并令其为零得出精确的极值位置X:X=−∂2D−1∂X2∂D∂X则有D(X)=D+12∂D T ∂X如果|D(X)|≥0.03,则保留该特征点,否则就丢弃。
为了去除不稳定的边缘特征点,可以获取特征点处的Hessian矩阵,主曲率可以通过一个2×2的Hessian矩阵H求出:H=[D xx D xy D xy D yy]设α和β分别为H阵的最大特征值和最小特征值,且α=rβ,则D(x,y,σ)的主曲率与特征值的大小成正比。
令:Tr(H)=D xx+D yy=α+βDet(H)=D xx D yy−(D xy)2=αβTr(H)2 Det(H)=(α+β)2αβ=(r+1)2r若Tr(H)2Det(H)<(r+1)2r(一般取r=10),则保留该特征点,否则就丢弃。
为了实现特征点的选编不变性,可以利用特征点的主方向来实现。
(x,y)处的梯度值和方向分别为:m(x,y)=√(L(x+1,y)−L(x−1,y))2+(L(x,y+1)−L(x,y−1))2θ(x,y)=tan−1(L(x,y+1)−L(x,y−1))/ L(x+1,y)−L(x−1,y)在以特征点为中心的邻域内进行采样,并用直方图统计邻域像素的梯度方向。
梯度直方图的范围0°~360°,其中每45°一个柱,共8个柱。
梯度直方图的峰值则代表了该特征点处邻域梯度的主方向。
这样对于每一个关键点,就拥有了三个信息:位置,尺度以及方向。
接下来就是为每一个关键点建立一个特征描述符。
首先将坐标轴旋转为特征点的方向,以保证旋转不变性,接下来以特征点为中心取16×16的窗口,然后在每个4×4的图像小块上计算8个方向的梯度方向直方图,绘制每个梯度方向的累加值。
此图中一共有4×4×8=128个数据,形成一个128维的SIFT特征向量即特征描述符。
这种邻域领域方向性信息联合的思想增强了算法抗噪声的能力,同时对于含有定位误差的特征匹配也提供了较好的容错性。
此时,SIFT特征向量已经去除了尺度变化、旋转等几何变形因素的影响,再继续将特征向量的长度归一化,则可以进一步去除光照变化的影响。
提取出图像的特征点之后,就要进行特征点的匹配。
本次实验以两个特征点描述子之间的欧氏距离作为特征点匹配的相似度准则。
假设特征点p和q的特征描述子分别为Des p和Des q,则其欧氏距离定义为:d=√∑(Des p(i)−Des q(i))2i=0 (127)关键点的匹配可以采用穷举法。
以待匹配图像的特征点R i为基准,在参考<图像中搜索与其最邻近的特征点S if以及次邻近的特征点S is,若满足d(R i,S if)d(R i,S is) Threshold则认为S if与R i为匹配的特征点对。
通过对阈值的设定,可以将两帧图像中没有匹配点的特征点去掉,只留下匹配的特征点对。
实验采用MATLAB编程,分别对一组交大图书馆的图像以及一组标准库中的图像进行特征点提取与匹配,结果如下图。
2.单应性矩阵计算设原图像中一点的坐标为(x ,y ,1)T,进行变换后该点的坐标为(x ’,y ‘,1)T ,则二者之间具有以下关系:[x ′′y ′′z ′′]=[h 11h 12h 13h 21h 22h 23h 31h 32h 33][x y 1][x ′y ′1]=1z ′′[x ′′y ′′z ′′]其中H=[h 11h 12h 13h 21h 22h 23h 31h 32h 33],为单应性矩阵(homography matrix )。
通常令h 33=1来归一化矩阵,这样,待求解的矩阵参数有8个,需要4个特征点对来求解。
求解算法如下:从匹配的特征点对集S 中取出 4 对不共线的点对,坐标为{(x i , y i ),(x i ′ ,y i ′)|i=1,2,3,4}x i ′(h 31x i +h 32y i +h 33)=h 11x i +h 12y i +h 13y i ′(h 31x i +h 32y i +h 33)=h 21x i +h 22y i +h 13可得:[ x 1y 11000x 2x 3x 4y 20y 30y 40101010 000x 1y 110x 20x 30x 40y 20y 30y 4010101 −x ′1x 1−x ′1y 1 −y ′1x 1−y ′1y 1−x ′2x 2−y ′2x 2−x ′3x 3−y ′3x 3−x ′4x 4−y ′4x 4−x ′2y 2−y ′2y 2−x ′3y 3−y ′3y 3−x ′4y 4−y ′4y 4 −x 1′−y 1′−x 2′−y 2′−x 3′−y 3′−x 4′−y 4′ ] [ h 11h 12h 13h 21h 22h 23h 31h 321] =[ 00000000]即: Ah = 0对矩阵A 进行奇异值分解得A =UDV T =U (d 11⋯d 19⋮⋱⋮d 91⋯d 99)(v 11⋯v 19⋮⋱⋮v 91⋯v 99)Th =[v 19…v 99]v 99上式h 各个元素即为所求。
3.匹配点对过滤(RANSAC )由于用穷举法得到的匹配的特征点对中会存在错误的匹配,影响两幅图像之间转换矩阵的求解精度,最后影响到全景图的拼接效果。
在这里,传统的最小二乘法容易失效,需要有一种方法来剔除匹配点对集合中错误的匹配对,并根据剔除了错误匹配对后集合中剩下的匹配点对计算出精确的转换矩阵。
所以在本次实验中利用RANSAC算法来计算单应性矩阵。
随机抽样一致性算法,即RANSAC(Random Sample Consensus)算法,它是根据一组包含异常数据的样本数据集,计算出数据的数学模型参数,得到有效样本数据的算法。
该算法的主要思想是通过多次的采样求解符合样本的数学模型参数,从中选取最符合整个样本数据集合的模型作为最佳模型,而符合最佳模型的样本点认为是精确的样本点(内点),不符合最佳模型的样本点则认为是存在误差的样本点(外点)。
具体做法如下:①将待拼接图像中剩余的特征点分别通过上一步求出的单应性矩阵映射到参考图像中,然后计算映射点的位置与该匹配点对的实际位置之间的欧式距离,d=(h11x i+h12y i+h13(h31x i+h32y i+h33)−xi′)2+(h21x i+h22y i+h23(h31x i+h32y i+h33)−yi′)2若距离小于阈值T,将其加入内点集合,记下内点集合中匹配点个数c,反之则加入外点集;②重复上述过程k次;③取k次计算结果中内点数目c最大的匹配点集合作为精确的匹配对集合;④根据初步精确的匹配对集合重新计算H矩阵。
运用RANSAC算法得到的精确匹配对如下图,对比可以看出,RANSAC算法剔除了许多错误的匹配对,明显的提高了匹配精度。
(其中阈值T设定为√20)采用RANSAC算法得到的匹配特征点用单应性矩阵变换后的图像4.图像拼接在两组图像中,将第二幅作为参考图像,用所求的H矩阵将第一幅图像进行转换,图像经过配准变换之后,再经过图像融合即可完成整个图像的拼接的工作。
拼接后的图像在过渡区域会产生明显的拼接缝隙,图像融合的目的就是使配准后的图像重叠区域的像素点平滑过渡,其主要思想是采用一定的策略确定重叠区域像素点的灰度值。
