回弹计算公式-
圆管折弯回弹计算公式

圆管折弯回弹计算公式圆管折弯回弹是指在圆管弯曲加工后,材料在释放应力后会有一定程度的回弹现象。
这种回弹现象会对弯曲加工的精度产生影响,因此需要进行准确的计算和控制。
在工程实践中,可以通过一定的计算公式来预测圆管折弯回弹的情况,从而进行相应的修正和控制。
圆管折弯回弹的计算公式可以通过理论分析和实验数据得出。
一般来说,圆管折弯回弹的计算公式包括了材料的弹性模量、材料的屈服强度、圆管的直径和壁厚等因素。
下面将介绍一些常见的圆管折弯回弹计算公式。
1. 简化的计算公式。
在一些简化的情况下,可以采用以下的简化计算公式来估计圆管的折弯回弹:ΔL = R × (1 cosθ)。
其中,ΔL为圆管的折弯回弹量,R为圆管的外径,θ为圆管的弯曲角度。
这个简化的计算公式适用于一些简单的情况,但在实际工程中可能会存在一定的误差。
2. 基于材料力学性能的计算公式。
在考虑材料的力学性能的情况下,可以采用以下的计算公式来估计圆管的折弯回弹:ΔL = (E × t × R) / (2 ×σ)。
其中,ΔL为圆管的折弯回弹量,E为材料的弹性模量,t为圆管的壁厚,R为圆管的外径,σ为材料的屈服强度。
这个计算公式考虑了材料的弹性模量和屈服强度对于回弹的影响,因此在工程实践中有一定的准确性。
3. 综合考虑的计算公式。
在实际工程中,圆管的折弯回弹受到多种因素的影响,因此可以采用综合考虑的计算公式来进行预测:ΔL = (E × t × R) / (2 ×σ) × (1 + K × (R/t)^n)。
其中,ΔL为圆管的折弯回弹量,E为材料的弹性模量,t为圆管的壁厚,R为圆管的外径,σ为材料的屈服强度,K为经验系数,n为经验指数。
这个综合考虑的计算公式综合考虑了材料的力学性能和圆管的几何参数对于回弹的影响,因此在工程实践中具有一定的准确性。
在实际工程中,可以根据具体的情况选择合适的计算公式来进行圆管折弯回弹的预测。
混凝土回弹换算

混凝土回弹换算摘要:一、混凝土回弹换算概述二、混凝土回弹值与强度关系三、回弹换算公式及应用四、影响回弹换算的因素五、提高回弹换算精度的方法六、结论正文:一、混凝土回弹换算概述混凝土回弹换算是一种通过测量混凝土弹性特性来评估其强度的一种方法。
回弹换算是基于回弹锤对混凝土试块进行冲击,并通过测量回弹锤的回弹高度来推断混凝土的弹性模量和强度。
回弹换算在混凝土强度检测中具有广泛的应用,尤其在大型混凝土结构物的检测中具有重要意义。
二、混凝土回弹值与强度关系混凝土回弹值与强度之间存在一定的相关性。
通常情况下,回弹值越高,混凝土强度越高。
然而,这种相关性并非线性,而是受到多种因素的影响。
因此,在进行回弹换算时,需要考虑这些因素以提高换算的准确性。
三、回弹换算公式及应用回弹换算公式通常包括以下几个参数:回弹高度(H)、回弹能量(E)和混凝土强度(F)。
常用的回弹换算公式为:F = E / (H + β)。
其中,β为换算系数,根据试验数据确定。
回弹换算公式在实际应用中,需要根据具体情况进行调整。
例如,在施工现场检测混凝土强度时,可以先对混凝土试块进行回弹测试,然后根据回弹值和已知的强度-回弹关系曲线,推算出混凝土的强度。
四、影响回弹换算的因素1.混凝土本身的性质:混凝土强度、弹性模量、泊松比等物理性能指标对回弹换算结果有较大影响。
2.回弹锤的性能:回弹锤的质量和弹性特性会影响回弹测试的结果,从而影响回弹换算的准确性。
3.测试方法:测试过程中回弹锤的冲击速度、冲击角度和试块的尺寸等因素都会影响回弹换算结果。
五、提高回弹换算精度的方法1.选择合适的回弹换算公式和换算系数,根据试验数据进行修正。
2.优化回弹测试方法,确保测试过程的准确性。
3.结合其他无损检测方法,如超声波、雷达等,综合评估混凝土强度。
4.对回弹测试数据进行统计分析,建立强度与回弹值的关系模型,提高换算精度。
六、结论混凝土回弹换算是一种实用的混凝土强度检测方法,但在实际应用中需要注意影响回弹换算精度的因素。
弹簧自由回弹速度计算公式

弹簧自由回弹速度计算公式弹簧是一种常见的机械零件,它具有弹性,可以在受到外力作用后发生形变,并在外力消失后恢复原状。
弹簧的回弹速度是指在受到外力拉伸或压缩后,释放外力后弹簧恢复原状的速度。
弹簧的回弹速度对于许多机械设备的设计和运行都具有重要的意义。
在实际工程中,我们需要根据弹簧的材料和尺寸参数来计算其回弹速度,以保证设备的正常运行和安全性。
本文将介绍弹簧自由回弹速度的计算公式及其应用。
弹簧的自由回弹速度计算公式如下:V = √(2 g h)。
其中,V表示弹簧的自由回弹速度,g表示重力加速度,h表示弹簧的最大形变量。
在这个公式中,重力加速度g是一个已知的常数,通常取9.8m/s^2。
弹簧的最大形变量h是指弹簧在受力时的最大形变量,可以通过实验或计算得到。
通过这个公式,我们可以很容易地计算出弹簧的自由回弹速度。
弹簧的自由回弹速度与其材料和尺寸参数有着密切的关系。
一般来说,弹簧的回弹速度与其材料的弹性模量和尺寸参数成正比。
弹性模量越大,弹簧的回弹速度就越大;弹簧的形变量越大,回弹速度也越大。
因此,在设计弹簧时,我们需要根据实际情况选择合适的材料和尺寸参数,以满足设备的要求。
弹簧的自由回弹速度在许多机械设备中都具有重要的作用。
例如,汽车的避震器中就使用了弹簧,它的回弹速度直接影响着汽车的行驶稳定性和舒适性。
另外,弹簧也广泛应用于工业生产中的各种机械设备中,如压力机、模具等。
在这些设备中,弹簧的回弹速度直接关系到设备的性能和安全性。
在实际工程中,我们可以通过计算弹簧的自由回弹速度来评估设备的性能和安全性。
如果弹簧的回弹速度过大或过小,都会对设备的运行产生不利影响。
因此,合理地计算和选择弹簧的材料和尺寸参数对于设备的设计和运行都具有重要的意义。
除了弹簧的回弹速度外,我们还需要考虑弹簧的寿命和稳定性。
在实际工程中,弹簧在长期使用过程中会发生疲劳变形,导致其性能下降甚至断裂。
因此,我们需要通过实验和计算来评估弹簧的寿命和稳定性,以保证设备的安全运行。
回弹法评定混凝土强度公式

回弹法评定混凝土强度公式
回弹法(Schmidt锤法)是一种常用于评定混凝土强度的简单、快捷、经济的实测方法。
该方法通过使用一支称为“Schmidt锤”的仪器来对混
凝土表面进行敲击,然后根据回弹度来评定混凝土的强度。
回弹法评定混
凝土强度的公式可以是:
强度=回弹值×施工基准回弹值/表格回弹值
其中,回弹值是敲击混凝土表面后,Schmidt锤的回弹高度;施工基
准回弹值是通过在施工前对强度已知的标准混凝土进行测试得到的回弹高度;表格回弹值是通过查阅标准回弹表或其他相关手册得到的回弹高度。
在使用回弹法评定混凝土强度时,需要注意以下几点:
1.根据实际情况确定回弹点的位置:回弹值的准确性受到混凝土表面
质量和回弹点位置的影响。
在混凝土表面有明显裂缝或不均匀的情况下,
选择回弹点需要慎重。
2.根据实际情况选择测试位置:混凝土强度可能存在空间变化,因此
选择测试位置应该根据实际情况进行合理的划分。
3.根据不同结构部位调整评定结果:不同部位的混凝土可能受到不同
的荷载和环境影响,所以在使用回弹法进行评定时,应该根据不同的结构
部位调整评定结果的依据。
4.在使用公式进行计算时,需要结合实际情况适当调整基准回弹值和
表格回弹值,以提高评定的准确性。
总而言之,回弹法评定混凝土强度的公式是一种经验公式,用于快速、简单地估计混凝土的强度。
但需要注意的是,仅凭回弹法得到的评定结果
不能完全代表混凝土的实际强度,对于有严格强度要求的工程项目,还需要进行其他更加准确的检测方法。
弯曲回弹计算公式探讨

弯曲回弹计算公式探讨
1弯曲回弹计算公式
弯曲回弹属于结构力学中一类常见的力学问题,是指在弯曲加载下,杆件经过一个形变后,杆件去除外力后,会出现反弹的现象,必须对反弹量进行计算才能够预测杆件在外力消除之后的变形量和安全性。
传统的弯曲回弹计算公式为:
冲量=f×l/E
其中,f为弯矩,l为杆件的总长,E为材料的弹性模量。
2弯曲复合回弹计算公式
传统的弯曲回弹计算公式只能求出弯曲的最大反弹量,然而现实中实际的杆件以及模型杆件都不可能是完全弯曲的,所以传统的公式在实际应用中并不能反映出杆件真实的状态,而弯曲复合回弹计算公式就是为了解决这一问题而提出的,其计算公式为:
冲量=f×l/E−f×l×D/(2EI)
其中,D为杆件的重心距离,I为杆件的抗弯抗弯矩系数。
3计算步骤
1.计算杆件的弹性模量E
2.计算杆件的弯矩f、总长l以及抗弯抗弯矩系数I
3.计算杆件的重心距离D
4.计算弯曲回弹或者弯曲复合回弹的冲量
4使用场景
弯曲回弹计算公式最主要的应用是结构力学中,比如当结构分析杆件载入转移矩现象时,必须进行弯曲复合回弹计算来确定结构安全性,这样才能够准确估算结构的变形量。
另外,弯曲回弹的计算公式在机械、机电、气动等行业中也有着广泛的应用。
回弹值计算(一)

回弹值计算(一)回弹值(Rebound Value)计算是衡量材料反弹能力的重要指标,也是评价物料耐久性的一种方法。
在现代科技领域中,回弹值计算得到广泛应用,如汽车制造、建筑工程、医疗设备制造和运动器材等。
本文将分析回弹值的概念、相关计算方法和实际应用。
一、回弹值的概念回弹值是指物料受到外力作用后,恢复原始形态的程度。
其定义为所测得的反弹高度与落下高度之比。
一般计算回弹值的仪器为回弹仪或静力回弹仪。
二、回弹值计算方法1. 图示法即根据已知的质量、高度和反弹高度,利用泰坦公式(也称重力势能转化公式)进行计算。
公式为:h’/h = (√(2gh)/√(2gh+h’v))^2其中,h’为反弹高度,h为落下高度,g为重力常数,v为回弹体重量。
2. 数值法采用数据统计的方法进行计算,将多组反弹高度和落下高度数据带入计算公式求平均值。
常用的计算公式如下:RV=(ΣHi/ΣDi)×100%其中,RV为回弹值,Hi为第i次反弹高度,Di为第i次落下高度。
三、回弹值的实际应用回弹值的测量在各个行业中都有广泛的应用。
以下是回弹值密切相关的领域及其应用:1. 汽车制造回弹值被运用在汽车座椅、毯地、挡泥板、防滑垫等零部件的生产中,以确保该部件在冲击后能够恢复到原始状态。
2. 建筑工程在地震工程和建筑物抗震设计方面,回弹值可以用来测量各种材料的振动特性,并考虑到材料本身的回弹性。
3. 医疗设备制造回弹值在医疗领域的应用很多,如测量床垫和手术敷料的弹性,配合更好地设计支架、假体和其他医疗器械。
4. 运动器材回弹值在体育器材领域中被广泛使用,如测量运动鞋的舒适性、保护性和耐用性,以提高运动员的安全性和运动享受度。
总之,回弹值计算是评估材料抗冲击性、耐久性和弹性的重要方法。
它在不同的领域中得到了广泛的应用,为各种材料的研发和生产提供了可靠的技术支持。
混凝土强度回弹计算方法excel

混凝土强度回弹计算方法excel
混凝土强度回弹计算方法excel,是一种常用的混凝土强度计算方法,通过excel表格进行计算,可以快速准确地得出混凝土的强度。
下面介绍混凝土强度回弹计算方法excel的具体步骤。
1. 准备数据
首先,需要准备混凝土的相关数据,包括水泥强度、水灰比、骨料种类和混凝土的龄期等。
这些数据可以通过实验或测量得到。
2. 输入数据
接下来,将准备好的数据输入到excel表格中,包括水泥强度、水灰比、骨料种类和混凝土的龄期等。
3. 计算回弹值
根据混凝土的龄期和骨料种类,计算出回弹值。
回弹值的计算公式为:Rc = 0.075F + 0.75G + 0.35S - 2.65,其中Rc为回弹值,F 为水泥强度(MPa),G为水灰比,S为骨料强度(MPa)。
4. 计算混凝土强度
根据混凝土的龄期、水泥强度、水灰比和骨料强度,计算出混凝土的强度。
混凝土强度的计算公式为:f = 1.42*Rc/S - 0.075,其中f为混凝土强度(MPa),Rc为回弹值,S为骨料强度(MPa)。
5. 输出结果
最后,将计算出的混凝土强度输出到excel表格中,即可得到混
凝土强度的计算结果。
回弹计算公式
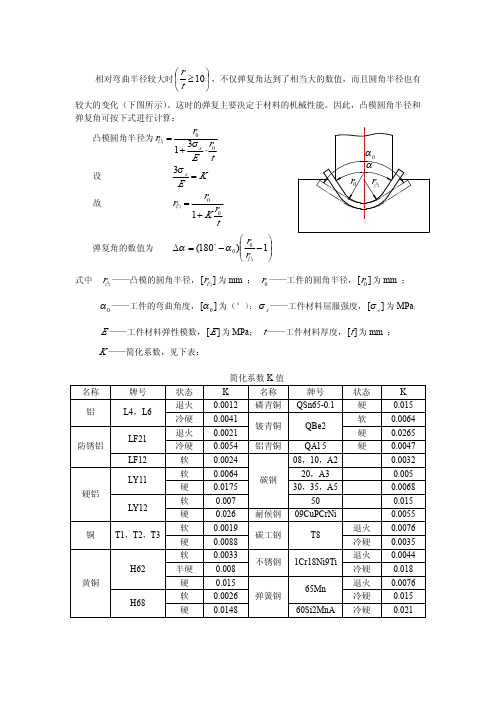
名称 磷青铜 铍青铜 铝青铜
牌号 QSn65-0.1 QBe2 QAl 5 08,10,A2 20,A3 30,35,A5 50 09CuPCrNi T8 1Cr18Ni9Ti 65Mn 60Si2MnA
状态 硬 软 硬 硬
K 0.015 0.0064 0.0265 0.0047 0.0032 0.005 0.0068 0.015 0.0055
相对弯曲半径较大时
r 10 ,不仅弹复角达到了相当大的数值,而且圆角半径也有 t
较大的变化(下图所示) 。这时的弹复主要决定于材料的机械性能。因此,凸模圆角半径和 弹复角可按下式进行计算: 凸模圆角半径为 r凸
设 故
r0 3 r 1 s 0 E t 3 s K E r0 r凸 r 1 K 0 t
r0 (180 0 ) r 1 凸
0 r0 r凸
弹复角的数值为
式中
r凸 ——凸模的圆角半径, [r凸 ] 为 mm ; r0 ——工件的圆角半径, [r0 ] 为 mm ; 0 ——工件的弯曲角度, [ 0 ] 为(°) ; s ——工件材料屈服强度, [ s ] 为 MPa; E ——工件材料弹性模数, [ E ] 为 MPa; t ——工件材料厚度, [t ] 为 mm ; K ——简化系数,见下表:
简化系数 K 值
名称 铝
牌号 L4,L6 LF21 LF12 LY11
状态 退火 冷硬 退火 冷硬 软 软 硬 软 硬 软 硬 软 半硬 硬 软 硬
K 0.0012 0.0041 0.0021 0.0054 0.0024 0.0064 0.0175 0.007 0.026 0.0019 0.0088 0.0033 0.008 0.015 0.0026 0.0148
回弹内插法的计算公式是

回弹内插法的计算公式是回弹内插法是一种常用的计算方法,主要用于确定材料的弹性模量。
在工程领域中,弹性模量是一个非常重要的参数,它可以帮助工程师们更好地了解材料的力学性能,从而为工程设计和材料选择提供参考依据。
回弹内插法是一种简单而有效的计算方法,下面我们将详细介绍回弹内插法的计算公式及其应用。
回弹内插法的计算公式如下:\[E = \frac{4L^3}{\pi d^2D}\]其中,E代表材料的弹性模量,L代表悬臂梁的长度,d代表悬臂梁的直径,D代表悬臂梁的挠度。
回弹内插法的计算步骤如下:1. 首先,需要准备一根悬臂梁,测量其长度(L)和直径(d)。
2. 然后,将悬臂梁放置在一个水平的支撑上,施加一个垂直于悬臂梁末端的力,使其产生一个小的挠度(D)。
3. 测量悬臂梁在受力后的挠度(D)。
4. 将测得的数据代入回弹内插法的计算公式中,即可得到材料的弹性模量(E)。
回弹内插法的原理是利用悬臂梁在受力后产生的挠度来计算材料的弹性模量。
根据悬臂梁的力学原理,可以推导出回弹内插法的计算公式。
通过测量悬臂梁的长度、直径和挠度,再代入计算公式中,就可以得到材料的弹性模量。
回弹内插法的优点是简单易行,不需要复杂的仪器设备,只需一根悬臂梁和简单的测量工具即可进行实验。
因此,回弹内插法在工程领域中得到了广泛的应用。
除了计算材料的弹性模量外,回弹内插法还可以用于材料的硬度测试。
在实际工程中,硬度测试是一项非常重要的工作,它可以帮助工程师们评估材料的耐磨性和耐久性。
利用回弹内插法进行硬度测试时,只需要将悬臂梁的长度、直径和挠度代入计算公式中,就可以得到材料的硬度值。
需要注意的是,回弹内插法在应用时需要考虑一些因素的影响。
例如,悬臂梁的材料和制造工艺会对实验结果产生影响,因此在进行实验时需要选择合适的悬臂梁,并严格控制实验条件。
此外,测量挠度时也需要注意减小误差,以保证实验结果的准确性。
总的来说,回弹内插法是一种简单而有效的计算方法,可以用于确定材料的弹性模量和硬度值。
回弹模量计算公式

回弹模量计算公式回弹模量(YoungModulus,缩写为YM)是材料力学中一个重要的参数,表征材料的弹性变形特性。
它是指当外力的大小趋于零时,材料的平衡形状和尺寸变化和外力之前线性变化的比例,也称为材料变形系数。
回弹模量是材料力学实验中测量和确定最常用的参数,它也是用来预测材料力学性能的唯一参数之一。
一般来说,回弹模量是指材料受到外力作用,在回复外力平衡状态时,其延伸量与外力之比例关系,用回弹模量YM表示。
它等于有限的变形和有限的外力之间的比值,可用下式表示:YM =σ/ε其中,σ表示外力的大小,ε表示变形的大小。
位移的大小根据变形量的大小计算,其计算公式为:Δs =s * L其中,εs表示变形量在恢复平衡状态时的变化量,L表示受力前的原始长度。
可以根据上面的公式得出回弹模量的计算公式:YM =σ*L/Δs为精确测定回弹模量,需要进行多遍试验,以确定外力σ和变形量εs之间的关系,然后根据试验结果,按以上公式算出材料的回弹模量。
实际测量过程中,应尽量确保外动力作用的方向与材料的轴向平行,以保证测量结果的准确性。
此外,实验中要注意材料的温度,并定期检查机械设备的工作情况,以确保实验结果的准确性。
回弹模量是材料力学中重要的参数,它能够反映材料弹性性能的好坏,也可以用来衡量材料的抗变形性能。
因此,广泛应用于材料力学研究、机械设计分析等领域,对于材料的实用性能和利用性有着重要意义。
回弹模量是比较容易测量的参数,但其准确性却不容小视。
正确的实验操作、准确的测量结果、合理的计算公式,都是测定回弹模量的关键所在。
因此,测量实验前应仔细准备,在实验测量过程中应更加谨慎,以期在测量中取得满意的结果。
回弹内插法的计算公式

回弹内插法的计算公式在工程和科学领域中,回弹内插法是一种常用的数值计算方法,用于估计两个已知数据点之间的数值。
这种方法通常用于插值温度、压力、密度等连续变量的数据。
回弹内插法的计算公式可以用来估计两个已知数据点之间的数值,从而帮助工程师和科学家们进行准确的数据分析和预测。
回弹内插法的计算公式可以表示为:\[ y = y_1 + \frac{x-x_1}{x_2-x_1} \times (y_2-y_1) \]在这个公式中,\( x_1 \) 和 \( x_2 \) 是已知数据点的自变量值,\( y_1 \) 和\( y_2 \) 是对应的因变量值,\( x \) 是要估计的自变量值,\( y \) 是通过回弹内插法计算得到的因变量值。
回弹内插法的计算公式基于线性插值的原理,即假设两个已知数据点之间的变化是线性的。
这种方法的优点是简单易懂,计算速度快,适用于连续变量的数据。
但是需要注意的是,回弹内插法只能用于已知数据点之间的估计,不能用于超出已知数据范围的预测。
下面我们通过一个例子来说明回弹内插法的计算过程。
假设有以下已知数据点:\( (x_1, y_1) = (2, 5) \)。
\( (x_2, y_2) = (4, 10) \)。
现在我们要估计当 \( x = 3 \) 时的 \( y \) 值。
根据回弹内插法的计算公式,我们可以得到:\[ y = 5 + \frac{3-2}{4-2} \times (10-5) \]\[ y = 5 + \frac{1}{2} \times 5 \]\[ y = 5 + 2.5 \]\[ y = 7.5 \]因此,当 \( x = 3 \) 时,根据回弹内插法的计算公式,我们估计得到的 \( y \) 值为 7.5。
通过这个例子,我们可以看到回弹内插法的计算公式是如何应用于估计两个已知数据点之间的数值的。
这种方法可以帮助工程师和科学家们在实际工作中进行准确的数据分析和预测。
回弹强度计算公式

回弹强度计算公式回弹强度是材料力学性能中的一个重要指标,它在工程领域和科学研究中都有着广泛的应用。
那咱们就来好好聊聊回弹强度计算公式这回事儿。
还记得我之前参与过的一个建筑项目,那是为一座小型图书馆进行结构评估。
在这个过程中,回弹强度的计算就成了关键的一环。
当时,我们的团队在现场拿着回弹仪,对混凝土柱子进行检测。
那回弹仪“啪啪”的声音,就好像在诉说着这些柱子的“秘密”。
回弹强度的计算公式看起来可能有点复杂,但其实只要咱们把它拆解开,一步步来,也就不难理解啦。
常见的回弹强度计算公式一般是基于回弹值、碳化深度以及一些修正系数来确定的。
比如说,对于混凝土构件,回弹强度 R 可以通过下面这个公式来计算:R = A × N - B × L在这个公式中,A 和 B 是根据试验得出的系数,N 是回弹值,L 是碳化深度。
这里的回弹值 N 可不是随便测一下就行的,得按照规范的操作方法,在构件表面均匀分布多个测点,然后取平均值。
就像我们在那个图书馆项目中,每个柱子上都测了至少 10 个点,力求数据准确。
而碳化深度 L 的测量也有讲究。
得先用酚酞试剂在构件表面喷一下,那些没变色的部分就是碳化区,然后用专门的工具测量深度。
再说修正系数,这可就更复杂啦。
它要考虑混凝土表面的平整度、是否潮湿、测试角度等等因素。
比如说,如果混凝土表面不平整,那就要乘以一个小于 1 的修正系数,来修正回弹值。
给您举个例子吧,假如我们测到的回弹值 N 是 35,碳化深度 L 是2.0mm,A 取值 0.025,B 取值 0.001。
那通过公式计算:R = 0.025 × 35 - 0.001 × 2.0 = 0.875 - 0.002 = 0.873(MPa)这只是一个非常简单的例子,实际情况中,计算可要复杂得多呢。
在实际应用中,回弹强度计算公式的准确性还受到很多因素的影响。
比如说,回弹仪的精度和校准情况,如果回弹仪本身就不准,那算出来的结果肯定不靠谱。
【模具知识】冲压模具回弹及其回弹计算公式

【模具知识】冲压模具回弹及其回弹计算公式回弹,设计师都会遇到,而且无法避免,只能想办法补偿或者降低影响。
那什么是回弹呢?金属材料在塑性弯曲时总是伴随著弹性变形,因此当弯矩去掉之后,弯曲件的弯曲半径变得与模具尺寸不一致,这种现象称为回弹。
而回弹的大小通常用角度回弹量∆a和曲率回弹量∆q来表示。
一.影响回弹的因素:1.材料的力学性能:回弹角的大小与材料的屈服点S与a正比,与弹性模数E 成反比.2.相对弯曲半径r/t愈大,则表示变形程度愈小,回弹愈大.3.弯曲中心角a:a愈大,则∆a愈大4.弯曲方式,校正弯曲的回弹角小于自由弯曲的回弹角.5.制件形状:u形状回弹角小于v形件,复杂的弯曲件, 一次弯曲成形,弯角数量越多,回弹量就越小.6.模具间隙:u形弯曲模的凸.凹每侧间隙z/h越大,则回弹与越大,z/2<t时,可以发生负回弹.二.回弹的计算由于影响回弹角的因素较多,因此要在理输上计算回弹角是有困难的,在模具设计时通常按实验总结的数据不修正,或经试衝后再修正.(一).当r/t<5时,直接放角度回弹即可不必缩R角.1).当t≤0.3,⍬=90º时,如图所示,分两次折弯且第一次折弯时,折弯点外移0.1~0.22).当t>0.3, ⍬=90º时,所图所示,分两次折弯,第一次折弯时,折弯点不用外移3). ⍬=90º时,一般一次成形,根据材质,料厚的不同,提供以下数据供参考.(4)U二)U当R/t≥5时,曲率回弹量比较大,需缩R角,其计算公式见R角回弹计算设计规范,在模具设计时,弯曲凸模圆角半径,R一般要比计算值R凸小,然后再加一步整形即可.产品回弹比较复杂,即使是相同材质的情况下,自身材料不同厚度、折弯角度、折弯内R都会对回弹产生很大影响。
不同材质就更不用说了。
因此,回弹并非一个公式即可完全解决,需要我们在理论的基础上进行实践调试,以得到最终合格产品。
回弹强度计算范文

回弹强度计算范文回弹强度是指材料在一定形变条件下的抗弹性变形能力,是衡量材料弹性的一种指标。
对于不同的材料来说,回弹强度的计算方法也有所不同。
本文将通过介绍金属材料和聚合物材料两种常见材料的回弹强度计算方法,来探讨回弹强度的计算原理。
对于金属材料来说,回弹强度的计算方法一般采用弹性回弹率。
弹性回弹率是指材料在经历一定形变后,恢复到初始形态的能力。
弹性回弹率的计算公式如下:弹性回弹率=(回弹高度/形变高度)×100%弹性回弹率越高,材料的回弹强度越大。
例如,假设有一块金属材料经受一定程度的压缩形变后,回弹高度为20mm,形变高度为100mm,则其弹性回弹率为(20 / 100)×100% = 20%。
对于聚合物材料来说,回弹强度的计算方法一般采用恢复率。
恢复率是指材料在一定形变条件下,恢复到初始状态的程度。
恢复率的计算公式如下:恢复率=(恢复高度/形变高度)×100%恢复率越高,材料的回弹强度越大。
例如,假设有一块聚合物材料经受一定程度的压缩形变后,恢复高度为15mm,形变高度为80mm,则其恢复率为(15 / 80)×100% = 18.75%。
除了以上的计算方法,还有一种常用的计算回弹强度的方法是利用回弹试验。
回弹试验是通过将材料进行一定程度的压缩形变后,测量其回弹高度或恢复高度来判断回弹强度的大小。
通过回弹试验可以快速准确地评估材料的回弹性能,广泛应用于材料科学和工程领域。
回弹强度的计算对于材料的使用和生产具有重要的意义。
通过对材料的回弹强度进行计算和评估,可以选择合适的材料来满足不同的工程需求。
在实际应用中,根据工程需求和材料特性,可以采用不同的回弹强度计算方法,并结合实验数据进行验证,以获得更加准确的结果。
总结起来,回弹强度的计算方法主要有弹性回弹率和恢复率两种。
弹性回弹率主要适用于金属材料,恢复率主要适用于聚合物材料。
此外,还可以通过回弹试验来评估材料的回弹性能。
管材冷弯回弹的计算公式

管材冷弯回弹的计算公式管材冷弯回弹的计算公式管材冷弯是制作弯头等曲线形状时常用的加工方法,通常采用机械压力把管材弯曲成所需的角度,达到所需的形状,该方法加工的管弯角度精度高、形状美观,但是会存在一个问题,就是管材冷弯后会出现回弹现象,导致制作出的曲线弯度和所期望的值误差较大。
因此,为了提高管材冷弯的精度,必须对其回弹效应进行分析和计算。
一、管材冷弯回弹的原理管材冷弯回弹的原理是由于管材在受到力的作用下,其内部发生了塑性变形,分子结构发生了改变,结晶颗粒变小,形成了残余应力,使管材在脱离力后,内部残余应力的作用下产生了回弹形变。
二、管材冷弯回弹的计算方法1、基本原理基于管材受到力的变形原理和材料力学基本公式,管材冷弯回弹的计算可以使用以下公式:ΔL = L×B×S/(2×R×E)其中:ΔL:回弹长度,即管材在力作用下发生的变形长度。
L:管材的原始长度。
B:弯曲角度,单位为角度。
S:钢管的剪切模量,单位为GPa。
R:管材弯曲半径,单位为毫米。
E:弹性模量,单位为GPa。
2、公式应用注意事项(1)公式只适合于弯曲角度小于90度的管材。
(2)公式中的剪切模量和弹性模量必须根据具体的材质型号确定,即硬度系数需要实际测试才能获得较好的效果。
(3)公式只考虑了单向弯曲回弹的问题,对于双向弯曲管材的设计,应进行独立分析。
三、例子应用比如一根钢管长度为6m,弯曲半径为300mm,弯曲角度为60度,材质为Q235的钢质管材,其弯曲回弹计算公式如下:ΔL = L×B×S/(2×R×E)ΔL = 6000×60×0.104/(2×300×2.06×10^5)ΔL= 4.17mm则该长度为6米,弯曲半径为300mm的60度钢质管材经过冷弯后会产生4.17毫米的回弹效应。
四、结论管材冷弯回弹的问题需要在设计过程中进行计算,采用上述公式可以计算出钢管的回弹量。
回弹值计算公式

回弹值计算公式常用的回弹值计算公式是弹性回弹比公式和回弹能量计算公式。
1.弹性回弹比公式:弹性回弹比定义为被测物体回弹高度与其初次下落高度之比。
公式如下:回弹比=(回弹高度/下落高度)×100%弹性回弹比公式适用于测量较小尺寸样品的回弹性能,例如橡胶小球、高尔夫球等。
这种方法简单易行,但只适用于较小物体,不能很好地描述回弹性能的差异。
2.回弹能量计算公式:回弹能量是一种衡量材料回弹性能的指标。
常用的回弹能量计算公式如下:回弹能量=(质量×重力加速度×下落高度)-(质量×重力加速度×回弹高度)回弹能量计算公式适用于测量较大尺寸样品的回弹性能,如篮球、足球等。
这种方法能够更准确地描述材料的回弹性能,但需要更复杂的实验设备和测量方法。
需要注意的是,回弹值计算公式只能作为参考,实际回弹性能还受到多种因素的影响。
例如材料的化学成分、物理结构、温度等都会对回弹性能产生影响。
最近,一种全新版的回弹值计算公式被提出,旨在综合考虑材料的力学性能和物理特性。
该公式基于材料的力学参数(如弹性模量、泊松比)、材料的物理特性(如密度)以及材料的几何形状(如厚度、面积)等因素。
该公式的表达式为:回弹值= (2 × 回弹能量× sqrt(π) × sqrt(厚度) × sqrt(面积) × sqrt(弹性模量) × sqrt(1-泊松比²)) / (密度× 下落高度²)这个全新版的回弹值计算公式考虑了更多因素的综合影响,使得回弹性能的评估更为准确。
同时,该公式也对材料的几何形状进行了考虑,更适用于不同形状和尺寸的材料。
需要注意的是,这个全新版的回弹值计算公式仍然需要根据具体的实验条件和测量数据进行确定。
同时,该公式也只适用于弹性材料的回弹性能评估,不能适用于其他性质的材料。
对于不同类型的材料,需要采用相应的测试方法和评估指标。
excel在砼回弹中公式计算

excel在砼回弹中公式计算在砼施工中,回弹是一个重要的指标,用于评估混凝土的质量和强度。
回弹指的是在混凝土浇筑后,用回弹锤对混凝土表面进行敲击后,测量回弹锤弹起的高度。
根据回弹锤的回弹高度,可以间接地推测出混凝土的抗压强度。
在砼回弹中,有一个常用的计算公式,即斯密特回弹公式(Schmidt Rebound Formula)。
这个公式是根据回弹高度和混凝土抗压强度之间的经验关系得出的,可以用来预测混凝土的抗压强度。
斯密特回弹公式的表达式如下:R = 100 × (h / H)其中,R是混凝土的回弹指数,h是回弹锤的回弹高度,H是回弹锤的自由落体高度。
根据斯密特回弹公式,可以通过测量回弹锤的回弹高度,计算出混凝土的回弹指数。
然后,利用回弹指数与混凝土抗压强度之间的经验关系,可以估计出混凝土的抗压强度。
不过需要注意的是,斯密特回弹公式是经验公式,其结果仅供参考,不能完全准确地预测混凝土的抗压强度。
在实际工程中,还需要结合其他因素进行综合评估。
除了斯密特回弹公式,还有其他一些回弹公式和方法,用于计算混凝土的抗压强度。
比如,斯科特回弹公式(Schot Rebound Formula)、奥尔松回弹公式(Olson Rebound Formula)等。
这些公式在一定程度上可以提供参考,但也存在一定的局限性。
在实际应用中,除了回弹测定法,还可以采用其他方法来评估混凝土的质量和强度。
比如,超声波检测法、钻孔取芯法等。
这些方法可以提供更为准确和直接的测量结果,但也需要专业设备和技术支持。
在砼回弹中,回弹公式是一种常用的计算方法,用于评估混凝土的抗压强度。
斯密特回弹公式是其中一种常用的公式,可以通过测量回弹锤的回弹高度,计算出混凝土的回弹指数。
然后,利用回弹指数与混凝土抗压强度之间的经验关系,可以估计出混凝土的抗压强度。
不过需要注意的是,回弹公式仅供参考,实际评估时还需结合其他因素和方法。
最后,为了确保混凝土质量和工程安全,建议在混凝土施工中,还应采用其他更为准确和直接的评估方法。
