基于供应中断风险的模糊多目标订单分配模型
基于改进模糊TOPSIS定权的供应商多选择目标规划方法

基于改进模糊TOPSIS定权的供应商多选择目标规划方法作者:郑皎章恒全焦俊来源:《软件导刊》2017年第11期摘要:针对多供应商选择规划模型中规划目标值设定的模糊性、不确定性以及目标间可能存在的冲突性,建立了基于多选择目标规划的多供应商选择规划模型。
同时考虑供应商评价指标间的相互影响关系对供应商综合表现水平的影响,采用模糊TOPSIS对供应商进行综合评价并定权,进而在MCGP模型中构建总采购价值目标。
采用相对偏好关系分析对三角模糊数进行去模糊化和距离计算,从而得到改进的模糊TOPSIS方法,有效减少了语义量化过程中评价信息的损失。
最后以实例验证了所提方法的可行性和有效性。
关键词关键词:供应商选择;多选择目标规划;TOPSIS;相对偏好关系分析DOIDOI:10.11907/rjdk.172756中图分类号:TP306文献标识码:A文章编号文章编号:16727800(2017)0110016060引言供应商选择是供应链管理的重要内容之一,可分为单供应商选择和多供应商选择两类。
在供应链全球化和敏捷化发展趋势下,多供应商选择问题成为研究的重点,该问题不仅需要选择供应商,而且需要确定各供应商的采购量。
合理选择供应商和分配采购量将直接关系到企业能否快速、低价和高质量地满足客户的产品服务需求并提高自身的核心竞争力。
然而在实际采购决策中,由于企业需求和供应环节的诸多不确定性因素以及决策者的主观偏好等问题,很难精确地确定出产品的需求量。
文献[1]针对供应链中零部件供应和产品需求的不确定性,构建了通用零部件供应商与多个专用零部件供应商之间的横向协同供应机制。
文献[2]研究了随机需求情况下三级物流服务供应链订单任务分配的问题。
目标规划(Goal Programming,GP)是解决多供应商选择问题的最主要方法,同时考虑到供应商选择的多目标性,许多研究将模糊多目标规划用于多供应商选择。
文献[3]提出了两阶段的供应商评价和订单分配方法,首先采用模糊全乘比例分析多目标优化方法对供应商进行主观性初选,然后再由模糊目标规划确定已选供货商采购量。
权威期刊《管理科学学报》杂志

刊名:管理科学学报Journal of Management Sciences in China主办:国家自然科学基金委员会管理科学部周期:月刊出版地:天津市语种:中文;开本:大16开ISSN:1007-9807CN:12-1275/G3邮发代号:6-89复合影响因子:2.876综合影响因子:1.538历史沿革:现用刊名:管理科学学报曾用刊名:决策与决策支持系统创刊时间:1992该刊被以下数据库收录:JST 日本科学技术振兴机构数据库(日)(2013)CSSCI 中文社会科学引文索引(2014—2015)来源期刊(含扩展版)核心期刊:中文核心期刊(2011)中文核心期刊(2008)中文核心期刊(2004)期刊荣誉:Caj-cd规范获奖期刊《管理科学学报》杂志期刊简介《管理科学学报》杂志是由国家新闻出版总署正式批准,由国家自然科学基金委员会管理科学部主办、面向国内外公开发行的专业学术期刊,具有正规的双刊号,其国内统一刊号:C N12-1275/G3,国际刊号:ISSN1007-9807。
本刊自1992年创刊以来,主要刊载有关管理科学的基础理论、方法与应用等学术性研究成果,以及已取得社会或经济效益的应用性研究成果,是我国管理科学领域具有权威性的一级学术刊物。
本刊的读者对象主要为从事管理科学研究和实践的管理科学工作者、管理工程技术人员,各行业、部门及企业管理人员,管理科学与经济管理院校师生等。
《管理科学学报》杂志期刊栏目设置本刊主要栏目:专论、综述、应用、专题、研究论文、研究简报、学术动态等。
论文快速发表绿色通道—期刊之家网发表流程:收稿---稿件初审---商定期刊---杂志社审稿---办理定金---修改定稿---确认---付余款---杂志社发采稿通知---发表见刊---接收期刊样册---知网收录论文刊发时间:从收到论文版面费起3-4个月(特殊情况除外),针对需要快速发表的作者提供绿色通道服务。
本站声明:期刊之家网与多家医学期刊结成了学术联盟,如果您有发表中国科技论文统计源期刊(中国科技核心期刊)、中文核心期刊、SCI收录期刊的需求,以及对于需要论文发票的作者可以与我们联系1、学术期刊论文发表时间安排等相关咨询联系刘编辑Q:1269292199或Q:26407343 87;2、不违反宪法和法律,不损害公共利益。
模糊多目标订单分配模型

负 的决 策变 量 ; i , , 为 给定 分 布 函数 的 b,一1 …
独立连 续随 机变量 ; i a 为 ~ 约束 条 件第 t 矗 ~
决 策变量 的相关 系数 和 口 是 i ~砌 约束 条件 满 足
的 概 率 水 平 ,< ≤ , 1 … , 0 i一 , m.
国家 自然 科 学 基 金 委 员会 创 新 群 体 项 目资 助 ( 准 号 :0 2 0 1 批 72 1 0 )
第 3 期
P /●\ r
潘
伟 , : 糊 多 目标 订单 分 配 模 型 等 模
P( 口 ≥b ∑ i , 优 () r∑ i≥ ) , 一1…, 7
Vo134 N o 3 . .
J n 0 0 u e2 1
模糊 多 目标订 单 分 配模 型 *
潘 伟 余 乐 安。 张金 隆 汪寿 阳。 ’
武汉 407) 3 0 4 北 京 1 O 9 ) 0 1 0 ( 汉大 学 经 济 与 管 理 学 院 ” 武 汉 武 4 0 7 ) ( 中 科技 大学 管理 学 院 3 0 2 华
在该 模型 中 , 符号 ~表示模 糊环 境 , 目标 函 在
数和 约束条 件 中的符 号 乏 表 示 大于 或者 等 于 , 相
反焉表 示小 于或者 等于 .
一
般 形式 的模糊 多 目标订单分 配模 型可 以表
_( 厂 ) 厂( ) P f ,d 一 1, , … k ,P一 志+ 1 … , , q () 4 () 5
足 ; a n发 展 了一 个 多 目标 线性订 单 分配模 型 Bl a ( MI P , MO L ) 该模 型 中供应商提供价格 折扣给采 购 者, 以鼓励 采购者下 大订单口 ;A d 构建 一个 线 mia 性模糊多 目标 供应 商选 择模 型 , 虑成 本 、 量 和 考 质 服务 3 目标 , 目标权 重提前给定_ . 个 且 4 ] 考虑到订 单分配 问题 自身 的特点及 目前研 究 方法 中存 在 的不足 , 文 假 设 市场 需求 是 一 个 随 本 机变量 , 确定线 性 的订 单分 配模型. 扩展 了模糊 其 多 目标线性 供应 商 选 择模 型 , 约束 条 件从 确 定 将 扩 展为 随机变量 , 如市 场需求 等.
供应链环境下库存的模糊多目标优化策略

供应链环境下库存的模糊多目标优化策略
田进凤Tian Jinfeng
【摘要】摘要:由于供应链中产品订货提前期的不确定性以及决策者对目标偏好和产品价格的模糊性,本文讨论了多级供应链库存控制的多个不可公度的模糊多目标决策问题,采用模糊数来描述产品市场价格和目标权重的模糊性,并利用交互式多目标线形加权优化算法对模型进行了分析和求解,从而使企业和供应链在库存管理方面获得双赢。
【期刊名称】价值工程
【年(卷),期】2010(029)014
【总页数】3
【关键词】供应链;库存控制;模糊偏好
0引言
随着社会经济发展的深度与广度的不断加大,企业管理问题日益复杂,各种因素相互交错,供应链管理系统内参数、变量预测模糊性十分明显。
因此,模糊理论工具在库存控制和供应链管理中的应用受到广泛关注。
Jayanta KUmar Dey等人给出了需求、提前期和库存成本均不确定的供应链库存模型,并且采用了人机交互方法最小化成本得到ParetO最优解的库存政策[l]o Cheng- Liang Chen和Wen-Cheng Lee提出了一种多产品、多阶段和多周期的计划模型,解决了具有不确定市场需求和产品价格的多级供应链的多个不可公度的目标[2]。
代颖和马祖军等研究了模糊需求环境下的连续盘点(Qj)库存模型[3]o朱新元和钟根元等人针对市场需求的不确定性,引入了模糊数学工具对需求不确定的二级供应链库存协调
问题进行了研究Z得到了供应链成员企业在面。
供应中断背景下航空物流服务供应链鲁棒优化

供应中断背景下航空物流服务供应链鲁棒优化作者:***来源:《物流技术》2021年第12期[摘要]基于供应中断的特殊背景,综合考虑由货运代理企业、主要航空物流企业和备用航空物流企业组成的多级、多服务产品航空物流服务供应链,利用区间分析法表达服务产品销售价格的不确定性,并在此基础上建立航空物流服务供应链鲁棒多目标优化模型,并对该模型进行了求解与检验。
结合数值算例结果,表明该模型能够在供应中断背景下,同时满足货运代理企业、主要航空物流企业和备用航空物流企业利润最大化的目标,对航空物流服务供应链进行了有效优化。
[关键词]供应中断;航空物流服务供应链;区间分析法;鲁棒优化[中图分类号]F274;F560.8[文献标识码]A[文章编号]1005-152X(2021)12-0106-06Robust Optimization of Aviation Logistics Service Supply Chain during Supply InterruptionLIU Wenjun(School of Logistics Engineering,Wuhan University of Technology,Wuhan 430063,China)Abstract:Under the special background of supply failure,the paper comprehensively considered the multi- level,multi- service/ product aviation logistics service supply chain composed of freight forwarders,major aviation logistics enterprises and backup aviation logistics enterprises,and used interval analysis to express the uncertainty in service/product sales price. On such basis,the paper established a robust multi- objective optimization model of the aviation logistics service supply chain,then solved and verified it. Combined with the result of a numerical example,it was shown that said model could maximize the profit of the freight forwarders,major aviation logistics enterprises and backup aviation logistics enterprises in event of supply failure,and effectively optimize the aviation logistics service supply chain.Keywords:supply disruption;aviation logistics service supply chain;interval analysis;robust optimization0引言经济全球化的大趋势营造了良好的开放环境,也为航空物流服务供应链的发展带来了巨大的机遇,如何实现航空物流服务供应链高效稳定发展,是摆在每一个供应链节点企业面前的首要问题[1]。
供应链中模糊多目标生产——配送计划模型及求解

供应链中模糊多目标生产——配送计划模型及求解李娜;李波【摘要】Production-distribution coordination optimization problems in supply chains have long attracted interest from both practitioners and academics. Because of the conflicting nature of the multiple objectives and the vagueness in related parameters, conventional deterministic methods are unsuitable for yielding an effective solution. This paper develops a fuzzy mathematical programming model to solve integrated multi-product and multi-plant problems with multiple fuzzy objectives. The proposed fuzzy multi-objective linear programming model attempts to simultaneously minimize total costs and total distribution time. Finally, an industrial case demonstrates the feasibility of applying the proposed model to a real-world integrated production-distribution coordination model in a supply chain under uncertain environments.% 供应链中的生产-配送协调优化已成为实践和学术界的热点。
基于模糊合作博弈的我国原油供应链协同利益分配模型研究
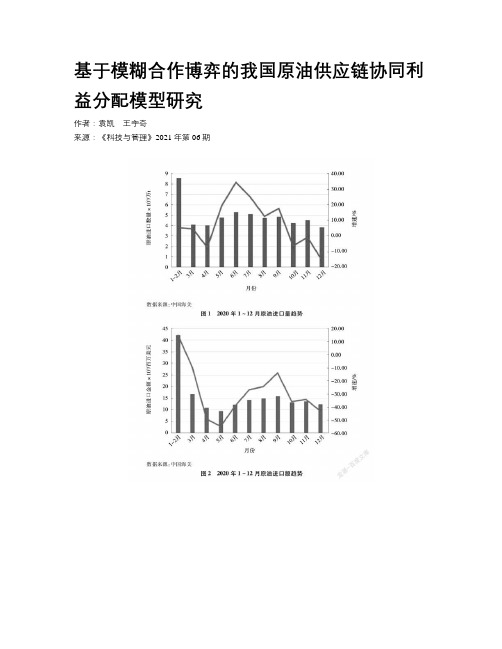
基于模糊合作博弈的我国原油供应链协同利益分配模型研究作者:袁凯王宇奇来源:《科技与管理》2021年第06期摘要:在原油供应链中,利益分配合理与否将直接影响供应链运行效率与稳定性。
在对原油供应链利益分配系统分析基础上,根据模糊合作博弈思想,构建以参与率为关键变量的原油供应链利益分配模型;利用遗传算法以及模糊Shapley值对模型进行求解;在利益分配修正过程中,考虑资源投入、成员地位、风险承担、创新能力4个因素,结合层次分析法以及模糊综合评价法进行量化修正。
科学合理的协同利益分配方案,可以更好整合和利用有限资源,最大程度保障供应链各成员企业的利益,提升供应链整体绩效水平,同时也为我国炼化企业运营管理提供新思路,降低经营风险以及采购成本。
关键词:利益分配;原油供应链;模糊合作博弈DOI:10.16315/j.stm.2021.06.010中图分类号: F274;F42622文献标志码: AResearch on collaborative benefit distribution model of China’s crude oil supply chain based on fuzzy cooperative GameYUAN Kai, WANG Yu-qi(School of Economics and Management, Harbin University of Science and Technology,Harbin 150080, China)Abstract:In the crude oil supply chain, whether the benefit distribution is reasonable or not will directly affect the operation efficiency and stability of the supply chain. Based on the analysis of the benefit distribution system of crude oil supply chain, according to the idea of fuzzy cooperative game, this paper constructs the benefit distribution model of crude oil supply chain with the participation rate as the key variable, and words out the model by using genetic algorithm and fuzzy Shapley value. Finally, in the process of benefit distribution correction, considering resource investment, membership, risk bearing, the four factors of innovation ability are quantitatively revised by combining analytic hierarchy process and fuzzy comprehensive evaluation method. Scientific and reasonable collaborative benefit distribution scheme can better integrate and make use of limited resources, maximize the interests of each member enterprise of the supply chain,improve the overall performance level of the supply chain, and provide new ideas for the operation and management of China’s refining and chemical enterprises, so as to reduce business risks and procurement costs.Keywords:benefit distribution; crude oil supply chain; fuzzy cooperative Game成員企业加入合作联盟的目的在于获得竞争优势以及更大的发展空间与机遇,使自身利益最大化,并使资源在更大范围内得到有效合理运用。
供应链环境下考虑中断风险的供应商订单竞争策略研究

供应链环境下考虑中断风险的供应商订单竞争策略研究作者:杨瑞玲杨晓艳来源:《现代管理科学》2021年第05期[摘要]為了研究中断环境下供应商订单竞争策略问题,构建由零售商和两个供应商组成的供应链,讨论三种策略模型。
两个供应商均未采取策略的基准模型、单个供应商降低中断风险策略模型、两个供应商均降低中断风险策略模型,运用Stackelberg博弈得到不同策略下的最优订货决策及利润,分析供应中断概率和批发价格的关系及这两个因素对采购量的影响程度。
此外,在降低供应中断风险策略中引入第三方投资企业,进一步分析供应商对第三方企业投资的选择决策。
研究表明:供应中断概率比批发价格对采购量的影响大、供应商与第三方投资企业合作时存在临界投资比并且临界投资值与供应商供应中断的概率有关。
借用Matlab工具进行数值仿真发现:相比于单个供应商降低供应中断风险策略,两个供应商均降低供应中断风险策略是可以增加总采购量的且该策略下的供应链利润优于其他策略模型下的利润,最后为供应商提供相应的决策建议。
[关键词]双供应商;订单竞争策略;第三方投资企业;中断风险;投资比一、引言及文献综述信息经济时代下,随着供应链网络结构的日益复杂以及人为破坏、疾病或自然灾害等事件发生的频率增加,供应商供应中断风险也在不断提升,供应中断是指供方不能按时、按质、按量向需方提供原材料或产品,进而破坏供应链的连续性。
供应商处于供应链中的上游位置,供应链中任何需求的满足都要追溯到供应商对订单的实现程度[1],供应商供应中断风险给供应企业自身和整条供应链带来巨大的经济及社会损失。
为了应对可能发生的供应中断风险事件,越来越多的零售商采用多源采购模式来实现自身产品需求的满足和盈利能力的提升。
零售商的多源采购模式往往会引起供应商对订单量的竞争,拥有同一零售商的供应商们通常会对价格、质量、供应中断风险等方面进行调整或投入以求获得零售商更多的采购量,但哪一种因素的调整对采购量的影响更大或者采取何种策略使供应链的利润更大呢?基于此,关于中断环境下两个供应商的订单竞争策略问题的研究有着重要意义。
采购量分配决策模糊规划模型

采购量分配决策模糊规划模型
王贤斌;周宝刚
【期刊名称】《运筹与管理》
【年(卷),期】2007(016)004
【摘要】供应商对形成企业的竞争力起着关键性的作用.采购决策中,采购商需要决策两方面的问题:应该选择哪些供应商以及在每一供应商应该采购多少.本文考虑了多目标性和目标的模糊性,同时为供应商选择和采购量分配提出了一个集成的决策模型.最后,通过一个算例阐释了该模型.
【总页数】3页(P157-159)
【作者】王贤斌;周宝刚
【作者单位】闽江学院,管理系,福建,福州,350108;闽江学院,管理系,福建,福
州,350108
【正文语种】中文
【中图分类】F274
【相关文献】
1.多周期多产品采购量分配优化模型 [J], 关志民;韩瑜
2.供货不足条件下的生鲜食品采购量分配模型 [J], 何利芳;陈奕娟;张诚一
3.基于价格折扣的采购量在供应商之间的分配决策 [J], 吴新宇;龚国华;林洪伟
4.模糊需求条件下的采购量分配优化模型 [J], 关志民;周宝刚
5.军用武器装备及配件采购决策模糊规划模型研究 [J], 金秀满;贾红梅;周言友;周立山;宋丽
因版权原因,仅展示原文概要,查看原文内容请购买。
模糊随机需求下的全球供应链订单分配

Order Assignment in Global Supply Chain with
Fuzzy Random Demands
作者: 葛娜;汪传旭
作者机构: 上海海事大学经济管理学院,上海200135
出版物刊名: 工业工程
页码: 82-88页
年卷期: 2012年 第6期
主题词: 模糊随机需求;订单分配;全球供应链
摘要:为了使全球供应链三方企业即供应商、第三方物流服务供应商和购买商的利润最大化,考虑了供应链中的模糊随机需求、关税和汇率等因素,从三方企业利润最大化角度出发,建立全球供应链订单分配的模糊随机多目标优化模型。
并借助矩阵转换,将模型转化为三方利润满意度最高的单目标优化模型进行求解,用Shapely值法对三方企业利润进行合理分配。
最后运用算例对模型进行仿真,并通过比较分析得出,基于三方企业利润最大化的订单分配模型所实现的全球供应链总利润要比基于一方企业或两方企业利润最大化的订单分配模型所实现的全球供应链总利润最少高出3.47%,验证了模型的有效性。
基于模糊混合群决策支持系统的 粮食供应链安全评估研究
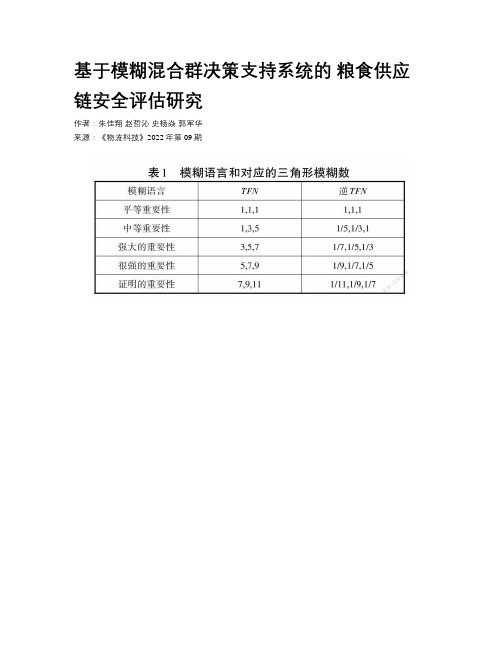
基于模糊混合群决策支持系统的粮食供应链安全评估研究作者:朱佳翔赵哲沁史杨焱郭军华来源:《物流科技》2022年第09期摘要:疫情影响下,全球产业链、价值链及供应链呈现“短链化”“缩链化”的新变化,粮食供应链安全再次成为世界瞩目的焦点。
针对粮食供应链安全的评估决策问题,文章将模糊层次分析法与模糊偏阶群决策法相结合,提出模糊混合群决策支持系统方法用于粮食供应链安全的评估决策。
通过大豆供应链安全评估案例验证模糊混合群决策支持系统的可行性,结果表明:(1)模糊混合群决策支持系统与传统的群决策支持系统相比,体系结构更加开放,有利于网络环境中多种决策的协同。
(2)模糊混合群决策支持系统中纳入交互式辅助决策,既保留了决策偏好的独立性,又消除了群决策小组不同偏好产生的冲突,有助于确保群决策质量。
(3)所提出模糊混合群决策支持系统方法具有较好的鲁棒性,可为我国粮食供应链安全的科学评估提供模糊混合群决策方法支持。
关键词:粮食供应链安全;模糊偏阶群决策;交互式辅助决策;模糊混合群决策支持系统中图分类号:F224 文献标识码:A DOI:10.13714/ki.1002-3100.2022.09.001Abstract: The global industrial chain, value chain and supply chain show new changesof“short chain”and“chain reduction”, and the food supply chain security has once again become the focus of world attention under the influence of the epidemic. For the assessment decision problem of food supply chain security, this paper combines fuzzy hierarchical analysis with fuzzy partial group decision method, and we propose fuzzy mixed group decision support system for the assessment decision of food supply chain security. The feasibility of fuzzy mixed group decision support system was verified by the soybean supply chain safety assessment case. The results show that:(1)Compared with the traditional fuzzy mixed group decision support system, the architecture is more open and is conducive to the coordination of multiple decisions in the network environment.(2)The inclusion of interactive assisted decision making in fuzzy mixed group decision support system retains the independence of decision preferences and eliminates the conflicts arising from the different preferences of group decision making groups, which helps to ensure the quality of group decisionmaking.(3)The proposed fuzzy mixed group decision support system method is robust and can provide fuzzy mixed group decision method support for the scientific evaluation of food supply chain security in China.Key words: food supply chain security; fuzzy partial order group decision-making; interactive auxiliary decision-making; fuzzy mixed group decision support system0 引言随着全球疫情、国际格局及经贸环境变化,粮食供应链安全成为供应链管理中的热门研究领域之一。
基于多目标规划的供应商订单分配方法研究

系。为了确保匹配方法是最优的,需要一个模型来决 定要使用的供应商数量,以及它们之间的订单数量分 配。该模型需满足以下条件。
目 标 函 数:总 采 购 花 费 最 小、质 量 合 格 数 量 最 多、准时交货数量最多、满足服务水平数量最多。
CHINA MANAGEMENT INFORMATIONIZATION / 123
企业管理
这些离不开供应链上各家企业的密切合作,特别是以 物流、资金流、信息流为纽带的互联互通,支撑了整个 产业链的发展。因此,为了科学规范管理物流、资金 流、信息流 3 个关键要素,使用科学的方法对供应商 订单进行合理分配十分必要。
2024 年 1 月 第 27 卷第 2 期
中国管理信息化 China Management Informationization
Jan.,2024 Vol.27,No.2
基于多目标规划的供应商订单分配方法研究
王 勋,晋严尊
(中国空空导弹研究院,河南 洛阳 471000)
[摘 要]制造企业在进行物资与服务采购时,对多源供应商一般采用固定的订单分配比例,但固定比例 分配订单在履约过程中,由于供应商订单与能力未精准匹配,客观造成了一些产品出现质量不稳定、未 按时交货的情况。为了使供应商能力和获得订单数量匹配,文章针对多源供应商的订单分配问题建立一 种基于多目标混合整数规划模型,该模型可以依据供应商过往的各项能力表现,确定使用的供应商数量 和订单分配数量,并考虑实际采购过程中阶梯降价的情况。使用供应商的实证数据进行求解后,结果显 示该模型具有良好的准确性和实用性,可以作出科学的采购决策,并为其他制造企业提供借鉴和参考。 [关键词]供应链管理;供应商选择;多目标规划;订单分配;物资采购 doi:10.3969/j.issn.1673 - 0194.2024.02.040 [中图分类号]F274 [文献标识码]A [文章编号]1673-0194(2024)02-0123-04
考虑供应中断风险的供应链集成优化模型

Economy and Law ·经济与法商业故事BUSINESS STORY考虑供应中断风险的供应链集成优化模型任文学(南京大学商学院,江苏南京210093)摘要:本课题是在确定性需求前提下,建立应对供应中断风险的供应链集成优化模型。
通过数值算例分析,研究供应中断风险下的最佳采购策略,从而为企业实际的供应链管理提供一些行动依据。
关键词:供应链中断;多源采购;产品替代1研究背景及意义在全球经济一体化背景下,产品分工日益精细,供应链网络越来越精细复杂。
面对变幻莫测的市场环境,供应链系统也越来越脆弱,一旦某个节点企业发生中断,便会依托网络传染至链条上的其他企业,最终将导致供应链巨大的效率损失。
因此,如何建立有效的快速响应系统减轻供应中断造成的损失,成为众学者关注的焦点。
本课题拟紧密联系当前实际,在多源采购策略和供应中断风险的理论基础上,建立在确定性需求前提下应对供应中断风险的集成优化模型,并设计相应的求解算法,利用数值算例分析验证模型的可行性与有效性,力求为企业实际的供应链管理提供一些行动依据。
2基础理论2.1供应链中断风险Tang (2006)认为供应链风险有两类,一类是运营风险,一类是中断风险。
中断风险是指存在于供应链外部的,如经济危机、地震、恐怖袭击等自然灾害或人为事件。
李勇建等(2012)认为,供应链中断是发生可能性较低的,但一旦发生,便会对供应链运作效率产生较大负面影响的事件,包括供应链系统内部事件(上下游企业发生意外事故、倒闭等)和供应链系统外事件(政治动荡、经济周期波动等)。
2.2多源采购策略李武(2009)指出,多源采购是指在有限的资源和不确定的供需条件下,制造商根据事先设定的目标或准则选定几个常用的供应商,再根据实际情况在供应商之间分配订单。
一旦某家供应商发生供应中断事件,可以从其他供应商获得紧急供应,保证生产的持续进行,这样就破除了采用单一的供应源造成的买方对供应商的过度依赖,省略了重新开发供应商的时间和流程,增加了应对供应中断风险的柔性。
考虑中断风险与模糊定价的闭环供应链网络设计模型

考虑中断风险与模糊定价的闭环供应链网络设计模型
吴功兴;孙兆洋;琚春华
【期刊名称】《计算机科学》
【年(卷),期】2022(49)7
【摘要】为缓解供应中断对企业的打击,文中提出了在竞争环境下考虑模糊定价和中断风险的双目标闭环供应链网络模型。
定义不确定需求为供应链及其竞争对手向客户提供的价格函数,使供应链在竞争环境中实现总利润最大化与碳排放量最小化。
文中基于可能性理论求解所提模型,将双目标模型转换为单目标模型,最后使用真实
案例进行数值算例分析。
结果表明,所提模型不仅可以增强供应链抵御风险的能力,
还有助于提高其在市场中的战略地位。
【总页数】6页(P220-225)
【作者】吴功兴;孙兆洋;琚春华
【作者单位】浙江工商大学管理工程与电子商务学院;中国标准化研究院高新技术
标准化研究所
【正文语种】中文
【中图分类】TP302
【相关文献】
1.考虑中断风险与库存成本的分销网络设计模型
2.考虑风险与资金约束的闭环供应链定价与回收决策
3.模糊需求下考虑政府奖惩的闭环供应链回收定价模型
4.模糊
环境下考虑供应中断的再制造闭环供应链研究5.考虑成员风险态度的零售商资金约束闭环供应链定价与回收决策
因版权原因,仅展示原文概要,查看原文内容请购买。
基于供应中断风险防范的供应商评价研究

基于供应中断风险防范的供应商评价研究李继勇;付继云;蔺正奇【摘要】供应链业务的全球展开、精益理念的发展,导致企业对供应商的依赖程度逐渐加大.然而,受现实风险因素影响,供应商通常是不可靠的,一旦发生供应中断,将会给企业造成巨大损失.供应商评价是防范供应中断风险的有效措施,为此,建立了基于供应中断风险防范的供应商评价指标体系,运用熵值法与模糊综合评价法构建评价模型,并通过实例计算出各供应商的综合实力,为企业选择合格供应商提供理论依据.【期刊名称】《河北工程大学学报(社会科学版)》【年(卷),期】2014(031)002【总页数】5页(P34-38)【关键词】供应中断风险;供应商评价;熵值法;模糊综合评价法【作者】李继勇;付继云;蔺正奇【作者单位】河北工程大学经管学院,河北邯郸056038;河北工程大学经管学院,河北邯郸056038;加州大学洛杉矶分校,洛杉矶CA90024【正文语种】中文【中图分类】F252供应商处于供应链的源头,对于下游采购企业的生存和发展起着重要作用。
但随着供应链业务的全球展开、精益理念的发展,企业为了降低库存成本,运用VMI、JIT等方法追求低库存,导致企业对供应商的依赖程度加大。
因为在现实中受多种风险因素的影响,供应商通常是不可靠的,随时会发生供应中断,给企业造成巨大损失。
因此,能否正确的对供应商进行评价、选择,以及对选择过程中存在的风险进行正确评价与防范,关系着整个供应链上的企业能否有效运营以及供应链效率的提升。
一、供应中断风险的涵义及防范的必要性目前在国内外文献中,因依据不同,对供应链中断风险的分类方法也不尽相同。
基于供应链风险的分类方法,将供应链中断风险分为发生概率较大、持续时间短、危害小且易于防范和控制的风险和发生概率小、持续时间长、危害大且不易于防范和控制的风险;基于中断来源,将其分为由自然事件和人为事件引发的中断;基于供应链失效的模式,将其分为供应商中断、交通中断、通信中断、设施中断、需求中断、违反货运制度等[1];基于供应链的构成,将其分为供应中断风险、协调中断风险和需求中断风险三种[2]。
不确定性供应链中基于模糊线性规划的订单分配方案

不确定性供应链中基于模糊线性规划的订单分配方案
王娟;尹小悦;陈昭玖
【期刊名称】《湘潭大学自然科学学报》
【年(卷),期】2016(038)003
【摘要】现实供应链中供应商具有多项不确定性,加大了订单合理分配的难度,为此提出一种基于模糊线性规划的订单分配方案.首先,运用模糊集理论来表示供应商指标中的不确定性.然后,根据供应商的输出指标,运用数据包络分析法对其进行效率评估并排序.最后,在综合考虑供应商交易效率、交货时间和采购成本下,利用提出的模糊线性规划模型求解订单分配方案.案例分析中,以各项指标的加权和评估了所得分配方案的性能.结果表明,该方法能够获得合理的分配方案且对不确定性具有鲁棒性.【总页数】5页(P108-112)
【作者】王娟;尹小悦;陈昭玖
【作者单位】赣南医学院人文社科学院,江西赣州341000;赣南医学院人文社科学院,江西赣州341000;江西农业大学经济管理学院,江西南昌330045
【正文语种】中文
【中图分类】O221;F273
【相关文献】
1.基于供应链中不确定性的生产计划研究 [J], 董鹏;崔爱平;董莉莉;仇莉
2.基于供应链中不确定性的生产计划研究 [J], 董鹏;崔爱平;董莉莉;仇莉
3.基于供应链中不确定性的生产计划研究 [J], 董鹏;崔爱平;董莉莉;仇莉
4.供应链协同与供应链绩效的关系研究——基于环境不确定性的调节作用 [J], 章怡心;李登科
5.考虑订单合同选择和生产不确定性的农产品供应链模型 [J], 覃丽萍
因版权原因,仅展示原文概要,查看原文内容请购买。
物流模式选择的模糊多目标决策模型

物流模式选择的模糊多目标决策模型物流模式选择是指在给定的情况下,根据多个目标和约束条件,选择适合的物流模式。
由于物流模式选择问题中存在多个冲突的目标,往往无法通过单一的目标函数进行优化。
因此,使用模糊多目标决策模型可以更好地解决这类问题。
模糊多目标决策模型是一种结合了模糊理论和多目标优化的决策方法。
它考虑了多个目标之间的相互关系和约束条件,并通过建立模糊关系来表达这种模糊性。
在物流模式选择中,可以将几个常见的目标作为权重来衡量物流服务水平、运输成本、交货时间、配送可靠性等因素。
模糊多目标决策模型的主要步骤如下:1.确定决策目标和约束条件:根据具体的物流模式选择问题,确定决策目标和相关的约束条件。
例如,目标可以包括服务水平、成本、时间等,约束条件可以包括运输能力、交通状况等。
2.建立模糊关系:对每个目标和约束条件进行模糊化处理,将其表示为模糊集合。
可以使用模糊数学中的隶属函数来描述每个目标和约束条件的模糊程度。
3.定义决策变量和决策规则:将物流模式作为决策变量,定义每个可能模式的模糊隶属函数。
根据已有的知识和经验,制定一套具体的决策规则。
4.模糊多目标优化:根据定义的决策规则,计算每个可能模式的模糊隶属度。
然后,利用模糊多目标优化算法(如模糊TOPSIS、模糊层次分析法等)确定最佳模式。
5.效果评估与调整:对于得到的最佳模式,进行效果评估和调整。
根据评估结果,可以对模糊隶属函数和决策规则进行调整,进一步改进模型效果。
总之,物流模式选择的模糊多目标决策模型能够处理多个冲突的目标和约束条件的问题,结合模糊理论,能够更好地考虑决策者的主观因素和不确定性。
在实际应用中,可以根据具体的情况进行调整和改进,以更好地满足实际需求。
基于模糊权重的多目标订单分配模型

Multi-Objective Order Allocation Model under
Fuzzy Weight
作者: 潘伟[1] 汪寿阳[2] 华国伟[2] 张金隆[3]
作者机构: [1]武汉大学经济与管理学院,湖北武汉430072 [2]中国科学院数学与系统科学研究院系统科学研究所,北京100190 [3]华中科技大学管理学院,湖北武汉430074
出版物刊名: 中国管理科学
页码: 80-85页
主题词: 模糊权重 模糊目标 订单分配 随机需求
摘要:随着竞争的日益加剧,采购成了影响企业生存和发展的关键因素。
在这种情况下,正确的订单分配是成功实行采购的关键。
实际上,影响订单分配的许多信息并不是确定的已知条件,例如目标、约束条件和影响权重等。
本文通过考虑上述信息的不确定性和模糊性,构建一个包含模糊目标、模糊权重和随机约束的订单分配模型。
然后,利用数值算例证明了模型的可解性。
最后,指出了未来可能的几个研究方向。
基于供应中断风险的模糊多目标订单分配模型

发展了多目标线性订单分配模型, 该模型中供应商提供价格折扣给采购者, 以鼓励 足.Balan 等 采购者下大订单.
①
[5 ]
提出了考
虑折扣价格的模糊供应商选择模型, 但其假设需
收稿日期: 2011-12-23; 修订日期: 2013-08-15. 基金项目: 国家自然科学基金资助项目( 71231007; 71103135) ; 2012 年武汉大学高水平国际期刊论文培育项目 ( 2012GSP028 ) ; 武汉大 “70 后” 学 2010 年度自主科研资助项目( 自然科学部分) ( 1101012) ; 武汉大学人文社会科学 学者学术发展团队资助项目. 作者简介: 潘 伟( 1976—) ,男,吉林扶余人,博士,副教授. Email: mrpanwei2000@ 163.com
i=1 j=1
≥ Dt
] ≥α
t
* t = 1, ... , q; i = 1, ... , n t ; j = 1, ... , m ti V t, i, j - 1 Y tij ≤ X t, i, j ≤ V t, i, j Y tij , m ti
Y tij ≤ 1,t = 1, ... , q; ∑ j=1
0
引
言
供应中断风险是种潜在的威胁, 它会利用供 应链系统的脆弱性, 破坏供应链系统, 给上下游企 业以及整个供应链带来损害和损失. Pan 等 等
[7 ] [6 ]
20 世纪 90 年代以来, 随着供应链管理思想 逐步地被接受和采用, 企业与供应商的关系演变 为合作伙伴, 比以价格为导向的传统模式要复杂 得多. 在供应链中, 一般工业企业采购成本约占总 成本的 70% , 在高新技术产品中, 采购成本与服 务费用则达到总成本的 80% 左右. 所以采购是影 响企业生存和发展的关键因素之一 . 而科学、 简 单、 实用的订单分配方法则是企业成功实行采购 的关键. 订单分配问题有诸多的影响因素, 选择最佳 的分配方案就要在各种各样的因素之间进行权 [1-2 ] .Pan 等[3]建立了关于信息服务企业的多目 衡 标线性订单分配模型, 它以折扣成本最小化为目 标, 同时考虑供应商的供应能力和价格随需求而
考虑动态服务能力的LSSC订单分配优化模型

考虑动态服务能力的LSSC订单分配优化模型范志强; 胡彦勇【期刊名称】《《计算机应用与软件》》【年(卷),期】2019(036)010【总页数】6页(P256-261)【关键词】动态服务能力; 物流服务供应链; 订单分配; 遗传算法【作者】范志强; 胡彦勇【作者单位】河南理工大学工商管理学院能源经济研究中心河南焦作454000【正文语种】中文【中图分类】TP39; F2520 引言随着服务经济的日益兴起以及客户需求的多样化、新颖化和个性化,传统的自营物流、第三方物流已经无法满足社会发展的需要,物流服务供应链(Logistics Service Supply Chain,LSSC)作为一种新兴的物流发展模式,正发挥着越来越重要的作用。
同时,也掀起了物流服务供应链的研究热潮,目前对物流服务供应链的研究主要集中于概念性、结构性、描述性的分析研究,包括其内涵结构、所具特征、利润分配、风险管理等方面,而对物流服务供应链核心问题之一的订单分配问题研究较少。
然而订单分配制约着物流服务供应链的响应速度、完成时效、服务质量等方面,并直接影响到订单任务是否能在合适的时间交给合适的供应商最合适的任务量,对物流服务供应链上企业的生存和发展起着至关重要的作用,所以对物流服务供应链上的订单分配问题进行研究是重要的也是必要的。
目前,在订单分配研究方面,大多集中在产品供应链领域,且多与供应商选择问题并行研究。
范志强[1]考虑了不良产品对订单分配的影响,构建了以交易成本、采购成本、不良产品数量与延迟交货数量最小化以及供应商评分最大化的多目标优化模型,并利用模拟退火算法进行求解;Moghaddam [2]以总利润、总缺陷部分、总交付后期部分以及候选供应商的相关经济风险等因素构建在不确定环境下的模糊多目标优化数学模型,并开发了一种与模糊目标规划相结合的蒙特-卡罗模拟方法,以确定所提出模型的整套帕累托最优解,以此进行供应商选择与订单分配;李占丞等[3]在允许延迟交货并提供相关折扣的情况下,构建订货量分配与订单排产联合优化模型,采用粒子群优化算法进行订单分配优化;Hamdan等[4]首先利用TOPSIS法与AHP法进行供应商选择,然后构造双目标整数规划模型,进行供应商选择与订单分配决策优化;黄辉等[5]针对现实生活中单一供应商可以供应多种产品种类,且根据采购量有一定的价格折扣的现状,构建了基于产能约束下的多目标供应商选择与订单分配模型,有效缓解了订单分配过程中出现的分配不均衡与不合理的问题;Hacer[6]采用决策试验与试验评估法(DEMATEL)与太古奇损失函数相结合的方法对供应商选择与订单分配进行优化;Lo等[7]对绿色供应商评估和订单分配进行了讨论研究,并提出了一种新的模型,该模型将最优-最差方法与理想解相似的订单偏好改进模糊技术和模糊多目标线性规划相结合,以解决绿色供应商选择和订单分配问题,最后通过电子公司的实际数据证明了所提方法的实用性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Pr
it
tiit来自1…, f( k) 是极小化目标或标准, 例如 这里: f( 1) , + 、 ; f ( k 1 ) , … , f ( q ) 价格 前值期等 是极大化目标 或标准, 例如质量、 服务等; g i( x) 是满足约束条件 t = 1, …, n 是非负的决策变量; 的可行解集合; x t , bi , i = 1, …, m 是给定分布函数的独立连续随机变 量; a it 代表 i - th 约束条件第 t - th 决策变量的相 0 < 关系数; β i 是 i - th 约束条件满足的概率水平, …,m. β i ≤ 1,i = 1, 典型的订单 分 配 问 题 , 其采购决策影响因 素主要包括成本 、 质量及配送情况 . 同时 , 每个供 应商作为独 立 的 个 体 , 都有他自己独特的产品 价格 、 配送历史 、 产品合格率及其产品供应能力 .
多目标线性 / 非线性规划模型为
( 10)
( 7)
在这里要最小化延迟交付率. 从多个供应商中采购多种产品的整数 最终,
∑ ∑ [∑ [ Ptij Xtij t=1 i=1 j=1
q nt m ti
+ dC ζ( X tij )
]]
( 成本) ( 11) ( 次品率) ( 12) ( 延迟交付率) ( 13) ( 供应能力) ( 14) ( 需求约束) ( 15) ( 16) ( 17) ( 18) ( 19)
[4 ] 变化等. Basnet 和 Leung 构建了多周期多目标 线性订单分配模型, 它考虑存储费用和需求的满
建
立了供应商选择模型, 考虑供应中断风险; 吴军 评述了有关供应链风险管理定量分析的一
[8 ]
些主要工作; 张煜等
研究了在零售商对供应商
安全状态信息未知的情况下, 零售商如何向供应 商提供两种不同性质的契约. 当然, 其它的影响因素也不容忽视, 当前, 订 单分配已经成为增强企业竞争力的必不可少的要 素, 订单分配的正确与否, 在产品质量、 库存、 生产 等诸多方面都对企业产生越来越大的影响. 然而 其中包含大量的不确定和模糊因素 , 针对这些, 国 内外研 究 者 做 出 了 许 多 卓 有 成 效 的 研 究 工 作. Balan 等[5] 建立了多目标模糊订单分配模型, 其 中主要有 3 个目标函数: 最小的成本、 最小的货物 中的废品率、 最小的延迟交付, 限制条件为满足顾 客需求及供应商的供应能力, 但在这个模型中 3 个目标的权重被假设为相同; Amid 等
在现存的关 于 订 单 分 配 模 型 中 , 研究者们很少 在一个模型 中 将 随 机 需 求 、 供应中断风险及价 格折扣等联 合 起 来 思 考 订 单 分 配 问 题 , 可是这 些现象往往却是同时存在的 . 为了解决这个实际 问题 , 本文 建 立 了 下 面 的 模 糊 多 目 标 订 单 分 配 模型 . 在这个订单分配问题中, 公司拥有多个供应 商, 其产品采购都是从其选择的供应商中进行. 下 面将详细地对模型进行讨论. 假设 失函数; 1) 不同的情景仅仅影响供应中断损
[9 ]
发展了多目标线性订单分配模型, 该模型中供应商提供价格折扣给采购者, 以鼓励 足.Balan 等 采购者下大订单.
①
[5 ]
提出了考
虑折扣价格的模糊供应商选择模型, 但其假设需
收稿日期: 2011-12-23; 修订日期: 2013-08-15. 基金项目: 国家自然科学基金资助项目( 71231007; 71103135) ; 2012 年武汉大学高水平国际期刊论文培育项目 ( 2012GSP028 ) ; 武汉大 “70 后” 学 2010 年度自主科研资助项目( 自然科学部分) ( 1101012) ; 武汉大学人文社会科学 学者学术发展团队资助项目. 作者简介: 潘 伟( 1976—) ,男,吉林扶余人,博士,副教授. Email: mrpanwei2000@ 163.com
如下形式 目标函数 min f( 1) , …, f( k) max f( k + 1) , …, f( q) 约束条件 x ∈ g i( x ) , g i( x ) = i = 1, …, m } ( 3) { ( ∑a x ≥ b ) ≥ β ,
n
购的 t - th 产品数量; Y tij i - th 供应商( Y tij = 1: 在 j - th 价格水平 时从 i - th 供应商采购 t - th 产品; 否则 Y tij = 0) ; P tij i - th 供应商在 j - th 价格水平时单位 t - th 产品价格; C ti F ti S ti Nt i - th 供应商的 t - th 产品供应能力; i - th 供应商 t - th 产品的延迟交付率; i - th 供应商 t - th 产品中的次品率; t - th 产品供应商的数目; i - th 供应商的 t - th 产品供应中
m ti
X tij ≤ C ti , 因为其实际供应的产品数量要受其 ∑ j=1 供应能力约束. 在情景分析中, 假设有 3 种场景, 每个不同的 场景中供应中断损失函数分别为 1) t - th 产品市场的供应能力远大于需求 dC 1( X tij ) = dp ti( X tij ) ·0 = 0 ( 5) 2) t - th 产品市场的供应与需求基本平衡 dC 2( X tij ) = dp ti( X tij ) θ t X tij ,θ t > 0 ( 6) 3) t - th 产品市场的供应能力远小于需求 dC3( Xtij ) = dpti( Xtij ) γt Xtij βt , γt , βt > 0 成本目标函数为 Z 1 = min∑ Pr ob( ζ)
2) 根据供应商列表, 公司选择产品提供者; 3) 公司对不同产品的需求都是服从正态分 布的随机变量; 4) 每种产品的价格都是随采购量而变化的 . 以下列出模型中的一些变量和参数 : 2, …, q) ; D t t - th 产品的市场需求( t = 1, V tij V* tij i - th 供应商在 j - th 价格水平时提供
dp ti( X tij ) 断出现概率;
dC ( X tij ) 在 情景下 t - th 产品的中断损失 函数; Z 目标函数. 这里, 产品 的 需 求 D t 是 正 态 分 布 的 随 机 变 量; X tij 是在 j - th 价格水平时从 i - th 供应商采购 的 t - th 产品数量;
— 46 —
[10-11 ]
管
理
科
学
学
报
2015 年 3 月
求为定值; 潘 伟 等 研究了信息不确定条件 下, 多目标供应商选择问题. 然而, 这些模型都没 有充分考虑供应中断和信息不确定等情况, 所以 为了提供更加符合现实情况的订单分配法案 , 本 文建立基于供应中断风险角度的模糊多目标订单 [12-17 ] 分配模型, 不仅将模糊集合论的思想和方法 并且结合供应风险管理的理念, 提出考 引入其中, 虑供应中断风险的订单分配模糊综合决策方法 . 本文主要通过对供应商供货的质量 、 价格、 服 务等因素的评价指标进行模糊描述, 运用模糊评 判的方法, 建立订单分配体系, 实现对订单进行智 能化的选择与评价. 扩展了模糊多目标订单分配 模型, 其主要创新点有以下 4 点: 1 ) 从确定约束 扩展到随机约束; 2 ) 添加了情境分析,定义了不 同情景下的供应中断损失函数; 3 ) 将隶属度函数 从线性扩展为一般形式即包含线性和非线性; 4 ) 考虑价格折扣.
* 稍小于 V tij( V tij = V tij - 1) ; i - th 供 应 商 的 t - th 产 品 价 格 变 化
1
1.1
模糊多目标订单分配模型
多目标订单分配模型 一般形式的多目标定单分配模型可以表示成
t - th 产品的最大供应量; m ti 数目; nt ( 1) ( 2) X tij t - th 产品的供应商数目; 在 j - th 价格水平时从 i - th 供应商采
第 18 卷第 3 期 2015 年 3 月
管 理 科 学 学 报 JOURNAL OF MANAGEMENT SCIENCES IN CHINA
Vol.18 No.3 Mar.2015
基于供应中断风险的模糊多目标订单分配模型
潘 伟
( 武汉大学经济与管理学院,武汉 430072)
①
摘要: 采购是影响企业生存和发展 的 关 键 因 素 之 一, 正 确 的 订单 分 配则 是 企业 成功 实 行 采购 管理的关键. 但影响订单分配的许 多 信息 并 不是 确 定的, 存 在着 供 应 中 断 的 风险. 文 章 在考 虑 供应中断风险的基础上, 结合不确定性的信息 和 线 性 / 非线 性的 隶属 度 函 数, 构 建 并分析 了 包 、 / . , 含模糊目标 随机约束和情景分析的多产品线性 非线性订单分配 模 型 然后 通过 数 值 算 例比 较了不同情景下企业的最优决策, 得到了管理上的一些启示. 关键词: 情景分析; 模糊目标; 供应中断; 随机需求 中图分类号: F275 文献标识码: A 文章编号: 1007 - 9807( 2015) 03 - 0045 - 07
第3期
潘
伟: 基于供应中断风险的模糊多目标订单分配模型
q nt mti
— 47 —
P
[ ∑∑X
nt m ti i=1 j=1
tij
≥ Dt
] ≥α
t
( 4)
Prob( ζ) ∑ ∑ [ ∑ [ Ptij Xtij + dCζ( Xtij ) ∑ t=1 i=1 j=1 ζ∈E
]]
( 8)
是 i - th 供应商能够提供 C ti 单位的产品, 这表明,
0
引
言
供应中断风险是种潜在的威胁, 它会利用供 应链系统的脆弱性, 破坏供应链系统, 给上下游企 业以及整个供应链带来损害和损失. Pan 等 等
