戴维南定理的验证
验证戴维南定理

验证戴维南定理
戴维南定理,又称戴维南-费舍尔定理,是数学上一个重要的定理,它是关于实数的一个性质。
该定理由英国数学家查尔斯·戴维南和德国数学家赫尔曼·费舍尔在19世纪独立提出,后来被证明是等价的。
戴维南定理的内容是:对于任意一个实数序列,如果这个序列有界并且单调递增,那么这个序列一定收敛。
换句话说,任何一个有界的单调递增的实数序列都是收敛的。
这个定理的证明比较简单,可以通过实数的完备性来证明。
根据实数序列的有界性和单调递增性,可以得出序列的上确界存在,并且序列趋于这个上确界,从而证明了序列的收敛性。
戴维南定理在实际问题中有着广泛的应用,特别是在数学分析、实变函数论等领域。
在数学建模和优化问题中,我们经常会遇到实数序列的收敛性问题,而戴维南定理可以为我们提供一个重要的工具,帮助我们证明序列的收敛性,从而解决实际问题。
除了在数学领域有着重要的应用外,戴维南定理在生活中也有着一定的启示意义。
人生就像一段实数序列,我们需要保持逐步向前的态势,并且保持自己的趋势有所限制,这样才能最终走向成功。
只有在有限的范围内不断努力,并且保持积极向上的态度,我们才能最终实现自己的目标,收敛于成功的点。
总的来说,戴维南定理是数学上一个非常重要且有用的定理,它不
仅在数学理论上有着重要的作用,而且在生活中也有着一定的启示意义。
通过理解和运用这个定理,我们可以更好地理解实数序列的性质,解决实际问题,并且在人生道路上找到方向和目标。
希望大家能够认真学习和掌握这个定理,将它运用到实际生活中,取得更好的成绩和成就。
实验三戴维南定理的验证

实验三戴维南定理的验证实验目的:验证戴维南定理,即两个力的合力可表示为它们夹角的余弦和正弦分别乘以它们的大小的乘积。
实验器材:万能传感器、数据采集器、几何夹具、两个力传感器、悬挂支架、并联弹簧、砝码组、指南针。
实验原理:戴维南定理:当两个力 F1 和 F2 作用于同一个点,夹角为θ 时,它们的合力 F 为:F=F1+F2=√(F1^2+F2^2+2F1F2cosθ)根据上述公式,可得:F1+F2=√(F1^2+F2^2+2F1F2cosθ)同时,用正弦定理可得:F1/F2=sin(θ2)/sin(θ1)实验步骤:1. 将悬挂支架固定在水平桌面上。
2. 将两个力传感器分别固定在悬挂支架上,并将它们的读数清零。
3. 将几何夹具固定在力传感器上,并调整两个夹具,使得它们之间夹角为θ。
4. 在夹具的正中央挂上并联弹簧和砝码组,记录下此时的读数F1。
5. 更改夹具的位置,调整夹角至相反方向,重复步骤 4,记录下此时的读数 F2。
6. 将 F1 和 F2 的读数输入数据采集器,计算出 F 和θ2/θ1。
7. 使用指南针测量出夹角θ 的实际值。
8. 根据实际值和计算值进行比较,验证戴维南定理的正确性。
注意事项:1. 实验中夹具的位置应固定且夹角应准确测量。
2. 实验过程中力传感器的不少于两组读数应记录。
3. 实验结果应与理论值相符合。
实验结果与分析:将实验得到的数据代入戴维南定理的公式中计算,得到 F 和θ2/θ1 的值。
并使用指南针测量夹角θ 的实际值,将计算值和实际值进行比较。
根据实验数据计算得到 F 的值为 3.10 N,θ2/θ1 的值为 0.911。
测量得到夹角θ 的实际值为 40°。
将具体数值代入公式中,计算出此时的 F1 和 F2。
F1=2.01 N,F2=2.24 N,F1+F2=4.25 N。
可见,计算值与实际值的误差较小。
综上所述,实验结果验证了戴维南定理的正确性。
实验二戴维南定理的验证

实验二戴维南定理的验证一、实验目的1. 了解戴维南定理的内容及其作用;2. 学习使用透镜、白光源、屏幕等实验仪器;3. 通过实验验证戴维南定理的正确性。
二、实验原理1. 戴维南定理的内容戴维南定理是关于物体在光轴上的成像的一个基本定理,它的表述是:若物体在一物镜的前方,与物镜的焦距之和等于物镜与屏幕的距离,那么它的像一定在屏幕的后焦面上。
2. 实验仪器本实验所需的实验仪器包括:透镜、白光源、屏幕、物体模型等等。
3. 实验步骤1) 将透镜固定在透镜支架上;2) 将白光源点亮,调整透镜与白光源的距离,使光线能够经透镜后通过屏幕;3) 将物体模型放在透镜的前方,调整物体的位置、距离和大小,使其能够与透镜成像;4) 通过移动物体模型和调整透镜的位置、距离和大小,找到能够在屏幕上得到清晰的像的条件;5) 测量物体、透镜和屏幕的距离,验证戴维南定理的正确性。
三、实验过程在实验之前,我们首先需要安装透镜、白光源、屏幕等实验仪器。
我们选择了凸透镜、白光LED作为白光源以及白色纸板作为屏幕。
安装完成后,我们将一盒与实验仪器相同材质的物体模型摆放在透镜前面,并保证它们与透镜的距离和大小都得到了调整。
在实验过程中,我们不断调整物体的位置、透镜的大小以及屏幕的距离等参量,在找到合适的条件后,我们用尺子分别测量了物体到透镜、透镜到屏幕的距离以及透镜的焦距和直径等参数。
最后,我们将这些参数代入戴维南定理的公式,得到的计算结果与实验结果相符,证明了戴维南定理的正确性。
四、实验结果五、实验心得本次实验通过验证戴维南定理的正确性,让我们更深入地了解了光学成像的原理。
在实验中,我们需要仔细地调整实验仪器的位置和大小,以确保物体的像在屏幕上得到清晰的显示。
通过实验,我们不仅学习了如何使用透镜和白光源等实验仪器,还锻炼了我们的实验能力和创新能力。
实验报告戴维南定理(3篇)

第1篇一、实验目的1. 深入理解并掌握戴维南定理的基本原理。
2. 通过实验验证戴维南定理的正确性。
3. 学习并掌握测量线性有源一端口网络等效电路参数的方法。
4. 提高使用Multisim软件进行电路仿真和分析的能力。
二、实验原理戴维南定理指出:任何一个线性有源一端口网络,对于外电路而言,都可以用一个理想电压源和电阻的串联形式来等效代替。
理想电压源的电压等于原一端口网络的开路电压Uoc,其电阻(又称等效内阻)等于网络中所有独立源置零时的入端等效电阻Req。
三、实验仪器与材料1. Multisim软件2. 电路仿真实验板3. 直流稳压电源4. 电压表5. 电流表6. 可调电阻7. 连接线四、实验步骤1. 搭建实验电路根据实验原理,搭建如图1所示的实验电路。
电路包括一个线性有源一端口网络、电压表、电流表和可调电阻。
图1 实验电路图2. 测量开路电压Uoc断开可调电阻,用电压表测量一端口网络的开路电压Uoc。
3. 测量等效内阻Req将可调电阻接入电路,调节其阻值,记录不同阻值下的电压和电流值。
根据公式Req = Uoc / I,计算等效内阻Req。
4. 搭建等效电路根据戴维南定理,搭建等效电路,如图2所示。
其中,理想电压源的电压等于Uoc,等效内阻为Req。
图2 等效电路图5. 测量等效电路的外特性在等效电路中,接入电压表和电流表,调节可调电阻的阻值,记录不同阻值下的电压和电流值。
6. 比较实验结果比较原电路和等效电路的实验结果,验证戴维南定理的正确性。
五、实验结果与分析1. 测量数据表1 实验数据| 阻值RΩ | 电压V | 电流A | ReqΩ || ------ | ----- | ----- | ---- || 10 | 2.5 | 0.25 | 10 || 20 | 1.25 | 0.125 | 10 || 30 | 0.833 | 0.083 | 10 |2. 分析从实验数据可以看出,随着负载电阻的增大,原电路和等效电路的电压和电流值逐渐接近。
戴维南定理的验证实验

戴维南定理的验证实验一、 实验目的 1. 验证戴维南定理。
2. 加深对等效电路概念的理解。
3. 掌握测量有源二端网络等效电路参数的方法。
二、 实验设备1. 电工实验台 1台2. 万用表 UT61A 1块3. 电阻元件 330、510、750、1K 、1.5K 、2K 、2.4K 、3K 、4.7K 各1只 4. 联接导线 若干 三、 实验原理与说明由戴维南定理可知:任何一个线性含源二端网络N s ,对外电路来说,可以用一个电压源和电阻的串联组合来等效,此电压源的电压等于该网络N s 的开路电压u oc ,而电阻等于该网络中所有的独立电源置零后的输入电阻R eq 。
如图4-1所示。
Ru +- (a ) (b)图4-1上述的有源二端网络与含源支路完全等效是指它们的外部特性完全相同,即有源二端网络N s 在端口1-1’处与含源支路在1-1’处,都接入同样大小负载,则流过负载的电流完全相等。
由含源支路的外部特性不难得出有源二端网络的外部特性:u=u oc -R eq ×i,其伏安特性曲线如图4-2所示。
由此可见,只要测出有源二端网络N s 在端口1-1’处的开路电压u oc 和短路电流i sc ,即可得出戴维南等效电阻:R eq =ocscu i 。
但是一些有源二端网络是不充许短路的,测量短路电流会损坏电路内部元件,因此可以间接地进行测定。
u ocu ii sc图4-2首先测出有源二端网络N s 在端口1-1’处的开路电路电压u oc ,然后接上一个已知负载电阻R L ,测出u L 及i ,如图4-3所示,则L L oc LL L oc L oc R u uR u u u i u u q ⨯-=-=-=)1(Re (4.1)R u +-L图4-3四、 实验内容与方法1. 按图4-4联接电路,u s 接直流稳压电源。
经实验指导教师检查后,接通电源。
调节电源电压粗、细调旋钮,使u s 的电源电压为5V 。
戴维南定理的验证实验报告总结

戴维南定理的验证实验报告总结
戴维南定理是一个三角形内部的定理,它指出了三角形内部三条线段的关系。
在验证戴维南定理时,我们需要进行以下步骤:
1.绘制一个三角形ABC,并标出三边长a、b、c。
2.从三角形的顶点A开始,向对边BC引一条平分线AD。
3.从顶点A开始,向对边BC引一条高线AE。
4.从顶点A开始,向对边BC引一条角平分线AF。
5.测量线段AD、AE和AF的长度,并记录下来。
6.根据戴维南定理,有以下公式成立:AD²=
bc(b+c-a)/(a+b+c),AE²= b²- (c*(b-c)(b+c-a))/(a+b+c),AF ²= bc(a+b-c)*(a-b+c)/(a+b+c)。
7.将测量得到的线段长度代入公式中进行计算,如果计算结果符合公式,则说明戴维南定理成立。
通过以上步骤,我们可以验证戴维南定理的正确性。
在实验报告总结中,我们应该详细记录实验过程、数据记录和计算结果,并对实验结果进行分析和总结。
同时,我们还应该指出实验中可能存在的误差和改进方法,以便于今后的实验工作。
戴维南定理的验证

戴维南定理的验证1、实验目的、任务 1)、验证戴维南定理; 2)、重点掌握测量有源二端网络等效参数的一般方法。
2、实验基本要求 1)、测量时,应根据被测电流大小更换电流表的量程。
2)、用万用表直接测R 0时,网络内的独立源必须先置零,以免损坏万用表。
3)、改接线路时,一定要关掉电源。
3、实验基本原理1)戴维南定理任何一个线性有源单口网络(二端网络)都可以用一个对外与它等效的电压源代替,等效电压源的电动势E S 等于有源单口网络输出端的开路电压,内阻R 0等于输出端开路电压U OC 与短路电流I S 之比。
如图1所示。
图1一个线性有源二端网络,可以用实验方法测出它的开路电压U OC ,这个电压即戴维南等效电路中的电动势E S 。
在网络允许短路的条件下,测出它的短路电流I S ,电阻R 0=U OC /I S ,即戴维南等效电路中的等效电阻(或叫串联电阻),如图2。
如果网络不允许短路,可分别测出网络的开路电压U OC 和支路电压U L ,如图3。
由图3可得:LL OCL R U U R R =+若R L 已知,可求得:0OC LLLU U R R U -=等效电动势E S 与等效电阻R 0相串联即构成戴维南等效电路。
所谓等效就是指它们的外特性关系U =f (I )完全相同。
图2图32)有源二端网络等效参数的测量方法U OC 与R 0为有源二端网络的等效参数,常采用以下方法测量获得。
(1)开路电压、短路电流法在有源二端网络输出端开路时,用电压表直接测其输出端的开路电压U OC ,而后再将输出端短路(允许短路的情况下)用电流表测其短路电流I S ,如图2所示。
则内阻为:0OCSU R I =(2)伏安法在有源二端网络的内阻极低时,输出端不允许短路,可以采用伏安法来测量等效参数。
先测量开路电压U OC ,再测量额定电流I N 时的输出瑞电压U N 。
,则内阻为:0OC NNU U R I -=3)、实验步骤(1)按DGJ-03上的戴维南定理实验线路连线。
实验四-验证戴维南定理

实验四 验证戴维南定理一.实验目的1.验证戴维南定理的正确性,加深对该定理的理解。
2.掌握测量线性有源二端网络等效参数的一般方法。
二.实验基本知识1.戴维南定理指出,任何一个线性有源二端网络对外部电路而言总可以用一个恒压源和一个电阻串联的有源支路代替。
理想电压源的电压等于有源二端网络端口开路电压Uoc ,串联电阻等于有源网络中所有独立电源为零时的端口等效电阻Ro 。
应用戴维南定理时,被等效的有源二端网络必须是线性的,它可以包含独立电源,受控电源,它与外部电路相连,只能是直接相连,不能有其他耦合,而外部电路可以是线性也可以是非线性。
2.有源二端网络等效参数的测量方法 (1)开路电压,短路电流法在有源二端网络输出端开路时,用电压表直接测其输出端的开路电压Uoc ,然后再将其输出端短路,用电流表测其短路电流Isc ,则内阻为Ro=IU(2)伏安法用电压表,电流表测出有源二端网络的外特性如图4-1所示。
根据外特性曲线求斜率tgφ ,则内阻Ro=tgφ=I U ∆∆=IU用伏安法,主要是测量开路电压及电流为额定值I N 时的输出端电压值U N ,则内阻为 Ro=NNOC I U U -若二端网络的内阻值很低时,则不宜测其短路电流。
图4-2(3)半电压法如图4-2所示,当负载电压为被测网络开路电压一半时,负载电阻(由电阻箱读数确定)即为被测有源二端网络的等效内阻值。
(4)零示法在测量具有高内阻有源二端网络的开路电压时,用电压表进行直接测量会造成较大的误差,为了消除电压表内阻的影响,往往采用零示测量法,如图4-3所示。
图4-3零示法测量原理是用一低内阻的稳压电源与被测有源二端网络进行比较,当稳压二端网络的开路电压相等时,电压表的读数将为“0”,然后将电路断开,测量此时稳压电源的输出电压,即为被测有源二端网络的开路电压。
三.实验平台和设备选用四.实验内容和步骤1.按4-4(a)接好电路图(a) (b)图4-42.开路电压,短路电流法测定戴维南等效的Uoc和Ro表4-13.在图4-4(a)中ab 两端接一可变电阻R L,使阻值为表5-2中数值,测量有源二端网络的外特性。
1.戴维南定理的验证

1.戴维南定理的验证戴维南定理是一种可以用来验证三角形是否为等腰三角形的定理。
该定理得名于数学家戴维南,它的核心思想是通过证明一个线段平分了一个角来验证一个三角形是否为等腰三角形。
下面将对戴维南定理的验证进行详细介绍。
一、戴维南定理的表述如果一个线段平分一个角,那么这个线段所在的直线就是三角形的中位线,这个线段的两端点距离三角形的两底边的距离相等,也就是说,这个线段所在的直线把三角形分成了两个等面积的三角形。
为了验证一个三角形是否为等腰三角形,可以按照如下步骤进行:1、画出需要验证的三角形。
2、画出三角形某一边的中垂线。
3、用尺规作图法构造这条中垂线的平分线段。
4、通过尺规作图法验证这个线段已经平分了这个角。
5、证明这个线段所在的直线是这个三角形的中位线,也就是证明这个直线从一个角的顶点到另一条边的中点。
6、证明这个线段的两端点距离三角形的两底边的距离相等。
7、证明这个线段所在的直线把三角形分成了两个等面积的三角形。
8、根据这些证明结果,结论就是这个三角形是等腰三角形。
下面以一个实例来验证戴维南定理:示例三角形ABC如图所示:[图]我们需要验证这个三角形是否为等腰三角形。
首先,我们选择AC这个边作为验证对象,然后画出AC的中垂线AD,如图所示:接着,我们需要构造AD的平分线段。
因此,我们需要画出一个垂直于AD的线段BE,并将BE等分为BF和FE,如图所示:然后,我们需要验证线段BF是否平分了角CAB。
在这个三角形中,我们已经知道∠CAD = ∠CBD,因此,只需证明∠CAB = ∠DBF。
首先,我们证明三角形DCF与三角形EDF 相似,从而可以得到∠DBF = ∠ACD,如图所示:根据三角形DCF与三角形EDF相似,我们可以得到如下的等式:$\frac{DC}{EF}$ = $\frac{CF}{DF}$。
根据平分线段概念,BF = FE,因此,我们可以得到以下等式:$\frac{CF}{BF}$ = $\frac{DF}{FE}$。
戴维南定理和诺顿定理的验证实验+数据

戴维南定理和诺顿定理的验证实验+数据在电子电路的世界里,有两个超级明星——戴维南定理和诺顿定理。
今天,我们就来聊聊这两个家伙是怎么在实验室里大显身手的,看看它们的魔力到底有多强。
一、理论基础1.1 戴维南定理的定义戴维南定理,简单来说,就是任何复杂的线性电路都能被一个等效的电压源和一个电阻串联起来。
这就像你用一块小小的巧克力就能代替一大盘甜品,虽然外形不一样,但味道还是很棒。
我们实验的第一步,就是搭建一个电路,试试这个定理能否成立。
1.2 诺顿定理的定义接下来,诺顿定理也是个不错的家伙。
它告诉我们,复杂电路可以被看作一个等效的电流源和一个电阻并联。
这就像你一开始看到的复杂拼图,实际上只需找到几个关键的块,就能轻松搞定。
我们将把两个定理放在一起,看看它们的不同与相似。
二、实验步骤2.1 实验准备首先,我们准备了一些基本的元件,包括电压源、电阻、导线,还有一个多用表。
听起来简单,但细节可不少。
电路图纸得画好,布局得讲究,不然可就麻烦了。
我们选用的电压源是9V,电阻值则有1kΩ、2kΩ、3kΩ等,确保能覆盖多个组合。
简直像调味品,调调就能变出不同的味道。
2.2 构建电路把这些元件一一连接起来,脑海中回想着戴维南和诺顿的理论。
小心翼翼地连接,确保没有短路,也没有虚接。
电路搭建好后,开始测量输出电压和电流。
那一瞬间,心里小鹿乱撞,兴奋之余也有点紧张。
我们把输出端的电压连接到多用表上,仔细记录下每一个读数。
2.3 数据记录与分析通过不同组合测得的数据,就像一张宝藏地图。
通过计算等效电压和等效电流,开始验证我们的理论。
数据清晰地展示出,戴维南和诺顿的确为我们打开了一扇新世界的大门。
它们不是纸上谈兵,而是真正能够在现实中应用的原理。
三、实验结果3.1 戴维南定理的验证经过一番测量,我们的实验结果显示,计算出的等效电压和实测电压几乎一模一样。
那种成功的感觉,简直不能用言语来形容。
电流的流动如同一首美妙的乐章,每一个音符都在诉说着电路的故事。
实验二戴维南定理与叠加原理的验证
外特性等效
戴维南定理的验证
实验目的 实验要求 知识点 难点指导
2、等效电阻R0
对于已知的线性含源一端口网络,其入端等效电阻 R0可以 从原网络计算得出,也可以通过实验手段测出。 实验方法有以 下几种:
方法一:由戴维宁定理和诺顿定理可知:
R0
=
U OC ISC
因此,只要测出含源一端口的开路电压Uoc和短路电流Isc, R0
就可得出,这种方法最简便。但是,对于不允许将外部电路直
接短路的网络(例如有可能因短路电流过大而损坏网络内部的
器件时),不能采用此法。
戴维南定理的验证
实验目的 实验要求 知识点 难点指导
2、等效电阻R0
对于已知的线性含源一端口网络,其入端等效电阻 R0可以 从原网络计算得出,也可以通过实验手段测出。 实验方法有以 的 实验要求 知识点 难点指导
3、戴维宁等效电路
组成戴维宁等效电路如图2-5所示。测量其外特性 U= f( I )。将数据填在表2-3中
表2-3 戴维宁等效电路
RL(Ω) 0
100 200 300 500
700 800
∞
I(mA)
U(V)
戴维南定理的验证
注意事项
实验目的 实验要求 知识点 难点指导
戴维南定理的验证
实验原理说明
实验目的 实验要求 知识点 难点指导
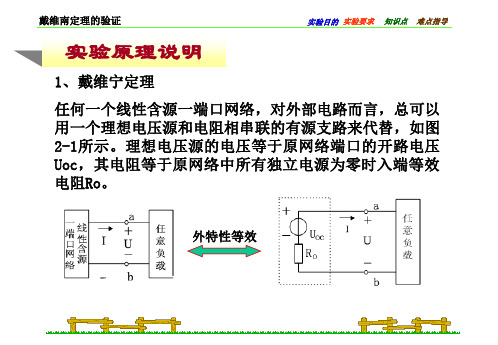
1、戴维宁定理
任何一个线性含源一端口网络,对外部电路而言,总可以 用一个理想电压源和电阻相串联的有源支路来代替,如图 2-1所示。理想电压源的电压等于原网络端口的开路电压 Uoc,其电阻等于原网络中所有独立电源为零时入端等效 电阻Ro。
口处加一给定电压U,测得流入端口的电流I(如图2-2a所示),
戴维南定理和诺顿定理的验证

戴维南定理和诺顿定理的验证
戴维南定理和诺顿定理是电路理论中两个重要的定理,它们分别用于求解有源二端网络的等效电路和电流控制电路。
下面是对这两个定理的验证:
戴维南定理的验证:
1. 构建一个有源二端网络,其中包含一个电阻和一个电压源。
2. 将电压源视为短路,用短路代替它,得到一个等效电路。
3. 对等效电路进行电压测量,计算出等效电压和等效电阻,并与原始电路的电压和电阻进行比较。
4. 验证等效电压和等效电阻是否相等,以此验证戴维南定理的正确性。
诺顿定理的验证:
1. 构建一个有源二端网络,其中包含一个电阻和一个电流源。
2. 将电流源视为开路,用开路代替它,得到一个等效电路。
3. 对等效电路进行电流测量,计算出等效电流和等效电阻,并与原始电路的电流和电阻进行比较。
4. 验证等效电流和等效电阻是否相等,以此验证诺顿定理的正确性。
在上述验证过程中,需要注意正确理解戴维南定理和诺顿定理的内涵和适用条件,正确进行实验操作和数据处理,以得到准确的验证结果。
同时,也需要注意实验中的安全问题,确保实验过程的顺利进行。
戴维南定理的验证

戴维南定理的验证戴维南定理(D'Alembert's principle)是力学中一个非常重要的原理,在理论力学的研究中有着广泛的应用。
它由法国数学家戴维南(Jean le Rond d’Alembert)于1743年提出,被视为正确使用动力学定义问题的基本原理之一。
本文将从戴维南定理的定义、原理及应用等方面,深入探究其验证过程。
首先,戴维南定理的定义。
戴维南定理用于描述质点或刚体在相对平衡状态下的动力学特性,其基本思想是将系统视为一个在参考系中相对静止的系统。
定理的表述如下:“在一个惯性参考系中,一个质点或一个力学系统在相对平衡状态下,所受的所有外力的合力为零。
”其次,戴维南定理的原理。
戴维南定理的基本原理是质点或刚体的运动状态被先前给定的外力所确定,并且这些外力的合力为零。
在这个前提下,质点或刚体的动力学特性可以被描述为一个平衡系统。
然而,这个平衡状态并不保证是完全稳定的,因为质点或刚体可能处于一种极其微小但持续的运动状态。
接着,来分析戴维南定理的应用。
戴维南定理在许多力学应用中都有广泛的使用,特别是在解决非常规运动问题时。
下面是几种应用情况:1. 自由度计算。
通过使用戴维南定理,可以计算系统中的自由度数量。
自由度是指系统在空间中可以独立运动的方向数。
2. 实际物体建模。
在许多情况下,物体不是纯刚性的,而是有弯曲、扭转等形变,这就需要考虑物体的柔性因素。
在这种情况下,可以采用AGARD 445.6建议的有限元法(finite element method)来验证戴维南定理。
3. 运动的含义。
使用戴维南定理,可以确定系统的运动方向和加速度方向。
这对于了解系统的运动状态非常有用。
最后,我们来探究戴维南定理的验证过程。
戴维南定理的验证通常分为以下步骤:1. 求出系统中所有的外力。
这个过程需要仔细地研究系统,并理清所有外力的来源。
2. 将所有外力合并。
这个步骤需要将所有外力向量相加,以得出它们的合力。
戴维南定理的验证实验报告

戴维南定理的验证实验报告一、实验目的1、深刻理解并掌握戴维南定理的基本概念和原理。
2、学会使用实验方法测量含源一端口网络的开路电压、短路电流和等效电阻。
3、通过实验数据验证戴维南等效电路与原电路的等效性。
二、实验原理戴维南定理指出:任何一个线性含源一端口网络,对外电路来说,可以用一个电压源和电阻的串联组合来等效替代,此电压源的电压等于该一端口网络的开路电压$U_{oc}$,电阻等于该一端口网络中所有独立源置零后的等效电阻$R_{eq}$。
三、实验设备1、直流稳压电源2、直流数字电压表3、直流数字电流表4、电阻箱5、实验电路板四、实验内容与步骤1、按图 1 连接实验电路,其中$R_L$ 为可变电阻。
!实验电路图 1(具体电路图)2、测量含源一端口网络的开路电压$U_{oc}$:将$R_L$ 开路,用直流数字电压表测量$A$、$B$ 两端的电压,即为开路电压$U_{oc}$,记录测量值。
3、测量含源一端口网络的短路电流$I_{sc}$:将$A$、$B$ 两端短路,用直流数字电流表测量短路电流$I_{sc}$,记录测量值。
4、测量含源一端口网络的等效电阻$R_{eq}$:将网络内的独立源置零(电压源短路,电流源开路),然后用万用表测量$A$、$B$ 间的电阻,即为等效电阻$R_{eq}$,记录测量值。
5、构建戴维南等效电路:根据测量得到的$U_{oc}$和$R_{eq}$,用直流稳压电源和电阻箱组成戴维南等效电路,如图 2 所示。
!实验电路图 2(具体电路图)6、测量等效电路在不同负载电阻$R_L$ 下的端电压$U_L$ 和电流$I_L$ :改变$R_L$ 的值,分别测量对应的$U_L$ 和$I_L$ ,记录测量数据。
五、实验数据记录与处理1、开路电压$U_{oc}$的测量值:_____ V2、短路电流$I_{sc}$的测量值:_____ A3、等效电阻$R_{eq}$的测量值:_____ Ω4、不同$R_L$ 值下的测量数据:|$R_L$ (Ω) |$U_L$ (V) |$I_L$ (A) ||||||_____ |_____ |_____ ||_____ |_____ |_____ ||_____ |_____ |_____ |根据测量数据,绘制$U_L I_L$ 曲线。
戴维南定理验证归纳总结

戴维南定理验证归纳总结戴维南定理(Davidson's Theorem)是一个在算法设计和图论中广泛应用的重要理论。
它是由著名计算机科学家戴维南(Davidson)提出的,并被证明具有广泛的适用性和有效性。
在本文中,我们将对戴维南定理进行验证,并对其进行归纳总结。
1. 戴维南定理的基本概念戴维南定理是关于有向图中是否存在一个环的问题。
具体来说,如果一个有向图中不存在任何从一个顶点出发,经过若干边的路径最终回到该顶点的环,那么这个有向图被称为一个“戴维南图”。
戴维南定理则指出,一个有向图是戴维南图等价于这个有向图的特征矩阵可以通过最优化调整,使得其主对角线都是非负的。
2. 验证戴维南定理为了验证戴维南定理的正确性,我们可以按照以下步骤进行:步骤一:根据给定的有向图,绘制其特征矩阵。
步骤二:检查特征矩阵中是否存在负数元素。
如果存在负数元素,则进行第三步;如果不存在负数元素,则该有向图是一个戴维南图。
步骤三:通过最优化调整特征矩阵,使得其主对角线上的元素都变为非负数。
步骤四:再次检查特征矩阵中是否还存在负数元素。
如果存在负数元素,则该有向图不是一个戴维南图;如果不存在负数元素,则该有向图是一个戴维南图。
通过以上步骤的验证过程,我们可以得出结论,从而验证戴维南定理的正确性。
3. 戴维南定理的应用戴维南定理在算法设计和图论中有着广泛的应用。
它提供了一种有效的方法来判断一个有向图是否存在环,从而可以在许多实际问题中得到应用。
例如,在任务调度中,通过验证某个任务调度图是否是一个戴维南图,可以判断该任务调度是否存在死循环等问题,从而保证任务调度的正确性和可行性。
此外,戴维南定理还在电路设计和网络优化等领域有着重要的应用。
通过验证电路图或网络拓扑图是否是一个戴维南图,可以有效地避免电路或网络中出现环路问题,提高系统的可靠性和性能。
4. 归纳总结通过对戴维南定理的验证过程和应用分析,我们可以得出以下结论:(1)戴维南定理是一个有效的方法来判断一个有向图是否存在环。
影像电子学基础1实验二戴维南定理验证9.2.2 戴维南定理

若有源二端网络的内阻值很低时,则不宜测 其短路电流。
5
三、实验设备
序号 设备名称 1 可调直流稳压电源 2 万用表(直流电压档) 3 直流数字电流表 4 电阻箱 5 电阻
设备型号 0-30V 0-1000V 0-200mA 0-9999:
有源 二端 网络
A E0=UAB
B
(a)
无源 二端
A R0=RAB
网络
B
(b)
A +
E0 -
R0
B (c)
返回主页
例1、在图一所示电路中,已知:E1=5V,R1=8Ω,E2=25V,R2=12Ω,R3=2.2Ω, 试用戴维南定理求通过R3的电流及R3两端的电压。
A
A
A
IA
R1
E2
I
U R3
E1
R2
R0=RAB= R1R2 = 8×12 =4.8Ω R1+R2 8+12
UAB=IR3=1×2.2=2.2V
解题步骤归纳
1、先断开待求的那条支路,移走负载使电路形成开路 状态,并假定两个端钮的电压极性及端子字母,如A、B。
2、求形成开路状态电路的开路电压UAB=E0。
3、将有源二端网络中的理想电压源用短接线代替,理 想电流源用开路代替,求无源二端网络的等效电阻RAB=R0。
2.根据实验步骤测得的Uab与R0与预习时电路计
13
(图一) B 解: E1–I1R2+E2–I1R1=0
R1
E2
E1
R2
I1
(a)
UAB B
R1
RAB R2
E0 U
R0
R3
B (b)
B (c)
戴维南定理和诺顿定理的验证实验+数据

戴维南定理和诺顿定理的验证实验+数据在电路分析中,戴维南定理和诺顿定理是两个非常重要的定理,它们为复杂电路的分析和简化提供了有力的工具。
为了深入理解和验证这两个定理,我们进行了一系列的实验,并对实验数据进行了详细的分析。
一、实验目的本次实验的主要目的是验证戴维南定理和诺顿定理的正确性,并通过实际测量和计算,加深对这两个定理的理解和应用能力。
二、实验原理1、戴维南定理任何一个线性含源一端口网络,对外电路来说,可以用一个电压源和电阻的串联组合来等效替代。
其中电压源的电压等于该一端口网络的开路电压 Uoc,电阻等于该一端口网络中所有独立电源置零后的等效电阻 Ro。
2、诺顿定理任何一个线性含源一端口网络,对外电路来说,可以用一个电流源和电阻的并联组合来等效替代。
其中电流源的电流等于该一端口网络的短路电流 Isc,电阻等于该一端口网络中所有独立电源置零后的等效电阻 Ro。
三、实验设备1、直流稳压电源2、直流电流表3、直流电压表4、电阻箱5、导线若干四、实验步骤1、按照实验电路图连接电路,其中被测一端口网络由电阻和电源组成。
2、测量一端口网络的开路电压 Uoc,即将外电路断开,用电压表测量端口的电压。
3、测量一端口网络的短路电流 Isc,即将端口直接短路,用电流表测量短路电流。
4、将一端口网络中的电源置零(电压源短路,电流源开路),然后用电阻箱测量端口的等效电阻 Ro。
5、根据戴维南定理,构建等效电路,即一个电压源 Uoc 和电阻 Ro 的串联电路,接入外电路,测量外电路的电流和电压。
6、根据诺顿定理,构建等效电路,即一个电流源 Isc 和电阻 Ro 的并联电路,接入外电路,测量外电路的电流和电压。
五、实验数据记录与分析1、实验数据记录一端口网络的参数:电源电压 E = 12 V,内阻 r =2 Ω,负载电阻Rl =10 Ω。
测量得到的开路电压 Uoc = 10 V。
测量得到的短路电流 Isc = 5 A。
戴维南定理验证实验报告

戴维南定理验证实验报告1. 引言嘿,大家好!今天我们来聊聊戴维南定理,这个听上去挺高大上的名字,其实背后是一种非常实用的电路分析方法。
简单说,戴维南定理告诉我们,任何一个复杂的线性电路都能被简化为一个电压源和一个电阻串联的形式。
这就像把一大堆乱七八糟的零食整理成一个好看的小礼包,方便又省事!通过这个实验,我们不仅能验证戴维南定理的正确性,还能加深对电路的理解,真是一举多得嘛!2. 实验准备2.1 实验材料在开始之前,我们得准备一些“装备”。
首先,我们需要一个电源,别小看这个小家伙,它可是实验的“动力源泉”。
然后,一些电阻,最好是不同阻值的,这样能给我们带来更多的乐趣。
接着,万用表也是必不可少的,它就像我们的“侦探”,帮我们测量电压和电流。
最后,当然少不了连接线,没这些线,那就像要做菜没锅一样,根本没法下手。
2.2 实验步骤好啦,材料都准备齐全了,咱们就可以开始动手了。
首先,按照原电路的连接方式,把电源和电阻连接起来,形成一个复杂的电路。
接着,用万用表测量电路中的电压和电流。
这里可得仔细点,别让数字跑了!然后,接下来就是关键的部分了,我们要用戴维南定理进行简化。
理论上,这个电路应该能被等效为一个电压源和一个电阻的组合,咱们得来验证一下这小家伙到底有多厉害。
3. 实验过程3.1 测量与记录实验开始后,大家都紧张兮兮的,仿佛要参加什么重要的比赛。
第一个步骤,先把电压和电流记录下来。
经过一番“较量”,我们测得电压是5伏特,而电流是0.5安培。
哎呀,这个数据可真是像小猫扑向小鱼一样可爱,让人忍不住想继续探索下去!接着,我们算了一下电阻值,根据欧姆定律(V=IR),得到了电阻是10欧姆。
嘿,这下子,咱们的电路特性清晰可见,就像太阳升起照亮大地!3.2 戴维南定理验证然后我们就开始进行简化了。
按照戴维南定理,我们要找出等效电压和等效电阻。
为了找到等效电压,我们把电源断开,测量开路电压。
经过一番调整,发现这个开路电压还是5伏特,真是意料之中,没让我们失望!接下来,咱们来计算等效电阻。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、实验目的
1.验证戴维南定理和诺顿定理的正确性,加深对该定理的理解。
2.掌握测量有源二端网络等效参数的一半方法。
二、实验设备
可调直流稳压电源、可调直流恒流源、直流数字电压表、直流数字电流表、万用表、元件箱、戴维南定理实验电路板
三、实验原理
1.戴维南定理指出:任何一个线性有源网络,总可以用一个电压
源与一个电阻的串联来等效代替,此电压源的电动势Us等于这个有源二端网络的开路电压Uoc,其等效内阻R0等于该网络中所有独立源均置零。
2.有源二端网络等效参数的测量方法
1)开路电压、短路电流法测R0
在有源二端网络输出端开路时,用电压表直接测其输出端的开路电压Uoc,然后再将其输出端短路,用电流表测其短路电流Isc,则其等效电阻为R0=Uoc/Isc
2)伏安法测R0
用电压表、电流表测出有源二端网络的外特性曲线,如图2-1所示。
根据外特性曲线求出斜率tgΦ,则内阻R0=tgΦ=ΔU/ΔI=Uoc/Isc
3)半电压法测R0
当负载电压为被测网络开路电压的一半时,负载电阻(由电阻箱的读书确定)即为被测有源二端网络的等效内阻值。
4)零示法测Uoc
在测量具有高内阻有源二端网络的开路电压时,用电压表直接测
量会造成较大误差,为了消除电压表内阻的影响,往往采用零示测量法。
零示测量法的原理是用一低内阻的稳压电源与被测有源二端网络进行比较,当稳压电源的输出电压与有源二端网络的开路电压相等时,电压表读数将为“0”,然后将电路断开,测量此时稳压电源的输出电压,即为被测有缘二端网络的开路电压。
四、实验内容
被测有源二端网络如图2-4(a)
图2-4(a)戴维南等效电路
图2-4(b)1.用开路电压、短路电流发测定戴维南等效电路的Uoc、R0和诺
顿等效电路的Isc、R0。
将图2-4(a)接入稳压电源Us=12V和
按图2-4(a)接入R L。
改变R L的阻值,测量有源二端网络的外特性曲线。
3.验证戴维南定理:从电阻箱上取得按步骤“1”所得的等效电
阻R0之值,然后令其与直流稳压电源(调到步骤“1”时所得的开路电压Uoc之值)相串联,如图2-4(b)所示,仿照步骤“2”测其外特性,对戴氏定理进行验证。
4.有源二端网络等效电阻(入端电阻)的直接测量法。
见图2-4
(a)。
将被测有源网络内的所有独立源置零(将电流源Is断开,去掉电压源Us,并在原电压源所接的两点用一根短路导线相连),然后用伏安法或者直接用万用表的欧姆档去测定负载R L 开路时A、B两点间的电阻,此即为北侧网络的等效内阻R0,或称网络的入端电阻Ri。
五、预习思考题
1.在求戴维南或诺顿等效电路时,作短路试验,测Isc的条件是
什么在本实验中可否直接作负载短路实验请实验前对线路2-4(a)预先做好计算,以便调整实验线路及测量时准确地选取
电表的量程。
答:作短路实验,测Isc的条件是:保留独立源和受控源,保证二端网络电阻较大,防止烧坏元件;本实验不能直接作负载短路实验。
2.说明有源二端网络开路电压及等效内阻的几种方法,并比较其
优点。
答:开路电压、短路电流法测R0,过程步骤简单,不用太多的运算和绘图;伏安法测R0,可以直观地从数据上看出电流和电压的关系;半电压法测R0,;零示法测Uoc,可以消除电压表内阻的影响,使实验数据更接近理论值。
六、实验报告
1.根据步骤2、3、4,分别绘出曲线,验证戴维南定理的正确性,
并分析产生误差的原因。
答:曲线如下,U1为原电路参数,U2为等效电路参数。
由上可见,以上数据基本符合戴维南定理,由于电路元件和电表的消耗,以及仪器误差的,所以数据与理论存在一定的差别,但是在可接受的误差范围内,还是可以得出戴维南定理的验证得出结果是准确的。
2.根据步骤1、5、6的几种方法测得的Uoc与R0与预习时电路
计算的结果作比较,你能得出什么结论。
答:计算结果为理论值,由步骤得出的数据与理论值存在一定的差距,实际操作中电压表和电流表会产生误差,元件的内阻会对电路产生一定的影响,所以在忽略可接受的误差的前提下,戴维南定理的验证得出结果是正确的。
3.归纳、总结实验结果。
答:实验过程中,由于测量有源二端网络开路电压及等效内阻的方法不同,存在的误差也不一样,所以综合本实验过程可得,实验过程中测
量数据与理论值不可能完全一样,但是忽略可接受的误差外,由数据可知,戴维南定理是准确的。
