数字电路与数字电子技术课后答案第四章(供参考)
数电第四章习题答案
第四章习题答案4.1 分析图4.1电路的逻辑功能解:(1)推导输出表达式Y2=X2;Y1=X1⊕X2;Y0=(MY1+X1⎺M)⊕X0A 、B 、C 、F 1、F 2分别表示被减数、减数、来自低位的借位、本位差、本位向高位的借位。
A BCF 1F 2-被减数减 数借 位差4.3分析图4.3电路的逻辑功能 解:(1)F 1=A ⊕B ⊕C ;F 2=(A ⊕B)C+AB (2)(3)4.4 设ABCD 是一个8421BCD 码,试用最少与非门设计一个能判断该8421BCD 码是否大于等于5的电路,该数大于等于5,F= 1;否则为0。
解:(1)列真值表10 1 1 010 1 0 100 1 0 000 0 1 110 1 1 100 0 1 000 0 0 100 0 0 0F A B C D Ø1 1 1 0Ø1 1 0 1Ø1 1 0 0Ø1 0 1 1Ø1 1 1 1Ø1 0 1 011 0 0 111 0 0 0F A B C D(2)写最简表达式F = A + BD + BC=⎺A · BD · BC&&&DBC AF&4.6 试设计一个将8421BCD码转换成余3码的电路。
(F2=⎺C⎺D+CD F1=⎺D 电路图略。
4.7 在双轨输入条件下用最少与非门设计下列组合电路:(1)F(ABC)=∑m(1,3,4,6,7)(2) F(ABCD)=∑m(0,2,6,7,8,10,12,14,15)解:F=⎺B⎺D+A⎺D+BC∑+∑m)3(φ(DCFAB,,,7,4,0(10=) ,)12),9,8,6,5,2(解:函数的卡诺图如下所示:4.10 电话室对3种电话编码控制,按紧急次序排列优先权高低是:火警电话、急救电话、普通电话,分别编码为11,10,01。
试设计该编码电路。
F 1=A+BF 2=BA +4.11 试将2/4译码器扩展成4/16译码器 解:A 3A 2A 1 A 0⎺Y 0⎺Y 1⎺Y 2⎺Y 3 ⎺Y 4 ⎺Y 5⎺Y 6⎺Y 7 ⎺Y 8⎺Y 9⎺Y 10⎺Y 11 ⎺ Y 12⎺Y 13⎺Y 14⎺Y 154.12 试用74138设计一个多输出组合网络,它的输入是4位二进制码ABCD ,输出为: F 1 :ABCD 是4的倍数。
数字电子技术第四章课后习题答案(江晓安等编)

第四章组合逻辑电路1. 解: (a)(b)是相同的电路,均为同或电路。
2. 解:分析结果表明图(a)、(b)是相同的电路,均为同或电路。
同或电路的功能:输入相同输出为“1”;输入相异输出为“0”。
因此,输出为“0”(低电平)时,输入状态为AB=01或103. 由真值表可看出,该电路是一位二进制数的全加电路,A为被加数,B为加数,C为低位向本位的进位,F1为本位向高位的进位,F2为本位的和位。
4. 解:函数关系如下:SF++⊕=+ABSABS BABS将具体的S值代入,求得F 312值,填入表中。
A A FB A B A B A A F B A B A A F A A F AB AB F B B A AB F AB B A B A B A AB F B A A AB F B A B A B A F B A AB AB B A B A F B B A B A B A B A B A B A F AB BA A A B A A B A F F B A B A F B A B A F A A F S S S S =⊕==+==+⊕===+⊕===⊕===⊕===+⊕===+=+⊕===⊕==+==⊕==Θ=+=+⊕===+++=+⊕===+=⊕===⊕==+=+⊕==+=+⊕===⊕==01111111011010110001011101010011000001110110)(01010100101001110010100011000001235. (1)用异或门实现,电路图如图(a)所示。
(2) 用与或门实现,电路图如图(b)所示。
6. 解因为一天24小时,所以需要5个变量。
P变量表示上午或下午,P=0为上午,P=1为下午;ABCD表示时间数值。
真值表如表所示。
利用卡诺图化简如图(a)所示。
化简后的函数表达式为D C A P D B A P C B A P A P DC A PD B A P C B A P A P F =+++=用与非门实现的逻辑图如图(b )所示。
数字电子技术基础(第四版)课后习题答案-第四章
第4章触发器[题4.1]画出图P4.1所示由与非门组成的基本RS触发器输出端Q、Q的电压波形,输入端S、R的电压波形如图中所示。
图P4.1[解]见图A4.1图A4.1[题4.2]画出图P4.2由或非门组成的基本R-S触发器输出端Q、Q的电压波形,输出入端S D,R D的电压波形如图中所示。
图P4.2[解]见图A4.2[题4.3]试分析图P4.3所示电路的逻辑功能,列出真值表写出逻辑函数式。
图P4.3 [解]:图P4.3所示电路的真值表S R Q n Q n+1 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 0* 1 110*由真值表得逻辑函数式 01=+=+SR Q R S Q nn[题4.4] 图P4.4所示为一个防抖动输出的开关电路。
当拨动开关S 时,由于开关触点接触瞬间发生振颤,D S 和D R 的电压波形如图中所示,试画出Q 、Q 端对应的电压波形。
图P4.4[解] 见图A4.4图A4.4[题4.5] 在图P4.5电路中,若CP 、S 、R 的电压波形如图中所示,试画出Q 和Q 端与之对应的电压波形。
假定触发器的初始状态为Q =0。
图P4.5[解]见图A4.5图A4.5[题4.6]若将同步RS触发器的Q与R、Q与S相连如图P4.6所示,试画出在CP信号作用下Q和Q端的电压波形。
己知CP信号的宽度tw= 4 t Pd 。
t Pd为门电路的平均传输延迟时间,假定t Pd≈t PHL≈t PLH,设触发器的初始状态为Q=0。
图P4.6图A4.6[解]见图A4.6[题4.7]若主从结构RS触发器各输入端的电压波形如图P4.7中所给出,试画Q、Q端对应的电压波形。
设触发器的初始状态为Q=0。
图P4.7[解] 见图A4.7图A4.7R各输入端的电压波形如图P4.8所示,[题4.8]若主从结构RS触发器的CP、S、R、D1S。
试画出Q、Q端对应的电压波形。
数字电路第四章习题答案

第四章习题4.4 由两个与非门构成的基本RS 触发器的输入如图P4.4所示,画出Q 和Q 端的波形。
图 P4.44.5 由两个或非门构成的基本RS 触发器的输入波形如图P4.5所示,画出输出Q 和Q 的波形。
图 P4.54.6 图P4.6是一个防抖动输出的开关电路。
当拨动开关S 时,由于开关触点接通瞬间发生振颤。
D S 和D R 的电压波形如图中所示,试画出Q 、Q 端对应的电压波形。
图P4.64.7 在同步RS触发器中,若CP、S、R的电压波形如图P4.7所示。
画出Q和Q端的波形。
设触发器的初始状态为Q=0。
图 P4.74.10 主从型JK触发器输入波形如图P4.10所示,画出输出端Q和Q的波形。
设触发器初始状态Q=0。
4.11 主从型JK 触发器组成图P4.11(a )所示电路,输入波形如图P4.11(b )所示,画出各触发器Q 端的波形。
(a )解:AB J 1 ,先画出J 的波形,然后画Q.。
4.12 主从型RS 触发器的CP 、S 、R 、DR各输入的电压波形如图P4.12所示,画出端Q 和Q 端对应的电压波形。
图 P4.124.14 维持阻塞D触发器构成图P4.14所示的电路,输入波形如图P4.14(b)所示。
画出各触发器Q段的波形。
触发器的初态均为0。
(b)图 P4.144.16 上升沿触发的维持阻塞型D触发器74LS74组成图(a)所示电路,输入波形如图(b)所示,画出Q1和Q2的波形,设Q初态为0。
4.20 画出图P4.20电路在图中所示CP、R信号作用下Q1、Q2、Q3的输出电压波形,并说明DQ1、Q2、Q3输出信号的频率与CP信号频率之间的关系。
CP1/21/4QQQ频率的、1/8。
、和的频率分别是、132。
数字电子技术基础(第4版)_课后习题答案

第一章1.1二进制到十六进制、十进制(1)(10010111)2=(97)16=(151)10 (2)(1101101)2=(6D)16=(109)10(3)(0.01011111)2=(0.5F)16=(0.37109375)10 (4)(11.001)2=(3.2)16=(3.125)10 1.2十进制到二进制、十六进制(1)(17)10=(10001)2=(11)16 (2)(127)10=(1111111)2=(7F)161621016210)3.19()1010 1(11001.101(25.7)(4))A D7030.6()0101 0000 0111 1101 0110 (0.0110(0.39)(3) B ====1.8用公式化简逻辑函数(1)Y=A+B (3)Y=1)=+(解:1A A 1)2(=+++=+++=+++=C B A C C B A C B Y CB AC B A Y ADC C B AD C B C B AD DC A ABD CD B A Y =++=++=++=)()(Y )4(解:(5)Y=0 (7)Y=A+CDE ABCD E C ABCD CE AD B BC CE AD B BC Y CE AD B BC B A D C AC Y =+=⋅+=+⋅=++++=)()()()()()6(解:CB AC B C B A A C B A C B A C B A C B C B A A C B A C B A C B A Y C B A C B A C B A Y +=++=+++=++++=++++⋅+=++++++=)())(())()(())()((8解:)(D A D A C B Y ++=)9(E BD E D BF E A AD AC Y ++++=)10(1.9 (a) C B C B A Y += (b) C B A ABC Y +=(c) ACD D C A D C A B A Y D AC B A Y +++=+=21,(d) C B A ABC C B A C B A Y BC AC AB Y +++=++=21, 1.10 求下列函数的反函数并化简为最简与或式(1)C B C A Y += (2)DC A Y++=CB C B AC C B AC B A BC AC C A B A BC AC C A B A Y BCAC C A B A Y +=++++=⋅+++=+++=+++=))((]))([())(())(()3(解: (4)C B A Y ++=DC ABD C B D C A D C B D A C A C D C B C A D A Y CD C B C A D A Y =++=+++=++++=+++=)())(())()(()5(解: (6)0=Y1.11 将函数化简为最小项之和的形式CB AC B A ABC BC A C B A C B A C B A ABC BC A CB A AC B B A BC A C B AC BC A Y CB AC BC A Y +++=++++=++++=++=++=)()()1(解:D C B A CD B A D C B A ABCD BCD A D C B A Y +++++=)(2)13()()()(3CD B A BCD A D BC A D C B A D C B A ABCD D ABC D C AB D C AB CD B A D C B A D C B A D C B A CD AB B A B A B A ACD D AC D C A D C A CD A D C A D C A D C A B BCD D BC D C B D C B CD B D C B D C B D C B A Y CDB A Y ++++++++++++=+++++++++++++++++++=++=解:)((4)CD B A D ABC D BC A D C AB D C AB CD B A ABCD BCD A Y +++++++= (5)MN L N M L N LM N M L N M L N M L Y +++++=1.12 将下列各函数式化为最大项之积的形式(1)))()((C B A C B A C B A Y ++++++= (2)))()((C B A C B A C B A Y ++++++= (3)76430M M M M M Y ⋅⋅⋅⋅= (4)13129640M M M M M M Y ⋅⋅⋅⋅⋅= (5)530M M M Y ⋅⋅=1.13 用卡诺图化简法将下列函数化为最简与或形式:(1)D A Y +=(3)1=Y (2)D C BC C A B A Y +++= (4)B AC B A Y ++=B A DC Y ++=AC B A Y +=(5)D C B Y ++= (6)C B AC B A Y ++=(7)C Y = (9)D C A C B D A D B Y +++=(8))14,11,10,9,8,6,4,3,2,1,0(),,,(m D C B A Y ∑= (10)),,(),,(741m m m C B A Y ∑=D A D C B Y ++=ABC C B A C B A Y ++=1.14化简下列逻辑函数(1)D C B A Y +++= (2)D C A D C Y += (3)C A D AB Y ++= (4)D B C B Y += (5)E D C A D A E BD CE E D B A Y +++++=1.20将下列函数化为最简与或式(1)AD D C B D C A Y ++= (2)AC D A B Y ++= (3)C B A Y ++= (4)D B A Y +=第二章2.1解:Vv v V V v T I mA I mA Vv T V v a o B o B BS B o B 10T 3.0~0(2.017.0230103.0207.101.57.05I V 5v 1021.5201.510V 0v )(i i ≈≈∴<=×≈=−≈∴−=×+−=截止,负值,悬空时,都行)饱和-=时,=当截止时,=当都行)=饱和,,-=悬空时,都行)饱和。
数电第四章习题答案

4.11图P4.11(a)所示各电路中,FF1~FF2均为边沿触发器:
1)写出各个触发器次态输出的函数表达式;
图P4.2
解答:见图A4.2
图A4.2
4.3一种特殊的RS触发器如图P4.3所示。
1)试列出状态转换真值表;
2)写出次态方程;
3)R与S是否需要约束条件?
图P4.3
解答:1)
①CP=0时,SS=1,RR=1,期间 ,状态保持。
2CP=1时,
即在CP=1的情况下:若R=0,S=0。则RR=1,SS=1,有 ,状态保持。
图P4.13
解答:根据电路图可知 ,而该电路中的触发器是CP上升沿触发的D触发器,其新态方程为: 。据已知的CP信号波形,可以画出A、B端的输出波形如图A4.13所示。
图A4.13
4.14什么是触发器的空翻现象?造成空翻的原因是什么?
解答:所谓触发器的“空翻”是指在同一个时钟脉冲作用期间触发器状态发生两次或两次以
图A4.17
4.18图P4.18一个扭环计数器,如果电路的初始状态为 ,试画出在一系列CP作用下的 、 、 、 波形(CP数目多于8)。
图P4.18
解答:从电路图可知, (CP上升沿时成立)
如果电路的初始状态为 ,可以画出在一系列CP作用下 、 、 、 的波形如图A4.18所示。
图A4.18
4.19据如图P4.19示的电路,试画出在8个CP作用下 、 、 的波形,假设电路的初始状态为 。
为使主从JK触发器按其特性表正常工作,在CP = 1期间,必须使JK端的状态保持
数字电路第四章答案

数字电路第四章答案【篇一:数字电路答案第四章时序逻辑电路2】p=1,输入信号d被封锁,锁存器的输出状态保持不变;当锁存命令cp=0,锁存器输出q?d,q=d;当锁存命令cp出现上升沿,输入信号d被封锁。
根据上述分析,画出锁存器输出q及 q的波形如习题4.3图(c)所示。
习题4.4 习题图4.4是作用于某主从jk触发器cp、j、k、 rd及 sd 端的信号波形图,试绘出q端的波形图。
解:主从jk触发器的 rd、且为低有效。
只有当rd?sd?1 sd端为异步清零和复位端,时,在cp下降沿的作用下,j、k决定输出q状态的变化。
q端的波形如习题4.4图所示。
习题4.5 习题4.5图(a)是由一个主从jk触发器及三个非门构成的“冲息电路”,习题4.5图(b)是时钟cp的波形,假定触发器及各个门的平均延迟时间都是10ns,试绘出输出f的波形。
cpf cp100ns10nsq(a)f30ns10ns(b)(c)习题4.5图解:由习题4.5图(a)所示的电路连接可知:sd?j?k?1,rd?f。
当rd?1时,在cp下降沿的作用下,且经过10 ns,状态q发生翻转,再经过30ns,f发生状态的改变,f?q。
rd?0时,经过10ns,状态q=0。
根据上述对电路功能的分析,得到q和f的波形如习题4.5图(c)所示。
习题4.6 习题4.6图(a)是一个1检出电路,图(b)是cp及j端的输入波形图,试绘出 rd端及q端的波形图(注:触发器是主从触发器,分析时序逻辑图时,要注意cp=1时主触发器的存储作用)。
cpj(a)qd(c)cp j(b)习题图解:分析习题4.6图(a)的电路连接:sd?1,k?0,rd?cp?q;分段分析习题4.6图(b)所示cp及j端信号波形。
(1)cp=1时,设q端初态为0,则rd?1。
j信号出现一次1信号,即一次变化的干扰,且k=0,此时q端状态不会改变;(2)cp下降沿到来,q端状态变为1,rd?cp,此时cp=0,异步清零信号无效;(3)cp出现上升沿,产生异步清零信号,使q由1变为0,在很短的时间里 rd又恢复到1;(4)同理,在第2个cp=1期间,由于j信号出现1信号,在cp下降沿以及上升沿到来后,电路q端和 rd端的变化与(2)、(3)过程的分析相同,其波形如习题4.6图(c)所示。
数字电子技术基础-课后习题答案第4章组合逻辑电路

第四章习题答案4-1(a)100A A F ⊕=,211A A F ⊕=,322A A F ⊕=,33A F =(b) 000B A C =,011111)()(C B A B A C ⊕+=,000B A S ⊕=,0111)(C B A S ⊕⊕= (c) B A AB F +=(同或)(d) B A AC F +=1,B A BC F +=2,C A BC F+=3, 4-2,F ,F ,F∑=)9,8,7,6,5(3m F ,∑=)9,4(2m F ,∑=)8,7,3,2(1m F ,∑=)8,6,3,1(0m F卡诺图化简D F =3,AD D C B F +=2,D A C B CD F ++=1,D B A D A F +=0,F ,F ,F∑=)9,8,7,6,5(3m Y ,∑=)9,4,3,2,1(2m Y , ∑=)8,7,4,3,0(1m Y ,∑=)8,6,4,2,0(0m Y用4-16线译码器实现987653F F F F F Y =,943212F F F F F Y =,874301F F F F F Y =,864200F F F F F Y =4-3将四片138译码器级联,ST 接高电平,ST 接低电平,ST 由译码控制3442A A ST =,3432A A ST =,3432A A ST =,3432A A ST =4-4113471347(1,3,4,7)F m m m m m F F F F ===∑ 2046046(0,4,6)F m m m m F F F ===∑4-51)一片8选1,输入A 、B 、C 分别接8选1的地址A 2,A 1,A 00,,1,17563420========D D D D D D D D D D2)两片8选1,输入A 、B 、C ,D 分别接4选1的地址012,,,A A A E1,01413121197651151084320================D D D D D D D D D D D D D D D D4-6A S SB A S S B A S S AB S S F 01010101)()(+⊕+++= A S S B A S S B A S S B S S A S S AB S S F 010*********+++++=将A S S ,,01分别接8选1的地址012,,A A A ,则输入端分别是0,1,,70635421========D D D D B D B D D D4-71) 输入A,B,C,D 分别接加法器的A 3,A 2,A 1,A 0, 加法器的B 3B 2B 1B 0=0011,CI=0 2) 输入A,B,C,D 分别接加法器的A 3,A 2,A 1,A 0, 加法器的B 3B 2B 1B 0=1101,CI=04-8假设四位被加数为ABCD ,加数为EFGH 输入A,B,C,D 分别接加法器的A 3,A 2,A 1,A 0, 加法器的B 3,B 2,B 1,B 0如下:M CI M H B M G B M F B M E B =⊕=⊕=⊕=⊕=,,,,01234-9真值表∑=)15,14,13,11,7(m F1)8选1数据选择器,将B A M ,,分别接8选1的地址012,,A A A ,则输入端分别是0,1,42107653========D D D D D C D D D2)用3-8译码器151413117151413117F F F F F m m m m m F ==4-10设三个开关分别为A,B,C ,开关的关闭为1,打开为0;灯的输出为F ,灯的亮为1,灭为0真值表C B A F =输入ABCD 分别接4-16译码器的地址段A 3,A 2,A 1,A 0 1) a 端:0158421=====D D D D D , 其余数据端接1 2) b 端:所有数据端均接1,1150=D D3) c 端:012109653======D D D D D D ,其余数据端接1 4) d 端:0158421=====D D D D D ,其余数据端接15) e 端:01514131187421=========D D D D D D D D D ,其余数据端接1 6) f 端:1150==D D ,其余数据端接07) g 端:08421====D D D D ,其余数据端接1设输出灯亮为1,灭为0真值表如下:1)4-16输入ABCD 分别接4-16译码器的地址段A 3,A 2,A 1,A 0(1) F 1端:143210=====D D D D D , 其余数据端接0 (2) F 2端:198765=====D D D D D , 其余数据端接0 (3) F3端:1151413121110======D D D D D D , 其余数据端接0 2)4位数据比较器实现用两片数据选择器,输入端ABCD 分别接两个比较器的A 3A 2A 1A 0,第一片比较器的B 3B 2B 1B 0=0101,第二片的B 3B 2B 1B 0=1001,两片的级联端0,1===<>=B A B A B A I I I ,则:B A I F <=11,B A I F >=23,212F F F =用4-16输入A 1A 0B 1B 0分别接4-16译码器的地址段A 3,A 2,A 1,A 0 (1) F 0端:1151375====D D D D , 其余数据端接0(2) F 1端:1141311976======D D D D D D , 其余数据端接0 (3) F 2端:1141110===D D D , 其余数据端接0 (4) F 3端:115=D , 其余数据端接04-141)只要把两片的B A I =直接相连就可以判断三个输入数据是否相等,假定输入为ABCD 四门课程,及格为1,不及格为0;输出F 为能否毕业,能够毕业为1,不能毕业为0。
数字电子技术基础第四章习题及参考答案

数字电子技术基础第四章习题及参考答案第四章习题1.分析图4-1中所示的同步时序逻辑电路,要求:(1)写出驱动方程、输出方程、状态方程;(2)画出状态转换图,并说出电路功能。
CPY图4-12.由D触发器组成的时序逻辑电路如图4-2所示,在图中所示的CP脉冲及D作用下,画出Q0、Q1的波形。
设触发器的初始状态为Q0=0,Q1=0。
D图4-23.试分析图4-3所示同步时序逻辑电路,要求:写出驱动方程、状态方程,列出状态真值表,画出状态图。
CP图4-34.一同步时序逻辑电路如图4-4所示,设各触发器的起始状态均为0态。
(1)作出电路的状态转换表;(2)画出电路的状态图;(3)画出CP作用下Q0、Q1、Q2的波形图;(4)说明电路的逻辑功能。
图4-45.试画出如图4-5所示电路在CP波形作用下的输出波形Q1及Q0,并说明它的功能(假设初态Q0Q1=00)。
CPQ1Q0CP图4-56.分析如图4-6所示同步时序逻辑电路的功能,写出分析过程。
Y图4-67.分析图4-7所示电路的逻辑功能。
(1)写出驱动方程、状态方程;(2)作出状态转移表、状态转移图;(3)指出电路的逻辑功能,并说明能否自启动;(4)画出在时钟作用下的各触发器输出波形。
CP图4-78.时序逻辑电路分析。
电路如图4-8所示:(1)列出方程式、状态表;(2)画出状态图、时序图。
并说明电路的功能。
1C图4-89.试分析图4-9下面时序逻辑电路:(1)写出该电路的驱动方程,状态方程和输出方程;(2)画出Q1Q0的状态转换图;(3)根据状态图分析其功能;1B图4-910.分析如图4-10所示同步时序逻辑电路,具体要求:写出它的激励方程组、状态方程组和输出方程,画出状态图并描述功能。
1Z图4-1011.已知某同步时序逻辑电路如图4-11所示,试:(1)分析电路的状态转移图,并要求给出详细分析过程。
(2)电路逻辑功能是什么,能否自启动?(3)若计数脉冲f CP频率等于700Hz,从Q2端输出时的脉冲频率是多少?CP图4-1112.分析图4-12所示同步时序逻辑电路,写出它的激励方程组、状态方程组,并画出状态转换图。
数字电子技术基础 第04章触发器习题解
Q
Q
R=1、S=0 不管原Q取0还是1使Q=0
R=0、S=1 不管原Q取0还是1使Q=1
R=1、S=1 使两个输出同时为0,是不允许出现 的,作为约束处理。
G1 ≥1
≥1 G2
将原状态作为变量,次态作为
R
S
函数列出特性表
R
S
Q n Q n+1
0
0
00
由状态转换表化简得 到特性方程
0
0
11
0
1
01
0
1
解:(1)特性方程为
Qn+1 1
=
D1 ,Q2n+1
=
D2
1D Q
驱动方程和输出方程为
C1
D1
=
n
Q2 , D2
=
Q1n , F
=
CP
⊕
Q1n
CP
代入得状态方程
Qn+1 1
=
Q
n 2
,
Q2n +
1
=
Q1n
从状态方程可得:
CP
Q1
1D Q
Q2
C1 R
=1 F
Q1
Q2 Q1n+1 Q2n+1 F
Q1
0
0
主从触发器有时钟控制,在CP=1期间接收数据,在 CP后沿发生翻转,不属于完全的时钟沿触发,有 一次变化缺点。
边沿触发器有时钟控制,在CP的边沿接收数据和发 生翻转,是一种较理想的触发器。
4.5 设图4.28中各触发器的初始状态皆为Q=0,画出在CP脉 冲连续作用下个各触发器输出端的波形图。
解:图1,2,5为时钟后沿翻 转,图3为时钟前沿翻转, 图4,6为保持原状态
数字电路第四章答案

数字电路第四章答案【篇一:数字电路答案第四章时序逻辑电路2】p=1,输入信号d被封锁,锁存器的输出状态保持不变;当锁存命令cp=0,锁存器输出q?d,q=d;当锁存命令cp出现上升沿,输入信号d被封锁。
根据上述分析,画出锁存器输出q及 q的波形如习题4.3图(c)所示。
习题4.4 习题图4.4是作用于某主从jk触发器cp、j、k、 rd及 sd 端的信号波形图,试绘出q端的波形图。
解:主从jk触发器的 rd、且为低有效。
只有当rd?sd?1 sd端为异步清零和复位端,时,在cp下降沿的作用下,j、k决定输出q状态的变化。
q端的波形如习题4.4图所示。
习题4.5 习题4.5图(a)是由一个主从jk触发器及三个非门构成的“冲息电路”,习题4.5图(b)是时钟cp的波形,假定触发器及各个门的平均延迟时间都是10ns,试绘出输出f的波形。
cpf cp100ns10nsq(a)f30ns10ns(b)(c)习题4.5图解:由习题4.5图(a)所示的电路连接可知:sd?j?k?1,rd?f。
当rd?1时,在cp下降沿的作用下,且经过10 ns,状态q发生翻转,再经过30ns,f发生状态的改变,f?q。
rd?0时,经过10ns,状态q=0。
根据上述对电路功能的分析,得到q和f的波形如习题4.5图(c)所示。
习题4.6 习题4.6图(a)是一个1检出电路,图(b)是cp及j端的输入波形图,试绘出 rd端及q端的波形图(注:触发器是主从触发器,分析时序逻辑图时,要注意cp=1时主触发器的存储作用)。
cpj(a)qd(c)cp j(b)习题图解:分析习题4.6图(a)的电路连接:sd?1,k?0,rd?cp?q;分段分析习题4.6图(b)所示cp及j端信号波形。
(1)cp=1时,设q端初态为0,则rd?1。
j信号出现一次1信号,即一次变化的干扰,且k=0,此时q端状态不会改变;(2)cp下降沿到来,q端状态变为1,rd?cp,此时cp=0,异步清零信号无效;(3)cp出现上升沿,产生异步清零信号,使q由1变为0,在很短的时间里 rd又恢复到1;(4)同理,在第2个cp=1期间,由于j信号出现1信号,在cp下降沿以及上升沿到来后,电路q端和 rd端的变化与(2)、(3)过程的分析相同,其波形如习题4.6图(c)所示。
数字电子技术基本(第四版)课后知识题目解析第四章
第4章触发器[题4.1]画出图P4.1所示由与非门组成的基本RS触发器输出端Q、Q的电压波形,输入端S、R的电压波形如图中所示。
图P4.1[解]见图A4.1图A4.1[题4.2]画出图P4.2由或非门组成的基本R-S触发器输出端Q、Q的电压波形,输出入端S D,R D的电压波形如图中所示。
图P4.2[解]见图A4.2[题4.3] 试分析图P4.3所示电路的逻辑功能,列出真值表写出逻辑函数式。
图P4.3[解]S R Q n Q n+1 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 0* 1 110*由真值表得逻辑函数式 01=+=+SR Q R S Q nn[题4.4] 图P4.4所示为一个防抖动输出的开关电路。
当拨动开关S 时,由于开关触点接触瞬间发生振颤,D S 和D R 的电压波形如图中所示,试画出Q 、Q 端对应的电压波形。
图P4.4[解]见图A4.4图A4.4[题4.5]在图P4.5电路中,若CP、S、R的电压波形如图中所示,试画出Q和Q端与之对应的电压波形。
假定触发器的初始状态为Q=0。
图P4.5[解]见图A4.5图A4.5[题4.6]若将同步RS触发器的Q与R、Q与S相连如图P4.6所示,试画出在CP 信号作用下Q和Q端的电压波形。
己知CP信号的宽度t w = 4 t Pd 。
t Pd为门电路的平均传输延迟时间,假定t Pd≈t PHL≈t PLH,设触发器的初始状态为Q=0。
图P4.6图A4.6[解]见图A4.6[题4.7]若主从结构RS触发器各输入端的电压波形如图P4.7中所给出,试画Q、Q 端对应的电压波形。
设触发器的初始状态为Q=0。
图P4.7[解] 见图A4.7图A4.7[题4.8]若主从结构RS触发器的CP、S、R、D R各输入端的电压波形如图P4.8所S。
试画出Q、Q端对应的电压波形。
示,1D图P4.8[解] 见图A4.8图A4.8[题4.9]已知主从结构JK触发器输入端J、K和CP的电压波形如图P4.9所示,试画出Q、Q端对应的电压波形。
数字电子技术第四章习题答案

第四章习题答案
4.1 Y=A’B’C’+A’BC+AB’C+ABC’
A 0 0 0 0 1 1 1 1 B 0 0 1 1 0 0 1 1 C 0 1 0 1 0 1 0 1 Y 1 0 0 1 0 1 1 0
三变量奇偶检测电 路,当输入便两种 有偶数个1 有偶数个1时,输出 否则为0 为1,否则为0。
《数字电子技术基础》第五版 数字电子技术基础》
4.12 用3线-8线译码器实现多输出逻辑函数。 线译码器实现多输出逻辑函数。 线 线译码器实现多输出逻辑函数
' ' Y1 = AC = AB ' C + ABC = m5 + m7 = ( m5 m7 )' = (Y5'Y7' )' ' ' ' ' Y2 = A ' B ' C + AB ' C '+ BC = ( m1m3 m4 m7 )' = (Y1'Y3'Y4'Y7' )' ' ' ' Y3 = B ' C '+ ABC ' = ( m0 m4 m6 )' = (Y0'Y4'Y6' )'
Y’2(2) 1 1 0 1 1
Y’2(1) 1 1 1 0 1
D2 1 1 1 1 0
设片1优先级别 设片 优先级别 最低, 优先 最低,片4优先 级别最高。 级别最高。 输出5位数为原 输出 位数为原 码D4D3D2D1D0
《数字电子技术基础》第五版 数字电子技术基础》
数电第四章练习册答案

数电第四章练习册答案问题1:解释什么是逻辑门,并给出常见的逻辑门类型。
答案:逻辑门是数字电路中的基本组件,用于实现基本的逻辑运算,如与(AND)、或(OR)、非(NOT)、异或(XOR)等。
常见的逻辑门类型包括:与门(AND)、或门(OR)、非门(NOT)、异或门(XOR)、与非门(NAND)、或非门(NOR)、同或门(XNOR)等。
问题2:描述二进制数和十进制数之间的转换方法。
答案:二进制数转换为十进制数的方法是将每个二进制位的值乘以其权重(2的幂),然后将结果相加。
十进制数转换为二进制数的方法是将十进制数除以2,取余数,然后继续除以2,直到结果为0。
问题3:什么是布尔代数?答案:布尔代数是一种数学系统,用于描述和操作逻辑运算。
它是数字电路设计中的基础,由布尔代数的基本原理和规则组成,如布尔代数的五个基本规则:交换律、结合律、分配律、德摩根定律和幂等律。
问题4:解释什么是组合逻辑电路,并给出一个例子。
答案:组合逻辑电路是一种数字电路,其输出仅依赖于当前的输入值,不包含存储元件。
一个常见的组合逻辑电路例子是加法器,它接受两个二进制数作为输入,并产生它们的和以及进位。
问题5:什么是时序逻辑电路?答案:时序逻辑电路是一种包含存储元件(如触发器)的数字电路,其输出不仅依赖于当前的输入值,还依赖于电路的历史状态。
一个常见的时序逻辑电路例子是寄存器,它可以存储一定数量的位,并在时钟信号的控制下更新其内容。
问题6:解释什么是触发器,并说明其功能。
答案:触发器是一种具有两个稳定状态的存储元件,它可以存储一位二进制信息。
触发器的功能是存储和转换信息,它们是构成更复杂时序逻辑电路的基本组件。
结束语:通过本章的练习,希望同学们能够加深对数字电子技术的理解,掌握逻辑门、二进制与十进制转换、布尔代数、组合逻辑电路和时序逻辑电路等基本概念和原理。
这些知识是数字电子技术领域的基石,对于未来深入学习和应用数字电路至关重要。
希望同学们能够不断练习,提高自己的理解和应用能力。
数字电子技术基础第四章习题答案
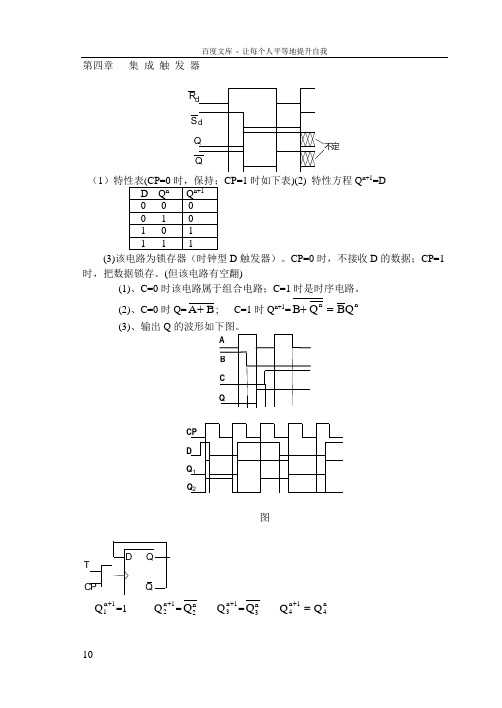
第四章 集 成 触 发 器R d S d Q Q不定(1CP=1时如下表)(2) 特性方程Q n+1=D(3)该电路为锁存器(时钟型D 触发器)。
CP=0时,不接收D 的数据;CP=1时,把数据锁存。
(但该电路有空翻)(1)、C=0时该电路属于组合电路;C=1时是时序电路。
(2)、C=0时Q=A B +; C=1时Q n+1=B Q BQ nn+= (3)、输出Q 的波形如下图。
A B C QCP D Q 1Q 2图DQ QCPTQ 1n 1+=1 Q 2n 1+=Q 2n Q n 13+=Q n3 Q Q 4n 14n +=1、CP 作用下的输出Q 1 Q 2和Z 的波形如下图;2、Z 对CP 三分频。
DQ QCPQ1DQ QQ2ZRd CP Q1Q2Z1由Q D J Q KQ J Q KQ n 1n n n n +==+=⋅得D 触发器转换为J-K 触发器的逻辑图如下面的左图;而将J-K 触发器转换为D 触发器的逻辑图如下面的右图CPD Q QJKQ QDQ QJ KCPCP B CACP X Q1Q2Z1、555定时器构成多谐振荡器2、u c, u o 1, u o 2的波形3、u o 1的频率f 1=1074501316..H z ⨯⨯≈ u o 2的频率f 2=158H z4、如果在555定时器的第5脚接入4V 的电压源,则u o 1的频率变为1113001071501232....H z ⨯⨯+⨯⨯≈图(a)是由555定时器构成的单稳态触发电路。
1、工作原理(略);2、暂稳态维持时间t w ==10ms(C 改为1μF);3、u c 和u o 的波形如下图:u ou ct t tu i (ms)(ms)(ms)5 10 25 30 45 503.33V4、若u i 的低电平维持时间为15m s ,要求暂稳态维持时间t w 不变,可加入微分电路由555定时器构成的施密特触发器如图(a)所示 1、电路的电压传输特性曲线如左下图; 2、u o 的波形如右下图;3、为使电路能识别出u i 中的第二个尖峰,应降低555定时器5脚的电压至3V 左右。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4) F=ΠM(5,7,13,15)
= BD
F= +
(5) F=ΠM(1,3,9,10,11,14,15)
= AC+ D
F = ( + )(B+ )
(6) F=∑m (0,2,4,9,11,14,15, 16,17,19,23,25,29,31)
F= + + BCD+ B E+AB E+ACDE+A +A E
= A⊙B⊙C
(6) = ⊙ ⊙
证:
左=
= [(A⊕B)+ ] (A⊙B)+C]
= (A⊙B) +[(A⊕B)C]
= +AB + BC+A C
右= ( ⊙ )⊙
= [( ⊙ ) + ]
= [( +AB) + ]
= +AB +
= +AB +(A⊕B)C
= +AB + BC+A C
9.证明
(1)如果a + b = c,则a + c = b,反之亦成立
(2)F在输入组合为1,3,5,7时使F=1
15.变化如下函数成另一种标准形式
(1) F=∑m (1,3,7)
(2) F=∑m (0,2,6,11,13,14)
(3) F=ΠM(0,3,6,7)
(4) F=ΠM(0,1,2,3,4,6,12)
解:
(1)F=ΠM(0,2,4,5,6)
(2)F=ΠM(1,3,4,5,7,8,9,10,12,15)
(3)F=∑m (1,2,4,5)
(4)F=∑m (5,7,8,9,10,11,13,14,15)
16.用图解法化简下列各函数
(1)化简题12中(1),(3),(5)
(2) F=∑m (0,1,3,5,6,8,10,15)
(3) F=∑m (4,5,6,8,10,13,14,15)
(4) F=ΠM(5,7,13,15)
( b )
图( 2 )
= D+B + D+ B
F= (A+ )( +C) B+ ) A+ ) =
(3) F= A + C+ CD
( b )
图( 3 )
= +AB
F= (A+C) + ) =
(4) F= AB+ C+ C
( b )
图( 4 )
= +
F = (A+C) (B+C) =
19.将下列各函数化简为与或非表达式,并用与或非门实现.
= ( +AB)(A+B)
= AB+AB
= AB=∑m (3)
=ΠM(0,1,2)
(2)F= (A⊕B)+ ( C+B )
= B+A + C+ B
= B+A + C
=∑m (1,2,3,4,5)
=ΠM(0,6,7)
12.用公式法化简下列各式
(1) F= A+AB +ABC+BC+B
解:
F= A(1+B +BC)+B(C+1) = A+B
(5)F= (x+y+z+ ) (v+x) ( +y+z+ )
解:
F`= xyz +vx+ yz
= vx+ yz +xyz
= vx+ yz
F``= F= (v+x) ( +y+z+ )
13.指出下列函数在什么输入组合时使F=0
(1) F=∑m (0,1,2,3,7)
(2) F=∑m (7,8,9,10,11)
= + +C+
=1
(4)x+wy+uvz
= (x+u+w) (x+u+y) (x+v+w) (x+v+y) (x+z+w) (x+z+y)
证:
对等式右边求对偶,设右边=F,则
F`= xuw+xuy+xvw+xvy+xzw+xzy
= xu (w+y)+xv (w+y) +xz (w+y)
= (w+y) (xu+xv+xz)
解:
y不一定等于z,因为若x = 0时,不论取何值则xy = xz = 0,逻辑与的特点,有一个为0则输出为0。
7.若已知x+y = x+z
Xy = xz问y = z吗?为什么?
解:
y等于z。因为若x = 0时,0+y = 0+z,∴y = z,所以xy = xz = 0,若x = 1时, x+y = x+z = 1,而xy = xz式中y = z要同时满足二个式子y必须等于z。
(3) F=∑m (0,1,4,5,12,13)
(4) F=ΠM(4,5,6,7,9,10,11,12)
解: 圈“1”格化简
(1)F=∑m (0,1,3,4,6,7,10,11,13,14,15)
( b )
图(1)
F= AC+BC+ D+ +ABD =
(2) F=∑m (0,2,3,4,5,6,7,12,14,15)
(2)如果 +ab = 0,则 = a +b
证:
(1)a + c = a ( )+ (a + b)
= a (ab+ )+ b
= ab+ b = b
(2) +ab = 0说明a = 或b =
= =
= ( + )(a+ )
= a + +
= a +
= a +b
10.写出下列各式F和它们的对偶式,反演式的最小项表达式
(1)F= ABCD+ACD+B
(2)F= A + B+BC
(3)F= +
解:
(1)F=∑m
=∑m (0,1,2,3,5,6,7,8,9,10,13,14)
F`=∑m (15,14,13,12,10,9,8,7,6,5,2,1)
(2)F=∑m (2,3,4,5,7)
=∑m (0,1,6)
F`=∑m (7,6,1)
8.用公式法证明下列个等式
(1) + +BC+ = +BC
证:
左= + BC +
= + BC + = (1+ ) + BC
= +BC =右边
(2) C +B D+ACD+ B + CD+B +BCD= C+B +BD
证:
左= ( C + CD+ACD )+(ABCD+BCD+B D)+(B D+B + B )
(7) F=∑m (0,2,4,5,7,9,13,14,15,16,18,20,21,23,25,29,30,31)
F= ACE+B E+BCD+ C +
17.将下列各函数化简成与非一与非表达式,并用与非门实现
(1) F=∑m (0,1,3,4,6,7,10,11,13,14,15)
(2) F=∑m (0,2,3,4,5,6,7,12,14,15)
(3)F=∑m (1,5,6,7,8,913,14,15)
=∑m (0,1,3,4,10,11,12)
F`=∑m (15,13,12,11,5,4,3)
11.将下列函数表示成最大项之积
(1) F= (A⊙B)(A+B)+(A⊙B)AB
(2) F= (A⊕B)+ (B⊕C)
解:
(1)F= (A⊙B) A+B+AB)
(5) F=ΠM(1,3,9,10,11,14,15)
(6) F=∑m (0,2,4,9,11,14,15,16,17,19,23,25,29,31)
(7) F=∑m (0,2,4,5,7,9,13,14,15,16,18,20,21,23,25,29,30,31)
解:
(1)化简题12中(1),(3),(5)
解:
(1)AB = 00或AB=11时F=1
(2)ABC110或111,或001,或011时F=1
(3)ABC = 100或101或110或111时F=1
3.用真值表证明下列等式.
(1) A+BC = (A+B) (A+C)
(2) BC+A C+AB = BC +AC +AB
(3) =ABC+
(4) AB+BC+AC=(A+B)(B+C)(A+C)
( b )
图( 2 )
F= C+BC+ +B + B =
(3) F=∑m (0,1,4,5,12,13)
( b )
F= +B =
图( 3 )
(4) F=ΠM(4,5,6,7,9,10,11,12)
( b )
图( 4 )
F = +ABD+ABC+ =
