资料分析公式大全
资料分析公式汇总

资料分析公式汇总在进行资料分析时,掌握一些关键的公式可以帮助我们更高效、准确地处理和解读数据。
以下是为大家汇总的一些常用公式:一、增长相关公式1、增长量=现期量基期量增长量用于衡量数据在一定时期内的绝对增长幅度。
2、增长率=增长量÷基期量×100%这个公式反映了数据增长的相对速度。
3、基期量=现期量÷(1 +增长率)当我们已知现期量和增长率,要求出之前某个时期的量时,就会用到这个公式。
4、现期量=基期量×(1 +增长率)通过基期量和增长率来计算当前时期的量。
二、比重相关公式1、比重=部分÷整体×100%比重表示部分在整体中所占的比例。
2、整体=部分÷比重已知部分和其占整体的比重,可求出整体的量。
3、部分=整体×比重根据整体的量和部分所占的比重,能计算出部分的量。
三、平均数相关公式1、平均数=总数÷个数这是计算平均数最基本的公式。
2、总数=平均数×个数当已知平均数和个数时,可求出总数。
四、倍数相关公式1、 A 是 B 的几倍:A÷B直接用 A 的数值除以 B 的数值,得到 A 是 B 的倍数。
2、 A 比 B 多几倍:(A B)÷B先计算 A 与 B 的差值,再除以 B 的数值。
五、隔年增长相关公式1、隔年增长率=现期增长率+间期增长率+现期增长率×间期增长率例如,今年的增长率为 r1,去年的增长率为 r2,那么隔年增长率就是 r1 + r2 + r1×r2 。
2、隔年基期量=现期量÷(1 +隔年增长率)六、年均增长相关公式1、年均增长量=(末期量初期量)÷年份差用于计算在一定年份内平均每年的增长量。
2、年均增长率=(末期量÷初期量)^(1÷年份差) 1七、混合增长率相关公式整体增长率介于部分增长率之间,且偏向于基期量大的部分增长率。
资料分析常考公式

资料分析常考公式一、基期与现期1.基期量=现期量-增长量=现期量/(1+r),当|r|≤5%,可化除为乘,现期量/(1+r)≈现期量×(1-r)2.现期量=基期量+增长量=基期量×(1+r)常见考法:基期量或现期量计算,基期量、现期量和差计算及大小比较。
基期比较:①当现期相差比较大,直接看量级;②现期相差不大,给出了现期和增长率,直接截位直除(根据选项差距来判断截取几位)。
二、增长量1.增长量=现期量-基期量(选项与材料精确度一样且尾数不同,可用尾数法;选项差距较大,首位法或者截位相加减)2.增长量=现期量×增长率/(1+增长率)(常用特殊分数法,增长率为正,用n+1;增长率为负,用n-1)3.年(月)均增长量=(末期-初期)/年(月)份差常见考法:增长量的计算及大小比较。
增长量比较口诀:“大大则大”,即当现期和增长率都大时,增长量也大;“一大一小”,主要看现期×增长率。
三、增长率r =(现期量-基期量)/基期量=增长量/基期量=现期量/基期量-1=增长量/(现期量-增长量)常见考法:增长率计算及大小比较增长率比较:①直接用现期量/基期量进行比较;②当基期量相差不大时,直接比较增长量大小;③分数比较(主要方法:首位法、截位直除、差分法)特殊增长率1.混合增长率:混合增长率介于部分增长率之间,且偏向基期较大的一方(用于判断大小范围);用线段法或十字交叉法估算具体数值。
2.间隔增长率:r=r1+r2+r1r2。
3.年均增长率:(1+年均增速)^n=末期/基期,n为年份差,计算时长代入10%、20%等中间值来判断年均增速的范围,进而确定选项。
四、比重1.比重=部分量/整体量,部分量=整体量×比重,整体量=部分量/比重2.现期比重=B/A (B为部分量,A为整体量)3.基期比重=B/A×(1+a)/(1+b)(B为部分量,b为部分量增速,A为整体量,a为整体量增速)4.两期比重差=B/A×(b-a)/(1+b)常见考法:比重计算和比较;两期比重判断:部分量增速大于整体量增速,比重上升;部分量增速小于整体量增速,比重下降。
资料分析计算公式整理

资料分析计算公式整理在进行资料分析时,掌握一些关键的计算公式是至关重要的。
这些公式能够帮助我们快速、准确地从大量的数据中提取有价值的信息,做出合理的判断和决策。
下面,我将为大家整理一些常见且实用的资料分析计算公式。
一、增长率相关公式1、增长率=(现期量基期量)÷基期量× 100%这是最基本的增长率计算公式。
例如,某公司去年的销售额为 100 万元,今年为 120 万元,那么今年的销售额增长率为(120 100)÷ 100 × 100% = 20%。
2、间隔增长率= r1 + r2 + r1×r2当涉及到间隔年份的增长率计算时,就需要用到这个公式。
假设第一年的增长率为 r1,第二年的增长率为 r2,那么从第一年到第二年的间隔增长率就是 r1 + r2 + r1×r2。
3、年均增长率=\(\sqrtn{\frac{现期量}{基期量}} 1 \)(n 为年份差)如果要计算一段时间内的平均增长率,就用这个公式。
比如,某地区 2010 年的 GDP 为 100 亿元,2020 年为 200 亿元,年份差为 10 年,那么年均增长率=\(\sqrt10{\frac{200}{100}} 1 \)。
1、比重=部分量÷整体量× 100%比如,某班级共有 50 名学生,其中男生 25 人,那么男生在班级中的比重就是 25÷50× 100% = 50%。
2、整体量=部分量÷比重已知部分量和比重,求整体量时使用。
假设某企业某产品的销售额占总销售额的 30%,该产品销售额为 100 万元,那么企业总销售额=100÷30% 。
3、部分量=整体量×比重当已知整体量和比重,求部分量时运用。
比如一个城市总人口为100 万人,其中老年人占比 20%,那么老年人的数量= 100×20% = 20 万人。
资料分析公式汇总

资料分析公式汇总资料分析公式的汇总在社会科学、自然科学、工程技术等领域,资料分析是一项非常重要的研究方法。
通过对大量的数据进行收集、整理和处理,可以得出对问题的解释和预测。
而资料分析公式则是在这个过程中广泛应用的一种工具。
本文将对一些常见的资料分析公式进行汇总和解释。
一、中心趋势测量公式1. 平均数公式:平均数是将一组数据的总和除以数据的个数得出的数值,用来代表这组数据的中心趋势。
计算公式如下:平均数 = 总和 / 数据个数2. 中位数公式:中位数是将一组数据按大小顺序排列后,位于中间位置的数值。
如果数据个数为奇数,则中位数就是中间的数值;如果数据个数为偶数,则中位数是中间两个数值的平均值。
3. 众数公式:众数是指在一组数据中出现频率最高的数值。
有时候一组数据中可能存在多个众数,这时可以将所有的众数列举出来。
二、离散程度测量公式1. 范围(R)公式:范围是用于度量一组数据的离散程度的指标,其计算公式如下:范围 = 最大值 - 最小值2. 方差(S²)公式:方差是一组数据偏离平均数的平方差的平均值,用于度量一组数据的离散程度。
计算公式如下:方差= ∑(Xi - 平均数)² / 数据个数3. 标准差(S)公式:标准差是方差的平方根,用于度量一组数据的离散程度的更常用指标。
计算公式如下:标准差= √方差三、相关关系测量公式1. 相关系数(r)公式:相关系数用于度量两组数据之间的相关性,其取值范围在-1到1之间。
相关系数越接近于1或-1,表示两组数据之间的相关性越强,越接近于0则表示两组数据之间的相关性越弱。
计算公式如下:相关系数r = ∑(Xi - 平均数X)(Yi - 平均数Y)/ √[∑(Xi - 平均数X)²] * √[∑(Yi - 平均数Y)²]2. 斯皮尔曼相关系数公式:斯皮尔曼相关系数也是度量两组数据之间的相关性的指标,但它适用于非线性关系的数据。
计算公式如下:斯皮尔曼相关系数 rs = 1 - 6 * ∑(Di²) / (n³ - n)四、回归关系测量公式1. 简单线性回归公式:简单线性回归是通过拟合一条直线来建立两组数据之间的线性关系,从而进行预测和解释的方法。
资料分析相关公式汇总

增长量相关1. 基期量已知现期量、增长率,基本公式:基期量=现期量/(1+增长率)。
已知现期量、增长量,基本公式:基期量=现期量-增长量。
2. 增长率已知基期量、增长量。
基本公式:增长率=增长量/基期量。
已知现期量、基期量。
基本公式: 增长率=(现期量-基期量)/基期量。
已知现期量、增长量。
基本公式:增长率=增长量/(现期量-基期量)。
3. 隔年增长率已知现期与间期的增长率,那么现期相对于基期的增长率为:隔年增长率=现期增长率+间期增长率+现期增长率*间期增长率。
比重相关1. 现期比重已知部分值、整体值,求比重。
基本公式:比重=部分值/整体值已知整体值、比重,求部分值。
基本公式:部分值=整体值*比重已知部分值、比重,求整体值。
基本公式:整体值=部分值/比重2. 基期比重部分值的现期量A,部分值的现期增长率q A,整体值的现期量B,整体值的现期增长率q B,则基期比重为:3. 比重变化分子部分所对应的增长速度>分母部分所对应的增长速度,则现期比重>基期比重,即比重值上升。
反之,平均数与倍数1. 平均数已知总体值、份数,求平均数。
基本公式:平均数=总数/份数2. 年均增长量已知末期值、初期値与年份差,求年均增长量。
基本公式:年均增长量=(末期量-初期量)/年份差3. 年均增长率已知末期值、初期值与年份差,求年均增长率。
基本公式:末期值=初期值×(1+年均增长率)N资料分析公式非常多,往往求解一个量就会有三四个公式,这时候就要求考生先看材料给了哪些数据,根据所给出的数据来决定用哪个公式,比如求解增长率的时候,给出增长量、基期值所用的公式和给出增长量、现期值所用的公式是不一样的,求解基期比重的时候,给出现期值、增长量和给出现期值、增长率所用的公式也是不一样的。
这里就要求各位考生熟悉掌握每一个公式和提前阅读材料。
大家如果记住了上面的公式,加上一些思维技巧,速度会很快提上来,就会做到事半功倍。
资料分析知识点公式总结

资料分析知识点公式总结资料分析是一种通过统计学和概率理论来获得和分析数据的方法。
它主要用于对数据进行模式、趋势和关系的识别。
资料分析通常通过使用数学公式来计算各种参数和统计量,从而得出对数据的解释和预测。
在本文中,我们将总结一些常见的资料分析知识点和公式。
1. 中心趋势中心趋势是数据集中值的度量。
常见的中心趋势包括平均数、中位数和众数。
平均数是一组数据的所有数值之和除以数据个数。
其公式为:\[\bar{x} = \frac{\sum_{i=1}^{n} x_i}{n}\]其中,\(\bar{x}\)代表平均数,\(x_i\)代表第i个数据值,n代表数据个数。
中位数是一组数据中居中位置的数值。
如果数据个数为奇数,中位数为排序后的中间值;如果数据个数为偶数,中位数为排序后中间两个值的平均数。
众数是一组数据中出现频率最高的数值。
2. 离散度离散度用于衡量一组数据的分散程度。
常见的离散度包括极差、方差和标准差。
极差是一组数据中最大值和最小值的差值。
方差是一组数据与其平均数之差的平方和的平均数。
其公式为:\[s^2 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n-1}\]其中,\(s^2\)代表方差,\(x_i\)代表第i个数据值,\(\bar{x}\)代表平均数,n代表数据个数。
标准差是方差的平方根。
其公式为:\[s = \sqrt{s^2}\]3. 相关性相关性用于衡量两组数据之间的关系。
常见的相关性包括协方差和相关系数。
协方差是一组数据对之间的平均偏差乘积。
其公式为:\[Cov(X, Y) = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{n}\]其中,\(Cov(X, Y)\)代表X和Y的协方差,\(x_i\)和\(y_i\)分别代表两组数据的第i个数值,\(\bar{x}\)和\(\bar{y}\)分别代表两组数据的平均数,n代表数据个数。
资料分析常用基础公式

资料分析常用基础公式在进行数据分析时,有一些常用的基础公式被广泛应用于统计分析和数据建模。
这些公式可以帮助我们理解数据、计算数据的统计特征以及推断数据的模式和趋势。
下面是一些常用的基础公式:1. 平均值(Mean):平均值是数据集所有观测值的总和除以观测值的个数。
平均值常用于描述数据的中心趋势。
公式:Mean = (x₁ + x₂ + ... + xn)/ n2. 中位数(Median):中位数是将数据集的观测值按升序排列后,位于中间位置的值。
中位数可以用来表示数据的中心位置,相比平均值,中位数对于极端值的鲁棒性更强。
公式:Median = ((n + 1)/ 2 )th observation3. 众数(Mode):公式:No explicit formula4. 标准差(Standard Deviation):标准差是观测值与平均值之间的偏离程度的度量。
标准差越大,观测值越分散。
公式:Standard Deviation = sqrt(( (x₁ - x̄)² + (x₂ - x̄)² + ... + (xn - x̄)² ) / n)5. 方差(Variance):方差是标准差的平方,它通过在标准差公式中去掉平方根而得到。
公式:Variance = ( (x₁ - x̄)² + (x₂ - x̄)² + ... + (xn - x̄)² ) / n6. 百分位数(Percentiles):百分位数是对数据集进行排序后的一些百分比处的值。
百分位数常用于描述数据分布的位置和统计特征。
公式:x_p=(p/100)*n(当p为整数时)7. 相关系数(Correlation coefficient):相关系数描述了两个变量之间的线性关系强度和方向。
相关系数的取值范围在-1到1之间,接近-1表示强负相关,接近1表示强正相关,接近0表示无线性关系。
(完整版)资料分析公式汇总
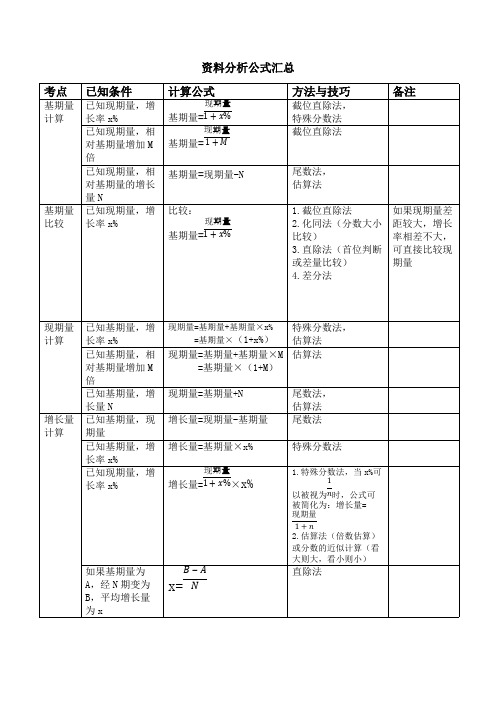
资料分析公式汇总考点已知条件计算公式方法与技巧备注已知现期量,增长率x%基期量=现期量1+x%截位直除法,特殊分数法已知现期量,相对基期量增加M 倍基期量=现期量1+M截位直除法基期量计算已知现期量,相对基期量的增长量N基期量=现期量-N尾数法,估算法基期量比较已知现期量,增长率x%比较:基期量=现期量1+x%1.截位直除法2.化同法(分数大小比较)3.直除法(首位判断或差量比较)4.差分法如果现期量差距较大,增长率相差不大,可直接比较现期量已知基期量,增长率x%现期量=基期量+基期量×x%=基期量×(1+x%)特殊分数法,估算法已知基期量,相对基期量增加M 倍现期量=基期量+基期量×M =基期量×(1+M )估算法现期量计算已知基期量,增长量N现期量=基期量+N 尾数法,估算法已知基期量,现期量增长量=现期量-基期量尾数法已知基期量,增长率x%增长量=基期量×x%特殊分数法已知现期量,增长率x%增长量=×x%现期量1+x% 1.特殊分数法,当x%可以被视为时,公式可1n 被简化为:增长量=现期量1+n2.估算法(倍数估算)或分数的近似计算(看大则大,看小则小)增长量计算如果基期量为A ,经N 期变为B ,平均增长量为xx=B ‒A N直除法增长量比较已知现期量,增长率x%增长量=×x%现期量1+x%1.特殊分数法,当x%可以被视为时,公式可1n被简化为:增长量=现期量1+n2.公式可变换为:增长量=现期量×,其中为x%1+x%x%1+x%增函数,所以现期量大,增长率大的情况下,增长量一定大已知基期量,增长量增长率=增长量基期量截位直除法,插值法已知现期量,基期量增长率=现期量‒基期量基期量截位直除法求平均增长率:如果基期量为A,第n+1期(或经n期)变为B,平均增长率为x%x%=-1nBA代入法,公式法B=A(1+X%)n当x%较小时可简化为B=A(1+nx%)求两期混合增长率:如果第一期和第二期增长率分别为r1和r2,那么第三期相对第一期增长率为r3r3= r1+r2+r1r2简单记忆口诀:连续增长,最终增长大于增长率之和;连续下降,最终下降小于增长率之和(正负号带进公式计算)求总体增长率:整体分为A,B两个部分,分别增长a%与b%,整体增长率x%x%=A×a%+B×b%A+B x%=a%+B(b%-a%)A+B已知总体增长率和其中一个部分的增长率,求另一部分的增长率增长率计算求混合增长率:整体为A,增长率为a%,分为两个部分B,C,增长率为b%和c%混合增长率a%介于b%和c%之间混合增长率大小居中增长率比较已知现期量与增长量比较增长率=代替增现期量基期量长率进行大小比较相当于分数大小比较发展速度已知现期量与基期量发展速度==1+增长率现期量基期量截位直除法,插值法已知部分增长量与整体增长量增长贡献量=部分增长量整体增长量截位直除法,插值法增长贡献率贡献率贡献率%=贡献量(产出量,所得量)投入量(消耗量,占用量)贡献率是指有效或有用成果数量与资源消耗及占用量之比,即投入量与产出量之比拉动增长求B拉动A增长几个百分点:如果B是A的一部分,B拉动A增长x%x%=B的增长量A的基期量截位直除法,插值法某部分现期量为A,整体现期量为为B现期比重=AB截位直除法,插值法某部分基期量为A,增长率a%,整体基期量为B,增长率b%现期比重=AB×1+a%1+b%一般先计算,然后AB根据a和b的大小判断大小某部分现期量为A,增长率a%,整体现期量为B,增长率b%基期比重=×AB1+b%1+a%一般先计算,然后AB根据a和b的大小判断大小比重计算求基期比重-现期比重:某部分现期量为A增长率a%,整体现期量为B,增长率b%两期比重差值计算:现期比重-基期比重=-×ABAB1+b%1+a%=×(1-)AB1+b%1+a%=×ABa%‒b%1+a%1.先根据a与b的大小判断差值计算结果是正数还是负数;2.答案小于|a-b|3.估算法(近似取整估算)4.直除法某部分现期量为A,整体现期量为B 现期比重=AB相当于分数大小比较,同上述做法比重比较基期比重与现期比重比较:某部分现期量为A,增长率a%,整体现期量为B,增长率b%基期比重=×AB1+b%1+a%直除法,当部分增长率大于整体增长率,则现期比重大于基期比重。
(完整版)资料分析公式汇总

资料分析公式汇总考点已知条件计算公式方法与技巧备注已知现期量,增长率x%基期量=现期量1+x%截位直除法,特殊分数法已知现期量,相对基期量增加M 倍基期量=现期量1+M截位直除法基期量计算已知现期量,相对基期量的增长量N基期量=现期量-N尾数法,估算法基期量比较已知现期量,增长率x%比较:基期量=现期量1+x%1.截位直除法2.化同法(分数大小比较)3.直除法(首位判断或差量比较)4.差分法如果现期量差距较大,增长率相差不大,可直接比较现期量已知基期量,增长率x%现期量=基期量+基期量×x%=基期量×(1+x%)特殊分数法,估算法已知基期量,相对基期量增加M 倍现期量=基期量+基期量×M =基期量×(1+M )估算法现期量计算已知基期量,增长量N现期量=基期量+N 尾数法,估算法已知基期量,现期量增长量=现期量-基期量尾数法已知基期量,增长率x%增长量=基期量×x%特殊分数法已知现期量,增长率x%增长量=×x%现期量1+x% 1.特殊分数法,当x%可以被视为时,公式可1n 被简化为:增长量=现期量1+n2.估算法(倍数估算)或分数的近似计算(看大则大,看小则小)增长量计算如果基期量为A ,经N 期变为B ,平均增长量为xx=B ‒A N直除法增长量比较已知现期量,增长率x%增长量=×x%现期量1+x%1.特殊分数法,当x%可以被视为时,公式可1n被简化为:增长量=现期量1+n2.公式可变换为:增长量=现期量×,其中为x%1+x%x%1+x%增函数,所以现期量大,增长率大的情况下,增长量一定大已知基期量,增长量增长率=增长量基期量截位直除法,插值法已知现期量,基期量增长率=现期量‒基期量基期量截位直除法求平均增长率:如果基期量为A,第n+1期(或经n期)变为B,平均增长率为x%x%=-1nBA代入法,公式法B=A(1+X%)n当x%较小时可简化为B=A(1+nx%)求两期混合增长率:如果第一期和第二期增长率分别为r1和r2,那么第三期相对第一期增长率为r3r3= r1+r2+r1r2简单记忆口诀:连续增长,最终增长大于增长率之和;连续下降,最终下降小于增长率之和(正负号带进公式计算)求总体增长率:整体分为A,B两个部分,分别增长a%与b%,整体增长率x%x%=A×a%+B×b%A+B x%=a%+B(b%-a%)A+B已知总体增长率和其中一个部分的增长率,求另一部分的增长率增长率计算求混合增长率:整体为A,增长率为a%,分为两个部分B,C,增长率为b%和c%混合增长率a%介于b%和c%之间混合增长率大小居中增长率比较已知现期量与增长量比较增长率=代替增现期量基期量长率进行大小比较相当于分数大小比较发展速度已知现期量与基期量发展速度==1+增长率现期量基期量截位直除法,插值法已知部分增长量与整体增长量增长贡献量=部分增长量整体增长量截位直除法,插值法增长贡献率贡献率贡献率%=贡献量(产出量,所得量)投入量(消耗量,占用量)贡献率是指有效或有用成果数量与资源消耗及占用量之比,即投入量与产出量之比拉动增长求B拉动A增长几个百分点:如果B是A的一部分,B拉动A增长x%x%=B的增长量A的基期量截位直除法,插值法某部分现期量为A,整体现期量为为B现期比重=AB截位直除法,插值法某部分基期量为A,增长率a%,整体基期量为B,增长率b%现期比重=AB×1+a%1+b%一般先计算,然后AB根据a和b的大小判断大小某部分现期量为A,增长率a%,整体现期量为B,增长率b%基期比重=×AB1+b%1+a%一般先计算,然后AB根据a和b的大小判断大小比重计算求基期比重-现期比重:某部分现期量为A增长率a%,整体现期量为B,增长率b%两期比重差值计算:现期比重-基期比重=-×ABAB1+b%1+a%=×(1-)AB1+b%1+a%=×ABa%‒b%1+a%1.先根据a与b的大小判断差值计算结果是正数还是负数;2.答案小于|a-b|3.估算法(近似取整估算)4.直除法某部分现期量为A,整体现期量为B 现期比重=AB相当于分数大小比较,同上述做法比重比较基期比重与现期比重比较:某部分现期量为A,增长率a%,整体现期量为B,增长率b%基期比重=×AB1+b%1+a%直除法,当部分增长率大于整体增长率,则现期比重大于基期比重。
资料分析相关公式

与增长有关的公式:1、增长量=今年的量-去年的量 2、增长率+增长率今年的量增长量=⨯1 3、-1去年的量今年的量 =去年的量今年的量-去年的量增长率= 4、增长率=去年的量×增长率 5、今年的量-增长量增长量增长率= 6、1+增长率今年的量去年的量=7、今年的量=去年的量×(1+增长率) 8、年份差末年的量-初年的量年均增长量= 9、-1年均增长率=年份差初年的量末年的量与隔年增长有关的公式(a1表示今年的增长率,a2表示去年的增长率)1、)()(今年的量前年的量=a211a 1+⨯+ 2、2a 2a 1a11⨯+⨯+)()(去年的量去年的增长量=3、)-1()隔年的增长率=(2a 11a 1+⨯+4、-1)(增长量的增长率=2a 1a 2a 1+ 与比重有关的公式(a1表示部分的增长率,a2表示整体的增长率) 1、整体的量部分的量比重=2、部分的量=比重×整体的量3、比重部分的量整体的量= 4、1a 1a21a +-今年的比重比重的差(百分点)=⨯5、比重的递推 %%b a Y X Y X ⨯=ca%则=cb%,=已知%%%则=%,=已知Y X Y X b c b a与平均量有关的公式(a1表示总数的增长率,a2表示份数的增长) 1、份数总数平均量= 2、a112a 1a +-的平均量平均量的增长量=今年 3、2a 12a 1a +-平均量的增长率=与倍数有关的公式1、BA是几倍=2、-1BA多几倍=3、是几倍-1=多几倍=增长率与指数有关的公式1、(指数-100)%=增长率 2、=是几倍指数100拉动增长和贡献率有关的公式1、总体去年的量部分的增长量拉动增长(百分点)=2、整体的增长量部分的增长量贡献率=3、贡献率拉动增长总体的增长率= 去年的和或差有关公式 12a 11a 1+++B A 去年的和或差=。
资料分析公式汇总(2024)

引言概述在现代社会中,大量的数据被和收集,而如何从这些海量的数据中提取有效的信息成为一个关键问题。
为了对这些数据进行分析和解释,研究者们开发出了各种各样的数据分析方法和公式。
本文将对一些常用的资料分析公式进行汇总和解析,以帮助读者更好地理解和应用这些方法。
正文内容一、描述性统计分析公式1.平均数(均值):用于计算数据集的平均值,通过求取所有数据的总和再除以数据的数量来得到。
2.中位数:将数据集按升序排列,找到中间位置的数值作为中位数,能更好地反映数据的集中趋势。
3.众数:指数据集中出现次数最多的数值,可用于描述数据的集中程度和典型值。
4.方差和标准差:用于衡量数据的离散程度,反映数据的分散情况。
方差是每个数据点与平均值的差的平方的平均值,而标准差是方差的平方根,提供了更直观的数据离散程度的度量。
二、相关性分析公式1.相关系数:用于衡量两个变量之间的线性相关程度,常用的有皮尔逊相关系数。
相关系数的取值范围是1到1,接近1表示正相关,接近1表示负相关,接近0表示无相关性。
2.协方差:用于衡量两个变量之间的总体相关程度,数值的正负反映了两个变量的联合变动方向。
3.假设检验:通过设定一个显著性水平来判断样本数据是否能够代表总体。
常用的假设检验方法包括t检验、F检验和卡方检验等。
三、回归分析公式1.简单线性回归:用于建立一个因变量和一个自变量之间的线性关系模型,通过最小二乘法估计回归系数。
2.多元线性回归:扩展了简单线性回归,通过引入多个自变量来建立回归模型。
3.逻辑回归:用于解决二分类问题,通过将线性回归的结果映射到一个概率范围内,来判断样本属于某一类别的概率。
四、聚类分析公式1.K均值聚类:通过将数据集划分为K个簇,使得簇内的数据相似度最大化,簇间相似度最小化。
2.层次聚类:通过逐渐合并或分解聚类簇来构建一个层次结构,能够展现不同层次的聚类结果。
3.密度聚类:通过样本点的密度来识别聚类簇,将密度较大的区域作为簇的中心。
资料分析计算公式整理超级有用

资料分析计算公式整理,超级有用在资料分析中,有许多常用的计算公式可以帮助我们理解和解释数据。
下面整理了一些超级有用的计算公式,帮助您进行数据分析。
1.平均值(Mean):平均值是一组数据的总和除以数据的个数。
它是最常用的描述数据集中趋势的指标,可以用于连续和离散数据。
公式:Mean = (x1 + x2 + . + xn) / n2.中位数(Median):中位数是将一组数据按照数值的大小排列,位于中间位置的数值。
它可以帮助我们了解数据的分布情况,特别是在存在异常值时更有用。
公式:如果数据个数为奇数,中位数是排序后的中间值;如果数据个数为偶数,中位数是排序后的中间两个数的平均值。
3.众数(Mode):众数是一组数据中出现次数最多的数值。
它可以帮助我们了解数据的集中趋势,特别是在离散数据中更常用。
4.方差(Variance):方差衡量了数据集合内个体值与其平均值的离散程度。
方差越大,数据的分布越分散。
公式:Variance = [(x1 - Mean)^2 + (x2 - Mean)^2 + . + (xn - Mean)^2] / n5.标准差(Standard Deviation):标准差是方差的平方根,用于衡量数据的离散程度。
它是最常用的描述数据分散情况的指标。
公式:Standard Deviation = √Variance6.相关系数(Correlation Coefficient):相关系数衡量了两个变量之间的线性关系强度和方向。
它的取值范围是-1到1,接近-1表示负相关,接近1表示正相关,接近0表示无相关。
公式:Correlation Coefficient = Covariance(x, y) / (Standard Deviation(x) * Standard Deviation(y))7.百分位数(Percentile):百分位数是一组数据中指定百分比位置处的数值。
它可以帮助我们了解数据的分布情况,例如中位数是50%百分位数。
资料分析计算公式整理

资料分析计算公式整理在进行资料分析时,掌握一些常用的计算公式能够帮助我们更高效、准确地处理数据和得出结论。
以下是对一些重要的资料分析计算公式的整理。
一、增长类计算公式1、增长量=现期量基期量例如,2022 年某公司的销售额为 100 万元,2021 年为 80 万元,那么增长量就是 100 80 = 20 万元。
2、增长率=增长量 ÷基期量 × 100%用上例的数据,增长率为(20 ÷ 80)× 100% = 25% 。
3、基期量=现期量 ÷(1 +增长率)假设 2023 年某产品的销量为 120 万件,同比增长 20%,则 2022 年的销量(基期量)为 120 ÷(1 + 20%)= 100 万件。
4、现期量=基期量 ×(1 +增长率)如果已知 2021 年某地区的人口为 50 万人,预计每年以 5%的速度增长,那么 2025 年的人口(现期量)为 50 ×(1 + 5%)^4 万人。
二、比重类计算公式1、比重=部分量 ÷整体量 × 100%比如,某班级男生有 20 人,全班共有 50 人,那么男生所占比重为(20 ÷ 50)× 100% = 40% 。
2、部分量=整体量 ×比重若已知某公司总利润为 1000 万元,其中 A 产品的利润占比为 30%,则 A 产品的利润为 1000 × 30% = 300 万元。
3、整体量=部分量 ÷比重比如某企业中研发部门的人数为 50 人,占总人数的 20%,则该企业总人数为 50 ÷ 20% = 250 人。
三、平均数类计算公式1、平均数=总数 ÷个数例如,某班级5 名学生的数学成绩分别为80、90、85、95、75 分,那么平均成绩为(80 + 90 + 85 + 95 + 75)÷ 5 = 85 分。
资料分析计算公式整理

资料分析计算公式整理在进行数据分析时,计算公式是一个非常重要的工具。
它们可以帮助我们对数据进行深入的理解和解释。
本文将整理一些常用的资料分析计算公式,以供参考使用。
一、中心趋势测量1. 平均值(Mean)平均值是最常用的中心趋势测量指标,用于衡量一组数据的集中程度。
计算公式如下:\[ \bar{x} = \frac{{x_1 + x_2 + \cdots + x_n}}{n} \]其中,\( x_1, x_2, \cdots, x_n \) 为数据集中的数据值,\( n \) 为数据点的个数。
2. 加权平均值(Weighted Mean)加权平均值是在计算平均值时,根据每个数据点的权重给予不同的重要程度。
计算公式如下:\[ \bar{x} = \frac{{w_1x_1 + w_2x_2 + \cdots + w_nx_n}}{w_1 + w_2 + \cdots + w_n} \]其中,\( w_1, w_2, \cdots, w_n \) 表示每个数据点的权重。
3. 中位数(Median)中位数是一组数据中的中间值,能够较好地反映数据的集中程度。
计算公式如下:若数据个数 \( n \) 为奇数:\[ \text{Median} = x_{\frac{n+1}{2}} \]若数据个数 \( n \) 为偶数:\[ \text{Median} = \frac{{x_{\frac{n}{2}} + x_{\frac{n}{2} + 1}}}{2} \]4. 众数(Mode)众数是一组数据中出现次数最多的数据值。
一组数据可能有一个或多个众数,也可能没有众数。
二、离散趋势测量1. 范围(Range)范围是一组数据的最大值与最小值之间的差异程度。
计算公式如下:\[ \text{Range} = \text{最大值} - \text{最小值} \]2. 四分位距(Interquartile Range,IQR)四分位距用于描述数据的分散程度,它是上四分位数与下四分位数之间的差异程度。
资料分析公式汇总

欢迎共阅资料分析公式汇总考点已知条件计算公式方法与技巧备注基期量计算已知现期量,增长率x%基期量=截位直除法,特殊分数法已知现期量,相对基期量增加M倍基期量=截位直除法已知现期量,相对基期量的增长量N基期量=现期量-N 尾数法,估算法基期量比较已知现期量,增长率x%比较:基期量=1.截位直除法2.化同法(分数大小比较)3.直除法(首位判断或差量比较)4.差分法如果现期量差距较大,增长率相差不大,可直接比较现期量现期量计算已知基期量,增长率x%现期量=基期量+基期量×x%=基期量×(1+x%)特殊分数法,估算法已知基期量,相对基期量增加M倍现期量=基期量+基期量×M=基期量×(1+M)估算法已知基期量,增长量N现期量=基期量+N 尾数法,估算法增长量计算已知基期量,现期量增长量=现期量-基期量尾数法已知基期量,增长率x%增长量=基期量×x% 特殊分数法已知现期量,增长率x%增长量=×x%1.特殊分数法,当x%可以被视为时,公式可被简化为:增长量=2.估算法(倍数估算)或分数的近似计算(看大则大,看小则小)如果基期量为A,经N期变为B,平均增长量为xx=直除法增长量已知现期量,增 1.特殊分数法,当x%可被简化为:增长量=2.公式可变换为:增长量=现期量×,其中为增函数,所以现期量大,增长率大的情况下,增长量一定大增长率计算已知基期量,增长量增长率=截位直除法,插值法已知现期量,基期量增长率=截位直除法求平均增长率:如果基期量为A,第n+1期(或经n期)变为B,平均增长率为x%x%=-1代入法,公式法B=A(1+X%)n当x%较小时可简化为B=A(1+nx%)求两期混合增长率:如果第一期和第二期增长率分别为r1和r2,那么第三期相对第一期增长率为r3r3=r1+r2+r1r2 简单记忆口诀:连续增长,最终增长大于增长率之和;连续下降,最终下降小于增长率之和(正负号带进公式计算)求总体增长率:整体分为A,B两个部分,分别增长a%与b%,整体增长率x%x%=x%=a%+已知总体增长率和其中一个部分的增长率,求另一部分的增长率求混合增长率:整体为A,增长率为a%,分为两个部分B,C,增长率为b%和c%混合增长率a%介于b%和c%之间混合增长率大小居中增长率比较已知现期量与增长量比较增长率=代替增长率进行大小比较相当于分数大小比较发展速度已知现期量与基期量发展速度==1+增长率截位直除法,插值法增长贡已知部分增长量截位直除法,=数量与资源消耗及占用量之比,即投入量与产出量之比拉动增长求B拉动A增长几个百分点:如果B是A的一部分,B拉动A增长x%x%=截位直除法,插值法比重计算某部分现期量为A,整体现期量为为B现期比重=截位直除法,插值法某部分基期量为A,增长率a%,整体基期量为B,增长率b%现期比重=一般先计算,然后根据a和b的大小判断大小某部分现期量为A,增长率a%,整体现期量为B,增长率b%基期比重=×一般先计算,然后根据a和b的大小判断大小求基期比重-现期比重:某部分现期量为A增长率a%,整体现期量为B,增长率b%两期比重差值计算:现期比重-基期比重=-×=×(1-)=×1.先根据a与b的大小判断差值计算结果是正数还是负数;2.答案小于|a-b|3.估算法(近似取整估算)4.直除法比重比较某部分现期量为A,整体现期量为B现期比重=相当于分数大小比较,同上述做法基期比重与现期比重比较:某部分现期量为A,增长率a%,整体现期量为B,增长率b%基期比重=×直除法,当部分增长率大于整体增长率,则现期比重大于基期比重。
资料分析公式汇总
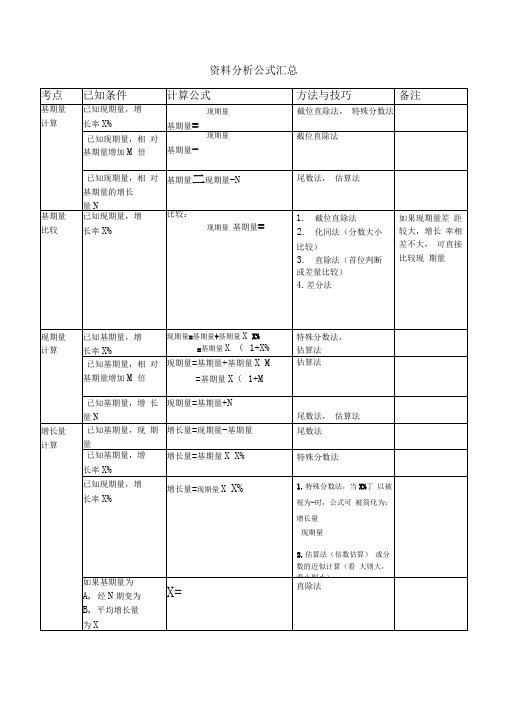
资料分析公式汇总增长量比较增长率计算增长率比较已知现期量,增长率X%已知基期量,增长量已知现期量,基期量求平均增长率: 如果基期量为A,第n+1期(或经n期)变为B,平均增长率为X% 求两期混合增长率:如果第一期和第二期增长率分别为r 1和「2, 那么第三期相对第一期增长率为「3求总体增长率:整体分为A,B两个部分,分别增长a%与b%整体增长率X% 求混合增长率:整体为A,增长率为a%分为两个部分B,C,增长率为b唏口C% 已知现期量与增长量增长量=现期量X X%增长量增长率-- -----增长率基期量丄现期量基期量增长率=基期量X%= --1r3= r i+r2+r 1「2x%=混合增长率a%介于b唏口C%之间现期量比较增长率=-期■^代替增基期量长率进行大小比较1.特殊分数法,当X%丁以被视为-时,公式可被简化为:增长量现期量2.公式可变换为:增长量=现期量X----- ,其中-------- 为增函数,所以现期量大,增长率大的情况下,增长量一定大截位直除法,插值法截位直除法代入法,公式法简单记忆口诀:连续增长,最终增长大于增长率之和;连续下降,最终下降小于增长率之和(正负号带进公式计算)x%=a%+混合增长率大小居中相当于分数大小比较nB=A (1+X%当X%较小时可简化为B=A (1+nX%已知总体增长率和其中一个部分的增长率,求另一部分的增长率发展速度增长贡献率已知现期量与基期量已知部分增长量与整体增长量贡献率现期量 .发展速度=甘甘口曰=1+增长率基期量丄和/工堆曰部分增长量—增长贡献量=齢《痕曰整体增长量贡献率%=贡献量(产岀量,所得量)截位直除法,插值法截位直除法,插值法贡献率是指有效或有用成果数量与资源消耗及占用量之比,即投入量与产出量之比拉动增长比重计算比重比较指数求B拉动A增长几个百分点:如果B是A的一部分,B拉动A增长X%某部分现期量为A,整体现期量为为B某部分基期量为A,增长率a% 整体基期量为B,增长率b% 某部分现期量为A,增长率a% 整体现期量为B,增长率b% 求基期比重-现期比重:某部分现期量为A增长率a%,整体现期量为B,增长率b%某部分现期量为A,整体现期量为B基期比重与现期比重比较:某部分现期量为A, 增长率a%整体现期量为B,增长率b%的增长量的基期量截位直除法,插值法现期比重=一现期比重=-基期比重二—X两期比重差值计算:现期比重-基期比重=一X( 1-=-X现期比重=-基期比重==X指数=基期量截位直除法,插值法一般先计算-,然后根据a和b的大小判断大小一般先计算-,然后根据a和b的大小判断大小1.先根据a与b的大小判断差值计算结果是正数还是负数;2.答案小于|a-b|3.估算法(近似取整估算)4.直除法相当于分数大小比较,同上述做法直除法,当部分增长率大于整体增长率,贝M期比重大于基期比重。
资料分析常用公式

资料分析常用公式1. 平均数公式平均数(Mean)是表示一组数据集中趋势的量数,计算公式为:$$\text{平均数} = \frac{\sum_{i=1}^{n} x_i}{n}$$其中,$ x_i $ 表示第 $ i $ 个数据,$ n $ 表示数据的总数。
平均数适用于描述数据的中心位置,常用于市场调查、产品评价等领域。
2. 中位数公式中位数(Median)是将一组数据从小到大(或从大到小)排列,位于中间位置的数值。
计算公式为:$$\text{中位数} = \begin{cases}x_{\frac{n+1}{2}} & \text{当 } n \text{ 为奇数时} \\\frac{x_{\frac{n}{2}} + x_{\frac{n}{2}+1}}{2} & \text{当 } n \text{ 为偶数时}\end{cases}$$中位数适用于描述数据的中心位置,特别适用于数据分布不均匀或存在异常值的情况。
3. 标准差公式标准差(Standard Deviation)是衡量一组数据离散程度的量数,计算公式为:$$\sigma = \sqrt{\frac{\sum_{i=1}^{n} (x_i \mu)^2}{n}}$$其中,$ \sigma $ 表示标准差,$ x_i $ 表示第 $ i $ 个数据,$ \mu $ 表示平均数,$ n $ 表示数据的总数。
标准差越大,表示数据的离散程度越大,反之越小。
4. 相关系数公式相关系数(Correlation Coefficient)用于衡量两个变量之间的线性关系程度,计算公式为:$$r = \frac{n(\sum xy) (\sum x)(\sum y)}{\sqrt{[n\sum x^2 (\sum x)^2][n\sum y^2 (\sum y)^2]}}$$其中,$ r $ 表示相关系数,$ x $ 和 $ y $ 分别表示两个变量,$ n $ 表示数据的总数。
