SPSS统计分析均值比较与T检验
一 均值比较和T检验及F检验

t
X1 X 2
2 X 2 X X 2 X1
2 1 2
n 1
=
79.5 71 9.1242 9.9402 2 0.704 9.124 9.940 10 1
பைடு நூலகம்
=3.459。 第三步 判断 根据自由度 df n 1 9 ,查 t 值表 t (9)0.05 2.262 , t (9)0.01 3.250 。由于实际计 算出来的 t =3.495>3.250= t (9)0.01 ,则 P 0.01 ,故拒绝原假设。 结论为:两次测验成绩有及其显著地差异。 由以上可以看出,对平均数差异显著性检验比较复杂,究竟使用 Z 检验还是使用 t 检 验必须根据具体情况而定,为了便于掌握各种情况下的 Z 检验或 t 检验,我们用以下一览表 图示加以说明。
已知时,用 Z
X
n
单总体
未知时,用 t
X (df n 1) S n
在这里, S 表示总体标准差的估计量,它与样本标准差 X 的关系是:
S
n X n 1
1 , 2 已知且是独立样本时,用
T 检验原理及公式
t 检验是用 t 分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著。 t 检验分为单总体 t 检验和双总体 t 检验。当总体呈正态分布,如果总体标准差未知,而且样 本容量 n <30,那么这时一切可能的样本平均数与总体平均数的离差统计量呈 t 分布。
对于要使用 T 检验进行均值比较的变量应该是正态分布的。 如果分析变量明显是非正态 分布的,应该选择非参数检验过程。
II 双总体 t 检验
双总体 t 检验是检验两个样本平均数与其各自所代表的总体的差异是否显著。双总体 t 检验又分为两种情况 一. 独立样本 t 检验 (检验假设:两个独立样本的 t 检验用于检验两个不相关的样本来自具有相同均值的 总体) 独立样本平均数的显著性检验。各实验处理组之间毫无相关存在,即为独立样本。该检 验用于检验两组非相关样本被试所获得的数据的差异性。 独立样本 T 检验要求被检验的两个样本方差要求具有齐性, 如果不齐, 使用校正公式计 算 T 值和自由度。因此,在输出结果中,应该先检查方差齐性(F 检验) ,根据齐性的结果, 在输出表格中选择 T 检验的结果。 二. 相关(配对)样本 t 检验。 (检验假设:配对样本 t 检验(Paired Sample T test)用于检验两个相关的样本是 否来自具有相同均值的总体) 相关样本平均数差异的显著性检验,用于检验匹配而成的两组被试获得的数据或同组 被试在不同条件下所获得的数据的差异性,这两种情况组成的样本即为相关样本或配对样 本。 现以相关检验为例,说明检验方法。因为独立样本平均数差异的显著性检验完全类似, 只不过 r 0 。 相关样本的 t 检验公式为:
spss结果中,F值,t值及其显著性sig的解释

spss结果中,F值,t值及其显著性sig的解释SPSS 结果中,F 值、t 值及其显著性 sig 的解释在进行数据分析时,尤其是运用 SPSS 这样的统计软件,我们常常会遇到 F 值、t 值以及显著性 sig 这些概念。
对于初学者来说,理解它们可能会有些困难,但一旦掌握,就能更好地解读数据和得出有意义的结论。
首先,咱们来说说F 值。
F 值通常出现在方差分析(ANOVA)中。
简单来讲,方差分析是用来比较两个或多个组的均值是否有显著差异。
那么 F 值是怎么来的呢?它其实是组间变异与组内变异的比值。
组间变异反映的是不同组之间的差异,组内变异则反映的是每组内部的差异。
如果F 值较大,就意味着组间变异相对于组内变异来说比较大,这就暗示着不同组的均值很可能存在显著差异。
举个例子,假设我们想研究不同教学方法对学生成绩的影响。
我们把学生分成三组,分别采用方法 A、方法 B 和方法 C 进行教学。
通过计算,得到了一个 F 值。
如果这个 F 值很大,那就说明这三种教学方法导致的学生平均成绩很可能是不一样的。
接下来,咱们聊聊 t 值。
t 值常见于 t 检验中,t 检验主要用于比较两组数据的均值是否有差异。
比如说,我们想知道男生和女生在某门课程上的平均成绩是否不同,这时候就可以用 t 检验。
计算得出的 t 值反映了两组均值差异的大小。
t 值的大小与两组均值的差异以及样本的标准差有关。
如果 t 值较大,就说明两组均值的差异在统计上很可能是显著的。
那什么是显著性 sig 呢?显著性 sig 其实就是用来判断我们观察到的差异到底是真实存在的,还是仅仅由于随机因素造成的。
通常,我们会设定一个显著性水平,比如 005 或者 001。
如果 sig值小于我们设定的显著性水平,就说明差异是显著的;反之,如果 sig值大于设定的显著性水平,就说明差异不显著,可能只是随机误差导致的。
比如说,我们得到的 sig 值是 003,而我们设定的显著性水平是 005,那么这就意味着我们观察到的差异是具有统计学意义的,不是偶然发生的。
均值比较和T检验

Spss16.0与统计数据分析均值比较和T检验20XX6月13日均值比较和T 检验统计分析常常采取抽取样本的方法,即从总体中随机抽取一定数量的样本进行研究来推论总体的特性。
但是,由于抽取的样本不一定具有完全代表性,样本统计量与总体参数间存在差异,所以不能完全的说明总体的特性。
同时,我们也可以知道,均值不等的两个样本不一定来自均值不同的整体。
对于如何避免这些问题,我们自然可以想均值比较和T 检验 1、Means 过程 1.1 Means 过程概述(1)功能:对数据进行进行分组计算,比较制定变量的描述性统计量包括均值、标准差 、总和、观测量数、方差等一系列单列变量描述性统计量,还可以给出方差分析表和线性检验结果。
(2)计算公式为: nxx ni i∑==1111.2问题举例:比较不同性别同学的体重平均值和方差。
数据如下表所示:体重表1.3用SPSS 操作过程截图:1.4 结果和讨论p{color:black;font-family:sans-serif;font-size:10pt;font-weight:normal} Your trial period for SPSS for Windows will expire in 14 days.p{color:0;font -family:Monospaced;font-size:13pt;font-style:normal;font-weight:normal;text-decoration:none}MEANS TABLES=体重 BY 性别/CELLS MEAN COUNT STDDEV VAR.MeansCase Processing SummaryCasesIncluded Excluded TotalN Percent N Percent N Percent体重* 性别24 100.0% 0 .0% 24 100.0%由SPSS 计算计算结果可知男同学体重平均值为:56.5,方差为54.091女同学体重平均值为43.833,方差为29.970。
第五章 SPSS参数检验1

作出决策
拒绝假设!
别无选择.
☺☺ ☺
☺☺ ☺☺
☺☺
抽取随机样本
☺X均=值20☺
原假设
(null hypothesis)
1. 又称“0假设”,研究者想收集证据予以反对的假设,用 H0表示
2. 所表达的含义总是指参数没有变化或变量之间没有关系 3. 最初被假设是成立的,之后根据样本数据确定是否有足够
的证据拒绝它
假设检验的理论依据
假设检验所以可行,其理论背景为 实际推断原理,即“小概率原理”
人们在实践中普遍采用的一个原则:
小概率事件在一次试验 中基本上不会发生 .
小概率原理及实际推理方法
1、小概率事件 如果在某次试验或观测中,某事件出现
的概率很小,这样的事件叫小概率事件。
2、小概率原理
小概率事件在一次试验或观测中几乎是不可能发 生的。
至此,SPSS将自动计算t统计量和对应的概 率p值。
• 推断储户一次平均存(取)款金额是否为2000 • 推断家庭人均住房面积的均值是否为20平方米
练习
根据各保险公司人员构成情况数据,对我国目 前保险公司从业人员的受高等教育的程度和年轻化 的程度进行推断:
• 保险公司具有高等教育水平的员工比例的平均值不 低于0.8;
解:研究者想收集证据予以证明的假设应该是“ 生产过程不正常”。建立的原假设和备择假设为
H0 : 10cm H1 : 10cm
提出假设
(例题分析)
• 【例】某品牌洗涤剂在它的产品说明书中声称 :平均净含量不少于500克。从消费者的利益 出发,有关研究人员要通过抽检其中的一批产 品来验证该产品制造商的说明是否属实。试陈 述用于检验的原假设与备择假设
3. 在一次试验中小概率事件一旦发生,我们就有 理由拒绝原假设
SPSS统计分析第四章均值比较与T检验

N 258 216
Mean $41441.8 $26031.9
Std. Dev iation $19,499.214 $7,558.021
Std. Error Mean $1213.97
$514.258
左第一栏为分析变量标签和分类变量标签 N观测量数目 Mean均值 Std. Deviation标准差 Std. Error Mean标准误
三、配对样本T检验
配对样本T检验(Paired Sample T test)用 于检验两个相关的样本是否来自具有相同均 值的总体。这种相关的或配对的样本常常来 自这样的实验结果,在实验中被观测对象在 实验前后均被观测。两个变量可以是before after,配对分析的测度也不是必须来自同一 个观测对象。一对可以两者组合而成。
练习题
已知某水样中含CaCO3的真值为20.7mg/L, 现用某方法重复测定该水样11次CaCO3的含 量(mg/L)为:20.99,20.41,20.10, 20.00,20.91,22.60,20.99,20.41, 20.00,23.00,22.00。问该方法测得的均值 是否偏高?
2、Independent Sample T test(独立样本T检验)
例题一
现有银行雇员工资为例,检验男女雇员现工 资是否有显著差异。一个是要比较salary变量 的均值,另一个是gender变量作为分水平变 量。 (data09--03) 。
分析变量的简单描述性统计量
Gender Current Salary Male
F emale
Group Statistics
如果你试图比较的变量明显不是正态分布的,则应该 考虑使用一种非参数检验过程(Nonparametric test)。 如果想比较的变量是分类变量,应该使用Crosstabs 功能。
spss均值检验(均数分析单样本t检验独立样本t检验)

在统计学中,我们往往从样本的特性推知随机变量总体的特性。
但由于总体中个体之间存在差异,样本的统计量和总体的参数之间往往会有误差。
因此,均值不相等的样本未必来自不同分布的总体,而均值相等的样本未必来自有相同分布的总体。
也就是说,如何从样本均值的差异推知总体的差异,这就是均值比较的内容。
SPSS提供了均值比较过程,在主菜单栏单击“Analyze”菜单下的“Compare Means”项,该项下有5个过程,如图4-1。
平均数比较Means过程用于统计分组变量的的基本统计量。
这些基本统计量包括:均值(Mean)、标准差(Standard Deviation)、观察量数目(Number of Cases)、方差(Variance)。
Means过程还可以列出方差表和线性检验结果。
[例子]调查了棉铃虫百株卵量在暴雨前后的数量变化,统计暴雨前和暴雨后的统计量,其数据如下:暴雨前 110 115 133 133 128 108 110 110 140 104 160 120 120暴雨后 90 116 101 131 110 88 92 104 126 86 114 88 112该数据保存在“DATA4-1.SAV”文件中。
1)准备分析数据在数据编辑窗口输入分析的数据,如图4-2所示。
或者打开需要分析的数据文件“DATA4-1.SAV”。
图4-2 数据窗口2)启动分析过程在SPSS主菜单中依次选择“Analyze→Compare Means→Means”。
出现对话框如图4-3。
图4-3 Means设置窗口3)设置分析变量从左边的变量列表中选中“百株卵量”变量后,点击变量选择右拉按钮,该变量就进入到因子变量列表“Dependent List:”框里,用户可以从左边变量列表里选择一个或多个变量进行统计。
从左边的变量列表中选中“调查时候”变量,点击“Independent List”框左边的右拉按钮,该变量就进入分组变量“IndependentList”框里,用户可以从左边变量列表里选择一个或多个分组变量。
spss统计分析教程-独立样本t检验(1)
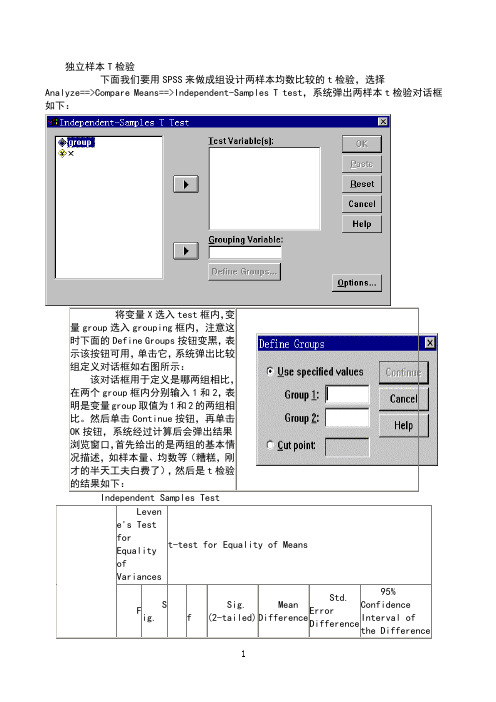
独立样本T检验下面我们要用SPSS来做成组设计两样本均数比较的t检验,选择Analyze==>Compare Means==>Independent-Samples T test,系统弹出两样本t检验对话框如下:将变量X选入test框内,变量group选入grouping框内,注意这时下面的Define Groups按钮变黑,表示该按钮可用,单击它,系统弹出比较组定义对话框如右图所示:该对话框用于定义是哪两组相比,在两个group框内分别输入1和2,表明是变量group取值为1和2的两组相比。
然后单击Continue按钮,再单击OK按钮,系统经过计算后会弹出结果浏览窗口,首先给出的是两组的基本情况描述,如样本量、均数等(糟糕,刚才的半天工夫白费了),然后是t检验的结果如下:Levene's TestforEqualityofVariancest-test for Equality of MeansFSig.tdfSig.(2-tailed)MeanDifferenceStd.ErrorDifference95%ConfidenceInterval ofthe Difference体方差是否齐,这里的戒严结果为F = ,p = ,可见在本例中方差是齐的;第二部分则分别给出两组所在总体方差齐和方差不齐时的t检验结果,由于前面的方差齐性检验结果为方差齐,第二部分就应选用方差齐时的t检验结果,即上面一行列出的t= ,ν=22,p=。
从而最终的统计结论为按α=水准,拒绝H0,认为克山病患者与健康人的血磷值不同,从样本均数来看,可认为克山病患者的血磷值较高。
SPSS对数据进行T检验统计分析

SPSS对数据进行T检验统计分析下面将做此项目的最后一个环节,即使用SPSS进行统计分析。
先用SPSS来做组设计两样本均数比较的T检验,其步骤如下。
(1)执行Analyze/Compare Means/Independent-Samples T test命令,打开如图1-43所示的对话框。
(2)在该对话框中选择X放入TEST列表框中,选择Group放入Grouping Variable文本框中,如图1-44所示。
图1-43 打开T检验对话框图1-44 选择入列表(3)单击Define Groups按钮,系统弹出比较组定义对话框,如图1-45所示。
(4)在该对话框中的两个值框中分别输入1和2,然后单击Continue按钮,如图1-46所示。
图1-45 比较组定义对话框图1-46 输入值(5)单击T检验对话框中的OK按钮,如图1-47所示。
图1-47 进行T检验(6)系统经过计算后,会弹出结果浏览窗口。
首先给出的是两组的基本情况描述,如样本量、均数等,然后是T检验的结果,如图1-48所示。
图1-48 T检验结果从上图中可见,结果分为两大部分:第一部分为Levene's方差检验,用于判断两体方差是否齐,这里的检验结果为F=0.032,p=0.860,可见在本例中方差齐;第二部分则分别给出两组所在部体方差齐和方差不齐时的T检验结果,即上面一行列出的T=2.542,V=22,p=0.019。
从而最终的统计结论为按=0.05水准,拒绝H0,认为克山病患者与健康人的血磷值是不同的。
从样本均数来看,可以确定克山病患者的血磷值较高。
《证券理论与实务》模块八考试精要(证券市场基础知识)模块八考试精要一、单项选择题1、涉及证券市场的法律、法规第一个层次是指()。
A、法律B、行政法规C、厂纪厂规D、部门规章2、涉及证券市场的法律、法规第二个层次是指()。
A、法律B、行政法规C、厂纪厂规D、部门规章3、涉及证券市场的法律、法规第三个层次是指()。
SPSS均值比较与T检验

.
7
H 西0 南财经大学出版社
5.1 统计推断与假设检验
2、假设检验的几个概念 (4) 概率p值
SPSS16.0与统计数据分析
p值是当零假设正确时,观测到的样本信息出现的概率。 如果这个概率很小,以至于几乎不可能在零假设正确时出现 目前的观测数据时,我们就拒绝零假设。p值越小,拒绝零假 设的理由就越充分。但怎样的p值才算“小”呢?通常是与预 先设定的显著性水平 值比较,若 值为0.05,p值小于0.05则 认为该概率值足够小,应拒绝零假设。
.
8
H 西0 南财经大学出版社
5.1 统计推断与假设检验
SPSS16.0与统计数据分析
3、假设检验的基本步骤
➢第1步 给出检验问题的原假设;
根据检验问题的要求,将需要检验的最终结果作为零假 设。例如,需要检验某学校的高考数学平均成绩是否同往年 的平均成绩一样,都为75,由此可做出零假设,H0 :75
④配对样本T检验(Paired-Sample T Test),用于检 验两个相关的样本是否来自具有相同均值的总体。
.
4
H 西0 南财经大学出版社
5.1 统计推断与假设检验
SPSS16.0与统计数据分析
2、假设检验的几个概念
(1)统计假设
➢ 原假设:在很多情况下,我们给出一个统计假设仅仅是
为了拒绝它。例如,如果我们要判断给定的一枚硬币是
.
3
西南财经大学出版社
5.1 统计推断与假设检验
SPSS16.0与统计数据分析
1、参数检验
①均值比较(Means),用于计算指定变量的 综合描述统计量;
Compare Means子菜单
②单样本T检验(One-Sample T Test),检验单个 变量的均值与假设检验值之间是否存在差异;
实验六——平均数分析与T检验

5.1.2 假设检验的基本思想
•
5.1.3 假设检验的基本步骤
依据假设检验的基本思想,假设检验可以总结 成为以下四大基本步骤: 第一,提出原假设(记为H0)。 • 即根据推断检验的目的,对待推断的总体参 数或分布提出一个基本假设。 第二,选择检验统计量。 • 在假设检验中,样本值(或更极端值)发生 的概率并不直接由样本数据得到,而是通过计算检 验统计量观测值发生的概率而间接得到。这些检验 统计量服从或近似服从某种已知的理论分布。对于 不同的假设检验问题以及不同的总体条件,会有不 同的选择检验统计量的理论、方法和策略。
定义两总体的标识值
框中输入一个数字,大于 等于该值的对应一个总体 ,小于该值的对应另一个 总体
•
本市户口和外地户口的家庭人均住房面积的样 本平均值有一定的差距。
结论
• • •
分析结论应通过两步完成: 第一步,两总体方差是否相等的F检验。 该检验的F统计量的观察值为65.469,对应 的概率P-为0.00。如果显著性水平a为0.05,由 于概率P-小于0.05,可以认为两总体的方差有显 著差异。 • 第二步,两总体均值的检验。 • t统计量的观测值为-3.369,对应的双尾概率 P-值为0.001.如果显著性水平a为0.05,由于概 率P-小于0.05,因此认为两总体的均值有显著地 差异,及本市户口的家庭人均住房面积的平均值存 在显著差异。
统计方法
描述统计
推断统计
估计
假设检验
参数检验
非参数检验
• 假设检验的基本思路是首先对总体参数提出假设,
然后再利用样本告之的信息去验证先前提出的假设 是否成立。 • 如果样本数据不能够充分证明和支持假设, 则在一定的条件下,应拒绝假设;相反,如果样本 数据不能够充分证明和支持假设是不成立的,则不 能推翻假设成立的合理性和真实性。 • 上述假设检验推断过程所依据的基本信念是 小概率原理,即发生概率很小的随机事件,在某一 次特定的实验中是几乎不可能发生的。
spss t检验 均数 标准差

spss t检验均数标准差SPSS t检验均数标准差。
SPSS(Statistical Product and Service Solutions)是一种统计分析软件,广泛应用于各个领域的数据分析和研究中。
在SPSS中,t检验是一种常用的假设检验方法,用于比较两组样本均数是否存在显著差异。
本文将介绍如何在SPSS中进行t 检验,并解释如何计算均数和标准差。
首先,我们需要明确t检验的基本概念。
t检验用于比较两组样本均数的差异是否显著。
在进行t检验之前,我们需要先对两组数据进行描述性统计分析,计算它们的均数和标准差。
均数是样本数据的平均值,用来衡量一组数据的集中趋势;标准差是样本数据的离散程度的度量,用来衡量数据的分散程度。
在SPSS中进行t检验,首先需要导入数据。
在“数据编辑器”中输入或导入两组数据,然后点击“分析”菜单中的“比较均数”选项。
在弹出的对话框中,选择“独立样本t检验”,将两组数据分别输入到“变量1”和“变量2”中,然后点击“确定”按钮进行分析。
SPSS将自动生成t检验的结果报告,其中包括了两组数据的均数、标准差、t 值、自由度和显著性水平等统计指标。
我们可以根据这些指标来判断两组数据的均数是否存在显著差异。
如果t值的绝对值较大,且显著性水平小于0.05,我们就可以拒绝原假设,认为两组数据的均数存在显著差异;反之,则接受原假设,认为两组数据的均数没有显著差异。
除了SPSS自动生成的结果报告,我们也可以手动计算两组数据的均数和标准差,然后利用t检验的公式来进行计算。
假设两组数据分别为X和Y,它们的均数分别为μ1和μ2,标准差分别为σ1和σ2,样本量分别为n1和n2,t值的计算公式为:t = (μ1 μ2) / √(σ1²/n1 + σ2²/n2)。
在计算t值之后,我们可以利用t分布表或SPSS软件来查找对应的显著性水平,从而判断两组数据的均数是否存在显著差异。
总之,t检验是一种常用的假设检验方法,用于比较两组样本均数的差异是否显著。
SPSS第5章 平均数比较

5.3.2 单一样本T检验过程选择
• 顺序单击“Analyze”→“Compare Means”→“One Sample T test”命令,可打开图5.3的对话框。“Test Variable”框中的变量是需要作检验的变量,要从源变 量框中选取某个变量进入该框,然后单击向右的箭头, 再在“Test Value”参数框中输入一个定值作为假设检 验值(总体参数)。 • “Options”对话框将给出置信水平“Confidence Interval”和缺失值“Missing Value”处置方式。置信水 平必须在1-99之间,如90、95,99等(一般取95)。 缺失值的处置方式一般有两种(图5.4):一种是只 要变量中含有缺失值,该组样本都被剔除(Exclude cases Listwise);另一种是尽可能保留样本,仅剔除 被分析变量的那个变量中含有缺失值的Cases。
•1、统计检验中的假设条件
•假设是进行检验的前提,是有待确认的一种事实。例 如,某样本是否满足正态分布,两样本平均数是否源 于同一总体等等。
•假设检验中,首先要建立一个关于总体参数的假设(原 假设),然后抽取样本,检验所做假设正确与否。在进行 研究时,往往需要根据已有的理论和经验,事先对研究结 果作出一种预想希望能证实的一种假设。这种假使叫科学 假设或被择假设,记为H1;而要对总体的某种假设(论断) 作出判断时,常要对相反的假设进行统计检验,称这个假 设为零假设(或虚无假设、无偏假设),记作H0。进行假 设检验的目的是为了推翻假设,主要是推翻假设时的犯错 误概率容易把握,而承认假设正确的概率不容易把握。 •假设建立得合适与否是决定检验成败的关键,统计中的 假设检验有两个基本要求。第一,建立假设的目的是为了 推翻原假设,因为推翻假设远远比承认原假设容易,因此, 真正需要证明的往往作为备择假设,即使不能推翻原假设, 也只能说,没有足够的证据推翻原假设。第二,原假设必 须是虚无(无显著性差异)假设,即必须包括等号,因为 所有的统计分析、统计计算都建立在这个基础之上;而备 择假设一定不能包含等号。
第五章 SPSS参数检验

配对样本的 t 检验 (数据形式)
观察序号
样本1
样本2
差值
1 2 M i M n
x 11 x 12 M x 1i M x 1n
x 21 x 22 M x 2i M x 2n
D1 = x 11 - x 21 D1 = x 12 - x 22 M D1 = x 1i - x 2i M D1 = x 1n- x 2n
1
2 2
总体2
抽取简单随机样 样本容量 n1 计算X1
计算每一对样本 的X1-X2
抽取简单随机样 样本容量 n2 计算X2
所有可能样本 的X1-X2
抽样分布
1 2
两个总体均值之差的检验 (12、 22 已知)
•
1.假定条件 (1)两个样本是独立的随机样本 (2)两个总体都是正态分布 (3)若不是正态分布, 可以用正态分布来近似(n130和 n230) 2.检验统计量为
1 2 0
5.5 两配对样本的T检验
5.5.1 两配对样本T检验的目的 (1)利用来自两个总体的配对样本,推断两个总体 的均值是否存在显著性差异。 (2)配对样本:个案在“前”“后”两种状态下, 或事物两个不同侧面的描述。 (3)要求: ①两配对样本的样本容量应该相等,两组样本观察 值的顺序一一对应,不能随意改变; ②样本来自的总体服从或近似服从正态分布。
5.2.2 单样本T检验的实现思路 • (1)提出原假设: H0 : 0
• (2)计算检验统计量和概率P值
X 0 t S n
(3)给定显著性水平与p值做比较:如果p值小于 显著性水平,小概率事件在一次实验中发生,则我 们应该拒绝原假设,反之就不能拒绝原假设。
5.2.3 单样本t检验的基本操作步骤
05SPSS-计量资料的统计分析-均数比较-t检验_6.8_L

计量资料的统计分析-均数比较两个均数比较的t 检验(t-test / Student’s t-test)就是以t分布为基础的假设检验方法,实际应用时,应弄清各种检验方法的用途、适用条件和注意事项。
SPSS在其分析菜单下的的均值比较中提供的t 检验方法过程有: 单样本t检验配对样本t检验独立样本t检验例3-5 某医生测量了36名从事铅作业男性工人的血红蛋白含量,算得其均数为130.83g/L,标准差为25.74g/L。
问从事铅作业工人的血红蛋白是否不同于正常成年男性平均值140g/L?附:36名从事铅作业男性工人的血红蛋白含量的原始数据112,137, 129,126,88, 90, 105, 178,130, 128,126,103,172,116,125, 90, 96, 62,157,151,135,113,175,129, 165, 171,128, 128,160,110,140,163,100, 129, 116,127。
SPSS软件操作-例3-051) 建立数据文件数据格式:1列36行,1个反应变量,变量名为“hb”。
2)过程操作界面SPSS软件操作-例3-053)结果N均值标准差均值的标准误血红蛋白含量36130.833325.74102 4.29017单个样本统计量单个样本检验检验值=140T df Sig.(双侧)均值差值差分的95%置信区间下限上限血红蛋白含量-2.13735.040-9.16667-17.8762-.4572例3-6 为比较两种方法对乳酸饮料中脂肪含量测定结果是否不同,随机抽取了10份乳酸饮料制品,分别用脂肪酸水解法和哥特里-罗紫法测定其结果如表3-5第(1)~(3)栏。
问两法测定结果是否不同?表3-5 两种方法对乳酸饮料中脂肪含量的测定结果(%)编号(1)哥特里-8罗紫法(29)脂肪酸水解法(3)差值d(4)=(2)-(3)10.8400.5800.260 20.5910.5090.082 30.6740.5000.174 40.6320.3160.316 50.6870.3370.350 60.9780.5170.461 70.7500.4540.291 80.7300.5120.218 9 1.2000.9970.203 100.8700.5060.364合计-- 2.724SPSS软件操作-例3-061) 建立数据文件数据格式:2列10行,2个反应变量,变量名为“x1”和“x2”。
spss配对样本t检验

spss配对样本t检验SPSS 配对样本 t 检验在数据分析的领域中,SPSS 配对样本 t 检验是一种常用且重要的统计方法。
它能够帮助我们比较配对数据之间的差异,从而得出有价值的结论。
那什么是配对样本呢?比如说,我们想要研究某种药物对患者治疗前后的效果,对同一批患者在治疗前和治疗后分别进行测量,这两组数据就是配对样本。
又或者,对同一组学生在考试前和考试后的成绩进行比较,这也是配对样本。
SPSS 配对样本 t 检验的基本原理是基于均值的比较。
它假设两组配对数据的差值服从正态分布。
如果这个假设成立,我们就可以通过计算 t 值来判断两组数据的均值是否存在显著差异。
接下来,让我们详细了解一下如何在SPSS 中进行配对样本t 检验。
首先,我们需要将数据正确地输入到 SPSS 软件中。
确保配对的两组数据在同一行,并且变量名清晰准确。
然后,在菜单栏中选择“分析” “比较均值” “配对样本 t 检验”。
这时候,会弹出一个对话框,我们需要将配对的两个变量选入“成对变量”框中。
点击“确定”后,SPSS 就会为我们输出一系列的结果。
其中最重要的就是 t 值和对应的 p 值。
t 值反映了两组数据均值差异的大小,而 p 值则告诉我们这个差异是否具有统计学意义。
一般来说,如果 p 值小于我们预先设定的显著性水平(通常为005),我们就可以认为两组数据的均值存在显著差异。
举个例子,假设我们研究一种新的减肥方法对体重的影响。
选取了10 名志愿者,在使用这种方法前测量了他们的体重,经过一段时间的干预后再次测量体重。
通过 SPSS 配对样本 t 检验,如果得出的 p 值小于 005,那么我们就可以说这种减肥方法对体重有显著的影响。
然而,在使用SPSS 配对样本t 检验时,也有一些需要注意的地方。
首先,要确保配对数据的合理性。
如果两组数据并不是真正的配对关系,那么使用这种方法得出的结果可能是错误的。
其次,要对数据进行正态性检验。
如果差值不服从正态分布,可能需要对数据进行转换或者使用非参数检验方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练习题
已知某水样中含CaCO3的真值为20.7mg/L, 现用某方法重复测定该水样11次CaCO3的含 量(mg/L)为:20.99,20.41,20.10, 20.00,20.91,22.60,20.99,20.41, 20.00,23.00,22.00。问该方法测得的均值 是否偏高?
使用MEANS过程求若干组的描述统计量, 目的在于比较。因此必须分组求均值。这是 与Descriptives过程不同之处。
MEANS过程的基本功能是分组计算指定变 量的描述统计量。包括均值、标准差、总和、 观测量数、方差等一系列单变量描述统计量。 还可以给出方差分析表和线性检验结果。
Mean过程的数据文件要求:至少有一个连续 变量、一个分类变量(离散变量)。对连续 变量求其基本描述统计量。分类变量用来分 组。
身高基本描述统计量
单样本T检验分析结果
95% Confidence Interval of the Difference(差值的95%置信 区间):95%的置信区间=均值±1.96标准误。根据上表95%置信 区间是143.048 ± 1.96×0.531即142.0~144.1之间。由此推出, 改范围与总体均数之差为142.0-142.3~144.1-142.3,即表中- 0.304和1.800的含义。实际上样本均值与总体均值142.3之间的差 值落在-0.301~1.800之间的占95%的范围包括0,由此得出样本 均数与总体均数无显著性差异。也就是样本均数与总体均数之差与 0无显著性差异。
Test for linearity:线性检验,输出R和R2,只有在控制变量有基本的控制级, 且自变量有三个水平以上时才能选用。
对第一层变量的方差分析结果
身高*年龄(方差分析的变量信息) :说明是分析不同年龄的身高均值间是 否存在显著性差异; Sum of Squares(偏差平方和);df(自由度);Mean square(均方);F(方差值); sig(P值); Between Groups(组间偏差平方和):由两部分组成:Linearity是由因变量与 控制变量之间的线性关系引起的;Deviation from linearity不是由因变量与控 制变量之间的线性关系引起的; Within Groups(组内偏差平方和):各组内的变异相对于组均值的变异; Total(偏差平方和的总和):为组间偏差平方和与组内偏差平方和之和。
以27个学生的身高为例说明操作步骤 (data11-01)
变量no编号,sex性别,age年龄,h身高,w 体重。
ANOVA table and eta:输出第一层控制变量给出的方差分析表和eta统计值η和 η2 。 η统计量表明因变量和自变量之间联系的强度。 η2 是组间平方和与总平 方和之比。
统计分析常常采取抽样研究的方法。即从总 体中随机抽取一定数量的样本进行研究来推 论总体的特性。由于总体中的每个个体间均 存在差异,即使严格遵守随机抽样原则也会 由于多抽到一些数值较大或较小的个体致使 样本统计量与总体参数之间有所不同。
由此可以得出这样的认识:均值不相等的两 个样本不一定来自均值不同的总体。 能否用 样本均数估计总体均数,两个变量均数接近 的样本是否来自均值相同的总体?换句话说, 两个样本某变量均值不同,其差异是否具有 统计意义,能否说明总体差异?这是各种研 究工作中经常提出的问题。这就要进行均值 比较。
Eta Squared:η2为组间偏差平方和与偏差 平方和总和之比。
练习题
已知97个被调查幼儿的体健资料并建立了 CHILD.sav数据文件。试按性别(X2)对身 高(X5)与体重(X4)做平均数分析。 CHILD.sav数据文件在SP11DATA文件夹下
二、T test过程
1、单一样本T检验(One-sample T Test) 检验单个变量的均值是否与给定的常数(一般为理 论值、标准值或经过大量观察所得的稳定值等)之间 存在差异。样本均数与总体均数之间的差异显著性 检验属于单一样本T检验。 举例:已知某地区12岁男孩平均身高为142.3cm。 1973年某市测量120名12岁男孩身高资料。分析该市 12岁男孩的身高与该地区平均身高有无明显差异。 建立数据库(data11--02)
Confidence interval:95%:置信区间项,可以自定义。 Missing Values:选择对缺失值的处理方法 Exclude cases analysis by analysis:带有缺失值的观测值当它 与分析有关时才被剔除; Exclude cases listwise:剔除所有列在Test、Grouping矩形框 中的变量带缺失值的项
F值的计算公式是:F=S12(较大)/S22(较小)
进行均值比较及检验的过程
MEANS 过程 T test 过程
单一样本T检验 独立样本的T检验 配对样本的T检验 单因素方差分析
一、MEANS过程
MEANS过程计算指定变量的综合描述统计 量。当观测量按一个分类变量分组时, MEANS过程可以进行分组计算。例如要计算 学生的平均身高,SEX变量把学生按性别分 为男、女生两组,MEANS过程可以分别计算 男、女生平均身高。用于形成分组的变量应 该是其值数量少且能明确表明其特征的变量。
对来自正态总体的两个样本进行均值比较常使用T检 验的方法。T检验要求两个被比较的样本来自正态总 体。两个样本方差相等与不等时使用的计算t值的公 式不同。
进行方差齐次性检验使用F检验。对应的零假设是: 两组样本方差相等。p值小于0.05说明在该水平上否 定原假设,方差不齐;否则两组方差无显著性差异。
线性检验结果
身高 * 年龄
Measures of Association
R
R Squared
.879
ห้องสมุดไป่ตู้
.772
Eta
Eta Squared
.915
.838
R是因变量身高的观测值与预测值之间的的相 关系数,R值越接近1 表明回归方程的预测性 越好;
Eta:即η值(0~1)说明因变量与自变量之 间的联系程度;
