哈夫曼编码信息论大作业

合集下载

信息论与编码试题集与答案(新)

1. 在无失真的信源中，信源输出由 H (X ) 来度量；在有失真的信源中，信源输出由 R (D ) 来度量。

2. 要使通信系统做到传输信息有效、可靠和保密，必须首先信源编码，然后_____加密____编码，再______信道_____编码，最后送入信道。

3. 带限AWGN 波形信道在平均功率受限条件下信道容量的基本公式，也就是有名的香农公式是log(1)C W SNR =+；当归一化信道容量C/W 趋近于零时，也即信道完全丧失了通信能力，此时E b /N 0为 -1.6 dB ，我们将它称作香农限，是一切编码方式所能达到的理论极限。

4. 保密系统的密钥量越小，密钥熵H (K )就越小，其密文中含有的关于明文的信息量I (M ；C )就越大。

5. 已知n ＝7的循环码42()1g x x x x =+++，则信息位长度k 为 3 ，校验多项式 h(x)= 31x x ++ 。

6. 设输入符号表为X ＝{0，1}，输出符号表为Y ＝{0，1}。

输入信号的概率分布为p ＝(1/2，1/2)，失真函数为d (0，0) = d (1，1) = 0，d (0，1) =2，d (1，0) = 1，则D min ＝ 0 ，R (D min )＝ 1bit/symbol ，相应的编码器转移概率矩阵[p(y/x )]＝1001⎡⎤⎢⎥⎣⎦；D max ＝ 0.5 ，R (D max )＝ 0 ，相应的编码器转移概率矩阵[p(y/x )]＝1010⎡⎤⎢⎥⎣⎦。

7. 已知用户A 的RSA 公开密钥(e,n )=(3,55)，5,11p q ==,则()φn = 40 ，他的秘密密钥(d,n )＝(27,55) 。

若用户B 向用户A 发送m =2的加密消息，则该加密后的消息为 8 。

二、判断题1. 可以用克劳夫特不等式作为唯一可译码存在的判据。

（√ ）2. 线性码一定包含全零码。

（√ ）3. 算术编码是一种无失真的分组信源编码，其基本思想是将一定精度数值作为序列的编码，是以另外一种形式实现的最佳统计匹配编码。

信息论课程实验报告—哈夫曼编码

else if(T[j].weight < T[*p2].weight)
*p2 = j;
}
}
void CreateHuffmanTree(HuffmanTree T)
{
int i,p1,p2;
InitHuffmanTree(T);
InputWeight(T);
for(i = n;i < m;i++)
4）依次继续下去，直至信源最后只剩下两个信源符号为止，将这最后两个信源符号分别用二元码符号“0”和“1”表示；
5）然后从最后—级缩减信源开始，进行回溯，就得到各信源符号所对应的码符号序列，即相应的码字。
四、实验目的：
(1)进一步熟悉Huffman编码过程；(2)掌握C语言递归程序的设计和调试技术。以巩固课堂所学编码理论的知识。
#include "stdio.h"
#include "stdlib.h"
#include <float.h>
#include <math.h>
#define n 8
#define m 2*n-1
typedef struct
{
float weight;
int lchild,rchild,parent;
}
}
void InputWeight(HuffmanTree T)
{
float temp[n] = {0.20,0.18,0.17,0.15,0.15,0.05,0.05,0.05};
for(int i = 0;i < n;i++)
T[i].weight = temp[i];
}

信息论综合性实验报告 Huffman编码及译码代码

Xx大学yy学院综合性设计性实验报告专业班级：学号：姓名：实验所属课程：信息论与编码技术实验室(中心)：信息科学与工程学院软件中心指导教师：实验完成时间： 2012 年 12 月 9 日一、设计题目：Huffman编码及译码二、实验内容及要求：<一>实验内容：对所给的字符串进行huffman的编译码；译码对应原始序列，在将编码进行移位操作时，再进行译码输出，得出误码率。

<二>实验要求：自己设计一段信源序列，利用Huffman编码对其进行编码，然后利用相应的译方法进行译码，同时考察译码错误对后续序列带来的影响。

三、实验过程(详细设计)：<一> huffman编码原理：Huffman编码是一种紧致编码，但编码序列的码并非是唯一的。

它是根据源数据各信号发生的概率进行编码，在源数据中出现的概率越大的信号，分配的码字越短；出现概率越小的信号，其码字越长，从而达到用尽可能少的码字表示源数据的目的。

Huffman编码的步骤如下：设信源X有m个符号（消息），信源概率分布如下：X = ⎧ x1, x2 ,..., x m ⎫⎩ p1 2 ,..., p m ⎭（1）把信源X 中的消息按概率从大到小的顺序排列；（2）把最后两个出现概率最小的消息合并成一个消息，从而使信源的消息数减少，并同时再按信源符号（消息）出现的概率从大到小排列；（3）重复上述2 个步骤，直到信源最后为一个序列只有一个1；（4）将被整合的消息分别赋予1 和0，并对最后的两个消息也相应地赋予1 和0.（5）通过以上步骤即可完成编码操作。

<二> huffman译码原理：通过在刚开始生成的随机编码序列，得到列出的0 1 序列与源字符串一一对应，就完成了译码。

而对错位后的编码序列，我只是只错位了前两个进行译码，效果不是很明显。

<三>算法设计：1、编码部分：（1）主函数主要用于调用前面所编写的各个函数模块，按照主函数（主函数代码如下）所列出来的调用顺序，进行一一叙述。

信息论实验报告(实验四、哈夫曼编码)

2、在分配码字长度时，首先将出现概率最小的两个符号的概率相加合成一个概率；
3、把这个合成概率看成是一个新组合符号地概率，重复上述做法直到最后只剩下两个符号概率为止；
4、完成以上概率顺序排列后，再反过来逐步向前进行编码，每一次有二个分支各赋予一个二进制码，可以对概率大的赋为零，概率小的赋为1；
5、从最后一级开始，向前返回得到各个信源符号所对应的码元序列，即相应的码字。
“1”，小的概率赋“0”。
（3）从最后一级开始，向前返回得到各个信源符号所对应的码元序列，即相应的码字。
（4）计算码字的平均码长得出最后的编码效率。
五、实验数据记录
六、实验结论与心得
通过本次实验，加强了对matlab程序的学习，进一步提高了我的编程能力。
如有侵权请联系告知删除，感谢你们的配合！
学生实验报告
院别
电子工程学院
课程名称
信息论与编码
班级
实验名称
实验四、哈夫曼编码
姓名
实验时间
学号
指导教师
成绩
报告内容
一、实验目的和任务
1、理解信源编码的意义；
2、熟悉MATLAB程序设计；
3、掌握哈夫曼编码的方法及计算机实现；
４、对给定信源进行香农编码，并计算编码效率；
二、实验原理介绍
1、把信源符号按概率大小顺序排列，并设法按逆次序分配码字的长度；
三、实验设备介绍
1、计算机
2、编程软件MATLAB6.5以上
四、实验内容和步骤
对如下信源进行哈夫曼编码，并计算编码效率。
（1）计算该信源的信源熵，并对信源概率进行排序
（2）首先将出现概率最小的两个符号的概率相加合成一个概率，把这个合成概率与其他的概率进行组合，得到一个新的概率组合，重复上述做法，直到只剩下两个概率为止。之后再反过来逐步向前进行编码，每一次有两个分支各赋予一个二进制码。对大的概率赋

信息论与编码习题与答案第五章

5-10 设有离散无记忆信源}03.0,07.0,10.0,18.0,25.0,37.0{)(=X P 。

（1）求该信源符号熵H(X)。

（2）用哈夫曼编码编成二元变长码，计算其编码效率。

（3）要求译码错误小于310-，采用定长二元码达到（2）中的哈夫曼编码效率，问需要多少个信源符号连在一起编？解：（1）信源符号熵为symbolbit x p x p X H i ii /23.203.0log 03.007.0log 07.010.0log 10.018.0log 18.025.0log 25.037.0log 37.0)(log )()(222222=------=-=∑ （2）1x 3x 2x 6x 5x 4x 0.370.250.180.100.070.030111110.100.200.380.621.0000011110110001001符号概率编码该哈夫曼码的平均码长为符号码元/3.2403.0407.0310.0218.0225.0237.0)(=⨯+⨯+⨯+⨯+⨯+⨯==∑iii K x p K 编码效率为9696.03.223.2)(===KX H η (3)信源序列的自信息方差为2222)(792.0)]([)]()[log ()(bit X H x p x p X i ii =-=∑σ7.00696.90)()(==+=εεη得，由X H X H53222102.6110)7.00(92.70)(⨯=⨯=≥-δεσX L 由切比雪夫不等式可得所以，至少需要1.62×105个信源符号一起编码才能满足要求。

5-12 已知一信源包含8个消息符号，其出现的概率}04.0,07.0,1.0,06.0,05.0,4.0,18.0,1.0{)(=X P ，则求：（1）该信源在每秒内发出1个符号，求该信源的熵及信息传输速率。

（2）对这8个符号作哈夫曼编码，写出相应码字，并求出编码效率。

信息论大作业

信息论大作业信息论大作业电子工程学院班号编码1．Huffman 编码原理：①将信源符号按概率从大到小的顺序排列，令p(x1)≥ p(x2)≥?≥ p(xn) ②给两个概率最小的信源符号p(xn-1)和p(xn)各分配一个码位“0”和“1”，将这两个信源符号合并成一个新符号，并用这两个最小的概率之和作为新符号的概率，结果得到一个只包含(n－1)个信源符号的新信源。

称为信源的第一次缩减信源，用S1表示。

③将缩减信源S1的符号仍按概率从大到小顺序排列，重复步骤2，得到只含(n －2)个符号的缩减信源S2。

④重复上述步骤，直至缩减信源只剩两个符号为止，此时所剩两个符号的概率之和必为1。

然后从最后一级缩减信源开始，依编码路径向前返回，就得到各信源符号所对应的码字。

2. 霍夫曼编码优缺点：1) 编出来的码都是异字头码，保证了码的唯一可译性。

2) 于编码长度可变。

因此译码时间较长，使得霍夫曼编码的压缩与还原相当费时。

3) 编码长度不统一，硬件实现有难度。

4) 对不同信号源的编码效率不同，当信号源的符号概率为2的负幂次方时，达到100％的编码效率；若信号源符号的概率相等，则编码效率最低。

5) 于0与1的指定是任意的，故上述过程编出的最佳码不是唯一的，但其平均码长是一样的，故不影响编码效率与数据压缩性能。

3.编码流程：读入一幅图像的灰度值; 1. 将矩阵的不同数统计在数组c的第一列中; 2. 将相同的数占站整个数组总数的比例统计在数组p中; 3. 找到最小的概率,相加直到等于1,把最小概率的序号存在tree第一列中,次小放在第二列,和放在p像素比例之后; 4. C数组第一维表示值,第二维表示代码数值大小,第三维表示代码的位数； 5. 把概率小的值为1标识，概率大的值为0标识； 6. 计算信源的熵；7. 计算平均码长；8. 计算编码效率’；9. 计算冗余度。

源程序：p=input(‘请输入数据:’); n=length(p); for i=1:n if p(i) fprintf(‘\\n 提示：概率值不能小于0!\\n’); p=input(‘请重新输入数据:’);end end if abs(sum(p))>1 fprintf(‘\\n 哈弗曼码中概率总和不能大于1!\\n’); p=input(‘请重新输入数据:’);end q=p; a=zeros(n-1,n); %生成一个n-1 行n 列的数组for i=1:n-1[q,l]=sort(q); a(i,:)=[l(1:n-i+1),zeros(1,i-1)];q=[q(1)+q(2),q(3:n),1];end for i=1:n-1 c(i,1:n*n)=blanks(n*n); end c(n-1,n)=‘0’;c(n-1,2*n)=‘1’; for i=2:n-1 c(n-i,1:n-1)=c(n-i+1,n*(find(a(n-i+1,:)==1 ))-(n-2):n*(find(a(n-i+1,:)==1))) ; c(n-i,n)=‘0’ ; c(n-i,n+1:2*n-1)=c(n-i,1:n-1) ; c(n-i,2*n)=‘1’ ;for j=1:i-1c(n-i,(j+1)*n+1:(j+2)*n)=c(n-i+1,n*(find( a(n-i+1,:)==j+1)-1)+1:n*find(a(n-i+1,:)==j +1)); end end%完成huffman 码字的分配for i=1:n h(i,1:n)=c(1,n*(find(a(1,:)==i)-1)+1:find(a (1,:)==i)*n);ll(i)=length(find(abs(h(i,:))~=32)); %计算每一个huffman 编码的长度end l=sum(p.*ll);%计算平均码长fprintf(‘\\n Huffman编码结果为:\\n’);h fprintf(‘\\n 编码的平均码长为:\\n’); l hh=sum(p.*(-log2(p))); %计算信源熵fprintf(‘\\n 信源熵为:\\n’);hh fprintf(‘\\n 编码效率为:\\n’); t=hh/l%计算编码效率运行结果为：请输入数据:[,,,,,,,] Huffman编码结果为: h = 1100 1101010111011 00010001 编码的平均码长为: l = 3 信源熵为: hh = 编码效率为: t = 编码：Fano 码: 费诺编码属于概率匹配编码，但它不是最佳的编码方法。

信息论与编码课程作业_huffman编码的matlab_实现

信息论与编码课程作业_huffman编码的matlab_实现信息论与编码课程作业——霍夫曼编码求信源熵和存储前后的信息量的变化一：设计目的：1、学习离散信源平均信息量的计算方法。

2、理解和掌握huffman 编码的基本原理，实现对信源符号的huffman 编码3、熟悉 Matlab 编程；二：设计原理和思路1.信源熵的计算：公式： 21()log a I a p = Matlab 实现：I=log2(1/p) 或I=-log2(p) 熵（平均自信息）的计算公式22111()log log qq i i i i i i H x p p p p ====-∑∑Matlab 实现：HX=sum(-x.*log2(x))；或者h=h-x(i)*log2(x(i));2.霍夫曼编码原理;分为两步，首先是码树形成过程：对信源概率进行合并形成编码码树。

然后是码树回溯过程：在码树上分配编码码字并最终得到Huffman 编码。

1、码树形成过程：将信源概率按照从小到大顺序排序并建立相应的位置索引。

然后按上述规则进行信源合并，再对信源进行排序并建立新的位置索引，直到合并结束。

在这一过程中每一次都把排序后的信源概率存入矩阵p 中，位置索引存入矩阵m 中。

这样，由排序之后的概率矩阵 p 以及索引矩阵m 就可以恢复原概率矩阵P 了，从而保证了回溯过程能够进行下去。

2、码树回溯过程：在码树上分配编码码字并最终得到Huffman 编码。

从索引矩阵M 的末行开始回溯。

(1) 在p 的末行2元素位置填入0和1。

(2) 根据该行索引1位置指示，将索引1位置的编码（‘1’）填入上一行的第一、第二元素位置，并在它们之后分别添加‘0’和‘1’。

(3) 将索引不为‘1’的位置的编码值（‘0’）填入上一行的相应位置（第3 列）。

(4) 以m的倒数第二行开始向上，重复步骤(1) ～(3)，直到计算至m的首行为止。

三：设计代码：>> clear all;format longdisp(strcat('信息论与编码课程作业——霍夫曼编码求信源熵和存储前后的信息量的变化',13));histgram=zeros(1,255);[c,map]=imread('C:\Documents and Settings\Administrator\桌面\infomation\lenna.bmp');x=rgb2gray(c);[a,b]=size(x);for i=1:afor j=1:bk=x(i,j);histgram(k)=histgram(k)+1;endendf=histgram/a/b;symbols=find(f~=0); %灰度值p=f(symbols); %概率L=length(p);pp=p;%霍夫曼编码m=zeros(L-1,L);for i=1:L-1[p,mark]=sort(p);m(L-i,1:L-i+1)=mark(1:L-i+1);p=[p(1)+p(2),p(3:L),1];endc=cell(L-1,L);c(1,1)={'0'};c(1,2)={'1'};for i=2:L-1;ind=find(m(i-1,:)==1);temp=char(c(i-1,ind));c(i,1)={[temp,'0']};c(i,2)={[temp,'1']};snc=find(m(i-1,:)~=1);for j=3:i+1;con=snc(j-2);c(i,j)=c(i-1,con);endendcodeL=[];averge_long=0;H1=0;disp(strcat('灰度值',32,32,32,'概率',32,32,32,32,32,32,32,32,32,'霍夫曼编码:'));for i=1:L;ind=find(m(L-1,:)==i);code=char(c(L-1,ind));codeLength(i)=length(code);averge_long=averge_long+pp(i)*codeLength(i);H1=H1+pp(i)*log2(1/pp(i));disp(strcat(32,num2str(symbols(i)),32,32,32,num2str(pp(i)),3 2,32, code));enddisp(strcat('信源熵=',num2str(H1),32,32,32,32,'平均码字长度=',num2str(averge_long),32,32,32,32,32,'压缩比=',num2str(8/averge_long)));四：设计运行结果：信息论与编码课程作业——霍夫曼编码求信源熵和存储前后的信息量的变化灰度值概率霍夫曼编码:30 1.5259e-005 101000111100001031 1.5259e-005 101000111100001136 1.5259e-005 101000111100000037 1.5259e-005 101000111100000139 6.1035e-005 1010001111000140 7.6294e-005 1110010101001041 6.1035e-005 0111010111011042 6.1035e-005 0111010111011143 9.1553e-005 1110010101001144 0.00018311 111011101010145 0.00021362 00111101101146 0.00022888 01110101111047 0.00024414 01110101111148 0.00039673 0011110110049 0.00048828 1010001110050 0.00065613 1110010101151 0.00090027 011101011052 0.00086975 001111011153 0.0013123 111001011054 0.0013733 111011101156 0.0018005 01110101057 0.0025177 11010001158 0.0036621 0111111059 0.0033722 0101111060 0.0046539 1100110161 0.0055847 1111010162 0.0061188 001001063 0.0080261 100111064 0.0075226 100001165 0.0083466 101010166 0.0088806 101111167 0.0092773 110011168 0.0095367 110101069 0.0086517 101101070 0.0084229 101011071 0.0075378 100010172 0.0071564 011011173 0.0061493 001001174 0.0056 1111011075 0.0053864 1110110076 0.0045319 1100011177 0.0043488 1011000178 0.0042114 1010111079 0.0039063 1000111180 0.0041199 1010100181 0.0035706 0110101182 0.0039368 1001011083 0.0037537 1000010084 0.003479 0110101086 0.0033417 0101101087 0.0032501 0100110088 0.0034027 0110000189 0.0031128 0011010090 0.0031433 0011110091 0.0036774 0111111192 0.0041046 1010011094 0.0038452 1000111095 0.004364 1011100096 0.0037842 1000110097 0.0037079 1000001198 0.0033722 0101111199 0.0040741 10100001 100 0.0040741 10100010 101 0.0038147 10001101 102 0.0040588 10011111 103 0.0041046 10100111 104 0.004364 10111001 105 0.0048218 11010111 106 0.0052185 11100100 107 0.0049591 11011010 108 0.005188 11100001 109 0.0047455 11010110 110 0.0052032 11100011 111 0.0054474 11110100 112 0.0057526 11111011 113 0.0065308 0100111 114 0.0079346 1001100 115 0.010223 1101111116 0.0095825 1101100 117 0.0089417 1100000 118 0.0086975 1011011 119 0.0081787 1010010 120 0.007782 1001001121 0.0066376 0101011 122 0.0059357 11111111 123 0.0056458 11110111 124 0.0051575 11100000 125 0.0052948 11101001 126 0.005188 11100010 127 0.0059814 0000001 128 0.0058594 11111101 129 0.0065613 0101010 130 0.0062561 0011011 131 0.006897 0110100132 0.0072479 0111011 133 0.0073242 0111110 134135 0.0075226 1000100 136 0.0077515 1001000138 0.008606 1011001139 0.0091095 1100100 140 0.012115 000010141 0.012115 000011142 0.012741 001110143 0.012329 001100144 0.010941 1111001145 0.010147 1101110146 0.0089417 1100001 147 0.0088043 1011101 148 0.0091095 1100101 149 0.010712 1110101150 0.011337 1111100151 0.010513 1110011152 0.012878 010000153 0.012268 001010154 0.013138 010100155 0.012238 001000156 0.012939 010001157 0.012115 000100158 0.012955 010010159 0.012207 000111160 0.011993 000001161 0.013916 011001162 0.012177 000110163 0.012299 001011164 0.0094604 1101001 165 0.0089874 1100010 166 0.0088501 1011110 167 0.0056915 11111010 168 0.0059357 0000000 169 0.0071716 0111001 170 0.0057678 11111100 171 0.0054016 11101111 172 0.0054169 11110001 173 0.0058746 11111110 174 0.0072937 0111100 175 0.0070953 0110110 176177 0.0061035 0001011 178 0.0054016 11110000 179 0.0053864 11101101 180 0.0046692 11010000182 0.0036774 10000000183 0.0033875 01100000184 0.0033264 01011000185 0.0031281 00110101186 0.0035706 01110000187 0.0033264 01011001188 0.0033569 01011011189 0.0036011 01110100190 0.0040436 10011110191 0.0034485 01100010192 0.0036774 10000001193 0.0032654 01001101194 0.0034485 01100011195 0.003006 00010100196 0.0033722 01011100197 0.0036774 10000010198 0.0042419 10110000199 0.0045166 11000110200 0.0041046 10101000201 0.0052643 11101000202 0.0050354 11011011203 0.0045319 11001100204 0.0039825 10011010205 0.0040588 10100000206 0.0039673 10010111207 0.0037537 10000101208 0.0033722 01011101209 0.0026703 111011100210 0.0022125 110100010211 0.0018768 101000110212 0.0015259 000101010213 0.0013428 1110010111214 0.0012665 1110010100215 0.0007782 0011110100216 0.00079346 0011110101217 0.00061035 10100011111218 0.00054932 10100011101219 0.00065613 11101110100220 0.00035095 111011101011 221 0.00033569 111001010101 222 0.00030518 101000111101 223 0.00021362 011101011100 224 0.00016785 1110111010100225 0.00019836 001111011010226 0.00015259 1110010101000227 0.00010681 0111010111010228 6.1035e-005 10100011110010230 3.0518e-005 101000111100110231 1.5259e-005 10100011110011110232 1.5259e-005 10100011110011111233 1.5259e-005 1010001111001110信源熵=7.2193 平均码字长度=7.2492 压缩比=1.1036五：设计新得体会：通过这学期对信息论和编码的学习，以及这次的设计，使我了解了很多东西，也使以前所学的知识得以巩固！，通过这次的设计，进一步学习了离散信源平均信息量、平均码长和压缩比的计算方法。

信息论与编码课程大作业

信息论与编码课程大作业
一、信源与信源编码
1、若信源包含N 个符号，在什么情况下熵最大？（10分）
最大的熵值是多少？（10分）
2、简述信源编码的两个作用。

（10分）
3、已知离散无记忆信源中各符号的概率空间为
X = 符号u1 u2 u3 u4
概率：1/2 1/4 1/8 1/8
(1)求信源的熵(10分)；
(2)对其进行哈夫曼编码(要求码方差较小)，写出过程(10分)；
(3)求出平均码长和编码效率(10分)。

4、举出学过的无失真与限失真编码方法，各1种。

（10分）
并选择一种，阐述其在实际中的应用（不少于200字）。

（10分）
5、编程题（20分）
二、信道与信道编码
1、对称信道容量公式？（10分）
在信源如何分布时达到信道容量？（10分）
2、信道编码的基本原理是什么？（10分）
3、对一个（4，2）码，其生成矩阵为
(1)写出伴随式译码表(10分)；
(2)接收序列R=1100，估算发码(10分)；
(3)判断码的检错能力(10分)。

4、举出两种常用的纠错码，（10分）
并选择一种，阐述其在实际中的应用（不少于200字）。

（10分）
5、编程题（20分）
说明：（1）按学号排列前30名同学完成信源与信源编码方面的作业，其余同学
完成信道与信道编码方面的作业。

（2）第5题编程题另付题目与具体要求，可在20道编程题中任选一道；
自己编写课程相关的其他程序也可以。

（3）第4题和第5题，任意两个同学不能雷同，否则均不能通过。

10010111G ⎡⎤=⎢⎥⎣⎦。

哈夫曼编码信息论大作业汇总

哈夫曼编码1.前言:H affman算法是个简单而高效的贪心算法，主要用来创建最优二叉树.可以在通讯时，对于出现频率较高的字符，用较少的比特数便可以进行通讯.从而节省通讯线路的资源消耗。

该算法在各类数据结构, 算法,组合数学，离散数学，图论等主题的书籍中都有所涉及。

故本文不再赘述，本文致力于用Haffman算法实现压缩与解压缩,采用的语言为C语言，编译环境VC++6.0.下面给出[1]中实现的Haffman树的结构及创建算法，有两点说明:a) 这里的Haffman树采用的是基于数组的带左右儿子结点及父结点下标作为存储结点的二叉树形式，这种空间上的消耗带来了算法实现上的便捷。

b) 由于对于最后生成的Haffman树，其所有叶子结点均为从一个内部树扩充出去的，所以，当外部叶子结点数为m个时，内部结点数为m-1.整个Haffman树的需要的结点数为2m-1. 2压缩过程的实现:压缩过程的流程是清晰而简单的:1创建Haffman树à2打开需压缩文件à3将需压缩文件中的每个ascii码对应的haffman编码按bit单位输出à4文件压缩结束。

其中，步骤1和步骤3是压缩过程的关键。

a) 步骤1:这里所要做工作是得到Haffman数中各叶子结点字符出现的频率并进行创建. 统计字符出现的频率可以有很多方法:如每次创建前扫描被创建的文件，“实时”的生成各字符的出现频率;或者是创建前即做好统计.本文采用后一种的方案,统计了十篇不同的文章中字符出现的频率。

当前，也可以根据被压缩文件的特性有针对性的进行统计，如要压缩C语言的源文件，则可事先对多篇C语言源文件中出现的字符进行统计,这样，会创建出高度相对较“矮”的Haffman树，从而提高压缩效果。

创建Haffman树的算法前文已有陈述，这里就不再重复了。

b) 步骤3: 将需压缩文件中的每个ascii码对应的haffman编码按bit单位输出.这是本压缩程序中最关键的部分:这里涉及“转换”和“输出”两个关键步骤:“转换”部分大可不必去通过遍历Haffman树来找到每个字符对应的哈夫曼编码，可以将每个Haffman码值及其对应的ascii码存放于如下所示的结构体中：2.算术编码(1)算术编码是把一个信源表示为实轴上0和1之间的一个区间，信源集合中的每一个元素都用来缩短这个区间。

信息论实验信源的二元Huffman编码

概率：0.18编码：111
概率：0.17编码：110
概率：0.01编码：1000
概率：0.15编码：101
概率：0.2编码：01
概率：0.19编码：00
概率：0.1编码：1001
平均码长为：2.72
编码效率为：0.959075
六．实验总结及心得体会
Huffman编码方法是《数据结构》课程中的一个重要内容，当时是用二叉树来实现的。在《信息论与编码》中，Huffman树的概念虽然提的很少，但整体思想仍然是相同的，因此编程过程还比较顺利。
for i=2:n-1
c(n-i,1:n-1)=c(n-i+1,n*(find(m(n-i+1,:)==1))-(n-2):n*(find(m(n-i+1,:)==1)));
c(n-i,n)='0';
c(n-i,n+1:2*n-1)=c(n-i,1:n-1);
c(n-i,2*n)='1';
for j=1:i-1
q=p;%信源的概率赋给q，以便后面排序、合并用
m=zeros(n-1,n);%定义m为零数组，记录排列顺序（小概率求和后再重新排列，这就存在排序的问题）
for i=1:n-1
[q,k]=sort(q);%k是排列后的顺序，sort(q)是对q进行升序
m(i,:)=[k(1:n-i+1),zeros(1,i-1)];%概率小的相加之后重新排序，排列顺序记录在m矩阵中
if (length(find(p<0))~=0)
error('数组中概率有负的');%p概率为负拒绝编码
end
if (abs(sum(p)-1)>10e-10)

信息论实验哈夫曼编码c语言

信息论实验哈夫曼编码c语言以下是使用C语言实现哈夫曼编码的示例代码：```cinclude <>include <>include <>define MAX_TREE_HT 100struct MinHeapNode {char data;unsigned freq;struct MinHeapNode left, right;};struct MinHeap {unsigned size;unsigned capacity;struct MinHeapNode array;};struct MinHeapNode newNode(char data, unsigned freq) {struct MinHeapNode temp = (structMinHeapNode)malloc(sizeof(struct MinHeapNode));temp->left = temp->right = NULL;temp->data = data;temp->freq = freq;return temp;}struct MinHeap createMinHeap(unsigned capacity) {struct MinHeap minHeap = (struct MinHeap)malloc(sizeof(struct MinHeap));minHeap->size = 0;minHeap->capacity = capacity;minHeap->array = (struct MinHeapNode)malloc(minHeap->capacity sizeof(struct MinHeapNode));return minHeap;}void swapMinHeapNode(struct MinHeapNode a, struct MinHeapNode b) {struct MinHeapNode t = a;a = b;b = t;}void minHeapify(struct MinHeap minHeap, int idx) {int smallest = idx;int left = 2 idx + 1;int right = 2 idx + 2;if (left < minHeap->size && minHeap->array[left]->freq < minHeap->array[smallest]->freq) {smallest = left;}if (right < minHeap->size && minHeap->array[right]->freq < minHeap->array[smallest]->freq) {smallest = right;}if (smallest != idx) {swapMinHeapNode(&minHeap->array[smallest], &minHeap->array[idx]);minHeapify(minHeap, smallest);}}int isSizeOne(struct MinHeap minHeap) {return (minHeap->size == 1);}void insertMinHeap(struct MinHeap minHeap, struct MinHeapNode minHeapNode) {minHeap->size++;int i = minHeap->size - 1;while (i && minHeapNode->freq < minHeap->array[(i - 1) / 2]->freq) {minHeap->array[i] = minHeap->array[(i - 1) / 2];i = (i - 1) / 2;}minHeap->array[i] = minHeapNode;}struct MinHeapNode extractMin(struct MinHeap minHeap) { struct MinHeapNode root = minHeap->array[0];minHeap->array[0] = minHeap->array[minHeap->size - 1]; --minHeap->size;minHeapify(minHeap, 0);return root;}void buildMinHeap(struct MinHeap minHeap) {int n = minHeap->size - 1;int i;for (i = (n - 1) / 2; i >= 0; --i) {minHeapify(minHeap, i);}}void printArr(int arr[], int n) {int i;for (i = 0; i < n; ++i) {printf("%d", arr[i]);if (i < n - 1) {printf(" ");} else {printf("\n");}}}int isLeaf(struct MinHeapNode root) {return !(root->left) && !(root->right);}void printCodes(struct MinHeapNode root, int arr[], int top) {if (root->left) {arr[top] = 0; // left branch -> 0 in binary tree representation.! So first bit of code for root will be '0'! So, '0' is the prefix for all left branches! Therefore, '。

信息论编码课程设计(用哈夫曼编码实现一个完整的压缩与解压程序)

课程设计任务书2011—2012学年第二学期专业：信息与计算科学学号：姓名：课程设计名称：信息论与编码课程设计设计题目：用哈夫曼编码实现一个完整的压缩与解压程序完成期限：自年月日至年月日共天一．设计目的1、深刻理解信源编码的基本思想与目的；2、理解哈夫曼编码方法的基本过程与特点；3、详细地理解文件的压缩与解压过程；4、提高综合运用所学理论知识独立分析和解决问题的能力；5、使用C语言进行编程。

二．设计内容假设已知一个文件内部所有的字符，编写适当函数，对其进行哈夫曼编码的编译，同时将其运用位操作进行压缩与解压，并且由其文件内字符长度的压缩和气原本长度进行计算，从而得出压缩率的大小。

三．设计要求1、编写的函数要有通用性；2、压缩的文件可以为任意文件，自由选择，并且解压其压缩后的文件显示其是否与原文件内容一致。

四．设计条件计算机、VC6.0编译环境五．参考资料李亦农、李梅《信息论基础教程》指导教师（签字）：教研室主任（签字）：批准日期：年月日哈夫曼编码(Huffman Coding)是一种编码方式，也是可变字长编码(VLC)的一种。

这种方法完全依据字符出现的概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫作哈夫曼编码。

对于M进制哈弗曼编码，为了提高编码效率，就要使长码的符号数量尽量少、概率尽量小，所以应使合并的信源符号位于缩减信源序列尽可能高的位置上，以减少再次合并的次数，充分利用短码。

本文将采用利用二进制哈夫曼编码来进行文件的压缩与解压。

在二进制哈夫曼编码中，得出码字、平均码长和编码效率，构造哈夫曼树，沿着根节点到叶节点从左到右依次为0、1，并且码字的频率由大到小排序。

在本文中采用Visual C++6.0进行编程，此程序中具有输入字符集大小和权值大小，构造哈夫曼树，并对原本的文件进行编码等功能。

关键词：哈弗曼编码；信源；哈夫曼树；Visual C++6.0；1课题描述 (1)2设计原理 (1)3 设计过程 (2)3.1软件介绍 (2)3.1.1 Visual C++ 6.0简介 (2)3.1.2主要部分 (2)3.2设计内容 (2)4编码程序分析及其结果 (3)总结 (7)参考文献 (7)1课题描述在这个信息量爆炸的时代，凡是能载荷一定信息量，且码字的平均长度最短，可分离的变长码的码字集合称为最佳变长码。

哈夫曼编码

南京工程学院通信工程学院《信息论与编码》大作业课程名称信息论与编码学生班级电子信息121学生姓名顾健实验成绩评定指导教师签字年月日基于C++语言的哈夫曼(Haffman)编码哈夫曼(Haffman)编码是一种常用的压缩编码方法，是哈夫曼于1952年为压缩文本文件建立的。

它的基本原理是按照概率大小顺序排列信源符号，并设法按逆顺序分配码字字长，使编码的码字为可辨识的。

哈夫曼码是最佳码。

二进制哈夫曼码的编码步骤如下：(1) 将q 个信源符号按概率分布)(i s p 的大小，以递减次序排列起来，设q p p p p ≥•••≥≥≥321(2) 用0和1码符号分别代表概率最小的两个信源符号，并将这两个概率最小的信源符号合并成一个符号，从而得到只包含q-1个符号的新信源，称为S 信源的缩减信源1S 。

(3) 把缩减信源1S 的符号仍按概率大小以递减次序排列，再将最后两个概率最小的符号合并成一个符号，并分别用0和1码符号表示，这样又形成了q-2个符号的缩减信源2S 。

(4) 依此继续下去，直至最后只剩两个符号为止。

将这最后两个信源符号分别用0和1码符号表示。

然后从最后一级缩减信源开始，向前返回，就得出各信源符号所对应的码符号序列，即对应的码字。

下面举一个具体的Huffman 编码的例子(如图1所示)：信源符号概率信源缩减过程编码码长1S 0.4 00 22S 0.2 10 2 3S 0.2 11 2 4S 010 3 5S 011 3 图1 Huffman 编码示例它的平均码长为)/(2.2305.0315.022.022.024.0)(51信源符号码符号=⨯+⨯+⨯+⨯+⨯=∑==i i i l s p L 信息熵为)/(08.2)log()(-)(51信源符号比特=∑==i i i s s p S H 编码效率为%5.94%1002.208.2)(=⨯==L S H η 哈夫曼编码方法得到的码并非是唯一的。

信息论大作业2课件

一、实验目的1、通过实验进一步理解霍夫曼编码、算术编码和LZ编码原理和方法2、熟悉matlab编程和GUI界面的设计二、实验原理1、赫夫曼（Huffman ）编码是1952年提出的，是一种比较经典的信息无损熵编码，该编码依据变长最佳编码定理，应用Huffman 算法而产生。

Huffman 编码是一种基于统计的无损编码。

设信源X 的信源空间为：⎩⎨⎧∙)()()()(:)(::][32121N N x P x P x P x P X P x x x X P X 其中，1)(1=∑=Ni i x P ，现用二进制对信源X 中的每一个符号i x (i=1,2,…N)进行编码。

根据变长最佳编码定理，Huffman 编码步骤如下：（1）将信源符号xi 按其出现的概率，由大到小顺序排列。

（2）将两个最小的概率的信源符号进行组合相加，并重复这一步骤，始终将较大的概率分支放在上部，直到只剩下一个信源符号且概率达到1.0为止；（3）对每对组合的上边一个指定为1，下边一个指定为0（或相反：对上边一个指定为0，下边一个指定为1）；（4）画出由每个信源符号到概率1.0处的路径，记下沿路径的1和0；（5）对于每个信源符号都写出1、0序列，则从右到左就得到非等长的Huffman 码。

Huffman 编码的特点是：（1）Huffman 编码构造程序是明确的，但编出的码不是唯一的，其原因之一是两个概率分配码字“0”和“1”是任意选择的（大概率为“0”，小概率为“1”，或者反之）。

第二原因是在排序过程中两个概率相等，谁前谁后也是随机的。

这样编出的码字就不是唯一的。

（2）Huffman 编码结果，码字不等长，平均码字最短，效率最高，但码字长短不一，实时硬件实现很复杂（特别是译码），而且在抗误码能力方面也比较差。

（3）Huffman 编码的信源概率是2的负幂时，效率达100%，但是对等概率分布的信源，产生定长码，效率最低，因此编码效率与信源符号概率分布相关，故Huffman 编码依赖于信源统计特性，编码前必须有信源这方面的先验知识，这往往限制了哈夫曼编码的应用。

信息论程序半字节哈弗曼重复码编译码

实验一英文半字节压缩编码技术实验二Huffman编码实验三重复码编译码方法实验一英文半字节压缩编码技术一、实验目的1、理解信源编码的作用和目的，掌握数据压缩的基本思想；2、掌握数据压缩中常用的比特流操作办法；3、掌握英文半字节压缩编码技术。

二、实验内容通过C语言编程，实现对一般英文文本文件的半字节压缩编码与译码程序，并观察编码、译码结果以及压缩效果。

三、实验原理对于一个通信系统来说，信息传输的有效性、可靠性、安全性和认证性是人们的主要目标。

其中，信息传输的有效性指的是尽可能的使用较短的时间和较少的设备等资源来传送尽可能多的信息，而这一目的主要是通过信源编码这个环节来实现的。

虽然有许许多多不同的信源编码方法，但总的说来，信源编码主要是通过减少或消除信源的剩余度来提高传输效率的。

而且，有时人们为了追求更高的传输效率，在满足实际需求的情况下，还允许在编译码过程中存在一定程度的失真，这就是所谓的有损压缩。

当然，针对不同的应用要求，可以选择不同的压缩编码办法，为了方便理解和实现，针对一般的英文文本，可以设计一种半字节压缩编码方法来实现数据的压缩。

（一）有损处理在一般英文文本中，除了大、小写英文字母外，还有多种不同的标点符号。

为了达到在不影响文章大意的前提下，尽可能的减少需编码的符号数，以提高信息传输效率的目的，可采取这样的处理方法：1) 所有的英文字母不区分大、小写(如：将所有的大写英文字母变成小写字母)；2) 保留标点符号：“，”、“。

”、“？”“：”和“”；3) 将“！”和“；”变为“。

”，其他符号全部变成“”。

这样，原来的英文文本就变成了一个新的文本，该文本全部由26个英文字母和“，”、“。

”、“？”、“：”以及“”这31种符号组成，而且，文章的大意并没有发生大的变化。

可以认为这种失真是在允许的失真范围之内的。

当然，为了简化操作，上面的第一步也可省略。

虽然这样会使输出文件中既有大写字符，又有小写字符，但只需在后面的编码操作时将大、小写等同处理，则同样达到了不区分大小写的目的。

信息论与编码课程大作业二进制哈夫曼编码

信息论与编码课程大作业题目：二进制哈夫曼编码学生姓名：学号： 00专业班级： 2010级电子信息班2013年 5月 18日二进制哈夫曼编码1、二进制哈夫曼编码的原理及步骤1、1信源编码的计算设有N 个码元组成的离散、无记忆符号集，其中每个符号由一个二进制码字表示，信源符号个数n 、信源的概率分布P={p(s i )},i=1,…..,n 。

且各符号xi的以li 个码元编码，在变长字编码时每个符号的平均码长为∑==ni li xi p L 1)( ；信源熵为：)(log )()(1xi p xi p X H ni ∑=-= ；唯一可译码的充要条件：11≤∑=-ni Ki m ；其中m 为码符号个数，n 为信源符号个数，Ki 为各码字长度。

构造哈夫曼数示例如下图所示。

1、2 二元霍夫曼编码规则（1）将信源符号依出现概率递减顺序排序。

（2）给两个概率最小的信源符号各分配一个码位“0”和“1”，将两个信源符号合并成一个新符号，并用这两个最小的概率之和作为新符号的概率，结果得到一个只包含（n-1）个信源符号的新信源。

称为信源的第一次缩减信源，用s1 表示。

（3）将缩减信源 s1 的符号仍按概率从大到小顺序排列，重复步骤(2)，得到只含（n-2）个符号的缩减信源s2。

（4）重复上述步骤，直至缩减信源只剩两个符号为止，此时所剩两个符号的概率之和必为 1，然后从最后一级缩减信源开始，依编码路径向前返回，就得到各信源符号所对应的码字。

1、3 二元哈夫曼编码流程图如下图所示。

2、二元哈夫曼编码程序p=input('please input a number:') %提示输入界面n=length(p);for i=1:nif p(i)<0fprintf('\n The probabilities in huffman can not less than 0!\n');p=input('please input a number:') %如果输入的概率数组中有小于 0 的值，endendif abs(sum(p)-1)>0fprintf('\n The sum of the probabilities in huffman can more than 1!\n');p=input('please input a number:') %如果输入的概率数组总和大于 1，则重endq=p;a=zeros(n-1,n); %生成一个 n-1 行 n 列的数组for i=1:n-1[q,l]=sort(q); %对概率数组q进行从小至大的排序，并且用l数组返回一个q排序前的顺序编号a(i,:)=[l(1:n-i+1),zeros(1,i-1)]; %由数组 l 构建一个矩阵，该矩阵表明概率合并q=[q(1)+q(2),q(3:n),1]; %将排序后的概率数组 q 的前两项，即概率最小的两endfor i=1:n-1c(i,1:n*n)=blanks(n*n);endc(n-1,n)='0'; %由于a矩阵的第n-1行的前两个元素为进行huffman编码加和运算时所得的最c(n-1,2*n)='1';for i=2:n-1c(n-i,1:n-1)=c(n-i+1,n*(find(a(n-i+1,:)==1))-(n-2):n*(find(a(n-i+1,:)==1))); c(n-i,n)='0'; %根据之前的规则，在分支的第一个元素最后补 0c(n-i,n+1:2*n-1)=c(n-i,1:n-1);c(n-i,2*n)='1'; %根据之前的规则，在分支的第一个元素最后补 1for j=1:i-1c(n-i,(j+1)*n+1:(j+2)*n)=c(n-i+1,n*(find(a(n-i+1,:)==j+1)-1)+1:n*find(a(n-i+1,: )==j+ 1));endend%完成 huffman 码字的分配for i=1:nh(i,1:n)=c(1,n*(find(a(1,:)==i)-1)+1:find(a(1,:)==i)*n);ll(i)=length(find(abs(h(i,:))~=32)); %计算每一个 huffman 编码的长度enddisp('二元霍夫曼编码平均码长')l=sum(p.*ll) %计算平均码长%fprintf('\n huffman code:\n');hdisp('信源熵')hh=sum(p.*(-log2(p))) %计算信源熵%fprintf('\n the huffman effciency:\n');disp('编码效率')t=hh/l %计算编码效率3、运行结果及分析当输入数据[,,,,,,,,]时3、1运行结果：please input a number:[,,,,,,,,] p =Columns 1 through 5Columns 6 through 9二元霍夫曼编码平均码长l =h =11101001110101111011111001111110001001信源熵hh =编码效率t =3、2分析：1、在哈弗曼编码的过程中，对缩减信源符号按概率有大到小的顺序重新排列，应使合并后的新符号尽可能排在靠前的位置，这样可使合并后的新符号重复编码次数减少，使短码得到充分利用。

算法实验2-哈夫曼编码实验报告

算法实验2-哈夫曼编码实验报告
哈夫曼编码又称为霍夫曼编码，是1952年由克劳德·哈夫曼（Claude Elwood Shannon）提出的一种数据压缩和编码方法。

它可以从一个字符串中挑选出重复出现频率较高的字母等字符，将这些字母用比它们出现次数少的符号代替，从而达到减少数据存储空间的目的。

哈夫曼编码在文件压缩和网络传输中有着巨大的应用。

哈夫曼编码的原理基于信息论，利用熵的概念来实现数据压缩和编码。

熵是信息源发送信息的期望的信息量的度量，也就是说，发送的信息越多，熵越大。

所以，哈夫曼编码就是根据被发送信息的可能性来构造字符编码的，这样就能够优化发送的信息长度，从而实现数据压缩。

哈夫曼编码的基本步骤是：首先，根据待编码的字符统计其出现的频率，形成一棵二叉树；接着，给每个最底层的叶子节点分配编码，这里使用的是0和1来代替；最后，把最底层节点上的编码和字母相关联形成一个字符集。

哈夫曼编码得到的编码串中每个字符的编码长度都不一样，每个字符的编码长度取决于它出现的频率。

出现次数越多的字符编码得越短，这就使得哈夫曼编码能够获得比其他编码更短的编码长度，从而更好地完成数据压缩任务。

哈夫曼编码是实现数据压缩和编码的一种有效方法，它可以将数据压缩到最小可能的体积，同时使用起来非常简单。

它非常适用于实施网络传输的压缩处理，可以有效减少传输所需的时间，提高数据传输的效率。

信息论编码作业

信息论编码一．信息论的认识1.消息是信息的载荷者。

信息是抽象的，消息是具体的。

要研究信息，还得从研究消息入手。

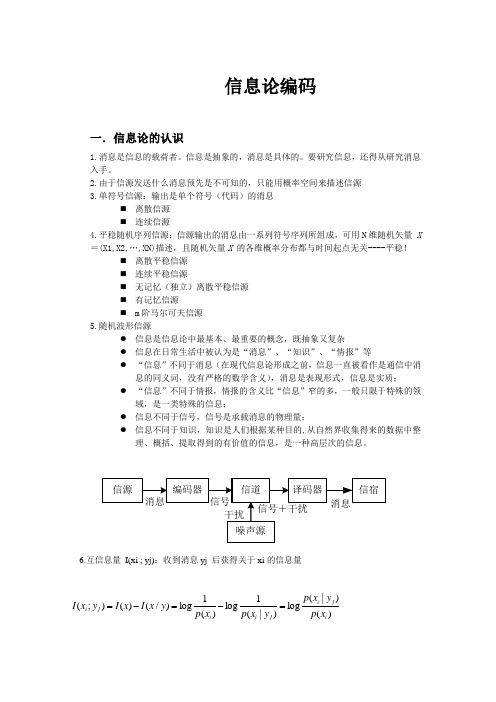
2.由于信源发送什么消息预先是不可知的，只能用概率空间来描述信源3.单符号信源：输出是单个符号（代码）的消息⏹ 离散信源 ⏹ 连续信源4.平稳随机序列信源：信源输出的消息由一系列符号序列所组成，可用N 维随机矢量 X ＝(X1,X2,…,XN)描述，且随机矢量X 的各维概率分布都与时间起点无关----平稳！⏹ 离散平稳信源 ⏹ 连续平稳信源⏹ 无记忆（独立）离散平稳信源 ⏹ 有记忆信源⏹ m 阶马尔可夫信源5.随机波形信源● 信息是信息论中最基本、最重要的概念，既抽象又复杂● 信息在日常生活中被认为是“消息”、“知识”、“情报”等● “信息”不同于消息（在现代信息论形成之前，信息一直被看作是通信中消息的同义词，没有严格的数学含义），消息是表现形式，信息是实质； ● “信息”不同于情报，情报的含义比“信息”窄的多，一般只限于特殊的领域，是一类特殊的信息；● 信息不同于信号，信号是承载消息的物理量；● 信息不同于知识，知识是人们根据某种目的,从自然界收集得来的数据中整理、概括、提取得到的有价值的信息，是一种高层次的信息。

6.互信息量 I(xi ; yj)：收到消息yj 后获得关于xi 的信息量)()|(log )|(1log )(1log )/()();(i j i j i i j i x p y x p y x p x p y x I x I y x I =-=-=即：互信息量表示先验的不确定性减去尚存的不确定性，这就是收信者获得的信息量对于无干扰信道，I(xi ; yj) = I(xi)；二．我们学到了1.离散信源熵和互信息定义具有概率为p（xi）的符号xi的自信息量为I(xi)=-logp（xi）信源输出的整体特征用平均自信息量，表示本身的特征用信源熵。

2.信道与信道容量信道分类：根据用户数量可分为单用户信道和多用户信道根据信道输入端和输出端的关系可分为无反馈信道和反馈信道。

西安电子科技大学信息论与编码作业

#include <iostream.h>#include <iomanip.h>#include <string.h>#include <malloc.h>#include <stdio.h>//typedef int TElemType;const int UINT_MAX=1000;char str[50];typedef struct{int weight,K;int parent,lchild,rchild;}HTNode,* HuffmanTree;typedef char **HuffmanCode;//-----------全局变量-----------------------HuffmanTree HT;HuffmanCode HC;int w[50],i,j,n;char z[50];int flag=0;int numb=0;// -----------------求哈夫曼编码-----------------------struct cou{char data;int count;}cou[50];int min(HuffmanTree t,int i){ // 函数void select()调用int j,flag;int k=UINT_MAX; // 取k为不小于可能的值,即k为最大的权值1000 for(j=1;j<=i;j++)if(t[j].weight<k&&t[j].parent==0)k=t[j].weight,flag=j;t[flag].parent=1;return flag;}//--------------------slect函数----------------------void select(HuffmanTree t,int i,int &s1,int &s2){ // s1为最小的两个值中序号小的那个int j;s1=min(t,i);s2=min(t,i);if(s1>s2)j=s1;s1=s2;s2=j;}}void HuffmanCoding(HuffmanTree &HT,HuffmanCode &HC,int *w,int n) { // w存放n个字符的权值(均>0),构造哈夫曼树HT,并求出n个字符的哈夫曼编码HCint m,i,s1,s2,start;//unsigned c,f;int c,f;HuffmanTree p;char *cd;if(n<=1)return;//检测结点数是否可以构成树m=2*n-1;HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode)); // 0号单元未用 for(p=HT+1,i=1;i<=n;++i,++p,++w){p->weight=*w;p->parent=0;p->lchild=0;p->rchild=0;}for(;i<=m;++i,++p)p->parent=0;for(i=n+1;i<=m;++i) // 建哈夫曼树{ // 在HT[1~i-1]中选择parent为0且weight最小的两个结点,其序号分别为s1和s2select(HT,i-1,s1,s2);HT[s1].parent=HT[s2].parent=i;HT[i].lchild=s1;HT[i].rchild=s2;HT[i].weight=HT[s1].weight+HT[s2].weight;}// 从叶子到根逆向求每个字符的哈夫曼编码HC=(HuffmanCode)malloc((n+1)*sizeof(char*));// 分配n个字符编码的头指针向量([0]不用)cd=(char*)malloc(n*sizeof(char)); // 分配求编码的工作空间cd[n-1]='\0'; // 编码结束符for(i=1;i<=n;i++){ // 逐个字符求哈夫曼编码start=n-1; // 编码结束符位置for(c=i,f=HT[i].parent;f!=0;c=f,f=HT[f].parent)// 从叶子到根逆向求编码if(HT[f].lchild==c)cd[--start]='0';elsecd[--start]='1';HC[i]=(char*)malloc((n-start)*sizeof(char)); // 为第i个字符编码分配空间strcpy(HC[i],&cd[start]); // 从cd复制编码(串)到HC }free(cd); // 释放工作空间}//--------------------- 获取报文并写入文件---------------------------------int InputCode(){//cout<<"请输入你想要编码的字符"<<endl;FILE *tobetran;if((tobetran=fopen("tobetran.txt","w"))==NULL){cout<<"不能打开文件"<<endl;return 0;}cout<<"请输入你想要编码的字符"<<endl;gets(str);fputs(str,tobetran);cout<<"获取报文成功"<<endl;fclose(tobetran);return strlen(str);}//--------------初始化哈夫曼链表--------------------------------- void Initialization(){ int a,k,flag,len;a=0;len=InputCode();for(i=0;i<len;i++){k=0;flag=1;cou[i-a].data=str[i];cou[i-a].count=1;while(i>k){if(str[i]==str[k]){a++;flag=0;}k++;if(flag==0)break;}if(flag){for(j=i+1;j<len;j++){if(str[i]==str[j])++cou[i-a].count;}}}n=len-a;for(i=0;i<n;i++){ cout<<cou[i].data<<" ";cout<<cou[i].count<<endl;}for(i=0;i<=n;i++){*(z+i)=cou[i].data;*(w+i)=cou[i].count;}HuffmanCoding(HT,HC,w,n);//------------------------ 打印编码-------------------------------------------cout<<"字符对应的编码为:"<<endl;for(i=1;i<=n;i++){puts(HC[i]);}//-------------------------- 将哈夫曼编码写入文件------------------------cout<<"下面将哈夫曼编码写入文件"<<endl<<"...................."<<endl;FILE *htmTree;char r[]={' ','\0'};if((htmTree=fopen("htmTree.txt","w"))==NULL){cout<<"can not open file"<<endl;return;}fputs(z,htmTree);for(i=0;i<n+1;i++){fprintf(htmTree,"%6d",*(w+i));fputs(r,htmTree);}for(i=1;i<=n;i++){fputs(HC[i],htmTree);fputs(r,htmTree);}fclose(htmTree);cout<<"已将字符与对应编码写入根目录下文件htmTree.txt中"<<endl<<endl;}//---------------------编码函数--------------------------------- void Encoding(){cout<<"下面对目录下文件tobetran.txt中的字符进行编码"<<endl; FILE *tobetran,*codefile;if((tobetran=fopen("tobetran.txt","rb"))==NULL){cout<<"不能打开文件"<<endl;}if((codefile=fopen("codefile.txt","wb"))==NULL){cout<<"不能打开文件"<<endl;}char *tran;i=99;tran=(char*)malloc(100*sizeof(char));while(i==99){if(fgets(tran,100,tobetran)==NULL){cout<<"不能打开文件"<<endl;break;}for(i=0;*(tran+i)!='\0';i++){for(j=0;j<=n;j++){if(*(z+j-1)==*(tran+i)){fputs(HC[j],codefile);if(j>n){cout<<"字符错误，无法编码!"<<endl; break;}}}}}cout<<"编码工作完成"<<endl<<"编码写入目录下的codefile.txt中"<<endl<<endl;fclose(tobetran);fclose(codefile);free(tran);}//-----------------译码函数---------------------------------void Decoding(){cout<<"下面对根目录下文件codefile.txt中的字符进行译码"<<endl; FILE *codef,*txtfile;if((txtfile=fopen("txtfile.txt","w"))==NULL){cout<<"不能打开文件"<<endl;}if ((codef=fopen("codefile.txt","r"))==NULL){cout<<"不能打开文件"<<endl;}char *work,*work2,i2;int i4=0,i,i3;unsigned long length=10000;work=(char*)malloc(length*sizeof(char));fgets(work,length,codef);work2=(char*)malloc(length*sizeof(char));i3=2*n-1;for(i=0;*(work+i-1)!='\0';i++){i2=*(work+i);if(HT[i3].lchild==0){*(work2+i4)=*(z+i3-1);i4++;i3=2*n-1;i--;}else if(i2=='0') i3=HT[i3].lchild;else if(i2=='1') i3=HT[i3].rchild;}*(work2+i4)='\0';fputs(work2,txtfile);cout<<"译码完成"<<endl<<"内容写入根目录下的文件txtfile.txt中"<<endl<<endl;free(work);free(work2);fclose(txtfile);fclose(codef);}//-----------------------打印编码的函数----------------------void Code_printing(){cout<<"下面打印根目录下文件CodePrin.txt中编码字符"<<endl; FILE * CodePrin,* codefile;if((CodePrin=fopen("CodePrin.txt","w"))==NULL){cout<<"不能打开文件"<<endl;return;}if((codefile=fopen("codefile.txt","r"))==NULL){cout<<"不能打开文件"<<endl;return;}char *work3;work3=(char*)malloc(51*sizeof(char));do{if(fgets(work3,51,codefile)==NULL){cout<<"不能读取文件"<<endl;break;}fputs(work3,CodePrin);puts(work3);}while(strlen(work3)==50);free(work3);cout<<"打印工作结束"<<endl<<endl;fclose(CodePrin);fclose(codefile);}//------------------------------- 打印译码函数---------------------------------------------void Code_printing1(){cout<<"下面打印根目录下文件txtfile.txt中译码字符"<<endl;FILE * CodePrin1,* txtfile;if((CodePrin1=fopen("CodePrin1.txt","w"))==NULL){cout<<"不能打开文件"<<endl;return;}if((txtfile=fopen("txtfile.txt","r"))==NULL){cout<<"不能打开文件"<<endl;return;}char *work5;work5=(char*)malloc(51*sizeof(char));do{if(fgets(work5,51,txtfile)==NULL){cout<<"不能读取文件"<<endl;break;}fputs(work5,CodePrin1);puts(work5);}while(strlen(work5)==50);free(work5);cout<<"打印工作结束"<<endl<<endl;fclose(CodePrin1);fclose(txtfile);}//------------------------打印哈夫曼树的函数----------------------- void coprint(HuffmanTree start,HuffmanTree HT){if(start!=HT){FILE * TreePrint;if((TreePrint=fopen("TreePrint.txt","a"))==NULL){cout<<"创建文件失败"<<endl;return;}numb++;//该变量为已被声明为全局变量coprint(HT+start->rchild,HT);cout<<setw(5*numb)<<start->weight<<endl;fprintf(TreePrint,"%d\n",start->weight);coprint(HT+start->lchild,HT);numb--;fclose(TreePrint);}}void Tree_printing(HuffmanTree HT,int w){HuffmanTree p;p=HT+w;cout<<"下面打印哈夫曼树"<<endl;coprint(p,HT);cout<<"打印工作结束"<<endl;}//------------------------主函数------------------------------------void main(){char choice;while(choice!='q'){ cout<<"\n******************************"<<endl;cout<<" 欢迎使用哈夫曼编码解码系统"<<endl;cout<<"******************************"<<endl;cout<<"(1)要初始化哈夫曼链表请输入'i'"<<endl; cout<<"(2)要编码请输入'e'"<<endl;cout<<"(3)要译码请输入'd'"<<endl;cout<<"(4)要打印编码请输入'p'"<<endl;cout<<"(5)要打印哈夫曼树请输入't'"<<endl;cout<<"(6)要打印译码请输入'y'"<<endl;if(flag==0)cout<<"\n请先初始化哈夫曼链表,输入'i'"<<endl;cin>>choice;switch(choice){case 'i':Initialization();break;case 'e':Encoding();break;case 'd':Decoding();break;case 'p':Code_printing();break;case 't':Tree_printing(HT,2*n-1); break;case 'y':Code_printing1();break;default:cout<<"input error"<<endl; }}free(z);free(w);free(HT);}费诺#include<iostream.h>#include<math.h>#define N 15int pa[N][N];void fano(float p[],int a[N][N],int n,int m,int k) {float g=0.0,h=0.0,d,b,c;int i,j,flase;if(n<m){for(i=n;i<=m;i++){g=p[i]+g;} g=g/2;for(i=n;i<=m;i++){h=h+p[i];if(h>g){d=h-p[i];b=h-g;c=g-d;if(c>b){for(j=n;j<=i;j++) a[j][k]=0;fano(p,a,n,i,k+1);for(j=i+1;j<=m;j++) a[j][k]=1;fano(p,a,i+1,m,k+1);}else{for(j=n;j<=i-1;j++) a[j][k]=0;fano(p,a,n,i-1,k+1);for(j=i;j<=m;j++) a[j][k]=1;fano(p,a,i,m,k+1);}break;}}}}void main(){int i,j,k[N],n,flase=0;float p[N],m,H=0.0,K=0.0,sum=0.0;cout<<"输入信源符号个数"<<endl;cin>>n;cout<<"输入各信源符号概率"<<endl;for(i=1;i<=n;i++){cin>>p[i];}for(i=1;i<=n;i++){sum=sum+p[i];}for(i=1;i<=n;i++){if(p[i]<0.0||p[i]>1.0||sum!=1.0){ cout<<"input gai lv error!";flase=1;break;}}if(flase==0){for(i=0;i<=n;i++)for(j=0;j<=n;j++){ pa[i][j]=10;}fano(p,pa,1,n,1);cout<<"信源费诺编码如下：\n";for(i=1;i<=n;i++){ k[i]=0;cout<<"x"<<i<<"="<<p[i]<<"\t码字为\t";for(j=1;j<=n;j++){if(pa[i][j]!=10){ cout<<pa[i][j];k[i]++;}}cout<<"\t码长为\t"<<k[i]<<endl;}for(i=1;i<=n;i++){H=-(p[i]*log(p[i])/log(2))+H;}cout<<"信源熵 H(X)="<<H<<" (比特/符号)"<<endl; for(i=1;i<=n;i++){K=p[i]*k[i]+K;}cout<<"平均码长 K="<<K<<" (比特/符号)"<<endl; cout<<"编码效率为 "<<(H/K)*100<<"%"<<endl;}//if(flase==0)cout<<endl;}//main()香农#include<iostream.h>#include<math.h>#include<iomanip.h>#include<stdlib.h>class T{public:T() {}~T();void Create();void Coutpxj();void Coutk();void Coutz();void Print();protected:int n;double *p;double *pxj;int *k;double *mz;};void T::Create(){cout<<"请输入信源符号个数:";cin>>n;p=new double[n];cout<<"请分别输入这"<<n<<"个概率:\n"; for(int i=0;i<n;i++)cin>>p[i];pxj=new double[n];k=new int[n];mz=new double[n];double sum=0.0;for(i=0;i<n;i++)sum+=p[i];if(sum!=1.0)throw 1;else{for(i=0;i<n;i++){int k=i;for(int j=i+1;j<n;j++)if(p[k]<p[j]) k=j;double m=p[i];p[i]=p[k];p[k]=m;}}}T::~T(){delete p;delete pxj;delete k;delete mz;}void T::Coutpxj(){pxj[0]=0;for(int i=1;i<n;i++){pxj[i]=0;for(int j=0;j<i;j++)pxj[i]+=p[j];}}void T::Coutk(){for(int i=0;i<n;i++){double d=(-1)*(log(p[i])/log(2)); if(d-(int)d>0) k[i]=(int)d+1;else k[i]=(int)d;}}void T::Print(){cout<<"Xi"<<setw(8)<<"P(xi)"<<setw(8)<<"Pa(xj)"<<setw(8)<<"Ki"<<setw(8)<<"码字"<<endl;for(int i=0;i<n;i++){ cout<<"X"<<i+1<<setw(8)<<setprecision(2)<<p[i] <<setw(8)<<setprecision(2)<<pxj[i] <<setw(8)<<k[i]<<" ";mz[i]=pxj[i];for(int j=0;j<k[i];j++){if(2*mz[i]-1>=0){cout<<1;mz[i]=2*mz[i]-1;}else{cout<<0;mz[i]=2*mz[i];}}cout<<endl;}double K=0.0,H=0.0,Y;for(i=0;i<n;i++){K+=(double)p[i]*k[i];H+=(-1)*p[i]*(log10(p[i])/log10(2.0)); }Y=H/K;cout<<"平均码长:"<<K<<endl;cout<<"信源熵:"<<H<<endl;cout<<"编码效率:"<<Y<<endl;}void main(){T t;int e;try{t.Create();t.Coutpxj();t.Coutk();t.Print();}catch(int e){if(e==1) cout<<"输入错误，请重新运行";} }。