第九章虚拟变量与CHOW检验
第9章 经典单方程计量经济学模型专门问题PPT课件

一个以性别为虚拟变量考察企业职工薪 金的模型:
Y i01 X i2 D ii
其中:Yi为企业职工的薪金,Xi为工龄, Di=1,若是男性,Di=0,若是女性。
7/17/2020
假定3>2,其几何意义:
保 健 支 出
大 学 教 育 高 中 教 育
低 于 中 学 教 育
收 入
7/17/2020
第9章 经典单方程计量经济学模型:
13
专门问题
• 还可将多个虚拟变量引入模型中以考察多种 “定性”因素的影响。
如在上述职工薪金的例中,再引入代表学 历的虚拟变量D2:
1 本科及以上学历
• 高中以下: E ( Y i|X i,D 1 0 ,D 2 0 ) 0 1 X i
7/17/2020
第9章 经典单方程计量经济学模型:
12
专门问题
• 高中: E ( Y i|X i , D 1 1 , D 2 0 ) ( 0 2 ) 1 X i
• 大学及其以上: E ( Y i|X i , D 1 0 , D 2 1 ) ( 0 3 ) 1 X i
7/17/2020
第9章 经典单方程计量经济学模型:
9
专门问题
• 可以通过传统的回归检验,对2的统计显著性 进行检验,以判断企业男女职工的平均薪金 水平是否有显著差异。
年 薪 Y
男 职 工
女 职 工
2
0
工 龄 X
7/17/2020
第9章 经典单方程计量经济学模型:
10
专门问题
又例:在横截面数据基础上,考虑个人保 健支出对个人收入和教育水平的回归。
金融计量经济第五讲虚拟变量模型和Probit、Logit模型

二、虚拟变量的设置原则
• 引入虚拟变量一般取0和1。
• 对定性因素一般取级别数减1个虚拟变量。例 子1:性别因素,二个级别(男、女)取一个 虚拟变量,D=1表示男(女),D=0表示女 (男)。
• 例子2:季度因素,四个季度取3个变量。
1, 一季度 D1 0, 其它季度
1, 二季度
D2
0,
其它季度
• 同样可以写成二个模型:
y ˆi ˆ0(ˆˆ1)x1iˆkxki D1
y ˆi ˆ0ˆ1x1iˆkxki
D0
• 可考虑同时在截距和斜率引入虚拟变量:
y i 0 0 D i (1 D i 1 ) x 1 i k x k iu i (5.
.
.
• 3、虚拟变量用于季节性因素分析。
•取
1, 当样本 i季为 度第 的数据 Di 0,其它季度的, i数 2,3据 ,4
• 工资模型为:
• Ii01 [S 1 (1 D 1 i D 2 i)S ( i S 1 )] 2 [D 2 i(S 2 S 1 ) D 1 i(S i S 1 ) ]3 D 2 i(S i S 2 ) u i (5.7
.
D2=1
S0
D1=1
S1
S2
.
• 作OLS得到参数估计值后,三个阶段的 报酬回归模型为: Iˆi ˆ0ˆ1Si, Si S1 Iˆi ˆ0ˆ1S1ˆ2(Si S1), S2Si S1 Iˆi ˆ0ˆ1S1ˆ2(S2S1)ˆ3(Si S2), Si S2
0.503543 0.500354 1.13E+03 1.99E+09 -13241.74 1.648066
Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic)
第九章:虚拟解释变量

[计量经济学讲义] 第九章:虚拟解释变量本章及下一章将变量类型由定量变量拓展到定性变量。
§1虚拟变量的性质1、变量的分类:定量变量:如收入、产量、价格、成本、高度等取值在一定分为内连续变化;定性变量:如性别、种族、肤色、宗教、国际、战争、地震、沿海省份等。
“量化”:将定性变量量化,可以根据其不同情况取值0或1。
2、虚拟变量(dummy variable ):取值为0、1等这样的变量。
虚拟变量有时也称为二值变量(binary variable)、二分变量(dichotomous variable)、定性变量(qualitative variable)、指标变量(indicator variable )3、ANOV A (方差分析analysis of variance ):解释变量全为虚拟变量例:i Y =α+βi D +i u其中i Y 表示教授年薪,i D =1,男教授i D =0,女教授(假定年龄、学位和经验可以忽略)女教授的平均年薪为:E(i Y |i D =0)=α;男教授的平均年薪为:E(i Y |i D =1)=α+β;一个例子(略)§2 一个定量变量和一个二分定性变量1、例子:i Y =1α+2αi D +βi X +i u其中i Y 表示教授年薪,i X 表示年龄,则有:女教授的平均年薪为:E(i Y |i X ,i D =0)=1α+βi X ;男教授的平均年薪为:E(i Y |i X ,i D =1)= 1α+2α+βi X ;(假设共同斜率)2、问:有截距项的情况下,区分两个类别要几个虚拟变量?答案是一个,否则有完全贡献性。
结论:有截距项的情况下,若一个定性变量有m 个类别,则仅引入m-1个虚拟变量。
3、0与1的分配问题。
4、基准(benchmark ):0类别的情况5、级差截距系数:D 的系数§3 一个定量变量和一个多分变量例子:假设在横截面数据的基础上,做个人保健支出对个人收入和教育水平的回归。
计量经济学 第2章 虚拟变量

第2章 虚拟变量
学习目标 案例简介 案例分析 问题探讨与思考 练习
学习目标
• 理解虚拟变量的设置 • 掌握虚拟变量模型的构建,并能对结果加以分析和解释 • 掌握CHOW检验等
案例简介
• 案例2.1利用某类酒的季节销售数据,分析酒的销售量的季节性变化,结果发现其受季节 变化的影响较大,因此这一类商品销售的商家可以根据分析结果,对自己经营的季节性变 化的商品进行合理的营销和库存安排。 • 由于1982年美国遭受到和平时期最严重的经济衰退,因此案例2.2中,在对1970~1995 年间美国个人可支配收入与个人储蓄之间的关系进行研究时,通过设置虚拟变量来具体分 析经济是否发生了结构性变化。该例子中同时介绍CHOW检验的应用。
1 1982 年以后 D 0 1982 及以前
估计结果
邹检验
结论
• 可以发现D和DX前面的系数都是显著的,因此1982年的经济衰退对美国个人储蓄与个人 可支配收入的关系有显著的影响,模型反应了1982年美国经济发生了结构性变化。
• CHOW检验统计量对应的P值为0.0004,因此拒绝经济结构没有发生显著性变化的原假设。
5.67
估计结果(三)
ˆ 76.56 1.76t 17.93d 0.45d t Y t 1 1
Ch9(new)

第 9章 虚拟变量回归模型9.1. 虚拟变量虚拟变量:用于反映定性变量,描述样本点是否具有某种属性或特征。
度量这种属性常用“1”表示有,0表示“没有”(不出现)。
例如:性别、种族、战争、区域、经济结构变化和季节效应等。
例1:研究薪金问题;薪水y i ,⎩⎨⎧=女性男性01i Dy i =α+βD i ++u i于是:.)1(,)(βαα+====i i i i D y E o D y E 表明男教授平均薪金为.βα+女教授为α。
例2:研究不同地区教师的工资差别,将一个国家分为3个地区(东中西),引进2个虚拟变量(为什么?),建立模型:y i =β1+β2D 2i +β3D 3i +u i⎩⎨⎧=othereastD i 011⎩⎨⎧=otherwest D i 012上述模型回归元全是的虚拟变量,这样的模型称为 ANOV A 模型。
9.2 ANOV A 模型ANOV A 模型用于分析不同子样本的均值在统计上的差异,类似与统计中比较均值差异的方差分析,所以被成为ANOV A 回归模型。
例: 美国公立学校教师的地区差别将美国分为东北(21个州)、南方(17个州)和西部地区(13个州),共3个属性,引进2个虚拟变量D 2i 和D 3i ,D 2i =1,如第i 个州属于东北区,否则D 2i =0; D 3i =1,如第i 个州属于南方区,否则D 3i =0。
模型为y i=β1+β2D2i+β3D3i+u i(9.1)东北区教师的平均工资:E(y i∣D2i=1, D3i=0)= β1+β2南方区和西部地区教师的平均工资分别为:E(y i∣D2i=0, D3i=1)= β1+β3E(y i∣D2i=0, D3i=0)= β1估计结果为:y i=26158.62-1734.473D2i-3264.615D3i+e i(9.1E)se=(1128.53) (1435.93) (1499.6)t=(23.18) (-1.21) (-2.18)(0.0000)(0.2330)(0.0349)R2=0.09东北区教师的平均工资:26158.62-1734.473=24424南方区教师的平均工资: 26158.62-3264.615=22894西部地区教师的平均工资:26158.62实际平均工资:东北区为24424.14;南方区为22894;西部区26158. 如何推断平均工资是否具有显著的地域差异?说明:1. 模型含截矩项时,虚拟变量个数为定性因素类别的个数减1.虚拟变量陷阱——完全多重共线性2. 不指定虚拟变量的类别(子样本)是比较的基准。
虚拟变量(中级计量经济学总结(四川大学,杨可扬)

虚拟变量(Wooldridge chapter 7 ,13and Gujarati chapter 9)本章所有内容都赋予一个统一的例题来总结:0121234 *** wage female married educ female married female educ married educ ub d d b b b b =+++ ++++ 显然本例是在研究性别、婚姻状况、教育状况同收入之间的 关系问题。
一,单个虚拟变量01 wage female ub d =++ 0 01(|0) (|1) E wage female E wage female b b d == ==+ 也就是说,男性的平均工资为 0 b ,而女性的平均工资为 01 b d + 。
检验 这两组平均工资是否显著不同只需检验 female 是否显著。
如果female 显著且 1ˆ d <0 则说明存在性别歧视。
这也是典型的用虚拟变量 来标志截距的不同。
换成对数——水平形式: 01 log() wage female u b d =++ 则男女之间工资 的百分比差异为: 1 100*[exp()1]d - 以下作一个简单的证明,表明以上公式不仅适用于虚拟变量:111011 101 101 10 1010log() log()log() log(/) / 1 %*100(1)*100 y x u y y y y y y e y y e y y y y e y bb b b b b b =++ -= = = - =- - D ==- 二,双个虚拟变量及其交互012 wage female married ub d d =+++ 02 012 (|0,) (|1,) E wage female married married E wage female married marriedb d b d d ==+ ==++ 因此 1 d 表示在给定婚姻状况条件下, 男女的工资差异。
虚拟变量(dummy variable)
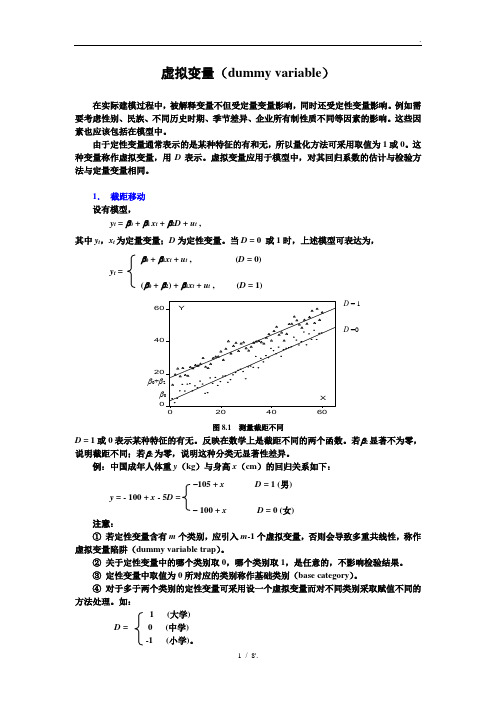
1(1978 - 1984)
中国进出口贸易总额数据(1950-1984)(单位:百亿元人民币)
年
trade
T
D
T*D
年
trade
T
D
T*D
1950
0.415
1
0
0
1968
1.085
19
0
0
1951
0.595
2
0
0
1969
1.069
20
0
0
1952
0.646
3
0
0
1970
1.129
21
0
0
1953
1(第2季度)
D2=
0(其他季度)
1(第3季度)
D3=
0(其他季度)
1(第4季度)
D4=
0(其他季度)
1(1998:1~2002:4)
DT=
0(1990:1~1997:4)
得估计结果如下:
GDPt= 1.1573+0.0668t+0.0775D2+0.2098D3+0.2349D4+1.8338DT-0.0654DTt
(50.8)(64.6) (3.7)(9.9) (11.0)(19.9) (-28.0)
R2=0.99, DW=0.9,s.e.=0.05, F=1198.4,T=52,t0.05 (52-7)= 2.01
对于1990:1~1997:4
GDPt= 1.1573+0.0668t+0.0775D2+0.2098D3+0.2349D4
首先看天津市粮食市场小麦批发价格的变化情况(图1)。1995年初,天津市粮食市场的小麦批发价格首先放开。在经历5个月的上扬之后,进入平稳波动期。从1996年8月份开始小麦批发价格一路走低。至2002年12月份,小麦批发价格降至是1160元/吨。
计量经济学重点

(|)i i i u Y E Y X =-第一章:计量经济学方法论计量经济学方法论大致地说,传统的计量经济学方法论按下列路线进行:(1)理论或假说陈述(2)数学模型设定(3)计量模型设定(4)获取数据 (5)参数估计(6)假设检验(7)预测(8)利用模型进行控制或制定政策 计量经济学所用数据的类型:(1)时间序列数据:对一个变量在不同时间取值的一组观测结果 (2)横截面数据:对一个或 多个变量在同一时间点上收集的数据 (3)混合数据:两者兼有(4)综列、纵列或微观综列数据:混合数据的特殊类型,指对相同的横截面的单元在时间轴上进行跟踪调查的数据。
第二章总体回归函数的概念:反映Y 的均值如何随X 的变化而变化的函数被称为总体回归函数(PRF )。
如:其中β1 和β2是未知但固定的参数,被称为回归系数 PRF 的随机设定:因为Y 是随机的,每个具体的Y 不可能恰好等于其均值,他们之间的离差被设定为一个随机扰动项:E(Y|Xi)被称为Yi 的系统性或确定性成分 ui 称为随机或非系统性成分在给定X 的条件下,随机扰动项的均值等于0 样本回归函数:SRF在大部分情况下,我们很难获得总体的数据,而是通过对总体的抽样来探索总体的性质。
类比于总体回归函数(总体Y 条件均值与X 的关系),可以定义样本回归函数:抽样Y 与X 之间的关系。
如:其中Yi (帽)是总体均值的估计量,β1(帽)和β2(帽)分别是β1和β2的估计量 随机形式的样本回归函数为:第三章估计量和估计量方差矩阵形式12(|)i i E Y X X ββ=+12ˆˆˆi i Y X ββ=+12ˆˆˆi ii Y X u ββ=++()()()11112222322211ˆ1ˆˆˆ1ˆˆˆˆˆˆ2'0ˆˆ''n n Y u X Y X u Y X u X Y u u Y X uY X u X Y X X X X Y ββββββββ-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥==+=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦=-=-∂=-=∂=()()ˆˆˆˆ最小二乘法的基本假定P51最小二乘法的假定漏了:没有完全多重共线性.判定系数:R2=ESS/TSS 假定1:参数线性模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• • • • • • • • • • • •
Variable C AGE EDU HILL MOU ROAD LAND IRRI RGIN DISS
Coefficient 1520.291 -9.528255 -138.9207 491.9524 135.0279 -180.0771 827.9669 -597.7996 -0.944183 7.665067
Chow预测检验
• Chow转折点检验方法存在一个问题,若某个子样本包 括的观察值太少,那么可能无法用其估计子模型。此 时可以考虑采用Chow预测检验。 • Chow预测检验同样需要将全部样本分为两个部分,检 验的步骤为:
– – – – 利用全部样本估计模型,得到RSSr; 利用第一个子样本(假定容量为T1)估计模型,得到RSSu ; 用估计的模型预测第二个子样本(假定容量为T2)的因变量; 计算F统计量: F RSSr RSSu T2
Std. Error 257.6199 4.416825 16.44906 124.4252 85.84877 149.4807 70.37880 118.0740 0.103780 2.227820
t-Statistic 5.901295 -2.157263 -8.445509 3.953801 1.572858 -1.204685 11.76444 -5.062923 -9.097896 3.440613
• 用全部数据做回归等同于加上k个约束条件,即两个方程 的所有参数都相同; • 用两组数据分别做回归则得到两套不同的截距和斜率系数 ,因而相应的自由度为T-2k,T为样本总量。
注:邹检验的自由度
• SSRR:T-K-1,在大样本条件下1可忽略 ,即T-K; • SSR1+SSR1:受约束增加一倍,即2K, 其自由度为T-2K; • SSRR-(SSR1+SSR1)自由度:T-K-(T2K)=k;
– 若预测与实际情况有很大偏差, RSSr会显著大于RSSu ,这意 味着两个子样本之间可能出现结构变化。
RSSu T1 k
自由度:
• SSRR=T1+T2-K-1,1忽略之后,即T1+T2K; • SSRU=T1-K-1,1忽略之后,即T1-K,因 为未受约束的样本量是预测之前的样本 量,即T1。
上章回顾
•自相关原因是什么? •如何检验自相关? •如何消除自相关?
第九章
虚拟变量及其设置的方法
虚拟变量
经济变量 可直接度量的变量 不可直接度量的变量 建立和应用计量经济学模型时,经常要考虑属性因素的 影响。例如,职业对个人收入的影响、战争与和平对经济发 展的影响、繁荣与萧条对就业的影响、文化程度对工资的影 响、自然灾害对农业生产的影响、季节对销售量的影响。所 以需要考虑是否在模型中引入属性因素。
•男职工本科以下学历的平均薪金:
E(Yi | X i , D1 1, D2 0) ( 0 2 ) 1 X i
•女职工本科以上学历的平均薪金:
E(Yi | X i , D1 0, D2 1) ( 0 3 ) 1 X i
•男职工本科以上学历的平均薪金:
案例1:地理区位影响
• 研究安徽省粮食可挖掘生产潜力的影响 因素,假说如下: • 人口的老化与非农化导致粮食生产潜力 没有挖掘; • 基础设施的不完善导致粮食生产潜力无 法实现。 • 地理区位因为即影响基础设施又影响劳 动力转移所以是比较重要的影响因素。
数据与虚拟变量设置
• 数据:共894个农户,分布区域包括:
• 大学及其以上: E(Yi | X i , D1 0, D2 1) ( 0 3 ) 1 X i 假定3>2,其几何意义:
大学教育 保健 支出 高中教育 低于中学教育
收入
• 还可将多个虚拟变量引入模型中以考察多种“定 性”因素的影响。
如在上述职工薪金的例中,再引入代表学历的虚拟 变量D2:
在 Eviews 中直接输入变量 data D1 D2 D3
季节 春季 夏季 秋季 冬季
D1 1 0 0 0
D2 0 1 0 0
D3 0 0 1 0
五、Chow检验
• 在现实生活中,有时会由于某些重大的政策和制度变 化或偶发事件,导致经济运行机制或行为改变。
– 不同的经济体制 – 不同的生产条件
• 对于计量经济学研究工作来说,这种情况表现为模型 的参数发生改变。 • 如果在样本资料所涉及的期间内发生过这样的情况, 那么就有必要检验模型参数的稳定性。 • Chow检验考虑样本是否包括了不同质的组,即检验不 同组间的参数是否相同。
Chow检验
• 在EVIWES中,Chow检验有两种不同的 方式:
Y 反常
正常
反常情况: Y = b0 + (b1+ b11)X + u 正常情况: Y = b0 + b1 X + u
b0 X
斜率发生了变化,可认为是虚拟变量 带来的影响。
例:根据消费理论,消费水平C主要取决于 收入水平Y,但在一个较长的时期,人们的消 费倾向会发生变化,尤其是在自然灾害、战 争等反常年份,消费倾向往往出现变化。这 种消费倾向的变化可通过在收入的系数中引 入虚拟变量来考察。
Prob. 0.0000 0.0313 0.0000 0.0001 0.1162 0.2287 0.0000 0.0000 0.0000 0.0006
案例2:CHOW检验
• 数据:安徽省粮食种植面积; • 目的:预测十二五我省粮食种植面积;
散点图:
一、虚拟变量的定义
根据属性类型,构造只取“0”或“1”的人工变量, 称为虚拟变量(Dummy Variable)。通常记为 D。 1 男 D= 0 女 含有虚拟变量的模型称为虚拟变量模型。
二、虚拟变量的引入
虚拟变量在模型中可以作解释变量,也可以作被解释 变量。一般是作解释变量。虚拟变量的引入有两种基本方 式:加法方式和乘法方式。
3、加法乘法并用
1 反常情况 D= 0 正常情况 Y=b0+b01D+b1 X+ b11D X
Y 反常 正常 b01 b0 X 截距和斜率均发生变化
反常情况: Y=(b0+b01)+(b1+b11) X 正常情况: Y = b0 + b1 X
4、临界指标的虚拟变量的引入
在经济发展的转折时期 Y 以 t* =1979 为转折期 以转折期的自变量 X 为临界值
• 我们将前者称作是无参数限制的模型,后者是 有参数限制的模型。 • 通过比较加上参数约束后是否使残差平方和显 著增大,我们可以检验模型是否存在结构变化 。
Chow检验
• 考虑分两个组的情况,检验过程分以下步骤:
– 依据对转折发生时间的了解,将全部样本分为两个部分; – 分别用两个组的数据做回归(即参数未受限制的情况) ,得到残 差平方和SSR1和SSR2(注意有RSSur=RSS1+RSS2); – 用全部数据做回归(即参数受限制的情况),得到残差平方和 SSR; SSR SSR1 SSR2 T 2 K – 计算F统计值 F SSR1 SSR2 K – 检验其显著性。
年薪 Y 男职工 女职工
2
0
工龄 X
又例:在横截面数据基础上,考虑个人保健支出 对个人收入和教育水平的回归。
教育水平考虑三个层次:高中以下, 高中, 大学及其以上
这时需要引入两个虚拟变量:
1 D1 0 高中 其他 1 D2 0 大学及其以上 其他
模型可设定如下: Yi 0 1 X i 2 D1 3 D2 i
1 D2 0
本科及以上学历
本科以下学历
职工薪金的回归模型可设计为:
Yi 0 1 X i 2 D1 3 D2 i
于是,不同性别、不同学历职工的平均薪金分别为:
•女职工本科以下学历的平均薪金:
E(Yi | X i , D1 0, D2 0) 0 1 X i
在E(i)=0 的初始假定下,高中以下、高中、大学 及其以上教育水平下个人保健支出的函数:
• 高中以下: • 高中:
E(Yi | X i , D1 0, D2 0) 0 1 X i
E(Yi | X i , D1 1, D2 0) ( 0 2 ) 1 X i
1 t t* D= 0 t < t* Y=b0+ b1X+ b2 (X X *)D 反常情况: Y=b0 b2 X *+ (b1+b2) X 正常情况: Y = b0 + b1 X
b0 X* X
两条不同时期的直线可在转折 期连起来成为一条折线
三、模型中引入虚拟变量的作用
1、分离异常因素的影响 2、检验不同的属性类别因素对因变量的影响 3、提高模型的精度
反常年份:
E(Ct | X t , Dt 0) 0 1 X t
书85页例4.5
• 假说:市场经济(经济制度)让农民对 价格更敏感。 • 注意:调整后的公式如下: • Y=b0+b1Pt+b2Xt+a1(PtDt) • 问: • 如果b1不显著,但 a1显著,说明了什么 ?本题假说是否正确? • 如果上述参数显著性正好相反呢?
如,设
1 Dt 0
正常年份 反常年份
消费模型可建立如下:
Ct 0 1 X t 2 Dt X t t
• 这里,虚拟变量D以与X相乘的方式引入了模型中 ,从而可用来考察消费倾向的变化。 • 假定E(i)= 0,上述模型所表示的函数可化为: 正常年份:
E(Ct | X t , Dt 1) 0 ( 1 2 ) X t
