Baltagi 面板数据计量分析一书数据2
面板数据分析PPT课件

相同(都是1),t 却因截面(时点)不同而异。可见时点固定效应 模型中的截距项t 包括了那些随不同截面(时点)变化,但不随个 体变化的难以观测的变量的影响。t 是一个随机变量。
以家庭消费性支出与可支配收入关系为例,“全国零售物价指数” 就是这样的一个变量。对于不同时点,这是一个变化的量,但是对 于不同省份(个体),这是一个不变化的量。
变换上式: yi = + X i ' +( i - + i ), i = 1, 2, …, N
称作平均数模型。对上式应用 OLS 估计,则参数估计量称作平均数 OLS 估 计量。此条件下的样本容量为 N,(T=1)。
如果 X i 与( i - + i )相互独立,和的平均数 OLS 估计量是一致估计量。
yit = + Xit ' +it, i = 1, 2, …, N; t = 1, 2, …, T 如果模型是正确设定的,且解释变量与误差项不相关,即 Cov(Xit,it) = 0。 那么无论是 N,还是 T,模型参数的混合最小二乘估计量都具有 一致性。 对于经济序列每个个体 i 及其误差项来说通常是序列相关的。NT 个相关 观测值要比 NT 个相互独立的观测值包含的信息少。从而导致误差项的标 准差常常被低估,估计量的精度被虚假夸大。
为误差项(标量),满足通常假定条件。Xit 为 k 1 阶回归变量列
向量(包括 k 个回归变量),为 k 1 阶回归系数列向量,则称此
模型为时点固定效应模型。
第8页/共30页
2.2.2 时点固定效应模型(time fixed effects model)
设定时点固定效应模型的原因。假定有面板数据模型
面板数据分析简要步骤与注意事项(面板单位根—面板协整—回归分析)(2)

面板数据分析简要步骤与注意事项(面板单位根—面板协整—回归分析)步骤一:分析数据的平稳性(单位根检验)按照正规程序,面板数据模型在回归前需检验数据的平稳性。
李子奈曾指出,一些非平稳的经济时间序列往往表现出共同的变化趋势,而这些序列间本身不一定有直接的关联,此时,对这些数据进行回归,尽管有较高的R平方,但其结果是没有任何实际意义的。
这种情况称为称为虚假回归或伪回归(spurious regression)。
他认为平稳的真正含义是:一个时间序列剔除了不变的均值(可视为截距)和时间趋势以后,剩余的序列为零均值,同方差,即白噪声。
因此单位根检验时有三种检验模式:既有趋势又有截距、只有截距、以上都无。
因此为了避免伪回归,确保估计结果的有效性,我们必须对各面板序列的平稳性进行检验。
而检验数据平稳性最常用的办法就是单位根检验。
首先,我们可以先对面板序列绘制时序图,以粗略观测时序图中由各个观测值描出代表变量的折线是否含有趋势项和(或)截距项,从而为进一步的单位根检验的检验模式做准备。
单位根检验方法的文献综述:在非平稳的面板数据渐进过程中,LevinandLin(1993) 很早就发现这些估计量的极限分布是高斯分布,这些结果也被应用在有异方差的面板数据中,并建立了对面板单位根进行检验的早期版本。
后来经过Levin et al. (2002)的改进,提出了检验面板单位根的LLC 法。
Levin et al. (2002) 指出,该方法允许不同截距和时间趋势,异方差和高阶序列相关,适合于中等维度(时间序列介于25~250 之间,截面数介于10~250 之间) 的面板单位根检验。
Im et al. (1997) 还提出了检验面板单位根的IPS 法,但Breitung(2000) 发现IPS 法对限定性趋势的设定极为敏感,并提出了面板单位根检验的Breitung 法。
Maddala and Wu(1999)又提出了ADF-Fisher和PP-Fisher面板单位根检验方法。
stata面板数据计量知识及参考资料

计量知识:1、横截面数据、时间序列、面板数据:横截面数据是在同一时间,不同统计单位相同统计指标组成的数据列。
横截面数据是按照统计单位排列的。
因此,横截面数据不要求统计对象及其范围相同,但要求统计的时间相同。
也就是说必须是同一时间截面上的数据。
,Pr i t emium ,1Pr i t emiun -H A Turnover Tutnover A H Size +/H A H SO SO +22/A H σσDummy时间序列数据:在不同时间点上收集到的数据,这类数据反映了某一事物、现象等随时间的变化状态或程度。
面板数据:是截面数据与时间序列数据综合起来的一种数据类型。
其有时间序列和截面两个维度,当这类数据按两个维度排列时,是排在一个平面上,与只有一个维度的数据排在一条线上有着明显的不同,整个表格像是一个面板,所以把panel data 译作“面板数据”。
举例:如:城市名:北京、上海、重庆、天津的GDP 分别为10、11、9、8(单位亿元)。
这就是截面数据,在一个时间点处切开,看各个城市的不同就是截面数据。
如:2000、2001、2002、2003、2004各年的北京市GDP 分别为8、9、10、11、12(单位亿元)。
这就是时间序列,选一个城市,看各个样本时间点的不同就是时间序列。
如:2000、2001、2002、2003、2004各年中国所有直辖市的GDP 分别为: 北京市分别为8、9、10、11、12;上海市分别为9、10、11、12、13;天津市分别为5、6、7、8、9;重庆市分别为7、8、9、10、11(单位亿元)。
这就是面板数据。
*变量合并2、截面数据,多重共线性和异方差都需要考虑,截面数据不需要检测DW 值!你做出来R 方比较小,可能原因是你的回归方程中没有纳入关键变量,建议你采用逐步回归方法,以提高R 方!对于截面数据来说,R 方一般在0.7左右都能接受!相关分析不是必要做的,在模型中加入什么变量进行回归,主要是依据前期的理论分析和研究目的!仅就计量回归而言,这些步骤只是告诉你,自变量与因变量的相关性会影响变量在模型中的显著性,而自变量间的相关则会带来多重共线性!3、线性相关,也叫自相关:可以用来看x和y的相关性,常用来考察各个x 自变量之间是否存在相关关系。
面板数据分析方法 ppt课件

it i t uit
i 1,2, N t 1,2,T
面板数据:多个观测对象的时间序列数据所组 成的样本数据。
i 反映不随时间变化的个体上的差异性,
被称为个体效应
t 反映不随个体变化的时间上的差异性,
被称为时间效应。
ppt课件 33
第二节 面板数据的模型形式
11,000 10,000 9,000 8,000 7,000 6,000 5,000 4,000 3,000 IP 2,000 3,000 5,000 7,000 9,000 11,000 13,000 CP_1996 CP_1997 CP_1998 CP_1999 CP_2000 CP_2001 CP_2002
安徽 北京 福建 河北 黑龙江 吉林 江苏 江西 辽宁 内蒙古 山东 上海 山西 天津 浙江
14000 12000 10000 8000 6000 4000 2000 0 1996 1997 1998 1999 2000 2001
浙江 山西 山东 辽宁 江苏
山西
14000 12000 10000 8000 6000 4000 2000
ppt课件
16
二、面板数据的分类
2.微观面板数据与宏观面板数据 微观面板数据一般指一段时期内不同个体或者家庭 的调查数据,其数据中往往个体单位较多,即 N较大( 通常均为几百或上千)而时期数 T较短(最短为两个时 期,最长一般不超过20个时期)。
ppt课件
17
二、面板数据的分类
2.微观面板数据与宏观面板数据 宏观面板数据通常为一段时间内不同国家或地区的 数据集合,其个体单位数量N不大(一般为7-200)而时 期数T较长(一般为20-60年)。
面板数据的常见处理 (2)

面板数据的常见处理面板数据是一种特殊的数据结构,通常用于经济学和社会科学研究中。
它由多个个体或单位在不同时间点上的观测值组成,可以用来分析个体或单位在时间上的变化以及它们之间的关系。
在处理面板数据时,常见的任务包括数据清洗、数据转换、数据描述统计和面板数据模型估计等。
一、数据清洗1. 缺失值处理:面板数据中常常存在缺失值,可以使用插补方法(如均值插补、回归插补等)填充缺失值,或者根据实际情况进行删除。
2. 异常值处理:通过观察和分析数据,识别和处理异常值,避免其对后续分析的影响。
二、数据转换1. 平衡面板数据:面板数据可能存在非平衡问题,即某些个体或单位在某些时间点上没有观测值。
可以通过删除非平衡部分或者进行插补来得到平衡面板数据。
2. 时间标识:为面板数据添加时间标识,方便后续的时间序列分析。
3. 数据排序:按照个体或单位的标识和时间标识对数据进行排序,以便后续的面板数据模型估计。
三、数据描述统计1. 平均值和标准差:计算面板数据的平均值和标准差,以了解变量的集中趋势和离散程度。
2. 相关系数:计算面板数据中不同变量之间的相关系数,以研究它们之间的关联关系。
3. 分组统计:根据个体或单位的特征变量,进行分组统计,比较不同组之间的差异。
四、面板数据模型估计1. 固定效应模型:通过引入个体或单位的固定效应,控制个体或单位特定的影响,估计面板数据模型。
2. 随机效应模型:通过引入个体或单位的随机效应,考虑个体或单位之间的随机差异,估计面板数据模型。
3. 差分估计:通过对面板数据进行差分,得到差分数据,进而估计面板数据模型。
总结:面板数据的常见处理包括数据清洗、数据转换、数据描述统计和面板数据模型估计等任务。
在处理面板数据时,需要注意缺失值和异常值的处理,对非平衡面板数据进行处理,添加时间标识和排序数据。
此外,还可以进行数据描述统计,如计算平均值、标准差和相关系数等。
最后,可以使用固定效应模型、随机效应模型或差分估计等方法进行面板数据模型估计。
《因果推断实用计量方法》大学教学课件--第8章-面板数据

可观测
随时间变化的 不随时间变化的 不随时间变化 随时间变化的
变量
变量
变量
变量
其中 是个体不可观测的不随时间变化的因素 ,u 是
个体不可观测的随时间变化的因素 。
面板数据因果关系分析的直观理解
面板数据的独特信息来源使得我们可以通过个体效应模型将不可观
测的不随时间变化的变量通过“控制”住。
如果 不存在,并且 , = 0,该
模型处理和一般横截面模型是一样的,使用简单OLS
就能得到无偏和一致估计值。
随机效应模型(Random Effects Model)
假设 存在,但由于 和与可观测变量不相关,E , =
不可观测
可观测
可观测
随时间变化 不随时间变化 不随时间变化
和随时间变化
的变量
的变量
的变量
其中干扰项 = + ,
面板数据因果关系分析的直观理解
通过面板数据,我们可以将模型改进为:
= +
+ +
ณ
+
ด
不可观测
不可观测
INCit 1EDU it 2GENDERi 1D1 2 D2 uit
ID
Year
INC
EDU
GENDER
D1
D2
1
2017
800
3
1
1
0
1
2018
1000
4
1
1
0
1
2019
1200
5
1
1
0
2
2017
1200
5
0
0
《面板数据分析》课件

面板数据分析的步骤
1
数据描述
对数据进行描述性统计,确定数据在时间和个体方面的特征。
2
ห้องสมุดไป่ตู้
分类讨论
分析不同情况下个体间行为的差异和影响因素,如何影响个体行为的内部因素和外部 环境。
3
建模和估计
根据分类讨论的结论,运用面板数据模型建立样本分布,通过极大似然法和广义矩估 计法进行参数估计。
4
结果解释
对估计的结果进行解释,如何分析因素对个体行为的影响和相关关系等。
生产领域
跟踪生产的进度和效果,寻找 提高生产效率的方法。
总结和展望
总结
面板数据分析是一种高通量数据分析方法,通 过对个体间微观差异的捕捉和分析,提高了分 析数据的精确性,研究结果更具有真实性和普 遍性。
展望
随着数据分析和研究技术的不断发展,面板数 据分析将进一步被广泛接受和使用,为各行各 业的发展与创新提供支持。
《面板数据分析》PPT课 件
欢迎各位来到《面板数据分析》课件。本课程将向大家介绍如何运用面板数 据分析各种数据,并运用不同的分析方法提升数据的价值。
面板数据的定义和特点
什么是面板数据?
面板数据指的是在一定时间内,对相同个体做重复观测所得到的数据。
面板数据的特点
相对于横截面数据和时间序列数据,面板数据能够更精确地反映个体间的差异和发展。
面板数据模型的建立
线性回归模型
用于研究数值型因变量和数值 型自变量之间的关系。
逻辑回归模型
用于研究分类因变量和数值型 自变量之间的关系。
混合效应模型
考虑组间差异和个体内部差异, 更为精确地分析面板数据的特 点。
面板数据分析的常用方法
1 固定效应模型
面板数据的计量经济分析

面板数据的计量经济分析1. 引言面板数据是研究中常用的一种数据形式,它包含多个个体在多个时间点上的观测值。
由于其具有横截面和时间序列的特点,面板数据通常可以提供比纯横截面数据或纯时间序列数据更大的信息量。
计量经济学的面板数据分析方法能够更准确地评估变量之间的关系,并对经济政策的效果进行研究。
本文将介绍面板数据的基本特征、主要的面板数据模型和计量经济学中常用的面板数据分析方法。
2. 面板数据的基本特征面板数据可以分为两种类型:平衡面板数据和非平衡面板数据。
平衡面板数据是指每个时间点上都有完整数据的面板,而非平衡面板数据则是至少有一个时间点上缺失了一些观测值的面板。
面板数据的分析需要考虑两个维度的异质性:个体异质性和时间异质性。
个体异质性是指不同个体之间的特征和行为存在差异,时间异质性是指同一时间点上不同个体之间的特征和行为存在差异。
3. 面板数据模型在计量经济分析中,有几种常用的面板数据分析模型。
3.1 固定效应模型固定效应模型假设每个个体的截距项是固定的,不随个体特征变化而变化。
通过固定效应模型,可以分离掉个体之间的异质性,使得我们更关注变量之间的关系。
固定效应模型的基本形式为:$$ y_{it} = \\alpha + \\beta X_{it} + \\gamma D_i + \\epsilon_{it}$$其中,y it是个体i在时间t的因变量观测值,X it是自变量观测值,D i是个体固定效应,$\\epsilon_{it}$是误差项。
3.2 随机效应模型随机效应模型假设个体截距项是随机的,并且与个体特征无关。
通过随机效应模型,可以同时考虑个体之间的异质性和变量之间的关系。
随机效应模型的基本形式为:$$ y_{it} = \\beta X_{it} + \\gamma D_i + \\alpha_i + \\epsilon_{it}$$其中,$\\alpha_i$是个体随机效应,$\\epsilon_{it}$是误差项。
面板数据分析方法及其应用

面板数据分析方法及其应用面板数据分析是一种经济学和统计学领域常用的数据分析方法,广泛应用于经济研究、社会科学研究以及商业分析等领域。
本文将介绍面板数据的概念和特点,然后探讨常见的面板数据分析方法,并引用实际案例展示面板数据分析方法的应用。
一、面板数据的概念和特点面板数据,又称为纵向数据或追踪数据,是指在一段时间内对相同的一组个体(如个人、企业等)进行观测得到的数据。
与横截面数据只在某一时间点上进行观测不同,面板数据可以提供个体在时间维度上的变化信息,对于研究个体之间的差异以及时间趋势的影响非常有用。
面板数据的特点主要包括两个方面:个体异质性和时间序列相关性。
个体异质性是指面板数据中不同个体之间存在差异,可以用于分析个体之间的差异成因;而时间序列相关性则是指面板数据中同一个体在不同时间点上的观测值之间存在相关性,可以用于分析时间因素对个体的影响。
二、面板数据分析方法1. 固定效应模型固定效应模型是最基础和最常用的面板数据分析方法之一,它通过引入个体固定效应来控制个体异质性,从而减少个体间的相关性。
固定效应模型的基本形式为:Y_it = α_i + βX_it + ε_it其中,Y_it代表第i个个体在第t个时间点的观测值,α_i代表个体i的固定效应,X_it代表自变量,β代表自变量的系数,ε_it代表随机误差项。
2. 随机效应模型随机效应模型是相对于固定效应模型而言的,它假设个体固定效应与自变量不相关,其随机性由随机效应体现。
随机效应模型的基本形式为:Y_it = γ_i + βX_it + ε_it其中,γ_i代表个体i的随机效应,其服从某个分布,其他符号的含义同固定效应模型。
3. 差分法差分法是利用面板数据的时间序列相关性来进行分析的方法,通过计算个体观测值之间的差分来消除个体固定效应,从而在分析时间序列的基础上探究因果关系。
差分法的基本思路是对面板数据进行两次差分,第一次是对个体间的差分,即将每个个体的观测值减去该个体在整个时间段上的平均值;第二次是对时间间的差分,即将每个个体的观测值减去前一个时间点的观测值。
面板数据的计量方法

面板数据的计量方法1.什么是面板数据?面板数据(panel data)也称时间序列截面数据(time series and cross section data)或混合数据(pool data)。
面板数据是截面数据与时间序列综合起来的一种数据资源,是同时在时间和截面空间上取得的二维数据。
如:城市名:北京、上海、重庆、天津的GDP分别为10、11、9、8(单位亿元)。
这就是截面数据,在一个时间点处切开,看各个城市的不同就是截面数据。
如:2000、2001、2002、2003、2004各年的北京市GDP分别为8、9、10、11、12(单位亿元)。
这就是时间序列,选一个城市,看各个样本时间点的不同就是时间序列。
如:2000、2001、2002、2003、2004各年中国所有直辖市的GDP分别为:北京市分别为8、9、10、11、12;上海市分别为9、10、11、12、13;天津市分别为5、6、7、8、9;重庆市分别为7、8、9、10、11(单位亿元)。
这就是面板数据。
2.面板数据的计量方法利用面板数据建立模型的好处是:(1)由于观测值的增多,可以增加估计量的抽样精度。
(2)对于固定效应模型能得到参数的一致估计量,甚至有效估计量。
(3)面板数据建模比单截面数据建模可以获得更多的动态信息。
例如1990-2000 年30 个省份的农业总产值数据。
固定在某一年份上,它是由30 个农业总产值数字组成的截面数据;固定在某一省份上,它是由11 年农业总产值数据组成的一个时间序列。
面板数据由30 个个体组成。
共有330 个观测值。
面板数据模型的选择通常有三种形式:混合估计模型、固定效应模型和随机效应模型第一种是混合估计模型(Pooled Regression Model)。
如果从时间上看,不同个体之间不存在显著性差异;从截面上看,不同截面之间也不存在显著性差异,那么就可以直接把面板数据混合在一起用普通最小二乘法(OLS)估计参数。
面板数据分析面板数据分析的理论进展单位根检验与协整检验.pptx

• Strauss(2000)使用三种方法(Abuaf和 Jorion(1990),LL方法,IPS方法),对从1929年到 1995年美国48州带趋势人均收入的数据进行单位根检 验,结论是拒绝有单位根的存在,并说明收敛的速率取 决于截距差异的假设、一阶自相关系数、滞后期和对 1973年石油危机造成趋势中断的适应性。
第28页/共33页
目前,已有一些专家正在探讨这些问题:
• Maddala和Wu(1999)自助法允许截面相关 • Pedroni(1997b)在他的PPP研究中,提出用基
于GLS修正来考虑在Panel个体之间存在的反馈 情况 • Hall等人(1999)提供了另一个同Pesaran和 Smith(1995)分析相反的例子,他们集中在 Panel协整的回归结构上 • Larsson、Lyhagen和 Lothgren(1998)按
第20页/共33页
Pedroni 协积检验:以 Engle-Granger 协积检验方法为基础构造检验统计量,标 准化以后渐近服从标准正态分布。(1999, 2004)
Kao 协积检验:以 Engle-Granger 协积检验方法为基础构造检验统计量,标准化 以后渐近服从标准正态分布。(1999)
Fisher 个体联合协积检验(combined individual test):由 Johansen 迹统计量推广 而成的检验方法。用个体的协积检验值构造一个服从 2 分布的累加统计量 检验面板数据的协积性。(Maddala and Wu 1999)
第21页/共33页
Pedroni协整检验:
• 以协整方程的回归残差为基础通过构造7个统计 量来检验面板变量间的协整关系。原假设:面板
检验。随后,Quah(1990)、Levin和Lin(1992)、 Im、Pesaran和Shin(1995)、Flôres等(Flôres et al.,1995)、O' Connell(1998)、Taylor和 Sarno(1998)、Maddala和吴(1999)、Groen (2000)、Chang(2000)和崔仁(In Choi, 2001)、白聚山和Ng(Jushan Bai ane Serena Ng, 2001)、Moon和Perron(2002)、Smith(2004) 和白仲林(2005)也相继提出了各种面板单位根检验 方法。通过蒙特卡罗模拟试验发现,与单变量时间序列 单位根检验相比较,各种面板数据单位根检验都不同程 度地提高了单位根检验的检验功效。
面板数据分析方法

面板数据分析方法
面板数据是指多个观察对象在同一时间序列下的数据。
面板数据分析方法可以帮助我们更好地理解时间序列数据,并进一步得出结论,这些数据通常用于经济学研究和社会科学研究。
以下是一些常用的面板数据分析方法:
1. 固定效应模型(Fixed Effects Model):固定效应模型是一种广泛应用于分析面板数据的方法。
它可以帮助我们控制可能影响结果的变量,并提高模型的可靠性和准确性。
2. 随机效应模型(Random Effects Model):随机效应模型与固定效应模型类似,但是它假设未观测到的变量对结果有影响,并对这种影响进行建模。
3. 差分法(Differences-in-Differences):差分法是一种比较两个实验组之间差异的方法。
在差分法中,我们比较一个实验组的结果与一个对照组的结果,以确定实验组的结果是否受到实验的影响。
4. 面板单位根检验(Panel Unit Root Test):面板单位根检验可以帮助我们确定一个时间序列是否具有单位根,这在面板数据分析中十分有用。
如果一个序列具有单位根,这意味着它是非平稳的,需要进行差分或其他方法来消除这种影响。
5. 面板数据模型选择(Model Selection):在进行面板数据分析时,我们需要选择一个合适的模型来准确地描述数据。
面板数据模型选择方法包括信息准则法、比较误差方差分解和Hausman检验等。
这些方法可以帮助我们更好地理解面板数据,并从中得出有意义的结论。
面板数据分析方法步骤全解

面板数据分析方法步骤全解面板数据分析方法步骤全解步骤一:分析数据的平稳性(单位根检验)按照正规程序,面板数据模型在回归前需检验数据的平稳性。
李子奈曾指出,一些非平稳的经济时间序列往往表现出共同的变化趋势,而这些序列间本身不一定有直接的关联,此时,对这些数据进行回归,尽管有较高的R平方,但其结果是没有任何实际意义的。
这种情况称为称为虚假回归或伪回归(spurious regression)。
他认为平稳的真正含义是:一个时间序列剔除了不变的均值(可视为截距)和时间趋势以后,剩余的序列为零均值,同方差,即白噪声。
因此单位根检验时有三种检验模式:既有趋势又有截距、只有截距、以上都无。
因此为了避免伪回归,确保估计结果的有效性,我们必须对各面板序列的平稳性进行检验。
而检验数据平稳性最常用的办法就是单位根检验。
首先,我们可以先对面板序列绘制时序图,以粗略观测时序图中由各个观测值描出代表变量的折线是否含有趋势项和(或)截距项,从而为进一步的单位根检验的检验模式做准备。
单位根检验方法的文献综述:在非平稳的面板数据渐进过程中,Levin andLin(1993) 很早就发现这些估计量的极限分布是高斯分布,这些结果也被应用在有异方差的面板数据中,并建立了对面板单位根进行检验的早期版本。
后来经过Levin et al. (2002)的改进,提出了检验面板单位根的LLC 法。
Levin et al. (2002) 指出,该方法允许不同截距和时间趋势,异方差和高阶序列相关,适合于中等维度(时间序列介于25~250 之间,截面数介于10~250 之间) 的面板单位根检验。
Im et al. (1997) 还提出了检验面板单位根的IPS 法,但Breitung(2000) 发现IPS 法对限定性趋势的设定极为敏感,并提出了面板单位根检验的Breitung 法。
Maddala and Wu(1999)又提出了ADF-Fisher和PP-Fisher面板单位根检验方法。
面板数据分析

面板数据分析引言面板数据,也称为纵向数据或长期追踪数据,是统计学中一种常见的数据类型。
它包含了多个观测单位(个体)在多个时间点上的观测数值,通常用于研究个体随时间变化的动态特征以及个体之间的差异。
本文将介绍面板数据分析的基本概念、应用场景以及常用的方法。
面板数据的特点面板数据与传统的横断面数据和时间序列数据相比,具有以下几个特点:1.面板数据可以捕捉到不同个体之间的差异,因为它包含了多个个体的观测值。
这使得面板数据分析更能够揭示个体之间的异质性。
2.面板数据可以捕捉到个体随时间的变化。
通过观察同一组个体在不同时间点上的观测值,我们可以分析其变化趋势以及时间的影响。
3.面板数据可以提供更准确的估计结果。
面板数据的观测值来自同一组个体,这意味着我们可以利用个体之间的差异来增加估计的准确性,减少估计的标准误差。
面板数据分析的应用场景面板数据分析在经济学、社会学、医学等领域都有广泛的应用。
以下是一些常见的应用场景:1.经济学中的面板数据分析可以用于研究个体或企业的投资行为、消费行为等经济决策的动态特征,从而为经济政策制定提供依据。
2.社会学中的面板数据分析可以用于研究个体或家庭的社会行为,如教育投资、就业状况等。
这些研究可以帮助我们了解社会问题的根源以及改善社会政策的方向。
3.医学中的面板数据分析可以用于研究疾病的发展过程以及治疗效果的评估。
通过观察患者在不同时间点上的生理指标变化,我们可以了解疾病的演变规律以及治疗手段的效果。
面板数据分析的方法面板数据分析有多种方法,下面介绍几种常用的方法:1.固定效应模型:固定效应模型是一种常用的面板数据分析方法,它将个体特定的固定效应引入模型中。
通过固定效应模型,我们可以分析个体固有的特征对观测值的影响。
2.随机效应模型:随机效应模型是另一种常用的面板数据分析方法,它将个体特定的随机效应引入模型中。
与固定效应模型不同,随机效应模型允许个体之间的差异是随机的,而不是固定的。
面板数据分析方法整理

让知识带有温度。
面板数据分析方法整理
面板数据分析方法
面板数据是指在时间序列上取多个截面,在这些截面上同时选取样本观测,也叫“平行数据”。
下面是我想跟大家共享的面板数据分析方法,欢迎大家扫瞄。
面板数据的分析方法
面板数据分析方法是最近几十年来进展起来的新的统计方法,面板数据可以克服时间序列分析受多重共线性的困扰,能够供应更多的信息、更多的变化、更少共线性、更多的自由度和更高的估量效率,而面板数据的单位根检验和协整分析是当前最前沿的领域之一。
在本文的讨论中,我们首先运用面板数据的单位根检验与协整检验来考察能源消费、环境污染与经济增长之间的长期关系,然后建立计量模型来量化它们之间的内在联系。
面板数据的单位根检验的方法主要有Levin,Lin and CHU(2023)提出的LLC检验方法。
Im,Pesearn,Shin(2023)提出的'IPS检验, Maddala 和Wu(1999),Choi(2023)提出的ADF和PP检验等。
面板数据的协整检验的方法主要有Pedroni[8] (1999,2023)和Kao(1999)提出的检验方法,这两种检验方法的原假设均为不存在协整关系,从面板数据中得到残差统计量进行检验。
Luciano(2023)中运用Monte Carlo模拟对协整检验的几种方法进行比较,说明在T较小(大)时,Kao检验比Pedroni 检验更高(低)的功效。
详细面板数据单位根检验和协整检验的方法见
文档内容到此结束,欢迎大家下载、修改、丰富并分享给更多有需要的人。
第1页/共1页。
第二代面板数据模型估计方法

第二代面板数据模型估计方法一、第二代面板数据模型的基本原理第二代面板数据模型也被称为固定效应模型或固定效应面板数据模型。
它的基本原理是将面板数据分为固定效应和时间效应两部分,并在模型中加入这两部分效应,使得模型能够更好地描述数据的特征。
固定效应代表了不随时间变化的个体特征,时间效应代表了随时间变化的普遍规律。
通过结合这两部分效应,第二代面板数据模型可以更准确地描述数据的动态变化过程。
第二代面板数据模型的数学表达形式如下:Yit = α + β1Xit + γ1D1i + γ2D2t + uit其中,Yit代表面板数据中第i个个体在第t个时间点的因变量值,α为常数项,β1为自变量的系数,Xit为自变量的取值,D1i为个体i的固定效应,D2t为时间t的时间效应,uit为误差项。
通过对个体和时间的固定效应进行控制,可以消除数据中的个体异质性和时间序列相关性,使得模型的估计更准确。
二、第二代面板数据模型的估计方法第二代面板数据模型的估计方法主要有最小二乘估计法(OLS)、固定效应估计法(FE)和随机效应估计法(RE)三种。
下面将分别介绍这三种方法的原理和应用。
1. 最小二乘估计法(OLS)最小二乘估计法是最常用的估计方法之一,它将面板数据视为一个普通的横截面数据集,忽略了数据中存在的时间序列和横截面的特性,因此在数据中存在个体异质性和时间序列相关性时,OLS估计的结果可能存在偏误。
但是在数据中不存在这些问题时,OLS估计是一种简单易行且有效的方法。
2. 固定效应估计法(FE)固定效应估计法是一种控制了个体固定效应的估计方法,通过固定效应的引入来消除数据中的个体异质性,从而提高模型的精确度。
FE估计方法可以通过变量差分(Difference-in-differences)或虚拟变量(Dummy Variable)等方式引入固定效应,从而得到更准确的估计结果。
3. 随机效应估计法(RE)随机效应估计法是一种通过随机生成时间变化的个体效应来控制个体异质性的估计方法,它能够更好地处理数据中存在的个体相关性和时间序列相关性。
第二讲 面板数据线性回归模型
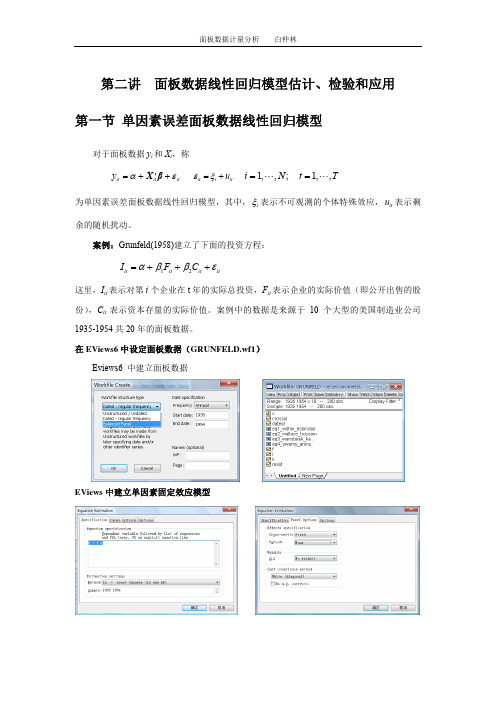
第二讲 面板数据线性回归模型估计、检验和应用 第一节 单因素误差面板数据线性回归模型对于面板数据y i 和X i ,称it it it y αε′=++X βit i it u εξ=+ 1,,;1,,i N t T ==""为单因素误差面板数据线性回归模型,其中,i ξ表示不可观测的个体特殊效应,it u 表示剩余的随机扰动。
案例:Grunfeld(1958)建立了下面的投资方程:12it it it it I F C αββε=+++这里,I it 表示对第i 个企业在t 年的实际总投资,F it 表示企业的实际价值(即公开出售的股份),C it 表示资本存量的实际价值。
案例中的数据是来源于10个大型的美国制造业公司1935-1954共20年的面板数据。
在EViews6中设定面板数据(GRUNFELD.wf1)Eviews6 中建立面板数据EViews 中建立单因素固定效应模型1.1 混合回归模型1 面板数据混合回归模型 假设1 ε ~ N (0, σ2I NT )对于面板数据y i 和X i ,无约束的线性回归模型是y i = Z i δi + εi i =1, 2, … , N(4.1)其中'i y = ( y i 1, … , y iT ),Z i = [ ιT , X i ]并且X i 是T×K 的,'i δ是1×(K +1)的,εi 是T×1的。
注意:各个体的回归系数δi 是不同的。
如果面板数据可混合,则得到有约束模型y = Z δ + ε(4.2)其中Z ′ = ('1Z ,'2Z , … ,'N Z ),u ′ = ('1ε,'2ε, … ,'N ε)。
2 混合回归模型的估计当满足可混合回归假设时,()1''ˆZ Z Z Y −=δ在假设1下,对于Grunfeld 数据,基于EViews6建立的混合回归模型3 面板数据的可混合性检验假设检验原理:基于OLS/ML 估计,对约束条件的检验。
面板数据分析

面板数据分析面板数据分析是一种常见的数据分析方法,通过对不同类型的面板数据进行统计和分析,可以帮助我们了解数据之间的关系和趋势。
面板数据通常指的是具有时间序列和横截面维度的数据,这种数据结构在经济学、社会学、医学等领域都有广泛的应用。
本文将介绍面板数据分析的基本概念和方法,并结合实例进行演示和说明。
面板数据的基本特征面板数据是一种既有时间序列又有横截面维度的数据结构,通常用于描述多个个体(如个人、家庭、公司等)在不同时间点上的变化。
面板数据可以分为平衡面板数据和非平衡面板数据两种类型。
平衡面板数据指的是在每个时间点上都有完整数据的面板,而非平衡面板数据则是在某些时间点上个体缺失数据的情况。
面板数据分析的基本方法面板数据分析通常涉及到固定效应模型、随机效应模型、面板数据单位根检验、汇总单位根检验等方法。
固定效应模型假设个体间的差异是固定的,而随机效应模型则假设个体间的差异是随机的。
面板数据单位根检验用于检验数据的平稳性,汇总单位根检验则是对所有面板单位进行单位根检验并进行拒绝或接受零假设。
面板数据分析的实例分析下面我们通过一个实例来演示面板数据分析的具体步骤。
假设我们有一个包含多个公司在不同时间点上销售额和成本数据的面板数据集,我们想要分析销售额和成本之间的关系。
首先,我们可以通过描述性统计分析来了解数据的基本特征,包括平均值、标准差、相关系数等。
然后,我们可以建立一个固定效应模型来分析销售额和成本之间的关系,控制个体特征和时间效应。
最后,我们可以进行假设检验来验证我们的模型是否显著,并通过模型拟合的结果来解释销售额和成本之间的关系。
总结面板数据分析是一种重要的数据分析方法,通过对具有时间序列和横截面特征的数据进行统计和建模,可以更好地了解数据的特性和规律。
在实际应用中,面板数据分析可以帮助我们进行效果评估、政策分析、市场预测等工作。
希望本文对你了解面板数据分析有所帮助。
