西电数据挖掘大作业k-means和k-medoids
4 第四章 聚类分析 -数据挖掘算法与应用(Python实现)-孙家泽-清华大学出版社

西安邮电大学
18
K-means算法概述
K-means算法对初始聚类中心较敏感,相似度 计算方式会影响聚类的划分。 常见的相似度计算方法有:
欧式距离 曼哈顿距离 闵可夫斯基距离
19
多选题 1分 对象i和对象j距离 d(i,j)满足性质( )
基于密度的聚类
➢常见的基于密度的方法:
➢ DBSCAN(具有噪声的基于密度的聚类方法) ➢ OPTICS(通过点排序识别聚类结构)
➢基于网格的方法把对象空间量化为有限个单元,形 成一个网络结构。所有的聚类操作都在这个网络结 构(即量化空间)上进行。这种方法主要优点是处 理速度很快,其处理时间通常独立于数据对象的个 数,而依赖于量化空间中每一维的单元数。
模式
聚类分析的目标
聚类分析的目标就是形成多个数据簇,并且数据 簇需要满足下面两个条件:
同一个簇内的数据尽量相似(high intra-class similarity);
不同簇的数据尽量不相似(low inter-class similarity)。
聚类分析常用算法介绍
常见的聚类分析算法有:
层次聚类算法
无论使用凝聚方法还是分裂方法,一个核心的问题是度量两 个簇间的距离,其中每个簇一般是一个对象集.
西安邮电大学
11
➢ 基于距离的聚类方法的缺点:只能发现球状的簇,难以发现任意形状的 簇。
➢ 基于密度的聚类:只要临近区域的密度(对象或数据点的数目)超过某 个临界值,就继续聚类。
优点:可以过滤掉“噪声”和“离群点”,发现任意形状的簇
第四章聚类分析
西安邮电大学
1
聚类分析
1. 聚类分析 2.基于划分的聚类方法 3.基于层次的聚类方法 4.基于密度的聚类方法 5.基于概率的聚类方法 6.聚类图数据
k-medoids 聚类公式字母公式

k-medoids 聚类算法是一种常用的基于距离的聚类方法,它主要用于将数据集中的数据点划分为若干个类别,使得同一类别内的数据点之间的相似度较高,不同类别之间的相似度较低。
与k-means 算法不同的是,k-medoids 算法使用代表性的数据点(medoids)来代表每个类别,从而使得对噪声和异常值更加稳健。
在k-medoids 聚类算法中,我们首先需要确定聚类的数量k,然后从数据集中随机选择k个数据点作为初始的medoids。
接下来的步骤是不断地迭代,直至收敛为止。
具体的迭代过程如下:1. 初始化:随机选择k个数据点作为初始的medoids。
2. 分配数据点:对于每个数据点,计算它与各个medoids 的距离,并将其分配到距离最近的medoids 所代表的类别中。
3. 更新medoids:对于每个类别,选择一个新的medoids 来代表该类别,使得该类别内所有数据点到新medoids 的距离之和最小。
4. 判断收敛:检查新的medoids 是否与旧的medoids 相同,若相同则停止迭代,否则继续进行迭代。
在k-medoids 聚类算法中,距离的计算可以使用各种不同的距离度量方式,例如欧氏距离、曼哈顿距离等。
对于大规模的数据集,k-medoids 算法可能会比k-means 算法更具有优势,因为它在每次迭代时只需要计算medoids 之间的距离,而不需要计算所有数据点之间的距离,从而可以减少计算量。
k-medoids 聚类算法是一种有效且稳健的聚类方法,它在处理一些特定情况下可以取得比k-means 更好的聚类效果。
通过对数据进行有效的分组和分类,k-medoids 聚类算法在数据挖掘和模式识别领域具有广泛的应用前景。
K-medoids clustering algorithm is a widely used distance-based clustering method for partitioning the data points in a dataset into several categories, in which the similarity of data points within the same category is relatively high, while the similarity between different categories is relatively low. Unlike the k-means algorithm, the k-medoids algorithm uses representative data points (medoids) to represent each category, making it more robust to noise and outliers.In the k-medoids clustering algorithm, the first step is to determine the number of clusters, denoted as k, and then randomly select k data points from the dataset as the initial medoids. The following steps involve iterative processes until the algorithm converges.The specific iterative process is as follows:1. Initialization: randomly select k data points as the initial medoids.2. Data point assignment: for each data point, calculate its distance to each medoid and assign it to the category represented by the nearest medoid.3. Update medoids: for each category, select a new medoid to represent the category, so that the sum of the distances from all data points in the category to the new medoid is minimized.4. Convergence check: check whether the new medoids are the same as the old medoids. If they are the same, stop the iteration; otherwise, continue the iteration.In the k-medoids clustering algorithm, various distance metrics can be used for distance calculation, such as Euclidean distance, Manhattan distance, etc. For large-scale datasets, the k-medoids algorithm may have advantages over the k-means algorithm because it only needs to calculate the distance betweenmedoids at each iteration, rather than calculating the distance between all data points, which can reduce theputational workload.In conclusion, the k-medoids clustering algorithm is an effective and robust clustering method that can achieve better clustering results than the k-means algorithm in certain situations. By effectively grouping and classifying data, the k-medoids clustering algorithm has wide application prospects in the fields of data mining and pattern recognition.Moreover, the k-medoids algorithm can be further extended and applied in various domains, such as customer segmentation in marketing, anomaly detection in cybersecurity, and image segmentation inputer vision. In marketing, k-medoids clustering can be used to identify customer segments based on their purchasing behavior, allowingpanies to tailor their marketing strategies to different customer groups. In cybersecurity, k-medoids can help detect anomalies by identifying patterns that deviate from the norm in network traffic or user behavior. Inputer vision, k-medoids can be used for image segmentation to partition an image into different regions based on similarity, which is useful for object recognition and scene understanding.Furthermore, the k-medoids algorithm can also bebined with other machine learning techniques, such as dimensionality reduction, feature selection, and ensemble learning, to improve its performance and scalability. For example, using dimensionality reduction techniques like principalponent analysis (PCA) can help reduce theputational burden of calculating distances in high-dimensional data, while ensemble learning methods like boosting or bagging can enhance the robustness and accuracy of k-medoids clustering.In addition, research and development efforts can focus on optimizing the k-medoids algorithm for specific applications and datasets, such as developing parallel and distributed versions of the algorithm to handle big data, exploring adaptive and dynamic approaches to adjust the number of clusters based on the data characteristics, and integrating domain-specific knowledge or constraints into the clustering process to improve the interpretability and usefulness of the results.Overall, the k-medoids clustering algorithm is a powerful tool for data analysis and pattern recognition, with a wide range of applications and potential for further advancements andinnovations. Its ability to handle noise and outliers, its flexibility in distance metrics, and its scalability to large-scale datasets make it a valuable technique for addressing real-world challenges in various domains. As the field of data science and machine learning continues to evolve, the k-medoids algorithm will likely remain an important method for uncovering meaningful insights fromplex data.。
聚类算法在医疗大数据上的应用研究

聚类算法在医疗大数据上的应用研究作者:王艳娥张拓杨倩来源:《电脑知识与技术》2020年第12期摘要:随着大数据技术的不断发展,医疗大数据的研究也成为我国医疗建设的重要一环,聚类能够挖掘出医疗大数据中潜在隐藏的信息,协助医生、医疗管理部门、科研所进行有效工作。
研究分析聚类算法K-means和K-medoids在医疗大数据的应用,从优化聚类算法降低时间复杂度、对高维医疗大数据进行特征提取降低维度、通过并行处理平台加速医疗数据的处理速度方面出发,阐明聚类算法在医疗大数据的数据预处理、数据分类、疾病预测等方面都广泛的应用。
随着并行处理平台的建设,聚类算法在医疗大数据的应用也将越来越广泛。
关键词:聚类算法;K-means;K-medoids;医疗大数据中图分类号:TP181 文献标识码:A文章编号:1009-3044(2020)12-0012-021聚类与医疗大数据聚类是数据挖掘中无监督学习分析数据常用的方法之一,通过聚类能够挖掘出数据集中隐藏的内在的联系。
医疗大数据的研究是我国医疗健康必经之路,通过聚类对医疗大数据进行分析,有效挖掘其隐藏的关联为临床诊断和医疗研究等提供有效的信息。
根据聚类原理的不同,聚类可分为层次聚类、划分式聚类、基于密度聚类和基于模型的方法,其中划分式聚类算法因为原理简单易于实现得到广泛的应用。
划分式聚类算法是按照相似性和相异性原则将数据集划分为k类。
采用划分式聚类算法分析数据时需要提前知道数据集的类数k,初始情况下,随机选择k个数据作为初始聚类中心,再按照相似行原则将其余数据划分给不同的类,然后根据优化目标重新选择新的聚类中心,直到满足给定的条件为止。
K-means算法和K-medoids算法是划分式聚类算法的典型代表,其中K-means算法因为运行速度快,在医疗大数据的应用中得到广泛的应用,K-medoids算法对噪声点的处理具有较好的效果也得到广泛的应用。
原理简单、易实现得到广泛的应用。
K-means聚类算法ppt课件

ppt课件.
1
K-means算法是很典型的基于距离的 聚类算法,采用距离作为相似性的评价指 标,即认为两个对象的距离越近,其相似 度就越大。
该算法认为类是由距离靠近的对象组 成的,因此把得到紧凑且独立的类作为最 终目标。
ppt课件.
2
假设数据集合为(x1, x2, …, xn),并 且每个xi为d维的向量,K-means聚类的目 的是,在给定分类组数k(k ≤ n)值的条 件下,将原始数据分成k类:
ppt课件.
4
数学表达式:
n:样本数。 k:样本分为k类。 rnk:第n个样本点是否属于第k类,属于则
rnk=1, 不属于则rnk=0。 μK:第k个中心点。
ppt课件.
5
k-means 要做的就是最小化
这个函数。
迭代的方法: 1、固定μK,得到rnk。 2、固定rnk,求出最优的μK。
ppt课件.
ppt课件.
12
K- medoids算法流程如下: 1、任意选取K个对象作为初始中心点 (O1,O2,…Oi…Ok)。 2、将余下的对象分到各个类中去(根据与 中心点最相近的原则); 3、对于每个类(Oi)中,顺序选取一个Or, 计算用Or代替Oi后的消耗—E(Or)。选择 E最小的那个Or来代替Oi。这样K个中心点 就改变了。
。不过,加上归一化规定,一个数据点的 隶属度的和总等于1:
ppt课件.
21
把n个元素xi(i=1,2,…,n)分为c个模糊组, 目标函数:
其中,m是大于1的实数,加权实数。uij 是xi属于类别j隶属度,cj是 类j的聚类中心。
ppt课件.
22
算法步骤: 1、用值在0,1间的随机数初始化隶属矩阵U,
基于KS抽样的k-medoids聚类初始中心选取法

基于KS抽样的k-medoids聚类初始中心选取法张晓东【摘要】The results of k-medoids clustering depend on initialseeds.Existing methods about seeds initialization cannot ensure the diversity of seeds.We proposed density peak Kennard-Stone (DPKS) sampling to choose seeds.Samples with high density are selected from initial data sets.Then less samples which are far away each other are chosen as the seeds by Kennard-Stone (KS) sampling.They will not be outlier and be more likely in different clusters.Experimental results demonstrate that,seed from DPKS gets more clusters than existing methods.Although the clustering accuracies of DPC and DPNM are comparable with that of DPKS,the proposed approach has less time consumption.That is because the proper seeds of DPKS reduces the number of iteration.Thus DPKS is an efficient and effective seeds initialization method.%经典的k-medoids聚类方法的聚类效果依赖于初始类中心的选择,而已有类中心选择方法不能确保类中心属于不同的类.针对此问题提出了密度峰值Kennard-Stone(Density peak Kennard-Stone,DPKS)类中心初始化方法,即先从原始数据集中选择一些高密度样本,再借助Kennard-Stone(KS)抽样从这些样本中选择距离较远的样本,这样确定的初始类中心不可能是离群点,而且更有可能属于不同的类.实验结果表明,DPKS比已有类中心选取法更容易获得不同类别的初始类中心.虽然DPC(Density peak clustering)和DPNM(Density peak optimized with new measure)与DPKS方法的聚类精度相差不大,但本文方法的聚类时间小于前两种方法,是一种快速有效的聚类方法.【期刊名称】《内蒙古工业大学学报(自然科学版)》【年(卷),期】2016(035)004【总页数】6页(P297-302)【关键词】k-medoids聚类;初始聚类中心;密度峰值;KS抽样【作者】张晓东【作者单位】包头师范学院网络信息中心,包头014030【正文语种】中文【中图分类】O212;O242实际中如果数据较多或问题繁杂难以统一处理,通常我们会将其进行归并,如医院按照病人病情分为不同科室处理;生物研究中根据古生物化石的骨骼形状和尺寸将它们分类;垃圾的分类回收等等。
聚类算法比较

聚类算法:1. 划分法:K-MEANS算法、K-M EDOIDS算法、CLARANS算法;1)K-means 算法:基本思想是初始随机给定K个簇中心,按照最邻近原则把待分类样本点分到各个簇。
然后按平均法重新计算各个簇的质心,从而确定新的簇心。
一直迭代,直到簇心的移动距离小于某个给定的值。
K-Means聚类算法主要分为三个步骤:(1)第一步是为待聚类的点寻找聚类中心(2)第二步是计算每个点到聚类中心的距离,将每个点聚类到离该点最近的聚类中去(3)第三步是计算每个聚类中所有点的坐标平均值,并将这个平均值作为新的聚类中心反复执行(2)、(3),直到聚类中心不再进行大范围移动或者聚类次数达到要求为止下图展示了对n个样本点进行K-means聚类的效果,这里k取2:(a)未聚类的初始点集(b)随机选取两个点作为聚类中心(c)计算每个点到聚类中心的距离,并聚类到离该点最近的聚类中去(d)计算每个聚类中所有点的坐标平均值,并将这个平均值作为新的聚类中心(e)重复(c),计算每个点到聚类中心的距离,并聚类到离该点最近的聚类中去(f)重复(d),计算每个聚类中所有点的坐标平均值,并将这个平均值作为新的聚类中心优点:1.算法快速、简单;2.对大数据集有较高的效率并且是可伸缩性的;3.时间复杂度近于线性,而且适合挖掘大规模数据集。
缺点:1. 在 K-means 算法中 K 是事先给定的,这个 K 值的选定是非常难以估计的。
2. 在 K-means 算法中,首先需要根据初始聚类中心来确定一个初始划分,然后对初始划分进行优化。
这个初始聚类中心的选择对聚类结果有较大的影响。
3. 从 K-means 算法框架可以看出,该算法需要不断地进行样本分类调整,不断地计算调整后的新的聚类中心,因此当数据量非常大时,算法的时间开销是非常大的。
4. 产生类的大小相差不会很大,对于脏数据很敏感。
2)K-M EDOIDS(k-medoids)算法与k-means很像,不一样的地方在于中心点的选取,在K-means中,我们将中心点取为当前cluster中所有数据点的平均值,在 K-medoids算法中,我们将从当前cluster 中选取这样一个点——它到其他所有(当前cluster中的)点的距离之和最小——作为中心点。
基于最小生成树的多层次k-Means聚类算法及其在数据挖掘中的应用

基于最小生成树的多层次k-Means聚类算法及其在数据挖掘中的应用金晓民;张丽萍【摘要】针对传统聚类算法存在挖掘效率慢、准确率低等问题,提出一种基于最小生成树的多层次k-means聚类算法,并应用于数据挖掘中.先分析聚类样本的数据类型,根据分析结果设计聚类准则函数;再通过最小生成树对样本数据进行划分,并选取初始聚类中心,将样本的数据空间划分为矩形单元,在矩形单元中对样本对象数据进行计算、降序和选取,得到有效的初始聚类中心,减少数据挖掘时间.实验结果表明,与传统算法相比,该算法可快速、准确地挖掘数据,且挖掘效率提升约50%.【期刊名称】《吉林大学学报(理学版)》【年(卷),期】2018(056)005【总页数】6页(P1187-1192)【关键词】最小生成树;多层次k-means聚类算法;数据挖掘【作者】金晓民;张丽萍【作者单位】内蒙古大学交通学院,呼和浩特010021;内蒙古自治区桥梁检测与维修加固工程技术研究中心,呼和浩特010070;内蒙古师范大学计算机科学技术学院,呼和浩特010022【正文语种】中文【中图分类】TP301数据挖掘就是从大量随机的、模糊的、有噪声的、不完全的数据中, 提取潜在的、未知的、隐含的、有应用价值的模式或信息的过程[1-3]. 数据挖掘中重要的步骤是聚类[4], 聚类将数据分为多个簇或类, 使相似度较高的对象在一个类中, 不同类别中的数据相似度较低[5]. 对稀疏和密集区域的识别通过聚类完成, 并通过聚类发现数据属性和分布模式间存在的关系[6]. 数据聚类广泛应用于医疗图像自动检测、客户分类、卫星照片分析、基因识别、空间数据处理和文本分类等领域[7].在低维情况下, 数据挖掘方法通过人眼进行模式识别及SOM(self organizing maps)可视化功能确定聚类的数目, 完成数据的挖掘, 该方法存在挖掘时间长和挖掘结果不准确的问题[8]. Means算法是数据聚类分析中常用的划分方法, 以准则函数和误差平方作为数据聚类的准则, 可快速、有效地完成大数据集的处理. MFA算法是一个优先考虑边权值进行社团划分的算法, 同时也继承了通过优化Q值进行社团划分的特点. 文献[9]提出了一种基于改进并行协同过滤算法的大数据挖掘方法, 通过分析协同过滤算法的执行流程, 针对传统协同过滤算法的不足, 从生成节点评分向量、获取相邻节点、形成推荐信息等方面对传统协同过滤算法进行改进, 得到了从运行时间、加速率和推荐精度三方面均运行效率较高的改进并行协同过滤算法. k-means算法依赖于数据输入的顺序和初始值的选择, 通过准则函数和误差平方对聚类效果进行测度, 各类的大小和形状差别较大[10]. 为了优化挖掘过程, 本文提出一种基于最小生成树的多层次k-means聚类算法对数据进行挖掘.1 数据类型与聚类准则函数设计1.1 聚类分析中的矩阵类型选取1) 数据矩阵. 数据矩阵表示一个对象的属性结果, 是数据之间的关系表, 每列都表示对象的一类属性, 每行表示数据对象, 如通过m个属性对数据对象进行描述, 属性一般为种类、高度等. n个对象中存在m个属性可通过n×m矩阵表示为(1)2) 差异矩阵. 数据对象之间的差异性用差异矩阵进行储存, 差异矩阵用n×n维矩阵表示, 其中d(i,j)为差异矩阵中的元素, 表示数据对象i和j之间存在的差异程度, 表达式为(2)差异矩阵中的元素d(i,j)≥0, 数据对象间的相似度越高, 该数据越接近于0;数据对象之间的相似度越低, 该数据越大.1.2 聚类准则和加权平均平方距离计算函数设计1) 误差平方和准则函数设计. 设X={x1,x2,…,xn}表示混合样本集, 通过相似性度量将混合样本集聚类成C个子集X1,X2,…,XC, 每个子集都表示一个数据的类型, 分别存在n1,n2,…,nC种样本. 采用准则函数和误差平方对数据聚类的质量进行衡量, 表达式为(3)其中: mj表示数据样本在类中的均值; JC表示准则函数, 是聚类中心和样本的函数, JC值越大, 表示聚类过程中存在的误差越大, 得到的聚类结果较差.2) 加权平均平方距离计算. 数据聚类过程中的加权平均平方距离和准则的表达式为(4)其中表示样本在数据类中的平均平方距离, 计算公式为(5)用数据的类间距离和准则Jb2及类间距离和准则Jb1对聚类结果类间存在的距离分布状态进行描述, Jb1和Jb2的计算公式为其中: mj表示样本在数据类别中的均值向量; m表示数据样本全部的均值向量; pj 表示数据类别的先验概率[11].2 算法设计2.1 基于最小生成树的初始中心点选取各矩形单元中存在的数据对象个数用最小生成树分割, 计算公式为(8)其中: RecU表示矩形单元; DataN表示样本数据的总数; SF表示细分因子; k表示聚类数. 最小生成树分割得到的矩形单元均值计算公式为(9)其中: S表示数据对象在矩形单元中的线性和; W表示矩形单元权重. 数据对象在各矩形单元中密集程度的计算公式为(10)其中: vi表示每个矩形单元的面积; ni表示数据对象在每个矩形单元中的数量; dmin和dmax分别表示矩阵单元中最小数据和最大数据的距离值.用最小生成树对样本数据X={x1,x2,…,xn}进行划分, CenterRecU表示分割后得到的矩形单元RecU, 其反映了样本数据集的分布状况. 采用数据集X′对集合CenterRecU进行表示, 用矩形单元密度对数据集X′进行降序排序, 初始聚类中心在数据集X′中选取, 记C={C1,C2,…,Ck}, 用矩形单元中心对数据集X′进行聚类, 得到k个类, 原始样本数据集的初始中心点通过在矩形单元中进行操作获得[12]. 2.2 算法描述设X1和X2表示样本的数据集, Dist(Ci,Cj)表示样本簇与样本簇之间的距离, 函数Dist(Ci,Cj)的表达式为(11)其中: Ci和Cj分别表示含有xi和xj的两个不同聚类簇; xi和xj分别表示数据集Xi和Xj中的样本点;用欧氏距离计算函数Dist(xi,xj)中数据间的距离; n1和n2表示数据对象在两个样本簇中的个数. 平均簇间距定义为(12)其中, Ci和Cj表示两个不同的聚类簇. 如果AvgDist(C)大于两个簇间的距离, 则不处理这两个簇, 继续比较, 直到AvgDist(C)小于两个簇之间的距离为止. 算法步骤如下:1) 通过k个中心点集C={C1,C2,…,Ck}构建最小生成树.2) 设Mi表示增量数据在第i个类中的总数, Gi表示第i个类中对象数据构成的集合. 对其他对象及相应的邻近类Ci进行搜索, 将搜索得到的数据划分到相应的集合Gi中.3) 从构建的最小生成树根节点向下出发, 搜索数据, 如果分裂点的坐标大于当前的坐标, 则搜索其左侧的空间;如果分裂点的坐标小于当前的坐标, 则搜索其右侧的坐标, 直至最小生成树的叶节点终止, 并对其进行标记, 记为Nearest. 计算与叶节点之间的距离, 并记为Distance.4) 计算每个目标点与节点之间的距离, 如果Distance大于与目标点的距离, 则将该节点更新为Nearest, 距离为Distance. 将目标点作为圆心、 Distance为半径画圆, 观察节点分类轴与所做圆是否相交. 若相交, 则向该节点的子节点进行搜索;若不相交, 则继续回溯, 当回溯到最小生成树的根节点时, 完成搜索. 此时最近的目标点聚类中心为最近点Nearest, 并在最近点Nearest中加入最近数据对象的聚类中心.5) 设Ci表示搜索得到的增量数据相应的最近聚类中心, 按下式对聚类中心进行更新:(13)6) 用式(12)比较k个聚类簇之间的距离, 如果平均簇间距AvgDist(C)大于两个簇之间的距离, 则对两个簇进行合并, 直到平均簇间距AvgDist(C)小于两个簇之间的距离为止. 用最小生成树得到的增量数据与初始聚类中心建立最小生成树, 用最近邻搜索方法将增量数据依次划分到相应的聚类中, 完成数据的聚类, 并根据类间的平均距离对聚类结果进行完善和修正, 获得最优的聚类结果, 完成数据挖掘.基于最小生成树的多层次k-means聚类算法流程如图1所示.图1 多层次k-means聚类算法流程Fig.1 Flow chart of multi-level k-means clustering algorithm3 算法应用实验1 为了验证基于最小生成树的多层次k-means聚类算法对数据挖掘的有效性, 下面对该算法进行测试, 操作系统为Windows7.0. 基于聚类结果越精准得到的数据挖掘结果越准确的原则, 分别采用基于最小生成树的多层次k-means聚类算法与传统k-means算法进行测试, 对比两种不同算法对数据挖掘过程中的聚类结果, 测试结果如图2所示, 图2中不同形状表示不同类别的数据.由图2可见: 采用基于最小生成树的多层次k-means聚类算法对数据进行聚类时, 可准确地对不同类别的数据进行划分; 采用传统k-means算法对数据进行聚类时,得到的分类中存在不同类别的数据, 聚类结果不准确. 因此, 基于最小生成树的多层次k-means聚类算法可准确地对数据进行挖掘.实验2 在k-means算法中, k值决定在该聚类算法中所要分配聚类簇的多少, 同时影响算法的聚类效果和迭代次数, 因此利用Canopy算法先进行粗略的聚类, 产生簇的个数为6, 即k-means算法的k=6.图2 两种不同算法的聚类结果Fig.2 Clustering results of two different algorithms在k=6的条件下, 为进一步验证本文算法的优越性, 在分类簇的划分过程中, 可用挖掘数据对象到簇中心的距离衡量算法的优劣. 聚类过程中, 距离计算次数能很好地衡量挖掘算法的相关性能. 通过对本文改进k-means算法和传统的MFA算法的距离计算次数进行比较, 完成性能对比, 对比结果如图3所示. 由图3可见, 本文提出的改进k-means算法得到的距离计算次数比传统MFA算法少, 随着计算挖掘控制维度的不断增加, 这种优势对比越来越明显. 与MFA算法相比, 在数据维度不断增加的集合中, 本文算法的效率提升约50%. 利用本文提出的改进k-means算法和MFA算法在运行实际效率上进行实验对比, 结果如图4所示. 由图4可见, 本文算法在每次迭代过程中, 在时间效率上都优于传统MFA算法, 且维度越大, 效果越明显.图3 不同算法的数据点距离计算数比较Fig.3 Comparison of calculation number of data points distance of different algorithms图4 不同算法迭代阶段的运行时间比较Fig.4 Comparison of running time of different algorithms in iterative stages由以上分析可知, 当k=6时, 本文提出的算法在时间效率上优于传统的MFA挖掘算法.图5 不同算法的效率测试结果比较Fig.5 Comparison of efficiency test resultsof different algorithms实验3 选择初始点和聚类迭代次数在数据挖掘中均较耗时的两个阶段, 分别采用基于最小生成树的多层次k-means聚类算法、文献[9]算法及传统MFA算法对数据进行挖掘, 对比不同算法进行数据挖掘的效率, 结果如图5所示.由图5可见, 采用基于最小生成树的多层次k-means聚类算法对数据进行挖掘时, 在选择初始点阶段的迭代次数较多, 在聚类阶段中的迭代次数较低. 采用其他算法对数据进行挖掘时, 在选择初始点阶段的迭代次数较少, 但在聚类阶段中的迭代次数较多. 对比基于最小生成树的多层次k-means聚类算法其他和算法的迭代次数可知, 基于最小生成树的多层次k-means聚类算法的总体迭代次数少于其他算法的总体迭代次数, 因此基于最小生成树的多层次k-means聚类算法对数据进行挖掘时迭代次数较少, 挖掘所用时间较短.综上可见, 针对传统聚类算法挖掘数据时, 存在挖掘结果不准确、挖掘时间长的问题, 本文提出了一种基于最小生成树的多层次k-means聚类算法, 解决了目前数据挖掘效率低的问题, 可有效提高信息检索率.参考文献【相关文献】[1] 林媛. 非结构化网络中有价值信息数据挖掘研究 [J]. 计算机仿真, 2017, 34(2): 414-417. (LIN Yuan. Research on Data Mining of Valuable Information in Unstructured Network [J]. Computer Simulation, 2017, 34(2): 414-417.)[2] 何拥军, 骆嘉伟, 余爱民. 多帧CT图像数据的测序数据挖掘与规律分析 [J]. 现代电子技术, 2017, 40(14): 106-108. (HE Yongjun, LUO Jiawei, YU Aimin. Sequencing Data Mining and Rules Analysis of Multi-frame CT Image Data [J]. Modern Electronics Technique, 2017, 40(14): 106-108.)[3] 贾瑞玉, 李振. 基于最小生成树的层次K-Means聚类算法 [J]. 微电子学与计算机, 2016, 33(3):86-88. (JIA Ruiyu, LI Zhen. The Level of K-Means Clustering Algorithm Based on the Minimum Spanning Tree [J]. Microelectronics & Computer, 2016, 33(3): 86-88.)[4] 王茜, 刘胜会. 改进K-Means算法在入侵检测中的应用研究 [J]. 计算机工程与应用, 2015,51(17): 124-127. (WANG Qian, LIU Shenghui. Application Research of Improved K-Means Algorithm in Intrusion Detection [J]. Computer Engineering and Applications, 2015, 51(17): 124-127.)[5] 杨辉华, 王克, 李灵巧, 等. 基于自适应布谷鸟搜索算法的K-Means聚类算法及其应用 [J]. 计算机应用, 2016, 36(8): 2066-2070. (YANG Huihua, WANG Ke, LI Lingqiao, et al. K-Means Clustering Algorithm Based on Adaptive Cuckoo Search and Its Application [J]. Journal of Computer Applications, 2016, 36(8): 2066-2070.)[6] 李洪成, 吴晓平, 陈燕. MapReduce框架下支持差分隐私保护的K-Means聚类算法 [J]. 通信学报, 2016, 37(2): 124-130. (LI Hongcheng, WU Xiaoping, CHEN Yan. K-Means Clustering Method Preserving Differential Privacy in MapReduce Framework [J]. Journal on Communications, 2016, 37(2): 124-130.)[7] 张顺龙, 庞涛, 周浩. 针对多聚类中心大数据集的加速K-Means聚类算法 [J]. 计算机应用研究, 2016, 33(2): 413-416. (ZHANG Shunlong, PANG Tao, ZHOU Hao. Accelerate K-Means for Multi-center Clustering of Big Datasets [J]. Application Research of Computers, 2016,33(2): 413-416.)[8] 陈平华, 陈传瑜. 基于满二叉树的二分K-Means聚类并行推荐算法 [J]. 计算机工程与科学, 2015, 37(8): 1450-1457. (CHEN Pinghua, CHEN Chuanyu. A Bisecting K-Means Clustering Parallel Recommendation Algorithm Based on Full Binary Tree [J]. Computer Engineering and Science, 2015, 37(8): 1450-1457.)[9] ZHU Li, LI Heng, FENG Yuxuan. Research on Big Data Mining Based on Improved Parallel Collaborative Filtering Algorithm [J]. Cluster Computing, 2018(5): 1-10.[10] França F O D. A Hash-Based Co-clustering Algorithm for Categorical Data [J]. Expert Systems with Applications, 2016, 64(12): 24-35.[11] 张睿, 熊金虎,汪东兴, 等. 基于体素邻域信息的均值漂移聚类算法检测fMRI激活区 [J]. 江苏大学学报(自然科学版), 2016, 37(5): 556-561. (ZHANG Rui, XIONG Jinhu, WANG Dongxing, et al. Detecting fMRI Activation by Mean-Shift Clustering Method Based on Voxel Neighborhood Information [J]. Journal of Jiangsu University (Natural Science Edition), 2016, 37(5): 556-561.)[12] 王永,万潇逸,陶娅芝, 等. 基于K-medoids 项目聚类的协同过滤推荐算法 [J]. 重庆邮电大学学报(自然科学版), 2017, 29(4): 521-526. (WANG Yong, WAN Xiaoyi, TAO Yazhi, et al. Collaborative Filtering Recommendation Algorithm Based on K-medoids Item Clustering [J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2017, 29(4): 521-526.)。
数据挖掘噪声数据处理综述

噪声数据处理综述摘要:噪声数据是指数据中存在着错误或异常(偏离期望值)的数据,不完整数据是指感兴趣的属性没有值.不一致数据则是数据内涵出现不一致的情况。
为了更好的论述什么是噪声数据处理,给出了两种噪声数据处理的算法:在属性级别上处理噪声数据的数据清洗算法和一种改进的应用于噪声数据中的KNN算法。
关键词: 噪声数据 噪声数据处理 数据清洗 KNN算法1. 概述噪声数据(noisy data)就是无意义的数据(meaningless data)。
这个词通常)的同义词使用。
但是,现在它的意义已经扩展到包作为损坏数据(corrupt data含所有难以被机器正确理解和翻译的数据,如非结构化文本。
任何不可被创造它的源程序读取和运用的数据,不管是已经接收的、存储的还是改变的,都被称为噪声。
噪声数据未必增加了需要的存储空间容量,相反地,它可能会影响所有数据挖掘(data mining)分析的结果。
统计分析可以运用历史数据中收集的信息来清除噪声数据从而促进数据挖掘。
引起噪声数据(noisy data)的原因可能是硬件故障、编程错误或者语音或光学字符识别程序(OCR)中的乱码。
拼写错误、行业简称和俚语也会阻碍机器读取。
噪声数据处理是数据处理的一个重要环节,在对含有噪声数据进行处理的过程中,现有的方法通常是找到这些孤立于其他数据的记录并删除掉,其缺点是事实上通常只有一个属性上的数据需要删除或修正,将整条记录删除将丢失大量有用的、干净的信息。
在数据仓库技术中,通常数据处理过程应用在数据仓库之前,其目的是提高数据的质量,使后继的联机处理分析(OLAP)和数据挖掘应用得到尽可能正确的结果。
然而,这个过程也可以反过来,即利用数据挖掘的一些技术来进行数据处理,提高数据质量。
2.噪声数据处理2.1在属性级别上噪声数据处理的数据清洗算法2.1.1 数据清洗和聚类分析介绍数据清洗包括许多的内容,文献【l】给出了详尽的介绍,其中噪声数据(包含错误或存在偏离期望的孤立点值)的处理是其中重要的一部分。
增量式K-Medoids聚类算法

增量式K-Medoids聚类算法
高小梅;冯志;冯兴杰
【期刊名称】《计算机工程》
【年(卷),期】2005(031)0z1
【摘要】聚类是一种非常有用的数据挖掘方法,可用于发现隐藏在数据背后的分组和数据分布信息.目前已经提出了许多聚类算法及其变种,但在增量式聚类算法研究方面所做的工作较少.当数据集因更新而发生变化时,数据挖掘的结果也应该进行相应的更新.由于数据量大,在更新后的数据集上重新执行聚类算法以更新挖掘结果显然比较低效,因此亟待研究增量式聚类算法.该文通过对K-Medoids聚类算法的改进,提出一种增量式K-Medoids聚类算法.它能够很好地解决传统聚类算法在伸缩性、数据定期更新时所面临的问题.
【总页数】3页(P181-183)
【作者】高小梅;冯志;冯兴杰
【作者单位】中国民航学院计算机科学与技术学院,天津,300300;中国民航学院计算机科学与技术学院,天津,300300;中国民航学院计算机科学与技术学院,天
津,300300
【正文语种】中文
【中图分类】TP311
【相关文献】
1.改进的电力负荷曲线集成K-medoids聚类算法 [J], 王华勇;韩松;肖孝天;杨超
2.基于全覆盖粒计算的K-medoids文本聚类算法 [J], 邹雪君;谢珺;任密蜂;续欣莹
3.一种基于标准差的K-medoids聚类算法 [J], 邓玉芳;张继福
4.基于k-medoids聚类算法的低压台区线损异常识别方法 [J], 薛明志;陈商玥;高强
5.基于K-Medoids聚类算法的电网工程数据处理技术研究 [J], 李斌;冯延明;刘伟;侯秀梅;陆杭
因版权原因,仅展示原文概要,查看原文内容请购买。
聚类分析—K-means and K-medoids聚类

3. 按下式重新计算k个聚类中心; xs s:label ( s ) j cj , j 1, 2,..., k Nj
4. 重复步骤2和步骤3,直到达到最大迭代次数为止。
2014-5-12
Matlab程序实现
function [M, j, e] = kmeans(X, K, Max_Its) [N,D]=size(X); I=randperm(N); M=X(I(1:K),:); Mo = M; for n=1:Max_Its for k=1:K Dist(:,k) = sum((X - repmat(M(k,:),N,1)).^2,2)'; end [i, j]=min(Dist, [], 2); for k=1:K if size(find(j==k))>0 M(k, :) = mean(X(find(j==k), :)); end end
10
9
例
10
10 9 8 7 6 5
9
8
8
7
7
6
6
5
5
4
4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10
将每个 对象赋 给最类 似的中 心
10 9 8 7 6 5 4 3 2 1 0
3 2 1 0 0 1 2 3 4 5 6 7 8 9 10
更新簇 的平均 值 重新赋值
4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10
聚类结果的质量用一个代价函数来估算, 该函数评估了 对象与其参照对象之间的平均相异度
E || p oi ||
k j 1 pC j
2014-5-12
2
数据挖掘-从海量数据中发现规则和规律

数据挖掘--从海量数据中发现规则和规律数据挖掘徐良为(日本数理系统株式会社)徐良为-----------基于数据挖掘进行工业上的品质管理和节省能源控制关键字:不确定性,知识发现,机器学习,品质改善,节省能源控制1 前言数据挖掘借助于计算机的存贮能力与计算能力,从海量的、复杂的数据中发现有价值的知识、规律性和要素之间的对应联系等等。
近年来,随着数据挖掘技术迅速的发展,在各种各样的行业中得到有效地运用和实践。
在这样的背景下,充满着复杂性、多样性和不确定性的社会中如何去理解和合理地判断、从已有的记录数据出发如何将其复杂的关联性要素进行清晰化模型化、如何将类似的东西合理地分类、计算不确定的事情的发生概率大小等等各类重要性有必要进行重新认识。
对于本文,作者从数据挖掘系统开发者的观点出发,结合以往的制造业质量管理和节省能源控制等项目的实施经验进行数据挖掘的基础技术介绍。
第二节是对数据挖掘过程的基本介绍,第三节是制造业的质量改进,第四节是关于产品的生产控制以及节省能源应用的例子。
最后一节叙述了数据挖掘将来的展望。
2 数据挖掘过程的基础我们经常会听到诸如“明日的最高气温是多少度”的问题,由于影响实际气温的因素有许许多多,包括一些人类无法预知的因素,所以要非常精确地说“明日的最高气温是25.4度”是很困难的。
但是如果根据最高与最低气温的记录得到“明日的最高气温是(-41,40.9)”谁都不会有异议。
但是这个范围太广了,如果说是北京,则根据当地气象状况得到(-9.2,39.5)的范围。
更进一步,能够加入季节、周边地区的气象状况等条件的话,这个温度的判断范围还会缩小。
但是这个范围始终是概率上的推定,还是有较小的可能性最终实际温度会偏离这个范围。
为了缩小范围,需要从海量且复杂的气象数据中将最高气温的关联原因找出来。
在这里,我们说:“推断明日的最高气温”这个话题其实是数据挖掘过程的一种基本形式。
图1 数据挖掘作业图数据挖掘过程中的几个主要步骤:(1)挖掘目标需明确化首先要清楚做什么。
kmedoids的轮廓系数__解释说明

kmedoids的轮廓系数解释说明1. 引言1.1 概述在聚类算法中,K-means是一种常用的方法,其通过将数据点划分为K个簇来实现聚类分析。
然而,当数据集包含离群点或者噪声数据时,传统的K-means 算法可能无法获取准确的聚类结果。
为了克服这一问题,K-medoids算法被提出并广泛应用于各种领域。
与K-means不同的是,K-medoids将簇中心选择为该簇内具有最小平均距离的对象,从而提高了对异常值和噪声数据的鲁棒性。
1.2 文章结构本文将详细介绍K-medoids算法及其在聚类分析中的应用。
首先,在第2节中我们将总览该算法,并解释其原理和流程;接着,在第3节中我们将介绍轮廓系数的概念和意义,并阐述轮廓系数在K-medoids中的作用;然后,在第4节中我们将给出研究方法与结果分析部分,包括数据集选择与预处理方法描述、实验设置与评估指标介绍以及实验结果分析与讨论;最后,在第5节中我们将对整篇文章进行总结,并展望未来关于K-medoids算法的研究方向。
1.3 目的本文的目的在于介绍K-medoids算法,并重点解释其应用中的一个重要指标——轮廓系数。
通过对该指标的全面分析,我们希望读者能够理解K-medoids算法及其在聚类分析中的优势,以及如何使用轮廓系数来评估聚类效果。
此外,通过实验结果分析与讨论部分,我们也将展示K-medoids算法在不同数据集上的性能表现,以验证其有效性和可靠性。
最后,我们还将探讨未来关于K-medoids 算法的研究方向,并给出相应建议和展望。
这样组织文章可以确保读者对文章结构有清晰的了解,并且能够准确把握每一节主题内容。
同时,在引言部分明确阐述了文章的概述、结构和目的,使得读者能够对整篇文章有一个整体认识并明白作者要传达的信息。
2. K-medoids算法2.1 总览K-medoids算法是一种用于聚类分析的方法,它是基于中心点(medoid)的概念进行计算的。
大数据挖掘算法篇之K-Means实例

⼤数据挖掘算法篇之K-Means实例⼀、引⾔ K-Means算法是聚类算法中,应⽤最为⼴泛的⼀种。
本⽂基于欧⼏⾥得距离公式:d = sqrt((x1-x2)^+(y1-y2)^)计算⼆维向量间的距离,作为聚类划分的依据,输⼊数据为⼆维数据两列数据,输出结果为聚类中⼼和元素划分结果。
输⼊数据格式如下:118223240.00.051.00.060.01.072.01.081.02.092.02.0102.00.0110.02.0127.06.0137.07.0147.08.0158.06.0168.07.0178.08.0188.09.0199.07.0209.08.0219.09.022⼆、欧⼏⾥得距离:欧⼏⾥得距离定义:欧⼏⾥得距离( Euclidean distance)也称欧⽒距离,在n维空间内,最短的线的长度即为其欧⽒距离。
它是⼀个通常采⽤的距离定义,它是在m维空间中两个点之间的真实距离。
在⼆维和三维空间中的欧式距离的就是两点之间的距离,⼆维的公式是d = sqrt((x1-x2)^+(y1-y2)^)三维的公式是d=sqrt((x1-x2)^+(y1-y2)^+(z1-z2)^)推⼴到n维空间,欧式距离的公式是d=sqrt( ∑(xi1-xi2)^ ) 这⾥i=1,2..nxi1表⽰第⼀个点的第i维坐标,xi2表⽰第⼆个点的第i维坐标n维欧⽒空间是⼀个点集,它的每个点可以表⽰为(x(1),x(2),...x(n)),其中x(i)(i=1,2...n)是实数,称为x的第i个坐标,两个点x和y=(y(1),y(2)...y(n))之间的距离d(x,y)定义为上⾯的公式.欧⽒距离看作信号的相似程度。
距离越近就越相似,就越容易相互⼲扰,误码率就越⾼。
三、代码⽰例1/****************************************************************************2* *3* KMEANS *4* *5*****************************************************************************/67 #include <stdio.h>8 #include <stdlib.h>9 #include <string.h>10 #include <conio.h>11 #include <math.h>1213// FUNCTION PROTOTYPES141516// DEFINES17#define SUCCESS 118#define FAILURE 019#define TRUE 120#define FALSE 021#define MAXVECTDIM 2022#define MAXPATTERN 2023#define MAXCLUSTER 10242526272829char *f2a(double x, int width){30char cbuf[255];31char *cp;33int d,s;34 cp=fcvt(x,width,&d,&s);35if (s) {36 strcpy(cbuf,"-");37 }38else {39 strcpy(cbuf,"");40 } /* endif */41if (d>0) {42for (i=0; i<d; i++) {43 cbuf[i+1]=cp[i];44 } /* endfor */45 cbuf[d+1]=0;46 cp+=d;47 strcat(cbuf,".");48 strcat(cbuf,cp);49 } else {50if (d==0) {51 strcat(cbuf,".");52 strcat(cbuf,cp);53 }54else {55 k=-d;56 strcat(cbuf,".");57for (i=0; i<k; i++) {58 strcat(cbuf,"0");59 } /* endfor */60 strcat(cbuf,cp);61 } /* endif */62 } /* endif */63 cp=&cbuf[0];64return cp;65 }6667686970// ***** Defined structures & classes *****71struct aCluster {72double Center[MAXVECTDIM];73int Member[MAXPATTERN]; //Index of Vectors belonging to this cluster 74int NumMembers;75 };7677struct aVector {78double Center[MAXVECTDIM];79int Size;80 };8182class System {83private:84double Pattern[MAXPATTERN][MAXVECTDIM+1];85 aCluster Cluster[MAXCLUSTER];86int NumPatterns; // Number of patterns87int SizeVector; // Number of dimensions in vector88int NumClusters; // Number of clusters89void DistributeSamples(); // Step 2 of K-means algorithm90int CalcNewClustCenters();// Step 3 of K-means algorithm91double EucNorm(int, int); // Calc Euclidean norm vector92int FindClosestCluster(int); //ret indx of clust closest to pattern93//whose index is arg94public:95void system();96int LoadPatterns(char *fname); // Get pattern data to be clustered97void InitClusters(); // Step 1 of K-means algorithm98void RunKMeans(); // Overall control K-means process99void ShowClusters(); // Show results on screen100void SaveClusters(char *fname); // Save results to file101void ShowCenters();102 };103//输出聚类中⼼104void System::ShowCenters(){105int i,j;106 printf("Cluster centers:\n");107for (i=0; i<NumClusters; i++) {108 Cluster[i].Member[0]=i;109 printf("ClusterCenter[%d]=(%f,%f)\n",i,Cluster[i].Center[0],Cluster[i].Center[1]); 110 } /* endfor */111 printf("\n");112 getchar();113 }114115//读取⽂件117 {118 FILE *InFilePtr;119int i,j;120double x;121if((InFilePtr = fopen(fname, "r")) == NULL)122return FAILURE;123 fscanf(InFilePtr, "%d", &NumPatterns); // Read # of patterns 18数据量124 fscanf(InFilePtr, "%d", &SizeVector); // Read dimension of vector 2维度125 fscanf(InFilePtr, "%d", &NumClusters); // Read # of clusters for K-Means 2簇126for (i=0; i<NumPatterns; i++) { // For each vector127for (j=0; j<SizeVector; j++) { // create a pattern128 fscanf(InFilePtr,"%lg",&x); // consisting of all elements129 Pattern[i][j]=x;130 } /* endfor */131 } /* endfor */132//输出所有数据元素133 printf("Input patterns:\n");134for (i=0; i<NumPatterns; i++) {135 printf("Pattern[%d]=(%2.3f,%2.3f)\n",i,Pattern[i][0],Pattern[i][1]);136 } /* endfor */137 printf("\n--------------------\n");138 getchar();139return SUCCESS;140 }141//***************************************************************************142// InitClusters *143// Arbitrarily assign a vector to each of the K clusters *144// We choose the first K vectors to do this *145//***************************************************************************146//初始化聚类中⼼147void System::InitClusters(){148int i,j;149 printf("Initial cluster centers:\n");150for (i=0; i<NumClusters; i++) {151 Cluster[i].Member[0]=i;152for (j=0; j<SizeVector; j++) {153 Cluster[i].Center[j]=Pattern[i][j];154 } /* endfor */155 } /* endfor */156for (i=0; i<NumClusters; i++) {157 printf("ClusterCenter[%d]=(%f,%f)\n",i,Cluster[i].Center[0],Cluster[i].Center[1]); //untransplant 158 } /* endfor */159 printf("\n");160 getchar();161 }162//运⾏KMeans163void System::RunKMeans(){164int converged;165int pass;166 pass=1;167 converged=FALSE;168//第N次聚类169while (converged==FALSE) {170 printf("PASS=%d\n",pass++);171 DistributeSamples();172 converged=CalcNewClustCenters();173 ShowCenters();174 getchar();175 } /* endwhile */176 }177//在⼆维和三维空间中的欧式距离的就是两点之间的距离,⼆维的公式是178//d = sqrt((x1-x2)^+(y1-y2)^)179//通过这种运算,就可以把所有列的属性都纳⼊进来180double System::EucNorm(int p, int c){ // Calc Euclidean norm of vector difference181double dist,x; // between pattern vector, p, and cluster182int i; // center, c.183char zout[128];184char znum[40];185char *pnum;186//187 pnum=&znum[0];188 strcpy(zout,"d=sqrt(");189 printf("The distance from pattern %d to cluster %d is calculated as:\n",p,c);190 dist=0;191for (i=0; i<SizeVector ;i++){192//拼写字符串193 x=(Cluster[c].Center[i]-Pattern[p][i])*(Cluster[c].Center[i]-Pattern[p][i]);194 strcat(zout,f2a(x,4));195if (i==0)196 strcat(zout,"+");197//计算距离198 dist += (Cluster[c].Center[i]-Pattern[p][i])*(Cluster[c].Center[i]-Pattern[p][i]);199 } /* endfor */201return dist;202 }203//查找最近的群集204int System::FindClosestCluster(int pat){205int i, ClustID;206double MinDist, d;207 MinDist =9.9e+99;208 ClustID=-1;209for (i=0; i<NumClusters; i++) {210 d=EucNorm(pat,i);211 printf("Distance from pattern %d to cluster %d is %f\n\n",pat,i,sqrt(d));212if (d<MinDist) {213 MinDist=d;214 ClustID=i;215 } /* endif */216 } /* endfor */217if (ClustID<0) {218 printf("Aaargh");219 exit(0);220 } /* endif */221return ClustID;222 }223//224void System::DistributeSamples(){225int i,pat,Clustid,MemberIndex;226//Clear membership list for all current clusters227for (i=0; i<NumClusters;i++){228 Cluster[i].NumMembers=0;229 }230for (pat=0; pat<NumPatterns; pat++) {231//Find cluster center to which the pattern is closest232 Clustid= FindClosestCluster(pat);//查找最近的聚类中⼼233 printf("patern %d assigned to cluster %d\n\n",pat,Clustid);234//post this pattern to the cluster235 MemberIndex=Cluster[Clustid].NumMembers;236 Cluster[Clustid].Member[MemberIndex]=pat;237 Cluster[Clustid].NumMembers++;238 } /* endfor */239 }240//计算新的群集中⼼241int System::CalcNewClustCenters(){242int ConvFlag,VectID,i,j,k;243double tmp[MAXVECTDIM];244char xs[255];245char ys[255];246char nc1[20];247char nc2[20];248char *pnc1;249char *pnc2;250char *fpv;251252 pnc1=&nc1[0];253 pnc2=&nc2[0];254 ConvFlag=TRUE;255 printf("The new cluster centers are now calculated as:\n");256for (i=0; i<NumClusters; i++) { //for each cluster257 pnc1=itoa(Cluster[i].NumMembers,nc1,10);258 pnc2=itoa(i,nc2,10);259 strcpy(xs,"Cluster Center");260 strcat(xs,nc2);261 strcat(xs,"(1/");262 strcpy(ys,"(1/");263 strcat(xs,nc1);264 strcat(ys,nc1);265 strcat(xs,")(");266 strcat(ys,")(");267for (j=0; j<SizeVector; j++) { // clear workspace268 tmp[j]=0.0;269 } /* endfor */270for (j=0; j<Cluster[i].NumMembers; j++) { //traverse member vectors271 VectID=Cluster[i].Member[j];272for (k=0; k<SizeVector; k++) { //traverse elements of vector273 tmp[k] += Pattern[VectID][k]; // add (member) pattern elmnt into temp 274if (k==0) {275 strcat(xs,f2a(Pattern[VectID][k],3));276 } else {277 strcat(ys,f2a(Pattern[VectID][k],3));278 } /* endif */279 } /* endfor */280if(j<Cluster[i].NumMembers-1){281 strcat(xs,"+");282 strcat(ys,"+");283 }285 strcat(xs,")");286 strcat(ys,")");287 }288 } /* endfor */289for (k=0; k<SizeVector; k++) { //traverse elements of vector290 tmp[k]=tmp[k]/Cluster[i].NumMembers;291if (tmp[k] != Cluster[i].Center[k])292 ConvFlag=FALSE;293 Cluster[i].Center[k]=tmp[k];294 } /* endfor */295 printf("%s,\n",xs);296 printf("%s\n",ys);297 } /* endfor */298return ConvFlag;299 }300//输出聚类301void System::ShowClusters(){302int cl;303for (cl=0; cl<NumClusters; cl++) {304 printf("\nCLUSTER %d ==>[%f,%f]\n", cl,Cluster[cl].Center[0],Cluster[cl].Center[1]); 305 } /* endfor */306 }307308void System::SaveClusters(char *fname){309 }四、主调程序1void main(int argc, char *argv[])2 {34 System kmeans;5/*6 if (argc<2) {7 printf("USAGE: KMEANS PATTERN_FILE\n");8 exit(0);9 }*/10if (kmeans.LoadPatterns("KM2.DAT")==FAILURE ){11 printf("UNABLE TO READ PATTERN_FILE:%s\n",argv[1]);12 exit(0);13 }1415 kmeans.InitClusters();16 kmeans.RunKMeans();17 kmeans.ShowClusters();18 }五、输出结果1 Input patterns:2 Pattern[0]=(0.000,0.000)3 Pattern[1]=(1.000,0.000)4 Pattern[2]=(0.000,1.000)5 Pattern[3]=(2.000,1.000)6 Pattern[4]=(1.000,2.000)7 Pattern[5]=(2.000,2.000)8 Pattern[6]=(2.000,0.000)9 Pattern[7]=(0.000,2.000)10 Pattern[8]=(7.000,6.000)11 Pattern[9]=(7.000,7.000)12 Pattern[10]=(7.000,8.000)13 Pattern[11]=(8.000,6.000)14 Pattern[12]=(8.000,7.000)15 Pattern[13]=(8.000,8.000)16 Pattern[14]=(8.000,9.000)17 Pattern[15]=(9.000,7.000)18 Pattern[16]=(9.000,8.000)19 Pattern[17]=(9.000,9.000)2021 --------------------2223 Initial cluster centers:24 ClusterCenter[0]=(0.000000,0.000000)25 ClusterCenter[1]=(1.000000,0.000000)262728 PASS=129 The distance from pattern 0 to cluster 0is calculated as:30 d=sqrt( .0000+ .0000)31 Distance from pattern 0 to cluster 0is0.0000003233 The distance from pattern 0 to cluster 1is calculated as:35 Distance from pattern 0 to cluster 1is1.0000003637 patern 0 assigned to cluster 03839 The distance from pattern 1 to cluster 0is calculated as:40 d=sqrt( 1.0000+ .0000)41 Distance from pattern 1 to cluster 0is1.0000004243 The distance from pattern 1 to cluster 1is calculated as:44 d=sqrt( .0000+ .0000)45 Distance from pattern 1 to cluster 1is0.0000004647 patern 1 assigned to cluster 14849 The distance from pattern 2 to cluster 0is calculated as:50 d=sqrt( .0000+ 1.0000)51 Distance from pattern 2 to cluster 0is1.0000005253 The distance from pattern 2 to cluster 1is calculated as:54 d=sqrt( 1.0000+ 1.0000)55 Distance from pattern 2 to cluster 1is1.4142145657 patern 2 assigned to cluster 05859 The distance from pattern 3 to cluster 0is calculated as:60 d=sqrt( 4.0000+ 1.0000)61 Distance from pattern 3 to cluster 0is2.2360686263 The distance from pattern 3 to cluster 1is calculated as:64 d=sqrt( 1.0000+ 1.0000)65 Distance from pattern 3 to cluster 1is1.4142146667 patern 3 assigned to cluster 16869 The distance from pattern 4 to cluster 0is calculated as:70 d=sqrt( 1.0000+ 4.0000)71 Distance from pattern 4 to cluster 0is2.2360687273 The distance from pattern 4 to cluster 1is calculated as:74 d=sqrt( .0000+ 4.0000)75 Distance from pattern 4 to cluster 1is2.0000007677 patern 4 assigned to cluster 17879 The distance from pattern 5 to cluster 0is calculated as:80 d=sqrt( 4.0000+ 4.0000)81 Distance from pattern 5 to cluster 0is2.8284278283 The distance from pattern 5 to cluster 1is calculated as:84 d=sqrt( 1.0000+ 4.0000)85 Distance from pattern 5 to cluster 1is2.2360688687 patern 5 assigned to cluster 18889 The distance from pattern 6 to cluster 0is calculated as:90 d=sqrt( 4.0000+ .0000)91 Distance from pattern 6 to cluster 0is2.0000009293 The distance from pattern 6 to cluster 1is calculated as:94 d=sqrt( 1.0000+ .0000)95 Distance from pattern 6 to cluster 1is1.0000009697 patern 6 assigned to cluster 19899 The distance from pattern 7 to cluster 0is calculated as: 100 d=sqrt( .0000+ 4.0000)101 Distance from pattern 7 to cluster 0is2.000000102103 The distance from pattern 7 to cluster 1is calculated as: 104 d=sqrt( 1.0000+ 4.0000)105 Distance from pattern 7 to cluster 1is2.236068106107 patern 7 assigned to cluster 0108109 The distance from pattern 8 to cluster 0is calculated as: 110 d=sqrt( 49.0000+ 36.0000)111 Distance from pattern 8 to cluster 0is9.219544112113 The distance from pattern 8 to cluster 1is calculated as: 114 d=sqrt( 36.0000+ 36.0000)115 Distance from pattern 8 to cluster 1is8.485281116117 patern 8 assigned to cluster 1123 The distance from pattern 9 to cluster 1is calculated as: 124 d=sqrt( 36.0000+ 49.0000)125 Distance from pattern 9 to cluster 1is9.219544126127 patern 9 assigned to cluster 1128129 The distance from pattern 10 to cluster 0is calculated as: 130 d=sqrt( 49.0000+ 64.0000)131 Distance from pattern 10 to cluster 0is10.630146132133 The distance from pattern 10 to cluster 1is calculated as: 134 d=sqrt( 36.0000+ 64.0000)135 Distance from pattern 10 to cluster 1is10.000000136137 patern 10 assigned to cluster 1138139 The distance from pattern 11 to cluster 0is calculated as: 140 d=sqrt( 64.0000+ 36.0000)141 Distance from pattern 11 to cluster 0is10.000000142143 The distance from pattern 11 to cluster 1is calculated as: 144 d=sqrt( 49.0000+ 36.0000)145 Distance from pattern 11 to cluster 1is9.219544146147 patern 11 assigned to cluster 1148149 The distance from pattern 12 to cluster 0is calculated as: 150 d=sqrt( 64.0000+ 49.0000)151 Distance from pattern 12 to cluster 0is10.630146152153 The distance from pattern 12 to cluster 1is calculated as: 154 d=sqrt( 49.0000+ 49.0000)155 Distance from pattern 12 to cluster 1is9.899495156157 patern 12 assigned to cluster 1158159 The distance from pattern 13 to cluster 0is calculated as: 160 d=sqrt( 64.0000+ 64.0000)161 Distance from pattern 13 to cluster 0is11.313708162163 The distance from pattern 13 to cluster 1is calculated as: 164 d=sqrt( 49.0000+ 64.0000)165 Distance from pattern 13 to cluster 1is10.630146166167 patern 13 assigned to cluster 1168169 The distance from pattern 14 to cluster 0is calculated as: 170 d=sqrt( 64.0000+ 81.0000)171 Distance from pattern 14 to cluster 0is12.041595172173 The distance from pattern 14 to cluster 1is calculated as: 174 d=sqrt( 49.0000+ 81.0000)175 Distance from pattern 14 to cluster 1is11.401754176177 patern 14 assigned to cluster 1178179 The distance from pattern 15 to cluster 0is calculated as: 180 d=sqrt( 81.0000+ 49.0000)181 Distance from pattern 15 to cluster 0is11.401754182183 The distance from pattern 15 to cluster 1is calculated as: 184 d=sqrt( 64.0000+ 49.0000)185 Distance from pattern 15 to cluster 1is10.630146186187 patern 15 assigned to cluster 1188189 The distance from pattern 16 to cluster 0is calculated as: 190 d=sqrt( 81.0000+ 64.0000)191 Distance from pattern 16 to cluster 0is12.041595192193 The distance from pattern 16 to cluster 1is calculated as: 194 d=sqrt( 64.0000+ 64.0000)195 Distance from pattern 16 to cluster 1is11.313708196197 patern 16 assigned to cluster 1198199 The distance from pattern 17 to cluster 0is calculated as: 200 d=sqrt( 81.0000+ 81.0000)201 Distance from pattern 17 to cluster 0is12.727922207 patern 17 assigned to cluster 1208209 The new cluster centers are now calculated as:210 Cluster Center0(1/3)( .000+ .000+ .000),211 (1/3)( .000+ 1.000+ 2.000)212 Cluster Center1(1/15)( 1.000+ 2.000+ 1.000+ 2.000+ 2.000+ 7.000+ 7.000+ 7.000+ 8 213 .000+ 8.000+ 8.000+ 8.000+ 9.000+ 9.000+ 9.000),214 (1/15)( .000+ 1.000+ 2.000+ 2.000+ .000+ 6.000+ 7.000+ 8.000+ 6.000+ 7.000+ 8.00 2150+ 9.000+ 7.000+ 8.000+ 9.000)216 Cluster centers:217 ClusterCenter[0]=(0.000000,1.000000)218 ClusterCenter[1]=(5.866667,5.333333)。
数据挖掘中三种典型聚类算法的分析比较
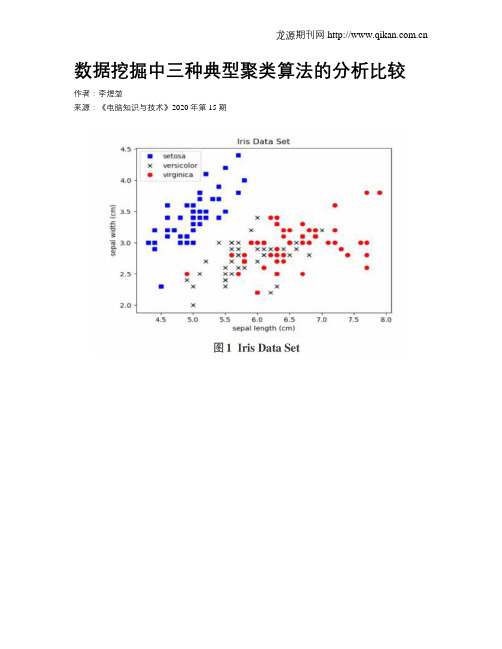
数据挖掘中三种典型聚类算法的分析比较作者:李煜堃来源:《电脑知识与技术》2020年第15期摘要:大数据时代从大量无序的数据中发现隐含的、有效的、有价值的、可理解的模式变得越发重要。
在此背景下,以数据挖掘众多算法中的聚类算法为切人点,选取三种典型的聚类算法——K-means算法、AGNES算法、DBSCAN算法,进行可视化聚类结果和FMI值比较分析,归纳出DBSCAN算法可以发现任意形状的簇类,AGNES算法和K-Means算法在中小型数据集中挖掘得到球形簇的效果较好。
關键词:聚类;K-means算法;AGNES算法;DBSCAN算法中图分类号:TP301 文献标识码:A文章编号:1009-3044(2020)15-0052-051引言聚类是通过发现数据集中数据之间的相关关系,将数据分类到不同的类或簇的过程。
聚类并不关心某一类别的信息,其目标是将相似的样本聚在一起,实现同一类对象的相似度尽可的大,而不同类对象之间的相似度尽可能地小。
因此,聚类算法只需要知道如何计算样本之间的相似性,就可以对数据进行聚类。
目前聚类的方法很多,根据基本思想的不同,大致可以将聚类算法分为五大类:层次聚类算法、分割聚类算法、基于约束的聚类算法、机器学习中的聚类算法和用于高维度的聚类算法。
选取划分聚类算法中传统的K-means算法、层次聚类算法中具有代表性的AGNES算法以及典型的基于密度的聚类算法DBSCAN等三种算法对不同数据集的聚类效果进行分析,归纳不同聚类算法优缺点。
2算法相关理论2.1 K-means算法的基本原理及实现步骤2.1.1 K-means算法的基本原理K-Means是典型的划分聚类算法,其中K表示的是聚类为k个簇,Means代表取每一个聚类中数据值的均值作为该簇的中心,或者称为质心,即用每一个类的质心对该簇进行描述。
K-Means算法的原理是对于给定的数据集,按照各数据点之间的距离大小关系,将数据集戈0分为K个簇。
三种常见的聚类算法的python实现kmeans、Hierarchicalclusteri。。。

三种常见的聚类算法的python实现kmeans、Hierarchicalclusteri。
聚类是机器学习、数据挖掘相关的⼀类很常见的问题。
关于聚类算法的介绍这⾥就不多写了,因为⽆论是教科书还是⽹络上都有太多的资料了。
这⾥,⽤⼀个《Programming Collective Intelligence》中的聚类例⼦,写⼏个经典聚类算法的实现,分别是hierachiclaCluster、kmeans、kmedoids。
另外,最近⼀直在看数据挖掘、⾃然语⾔处理相关的东西,通过看资料发现有些东西很好理解,但是长时间不⽤的话,过⼀段时间就忘记得差不多了。
其实换个⾓度想,也是⾃⼰对这些东西理解得不深刻。
我觉得踏踏实实的实现这些算法是必要的,因为在实现过程中,我们可以发现哪些地⽅是算法的核⼼思想,哪些地⽅是性能瓶颈,这也为进⼀步优化提供了基础。
问题背景及数据集:blog的聚类。
如何判断两个blog是相似的呢?由于相关的博客的主题内容应该是相同的,即会出现很多相同的词。
于是我们为每个blog定义⼀个向量,该向量的维度为数据集中所有出现的不同词的个数,向量的值为对应词出现的次数。
判断两个向量间的相似性,我们使⽤算法。
测试数据集描述:数据集,该数据集第⼀⾏包含所有数据集中出现的不同词,共有m个,剩下所有⾏,每⼀⾏对应⼀篇blog,共m+1列,⽤tab分开。
第⼀列为博客名,接下来m列为⼀个向量,代码每个词出现的次数。
接下来就聚类吧~Hierachical clustering :维基百科:kmeans clustering :维基百科:kmedoids clustering :维基百科:虽然上⾯三种算法都很好理解,但是这都是基础算法,要想深⼊,还有很多很多相关问题需要解决,⽐如k如何设置;随机选取初始点的问题等等,⽽且如何选取好⽤的聚类算法也值得商榷。
github代码位置:clusterBase.py ⽤来导⼊数据from math import sqrtdef importData(FIFE = 'blogdata.txt') :blogwords = []blognames = []f = open(FIFE, 'r')words = f.readline().split()#//remove '\r\n'for line in f:blog = line[:-2].split('\t')blognames.append(blog[0])blogwords.append([int(word_c) for word_c in blog[1:]] )return blogwords,blognamesdef pearson_distance(vector1, vector2) :"""Calculate distance between two vectors using pearson methodSee more : /wiki/Pearson_product-moment_correlation_coefficient"""sum1 = sum(vector1)sum2 = sum(vector2)sum1Sq = sum([pow(v,2) for v in vector1])sum2Sq = sum([pow(v,2) for v in vector2])pSum = sum([vector1[i] * vector2[i] for i in range(len(vector1))])num = pSum - (sum1*sum2/len(vector1))den = sqrt((sum1Sq - pow(sum1,2)/len(vector1)) * (sum2Sq - pow(sum2,2)/len(vector1)))if den == 0 : return 0.0return 1.0 - num/denhierachiclaCluster.py注意distances字典的使⽤,可以减少⼤量重复的计算另外这个聚类算法,最终⽣成的是⼀颗树形结构。
聚类分析—K-means and K-medoids聚类要点

2018/10/5
在图像分割上的简单应用(续)
分割后的效果
注:最大迭代次数为20次,需运行多次才有可能得到较好的效果。
2018/10/5
在图像分割上的简单应用(续)
例 2:
注:聚类中心个数为5,最大迭代次数为10。
2018/1Байду номын сангаас/5
k-平均聚类算法(续)
优点: 相对有效性: O(tkn),
其中 n 是对象数目, k 是簇数目, t 是迭代次数; 通常, k, t << n.
2018/10/5
PAM
PAM (Partitioning Around Medoids) (Kaufman and Rousseeuw, 1987)
是最早提出的k-中心点聚类算法 基本思想:
随机选择k个代表对象
反复地试图找出更好的代表对象: 分析所有可能的对象对,每个对 中的一个对象被看作是代表对象, 而另一个不是. 对可能的各种组合, 估算聚类结果的质量
2018/10/5
k-中心点聚类方法(续)
找聚类中的代表对象(中心点)
PAM (Partitioning Around Medoids, 1987)
首先为每个簇随意选择选择一个代表对象, 剩余的对象根 据其与代表对象的距离分配给最近的一个簇; 然后反复地 用非代表对象来替代代表对象,以改进聚类的质量 PAM 对于较小的数据集非常有效, 但不能很好地扩展到大 型数据集
k-平均值(MacQueen’67): 每个簇用该簇中对象的平均值来表示
k-中心点或 PAM (Partition around medoids) (Kaufman & Rousseeuw’87): 每个簇用接近聚类中心的一个对象来表示
基于差分隐私保护的KDCK-medoids动态聚类算法

基于差分隐私保护的KDCK-medoids动态聚类算法
马银方;张琳
【期刊名称】《计算机科学》
【年(卷),期】2016(043)0z2
【摘要】K-medoids算法对初始中心点敏感,不能有效地对动态数据进行聚类,且需要对相关的隐私数据进行保护.针对这些问题,提出了基于差分隐私保护的KDCK-medoids动态聚类算法.该算法在采用差分隐私保护技术的基础上将KD-树优化选取出的k个聚类中心和增量数据相结合建立新的KD-树,然后采用近邻搜索策略将增量数据分配到与其相应的聚类簇中,从而完成最终的动态聚类.通过实验分别对小数据集和多维的大数据集的聚类准确率及运行时间进行了分析,同时也对采用差分隐私保护技术的KDCK-medoids算法在不同数据集上的有效性进行了评估.实验结果表明,基于差分隐私保护的KDCK-medoids动态聚类算法能够在实现隐私保护的同时快速高效地处理增量数据的动态聚类问题.
【总页数】5页(P368-372)
【作者】马银方;张琳
【作者单位】南京邮电大学计算机学院南京210003;南京邮电大学计算机学院南京210003
【正文语种】中文
【中图分类】TP393
【相关文献】
1.基于差分隐私保护的DP-DBScan聚类算法研究 [J], 吴伟民;黄焕坤
2.基于差分隐私保护的DPk-medoids聚类算法 [J], 高瑜;田丰;吴振强
3.基于拉普拉斯机制的差分隐私保护k-means++聚类算法研究 [J], 傅彦铭;李振铎
4.基于差分隐私保护的谱聚类算法 [J], 郑孝遥;陈冬梅;刘雨晴;尤浩;汪祥舜;孙丽萍
5.基于B+树索引的动态社会网络差分隐私保护 [J], 刘振鹏;王烁;贺玉鹏;李小菲因版权原因,仅展示原文概要,查看原文内容请购买。
k模检测标准-概念解析以及定义

k模检测标准-概述说明以及解释1.引言1.1 概述概述部分的内容:在如今的信息时代,数据分析和机器学习已经成为了各个行业中不可或缺的一部分。
而在数据分析过程中,我们常常需要对数据进行聚类和分类的操作,以便更好地理解和利用这些数据。
而k-均值聚类算法是一种常用的数据聚类算法,它可以将数据集分为k个不相交的簇,每个簇代表一类数据。
而为了确保聚类结果的准确性和可靠性,我们需要使用k-均值聚类算法的标准来检测聚类效果。
本文就是要介绍和讨论这些k-均值聚类算法的检测标准。
通过对不同的检测标准的分析与比较,我们可以选择适合当前数据集的合适的检测标准,帮助我们评估聚类结果的质量和可靠性。
在接下来的章节中,我们将首先简要介绍文章的结构和目的,然后详细讨论k-均值聚类算法中的三个要点:第一个要点是聚类中心的选择,第二个要点是簇的分配和更新,第三个要点是聚类结果的评估。
最后,我们将在结论部分对本文进行总结,并给出一些关于k-均值聚类算法的实际应用和未来研究的建议。
本文将为读者提供全面的理论和实践指南,帮助大家更好地理解和使用k-均值聚类算法,并希望本文对于相关领域的研究者和从业者有所启发和帮助。
1.2文章结构文章结构部分的内容应该包含对整篇文章的章节划分和内容安排的介绍。
下面是一个可能的内容示例:2. 文章结构本篇文章主要包括三个大的部分,分别是引言、正文和结论。
以下是对各个部分的详细描述:2.1 引言部分引言部分是整篇文章的开端,旨在向读者介绍本文的主题和背景。
首先,我们将提供对k模检测标准的概述,解释该标准的含义和应用场景。
接着,通过介绍本文的结构和目的,读者可以清晰地了解整篇文章的内容和组织方式。
最后,我们将对整个引言部分进行总结,为接下来的正文做好铺垫。
2.2 正文部分正文部分是本篇文章的核心部分,主要阐述k模检测标准的相关要点。
我们将以三个要点为主线展开讨论。
首先,在第一个要点中,我们将介绍k模检测标准的背景和起源,并详细解释其相关的理论基础和概念。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西电数据挖掘大作业k-m e a n s和k-m e d o i d s -标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII题目:数据挖掘学院:电子工程学院专业:智能科学与技术学生姓名: **学号: 02115***k-means实验报告一、waveform数据1、算法描述1.从数据集中任意选取k个赋给初始的聚类中心c1,c2, …, c k;2.对数据集中的每个样本点x i,计算其与各个聚类中心c j的欧氏距离并获取其类别标号:3.按下式重新计算k个聚类中心;重复步骤2和步骤3,直到达到最大迭代次数为止2、实验结果二、图像处理1、算法描述同上;2、实验结果代码:k_means:%%%%%%%%%K_means%%%%%%%% %%%%%%%%%函数说明%%%%%%%%%输入:% sample——样本集;% k ——聚类数目;%输出:% y ——类标(从0开始) % cnew ——聚类中心% n ——迭代次数function [y cnew n]=k_means(sample,k)[N V]=size(sample); %N为样本的个数 K为样本的维数y=zeros(N,1); %记录样本类标dist=zeros(1,k);rand_num=randperm(N);cnew=(sample(rand_num(1,1:k),:));%随机初始化聚类中心cold=zeros(k,V);n=0;while(cold~=cnew)cold=cnew;n=n+1; %记录迭代次数%对样本进行重新分类for i=1:Nfor j=1:kif(V==1)dist(1,j)=abs(sample(i,:)-cold(j,:));elsedist(1,j)=norm(sample(i,:)-cold(j,:));endendfor s=1:kif(dist(1,s)==min(dist))y(i,1)=s-1;endendend%更新聚类中心cnew=zeros(k,V);flag=zeros(k,1);for i=1:Nfor j=1:kif (y(I,1)==j-1)flag(j,1)=flag(j,1)+1;cnew(j,☺=cnew(j,☺+sample(I,☺;endendendfor j=1:kcnew(j,☺=cnew(j,☺/flag(j,1);endendk_means_waveform:clear;clc;%%%%%%%%%数据读入%%%%%%%data=load('G:\西电\2014大三下\大作业\Data Mining\k_means\waveform.data');[N K]=size(data); %数据集的数目data0=zeros(1,K);data1=zeros(1,K);data2=zeros(1,K);for i=1:Nif(data(i,K)==0)data0=cat(1,data(i,:),data0);elseif(data(i,K)==1)data1=cat(1,data(i,:),data1);elsedata2=cat(1,data(i,:),data2);endendsample=cat(1,data0(1:100,:),data1(1:100,:),data2(1:100,:));label=sample(:,K); %样本的正确类标sample=sample(:,1:K-1); %样本集k=3; %聚类中心的数目%%%%%%%%%K_means%%%%%%%%[y cnew n]=k_means(sample,k);%%%%%%%%%%正确率统计%%%%%%%sum=zeros(1,6);[N V]=size(sample);for i=1:Nif(y(i,1)==label(i,1))sum(1,1)=sum(1,1)+1;endendfor i=1:Nif((y(i,1)+label(i,1))==2)sum(1,2)=sum(1,2)+1;endendfor i=1:Nif(((y(i,1)==0)&&(label(i,1)==0))||((y(i,1)==1)&&label(i,1)==2)||((y( i,1)==2)&&label(i,1)==1))sum(1,3)=sum(1,3)+1;endendfor i=1:Nif(((y(i,1)==0)&&(label(i,1)==1))||((y(i,1)==1)&&label(i,1)==0)||((y( i,1)==2)&&label(i,1)==2))sum(1,4)=sum(1,4)+1;endendfor i=1:Nif(((y(i,1)==0)&&(label(i,1)==1))||((y(i,1)==1)&&label(i,1)==2)||((y( i,1)==2)&&label(i,1)==0))sum(1,5)=sum(1,5)+1;endendfor i=1:Nif(((y(i,1)==0)&&(label(i,1)==2))||((y(i,1)==1)&&label(i,1)==0)||((y( i,1)==2)&&label(i,1)==1))sum(1,6)=sum(1,6)+1;endendsum=sum/N;creatrate=max(sum);disp('循环次数:');disp(n);disp('聚类中心为:');disp(cnew);disp('正确率为:');disp(creatrate);k_means_picture:clear;clc;%%%%%%%%%数据读入%%%%%%%I1=imread('G:\西电\2014大三下\大作业\Data Mining\ k_means\lena.jpg');I2=rgb2gray(I1);%转化为灰度图像I=im2double(I2);[num v]=size(I);sample=reshape(I,v*num,1);%样本集k=2; %聚类中心的数目%%%%%%%%%K_means%%%%%%%%[y cnew n]=k_means(sample,k);%%%%%%%%v%%%%%%%%I3=sample;if(cnew(1,1)>=cnew(2,1))F0=255;F1=0;F0=0;F1=255;endfor i=1:num*vif(y(i,1)==0)I3(i,1)=F0;elseI3(i,1)=F1;endendI3=reshape(I3,num,v);figure(1)subplot(1,3,1);imshow(I1);title('原图像');subplot(1,3,2);imshow(I2);title('灰度图像');subplot(1,3,3);imshow(I3);title('二值化图像');k_medoids实验报告一、 waveform数据1、算法描述(1)随机选择k个对象作为初始的代表对象;(2) repeat(3) 指派每个剩余的对象给离它最近的代表对象所代表的簇;(4) 随意地选择一个非代表对象Orandom;(5) 计算用Orandom代替Oj的总代价S;(6) 如果S<0,则用Orandom替换Oj,形成新的k个代表对象的集合;(7) until 不发生变化2、实验结果二、图像处理1、算法描述同上;2、实验结果代码:k_medoids:%%%%%%%%k_medoids%%%%%%%%%%%%%%%%%º函数说明%%%%%%%%%%输入:% sample——数据集% k——聚类数目;%输出:% y——类标;% med ——聚类中心点function [y med]=k_medoids(sample,k)[N V]=size(sample); %N为样本数目 V为样本为数%聚类中心的随机初始化rbowl=randperm(N);med=sample(rbowl(1,1:k),:);temp=zeros(N,2);dist=zeros(1,k);index=rbowl(1,k);Eold=0;Enew=1000;while(abs(Enew-Eold)>0.001)%将所有样本分配到最近的代表点for i=1:Nfor j=1:kdist(1,j)=norm(sample(i,:)-med(j,:));endtemp(i,1)=min(dist);for s=1:kif(dist(1,s)==temp(i,1))temp(i,2)=s;endendendy=temp(:,2);Eold=sum(temp(:,1));%随机的选择一个非代表点,生成新的代表点集合index=index+1;med_temp=med;E=zeros(1,k);for j=1:kmed_temp(j,:)=sample(index,:);%将所有样本分配到最近的代表点for i=1:Nfor t=1:kdist(1,t)=norm(sample(i,:)-med_temp(t,:));endtemp(i,1)=min(dist);for s=1:kif(dist(1,s)==temp(i,1))temp(i,2)=s;endendendE(1,j)=sum(temp(:,1));endEnew=min(E);for t=1:kif(E(1,t)==Enew)obest=t;endendif(Enew<Eold)med(obest,:)=sample(index,:);elseEnew=Eold;endendk_medoids_waveform:clear;clc;%%%%%%%%%Êý¾Ý¶ÁÈë%%%%%%%data=load(' G:\西电\2014大三下\大作业\Data Mining\ k_medoids\waveform-+noise.data');[N K]=size(data); %数据集的数目data0=zeros(1,K);data1=zeros(1,K);data2=zeros(1,K);for i=1:Nif(data(i,K)==0)data0=cat(1,data(i,:),data0);elseif(data(i,K)==1)data1=cat(1,data(i,:),data1);elsedata2=cat(1,data(i,:),data2);endendsample=cat(1,data0(1:100,:),data1(1:100,:),data2(1:100,:));label=sample(:,K); %Ñù±¾µÄÕýÈ·Àà±êsample=sample(:,1:K-1); %Ñù±¾¼¯k=3; %聚类中心的数目%%%%%%%%%%k_medoids%%%%%%%[y med]=k_medoids(sample,k);%%%%%%%%%%正确率统计Æ%%%%%%%sum=zeros(1,6);[N V]=size(sample);for i=1:Ny(i,1)=y(i,1)-1;endfor i=1:Nif(y(i,1)==label(i,1))sum(1,1)=sum(1,1)+1;endendfor i=1:Nif((y(i,1)+label(i,1))==2)sum(1,2)=sum(1,2)+1;endendfor i=1:Nif(((y(i,1)==0)&&(label(i,1)==0))||((y(i,1)==1)&&label(i,1)==2)||((y( i,1)==2)&&label(i,1)==1))sum(1,3)=sum(1,3)+1;endendfor i=1:Nif(((y(i,1)==0)&&(label(i,1)==1))||((y(i,1)==1)&&label(i,1)==0)||((y( i,1)==2)&&label(i,1)==2))sum(1,4)=sum(1,4)+1;endendfor i=1:Nif(((y(i,1)==0)&&(label(i,1)==1))||((y(i,1)==1)&&label(i,1)==2)||((y( i,1)==2)&&label(i,1)==0))sum(1,5)=sum(1,5)+1;endendfor i=1:Nif(((y(i,1)==0)&&(label(i,1)==2))||((y(i,1)==1)&&label(i,1)==0)||((y( i,1)==2)&&label(i,1)==1))sum(1,6)=sum(1,6)+1;endendsum=sum/N;creatrate=max(sum);disp('¾ÛÀàÖÐÐÄΪ£º');disp(med);disp('ÕýÈ·ÂÊΪ£º');disp(creatrate);k_medoids_picture:clear;clc;%%%%%%%%%Êý¾Ý¶ÁÈë%%%%%%%I0=imread(' G:\西电\2014大三下\大作业\Data Mining\ k_medoids\lena.jpg'); D=0.001;I1=imnoise(I0,'gaussian',0,D);%加噪声I2=rgb2gray(I1);%转化为灰度图像I=im2double(I2);[num v]=size(I);sample=reshape(I,v*num,1);%Ñù±¾¼¯k=2; %¾ÛÀàÖÐÐĵÄÊýÄ¿%%%%%%%%%K_means%%%%%%%%[y med]=k_medoids(sample,k); %%%%%%%%图像显示¾%%%%%%%%I3=sample;if(med(1,1)>=med(2,1))F0=255;F1=0;elseF0=0;F1=255;endfor i=1:num*vif(y(i,1)==1)I3(i,1)=F0;elseI3(i,1)=F1;endendI3=reshape(I3,num,v);figure(1)subplot(1,4,1);imshow(I0);title('原图像');subplot(1,4,2);imshow(I1);title('加噪声后的图像');subplot(1,4,3);imshow(I2);title('灰度图像');subplot(1,4,4);imshow(I3);title('二值化图像');。
