模式识别fisher判别
【线性判别】Fisher线性判别(转)

【线性判别】Fisher线性判别(转)今天读paper遇到了Fisher线性判别的变体,所以来学习⼀下,所以到时候⼀定要把PRMl刷⼀遍呀在前⽂《贝叶斯决策理论》中已经提到,很多情况下,准确地估计概率密度模型并⾮易事,在特征空间维数较⾼和样本数量较少的情况下尤为如此。
实际上,模式识别的⽬的是在特征空间中设法找到两类(或多类)的分类⾯,估计概率密度函数并不是我们的⽬的。
前⽂已经提到,正态分布情况下,贝叶斯决策的最优分类⾯是线性的或者是⼆次函数形式的,本⽂则着重讨论线性情况下的⼀类判别准则——Fisher判别准则。
为了避免陷⼊复杂的概率的计算,我们直接估计判别函数式中的参数(因为我们已经知道判别函数式是线性的)。
⾸先我们来回顾⼀下线性判别函数的基本概念:应⽤统计⽅法解决模式识别问题时,⼀再碰到的问题之⼀就是维数问题。
在低维空间⾥解析上或计算上⾏得通的⽅法,在⾼维空间⾥往往⾏不通。
因此,降低维数有时就会成为处理实际问题的关键。
问题描述:如何根据实际情况找到⼀条最好的、最易于分类的投影线,这就是Fisher判别⽅法所要解决的基本问题。
考虑把d维空间的样本投影到⼀条直线上,形成⼀维空间,即把维数压缩到⼀维。
然⽽,即使样本在d维空间⾥形成若⼲紧凑的互相分得开的集群,当把它们投影到⼀条直线上时,也可能会是⼏类样本混在⼀起⽽变得⽆法识别。
但是,在⼀般情况下,总可以找到某个⽅向,使在这个⽅向的直线上,样本的投影能分得开。
下图可能会更加直观⼀点:从d维空间到⼀维空间的⼀般数学变换⽅法:假设有⼀集合Г包含N个d维样本x1, x2, …, xN,其中N1个属于ω1类的样本记为⼦集Г1, N2个属于ω2类的样本记为⼦集Г2 。
若对xn的分量做线性组合可得标量:yn = wTxn, n=1,2,…,N这样便得到N个⼀维样本yn组成的集合,并可分为两个⼦集Г1’和Г2’ 。
实际上,w的值是⽆关紧要的,它仅是yn乘上⼀个⽐例因⼦,重要的是选择w的⽅向。
模式识别FISHER线性判别实验

模式识别FISHER线性判别实验
人工知能领域中的模式识别是计算机实现人类识别物体的能力的一种
技术。
它的主要目的是根据给定模式的样本及其特征,自动识别出新的样
本的特征并做出判断。
其中最著名的技术之一就是FISHER线性判别法。
FISHER线性判别法基于正态分布理论,通过计算样本的统计特征来
分类,它是一种基于参数的最优分类算法。
算法的基本思想是通过计算两
个类别的最大类间差异度,以及最小类内差异度,来有效地分类样本。
具
体而言,FISHER线性判别法即求出一个线性超平面,使这个超平面把样
本区分开来,使样本离类中心向量之间的距离最大,同时使类中心向量之
间的距离最小。
FISHER线性判别法的具体实现过程如下:
1.准备好建立模型所需要的所有数据:训练样本集,其样本特征与对
应的类标号。
2.确定每个类的类中心向量c_1,c_2,…,c_m,其中m为类的数目。
3.根据类中心向量求出类间离散度矩阵S_b和类内离散度矩阵S_w。
4.将S_b与S_w相除,得到S_b/S_w,从而求出矩阵的最大特征值
λ_1及最小特征值λ_n。
5.将最大特征值λ_1进行特征值分解,求出其特征向量w,求出判
定函数:
f(x)=w·x+w_0。
6.根据判定函数,将样本进行分类。
魏尔斯特拉斯判别法

魏尔斯特拉斯判别法
拉斯判别法(Fisher discrimination),又称魏尔斯-拉普拉斯判别式,是概率论中的一种模式识别算法。
这种方法源于一九三五年爱因斯坦颁奖典礼上提出的魏尔斯定理,由Ronald A. Fisher利用贝叶斯定理建立而成。
该方法的基本思想是对类的期望总密度进行估计,在此基础上构造出把类别隔离开来的线性判别式,用来识别新样本。
它以类内样本的类内散度矩阵(within-class scatter matrix)和类间散度矩阵(between-class scatter matrix)为依据,构建决策边界,此处的决策边界满足最优类内距离和最大类间距离的性质。
拉斯判别法属于线性判别(linear discrimination)的一种,它的特点是用一个线性判别式来区分类型,具有计算简单、实现方便等特点,因而被人们广泛使用,拉斯判别法也称为线性判别分析(linear discriminant analysis, LDA)。
fisher判别式

Fisher 线性判别式前面讲过的感知器准则、最小平方和准则属于用神经网络的方法解决分类问题。
下面介绍一种新的判决函数分类方法。
由于线性判别函数易于分析,关于这方面的研究工作特别多。
历史上,这一工作是从R.A.Fisher 的经典论文(1936年)开始的。
我们知道,在用统计方法进行模式识别时,许多问题涉及到维数,在低维空间行得通的方法,在高维空间往往行不通。
因此,降低维数就成为解决实际问题的关键。
Fisher 的方法,实际上涉及维数压缩。
如果要把模式样本在高(d )维的特征向量空间里投影到一条直线上,实际上就是把特征空间压缩到一维,这在数学上容易办到。
另外,即使样本在高维空间里聚集成容易分开的群类,把它们投影到一条任意的直线上,也可能把不同的样本混杂在一起而变得无法区分。
也就是说,直线的方向选择很重要。
在一般情况下,总可以找到某个最好的方向,使样本投影到这个方向的直线上是最容易分得开的。
如何找到最好的直线方向,如何实现向最好方向投影的变换,是Fisher 法要解决的基本问题。
这个投影变换就是我们寻求的解向量*w 。
1.线性投影与Fisher 准则函数在21/w w 两类问题中,假定有n 个训练样本),....,2,1(n k x k =其中1n 个样本来自i w 类型,2n 个样本来自j w 类型,21n n n +=。
两个类型的训练样本分别构成训练样本的子集1X 和2X 。
令:k Tk x w y =,n k ,...,2,1= (4.5-1)k y 是向量k x 通过变换w 得到的标量,它是一维的。
实际上,对于给定的w ,k y 就是判决函数的值。
由子集1X 和2X 的样本映射后的两个子集为1Y 和2Y 。
因为我们关心的是w 的方向,可以令1||||=w ,那么k y 就是k x 在w 方向上的投影。
使1Y 和2Y 最容易区分开的w 方向正是区分超平面的法线方向。
如下图:图中画出了直线的两种选择,图(a)中,1Y 和2Y 还无法分开,而图(b)的选择可以使1Y 和2Y 区分开来。
基于主成分分析与Fisher判别分析法的矿井突水水源识别方法

基于主成分分析与Fisher判别分析法的矿井突水水源识别方法一、概述矿井突水作为矿山生产过程中的一大安全隐患,其准确识别对于预防突水事故、保障矿山安全生产具有重要意义。
传统的矿井突水水源识别方法往往依赖于经验判断和单一的水质指标分析,这些方法不仅效率低下,而且识别准确率难以保证。
开发一种高效、准确的矿井突水水源识别方法成为当前矿山安全领域亟待解决的问题。
主成分分析(PCA)和Fisher判别分析法是两种常用的数据处理和模式识别方法,它们在不同的领域中都得到了广泛的应用。
PCA通过降维的方式将多个指标转化为少数几个综合指标,这些综合指标能够反映原来指标的大部分信息,且相互独立,避免了信息的重叠。
而Fisher判别分析法则是一种线性分类器,通过求解最优的权向量和阈值,将样本投影到一条直线上,然后选择一个阈值将两类分开。
这两种方法的结合,可以实现对矿井突水水源的高效、准确识别。
本文将详细介绍基于主成分分析与Fisher判别分析法的矿井突水水源识别方法。
通过PCA对矿井突水水源的多项指标进行降维处理,提取出主要的综合指标。
利用Fisher判别分析法对这些综合指标进行分类判别,从而实现对矿井突水水源的准确识别。
通过实例验证和对比分析,证明该方法的可行性和优越性,为矿山安全生产提供有力的技术支持。
1. 矿井突水问题的严重性及其对矿井安全生产的影响矿井突水问题一直是采矿行业面临的一项重大挑战,其严重性不容忽视。
突水事件往往伴随着大量的地下水涌入矿山坑道,使得施工条件变得极为复杂,采矿成本大幅上升。
更为严重的是,突水不仅影响正常的采矿生产,甚至可能导致淹井事故的发生,给矿山工程和人员安全带来严重威胁。
在突水事故发生时,大量水流的涌入使得井巷和矿山设备遭受淹没,进而造成人员伤亡和财产损失。
突水事件还会对采矿生产造成直接影响,导致产量减少,甚至使部分矿区因无法继续开采而报废,给矿山的经济效益和资源利用带来巨大损失。
模式识别第四章线性判别函数优秀课件

g(x)=0, 可将其任意分类或拒绝
线性判别函数的几何意义
决策面(decision boundary)H方程:g(x)=0
向量w是决策面H的法向量
g(x)是点x到决策面H的距离的一种代数度量
w
x xp r
w w
,
g(x) r w
x2
x
r是x到H的垂直距离
r
x p是x在H 上的投影向量
xp
当 n 和 ( x p) 夹角小于90度时,即 x 在 n 指向的半空间中
当 n 和 ( x p) 夹角大于90度时,即 x 在 n 背向的半空间中
由于 w 0 ,故 nT ( x p) 和 wT x w0 同号
广义线性判别函数
线性判别函数是形式最为简单的判别函数, 但是它不能用于复杂情况。
模式识别问题就是根据模式X的n个特征来判 别模式属于ω1 ,ω2 , … , ωc 类中的那一类。
判别函数:表示类分界面的函数。
判别函数(续)
x2
•
•••••••••2 ••••••••••••1
o x1
两类的分类问题,它们的边界线就是一个判别函数
判别函数(续)
X轴
两类问题中线性不可分的实例
模式识别第四章线性判别函数
主要内容
引言 Fisher线性判别 感知器准则 最小平方误差准则 多类问题 分段线性判别函数
4.1 引言
分类器
x1
g1
功能结构
x2
g2
MAX
a(x)
基于样本的Bayes分类
. .
. . .
器:通过估计类条件 概率密度函数,设计
.
xn
gc
相应的判别函数
判别分析公式Fisher线性判别二次判别

判别分析公式Fisher线性判别二次判别判别分析是一种常用的数据分析方法,用于根据已知的类别信息,将样本数据划分到不同的类别中。
Fisher线性判别和二次判别是两种常见的判别分析方法,在实际应用中具有广泛的应用价值。
一、Fisher线性判别Fisher线性判别是一种基于线性变换的判别分析方法,该方法通过寻找一个合适的投影方向,将样本数据投影到一条直线上,在保持类别间离散度最大和类别内离散度最小的原则下实现判别。
其判别函数的计算公式如下:Fisher(x) = W^T * x其中,Fisher(x)表示Fisher判别函数,W表示投影方向的权重向量,x表示样本数据。
具体来说,Fisher线性判别的步骤如下:1. 计算类别内离散度矩阵Sw和类别间离散度矩阵Sb;2. 计算Fisher准则函数J(W),即J(W) = W^T * Sb * W / (W^T * Sw * W);3. 求解Fisher准则函数的最大值对应的投影方向W;4. 将样本数据投影到求得的最优投影方向上。
二、二次判别二次判别是基于高斯分布的判别分析方法,将样本数据当作高斯分布的观测值,通过估计每个类别的均值向量和协方差矩阵,计算样本数据属于每个类别的概率,并根据概率大小进行判别。
二次判别的判别函数的计算公式如下:Quadratic(x) = log(P(Ck)) - 0.5 * (x - μk)^T * Σk^-1 * (x - μk)其中,Quadratic(x)表示二次判别函数,P(Ck)表示类别Ck的先验概率,x表示样本数据,μk表示类别Ck的均值向量,Σk表示类别Ck的协方差矩阵。
具体来说,二次判别的步骤如下:1. 估计每个类别的均值向量μk和协方差矩阵Σk;2. 计算每个类别的先验概率P(Ck);3. 计算判别函数Quadratic(x);4. 将样本数据划分到概率最大的类别中。
判别分析公式Fisher线性判别和二次判别是常见的判别分析方法,它们通过对样本数据的投影或概率计算,实现对样本数据的判别。
模式识别K近邻和FISHER

(仅一块截屏中就有 8 处分类错误。) 附全部代码: import java.io.*; public class Kalg { public static final int N = 40; public static final int M = 4; public static final int K = 50; public static final int L = 80; public static final int f = 30; public static void main(String[] args) { String s = null; double arr[][] = new double[N][M]; double arr2[][] = new double[N][M];
对 50 个 Iris-versicolor 全部分类正确,对 Iris-virginica 仅有一处分类错误。综合正确率达到 99%。 k = 2 时,出现了数个无法区分的样本以及被错分的样本。统计综合正确率为 93%。 以下为截图。(共一百组待测数据,截屏仅显示部分)
依次类推分别验证了 k = 3,4,5...,正确率分别为 94%,94%,95%...,总体来说正确率在 93% 到 95%之间,但是当 k 取值比较大时,如取 20,25,正确率就会有所下降,有时可以到到 了 90%之下。(共一百组待测数据,截屏仅显示部分)
String daice_arrstr2[] = s.split(","); for (int j = 0; j < daice_arrstr2.length; j++) { daice_arr2[row4][j] = Double.parseDouble(daice_arrstr2[j]); } row4++; } br4.close(); } catch (FileNotFoundException e) { // TODO Auto-generated catch block e.printStackTrace(); } catch (IOException e) { // TODO Auto-generated catch block e.printStackTrace(); } for (int i = 0; i < K; i++) check(arr, arr2, daice_arr[i][0], daice_arr[i][1], daice_arr[i][2], daice_arr[i][3], f); System.out.println("**********above is Iris-versicolor below is Iris-virginica**********"); for (int i = 0; i < K; i++) check(arr, arr2, daice_arr2[i][0], daice_arr2[i][1], daice_arr2[i][2], daice_arr2[i][3], f); } public static void check(double[][] a, double[][] b, double x, double y, double z, double h, int k) { double ARR[] = new double[N]; double ARR2[] = new double[N]; double temp; int flag = 0; int arr = 0; int arr2 = 0; for (int i = 0; i < N; i++) ARR[i] = (a[i][0] - x) * (a[i][0] - x) + (a[i][1] - y) * (a[i][1] - y) + (a[i][2] - z) * (a[i][2] - z) + (a[i][3] - h) * (a[i][3] - h); for (int i = 0; i < N; i++) for (int j = 0; j < N - i - 1; j++) if (ARR[j] > ARR[j + 1]) { temp = ARR[j]; ARR[j] = ARR[j + 1];
模式识别Fisher线性判别实验

模式识别Fisher线性判别实验实验三 Fisher线性判别实验姓名:徐维坚学号:2220103484 日期:2012/7/7 一、实验目的:1)加深对Fisher线性判别的基本思想的认识和理解。
2)编写实现Fisher线性判别准则函数的程序。
二、实验原理:1.基本原理:一般情况下,我们总可以找到某个方向,使得这个方向的直线上,样本的投影能分开的最好,而Fisher法所要解决的基本问题就是找到这条最好的、最易于分类的投影线。
X先从d维空间到一维空间的一维数学变换方法。
假设有一集合包含N个d维样本,其中个属于类的样本记为子集,个属于类的样本记为。
x,x,...,x,N,XNX212N11122若对的分量做线性组合可得标量 xN T, n,1,2,...,Ny,wxinn这样便得到N个一维样本组成的集合,并可分为两个子集和。
的绝对值是无关ywYYn12紧要的,它仅使乘上一个比例因子,重要的是选择的方向,从而转化为寻找最好的投ywn*w影方向,是样本分开。
2.基本方法:先定义几个基本参量:m(1)各类样本均值向量 i1m,x,i,1,2 ,iNx,XiSS(2)样本类内离散度矩阵和总类内离散度矩阵 i,TS,(x,m)(x,m),i,1,2 i,iix,XiS,S,S ,12S(3)样本类间离散度矩阵 bTS,(m,m)(m,m) 1212b(m,m)我们希望投影后,在低维空间里个样本尽可能的分开些,即希望两类均值越大越12Authord: Vivid Xu;好,同时希望各类样本内部尽量密集,即越小越好。
因此,我们定义Fisher 准则函数为 Si2,(mm)12 ,J(w)F,SS12但不显含,因此必须设法将变成的显函数。
wwJ(w)J(w)FF由式子111TTTm,y,wx,w(x),wm ,,,iiNNN,,,yYxXxXiiiiii2TT2TTT (m,m),(wm,wm),w(m,m)(m,m)w,wSw12121212bTTTTT22S,(y,m),(wx,wm),w(x,m)(x,m)w,wSw ,,iiiiii,,yYyYii从而得到TwSwbJw, (),FTwSw,*w采用Lagrange乘子法求解它的极大值TT L(w,,),wSw,,(wSw,c),b**对其求偏导,得,即 Sw,,Sw,0b,** Sw,,Swb,从而我们很容易得到*,1*,1T* ,w,S(Sw),S(m,m)R,其中R,(m,m)w,,b1212R*1,w,S(m,m) ,12,R/,忽略比例因子,得*1, w,S(m,m),12这就是我们Fisher准则函数J(w)取极大值时的解。
fisher判别函数

Fisher判别函数,也称为线性判别函数(Linear Discriminant Function),是一种经典的模式识别方法。
它通过将样本投影到一维或低维空间,将不同类别的样本尽可能地区分开来。
一、算法原理:Fisher判别函数基于以下两个假设:1.假设每个类别的样本都服从高斯分布;2.假设不同类别的样本具有相同的协方差矩阵。
Fisher判别函数的目标是找到一个投影方向,使得同一类别的样本在该方向上的投影尽可能紧密,而不同类别的样本在该方向上的投影尽可能分开。
算法步骤如下:(1)计算类内散度矩阵(Within-class Scatter Matrix)Sw,表示每个类别内样本之间的差异。
Sw = Σi=1 to N (Xi - Mi)(Xi - Mi)ᵀ,其中Xi 表示属于类别i 的样本集合,Mi 表示类别i 的样本均值。
(2)计算类间散度矩阵(Between-class Scatter Matrix)Sb,表示不同类别之间样本之间的差异。
Sb = Σi=1 to C Ni(Mi - M)(Mi - M)ᵀ,其中 C 表示类别总数,Ni 表示类别i 中的样本数量,M 表示所有样本的均值。
(3)计算总散度矩阵(Total Scatter Matrix)St,表示所有样本之间的差异。
St =Σi=1 to N (Xi - M)(Xi - M)ᵀ(4)计算投影方向向量w,使得投影后的样本能够最大程度地分开不同类别。
w= arg max(w) (wᵀSb w) / (wᵀSw w),其中w 表示投影方向向量。
(5)根据选择的投影方向向量w,对样本进行投影。
y = wᵀx,其中y 表示投影后的样本,x 表示原始样本。
(6)通过设置一个阈值或使用其他分类算法(如感知机、支持向量机等),将投影后的样本进行分类。
二、优点和局限性:Fisher判别函数具有以下优点:•考虑了类别内和类别间的差异,能够在低维空间中有效地区分不同类别的样本。
模式识别——感知器准则与Fisher算法实验-推荐下载

1、复习感知器算法; 2、写出实现批处理感知器算法的程序 1)从 a=0 开始,将你的程序应用在 ω1 和 ω2 的训练数据上。记下收敛的步 数。 2)将你的程序应用在 ω2 和 ω3 类上,同样记下收敛的步数。 3)试解释它们收敛步数的差别。 3、提高部分:ω3 和 ω4 的前 5 个点不是线性可分的,请手工构造非线性映 射,使这些点在映射后的特征空间中是线性可分的,并对它们训练一个感
本实验通过编制程序让初学者能够体会 Fisher 线性判别的基本思路,理解线性判别的 基本思想,掌握 Fisher 线性判别问题的实质。
2、[实验内容]
1.实验所用样本数据如表 2-1 给出(其中每个样本空间(数据)为两维, x 1 表示第一维的值、x 2 表示第二维的值),编制程序实现 ω1、ω 2 类 ω 2、ω 3 类的分类。分析分类器算法的性能。
x1 X
xd
根据 Fisher 选择投影方向 W 的原则,即使原样本向量在该方向上的投影能兼顾类间分
布尽可能分开,类内样本投影尽可能密集的要求,用以评价投影方向 W 的函数为:
J F (W ) (m~S~112m~S~222)2
W * SW1(m1 m2 )
上面的公式是使用 Fisher 准则求最佳法线向量的解,该式比较重要。另外,该式这种
2
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置2试时32卷,3各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并25工且52作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
实验1 Fisher线性判别实验
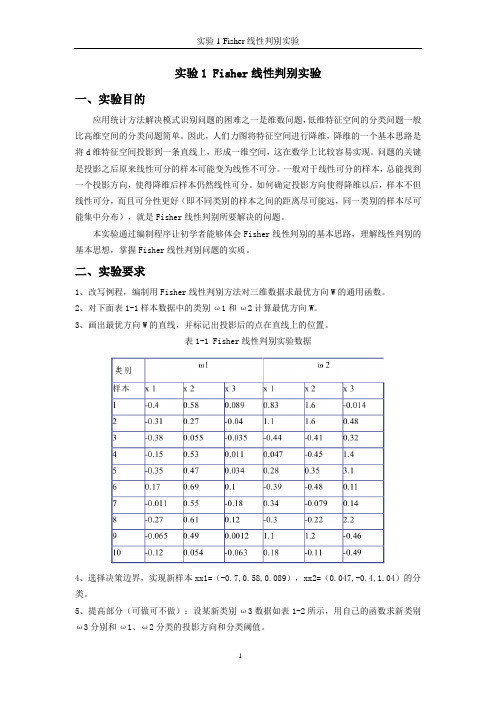
实验1 Fisher线性判别实验一、实验目的应用统计方法解决模式识别问题的困难之一是维数问题,低维特征空间的分类问题一般比高维空间的分类问题简单。
因此,人们力图将特征空间进行降维,降维的一个基本思路是将d维特征空间投影到一条直线上,形成一维空间,这在数学上比较容易实现。
问题的关键是投影之后原来线性可分的样本可能变为线性不可分。
一般对于线性可分的样本,总能找到一个投影方向,使得降维后样本仍然线性可分。
如何确定投影方向使得降维以后,样本不但线性可分,而且可分性更好(即不同类别的样本之间的距离尽可能远,同一类别的样本尽可能集中分布),就是Fisher线性判别所要解决的问题。
本实验通过编制程序让初学者能够体会Fisher线性判别的基本思路,理解线性判别的基本思想,掌握Fisher线性判别问题的实质。
二、实验要求1、改写例程,编制用Fisher线性判别方法对三维数据求最优方向W的通用函数。
2、对下面表1-1样本数据中的类别ω1和ω2计算最优方向W。
3、画出最优方向W的直线,并标记出投影后的点在直线上的位置。
表1-1 Fisher线性判别实验数据4、选择决策边界,实现新样本xx1=(-0.7,0.58,0.089),xx2=(0.047,-0.4,1.04)的分类。
5、提高部分(可做可不做):设某新类别ω3数据如表1-2所示,用自己的函数求新类别ω3分别和ω1、ω2分类的投影方向和分类阈值。
表1-2 新类别样本数据三、部分参考例程及其说明求取数据分类的Fisher投影方向的程序如下:其中w为投影方向。
clear %Removes all variables from the workspace.clc %Clears the command window and homes the cursor.% w1类训练样本,10组,每组为行向量。
w1=[-0.4,0.58,0.089;-0.31,0.27,-0.04;-0.38,0.055,-0.035;-0.15,0.53,0. 011;-0.35,0.47,0.034;...0.17,0.69,0.1;-0.011,0.55,-0.18;-0.27,0.61,0.12;-0.065,0.49,0.0012;-0 .12,0.054,-0.063];% w2类训练样本,10组,每组为行向量。
距离判别法贝叶斯判别法和费歇尔判别法的异同

距离判别法、贝叶斯判别法和费歇尔判别法的异同引言在模式识别领域,判别分析是一种常用的方法,用于将数据样本划分到不同的类别中。
距离判别法、贝叶斯判别法和费歇尔判别法是判别分析中常见的三种方法。
本文将对这三种方法进行比较,探讨它们的异同。
一、距离判别法距离判别法是一种基于距离度量的判别分析方法。
它的基本思想是通过计算样本点与各个类别中心的距离,将样本划分到距离最近的类别中。
常见的距离判别法有欧氏距离判别法和马氏距离判别法。
1. 欧氏距离判别法欧氏距离判别法是一种简单直观的距离判别方法。
它通过计算样本点与各个类别中心之间的欧氏距离,将样本划分到距离最近的类别中。
算法步骤如下: 1. 计算各个类别的中心点,即各个类别样本点的均值向量。
2. 对于给定的待判样本点,计算其与各个类别中心点的欧氏距离。
3. 将待判样本点划分到距离最近的类别中。
2. 马氏距离判别法马氏距离判别法考虑了各个类别的协方差矩阵,相比于欧氏距离判别法更加准确。
它通过计算样本点与各个类别中心之间的马氏距离,将样本划分到距离最近的类别中。
算法步骤如下: 1. 计算各个类别的中心点,即各个类别样本点的均值向量。
2. 计算各个类别的协方差矩阵。
3. 对于给定的待判样本点,计算其与各个类别中心点之间的马氏距离。
4. 将待判样本点划分到距离最近的类别中。
二、贝叶斯判别法贝叶斯判别法是一种基于贝叶斯理论的判别分析方法。
它的基本思想是通过计算后验概率,将样本划分到具有最高后验概率的类别中。
常见的贝叶斯判别法有贝叶斯最小错误率判别法和贝叶斯线性判别法。
1. 贝叶斯最小错误率判别法贝叶斯最小错误率判别法是一种理论上最优的判别方法。
它通过计算后验概率,将样本划分到具有最高后验概率的类别中。
算法步骤如下: 1. 计算各个类别的先验概率。
2. 计算给定样本点在各个类别下的条件概率。
3. 计算给定样本点在各个类别下的后验概率。
4. 将待判样本点划分到具有最高后验概率的类别中。
fisher判别的决策面方程

fisher判别的决策面方程Fisher判别的决策面方程是一种常用的分类算法,在模式识别和机器学习领域有着广泛的应用。
它通过线性判别分析来寻找一个最优的超平面,将不同类别的样本点尽可能地分开。
本文将介绍Fisher 判别的决策面方程及其原理,以及在实际应用中的一些注意事项。
Fisher判别的决策面方程可以表示为:w^T * x + b = 0其中,w是一个n维的权重向量,x是一个n维的输入向量,b是一个常数。
决策面方程将输入向量映射到一个超平面上,根据超平面上的位置来判断输入向量属于哪个类别。
Fisher判别的原理是寻找一个投影矩阵W,通过将输入数据映射到一个低维的子空间中,使得同类样本点的投影尽可能的靠近,不同类样本点的投影尽可能的分开。
具体的步骤如下:1. 计算各个类别的均值向量:m1, m2, ..., mc。
其中c表示类别的个数,m表示均值向量。
2. 计算类内离散度矩阵Sw和类间离散度矩阵Sb。
类内离散度矩阵Sw表示类别内部的散布情况,计算公式为:Sw = Σ(xi - mi)(xi - mi)^T类间离散度矩阵Sb表示不同类别之间的散布情况,计算公式为:Sb = Σ(Ni)(mi - m)(mi - m)^T其中,xi表示第i个样本点,mi表示第i类样本的均值向量,N 表示每个类别的样本个数,m表示所有样本的总体均值向量。
3. 计算特征值和特征向量。
将Sw的逆矩阵与Sb相乘,得到矩阵M = Sw^(-1) * Sb。
计算矩阵M的特征值和特征向量,选择特征值最大的k个特征向量作为投影矩阵W。
4. 根据投影矩阵W,将输入向量x映射到低维的子空间中。
计算投影后的向量y = W^T * x,其中y是一个k维的向量。
5. 根据投影后的向量y,通过线性判别分析找到一个最优的超平面。
根据训练样本的类别信息,通过最小化类内离散度和最大化类间离散度的准则函数来确定超平面的权重向量w和常数b。
Fisher判别的决策面方程可以通过上述步骤得到,它能够有效地将不同类别的样本点分开,提高分类的准确性。
fisher判别式 -回复

fisher判别式-回复【Fisher判别式】一种经典的模式分类方法在机器学习领域,有很多用于模式分类的方法,其中之一就是Fisher判别式。
Fisher判别式是通过线性变换将样本投影到低维空间中,从而实现样本分类的一种方法。
本文将详细介绍Fisher判别式的原理和步骤,并解释该方法在实际应用中的意义。
一、Fisher判别式的原理Fisher判别式的思想是通过找到一个投影方向,使得在该方向上不同类别的样本具有最大的类间距离(即类别间的差异最大),同时最小化类内的方差(即类别内的相似性最小)。
通过这样的投影,我们可以将高维的数据映射到低维的空间中,从而方便进行分类。
具体而言,Fisher判别式考虑了两个指标:类间散度矩阵和类内散度矩阵。
类间散度矩阵衡量的是不同类别之间的差异,而类内散度矩阵则衡量的是同一类别内样本的相似程度。
通过最大化类间散度矩阵与最小化类内散度矩阵的比值,我们可以得到Fisher判别式。
二、Fisher判别式的步骤1. 数据预处理:首先,我们需要收集样本数据,确保该数据集包含了不同的类别。
在收集样本数据后,我们需要对其进行预处理,包括特征选择和数据标准化等操作,以确保数据符合Fisher判别式的前提条件。
2. 计算类内散度矩阵和类间散度矩阵:在第一步的基础上,我们需要计算类内散度矩阵和类间散度矩阵。
类内散度矩阵可以通过计算各类别样本的协方差矩阵并进行加权求和得到,而类间散度矩阵可以通过计算不同类别之间均值差的协方差矩阵得到。
3. 计算投影方向:接下来,我们需要计算投影方向。
这可以通过求解广义特征值问题来实现,其中需要同时考虑类内散度矩阵和类间散度矩阵。
通过求解该特征值问题,我们可以得到投影方向。
4. 数据投影和分类:最后,我们需要将原始数据投影到低维空间中,并进行分类预测。
对于新的样本数据,我们可以使用投影方向将其映射到低维空间,并使用训练得到的分类器对其进行分类。
三、Fisher判别式的应用意义Fisher判别式在实际应用中具有广泛的应用意义。
(模式识别)Fisher线性判别

Fisher 判别
各类样本均值
1
mi Ni yi y, i 1, 2
样本类内离散度和总类内离散度
Si ( y mi )2, i 1,2 yi
样本类间离散度
Sw S1 S2 Sb (m1 m2 )2
以上定义描述d维空间样本点到一向量投影的分 散情况,因此也就是对某向量w的投影在w上的 分布。样本离散度的定义与随机变量方差相类似
Sw1(m1 m2 )R
w*
R
Sw1(m1
m2 )
Sw1(m1 m2 )
10
8
判别函数的确定
Fisher 判别
前面讨论了使Fisher准则函数极大的d维向 量w*的计算方法,判别函数中的另一项w0 (阈值)可采用以下几种方法确定:
w0
m1
2
m2
w0
N1m1 N2m2 N1 N2
m
w0
m1
m2 2
lnP(1) / P( 1 y wT x w0 0 x 2
Fisher线性判别
线性判别函数y=g(x)=wTx:
• 样本向量x各分量的线性加权 • 样本向量x与权向量w的向量点积 • 如果|| w ||=1,则视作向量x在向量w上的投
影
Fisher准则的基本原理:找到一个最合适的 投影轴,使两类样本在该轴上投影之间的距 离尽可能远,而每一类样本的投影尽可能紧 凑,从而使分类效果为最佳。
Si (x mi )(x mi )T , i 1,2 xi
Sw S1 S2
样本类间离散度矩阵Sb:Sb (m1 m2 )(m1 m2 )T
离散矩阵在形式上与协方差矩阵很相似,但协方 差矩阵是一种期望值,而离散矩阵只是表示有限 个样本在空间分布的离散程度
fisher感知器算法的原理

fisher感知器算法的原理Fisher感知器算法是一种模式识别算法,用于解决二分类问题。
它基于Fisher线性判别分析(Fisher Linear Discriminant Analysis,简称FLDA)的原理。
FLDA通过将数据投影到低维空间,使得同一类别的样本尽可能靠近,不同类别的样本尽可能分开。
具体来说,FLDA的目标是最大化类间方差与最小化类内方差的比值。
Fisher感知器算法将FLDA应用于二分类任务中。
它假设数据可以通过一个线性函数进行分类,即假设存在一个权重向量w 和偏置b,使得对于每个样本x,如果w·x + b > 0,则将其分类为正类,否则分类为负类。
Fisher感知器算法的训练过程如下:1. 初始化权重向量w和偏置b。
2. 选择一个样本x,计算 w·x + b 的值。
3. 如果 w·x + b > 0,并且x属于正类,则保持w和b不变。
4. 如果 w·x + b > 0,并且x属于负类,则将w向量朝负梯度方向调整,使得 w·x + b 变小。
5. 如果 w·x + b < 0,并且x属于负类,则保持w和b不变。
6. 如果 w·x + b < 0,并且x属于正类,则将w向量朝正梯度方向调整,使得 w·x + b 变大。
7. 重复步骤2-6,直到收敛或达到最大迭代次数。
在训练过程中,Fisher感知器算法会根据样本点的分类结果对参数进行调整,以找到一个能够最大化类间方差与最小化类内方差的超平面,从而实现对数据的最优分类。
fisher判别原理

fisher判别原理Fisher判别原理引言:Fisher判别原理是一种经典的模式分类方法,它基于统计学原理,通过对样本数据的分析,将数据投影到一条直线上,使得同类样本的投影点尽可能地紧密,不同类别的样本的投影点尽可能地分散。
本文将对Fisher判别原理进行详细介绍,并探讨其在实际应用中的优缺点。
一、Fisher判别原理的基本思想Fisher判别原理由英国统计学家R.A. Fisher在20世纪30年代提出。
它的基本思想是找到一个投影方向,使得同类样本的投影点尽可能地接近,不同类别的样本的投影点尽可能地远离。
具体来说,假设有两类样本,每个样本有n个特征,我们可以将每个样本表示为一个n维向量。
Fisher判别原理的目标是找到一个n维向量w,使得同类样本在w的投影上的方差尽可能小,不同类样本在w的投影上的方差尽可能大。
二、Fisher判别准则函数的推导为了找到最佳的投影方向w,可以定义Fisher判别准则函数J(w),该函数的表达式为同类样本投影点方差的倒数与不同类样本投影点方差之和的比值。
推导过程中,需要计算样本的均值和协方差矩阵,并利用最大化准则函数的方法求解最优方向w。
最终的解析解为特征值问题,求解该问题可以得到最佳的投影方向w。
三、Fisher判别原理的优缺点Fisher判别原理作为一种经典的模式分类方法,具有以下优点:1. Fisher判别原理能够有效地降低数据维度。
通过将n维样本数据投影到一维或低维空间,可以减少特征维度,提高计算效率。
2. Fisher判别原理对于噪声数据具有一定的鲁棒性。
由于Fisher判别准则函数考虑了类内方差和类间方差的比值,因此可以减少噪声对分类结果的影响。
然而,Fisher判别原理也存在一些缺点:1. Fisher判别原理假设样本数据满足高斯分布,如果样本不满足高斯分布,可能会导致分类效果下降。
2. Fisher判别原理只考虑了样本的线性投影,对于非线性分类问题效果有限。
模式识别练习题(简答和计算)

1、试说明Mahalanobis 距离平方的定义,到某点的Mahalanobis 距离平方为常数的轨迹的几何意义,它与欧氏距离的区别与联系。
答:M ahalanobis距离的平方定义为:其中x,u 为两个数据,Z- ¹是一个正定对称矩阵(一般为协方差矩阵)。
根据定义,距某一点的Mahalanobis 距离相等点的轨迹是超椭球,如果是单位矩阵Z, 则M ahalanobis距离就是通常的欧氏距离。
2、试说明用监督学习与非监督学习两种方法对道路图像中道路区域的划分的基本做法,以说明这两种学习方法的定义与它们间的区别。
答:监督学习方法用来对数据实现分类,分类规则通过训练获得。
该训练集由带分类号的数据集组成,因此监督学习方法的训练过程是离线的。
非监督学习方法不需要单独的离线训练过程,也没有带分类号(标号)的训练数据集,一般用来对数据集进行分析,如聚类,确定其分布的主分量等。
就道路图像的分割而言,监督学习方法则先在训练用图像中获取道路象素与非道路象素集,进行分类器设计,然后用所设计的分类器对道路图像进行分割。
使用非监督学习方法,则依据道路路面象素与非道路象素之间的聚类分析进行聚类运算,以实现道路图像的分割。
3、已知一组数据的协方差矩阵为, 试问(1)协方差矩阵中各元素的含义。
(2)求该数组的两个主分量。
(3)主分量分析或称K-L 变换,它的最佳准则是什么?(4)为什么说经主分量分析后,消除了各分量之间的相关性。
答:协方差矩阵为, 则(1)对角元素是各分量的方差,非对角元素是各分量之间的协方差。
(2)主分量,通过求协方差矩阵的特征值,用得(A- 1)²=1/4,则,相应地:A=3/2, 对应特征向量为,,对应0 这两个特征向量,即为主分量。
K-L 变换的最佳准则为:(3)对一组数据进行按一组正交基分解,在只取相同数量分量的条件下,以均方误差计算截尾误差最小。
(4)在经主分量分解后,协方差矩阵成为对角矩阵,因而各主分量间相关性消除。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
论文(设计)《模式识别》题目Fisher线性判别的基本原理及应用Fisher判别准则一、基本原理思想Fisher线性判别分析的基本思想:通过寻找一个投影方向(线性变换,线性组合),将高维问题降低到一维问题来解决,并且要求变换后的一维数据具有如下性质:同类样本尽可能聚集在一起,不同类的样本尽可能地远。
Fisher线性判别分析,就是通过给定的训练数据,确定投影方向W和阈值y0,即确定线性判别函数,然后根据这个线性判别函数,对测试数据进行测试,得到测试数据的类别。
二、算法的实现及流程图1 算法实现 (1)W 的确定x 1m x, 1,2ii X ii N ∈==∑各类样本均值向量mi样本类内离散度矩阵和总类内离散度矩阵Tx S (x m )(x m ), 1,2ii i i X i ∈=--=∑样本类间离散度矩阵T1212S (m m )(m m )b =--在投影后的一维空间中,各类样本均值。
样本类内离散度和总类内离散度。
样本类间离散度。
Fisher 准则函数满足两个性质:·投影后,各类样本内部尽可能密集,即总类内离散度越小越好。
·投影后,各类样本尽可能离得远,即样本类间离散度越大越好。
根据这个性质确定准则函数,根据使准则函数取得最大值,可求出W :。
(2)阈值的确定采取的方法:【1】【2】【3】(3)Fisher 线性判别的决策规则对于某一个未知类别的样本向量x ,如果y=W T·x>y0,则x ∈w1;否则x ∈w2。
2 流程图归一化处理载入训练数据三、实验仿真1.实验要求试验中采用如下的数据样本集:ω1类: (22,5),(46,33),(25,30),(25,8),(31, 3),(37,9),(46,7),(49,5),(51,6),(53,3)(19,15),(23,18),(43,1),(22,15),(20,19),(37,36),(22,22),(21,32),(26,36),(23,39)(29,35),(33,32),(25,38),(41,35),(33,2),(48,37)ω2类: (40,25),(63,33),(43,27),(52,25),(55,27),(59,22) ,(65,59),(63,27)(65,30),(66,38),(67,43),(52,52),(61,49) (46,23),(60,50),(68,55) (40,53),(60,55),(55,55) (48,56),(45,57),(38,57) ,(68,24)在实验中采用Fisher线性判别方法设计出每段线性判别函数。
2.算法程序(matlab编程)%程序代码1在matlab中画出w1,w2类样本点clearclc%w1,w2类两类样本点值w1=[22,46,25,25,31,37,46,49,51,53,19,23,43,22,20,37,22,21,26,23,29,33,2 5,41,33,48;5,33,30,8,3,9,7,5,6,3,15,18,1,15,19,36,22,32,36,39,35,32,38, 35,2,37]';N1=length(w1); %w1类样本点的个数plot(w1(:,1),w1(:,2),'color','r','linestyle','none','marker','o','linew idth',1.5);hold on;w2=[40,63,43,52,55,59,65,63,65,66,67,52,61,46,60,68,40,60,55,48,45,38,6 8;25,33,27,25,27,22,59,27,30,38,43,52,49,23,50,55,53,55,55,56,57,57,24] ';N2=length(w2); %w2类样本点的个数plot(w2(:,1),w2(:,2),'color','b','linestyle','none','marker','+','linew idth',1.5);hold on;xlabel('x1');ylabel('x2');title('fisher准则的应用');%程序代码2在matlab中画出w1,w2类样本点的投影方向%计算w1,w2类的样本均值average1=mean(w1);average2=mean(w2);%计算w1,w2类内离散度矩阵S1和S2和总类内离散度矩阵SwS1=zeros(2,2);for i=1:N1S1=S1+(w1(i,:)-average1)'*(w1(i,:)-average1); endS2=zeros(2,2);for j=1:N2S2=S2+(w2(j,:)-average2)'*(w2(j,:)-average2); endSw=S1+S2;%计算投影向量ww=inv(Sw)*(average1-average2)';%»³ö¹ýÔµãµÄͶӰÏßk=w(2,1)/w(1,1);x1=[-20:0.1:100];x2=k*x1;plot(x1,x2,'color','k');hold on;%程序代码3在matlab中画出w1,w2类样本点的投影点和分界线for i=1:N1x1=(w1(i,1)+k*w1(i,2))/(k*k+1);x2=k*x1;plot(x1,x2,'color','r','marker','o');endx1=(w2(j,1)+k*w2(j,2))/(k*k+1);x2=k*x1;plot(x1,x2,'color','b','marker','+');endx1=[0:0.1:100];x2=(-1/k)*(x1-w1(16,1)+w2(22,1))+w1(16,2)+w2(22,2);plot(x1,x2,'color','k');hold on;x1=[0:0.1:100];x2=(-1/k)*(x1-w1(10,1)+w2(4,1))+w1(10,2)+w2(4,2);plot(x1,x2,'color','k');hold on;经过fisher方法的第一次分割后,w1类和w2类共有10个样本点混合如上图所示。
此时考虑对剩余的不可分样本点再利用fisher方法分割.如此往复,便可最终能够将w1类和w2类的所有样本分开。
%对剩余的样本点再利用fisher准则进行分割new1=[46,51,53,37,41,48;33,6,3,36,35,37]';new2=[40,43,52,46;25,27,25,23]';average1=mean(new1);average2=mean(new2);S1=zeros(2,2);S1=S1+(new1(i,:)-average1)'*(new1(i,:)-average1); endS2=zeros(2,2);for j=1:4S2=S2+(new2(j,:)-average2)'*(new2(j,:)-average2); endSw=S1+S2;%求投影向量ww=inv(Sw)*(average1-average2)';%画出过原点的投影线k=w(2,1)/w(1,1);x1=[-20:0.1:100];x2=k*x1;plot(x1,x2,'color','k');hold on;%画出剩余样本点的投影点for i=1:6x1=(new1(i,1)+k*new1(i,2))/(k*k+1);x2=k*x1;plot(x1,x2,'color','r','marker','o');endfor j=1:4x1=(new2(j,1)+k*new2(j,2))/(k*k+1);x2=k*x1;plot(x1,x2,'color','b','marker','+');end重复以上步骤,直到w1类和w2类两类样本点最终分开为止。
以此类推分割,代码有点冗余.不在此呈现。
matlab最终的仿真结果如下图所示。
四、实验总结实验结果与预期的有点差距,在进行第二次分割后,投影的方向与心里所想的投影方向有点不同,经过多次修改程序,最终得出结果如上图,但仍然不是令人满意。
从这次的试验中,我收获挺多的。
要加深对课本的理解,更要上机动手实践,理论与实践相结合,才能达到最终深刻理解其中的含义。
matlab最终的仿真结果如下图所示。
四、实验总结实验结果与预期的有点差距,在进行第二次分割后,投影的方向与心里所想的投影方向有点不同,经过多次修改程序,最终得出结果如上图,但仍然不是令人满意。
从这次的试验中,我收获挺多的。
要加深对课本的理解,更要上机动手实践,理论与实践相结合,才能达到最终深刻理解其中原理的含义。
