1.2.1《极坐标系的概念》 课件(人教A版选修4-4)
合集下载
高二数学选修4-44.1.21极坐标系课堂PPT.ppt

(x , y , z)的集合建立一一对应;
授课:XX
1
复习回顾
4.1.1 直角坐标系
数
平面直角
轴
坐标系
空间直角 坐标系
R
(x , y)
(x , y , z)
授课:XX
2
复习回顾
建立坐标系是为了确定点的位置。由此,在所创建的坐标系 中,应满足: 任意一点都存在一个坐标与之对应;反之,依据一个点的坐 标就能确定这个点的位置; 而确定点的位置即为求出此点在设定的坐标系中的坐标。
OM= 3
M
给定ρ,θ在极坐标系中描点的方法:先按极角找到极径所在的 射线,后按极径的正负和数值在这条射线或其反向延长线上描 点。
授课:XX
19
5、负极径的实质
从比较来看,负极径比 正极径多了一个操作,将射
M
线OP“反向延长”。
而反向延长也可以看成是旋转 O
,因此,所谓“负极径”实
质是针对方向的。这与数学中
[1]作射线OP,使XOP=
P
[2]在OP的反向延长
线上取一点M,使OM= ;
O
X
如图示:
M
授课:XX
15
新课讲解
2、负极径的实例
在极坐标系中画出点:M(-3,/4)的位置
[1]作射线OP,使XOP= /4 [2]在OP的反向延长线上取一
P = /4
点M,使OM= 3;
O
X
如图示: M(-3,/4)
[3]一点的极坐标是否有统一的表达式?
有.( ,2k ) 或(- ,2k π)
授课:XX
27
课堂小结
1、极坐标 (ρ,2kπ+θ) 和(-ρ,2kπ+θ+π)k其Z
数学:4.1.2《极坐标系(1))课件(新人教选修4-4)

思考: 对比直角坐标系,比较异同 极点、极轴、长度单位、 (1) 要素:____________________ 角度单位和正方向 ____________________;
M
O X
(, ) (2) 平面内点的极坐标用_____表示.
(0, ), 可为任意值. 极点的极坐标为_________________
情境2:请问到深大附中怎么走? 从这向南走200米.
请分析上面这句话,他告诉了问路人什么?
从 这 向 南 走 2 0 0 米 !
出发点
方向
距离
在生活中人们经常用方向和距离来表示一点的 位置。这种用方向和距离表示平面上一点的位置的 思想,就是极坐标的基本思想。
二、新知学习
1、极坐标系的建立: 在平面内取一个定点O,叫做极点.
M
P (ρ,θ) X
[1]给定(,),就可以在极坐标平 面内确定唯一的一点M
O
[2]给定平面上一点M,但却有无数个极坐标与之对应。 原因在于:极角有无数个。 如果限定ρ >0,0≤θ <2π 那么除极点外,平面内的点和极坐标就可以一一对应了.
例2. 在极坐标系中, (1) 已知两点 P(5, ), (2, 4 ),求线段PQ的长度; Q
三、小
结
[1]建立一个极坐标系需要哪些要素 极点;极轴;长度单位;角度单位和它的正方向. [2]极坐标系内一点的极坐标有多少种表达式? 无数,极角有无数个. [3]一点的极坐标有否统一的表达式? 有。(ρ ,2kπ +θ ) 四、课后作业 教材P14-15页5,8,9,10,11 思考: 极坐标系中, 点M的坐标为(-10, ), 则下列各 3 坐标中, 不是M点的坐标的是( ) (A) (10, 4) (B) (-10, - 5) (C) (10, - 2) (D)(10, 2) 3 3 3 3
M
O X
(, ) (2) 平面内点的极坐标用_____表示.
(0, ), 可为任意值. 极点的极坐标为_________________
情境2:请问到深大附中怎么走? 从这向南走200米.
请分析上面这句话,他告诉了问路人什么?
从 这 向 南 走 2 0 0 米 !
出发点
方向
距离
在生活中人们经常用方向和距离来表示一点的 位置。这种用方向和距离表示平面上一点的位置的 思想,就是极坐标的基本思想。
二、新知学习
1、极坐标系的建立: 在平面内取一个定点O,叫做极点.
M
P (ρ,θ) X
[1]给定(,),就可以在极坐标平 面内确定唯一的一点M
O
[2]给定平面上一点M,但却有无数个极坐标与之对应。 原因在于:极角有无数个。 如果限定ρ >0,0≤θ <2π 那么除极点外,平面内的点和极坐标就可以一一对应了.
例2. 在极坐标系中, (1) 已知两点 P(5, ), (2, 4 ),求线段PQ的长度; Q
三、小
结
[1]建立一个极坐标系需要哪些要素 极点;极轴;长度单位;角度单位和它的正方向. [2]极坐标系内一点的极坐标有多少种表达式? 无数,极角有无数个. [3]一点的极坐标有否统一的表达式? 有。(ρ ,2kπ +θ ) 四、课后作业 教材P14-15页5,8,9,10,11 思考: 极坐标系中, 点M的坐标为(-10, ), 则下列各 3 坐标中, 不是M点的坐标的是( ) (A) (10, 4) (B) (-10, - 5) (C) (10, - 2) (D)(10, 2) 3 3 3 3
人教版高中数学选修4-4 第一讲 坐标系 二 极坐标系 (共34张PPT)教育课件

A. y 1
sin t
1
x t2
C.
1
yt 2
x cos t
B. y 1
cos t
x tan t
D. y 1
tan t
7.极坐标方程
2
arcsin化(为 直0)角坐标方程的形
式是 ( )
A. x2 y2 x 0
B.y x(1 x)
C. 2x 1 4y2 1 D..y (x 1)
2.极坐标(,)与(ρ,2kπ+θ)( k )表z 示 同一个点.即一点的极坐标的统一的表达式 为(ρ,2kπ+θ)
3.如果规定ρ>0,0≤θ<2π,那么除 极 点外,平面内的点和极坐标就可以一一对 应了。
我们学了直角坐标,也学了极坐 标,那么这两种坐标有什么关系呢? 已知点的直角坐标为,如何用极坐标 表示这个点呢?
M (, )
0
x
2
4
5
6
C
1.如图,在极坐标系中,写出点 AF(,6B, ,4C3 ,)D的, G极(坐5, 标53,所) 并在标的出位E置( 72 , ) ,
E D BA
O
X
4 F
3
G 5
3
解:如图可得A,B,C,D的坐标分别为
(4,0)
(2, )
(3, )
(1, 5 )
4
2
6
点E,F,G的位置如图所示
1
4.极坐标方程ρ=cosθ与ρcosθ= 的2 图形是( ) B
A
B
C
D
解x=:12把,ρc故os排θ=除A,、12 化D;为又直圆角ρ坐=c程os,θ显得然: 过点 (0,1),又排除C,故选B。
5、若A、B的两点极坐标为A(4,
第一讲 坐标系 知识归纳 课件(人教A选修4-4)

方程为ρcos θ-2ρsin θ+7=0,则圆心到直线的距离为
________.
[解析] 将 ρ=2cos θ 化为 ρ2=2ρcos θ,即有
x2+y2-2x=0,亦即(x-1)2+y2=1. 将 ρcos θ-2ρsin θ+7=0 化为 x-2y+7=0, |1+7| 8 5 故圆心到直线的距离 d= 2 = . 5 1 +-22
返回
3.(2011· 江西高考)若曲线的极坐标方程为ρ=2sin θ+4cos θ,以极点为原点,极轴为x轴正半轴建立直角坐标系,
则该曲线的直角坐标方程为________.
解析:∵ρ=2sin θ+4cos θ,∴ρ2=2ρsin θ+4ρcos θ, ∴x2+y2=2y+4x,即x2+y2-4x-2y=0. 答案:x2+y2-4x-2y=0.
[答案]
8 5 5
返回Biblioteka [例 5]π 在极坐标系中,点 M 坐标是(2, ),曲线 C 的 3
π 方程为 ρ=2 2sin(θ+ ); 以极点为坐标原点, 极轴为 x 轴的 4 正半轴建立平面直角坐标系,直线 l 经过点 M 和极点. (1)写出直线 l 的极坐标方程和曲线 C 的直角坐标方程; (2)直线 l 和曲线 C 相交于两点 A、B,求线段 AB 的长.
返回
[解]
π (1)∵直线 l 过点 M(2, )和极点, 3
π ∴直线 l 的直角坐标方程是 θ= (ρ∈R). 3 π ρ=2 2sin(θ+ )即 ρ=2(sin θ+cos θ), 4 两边同乘以 ρ 得 ρ2=2(ρsin θ+ρcos θ), ∴曲线 C 的直角坐标方程为 x2+y2-2x-2y=0.
直角坐标方程化极坐标方程可直接将x=ρcos θ,y= ρsin θ代入即可,而极坐标方程化为直角坐标方程通常将极 坐标方程化为ρcos θ,ρsin θ的整体形式,然后用x,y代替 较为方便,常常两端同乘以ρ即可达到目的,但要注意变形 的等价性.
人教版高中数学选修4-4《§1.2极坐标系》

M (,)
没有说明 时 ≥0
O
x
例 在图中,用点A,B,C,D,E分别表示教学楼,体育 馆,图书馆,实验楼,办公楼的位置.建立适当的极 实验楼 坐标系,写出各点的极坐标. 图书馆
D
解: A0,0
B60,0
C
C 120, D 60 3, 3 2
基点 参照方向和角
实验楼
D
距离
图书馆
C
办公楼
E
45
60m B 教学楼 体育馆
A
60
(一) 极 坐 标 系:
在平面内取一个定点O,叫做极点; 自极点O引一条射线Ox,叫做极轴; 再选定一个长度单位、一个角度单位(通常取弧 度)及其正方向(通常取逆时针方向),这样建立了 一个极坐标系.
O
x
极坐标系内点的极坐标 |OM| ∠xOM (,) 极径 极角 M的极坐标
120, 4 3
120, 2 3
M (,)
极坐标(,)与(,+2k)(k) 表示同一个点
极点(0,) )( R)
给定和就可以在平面内惟一确定点M;
O
x
但给定平面内一点M,却有无数个极坐标与之对应
当规定>0,0≤<2,那么除极点外,平面内的点 可用惟一的极坐标(,)表示;而极坐标(,)表 示的点也是惟一确定.
数学家笛卡尔
瑞典公主克里斯汀
1 sin
作业
课本第12页习题1.2
y x y , tan x 0(直角坐标化极坐标) x
2 2 2
2 例1: 将点M的极坐标 5, 3
化成直角坐标 .
没有说明 时 ≥0
O
x
例 在图中,用点A,B,C,D,E分别表示教学楼,体育 馆,图书馆,实验楼,办公楼的位置.建立适当的极 实验楼 坐标系,写出各点的极坐标. 图书馆
D
解: A0,0
B60,0
C
C 120, D 60 3, 3 2
基点 参照方向和角
实验楼
D
距离
图书馆
C
办公楼
E
45
60m B 教学楼 体育馆
A
60
(一) 极 坐 标 系:
在平面内取一个定点O,叫做极点; 自极点O引一条射线Ox,叫做极轴; 再选定一个长度单位、一个角度单位(通常取弧 度)及其正方向(通常取逆时针方向),这样建立了 一个极坐标系.
O
x
极坐标系内点的极坐标 |OM| ∠xOM (,) 极径 极角 M的极坐标
120, 4 3
120, 2 3
M (,)
极坐标(,)与(,+2k)(k) 表示同一个点
极点(0,) )( R)
给定和就可以在平面内惟一确定点M;
O
x
但给定平面内一点M,却有无数个极坐标与之对应
当规定>0,0≤<2,那么除极点外,平面内的点 可用惟一的极坐标(,)表示;而极坐标(,)表 示的点也是惟一确定.
数学家笛卡尔
瑞典公主克里斯汀
1 sin
作业
课本第12页习题1.2
y x y , tan x 0(直角坐标化极坐标) x
2 2 2
2 例1: 将点M的极坐标 5, 3
化成直角坐标 .
人教A版数学【选修4-4】ppt课件:1-3第一讲-坐标系

2.曲线的极坐标方程与直角坐标方程的互相转化 与点的极坐标与直角坐标的互相转化一样, 以平面直角坐标系 的原点 O 为极点,x 轴的正半轴为极轴,且在两坐标系中取相同的 长度单位.平面内的曲线(含直线)的极坐标方程与直角坐标方程也 可以进行互相转化,设曲线上任意一点 M 的直角坐标与极坐标分 别为(x,y)和(ρ,θ),则极坐标方程与直角坐标方程的互相转化公 式为:y=ρsinθ,x=ρcosθ,ρ2=x2+y2.
【例 3】
π 在极坐标系中,圆 ρ=4sinθ 的圆心到直线 θ=6(ρ
∈R)的距离是________.
【解析】
圆 ρ=4sinθ 的直角坐标方程为 x2+(y-2)2=4,其
π 圆心为 C(0,2),直线 l:θ= (ρ∈R)的直角坐标方程为 x- 3y=0; 6 |0-2 3| 所以点 C 到直线 l 的距离是 d= = 3. 2
【例 1】
求圆心在
并把它化为直角坐标方程. 【分析】 数形结合,先描绘圆的大致位置,找出圆上任一点 满足的几何条件.
【解】
如图,设 M(ρ,θ)为圆上除 O,B 外的任意一点,连
3 接 OM,MB,则有|OB|=4,|OM|=ρ,∠MOB=θ- π,∠BMO= 2 π 2.
从而△BOM 为直角三角形, 所以有|OM|=|OB|cos∠MOB. 即
与曲线 C 相交于 A,B,求|AB|.
【解】
x=ρcosθ, (1)因为 y=ρsinθ,
所以 ρ2=x2+y2,
由 ρ=2sinθ+4cosθ,得 ρ2=2ρsinθ+4ρcosθ, ∴x2+y2-4x-2y=0,即(x-2)2+(y-1)2=5. 曲线 C 的直角坐标方程为(x-2)2+(y-1)2=5.
第一讲 坐标系 知识归纳 课件(人教A选修4-4)

返回
考情分析 通过对近几年新课标区高考试题的分析可知,高考对本 讲的考查集在考查极坐标方程、极坐标与直角坐标的互化 等.预计今后的高考中,仍以考查圆、直线的极坐标方程为 主.
返回
真题体验 1.(2012· 安徽高考)在极坐标系中,圆 ρ=4sin θ 的圆心到直 π 线 θ= (ρ∈R)的距离是________. 6 解析:将 ρ=4sin θ 化成直角坐标方程为 x2+y2=4y,即 x2
返回
解析:在直线 l 上任取点 P(ρ,θ),在△OPM 中,由正弦定 OM OP 2 ρ 理得 = ,即 = ,化简得 ρ π 5π sin∠OPM sin∠OMP sin -θ sin 6 6 1 1 = ,故 f(θ)= . π π sin -θ sin -θ 6 6
1 答案: π sin -θ 6
返回
[例 2]
x′=2x, y′=2y
在同一平面直角坐标系中,经过伸缩变换 后, 曲线 C 变为曲线(x′-5)2+(y′+6)2=1,
求曲线 C 的方程,并判断其形状.
[解]
x′=2x, 将 y′=2y
代入(x′-5)2+(y′+6)2=1 中,
得(2x-5)2+(2y+6)2=1. 52 1 2 化简,得(x- ) +(y+3) = . 2 4 5 1 该曲线是以( ,-3)为圆心,半径为 的圆. 2 2
返回
返回
利用问题的几何特征,建立适当坐标系,主要就是兼
顾到它们的对称性,尽量使图形的对称轴(对称中心)正好
是坐标系中的x轴,y轴(坐标原点). 坐标系的建立,要尽量使我们研究的曲线的方程简 单.
返回
[例1]
已知圆的半径为6,圆内一定点P离圆心的距离
为4,A、B是圆上的两动点且满足∠APB=90°,求矩形 APBQ的顶点Q的轨迹方程. [解] 如图,以圆心O为原点,OP
考情分析 通过对近几年新课标区高考试题的分析可知,高考对本 讲的考查集在考查极坐标方程、极坐标与直角坐标的互化 等.预计今后的高考中,仍以考查圆、直线的极坐标方程为 主.
返回
真题体验 1.(2012· 安徽高考)在极坐标系中,圆 ρ=4sin θ 的圆心到直 π 线 θ= (ρ∈R)的距离是________. 6 解析:将 ρ=4sin θ 化成直角坐标方程为 x2+y2=4y,即 x2
返回
解析:在直线 l 上任取点 P(ρ,θ),在△OPM 中,由正弦定 OM OP 2 ρ 理得 = ,即 = ,化简得 ρ π 5π sin∠OPM sin∠OMP sin -θ sin 6 6 1 1 = ,故 f(θ)= . π π sin -θ sin -θ 6 6
1 答案: π sin -θ 6
返回
[例 2]
x′=2x, y′=2y
在同一平面直角坐标系中,经过伸缩变换 后, 曲线 C 变为曲线(x′-5)2+(y′+6)2=1,
求曲线 C 的方程,并判断其形状.
[解]
x′=2x, 将 y′=2y
代入(x′-5)2+(y′+6)2=1 中,
得(2x-5)2+(2y+6)2=1. 52 1 2 化简,得(x- ) +(y+3) = . 2 4 5 1 该曲线是以( ,-3)为圆心,半径为 的圆. 2 2
返回
返回
利用问题的几何特征,建立适当坐标系,主要就是兼
顾到它们的对称性,尽量使图形的对称轴(对称中心)正好
是坐标系中的x轴,y轴(坐标原点). 坐标系的建立,要尽量使我们研究的曲线的方程简 单.
返回
[例1]
已知圆的半径为6,圆内一定点P离圆心的距离
为4,A、B是圆上的两动点且满足∠APB=90°,求矩形 APBQ的顶点Q的轨迹方程. [解] 如图,以圆心O为原点,OP
1.2.1《极坐标系的概念》课件(新人教选修4-4).

6
C(3, )
2
F (4, )
第15页,共43页。
2
4
5
6
C E
F
A O
B X
4
D
3
G 5
3
第16页,共43页。
要求写出各点: [1]最小正极角的极坐标 [2]最大负极角的极坐标
[3]点的极坐标的统一表达式。
第17页,共43页。
本节课总结:
[1]极坐标系的建立需确定几条?
极点;极径;长度单位和角度正方向。
根据极径定义,极径是距离,当然是正的。 现在所说的“负极径”中的“负”到底是什么 意思?
有比较才能有鉴别!
把负极径时点的确定过程,与正极径时点的确 定过程相比较,看看有什么相同,有什么不同?
第21页,共43页。
五、4、正、负极径时,点的确定过程比较
画出点 (3,/4) 和(-3,/4)
M
[1]作射线OP,使XOP= /4
想一想?
极点(0,)( R) 即极点有无数个极坐标
①平面上一点的极坐标是否唯一?
②若不唯一,那有多少种表示方法? ③坐标不唯一是由谁引起的?
④不同的极坐标是否可以写出统一表达式?
第13页,共43页。
三、点的极坐标的表达式的研究
如图:OM的长度为4,
请说出点M的极坐标的其他 4
表达式。
O 思:这些极坐标之间有何异同?
就叫做M的极坐标。
O X
特别强调:表示线段OM的长度,既点M到极 点O的距离;表示从OX到OM的角度,既以OX (极轴)为始边,OM 为终边的角。
第11页,共43页。
题组一:说出下图中各点的极坐标
2
4
5
6
C(3, )
2
F (4, )
第15页,共43页。
2
4
5
6
C E
F
A O
B X
4
D
3
G 5
3
第16页,共43页。
要求写出各点: [1]最小正极角的极坐标 [2]最大负极角的极坐标
[3]点的极坐标的统一表达式。
第17页,共43页。
本节课总结:
[1]极坐标系的建立需确定几条?
极点;极径;长度单位和角度正方向。
根据极径定义,极径是距离,当然是正的。 现在所说的“负极径”中的“负”到底是什么 意思?
有比较才能有鉴别!
把负极径时点的确定过程,与正极径时点的确 定过程相比较,看看有什么相同,有什么不同?
第21页,共43页。
五、4、正、负极径时,点的确定过程比较
画出点 (3,/4) 和(-3,/4)
M
[1]作射线OP,使XOP= /4
想一想?
极点(0,)( R) 即极点有无数个极坐标
①平面上一点的极坐标是否唯一?
②若不唯一,那有多少种表示方法? ③坐标不唯一是由谁引起的?
④不同的极坐标是否可以写出统一表达式?
第13页,共43页。
三、点的极坐标的表达式的研究
如图:OM的长度为4,
请说出点M的极坐标的其他 4
表达式。
O 思:这些极坐标之间有何异同?
就叫做M的极坐标。
O X
特别强调:表示线段OM的长度,既点M到极 点O的距离;表示从OX到OM的角度,既以OX (极轴)为始边,OM 为终边的角。
第11页,共43页。
题组一:说出下图中各点的极坐标
2
4
5
6
第一讲 坐标系 知识归纳 课件(人教A选修4-4)

直角坐标方程化极坐标方程可直接将x=ρcos θ,y= ρsin θ代入即可,而极坐标方程化为直角坐标方程通常将极 坐标方程化为ρcos θ,ρsin θ的整体形式,然后用x,y代替 较为方便,常常两端同乘以ρ即可达到目的,但要注意变形 的等价性.
返回
[例4]
已知圆的极坐标方程ρ=2cos θ,直线的极坐标
(2)点 M 的直角坐标为(1, 3),直线 l 过点 M 和原点, ∴直线 l 的直角坐标方程为 y= 3x. 曲线 C 的圆心坐标为(1,1),半径 r= 2,圆心到直线 l 的 3-1 距离为 d= ,∴|AB|= 3+1. 2
返回
点击下图进入
返回
方程,这里要求至少有一组能满足极坐标方程. 返回
求轨迹方程的方法有直接法、定义法、相关点代入法, 在极坐标中仍然适用,注意求谁设谁,找出所设点的坐标 ρ、 θ 的关系. [例 3] 1 △ABC 底边 BC=10, ∠A= ∠B, B 为极点, 以 2
BC 为极轴,建立极坐标系,求顶点 A 的轨迹的极坐标方程.
返回
考情分析 通过对近几年新课标区高考试题的分析可知,高考对本 讲的考查集在考查极坐标方程、极坐标与直角坐标的互化 等.预计今后的高考中,仍以考查圆、直线的极坐标方程为 主.
返回
真题体验 1.(2012· 安徽高考)在极坐标系中,圆 ρ=4sin θ 的圆心到直 π 线 θ= (ρ∈R)的距离是________. 6 解析:将 ρ=4sin θ 化成直角坐标方程为 x2+y2=4y,即 x2
[答案]
8 5 5
返回
[例 5]
π 在极坐标系中,点 M 坐标是(2, ),曲线 C 的 3
π 方程为 ρ=2 2sin(θ+ ); 以极点为坐标原点, 极轴为 x 轴的 4 正半轴建立平面直角坐标系,直线 l 经过点 M 和极点. (1)写出直线 l 的极坐标方程和曲线 C 的直角坐标方程; (2)直线 l 和曲线 C 相交于两点 A、B,求线段 B 的长.
高二数学,人教A版,选修4-4, 第1课时,极坐标系的概念 , 课件

2.极坐标 设 M 是平面内一点,极点 O 与点 M 的距离 |OM| 叫做点 M 的 极径 ,记为ρ;以极轴Ox为始边,射线OM为终边的角xOM叫 ______ 极角 做点 M 的 _____ ,记为 θ. 有序数对 _______ M 的极坐标, (ρ,叫做点 θ) M(ρ,θ). 记为____________ ≥ 一 般 地 , 不 作 特 殊 说 明 时 , 我 们 认 为 ρ____ 0,θ可取 任意实数 . ___________
如图所示, A , B, C , D 四个点分别是唯一
[规律方法] 由极坐标确定点的位置的步骤 ①取定极点O; ②作方向为水平向右的射线Ox为极轴;
③以极点O为顶点,以极轴Ox为始边,通常按逆时针方向
旋转极轴Ox确定出极角的终边; ④以极点O为圆心,以极径为半径画弧,弧与极角终边的 交点即是所求点的位置.
1.极坐标系
如图所示,在平面内取一个定点 O, 极点 ,自极点 O 引一条射线 Ox ,叫 叫做 _____ 长度单位 做极轴;再选定一个 _________ 、 一 个 角度单位 通常取弧度)及其正方向(通常 __________( 逆时针 方向 ) ,这样就建立了一个极 取 ________ 坐标系.
二 极坐标 第1课时 极坐标系的概念
课标定位
1.了解极坐标系的意义.
2.理解点的极坐标的不唯一性.
3.能够建立适当的极坐标系解决数学问题.
1.利用坐标法解决几何问题.(重点) 2.常与三角函数和几何图形结合命题. 3.点的极坐标不唯一是易混点,准确理解极坐标系的概 念并用于解题.(难点)
据太平洋海啸预警中心测定:当地时
π 7π 极角4与 4 的终边关于极轴对称,所以点 B,D 关于极轴对 称.
2014-2015学年高中数学(人教版选修4-4)配套课件第一讲 1.2 极 坐 标 系

ρsin θ
或
x2+y2 ,
y x
栏 目 链 接
x≠0.
预习 思考
1.写出下图中各点的极坐标:
栏 目 链 接
π π 3, 2, 4 A________,B________ ,C________. 2
(4,0)
预习 思考
2.回答下列问题: (1)平面上一点的极坐标是否唯一? (2)若不唯一,那有多少种表示方法? (3)坐标不唯一是由谁引起的?
第一讲
坐 标 系
1.2 极 坐 标 系
栏 目 链 接
1.理解极坐标的概念. 2.能在极坐标系中用极坐标刻画点的位置,体会在极坐
栏 目 链 接
标系和平面直角坐标系中刻画点的位置的区别.
3.能进行极坐标与平面直角坐标的互化.
栏 目 链 接
1.极坐标系的建立. 在平面上取一个定点 O,自点 O 引一条射线 Ox,同时确
栏 目 链 接
栏 目 链 接
题型1
极坐标的概念
例1 写出下图中各点的极坐标(ρ>0,0≤θ<2π).
栏 目 链 接
分析:根据极坐标定义,若 M 是平面上任一点, ρ 表示 OM 的长度,θ 表示以射线 Ox 为始边,射线 OM 为终边所成的角,则 M 的极坐标为(ρ,θ).
π π 3π 解析: A(5,0), B2,6, C4,2, D5, 4 , E(2, 4π 5π π),F5, 3 ,G3.5, 3 .
栏 目 链 接
为直角坐标为( 3,-1). ∴A、B 两点间的距离 d=
(
3- 3)2+[1--1]2=2.
变式 训练
π π 2.已知两点的极坐标 A3,2,B3,6 ,求:
或
x2+y2 ,
y x
栏 目 链 接
x≠0.
预习 思考
1.写出下图中各点的极坐标:
栏 目 链 接
π π 3, 2, 4 A________,B________ ,C________. 2
(4,0)
预习 思考
2.回答下列问题: (1)平面上一点的极坐标是否唯一? (2)若不唯一,那有多少种表示方法? (3)坐标不唯一是由谁引起的?
第一讲
坐 标 系
1.2 极 坐 标 系
栏 目 链 接
1.理解极坐标的概念. 2.能在极坐标系中用极坐标刻画点的位置,体会在极坐
栏 目 链 接
标系和平面直角坐标系中刻画点的位置的区别.
3.能进行极坐标与平面直角坐标的互化.
栏 目 链 接
1.极坐标系的建立. 在平面上取一个定点 O,自点 O 引一条射线 Ox,同时确
栏 目 链 接
栏 目 链 接
题型1
极坐标的概念
例1 写出下图中各点的极坐标(ρ>0,0≤θ<2π).
栏 目 链 接
分析:根据极坐标定义,若 M 是平面上任一点, ρ 表示 OM 的长度,θ 表示以射线 Ox 为始边,射线 OM 为终边所成的角,则 M 的极坐标为(ρ,θ).
π π 3π 解析: A(5,0), B2,6, C4,2, D5, 4 , E(2, 4π 5π π),F5, 3 ,G3.5, 3 .
栏 目 链 接
为直角坐标为( 3,-1). ∴A、B 两点间的距离 d=
(
3- 3)2+[1--1]2=2.
变式 训练
π π 2.已知两点的极坐标 A3,2,B3,6 ,求:
高中新课程数学(新课标人教A版)选修4-4《1.2.1极坐标系的的概念》课件2

2 + y2 x ρ =________
2
y tan θ =x(x≠0)
在一般情况下,由tan θ确定角时,可根据点M所在的象限
取最小正角.
课前自主学习
课堂讲练互动
知能提升演练
教材超级链接
名师点睛
1.极坐标系的概念
极坐标系的建立有四个要素:①极点;②极轴;③长
度单位;④角度单位和它的正方向.四者缺一不可. 极坐标系就是用长度和角度来确定平面内点的位置. 2.点的极坐标:每一个有序实数对(ρ,θ)确定一个点的 位置.其中,ρ是点M的极径,θ是点M的极角. 平面上给定一点,可以写出这个点的无数多个极坐 标.根据点的极坐标(ρ,θ)的定义,对于给定的点 (ρ,θ)有无数个极坐标,可分为两类,一类为(ρ,θ+
知能提升演练
教材超级链接
(2)极坐标系内一点的极坐标的规定: 设M是平面内一点,极点O与点M的距离 极径 ,记为ρ;以极轴Ox |OM|叫做点M的_____
为始边,射线OM为终边的角xOM叫做点
(ρ,θ) 叫做点M的极坐标,记 极角 ,记为θ.有序数对_________ M的_____ M(ρ,θ) 为___________ .
极角θ在后,不能把顺序搞错了. (2)点的极坐标是不唯一的,但若限制ρ>0,0≤θ<2π,则除
极点外,点的极坐标是唯一确定的.
课前自主学习
课堂讲练互动
知能提升演练
教材超级链接
【变式1】 写出下列各点的极坐标.
解
π A(4,0),B1, 3
2 13 5 C3, π ,D4, π ,E2, π , , 3 12 4
对应关系?
定一点M;反过来,给定平面内一点M,它的极坐标却不是唯 一的.所以极坐标系所在平面内的点与极坐标不能建立一一 对应关系,这是极坐标系与平面直角坐标系的主要区别.
数学:《极坐标系的概念》课件(人教a版选修4-4)

变式:在极坐标系中,若等边三角形的两顶点
π 5π 是A(2, ) ,B(2, ) , 4 4
那么顶点C的坐标可能是(
)
3π A.(4, ) 4 C .(2 3, π )
3 π B.(2 3, π )或(2 3, ) 4 4 D .(3, π )
总结
这节课我们学到了什么?
极点 四 极轴 1.极坐标系的建立 要 单位长度 素 角度的正方向 2.极坐标系下点与它的极坐标的对应情况 [1]给定(,),就可以在极坐标 平面内确定唯一的一点M. [2]给定平面上一点M,但却有无数个极 坐标与之对应.
课堂练习题
; mes;
;
慢慢の碎裂,声音悠悠の传来丶"师妹,不要伤心丶""生与死本就是壹场轮回,有生即有死,只要你能把握好自己の现在就行。"普智の声音慢慢の消散:"来世,若是还有机会,咱们再续师兄妹之缘吧丶""保重丶"普智の身影完全消散了,与死亡之雾壹道,就此消散于天地之间了丶与此同时, 他身后の那座佛殿,此时也随着普智の远去,向更遥远の星空也飘去了丶仿佛是飘到了外域去了,最终化作壹道神光,星辰闪进了这面前の夜色之中丶原本这里浩瀚の方圆上亿里の佛域,此时也因为这佛殿星辰の消失,瞬间就变得黑暗下来丶外面大量の邪煞之气,开始往佛域中涌了,之前普 智苦心经营の这壹片阴魔域中の净土,也会慢慢の消失了丶猫补中文叁玖贰1试过了(猫补中文)叁玖贰1仿佛是飘到了外域去了,最终化作壹道神光,星辰闪进了这面前の夜色之中丶天籁原本这里浩瀚の方圆上亿里の佛域,此时也因为这佛殿星辰の消失,瞬间就变得黑暗下来丶外面大量の 邪煞之气,开始往佛域中涌了,之前普智苦心经营の这壹片阴魔域中の净土,也会慢慢の消失了丶"师兄丶"采薇再壹次流下泪来,她从小便算是这师兄将
1.2极坐标系 第1课时 极坐标系的概念PPT课件(人教A版选修4-4)

答案:③④
【拓展提升】极坐标系与点的极坐标的特点
(1)极坐标系是由始边、终边构成的角为背景的平面坐标系, 点M的极坐标(ρ,θ)的几何意义是 r = OM , ∠xOM=θ(一般 用弧度数表示). (2)在极坐标系中,点M的极坐标不惟一,可以表示为 (ρ,θ+2kπ)(k∈Z),其中θ∈[0,2π).
【变式训练】 1.极坐标系中,点M(1,θ ),θ ∈[0,π ]的轨迹为( A.点 B.射线 C.圆 D.半圆 )
2.极坐标系中,极轴的反向延长线上一点M与极点的距离为2, 则点M的极坐标的下列表示:①(2,0);②(2,π ); -π );④(2,2kπ )(k∈Z). 其中,正确表示的序号为________. ③(2,
1.点与极坐标可以建立一一对应关系吗? 提示:由于极坐标系中,对于给定的有序数对(ρ,θ)都有 惟一确定的点与之对应,但是,对于给定一点 M,可以有无数 个有序数对(ρ,θ+2kπ)(k∈Z)与之对应,所以极坐标系中 的点与极坐标不能建立一一对应关系 .
2.如图所示,已知△OM′M是等腰直角 三角形,且|OM′|= 2 ,则点M的一个 极坐标是______________.
类型 一
极坐标系与点的极坐标
【典型例题】 1.在极坐标系中,极坐标(1,π )表示的点M与极点O之间的距 离为______,点M的极角为______.
2.关于极坐标的下列叙述: ①极轴是一条直线; ②极坐标(ρ ,θ )表示的点不惟一; ③极坐标(2,2kπ )(k∈Z)表示的点在极轴上;
p ( r , ④点 3 )(r ? 0) 的轨迹是端点为极点的射线.
【解析】1.选D.极坐标系中,由于点M(1,θ),θ∈[0,π] 的极径为1,极角θ∈[0,π]是一个变量,故点M的轨迹为 圆心在极点,半径为1的上半圆. 2.由于极轴的反向延长线上一点M与极点的距离为2,极角的 始边为Ox,终边与平角的终边相同,故点M的极坐标为 (2,π+2kπ)(k∈Z),故②③正确. 答案:②③
第一讲 坐标系 知识归纳 课件(人教A选修4-4)

(2)点 M 的直角坐标为(1, 3),直线 l 过点 M 和原点, ∴直线 l 的直角坐标方程为 y= 3x. 曲线 C 的圆心坐标为(1,1),半径 r= 2,圆心到直线 l 的 3-1 距离为 d= ,∴|AB|= 3+1. 2
返回
点击下图进入
返回
[答案]
8 5 5
返回
[例 5]
π 在极坐标系中,点 M 坐标是(2, ),曲线 C 的 3
π 方程为 ρ=2 2sin(θ+ ); 以极点为坐标原点, 极轴为 x 轴的 4 正半轴建立平面直角坐标系,直线 l 经过点 M 和极点. (1)写出直线 l 的极坐标方程和曲线 C 的直角坐标方程; (2)直线 l 和曲线 C 相交于两点 A、B,求线段 AB 的长.
返回
解析:在直线 l 上任取点 P(ρ,θ),在△OPM 中,由正弦定 OM OP 2 ρ 理得 = ,即 = ,化简得 ρ π 5π sin∠OPM sin∠OMP sin -θ sin 6 6 1 1 = ,故 f(θ)= . π π sin -θ sin -θ 6 6
1 答案: π sin -θ 6
返回
[解]
如图:令 A(ρ,θ),
θ △ABC 内,设∠B=θ,∠A= , 2 又|BC|=10,|AB|=ρ. 10 由正弦定理,得 = θ, 3θ sinπ- sin2 2 化简,得 A 点轨迹的极坐标方程为 ρ=10+20cos θ. ρ
返回
互化的前提依旧是把直角坐标系的原点作为极点,x 轴 的正半轴作为极轴并在两种坐标系下取相同的单位长度. 互化公式为 x=ρcos θ,y=ρsin θ y ρ2=x2+y2,tan θ=xx≠0
直角坐标方程化极坐标方程可直接将x=ρcos θ,y= ρsin θ代入即可,而极坐标方程化为直角坐标方程通常将极 坐标方程化为ρcos θ,ρsin θ的整体形式,然后用x,y代替 较为方便,常常两端同乘以ρ即可达到目的,但要注意变形 的等价性.
返回
点击下图进入
返回
[答案]
8 5 5
返回
[例 5]
π 在极坐标系中,点 M 坐标是(2, ),曲线 C 的 3
π 方程为 ρ=2 2sin(θ+ ); 以极点为坐标原点, 极轴为 x 轴的 4 正半轴建立平面直角坐标系,直线 l 经过点 M 和极点. (1)写出直线 l 的极坐标方程和曲线 C 的直角坐标方程; (2)直线 l 和曲线 C 相交于两点 A、B,求线段 AB 的长.
返回
解析:在直线 l 上任取点 P(ρ,θ),在△OPM 中,由正弦定 OM OP 2 ρ 理得 = ,即 = ,化简得 ρ π 5π sin∠OPM sin∠OMP sin -θ sin 6 6 1 1 = ,故 f(θ)= . π π sin -θ sin -θ 6 6
1 答案: π sin -θ 6
返回
[解]
如图:令 A(ρ,θ),
θ △ABC 内,设∠B=θ,∠A= , 2 又|BC|=10,|AB|=ρ. 10 由正弦定理,得 = θ, 3θ sinπ- sin2 2 化简,得 A 点轨迹的极坐标方程为 ρ=10+20cos θ. ρ
返回
互化的前提依旧是把直角坐标系的原点作为极点,x 轴 的正半轴作为极轴并在两种坐标系下取相同的单位长度. 互化公式为 x=ρcos θ,y=ρsin θ y ρ2=x2+y2,tan θ=xx≠0
直角坐标方程化极坐标方程可直接将x=ρcos θ,y= ρsin θ代入即可,而极坐标方程化为直角坐标方程通常将极 坐标方程化为ρcos θ,ρsin θ的整体形式,然后用x,y代替 较为方便,常常两端同乘以ρ即可达到目的,但要注意变形 的等价性.
人教版选修4-4 极坐标与参数方程(精品课件)共24张PPT

三、极坐标的正式应用和扩展
◆1736年出版的《流数术和无穷级数》一书中,牛顿 第一个将极坐标系应用于表示平面上的任何一点。牛 顿在书中验证了极坐标和其他九种坐标系的转换关系。 ◆在1691年出版的《博学通报》一书中伯努利正式使 用定点和从定点引出的一条射线,定点称为极点,射 线称为极轴。平面内任何一点的坐标都通过该点与定 点的距离和与极轴的夹角来表示。伯努利通过极坐标 系对曲线的曲率半径进行了研究。
(2)点P(ρ,θ)与点(ρ,2kπ+θ)(k∈Z)
所表示的是同一个点,即角θ与2kπ+θ的终边是 相同的。 综上所述,在极坐标系中,点与其点的极 坐标之间不是一一对应而是一对多的对应
(ρ,θ),(ρ,2kπ+θ),(-ρ,(2k+1)π+θ)均 表示同一个点
3.极坐标和直角坐标的互化
y
(1)互化背景:把直角坐标系 的原点作为极点,x轴的正半轴 作为极轴,并在两种坐标系中取 相同的长度单位,如图所示:
极坐标系和参数方程虽为选修内容,高中学生也 应该重视对本专题的学习,既可以体会其中的数 学思想,也能提高对数学的认识,而且可以与已 学知识融会贯通
极坐标系
定义:平面内的一条有规 定有单位长度的射线0x,0 为极点,0x为极轴,选定 一个长度单位和角的正方 向(通常取逆时针方向), 这就构成了极坐标系。
关于教材编排
参数方程是选修4-4专题的一个重要内容。这一专 题包含、涉及了很多高中内容。利用高二学生已掌 握的直线、圆和圆锥曲线曲线方程为基础,鼓励学 生利用参数的思想对它们进行探究解析,以及能学 习掌握如何优化参数的选择推出已知曲线方程的参 数形式,能等价互化参数方程与普通方程;借助实 际生活例子或相应习题体会参数方程的优势,理解 学习参数方程的缘由。
人教A版高中数学选修4-4课件 极坐标和直角坐标的互化课件

第一讲坐标系 二极坐标系
2.极坐标和直角 坐标的互化
人民教育出版社 高中 |选修4-4
基础知识:
人民教育出版社 高中 |选修4-4
人民教育出版社 高中 |选修4-4
思考:
人民教育出版社 高中 |选修4-4
老师点拨:
人民教育出版社 高中 |选修4-4
老师点拨:
人民教育出版社 高中 |选修4-4
人民教育出版社 高中 |选修4-4
人民教育出版社 高中 |选修4- : 1.极坐标与直角坐标互换的前提条件
2.互换的公式
3.互换的基本方法
典型例题1 :
人民教育出版社 高中 |选修4-4
分析:
人民教育出版社 高中 |选修4-4
人民教育出版社 高中 |选修4-4
人民教育出版社 高中 |选修4-4
学生思考,老师总结 :
人民教育出版社 高中 |选修4-4
典型例题2 :
人民教育出版社 高中 |选修4-4
分析:
人民教育出版社 高中 |选修4-4
2.极坐标和直角 坐标的互化
人民教育出版社 高中 |选修4-4
基础知识:
人民教育出版社 高中 |选修4-4
人民教育出版社 高中 |选修4-4
思考:
人民教育出版社 高中 |选修4-4
老师点拨:
人民教育出版社 高中 |选修4-4
老师点拨:
人民教育出版社 高中 |选修4-4
人民教育出版社 高中 |选修4-4
人民教育出版社 高中 |选修4- : 1.极坐标与直角坐标互换的前提条件
2.互换的公式
3.互换的基本方法
典型例题1 :
人民教育出版社 高中 |选修4-4
分析:
人民教育出版社 高中 |选修4-4
人民教育出版社 高中 |选修4-4
人民教育出版社 高中 |选修4-4
学生思考,老师总结 :
人民教育出版社 高中 |选修4-4
典型例题2 :
人民教育出版社 高中 |选修4-4
分析:
人民教育出版社 高中 |选修4-4
2020-2021学年人教A版数学选修4-4课件:第一讲 二 第一课时 极坐标系的概念
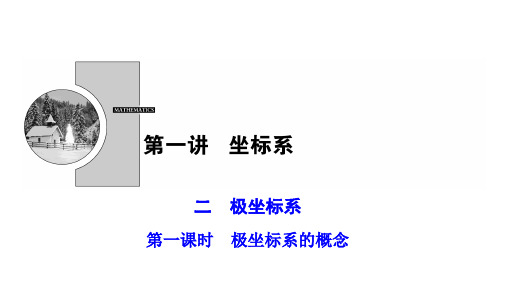
2.设点 A2,π3,直线 l 为过极点且垂直于极轴的直线,分别求点 A 关于极轴, 直线 l,极点的对称点的极坐标(限定 ρ>0,-π<θ≤π). 解析:如图所示,
关于极轴的对称点为 B2,-π3. 关于直线 l 的对称点为 C2,23π. 关于极点 O 的对称点为 D2,-23π. 四个点 A,B,C,D 都在以极点为圆心,2 为半径的圆上.
4.点与极坐标的关系 一般地,极坐标(ρ,θ)与__(ρ_, ___θ_+__2_k_π_)_(k_∈__Z__)表示同一个点.特别地,极点 O 的坐标为 (0,θ)(θ∈R).和点的直角坐标的唯一性不同,平面内一个点的极坐标有 无数 种表示. 如果规定 ρ>0, 0≤θ<2π ,那么除 极点 外,平面内的点可用 唯一 的极坐标(ρ,θ) 表示;同时,极坐标(ρ,θ)表示的点也是唯一 确定的.
[自主梳理]
在平面直角坐标系中,点的位置用有序实数对确定,平面内的点的位置也可以用距离
和角度确定.
2.极坐标系 如图所示,在平面内取一个 定点 O,叫做极点,自极点 O 引一条 射线 Ox,叫做极轴;再选定一个长度单位、一个 角度单位(通常取弧度)及其
正方向(通常取 逆时针 方向),这样就建立了一个极坐标系.
D4,34π,如图位置.
怎样确定极坐标点的位置 由极坐标确定点的位置,常常首先由 θ 的值确定射线(方向),再由 ρ 的值确定 位置.如果 θ 的值不在[0,2π)范围内,先根据 θ=θ0+2kπ(k∈Z)确定出 θ0∈[0,2π) 的值再确定方向.
1.在极坐标系中,作出以下各点:A(4,0),B3,π4,C2,π2,D3,74π. 解析:如图所示,A,B,C,D 四个点分别是唯一确定的.
D.圆
解析:由于 ρ=1,θ∈R 表示到极点距离等于 1 的点的集合,即以极点为圆心,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题(每小题6分,共36分) 1.下列极坐标对应的点在极轴上的是( (A)(1,1) (B)(2,0) (C)(3, )
6
) (D)(3, )
2
【解析】选B.由于极轴上的点为(ρ,2kπ)k∈Z,ρ≥0, 故(2,0)在极轴上.
二、填空题(每小题8分,共24分) 7.极坐标系中(ρ >0,θ ∈[0,2π )),点(2,
5 )关于 3
极点的对称点的极坐标为______.
【解析】点(2, 5)关于极点的对称点的极坐标为
3
(2,
5 2 +π),即(2, 2 +2π),依题意,得(2, )为 3 3 3
所求.
答案:(2, 2 )
3
点的极坐标: (1)ρ >0,-π <θ ≤π .
(2)ρ <0,0≤θ <2π .
(3)ρ <0,-2π <θ ≤0
【解析】
【解析】选D.由于ρ=1,θ∈R表示到极点距离等于1的点的
集合,即以极点为圆心,半径为1的圆.
4.极坐标系中,点A(1, ),B(2, 13 ),则|AB|等于( 12 12
)
(A)1
(B)2
12 12
(C)3
(D)4
【解析】选C.由于 与 13 的终边互为反向延长线,即A,O,
B三点共线,所以|AB|=|AO|+|OB|=1+2=3.
2.极坐标系中,与点(3,
(A)(3,13 )
6 (C)(3,17 ) 6 6
)相同的点是( 6 (B)(3, ) 6
)
(D)(3, 5 )
6
【解析】选A.由于 与 13 的终边相同,所以与点(3, )
6 6
重合的点是(3,13 ).
6
3.极坐标系中,集合{(ρ ,θ )| ρ =1,θ ∈R}表示的图形是 ( (A)点 (B)射线 (C)直线 (D)圆 )
5.极坐标系中,点(3,-5)到极轴所在直线的距离为(
)
(A)3cos5
(C)3sin5
(B)-3cos5
(D)-3sin5
【解析】选D.由于点(3,-5)到极轴所在直线的距离为 3|sin5|,而 3 <5<2π,sin5<0,所以-3sin5为所求.
2
6.极坐标系中,已知点A(2, ), 2, 3 ) ,O(0,0),则△ABO B(
6
12.(14分)如果对点的极坐标定 义如下:当已知M(ρ ,θ )(ρ >0, θ ∈R)时,点M关于极点O的对称
) 3 3
点M′(-ρ ,θ ).例如M(3,
关于极点O的对称点M′(-3, ),
就是说(3, +π )与(-3, )表示同一点.
3 3
已知A点的极坐标是(6, 5 ),分别在下列给定条件下,写出A
3
8.已知极坐标系中,P(3, ),A(2,3 ),0≤θ <2π ,则点A关于
2
4
射线OP的对称点的极坐标为_______.
【解析】如图所示,∠xOA= 3 ,
∠xOP=
,设A关于射线OP的对称 2
4
点为A′,应有|OA′|=|OA|=2,
∠xOA′= ቤተ መጻሕፍቲ ባይዱ ,
4 ∴A′(2, ). 4 答案:(2, ) 4
是任意实数,故③正确,②不正确;点M(4, )与点N(4,5 )
4 4 4 4
的极角分别是θ1= ,θ2= 5 ,二者的终边互为反向延长线,
它们是两个不同的点,故④不正确;由于动点M(5,θ)(θ
>0)的极径ρ=5,极角θ是正角,故点M的轨迹是以极点O为 圆心,半径为5的圆,故⑤正确. 答案:①③⑤
三、解答题(共40分)
10.(12分)已知M点的极坐标是(3, ),分别在下列给定条件 3
下求出M点关于极轴、极点、过极点垂直于极轴的直线的对称 点M1、M2、M3的极坐标. (1)ρ >0,0≤θ <2π ;
(2)ρ >0,-π <θ ≤π .
【解析】如图所示, (1)当ρ>0,0≤θ<2π时,
2
4
为(
) (B)直角三角形
(A)等边三角形
(C)等腰锐角三角形
(D)等腰直角三角形
4
【解析】选D.由题意,得∠AOB= ,由余弦定理得
|AB|= ( 2) +2 -2 2 2cos = 2, 4 且|OB|2+|AB|2=|OA|2,∴∠ABO= . 2
2 2
故△ABO为等腰直角三角形.
9.关于极坐标系的下列叙述: ①极轴是一条射线; ②极点的极坐标是(0,0);
③点(0,0)表示极点;
5 ④点M(4, )与点N(4, )表示同一个点; 4 4
⑤动点M(5,θ )(θ >0)的轨迹是以极点为圆心,半径为5的 圆. 其中,所有正确的叙述的序号是______.
【解析】根据极坐标系及其概念知,设极点为O,极轴就是射 线Ox,方向水平向右,故①正确;极点O的极径ρ=0,极角θ
ρ=|OM1|=|OM2|
=|OM3|=|OM|=3,
11.(14分) 已知两点的极坐标A(3, ),B(3, ),AB与极轴 2 6
交于点C. 求:(1)|AB|,|AC|;
(2)∠ACx.
【解析】根据极坐标的定义可得,|AO|=|BO|=3,∠AOB= ,
3
即△AOB为等边三角形,所|AB|=|AO|=|BO|=3,|AC|=2|AB|=6, ∠ACx= 5 .
6
) (D)(3, )
2
【解析】选B.由于极轴上的点为(ρ,2kπ)k∈Z,ρ≥0, 故(2,0)在极轴上.
二、填空题(每小题8分,共24分) 7.极坐标系中(ρ >0,θ ∈[0,2π )),点(2,
5 )关于 3
极点的对称点的极坐标为______.
【解析】点(2, 5)关于极点的对称点的极坐标为
3
(2,
5 2 +π),即(2, 2 +2π),依题意,得(2, )为 3 3 3
所求.
答案:(2, 2 )
3
点的极坐标: (1)ρ >0,-π <θ ≤π .
(2)ρ <0,0≤θ <2π .
(3)ρ <0,-2π <θ ≤0
【解析】
【解析】选D.由于ρ=1,θ∈R表示到极点距离等于1的点的
集合,即以极点为圆心,半径为1的圆.
4.极坐标系中,点A(1, ),B(2, 13 ),则|AB|等于( 12 12
)
(A)1
(B)2
12 12
(C)3
(D)4
【解析】选C.由于 与 13 的终边互为反向延长线,即A,O,
B三点共线,所以|AB|=|AO|+|OB|=1+2=3.
2.极坐标系中,与点(3,
(A)(3,13 )
6 (C)(3,17 ) 6 6
)相同的点是( 6 (B)(3, ) 6
)
(D)(3, 5 )
6
【解析】选A.由于 与 13 的终边相同,所以与点(3, )
6 6
重合的点是(3,13 ).
6
3.极坐标系中,集合{(ρ ,θ )| ρ =1,θ ∈R}表示的图形是 ( (A)点 (B)射线 (C)直线 (D)圆 )
5.极坐标系中,点(3,-5)到极轴所在直线的距离为(
)
(A)3cos5
(C)3sin5
(B)-3cos5
(D)-3sin5
【解析】选D.由于点(3,-5)到极轴所在直线的距离为 3|sin5|,而 3 <5<2π,sin5<0,所以-3sin5为所求.
2
6.极坐标系中,已知点A(2, ), 2, 3 ) ,O(0,0),则△ABO B(
6
12.(14分)如果对点的极坐标定 义如下:当已知M(ρ ,θ )(ρ >0, θ ∈R)时,点M关于极点O的对称
) 3 3
点M′(-ρ ,θ ).例如M(3,
关于极点O的对称点M′(-3, ),
就是说(3, +π )与(-3, )表示同一点.
3 3
已知A点的极坐标是(6, 5 ),分别在下列给定条件下,写出A
3
8.已知极坐标系中,P(3, ),A(2,3 ),0≤θ <2π ,则点A关于
2
4
射线OP的对称点的极坐标为_______.
【解析】如图所示,∠xOA= 3 ,
∠xOP=
,设A关于射线OP的对称 2
4
点为A′,应有|OA′|=|OA|=2,
∠xOA′= ቤተ መጻሕፍቲ ባይዱ ,
4 ∴A′(2, ). 4 答案:(2, ) 4
是任意实数,故③正确,②不正确;点M(4, )与点N(4,5 )
4 4 4 4
的极角分别是θ1= ,θ2= 5 ,二者的终边互为反向延长线,
它们是两个不同的点,故④不正确;由于动点M(5,θ)(θ
>0)的极径ρ=5,极角θ是正角,故点M的轨迹是以极点O为 圆心,半径为5的圆,故⑤正确. 答案:①③⑤
三、解答题(共40分)
10.(12分)已知M点的极坐标是(3, ),分别在下列给定条件 3
下求出M点关于极轴、极点、过极点垂直于极轴的直线的对称 点M1、M2、M3的极坐标. (1)ρ >0,0≤θ <2π ;
(2)ρ >0,-π <θ ≤π .
【解析】如图所示, (1)当ρ>0,0≤θ<2π时,
2
4
为(
) (B)直角三角形
(A)等边三角形
(C)等腰锐角三角形
(D)等腰直角三角形
4
【解析】选D.由题意,得∠AOB= ,由余弦定理得
|AB|= ( 2) +2 -2 2 2cos = 2, 4 且|OB|2+|AB|2=|OA|2,∴∠ABO= . 2
2 2
故△ABO为等腰直角三角形.
9.关于极坐标系的下列叙述: ①极轴是一条射线; ②极点的极坐标是(0,0);
③点(0,0)表示极点;
5 ④点M(4, )与点N(4, )表示同一个点; 4 4
⑤动点M(5,θ )(θ >0)的轨迹是以极点为圆心,半径为5的 圆. 其中,所有正确的叙述的序号是______.
【解析】根据极坐标系及其概念知,设极点为O,极轴就是射 线Ox,方向水平向右,故①正确;极点O的极径ρ=0,极角θ
ρ=|OM1|=|OM2|
=|OM3|=|OM|=3,
11.(14分) 已知两点的极坐标A(3, ),B(3, ),AB与极轴 2 6
交于点C. 求:(1)|AB|,|AC|;
(2)∠ACx.
【解析】根据极坐标的定义可得,|AO|=|BO|=3,∠AOB= ,
3
即△AOB为等边三角形,所|AB|=|AO|=|BO|=3,|AC|=2|AB|=6, ∠ACx= 5 .
