热辐射基本定律及辐射特性
传热学-热辐射基本定律和辐射特性

C1 (λT
eC2 /(λT )
)−5
d −1
(
λT
)
=
f
(λT )
f(λT)称为黑体辐射函数,表示温度为T 的黑体所发射的辐射能 中在波段0~λ内的辐射能所占的百分数。
利用黑体辐射函数数值表(360页表8-1)可以很容易地用 下式计算黑体在某一温度下发射的任意波段的辐射能量:
Eb(λ1−λ2 ) = ⎡⎣ Fb(0−λ2 ) − Fb(0−λ1) ⎤⎦ Eb
∫ 显然有
Eb =
∞ 0
Ebλ
d
λ
普朗克定律解释了黑体辐射能按波长分布的规律:
Ebλ
=
c1λ−5
ec 2
(λT )
−1
式中,Ebλ—黑体光谱辐射力,W/m3
λ— 波长,m ; T — 黑体温度,K ; c1 — 第一辐射常数,3.7419×10-16 W⋅m2; c2 — 第二辐射常数,1.4388×10-2 W⋅K;
8.1.2 从电磁波角度描述热辐射的特性
8.1.2 从电磁波角度描述热辐射的特性
c 电磁波的数学描述: = λν
c — 电磁波传播速度, m/s ν — 频率, 单位 1/s λ — 波长, 常用μm为单位
从理论上说,物体热辐射的电磁波波长范围可以包括整个波谱,即波长从零到无穷大 然而,在工业上所遇到的温度范围内,即2000K以下,有实际意义的热辐射波长位于 0.38—100μm之间,且大部分能量位于红外线区段的0.76—20μm范围内,而在可见 光区段、即波长为0.38—0.76μm 的区段,热辐射能量的比重不大
τ =0, α + ρ =1
第七章 热辐射基本定律及物体的辐射特性

本质原因:物体对不同波长 的光谱吸收比 ( ) 不同
4、灰体——光谱吸收比 ( ) 与波长无关的物体 • ( ) 常数 •灰体吸收比 与外界条件无关 •灰体同黑体一样,是一种理想物体
实际物体常可看作灰体的条件:
1)热辐射能量集中在 0.76 10 m 红外线内, 而 ( ) 在此区内近似不变的物体 2)对投入的热辐射波长范围具有等 ( ) 的物体
若投入辐射来自黑体( T2 )(吸收物体温度 T1 ),则
0
( , T1 ) Eb (T2 )d
0
Eb (T2 )d
0
( , T1 ) Eb (T2 )d T24
(7-23b)
f (T1 , T2,表面1性质)
若投入辐射来自实际物体(T2 ),则
(7-3)
(7-4)
漫反射 (一般工程材料表面形成)
液体
四、几个名词 1、黑体——物体的吸收比 1 ( 0)
2、镜体——物体的镜面反射比 1 ( 0) 3、白体——物体的漫反射比 1 4、透明体——物体的穿透比 1 ( 0)
3、斯忒藩-玻耳兹曼定律(俗称四次方定律) ——黑体辐射力 Eb
T
Eb Eb d
0
0
c1 5 4 d T ec2 ( T ) 1
黑体辐射常数
(7-9)
8 2 4 其中 5.67 × 10 W (m K )
或
其中
T 4 Eb c0 ( ) 100 ,
b) T 1000 则 Fb (0 ) 0.05%
热辐射基本定律及物体的辐射特性

5、光谱辐射(单色辐射) 对于某一特定波长下的辐射称为光谱辐射或单
色辐射。 对光谱辐射相应有光谱吸收比、光谱反射比和
光谱透射比。 1
()() () 1
关于物体的颜色
我们所看到的物体颜色是由于从该表面发出的 单色光线(辐射)投入到了我们的眼睛。
而从表面发出的辐射可能是自身发射的,也可 能是反射投入其表面上的可见光。
的份额分别称为吸收比、反射比 和透射比 。
G
G
G G
G G
1
3、镜反射和漫反射 视物体表面状况(平整程度)和投入辐射的波
长,表面的反射又分为镜反射和漫反射。
(a)镜反射
(b)漫反射
漫反射是把来自任意方向、任意波长的投入辐
射以均匀的强度(不是“能量”)反射到半球空间所 有方向上去。注:除了经特殊处理的金属表面,大
如果仅考虑某特定
p
波长的辐射,那么相应
可见辐射
的量被称为定向光谱辐
面积
射强度 L(,) 。
dA
(4) 定向辐射力
是指单位时间、单位辐射面积向空间指定方向
所在的单位立体角内发射的全波段辐射能量。用
符号 E 表示。
E
d()
dAd
因此可得:
E L()cos
E 2Ed
§8-2 黑体辐射的基本定律
一、黑体与黑体模型
三、斯忒藩-玻耳兹曼定律
黑体辐射的辐射力与温度的关系遵循斯忒藩-波 尔兹曼定律:
E b0 E d0 eC C 2/1 T 5 1dT4
Eb T4
Eb
C0
T 4 100
5.67108 W/2(m K4)
C05.67W/2(m K4)
波段范围内辐射力的计算
热辐射基本定律及物体的辐射特性

第八章 热辐射基本定律及物体的
14
辐射特性
在许多实际问题中,往往需要确定某一特定波长区段内的辐射能量。 黑体在[λ1,λ2]区段所发出的辐射能为(见图7-7)
Eb
2 1
Ebd
通常把这一波段的辐射能表示成同温下黑体辐射力(0-∞)的
百分数,记为Fb(λ1-λ2)。于是
Fb(12) 01 2EEbbddT14 12Ebd
对于服从兰贝特定律的辐射,其定向辐射强度L与辐射力E之间有如 下关系:
Байду номын сангаас
第八章 热辐射基本定律及物体的
16
辐射特性
(1)定向辐射强度
① 先引入立体角的概念(见图7-8)
平面角:θ=s/r [rad](弧度) 式中: 弧长s、半径r 。
立体角:Ω=Ac/r2
式中:Ac —半球体表面被立体角切割的面积, r—球体的半径。
对半球,面积为2πr2,立体角为2π[ sr](球面度)。 微元立体角:dΩ= dAC/r2
(2)单色辐射力Eλ:在热辐射的整个波谱内,不同波长发射出的 辐射能是不同的。见图7-6。对特定波长λ来说:
从λ到λ+dλ区间发射出的能量为dE。则
E
dE
d
第八章 热辐射基本定律及物体的
10
辐射特性
单位时间内物体的单位表面积向半球空间所有方向发射出去的某一 特定波长的辐射能。称为单色辐射力。[w/m3]。
图7-6 Planck 定律的图示
第八章 热辐射基本定律及物体的
12
辐射特性
最大单色辐射力所对应的波长λm亦随温度不同而变化。随着 温度的增高,曲线的峰值向左移动,即移向较短的波长。最大单色 辐射力所对应的波长λm与温度T之间存在着如下的关系:
辐射传热-热辐射基本定律和辐射特性

4.1.1热辐射的定义及基本性质1.热辐射定义热辐射-Thermal Radiation物体由于热的原因(温度高于0 K)而发射电磁波的现象只要温度高于0 K,就会不停地向周围空间发出热辐射1.热辐射定义辐射换热-Radiation Heat Transfer物体之间通过热辐射交换热量的过程当系统达到热平衡时,辐射换热量为零,热辐射仍然不断进行2.热辐射特点近程及远程效应∞-44w T T 而与成正比∞-w T T 换热不再与成正比,伴随能量形式的转变可以在真空中传播可穿过真空或低温区(好处-航天器散热;坏处-保温瓶散热)辐射能与温度和波长均有关具有强烈的方向性3.热辐射具有电磁波的共性f=C电磁波谱激光红宝石0.6943μmCO210.6μm氦氖0.6328μm微波加热原理?高频电磁波300-300000 MHz (相应波长100-0.1cm),使生物组织内偶极分子及蛋白质极性侧链以极高频率振荡,增加分子运动从而导致热量产生热辐射理论上覆盖整个电磁波谱对于太阳辐射(约5800K ):0.2~2μm可见光:0.38~0.76μm红外线:0.76~25~1000μm一般工业范围内(2000K 以下):0.38~100μm0.76~20μm远红外加热技术4.物体对热辐射的吸收、反射和穿透当热辐射投射到物体表面上时,一般会发生吸收、反射和穿透。
transmissivityabsorptivity reflectivity物体对热辐射的吸收、反射和穿透热辐射-Thermal Radiation5.反射同样具有镜反射和漫反射的分别镜反射漫反射对于大多数的固体和液体1,0=+=ρατ1,0=+=ταρ对于不含颗粒的气体只涉及表面整个气体容积假想的1=α1=ρ1=τ透明体黑体镜体或白体三种理想情形4.1.2黑体模型1.黑体定义(Blackbody)可以全部吸收透射到其表面上的所有波长的辐射能( =1)【不存在任何反射和透射】室温条件下:能量集中在长波电磁辐射和远红外波段到一定温度:开始发出可见光【钢材升温过程】 黑体不见得就是黑色的【取决于温度】2.黑体模型理想化模型:自然界并不存在严格意义上的黑体 人工模型黑体模型✓小孔面积占空腔内壁总面积的比值越小,小孔就越接近黑体✓若这个比值小于0.6%,当内壁吸收比为0.6时,计算表明,小孔的吸收比可达99.6%带有小孔的温度均匀的空腔✓温度均匀【保证辐射均匀且各向同性】✓具有黑体性质【小孔及空腔内部】✓举例:晴天远眺窗口黑洞洞的枪口3. 黑体应用黑体炉对辐射温度计的校准、检定,通常采用比较法,就是通过高稳定度的辐射源(通常为黑体辐射源)和其他配套设备,将标准器所复现的温度与被检辐射温度计所复现的温度进行比较,以判断其是否合格或给出校准结果。
传热学-第七章热辐射基本定律及物体的辐射特性

在单位立体角内发射的一切波长的能量,参见图8-10。 d( , ) L( , ) dA cos d (6) Lambert 定律(黑体辐射的第 三个基本定律)
d( , ) L cos dA d
第八章 热辐射基本定律和辐射特性 24
本节中,还有几点需要注意
1. 将不确定因素归于修正系数,这是由于热辐射非常复杂,
很难理论确定,实际上是一种权宜之计; 2. 服从Lambert定律的表面成为漫射表面。虽然实际物体的 定向发射率并不完全符合Lambert定律,但仍然近似地认 为大多数工程材料服从Lambert定律,这有许多原因;
3. 物体表面的发射率取决于物质种类、表面温度和表面状况。
这说明发射率只与发射辐射的物体本身有关,而不涉及外
界条件。
第八章 热辐射基本定律和辐射特性 25
§8-4
实际物体对辐射能的吸收与辐射的关系
上一节简单介绍了实际物体的发射情况,那么当外界 的辐射投入到物体表面上时,该物体对投入辐射吸收 的情况又是如何呢?本节将对其作出解答。
1
0
( , T1 ) b ( , T2 ) Eb (T2 )d
0
b ( , T2 ) Eb (T2 )d
0
( , T1 ) Eb (T2 )d
0
Eb (T2 )d
T24 f (T1 , T2 , 表面1的性质)
图8-19给出了一些材料对黑体辐射的吸收比与温度的关系。
第八章 热辐射基本定律和辐射特性
21
对应于黑体的辐射力Eb,光谱辐射力Eb和定向辐射强度L, 分别引入了三个修正系数,即,发射率,光谱发射率( )和定 向发射率( ),其表达式和物理意义如下 实际物体的辐射力与 黑体辐射力之比: 实际物体的光谱辐射 力与黑体的光谱辐射 力之比: 实际物体的定向辐射 强度与黑体的定向辐 射强度之比:
传热学第8章热辐射基本定律和辐射特性

1. 立体角
A r2
sr 球面度
对整个半球:
A 2r 2 2 sr
对微元立体角:
d
dA r2
s in dd
sr
n θ
dΩ r dA1
立体角定义
dθ dA2
φ dφ
r sind
rd
dA2
2. 定向辐射强度(辐射强度) 物体单位时间单位可见辐射面积单位立体角
内发出的辐射能量。
L( ,) d
n
W /(m2 sr)
引入辐射比 Fb(1 2 )
0
1
2
黑体波段内的辐射力
F b(12 )
E d 2
1
b
0 Eb d
1
0T 4
E d 2
1
b
F F b(02 )
b(01 )
其中: Fb(0) 为黑体辐射函数(表8-1)
则波段内黑体辐射力:
Eb(1 2 ) [Fb(02 ) Fb(01 ) ]Eb
8.2.3 兰贝特定律
dф
dAcosd
θ
dA2
对各向同性物体表面:
dΩ
L( ,) L( )
dA1
dA1cosθ
3. 定向辐射力 单位时间单位面积物体表面向某个方向发射
单位立体角内的辐射能, 称为该物体表面在该 方向上的定向辐射力。Eθ,W/(m2.sr)
4. 兰贝特定律 黑体的定向辐射强度与方向无关, 即半球空间各方向上的辐射强度都相等。
热辐射投射到固体,液体表面上:
1 0
表面性
热辐射投射到气体表面上:
1 0 容积性
(3)固体表面的两种反射现象 ✓镜反射 (Specular reflection) ✓漫反射 (Diffuse reflection) 主要取决于固体表面不平整尺寸 的大小(表面粗糙度)。
传热学-第七章热辐射基本定律及物体的辐射特性

定律 表示式 说明
韦恩位移定律 λmax = b / T 黑体辐射波长与温度的关系
理想黑体的辐射特性
理想黑体具有尽可能高的吸收率和发射率,同时它是完美的热辐射体,能够根据其温度和波长分布发射出连续 的辐射能量。
实际物体的辐射特性
实际物体的辐射特性受到其表面性质的影响。反射率与吸收率、发射率与辐射率以及雷诺茨定律帮助我们了解 和描述实际物体的辐射情况。
反射率与吸收率
实际物体吸收和反射辐射能量 的能力
发射率与辐射率
实际物体辐射能量的发出能力
雷诺茨定律
物体在达到热平衡后,各表面 温度和总发射能力一致
热辐射的应用和实例
热辐射广泛应用于热工技术、太阳能技术、计算机热管理等领域。例如,太阳能电池利用光照下的热辐射转换 为电能。
太阳能电池
利用光照下的热辐射转换为电能
传热学-第七章热辐射基 本定律及物体的辐射特性
了解热辐射的基本概念和定义,掌握热辐射的三大基本定律:斯特藩-玻尔兹 曼定律,基尔霍夫定律和韦恩位移定律。
斯特藩-玻尔兹曼定律
斯特藩-玻尔兹曼定律揭示了黑体辐射功率与温度的关系,P = εσT4,其中P为辐射功率,ε为辐射率,σ为斯特 藩-玻尔兹曼常数。
定律 表示式 说明
斯特藩-玻尔兹曼定律 P = εσT4 黑体辐射功率与温度的关系
基尔霍夫定律
基尔霍夫定律阐明了一个物体表面的吸收率和发射率相等,α = ε。
1 基尔霍夫定律
物体表面的吸收率和发射率相等
韦恩位移定律
韦恩位移定律描述了黑体辐射波长与黑体温度之间的关系,λmax = b / T,其中λmax是峰值辐射波长,b是韦恩 位移常数。
总结和要点
• 热辐射包括斯特藩-玻尔兹曼定律、基尔霍夫定律和韦恩位移定律 • 理
传热学热辐射基本定律和辐射特性课件

工业辐射加热与冷却
工业辐射加热
利用辐射方式将热量传递给物料 ,实现高效、均匀的加热效果。
工业辐射冷却
利用辐射方式将热量传递给冷却 介质,实现高效、快速的冷却效
果。
工业辐射干燥
利用辐射方式将热量传递给物料 ,实现快速、均匀的干燥效果。
05
热辐射研究展望
新型热辐射材料研究
总结词
随着科技的发展,新型热辐射材料的研究成为传热学领域的重要方向。
详细描述
通过研究热辐射与大气、水体和地表 的相互作用,可以深入了解地球系统 的能量平衡和蔼候变化机制。同时, 这种研究也为可再生能源的利用和环 境保护提供了理论支持。
热辐射在新能源领域的应用研究
总结词
热辐射在新能源领域的应用研究具有广阔的前景。
详细描述
利用热辐射进行光热转换,可以实现太阳能的利用和转化。此外,热辐射在高温核聚变、磁流体发电和地热能利 用等领域也有着重要的应用价值。通过深入研究热辐射在这些新能源领域的应用,有望为解决能源危机和环境污 染问题提供新的解决方案。
意义。
吸取率
总结词
详细描述
吸取率是物体吸取热辐射能量的能力,它 决定了物体对热辐射的吸取程度。
吸取率表示物体在特定温度下吸取的热量 与入射到物体上的总热量之比。物体的吸 取率与其发射率和反射率有关。
总结词
详细描述
吸取率的值介于0和1之间,完全吸取的物 体吸取率为1,完全不吸取的物体吸取率为 0。
了解物体的吸取率对于设计热辐射系统、 控制热能传递和优化热能利用具有重要意 义。
普朗克辐射定律
总结词
普朗克辐射定律描述了黑体光谱辐射的能量散布。
详细描述
普朗克辐射定律指出,黑体的光谱辐射强度与波长、温度有关。在任意波长下 ,黑体的光谱辐射强度与温度成正比。该定律是量子力学的基础之一,适用于 所有温度下的黑体辐射。
第八章-热辐射基本定律和辐射基本特性分解

8-3 灰体和基尔霍夫定律
一、实际物体的辐射特性和发射率
▲光谱辐射力随波长呈现不规则的变化;
实际物体 辐射特性:
▲辐射力并不严格地同热力学温度四次方成正比;
▲定向辐射强度在不同方向上有变化谱发射率( )
—修正光谱辐射力Eb
定向发射率( )
—修正定向辐射强度I
★发射率(黑度)ε—— 实际物体的辐射力与同温度下黑体的辐射力的比值。
固体和液体对辐射能的吸收和反射基本上属于表面效应: 金属的表面层厚度小于1m;绝大多数非金属的表面层厚度小 于1mm。
二、黑体模型
能吸收投入到其表面上的所有热辐射能的物体,是 一种科学假想的物体,现实中并不存在。
黑体: 白体或镜体:
1
1
透明体:
1
煤烟、炭黑、粗糙的钢板 0.9以上
黑体吸收和发射辐射能的能力最强
热辐射是热量传递的 基本方式之一,以热辐 射方式进行的热量交换 称为辐射换热。
传热学
第八章 热辐射基本定律和辐射特性
§8-1 热辐射现象的基本概念
1. 热辐射特点
(1) 定义:由热运动产生的,以电磁波形式传递的能量;
(2) 特点:a 任何物体,只要温度高于0K,就会不停地向周
围空间发出热辐射;b 可以在真空中传播;c 伴随能量形
可见光波段的辐射能量比例为 0.545 8-0.099 32 = 0.446 5
0.76 m ~ 40 m红外波段的辐射能量比例
1.0-0.545 8 = 0.454 2
计算表明: (1) 大气层外太阳辐射中可见光的能量比例接近45%,而
40 m以内的红外辐射也占大约45%。 (2) 太阳辐射温度下,40m以上的红外辐射能量几乎为零。
传热学热辐射基本定律和辐射特性

黑色油漆对可见光吸收比约0.9 。
4.温室效应
暖房: 玻璃和塑料薄膜对λ< 3μm太阳辐射的穿透率很高 对内部的物体热辐射 λ> 3μm常温辐射的穿透率很低
•温室气体:CO2、CFC制冷剂(R12等)对≥3μm的 红外波段吸收率高,而对于太阳辐射穿透率高
光谱辐射力特征: 光谱辐射力随温度升高而增加;
光谱辐射力随波长增加先增后减,具有最大Ebλ 光谱辐射力最大处的波长随温度不同而不同,随温度增加,λmax减小
(2) 维恩位移定律
光谱辐射力最大处的波长λmax与绝对温度T 的乘积为常数。 λmaxT = 2.898×10-3m·K≈ 2.9×10-3m·K =2900μm·K
E
d( )
dA d
E 2 E d
d():面积dA的微元面积,向空间纬度角方向的微 元立体角d内辐射的能量
兰贝特定律—— 黑体按空间方向的分布规律
表述1:黑体辐射的定向辐射强度与方向无关,即半球空间的各方向上的定 向辐射强度相等:
d( ) dAcos d
=I b
const
表述2:黑体单位辐射面积,单位立体角的定向辐射力
说明: (1)工程上遇到温度范围,热射线集中在红外范 围内( 0.76~20μm ) (2)太阳辐射可见光占44.8%,红外线占45.1%, 紫外线占10.1% (3)常温20℃以下物体辐射几乎在3μm以上的红 外。
➢ 物体表面对热辐射的作用
(1)物体对热辐射的吸收、反射与穿透
根据能量守恒,有以下平衡方程:
微元立体角
d
dAc r2
➢ 黑体的定向辐射强度和定向辐射力:
E
d( )
dA d
实验测定 黑体
Eb,
第八章 热辐射基本定律和辐射特性(20190415)

E Eb
0 ()Ebd T4
实际物体光谱辐射力小于同温度 下黑体同一波长的光谱辐射力。
实际物体光谱辐射力随波长和方 向作不规则变化。
与波长无关----灰体
8.3 实际固体和液体的辐射特性
3 实际物体的定向辐射强度
定向发射率及其随θ角的变化规律
实际物体的定向辐射强度与 黑体的定向辐射强度之比为 定向发射率(定向黑度):
第八章 热辐射基本定律和辐射特性
主讲人:潘冬梅 华南理工大学机械与汽车工程学院
主要内容
8.1 热辐射现象的基本概念 8.2 黑体热辐射的基本定律 8.3 实际固体和液体的辐射特性 8.4 实际物体对辐射能的吸收与辐射的关系
8.1 热辐射现象的基本概念
8.1 热辐射现象的基本概念
1 热辐射的特性
辐射力与黑体半球总辐射力之比。
E E Eb T 4
实际物体的辐射力可以表示为:
E
Eb
T
4
C0
(T 100
)
4
一般通过实验测得,只取 决于物体本身
8.3 实际固体和液体的辐射特性
2 实际物体的光谱辐射力
光谱发射率(单色黑度) ε(λ) = Eλ Ebλ
实际物体的光谱发射率与发射率
1
d
T 4
8.2 黑体热辐射的基本定律
黑体2 辐普射朗函克数定(律黑体辐射能按波段的分布)
从0到某个波长的波段的黑体辐射能
Eb(0 ) 0 Eb d
这份能量在黑体辐射力中所占的百分数为:
可查表
P360
Fb(0)
0 Eb d T 4
热辐射基本定律和辐射特性

例7-1:试分别计算温度为2000K和5800K的黑
体的最大光谱辐射力所对应的波长m 。
解:按 m T2.910 3m K计算:
当T=2000K时, m2.9 210 0 3K m 0K 01.4 510 6m
当T=5800K时,
m2.9 518 0 3K m 0K 00.510 6m
可见工业上一般高温辐射(2000K内),黑体最大光 谱辐射力的波长位于红外线区段,而太阳辐射 (5800K)对应的最大光谱辐射的波长则位于可见光 区段。
dω为微元立体角
E
d 2Q
ddA
方向辐射力与辐射力之间的关系: E
E d
2
dQ
df
dQλ
r
dφ
dA
dA
(a)微元表面总辐射 (b)微元表面单色辐射
dA
(c)微元表面方向辐射
立体角是用来衡量空间中的面相对于某一点所 张开的空间角度的大小,如图c所示,其定义为:
d df r 2
df为空间中的微元面积,r为该面积与发射点之 间的距离。
普朗克定律表示的是黑体的辐射能按波长的分
布规律,给出了黑体的单色辐射力与热力学温 度T、波长之间的函数关系,由量子理论得到 的数学表达式为:
Eb
c1
5 ec2 (T )
1
c1为第一辐射常数,c1=3.74210-16W·m2; c2为第二辐射常数,c2=1.4388 10-2m·K
图中给出了在温度为参变量下的单色辐射力随
解:在热平衡条件下,黑体温度与室温相同, 辐射力为:Eb1c01T104 05.67m2W K4217 2 07 04 3K4
45W 9 2 /m
327℃黑体的辐射力为
《传热学》第8章-热辐射基本定律及物体的辐射特性
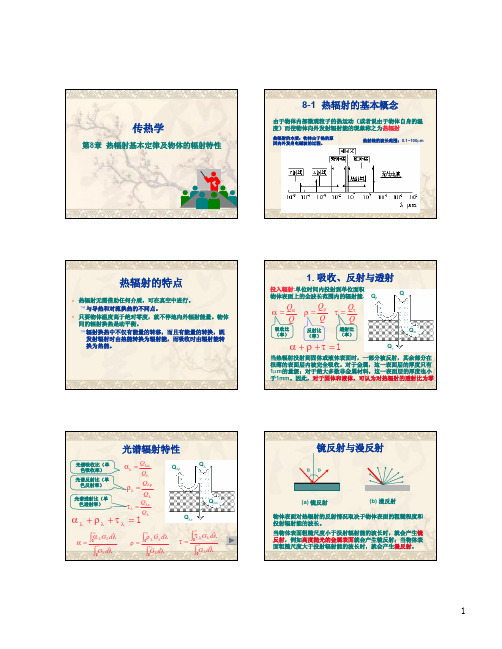
2. 斯忒藩—玻耳兹曼定律
v 斯忒藩(J. Stefan)—玻耳兹曼(D. Boltzmann)定律确 定了黑体的辐射力Eb与热力学温度T之间的关系
v 斯忒藩在1879年从实验中得出,后来玻耳兹曼于1884年运
用热力学理论进行了证明。
斯忒藩—玻耳兹曼 常数,又称为黑体
辐射常数
Eb = σT 4
σ= 5.67×10-8
光谱辐射力: 只对某一波长辐射能的辐射力, Eλ ,单位为W/m3。
∞
∫ E =
E
0
λ
dλ
定向辐射力: 单位时间内,单位面积物体表面向某个方向发射 的单位立体角内的辐射能 , Eθ,单位是W/(m2⋅Sr)。
∫ E = Ω=2π Eθ dΩ
∫ E = L(θ) cosθdΩ Ω =2π
2
8-2 黑体辐射的基本定律
∫ ∫ Fb(λ1−λ2 ) =
Eb(λ1 −λ2 ) Eb
=
λ2 0
Ebλ dλ
−
Eb
λ1 0
Ebλ dλ
Eb
=
Fb (0−λ2 ) −
Fb (0−λ1 )
[ ] E = b(λ1 −λ2 ) Fb(0−λ2T ) − Fb (0−λ1T ) Eb
例题
v 试计算太阳辐射中可见光所占的比例。
解:太阳可认为是表面温度为T = 5762 K的黑体,可见光的 波长范围是0.38~0.76µm ,即λ1 = 0.38 µm , λ2 = 0.76 µm , 于是
∞
2 Ebλ dλ Eb
Fb(0−2) =0.02 .6341
= 0.45Fb(0−2) + 0.1(1− Fb(0−2) )
0.1
No.20 1130 8 热辐射的基本定律和辐射特性
4、 兰贝特(Lambert)定律: 描述黑体在某一温度下所辐射的全 部波长的能量沿半球空间方向上的分布规律。
13
二、 实际固体和液体的吸收特性
对于黑体 发射率 1 吸收比 1 那么 对于实际物体 发射率 1 吸收比 1 那么 ? 那么对实际物体发射率和吸收比之间存在什么关系?为了进行研究,首先定义两 个概念。
1、吸收比和光谱吸收比
吸收比: 物体对投入辐射所吸收的百分数
26
作一名聪明 好学的好孩 子,上课注 意听讲。。
27
第八章
热辐射基本定律及 物体的辐射特性
主要内容:
8.1 热辐射现象的基本概念
8.2 黑体热辐射的基本定律 8.3 实际固体和液体的辐射特性 8.4 实际物体对辐射能的吸收与辐射的关系
2
Quick Review
黑体辐射定律小结:
1、 普朗克(Planck)定律: 描述黑体在某一温度下向半球空间所 有方向辐射的能量沿波长分布的规律。
(T ) (T25 )
?
结论:
1、实际物体的辐射和吸收特性与波长、方向等因素有关,不 同于黑体。
2、工程上, 实际物体可处理为服从兰贝特定律, 即实际物体各 个方向的定向辐射强度相等(漫射体), I E / ;而且可以进 一步处理为灰体, 即物体的光谱吸收比与外界投入波长无 关, (T ) (T ) 。从而实际物体最终可以处理为漫灰体。 3、引入平均发射率以后,实际物体的发射力按照公式 E T 4 计算。 4、实际物体的平均发射率近似等于其法向发射率, n 查实际物体的法向发射率得到的值可以作为平均发射率使 用。
传热学-第八章 热辐射特性

§ 8-3 固体和液体的辐射特性
发射率 前面定义了黑体的发射特性:同温度下,黑体发射热辐 射的能力最强,包括所有方向和所有波长;
真实物体表面的发射能力低于同温度下的黑体;
因此,定义了发射率 (也称为黑度) :相同温度下,实际 物体的半球总辐射力与黑体半球总辐射力之比:
E E 4 Eb T
c2 T
5
0
1
d T
0
内所发射的辐射力:
Eb 1 2 Fb 0 2 Fb 0 1 Eb
图8-7 特定波长区段内的黑体辐射力
11
立体角
定义:球面面积除以球半径的平方称为立体角,单位:sr(球面度)
dAc rd r sin d d 2 sin d d 2 r r
0.76 0.38
Eb dλ=0.45Fb0.380.76 Eb
E 0.380.76 E
§8-4
实际物体对辐射能的吸收与辐射的关系
上一节简单介绍了实际物体的发射情况,那么当外界 的辐射投入到物体表面上时,该物体对投入辐射吸收 的情况又是如何呢?
Semi-transparent medium
吸收比为
吸收的总能量 1 投入的总能量
0
( , T1 ) ( , T2 ) Eb (T2 )d
0
( , T2 ) Eb (T2 )d
f (T1 , T2 , 表面1的性质, 表面2的性质)
32
如果投入辐射来自黑体,由于 b ( , T2 ) 1 ,则上式可为
第八章 热辐射基本定律 和辐射特性
1
§8-1 热辐射的基本概念
8.热辐射基本定率与辐射特性

8.2.3 Stefan-Boltzmann定律 E b0 E b d0 ec2c (1 T )5 1dT4
式中,σ= 5.67×10-8 w/(m2K4),是Stefan-Boltzmann常数。
波段辐射与辐射函数
黑体在波长λ1和λ2区段内所发 射的辐射力,如图所示:
Eb1~2
1 T 2 μ m 25 K 0 50 μ0 K m 0
查表得
Fb0~2 0.6341
1Fb0~221Fb0~2
0.450.63401.110.6341
0.322
E E b 0 .3 2 5 .6 2 1 7 8 0 W m 2K 4 25 K 4 00
7 .1 1 35 W 0m 2
辐射力与定向辐射力间的关系
E0 2E d 0 2I,co d s
辐射力与定向辐射强度的关系
E02I,cods
8.2.2 Planck定律
Eb
c15
ec2 (T) 1
式中,λ— 波长,m ;T — 黑体温 度,K ;c1 — 第一辐射常数, 3.742×10-16 Wm2; c2 — 第二辐射 常数,1.4388×10-2 WK;
定义为单位时间单位辐射面积向半球空间某一方向 上单位立体角内发出的所以波长的辐射能。
E
d dA d
★ 定向辐射力以单位实际辐射面积为度量依据, 而定向辐射强度以单位可见面积为度量依据
辐射力与光谱辐射力间的关系
E Ed 0
辐射强度与光谱辐射强度间的关系
I,0I,d
定向辐射力与定向辐射强度的关系
E I,co s
米的宇宙射线。 • 由于热的原因而产生的电磁波辐射称为热辐射。
热辐射区别于导热、对流的特点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E E Eb T 4
上面公式只是针对光谱和方向平均的情况,但是,实际 上,真实表面的发射能力随光谱和方向变化。
2、 实际物体的光谱辐射力
光谱发射率:实际物体的光谱辐射力与黑体的光谱 辐射力之比
Eλ
E ε Eb
ε
E Eb
ε( )E d
b 0
T 4
光谱吸收比:物体吸收某一特定波长辐射能的百分数。 表征物体对某一波长辐射能吸收特性的物理量。
几种金属材料的光谱吸收比
几种非金属材料的光谱吸收比 辐射特性随波长变化的性质称为辐射特性对波长的选择性。
实际物体的吸收比 :取决于物体本身材料的种类、温度及表面
性质,还与投入辐射的波长分布有关,因此与投入辐射能的发 射体温度有关。
的能量总和。 (W/m2); 光谱辐射力Eλ: 单位时间内,单位波长范围内(包含某一给定波长),物体的 单位表面积向半球空间发射的能量。 (W/m3); E、Eλ关系:
E
0
E d
黑体一般采用下标b表示,如黑体的辐射力为Eb,黑体的
光谱辐射力为Ebλ
立体角
定义:球面面积除以球半径的平方称为立体角,单位: sr(球面度),如图所示:
2、热辐射
由于物体内部微观粒子的热运动而使物体向外发射辐射能的
现象。 (1)热辐射的主要特点
a. 所有温度大于0 K的物体都具有发射热辐射的能力,温 度愈高,发射热辐射的能力愈强。 发射热辐射时: 内热能 辐射能 ; b. 所有实际物体都具有吸收热辐射的能力 物体吸收热辐射时: 辐射能 内热能 ; c. 热辐射不依靠中间媒介,可以在真空中传播,且传播效 率最高; d. 物体间以热辐射方式进行的热量 高温 传递是双向的。 物体
Wien位移定律给出λm与T 的关系:
mT 2.8976 103 m K
(2) Stefan-Boltzmann定律
0
E b d
c1 5 ec
2
0
( T )
1
d T 4 E b
即Eb T 4
式中,σ= 5.67×10-8 W/(m2K4),
3、实际物体的定向辐射强度
定向发射率:实际物体的定向辐射强度与黑体的定向发射 强度之比 I ( ) I ( ) ( ) Ib ( ) Ib 几种非导电体材料在不同 方向上的定向发射率 ( ) (t=0~90℃)
几种金属导体在不同方向上的定向发射 ( )(t=150℃)
对应于黑体的辐射力Eb,光谱辐射力Eb和定向辐射强度I,
力之比:实际物体的定向辐射Fra bibliotek强度与黑体的定向发
射强度之比:
因此,实际物体的光谱发射率并不是常数;定向发射率 也并不完全符合Lambert定律。
实际物体辐射的简化处理方式
1. 光谱发射率( )为常数==>灰体假设; 2. 定向发射率( )为常数==>漫射表面假设;
8.4 实际物体的吸收比和基尔霍夫定律
低温 物体
(2)物体对热辐射的吸收、反射和穿透
当热辐射投射到物体表面上时,一般会发生三种现象,即 吸收、反射和穿透,如图所示。
Q Q Q Q
Q Q Q 1 Q Q Q 1
对于大多数的固体和液体:
对于不含颗粒的气体:
0, 1 0, 1
d( ) =I dA cos d
I为常数,与θ 无关。
dA cos 称为可见面积
2、黑体辐射的三个基本定律及相关性质
(1) Planck定律
Eb
c15 ec
2
( T )
1
式中,Ebλ光谱辐射力,W/m3;λ:波长,m ;T :黑体 温度,K ; c1 :第一辐射常数,3.742×10-16 Wm2; c2 :第二辐射常数,1.4388×10-2 WK; 根据上式可得:不同温度 下Ebλ随波长λ的变化曲线。
2
实际物体的辐 射定律
假定物体的辐 射定律
ε 不随波长变 化,灰体 ε不随发射角变 化,漫射表面
E = T 4
1
E Eb I Ib
光谱辐射力 定向辐射力
( T )
d( ) I cos dA d
辐射力:半球空间、全部波长;E,W/m2 光谱辐射力:半球空间、某段波长;Eλ,W/(m2.μm) 定向辐射力:单位面积,单位立体角、全部波长,Icosθ,W/(m2.sr)
5. 漫灰表面的概念。
6. 维恩位移定律的表达式。 试考虑一下它在自然科学及工 程应用中的作用。 7. 四个黑体辐射基本定律的物理意义及计算应用。
f — 频率, 单位 s-1。
电磁波的波谱
射线: < 5×10-5 m
X射线: 5×10-7 m < < 5×10-2 m 紫外线: 4×10-3 m < < 0.38 m 可见光: 0.38 m < < 0.76 m 红外线: 0.76 m < < 103 m 无线电波: > 103 m
E
I cos d I
Lambert定律图示
8.3 固体和液体的辐射特性
定向辐射强度
光谱辐射力
1、实际物体发射率
同温度下,黑体发射热辐射的能力最强;
真实物体表面的发射能力低于同温度下的黑体;
发射率 (也称为黑度) :相同温度下,实际物体的辐射
力与黑体辐射力之比:
定向辐射强度:单位可见面积、单位立体角、全部波长,I,W/(m2.sr)
三者关系
E E d
0
E
I cos d
思考题:
1. 什么是黑体、 灰体? 实际物体在什么样的条件下可以看 成是灰体? 2. 光谱辐射力,定向辐射强度和辐射力的物理意义。它们 之间有什么关系? 3. 物体的发射率,吸收率,反射率,穿透率是怎样定义? 发射率和反射率有何不同?
固体表面镜反射与漫反射
镜反射 对于镜体或白体:
对于透明体:
漫反射
1
1
3、黑体模型
黑体是指能吸收投入到其面上
所有热辐射能的物体,是一种
科学假想的物体。
现实生活中不存在,但却可以
人工制造出近似的人工黑体。
人工黑体模型
8.2 黑体热辐射的基本定律
1、热辐射能量的表示方法 辐射力E:
单位时间内,物体的单位表面积向半球空间发射的所有波长
第八章 热辐射基本定律及辐射特性
8.1 热辐射的基本概念
1、辐射:电磁波传递能量的现象。
辐射的两种理论 :电磁理论与量子理论 电磁波的数学描述: c f
c — 某介质中传播速率, c c0 n
c0 3.0 10
8
m/s 为真空中的光速;
n 为介质的折射率。
— 波长, 常用m为单位, 1m = 10-6 m。
dAc d 2 r
dAc rd r sin d d sin d d
定向辐射强度 I 辐射强度:空间某一表面在单位时间,与辐射方向垂直的单 位面积上,单位立体角发射的波长为0 ~ ∞的能量,用I表示。 空间某一表面,面积为dA的黑体微元,在微元立体角dΩ内 辐射出去的能量为dΦ,则
重要推论:
1、吸收辐射能能力愈强的物体,发射辐射能能力也愈强。
2、在温度相同的物体中,黑体吸收辐射能的能力最强,发 射辐射能的能力也最强。 漫射灰体:辐射特性与角度和波长无关,只是温度的函数
T T
本章小结
辐射能力 辐射力
黑体的辐射定律
Eb = T 4
Eb c15 ec
Stefan-Boltzmann常数。
Planck定律与Stefan-Boltzmann定律的关系
(3) Lambert 定律
Lambert 定律:单位时间内,黑体单位可见面积,在单位 立体角中辐射出去的能量相等,或定向辐射强度I是常数。 Lambert 定律也称为余弦定律。单位时间内,黑体单位面 积,在单位立体角中辐射出去的能量随天顶角呈余弦规律 变化。 对上式沿半球方向积分,可获得了半球辐射力 E: Lambert定律与Stefan-Boltzmann 定律的关系
工程上的热辐射主要位于
0.76~10 m的红外波长范围
内,绝大多数工程材料的光 谱辐射特性在此波长范围内
变化不大,因此在工程计算
时可以近似地当作灰体处理。
一些材料对黑体辐射的吸收
比随黑体温度的变化。
基尔霍夫定律
基尔霍夫定律揭示了物体吸收辐射能的能力与发射辐射能
的能力之间的关系,其表达式为
,, T ,, T
分别引入了三个修正系数,即(总)发射率,光谱发射率 ( ) 和定向发射率 ( ),其表达式和物理意义如下 实际物体的辐射力与 黑体发射力之比: 实际物体的光谱辐射 力与黑体的光谱发射
E Eb
0
( ) Eb d T 4
E ( ) Eb
I ( ) I ( ) ( ) Ib ( ) Ib
