计数问题之递推法例题讲解3

合集下载

奥数讲义计数专题：归纳与递推

华杯赛计数专题：归纳与递推基础知识：1.递推的基本思想：从简单情况出发寻找规律，逐步找到复杂问题的解法。

2.基本类型：上楼梯问题、直线分平面问题、传球法、圆周连线问题。

3.递推分析的常用思路：直接累加、增量分析、从复杂化归简单。

例题：例1.一个楼梯共有10级台阶，规定每步可以迈一级台阶或二级台阶.走完这10级台阶，一共可以有多少种不同的走法？【答案】89种【解答】设n级台阶有a n种走法，则a n=a n-1+a n-21级有1种走法；2级有（1+1和2）2种走法；3级有（1+1+1、2+1和1+2）3种走法；4级有3+2=5种走法；5级有3+5=8种走法；6级有5+8=13种走法；7级有8+13=21种走法；8级有13+21=34种走法；9级有21+34=55种走法；10级有34+55=89种走法例2.小悦买了10块巧克力，她每天最少吃一块，最多吃3块，直到吃完，共有多少种吃法？【答案】274种【解答】通过枚举法和递推法：设n块糖有a n种走法，则a n=a n-1+a n-2+ a n-31块糖有1种吃法；2块糖有2种吃法； 3块糖有4种吃法； 4块糖有1+2+4=7种吃法； 5块糖有2+4+7=13种吃法； 6块糖有4+7+13=24种吃法； 7块糖有7+13+24=44种吃法； 8块糖有13+24+44=81种吃法；9块糖有24+44+81=149种吃法；10块糖有44+81+149=274种吃法。

例3.用1×2的小方格覆盖2×7的长方形，共有多少种不同的覆盖方法？【答案】21种【解答】2×1的方格有1种盖法；2×2的方格有2种盖法；2×3的方格有2+1=3种盖法；2×4的方格有3+2=5种盖法；2×5的方格有3+5=8种盖法；2×6的方格有5+8=13种盖法；2×7的方格有8+13=21种盖法。

例4.如果在一个平面上画出4条直线，最多可以把平面分成几个部分？如果画20条直线，最多可以分成几个部分？【答案】211个【解答】1条直线将平面分成1+1=2部分；2条直线最多将平面分成1+2+1=4部分；3条直线最多将平面分成1+2+3+1=7部分；4条直线最多将平面分成1+2+3+4+1=11部分……20条直线最多将平面分成1+2+3+……+20+1=211部分；例5.甲、乙、丙三名同学练习传球，每人都可以把球传给另外两个人中的任意一个.先由甲发球，经过6次传球后球仍然回到了甲的手中.请问：整个传球过程共有多少种不同的可能？【答案】89种【解答】通过递推，可知0次传球到甲有1种；1次传球到甲有0种；2次传球到甲有2种；3次传球到甲有2种；4次传球到甲有6种；5次传球到甲有10种；6次传球到甲有22种。

递推法解计数问题例析

递推法解计数问题例析发布时间：2021-06-22T11:22:52.897Z 来源：《中小学教育》2021年第2月6期（下）作者：张淑云[导读] 计数问题是学习和生活中经常遇到的一类问题张淑云湖南省冷水江市铎山镇中心小学 417508摘要：计数问题是学习和生活中经常遇到的一类问题，它的表现形式多样,处理方法灵活,其中递推法是处理复杂计数问题的一种重要方法。

本文通过几个典型例子，说明递推法在解计数问题中的应用。

关键词：计数问题，递推法，例析意大利著名数学家斐波那契（约1170—1250）有一部传世之作《算术之法》，其中提出了一个饶有趣味的问题：假定一对刚出生的兔子一个月就能长成大兔子，再过一个月就开始生下一对小兔子，并且以后每个月都生一对小兔子。

设所生一对兔子为一雌一雄，且均无死亡。

问一对刚出生的小兔一年内可以繁殖成多少对兔子？对于斐波那契提出的这个“兔子繁殖问题”，我们不妨一个月一个月向后推算：开始时有一对小兔，即a0=1；第1个月，这对小兔长成一对大兔，即a1=1；第2个月，这对大兔产下一对小兔，此时共有两对兔子，即a2=2；第3个月，原来的大兔产下一对小兔，第2个月出生的一对小兔长成大兔，即a3=3；第4个月，原来的和第2个月出生的兔子各产下一对小兔，而第3个月出生的一对小兔长成大兔，此时共有5对兔子，即a4=5；…… 如果按照上述“连锁反应”式地繁殖小兔，来推算出一年（12个月）内可以繁殖成多少对兔子，我们确实要费一番功夫。

因此，我们需要找出一个简捷的“连锁反应关系式”来解出a12。

设第n个月共有an对兔子，则an是由两部分构成的，其中一部分是第（n-1）个月的兔子对数an-1；第二部分是由an-2对兔子所生的小兔，共有an-2对。

所以an=an-1+ an-2。

由于a0=1，a1=1，因此每个月的兔子对数依次为：1，1，2，3，5，8，13，21，34，55，89，144，233，…。

小学六年级奥数第6讲计数方法之标数法、递推法

【例6】(★★★) 如下图，一只蜜蜂从A处出发，回到家里B处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？
A
B
【例7】(★★★) 一个楼梯共有12级台阶，规定每步可以迈1级台阶或2级台阶，最多可以迈3级台阶，从地面到最上面1级台阶，一共可以有多少种不同的走法？
【例8】(★★★) 在平面上画8个圆，最多可以把平面分成_______部分。
计数方法之标数法、递推法
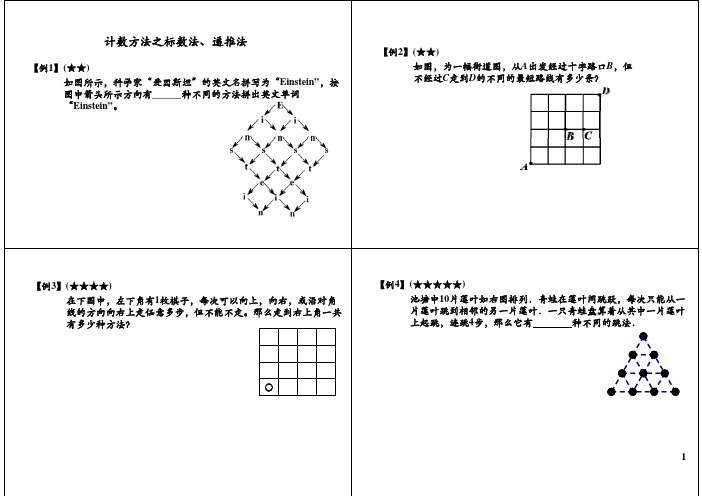
【例1】(★★) 如图所示，科学家“爱因斯坦”的英文名拼写为“Einstein”，按图中箭头所示方向有______种不同的方法拼出英文单词 “Einstein”。
【例2】(★★) 如图，为一幅街道图，从A出发经过十字路口B，但不经过C走到D的不同的最短路线有多少条？
【例3】(★★★★) 在下图中，左下角有1枚棋子，每次可以向上，向右，或沿对角线的方向向右上走任意多步，但不能不走。那么走到右上角一共有多少种方法？
ห้องสมุดไป่ตู้
【例4】(★★★★★)
池塘中10片莲叶如右图排列．青蛙在莲叶间跳跃，每次只能从一
片莲叶跳到相邻的另一片莲叶．一只青蛙盘算着从其中一片莲叶
上起跳，连跳4步，那么它有
种不同的跳法．
○
1
【例5】(★★★★★) 游乐园门票1元1张，每人限购1张.现有10个小朋友排队购买，其中5个小朋友只有1元的钞票，另外5个小朋友只有2元的钞票，售票员没有零钱。10个小朋友排队，不同的排队方法总共有10！＝3628800种，问其中有______种排队方法，售票员总能找的开零钱。
【例9】(★★★★) 一个长方形把平面分成两部分，那么10个长方形最多把平面分成 _______部分.

计数中的递推关系

计数中的递推关系作者：周文国来源：《中学课程辅导高考版·学生版》2012年第02期利用递推关系求解计数问题是处理排列组合问题的一种有效方法，可从简单的情形着手，逐步递推到一般的情形.现在举例说明如何挖掘和利用计数中的递推关系：一、一阶递推式之整点个数问题例1在直角坐标系中，定义横纵坐标都为整数的点为“整点”，则集合M={(x,y)||x|+|y|≤n,n∈N*}所表示的区域中有多少个整点？分析：可从n分析到n+1进行解决．解：如图，设正方形G n所确定的整点个数为f(n)，则容易知道f(1)=5，当n增加到n+1时，在第一象限就增加了n个整点，由对称性：f(n+1)=f(n)+4n+4，累加知道f(n)=2n2+2n+1，故在n=5时所确定的整点的个数共有f(5)=61个．点评：从f(n)到f(n+1)来分析点的个数的变化．二、一阶递推式之涂色问题例2把一个圆分成n个扇形（n≥2），依次记为D1、D2、……、D n－1、D n，每个扇形都可以用三种不同颜色中的任何一种涂色，要求相邻的扇形颜色不同，若n=4，则共有种不同涂色方法．分析：设涂色方法共有f(n)种，当n=2时，f(2)=6，下面寻求f(n)的递推关系即可．解：D1有3种涂色方法，D2有2种涂色方法，……，D n－1有2种涂色方法，D n仍然有2种涂色方法（不论是否与D1同色），这样共有3×2n－1种涂色方法，这3×2n－1种涂色方法可分为两类：（1）D n与D1同色，虽然与要求不符合，但可以认为D n与D1合为一个扇形，此时涂色方法有f(n－1)种；（2）D n与D1不同色，此时涂色方法有f(n)种．于是3×2n－1=f(n)+f(n－1)，利用数列求和可得到：f(n)=2n+2·(－1)n(n≥2)．则当n=4时，f(4)=18，共有18种不同涂色方法．点评：利用递推式可找出D1、D2、…、D n－1、D n之间的关系，从而确定不同的涂色方法．三、二阶递推式例3一楼梯共有12级，每步可以向上跨1级或2级，共有种上楼梯的方法．分析：设跨到n级楼梯共有f(n)种走法，由题意，跨到n级楼梯需要从n－2级跨到，或从n－1级跨到，前者有f(n－2)种走法，后者有f(n－1)种走法．解：由分类计数原理可以知道f(n)=f(n－1)+f(n－2)，则容易知道f(1)=1，f(2)=2，f(3)=3， f(4)=5，…，故共有f(12)=f(11)+f(10)=233种上楼梯的方法．点评：从解答中可以看到若求f(12)，则必须知道f(11)和f(10)才能解答．四、双元递推式例4用1，2，3这3个数字来构造四位数，但不允许相邻的1出现在四位数中，则这样的四位数共有个．分析：设用1，2，3这3个数字来构造n位数：末位数字为1的有f(n)个，末位数字不为1的有g(n)个，则所有满足条件的n位数共有f(n)+g(n)个，再分这两种情况分析．解：考虑由1，2，3构成的n+1位数：（1）末位数字为1，此类数可由满足要求的n位数中末位不为1的数末位添上1而得到的，故此类数有g(n)个；（2）末位数字不为1，此类数可由满足要求的n位数中末位添上2或3而得到的，故此类数有2［f(n)+g(n)］个．于是f(n+1)=g(n)g(n+1)=2［f(n)+g(n)］，由f(1)=1g(1)=2 ，得到n=4时，f(4)+g(4)=60．点评：通过f(n+1)和g(n+1)双元递推，则问题比较容易解决．（作者：周文国，江苏张家港职业教育中心)。

【详解】六年级(上)第03讲递推计数仅答案

第三讲递推计数例题例1．答案：927详解：将作文数量与完成作文的方法数列成一张表格，如下所示：下面解释一下这张数表是如何累加得到的．写1、2、3篇作文的方法数可以枚举得到．写4篇作文的完成方法数可以分三类去数：如果第一天写1篇，那么参考数表可得，剩下3篇有4种完成方法；如果第一天写2篇，同样参考数表可得，剩下2篇有2种完成方法；如果第一天写3篇，那么剩下1篇还有1种完成方法——因此4篇作文的完成方法总数为1247++=，如上表箭头所示．接着分析5篇作文的完成方法数，仍然分三类：第一天写1篇，那么参考数表可得，剩下4篇还有7种完成方法；第一天写2篇，那么剩下3篇还有4种完成方法；第一天写3篇，那么剩下2篇还有2种完成方法——因此5篇作文的完成方法数等于24713++=……以此类推便可填满整张表格．例2．答案：28详解：我们同样可以列出一个递推数列，将其表示如下：下面详细说明该问题的递推规律．覆盖1×3、2×3和3×3方格表的方法数可以枚举得到．接着分析覆盖4×3的表格有几种覆盖方法．如下图所示，左上角的阴影方格在覆盖的时候有两种方法：竖着覆盖或横着覆盖．当竖着覆盖时，余下部分恰好是一个3×3的方格表，覆盖方法数为2；当横着覆盖时，其下方的方格只能被横放的纸片盖住，因此只剩下一个1×3的方格表需要覆盖，方法数为1．由此可得4×3表格的方法数为2+1=3．用同样的方法分析5×3的方格表，可得其覆盖方法数等于43⨯的方法数加上23⨯的方法数，因此等于314+=．接着以此类推即可．例3．答案：5051详解：我们同样可以列出一个递推数列，将其写为如下的一张数表：余下部分是33⨯的方格表，覆盖方法有2种．阴影方格下方的格子只能用横放的纸片盖住，因此只剩下13⨯的方格表需要覆盖下面详细说明该递推过程．平面上有1、2、3条直线的情形画图即可解决，我们从第4条直线开始分析．如右图所示，当画上第4条直线时，会把原有的区域一分为二（如编号为I 、II 、III 、IV 的4个区域），因此会增加4个新区域．而之所以能产生4个新区域，就是由于第4条直线会与原有的3条直线产生3个交点，而这3个交点会把第4条直线分为4部分，每一部分都会位于一个原有的区域中，因此每一部分都就会把原有的某个区域一分为二，因此直线被分为几部分，区域数量自然也就增加几部分．上述逻辑关系在下方右侧有明确的表示．由此可得，增加到第n 条直线就会增加n 个新区域，因此答案是()22341005051+++++=．例4．答案：1641详解：本题的方法称为“传球法”．传球法在很多问题中有着广泛的应用．如右侧表格所示，除了第“0”行外，其余每一行的数量都是由上一行的数量通过某种规则累加得到的．比如第“1”行A 下方的0，就是通过第“0”行B 、C 、D 的数量相加得到的；第“3”行B 下方的7，就是通过第“2”行A 、C 、D 的数量相加得到的；第“4”行C 下方的20，就是通过第“5”行A 、B 、D 的数量相加得到的；第“6”行D 下方的182，就是通过第“5”行A 、B 、C 的数量相加得到的．之所以有这样的累加规则，就是因为A 想拿球，必须由B 、C 、D传球给他，所以他下方的数也必须由B 、C 、D 累加给他我们不停地将数表向下累加，每传一次球就多累加一行，最后得到第“8”行．这一行的四个数分别为1641、1640、1640和1640．他们分别表示8次传球后，由A 、B 、C 、D 拿球的传球方法数．由于题目要求最后球回到A 手中，因此答案为1641种．III IIIIV增加第n 条直线产生1n -个交点第n 条直线被分成n 部分直线的每一部分都分出一个新区域增加n 个新区域…例5．答案：1224详解：我们把这个七位数看作是1、2、3三个人之间传6次球的一个传球顺序，具体的传球规则是：1能传球给2、3，但不能给自己；2、3都能传球给1、2、3．依据“传球规则决定累加规则”，我们可以列出如右表所示的一张递推表格．表格的第“0”行是发球行，对应的是这个七位数的首位数字．由于1、2、3都能作首位，因此第“0”行写的都是1．接着按照传球规则累加即可．表格中第“6”行（最后一行）中的三个数分别表示第六次传球后，球在1、2、3手中的方法数，对于七位数而言，就是表示分别以1、2、3结尾的符合题意的七位数有多少个．所以最后答案应该把它们全加起来，等于328+448+448=1224．例6．答案：42详解：我们依照连续偶数的次序进行递推累加．（1）圆周上有2个点，只有1种连法．（2）圆周上有4个点，只有2种连法．（3）圆周上有6个点A 1、A 2、A 3、A 4、A 5、A 6（如下左图），那么与A 1相连的点只能是A 2、A 4或A 6．依次分三类情况讨论：第一，A 1连A 2，剩下4个点连法数为2；第二，A 1连A 4，剩下4个点连法数为1；第三，A 1连A 4，剩下4个点连法数也为2．由此可得，6个点共有5种不同的连法．（4）如果圆周上有8个点A 1、A 2、A 3、A 4、A 5、A 6、A 7、A 8（如下右图），那么与A 1相连的点有四种可能，分别是A 2、A 4、A 6或A 8．以此分四类讨论，共14种方法．（5）如果圆周上有10个点，同样考虑能与A 1相连的点，分五类讨论，如下图所示．共42种方法．评析：本题虽然不像之前那样，只遵循一个简单的累加规则，但也仍然是一个由小求大的递推过程：3 46A 3 46A 3 46A 3 46A 3 46A 剩余8个点共14种方法剩余26+个点共15⨯种方法剩余44+个点共22⨯种方法剩余26+个点共15⨯种方法剩余8个点共14种方法A 还剩4个点， 2种方法．1种方法．还剩4个点，2种方法．剩余42+个点，方法数为21⨯．42+个方法数为1⨯．还剩6个点，共5种方法．在求解6个点的方法数时，会用到2个、4个点的方法数；在求解8个点的方法数时，也会用到2个、4个、6个点的方法数；而在求解10个点的方法数时，则会用到2个、4个、6个、8个点的方法数……由此可见“由小求大”应该说是递推法真正的内涵．我们再处理问题时，要有能力将数目较大的情形通过变形，化归为数目较小的情形来解决．另外，请大家观察右图．从A处出发，每次只能向右或向上走一步，那么从A到B、C、D、E、F的最短路径分别有多少？大家不妨用标数法（参考四年级上册第16讲《加法原理与乘法原理》）自己做一做，在把相应的结果与本题的结果对照一下，你能发现其中的奥妙吗？ABCDEF练习1、答案：12简答：仿照例题1进行分类讨论，列出如下数表进行累加即可，注意累加规则．练习2、答案：21简答：仿照例题2，找到左上角的方格，按照该方格是横着覆盖还是竖着覆盖分两类讨论即可得递推规则．练习3、答案：1276简答：本题与直线分平面的问题本质相同，因此与例题3类似进行递推即可．如下表所示练习4、答案：434后的拿球人不是发球人这一点要注意！2+4+1. 答案：89 简答：简答：简答：略． 4. 答案：3277简答：如右表所示，用传球法列表解决．传球规则是：0不能发球，其它都可以发球；传球不能传给自己，只能传给别人；总共传球传6次． 5. 答案：29简答：如下方左图所示，和例题2类似，找到某个方格，依据这个方格是横着覆盖还是竖着覆盖分两种情况讨论．情况一，横着覆盖：这类情况其实就是的覆盖方法，利用练习2的分析方法和相关结论，可得答案为21．情况二，竖着覆盖：在这类情况下，有另外四个格子的覆盖方法唯一确定，如下方右图中的虚线所示，剩下需要覆盖的是一个的方格表，其方法数量也可参考练习2的分析方法和相关结论来取得，答案为8．上述两种情况相加，可得答案为．21829+= 52⨯ 72⨯。

递推计数与对应计数[高效]

递推计数与对应计数一.对应计数法:要计算一个有限集A 的元素个数,若直接计算比较困难时,我们可设法寻找一个便于计算其元素个数的集合B ,并且建立一个A 到B 上的一一对应f ,于是由A B =得到A 的元素个数,这种计数方法就是对应计数方法.运用这种方法的关键是寻找一个便于计算其元素个数的集合B 及如何在A 与B 建立一一对应.例1 圆周上有()4m m ≥个点,每两点连一条弦,如果没有三条弦交于一点(端点除外),问,这些弦在圆内一共有多少个交点?解:圆周上任四点之间所连的弦中在圆内恰有一个交点,反之,圆内的任何一个交点,是由两条弦相交而得,这两条弦对应于圆周上四个点.这样交点与圆周上的四点组之间构成了一个一一对应关系,所以共有4m C 个交点.例2 正方体的12条棱,12条面对角线及4条体对角线,这28条线中,异面直线有几对?解:从正方体的8个顶点中取四个不共面的顶点组成一个四面体,在该四面体的棱所在直线中有3对异面直线;反之,每一对异面线段的四个顶点对应于正方体的4个不共面的顶点.从正方体的8个顶点中取四个不共面的顶点有486658C --=种方法,所以异面直线的对数为358174⨯=.例3 从m n ⨯的棋盘中,取出一个由三个方格组成的L 形,有多少种不同的取法?解:棋盘中的每一个内部点A 都对应于四个L 形,反之每一个L 形都对应于一个内部点A .m n ⨯的棋盘共有()()11m n --个内部点,所以不同的取法有()()411m n --种.例4 从19,,3,2,1 中,按从小到大的顺序选取4321,,,a a a a 四个数,使得21322,3a a a a -≥-≥,434≥-a a .问符合上述要求的不同取法有多少种?解:等价于去掉六个数,从1,2,3,,13 中,按从小到大的顺序选取1234,,,b b b b 四个数共有多少种取法,有413715C =种方法.在此基础上取11223344,1,3,6a b a b a b a b ==+=+=+即可.例5 从集合{}1,2,3,,49 中取出6个不同的数,使得其中至少有两个相邻,不同的取法有几种?A解:从集合{}1,2,3,,49 中取出6个不同的数123456,,,,,a a a a a a 有649C 种不同取法.若这些数互不相邻,则12345611234544a a a a a a ≤<-<-<-<-<-≤,即等价于从44个数中选6个不同的数,它们从小到大依次为123456,,,,,b b b b b b ,然后令()11,2,,6i i a b i i =+-= ,这样得到的6个数123456,,,,,a a a a a a 即满足条件,反之亦然.所以不同的取法有664944C C -种.例6 圆周上有n 个点(6)n ≥,每两个点连一线段,假设任三条线段在圆内不共点,于是三条两两相交的线段构成一个三角形,试求这些三角形的个数?解:设三角形的顶点有i 个在圆内,3i -个在圆周上,这类三角形的全体为(0,1,2,3)i I i =. 则30nI C =.对1I ∆∈,有一内点O 为∆的顶点,内点O 为二条线段的交点,对应圆上四点1234,,,A A A A ,13A A 与24A A 交于点O .即内点全体与圆周上四点组全体之间构成一个一一对应,而每个内点O ,又有四个1I 中的∆与之对应,故414n I C =.对2I ∆∈,圆周上任取n 点中的5点,对应2I 中5个∆;反之对每一个2I ∆∈,延长∆的边与圆周交于5个点,使此∆为5点对应的5个∆之一,故525n I C =.对3I ∆∈,则∆三内点确定三条线段交圆周6个点,反之也对,故63n I C =.综上,所以三角形总数为:345645n n n nC C C C +++. 评析:一一映射与倍数映射是转化抽象的,复杂的计数问题的常用方法,但恰当的构造映射是解决问题的关键.二.递推计数法:通过引入数列,建立递推关系来计数的方法称为递推计数法.运用递推方法计数的一般步骤是:(1)求初始值;(2)建立递推关系;(3)利用递推关系求解.例7 由0,1,2,3组成的长度为n 的数字串中,求没有两个0相邻的数字串的个数.解:设所求数字串的个数为n a ,则长度为n 的数字串可以分为两类:(1)数字串中第一位不为0,则第一位为1,2,3之一,而剩下的长度为1n -的数字串中无两个0相邻的个数为1n a -,由分步计数原理,共有13n a -个;(2) 数字串中第一位为0,则第二位为1,2,3之一,而剩下的长度为2n -的数字串中无两个0相邻的个数为2n a -,由分步计数原理,共有23n a -个;因此我们得到递推关系式()12333n n n a a a n --=+≥,它的特征方程为233x x =+,特征根为32x ±=,结合初始值124,15a a ==,易得213213422422n nn a +--=+⎝⎭⎝⎭.例8 4个人互相传球,接球后即传给别人,首先由甲发球,并把它当作第一次传球.求经过n 次传球后,球又回到甲手中的传球方法数.解:设传球方法数为n a ,则120,3a a ==.由甲开始传球1n -次,总传球数为13n -,若经过n 次传球后,球又回到甲手中,则倒数第二次球在另外三个人手中,共有113n n a ---种传法,由此我们得到递推关系式()1132n n n a a n ---=≥,变形为1111134334n n n n a a --⎛⎫-=-- ⎪⎝⎭,所以()133111134434nn n n n n a a -+⋅-⎛⎫-=--⇒=⎪⎝⎭.例9 有人要上楼,此人每步能向上走1阶或2阶,如果一层楼有18阶,他上一层楼有多少种不同的走法?解(一):此人上楼最多走18步,最少走9步.这里用1817169,,,,a a a a 分别表示此人上楼走18步,17步,16步,…,9步时走法(对于任意前后两者的步数,因后者少走2步1阶,而多走1步2阶,计后者少走1步)的计数结果.考虑步子中的每步2阶情形,易得0118181717C ,C a a ==,29161699C ,,C a a == .综上,他上一层楼共有01291817169C C C C 11712014181++++=++++= 种不同的走法.解(二):设n F 表示上n 阶的走法的计数结果.显然,121,2F F ==.对于34,,F F 起步只有两种不同走法:上1阶或上2阶.因此对于3F ,第1步上1阶的情形,还剩312-=阶,计2F 种不同的走法；对于第1步上2阶的情形,还剩321-=阶,计1F 种不同的走法.总计321213F F F =+=+=.一般地,对于n F ,第一步走1阶,剩下的1n -阶有1n F -种不同的走法;第一步走2阶,剩下的2n -步有2n F -种不同的走法.所以得到递推关系12n n n F F F --=+.依次递推得到:432543181716325,538,,258415974181F F F F F F F F F =+=+==+=+==+=+= .例10 求n 位十进制数中出现偶数个6的数的个数.解:设n a 为n 位十进制数中出现偶数个6的数的个数,n b 为n 位十进制数中出现奇数个6的数的个数.则有111199n n n n n n a a b b b a ----=+⎧⎨=+⎩,且118,9a b ==.从而12212991880n n n n n n a a b a a a -----=++=-,利用特征根法,∴117981022n n n a --=⋅+⋅.。

(小学奥数)计数之递推法

7-6-4.計數之遞推法教學目標前面在講加法原理、乘法原理、排列組合時已經穿插講解了計數中的一些常用的方法，比如枚舉法、樹狀圖法、標數法、捆綁法、排除法、插板法等等，這裏再集中學習一下計數中其他常見的方法，主要有歸納法、整體法、對應法、遞推法．對這些計數方法與技巧要做到靈活運用．例題精講對於某些難以發現其一般情形的計數問題，可以找出其相鄰數之間的遞歸關係，有了這一遞歸關係就可以利用前面的數求出後面未知的數，這種方法稱為遞推法．【例 1】每對小兔子在出生後一個月就長成大兔子，而每對大兔子每個月能生出一對小兔子來．如果一個人在一月份買了一對小兔子，那麼十二月份的時候他共有多少對兔子？【考點】計數之遞推法【難度】3星【題型】解答【解析】第一個月，有1對小兔子；第二個月，長成大兔子，所以還是1對；第三個月，大兔子生下一對小兔子，所以共有2對；第四個月，剛生下的小兔子長成大兔子，而原來的大兔子又生下一對小兔子，共有3對；第五個月，兩對大兔子生下2對小兔子，共有5對；……這個特點的說明每月的大兔子數為上月的兔子數，每月的小兔子數為上月的大兔子數，即上上月的兔子數，所以每月的兔子數為上月的兔子數與上上月的兔子數相加．依次類推可以列出下表：經過月數：---1---2---3---4---5---6---7---8---9---10---11---12兔子對數：---1---1---2---3---5---8--13--21--34--55--89—144，所以十二月份的時候總共有144對兔子．【答案】144【例 2】樹木生長的過程中，新生的枝條往往需要一段“休息”時間供自身生長，而後才能萌發新枝．一棵樹苗在一年後長出一條新枝，第二年新枝“休息”，老枝依舊萌發新枝；此後，老枝與“休息”過一年的枝同時萌發，當年生的新枝則依次“休息”．這在生物學上稱為“魯德維格定律”．那麼十年後這棵樹上有多少條樹枝？【考點】計數之遞推法【難度】3星【題型】解答【解析】一株樹木各個年份的枝椏數，構成斐波那契數列：1，2，3，5，8，13，21，34，55，89，……所以十年後樹上有89條樹枝．【答案】89【例 3】一樓梯共10級，規定每步只能跨上一級或兩級，要登上第10級，共有多少種不同走法？【考點】計數之遞推法【難度】4星【題型】解答【解析】登1級2級3級4級 ...... 10級1種方法 2種3種5種 ...... ？我們觀察每級的種數，發現這麼一個規律：從第三個數開始，每個數是前面兩個數的和；依此規律我們就可以知道了第10級的種數是89.其實這也是加法的運用：假如我們把這個人開始登樓梯的位置看做A0，那麼登了1級的位置是在A1，2級在A2... A10級就在A10．到A3的前一步有兩個位置；分別是A2和A1．在這裏要強調一點，那麼A2到A3 既然是一步到了，那麼A2、A3之間就是一種選擇了；同理A1到A3也是一種選擇了．同時我們假設到n級的選擇數就是An．那麼從A0到A3就可以分成兩類了：第一類：A0 ---- A1 ------ A3 ，那麼就可以分成兩步．有A1×1種，也就是A1 種；(A1 ------ A3 是一種選擇)第二類：A0 ---- A2 ------ A3，同樣道理有A2 ．類類相加原理：A3 = A1 ＋A2，依次類推An = An-1 + An-2．【答案】89【鞏固】一樓梯共10級，規定每步只能跨上一級或三級，要登上第10級，共有多少種不同走法？【考點】計數之遞推法【難度】4星【題型】解答【解析】登 1級 2級 3級 4級 5級 ...... 10級1種方法 1種 2種 3種 4種...... ？我們觀察每級的種數，發現這麼一個規律：從第三個數開始，每個數是前面相隔的兩個數的和；依此規律我們就可以知道了第10級的種數是28. 【答案】28【例 4】 1×2的小長方形(橫的豎的都行)覆蓋2×10的方格網，共有多少種不同的蓋法．【考點】計數之遞推法【難度】4星【題型】解答【解析】如果用12⨯的長方形蓋2n ⨯的長方形，設種數為n a ,則11a =，22a =,對於3n ≥，左邊可能豎放1個12⨯的，也可能橫放2個12⨯的，前者有-1n a 種，後者有-2n a 種，所以-1-2n n n a a a =+,所以根據遞推，覆蓋210⨯的長方形一共有89種．【答案】89【例 5】用13⨯的小長方形覆蓋38⨯的方格網，共有多少種不同的蓋法？【考點】計數之遞推法【難度】5星【題型】解答【解析】如果用13⨯的長方形蓋3n ⨯的長方形，設種數為n a ,則11a =，21a =,32a =,對於4n ≥，左邊可能豎放1個13⨯的，也可能橫放3個13⨯的，前者有-1n a 種，後者有a 種，所以a a a =+,依照這條遞推公式列表：31⨯32⨯33⨯34⨯35⨯36⨯37⨯38⨯1 1234 6 9 13所以用13⨯的小長方形形覆蓋38⨯的方格網，共有13種不同的蓋法．【答案】13【例 6】有一堆火柴共12根，如果規定每次取1～3根，那麼取完這堆火柴共有多少種不同取法？【考點】計數之遞推法【難度】4星【題型】解答【解析】取1根火柴有1種方法，取2根火柴有2種方法，取3根火柴有4種取法，以後取任意根火柴的種數等於取到前三根火柴所有情況之和，以此類推，取完這堆火柴一共有927種方法．【答案】927【巩固】一堆蘋果共有8個，如果規定每次取1～3個，那麼取完這堆蘋果共有多少種不同取法？【考點】計數之遞推法【難度】4星【題型】解答【解析】取1個蘋果有1種方法，取2個蘋果有2種方法，取3個蘋果有4種取法，以後取任意個蘋果的種數等於取到前三個蘋果所有情況之和，以此類推，取完這堆蘋果一共有81種方法．【答案】81【例 7】有10枚棋子，每次拿出2枚或3枚，要想將10枚棋子全部拿完，共有多少種不同的拿法？【考點】計數之遞推法【難度】4星【題型】解答【解析】本題可以採用遞推法，也可以進行分類討論，當然也可以直接進行枚舉．(法1)遞推法．假設有n 枚棋子，每次拿出2枚或3枚，將n 枚棋子全部拿完的拿法總數為n a 種．則21a =，31a =，41a =．由於每次拿出2枚或3枚，所以32n n n a a a --=+(5n ≥)．所以，5232a a a =+=；6342a a a =+=；7453a a a =+=；8564a a a =+=；9675a a a =+=；10787a a a =+=．即當有10枚棋子時，共有7種不同的拿法． (法2)分類討論．由於棋子總數為10枚，是個偶數，而每次拿2枚或3枚，所以其中拿3枚的次數也應該是偶數．由於拿3枚的次數不超過3次，所以只能為0次或2次．若為0次，則相當於2枚拿了5次，此時有1種拿法；若為2次，則2枚也拿了2次，共拿了4次，所以此時有246C =種拿法．根據加法原理，共有167+=種不同的拿法．【答案】7【例 8】如下圖，一只蜜蜂從A 處出發，回到家裏B 處，每次只能從一個蜂房爬向右側鄰近的蜂房而不准逆行，共有多少種回家的方法？【考點】計數之遞推法【難度】4星【題型】解答BA AB 1357946821235813213455891【解析】蜜蜂“每次只能從一個蜂房爬向右側鄰近的蜂房而不准逆行”這意味著它只能從小號碼的蜂房爬近相鄰大號碼的蜂房．明確了行走路徑的方向，就可以運用標數法進行計算．如右圖所示，小蜜蜂從A 出發到B 處共有89種不同的回家方法．【答案】89【鞏固】小蜜蜂通過蜂巢房間，規定只能由小號房間進入大號房間問小蜜蜂由A 房間到達B 房間有多少種方法？【考點】計數之遞推法【難度】4星【題型】解答【解析】斐波那契數列第八項．21種．【答案】21【例 9】如下圖，一只蜜蜂從A 處出發，回到家裏B 處，每次只能從一個蜂房爬向右側鄰近的蜂房而不准逆行，共有多少種回家的方法？【考點】計數之遞推法【難度】4星【題型】解答BA【解析】按照蜜蜂只能從小號碼的蜂房爬近相鄰大號碼的蜂房的原則，運用標號法進行計算．如右圖所示，小蜜蜂從A 出發到B 處共有296種不同的回家方法．【答案】296【例 10】對一個自然數作如下操作：如果是偶數則除以2，如果是奇數則加1，如此進行直到得數為1操作停止．問經過9次操作變為1的數有多少個？【考點】計數之遞推法【難度】4星【題型】解答【解析】可以先嘗試一下，倒推得出下麵的圖：2410131112514302831643215167683421其中經1次操作變為1的1個，即2，經2次操作變為1的1個，即4，經3次操作變為1的2個，是一奇一偶，以後發現，每個偶數可以變成兩個數，分別是一奇一偶，每個奇數變為一個偶數，於是，經1、2、…次操作變為1的數的個數依次為：1，1，2，3，5，8，…這一串數中有個特點：自第三個開始，每一個等於前兩個的和，即即經過9次操作變為1的數有34個. 為什麼上面的規律是正確的呢？道理也很簡單. 設經過n 次操作變為1的數的個數為n a ,則1a =1，2a =1，3a =2，…從上面的圖看出，1n a +比n a 大.一方面，每個經過n 次操作變為1的數，乘以2，就得出一個偶數，經過1n +次操作變為1；反過來，每個經過1n +次操作變為1的偶數，除以2，就得出一個經過n 次操作變為1的數. 所以經過n 次操作變為1的數與經過1n +次操作變為1的偶數恰好一樣多.前者的個數是n a ,因此後者也是n a 個. 另一方面，每個經過n 次操作變為1的偶數，減去1，就得出一個奇數，它經過1n +次操作變為1，反過來.每個經過1n +次操作變為1的奇數，加上1，就得出一個偶數，它經過n 次操作變為1. 所以經過n 次操作變為1的偶數經過1n +次操作變為1的奇數恰好一樣多.而由上面所說，前者的個數就是1n a -,因此後者也是1n a -.經過n +1次操作變為1的數，分為偶數、奇數兩類，所以11n n n a a a +-=+，即上面所說的規律的確成立. 【答案】34【例 11】有20個石子，一個人分若干次取，每次可以取1個，2個或3個，但是每次取完之後不能留下質數個，有多少種方法取完石子？（石子之間不作區分，只考慮石子個數）【考點】計數之遞推法【難度】5星【題型】解答【解析】如果沒有剩下的不能使質數這個條件，那麼遞推方法與前面學過的遞推法相似，只不過每次都是前面3個數相加．現在剩下的不能是質數個，可以看作是質數個的取法總數都是0，然後再進行遞推．【答案】25【鞏固】有20個相同的棋子，一個人分若干次取，每次可取1個，2個，3個或4個，但要求每次取之後留下的棋子數不是3或4的倍數，有種不同的方法取完這堆棋子.【考點】計數之遞推法【難度】5星【題型】填空【解析】把20、0和20以內不是3或4的倍數的數寫成一串，用遞推法把所有的方法數寫出來：【答案】54【例 12】4個人進行籃球訓練，互相傳球接球，要求每個人接球後馬上傳給別人，開始由甲發球，並作為第一次傳球，第五次傳球後，球又回到甲手中，問有多少種傳球方法？【考點】計數之遞推法【難度】5星【題型】解答【解析】設第n 次傳球後，球又回到甲手中的傳球方法有n a 種．可以想像前1n -次傳球，如果每一次傳球都任選其他三人中的一人進行傳球，即每次傳球都有3種可能，由乘法原理，共有11333333n n --⨯⨯⨯=()个…(種)傳球方法．這些傳球方法並不是都符合要求的，它們可以分為兩類，一類是第1n -次恰好傳到甲手中，這有1n a -種傳法，它們不符合要求，因為這樣第n 次無法再把球傳給甲；另一類是第1n -次傳球，球不在甲手中，第n 次持球人再將球傳給甲，有n a 種傳法．根據加法原理，有11133333n n n n a a ---+=⨯⨯⨯=(个…)．由於甲是發球者，一次傳球後球又回到甲手中的傳球方法是不存在的，所以10a =．利用遞推關係可以得到：2303a =-=，33336a =⨯-=，4333621a =⨯⨯-=，533332160a =⨯⨯⨯-=．這說明經過5次傳球後，球仍回到甲手中的傳球方法有60種．本題也可以列表求解．由於第n 次傳球後，球不在甲手中的傳球方法，第1n +次傳球後球就可能回到甲手中，所以只需求出第四次傳球後，球不在甲手中的傳法共有多少種．從表中可以看出經過五次傳球後，球仍回到甲手中的傳球方法共有60種．【答案】60【鞏固】五個人互相傳球，由甲開始發球，並作為第一次傳球，經過4次傳球後，球仍回到甲手中．問：共有多少種傳球方式？【考點】計數之遞推法【難度】5星【題型】解答【解析】遞推法．設第n 次傳球後球傳到甲的手中的方法有n a 種．由於每次傳球有4種選擇，傳n 次有4n 次可能．其中有的球在甲的手中，有的球不在甲的手中，球在甲的手中的有n a 種，球不在甲的手中的，下一次傳球都可以將球傳到甲的手中，故有1n a +種．所以14n n n a a ++=．由於10a =，所以12144a a =-=，232412a a =-=，343452a a =-=．即經過4次傳球後，球仍回到甲手中的傳球方法有52種．【答案】52【例 13】設A、E為正八邊形ABCDEFGH的相對頂點，頂點A處有一只青蛙，除頂點E外青蛙可以從正八邊形的任一頂點跳到其相鄰兩個頂點中任意一個，落到頂點E時青蛙就停止跳動，則青蛙從頂點A出發恰好跳10次後落到E的方法總數為種．【考點】計數之遞推法【難度】5星【題型】填空【關鍵字】清華附中【解析】可以使用遞推法．回到A跳到B或H跳到C或G跳到D或F停在E1步 12步 2 13步 3 14步 6 4 25步10 46步20 14 87步34 148步68 48 289步116 48其中，第一列的每一個數都等於它的上一行的第二列的數的2倍，第二列的每一個數都等於它的上一行的第一列和第三列的兩個數的和，第三列的每一個數都等於它的上一行的第二列和第四列的兩個數的和，第四列的每一個數都等於它的上一行的第三列的數，第五列的每一個數都等於都等於它的上一行的第四列的數的2倍．這一規律很容易根據青蛙的跳動規則分析得來．所以，青蛙第10步跳到E有48296⨯=種方法．【答案】96【鞏固】在正五邊形ABCDE上，一只青蛙從A點開始跳動，它每次可以隨意跳到相鄰兩個頂點中的一個上，一旦跳到D點上就停止跳動．青蛙在6次之內(含6次)跳到D點有種不同跳法．【考點】計數之遞推法【難度】5星【題型】填空ABEC D【解析】採用遞推的方法．列表如下：跳到A跳到B跳到C停在D跳到E 1步 1 12步 2 1 13步 3 1 24步 5 3 25步8 3 56步13 8 5其中，根據規則，每次可以隨意跳到相鄰兩個頂點中的一個上，一旦跳到D 點上就停止跳動．所以，每一步跳到A的跳法數等於上一步跳到B和E的跳法數之和，每一步跳到B的跳法數等於上一步跳到A和C的跳法數之和，每一步跳到C的跳法數等於上一步跳到B的跳法數，每一步跳到E的跳法數等於上一步跳到A的跳法數，每一步跳到D的跳法數等於上一步跳到C或跳到E的跳法數．觀察可知，上面的遞推結果與前面的枚舉也相吻合，所以青蛙在6次之內(含6次)跳到D點共有1123512++++=種不同的跳法．【答案】12【例 14】有6個木箱，編號為1，2，3，……，6，每個箱子有一把鑰匙，6把鑰匙各不相同，每個箱子放進一把鑰匙鎖好．先挖開1，2號箱子，可以取出鑰匙去開箱子上的鎖，如果最終能把6把鎖都打開，則說這是一種放鑰匙的“好”的方法，那麼“好”的方法共有種．【考點】計數之遞推法【難度】5星【題型】填空【關鍵字】迎春杯，中年級組，決賽【解析】(法1)分類討論．如果1，2號箱中恰好放的就是1，2號箱的鑰匙，顯然不是“好”的方法，所以“好”的方法有兩種情況：⑴1，2號箱的鑰匙恰有1把在1，2號箱中，另一箱裝的是3～6箱的鑰匙．⑵1，2號箱的鑰匙都不在1，2號箱中．對於⑴，從1，2號箱的鑰匙中選1把，從3～6號箱的鑰匙中選1把，共有248⨯=(種)⨯=(種)選法，每一種選法放入1，2號箱各有2種放法，共有8216放法．不妨設1，3號箱的鑰匙放入了1，2號箱，此時3號箱不能裝2號箱的鑰匙，有3種選法，依次類推，可知此時不同的放法有3216⨯⨯=(種)．所以，第⑴種情況有“好”的方法16696⨯=(種)．對於⑵，從3～6號箱的鑰匙中選2把放入1，2號箱，有4312⨯=(種)放法．不妨設3，4號箱的鑰匙放入了1，2號箱．此時1，2號箱的鑰匙不可能都放在3，4號箱中，也就是說3，4號箱中至少有1把5，6號箱的鑰匙．如果3，4號箱中有2把5，6號箱的鑰匙，也就是說3，4號箱中放的恰好是5，6號箱的鑰匙，那麼1，2號箱的鑰匙放在5，6號箱中，有224⨯=種放法；如果3，4號箱中有1把5，6號箱的鑰匙，比如3，4號箱中放的是5，1號箱的鑰匙，則只能是5號箱放6號箱的鑰匙，6號箱放2號箱的鑰匙，有212⨯=種放法；同理，3，4號箱放5，2號箱或6，1號箱或6，2號箱的鑰匙，也各有2種放法．所以，第⑵種情況有“好”的放法()1242222144⨯++++=(種)．所以“好”的方法共有96144240+=(種)．(法2)遞推法．設第1，2，3，…，6號箱子中所放的鑰匙號碼依次為1k ，2k ，3k ，…，6k ．當箱子數為n (2n ≥)時，好的放法的總數為n a ．當2n =時，顯然22a =(11k =，22k =或12k =，21k =)．當3n =時，顯然33k ≠，否則第3個箱子打不開，從而13k =或23k =，如果13k =，則把1號箱子和3號箱子看作一個整體，這樣還是鎖著1，2兩號鑰匙，撬開1，2兩號箱子，那麼方法有2a 種；當23k =也是如此．於是2n =時的每一種情況對應13k =或23k =時的一種情況，這樣就有3224a a ==．當4n ≥時，也一定有n k n ≠，否則第n 個箱子打不開，從而1k 、2k 、……、1n k -中有一個為n ，不論其中哪一個是n ，由於必須要把該箱子打開才能打開n 號箱子，所以可以將鎖著這把鑰匙的箱子與第n 號箱子看作1個箱子，於是還是鎖著1k 、2k 、……、1n k -這()1n -把鑰匙，需要撬開1，2兩號箱子，所以每種情況都有1n a -種．所以()11n n a n a -=-．所以，6542554543225!240a a a a ==⨯==⨯⨯⨯=⨯=，即好的方法總數為240種．【答案】240【鞏固】有10個木箱，編號為1，2，3，……，10，每個箱子有一把鑰匙，10把鑰匙各不相同，每個箱子放進一把鑰匙鎖好．先挖開1，2號箱子，可以取出鑰匙去開箱子上的鎖，如果最終能把10把鎖都打開，則說這是一種放鑰匙的“好”的方法，那麼“好”的方法共有種．【考點】計數之遞推法【難度】5星【題型】填空【解析】遞推法．設第1，2，3，…，6號箱子中所放的鑰匙號碼依次為1k ，2k ，3k ，…，6k ．當箱子數為n (2n ≥)時，好的放法的總數為n a ．當2n =時，顯然22a =(11k =，22k =或12k =，21k =)．當3n =時，顯然33k ≠，否則第3個箱子打不開，從而13k =或23k =，如果13k =，則把1號箱子和3號箱子看作一個整體，這樣還是鎖著1，2兩號鑰匙，撬開1，2兩號箱子，那麼方法有2a 種；當23k =也是如此．於是2n =時的每一種情況對應13k =或23k =時的一種情況，這樣就有3224a a ==．當4n ≥時，也一定有n k n ≠，否則第n 個箱子打不開，從而1k 、2k 、……、1n k -中有一個為n ，不論其中哪一個是n ，由於必須要把該箱子打開才能打開n 號箱子，所以可以將鎖著這把鑰匙的箱子與第n 號箱子看作1個箱子，於是還是鎖著1k 、2k 、……、1n k -這()1n -把鑰匙，需要撬開1，2兩號箱子，所以每種情況都有1n a -種．所以()11n n a n a -=-．所以，109829989876543229!=725760a a a a ==⨯==⨯⨯⨯⨯⨯⨯⨯=⨯，即好的方法總數為725760種．【答案】725760。

计数问题之递推法例题讲解【三篇】

计数问题之递推法例题讲解【三篇】分析与解答：如果我们通过计算找到答案比较麻烦，所以我们先从最简单的情况入手。

9×9＝81，有1个奇数；99×99＝99×(100－1)＝9900－99＝9801，有2个奇数；999×999＝999×(1000－1)＝99900－999＝998001，有3个奇数；……从而可知，999…999×999…999的乘积*有10个奇数。

【第二篇】例题：分析与解答：这道题我们能够采用分别求出每个数的立方是多少，再求和的方法来解答。

但是，这样计算的工作量比较大，我们能够从简单的情况开始研究。

【第三篇】例题： 2000个学生排成一行，依次从左到右编上1～2000号，然后从左到右按一、二报数，报一的离开队伍，剩下的人继续按一、二报数，报一的离开队伍，…… 按这个规律如此下去，直至当队伍只剩下一人为止。

问：这时一共报了多少次？最后留下的这个人原来的号码是多少？分析与解答：难的不会想简单的，数大的不会想数小的。

我们先从这2000名同学中选出20人代替2000人实行分析，试着找出规律，然后再用这个规律来解题。

这20人第一次报数后共留下10人，因为20÷2＝10 ，这10人开始时的编号依次是：2、4、6、8、10、12、14、16、18、20，都是2的倍数。

第二次报数后共留下5人，因为10÷2＝5 ，这5人开始时的编号依次是： 4、8、12、16、20，都是4的倍数，也就是2×2的倍数。

第三次报数后共留下2人，因为5÷2＝2 ……1 ，这2人开始时的编号依次是： 8、16，都是8的倍数，也就是2×2×2的倍数。

第四次报数后共留下1人，因为2÷2＝1 ，这1人开始时的编号是：16，都是8的倍数，也就是2×2×2×2的倍数。

由此能够发现，第n次报数后，留下的人的编号就是n个2的连乘积，这是一个规律。

【奥赛】小学数学竞赛：计数之递推法.学生版解题技巧培优易错难

【例 3】一楼梯共10级，规定每步只能跨上一级或两级，要登上第10级，共有多少种不同走法？
【巩固】一楼梯共10级，规定每步只能跨上一级或三级，要登上第10级，共有多少种不同走法？
【例 4】1×2的小长方形(横的竖的都行)覆盖2×10的方格网，共有多少种不同的盖法．
【例 5】用的小长方形覆盖的方格网，共有多少种不同的盖法？
【巩固】小蜜蜂通过蜂巢房间，规定只能由小号房间进入大号房间问小蜜蜂由房间到达房间有多少种方法？
【例 9】如下图，一只蜜蜂从A处出发，回到家里B处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？
【例 10】对一个自然数作如下操作：如果是偶数则除以2，如果是奇数则加1，如此进行直到得数为1操作停止．问经过9次操作变为1的数有多少个？
【例 1】每对小兔子在出生后一个月就长成大兔子，而每对大兔子每个月能生出一对小兔子来．如果一个人在一月份买了一对小兔子，那么十二月份的时候他共有多少对兔子？
【例 2】树木生长的过程中，新生的枝条往往需要一段“休息”时间供自身生长，而后才能萌发新枝．一棵树苗在一年后长出一条新枝，第二年新枝“休息”，老枝依旧萌发新枝；此后，老枝与“休息”过一年的枝同时萌发，当年生的新枝则依次“休息”．这在生物学上称为“鲁德维格定律”．那么十年后这棵树上有多少条树枝？
【例 6】有一堆火柴共12根，如果规定每次取1～3根，那么取完这堆火柴共有多少种不同取法？
【巩固】一堆苹果共有8个，如果规定每次取1～3个，那么取完这堆苹果共有多少种不同取法？
【例 7】有10枚棋子，每次拿出2枚或3枚，要想将10枚棋子全部拿完，共有多少种不同的拿法？
【例 8】如下图，一只蜜蜂从处出发，回到家里处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？

小学奥数递推方法的概述及解题技巧参考

小学奥数递推方法的概述及解题技巧参考
含义：在不少计数问题中，要很快求出结果是比较困难的'，有时可先从简单情况入手，然后从某一种特殊情况逐渐推出与以后比较复杂情况之间的关系，找出规律逐步解决问题，这样的方法叫递推方法。

问题：线段AB上共有10个点(包括两个端点)，那么这条线段上一共有多少条不同的线段?
分析与解答：从简单情况研究起：
AB上共有2个点，有线段：1条
AB上共有3个点，有线段：1+2=3(条)
AB上共有4个点，有线段：1+2+3=6(条)
AB上共有5个点，有线段：1+2+3+4=10(条)
……
AB上共有10个点，有线段：1+2+3+4+…+9=45(条)
一般地，AB上共有n个点，有线段：
1+2+3+4+…+(n-1)=n×(n-1)÷2
即：线段数=点数×(点数-1)÷2
【小学奥数递推方法的概述及解题技巧参考】。

奥数计数问题之递推法例题讲解【三篇】

奥数计数问题之递推法例题讲解【三篇】导读：本文奥数计数问题之递推法例题讲解【三篇】，仅供参考，如果觉得很不错，欢迎点评和分享。

【第一篇】例题：平面上有10个圆，最多能把平面分成几部分？分析与解答：直接画出10个圆不是好办法，先考虑一些简单情况。

一个圆最多将平面分为2部分；二个圆最多将平面分为4部分；三个圆最多将平面分为8部分；当第二个圆在第一个圆的基础上加上去时，第二个圆与第一个圆有2个交点，这两个交点将新加的圆弧分为2段，其中每一段圆弧都将所在平面的一分为二，所以所分平面部分的数在原有的2部分的基础上增添了2部分。

因此，二个圆最多将平面分为2＋2＝4部分。

同样道理，三个圆最多分平面的部分数是二个圆分平面为4部分的基础上增加4部分。

因此，三个圆最多将平面分为2＋2＋4＝8部分。

由此不难推出：画第10个圆时，与前9个圆最多有9×2＝18个交点，第10个圆的圆弧被分成18段，也就是增加了18个部分。

因此，10个圆最多将平面分成的部分数为：2＋2＋4＋6＋…＋18＝2＋2×（1＋2＋3＋ (9)＝2＋2×9×（9＋1）÷2＝92类似的分析，我们可以得到，n个圆最多将平面分成的部分数为：2＋2＋4＋6＋…＋2（n－1）＝2＋2×[1＋2＋3＋…＋（n－1）]＝2＋n（n－1）＝n2－n＋2 【第二篇】例题：有8块相同的巧克力糖，从今天开始每天至少吃一块，最多吃两块，吃完为止，共有多少种不同的吃法？分析与解答：【第三篇】例题： 4个人进行篮球训练，互相传球接球，要求每个人接球后马上传给别人，开始由甲发球，并作为第一次传球，第五次传球后，球又回到甲手中，问有多少种传球方法？分析与解答：。

计数之递推法

7-6-4计数之递推法教学目标前面在讲加法原理、乘法原理、排列组合时已经穿插讲解了计数中的一些常用的方法，比如枚举法、树形图法、标数法、捆绑法、排除法、插板法等等，这里再集中学习一下计数中其他常见的方法，主要有归纳法、整体法、对应法、递推法．对这些计数方法与技巧要做到灵活运用．例题精讲对于某些难以发现其一般情形的计数问题，可以找出其相邻数之间的递归关系，有了这一递归关系就可以利用前面的数求出后面未知的数，这种方法称为递推法．【例1】每对小兔子在出生后一个月就长成大兔子，而每对大兔子每个月能生出一对小兔子来．如果一个人在一月份买了一对小兔子，那么十二月份的时候他共有多少对兔子？【例2】树木生长的过程中，新生的枝条往往需要一段“休息”时间供自身生长，而后才能萌发新枝．一棵树苗在一年后长出一条新枝，第二年新枝“休息”，老枝依旧萌发新枝；此后，老枝与“休息”过一年的枝同时萌发，当年生的新枝则依次“休息”．这在生物学上称为“鲁德维格定律”．那么十年后这棵树上有多少条树枝？【例3】一楼梯共10级，规定每步只能跨上一级或两级，要登上第10级，共有多少种不同走法？【巩固】一楼梯共10级，规定每步只能跨上一级或三级，要登上第10级，共有多少种不同走法？【例4】1×2的小长方形(横的竖的都行)覆盖2×10的方格网，共有多少种不同的盖法．【例5】用13⨯的方格网，共有多少种不同的盖法？⨯的小长方形覆盖38【例6】有一堆火柴共12根，如果规定每次取1～3根，那么取完这堆火柴共有多少种不同取法？【巩固】一堆苹果共有8个，如果规定每次取1～3个，那么取完这堆苹果共有多少种不同取法？【例7】有10枚棋子，每次拿出2枚或3枚，要想将10枚棋子全部拿完，共有多少种不同的拿法？【例8】如下图，一只蜜蜂从A处出发，回到家里B处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？AB【巩固】小蜜蜂通过蜂巢房间，规定只能由小号房间进入大号房间问小蜜蜂由A房间到达B房间有多少种方法？【例9】如下图，一只蜜蜂从A处出发，回到家里B处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？【例10】对一个自然数作如下操作：如果是偶数则除以2，如果是奇数则加1，如此进行直到得数为1操作停止．问经过9次操作变为1的数有多少个？【例11】有20个石子，一个人分若干次取，每次可以取1个，2个或3个，但是每次取完之后不能留下质数个，有多少种方法取完石子？（石子之间不作区分，只考虑石子个数）【巩固】有20个相同的棋子，一个人分若干次取，每次可取1个，2个，3个或4个，但要求每次取之后留下的棋子数不是3或4的倍数，有种不同的方法取完这堆棋子.【例12】4个人进行篮球训练，互相传球接球，要求每个人接球后马上传给别人，开始由甲发球，并作为第一次传球，第五次传球后，球又回到甲手中，问有多少种传球方法？【巩固】五个人互相传球，由甲开始发球，并作为第一次传球，经过4次传球后，球仍回到甲手中．问：共有多少种传球方式？【例13】设A、E为正八边形ABCDEFGH的相对顶点，顶点A处有一只青蛙，除顶点E外青蛙可以从正八边形的任一顶点跳到其相邻两个顶点中任意一个，落到顶点E时青蛙就停止跳动，则青蛙从顶点A出发恰好跳10次后落到E的方法总数为种．【巩固】在正五边形ABCDE上，一只青蛙从A点开始跳动，它每次可以随意跳到相邻两个顶点中的一个上，一旦跳到D点上就停止跳动．青蛙在6次之内(含6次)跳到D点有种不同跳法．【例14】有6个木箱，编号为1，2，3，……，6，每个箱子有一把钥匙，6把钥匙各不相同，每个箱子放进一把钥匙锁好．先挖开1，2号箱子，可以取出钥匙去开箱子上的锁，如果最终能把6把锁都打开，则说这是一种放钥匙的“好”的方法，那么“好”的方法共有种．【巩固】有10个木箱，编号为1，2，3，……，10，每个箱子有一把钥匙，10把钥匙各不相同，每个箱子放进一把钥匙锁好．先挖开1，2号箱子，可以取出钥匙去开箱子上的锁，如果最终能把10把锁都打开，则说这是一种放钥匙的“好”的方法，那么“好”的方法共有种．。

一、递推的方法

一、递推的方法在不少计数问题中，要很快求出结果是比较困难的，有时可先从简单情况入手，然后从某一种特殊情况逐渐推出与以后比较复杂情况之间的关系，找出规律逐步解决问题，这样的方法叫递推方法。

例2 计算13＋23＋33＋43＋53＋63＋73＋83＋93＋103的值。

这道题我们可以采用分别求出每个数的立方是多少，再求和的方法来解答。

但是，这样计算的工作量比较大，我们可以从简单的情况开始研究。

13＋23＝9＝32＝(1＋2)213＋23＋33＝36＝62＝(1＋2＋3)213＋23＋33＋43＝100＝102＝(1＋2＋3＋4)2……这样我们可以得到：13＋23＋33＋43＋53＋63＋73＋83＋93＋103＝(1＋2＋3＋4＋5＋6＋7＋8＋9＋10)2＝552＝3025所以 13＋23＋33＋……＋ｎ3＝(1＋2＋3＋……＋ｎ)2例3 2000个学生排成一行，依次从左到右编上1～2000号，然后从左到右按一、二报数，报一的离开队伍，剩下的人继续按一、二报数，报一的离开队伍，……按这个规律如此下去，直至当队伍只剩下一人为止。

问：这时一共报了多少次？最后留下的这个人原来的号码是多少？难的不会想简单的，数大的不会想数小的。

我们先从这2000名同学中选出20人代替2000人进行分析，试着找出规律，然后再用这个规律来解题。

这20人第一次报数后共留下10人，因为20÷2＝10 ，这10人开始时的编号依次是：2、4、6、8、10、12、14、16、18、20，都是2的倍数。

第二次报数后共留下5人，因为10÷2＝5 ，这5人开始时的编号依次是： 4、8、12、16、20，都是4的倍数，也就是2×2的倍数。

第三次报数后共留下2人，因为5÷2＝2 ……1 ，这2人开始时的编号依次是： 8、16，都是8的倍数，也就是2×2×2的倍数。

第四次报数后共留下1人，因为2÷2＝1 ，这1人开始时的编号是：16，都是8的倍数，也就是2×2×2×2的倍数。

高斯小学奥数六年级上册含答案第03讲递推计数

第三讲递推计数有许多计数问题很复杂，直接处理比较困难，此时硬碰硬是不行的．一个比较有效的策略是退而求其次：先考虑该问题的简单情形，看看简单情形如何处理；在解决了简单情形后，再考虑如何利用简单情形的结论来解决更复杂的问题……这个由简单到复杂的推导过程就叫“递推”．那如何利用“递推法”来解决计数问题呢？下面我们就来看几个例子．例1．老师给小高布置了12篇作文，规定他每天至少写1篇．如果小高每天最多能写3篇，那么共有多少种不同的完成方法？（小高每天只能写整数篇）「分析」从简单情况入手，看看能否找到合适的突破口．如果老师只布置1篇作文，小高有多少种不同的完成方法？如果老师布置2篇作文，小高有多少种不同的完成方法？如果老师布置3篇、4篇、……小高又分别有多少种不同的完成方法？篇数由少到多，完成方法数也会逐渐变多，这其中有什么规律呢？练习1、一个楼梯共有12级台阶，规定每步可以迈二级台阶或三级台阶．走完这12级台阶，共有多少种不同的走法？⨯的方格表，共有多少种覆盖方法？例2．用10个13⨯的长方形纸片覆盖一个103「分析」与例1的类似，我们还是从简单情形入手找递推关系．可具体从什么样的情形入手呢？⨯的方格表，共有多少种覆盖方法？练习2、用7个12⨯的长方形纸片覆盖一个72例3．在一个平面上画出100条直线，最多可以把平面分成几个部分？「分析」当直线数量不多时，画图数一数即可．但现在有100条，画图数并不现实．我们不妨在纸上将直线逐一画出，并在画的过程中仔细观察：每增加一条直线，平面被分成的部分会增加多少？这个增量．．有什么变化规律？练习3、如果在一个圆内画出50条直线，最多可以把圆分成多少部分？下面我们来学习一类很经典的递推计数问题——传球问题．例4．四个人分别穿着红、黄、绿、蓝四种颜色的球衣练习传球，每人都可以把球传给另外三个人中的任意一个．先由红衣人发球，并作为第1次传球，经过8次传球后球仍然回到红衣人手中．请问：整个传球过程共有多少种不同的可能？「分析」看到这个问题，很多同学可能想通过树形图来求解，我们不妨来试一试．设穿着红、黄、绿、蓝四种颜色球衣的人分别是A 、B 、C 、D ．如下图，最开始时，球在A 手上，第一次传球由A 传给B 、C 、D ，也就是第一层有三个字母就够了．然后B 、C 、D 都会继续往下传球，各有3种传法，传到第二层需要9个字母．再传到第三层，需要27个字母……每一层需要的字母增加迅猛！如果传8次球，到最后一层会用到836561 个字母，这要多大的一个树形图啊！可见画树形图的方案不可行．但树形图对这道题就没有用了吗？并非如此．它可以帮助我们找出传球过程中所隐藏的递推关系．事实上，我们并不关心树形图长啥样，我们关心的是数量——树形图每一层分支的数量．因此，只要知道每一层各字母出现的次数就可以了，我们不妨制作一个表格来统计这个次数．如下表，我们用第一列来表示层数，第一行来表示每个人，其余空格用于填写字母在该层中出现的次数．请你从上方的树形图中数一数，填出表格中的前几行．然后思考一下：这其中隐藏着什么样的递推关系？BC DACDABDABCAB C D A B D A B C B C D A C D A B C B C D A C D A B D练习4、三个人分别穿着红、黄、蓝三种颜色的球衣练习传球，每人都可以把球传给另外两个人中的任意一个．先由红衣人发球，并作为第1次传球，经过7次传球后传到蓝衣人手中．请问：整个传球过程共有多少种不同的可能？解传球问题的方法称为“传球法”．“传球法”是递推法的一种特殊形式，是一种极其实用的数表累加计数法．例5．一个七位数，每一位都是1、2或者3，而且没有连续的两个1，这样的七位数一共有多少个？「分析」这道题与前面两道题有何异同？应该如何求解呢？前面的计数问题，递推关系都表现为数列、数表的简单累加，但这不是递推的全部．简单累加只是递推的一种表现形式，递推还有很多其它形式．下面我们就来看一道无法通过简单累加求解的计数问题．例6．圆周上有10个点A1、A2、L、A10，以这些点为端点连接5条线段，要求线段之间没有公共点，共有多少种连接方式？「分析」圆周上10个点，连5条线段，连法很多，很难直接画出来枚举．像这类问题，我们同样还是从简单的情况入手．那么是应该按1个点、2个点、3个点、……这样依次计数，来找递推关系吗？神奇的汉诺塔一位法国数学家曾编写过一个印度的古老传说：在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针．印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔．不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面．僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽．不管这个传说的可信度有多大，如果考虑一下把64片金片，由一根针上移到另一根针上，并且始终保持上小下大的顺序．这需要多少次移动呢?这里需要递归的方法．假设有n 片，移动次数是()f n ．显然(1)1f =，(2)3f =，(3)7f =，且(1)2()1f k f k +=+．此后不难证明()21n f n =-．64n =时，64(64)2118446744073709551615f =-=．假如每秒钟一次，共需多长时间呢？一个平年365天有31536000 秒，闰年366天有31622400秒，平均每年31556952秒，计算一下，18446744073709551615/31556952=584554049253.855年．这表明移完这些金片需要5845亿年以上，而地球存在至今不过45亿年，太阳系的预期寿命据说也就是数百亿年．真的过了5845亿年，不说太阳系和银河系，至少地球上的一切生命，连同梵塔、庙宇等，都早已经灰飞烟灭．课堂内外作业1. 有10个蛋黄派，萱萱每天吃1个或2个，那么共有多少种不同的吃法？2. 甲、乙两人玩抓石子游戏，共有12个石子，甲先乙后轮流抓取．每次可以抓取其中的2个、3个或4个，直到最后抓取完毕为止．那么共有多少种抓取石子的方案？3. 用直线把一个平面分成100部分，至少要在平面上画几条直线？4. 一个七位数，它由数字0、1、2、3、4组成，相邻位置上的数字不相同，并且个位数字是2．这样的七位数有多少个？5. 用8个的长方形纸片覆盖下面的方格表，共有多少种覆盖方法？12第五讲进位制问题例题：例7．答案：（1）31023、3735、11B9、7DD ；（2）257；（3）1742详解：（1）（2）32025051525257⨯+⨯+⨯+⨯=；（3）3202120121122121742⨯+⨯+⨯+⨯=．例8．答案：（1）5；（2）13121、731 详解：三进制转九进制从右往左两位两位转换；二进制转四进制从右往左两位两位转换；二进制转八进制从右往左三位三位转换．例9．答案：15031 详解：列竖式计算．例10．答案：212．a =5、b =5、c =2例11．答案：10个详解：若要称量1克的重量必须有1克的砝码，若要称量2克的重量必须有2克的砝码，依次类推可得：1+2+4+8+16+32+64+128+256+512，此时可以称量1克到1023克的所有重量，此时需要10个砝码．例12．答案：12...... 3 ...... 2 ...... 1 0 (3)...... 2 ...... 3 (7) (3)…… 9 ……12 (1) (1)...... 13 ...... 13 (7)详解：所看页数列为1、1、2、4、8、……、256、512、989．练习：6. 答案：554；2781；195；7227. 答案：161578. 答案：212349. 答案：248．a =5、b =0、c =3作业：1. 答案：（1）354；（2）458；（3）C 30；（4）14443；（5）433；（6）852. 答案：（1）1131；（2）123123. 答案：100简答：a 很容易知道只能为1，再根据进位制展开解方程得出b 、c 均为0，所以原数十进制是100．4. 答案：22简答：由题意有，其中a 、b 、c 均小于3，则有，化简得，符合条件的a 、b 、c 为2、1、1，化成十进制是22．5. 答案：24简答：由题意有，其中a 、b 均要大于7，则有，符合条件的最小的a 、b 为15、9，和是24．4774a b +=+ ()()4774a b = 815a b c =+ 93164a b c c b a ++=++ ()()34abc cba =。

第三讲 ——递推计数

第三讲递推计数知识精讲有许多计数问题很复杂，直接处理比较困难，此时硬碰硬是不行的.一个比较有效的策略是退而求其次：先考虑该问题的简单情形，看看简单情形如何处理；在解决了简年情形后，再考虑如何利用简单情形的结论来解决更复杂的问题……这个由简单到复杂的推导过程就叫“递推”。

那如何利用“递推法”来解决计数问题呢？下面我们就来看几个例子.例1、老师给小高布置了 12篇作文，规定他每天至少写1篇.如果小高每天最多能写3篇，那么共有多少种不同的完成方法?（小高每天只能写整数篇）练习1 、一个楼梯一共有12级台阶，规定每步可以迈二级台阶或三级台阶，走完这12级台阶共有多少种不同的走法？例2、用10个1×3的长方形纸片覆盖一个10×3的方格表，共有多少种覆盖方法？练习2、用7个1×2的长方形纸片覆盖一个7×2的方格表，共有多少种覆盖方法？例3、在一个平面上画出100条线，最多可以把平面分成几部分？练习3、如果在一个圆内画出50条直线，最多可以把圆分成多少部分?例题4四个人分别穿着红、黄、绿、蓝四种颜色的球衣练习传球，每人都可以把球传给另外三个人中的任意一个.先由红衣人发球，并作为第1次传球, 经过8次传球后球仍然回到红衣人手中.请问：整个传球过程共有多少种不同的可能？练习4三个人分别穿着红、黄、蓝三种颜色的球衣练习传球，每人都可以把球传给另外两个人中的任意一个.先由红衣人发球，并作为第1次传球，经过7次传球后传到蓝衣人手中.请问：整个传球过程共有多少种不同的可能？极限挑战例题5 一个七位数，每一位都是1、2或者3，而且没有连续的两个1，这样的七位数一共有多少个？例题6 圆周上有10个点1021,,A A A ,以这些点为端点连接5条线段，要求线段之间没有公共点，共有多少种连接方式？作业1、有10个蛋黄派，萱萱每天吃1个或2个，那么共有多少种不同的吃法？2、甲、乙两人玩抓石子游戏，共有12个石子，甲先乙后轮流抓取，每次可以抓取其中的2个 3个或4个，直到最后抓取完毕为止.那么共有多少种抓取石子的方案？3、用直线把一个平面分成100部分，至少要在平面上画几条直线?4、一个七位数，它由数字0、 1、2、3、4组成，相邻位置上的数字不相同，并且个位数字是2。

小学奥数：计数之递推法.专项练习及答案解析

7-6-4.计数之递推法教学目标前面在讲加法原理、乘法原理、排列组合时已经穿插讲解了计数中的一些常用的方法，比如枚举法、树形图法、标数法、捆绑法、排除法、插板法等等，这里再集中学习一下计数中其他常见的方法，主要有归纳法、整体法、对应法、递推法．对这些计数方法与技巧要做到灵活运用．例题精讲对于某些难以发现其一般情形的计数问题，可以找出其相邻数之间的递归关系，有了这一递归关系就可以利用前面的数求出后面未知的数，这种方法称为递推法．【例 1】每对小兔子在出生后一个月就长成大兔子，而每对大兔子每个月能生出一对小兔子来．如果一个人在一月份买了一对小兔子，那么十二月份的时候他共有多少对兔子？【考点】计数之递推法【难度】3星【题型】解答【解析】第一个月，有1对小兔子；第二个月，长成大兔子，所以还是1对；第三个月，大兔子生下一对小兔子，所以共有2对；第四个月，刚生下的小兔子长成大兔子，而原来的大兔子又生下一对小兔子，共有3对；第五个月，两对大兔子生下2对小兔子，共有5对；……这个特点的说明每月的大兔子数为上月的兔子数，每月的小兔子数为上月的大兔子数，即上上月的兔子数，所以每月的兔子数为上月的兔子数与上上月的兔子数相加．依次类推可以列出下表：经过月数：---1---2---3---4---5---6---7---8---9---10---11---12兔子对数：---1---1---2---3---5---8--13--21--34--55--89—144，所以十二月份的时候总共有144对兔子．【答案】144【例 2】树木生长的过程中，新生的枝条往往需要一段“休息”时间供自身生长，而后才能萌发新枝．一棵树苗在一年后长出一条新枝，第二年新枝“休息”，老枝依旧萌发新枝；此后，老枝与“休息”过一年的枝同时萌发，当年生的新枝则依次“休息”．这在生物学上称为“鲁德维格定律”．那么十年后这棵树上有多少条树枝？【考点】计数之递推法【难度】3星【题型】解答【解析】一株树木各个年份的枝桠数，构成斐波那契数列：1，2，3，5，8，13，21，34，55，89，……所以十年后树上有89条树枝．【答案】89【例 3】一楼梯共10级，规定每步只能跨上一级或两级，要登上第10级，共有多少种不同走法？【考点】计数之递推法【难度】4星【题型】解答【解析】登 1级 2级 3级 4级 ...... 10级1种方法 2种 3种 5种 ...... ？我们观察每级的种数，发现这么一个规律：从第三个数开始，每个数是前面两个数的和；依此规律我们就可以知道了第10级的种数是89.其实这也是加法的运用：假如我们把这个人开始登楼梯的位置看做A 0，那么登了1级的位置是在A 1，2级在A 2... A 10级就在A 10．到A 3的前一步有两个位置；分别是A 2 和A 1 ．在这里要强调一点，那么A 2 到A 3 既然是一步到了，那么A 2 、A 3之间就是一种选择了；同理A 1 到A 3 也是一种选择了．同时我们假设到n 级的选择数就是An ．那么从A 0 到A 3 就可以分成两类了：第一类：A 0 ---- A 1 ------ A 3 ，那么就可以分成两步．有A 1×1种，也就是A 1 种；(A 1 ------ A 3 是一种选择)第二类：A 0 ---- A 2 ------ A 3，同样道理有A 2 ．类类相加原理：A 3 = A 1 ＋A 2，依次类推An = An -1 + An -2．【答案】89【巩固】一楼梯共10级，规定每步只能跨上一级或三级，要登上第10级，共有多少种不同走法？【考点】计数之递推法【难度】4星【题型】解答【解析】登 1级 2级 3级 4级 5级 ...... 10级1种方法 1种 2种 3种 4种...... ？我们观察每级的种数，发现这么一个规律：从第三个数开始，每个数是前面相隔的两个数的和；依此规律我们就可以知道了第10级的种数是28.【答案】28【例 4】 1×2的小长方形(横的竖的都行)覆盖2×10的方格网，共有多少种不同的盖法．【考点】计数之递推法【难度】4星【题型】解答【解析】如果用12⨯的长方形盖2n ⨯的长方形，设种数为n a ,则11a =，22a =,对于3n ≥，左边可能竖放1个12⨯的，也可能横放2个12⨯的，前者有-1n a 种，后者有-2n a 种，所以-1-2n n n a a a =+,所以根据递推，覆盖210⨯的长方形一共有89种．【答案】89【例 5】用13⨯的小长方形覆盖38⨯的方格网，共有多少种不同的盖法？【考点】计数之递推法【难度】5星【题型】解答【解析】如果用13⨯的长方形盖3n ⨯的长方形，设种数为n a ,则11a =，21a =,32a =,对于4n ≥，左边可能竖放1个13⨯的，也可能横放3个13⨯的，前者有-1n a 种，后者有a 种，所以a a a =+,依照这条递推公式列表：【答案】13【例 6】有一堆火柴共12根，如果规定每次取1～3根，那么取完这堆火柴共有多少种不同取法？【考点】计数之递推法【难度】4星【题型】解答【解析】取1根火柴有1种方法，取2根火柴有2种方法，取3根火柴有4种取法，以后取任意根火柴的种数等于取到前三根火柴所有情况之和，以此类推，参照上题列表如【答案】927【巩固】一堆苹果共有8个，如果规定每次取1～3个，那么取完这堆苹果共有多少种不同取法？【考点】计数之递推法【难度】4星【题型】解答【解析】取1个苹果有1种方法，取2个苹果有2种方法，取3个苹果有4种取法，以后取任意个苹果的种数等于取到前三个苹果所有情况之和，以此类推，参照上题列表如【答案】81【例 7】有10枚棋子，每次拿出2枚或3枚，要想将10枚棋子全部拿完，共有多少种不同的拿法？【考点】计数之递推法【难度】4星【题型】解答【解析】本题可以采用递推法，也可以进行分类讨论，当然也可以直接进行枚举． (法1)递推法．假设有n 枚棋子，每次拿出2枚或3枚，将n 枚棋子全部拿完的拿法总数为n a 种．则21a =，31a =，41a =．由于每次拿出2枚或3枚，所以32n n n a a a --=+(5n ≥)．所以，5232a a a =+=；6342a a a =+=；7453a a a =+=；8564a a a =+=；9675a a a =+=；10787a a a =+=．即当有10枚棋子时，共有7种不同的拿法．(法2)分类讨论．由于棋子总数为10枚，是个偶数，而每次拿2枚或3枚，所以其中拿3枚的次数也应该是偶数．由于拿3枚的次数不超过3次，所以只能为0次或2次．若为0次，则相当于2枚拿了5次，此时有1种拿法；若为2次，则2枚也拿了2次，共拿了4次，所以此时有246C =种拿法．根据加法原理，共有167+=种不同的拿法．【答案】7【例 8】如下图，一只蜜蜂从A 处出发，回到家里B 处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？【考点】计数之递推法【难度】4星【题型】解答BAA B 1357946821235813213455891【解析】蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”这意味着它只能从小号码的蜂房爬近相邻大号码的蜂房．明确了行走路径的方向，就可以运用标数法进行计算．如右图所示，小蜜蜂从A 出发到B 处共有89种不同的回家方法．【答案】89【巩固】小蜜蜂通过蜂巢房间，规定只能由小号房间进入大号房间问小蜜蜂由A 房间到达B房间有多少种方法？【考点】计数之递推法【难度】4星【题型】解答【解析】斐波那契数列第八项．21种．86427531【答案】21【例 9】如下图，一只蜜蜂从A 处出发，回到家里B 处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？【考点】计数之递推法【难度】4星【题型】解答BA【解析】按照蜜蜂只能从小号码的蜂房爬近相邻大号码的蜂房的原则，运用标号法进行计算．如右图所示，小蜜蜂从A 出发到B 处共有296种不同的回家方法．【答案】296【例 10】对一个自然数作如下操作：如果是偶数则除以2，如果是奇数则加1，如此进行直到得数为1操作停止．问经过9次操作变为1的数有多少个？【考点】计数之递推法【难度】4星【题型】解答【解析】可以先尝试一下，倒推得出下面的图：2410131112514302831643215167683421其中经1次操作变为1的1个，即2，经2次操作变为1的1个，即4，经3次操作变为1的2个，是一奇一偶，以后发现，每个偶数可以变成两个数，分别是一奇一偶，每个奇数变为一个偶数，于是，经1、2、…次操作变为1的数的个数依次为：1，1，2，3，5，8，…这一串数中有个特点：自第三个开始，每一个等于前两个的和，即即经过9次操作变为1的数有34个.为什么上面的规律是正确的呢？道理也很简单. 设经过n 次操作变为1的数的个数为n a ,则1a =1，2a =1，3a =2，… 从上面的图看出，1n a +比n a 大.一方面，每个经过n 次操作变为1的数，乘以2，就得出一个偶数，经过1n +次操作变为1；反过来，每个经过1n +次操作变为1的偶数，除以2，就得出一个经过n 次操作变为1的数. 所以经过n 次操作变为1的数与经过1n +次操作变为1的偶数恰好一样多.前者的个数是n a ,因此后者也是n a 个.另一方面，每个经过n 次操作变为1的偶数，减去1，就得出一个奇数，它经过1n +次操作变为1，反过来.每个经过1n +次操作变为1的奇数，加上1，就得出一个偶数，它经过n 次操作变为1. 所以经过n 次操作变为1的偶数经过1n +次操作变为1的奇数恰好一样多. 而由上面所说，前者的个数就是1n a -,因此后者也是1n a -.经过n +1次操作变为1的数，分为偶数、奇数两类，所以11n n n a a a +-=+，即上面所说的规律的确成立.【答案】34【例 11】有20个石子，一个人分若干次取，每次可以取1个，2个或3个，但是每次取完之后不能留下质数个，有多少种方法取完石子？（石子之间不作区分，只考虑石子个数）【考点】计数之递推法【难度】5星【题型】解答【解析】如果没有剩下的不能使质数这个条件，那么递推方法与前面学过的递推法相似，只不过每次都是前面3个数相加．现在剩下的不能是质数个，可以看作是质数个的取法总数都是0，然后再进行递推．【答案】25【巩固】有20个相同的棋子，一个人分若干次取，每次可取1个，2个，3个或4个，但要求每次取之后留下的棋子数不是3或4的倍数，有种不同的方法取完这堆棋子.【考点】计数之递推法【难度】5星【题型】填空【解析】把20、0和20以内不是3或4的倍数的数写成一串，用递推法把所有的方法数写出来：【答案】54【例 12】 4个人进行篮球训练，互相传球接球，要求每个人接球后马上传给别人，开始由甲发球，并作为第一次传球，第五次传球后，球又回到甲手中，问有多少种传球方法？【考点】计数之递推法【难度】5星【题型】解答【解析】设第n 次传球后，球又回到甲手中的传球方法有n a 种．可以想象前1n -次传球，如果每一次传球都任选其他三人中的一人进行传球，即每次传球都有3种可能，由乘法原理，共有11333333n n --⨯⨯⨯=144424443()个…(种)传球方法．这些传球方法并不是都符合要求的，它们可以分为两类，一类是第1n -次恰好传到甲手中，这有1n a -种传法，它们不符合要求，因为这样第n 次无法再把球传给甲；另一类是第1n -次传球，球不在甲手中，第n 次持球人再将球传给甲，有n a 种传法．根据加法原理，有11133333n n n n a a ---+=⨯⨯⨯=14444244443(个…)．由于甲是发球者，一次传球后球又回到甲手中的传球方法是不存在的，所以10a =．利用递推关系可以得到：2303a =-=，33336a =⨯-=，4333621a =⨯⨯-=，533332160a =⨯⨯⨯-=．这说明经过5次传球后，球仍回到甲手中的传球方法有60种．本题也可以列表求解．由于第n 次传球后，球不在甲手中的传球方法，第1n +次传球后球就可能回到甲手中，所以只需求出第四次传球后，球不在甲手中的传法共有多少种．从表中可以看出经过五次传球后，球仍回到甲手中的传球方法共有60种．【答案】60【巩固】五个人互相传球，由甲开始发球，并作为第一次传球，经过4次传球后，球仍回到甲手中．问：共有多少种传球方式？【考点】计数之递推法【难度】5星【题型】解答【解析】递推法．设第n 次传球后球传到甲的手中的方法有n a 种．由于每次传球有4种选择，传n 次有4n 次可能．其中有的球在甲的手中，有的球不在甲的手中，球在甲的手中的有n a 种，球不在甲的手中的，下一次传球都可以将球传到甲的手中，故有1n a +种．所以14n n n a a ++=．由于10a =，所以12144a a =-=，232412a a =-=，343452a a =-=．即经过4次传球后，球仍回到甲手中的传球方法有52种．【答案】52【例 13】设A 、E 为正八边形ABCDEFGH 的相对顶点，顶点A 处有一只青蛙，除顶点E 外青蛙可以从正八边形的任一顶点跳到其相邻两个顶点中任意一个，落到顶点E 时青蛙就停止跳动，则青蛙从顶点A 出发恰好跳10次后落到E 的方法总数为种．【考点】计数之递推法【难度】5星【题型】填空【关键词】清华附中【解析】可以使用递推法．回到A 跳到B 或H 跳到C 或G 跳到D 或F 停在E 1步 12步 2 13步 3 14步 6 4 25步 10 46步 20 14 87步 34 148步 68 48 289步 116 48其中，第一列的每一个数都等于它的上一行的第二列的数的2倍，第二列的每一个数都等于它的上一行的第一列和第三列的两个数的和，第三列的每一个数都等于它的上一行的第二列和第四列的两个数的和，第四列的每一个数都等于它的上一行的第三列的数，第五列的每一个数都等于都等于它的上一行的第四列的数的2倍．这一规律很容易根据青蛙的跳动规则分析得来．所以，青蛙第10步跳到E 有48296⨯=种方法．【答案】96【巩固】在正五边形ABCDE 上，一只青蛙从A 点开始跳动，它每次可以随意跳到相邻两个顶点中的一个上，一旦跳到D 点上就停止跳动．青蛙在6次之内(含6次)跳到D 点有种不同跳法．【考点】计数之递推法【难度】5星【题型】填空AB C D E【解析】采用递推的方法．列表如下：跳到A 跳到B 跳到C 停在D 跳到E1步 1 12步 2 1 13步 3 1 24步 5 3 25步 8 3 56步 13 8 5其中，根据规则，每次可以随意跳到相邻两个顶点中的一个上，一旦跳到D 点上就停止跳动．所以，每一步跳到A 的跳法数等于上一步跳到B 和E 的跳法数之和，每一步跳到B 的跳法数等于上一步跳到A 和C 的跳法数之和，每一步跳到C 的跳法数等于上一步跳到B 的跳法数，每一步跳到E 的跳法数等于上一步跳到A 的跳法数，每一步跳到D 的跳法数等于上一步跳到C 或跳到E 的跳法数．观察可知，上面的递推结果与前面的枚举也相吻合，所以青蛙在6次之内(含6次)跳到D 点共有1123512++++=种不同的跳法．【答案】12【例 14】有6个木箱，编号为1，2，3，……，6，每个箱子有一把钥匙，6把钥匙各不相同，每个箱子放进一把钥匙锁好．先挖开1，2号箱子，可以取出钥匙去开箱子上的锁，如果最终能把6把锁都打开，则说这是一种放钥匙的“好”的方法，那么“好”的方法共有种．【考点】计数之递推法【难度】5星【题型】填空【关键词】迎春杯，中年级组，决赛【解析】 (法1)分类讨论．如果1，2号箱中恰好放的就是1，2号箱的钥匙，显然不是“好”的方法，所以“好”的方法有两种情况：⑴1，2号箱的钥匙恰有1把在1，2号箱中，另一箱装的是3～6箱的钥匙．⑵1，2号箱的钥匙都不在1，2号箱中．对于⑴，从1，2号箱的钥匙中选1把，从3～6号箱的钥匙中选1把，共有248⨯=(种)选法，每一种选法放入1，2号箱各有2种放法，共有8216⨯=(种)放法．不妨设1，3号箱的钥匙放入了1，2号箱，此时3号箱不能装2号箱的钥匙，有3种选法，依次类推，可知此时不同的放法有3216⨯⨯=(种)．所以，第⑴种情况有“好”的方法16696⨯=(种)．对于⑵，从3～6号箱的钥匙中选2把放入1，2号箱，有4312⨯=(种)放法．不妨设3，4号箱的钥匙放入了1，2号箱．此时1，2号箱的钥匙不可能都放在3，4号箱中，也就是说3，4号箱中至少有1把5，6号箱的钥匙．如果3，4号箱中有2把5，6号箱的钥匙，也就是说3，4号箱中放的恰好是5，6号箱的钥匙，那么1，2号箱的钥匙放在5，6号箱中，有224⨯=种放法；如果3，4号箱中有1把5，6号箱的钥匙，比如3，4号箱中放的是5，1号箱的钥匙，则只能是5号箱放6号箱的钥匙，6号箱放2号箱的钥匙，有212⨯=种放法；同理，3，4号箱放5，2号箱或6，1号箱或6，2号箱的钥匙，也各有2种放法．所以，第⑵种情况有“好”的放法()1242222144⨯++++=(种)．所以“好”的方法共有96144240+=(种)．(法2)递推法．设第1，2，3，…，6号箱子中所放的钥匙号码依次为1k ，2k ，3k ，…，6k ．当箱子数为n (2n ≥)时，好的放法的总数为n a ．当2n =时，显然22a =(11k =，22k =或12k =，21k =)．当3n =时，显然33k ≠，否则第3个箱子打不开，从而13k =或23k =，如果13k =，则把1号箱子和3号箱子看作一个整体，这样还是锁着1，2两号钥匙，撬开1，2两号箱子，那么方法有2a 种；当23k =也是如此．于是2n =时的每一种情况对应13k =或23k =时的一种情况，这样就有3224a a ==．当4n ≥时，也一定有n k n ≠，否则第n 个箱子打不开，从而1k 、2k 、……、1n k -中有一个为n ，不论其中哪一个是n ，由于必须要把该箱子打开才能打开n 号箱子，所以可以将锁着这把钥匙的箱子与第n 号箱子看作1个箱子，于是还是锁着1k 、2k 、……、1n k -这()1n -把钥匙，需要撬开1，2两号箱子，所以每种情况都有1n a -种．所以()11n n a n a -=-．所以，6542554543225!240a a a a ==⨯==⨯⨯⨯=⨯=L ，即好的方法总数为240种．【答案】240【巩固】有10个木箱，编号为1，2，3，……，10，每个箱子有一把钥匙，10把钥匙各不相同，每个箱子放进一把钥匙锁好．先挖开1，2号箱子，可以取出钥匙去开箱子上的锁，如果最终能把10把锁都打开，则说这是一种放钥匙的“好”的方法，那么“好”的方法共有种．【考点】计数之递推法【难度】5星【题型】填空【解析】递推法．设第1，2，3，…，6号箱子中所放的钥匙号码依次为1k ，2k ，3k ，…，6k ．当箱子数为n (2n ≥)时，好的放法的总数为n a ．当2n =时，显然22a =(11k =，22k =或12k =，21k =)．当3n =时，显然33k ≠，否则第3个箱子打不开，从而13k =或23k =，如果13k =，则把1号箱子和3号箱子看作一个整体，这样还是锁着1，2两号钥匙，撬开1，2两号箱子，那么方法有2a 种；当23k =也是如此．于是2n =时的每一种情况对应13k =或23k =时的一种情况，这样就有3224a a ==．当4n ≥时，也一定有n k n ≠，否则第n 个箱子打不开，从而1k 、2k 、……、1n k -中有一个为n ，不论其中哪一个是n ，由于必须要把该箱子打开才能打开n 号箱子，所以可以将锁着这把钥匙的箱子与第n 号箱子看作1个箱子，于是还是锁着1k 、2k 、……、1n k -这()1n -把钥匙，需要撬开1，2两号箱子，所以每种情况都有1n a -种．所以()11n n a n a -=-．所以，109829989876543229!=725760a a a a ==⨯==⨯⨯⨯⨯⨯⨯⨯=⨯L ，即好的方法总数为725760种．【答案】725760。

小学奥数计数之递推法(完整版)

小学奥数计数之递推法7-6-4.计数之递推法教学目标前面在讲加法原理、乘法原理、排列组合时已经穿插讲解了计数中的一些常用的方法，比如枚举法、树形图法、标数法、捆绑法、排除法、插板法等等，这里再集中学习一下计数中其他常见的方法，主要有归纳法、整体法、对应法、递推法．对这些计数方法与技巧要做到灵活运用．例题精讲对于某些难以发现其一般情形的计数问题，可以找出其相邻数之间的递归关系，有了这一递归关系就可以利用前面的数求出后面未知的数，这种方法称为递推法．【例 1】每对小兔子在出生后一个月就长成大兔子，而每对大兔子每个月能生出一对小兔子来．如果一个人在一月份买了一对小兔子，那么十二月份的时候他共有多少对兔子？【考点】计数之递推法【难度】3星【题型】解答【解析】第一个月，有1对小兔子；第二个月，长成大兔子，所以还是1对；第三个月，大兔子生下一对小兔子，所以共有2对；第四个月，刚生下的小兔子长成大兔子，而原来的大兔子又生下一对小兔子，共有3对；第五个月，两对大兔子生下2对小兔子，共有5对；……这个特点的说明每月的大兔子数为上月的兔子数，每月的小兔子数为上月的大兔子数，即上上月的兔子数，所以每月的兔子数为上月的兔子数与上上月的兔子数相加．依次类推可以列出下表：经过月数：---1---2---3---4---5---6---7---8---9---10---11---12兔子对数：---1---1---2---3---5---8--13--21--34--55--89—144，所以十二月份的时候总共有144对兔子．【答案】144【例 2】树木生长的过程中，新生的枝条往往需要一段“休息”时间供自身生长，而后才能萌发新枝．一棵树苗在一年后长出一条新枝，第二年新枝“休息”，老枝依旧萌发新枝；此后，老枝与“休息”过一年的枝同时萌发，当年生的新枝则依次“休息”．这在生物学上称为“鲁德维格定律”．那么十年后这棵树上有多少条树枝？【考点】计数之递推法【难度】3星【题型】解答【解析】一株树木各个年份的枝桠数，构成斐波那契数列：1，2，3，5，8，13，21，34，55，89，……所以十年后树上有89条树枝．【答案】89【例 3】一楼梯共10级，规定每步只能跨上一级或两级，要登上第10级，共有多少种不同走法？【考点】计数之递推法【难度】4星【题型】解答【解析】登 1级 2级 3级 4级 ...... 10级1种方法 2种 3种 5种 ...... ？我们观察每级的种数，发现这么一个规律：从第三个数开始，每个数是前面两个数的和；依此规律我们就可以知道了第10级的种数是89.其实这也是加法的运用：假如我们把这个人开始登楼梯的位置看做A 0，那么登了1级的位置是在A 1，2级在A 2... A 10级就在A 10．到A 3的前一步有两个位置；分别是A 2 和A 1 ．在这里要强调一点，那么A 2 到A 3 既然是一步到了，那么A 2 、A 3之间就是一种选择了；同理A 1 到A 3 也是一种选择了．同时我们假设到n 级的选择数就是An ．那么从A 0 到A 3 就可以分成两类了：第一类：A 0 ---- A 1 ------ A 3 ，那么就可以分成两步．有A 1×1种，也就是A 1 种；(A 1 ------ A 3 是一种选择)第二类：A 0 ---- A 2 ------ A 3，同样道理有A 2 ．类类相加原理：A 3 = A 1 ＋A 2，依次类推An = An -1 + An -2．【答案】89【巩固】一楼梯共10级，规定每步只能跨上一级或三级，要登上第10级，共有多少种不同走法？【考点】计数之递推法【难度】4星【题型】解答【解析】登 1级 2级 3级 4级 5级 ...... 10级1种方法 1种 2种 3种 4种...... ？我们观察每级的种数，发现这么一个规律：从第三个数开始，每个数是前面相隔的两个数的和；依此规律我们就可以知道了第10级的种数是28.【答案】28【例 4】 1×2的小长方形(横的竖的都行)覆盖2×10的方格网，共有多少种不同的盖法．【考点】计数之递推法【难度】4星【题型】解答【解析】如果用12⨯的长方形盖2n ⨯的长方形，设种数为n a ,则11a =，22a =,对于3n ≥，左边可能竖放1个12⨯的，也可能横放2个12⨯的，前者有-1n a 种，后者有-2n a 种，所以-1-2n n n a a a =+,所以根据递推，覆盖210⨯的长方形一共有89种．【答案】89【例 5】用13⨯的小长方形覆盖38⨯的方格网，共有多少种不同的盖法？【考点】计数之递推法【难度】5星【题型】解答【解析】如果用13⨯的长方形盖3n ⨯的长方形，设种数为n a ,则11a =，21a = ,32a = ,对于4n ≥，左边可能竖放1个13⨯的，也可能横放3个13⨯的，前者有-1n a 种，后者有-3n a 种，所以-1-3n n n a a a =+,依照这条递推公式列表：31⨯ 32⨯ 33⨯ 34⨯ 35⨯ 36⨯ 37⨯ 38⨯1 1234 6 9 13所以用13⨯的小长方形形覆盖38⨯的方格网，共有13种不同的盖法．【答案】13【例 6】有一堆火柴共12根，如果规定每次取1～3根，那么取完这堆火柴共有多少种不同取法？【考点】计数之递推法【难度】4星【题型】解答【解析】取1根火柴有1种方法，取2根火柴有2种方法，取3根火柴有4种取法，以后取任意根火柴的种数等于取到前三根火柴所有情况之和，以此类推，参照上题列表如下： 1根 2根 3根 4根 5根 6根 7根 8根 9根 10根 11根 12根1 2 4 7 13 24 44 81 149 274 504 927取完这堆火柴一共有927种方法．【答案】927【巩固】一堆苹果共有8个，如果规定每次取1～3个，那么取完这堆苹果共有多少种不同取法？【考点】计数之递推法【难度】4星【题型】解答【解析】取1个苹果有1种方法，取2个苹果有2种方法，取3个苹果有4种取法，以后取任意个苹果的种数等于取到前三个苹果所有情况之和，以此类推，参照上题列表如下：1个 2个 3个 4个 5个 6个 7个 8个1 2 4 7 13 24 44 81取完这堆苹果一共有81种方法．【答案】81【例 7】有10枚棋子，每次拿出2枚或3枚，要想将10枚棋子全部拿完，共有多少种不同的拿法？【考点】计数之递推法【难度】4星【题型】解答【解析】本题可以采用递推法，也可以进行分类讨论，当然也可以直接进行枚举．(法1)递推法．假设有n 枚棋子，每次拿出2枚或3枚，将n 枚棋子全部拿完的拿法总数为n a 种．则21a =，31a =，41a =．由于每次拿出2枚或3枚，所以32n n n a a a --=+(5n ≥)．所以，5232a a a =+=；6342a a a =+=；7453a a a =+=；8564a a a =+=；9675a a a =+=；10787a a a =+=．即当有10枚棋子时，共有7种不同的拿法．(法2)分类讨论．由于棋子总数为10枚，是个偶数，而每次拿2枚或3枚，所以其中拿3枚的次数也应该是偶数．由于拿3枚的次数不超过3次，所以只能为0次或2次．若为0次，则相当于2枚拿了5次，此时有1种拿法；若为2次，则2枚也拿了2次，共拿了4次，所以此时有246C =种拿法．根据加法原理，共有167+=种不同的拿法．【答案】7【例 8】如下图，一只蜜蜂从A 处出发，回到家里B 处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？【考点】计数之递推法【难度】4星【题型】解答【解析】蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”这意味着它只能从小号码的蜂房爬近相邻大号码的蜂房．明确了行走路径的方向，就可以运用标数法进行计算．如右图所示，小蜜蜂从A 出发到B 处共有89种不同的回家方法．【答案】89【巩固】小蜜蜂通过蜂巢房间，规定只能由小号房间进入大号房间问小蜜蜂由A 房间到达B房间有多少种方法？【考点】计数之递推法【难度】4星【题型】解答【解析】斐波那契数列第八项．21种．【答案】21【例 9】如下图，一只蜜蜂从A 处出发，回到家里B 处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？【考点】计数之递推法【难度】4星【题型】解答【解析】按照蜜蜂只能从小号码的蜂房爬近相邻大号码的蜂房的原则，运用标号法进行计算．如右图所示，小蜜蜂从A 出发到B 处共有296种不同的回家方法．【答案】296【例 10】对一个自然数作如下操作：如果是偶数则除以2，如果是奇数则加1，如此进行直到得数为1操作停止．问经过9次操作变为1的数有多少个？【考点】计数之递推法【难度】4星【题型】解答【解析】可以先尝试一下，倒推得出下面的图：BA AB 135794682123581321345589186427531BA其中经1次操作变为1的1个，即2，经2次操作变为1的1个，即4，经3次操作变为1的2个，是一奇一偶，以后发现，每个偶数可以变成两个数，分别是一奇一偶，每个奇数变为一个偶数，于是，经1、2、…次操作变为1的数的个数依次为：1，1，2，3，5，8，…这一串数中有个特点：自第三个开始，每一个等于前两个的和，即即经过9次操作变为1的数有34个.为什么上面的规律是正确的呢？道理也很简单. 设经过n 次操作变为1的数的个数为n a ,则1a =1，2a =1，3a =2，… 从上面的图看出，1n a +比n a 大.一方面，每个经过n 次操作变为1的数，乘以2，就得出一个偶数，经过1n +次操作变为1；反过来，每个经过1n +次操作变为1的偶数，除以2，就得出一个经过n 次操作变为1的数. 所以经过n 次操作变为1的数与经过1n +次操作变为1的偶数恰好一样多.前者的个数是n a ,因此后者也是n a 个.另一方面，每个经过n 次操作变为1的偶数，减去1，就得出一个奇数，它经过1n +次操作变为1，反过来.每个经过1n +次操作变为1的奇数，加上1，就得出一个偶数，它经过n 次操作变为1. 所以经过n 次操作变为1的偶数经过1n +次操作变为1的奇数恰好一样多.而由上面所说，前者的个数就是1n a -,因此后者也是1n a -.经过n +1次操作变为1的数，分为偶数、奇数两类，所以11n n n a a a +-=+，即上面所说的规律的确成立.【答案】34【例 11】有20个石子，一个人分若干次取，每次可以取1个，2个或3个，但是每次取完之后不能留下质数个，有多少种方法取完石子？（石子之间不作区分，只考虑石子个数）【考点】计数之递推法【难度】5星【题型】解答【解析】如果没有剩下的不能使质数这个条件，那么递推方法与前面学过的递推法相似，只不过每次都是前面3个数相加．现在剩下的不能是质数个，可以看作是质数个的取法总数都是0，然后再进行递推．【答案】25【巩固】有20个相同的棋子，一个人分若干次取，每次可取1个，2个，3个或4个，但要2410131112514302831643215167683421求每次取之后留下的棋子数不是3或4的倍数，有种不同的方法取完这堆棋子.【考点】计数之递推法【难度】5星【题型】填空【解析】把20、0和20以内不是3或4的倍数的数写成一串，用递推法把所有的方法数写出来：【答案】54【例 12】 4个人进行篮球训练，互相传球接球，要求每个人接球后马上传给别人，开始由甲发球，并作为第一次传球，第五次传球后，球又回到甲手中，问有多少种传球方法？【考点】计数之递推法【难度】5星【题型】解答【解析】设第n 次传球后，球又回到甲手中的传球方法有n a 种．可以想象前1n -次传球，如果每一次传球都任选其他三人中的一人进行传球，即每次传球都有3种可能，由乘法原理，共有11333333n n --⨯⨯⨯=()个…(种)传球方法．这些传球方法并不是都符合要求的，它们可以分为两类，一类是第1n -次恰好传到甲手中，这有1n a -种传法，它们不符合要求，因为这样第n 次无法再把球传给甲；另一类是第1n -次传球，球不在甲手中，第n 次持球人再将球传给甲，有n a 种传法．根据加法原理，有11133333n n n n a a ---+=⨯⨯⨯=(个…)．由于甲是发球者，一次传球后球又回到甲手中的传球方法是不存在的，所以10a =．利用递推关系可以得到：2303a =-=，33336a =⨯-=，4333621a =⨯⨯-=，533332160a =⨯⨯⨯-=．这说明经过5次传球后，球仍回到甲手中的传球方法有60种．本题也可以列表求解．由于第n 次传球后，球不在甲手中的传球方法，第1n +次传球后球就可能回到甲手中，所以只需求出第四次传球后，球不在甲手中的传法共有多少种．从表中可以看出经过五次传球后，球仍回到甲手中的传球方法共有60种．【答案】60【巩固】五个人互相传球，由甲开始发球，并作为第一次传球，经过4次传球后，球仍回到甲手中．问：共有多少种传球方式？【考点】计数之递推法【难度】5星【题型】解答【解析】递推法．设第n 次传球后球传到甲的手中的方法有n a 种．由于每次传球有4种选择，传n 次有4n 次可能．其中有的球在甲的手中，有的球不在甲的手中，球在甲的手中的有n a 种，球不在甲的手中的，下一次传球都可以将球传到甲的手中，故有1n a +种．所以14n n n a a ++=．由于10a =，所以12144a a =-=，232412a a =-=，343452a a =-=．即经过4次传球后，球仍回到甲手中的传球方法有52种．【答案】52【例 13】设A 、E 为正八边形ABCDEFGH 的相对顶点，顶点A 处有一只青蛙，除顶点E外青蛙可以从正八边形的任一顶点跳到其相邻两个顶点中任意一个，落到顶点E 时青蛙就停止跳动，则青蛙从顶点A 出发恰好跳10次后落到E 的方法总数为种．【考点】计数之递推法【难度】5星【题型】填空【关键词】清华附中【解析】可以使用递推法．回到A 跳到B 或H 跳到C 或G 跳到D 或F 停在E1步 12步 2 13步 3 14步 6 4 25步 10 46步 20 14 87步 34 148步 68 48 289步 116 48其中，第一列的每一个数都等于它的上一行的第二列的数的2倍，第二列的每一个数都等于它的上一行的第一列和第三列的两个数的和，第三列的每一个数都等于它的上一行的第二列和第四列的两个数的和，第四列的每一个数都等于它的上一行的第三列的数，第五列的每一个数都等于都等于它的上一行的第四列的数的2倍．这一规律很容易根据青蛙的跳动规则分析得来．所以，青蛙第10步跳到E 有48296⨯=种方法．【答案】96【巩固】在正五边形ABCDE 上，一只青蛙从A 点开始跳动，它每次可以随意跳到相邻两个顶点中的一个上，一旦跳到D 点上就停止跳动．青蛙在6次之内(含6次)跳到D 点有种不同跳法．【考点】计数之递推法【难度】5星【题型】填空【解析】采用递推的方法．列表如下：跳到A 跳到B 跳到C 停在D 跳到E1步 1 12步 2 1 13步 3 1 24步 5 3 25步 8 3 56步 13 8 5其中，根据规则，每次可以随意跳到相邻两个顶点中的一个上，一旦跳到D 点上就停止跳动．所以，每一步跳到A 的跳法数等于上一步跳到B 和E 的跳法数之和，每一步跳到B 的跳法数等于上一步跳到A 和C 的跳法数之和，每一步跳到C 的跳法数等于上一步跳到B 的跳法数，每一步跳到E 的跳法数等于上一步跳到A 的跳法数，AB C DE每一步跳到D 的跳法数等于上一步跳到C 或跳到E 的跳法数．观察可知，上面的递推结果与前面的枚举也相吻合，所以青蛙在6次之内(含6次)跳到D 点共有1123512++++=种不同的跳法．【答案】12【例 14】有6个木箱，编号为1，2，3，……，6，每个箱子有一把钥匙，6把钥匙各不相同，每个箱子放进一把钥匙锁好．先挖开1，2号箱子，可以取出钥匙去开箱子上的锁，如果最终能把6把锁都打开，则说这是一种放钥匙的“好”的方法，那么“好”的方法共有种．【考点】计数之递推法【难度】5星【题型】填空【关键词】迎春杯，中年级组，决赛【解析】 (法1)分类讨论．如果1，2号箱中恰好放的就是1，2号箱的钥匙，显然不是“好”的方法，所以“好”的方法有两种情况：⑴1，2号箱的钥匙恰有1把在1，2号箱中，另一箱装的是3～6箱的钥匙．⑴1，2号箱的钥匙都不在1，2号箱中．对于⑴，从1，2号箱的钥匙中选1把，从3～6号箱的钥匙中选1把，共有248⨯=(种)选法，每一种选法放入1，2号箱各有2种放法，共有8216⨯=(种)放法．不妨设1，3号箱的钥匙放入了1，2号箱，此时3号箱不能装2号箱的钥匙，有3种选法，依次类推，可知此时不同的放法有3216⨯⨯=(种)．所以，第⑴种情况有“好”的方法16696⨯=(种)．对于⑴，从3～6号箱的钥匙中选2把放入1，2号箱，有4312⨯=(种)放法．不妨设3，4号箱的钥匙放入了1，2号箱．此时1，2号箱的钥匙不可能都放在3，4号箱中，也就是说3，4号箱中至少有1把5，6号箱的钥匙．如果3，4号箱中有2把5，6号箱的钥匙，也就是说3，4号箱中放的恰好是5，6号箱的钥匙，那么1，2号箱的钥匙放在5，6号箱中，有224⨯=种放法；如果3，4号箱中有1把5，6号箱的钥匙，比如3，4号箱中放的是5，1号箱的钥匙，则只能是5号箱放6号箱的钥匙，6号箱放2号箱的钥匙，有212⨯=种放法；同理，3，4号箱放5，2号箱或6，1号箱或6，2号箱的钥匙，也各有2种放法．所以，第⑴种情况有“好”的放法()1242222144⨯++++=(种)．所以“好”的方法共有96144240+=(种)．(法2)递推法．设第1，2，3，…，6号箱子中所放的钥匙号码依次为1k ，2k ，3k ，…，6k ．当箱子数为n (2n ≥)时，好的放法的总数为n a ．当2n =时，显然22a =(11k =，22k =或12k =，21k =)．当3n =时，显然33k ≠，否则第3个箱子打不开，从而13k =或23k =，如果13k =，则把1号箱子和3号箱子看作一个整体，这样还是锁着1，2两号钥匙，撬开1，2两号箱子，那么方法有2a 种；当23k =也是如此．于是2n =时的每一种情况对应13k =或23k =时的一种情况，这样就有3224a a ==．当4n ≥时，也一定有n k n ≠，否则第n 个箱子打不开，从而1k 、2k 、……、1n k -中有一个为n ，不论其中哪一个是n ，由于必须要把该箱子打开才能打开n 号箱子，所以可以将锁着这把钥匙的箱子与第n 号箱子看作1个箱子，于是还是锁着1k 、2k 、……、1n k -这()1n -把钥匙，需要撬开1，2两号箱子，所以每种情况都有1n a -种．所以()11n n a n a -=-．所以，6542554543225!240a a a a ==⨯==⨯⨯⨯=⨯=，即好的方法总数为240种．【答案】240【巩固】有10个木箱，编号为1，2，3，……，10，每个箱子有一把钥匙，10把钥匙各不相同，每个箱子放进一把钥匙锁好．先挖开1，2号箱子，可以取出钥匙去开箱子上的锁，如果最终能把10把锁都打开，则说这是一种放钥匙的“好”的方法，那么“好”的方法共有种．【考点】计数之递推法【难度】5星【题型】填空【解析】递推法．设第1，2，3，…，6号箱子中所放的钥匙号码依次为1k ，2k ，3k ，…，6k ．当箱子数为n (2n ≥)时，好的放法的总数为n a ．当2n =时，显然22a =(11k =，22k =或12k =，21k =)．当3n =时，显然33k ≠，否则第3个箱子打不开，从而13k =或23k =，如果13k =，则把1号箱子和3号箱子看作一个整体，这样还是锁着1，2两号钥匙，撬开1，2两号箱子，那么方法有2a 种；当23k =也是如此．于是2n =时的每一种情况对应13k =或23k =时的一种情况，这样就有3224a a ==．当4n ≥时，也一定有n k n ≠，否则第n 个箱子打不开，从而1k 、2k 、……、1n k -中有一个为n ，不论其中哪一个是n ，由于必须要把该箱子打开才能打开n 号箱子，所以可以将锁着这把钥匙的箱子与第n 号箱子看作1个箱子，于是还是锁着1k 、2k 、……、1n k -这()1n -把钥匙，需要撬开1，2两号箱子，所以每种情况都有1n a -种．所以()11n n a n a -=-．所以，109829989876543229!=725760a a a a ==⨯==⨯⨯⨯⨯⨯⨯⨯=⨯，即好的方法总数为725760种．【答案】725760。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

计数问题之递推法例题讲解3
例题：2000个学生排成一行，依次从左到右编上1～2000号，然后从左到右按一、二报数，报一的离开队伍，剩下的人继续按一、二报数，报一的离开队伍，按这个规律如此下去，直至当队伍只剩下一人为止。

问：这时一共报了多少次？最后留下的这个人原来的号码是多少？
分析与解答：
难的不会想简单的，数大的不会想数小的。