加速寿命试验理论依据
加速寿命实验设计

加速寿命实验设计
实验设计关键因素
实验设计关键因素
实验目标定义
1.明确实验目的:确定实验目标,明确希望通过实验解决什么问题或验证什么假设。 2.量化实验指标:将实验目标量化,以便更准确地衡量实验结果。 3.考虑实验限制:考虑实验资源、时间和预算等方面的限制,确保实验设计具有可行性。
实验样本选择与处理
1.样本来源:确定样本来源,确保样本具有代表性和可靠性。 2.样本数量:根据实验需求和统计方法,确定所需的样本数量。 3.样本处理:确定样本处理方法,以消除干扰因素或确保实验条件的一致性。
实验设计关键因素
▪ 实验变量与控制
1.变量识别:识别实验中的所有变量,包括自变量、因变量和 潜在干扰变量。 2.变量控制:确定控制变量的方法,以减少干扰因素对实验结 果的影响。 3.变量测量:选择可靠的测量工具或方法,以确保变量测量的 准确性和客观性。
实验结果的可靠性评估
1.对实验过程进行回顾,确认是否存在可能影响实验结果可靠 性的因素。 2.对实验数据进行交叉验证,确保实验结果的稳定性和可重复 性。 3.对实验结果的不确定性进行评估,为后续决策提供可靠的依 据。
实验结果应用与探讨
▪ 实验结果的应用前景探讨
1.根据实验结果,探讨可能的应用场景和实际价值。 2.分析实验结果的应用前景,评估其推广潜力和市场前景。 3.针对实验结果的应用,提出改进和优化建议,提高其实用性和竞争力。
实验数据与结果分析
▪ 数据分析方法
1.掌握常用的数据分析方法,如回归分析、方差分析等。 2.根据实验目的选择合适的数据分析方法。 3.利用数据分析软件进行分析,得出结果。
▪ 实验结果展示
1.将实验结果以清晰、简明的方式展示出来。 2.对比不同实验条件下的结果,分析差异。 3.对实验结果进行解释和说明。
加速寿命试验

1.MTBF測試原理
1.1.9 反乘冪法則(Inverse Power Law)適用於金屬和非金 屬材料,軸承和電子裝備等. 1.1.10.復合模式(Combination Model)適用於同時考慮溫度 與電壓作為環境應力的電子材料,如電容. 1.1.11.一般情況下,主動電子零件完全適用阿氏模型,而電子 和資訊類成品也可適用阿氏模型,原因是成品類的失效 模式是由大部分主動式電子零件所構成.因此,阿氏模 型,廣泛應用於電子﹑資訊行業.
1.MTBF測試原理
1.2.2. 加速因子
加速因子即為產品在使用條件下的壽命和高測試應力條件下 的壽命的比值.
如果產品壽命適用於阿氏模型,則其加速因子為:
Vu為使用條件下的絕對溫度 Va為加速條件下的絕對溫度 B=EA/K
1.MTBF測試原理
1.2.3.加速因子中活化能Ea的計算 活化能是分子與化學或物理作用中需具備的能量,單位 是電子伏特Ev. 當試驗的溫度與使用溫度差距範圍不大時, 則Ea可設為常數. Ea= K* (Inλa – Inλn)/(1/Tn-1/Ta) λa為加速溫度時的失效率 λn為正常溫度時的失效率 Tn, Ta均為絕對溫度0K λa和λn可以以試驗的方式的得出,但需要較長的試驗時 間.而且新機種的失效率很難在短時間內得出.
MTB F 計算方法概論
加速寿命试验的理论模型与试验方法

产品可靠性试验6.2.1 可靠性试验的意义与分类可靠性试验是为分析、评价、提高或保证产品的可靠性水平而进行的试验。
产品的研制者通过试验获得产品设计、鉴定所需的可靠性数据(可靠性测定试验)。
通过试验暴露产品缺陷,改进设计并获得可靠性增长信息(可靠性增长试验)。
产品的制造者通过试验剔除零件批中的不合格品或暴露整机缺陷,消除早期故障(可靠性筛选或老化试验老化试验不是消除早期故障的)产品使用者通过试验验证产品批可靠性水平以保证接收的产品批达到规定要求(可靠性接收试验)。
政府或行业管理部门通过试验获得数据库所需基础可靠性数据(可靠性测定试验),认证产品可靠性等级(可靠性验证试验),进行产品的可靠性鉴定与考核(可靠性鉴定试验)。
本节主要介绍可靠性测定试验,这是为获得产品可靠性特征量的估计值而进行的试验,根据需要可由试验结果给出可靠性特征量的点估计值和给定置信度下的区间估计。
由于可靠性试验往往是旷日持久的试验,为节省时间与费用常采用加速试验的方式。
本节将介绍某些加速寿命试验的理论模型与试验方法。
6.2.2 指数分布可靠性测定试验大多数电子元器件、复杂机器及系统的寿命都服从指数分布。
其待估参数为故障率λ,其他可靠性指标可利用估计值进行计算MTBF 已经有平均的意思了1.定时截尾试验(1)点估计试验进行至事先规定的截尾时间t c停止试验,设参与试验的n个样本中有r个发生关联故障,则由极大似然估计理论得出的故障率点估计值为式中t i——第I个关联故障发生前工作时间(i=1,…,r)。
若在试验过程中及时将已故障产品修复或替换为新产品继续试验,则为有替换的定时截尾试验。
此时λ的点估计为(2)区间估计对于无替换和有替换的定时截尾试验,其给定置信度为1-α的双侧置信区间为[λL,λU],则式中——自由度为υ的分布的概率为的下侧分位点;T——总试验时间(3)零故障数据的区间估计当定时截尾试验在(0,t c)内的故障数r=0时,可由式(4)给出。
加速寿命试验的理论基础_

加速寿命试验的理论基础(Ⅰ)Ξ杨宇航1,周源泉2(1.北京航空航天大学经济管理学院,北京100083;21北京强度与环境研究所,北京100076) 摘 要:提出了有效的加速寿命试验对加速系数的要求,讨论了加速系数的性质与用途,并给出了常见的失效分布族。
关键词:加速寿命试验;加速系数;分布参数;失效模式;失效机理中图分类号:V430 文献标识码:A 文章编号:100124055(2001)0420276204Theoretical foundation of accelerated life testing(Ⅰ)Y ANG Y u2hang1,ZH OU Y uan2quan2(11School of Economic Management,Beijing Univ.of Aeronautics and Astronautics,Beijing100083,China;21Beijing Inst.of S tructure and Environment,Beijing100076,China)Abstract: F or accelerated factor(AF),the demand of the effective accelerated life testing(A LT)were presented.The properties and uses of accelerated factor were discussed.And the comm on failure distribulions were given.K ey w ords: Acceleration life test;Acceleration factor;Distributed parameter;Failure mechanism;Failure m ode1 引 言加速寿命试验(Accelerated Life T esting,简称A LT)迄今已发展成为可靠性工程的一门较成熟的独立分支,已有数以百计的论文发表和一些专著[1]出版及标准的推行。
加速寿命试验理论依据

加速寿命试验理论依据加速试验电子元器件的失效原因与器件本身所选用的材料、材料之间、器件表面或体内、金属化系统以及封装结构中存在的各种化学、物理的反应有关。
器件从出厂经过贮存、运输、使用到失效的寿命周期,无时无刻不在进行着缓慢的化学物理变化。
在各种外界环境下,器件还会承受了各种热、电、机械应力,会使原来的化学物理反应加速,而其中温度应力对失效最为敏感。
实践证明,当温度升高以后,器件劣化的物理化学反应加快,失效过程加速,而Arrhenius模型就总结了由温度应力决定的化学反应速度依赖关系的规律性,为加速寿命试验提供了理论依据。
1. 以温度应力为加速变量的加速方程由Arrhenius总结的经验公式如下(8.5)式中,dM/dt是化学反应速率,A是常数,E a是引起失效或退化过程的激活能,k是玻尔兹曼常数,T是绝对温度。
当器件在t0时刻处于正常状态数为M0,到t1时刻,器件处于失效状态数为M1。
如果温度与时间无关,则积分式(8.1)得(8.6)令DM=M1-M0,t=t1-t0,得到(8.7)取对数(8.8)可写成(8.9)其中(8.10)上式就是根据Arrhenius模型得到的以温度应力为加速度变量的加速方程。
用此方程来解释器件的高温贮存寿命试验是非常成功的。
式中,t表示器件产品达到某一F(t)的时间,它的对数与绝对温度的倒数成线性关系。
若用t~1/T单边对数坐标纸绘图,则可得到一条直线,然后用图估计法或数值法推算出器件在不同温度下的寿命值。
由式(8.1)可计算得到方程的斜率b、截距α和激活能Ea ,当T1>T2时(8.11)激活能E a与方程的斜率b与器件的失效模式与失效机理有关。
根据多年来的实践积累,有关半导体器件与微电路不同失效模式与机理的激活能数据列于表8.8。
http://Kê。
图8.3 不同激活能时温度与寿命的关系以激活能E a作为参数,可以绘出不同E a时温度与寿命的关系,如图8.3所示。
电子元器件加速寿命试验试验报告

试验报告1、引言加速寿命试验(Accelerated life test,ALT)是一种对受试品施加不同应力,从而快速暴露产品的缺陷,进而确定产品工作极限和破坏极限,以及发现并消除缺陷及潜在缺陷的试验程序,它利用阶梯应力方式施加在受试品上,施加在受试品上的应力有振动、高低温、湿度、电应力开关循环、极限电压及极限频率等。
ALT试验的主要目的是增加产品的设计极限值,迅速找出产品设计及制造的缺陷,通过根因分析并消除缺陷,从而增加产品可靠度并缩短研发时间和减少研发费用目前,加速寿命试验已在电子元器件研发制造中广泛应用。
所以加速寿命试验是在进行合理工程及统计假设的基础上,利用与物理失效规律相关的统计模型对在超出正常应力水平的加速环境下获得的信息进行转换,得到产品在额定应力水平下的特征可复现的数值估计的一种试验方法。
目前应用最广的加速寿命试验是恒加试验。
恒定应力加速度寿命试验方法已被IEC标准采用。
其中加速试验程序包括对样品周期测试的要求、热加速电耐久性测试的试验程序等,可操作性较强。
恒加方法造成的失效因素较为单一,准确度较高。
国外已经对不同材料的异质结双极晶体管(HBT)、CRT阴极射线管、赝式高电子迁移率晶体管开关(PHEMT switch)、多层陶瓷芯片电容等电子元器件做了相关研究。
恒加试验一般需要约1000 h,总共要取上百个样品,要求应力水平数不少于3个。
每个应力下的样品数不少于10个,特殊产品不少于5只。
每一应力下的样品数可相等或不等,高应力可以多安排一些样品。
步加试验只需1组样品,最好至少安排4个等级的应力,每级应力的失效数不少于3个,这样才能保证数据分析的合理性。
另外一种方法是步进应力加速寿命试验。
步加试验时,先对样品施加一接近正常值的应力,到达规定时间或失效数后,再将应力提高一级,重复刚才的试验,一般至少做三个应力级。
恒加试验已经成熟地应用于包括航空、机械、电子等多个领域。
步加试验往往作为恒定应力加速寿命试验的预备试验,用于确定器件承受应力的极大值。
电池寿命试验

结语
综上所述:
1、通过高温加速试验方法可以推算出锂电池的激活能Ea约为0.6eV,由 以上数据分析结果可知,该电池的加速因子AF在60 ℃时相当于20 ℃温 度下的17.3倍。;
2、根据加速寿命试验验证的结果,可以说明评估锂亚电池在60 ℃存放 200天的贮存性能,即等效为评估锂亚电池常温存放约10年贮存性能。
电池寿命试验
1、概述 2、加速寿命试验的理论依据 3、加速寿命试验的情况说明 4、结论
ቤተ መጻሕፍቲ ባይዱ 关于进行锂电池加速寿命试验的概述
对于智能表计,无论是电表、水表、气表,还是热表,均需要使用 电池作为实时时钟电源,记忆体后备电源或动力电源。而锂/亚硫酰 氯电池(以下简称锂亚电池)已经成为各种智能表计的首选电池品种。 因此,对锂/亚硫酰氯电池进行可靠性研究分析具体有重要意义,其 中最关键的是评估锂/亚硫酰氯电池贮存寿命,而对其进行长期寿命 试验是通常被采用的可靠性评估手段之一。 然而,长期寿命试验需要较长的时间,视不同情况可能达到 10年以上,浪费人力物力。为了缩短时间、节约样品与费用、快 速地评价产品的可靠性,就需要做加速寿命试验。 本文主要就是通过设计试验,监测研究ER14250电池在不同环 境温度下的剩余容量变化,计算该电池的激活能(Ea),从而可 以得出该类电池的加速试验寿命模型以及不同温度下的加速因子。
根据电池的应用特性,在试验中取剩余容量值的变化监测电池 是否失效,认为当电池在定时监测时330Ω 负载恒阻放电容量值小 于额定容量的20%就认为电池失效,以此统计出电池失效数据,然 后用线性外延法计算出电池在不同温度下的储存寿命,即MTTF值 (对于此电池为不可修复产品,不可采用MTBF),数据和计算过 程见表1,其中电池容量为平均值。
I/T
寿命试验的目的及加速试验理论基础

寿命试验的目的及加速试验理论基础寿命试验的目的了解和掌握产品的故障信息,解决产品寿命周期内质量问题。
13提供产品的寿命指标(包括质保期、首翻期、翻修间隔、总寿命)了解产品的寿命特征、失效规律。
2加速试验概述加速试验概述加速试验概述元器件的寿命与应力之间的关系,是以一定的物理模型为依据的。
常见的物理模型:◆失效率模型◆应力与强度模型◆最弱链条模型◆反应速度模型加速试验概述失效率模型失效率模型是将失效率曲线划分为早期失效、随机失效和磨损失效三个阶段,并将每个阶段的产品失效机理与其失效率相联系起来。
典型的失效率曲线)(t加速试验概述应力与强度模型研究实际环境应力与产品所能承受的强度的关系。
应力与强度均为随机变量,因此,产品的失效与否将决定于应力分布和强度分布。
随着时间的推移,产品的强度分布将逐渐发生变化,如果应力分布与强度分布一旦发生了干预,产品就会出现失效。
因此,研究应力与强度模型对了解产品的环境适应能力是很重要的。
最弱链条模型最弱链条模型是基于元器件的失效是发生在构成元器件的诸因素中最薄弱的部位这一事实而提出来的。
这种模型,对于研究电子产品在高温下发生的失效现象最为有效,因为这类失效正是由于元器件内部潜在的微观缺陷和污染,在经过制造和使用后而逐渐显露出来的。
暴露最显著、最迅速的地方,就是最薄弱的地方,也是最先失效的地方。
反应速度模型反应速度模型反映了反应速度与温度的关系。
元器件的失效是由于微观的分子与原子结构发生了物理或化学的变化而引起的,从而导致在产品特性参数上的退化,当这种退化超过了某一界限,就发生失效。
阿列尼乌斯模型和爱林模型。
加速寿命试验的加速模型 标准

加速寿命试验的加速模型标准【加速寿命试验的加速模型标准】1. 引言在工程领域,对产品的寿命进行评估和预测是非常重要的,尤其是在一些对产品寿命要求较高的行业,比如航空航天、汽车、医疗器械等。
加速寿命试验是一种常见的手段,通过在相对较短的时间内模拟产品使用过程的加速速度,以求得产品的可靠性和寿命指标。
而加速寿命试验的加速模型标准则是对试验过程中使用的加速模型进行规范和标准化,以确保试验结果的可靠性和可比性。
2. 加速寿命试验的基本原理在进行加速寿命试验时,需要首先确定试验过程中所使用的加速模型。
加速模型是指在实验室条件下对产品进行加速老化或破坏的方法和技术,以求得产品在实际使用环境下的寿命。
常见的加速模型包括温度应力模型、湿度应力模型、压力应力模型等。
这些加速模型都是基于一定的物理和化学原理建立起来,通过模拟产品在实际使用过程中所受到的环境应力,来加速产品老化和失效的过程。
3. 加速寿命试验的加速模型标准针对不同的产品和行业,加速寿命试验的加速模型标准有所不同。
一般来说,国际上对加速寿命试验的加速模型标准进行了规范和统一,比如ISO 9227对盐雾试验的加速模型进行了规范,ISO 6270对循环试验的加速模型进行了规范等。
这些标准主要包括了试验条件、试验方法、试验过程中的监测和记录要求等内容,以确保试验过程中的可靠性和可比性。
4. 个人观点在加速寿命试验中,选择合适的加速模型标准是非常重要的。
一个合适的加速模型标准可以有效地加速产品老化和失效的过程,节约时间和成本。
然而,在选择加速模型标准时,需要充分考虑产品的实际使用环境和应力条件,以及试验过程中的可靠性和可比性要求。
针对一些特殊的产品和行业,也需要根据实际情况进行定制化的加速模型标准,以满足产品寿命评估和预测的需要。
5. 总结加速寿命试验的加速模型标准是对试验过程中所使用的加速模型进行规范和标准化的重要手段。
选择合适的加速模型标准可以有效地加速产品老化和失效的过程,节约时间和成本。
寿命测试的原理和方法

寿命测试的原理和方法寿命测试是一种用于评估产品、设备或材料的寿命、稳定性和可靠性的方法。
它旨在模拟真实使用环境中的周期性应力加载和时间依赖行为,并通过测量和分析设备或材料在测试条件下的性能变化来预测其在实际使用中的寿命。
以下是寿命测试的原理和方法的详细解释。
一、寿命测试的原理:1.加速寿命测试原理:加速寿命测试是通过增加设备或材料所受到的应力水平来缩短测试时间,以模拟产品在正常使用过程中所经历的应力水平。
该原理基于物质在应力作用下会发生劣化、老化或失效,应力越大,劣化速度越快,因此可以通过提高应力水平来推断设备或材料的寿命。
2.时间渗透原理:时间渗透是指随着时间的推移,物质内部会发生微小的体积或化学变化。
通过在寿命测试中测量和记录这些微小变化,可以预测设备或材料的寿命。
这些变化可以是材料的化学成分变化、厚度的变化、重量的减少、弯曲或拉伸的蠕变等。
3.可靠性原理:可靠性是指设备或材料在一定时间内能够正常工作或性能稳定的能力。
寿命测试旨在评估设备或材料的可靠性,通过模拟真实使用环境中的应力和条件,利用统计学方法分析和计算设备或材料的故障概率,从而预测其在实际使用中的可靠性。
二、寿命测试的方法:1.加速应力测试:加速应力测试是通过将设备或材料暴露在高温、低温、湿度、氧化、辐射等极端条件下,以增加其受到的应力水平。
根据设备或材料的特性,可以选择合适的应力类型和水平,并持续一定的时间进行测试。
这种方法可以快速获得设备或材料在极端条件下的性能表现,更准确地预测其在实际使用中的寿命。
2.循环应力测试:循环应力测试是通过重复加载和卸载设备或材料来模拟其在实际使用中所受到的周期性应力。
这种方法可以检测设备或材料在重复应力的作用下的性能变化,并通过持续的监测和测量来评估其寿命和稳定性。
循环应力测试通常通过机械装置、液压装置、热胀冷缩等方式来实现。
3.退化测试:退化测试是针对一些易失效设备或材料进行的测试,目的是在短时间内模拟其长期使用过程中所受到的退化或劣化。
2.5 加速寿命试验

2.5 加速寿命试验
e.g., 人造卫星上所使用的电子元器件要求 失效率λ=2.6×10-8/小时(7级) 实验方案一: 抽取1000只 允许5元件失效 试验时间 22年 5700年
天津大学电子信息工程学院
λ=2.6×10-8/小时 λ=10-10/小时
微电子可靠性原理
微电子可靠性原理
天津大学电子信息工程学院
2.5 加速寿命试验
金属膜电阻器耐高温、高湿试验: 240 h,加满负荷250 V,RH85%~98%,温度 从-10℃到+80℃循环三次,ΔR/R≤0.4%;
成品电阻器的生产及结构
微电子可靠性原理
天津大学电子信息工程学院
2.5 加速寿命试验
微电子可靠性原理
微电子可靠性原理
天津大学电子信息工程学院
2.5 加速寿命试验
恒定应力加速寿命试验 加速应力水平的个数k≥4; S1和Sk确定后,S2,…,Sk-1应当分散,使 相邻应力水平间隔比较合理;
一般原则: 使k个加速应力水平S1,S2,…,Sk成等间隔;
微电子可靠性原理 天津大学电子信息工程学院
2.5 加速寿命试验
t0 ( F0 ) V1 c ( ) t1 ( F0 ) V0
艾林(Eyring)模型
微电子可靠性原理 天津大学电子信息工程学院
2.5 加速寿命试验
5次方10度法则 某些电子元器件的寿命与电压的5次方成反比; 对于温度,每上升10℃,其寿命将缩减一半。 这种寿命与应力的关系称“5次方10度法则” 加速系数
微电子可靠性原理 天津大学电子信息工程学院
2.5 加速寿命试验
化学反应速率与温度之间的关系表达式
加速寿命试验方法及其在航空机轮中的应用
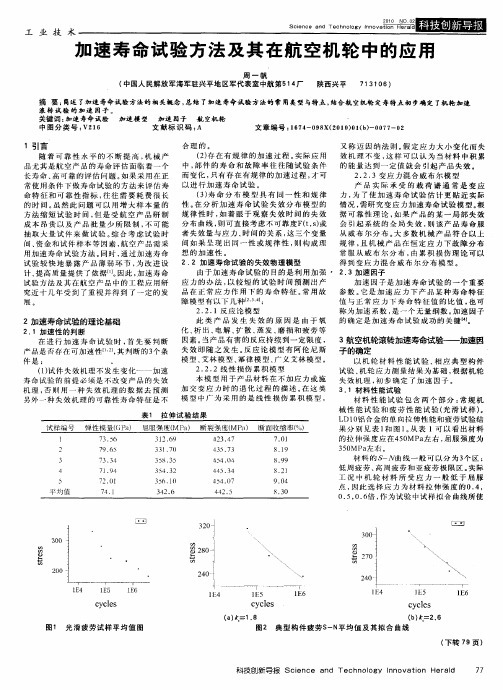
又 称 迈 因 纳 法 则 。 定 应 力 大 小 变 化 而 失 假 ( ) 在 有 规 律 的 加 速 过 程 。 际 应 用 效 机 理 不 变 , 样 可 以 认 为 当材 料 中 积 累 2存 实 这 中 , 件 的 寿 命 和 故 障 率 往 往 随 试 验 条 件 的 能 量 达 到 一 定 值 就 会 引 起 产 品 失 效 。 部 而变 化 , 有 存 在 有规 律 的加 速 过 程 , 可 只 才 2 2 3变 应 力 混 合 威 布 尔 模 型 .. 以 进 行 加 速 寿 命试 验 。 产 品 实 际 承 受 的 载 荷 谱 通 常 是 变 应 ( ) 命 分 布 模 型 具 有 同 一 性 和 规 律 力 , 了 使 加 速 寿 命 试 验 估 计 更 贴 近 实 际 3寿 为 性 。 分 析 加 速 寿 命 试 验 失 效 分 布 模 型 的 情 况 , 研 究 变应 力加 速 寿 命 试 验 模 型 。 在 需 根 规 律 性 时 , 着 眼 于 观 察 失 效 时 间 的 失 效 据 可 靠 性 理 论 , 果 产 品 的 某 一 局 部 失效 如 如 分 布 曲线 , 则可 直 接 考 虑不 可 靠 度 F t s或 会 引 起 系 统 的 全 局 失 效 , 该 产 品寿 命服 (,) 则 者 失 效 量 与 应 力 、 间 的关 系 , 三 个 变 量 从 威 布 尔 分 布 。 多 数 机 械 产 品 符 合 以上 时 这 大 间如 果 呈 现 出 同 一 性 或 规 律 性 , 构 成 理 规 律 , 机 械 产 品在 恒 定 应 力 下 故 障 分 布 则 且 想 的加 速 性 。 常服从 威布尔分 布 , 由累 积 损 伤 理 论 可 以 2. 加速 寿命 试 验 的失 效物 理 模型 2 得 到 变 应 力混 合 威 布 尔 分 布 模 型 。 由 于加 速 寿 命 试 验 的 目的 是 利 用加 强 ・ 2。 3加 速 因子 应 力 的 办 法 , 较 短 的 试 验 时 间 预 测 出产 以 加 速 因 子 是 加 速 寿 命 试 验 的 一 个 重 要 品 在 正 常 应 力 作 用 下 的 寿 命 特 征 。 用 故 参 数 。 常 它是 加 速 应 力 下 产 品某 种 寿 命 特 征 障 模 型 有 以下 几 种 _ 1 2 : 值 与 正 常 应 力 下 寿 命 特 征 值 的 比 值 , 可 也 2. 1反 应 论 模 型 2. 称 为加 速 系数 , 一 个 无 量 纲 数 。 速 因子 是 加 此 类 产 品 发 生 失 效 的 原 因 是 由 于 氧 的 确 定 是 加 速 寿 命 试 验 成 功 的关 键 『。 4 】 化、 出、 析 电解 、 散 、 发 、 损 和 疲 劳 等 扩 蒸 磨 因 素 。 产 品有 害 的 反 应 持 续 到 一定 限 度 , 3 空机轮滚转 加速 寿命试验一 加速 因 当 航 失 效 即随 之 发 生 。 应 论 模 型 有 阿 伦 尼 斯 子的确定 反 模型、 林模型、 艾 幂律 模 型 、 义 艾林 模 型 。 广 以 机 轮 材 料 性 能 试 验 、 应 典 型 构 件 相 2. 2线 性 损 伤 累积 模 型 2. 试 验 、 轮 应 力 测 量 结 果 为 基础 , 据 机 轮 机 根 本 模 型 用于 产 品 材料 在 不 加 应 力 或 施 失效 机理 , 步 确 定 了 加 速 因 子 。 初 加 交 变 应 力 时 的 退 化 过 程 的 描 述 在 这 类 3. 1材料 性能试 验 模 型 中广 为 采 用 的 是 线 性 损 伤 累 积 模 型 , 材料性 能试 验包含 两个部 分 : 常规 机
加速寿命试验的理论基础(ⅰ)

加速寿命试验的理论基础(ⅰ)摘要:本文旨在探讨加速寿命试验的理论基础(ⅰ)。
使用数学模型来分析可能对加速寿命试验有影响的各种参数;介绍了它们之间的关系,并研究了在不同情况下的加速寿命试验的衍生参数。
通过对各种因素的研究,本文为进行加速寿命试验时挑选正确参数提供了理论支持。
关键词:加速寿命试验,参数研究,数学模型,理论基础正文:加速寿命试验是一种为确定产品性能下限所采用的方法,它基于物理、热力学和化学定律,可有效预测产品在一定环境下的变化趋势。
本文首先介绍了加速寿命试验的理论基础(ⅰ),即通过各种环境参数(如温度、湿度、曝光等),来实现加速老化和模拟真实环境的寿命研究。
然后,利用数学模型探究不同参数之间的关系,了解加速寿命试验的衍生参数,为今后选择合适的参数提供参考。
最后,总结研究成果,指出加速寿命试验的理论基础(ⅰ)提供了一种快速、准确、经济的研究工具来超越实际使用时间限制,以实现对产品和服务质量的更高要求。
加速寿命试验可以广泛应用于各种场景,如医药、食品安全、材料科学领域等。
例如,在医药领域,加速寿命试验可以模拟常见的疾病状态,例如衰老过程、抗炎过程以及对药物作用的反应。
在食品安全研究中,可以用它研究不同保鲜剂的有效性,以及能否维持产品的质量和安全性。
在材料科学中,加速寿命试验能够测定塑料、橡胶等的耐久性,以及对不同温度和环境影响的程度。
此外,它还可以用于研究可再生能源的可靠性,并可以应用于电子产品等多种其他产品在使用过程中可能出现的问题。
总之,加速寿命试验是一个非常有用的工具,它可以在大大缩短时间的情况下,对产品在不同条件下的性能和持久性进行测试,为开发者提供正确、可靠的参考。
随着加速寿命试验理论的不断发展,它将提高了我们产品的质量和可靠性,为人类带来更多的便利和安全。
加速寿命试验也有着广泛的实用性,如环境污染、电气安全和机械可靠性等。
例如,为了保护环境,研究人员可以使用加速寿命试验来研究不同材料的持久性,例如氧化物、碳纤维和混合材料等,从而制定出可行的废弃和处理计划。
失效物理模型与加速寿命试验

XI’AN JIAOTONG UNIVERSITY
加速寿命试验统计分布
3.恒应力加速寿命的估计 恒应力加速寿命的估计
1 基本假设 威布尔分布
A、所用应力Si下都服从威布尔分布 、所用应力 B、m相同 、 相同 C、lnη=a+bФ(S) 、 η=a+bФ
mi t Fi (ti ) = 1 − exp − i ηi
Ф(T)=1/T Ф(V)=lnV
τ=
E 1 1 t0 ( F0 ) = exp ( − ) t1 ( F0 ) k T0 T1
XI’AN JIAOTONG UNIVERSITY
加速寿命试验统计分布
(2) 以电应力为变量的加速方程
1 t= KV c
K和c的计算 和 的计算
lgt=-clgV-lgK
加速系数
t0 ( F0 ) V1 = τ= t1 ( F0 ) V0
− ∂M = R (t ) = Ae kT ∂t E
M-元器件某特性量或退化量 A-系数 E-某种反应的激活能 k-玻尔兹曼(Boltzman)常数,0.8617×10-4eV/K T-绝对温度
XI’AN JIAOTONG UNIVERSITY
反应速度论- Eyring模型
在Arrhenius中只考虑了温度应力 考虑温度在内的多种应力和寿命的关系,其反应速率: R(T,S)=R0f1f2 S-非温度应力 R0=a(k/h)Texp(-E/(kT))-只有温度应力时的艾林反应速率 h-普朗克常量 f1=exp(CS)-考虑非温度应力存在时对能量分布的修正因子 f2=exp(DS)-考虑非温度应力存在时对激活能的修正因子 a,C,D-待定常数 电应力对寿命的影响
寿命的可靠性综论(四)——使用寿命的加速寿命试验

使 用寿命 的加速寿命试验
何 国伟 1 角 淑 媛 2
( .原航天 工业 总公 司 质量 司 ,北 京 10 3 ;2 中国航天 标准化 与产 品保证 研究 院 ,北 京 10 7 ) 1 0 80 . 0 0 1
摘 要 产 品寿命 ( 包括使 用寿命 )取决 于环境 、材料 、结构 、装 配、加 工等 多种应 力 因素 。 但在 产品研 发阶段 .开展使 用条件下 的几年 甚至几十年的寿命试 验来得 出产品寿命 可靠性的规律是 不现 实的。 因此 ,只能用一、 两种主要 因素的加速 寿命试验 结果 来外推或 用相 似产品 法综合估算 寿 命 可靠性规律 ,以此作为维修性设计及确定寿命周期成本 ( C )的依据 。实际工作 中,必须开展使 LC
推估 计 的误 差 在 3 % 以 内 .已经 算 是 相 当好 了 。 0
又如 对裂 纹 扩展 寿命 的数 学模 型 P r 公式 .美 国 ai s
机械 学 会推 荐 安 全 系数 为 2 .即 如果 该 模 型 外 推 O
应 力循 环 2 16 .则 认 为 该 产 品 的使 用 寿命 为 X0 次 ls 。在 产 品研 发 阶段 必须 对 一 、两 种 关键 应 力 0次
的应 力 ( 括 温度 、 温 度 冲击 、 电 压 、振 动 ,等 包 等 )持 续 到一定 程度 .元器 件就 会从 正常 状态转 化
为 蜕化 状态 但 从正 常 状态进 到 蜕化状 态 要越过 能 垒 。越 过 能 垒需 要 的能量 叫激活 能 ( E ,其 概 率 △ )
品寿命 的 主要是温 度及 电压两 种应力 很 多理论 及 试 验都 重点 考虑这 两种 应力 。实 际上 ,温度循 环对 寿 命影 响相 当大 。有 试验 总结 .与 e ’ 1(- ) ‘ [ e- 。 n n I v
加速寿命试验的理论模型与试验方法

6.2 产品可靠性试验6.2.1 可靠性试验的意义与分类可靠性试验是为分析、评价、提高或保证产品的可靠性水平而进行的试验。
产品的研制者通过试验获得产品设计、鉴定所需的可靠性数据(可靠性测定试验)。
通过试验暴露产品缺陷,改进设计并获得可靠性增长信息(可靠性增长试验)。
产品的制造者通过试验剔除零件批中的不合格品或暴露整机缺陷,消除早期故障(可靠性筛选或老化试验老化试验不是消除早期故障的)产品使用者通过试验验证产品批可靠性水平以保证接收的产品批达到规定要求(可靠性接收试验)。
政府或行业管理部门通过试验获得数据库所需基础可靠性数据(可靠性测定试验),认证产品可靠性等级(可靠性验证试验),进行产品的可靠性鉴定与考核(可靠性鉴定试验)。
本节主要介绍可靠性测定试验,这是为获得产品可靠性特征量的估计值而进行的试验,根据需要可由试验结果给出可靠性特征量的点估计值和给定置信度下的区间估计。
由于可靠性试验往往是旷日持久的试验,为节省时间与费用常采用加速试验的方式。
本节将介绍某些加速寿命试验的理论模型与试验方法。
6.2.2 指数分布可靠性测定试验大多数电子元器件、复杂机器及系统的寿命都服从指数分布。
其待估参数为故障率λ,其他可靠性指标可利用估计值进行计算MTBF 已经有平均的意思了1.定时截尾试验(1)点估计试验进行至事先规定的截尾时间t c停止试验,设参与试验的n个样本中有r个发生关联故障,则由极大似然估计理论得出的故障率点估计值为式中t i——第I个关联故障发生前工作时间(i=1,…,r)。
若在试验过程中及时将已故障产品修复或替换为新产品继续试验,则为有替换的定时截尾试验。
此时λ的点估计为(2)区间估计对于无替换和有替换的定时截尾试验,其给定置信度为1-α的双侧置信区间为[λL,λU],则式中——自由度为υ的分布的概率为的下侧分位点;T——总试验时间(3)零故障数据的区间估计当定时截尾试验在(0,t c)内的故障数r=0时,可由式(4)给出。
加速寿命试验的原理

效果 ������ 通过缩短试验周期和开发周期 ,最终可以降低开发费用; ������ 尽快可以收集到为了评价设计的产品的性能信息和潜在的故障模 式, 设计上的弱点, 重要器件的确认等有关可靠性的信息; ������ 尽快地推定使用条件下的可靠性尺度 (故障率, 寿命等 ),可以保 证可靠性。
快速的技术发展,增 加了未知的因数
其他 性能
性能 电性能
维卡软化点 热变形温度 热膨胀性
导电性
介电常数
表面电阻/体积电阻(率)
镀层/涂层
附着力
厚度
性能
稳定性
颜色
硬度
可靠性检测
半成品/成品的可靠性测试
安
装
工 作
环 境
存 储 环 境
环
境
使
半成品/成品
用
环
境
滥 用 情 况
耐久性 测试
温度寿 命试验
调压器 测试
振动测试
冷热 冲击
气体 腐蚀
加速寿命试验概要
1.4 应力施加的方法
应力
恒定应力加速试验(constant-stress accelerated test) • 应力施加方法中的最代表性的方法 • 将一定水准的应力维持到试验结束时间为止的方法
应力
步进应力加速试验(step-stress accelerated test) • 将应力水准变为阶梯形的(主要是增加)实验方法
开发危险的减少 以及可靠性的保证
快速的市场进入 或交期的缩短
预防市场故障 (A/S, 索赔等 )
加速 试验
加速寿命试验概要
1.3 加速方法 时间加速 增加连续或间歇动作的次数来进行加速的方法 (进行30000次的行程大于50%全行程和频率大于5次/min的启闭动作) 利用退化特性的加速 • 对于使用时间, 具有退化特性的项目 • 严密的意义上讲不能说是加速, 但是缩短时间的这点上, 可以认为是加速的一种形式应 力(温度, 湿度, 振动, 电压, 压力等 )加速 • 把应力设计加严后做试验并促进故障的 • 所谓的加速试验一般表示为对应力的加速 • Strength < Stress : 故障
寿命测试的原理和方法

寿命测试的原理和方法以寿命测试的原理和方法为标题,我们来探讨一下寿命测试的基本原理以及常用的方法。
一、寿命测试的原理寿命测试是指通过一系列的实验和观测,评估或预测一个产品、系统或设备的寿命期限。
其原理基于以下几个方面:1. 加速模型:寿命测试中常用的一个原理是加速模型,即通过模拟产品在实际使用中的环境、载荷和应力条件,加速产品的老化过程,以便在短时间内得到相对准确的寿命预测。
加速模型的建立需要对产品的应力-寿命关系进行分析和建模,以确定加速因子和寿命加速方程。
2. 应力源:寿命测试需要对产品施加一定的应力,以模拟实际使用环境中的应力情况。
常见的应力源包括温度、湿度、电压、电流、振动、冲击等。
通过控制和调整这些应力因素,可以对产品进行不同类型的寿命测试。
3. 故障分析:寿命测试的原理还包括对产品在寿命期间可能出现的故障进行分析。
通过观察和记录产品在测试过程中的故障情况,可以对产品的寿命进行评估和预测。
故障分析可以帮助确定产品的弱点和故障模式,进而改善产品的设计和制造过程。
二、寿命测试的方法1. 加速寿命测试:这是最常用的寿命测试方法之一。
加速寿命测试通过对产品施加加速应力,使其在较短时间内达到与实际使用条件下相当的老化程度。
加速寿命测试可以通过控制温度、湿度、电压等因素来实现。
例如,在电子产品的寿命测试中,可以通过提高温度和电压来加速产品老化。
2. 基于可靠性统计的寿命测试:这种方法是通过一定数量的产品进行寿命测试,并根据统计分析和可靠性理论来评估和预测产品的寿命。
该方法适用于大规模生产的产品,可以通过抽样测试来代表整个产品批次的寿命情况。
3. 试验台架寿命测试:这种方法适用于某些特定类型的产品,例如发动机、机械设备等。
通过搭建试验台架,模拟产品在实际使用中的工作环境和载荷,对产品进行长时间的运行和测试,以评估其寿命。
4. 加速退化测试:这种方法是通过对产品进行加速退化测试,观察和记录产品在不同寿命阶段的性能变化情况,以评估其寿命。
加速寿命试验的理论模型与试验方法

产品可靠性试验6.2.1 可靠性试验的意义与分类可靠性试验是为分析、评价、提高或保证产品的可靠性水平而进行的试验。
产品的研制者通过试验获得产品设计、鉴定所需的可靠性数据(可靠性测定试验)。
通过试验暴露产品缺陷,改进设计并获得可靠性增长信息(可靠性增长试验)。
产品的制造者通过试验剔除零件批中的不合格品或暴露整机缺陷,消除早期故障(可靠性筛选或老化试验老化试验不是消除早期故障的)产品使用者通过试验验证产品批可靠性水平以保证接收的产品批达到规定要求(可靠性接收试验)。
政府或行业管理部门通过试验获得数据库所需基础可靠性数据(可靠性测定试验),认证产品可靠性等级(可靠性验证试验),进行产品的可靠性鉴定与考核(可靠性鉴定试验)。
本节主要介绍可靠性测定试验,这是为获得产品可靠性特征量的估计值而进行的试验,根据需要可由试验结果给出可靠性特征量的点估计值和给定置信度下的区间估计。
由于可靠性试验往往是旷日持久的试验,为节省时间与费用常采用加速试验的方式。
本节将介绍某些加速寿命试验的理论模型与试验方法。
6.2.2 指数分布可靠性测定试验大多数电子元器件、复杂机器及系统的寿命都服从指数分布。
其待估参数为故障率λ,其他可靠性指标可利用估计值进行计算MTBF已经有平均的意思了1.定时截尾试验(1)点估计试验进行至事先规定的截尾时间t c停止试验,设参与试验的n个样本中有r个发生关联故障,则由极大似然估计理论得出的故障率点估计值为式中t i——第I个关联故障发生前工作时间(i=1,…,r)。
若在试验过程中及时将已故障产品修复或替换为新产品继续试验,则为有替换的定时截尾试验。
此时λ的点估计为12(2)区间估计 对于无替换和有替换的定时截尾试验,其给定置信度为1-α的双侧置信区间为[λL ,λU ],则式中——自由度为υ的分布的概率为的下侧分位点;T ——总试验时间(3)零故障数据的区间估计 当定时截尾试验在(0,t c )内的故障数r=0时,可由式(4)给出。
加速寿命试验及其在电子产品上的应用

1 引言
加速寿命试验是电子元器件可靠性试验中的一项重 要的试验手段,对于可靠性水平较高的产品按照恒定失效 率假设下的失效率与平均无故障时间的验证试验方案进行 寿命评价需要很长的试验周期和大量的试验样品,试验成 本相对较高。加速寿命试验是一种可在短时间内获得产品 失效率数据的方法,它要求了解在正常应力下的主要失效 机理与失效模式、环境应力水平与产品寿命特征的关系, 一旦求得这种关系,即可确定有关应用环境的失效率估计 值。加速寿命试验可以有效获得零件、部件或系统的失效 率,可以减少测定低失效率产品寿命试验时间,是一种十 分有效的寿命试验方法[1-2]。
t=[M2M1)/A0]exp(E/kT)
(公式2)
当退化量M2达到某个值Mp时,则认为该器件失效,
而影响到由产品构成设备的性能参数或工作。这时的时间
差(t2-t1)就是产品从t1开始延续的寿命L。即
ln L = ln M p − M1 + ∆E
A0
kT
(公式3)
令A=ln[(Mp-M1)/A0],B=E/k,得lnL=A+(B/T)。式
序进应力加速寿命试验将试样从低应力开始试验,应 力水平试验时间等速升高,直到一定数量的失效发生或者 到了应力水平的极限为止。
基金项目:2017年工业转型升级(中国制造2025)资金(部门预算)—智能家电及高端消费类电子产品可靠性设计技术推广应用项目(项目中 标编号:TC170A5UG/2)
68 │SMART FACTORY│智慧工厂
│
《智慧工厂》Smart factory February 2018
67
加速寿命试验及其在电子产品上的应用
Accelerated Life Testing and Application in Electronic Products
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
加速寿命试验理论依据
电子元器件的失效原因与器件本身所选用的材料、材料之间、器件表面或体内、金属化系统以及封装结构中存在的各种化学、物理的反应有关。
器件从出厂经过贮存、运输、使用到失效的寿命周期,无时无刻不在进行着缓慢的化学物理变化。
在各种外界环境下,器件还会承受了各种热、电、机械应力,会使原来的化学物理反应加速,而其中温度应力对失效最为敏感。
实践证明,当温度升高以后,器件劣化的物理化学反应加快,失效过程加速,而Arrhenius模型就总结了由温度应力决定的化学反应速度依赖关系的规律性,为加速寿命试验提供了理论依据。
1. 以温度应力为加速变量的加速方程
由Arrhenius总结的经验公式如下
(8.5)
式中,dM/dt是化学反应速率,A是常数,E a是引起失效或退化过程的激活能,k是玻尔兹曼常数,T是绝对温度。
当器件在t0时刻处于正常状态数为M0,到t1时刻,器件处于失效状态数为M1。
如果温度与时间无关,则积分式(8.1)得
(8.6)
令DM=M1-M0,t=t1-t0,得到
(8.7)
取对数
(8.8)
可写成
(8.9)
其中
(8.10)
上式就是根据Arrhenius模型得到的以温度应力为加速度变量的加速方程。
用此方程来解释器件的高温贮存寿命试验是非常成功的。
式中,t表示器件产品达到某一F(t)的时间,它的对数与绝对温度的倒数成线性关系。
若用t~1/T单边对数坐标纸绘图,则可得到一条直线,然后用图估计法或数值法推算出器件在不同温度下的寿命值。
由式(8.1)可计算得到方程的斜率b、截距α和激活能E a,当T1>T2时
(8.11)激活能E a与方程的斜率b与器件的失效模式与失效机理有关。
根据多年来的实践积累,有关半导体器件与微电路不同失效模式与机理的激活能数据列于表8.8。
表8.8 失效模式、失效机理与激活能
失效模式失效机理激活能(eV)阈值电压漂移离子性(SiO2中的钠离子漂移) 1.0~1.4
阈值电压漂移离子性(Si-SiO2界面的低阻挡层) 1.0
漏电流增加形成反型层(MOS器件)0.8~1.4
漏电流增加隧道效应(二极管)0.5
电流增益下降因水分加速离子移动0.8 开路铝的腐蚀0.6~0.9
开路铝的电迁移0.6
短路氧化膜击穿0.3
http://Kê。
图8.3 不同激活能时温度与寿命的关系
以激活能E a作为参数,可以绘出不同E a时温度与寿命的关系,如图8.3所示。
可见,激活能越大,曲线倾斜越大,与温度的关系越密切。
加速系数τ的计算方法是:设在基准应力条件下做试验达到累积失效概率F0所需的时间为t0(F0),施加某种应力条件下进行加速寿命试验达到相同的累计失效概率所需的时间为t0(F0),则两者的比值即为加速系数t。
由基准温度T0升至高温T1条件下的加速系数为
(8.12)由上式可看出,激活能越大,加速系数越大,越容易被加速失效,加速试验的效果越明显。
在不同温度应力下,激活能与加速系数的关系,如图8.4所示。
图8.4 激活能与加速系数的关系
2. 以电应力为加速变量的加速方程
器件失效除了与温度应力有关外,与电应力也有密切关系。
电应力也会促使器件内部产生离子迁移、质量迁移等,造成短路、击穿断路失效等。
器件在电流、电压或功率等电应力作用下,应力越强,失效速率越快,器件寿命越短,爱伦模型总结了器件寿命与电应力之间的逆幂律关系,即
(8.13)
式中,t是电子元器件的寿命,k、c是常数,V是施加在电子元器件上的电应力。
这就是以电应力为加速变量的加速方程。
将上式取对数后,可得到k、c值。
当V2>V1时,
http://可靠性.com
(8.14) 在确定k、c之后,可根据上式,利用图估法或数值计算法评估器件在不同电应力下的寿命或失效率。
加速系数t的计算可按下式计算
(8.15)
对于某些微电子器件,若已知c和t,只要做一次施加高压V1下的加速寿命试验确定t1(F0),再根据上式,即可得到在正常电应力V0下的失效时间t0(F0)。
在加速寿命试验中,也有用湿度做加速变量的,也有同时采用湿度应力和电应力进行加速的,如THB(高温,高湿、偏置)加速试验,其主要目的是评价器件的耐潮寿命,采用的公式为
(8.16)
式中,t是平均寿命,exp(E a/kT)是Arrhenius模型方程因子,f(RH)是相对湿度函数,可表示为
(8.17)中国可靠性网可靠性、com
是爱伦模型因子。
