暴强Dijkstra算法求任意两点间最短路径(matlab程序)
Dijkstra求最短路的MATLAB程序(含注释)

Dijkstra求解最短路(含注释)function [P,D]=dijkstra_pt(A,sv)%Dijkstra法求解最短路%A为邻接矩阵;%sv为寻求最短路的起始点%P为所有点的P标号,即路权值%D为sv到所有结点的最短路径矩阵%2010年8月28日凌晨1:41[n,n]=size(A);s=sv;T=inf.*ones(1,n);%T标号初始化P=inf.*ones(1,n);%P标号初始化Tv=1:1:n;%具有T标号的点,初始时,所有点均为T标号v=zeros(1,n);%结点的前驱,初始时,均为0Tm=zeros(n,n);%所有点从P标号变为T标号的过程矩阵P(s)=0;for i=1:n%将所有结点从P标号变为T标号的过程Pv(i)=s;%Pv具有P标号的结点Tv=Tmark(Tv,s);%删去具有P标号的结点Tm(s,:)=A(s,:);for k=Pv%将具有P标号的点赋值无穷大,从而不影响后面的程序取最小值Tm(s,k)=inf;T(k)=inf;endfor k=Tv%一次修改P标号点所对应的T标号点的T标号Tm(s,k)=Tm(s,k)+P(s);endfor k=Tv[x,val]=min([T(k),Tm(s,k)]);T(k)=x;%二次修改P标号点所对应的T标号点的T标号if val==2v(k)=s;%修改P标号点所对应的T标号点的前驱endend[x,val]=min(T);%寻找P标号点if x==infbreak;ends=val;P(s)=x;%修改P标号end%下面求解从sv到各点的最短路矩阵aad=zeros(1,n);%最短路临时存储向量for i=n:-1:1w=i;for k=1:n%将sv到i点的最短路倒序存储在aad中if w==0break;endaad(k)=w;w=v(w);if w==svaad(k+1)=w;break;endendfor l=1:n%将sv到i点的最短路顺序存储在D中if aad(l)==svk=1;for j=l:-1:1D(i,k)=aad(j);k=k+1;endendendaad=zeros(1,n);end[g,h]=size(D);for i=1:g%将与最短路径无关的点赋值NaNfor j=1:h%con由上面计算得到if D(i,j)==0D(i,j)=NaN;endendend%下面为在T标号结点集合中删除P标号的子函数function Tvad=Tmark(Tv,vm)tg=length(Tv);for i=1:tgif Tv(i)==vm;wd=i;break;endendTvad=[Tv(1,1:wd-1),Tv(1,wd+1:tg)];。
Dijkstra、Floyd算法Matlab_Lingo实现

Dijkstra算法Matlab实现。
%求一个点到其他各点的最短路径function [min,path]=dijkstra(w,start,terminal)%W是邻接矩阵%start是起始点Array %terminal是终止点%min是最短路径长度%path是最短路径n=size(w,1);label(start)=0;f(start)=start;for i=1:nif i~=startlabel(i)=inf;endends(1)=start;u=start;while length(s)<nfor i=1:nins=0;forif i==s(j)ins=1;endendif ins==0v=i;if label(v)>(label(u)+w(u,v))label(v)=(label(u)+w(u,v));f(v)=u;endendendv1=0;k=inf;for i=1:nins=0;for j=1:length(s)if i==s(j)ins=1;endend-if ins==0v=i;if k>label(v)k=label(v);v1=v;endendends(length(s)+1)=v1;u=v1;endmin=label(terminal);path(1)=terminal;i=1;while path(i)~=startpath(i+1)=f(path(i));i=i+1 ;endpath(i)=start;L=length(path);path=path(L:-1:1);Floyd算法:matlab程序:%floyd算法,function [D,path,min1,path1]=floyd(a,start,terminal)%a是邻接矩阵%start是起始点%terminal是终止点%D是最小权值表D=a;n=size(D,1);path=zeros(n,n);for i=1:nfor j=1:nif D(i,j)~=infpath(i,j)=j;endendendfor k=1:nfor i=1:nfor j=1:nif D(i,k)+D(k,j)<D(i,j)-D(i,j)=D(i,k)+D(k,j);path(i,j)=path(i,k);endendendendif nargin==3min1=D(start,terminal);m(1)=start;i=1;path1=[ ];while path(m(i),terminal)~=terminalk=i+1;m(k)=path(m(i),terminal);i=i+1;endm(i+1)=terminal;path1=m;end1 6 5 5 5 66 2 3 4 4 65 2 3 4 5 45 2 3 4 5 61 4 3 4 5 11 2 4 4 1 6Floyd算法:Lingo程序:!用LINGO11.0编写的FLOYD算法如下;model:sets:nodes/c1..c6/;link(nodes,nodes):w,path; !path标志最短路径上走过的顶点;endsetsdata:path=0;w=0;@text(mydata1.txt)=@writefor(nodes(i):@writefor(nodes(j):-@format(w(i,j),' 10.0f')),@newline(1));@text(mydata1.txt)=@write(@newline(1));@text(mydata1.txt)=@writefor(nodes(i):@writefor(nodes(j):@format(path(i,j),' 10.0f')),@newline(1));enddatacalc:w(1,2)=50;w(1,4)=40;w(1,5)=25;w(1,6)=10;w(2,3)=15;w(2,4)=20;w(2,6)=25;w(3,4)=10;w(3,5)=20;w(4,5)=10;w(4,6)=25;w(5,6)=55;@for(link(i,j):w(i,j)=w(i,j)+w(j,i));@for(link(i,j) |i#ne#j:w(i,j)=@if(w(i,j)#eq#0,10000,w(i,j)));@for(nodes(k):@for(nodes(i):@for(nodes(j):tm=@smin(w(i,j),w(i,k)+w(k,j));path(i,j)=@if(w(i,j)#gt# tm,k,path(i,j));w(i,j)=tm)));endcalcend无向图的最短路问题Lingomodel:sets:cities/1..5/;roads(cities,cities):w,x;endsetsdata:w=0;enddatacalc:w(1,2)=41;w(1,3)=59;w(1,4)=189;w(1,5)=81;w(2,3)=27;w(2,4)=238;w(2,5)=94;w(3,4)=212;w(3,5)=89;w(4,5)=171;@for(roads(i,j):w(i,j)=w(i,j)+w(j,i));@for(roads(i,j):w(i,j)=@if(w(i,j) #eq# 0, 1000,w(i,j)));endcalcn=@size(cities); !城市的个数;min=@sum(roads:w*x);@for(cities(i)|i #ne#1 #and# i #ne#n:@sum(cities(j):x(i,j))=@sum(cities(j):x(j,i)));@sum(cities(j):x(1,j))=1;-@sum(cities(j):x(j,1))=0; !不能回到顶点1;@sum(cities(j):x(j,n))=1;@for(roads:@bin(x));endLingo编的sets:dian/a b1 b2 c1 c2 c3 d/:;link(dian,dian)/a,b1 a,b2 b1,c1 b1,c2 b1,c3 b2,c1 b2,c2 b2,c3 c1,d c2,d c3,d/:x,w;endsetsdata:w=2 4 3 3 1 2 3 1 1 3 4;enddatamin=@sum(link:w*x);@for(link:@bin(x));n=@size(dian);@sum(link(i,j)|i#eq#1:x(i,j))=1;@sum(link(j,i)|i#eq#n:x(j,i))=1;@for(dian(k)|k#ne#1#and#k#ne#n:@sum(link(i,k):x(i,k))=@sum(link(k,i):x(k,i)));- sets:dian/1..5/:level; !level(i)表示点i的水平,用来防止生产圈;link(dian,dian):d,x;endsetsdata:d=0 41 59 189 8141 0 27 238 9459 27 0 212 89189 238 212 0 17181 94 89 171 0;enddatan=@size(dian);min=@sum(link(i,j)|i#ne#j:d(i,j)*x(i,j));@sum(dian(j)|j#gt#1:x(1,j))>1;@for(dian(i)|i#gt#1:@sum(dian(j)|j#ne#i:x(j,i))=1);@for(dian(i)|i#gt#1:@for(dian(j)|j#ne#i#and#j#gt#1:level(j)>level(i)+x(i,j)-(n-2)*(1-x(i,j))+(n-3)*x(j, i)));@for(dian(i)|i#gt#1:level(i)<n-1-(n-2)*x(1,i));@for(dian(i)|i#gt#1:@bnd(1,level(i),100000));@for(link:@bin(x));。
Dijkstra算法求最短路径

在交通网络中,常常会提出许多这样的问题:两地之间是否有路相通?在有多条通路的情况下,哪一条最近?哪一条花费最少等。
交通网络可以用带权图表示,图中顶点表示域镇,边表示两城之间的道路,边上权值可表示两城镇间的距离,交通费用或途中所需的时间等。
以上提出的问题就是带权图中求最短路径的问题,即求两个顶点间长度最短的路径。
最短路径问题的提法很多。
在这里仅讨论单源最短路径问题:即已知有向图(带权),我们希望找出从某个源点S∈V到G中其余各顶点的最短路径。
例如:下图(有向图G14),假定以v1为源点,则其它各顶点的最短路径如下表所示:图G14从有向图可看出,顶点v1到v4的路径有3条:(v1,v2,v4),(v1,v4),(v1,v3,v2,v4),其路径长度分别为:15,20和10。
因此v1到v4的最短路径为(v1,v3,v2,v4 )。
为了叙述方便,我们把路径上的开始点称为源点,路径的最后一个顶点为终点。
那么,如何求得给定有向图的单源最短路径呢?迪杰斯特拉(Dijkstra)提出按路径长度递增产生诸顶点的最短路径算法,称之为迪杰斯特拉算法。
迪杰斯特拉算法求最短路径的实现思想是:设有向图G=(V,E),其中,V={0,2,…,n-1},cost是表示G的邻接矩阵,G.arcs [i][j] .adj 表示有向边<i,j>的权。
若不存在有向边<i,j>,则G.arcs [i][j] .adj 的权为无穷大(这里取值为32767)。
设S是一个集合,其中的每个元素表示一个顶点,从源点到这些顶点的最短距离已经求出。
设顶点v0为源点,集合S的初态只包含顶点v0。
数组D记录从源点到其他各顶点当前的最短距离,其初值为D[i]= G.arcs[v0][i].adj ,i=1,…,n-1。
从S之外的顶点集合V-S 中选出一个顶点w,使D[w]的值最小。
于是从源点到达w只通过S 中的顶点,把w加入集合S中调整D中记录的从源点到V-S中每个顶点v的距离:从原来的D[v] 和D[w]+ G.arcs [w][v] .adj中选择较小的值作为新的D[v]。
matlab中求最短路径的函数

matlab中求最短路径的函数在matlab中,有多种方法可以求解最短路径问题。
其中,较为常用的方法包括Dijkstra算法、Bellman-Ford算法和Floyd算法等。
这些方法对应的函数分别为dijkstra、bellmanford和floyd。
以下是这些函数的使用方法:1. dijkstra函数dijkstra函数可以求解带权有向图的单源最短路径问题。
其使用方法如下:[d,path] = dijkstra(W,s,t)其中,W为带权邻接矩阵,s为源节点,t为目标节点。
函数返回最短路径长度d和路径path。
例如,假设有以下带权有向图:W = [0 1 12 0;0 0 9 3;0 0 0 0;0 0 4 0];其中,0表示两节点之间没有边相连。
则可以使用以下代码求解1号节点到4号节点的最短路径:[d,path] = dijkstra(W,1,4)最短路径长度为7,路径为[1 2 4]。
2. bellmanford函数bellmanford函数可以求解带权有向图的单源最短路径问题,但是可以处理负权边。
其使用方法如下:[d,path] = bellmanford(W,s,t)其中,W为带权邻接矩阵,s为源节点,t为目标节点。
函数返回最短路径长度d和路径path。
例如,假设有以下带权有向图:W = [0 1 12 0;-4 0 9 3;0 0 0 0;0 0 4 0];其中,负权边被用负数表示。
则可以使用以下代码求解1号节点到4号节点的最短路径:[d,path] = bellmanford(W,1,4)最短路径长度为-1,路径为[1 2 4]。
3. floyd函数floyd函数可以求解带权有向图的所有节点之间的最短路径问题。
其使用方法如下:[D,path] = floyd(W)其中,W为带权邻接矩阵。
函数返回最短路径长度矩阵D和路径矩阵path。
例如,假设有以下带权有向图:W = [0 1 12 0;0 0 9 3;0 0 0 0;0 0 4 0];则可以使用以下代码求解所有节点之间的最短路径:[D,path] = floyd(W)最短路径长度矩阵为:D = [0 1 10 4;Inf 0 9 3;Inf Inf 0 Inf;Inf Inf 4 0];其中,Inf表示两节点之间不存在路径。
利用MATLAB实现Dijkstra算法
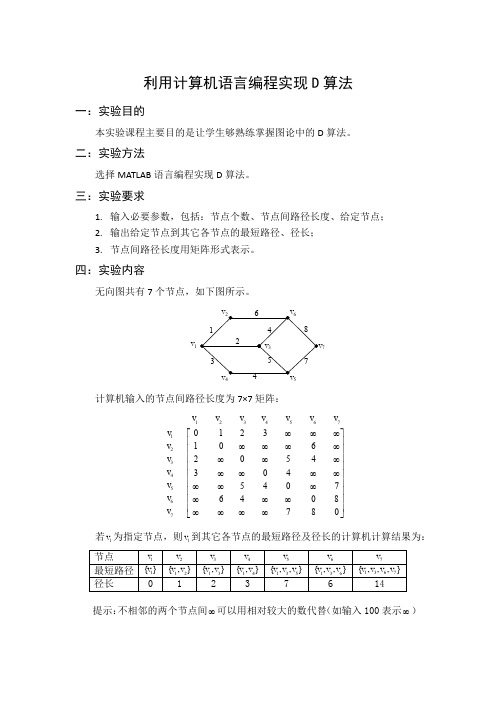
利用计算机语言编程实现D算法一:实验目的本实验课程主要目的是让学生够熟练掌握图论中的D算法。
二:实验方法选择MATLAB语言编程实现D算法。
三:实验要求1.输入必要参数,包括:节点个数、节点间路径长度、给定节点;2.输出给定节点到其它各节点的最短路径、径长;3.节点间路径长度用矩阵形式表示。
四:实验内容无向图共有7个节点,如下图所示。
v1457计算机输入的节点间路径长度为7×7矩阵:12345671 2 3 4 5 6 7012310620543045407 6408780⎡⎤∞∞∞⎢⎥∞∞∞∞⎢⎥⎢⎥∞∞∞⎢⎥∞∞∞∞⎢⎥⎢⎥∞∞∞⎢⎥∞∞∞⎢⎥⎢⎥∞∞∞∞⎣⎦v v v v v v vvvvvvvv若1v为指定节点,则1v到其它各节点的最短路径及径长的计算机计算结果为:提示:不相邻的两个节点间∞可以用相对较大的数代替(如输入100表示∞)五:实验原理1. D 算法原理已知图G=(V,E),将其节点集分为两组:置定节点集p G 和未置定节点集p G G -。
其中p G 内的所有置定节点,是指定点s v 到这些节点的路径为最短(即已完成最短路径的计算)的节点。
而p G G -内的节点是未置定节点,即s v 到未置定节点距离是暂时的,随着算法的下一步将进行不断调整,使其成为最短径。
在调整各未置定节点的最短径时,是将p G 中的节点作为转接点。
具体地说,就是将p G 中的节点作为转接点,计算(s v ,j v )的径长(j p v G G ∈-),若该次计算的径长小于上次的值,则更新径长,否则,径长不变。
计算后取其中径长最短者,之后将j v 划归到p G 中。
当(p G G -)最终成为空集,同时p G G =,即求得s v 到所有其他节点的最短路径。
j w 表示s v 与其他节点的距离。
在p G 中,i w 表示上一次划分到p G 中的节点iv 到s v 得最短路径。
在 p G G -中,表示s v 到j v (j p v G G ∈-)仅经过p G 中的节点作为转接点所求得的该次的最短路径的长度。
dijkstra算法缺点及matlab程序

Dijkstra算法Dijkstra(迪杰斯特拉)算法是典型的最短路径路由算法,用于计算一个节点到其他所有节点的最短路径。
主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
其基本原理是:每次新扩展一个距离最短的点,更新与其相邻的点的距离。
当所有边权都为正时,由于不会存在一个距离更短的没扩展过的点,所以这个点的距离永远不会再被改变,因而保证了算法的正确性。
不过根据这个原理,用Dijkstra求最短路的图不能有负权边,因为扩展到负权边的时候会产生更短的距离,有可能就破坏了已经更新的点距离不会改变的性质。
Dijkstra 算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
Dijkstra算法是很有代表性的最短路算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。
Dijkstra一般的表述通常有两种方式,一种用永久和临时标号方式,一种是用OPEN, CLOSE表方式,Drew为了和下面要介绍的A* 算法和D* 算法表述一致,这里均采用OPEN,CLOSE表的方式。
其采用的是贪心法的算法策略大概过程:创建两个表,OPEN, CLOSE。
OPEN表保存所有已生成而未考察的节点,CLOSED表中记录已访问过的节点。
1.访问路网中距离起始点最近且没有被检查过的点,把这个点放入OPEN 组中等待检查。
2.从OPEN表中找出距起始点最近的点,找出这个点的所有子节点,把这个点放到CLOSE表中。
3.遍历考察这个点的子节点。
求出这些子节点距起始点的距离值,放子节点到OPEN表中。
4.重复第2和第3步,直到OPEN表为空,或找到目标点。
①function [l,z]=Dijkstra(W)n = size (W,1);for i = 1 :nl(i)=W(1,i);z(i)=1;endi=1;while i<=nfor j =1 :nif l(i)>l(j)+W(j,i)l(i)=l(j)+W(j,i);z(i)=j;if j<ii=j-1;endendendi=i+1;end% W =[ 0 2 1 8 Inf Inf Inf Inf % 2 0 Inf 6 1 Inf InfInf% 1 Inf 0 7 Inf Inf 9 Inf% 8 6 7 0 5 12 Inf% Inf 1 Inf 5 0 3 Inf9% Inf Inf Inf 1 3 0 46% Inf Inf 9 2 Inf 4 03% Inf Inf Inf Inf 9 6 30 ];②========================================================Dijkstra的matlab实现代码=========================================================function [d,DD]=dijkstra(D,s)%Dijkstra最短路算法Matlab程序用于求从起始点s到其它各点的最短路%D为赋权邻接矩阵%d为s到其它各点最短路径的长度%DD记载了最短路径生成树[m,n]=size(D);d=inf.*ones(1,m);d(1,s)=0;dd=zeros(1,m);dd(1,s)=1;y=s;DD=zeros(m,m);DD(y,y)=1;counter=1;while length(find(dd==1))<Mfor i=1:mif dd(i)==0d(i)=min(d(i),d(y)+D(y,i));endendddd=inf;for i=1:mif dd(i)==0&&d(i)<DDDddd=d(i);endendyy=find(d==ddd);counter=counter+1;DD(y,yy(1,1))=counter;DD(yy(1,1),y)=counter;y=yy(1,1);dd(1,y)=1;end③没有用过这个算法,请大家指点一下对于下面的路径矩阵怎样求取从1到7的最短路径的使用方法(急着用,谢谢了):%关键在于怎样输出途经结点或边的位置1~9clear;clc;ko=10000;mp(1,:)=[0 628.4 400 ko ko ko 728.4 ko ko];mp(2,:)=[zeros(1,2) ko 900 ko ko ko ko ko];mp(3,:)=[zeros(1,3) ko ko 700 ko ko ko];mp(4,:)=[zeros(1,4) 400 ko ko ko ko];mp(5,:)=[zeros(1,5) ko ko ko 628.4];mp(6,:)=[zeros(1,6) ko ko 200];mp(7,:)=[zeros(1,7) 800 ko];mp(8,:)=[zeros(1,8) 1028.4];mp(9,:)=zeros(1,9);mr=mp+mp';附:dijkstra算法代码[m,n]=size(D);d=inf.*ones(1,m);d(1,s)=0;dd=zeros(1,m);dd(1,s)=1;y=s;DD=zeros(m,m);DD(y,y)=1;counter=1;while length(find(dd==1))<Mfor i=1:mif dd(i)==0d(i)=min(d(i),d(y)+D(y,i));endendddd=inf;for i=1:mif dd(i)==0&&d(i)<DDDddd=d(i);endendyy=find(d==ddd);counter=counter+1;DD(y,yy(1,1))=counter;DD(yy(1,1),y)=counter;y=yy(1,1);dd(1,y)=1;endFloyd算法描述:设A = (aij )n×n为赋权图G = (V, E, F)的权矩阵, dij表示从vi到vj点的距离, rij表示从vi到vj点的最短路中一个点的编号.①赋初值. 对所有i, j, dij = aij, rij = j. k = 1. 转向②.②更新dij , rij . 对所有i, j, 若dik + dk j<dij , 则令dij = dik + dkj , rij = k, 转向③;③终止判断. 若k = n终止; 否则令k = k + 1, 转向②.最短路线可由rij得到.Matlab程序:%floyd1.m文件function [d,r1]=floyd1(vx,vy)b=inf;a= [ 0 2 8 1 b b b b2 0 6 b 1 b b b8 6 0 7 5 1 2 b1 b 7 0 b b 9 bb 1 5 b 0 3 b 8b b 1 b 3 0 4 6b b 2 9 b 4 0 3b b b b 8 6 3 0 ];d=a;vx=vx+1;vy=vy+1;global r;r=a;for i=1:8for j=1:8d(i,j)=a(i,j);r(i,j)=j;k=1;endendfor k=1:8for i=1:8for j=1:8if d(i,k)+d(k,j)<d(i,j)d(i,j)=d(i,k)+d(k,j);r(i,j)=k;endendendendr1=r-1;fun3(vx,vy);%fun3.m文件function fun3(vx,vy)global rt=r(vx,vy);if vy==treturnelsefun3(vx,t);disp(t-1);fun3(t,vy);end。
最短路dijkstra算法Matlab程序

function [c0,c,path0,path]=dijkstra(s,t,C,flag)% Use the Dijkstra's algorithm to find the shortest path from% s to t and can also find the shortest path between s and all% the other points.% Reference: Graph Theory with Applications by J. A. Bondy and% U. S. R. Murty.% Input -- s is the starting point and also is the point s.% -- t is the given terminal point and is the point t.% -- C \in R^{n \times n}is the cost matrix, where% C(i,j)>=0 is the cost from point i to point j.% If there is no direct connection between point i and% j, C(i,j)=inf.% -- flag: if flag=1, the function just reports the% shortest path between s and t; if flag~=1, the% function reports the shortest path between s and t,% and the shortest paths between s and other points.% Output -- c0 is the minimal cost from s to t.% -- path0 denotes the shortest path form s to t.% -- c \in R{1\times n} in which the element i is the% minimal cost from s to point i.% -- path \in R^{n \times n} in which the row i denotes% the shortest path from s to point i.% Copyright by MingHua Xu(徐明华), Changhzou University, 27 Jan. 2014. s=floor(s);t=floor(t);n=size(C,1);if s<1 || t < 1 || s > n || t > nerror(' The starting point and the terminal point exceeds the valid range');endif t==sdisp('The starting point and the terminal point are the same points');endlabel=ones(1,n)*inf;label(s)=0;S=[s];Sbar=[1:s-1,s+1:n];c0=0;path=zeros(n,n);path(:,1)=s;c=ones(1,n)*inf;parent=zeros(1,n);i=1; % number of points in point set S.while i<n% for each point in Sbar, replace label(Sbar(j)) by% min(label(Sbar(j)),label(S(k))+C(S(k),Sbar(j)))for j=1:n-ifor k=1:iif label(Sbar(j)) > label(S(k))+C(S(k),Sbar(j))label(Sbar(j))=label(S(k))+C(S(k),Sbar(j));parent(Sbar(j))=S(k);endendend% Find the minmal label(j), j \in Sbar.temp=label(Sbar(1));son=1;for j=2:n-iif label(Sbar(j))< temptemp=label(Sbar(j));son=j;endend% update the point set S and SbarS=[S,Sbar(son)];Sbar=[Sbar(1:son-1),Sbar(son+1:n-i)];i=i+1;% if flag==1, just output the shortest path between s and t.if flag==1 && S(i)==tson=t;temp_path=[son];if son~=swhile parent(son)~=sson=parent(son);temp_path=[temp_path,son];endtemp_path=[temp_path,s];endtemp_path=fliplr(temp_path);m=size(temp_path,2);path0(1:m)=temp_path;c_temp=0;for j=1:m-1c_temp=c_temp+C(temp_path(j),temp_path(j+1));endc0=c_temp;path(t,1:m)=path0;c(t)=c0;returnendend% Form the output resultsfor i=1:nson=i;temp_path=[son];if son~=swhile parent(son)~=sson=parent(son);temp_path=[temp_path,son];endtemp_path=[temp_path,s];endtemp_path=fliplr(temp_path);m=size(temp_path,2);path(i,1:m)=temp_path;c_temp=0;for j=1:m-1c_temp=c_temp+C(temp_path(j),temp_path(j+1));endc(i)=c_temp;c0=c(t);path0=path(t,:);endreturn。
D_i_j_k_s_t_r_a最短路算法MATLAB程序_

从起点sb到终点db通用的Dijkstra标号算法程序function [mydistance,mypath]=mydijkstra(a,sb,db);% 输入:a—邻接矩阵,a(i,j)是指i到j之间的距离,可以是有向的% sb—起点的标号, db—终点的标号% 输出:mydistance—最短路的距离, mypath—最短路的路径n=size(a,1); visited(1:n) = 0;distance(1:n) = inf; distance(sb) = 0; %起点到各顶点距离的初始化visited(sb)=1; u=sb; %u为最新的P标号顶点parent(1:n) = 0; %前驱顶点的初始化for i = 1: n-1id=find(visited==0); %查找未标号的顶点for v = idif a(u, v) + distance(u) < distance(v)distance(v) = distance(u) + a(u, v); %修改标号值parent(v) = u;endendtemp=distance;temp(visited==1)=inf; %已标号点的距离换成无穷[t, u] = min(temp); %找标号值最小的顶点visited(u) = 1; %标记已经标号的顶点endmypath = [];if parent(db) ~= 0 %如果存在路!t = db; mypath = [db];while t ~= sb %从终点db开始回溯p = parent(t);mypath = [p mypath];t = p;endendmydistance = distance(db);例题:运筹学教材P205 第七题D=[0 3 6 1 inf inf inf inf;inf 0 2 inf 4 6 inf inf;inf inf 0 inf inf 5 inf inf;inf inf 4 0 inf 3 6 inf;inf inf inf inf 0 inf inf 7;inf inf inf inf inf 0 7 11;inf inf inf inf inf inf 0 8;inf inf inf inf inf inf inf 0]在command window输入:[mydistance,mypath]=mydijkstra(D,1,8);。
暴强Dijkstra算法求任意两点间最短路径(matlab程序)

暴强D i j k s t r a算法求任意两点间最短路径(m a t l a b程序)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN效果展示:开头输入的是点的序列号(表示第几个点),显示的是最短路径的走法(同样以点的序列号显示,表示途径的第几个点)。
%编写m文件function [distance,path]=dijkstra(A,s,e)% [DISTANCE,PATH]=DIJKSTRA(A,S,E)% returns the distance and path between the start node and the end node.%% A: adjcent matrix% s: start node% e: end node% initializen=size(A,1); % node numberD=A(s,:); % distance vectorpath=[]; % path vectorvisit=ones(1,n); % node visibilityvisit(s)=0; % source node is unvisibleparent=zeros(1,n); % parent node% the shortest distancefor i=1:n-1 % BlueSet has n-1 nodestemp=zeros(1,n);count=0;for j=1:nif visit(j)temp=[temp(1:count) D(j)];elsetemp=[temp(1:count) inf];endcount=count+1;end[value,index]=min(temp);j=index; visit(j)=0;for k=1:nif D(k)>D(j)+A(j,k)D(k)=D(j)+A(j,k);parent(k)=j;endendenddistance=D(e);% the shortest distance pathif parent(e)==0return;endpath=zeros(1,2*n); % path preallocationt=e; path(1)=t; count=1;while t~=s && t>0p=parent(t);path=[p path(1:count)];t=p;count=count+1;endif count>=2*nerror(['The path preallocation length is too short.',... 'Please redefine path preallocation parameter.']);endpath(1)=s;path=path(1:count);%算法实现clc; clear; close all;%% 载入设置数据lines = load(''); %点与点之间的距离矩阵A=lines;A(find(A>10))=inf; %对步长的限制,根据自己的要求决定!我们在此选择10. % A就是连接矩阵,其中对角线为0,表示本身% 有连接关系的就对应线的长度% 没有连接关系的就对应inf%% 下面的是dijstra算法,有两种方式可以调用s =input('输入起点'); % 起点(点的序号)e =input('输入终点'); % 终点(点的序号)[distance,path0] = dijkstra(A,s,e);fprintf('\n Use Dijkstra the Min Distance is: %.5f \n', distance);fprintf('\n Use Dijkstra the Min Distance path is: \n');disp(path0);A1 = A;A1(isinf(A1)) = 0;[d, p, pred] = graphshortestpath(sparse(A1), s, e);fprintf('\n Use graphshortestpath the Min Distance is: %.5f \n', d);fprintf('\n Use graphshortestpath the Min Distance path is: \n');disp(p);for i = 1 : length(path0)if i == length(path0)temp = [path0(1) path0(i)];elsetemp = [path0(i) path0(i+1)];endend。
dijkstra算法原理及MATLAB代码

Dijkstra算法是寻找最短路径的一种搜索算法,由荷兰科学家提出。
1)算法思想:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径, 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。
在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v 到U中任何顶点的最短路径长度。
此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
2)算法步骤:a.初始时,S只包含源点,即S={v},v的距离为0。
U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则<u,v>正常有权值,若u不是v的出边邻接点,则<u,v>权值为∞。
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
算法描述:通过为每个节点保留目前为止所找到的从s到e的最短路径。
为了记录最佳路径轨迹,记录路径上每个节点的前趋,通过回溯法找出最短路径轨迹。
过程如下:在网上搜索一些版本的Matlab实现方法,感觉都有些毛病。
经过修改,得到比较好的效果。
[cpp]view plain copy1.function [ distance path] = Dijk( W,st,e )2.%DIJK Summary of this function goes here3.% W 权值矩阵 st 搜索的起点 e 搜索的终点4.n=length(W);%节点数5. D = W(st,:);6.visit= ones(1:n); visit(st)=0;7.parent = zeros(1,n);%记录每个节点的上一个节点8.9.path =[];10.11.for i=1:n-112. temp = [];13. %从起点出发,找最短距离的下一个点,每次不会重复原来的轨迹,设置visit判断节点是否访问14.for j=1:n15.if visit(j)16. temp =[temp D(j)];17.else18. temp =[temp inf];19. end20.21. end22.23. [value,index] = min(temp);24.25. visit(index) = 0;26.27. %更新如果经过index节点,从起点到每个节点的路径长度更小,则更新,记录前趋节点,方便后面回溯循迹28.for k=1:n29.if D(k)>D(index)+W(index,k)30. D(k) = D(index)+W(index,k);31. parent(k) = index;32. end33. end34.35.36.end37.38.distance = D(e);%最短距离39.%回溯法从尾部往前寻找搜索路径40.t = e;41.while t~=st && t>042. path =[t,path];43. p=parent(t);t=p;44.end45.path =[st,path];%最短路径46.47.48.end测试:测试用例1[cpp]view plain copy1.W=[0 50 inf 40 25 102. 50 0 15 20 inf 253. inf 15 0 10 20 inf4. 40 20 10 0 10 255. 25 inf 20 10 0 556. 10 25 inf 25 55 0];[cpp]view plain copy1.[cpp]view plain copy1.[distance,path]=Dijk(W,1,4);>> distancedistance =35>> pathpath =1 6 4从节点1到节点4最短距离路径为1-->6-->4, 最短距离为35测试用例2[html]view plain copy1.W=[0 1 3 42. 1 0 2 inf3. 3 2 0 54. 4 inf 5 0];[html]view plain copy1.[distance,path]=Dijk(W,2,4);>> distancedistance =5>> pathpath =2 1 4从节点2到节点4最短距离路径为2-->1-->4, 最短距离为5。
Dijkstra求用matlab解最短路问题的程序

% Dijkstra's Shortest Path%% final = dijkstra( A, x, y )%% Description: returns the shortest path from x to y given adjacency % matrix A. Utilizes Dijkstra's shortest path algorithm.%% A = adjacency matrix of the graph (includes point x and y)% x = intial node% y = terminal node% IN = set of nodes whose shortest path from x is known% z,p = temporary nodes% d = vector of lengths from initial point. i.e. d(p) = x to p% s = vector of the previous node on a shortest path for any node %% Author: Josh Eads% Date: 1/23/2006function final = dijkstra( A, x, y )%modify A so that lengths of 0 are invalid (-1)A(find(A == 0)) = NaN;%initialize IN to include only xIN = x;%initialize ss = zeros(1,length(A));%initialize d & d(x) (distance to self)d = zeros(1,length(A));d(x) = 0;%loop through all the nodes in Afor z = 1:length(A)%don't calculate values already in IN%if ~(find(IN == z))if ~isWithin(IN, z)%grab the distance from x to z from A (-1 denotes unreachable)d(z) = A(x,z);%set the previous node to xs(z) = x;endend%process nodes into IN%while y isn't in set IN%while ~(find(IN == y))while ~isWithin(IN, y)tempMin = [];%add the node not in IN with the minimum distance into INfor z = 1:length(A)%if z isn't in IN%if ~(find(IN == z))if ~isWithin(IN, z)tempMin = [tempMin, d(z)];endend%find the minimum value from tempMinp = min(tempMin);%find the minimum distance nodessearch = find(d == p);%cycle through all the minimum distance nodes until one not in IN is %foundfor i = 1:length(search)search = find(d == p);%store in p if the node isn't in INif( ~isWithin(IN, search(i)) )p = search(i);break;endend%add node p into ININ = [IN, p];%recompute d for all non-IN nodes, and adjust sfor z = 1:length(A)%if z isn't in IN%if ~(find(IN == z))if ~isWithin(IN, z)oldDistance = d(z);%if the new path is shorter for z, update d(z)d(z) = min(d(z), d(p) + A(p,z));%if the new and old distances don't match, update s(z)if ~(d(z) == oldDistance)s(z) = p;endendendend%write the shortest path to finalfinal = y;z = y;while (z == x) == 0final = [final, s(z)];z = s(z);endfinal=fliplr(final);% isWithin Function% source = matrix to search through% search = item to search for%% returns - true if search is within source function truth = isWithin(source, search)truth = 0;for i = 1:length(source)if(source(i) == search)truth = 1;endend。
matlab计算节点之间最短距离

matlab计算节点之间最短距离在计算机科学中,图是一种常用的数据结构,用于表示对象之间的关系。
其中,节点表示对象,边表示两个对象之间的关系。
图包含了许多重要的问题,如最短路径问题,它是一种在有向或无向图中寻找两个节点之间最短路径的算法。
在MATLAB中,有几种方法可以计算图中节点之间的最短距离,包括Dijkstra算法、A*算法和Floyd-Warshall算法。
这些算法是根据不同的原理设计的,各有优缺点。
Dijkstra算法是在有向图中找到从一个寻点到另一个节点的最短路径的常用算法。
算法从起点开始,跟踪到目前为止在最短路径上距离最小的节点,并将其添加到已访问节点的列表中。
然后,它更新与该节点相邻的节点的距离,如果新的距离比之前的距离短,则更新其距离。
最后,它会从未访问过的节点中选出下一个最短路径节点。
该算法需要一个图,一个起点和一个终点。
A*搜索是另一种常用的算法,通常用于在指定的有向图中查找最短路径。
其特点是采用启发式估价函数,以查找节点之间最短路径的代价。
算法将节点按其启发式估价函数的评估值存储,这样可以保证算法总是从最有希望的节点开始移动。
它在一些特定的情况下可以比Dijkstra的算法更快地找到最短路径。
Floyd算法也是一种流行的最短路径算法,可以计算两个节点之间的最短路径,还可以计算任意两个节点之间的最短路径。
该算法由Discrete Mathematics中的Robert W. Floyd提出。
该算法使用动态规划来计算每个节点之间的最短路径。
在对每个节点进行计算后,可以找到任意两个节点之间的最短路径。
总之,计算节点之间最短距离是计算机图形学,图像处理和机器学习等领域中非常重要的问题。
在MATLAB中,可以使用Dijkstra算法、A*算法或Floyd算法来解决它。
这些算法都有自己的优缺点,因此,在选择算法时需要考虑系统需求和计算资源等因素。
matlab计算最短路径讲述

湖南大学MATLAB实训报告题目:matlab计算最短路径问题学院名称:信息科学与工程学院专业班级:软件工程四班学生姓名:彭天越学号: 20112601416 日期: 2013年7月3号目录题目 (2)问题描述 (3)(1)根据无向图A,使用Di.jistra算法 (3)(2)根据有向图B,使用Warshall-Floyd算法 (4)思路及代码 (4)(1)思路 (4)(2)源代码 (5)测试结果说明 (10)(1)Di.jistra算法 (10)(2)Floyd算法 (11)小结 (11)题目求下图中顶点ν1到顶点ν11的最短距离和最短路(2学分)B.有向图问题描述(1)根据无向图A,使用Di.jistra算法(2)根据有向图B,使用Warshall-Floyd算法思路及代码(1)思路(1)Dijkstra算法使用范围:1)寻求从一固定顶点到其余各点的最短路径;2)有向图、无向图和混合图;3)权非负.算法思路:采用标号作业法,每次迭代产生一个永久标号, 从而生长一颗以v为根的最短路树,在这颗树上每个顶点与根节点之间的路径皆为最短路径. 诉法步骤:S: 具有永久标号的顶点集;l(v): v的标记; f(v):v的父顶点,用以确定最短路径;输入加权图的带权邻接矩阵w=[w(vi ,vj)]nxm.1)初始化令l(v0)=0,S=Φ;∀ v≠v,l(v)=∞;2)更新l(v), f(v)寻找不在S中的顶点u,使l(u)为最小.把u加入到S中,然后对所有不在S中的顶点v,如l(v)>l(u)+w(u,v),则更新l(v),f(v), 即l(v)←l(u)+w(u,v),f(v)←u;3)重复步骤2), 直到所有顶点都在S中为止.(2)Floyd算法使用范围:1)求每对顶点的最短路径;2)有向图、无向图和混合图;算法思想:直接在图的带权邻接矩阵中用插入顶点的方法依次递推地构造出n个矩阵D(1), D(2), …, D(n), D(n)是图的距离矩阵, 同时引入一个后继点矩阵记录两点间的最短路径.算法步骤:d(i,j) : i到j的距离;path(i,j): i到j的路径上i的后继点;输入带权邻接矩阵a(i,j).1)赋初值对所有i,j, d(i,j)←a(i,j) , path(i,j)←j,k=l.2)更新d(i,j) , path(i,j)对所有i,j, 若d(i,k)+d(k,j)<d(i,j),则d(i,j)←d(i,k)+d(k,j) , path(i,j)←path(i,k) , k ←k+1 3)重复2)直到k=n+1(2)源代码(1)Dijkstra.m文件%计算最短路径(Dijkstra算法)%min表示最短的距离%path表示最短路径%w表示邻接矩阵%start表示开始点%terminal表示终止点function [min,path]=dijkstra(w,start,terminal)n=size(w,1); %计算邻接矩阵的行数label(start)=0; f(start)=start;%初始化for i=1:nif i~=startlabel(i)=inf;endends(1)=start; u=start;%更新最短路径直到所有顶点都遍历while length(s)<nfor i=1:nins=0;for j=1:length(s)if i==s(j)ins=1;endendif ins==0v=i;if label(v)>(label(u)+w(u,v)) label(v)=(label(u)+w(u,v)); f(v)=u;endendend%v1=0;k=inf;for i=1:nins=0;for j=1:length(s)if i==s(j)ins=1;endendif ins==0v=i;if k>label(v)k=label(v);v1=v;endendends(length(s)+1)=v1;u=v1;end%求出最短距离与最短路径min=label(terminal); path(1)=terminal;i=1;while path(i)~=startpath(i+1)=f(path(i));i=i+1 ;endpath(i)=start;L=length(path);path=path(L:-1:1);%循环输出路径text01.m脚本文件进行测试clear;clc;fprintf('计算最短路径(Dijkstra算法)\n');x=[0,2,1,8,inf,inf,inf,inf,inf,inf,inf;2,0,inf,6,1,inf,inf,inf,inf,inf,inf;1,inf,0,7,inf,inf,9,inf,inf,inf,inf;8,6,7,0,5,1,2,inf,inf,inf,inf;inf,1,inf,5,0,3,inf,2,1,inf,inf;inf,inf,inf,1,3,0,4,inf,6,inf,inf;inf,inf,9,2,inf,4,0,inf,3,1,inf;inf,inf,inf,inf,2,inf,inf,0,7,inf,inf;inf,inf,inf,inf,inf,6,3,7,0,1,2;inf,inf,inf,inf,inf,inf,1,inf,1,0,1;inf,inf,inf,inf,inf,inf,inf,inf,2,1,0]%x=input('输入邻接矩阵:');start=input('输入起点:');terminal=input('输入终点:');fprintf('计算结果如下:');[min,path_way]=dijkstra(x,start,terminal)Floyd.m函数%计算最短路径(Floyd算法)%[D,path,min1,path1]=floyd(a,start,terminal)返回矩阵D, path; 并返回start与terminal之间的最短距离min1和最短路径path1.%path(i,j): 表示i到j的路径上i的后继点;%D(i,j) : 表示i到j的距离;%输入带权邻接矩阵a(i,j).%1)赋初值% 对所有i,j, D(i,j)<-a(i,j) , path(i,j)<-j%2)更新D(i,j) , path(i,j)% 对所有i,j, 若D(i,k)+D(k,j)<d(i,j),则% D(i,j)<-D(i,k)+D(k,j) , path(i,j)<-path(i,k) , k<-k+1 %3)重复2)直到k=n+1function [D,path,min1,path1]=floyd(a,start,terminal)D=a;n=size(D,1);path=zeros(n,n);%初始化for i=1:nfor j=1:nif D(i,j)~=infpath(i,j)=j;endendendfor k=1:nfor i=1:nfor j=1:nif D(i,k)+D(k,j)<D(i,j)D(i,j)=D(i,k)+D(k,j);path(i,j)=path(i,k);endendendendif nargin==3%参数个数为3的时候执行min1=D(start,terminal);%最短距离m(1)=start;i=1;path1=[ ]; %计算最短路径while path(m(i),terminal)~=terminalk=i+1;m(k)=path(m(i),terminal);i=i+1;endm(i+1)=terminal;path1=m;endtext02.m脚本文件,进行测试clear;clc;fprintf('计算最短路径(Floyd算法)\n');x=[0,2,inf,8,inf,inf,inf,inf,inf,inf,inf; inf,0,inf,6,1,inf,inf,inf,inf,inf,inf;1,inf,0,inf,inf,inf,9,inf,inf,inf,inf;inf,inf,7,0,inf,inf,inf,inf,inf,inf,inf;inf,inf,inf,5,0,inf,inf,inf,1,inf,inf;inf,inf,inf,1,3,0,4,inf,inf,inf,inf;inf,inf,inf,2,inf,inf,0,inf,3,1,inf;inf,inf,inf,inf,2,inf,inf,0,inf,inf,inf;inf,inf,inf,inf,inf,6,inf,7,0,inf,inf;inf,inf,inf,inf,inf,inf,inf,inf,1,0,1;inf,inf,inf,inf,inf,inf,inf,inf,2,inf,0]%x=input('输入邻接矩阵:');start=input('输入起点:');terminal=input('输入终点:');fprintf('计算结果如下:');[D,path,min,path_way]=floyd(x,start,terminal)测试结果说明(1)Di.jistra算法根据无向图A,可以知道matlab计算出来的结果是正确的湖南大学(2)Floyd算法根据有向图B,可以知道matlab计算出来的结果是正确的小结Matlab 现在的发展已经使其成为一种集数值运算、符号运算、数据可视化、图形界面设计、程序设计、仿真、图像处理、电路设计等多种功能于一体的集成化软件,在矩阵方面等处理占据很大的优势,图论中的很多问题均能通过matlab 来解决,方便而高效,比如哥尼斯堡七桥问题,连通性邻接矩阵等概念的提出,更便于解决图论中的计算最短路径的问题,要熟练掌握一门语言,乃至精通就必须要多练多动手自己多思考,然后要懂得充分的利用可靠资源!11。
基于 dijsktra 算法的最短路径求解

基于dijsktra 算法的最短路径求解
Dijkstra 算法是一种贪心算法,用于解决带权重边的单源最短路径问题,可以用来求解任意两个节点之间的最短路径,它的时间复杂度为O(V^2),其中V 是节点数量。
以下是Dijkstra 算法的具体步骤:
1. 定义一个数组dist,表示每个节点到源节点的最短距离,初始时所有节点的距离设为无穷大,源节点的距离设为0。
2. 定义一个数组visited,表示每个节点的访问状态,初始时所有节点都未被访问。
3. 以源节点为起点,将dist[s] 设为0。
4. 对于每个未被访问的节点,找到到源节点距离最短的节点u,将其标记为已访问,并更新与u 相邻的节点的最短距离,具体方法为:对于所有与u 相邻的节点v,如果dist[v] > dist[u] + w(u, v)(其中w(u, v) 表示u 到v 的边权重),则更新dist[v] = dist[u] + w(u, v)。
5. 重复步骤4 直到所有节点都被访问。
最终,dist 数组中存储的即为源节点到其它所有节点的最短路径长度。
如果需要求源节点到目标节点的最短路径,可以使用回溯法,从目标节点开始,依次沿着dist 值不断递减的路径找到源节点。
Dijkstra算法,最短路径路由算法matlab代码

Dijkstra算法,最短路径路由算法matlab代码Dijkstra算法是⼀种最短路径路由算法,⽤于计算⼀个节点到其他所有节点的最短路径。
主要特点是以起始点为中⼼向外层层扩展,直到扩展到终点为⽌。
Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率较低。
算法详细解释各⽹站都有,不太难。
下边是对下图从D开始到A节点寻找最短路径的matlab代码,个⼈原创。
%% Dijkstra算法%by Jubobolv369 at 2022/1/22clc;clear;close all;%% 初始化带权邻接矩阵,起点、终点等initRoute=[0 12 inf inf inf 16 14;12 0 10 inf inf 7 inf;inf 10 0 3 5 6 inf;inf inf 3 0 4 inf inf;inf inf 5 4 0 2 8;16 7 6 inf 2 0 9;14 inf inf inf 8 9 0;];[row,column]=size(initRoute);start_node=4;end_node=1;close_list=[];open_list=[];%closelist中加⼊初始节点close_list=[start_node,start_node,0];%% 如果closelist中没有终点,则遍历节点,通过⽐较逐渐加⼊节点到closelist。
while isempty(find(close_list(:,1) == end_node))[last1,~]=size(close_list);%获取closelist的最后⼀⾏的索引now_node=close_list(last1,1);%当前节点编号now_length=close_list(last1,3);%当前最优长度[last2,~]=size(open_list); %%获取openlist的最后⼀⾏的索引now_list=initRoute(now_node,:); %从原始矩阵中取初当前节点的边权值i=1;%% 更新openlistfor j=1:column%如果第j个节点可达、不是⾃⾝且不在close_list中,该点可能需要改动或添加到openlist中if now_list(j)~=inf && now_list(j)~=0 && isempty(find(close_list(:,1) == j))if last1==1open_list(i,1)=j;open_list(i,2)=now_node;open_list(i,3)=now_list(j);i=i+1;%如果不在openlist中,就将其添加到其中,否则将通过当前⽗节点到此节点的权值与之前的作⽐较elsek=find(open_list(:,1) == j);if isempty(k)open_list(last2+i,1)=j;open_list(last2+i,2)=now_node;open_list(last2+i,3)=now_list(j)+now_length;i=i+1;elseif open_list(k,3)>(now_list(j)+now_length) %若現在的路徑⾧度⼩,則更新路徑open_list(k,1)=j;open_list(k,1)=j;open_list(k,2)=now_node;open_list(k,3)=now_list(j)+now_length;endendendend%% 更新closelist和openlist。
dijkstra matlab 代码

Dijkstra算法是一种用于寻找图中单源最短路径的算法,由荷兰计算机科学家艾兹赫·迪科斯彻尔(Edsger Dijkstra)于1956年提出。
它主要用于计算从一个节点到其他所有节点的最短路径,通过不断更新起始节点到其他节点的最短距离来实现。
Dijkstra算法的基本思想是利用贪心算法,不断更新起始节点到其他节点的最短距离,直到所有节点的最短路径都被找到。
这个过程中,算法会维护一个距离数组,来记录起始节点到其他节点的最短距离,通过不断更新这个数组来找到最短路径。
对于一幅图G,Dijkstra算法可以描述如下:1. 初始化起始节点到其他所有节点的距禫数组,将起点到自己的距离设为0,其他节点的距离设为无穷大。
2. 从起始节点开始,选择距离数组中距离最小的节点,标记为已访问。
3. 遍历该节点的所有邻接节点,更新距离数组中的距离,如果有更短的路径,则更新距离数组。
4. 重复步骤2和3,直到所有节点都被访问过。
在Matlab中,我们可以通过编写Dijkstra算法的代码来实现对图的最短路径计算。
下面是一个简单的Dijkstra算法的Matlab实现:```matlabfunction [dist, path] = Dijkstra(graph, start)n = length(graph); 获取图的节点个数dist = inf(1, n); 距离数组初始化为无穷大path = ones(1, n) * -1; 路径数组初始化为-1visited = false(1, n); 标记数组初始化为falsedist(start) = 0; 起始节点到自己的距离为0for i = 1:n[mindist, u] = min(dist(~visited)); 找到距离数组中未访问节点的最小值以及对应的节点visited(u) = true; 标记该节点为已访问for v = 1:nif ~visited(v) graph(u, v) > 0 dist(u) + graph(u, v) < dist(v) 如果节点未访问且存在边u到v,并且通过u到v的距离小于dist(v) dist(v) = dist(u) + graph(u, v); 更新起始节点到v的距离path(v) = u; 记录最短路径中v的前驱节点endendendend```在这段Matlab代码中,我们首先定义了一个函数Dijkstra,输入参数为图graph和起始节点start,输出参数为距离数组dist和路径数组path。
dijkstra算法

1、(求两点之间的最短路程)Dijkstra算法的MATLAB程序dijkstra.m如下:% Dijkstra’s Algorithmfunction [S, D]= dijkstra (i,m,W)% i为最短路径的起始点,m为图顶点数,W为图的带权邻接矩阵% 不构成边的两顶点之间用inf 表示% S的每一列从上到下记录了从始点到终点的最短路径所经顶点的序号% D是一个行向量,记录了S中所示路径的大小dd=[ ];tt=[ ];ss=[ ];ss(1,1)=i; v=1:m; v(i)=[ ];dd=[0;i];% dd的第二行是每次求出的最短路径的终点,第一行是最短路径的值kk=2; [mdd,ndd]=size(dd);while ~isempty(v)[tmpd,j]=min(W(i,v));tmpj=v(j);for k=2:ndd[tmp1,jj]=min(dd(1,k)+W(dd(2,k),v));tmp2=v(jj);tt(k-1,:)=[tmp1,tmp2,jj];endtmp=[tmpd,tmpj,j;tt]; [tmp3,tmp4]=min(tmp(:,1));if tmp3==tmpd,ss(1:2,kk)=[i;tmp(tmp4,2)];else, tmp5=find(ss(:,tmp4)~=0); tmp6=length(tmp5);if dd(2,tmp4)==ss(tmp6,tmp4)ss(1:tmp6+1,kk)=[ss(tmp5,tmp4); tmp(tmp4,2)];else, ss(1:3,kk)=[i; dd(2,tmp4); tmp(tmp4,2)];endenddd=[dd,[tmp3;tmp(tmp4,2)]];v(tmp(tmp4,3))=[ ];[mdd,ndd]=size(dd);kk=kk+1;endS=ss;D=dd(1,: );。
matlab两点间最短路径

matlab两点间最短路径两点间最短路径是指在一个图中,找出连接两个给定节点的最短路径,即路径上的边权重之和最小。
在Matlab中,我们可以使用图论算法来解决这个问题。
本文将介绍如何使用Matlab来计算两点间的最短路径,以及一些应用场景和实例。
我们需要创建一个图对象,并定义节点和边的信息。
在Matlab中,可以使用graph函数来创建一个图对象。
假设我们有一个包含n个节点的图,节点之间的连接关系可以用一个邻接矩阵来表示。
邻接矩阵A的第i行第j列的元素表示节点i和节点j之间的边权重。
如果节点i和节点j之间没有边,则对应的元素为0。
接下来,我们可以使用图对象的shortestpath函数来计算两点间的最短路径。
该函数的输入参数包括图对象、起始节点和目标节点。
函数将返回一个包含最短路径节点索引的数组。
如果不存在连接起始节点和目标节点的路径,则返回空数组。
下面是一个简单的示例,演示如何使用Matlab计算两点间的最短路径:```% 创建一个包含5个节点的图对象G = graph([1 1 2 2 3 4 4 5], [2 3 3 4 5 1 5 3]);% 计算节点1到节点5的最短路径path = shortestpath(G, 1, 5);% 打印最短路径节点索引disp(path);```上述示例中,我们创建了一个包含5个节点的图对象G。
然后,我们使用shortestpath函数计算节点1到节点5的最短路径。
最后,我们将结果打印出来。
除了计算两点间的最短路径,Matlab还提供了其他一些与图相关的函数和工具。
例如,我们可以使用graphallshortestpaths函数来计算图中所有节点对之间的最短路径。
我们还可以使用plot函数将图对象可视化,以便更直观地理解图的结构和节点之间的连接关系。
两点间最短路径在实际应用中有很多用途。
例如,在交通网络中,我们可以使用最短路径算法来计算从一个地点到另一个地点的最短驾驶路径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
效果展示:
开头输入的是点的序列号(表示第几个点),显示的是最短路径的走法(同样以点的序列号显示,表示途径的第几个点)。
%编写m文件
function [distance,path]=dijkstra(A,s,e)
% [DISTANCE,PA TH]=DIJKSTRA(A,S,E)
% returns the distance and path between the start node and the end node.
%
% A: adjcent matrix
% s: start node
% e: end node
% initialize
n=size(A,1); % node number
D=A(s,:); % distance vector
path=[]; % path vector
visit=ones(1,n); % node visibility
visit(s)=0; % source node is unvisible
parent=zeros(1,n); % parent node
% the shortest distance
for i=1:n-1 % BlueSet has n-1 nodes
temp=zeros(1,n);
count=0;
for j=1:n
if visit(j)
temp=[temp(1:count) D(j)];
else
temp=[temp(1:count) inf];
end
count=count+1;
end
[value,index]=min(temp);
j=index; visit(j)=0;
for k=1:n
if D(k)>D(j)+A(j,k)
D(k)=D(j)+A(j,k);
parent(k)=j;
end
end
end
distance=D(e);
% the shortest distance path
if parent(e)==0
return;
end
path=zeros(1,2*n); % path preallocation
t=e; path(1)=t; count=1;
while t~=s && t>0
p=parent(t);
path=[p path(1:count)];
t=p;
count=count+1;
end
if count>=2*n
error(['The path preallocation length is too short.',...
'Please redefine path preallocation parameter.']);
end
path(1)=s;
path=path(1:count);
%算法实现
clc; clear; close all;
%% 载入设置数据
lines = load('Distance.txt'); %点与点之间的距离矩阵
A=lines;
A(find(A>10))=inf; %对步长的限制,根据自己的要求决定!我们在此选择10. % A就是连接矩阵,其中对角线为0,表示本身
% 有连接关系的就对应线的长度
% 没有连接关系的就对应inf
%% 下面的是dijstra算法,有两种方式可以调用
s =input('输入起点'); % 起点(点的序号)
e =input('输入终点'); % 终点(点的序号)
[distance,path0] = dijkstra(A,s,e);
fprintf('\n Use Dijkstra the Min Distance is: %.5f \n', distance);
fprintf('\n Use Dijkstra the Min Distance path is: \n');
disp(path0);
A1 = A;
A1(isinf(A1)) = 0;
[d, p, pred] = graphshortestpath(sparse(A1), s, e);
fprintf('\n Use graphshortestpath the Min Distance is: %.5f \n', d);
fprintf('\n Use graphshortestpath the Min Distance path is: \n');
disp(p);
for i = 1 : length(path0)
if i == length(path0)
temp = [path0(1) path0(i)];
else
temp = [path0(i) path0(i+1)];
end
end。
