工程常用几何体面积体积计算公式

几何体的表面积和体积公式大全

几何体的表面积和体积公式大全几何体的表面积,体积计算公式1、圆柱体:表面积:2πRr+2πRh 体积:πR²h (R为圆柱体上下底圆半径,h为圆柱体高)2、圆锥体:表面积:πR²+πR[(h²+R²)的平方根] 体积:πR²h/3 (r为圆锥体低圆半径,h为其高, 3、正方体a－边长,S＝6a²,V＝a³4、长方体a－长,b－宽,c－高S＝2(ab+ac+bc) V＝abc5、棱柱S－底面积h－高V＝Sh6、棱锥S－底面积h－高V＝Sh/37、棱台S1和S2－上、下底面积h－高V＝h[S1+S2+(S1S2)^1/2]/38、拟柱体S1－上底面积,S2－下底面积,S0－中截面积h－高,V＝h(S1+S2+4S0)/69、圆柱r－底半径,h－高,C—底面周长S底—底面积,S侧—侧面积,S表—表面积C＝2πrS底＝πr²,S侧＝Ch ,S表＝Ch+2S底,V＝S底h＝πr²h10、空心圆柱R－外圆半径,r－内圆半径h－高V＝πh(R^2-r^2)11、直圆锥r－底半径h－高V＝πr^2h/312、圆台r－上底半径,R－下底半径,h－高V＝πh(R²＋Rr＋r²)/313、球r－半径d－直径V＝4/3πr^3＝πd^3/614、球缺h－球缺高,r－球半径,a－球缺底半径V＝πh(3a²+h²)/6 ＝πh²(3r-h)/315、球台r1和r2－球台上、下底半径h－高V＝πh[3(r1²＋r2²)+h²]/616、圆环体R－环体半径D－环体直径r－环体截面半径d－环体截面直径V＝2π2Rr²＝π2Dd²/417、桶状体D－桶腹直径d－桶底直径h－桶高V＝πh(2D²＋d²)/12 ,(母线是圆弧形,圆心是桶的中心)V＝πh(2D²＋Dd＋3d²/4)/15 (母线是抛物线形)。

各种形体面积体积计算公式

各种形体面积体积计算公式
一、立体
1.椎体
椎体的表面积公式为：S=2πrh；椎体的体积公式为：V=1/3πr^2h，其中r为椎体半径，h为椎体的高。

2.圆柱体
圆柱体的表面积公式为：S=2πrh+2πr2；圆柱体的体积公式为：
V=πr²h，其中r为圆柱体底面的半径，h为圆柱体的高。

3.球体
球体的表面积公式为：S=4πr²；球体的体积公式为：V=4/3πr³，其中r为球体的半径。

4.圆锥体
圆锥体的表面积公式为：S=πrl+πrs；圆锥体的体积公式为：
V=1/3πr²h，其中r为圆锥体的底面半径，l为圆锥体的底面周长，h为圆锥体的高。

5.正方体
正方体的表面积公式为：S=6a²；正方体的体积公式为：V=a³，其中a为正方体的边长。

6.平行四边体
平行四边体的表面积公式为：S=2a²+2b²；平行四边体的体积公式为：V=a²b，其中a为平行四边体的底面的长度，b为平行四边体的底面的宽度。

二、平面
1.三角形
三角形的面积公式为：S=1/2absinC，其中a、b为三角形的两边，C
为三角形的夹角（以弧度为单位）。

2.矩形
矩形的面积公式为：S=ab，其中a为矩形的长，b为矩形的宽。

3.正方形
正方形的面积公式为：S=a²，其中a为正方形的边长。

4.圆
圆的面积公式为：S=πr²，其中r为圆的半径。

常见几何体的表面积体积公式

常见几何体的表面积体积公式1、长方体V：体积s：面积a：长b：宽h：高(1)表面积(长×宽+长×高+宽×高)×2 {S=2(ab+ah+bh)(2)体积=长×宽×高（V=abh）2、圆柱体v：体积h：高s;底面积r：底面半径c：底面周长(1)侧面积=底面周长×高(2)表面积=侧面积+底面积×2(3)体积=底面积×高（4）体积＝侧面积÷2×半径3、圆锥体v：体积h：高s;底面积r：底面半径体积=底面积×高÷34、正方体V：体积s：面积a：边长体积：边长×边长×边长扩展资料周长：1、正方形C周长S面积a边长周长＝边长×4（C=4a）面积=边长×边长（S=a×a）2、长方形C周长S面积a边长周长=(长+宽)×2（C=2(a+b)）面积=长×宽（S=ab）3、三角形s面积a底h高面积=底×高÷2（s=ah÷2）三角形高=面积×2÷底三角形底=面积×2÷高4、平行四边形s面积a底h高面积=底×高（s=ah）5、梯形s面积a上底b下底h高面积=(上底+下底)×高÷2（s=(a+b)×h÷2）6、圆形S面积C周长πd=直径r=半径(1)周长=直径×π=2×π×半径（C=πd=2πr）(2)面积=半径×半径×π。

工程常用面积体积计算公式

工程常用面积体积计算公式工程中常用的面积和体积计算公式非常多，涉及到各种建筑、土木、机械、电力等不同领域的工程。

以下是一些常见的面积和体积计算公式的示例：1.平面图形的面积计算公式：-长方形的面积公式：面积=长×宽-正方形的面积公式：面积=边长×边长-圆的面积公式：面积=π×半径×半径-椭圆的面积公式：面积=π×长轴半径×短轴半径-三角形的面积公式：面积=底边长×高/22.三维几何体的体积计算公式：-立方体的体积公式：体积=边长×边长×边长-直方体的体积公式：体积=长×宽×高-圆柱体的体积公式：体积=圆的面积×高-圆锥体的体积公式：体积=圆锥的底面积×高/3-球体的体积公式：体积=4/3×π×半径×半径×半径3.土木工程中的体积计算公式：-坝体体积计算公式：体积=坝顶长度×每个梯段高度之和-挡土墙体积计算公式：体积=墙底长度×每个梯段高度之和-坡道体积计算公式：体积=坡度×坡道宽度×坡道长度-水库库容计算公式：体积=水库底面积×水位高度4.电力工程中的体积计算公式：-电容器体积计算公式：体积=电容量/电容器电压-变压器体积计算公式：体积=功率/变压器容量密度5.机械工程中的体积计算公式：-内燃机汽缸体积计算公式：体积=π×活塞直径×活塞行程×气缸数量这只是一些常见的面积和体积计算公式示例，实际应用中还有许多其他的公式，根据具体工程的需求会有所不同。

在工程实践中，我们还需要考虑到各种误差和修正因素，以及特殊形状和复杂结构的计算方法。

因此，在实际应用中，需要根据具体情况进行计算并选择合适的公式。

空间几何体表面积和体积公式

空间几何体表面积和体积公式
空间几何体表面积和体积公式如下:
表面积公式:
S = 2 × (a + b + c)
其中,a、b、c分别表示几何体的长、宽、高。

体积公式:
V = a × b × c
其中,a、b、c分别表示几何体的长、宽、高。

还有一些常用的表面积和体积公式:
1. 如果一个几何体只有一个面是正方形或正多边形,那么它的
表面积和体积都可以用一个简单的公式计算:S = 4a,V = a × b。

2. 如果一个几何体的边长为c,那么它的表面积可以表示为:S = 2 × (c + d),其中d表示几何体的长宽比。

体积可以表示为:V = c ×d。

3. 如果一个几何体是正多边形,且每个内角都相等,那么它的表
面积和体积都可以用一个复杂的公式计算:S = (n-2) × 4a,V = (n-2) × a × b。

其中n表示正多边形的边数。

4. 如果一个几何体只有一个面是矩形或圆形,那么它的表面积
和体积都可以用一个简单的公式计算:S = a + b + c,V = π× r ×(a + b + c)。

其中π是圆周率,r表示几何体的半径。

这些公式只是一些基本的几何公式,实际上还有很多更复杂的公
式可以用于计算几何体的性质。

了解这些基本的公式有助于我们更方
便地计算几何体的面积和体积。

体积公式大全-互联网类

体积公式大全－互联网类一、关键信息1、常见几何体体积公式11 长方体体积公式：长×宽×高12 正方体体积公式：棱长×棱长×棱长13 圆柱体体积公式：底面积×高（π×半径²×高）14 圆锥体体积公式：1/3×底面积×高（1/3×π×半径²×高）15 球体体积公式：4/3×π×半径³2、体积单位换算公式21 1 立方米＝ 1000 立方分米22 1 立方分米＝ 1000 立方厘米23 1 立方厘米＝ 1000 立方毫米3、体积计算的应用领域31 建筑工程32 制造业33 物理学34 数学教育二、体积公式详细说明1、长方体体积公式长方体体积的计算基于其长度、宽度和高度。

公式为 V ＝ l × w × h，其中 V 表示体积，l 表示长度，w 表示宽度，h 表示高度。

例如，一个长方体的长为 5 厘米，宽为 3 厘米，高为 2 厘米，其体积为 5 × 3 × 2＝ 30 立方厘米。

11 长方体体积公式的推导长方体可以看作是由无数个相同的小立方体堆积而成。

每个小立方体的体积为 1 立方单位，长方体所含小立方体的数量即为其体积。

通过计算长、宽、高方向上小立方体的个数，相乘即可得到总体积。

12 长方体体积公式的应用场景长方体在日常生活中非常常见，如房屋的房间、冰箱的内部空间、书本的形状等。

在建筑设计、物流包装等领域，准确计算长方体的体积对于空间规划和材料用量的估算至关重要。

2、正方体体积公式正方体是一种特殊的长方体，其所有棱长相等。

体积公式为 V ＝ a³，其中 a 表示棱长。

例如，一个正方体的棱长为 4 厘米，其体积为 4³＝64 立方厘米。

21 正方体体积公式的推导与长方体类似，正方体也可以看作是由小立方体堆积而成，由于其棱长相等，所以体积为棱长的立方。

土方计算公式

1，建筑土方开挖工程量计算公式：圆柱体：体积=底面积×高长方体：体积=长×宽×高正方体：体积＝棱长×棱长×棱长．锥体: 底面面积×高÷3台体: V=[ S上+√(S上S下)+S下]h÷3球缺体积公式＝πh²(3R-h)÷3球体积公式：V＝4πR³/3棱柱体积公式：V＝S底面×h＝S直截面×l （l为侧棱长,h为高)棱台体积：V=〔S1＋S2＋开根号（S1*S2）〕／3*h注：V：体积；S1：上表面积；S2：下表面积；h：高。

------几何体的表面积计算公式圆柱体:表面积:2πRr+2πRh 体积:πRRh (R为圆柱体上下底圆半径,h为圆柱体高) 圆锥体:表面积:πRR+πR[(hh+RR)的平方根] 体积: πRRh/3 (r为圆锥体低圆半径,h为其高, 平面图形名称符号周长C和面积S正方形a—边长C＝4a S＝a2 长方形a和b－边长C＝2(a+b) S＝ab 三角形a,b,c－三边长h－a边上的高s－周长的一半A,B,C－内角其中s＝(a+b+c)/2 S＝ah/2＝ab/2•sinC ＝[s(s-a)(s-b)(s-c)]1/2＝a2sinBsinC/(2sinA) 四边形d,D－对角线长α－对角线夹角S＝dD/2•sinα 平行四边形a,b－边长h－a边的高α－两边夹角S ＝ah＝absinα 菱形a－边长α－夹角D－长对角线长d－短对角线长S＝Dd/2＝a2sinα 梯形a和b－上、下底长h－高m－中位线长S＝(a+b)h/2＝mh 圆r－半径d－直径C＝πd＝2πr S＝πr2＝πd2/4 扇形r—扇形半径a—圆心角度数C＝2r＋2πr×(a/360) S＝πr2×(a/360) 弓形l－弧长S＝r2/2•(πα/180-sinα)b－弦长＝r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2h－矢高＝παr2/360 - b/2•[r2-(b/2)2]1/2r－半径＝r(l-b)/2 + bh/2α－圆心角的度数≈2bh/3 圆环R－外圆半径S＝π(R2-r2)r－内圆半径＝π(D2-d2)/4D－外圆直径d－内圆直径椭圆D－长轴S＝πDd/4d－短轴2，建筑工程量计算公式：计算挖土方的体积：土方体积＝挖土方的底面积*挖土深度。

常用形体体积面积计算公式大全

常用形体体积面积计算公式大全以下是常用的形体体积和面积计算公式：
1.立方体：
-体积公式：V=s^3(s为立方体的边长)
-表面积公式：A=6s^2
2.球体：
-体积公式：V=(4/3)πr^3(r为球的半径)
-表面积公式：A=4πr^2
3.圆柱体：
-体积公式：V=πr^2h(r为圆柱的底面半径，h为高)
-表面积公式：A=2πr(r+h)+2πr^2
4.圆锥体：
-体积公式：V=(1/3)πr^2h(r为圆锥的底面半径，h为高) -表面积公式：A=πr(r+√(r^2+h^2))
5.圆环：（两个同心圆之间的区域）
-面积公式：A=π(R^2-r^2)(R为大圆半径，r为小圆半径)
6.正方形：（四边相等，每个角为直角的四边形）
-面积公式：A=a^2(a为边长)
7.长方形：（四边都不相等，每个角为直角的四边形）
-面积公式：A=l×w(l为长，w为宽)
8.三角形：
- 面积公式：A = (1/2)bh (b为底边长，h为高)
9.梯形：（有两个平行的底边）
-面积公式：A=(1/2)(a+b)h(a和b为两个底边的长度，h为高)
10.五边形：
- 面积公式：A = (1/4)sqrt(5(5+2sqrt(5)))a^2 (a为边长)
11.六边形：
-面积公式：A=(3√3)/2a^2(a为边长)
12.椭圆：
- 面积公式：A = πab (a为长轴的一半，b为短轴的一半)
这些是常见的形体体积和面积计算公式，可以帮助你快速计算各种形状的物体的体积和面积。

几何体的表面积和体积公式

几何体的表面积和体积公式一、柱体。

1. 棱柱。

- 表面积公式：- 直棱柱的表面积S = 2S_底+S_侧，其中S_底为底面多边形的面积，S_侧为侧面积。

若直棱柱底面多边形的边长为a，边数为n，棱柱的高为h，则S_侧=nah。

- 体积公式：V = S_底h，h为棱柱的高。

2. 圆柱。

- 表面积公式：S = 2π r^2+2π rh，其中r为底面半径，h为圆柱的高。

- 体积公式：V=π r^2h。

二、锥体。

1. 棱锥。

- 表面积公式：S = S_底+S_侧，棱锥的侧面积S_侧等于各个侧面三角形面积之和。

若棱锥底面多边形的边长为a，边数为n，斜高（侧面三角形底边上的高）为h'，则S_侧=(1)/(2)nah'。

- 体积公式：V=(1)/(3)S_底h，h为棱锥的高。

2. 圆锥。

- 表面积公式：S=π r^2+π rl，其中r为底面半径，l为母线长。

- 体积公式：V = (1)/(3)π r^2h，h为圆锥的高。

三、台体。

1. 棱台。

- 表面积公式：S = S_上底+S_下底+S_侧，棱台的侧面积S_侧=(1)/(2)(n(a + b)h')，其中n为底面边数，a为上底面多边形的边长，b为下底面多边形的边长，h'为斜高。

- 体积公式：V=(1)/(3)h(S_上底+S_下底+√(S_上底)S_{下底})，h为棱台的高。

2. 圆台。

- 表面积公式：S=π r^2+π R^2+π l(R + r)，其中r为上底面半径，R为下底面半径，l为母线长。

- 体积公式：V=(1)/(3)π h(r^2+R^2+rR)，h为圆台的高。

四、球体。

- 表面积公式：S = 4π R^2，其中R为球的半径。

- 体积公式：V=(4)/(3)π R^3。

各形状物体体积计算公式

常用体积及表面积计算公式一些数学的体积和表面积计算公式3 立方图形名称符号面积S和体积V正方体 a－边长 S＝6a2 V＝a3长方体 a－长 b－宽 c－高 S＝2(ab+ac+bc)V＝abc棱柱 S－底面积 h－高 V＝Sh棱锥 S－底面积 h－高 V＝Sh/3棱台 S1和S2－上、下底面积h－高 V＝h[S1+S2+(S1S2)1/2]/3正棱台拟柱体 S1－上底面积 S2－下底面积 S0－中截面积 h－高V＝h(S1+S2+4S0)/6圆柱 r－底半径 h－高 C—底面周长S底—底面积 S侧—侧面积S表—表面积C＝2πrS底＝πr2 S侧＝Ch S表＝Ch+2S底V＝S底h＝πr2h空心圆柱 R－外圆半径 r－内圆半径h－高V＝πh(R2-r2)直圆锥 r－底半径 h－高V＝πr2h/3圆台 r－上底半径 R－下底半径 h－高V＝πh(R2＋Rr＋r2)/3球 r－半径 d－直径V＝4/3πr3＝πd2/6球缺 h－球缺高 r－球半径 a－球缺底半径V＝πh(3a2+h2)/6 ＝πh2(3r-h)/3 a2＝h(2r-h)球台 r1和r2－球台上、下底半径 h－高V＝πh[3(r12＋r22)+h2]/6圆环体 R－环体半径 D－环体直径 r －环体截面半径 d－环体截面直径V＝2π2Rr2＝π2Dd2/4桶状体 D－桶腹直径 d－桶底直径 h －桶高V＝πh(2D2＋d2)/12 (母线是圆弧形,圆心是桶的中心)V＝πh(2D2＋Dd＋3d2/4)/15 (母线是抛物、、长方形的周长=（长+宽）×2正方形的周长=边长×4长方形的面积=长×宽正方形的面积=边长×边长三角形的面积=底×高÷2平行四边形的面积=底×高梯形的面积=（上底+下底）×高÷2 直径=半径×2 半径=直径÷2圆周率×半径×2圆的面积=圆周率×半径×半径长方体的表面积=（长×宽+长×高＋宽×高）×2长方体的体积=长×宽×高正方体的表面积=棱长×棱长×6正方体的体积=棱长×棱长×棱长圆柱的侧面积=底面圆的周长×高圆柱的表面积=上下底面面积+侧面积圆柱的体积=底面积×高圆锥的体积=底面积×高÷3长方体（正方体、圆柱体）的体积=底面积×高平面图形名称符号周长C和面积S正方形a—边长C＝4aS＝a2长方形a和b－边长C＝2(a+b)S＝ab三角形a,b,c－三边长h－a边上的高s－周长的一半A,B,C－内角其中s＝(a+b+c)/2 S＝ah/2＝ab/2·sinC＝[s(s-a)(s-b)(s-c)]1/2＝a2sinBsinC/(2sinA)四边形d,D－对角线长α－对角线夹角S＝dD/2·sinα平行四边形a,b－边长h－a边的高α－两边夹角S＝ah＝absinα菱形a－边长α－夹角D－长对角线长d－短对角线长S＝Dd/2＝a2sinα梯形a和b－上、下底长h－高m－中位线长S＝(a+b)h/2＝mh圆r－半径d－直径C＝πd＝2πr扇形r—扇形半径a—圆心角度数C＝2r＋2πr×(a/360)S＝πr2×(a/360)弓形l－弧长b－弦长h－矢高r－半径α－圆心角的度数S＝r2/2·(πα/180-sinα) ＝r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2＝παr2/360 - b/2·[r2-(b/2)2]1/2＝r(l-b)/2 + bh/2≈2bh/3圆环R－外圆半径r－内圆半径D－外圆直径d－内圆直径S＝π(R2-r2)＝π(D2-d2)/4椭圆D－长轴d－短轴S＝πDd/4立方图形名称符号面积S和体积V正方体a－边长S＝6a2V＝a3长方体a－长b－宽c－高S＝2(ab+ac+bc)V＝abc棱柱S－底面积h－高V＝Sh棱锥S－底面积h－高V＝Sh/3棱台S1和S2－上、下底面积h－高V＝h[S1+S2+(S1S1)1/2]/3拟柱体S1－上底面积S2－下底面积S0－中截面积h－高V＝h(S1+S2+4S0)/6圆柱r－底半径h－高C—底面周长S底—底面积S侧—侧面积S表—表面积C＝2πrS表＝Ch+2S底V＝S底h＝πr2h空心圆柱R－外圆半径r－内圆半径h－高V＝πh(R2-r2)直圆锥r－底半径h－高V＝πr2h/3圆台r－上底半径R－下底半径h－高V＝πh(R2＋Rr＋r2)/3球r－半径d－直径V＝4/3πr3＝πd2/6球缺h－球缺高r－球半径a－球缺底半径V＝πh(3a2+h2)/6＝πh2(3r-h)/3a2＝h(2r-h)球台r1和r2－球台上、下底半径h－高V＝πh[3(r12＋r22)+h2]/6圆环体R－环体半径D－环体直径r－环体截面半径d－环体截面直径V＝2π2Rr2＝π2Dd2/4桶状体D－桶腹直径d－桶底直径h－桶高V＝πh(2D2＋d2)/12(母线是圆弧形,圆心是桶的中心)V＝πh(2D2＋Dd＋3d2/4)/15(母线是抛物线形)棱台体体积计算公式：V=（1/3）H（S上＋S下＋√[S上×S下]）H是高，S上和S下分别是上下底面的面积。

几何体体积计算公式

几何体体积计算公式圆柱体的体积公式：体积=底面积×高，如果用h代表圆柱体的高，则圆柱＝S底×h长方体的体积公式：体积=长×宽×高如果用a、b、c分别表示长方体的长、宽、高则长方体体积公式为：V长=abc正方体的体积公式：体积＝棱长×棱长×棱长．如果用a表示正方体的棱长，则正方体的体积公式为V正＝a·a·a＝a³锥体的体积=底面面积×高÷3 V 圆锥＝S底×h÷3台体体积公式:V=[ S上+√(S上S下)+S下]h÷3圆台体积公式:V=(R²+Rr+r²)hπ÷3球缺体积公式＝πh²(3R-h)÷3球体积公式：V＝4πR³/3棱柱体积公式：V＝S底面×h＝S直截面×l （l为侧棱长,h为高)棱台体积：V=〔S1＋S2＋开根号（S1*S2）〕／3*h注：V：体积；S1：上表面积；S2：下表面积；h：高。

几何体的表面积计算公式圆柱体:表面积:2πRr+2πRh 体积:πRRh (R为圆柱体上下底圆半径,h为圆柱体高) 圆锥体:表面积:πRR+πR[(hh+RR)的平方根] 体积: πR Rh/3 (r为圆锥体低圆半径,h为其高, 平面图形名称符号周长C和面积S正方形a—边长C＝4a S＝a2 长方形a和b－边长C＝2(a+b) S＝ab 三角形a,b,c－三边长h－a边上的高s－周长的一半A,B,C－内角其中s＝(a+b+c)/2 S＝ah/2＝ab/2·sinC ＝[s(s-a)(s-b)(s-c)]1/2＝a2sinBsinC/(2sinA) 四边形d,D－对角线长α－对角线夹角S＝dD/2·sinα 平行四边形a,b－边长h－a边的高α－两边夹角S＝ah＝absinα 菱形a－边长α－夹角D－长对角线长d－短对角线长S＝Dd/2＝a2sinα 梯形a和b－上、下底长h－高m－中位线长S＝(a+b)h/2＝mh 圆r－半径d－直径C＝πd＝2πr S＝πr2＝πd2/4 扇形r—扇形半径a—圆心角度数C＝2r＋2πr×(a/360) S＝πr2×(a/360) 弓形l－弧长S＝r2/2·(πα/180-sinα)b－弦长＝r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2h－矢高＝παr2/360 - b/2·[r2-(b/2)2]1/2r－半径＝r(l-b)/2 + bh/2α－圆心角的度数≈2bh/3 圆环R－外圆半径S＝π(R2-r2)r－内圆半径＝π(D2-d2)/4D－外圆直径d－内圆直径椭圆D－长轴S＝πDd/4d－短轴（一）面积1、正方形S= a2(a为正方形边长)2、长方形S= a × b 长方形(a、b分别为长、宽)3、三角形S= b × h÷2 角形（b、h分别为底边长和高）4、梯形S=（a+b）× h÷2（a、b、h分别为上底长、下底长和高）形5、圆形S=3.14×d 2 ÷ 4（d为直径）（二）圆周长与直径的关系L=3.14 ×d c 长方体（三）体积1、长方体V=a × b × c(a、b、c分别为长、宽、高)2、圆柱体V= S×h（S、h 分别为底面积和高）3、圆锥体V=S × h ÷ 3（S、h 分别为底面积和高）圆柱体4、长方截锥体V=（S1+S2+ S1×S2 ）× h ÷ 3(S1、S2和h分别为上下底面积和高)5、圆台体V=（d12 + d1×d2 + d22）÷ 12 × h ×3 .14(d1、d2和h分别为上下底直径和高) 长方截锥体圆台体。

体积和表面积的概念和计算

体积和表面积的概念和计算体积和表面积是数学中涉及到的两个重要概念，它们在几何学、物理学以及工程领域中都有着广泛的应用。

本文将介绍体积和表面积的定义以及它们的计算方法，帮助读者更好地理解和运用这两个概念。

一、体积的概念和计算体积是指物体所占据的空间大小，通常用单位立方米（m³）或立方厘米（cm³）来表示。

对于一些简单的几何体，可以通过基本的公式来计算其体积。

1. 立方体的体积计算公式：立方体是边长相等的正方体，其体积计算公式为边长的三次方。

假设立方体的边长为a，则其体积V可以通过公式V=a³来计算。

2. 直方体的体积计算公式：直方体与立方体类似，但其三个边长不一定相等。

对于直方体，可以通过长度、宽度和高度的乘积来计算。

假设直方体的长度为L，宽度为W，高度为H，则其体积V可以通过公式V=L×W×H来计算。

3. 圆柱体的体积计算公式：圆柱体是一个由底面圆和柱体侧面构成的几何体。

对于圆柱体，可以通过底面圆的面积和高度来计算其体积。

假设底面圆的半径为r，高度为h，则其体积V可以通过公式V=πr²h来计算，其中π约等于3.14159。

4. 其他几何体的体积计算：对于其他更为复杂的几何体，计算其体积可能需要使用不同的公式或方法，例如球体、棱锥等。

这些公式可以在相关的数学书籍或在线资源中找到。

在实际应用中，也可以利用测量方法来获取几何体的体积。

二、表面积的概念和计算表面积是指几何体外部所占据的空间大小，在物理学和工程领域中常用于表示物体的包裹面积或接触面积。

不同的几何体有不同的计算方法来求解其表面积。

1. 立方体的表面积计算公式：立方体的六个面都是正方形，且边长相等。

因此，计算立方体的表面积，只需将一个正方形的面积乘以6即可。

假设立方体的边长为a，则其表面积S可以通过公式S=6a²来计算。

2. 直方体的表面积计算公式：直方体的表面积计算方法与立方体类似，只是需要考虑到不同的长方形面的尺寸。

常用形体体积面积计算公式大全

常用形体体积面积计算公式大全形体的体积和面积是几何学中重要的概念，常用于计算物体的大小和空间占用。

本文将介绍一些常用的形体体积和面积计算公式，包括立方体、长方体、球体、圆柱体、圆锥体等常见的几何形体。

1.立方体：立方体是一种具有六个相等的正方形面的形体，它的体积和表面积可以通过以下公式计算：-体积公式：V=a^3，其中a表示立方体的边长。

-表面积公式：A=6a^22.长方体：长方体是一种具有六个面的形体，每个面都是矩形，它的体积和表面积可以通过以下公式计算：- 体积公式：V = lwh，其中l表示长方体的长度，w表示宽度，h表示高度。

- 表面积公式：A = 2lw + 2lh + 2wh3.球体：球体是一种具有球面的形体，它的体积和表面积可以通过以下公式计算：-体积公式：V=(4/3)πr^3，其中r表示球体的半径。

-表面积公式：A=4πr^24.圆柱体：圆柱体是一种具有两个平行圆底和侧面的形体，它的体积和表面积可以通过以下公式计算：-体积公式：V=πr^2h，其中r表示圆柱体的底面半径，h表示圆柱体的高度。

- 表面积公式：A = 2πrh + 2πr^25.圆锥体：圆锥体是一种具有一个圆锥形底面和一个顶点的形体，它的体积和表面积可以通过以下公式计算：-体积公式：V=(1/3)πr^2h，其中r表示圆锥体的底面半径，h表示圆锥体的高度。

-表面积公式：A=πr(r+√(r^2+h^2))6.整体公式：对于一些复合的形体或不规则的形体，可以使用下列常用的整体公式进行体积和表面积的计算：-立方体和长方体的合并体积公式：V=V1+V2，其中V1和V2分别为两个立方体或长方体的体积。

-球体的切割体积公式：V=V1-V2，其中V1为球体的体积，V2为切割球体的体积。

-面积的整体公式：A=A1+A2+...+An，其中A1，A2，...，An分别为各个面的面积。

这些公式是几何学中常用的形体体积和面积计算公式，可以帮助我们计算各种形体的大小和空间占用。

几何体面积体积计算公式大全

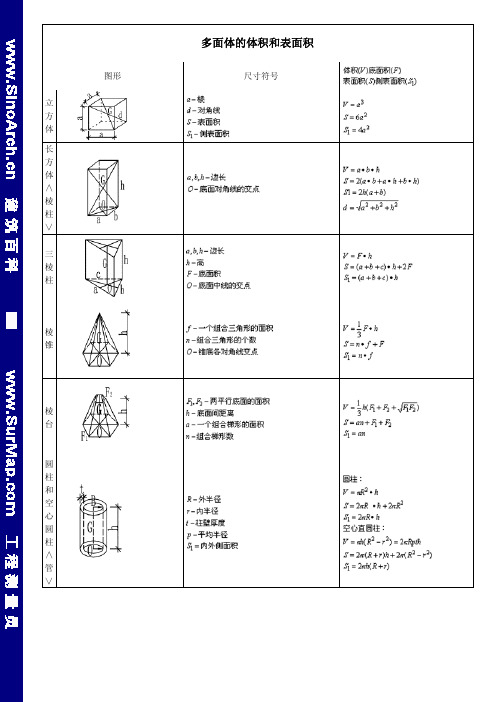
几何体面积体积计算公式大全几何体体积公式立体几何体积公式几何体面积公式几何体表面积公式几何体的表面积和体积几何体公式圆面积的计算公式面积计算公式扇形面积的计算公式
图形
立方体长方体 ∧ 棱柱 ∨
三棱柱
棱锥
棱台
圆柱和空心圆柱 ∧ 管 ∨
多面体的体积和表面积
尺寸符号
斜线直圆柱
直圆锥
圆台
球
球扇形 ∧ 球楔 ∨
球缺
圆环体 ∧ 胎 ∨
球带体
桶形
椭
球
a,b,c-半轴
体
交叉圆柱体
梯形体
正方形
长方形
三角形式
尺寸符号
面积（F）表面积（S）
任意四边
形
正多边形
菱形
梯形
圆形
椭圆形
扇形
弓形
a·b-主轴
F= (π/4) a·b
圆环
部分圆环
新月形
L d/10 P 0.40 抛物线形
等多边形
2d/10 3d/10 4d/10 0.79 1.18 1.56
5d/10 6d/10 7d/10 1.91 2.25 2.55

几何体面积体积计算公式大全

圆环
部分圆环
新月形
L d/10 P 0.40 抛物线形
等多边形
2d/10 3d/10 4d/10 0.79 1.18 1.56
5d/10 6d/10 7d/10 1.91 2.25 2.55
几何体面积体积计算公式大全几何体公式体积计算公式面积计算公式圆面积的计算公式棱台体积计算公式扇形面积的计算公式椎体体积计算公式圆面积计算公式扇形面积计算公式
图形
立方体长方体 ∧ 棱柱 ∨
三棱柱
棱锥
棱台
圆柱和空心圆柱 ∧ 管 ∨
多面体的体积和表面积
锥
圆台
球
球扇形 ∧ 球楔 ∨
球缺
圆环体 ∧ 胎 ∨
球带体
桶形
椭
球
a,b,c-半轴
体
交叉圆柱体
梯形体
正方形
长方形
三角形
平行四边
形
图形
常用图形求面积公式
尺寸符号
面积（F）表面积（S）
任意四边
形
正多边形
菱形
梯形
圆形
椭圆形
扇形
弓形
a·b-主轴
F= (π/4) a·b

几何体体积计算公式

几何体体积计算公式圆柱体的体积公式：体积=底面积X高，如果用h代表圆柱体的高，则圆柱=$底如长方体的体积公式：体积=长乂宽乂高如果用a、b、c分别表示长方体的长、宽、高则长方体体积公式为：V长=abc正方体的体积公式：体积=棱长X棱长X棱长.如果用a表示正方体的棱长，则正方体的体积公式为V ^=a-a-a=a3锥体的体积=底面面积X高!3 V圆锥=$底xh-3台体体积公式：V=[ S上+WS上S下)+S下]h：3圆台体积公式:V=(R2+Rr+r2)hn-3球缺体积公式=nh2(3R-h)-3球体积公式：V=4nR3/3棱柱体积公式：V=S底面xh = S直截面xl (I为侧棱长,h为高)棱台体积：V=〔S1+S2+开根号(S1*S2)〕/3*h注：V：体积；S1 ：上表面积；S2：下表面积；h：高。

几何体的表面积计算公式圆柱体:表面积:2nRr+2nRh体积:nRRh (R为圆柱体上下底圆半径,h为圆柱体高)圆锥体：表面积:nRR+nR[(hh+RR)的平方根]体积:nR Rh/3 (r为圆锥体低圆半径,h为其高，平面图形名称符号周长C和面积S正方形a—边长C=4a S=a2长方形a和b一边长C=2(a+b) S=ab三角形a,b,c一三边长h—a边上的高s一周长的一半A,B,C 一内角其中s=(a+b+c)/2 S=ah/2=ab/2-sinC =[s(s-a)(s-b)(s-c)]1/2=a2sinBsinC/(2sinA)四边形d,D—对角线长a一对角线夹角S=dD/2・sina平行四边形a,b一边长h—a边的高a一两边夹角S=ah=absina菱形a-边长。

一夹角D-长对角线长d-短对角线长S=Dd/2= a2sina梯形a 和b・上、下底长h・高m・中位线长S=(a+b)h/2=mh圆「一半径d—直径C=nd=2nrS=nr2=nd2/4扇形r—扇形半径a—圆心角度数C=2r+2nrx(a/360) S=nr2x(a/360)弓形I一弧长S = r2/2・(na/180-sina)b・弦长=r2arccos[(r-h)/r] - (r-h)(2rh-h2)1/2h・矢高 =nar2/360 - b/2・[r2-(b/2)2]1/2「一半径 =r(I-b)/2 + bh/2。

工程常用面积体积计算公式

工程常用面积体积计算公式在工程中，常常需要计算面积和体积，以确定材料的用量、空间的大小等。

以下是一些常用的面积和体积计算公式：一、平面图形的面积计算：1.矩形的面积（或正方形的面积）：面积=长×宽2.三角形的面积：面积=（底边长×高）/23.梯形的面积：面积=（上底长+下底长）×高/24.平行四边形的面积：面积=底边长×高5.圆的面积：面积=π×半径的平方（其中π可以取3.14或22/7）6.扇形的面积：面积=π×半径的平方×（度数/360）（度数为扇形的角度）二、立体图形的体积计算：1.立方体的体积：体积=长×宽×高2.正方体的体积：体积=边长的立方3.圆柱的体积：体积=π×半径的平方×高（其中π可以取3.14或22/7）4.锥体的体积：体积=（底面积×高）/35.球体的体积：体积=（4/3）×π×半径的立方6.角锥的体积：体积=（底面积×高）/3（其中，不规则三角形的底面积计算方式同三角形面积的公式）三、其他常用的面积和体积计算公式：1.圆环的面积：面积=π×（外半径的平方-内半径的平方）2.圆台的体积：体积=（底面积+顶面积+侧面积）/33. 正多边形的面积：面积 = （n × 边长× 边长）/ （4 × tan （π / n））（其中 n 为边的数量）4.棱柱的体积：体积=底面积×高这些公式是工程中常用的面积和体积计算公式，通过灵活运用这些公式，可以有效地计算出所需的面积和体积值，从而进行工程设计和规划。

同时，在实际应用中，还需要注意单位的转换和准确性，以及考虑到材料的浪费和排除不规则因素对计算结果的影响。