球的体积和表面积公式具体推导过程
球的表面积公式的四种推导方法

球的表面积公式的四种推导方法1. 推导方法一:通过球的体积公式推导表面积公式我们知道球的体积公式为 V = 4/3 * π * r^3(其中 V 表示体积,r 表示球的半径)。
若将球的体积公式对 r 进行求导,得到 dV/dr = 4/3 * π * 3 * r^2 = 4πr^2。
则球的表面积 S = dV/dr * dr = 4πr^2 * dr。
所以,球的表面积公式为 S = 4πr^2。
2. 推导方法二:通过球的面积元素推导表面积公式假设球上存在一个面积元素 dS,该面积元素可以近似看做一个平行于球心的正切平面圆形。
则该面积元素的面积可以表示为 dS = 2πr * dr(其中 dr 表示该元素在球半径方向上的微小长度)。
将所有的面积元素叠加起来,即可得到球的表面积S。
因此,S = ∫(0到R) 2πr * dr,其中 R 表示球的半径。
通过对上式积分,可得球的表面积公式为 S = 4πr^2。
3. 推导方法三:通过球的经纬度线推导表面积公式将球看做由无数个圆形经线和纬线组成的网格,每个经线的长度为 2πr,而每个纬线的长度则随着纬度的变化而变化。
设每个纬线的长度为 L(θ),其中θ表示纬度角,则球的表面积可以近似表示为 S ≈∫(0到π) L(θ) * 2πr * dθ。
由于每个纬线的长度为 L(θ) ≈ 2πr * sinθ,带入上式,我们得到 S ≈∫(0到π) 2πr * sinθ * 2πr * dθ。
通过对上式积分,可得球的表面积公式为 S = 4πr^2。
4. 推导方法四:通过球的半径切割推导表面积公式将球以半径 r 为切割点分为无数个无穷小带状面元,每个面元的宽度为 dθ,并且在纬度上有微小的长度 ds。
则球的表面积可以近似表示为 S ≈∫(0到2π) ∫(0到r) ds dθ。
由于每个面元的长度可以表示为 ds = r * dθ,带入上式,我们得到 S ≈∫(0到2π) ∫(0到r) r * dθ * dθ。
球的体积和表面积公式具体推导过程

1..3.2球的体积和表面积(1)设球的半径为R ,将半径OAn 等分,过这些分点作平面把半球切割成n 层,每一层都是近似于圆柱形状的“小圆片”,这些“小圆片”的体积之和就是半球的体积。
由于“小圆片”近似于圆柱形状,所以它的体积也近似于圆柱的体积.它的高就是“小圆片”的厚度n R ,底面就是“小圆片”的下底面。
由勾股定理可得第i 层(由下向上数)“小圆片”的下底面半径: 22)]1([--=i n R R r i ,(i =1,2,3,···,n )第i 层“小圆片”的体积为:V ≈π2i r ·n R =⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--2311n i n R π,(i =1,2,3,···,n ) 半球的体积:V 半径=V 1+V 2+···+Vn ≈n R 3π{1+(1-221n )+(1-222n )+···+[1-22)1(n n -]} =n R 3π[n -2222)1(21n n -+•••++](注:)12)(1(6121222++=+•••++n n n n ) =n R 3π[n -6)12()1(12--•n n n n =236)12)(1(1(n n n R ---π)=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---6)12)(11(13n n R π ①当所分的层数不断增加,也就是说,当n 不断变大时,①式越来越接近于半球的体积,如果n 无限变大,就能由①式推出半径的体积。
事实上,n 增大,n 1就越来越小,当n 无限大时,n 1趋向于0,这时,有 V 半径=332R π,所以,半径为R 的球的体积为: V =334R π1.。
3。
2球的体积和表面积(2)球的表面积推导方法(设球的半径为R ,利用球的体积公式推导类似方法)(1)分割。
把球O 的表面分成n 个“小球面片”,设它们的表面积分别是S 1,S 2,……Sn ,那么球的表面积为:S =S 1+S 2+……+Sn把球心O 和每一个“小球面片”的顶点连接起来,整个球体被分成n 个以“小球 面片”为底,球心为顶点的“小锥体”.例如,球心与第i 个“小球面片”顶点相连后就得到一个以点O 为顶点,以第i 个“小球面片”为底面的“小锥体"。
球体的表面积和体积计算

球体的表面积和体积计算球体是一种简单而常见的几何图形,它具有很多独特的性质和特点。
在数学和物理学中,计算球体的表面积和体积是一个基本而重要的问题。
在本文中,我们将介绍如何准确计算球体的表面积和体积。
一、球体的表面积计算公式要计算球体的表面积,我们可以使用以下公式:S = 4πr²其中,S表示球体的表面积,π是圆周率(约为3.14159),r是球体的半径。
这个公式的推导过程较为复杂,我们可以简单解释一下。
我们可以将球体看作由无数微小的面元组成,每个面元都是一个微小的圆形。
球体的表面积就是这些微小圆形的面积之和。
而每个微小圆形的半径都等于球体的半径r,因此我们可以将每个微小圆形的面积表示为πr²。
最后,将所有的微小圆形面积之和即得到了球体的表面积。
二、球体的体积计算公式要计算球体的体积,我们可以使用以下公式:V = (4/3)πr³其中,V表示球体的体积,π是圆周率,r是球体的半径。
这个公式的推导也较为复杂,我们可以简单解释一下。
我们可以将球体看作无数个微小的圆柱体叠加而成。
每个微小圆柱体的体积可以表示为πr²h,其中h是圆柱体的高度,也就是球体半径r对应的微小圆柱体的高度。
由于球体是各向同性的,每个微小圆柱体的高度都等于r。
因此,我们将微小圆柱体的体积表示为πr²r,即πr³。
最后将所有微小圆柱体的体积之和即得到了球体的体积。
三、实例应用假设我们需要计算一个半径为5cm的球体的表面积和体积。
根据上述公式,我们可以按照以下步骤进行计算:1. 计算表面积:S = 4πr²= 4 × 3.14159 × 5²≈ 314.159 cm²2. 计算体积:V = (4/3)πr³= (4/3) × 3.14159 × 5³≈ 523.599 cm³因此,半径为5cm的球体的表面积约为314.159 cm²,体积约为523.599 cm³。
球体的体积与表面积关系推导

球体的体积与表面积关系推导在数学中,球体是一种具有无限多个对称中心的几何体。
球体的特点是其表面上的每一点到中心的距离都相等,这个距离被称为半径。
通过研究球体的体积与表面积之间的关系,我们可以更深入地了解球体的性质和特点。
一、球体的定义及基本公式球体是由三维空间中所有到中心点距离小于等于给定半径的点构成的集合。
球体的体积和表面积可以通过以下公式计算得出:1. 球体的体积公式:V = (4/3)πr^3其中,V表示球体的体积,π是圆周率,r是球体的半径。
2. 球体的表面积公式:A = 4πr^2其中,A表示球体的表面积,π是圆周率,r是球体的半径。
二、推导球体体积与表面积的关系我们可以通过对球体的切割和展开来推导球体的体积与表面积之间的关系。
1. 切割与展开球体将球体沿着两个垂直于彼此的坐标轴切割,并沿着这两个切割面将球体展开。
2. 形成球冠和圆盘我们可以看到,切割后的球体被分成许多球冠和圆盘。
球冠是由球的表面和两个切割面构成的部分,圆盘是由两个切割面和球的表面构成的部分。
3. 计算球冠的体积对于一个球冠,它的体积可以通过计算一个圆台的体积得出。
圆台的体积公式为:Vc = (1/3)π(h^2)(R + r)其中,Vc表示球冠的体积,h表示球冠的高度,R表示球冠的大半径,r表示球冠的小半径。
4. 计算圆盘的面积对于一个圆盘,它的面积可以通过计算一个矩形的面积得出。
矩形的面积公式为:Ac = 2πr * h其中,Ac表示圆盘的面积,r表示圆盘的半径,h表示圆盘的周长。
5. 求和计算球体的体积将所有球冠的体积相加,可以得到整个球体的体积。
同理,将所有圆盘的面积相加,可以得到整个球体的表面积。
V = Vc1 + Vc2 + Vc3 + ... + VcnA = Ac1 + Ac2 + Ac3 + ... + Acn三、结论与应用通过上述的推导过程,我们可以得出一个结论:球体的体积与表面积之间存在着特殊的关系。
球的表面积和体积计算

球的表面积和体积计算球是一种常见的几何图形,其表面积和体积的计算是我们在数学和物理学中经常遇到的问题。
本文将介绍如何准确计算球的表面积和体积,并提供相应的公式和计算步骤。
一、球的表面积计算表面积是指球外部各个点的总面积,计算球的表面积可以使用球的半径来确定。
使用以下公式计算球的表面积:S = 4πr²其中,S表示球的表面积,π表示圆周率,r表示球的半径。
例如,如果球的半径为5厘米,则可以通过代入公式计算出球的表面积:S = 4π * (5²) = 4π * 25 ≈ 314.16 cm²所以,半径为5厘米的球的表面积约为314.16平方厘米。
二、球的体积计算体积是指球所占据的空间大小,计算球的体积同样使用球的半径作为计算依据。
使用以下公式计算球的体积:V = (4/3)πr³其中,V表示球的体积,π表示圆周率,r表示球的半径。
以半径为5厘米的球为例,可以通过代入公式计算出球的体积:V = (4/3)π * (5³) = (4/3)π * 125 ≈ 523.6 cm³因此,半径为5厘米的球的体积约为523.6立方厘米。
综上所述,球的表面积和体积的计算分别使用了公式S = 4πr²和V = (4/3)πr³,其中S表示球的表面积,V表示球的体积,r表示球的半径,π表示圆周率。
通过代入球的半径值,可以准确计算出球的表面积和体积。
请注意,在实际计算过程中,需要注意单位的统一,并按照所需精度进行四舍五入。
此外,要正确使用圆周率π的值,常见的取值为3.14或3.1415926。
总结:球的表面积和体积计算是一种常见的数学问题,掌握计算球的表面积和体积的公式和步骤能够帮助我们更好地理解和应用几何学和物理学知识。
在实际应用中,需要注意单位的转换和精度的控制,以获得准确的计算结果。
圆球的体积与表面积

圆球的体积与表面积对于一个圆球来说,它的体积和表面积是直接相关的。
体积是指圆球所占据的三维空间的大小,而表面积则是圆球外表面的面积。
在本文中,将详细探讨圆球的体积和表面积之间的数学关系,并介绍如何计算和应用这些概念。
一、圆球的体积要计算一个圆球的体积,我们需要知道它的半径。
半径是指从圆球的中心到球面上任意一点的距离。
假设圆球的半径为r,则它的体积可以通过下面的公式计算:V = (4/3)πr³其中,V表示圆球的体积,π约等于3.14159。
这个公式可以从球体的几何性质推导得出,具体的证明过程可以参考数学教材或相关资料。
需要注意的是,计算体积时半径的单位应保持一致,例如都是以厘米或者米为单位。
举个例子,如果我们有一个半径为5厘米的圆球,那么它的体积可以通过将半径代入公式中计算得出:V = (4/3)π(5³) ≈ 523.6 cm³所以这个圆球的体积约为523.6立方厘米。
二、圆球的表面积圆球的表面积是指其外表面的总面积。
同样,要计算一个圆球的表面积,我们只需要知道它的半径。
圆球的表面积可以通过以下公式计算:A = 4πr²其中,A表示圆球的表面积,π约等于3.14159,r表示圆球的半径。
同样需要注意,半径的单位在计算表面积时应保持一致。
以刚才的例子为参考,如果我们有一个半径为5厘米的圆球,那么它的表面积可以通过将半径代入公式中计算得出:A = 4π(5²) ≈ 314.16 cm²所以这个圆球的表面积约为314.16平方厘米。
三、体积与表面积的关系从上述的计算公式中可以看出,圆球的体积与半径的立方成正比,而表面积与半径的平方成正比。
也就是说,如果我们将半径增加一倍,那么圆球的体积将增加8倍,而表面积将增加4倍。
这个关系在实际生活中具有一定的应用价值。
例如,在设计装饰物品时,如果我们希望增加物体的体积,我们可以通过增加半径来实现。
而如果我们想要增加物体的表面积,我们可以通过减小半径来实现。
球体的体积与表面积计算方法

球体的体积与表面积计算方法球体是一种常见的几何体,球体的体积和表面积是我们经常需要计算的量。
本文将介绍球体的体积与表面积计算方法及其推导过程。
一、球体的体积计算方法要计算一个球体的体积,我们需要知道球的半径。
球体的体积可以通过以下公式来计算:V = (4/3)πr³其中,V表示球体的体积,π近似为3.14159,r表示球体的半径。
这个公式是根据球体的几何性质推导出来的。
具体计算过程如下:1. 确定球体的半径r;2. 将半径r的值代入公式V = (4/3)πr³中;3. 按照计算器的要求进行计算,得到球体的体积V。
例如,如果球体的半径r为10cm,那么根据公式V = (4/3)πr³,计算得到该球体的体积为:V = (4/3) × 3.14159 × 10³ ≈ 4188.79 cm³所以,球体的体积约为4188.79 cm³。
二、球体的表面积计算方法球体的表面积也是通过球的半径来计算的。
球体的表面积可以通过以下公式来计算:A = 4πr²其中,A表示球体的表面积,π近似为3.14159,r表示球体的半径。
具体计算过程如下:1. 确定球体的半径r;2. 将半径r的值代入公式A = 4πr²中;3. 按照计算器的要求进行计算,得到球体的表面积A。
例如,如果球体的半径r为10cm,那么根据公式A = 4πr²,计算得到该球体的表面积为:A = 4 × 3.14159 × 10² ≈ 1256.64 cm²所以,该球体的表面积约为1256.64 cm²。
综上所述,球体的体积与表面积计算方法基于球的半径,通过相应的公式进行计算。
需要注意的是,在计算过程中要保留足够的小数位数,以提高计算的准确性。
值得一提的是,这些计算方法不仅适用于正规球体,对于近似球体(如地球)同样适用。
球体的表面积和体积计算

球体的表面积和体积计算球体是一种几何体,具有独特的形状和特点。
计算球体的表面积和体积是数学中的基本问题之一。
本文将详细介绍如何准确计算球体的表面积和体积。
一、球体的表面积计算表面积是指球体上所有表面的总面积。
对于球体,其表面积的计算公式如下:A = 4πr²其中,A代表表面积,π代表圆周率(取近似值3.14159),r代表球体的半径。
在计算球体表面积时,首先需要确定球体的半径,然后将半径代入表面积公式进行计算。
下面通过一个例子来说明具体的计算步骤。
例:计算半径为5 cm的球体的表面积。
解:根据公式A = 4πr²,将r替换为5,得到A = 4π(5)² = 4π(25) = 100π cm²。
所以,半径为5 cm的球体的表面积为100π cm²。
二、球体的体积计算体积是指球体的内部空间容纳的大小。
对于球体,其体积的计算公式如下:V = (4/3)πr³其中,V代表体积,π代表圆周率,r代表球体的半径。
在计算球体的体积时,同样需要确定球体的半径,然后将半径代入体积公式进行计算。
下面通过一个例子来说明具体的计算过程。
例:计算半径为2 m的球体的体积。
解:根据公式V = (4/3)πr³,将r替换为2,得到V = (4/3)π(2)³ =(4/3)π(8) = (32/3)π m³。
所以,半径为2 m的球体的体积为(32/3)π m³。
综上所述,球体的表面积和体积的计算公式为A = 4πr²和V =(4/3)πr³。
通过确定球体的半径,将半径代入相应的公式中,即可准确计算出球体的表面积和体积。
提示:在实际问题中,有时需要对球体进行单位转换。
例如,将球的半径从厘米转换为米,需要注意单位换算的正确性。
此外,在使用计算器进行计算时,应尽量保留较精确的数值,只在最后的结果中进行取舍。
请根据实际情况灵活运用上述公式,准确计算球体的表面积和体积。
球体表面积和体积公式

球体表面积和体积公式球体是一个非常常见的几何形状,它具有许多独特的性质和特征。
在这篇文章中,我们将重点介绍球体的表面积和体积公式,以及它们的应用。
一、球体的表面积公式球体的表面积是指球体外部所有点的集合所形成的曲面的总面积。
球体表面积的计算公式如下:S = 4πr^2其中,S表示球体的表面积,π是一个数学常数,约等于3.14159,r是球体的半径。
这个公式的推导可以通过将球体划分为无数个微小的表面元素,并对每个表面元素的面积进行累加得到。
然而,在这里我们不会对公式的推导过程进行详细讲解。
二、球体的体积公式球体的体积是指球体内部所有点的集合所形成的空间的总体积。
球体体积的计算公式如下:V = (4/3)πr^3其中,V表示球体的体积,π是一个数学常数,约等于3.14159,r 是球体的半径。
这个公式的推导可以通过将球体划分为无数个微小的体积元素,并对每个体积元素的体积进行累加得到。
同样,在这里我们不会对公式的推导过程进行详细讲解。
三、球体表面积和体积的应用球体的表面积和体积公式在许多领域都有着广泛的应用。
1. 建筑工程:在建筑设计中,球体的表面积公式可以用于计算建筑物的外墙面积,从而确定建筑材料的使用量。
而球体的体积公式则可以用于计算建筑物内部空间的容积,从而确定建筑物的可使用面积。
2. 包装设计:在包装设计中,球体的表面积公式可以用于计算圆形容器的外表面积,从而确定包装纸的大小。
而球体的体积公式则可以用于计算圆形容器的容积,从而确定包装物的容量。
3. 天文学:在天文学中,球体的表面积公式可以用于计算恒星的表面积,从而确定恒星的辐射能力。
而球体的体积公式则可以用于计算行星的体积,从而确定行星的质量。
4. 地理学:在地理学中,球体的表面积公式可以用于计算地球的表面积,从而确定地球的大小。
而球体的体积公式则可以用于计算地球的体积,从而确定地球的体积。
除了上述应用领域,球体的表面积和体积公式还可以在数学、物理、化学等学科中找到许多其他的应用。
球的表面积体积计算公式及推导过程

球的表面积体积计算公式及推导过程球的表面积公式是什么球体的计算公式半径是R的球的体积计算公式是:V=(4/3)πR^3(三分之四乘以π乘以半径的三次方)V=(1/6)πd^3 (六分之一乘以π乘以直径的三次方)半径是R的球的表面积计算公式是:S=4πR^2(4倍的π乘以R的二次方) 球体体积计算公式V=(4/3)πr^3解析:三分之四乘圆周率乘半径的三次方。
球体:“在空间内一中同长谓之球。
”定义:(1)在空间中到定点的距离等于或小于定长的点的集合叫做球体,简称球。
(从集合角度下的定义)(2)以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体(solid sphere),简称球。
(从旋转的角度下的定义)(3) 以圆的直径所在直线为旋转轴,圆面旋转180°形成的旋转体叫做球体(solid sphere),简称球。
(从旋转的角度下的定义)(4)在空间中到定点的距离等于定长的点的集合叫做球面即球的表面。
这个定点叫球的球心,定长叫球的半径。
推导过程球体表面积公式S(球面)=4πr^2运用第一数学归纳法:把一个半径为R的球的上半球横向切成n份,每份等高并且把每份看成一个圆柱,其中半径等于其底面圆半径则从下到上第k个圆柱的侧面积S(k)=2πr(k)×h其中h=R/n,r(k)=√[R^2;-﹙kh^2;]=2πR^2;×√[1/n^2;-(k/n^2)^2;] 则S(1)+S(2)+……+S(n)当n取极限(无穷大)的时候,半球表面积就是2πR^2;球体乘以2就是整个球的表面积4πR^2;球体性质用一个平面去截一个球,截面是圆面。
球的截面有以下性质:1球心和截面圆心的连线垂直于截面。
2球心到截面的距离d与球的半径R及截面的半径r有下面的关系:r^2=R^2-d^2球面被经过球心的平面截得的圆叫做大圆,被不经过球心的截面截得的圆叫做小圆。
在球面上,两点之间的最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度,我们把这个弧长叫做两点的球面距离。
球体表面积和体积的公式

球体表面积和体积的公式一、球体表面积公式。
1. 公式内容。
- 球体的表面积公式为S = 4π r^2,其中S表示球体的表面积,r表示球的半径,π是圆周率,通常取3.14。
2. 公式推导(高中阶段了解)- 可以通过对球体进行无限分割,将球体表面分割成无数个小的曲面三角形。
利用极限的思想,当分割得足够细时,这些小曲面三角形的面积之和就近似等于球体的表面积。
- 从数学分析的角度,利用球坐标变换等高等数学方法可以严格推导出这个公式。
3. 应用示例。
- 例:已知一个球的半径r = 5厘米,求这个球的表面积。
- 解:根据球体表面积公式S = 4π r^2,将r = 5代入公式,可得S=4×3.14×5^2=4×3.14×25 = 314(平方厘米)。
二、球体体积公式。
1. 公式内容。
- 球体的体积公式为V=(4)/(3)π r^3,其中V表示球体的体积,r表示球的半径,π是圆周率,通常取3.14。
2. 公式推导(高中阶段了解)- 可以使用祖暅原理(等积原理)来推导球体体积公式。
将一个半球体与一个底面半径和高都等于球半径r的圆柱体挖去一个底面半径和高都为r的圆锥体进行对比,利用祖暅原理可知它们的体积相等,从而推导出球体体积公式。
- 从高等数学角度,也可以通过三重积分等方法进行推导。
3. 应用示例。
- 例:已知球的半径r = 3厘米,求这个球的体积。
- 解:根据球体体积公式V = (4)/(3)π r^3,将r = 3代入公式,可得V=(4)/(3)×3.14×3^3=(4)/(3)×3.14×27 = 113.04(立方厘米)。
高中数学必修二运用球的体积公式来推导球的表面积公式

运用球的体积公式来推导球的表面积公式第一步:分割如图,把球O 的表面分成n 个“小球面片”,设它们的表面积分别为12,,,n S S S •••,那么,球的表面积12nS S S S =++•••+把球心O 和每一个“小球面片”的顶点连接起来,整个球体就被分割成n 个以这些“小球面片”为底,球心为顶点的“准锥体”。
这样的“准锥体”的底面是球面的一部分,底面是“曲”的。
第二步:近似求和设n 个“准锥体”的体积分别为12,n V V V •••,(1)这n 个 “准锥体”的体积与球的体积有怎样的关系呢? 球体的体积31243n V V V V R π=++•••+= (2)怎样求每一个“准锥体”的体积呢?你会算吗?怎样处理呢?如果每一个“小球面片”都非常小,那么“准锥体”的底面几乎是平的。
这时,每一个“准锥体”就近似于棱锥。
所以,我们用相应的棱锥的体积作为“准锥体”体积的近似值。
棱锥底面面积近似取为i S ,设棱锥的高为i h ,(如图)i S i h iR 以平代曲 R于是棱锥的体积为13i i S h ,这样相应“准锥体”的体积i V ≈13i i S h (1,2,3,,)i n =••• 所以“准锥体”的体积之和的近似值即球体的体积V ≈1122111333n n S h S h S h ++•••+(3)怎样提高这个近似值的精确度呢? 第三步:取极限分割越细密,也就是每一个“小球面片”越小,几乎是平的,“准锥体”就越接近棱锥,精确度就越高。
但只要分割份数是一个有限值,误差就一定存在, 得到的始终是一个近似值。
O O R iS(4)那么怎样把这个近似值转化为准确值呢?这是一个比较深奥的问题,要用到高等数学的极限思想,教者简单介绍极限思想。
于是V =1211()33n S S S R RS ++•••+=,而我们已知球的体积343V R π=,所以球的表面积S =24R π。
推导公式球的表面积与体积计算公式

推导公式球的表面积与体积计算公式球的表面积和体积是我们在数学课上经常会接触到的内容。
它们的求解是十分重要的,尤其是在物理学和工程学等领域中。
在本文中,我们将推导出球的表面积和体积的计算公式。
假设有一个半径为r的球体。
我们首先来推导球的表面积公式。
球的表面积由许多小的表面元素组成,每个表面元素都是一个微小的平面圆盘。
我们可以将球体切割成很多个这样的平面圆盘,然后将其展开。
你可以想象成类似于展开一个橙子的皮一样。
每个小平面圆盘的面积可以表示为2πRh,其中R是该平面圆盘的半径,h是平面圆盘到球心的距离(也就是球的半径r)。
由于球的所有小平面圆盘都具有相同的半径和距离,我们可以将所有小平面圆盘的面积相加,从而得到整个球的表面积。
但是,为了简化计算,我们可以将球体切割成无数个特别小的表面元素。
当我们将这些表面元素展开时,它们将形成一个长方形,其中一条边的长度是球的周长(2πr),另一条边的长度是展开后的球体的高度(r)。
因此,球体的表面积S可以表示为:S = 2πr * r = 4πr²现在,我们来推导球的体积公式。
球体的体积可以看作是无数个特别小的体积元素的总和。
我们可以将球体划分为无数个小体积元素,类似于将一个柠檬切成无数个小块。
每个小体积元素可以看作是一个半径为r的球形圆柱体,其高度为h。
根据几何学知识,圆柱体的体积可以表示为πR²h,其中R是圆柱体底面的半径,也就是球的半径r。
由于球的所有小体积元素具有相同的半径和高度,我们可以将所有小体积元素的体积相加,从而得到整个球的体积。
但是,为了简化计算,我们可以将球体划分为无数个无限小的体积元素。
这样,当我们将它们全部相加时,它们的体积和球的体积几乎一样。
这就等价于求解一个无穷小的球的体积。
根据微积分的知识,无穷小的球的体积可以表示为dV = πr²dh,其中dh是无穷小的高度变化。
我们可以积分这个无穷小的体积元素,从球的底部(h=0)到顶部(h=r),得到整个球的体积V:V = ∫[0,r] πr²dh = πr²h∣∣[0,r] = πr²r = 4/3πr³综上所述,球的表面积公式为S = 4πr²,球的体积公式为V = 4/3πr³。
半球体积公式和表面积

半球体积公式和表面积
一、半球体积公式。
1. 公式推导。
- 球的体积公式为V = (4)/(3)π r^3(其中r为球的半径)。
- 半球的体积就是球体积的一半,所以半球体积公式V_半球=(1)/(2)×(4)/(3)π r^3=(2)/(3)π r^3。
2. 示例。
- 已知半球的半径r = 3,求半球的体积。
- 根据半球体积公式V_半球=(2)/(3)π r^3,将r = 3代入公式,可得
V_半球=(2)/(3)π×3^3=(2)/(3)π×27 = 18π。
二、半球表面积公式。
1. 公式推导。
- 球的表面积公式为S = 4π r^2。
- 半球的表面积由半球面和底面圆两部分组成。
半球面的面积是球表面积的一半,即(1)/(2)×4π r^2=2π r^2,底面圆的面积为π r^2。
- 所以半球的表面积公式S_半球=2π r^2+π r^2=3π r^2。
2. 示例。
- 已知半球的半径r = 2,求半球的表面积。
- 根据半球表面积公式S_半球=3π r^2,将r = 2代入公式,可得
S_半球=3π×2^2=3π×4 = 12π。
图解球体表面积和体积正确计算方法及计算公式
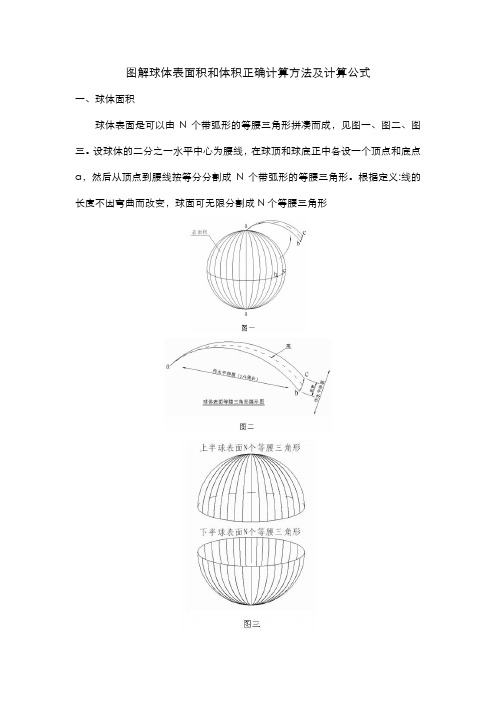
图解球体表面积和体积正确计算方法及计算公式一、球体面积球体表面是可以由N个带弧形的等腰三角形拼凑而成,见图一、图二、图三。
设球体的二分之一水平中心为腰线,在球顶和球底正中各设一个顶点和底点a,然后从顶点到腰线按等分分割成N个带弧形的等腰三角形。
根据定义:线的长度不因弯曲而改变,球面可无限分割成N个等腰三角形如图二、图四、图五所示,所有分割好带弧形的等腰三角形都可以自然平展成标准的等腰三角形,亦可将等腰三角形拼凑成方形。
在理解上述图例球体表面和等腰三角形的关系后,我们可以对球体表面积的计算有比较清晰的判断。
即,球体表面可以分割成N个相等的等腰三角形,等腰三角形亦可拼凑成方形,由此推导出球体面积可以用矩形公式计算。
即S = 长×宽,如果我们设球体1/4之一的周长为宽,设球体的周长为长,则球体表面积公式为:S=1/4周长×周长(见图六)例1:已知球体直径是1个单位,求球体表面积(用上述最新推导公式S=1/4周长×周长)S =(3。
14159÷4)×3.14159 = 2。
4674㎡二、球体体积设以球心作一条垂线或水平中心线,然后以垂线或水平中心向外将球体按等分无限分割成N个半圆楔形体。
见图七、图八。
球体分割完成后,将半圆楔形体镜像排列成圆柱体,见图九、图十。
从图七、图八、图九、图十看,球体从中心按等分分割成半圆楔形体后可以排列堆砌成圆柱体,根据计算得出定义:与球体同直径同体积的圆柱体的柱高正好是球体周长的1/4。
则球体体积公式为:V =πR平方×周长的1/4或:V = D(直径的三次方)×0.616849233例2:已知球体直径是1个单位,求球体体积(用上述最新推导公式)V =πR平方×周长的1/4= 3.14159×0.25×0.7853975= 0.616849233三、公知公式在球体面积、体积计算中出现的错误1、球体面积如何检验球体面积计算的正确,最好的方法就是用计算结果制成N个等腰三角形的薄膜反贴球体表面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1..3.2球的体积和表面积(1)
设球的半径为R ,将半径OAn 等分,过这些分点作平
面把半球切割成n 层,每一层都是近似于圆柱形状的“小
圆片”,这些“小圆片”的体积之和就是半球的体积。
由于“小圆片”近似于圆柱形状,所以它的体积也近似于圆柱的体积。
它的高就是“小圆片”的厚度
n R ,底面
就是“小圆片”的下底面。
由勾股定理可得第i 层(由下向上数)“小圆片”的下底面半径: 2
2)]1([--=i n R R r i ,(i =1,2,3,···,n )
第i 层“小圆片”的体积为:
V ≈π2i r ·n R =⎥⎥⎦
⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--2311n i n R π,
(i =1,2,3,···,n ) 半球的体积:V 半径=V 1+V 2+···+Vn ≈n R 3π{1+(1-221n )+(1-222n )+···+[1-2
2)1(n n -]} =n R 3π[n -2222)1(21n n -+•••++](注:)12)(1(6
121222++=+•••++n n n n ) =n R 3π[n -6)12()1(12--•n n n n =236)12)(1(1(n n n R ---π)=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---6)12)(11(13n n R π ①
当所分的层数不断增加,也就是说,当n 不断变大时,①式越来越接近于半球的
体积,如果n 无限变大,就能由①式推出半径的体积。
事实上,n 增大,
n 1就越来越小,当n 无限大时,n 1趋向于0,这时,有 V 半径=332R π,所以,半径为R 的球的体积为: V =33
4R π
1..3.2球的体积和表面积(2)
球的表面积推导方法(设球的半径为R ,利用球的体积公式推导类似方法)
(1)分割。
把球O 的表面分成n 个“小球面片”,设它们的表面积分别是S 1,S 2,……
Sn ,那么球的表面积为:S =S 1+S 2+……+Sn
把球心O 和每一个“小球面片”的顶点连接起来,整个球体被分成n 个以“小球
面片”为底,球心为顶点的“小锥体”。
例如,球心与第i 个“小球面片”顶点相连后 就得到一个以点O 为顶点,以第i 个“小球面片”为底面的“小锥体”。
这样“小锥体” 的底面是球面的一部分,底面是“曲”的。
如果每一个“小球面片”都非常小,那么
“小锥体”的底面几乎是“平”的,(好象地球一样),这时,每一个“小锥体”就近
似于棱锥,它们的高近似于球的半径R 。
(2)求近似和。
设n 个“小锥体”的体积分别为V 1,V 2, (V)
那么球的体积为:V =V 1+V 2+ (V)
由于“小锥体”近似于棱锥,所以我们用相应棱锥的体积作为“小锥体”体积的
近似值。
第i 个“小锥体”对应的棱锥以点O 为顶点,以点O 与第i 个“小球面片”
顶点的连线为棱。
设它的高为h i ,底面面积为S ’i ,于是,它的体积为:
V ’i =3
1h i S ’i ,(i =1,2,…,n ) 这样就有:V i ≈3
1h i S ’i ,(i =1,2,…,n ) V ≈31(h 1 S ’1+h 2 S ’2 +…+h n S ’n ) ①
(3)转化为球的表面积。
分割得越细密,也就是每一个“小球面片”越小,“小锥体”就越接近于棱锥,如果分割无限加细,每一个“小球面片”都无限变小,那么h i (i =1,2,…,n )就趋向于R ,S ’i 就趋向于 S i ,于是,由①可得:V =3
1RS 又V =334R π,所以,有334R π=3
1RS 即: S =4πR 2。
