程序设计实训题3
国开电大 网络编程 实训三:随机显示题头图片

国开电大网络编程实训三:随机显示题头图片简介本文档将介绍国开电大网络编程实训三中的随机显示题头图片的实施方法。
背景在网络编程实训三中,我们需要实现一个功能,在网页头部随机显示一张图片。
这个功能旨在提升用户体验和吸引用户的注意力。
实施方法以下是实现随机显示题头图片的简单步骤:1. 收集图片:首先,我们需要收集一系列适用于题头的图片。
可以选择与网页内容相关的图片,或者能够吸引用户的图片。
2. 图片路径列表:将收集到的图片路径以列表的形式保存。
可以在代码中定义一个列表,并将图片路径作为元素添加到其中。
3. 随机选择图片:使用随机函数,从图片路径列表中随机选择一个图片路径。
5. 页面美化(可选):可以为图片添加额外样式,如设置图片的宽度、高度、边框等,以适应网页的布局和设计。
示例代码以下是一个示例代码片段,展示了如何实现随机显示题头图片的功能:<head><title>随机显示题头图片</title><style>header-image {width: 100%;height: auto;}</style></head><body><header><img id="header-image" src="path_to_random_image"alt="Header Image"></header><!-- 其他页面内容 --></body>注意事项- 确保图片路径列表包含正确的图片路径。
- 根据需要更新图片路径列表,以显示不同的题头图片。
- 可根据实际情况对页面进行美化调整。
结论通过实施以上步骤,我们能够在网页中实现随机显示题头图片的功能,提升网页的外观和用户体验。
以上是实现随机显示题头图片的简单方法说明。
2019第十届蓝桥杯单片机省赛——程序设计题
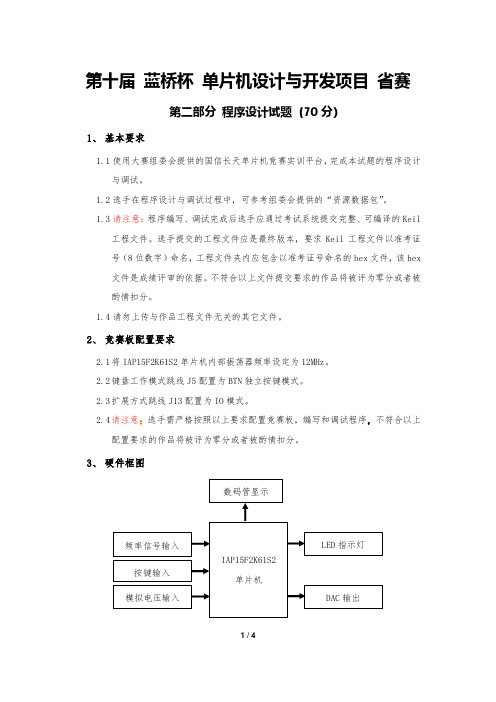
第十届 蓝桥杯 单片机设计与开发项目 省赛第二部分 程序设计试题(70分)1、 基本要求1.1 使用大赛组委会提供的国信长天单片机竞赛实训平台,完成本试题的程序设计与调试。
1.2 选手在程序设计与调试过程中,可参考组委会提供的“资源数据包”。
1.3 请注意:程序编写、调试完成后选手应通过考试系统提交完整、可编译的Keil工程文件。
选手提交的工程文件应是最终版本,要求Keil 工程文件以准考证号(8位数字)命名,工程文件夹内应包含以准考证号命名的hex 文件,该hex 文件是成绩评审的依据。
不符合以上文件提交要求的作品将被评为零分或者被酌情扣分。
1.4 请勿上传与作品工程文件无关的其它文件。
2、 竞赛板配置要求2.1 将IAP15F2K61S2单片机内部振荡器频率设定为12MHz 。
2.2 键盘工作模式跳线J5配置为BTN 独立按键模式。
2.3 扩展方式跳线J13配置为IO 模式。
2.4 请注意:选手需严格按照以上要求配置竞赛板,编写和调试程序,不符合以上配置要求的作品将被评为零分或者被酌情扣分。
3、 硬件框图IAP15F2K61S2单片机LED 指示灯模拟电压输入频率信号输入数码管显示DAC 输出按键输入图1 系统硬件框图4、功能描述4.1基本功能1)测量竞赛板上电位器RB2输出的模拟电压信号和NE555模块输出的频率信号,以数码管、LED等外围设备进行数据呈现。
(P34与SIGNAL2)频率测量功能需将竞赛板J3-SIGNAL引脚与P34引脚短接。
的短接可以使用竞赛板上超声/红外切换等与本试题功能要求无关的跳线帽完成)。
3)使用PCF8591测量电位器RB2的输出电压,并根据试题要求通过其DAC功能输出该电压值。
4)电压、频率数据刷新时间要求●电压数据刷新时间≤0.5秒。
●频率数据刷新时间≤1秒。
5)电压、频率数据测量范围要求●电压数据测量范围:电位器RB2输出的最小电压值到最大电压值。
国开电大 JavaScript程序设计 实训三:随机显示题头图片

1. 题目随机显示题头图片。
2. 目的(1)掌握图像显示的基本知识。
(2)掌握对象建立的方法。
(3)掌握Math的使用方法。
(3)会应利用随机函数编写应用程序。
3. 内容结合一个具体应用的需求,设计随机显示题头的程序。
4. 要求(1)针对一个具体应用的需求,设计界面。
(2)使用对象的方式存储图像信息,利用随机函数抽取图像。
代码示例:#lr_systembox{ width:980px; height:50px; background-color:#CCC; position:relative; margin:0 auto; z-index:100000;}.lr_systembtn{ width:201px; height:35px; line-height:33px;position:absolute; top:0px; right:0px; z-index:100004;}.lr_systembtn .lr_abtn{ width:100%; height:35px; display:block; font-size:15px; font-weight:bold;color:#666666;background-image:url(lr_images/btn_system.png);background-repeat:no-repeat;background-position:left top;}.lr_systembtn .lr_abtn:hover{color:#333333;background-position:left bottom;}.lr_systembtn .lr_abtn span{ padding-left:28px;}.lr_menu{ width:184px; padding:8px 6px 8px 6px; background-color:#ffffff; border:#ACACAC solid 2px;filter:alpha(opacity=90);opacity: 0.90;position:absolute; top:35px; right:0px;z-index:100005;display:none;}.lr_menu dl{width:100%; display:block; overflow:hidden;}.lr_menu a{ width:100%;display:block; color:#666666;border-bottom:#ACACAC dashed 1px;height:30px; line-height:30px; font-size:14px;background-image: url(lr_images/jt1.gif);background-repeat:no-repeat;background-position:6px center;}.lr_menu a:hover{background-color:#E2E2E2; color:#333333; text-decoration:none;}.lr_menu dt{}.lr_menu dt a{font-weight:bold;text-indent:14px;}.lr_menu dd a{text-indent:24px;background-position:16px center;}<div id="lr_systembox"><div id="lr_systembtn" class="lr_systembtn"><a href="#" class="lr_abtn"><span> </span></a><div id="lr_menu" class="lr_menu"><dl><dt><a href="/js/" target="_blank">jquery特效</a></dt> </dl><dl><dt><a href="/js/nav/" target="_blank">导航菜单</a></dt><dd><a href="#" target="_blank">三级菜单测试</a></dd><dd><a href="#" target="_blank">三级菜单测试</a></dd></dl><dl><dt><a href="/js/slide/" target="_blank">焦点幻灯片</a></dt></dl><dl><dt><a href="/js/texiao/" target="_blank">网页特效</a></dt></dl><dl><dt><a href="/qqkefu/" target="_blank">qq在线客服代码</a></dt></dl><dl><dt><a href="/jquery_tanchu/" target="_blank">jquery 弹出层</a></dt></dl></div></div></div>。
C语言实训商店商品管理信息系统

附录 A 程序清单……………………………………………………………… 附录 B 用户使用说明书……………………………………………………… 参考文献…………………………………………………………………………
销售量(用#结束输入):");
scanf("%d",&temp.xsl);
printf("
销售额(用#结束输入):");
scanf("%f",&z);
temp.xse=z;
printf("
剩余数(用#结束输入):");
scanf("%d",&temp.sys);
printf("
毛利(用#结束输入):");
为了实现上述功能,有关语句都应放在 do-while 循环体中。 设计算法时应考虑如何时程序具有容错能力。例如,当用户在应答是否继续时, 如果输入的是合法数据(即 y、Y、n 或 N),则程序继续下一步操作;如果输入 的是非法数据(即 y、Y、n 或 N 以外的字符),则应让用户重新输入,这时需要 在是否继续的问题上加一个循环判断,这种功能常用 do-while 实现。 (4)流程图(如下图所示):
|
1——按原来顺序显示
|
|
2——按销售额高低显示
|
|
3——按毛利高低显示
|
|
4——返回
|
|
0——退出系统
|
(完整word版)单片机C语言程序设计实训100例
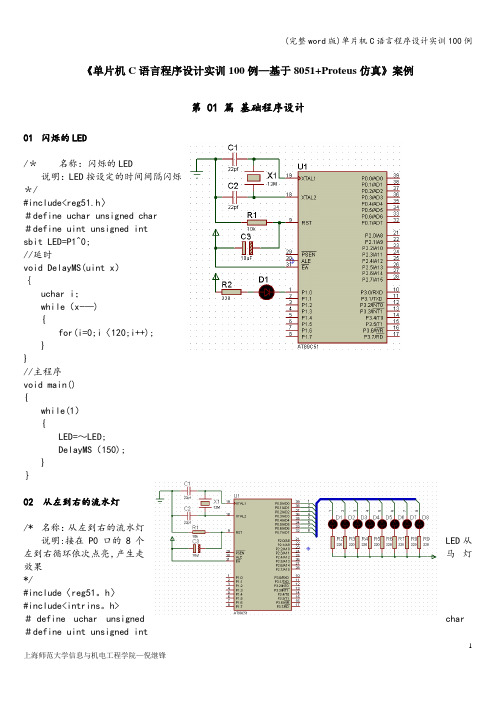
《单片机C语言程序设计实训100例—基于8051+Proteus仿真》案例第 01 篇基础程序设计01 闪烁的LED/*名称:闪烁的LED说明:LED按设定的时间间隔闪烁*/#include<reg51.h〉#define uchar unsigned char#define uint unsigned intsbit LED=P1^0;//延时void DelayMS(uint x){uchar i;while(x-—){for(i=0;i〈120;i++);}}//主程序void main(){while(1){LED=~LED;DelayMS(150);}}02 从左到右的流水灯/* 名称:从左到右的流水灯说明:接在P0口的8个LED从左到右循环依次点亮,产生走马灯效果*/#include〈reg51。
h〉#include<intrins。
h>#define uchar unsigned char #define uint unsigned int//延时void DelayMS(uint x){uchar i;while(x—-){for(i=0;i〈120;i++);}}//主程序void main(){P0=0xfe;while(1){P0=_crol_(P0,1); //P0的值向左循环移动DelayMS(150);}}03 8只LED左右来回点亮/*名称:8只LED左右来回点亮说明:程序利用循环移位函数_crol_和_cror_形成来回滚动的效果*/#include<reg51.h>#include〈intrins.h>#define uchar unsigned char #define uint unsigned int//延时void DelayMS(uint x){uchar i;while(x——){for(i=0;i〈120;i++);}}//主程序void main(){uchar i;P2=0x01;while(1){for(i=0;i〈7;i++){P2=_crol_(P2,1); //P2的值向左循环移动DelayMS(150);}for(i=0;i<7;i++){P2=_cror_(P2,1); //P2的值向右循环移动DelayMS(150);}}}04 花样流水灯/* 名称:花样流水灯说明:16只LED分两组按预设的多种花样变换显示*/#include<reg51。
头哥实训程序设计部分指针三

头哥实训程序设计部分指针三指针是C/C++中非常重要的概念,它可以用于操作内存,动态分配内存,以及在函数间传递参数等。
以下是指针的进阶应用。
1. 指针和数组:数组名其实就是一个指向数组第一个元素的指针,因此可以使用指针来访问数组元素。
例如:c++int numbers[5] = {1, 2, 3, 4, 5};int* ptr = numbers; 将数组的首地址赋值给指针for (int i = 0; i < 5; i++) {cout << *ptr << " "; 输出指针指向的元素值ptr++; 移动指针到下一个元素}2. 动态内存分配:通过使用`new`关键字可以动态分配内存,返回一个指向所分配内存的指针。
可以使用指针来访问和操作动态分配的内存。
例如:c++int* ptr = new int; 动态分配一个int类型的内存空间*ptr = 123; 使用指针来操作动态分配的内存cout << *ptr; 输出指针指向的内存的值delete ptr; 释放动态分配的内存3. 指针和函数参数:指针可以在函数中用于传递参数,实现对参数的修改。
通过传递指针作为函数参数,可以直接操作函数外部的变量。
例如:c++void increment(int* num) {(*num)++; 通过指针直接修改函数外部的变量}int main() {int number = 10;increment(&number); 传递指向number的指针cout << number; 输出11return 0;}以上是指针的一些常见用法,掌握好指针的使用可以提高C/C++程序的灵活性和效率。
但指针也需要小心使用,避免空指针、野指针等错误。
python程序设计实训题目

python程序设计实训题目
当涉及到实训题目,有很多不同的选择,因为实训题目可以涉
及很多不同的主题和概念。
以下是一些可能的 Python 程序设计实
训题目:
1. 创建一个学生管理系统,其中可以添加、删除和查找学生信息,包括姓名、年龄和成绩。
2. 编写一个简单的计算器程序,可以执行加减乘除等基本运算。
3. 开发一个简单的待办事项应用,可以添加、删除和编辑待办
事项,并且可以按照日期进行排序。
4. 设计一个简单的电子商务网站后端,包括用户登录、商品展示、购物车管理等功能。
5. 编写一个简单的文本编辑器,可以打开、编辑和保存文本文件。
这些是仅供参考的一些可能的实训题目,具体的题目可以根据
课程要求和学生能力进行调整和定制。
希望这些题目可以帮助您开始思考您的实训课题。
面向对象程序设计实训

1) 观看老师运行一个简单的java聊天程序。
2) 新建一个Hello.java程序,在控制台打印“欢迎使用本聊天系统!”。
3) 新建一个Test类,在test类中打印下面表达式的运算结果,设a=3,b=-5,f=true:(1) --a % b ++ (2) (a>=1&&a<=12?a:b)4) 阅读TestWhat的源代码,编译并运行,并在老师的要求下使代码规范化。
5) 编写并运行一个字符界面的Java Application,接收用户输入的一个字符,并把该字符打印在屏幕上。
6) 新建一个工程,新建一个包(basic),新建一个类,在类里面写一个方法用来判断三角形的三条边能否构成三角形,并要求能判断出是等腰等边还是普通三角形,在main函数里面实例化对象,调用该方法。
7) 新建另一包(test),然后新建另一个类,测试能不能调用步骤1中的方法.8)Java API有一个类java.util.GregorianCalendar,可用来获得某个日期的年、月、日,用无参数的构造函数创建当前日期的实例,get(GregorianCalendar.YEAR),get(GregorianCalendar.MONTH),get(GregorianCalendar.DAY_OF_MONTH)返回日期的年、月、日。
写程序显示当前的年、月、日。
9)创建聊天程序中的用户类(User),用户拥有自己的名称、出生年份、年龄、密码等信息。
其中年龄要通过出生年份计算出来。
10)考虑以上User类各种方法的访问性,并设计出合理的访问控制修饰符。
11)定义矩形类和它的子类正方形类,并增加一个Printable接口,用于以字符和图形的方式打印矩形和正方形的信息。
(1)定义矩形类,用户输入矩形的长与宽,程序计算其面积和周长;(2)定义矩形类的派生类---正方形类。
正方形类的操作同样是求周长和面积;(3)定义一个接口Printable,其中包括一个方法printWay(),这个方法没有形参,返回值为空;(4)改写矩形类,使之实现Printable接口,用printWay()将矩形的相关信息(长、宽、周长、面积)打印在屏幕上;(5)改写正方形类,重载printWay()方法,将正方形的边长、周长、面积打印在屏幕上;(6)在Printable接口中增加一个新的printWay(char)方法,并改写矩形类、正方形类定义。
C语言程序设计综合实训题目

一、参考题目及选题(1)学生信息管理系统设计问题描述:学生信息包括:学号, 姓名, 年龄, 性别, 出生年月, 政治面貌, 籍贯, 家庭住址, 电话, E-mail等。
试设计一学生信息管理系统, 使之能提供以下功能:(1)系统以菜单方式工作(2)学生信息录入功能(学生信息用文件保存)(3)学生信息浏览功能(4)学生信息排序、查询功能对信息进行排序, 可以按学号, 按姓名, 按性别, 按出生年月日, 按籍贯进行查询(5)信息统计a) 可以按性别, 按出生年, 按籍贯统计学生人数b) 可以按班级统计学生人数c) 可以按政治面貌统计学生人数按班级统计学生党员人数, 团员人数, 以及所占比例, 设计并输出统计报表。
(6)学生信息的删除与修改●设计要求:●界面比较美观;有一定的容错能力, 比如输入的成绩不在0~100之间, 就提示不合法, 要求重新输入;●最好用链表的方式实现。
算法分析:首先, 一个学生包括这么多的属性, 应该考虑定义一个结构, 其次, 我们应该考虑数据的存储形式:是定义一个数组来存储, 还是定义一个链表呢?在这里假如我们以数组的方式来存储, 当然可以, 但是我们知道, 假如我们定义一个数组的话, 我们首先必须知道学生人数大概是多少, 以便我们确定数组的大小, 但是题目中没有给出, 而且题目要求中有大量的删除、插入操作, 所以用链表的方式比较方便。
对于菜单的实现, 其实也比较简单, 首先我们用printf语句把程序的功能列出来, 然后等待用户输入而执行不同的函数, 执行完了一个功能后又回到菜单。
文件的读写操作大家参照书中的有关文件的章节。
(2)、学生综合测评系统每个学生的信息为: 学号、姓名、性别、家庭住址、联系电话、语文、数学、外语三门单科成绩、考试平均成绩、考试名次、同学互评分、品德成绩、任课教师评分、综合测评总分、综合测评名次。
考试平均成绩、同学互评分、品德成绩、任课教师评分分别占综合测评总分的60%, 10%, 10%, 20%。
java程序设计 实训题目

java程序设计实训题目
以下是一些Java程序设计实训题目,供您参考:
1. 编写一个Java程序,实现一个简单的计算器,可以进行加、减、乘、除
运算。
要求使用面向对象的思想,将计算器的功能封装在一个类中,并提供一个主函数用于测试。
2. 编写一个Java程序,实现一个简单的文本编辑器,可以打开、保存、编
辑和打印文本文件。
要求使用Java的I/O流和文件操作类库,以及图形用
户界面库(如Swing或JavaFX)。
3. 编写一个Java程序,实现一个简单的聊天室,支持多人同时在线聊天。
要求使用Java的多线程机制和网络编程技术(如Socket编程),并实现基本的用户注册、登录和消息发送功能。
4. 编写一个Java程序,实现一个简单的数据库管理系统,可以创建、删除、查询和更新数据库中的记录。
要求使用Java的JDBC API连接数据库,并
使用SQL语句进行操作。
5. 编写一个Java程序,实现一个简单的图像处理软件,可以对图像进行缩放、旋转、裁剪和滤镜处理。
要求使用Java的图像处理库(如Java Advanced Imaging API)和图形用户界面库(如Swing或JavaFX)。
6. 编写一个Java程序,实现一个简单的邮件发送系统,可以发送HTML格式的邮件。
要求使用Java的邮件发送库(如JavaMail API),并支持SMTP协议和附件上传功能。
7. 编写一个Java程序,实现一个简单的在线考试系统,可以随机生成试题、计时考试时间并自动评分。
要求使用Java的多线程机制和网络编程技术(如Socket编程),并实现基本的用户登录、答题和提交功能。
第3章结构化程序设计习题答案

《C语言程序设计(Visual C++6.0环境)》习题答案习题三一、选择题1.C2.A3.C4.D5.C6.B二、填空题1、<CR>12、$$$$$$$$$$$$$$$$$$$$3、89104、0 01 12 3三、思考题1、32、1,53、循环条件由-1开始一直减1,永远不能得0,因此循环条件恒为真,无法结束,造成死循环。
4、无限循环四、编程题1、用if语句编程,输入一个数,输出这个数的绝对值。
#include "stdio.h"main(){int m,n; /*或者定义成实型*/printf("请输入一个整数: ");scanf("%d",&m);if(m>=0)n=m;elsen=-m;printf("%d的绝对值是:%d",m,n);}2、设计一种程序,输入一个整数,判断它的奇偶性。
#include "stdio.h"main(){int m;printf("请输入一个整数: ");scanf("%d",&m);if(m%2==0) /*或写为!(m%2) 或者m==m/2*2 均可*/printf("%d是偶数",m);elseprintf("%d是奇数",m);}3、假设星期一至星期五每工作1小时的工资是20元,星期六和星期日每工作1小时的工资是平时的3倍,其中工资的4.5%是税金。
请输入一周各天工作的小时数,然后列出该周实际领取的工资及税金。
#include "stdio.h"main(){ int day,h;float gz,sj;gz=0;printf("input weekday1---7:hours\n");for(day=1;day<=7;day++){ printf("%d--:\n",day);scanf("%d",&h);if(day<=5)gz=gz+h*20;elsegz=gz+h*20*3;}sj=gz*0.045;printf("gz=%.2f,sj=%.2f\n",gz,sj);}4、用if语句和switch语句分别编写程序,实现以下功能:从键盘输入数字1,2,3,4,分别显示excellent,good,pass,fail:输入其他键时显示error。
微机原理 实验三 分支结构程序设计

实验3 分支结构程序设计—转移指令
一、项目(实训)名称:
分支结构程序设计—转移指令
二、项目(实训)学时数:
学时数:4
三、项目(实训)目标:
1)熟悉8086CPU的寻址方式和指令系统。
2)掌握汇编语言程序设计上机步骤。
3)用实例上机调试。
四、项目(实训)中的具体任务:
1)熟悉8086/8088 的指令系统分支结构程序。
.
2)按汇编语言程序设计上机步骤上机。
3)初步学会编写和调试分支结构程序。
五、教师知识和能力要求:
要求教师熟悉微机的结构和工作原理,熟悉8086CPU的寻址方式和指令系统,掌握汇编语言程序设计上机步骤。
掌握MASM和TASM汇编程序的安装方法。
六、学生知识和能力准备:
认真阅读8086CPU的寻址方式和指令系统。
编写分支结构汇编语言程序。
做好实验工具软件和资料准备。
七、工具与设备:
八、辅助教学资料:
汇编语言程序设计韩海编
九、实施步骤与技术要点:
题目:用跳转语句实现从键盘接收一个字符,如果是小写字母则输出“L”,大写字母则输出“U”,数字则输出“N”,都不是则输出“*”。
输入回车停止输入。
如下图所示:
1.画出程序流程图,编写源程序:
2.用汇编程序产生目标文件:
3.用LINK.EXE程序产生可执行文件:
4.运行可执行文件:
十、考核或评价标准:
1. 检查上机步骤及调试结果:(60分)
2.程序分析正确性:(20分),
3.结合思考题答辩情况(20分),综合评定成绩。
C语言程序设计(第2版)-- 课后题答案

《C语言程序设计能力教程(第二版)》课后作业及实训题参考答案第1章进入C语言程序世界二、1. I love China!printf("we are students.\n")2. 6项目实训题参考答案1.编写一个C程序,输出以下信息:* * * * * * * * * * * * * * * * * * * *I am a student!* * * * * * * * * * * * * * * * * * * *main(){ printf("********************\n");printf(" I am a student!\n ");printf("********************\n");}2.已知立方体的长、宽、高分别是10cm、20cm、15cm,编写程序,求立方体体积。
解:main(){int a,b,c,v;a=10;b=20;c=15;v=a*b*c;printf("v=%d",v);}本程序运行结果为:v=3000第2章编制C程序的基础知识一选择题C B A B A C C二操作题,2,-8,23.000000,2.500000,-8.0000002. ABC DEFGHwhy is 21+35 equal 523.3 14 32 31 24. aa bb cc abcA N项目实训题1.定义一个符号常量M为5和一个变量n值为2,把它们的乘积输出。
#define M 5main(){ int n,c;n=2; c=M*n;printf("%d\n",c); }2.编程求下面算术表达式的值。
(1)x+a%3*(int)(x+y)%2/4,设x=2.5,a=7,y=4.7;(2)(float)(a+b)/2+(int)x%(int)y,设a=2,b=3,x=3.5,y=2.5。
python语言程序设计实训微课版答案刘立群

python语言程序设计实训微课版答案刘立群1、CIDR 技术的作用是()。
易[单选题] *A.把小的网络汇聚成大的超网(正确答案)B.多个主机共享同一个网络地址C.把大的网络划分成小的子网D.将本地IP 地址转换成全球IP 地址2、若要将一些文本内容设置为黑体字,则将文本选中,然后()。
[单选题] *A. 单击“(正确答案)B”按钮B. 单击“U”按钮C. 选择3、如果子网掩码是...,那么主机... 所在的驻留子网是()。
中[单选题] *A....B....C....(正确答案)D....4、D:编辑器移动硬盘或优盘连接计算机所使用的接口通常是______。
[单选题] *A:RS-232C接口B:并行接口C:USB(正确答案)5、73.以.jpg为扩展名的文件通常是()[单选题] *A.文本文件B.音频信号文件C.图像文件(正确答案)D.视频信号文件6、双绞线线缆色标由白橙、橙()组成。
*A白蓝、蓝(正确答案)B白棕、棕(正确答案)C白灰、灰D白绿、绿(正确答案) 双绞线()基本都已退出市场。
*7、允许多个用户可以交互方式使用计算机的操作系统是()。
[单选题] * A.分时操作系统B.批处理单道系统C.实时操作系统D.批处理多道系统(正确答案)8、一个端口的交换机的冲突域和广播域的个数分别是()。
中[单选题] *A. ,B . ,(正确答案)C. ,D. ,9、当要引用的公式与包含公式的单元格的位置无关时,可以使用()引用方式。
[单选题] *A.混合引用B.相对引用C.绝对引用(正确答案)10、计算机的性能主要决定于()。
[单选题] *A.内存容量B.磁盘容量C.CPU型号(正确答案)D.价格高低11、68.下列软件中,属于应用软件的是()。
[单选题] *A.WindowsXPB.PowerPoint 2003(正确答案)C.UNIXD.Linx12、计算机网络的应用范围不包含()。
[单选题] *A商业运用B登月(正确答案)C移动用户D家庭运用13、WPS演示文稿“动画”菜单中的“自定义动画”命令,用于设置放映时()。
C语言程序设计(第2版)-- 课后题答案.

《C语言程序设计能力教程(第二版)》课后作业及实训题参考答案第1章进入C语言程序世界二、1. I love China!printf("we are students.\n")2. 6项目实训题参考答案1.编写一个C程序,输出以下信息:* * * * * * * * * * * * * * * * * * * *I am a student!* * * * * * * * * * * * * * * * * * * *main(){ printf("********************\n");printf(" I am a student!\n ");printf("********************\n");}2.已知立方体的长、宽、高分别是10cm、20cm、15cm,编写程序,求立方体体积。
解:main(){int a,b,c,v;a=10;b=20;c=15;v=a*b*c;printf("v=%d",v);}本程序运行结果为:v=3000第2章编制C程序的基础知识一选择题C B A B A C C二操作题,2,-8,23.000000,2.500000,-8.0000002. ABC DEFGHwhy is 21+35 equal 523.3 14 32 31 24. aa bb cc abcA N项目实训题1.定义一个符号常量M为5和一个变量n值为2,把它们的乘积输出。
#define M 5main(){ int n,c;n=2; c=M*n;printf("%d\n",c); }2.编程求下面算术表达式的值。
(1)x+a%3*(int)(x+y)%2/4,设x=2.5,a=7,y=4.7;(2)(float)(a+b)/2+(int)x%(int)y,设a=2,b=3,x=3.5,y=2.5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基础实训21
5. 分解质因数
整数分解质因数是最基本的分解。
例如,90=2*3*3*5, 1960=2^3*5*7^2,前者为质因数乘积形式,后者为质因数的指数形式。
把指定区间上的所有整数分解质因数,•每一整数表示为质因数从小到大顺序的乘积形式。
如果被分解的数本身是素数,则注明为素数。
例如, 92=2*2*23, 91(素数!)。
分解:
1671861=
5845271=
(1)设计要点
对每一个被分解的整数i,赋值给b(以保持判别运算过程中i不变),用k(从2开始递增取值)试商:
若不能整除,说明该数k不是b的因数,k增1后继续试商。
若能整除,说明该数k是b的因数,打印输出"k*";b除以k的商赋给b(b=b/k)•后继续用k试商(注意,可能有多个k因数),直至不能整除,k增1后继续试商。
按上述从小至大试商确定的因数显然为质因数。
循环取值k的终值如何确定,一定程度上决定了程序的效率。
终值定为i-1或i/2,无效循环太多。
循环终值定为i的平方根sqrt(i)可大大精简试商次数,此时如果有大于sqrt(i)的因数(至多一个!)•,在试商循环结束后要注意补上,不要遗失。
如果整个试商后b的值没有任何缩减,仍为原待分解数i,说明i是素数,作素数说明标记。
(2)质因数分解乘积形式程序设计
// 质因数分解乘积形式
#include"math.h"
#include <stdio.h>
void main()
{long int b,i,k,m,n,w=0;
printf("[m,n]中整数分解质因数(乘积形式).\n");
printf("请输入m,n:");
scanf("%ld,%ld",&m,&n);
for(i=m;i<=n;i++) // i为待分解的整数
{ printf("%ld=",i);
b=i;k=2;
while(k<=sqrt(i)) // k为试商因数
{if(b%k==0)
{b=b/k;
if(b>1)
{printf("%ld*",k);
continue; // k为质因数,返回再试
}
if(b==1) printf("%ld\n",k);
}
k++;
}
if(b>1 && b<i)
printf("%ld\n",b); // 输出大于i平方根的因数
if(b==i)
{printf("(素数!)\n");w++;} // b=i,表示i无质因数
}
printf("其中共%d个素数.\n",w);
}
1671861=3*31*17977
5845271=233*25087
6. 构建横竖折对称方阵
试观察图所示的横竖折对称方阵的构造特点,总结归纳其构造规律,设计并输出n(奇数)阶对称方阵。
图 7阶横竖对称方阵
输出15阶、19阶横竖折对称方阵。
解: 这是一道培养与锻炼观察能力、归纳能力与设计能力的有趣案例。
设置2维数组a[n][n]存储n阶方阵的元素,数组a[n][n]就是数据结构。
本案例求解算法主要是给a数组赋值与输出。
一个一个元素赋值显然行不通,必须根据方阵的构造特点,归纳其构建规律,分区域给各元素赋值。
(1)构造规律与赋值要点
观察横竖折对称方阵的构造特点,方阵横向与纵向正中有一对称轴。
两对称轴所分4个小矩形区域表现为同数字横竖折递减,至4顶角元素为1。
设阶数n(奇数)从键盘输入,对称轴为m=(n+1)/2。
设置2维a数组存储方阵中元素,行号为i,列号为j,a[i][j]为第i行第j列元素。
可知主对角线(从左上至右下)有:i=j;
次对角线(从右上至左下)有:i+j=n+1。
按两条对角线把方阵分成上部、左部、右部与下部4个区,如图所示。
图对角线分成的4个区
对角线上元素可归纳到上、下部,即上、下部区域带等号即可。
上、下部按列号j的函数abs(m-j)赋值:
if(i+j<=n+1 && i<=j || i+j>=n+1 && i>=j)
a[i][j]=abs(m-j);
左、右部按行号i的函数abs(m-i)赋值:
if(i+j<n+1 && i>j || i+j>n+1 && i<j)
a[i][j]=abs(m-i);
输出时,按a[i][j]打印。
(2)程序设计
// 横竖折对称方阵
#include <stdio.h>
#include <math.h>
void main()
{int i,j,m,n,a[30][30]; // 定义数据结构
printf(" 请确定方阵阶数(奇数)n: "); scanf("%d",&n);
if(n%2==0) {printf(" 请输入奇数!");return;}
m=(n+1)/2;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{ if(i+j<=n+1 && i<=j || i+j>=n+1 && i>=j)
a[i][j]=abs(m-j); // 方阵上、下部元素赋值 if(i+j<n+1 && i>j || i+j>n+1 && i<j)
a[i][j]=abs(m-i); // 方阵左、右部元素赋值 }
printf(" %d阶对称方阵为:\n",n);
for(i=1;i<=n;i++)
{ for(j=1;j<=n;j++) // 输出对称方阵
printf("%3d",a[i][j]);
printf("\n");
}
}
7. n个1 整除
一个整数为n个1,它能被指定正整数p(约定为个位数字非5的奇数)整除,问n至少为多大?
输入p,输出n。
p=57, n=
p=2011, n=
8. 基于素数的代数和
定义s(n)=1*3-3*5-5*7+7*9+9*11±…-25*27±…±(2n-1)*(2n+1)
(一般项(2k-1)*(2k+1)的符号识别:当(2k-1)与(2k+1)中有且只有一个素数,取“+”;其余取“-”。
)
1) 求s(1000)。
2) 设1<=n<=1000,当n为多大时,s(n)最大。
3) 设1<=n<=1000,当n为多大时,s(n)最小。
9. 三组平方
把1,2,...,9这9个数字分成三个组,每组至少一个数字,使得这三个组中的所有数字分别能排列成平方数a,b,c(a<b<c)。
设计程序,求出满足要求的所有分法(若某一分法中某组的数字能排列成不同的平方数,例如1369=37^2,1936=44^2,这只算一种分法)。
