精品—国债期限结构-mba智库百科-国债期限 国债期限结构
我国国债利率期限结构存在的问题及建议

我国国债利率期限结构存在的问题及建议[摘要] 由于我国的金融市场还处于发展阶段,利率市场化不够发达,因此我国利率期限结构还存在很多不合理的地方。
本文对期限结构进行了剖析,指出了存在的问题,基于这些分析,提出了进一步健全我国债券市场利率期限结构的建议。
[关键词] 国债利率期限结构投资行为债券市场从1981年我国开始恢复了国债发行,在二十多年里国债市场有了长足的发展,不仅国债发行规模逐渐扩大,国债品种越来越多样化,而且国债发行和流通机制也逐步优化。
同时国债的发行方式日益市场化,经历了从传统的行政动员和行政分配,到1991年的承购包销,进而到现在的“基数认购、区间投标、差额招标、余额分销”,以及“自由投标、变动价位、二次加权、全额招标”的招标方式的演变。
我国债券市场经历了实物券柜台市场、上海证券交易所为代表的场内债券市场和银行间债券市场为代表的场外债券市场三个主要阶段的发展过程。
1997年6月以后商业银行退出交易所债券市场,将其所持有的国债、融资券和政策性金融债统一托管于中央国债登记结算公司,并可进行债券回购和现券买卖,银行间债券市场就此启动。
截至2004年底,银行间债券市场开户的投资者总数达5354家,涵盖商业银行、非银行金融机构、信用社、证券公司、保险公司及其它非金融机构类投资者,其组织成员已经基本覆盖了我国金融体系,一个开放的、具有较大规模的合格机构投资者市场已经形成。
2004年财政部通过银行间债券市场发行了14期共亿元记账式国债,其中跨市场国债有8期共亿元,占整个发行量的%。
但由于我国债券市场起步较晚,目前还不够完善,存在着以下问题。
一、我国国债期限结构存在的问题1.国债期限结构较为单一由于我国短期和长期国债的发行规模较小,15年期以上的国债品种较少,5年~15年期国债在可流通国债中占绝对比重。
从资金供求情况来看,市场上的长期资金供大于求投资行为短期化证券投资行为短期化。
我国的资本市场是一个新兴市场,也是一个转轨的市场。
最新-国债市场的利率期限结构分析与20年期国债的投资机会 精品

国债市场的利率期限结构分析与20年期国债的投资机会一、目前国债市场的利率期限结构与收益率分析目前,上交所国债市场上仅有8只国债品种,均为中长期附息国债。
在目前宏观经济平稳运行,市场利率持续保持低水平的情况下,国债无疑成为各类机构投资者组合投资的必选投资工具。
其安全性,流动性以及相对于银行存款较高的收益性受到投资者的普遍青睐。
8只国债品种票面利率随着利率下调逐渐走低。
其中发行最早的96国债6,票面利率高达1183,到2001年发行的21国债3固定票面利率仅为327。
但是,对于固定收入债券而言,票面利率高低仅能表征其发行时债券所具有的本征价值。
就上市交易的国债而言,由于价格波动,票面利率无法真实反映某一国债内在投资价值。
因此,必须借助于现金流贴现模型以及利率期限结构分析来评价国债的内在投资价值。
对于附息国债,评价其内在价值的贴现模型为其中债券价格每年的息票债券的面值内在收益率利用该模型可以计算出目前上交所上市的8只国债的内在收益率,如表1所示。
证券代码国债名称到期期限年内部收益率票面利率发行金额亿元期限年起息日到期日00069696国债64843411183250101996614201961400089696国债821927285620191996111201911100970497国债460653329781301019979520199500990599国债5602233132816081999820201982000990899国债8711733133200101999923201992301000420国债4878259一年存款利率+浮动062140102000523201952301001020国债106293256一年存款利率+浮动0381207200011142019111401010321国债3615313327120720014242019424另一方面,我们知道,债券的收益率与到期期限有一定关系,这种关系称为利率的期限结构。
债券发行了解债券的期限结构

债券发行了解债券的期限结构债券发行:了解债券的期限结构债券作为一种重要的金融工具,被广泛用于筹集资金和扩大企业规模。
债券的期限结构是指债券在发行时确定的到期时间,它在债券市场中起着重要的作用。
本文将对债券的期限结构进行深入解析,以帮助读者更好地了解债券发行。
一、短期债券短期债券是指到期时间在一年以内的债券。
这类债券通常以短期利率为基准确定其利息,比如公开市场操作利率等。
短期债券的特点是流动性较高,回报较低。
由于期限较短,债券持有者往往可以在较短时间内将其兑换成现金,因此相对风险较小。
二、中期债券中期债券是指到期时间在一年至十年之间的债券。
这类债券的利息通常由市场供求关系和市场预期决定。
中期债券的特点是回报稳定性较好,相对较为灵活。
其期限长于短期债券,但相对于长期债券而言,风险较小。
对于投资者来说,持有中期债券可以在一定程度上平衡流动性和风险。
三、长期债券长期债券是指到期时间在十年以上的债券。
这类债券常常以长期利率为基准确定其利息,比如国债利率等。
长期债券的特点是回报相对较高,但因其期限较长,其持有者需要承担更大的风险。
由于长期债券的流动性较差,投资者在持有期间往往需要考虑到市场波动等因素对债券价格的影响。
四、零息债券零息债券是指在发行过程中不支付现金利息的债券。
其回报主要来自于债券在到期时的折价或是溢价。
这类债券通常用于企业资金筹集或是投资者的投资组合调整。
零息债券的特点是在投资期间没有支付利息,投资者可以通过购买低折扣的零息债券,在到期时获得额外的回报。
五、可转换债券可转换债券是指在一定期限内可以将债券转换为公司股票的债券。
这类债券在发行时通常享有较低的利率,但投资者可以在特定时间段内将债券转换为股票,从而获得更高的回报。
可转换债券的特点是投资者可以根据市场行情和个人需求自主决定是否转换为股票,具有一定的灵活性。
六、固定利率债券和浮动利率债券固定利率债券是指在债券发行时确定了固定利率的债券。
这类债券的利息在持有期间保持不变,投资者可以在购买时就确定未来的回报。
宏观经济环境中的国债利率期限结构

于短期国债。
03 宏观经济环境对国债利率 期限结构的影响
经济周期对国债利率期限结构的影响
经济繁荣期
随着经济增长和就业率的提高,企业 和个人的收入增加,对未来经济形势 的预期也较为乐观,这会推动国债利 率期限结构上升。
经济衰退期
相反,当经济处于衰退期时,企业和 个人的收入减少,对未来经济形势的 预期也变得较为悲观,这会导致国债 利率期限结构下降。
宏观经济环境中的国债利率期限结 构
汇报人: 2023-12-01
目录
• 引言 • 国债利率期限结构概述 • 宏观经济环境对国债利率期限结构的影响 • 国债利率期限结构的风险管理 • 国债利率期限结构的定价模型 • 结论与展望
01 引言
研究背景和意义
金融市场的稳定性和发展水平是衡量一个国家经济实力的重要指标,而国债作为 金融市场上重要的投资工具,其利率期限结构对于投资者和管理者而言都具有重 要的意义。
国债利率期限结构对宏观经济变化具有敏感性
研究结果表明,当经济增长率、CPI等宏观经济变量发生变化时,国债利率期限结构会相 应地发生变化。
研究不足与展望
研究样本有限
未考虑市场微观结构因素
本研究使用的数据样本有限,可能影响研 究结果的普遍性和适用性。
本研究未考虑市场微观结构因素对国债利 率期限结构的影响,这可能对研究结果产 生一定的影响。
通货膨胀对国债利率期限结构的影响
温和通胀
在温和通胀的环境下,物价逐渐上涨,但上涨速度较慢,这种环境下国债利率 期限结构可能会保持相对稳定。
高通胀
然而,当通胀率较高时,物价快速上涨,货币购买力下降,这会导致国债利率 期限结构上升,以补偿投资者因物价上涨而遭受的购买力损失。
我国国债期限结构分析
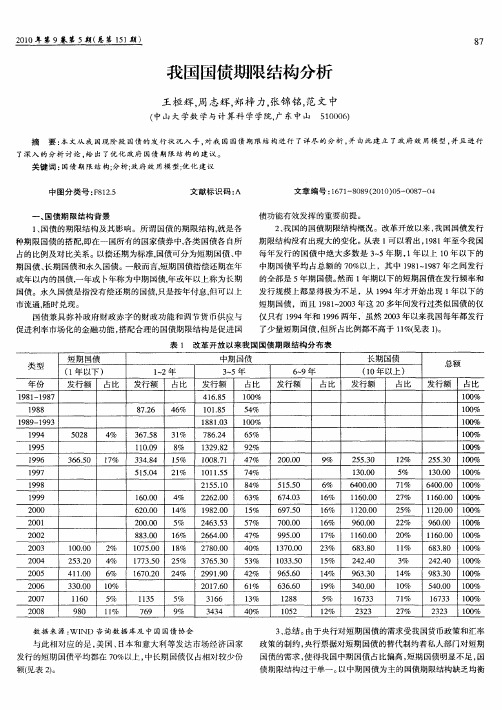
的全部 是 5 年期 国债 。 而 1 然 年期 以下 的短期国债在发行频率和
发行规 模上都显得极为不足 ,从 19 9 4年才开始出现 1 年以下的 短期国债 ,而且 1 8 ~ 0 3年这 2 9 12 0 0多年间发行过类似国债 的仅
1 Oo 6 .0 6 00 2 .0 2 0o 0 .0 8 3o 8 .0 1 7 .0 0 50 l 7 .0 7 35 1 7 .0 6 02
4 % 1 % 4 5 % 1 % 6 1 % 8 2 % 5 2 % 4
2 6 .0 2 20 1 8 .0 9 20 2 6 .3 4 35 2 6 .0 6 40 2 8 .O 7 00 3 6 .0 7 53 2 919 9 .0 2 l .O 0 76
长期 国债
6 9年  ̄ 发 行 额 占 比 (O年 以上 ) 1 发行 额 占 比
总额
发行 额 占比
10 o % lo 0 % 1o 0 %
1 % 0o
占 比
10 o % 5 % 4 10 0 %
6 5%
5 8 02
4%
36 58 7.
31 %
78 2 6.4
1 9 95 1 9 96 1 9 97
1 8 99
1 OO 1 .9 3 65 6 .O 1 % 7 3 48 3 .4 5 50 1 .4
8 % 1 % 5 2 % 1
1 2 .2 3 98 1 o .1 o 87 1 1 .5 0 15
21 1 55.O
9 % 2 4 % 7 7 % 4
什么是国债期限结构

什么是国债期限结构国债结构,是指一个国一家各种性质债务的互相搭配以及债务收入来源和发行期限的有机结合。
主要包括国债期限结构、利率结构、品种结构等。
造成国债结构不合理的原因在于国债发行市场的不完善。
中国国债结构不合理对国债风险的影响主要体现在两个方面:第一,品种结构不合理。
主要体现在凭证式国债发行量过大对发债人的潜在风险方面。
按当年凭证式国债发行额与当年全部国债发行额之比计算,1997年的为67.65%, 1998年的为57.8%, 1999年的为38.1%。
凭证式国债则凭借其代理发行机构网点多,购买方便,受到了居民个人的欢迎,在一定程度上弥补了国债市场不发达的缺陷。
但我们目前发行的凭证式国债都有.提前兑付条款,这给发行人带来潜在的风险。
提前兑付的条款原则上要求发债人必须保持一定的备付金比率。
现在凭证式国债的备付责任是由代理发行银行承担的。
第二,国债期限结构不合理。
国债期限结构主要反映每年国债发行额或是国债余额中各种期限的国债比重。
中国国债的期限单一,缺乏合理的分布,发行的国债绝大多数是2至5年的,短期国债和长期国债很少,从而造成还债压力的不均衡分布。
“九五”计划期间的债务压力急剧增加的原因正是以往国债期限不合理和随着1994年以来国债规模的急剧膨胀而又没有及时调整国债期限结构造成的。
因此,期限结构中存在的问题不可小视,它目前已成为影响国债风险的重要因素。
如果出现资金紧张的现象,代理发行银行首先是要保证其自身的支付需要,可能就会影响凭证式国债提前兑付条款的实现.损毁国债的信誉;如果出现了较极端的情况,比如,市场利率大幅上涨,凭证式国债的提前兑付就可能会集中出现,发债人必须增加发债规模以应付兑付,又可能拉动市场利率更加上扬,提前兑付的投资者就更多,陷入恶性循环,有可能迫使政府过度发行国债。
设计国债期限结构时应考虑的因素1国债期限结构应当与财政支出结构相适应。
应根据政府需要资金的性质来决定国债发行期限的长短。
我国国债利率期限结构存在的问题及建议

我国国债利率期限结构存在的问题及建议问题概述国债是政府在国内和国际资本市场筹措资金的重要工具,也是国家财政收支的重要途径之一。
国债的期限结构是指不同期限的国债利率水平之间的关系,其反映了市场对未来经济发展的预期和风险偏好的变化,对宏观经济运行、货币政策实施、债券市场发展等方面都有一定的影响。
但是,我国国债利率期限结构存在以下问题:1. 债券收益率曲线过于平缓我国国债利率期限结构过于平缓,这可能会给借贷人产生一种误导,让他们觉得风险并不增加,从而不愿意支付更高的利率。
这种情况将会使整个债券市场的利率结构变得非常平坦,并影响银行和其他金融机构的贷款决策。
2. 期限短的国债利率过高我国政府在短期债券市场上的财政资金需求相对较大,而且短期债券的供给又相对较少,这导致短期国债的利率过高。
同时,由于市场对于未来经济发展的预期通常是向上的,这种预期会造成短期国债的收益率比长期国债更高,从而导致短期国债的需求过度增加。
3. 投资者对于未来的预期不同导致议贴现率的波动国债利率期限结构方程的变化主要来自于政策因素、宏观经济预期和市场风险偏好的变化,而这些变化又受到不同投资者对未来的预期及预期与实际表现之间的差距的影响。
当这些因素的变化引起议贴现率波动时,对经济主体和市场会带来一定的影响。
建议方案为了解决上述问题,我们提出以下建议:1. 增加政府债券发行量在国内和国际市场上增加政府债券的发行量可以缓解短期债券供给不足的问题,有效避免影响短期国债的利率水平过高。
2. 扩大债券市场规模为了提高长期债券的投资需求,我们应该加大债券市场的深度和广度,增加境内外投资者对于债券市场的信心和热情。
这样可以从根本上改变债券利率期限结构偏平的状况。
3. 加强政策引导政府可以通过货币政策、财政政策和税收等多重手段来引导市场实现对期限结构向上倾斜的预期,从而提高短期债券的供给与流动性,避免出现价格被外界冲击的情况。
4. 完善信息披露制度债券市场的长期健康发展需要完善的信息披露制度和规范的投资者教育,可以较好地提升投资者的投资信心和理性参与债券市场。
什么是债券的期限结构

什么是债券的期限结构在金融世界里,债券是一种常见的投资工具。
而债券的期限结构,则是理解债券市场的一个重要概念。
首先,咱们来通俗地讲讲什么是债券。
想象一下,你把钱借给了一个机构或者政府,他们给你一张借条,承诺在未来的某个时间连本带利地还给你,这张借条就是债券。
而这个未来的时间,就是债券的期限。
那债券的期限结构呢,其实就是不同期限的债券在市场上的利率关系。
简单说,就是比较一下 1 年期债券的利率、3 年期债券的利率、5年期债券的利率等等,看看它们之间有什么样的规律和特点。
为什么要研究债券的期限结构呢?这对投资者和整个金融市场都非常重要。
对于投资者来说,了解债券的期限结构能帮助他们做出更明智的投资决策。
比如说,如果短期债券的利率比较高,而你又预计未来利率会下降,那投资短期债券可能更划算;反之,如果长期债券的利率诱人,而你觉得利率会长期保持稳定或者上升,长期债券也许是个不错的选择。
对于金融市场来说,债券的期限结构反映了市场对经济前景的预期。
如果市场普遍认为经济会增长,通货膨胀可能上升,那么长期债券的利率通常会上升,期限结构可能会变得更陡峭。
反之,如果市场预期经济衰退,利率可能下降,期限结构可能会变得平缓。
接下来,咱们深入了解一下债券期限结构的几种常见形态。
第一种是向上倾斜的期限结构,也叫正常的期限结构。
这意味着长期债券的利率高于短期债券的利率。
这通常发生在经济扩张时期,市场预期未来通货膨胀会上升,所以要求更高的回报来补偿长期投资的风险。
第二种是向下倾斜的期限结构,也叫反向的期限结构。
在这种情况下,短期债券的利率高于长期债券的利率。
这可能暗示市场预期经济即将衰退,未来利率会下降。
第三种是水平的期限结构,就是短期和长期债券的利率差不多。
这一般表示市场对未来经济和利率的走势没有明确的预期。
那债券的期限结构是怎么形成的呢?有几个关键因素在起作用。
首先是市场对未来利率的预期。
如果大家觉得未来利率会上升,那么长期债券的利率就会相对较高,以吸引投资者购买。
论我国国债的期限结构及其政策建议

定 的风 险 , 体 表 现 在 : 具
1 .中 国 国 债 总 体 平 均 期 限 较 短
和 1 年 期 的 长 期 债 ( 见 表 1。 O 参 )
1 9 年 、 9 8 年 和 1 9 年 3 年 的 短 期 国 97 19 99 债 没 有 发 行 ,o O 年 又 恢 复 了 短 期 国 债 的 发 20 行 , 是 所 占 比 例 很 小 ( 见 表 2 。从 总 体 来 看 , 但 参 ) 短期 国债相对 于国债 总规模来 说 比例较 小 , 期 限 较 长 的 1 年 乃 至 2 年 的 长 期 国 债 数 量 较 0 O
国 债 的 反 复 发 行 虽 然 可 以 筹 到 长 期 资 金 , 其 但
l9 90
l 9I 9 l9 92 l9 93 I9 94 l9 95 19 96 l9 97 5 7 0 2
J
9 6 34 l3 7 0 7
I 9 41 9 8l 8 4
一
,
且 发 行 节 奏 和 发 行 期 限 无 均 衡 性 。 我 国
注 : ・为2 0 1 0 0年 1 月底 发行数量 。2 以上数据 根据 历年国债发行数据整理得到 1
1 8 年 至 1 9 年 的 国 债 多 是 3 年 期 、 年 期 9 1 9 7 5 和 1 年 期 ,9 4 年 开 始 有 了 半 年 、 0 19 1年 和 2 年
进 ~ 级 市 场 的 发 行 和 二 级 市 场 的 流 通 ;反 之 ,
债 的 期 限 结 构 , 短 中 长 不 同 期 限 的 国 债 即
表 1 时间( ) 年
I 8l l 8 9 — 96 l8 97 l8 98
中 国 营债 期 限 结构 列 裹 三个 月 六个 月 一 年 二 年 三年
宏观经济环境中的国债利率期限结构

宏观经济环境中的国债利率期限结构国债利率期限结构可以理解为一个国家的财政货币政策对期限不同的国债利率的影响或调节。
国债利率期限结构反映了政府在宏观经济环境中对资金供给和需求的调节能力。
近年来,国家金融机构和学者对国债利率期限结构的重视程度越来越高,原因在于国债利率的期限结构会直接影响政府支持经济发展的能力,同时也会影响各项金融机构及市场投资者的投资行为。
一方面,国债利率期限结构可能是相对稳定的,另一方面,它也会随着宏观经济环境而变化。
在经济繁荣时期,政府将会尽量把利率作为一种重要的管理工具,以调节经济增长,把短期利率提高,以降低经济过度投资的风险,而使得长期利率也大大增加。
相反,在经济衰退时期,政府将会把利率作为激励工具,尽量降低短期利率和长期利率,鼓励投资,以促进经济发展。
此外,国债利率期限结构也会受到外部因素的影响,比如国际投资者对国内利率的预期,货币贬值,以及国际金融市场投资者在流动性上的需求等因素。
国债利率期限结构

国债利率期限结构模型静态估计的实证比较制作人:进击的樱桃荚国债利率期限结构模型静态估计的实证比较一、引言利率是金融市场的核心,准确构造利率期限结构,对于固定收益证券、利率衍生工具的定价及利率风险管理等具有重要意义。
在成熟的金融市场中,国债利率最直接反映了市场的交易者对市场资金供求状况的真实感受以及资金的准确价格,因此可以根据二级市场上国债的交易价格及变动来估计和分析市场基准利率的期限结构及其动态变化。
随着我国利率市场化改革的进展和债券市场的规范发展,中央银行将逐步放松对商业银行存贷款利率的管制,更多地依靠公开市场业务形成市场基准利率。
因此,根据债券交易价格构造利率期限结构,将越来越具有实用性。
利率期限结构是在某个时点上不同期限的利率所组成的一条利率曲线。
它是债券市场中最为重要的概念之一,体现了利率与剩余期限之间的关系。
从横截面的角度看,利率期限结构可以用一条无风险债券的收益率曲线表示。
当前市场上构建收益率曲线用的是到期收益率,而到期收益率编制的曲线只能得到收益率曲线的一个大致近似,即期收益率才是收益率曲线的精确反映。
然而即期收益率并不能直接从市场上观察,因此只有通过拟合估计才能得到。
利率期限结构的估计方法有很多,常用的主要有息票剥离(Bootstrap method)、样条估计(Spline approximation)和Nelsen—Siegel方法(包括改进的Nelsen—Siegel—Svennson方法等,以下简称NS和NSS模型。
考虑到期限结构构造方法的多样性和中国债券市场的特殊性,有必要对上述不同模型方法进行比较系统的横向对比研究。
本文选择Nelson—Siegel模型、Nelsen—Siegel—Svennson模型、多项式样条法及指数样条法这4种最常用的构造方法进行实证分析,研究其不同构造特点及各自的适用性问题。
选取2007年12月10日的全国间固定收益债券的各项数据,运用多项式样条、指数样条、NS、NSS 拟合数据,做出参数估计,并给出利率期限结构曲线、债券定价误差,最后比较分析结果。
国债期限结构问题初探

3 发 行 各 种 不 同 期 限 的 国 债 有 利 于 政 府 合 理 安 排 . 债 务 的 偿 还 。 期 限 结 构 单 一 容 易 造 成 国 债 偿 还 期 过 于 集
各 自所 占的 比 例 及 对 比 关 系 。研 究 国 债 的 期 限 结 构 问题
的重 要意 义在 于 ,国债 兼具 弥 补政 府 的财政 赤 字 的财政 功 能 和调 节货 币供 应 与货 币流 通 效率 的金 融功 能 ,而这
一
手 续 费 以及 券 面 印制 费和 债务 资金 的在 途 占压 费用 。发 行 不 同 期 限 的 国 债 ,有 利 于 降 低 发 行 利 率 。 如 果 政 府 只 发 行 一种 期 限的 国债 ,会 造成 相 应市 场 资金 的需 求大 于 供 给 , 而 引起该 品种 的发 行利 率上 升 。其 次 , 利率 市 从 在 场 化 的 条 件 下 ,市 场 利 率 随 着 经 济 周 期 的 波 动 而 变 化 。 在 不 同期 限的 国债 中进行 选 择 ,有 利于 政 府相 机 行 事 , 减小偿 债 成本 。 在经 济 衰退 时 ,发行 固定利 率 的长期 国 债可 以缩小利 息成本 开 支 ;在 经济 繁 荣 时期 ,市场利 率 高 , 府应 该 尽量避 免发行 长 期 国债 。 政
我国国债期限结构分析_王桓辉
本,包含着降低发行利率、手续费以及券面印制费和债务资金的 在途占压费用。发行不同期限的国债,有利于降低发行利率。如果 政府只发行一种期限的国债,会造成相应市场资金的需求大于供 给,从而引起该品种的发行利率上升。其次,在利率市场化的条件 下,市场利率随着经济周期的波动而变化。在不同期限的国债中 进行选择,有利于政府相机行事,减小偿债成本。在经济衰退时, 发行固定利率的长期国债可以缩小利息成本开支;在经济繁荣时 期,市场利率高,政府应该尽量避免发行长期国债。
正建立效用模型,求出各个期限的国债所带来的效用,从而能为
国家的债券发行作出决策。
(二)模型建立。
1、消费者需求。根据流动性偏好,人们普遍比较喜欢短期流
动性较高的债券,随着债券期限的增加,人们对它的需求应该是
递减的。为了简单起见,我们假设债券的需求和期限成线性关系,
更为直观的,我们假设总共有 800 人参与购买债券,期限每多 1
为了更加合理,我们采用加权平均,这里我们要引入一个权 重,由于在决定政府发债行为中,人们的满意度应该是首先要得 到考虑的,因为政府融资时先要考虑人们的需求,这样才能成功
我们分别求出从第一年到第十年的效用,十二年,十五年的 效用(见下表)
债券期限 三月 九月 六月 效用 160 169 165
一年 二年 三年 四年 五年 六年 七年 173 182 187 186 184 179 173
为了?加合?我们采用加权平均这?我们要引入一个权重由于在决定政府发债?为中人们的满意度应该是首先要得到考虑的因为政府融资时先要考虑人们的需求这样才能成功债券期限效用三月160九月169六月165一?173二?182三?187四?186我们分别求出从第一?到第十?的效用十二?十五?的效用见下表五?184六?179七?173八?164九?154十?十二?142115十五?66三模型讨论与分析
什么是债券期限结构如何分析它

什么是债券期限结构如何分析它在金融领域,债券期限结构是一个重要的概念。
它不仅对投资者的决策有着关键影响,也能反映出市场的预期和经济的状况。
那么,究竟什么是债券期限结构?又该如何对其进行分析呢?让我们一起来探讨一下。
债券期限结构,简单来说,就是在某一特定时点,不同期限债券的收益率与到期期限之间的关系。
它以收益率曲线的形式呈现,直观地展示了不同期限债券的收益率水平。
想象一下,有一系列不同到期期限的债券,比如1 年、2 年、5 年、10 年等等。
每个债券都有自己对应的收益率。
把这些期限和收益率一一对应起来,连成一条曲线,这就是债券期限结构曲线。
为什么债券期限结构如此重要呢?首先,它为投资者提供了一个参考框架。
投资者可以通过观察收益率曲线的形状和变化,来决定投资哪种期限的债券。
其次,它对金融机构的资产负债管理至关重要。
金融机构需要根据期限结构来合理配置资产和负债,以降低风险和提高收益。
此外,债券期限结构还能反映市场对未来经济走势和通货膨胀的预期。
那么,如何分析债券期限结构呢?一种常见的方法是观察收益率曲线的形状。
通常情况下,收益率曲线可能呈现出以下几种形状:向上倾斜的收益率曲线,也称为正常的收益率曲线。
在这种情况下,长期债券的收益率高于短期债券的收益率。
这通常意味着市场预期经济增长、通货膨胀上升,或者投资者对长期投资要求更高的回报。
向下倾斜的收益率曲线,又称倒置的收益率曲线。
此时,长期债券的收益率低于短期债券的收益率。
这可能是市场预期经济衰退、通货膨胀下降的信号,也可能反映出短期资金紧张而长期资金相对充裕的状况。
水平的收益率曲线,表示不同期限的债券收益率大致相同。
这可能暗示市场对未来经济走势的不确定性较大,或者短期和长期的供求关系相对平衡。
除了观察形状,我们还可以比较不同时期的收益率曲线。
如果收益率曲线整体上移,意味着债券的收益率普遍上升,可能是由于市场利率上升、通货膨胀预期增强等原因。
反之,如果收益率曲线整体下移,则表示债券收益率普遍下降,可能反映了市场利率下降、经济增长放缓等情况。
国债管理

名词解释1公(国)债期限结构国债期限结构是指不同期限的国债占国债总量的比例,是政府债务结构的重要组成部分,对国债的顺利发行、流通、偿还以及政府对经济的调控都有重要的影响。
2记账式国(公)债记账式国债又名无纸化国债,准确定义是由财政部通过无纸化方式发行的、以电脑记账方式记录债权,并可以上市交易的债券。
3公(国)债的负担率国债负担率又称国民经济承受能力,是指国债累计余额占国内生产总值( GDP) 的比重。
这一指标着眼于国债存量,反映了整个国民经济对国债的承受能力。
国际公认的国债负担率的警戒线为发达国家不超过60%,发展中国家不超过45%。
4公债管理政府围绕公债运行过程所进行的决策、组织、规划、指导、监督和调节等一系列工作。
5纯券过户纯券过户简称FOP(Free of Payment),是指债券交割不以资金支付为条件的结算方式,即结算双方只要求中央结算公司办理债券的交割,款项支付自行办理。
这是一种交易双方建立在互相了解和信任基础上的一种结算方式,也是国外发达市场常用的一种结算方式。
6国债国债,又称国家公债,是国家以其信用为基础,按照债的一般原则,通过向社会筹集资金所形成的债权债务关系。
国债是由国家发行的债券,是中央政府为筹集财政资金而发行的一种政府债券,是中央政府向投资者出具的、承诺在一定时期支付利息和到期偿还本金的债权债务凭证,由于国债的发行主体是国家,所以它具有最高的信用度,被公认为是最安全的投资工具。
7国债对税收的平滑作用8国债期权国债期权是购买者能有权利而非义务地以一预定价格买入或卖出一特定数量的中长期债券。
若期权被执行,期权的卖方有义务交付特定的证券--实物交付。
绝大多数场外交易按期权履约价格和结算日的现货市场价格的差额进行现金结算。
现货债券期权提供了一种防止一特定证券反向利率波动的对冲方法,同时又能从有利的利率波动中获利。
9国债偿债率公债偿债率指政府当年的债务还本付息支出与财政收入之间的比例关系,它反映了财政的债务清偿能力。
投资项目管理师宏观经济政策:国债的结构

投资项目管理师宏观经济政策:国债的结构
(1)国债的期限结构
国债的期限结构是指不同期限的国债占国债总量的比例,是政府债务结构的重要组成部分。
在现代社会,长、中、短期国债要优于单一长期或短期的国债结构。
我国国债期限结构中,中期国债数量较大,长期和短期国债较少。
(2)国债的持有者结构
国债的持有者结构也叫做国债的投资人结构,是国债在不同投资群体之间的分布比例。
在我国国债持有者结构中,个人持有者所占比重较大,而机构投资者所占比重较小。
一般来讲,市场经济国家的国债持有者结构中,机构投资者所占的比重较高。
因此,提高机构投资者的国债持有比重应是我国国债结构调整的一个方向。
重庆高级经济师重点:国债的种类和结构

重庆⾼级经济师重点:国债的种类和结构2016年重庆⾼级经济师重点:国债的种类和结构 2016年的⾼级经济师考试虽然还有很久才到,但是复习的事情是绝对不能落下的。
为了帮助⼴⼤考⽣有效备考2016年⾼级经济师考试,应届毕业⽣⽹⼩编挣了了⼀些相关的知识点,希望对您通过2016年⼈⼒资源管理师考试有所帮助! 国债的种类和结构 1.国债的结构 国债结构是指⼀国各种债务的相互搭配和有机组合,选择何种国债结构是⼀国经济政策和财政政策的重要内容。
(1)国债的期限结构。
即国家长、中、短期国债的搭配。
由于长期国债的偿还期⼀般在5年以上,在此期间,国债资⾦的'使⽤权完全掌握在政府⼿中,可以安排建设周期较长的建设项⽬,有助于基础产业和基础设施的发展。
⽽短期国债由于使⽤期限较短,政府使⽤这笔资⾦会受到⼀定的限制。
因此,发⾏长期国债对国家⽐较有利。
(2)国债持有者结构。
即各类企业、机构和各阶层居民认购国债的⽐例,⼜称为国债资⾦来源结构。
国债持有者也称应债主体,其存在是国债能够发⾏的前提。
不同类型的国债持有者,其应债能⼒是不同的。
⼀般情况下,国债持有者越集中,国债的发⾏成本越低,管理越容易。
2.国债的种类 由于举债的对象、举债的⽅式和举债的⽬的不同,我国的国债种类可从不同⾓度划分: (1)按国债筹措和发⾏的期限,可分为长期国债、中期国债和短期国债。
⼀般5年期以上的称为长期国债,1年期以内的称为短期国债,介于两者之间的称为中期国债。
(2)按国债筹措和发⾏的地区,可分为内债和外债。
(3)按国债举借的形式,可分为国家借款和发⾏债券。
(4)按国债的举借对象和⽤途,可分为不同的债种。
恢复发⾏国债后,我国先后发⾏了 国库券、重点建设债券、财政债券、国家建设债券、特种国债、保值国债、转换债、特种定向债券、专项国债、定向国债和特别国债等。
除了特种国债只向企业和单位机构发⾏财政债券、专项国债和定向国债只向银⾏及⾦融机构发⾏,特种定向债券向养⽼保险基⾦、待业保险基⾦及其他社会保险基⾦定向发⾏外,其他债种均同时向企业、单位和居民个⼈发⾏。
我国国债期限结构亟待完善

我国国债期限结构亟待完善
姚新民
【期刊名称】《上海财税》
【年(卷),期】2001(000)007
【摘要】国债的期限构成是与其基本功能相匹配的,并受到国债市场投资者结构的制约。
1.国债弥补财政赤字的功能要求国债期限构成偏向中长期。
在市场经济体制下,弥补财政赤字一般说来有三种措施,即增加税收、增发通货和发行国债。
发行国债筹资仅是社会资金使用权的暂时转移,在正常情况下,一般不会招致无度的通货膨胀,它可迅速、灵活和有效地弥补财政赤字,是弥补财政赤字的一种最基本方式。
【总页数】3页(P32-34)
【作者】姚新民
【作者单位】上海证券有限责任公司
【正文语种】中文
【中图分类】F8
【相关文献】
1.我国国债市场亟待改革的完善 [J], 张大龙
2.从国债规模的迅速扩张看我国国债的期限结构 [J], 唐祥来
3.我国国债市场利率期限结构存在的问题及其完善 [J], 翟微澜;张晓明
4.我国国债利率期限结构的实证研究——基于2009年12月4日上交所17支国
债最新价格 [J], 曾幸幸
5.完善我国国债期限结构的思考 [J], 何丽华;郭君;林青
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品—国债期限结构-mba智库百科|国债期限国债期限结构国债期限中国宏观经济环境中的国债利率期限结构基于动态随机一般均衡模型的研究本文节选于沈鑫博士毕业论文第二章,三类理论分支为主线,辅以其他相关理论、典型事实和利率期限结构与政策的结合应用,对现有相关文献进行梳理。
利率期限结构理论包含三个分支:纯粹预期理论(Pure Expectations Hypothesis)、流动性偏好理论(Liquidity Preference Theory)和市场分割理论(Market Segmentation Theory)。
研究对象包含静态的收益率曲线(Yield Curve)形状及其形成原因,和动态的演变过程。
本章以三类理论分支为主线,辅以其他相关理论、典型事实和利率期限结构与政策的结合应用,对现有相关文献进行梳理。
(一)纯粹预期理论纯粹预期理论有两种形式:强纯粹预期形式和弱纯粹预期形式。
强纯粹预期形式认为长期国债收益率等于到期前预期短期收益率的几何平均值,即在无套利假设下,应用该理论可以得出当前远期利率是对未来即期利率的无偏估计的结论,其隐含假设是各到期期限的国债之间是完全可替代的或市场参与者是风险中性的,收益率曲线的形状取决于国债市场参与者对未来利率的预期;弱纯粹预期形式认为长期国债收益率等于到期前预期短期收益率的几何平均值加一个不随时间变化、但随期限变化的风险溢价(Term Premium或Risk Premium)。
纯粹预期利率很好地解释了整条收益率曲线同向变化的情况。
与此同时,由于国债价格与收益率关系式中的指数函数为凸函数,Jensen不等式使得更长期国债(20年期以上)的收益率低于长期国债收益率,这与国债市场比较发达的美国等国利率期限结构的典型事实相符。
纯粹预期理论,特别是其强形式,较为简单,如果能够通过经验事实检验,那么通过任意时刻的利率期限结构可以反解出当时市场对未来短期利率的预期。
但是,一般情况下,收益率曲线是向上倾斜且凹的,这就意味着预期短期利率将随期限的加长而变得无穷大。
这显得有悖常理,因此强纯粹预期理论逐渐被其弱形式取代。
由于弱纯粹预期理论认为长期国债收益率与到期前预期短期收益率的几何平均值相差一个固定的常数,长期收益率的变化完全由预期短期利率的变化导致,故而,即便不求出这个常数的大小,通过观察长期收益率的变化同样可以解读国债市场参与者对未来短期利率与经济形势预期的变化。
至此,判断纯粹预期理论正确与否的关键归结于该理论是否与经验事实相符。
国内外众多学者对这一问题进行了实证检验。
Campbell and Shiller(1991)的方法影响较为广泛,他们提出了两个检验方法,用以验证纯粹预期理论的一个等价命题:更加陡峭的收益率曲线意味着长、短期预期利率均会上升,反之亦然。
他们的第一个检验直接应用了弱纯粹预期理论:即加权预期短期利率的变化对收益率曲线斜率的回归。
(2.1)式的被解释变量可被视为市场对t至t+m时段内预期无误形况下,完全预期到的期限溢价(Term Spread)。
如果纯粹预期理论正确,那么回归系数(应该等于1。
第二个检验是预期t+m至t+n时段的未来利率等于该时段的当前远期利率:即长期利率变化对收益率曲线斜率的回归。
同样,如果纯粹预期理论正确,那么回归系数b应该等于1。
Gürkaynak Sack and Wright(2007)和Gürkaynak and Wright(2010) 使用时间跨度为40年的月度美国样本对这两个回归式进行了检验,结果发现第一个大于0但小于1,否定纯粹预期理论;第二个小于1、显著不为1且随n的增加变得更小。
跟据纯粹预期理论,当收益率曲线更加陡峭时,长期利率应该上升,但检验结果为下降。
Shiller(1979)对此的解释是,长期收益率的波动率如此大以至于它很难被认为是预期短期利率均值的预期。
Fama and Bliss(1987)、Backus,Foresi and Mozumdar et al.(2001)、Duffee(2002)和Cochrane and Piazzesi(2005、2008)利用持有期收益率和即期收益率之间的回归对纯粹预期理论进行了检验。
由于该理论认为风险溢价为常数,因此事前(Ex-ante)超额持有期收益应为常数。
以Cochrane and Piazzesi(2008)为例:如果纯粹预期理论成立,则所有斜率系数都应该为0。
回归结果同样否定了该理论,且回归式的R2在12%至20%之间。
(二)流动性偏好理论流动性偏好理论可谓是固定收益研究领域应用最为广泛的理论分支。
该理论承认风险溢价的存在,认为与长期债券相比,短期债券的风险更小,债券市场参与者更加倾向持有短期债券,因此为了补偿长期债券持有者所面临的更多风险,长期收益率应为预期短期收益率和风险溢价之和。
正是因为风险溢价的存在,长期收益率通常高于短期收益率,使收益率曲线向上倾斜。
需要强调的是,在考虑不同交易情况时,风险溢价中的风险所指内容不同:当国债持有者意欲将国债持有至到期时,他面临的风险只有通胀风险(Inflation Risk);而当他意欲在到期前将国债出售的话,他还会因为出售日利率与当前远期利率可能不同而面临利率风险(Interest Rates Risk),或称价格风险(Price Risk)。
流动性偏好理论更多地研究第二种情况。
流动性偏好理论经历了从简单的仿射利率期限结构模型(Affine Term Structure Model),到宏观金融模型(Macro-finance Model),再到DSGE模型的发展历程。
各类模型均着重考察利率期限结构的动态过程,它们之间的最显著区别在于驱动收益率曲线变动的因素不同,宏观经济环境在利率期限结构形成过程中的作用逐步被深化。
1、仿射利率期限结构模型预测利率走势和解释利率期限结构的成因一直是金融业界与学术界十分关注的问题。
Campbell and Shiller(1991)、Cohrane and Piazzesi(2005)、Diebold and Li(2006)等学者倾向使用V AR模型预期未来利率。
但是直接假设各期限利率服从V AR过程难以保证其预测结果不存在套利机会。
而无套利一直是金融工程学科的基本假设条件,因此需要对V AR模型进行适当的调整。
仿射利率期限结构模型由此产生。
这类模型中随机折现因子(Stochastic Discount Factor,以下简称为SDF)的使用以及债券收益率的递归求解保证了无套利条件。
仿射利率期限结构模型大致包含三个部分:1. 决定利率期限结构的因子(Factor),记为X,是k*1维向量,服从V AR过程,这些因子可以是可被观察(Observed)的,或者是不可被观察到(Latent)的:其中a为k*1向量,b为k*k矩阵,c为k*1向量,t+1为k个独立同分布、服从正态分布的随机变量。
在金融数学和金融工程领域,(2.6)式多以连续时间形式存在:其中((Xt)和((Xt)分别代表漂移(Drift)系数和扩散(Diffuse)系数,它们可能与Xt有关,Wt是标准Wiener过程。
如果Xt仅是短期利率rt1,服从Ornstein-Uhlenbeck过程且漂移系数为固定常数,则该模型是V asicek(1977)模型;如果((Xt)= (( rt1)1/2,则是Cox-Ingersoll-Ross(1985)模型等。
2. 短期利率rt1是这些因子的仿射函数:3. 服从几何正态分布(Lognormal)的SDF,Mt+1:在应用时,第一部分有时以经测度变换后的风险中性(Risk-neutral)形式存在:由SDF的定义,债券价格为:Langetieg (1980)的推导指出,在(2.6)、(2.8)和(2.9)的基础上,其他期限收益率满足:其中An为常数,Bn为k*1维向量,两者由递归式定义:仿射利率期限结构模型结构简单、易于处理,且构成模型的三个部分几乎可以解释收益率曲线所有可能的变动方式(Litterman and Scheinkman,1991),因此在学术界被广泛使用(例如,Duffie and Kan,1996、Dai and Singleton,2000、Dai and Singleton,2002、Duffie,2002、Kim and Orphanides 2005、Kim and Wright,2005等)。
在这些应用中,因子Xt大多只包含三个元素,可分别代表收益率曲线的水平(Level)、斜率(Slope)与凸性(Curvature)。
以Christensen,Lopez and Rudebusch(2010)为例,该文中三个不可观测的因子满足:在这样的假设条件下,(2.10)式可近似地表示为:(2.13)式等同于Nelson and Siegel (1987)的多项式拟合。
仿射利率期限结构模型能够利用较少的变量很好地拟合利率期限结构的静态特征和动态行为,并对众多典型事实进行合理地解释。
但是由于这类模型的初始用途是预期未来利率,决定利率期限结构的因子都是不可观测的,没有响应的经济学意义,从而无从考察利率期限结构的形成原因(Rudebusch and Wu,2008) 和利率与宏观经济变量之间的联系(Andreasen,2008)。
为了解释形成利率期限结构的经济学原因,学者们在仿射利率期限结构模型的基础上提出了宏观金融模型。
2、宏观金融模型宏观金融模型将一些重要的宏观经济变量视为决定利率期限结构的因子,考察宏观经济环境对形成收益率曲线的作用和影响。
按照引入宏观经济变量方式的不同,宏观金融模型又可细分为简约宏观金融模型(Simple Macro-finance Model)和结构宏观金融模型(Structural Macro-finance Model)。
3、基于消费的资本资产定价模型仿射利率期限结构模型和宏观金融模型的实证分析结果较好,可以完美地拟合向上倾斜且凹的收益率曲线,但是它们使用的SDF仍是基于统计意义并考虑到处理的难以程度之后而得出的。
在金融资产定价研究领域,另一类研究方法是使用通过消费效用最大化得到的SDF对金融资产进行定价,即基于消费的资本资产定价模型(The Consumption Capital Asset Pricing Model,CCAPM)。
这类模型的SDF具有微观经济学基础,因此一些学者意欲通过CCAPM的SDF研究利率期限结构问题。
但是在这一理论应用之初,即便所有其他变量使用随意性较大的外生过程刻画,模型仍无法得出收益率曲线的最基本事实向上倾斜,即风险溢价为正数。
