高斯消元法c++代码
C++实验报告高斯消元法

高斯肖元法C++上机实验报告学生姓名: 学 号: 专业班级: 实验类型: 综合一 实验项目名称全选主元高斯消去法解线性方程组 二 实验原理设有n 元线性方程组(考虑便于C++程序数组表示,方程的下标从0开始),0000110,1100000110,111101,111,111n n n n n n n n n n a x a x a x b a x a x a x b a x a x a x b ---------+++=⎧⎪+++=⎪⎨⎪⎪+++=⎩写为矩阵形式为Ax=b,其中A 为线性方程组的系数矩阵,x 为列向量,是方程组的解,b 也是列向量.一般来讲,可以假定矩阵A 是非奇异阵。
(n 阶矩阵A 的行列式不为零,即 |A|≠0,则称A 为非奇异矩阵)00010,10111,1,01,11,1n n n n n n a a a a a a A a a a ----⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,011n x x x x -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ ,011n b b b b -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦将系数矩阵A 和向量b 放在一起,形成增广矩阵B :00010,010111,11,01,11,11(,)n n n n n n n a a a b a a a b b A b a a a b -----⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦全选主元消去就在矩阵B 上进行,整个过程分为如下两个步骤: 第一步:消去过程。
对于k 从0开始到n-2结束,进行以下三步。
1. 首先,从系数矩阵A 的k 行k 列开始的子矩阵中选取绝对值最大的元素作为主元素。
例如:11,max 0i j ij k i n k j na a ≤<≤<=≠然后交换B的第k行与第1i行,第k列与第1k列,这样,这个子矩阵中具有最大绝对值的元素被交换到k行k列的位置上.2.其次,进行归一化计算。
计算方法为:/,1,,1/kj kj kkk k kka a a j k nb b a==+-⎧⎪⎨=⎪⎩3.最后进行消去计算:,,1,,1,1,,1 ij ij ik kji i ik ka a a a j i k nb b a b i k n=-=+-⎧⎪⎨=-=+-⎪⎩第二步,回带过程:111,111/,2,,1,0 n n n nni i ij jj ix b ax b a x i n-----=+=⎧⎪⎨=-=-⎪⎩∑三代码的实现整个程序分为5个独立文件,Matrix.h文件中包括矩阵类Matrix的定义,Matrix.cpp文件中包括该类成员函数的实现,LinearEqu.h文件中包括线性方程组类LinearEqu的定义,LinearEqu.cpp文件中包括该类的成员函数实现文件;7-9.cpp文件包括程序的主函数,主函数中定义了一个类LinearEqu的对象,通过这个对象求解一个四元线性方程组。
列主元高斯消元法的C语言编程

基本思想:用高斯消元法求解线性方程组时,为避免小的主元,在进行第 k 步消元前,应该在第 k 列 元素 aik (i k , , n ) 中找出第一个出现的绝对值最大者, 例如 | aik k | max | aik | , 再把第 ik 个方程与第 k
k ≤i≤n (k ) (k ) (k )
x[k-1]=0.0; for(j=k+1;j<=n;j++) x[k-1]+=A[k-1][j-1]*x[j-1]; x[k-1]=(A[k-1][n]-x[k-1])/A[k-1][k-1]; } //在屏幕上输出结果 for(i=0;i<=n-1;i++) printf("%f\n",x[i]); } void main() { double A[N][N+1]={{0,2,-0.1,7,76.2},{6,0,3,-5,15},{3,1,2,5,86},{2,4,1,0,48}}; double x[N]={0}; Gause_pivot(N,A,x); }
个方程进行交换,使 aik k 成为主元。我们称这个过程为选主元。由于只在第 k 列元素中选主元,通常也称 为按列编程
列主元高斯消元法的 C 语言程序代码如下: #include<stdio.h> #include<math.h> #include<iostream.h> #define N 4 void Gause_pivot(int n,double A[N][N+1],double x[]) { //高斯消元 int i,j,k; for(k=1;k<=n-1;k++) { //选主元 int ii,jj,kk,row; double max,temp; ii=1;kk=k; max=A[ii-1+(kk-1)][kk-1]; for(jj=ii+1;jj<=n;jj++) { if (fabs(A[jj-1+(kk-1)][kk-1])>fabs(max)) { max=A[jj-1+(kk-1)][kk-1]; row=jj+(kk-1); } } for(ii=1;ii<=n+1;ii++) { temp=A[kk-1][ii-1]; A[kk-1][ii-1]=A[row-1][ii-1]; A[row-1][ii-1]=temp; } for(i=k+1;i<=n;i++) for(j=k+1;j<=n+1;j++) A[i-1][j-1]-=A[k-1][j-1]*A[i-1][k-1]/A[k-1][k-1]; } //回代求解 x[n-1]=A[n-1][n]/A[n-1][n-1]; for(k=n-1;k>=1;k--) {
实验三 编程实现列主元高斯消去法

实验三编程实现列主元高斯消去法1.实验目的:实现高斯主消元法,对计算过程加深理解。
2.实验内容:编写c++程序,实现对角占优方程组的编程求解。
3.实验步骤1、设计方程组的存储为二位数组,最大方程组数为100,第i行j列的元素值代表第i个方程的第j个系数,输入时没有的系数项填0。
2 对于每个方程按主消元法从0~n-1依次消元。
3迭代求解,对于第i个未知数的值,依次迭代i+1~n-1已求出的结果4.实验结果分析:对于除数很小的情况程序不能很好的解决,对于不是对角占优的也不能搜索出主元素,以后在进一步解决上述问题。
#include<iostream>using namespace std;const int MAX=100;double str[MAX][MAX];int main(){while(1){cout<<"输入方程组个数0<n<100"<<endl;int n,m,i,j,k,flag=0;cin>>n;if(n<=0||n>=100)break;cout<<"输入方程组的系数"<<endl;for(i=0;i<n;i++){for(j=0;j<=n;j++){cin>>str[i][j];if(i==j&&str[i][j]==0)flag=1;}}if(flag==1){cout<<"方程组不是对角占优的,此程序不能解决"<<endl;system("pause");return 0;}for(i=0;i<n;i++){for(j=n;j>=i;j--)//对角变一str[i][j]/=str[i][i];for(k=i+1;k<n;k++)//方程消元{double tem=str[k][i]/str[i][i];for(j=i;j<=n;j++){str[k][j]-=str[i][j]*tem;}}}double ans[MAX]={0};ans[n-1]=str[n-1][n];for(i=n-2;i>=0;i--){ans[i]=str[i][n];for(j=n-1;j>i;j--)ans[i]-=str[i][j]*ans[j];}for(i=0;i<n;i++)cout<<"X"<<i+1<<" = "<<ans[i]<<endl;system("pause");}}。
高斯方法解线性方程组c程序

高斯消去法和高斯主元消去法解线性方程组:高斯消元法:#include<stdio.h>#include<math.h>main(){int gauss(int n,double a[],double b[]); int i;double a[3][3]={{3,-1,4},{-1,2,-2},{2,-3,-2}}; double b[3]={7,-1,0};if(gauss(3,&a[0][0],b)!=0)for(i=0;i<=2;i++)printf("\nx[%d]=%f\n",i,b[i]);}int gauss(int n,double a[],double b[]) {int i,k,j,p,q;double d,t;for(k=0;k<=n-2;k++){d=a[k*n+k];if(d==0)return(0);for(j=k+1;j<=n-1;j++){p=k*n+j;a[p]=a[p]/d;}b[k]=b[k]/d;for(i=k+1;i<=n-1;i++){for(j=k+1;j<=n-1;j++){p=i*n+j;a[p]=a[p]-a[i*n+k]*a[k*n+j];}b[i]=b[i]-a[i*n+k]*b[k];}}d=a[(n-1)*n+n-1];if(fabs(d)+1.0==1.0){printf("fail\n");return(0);}b[n-1]=b[n-1]/d;for(k=n-2;k>=0;k--){t=0.0;for(j=k+1;j<=n-1;j++)t=t+a[k*n+j]*b[j];b[k]=b[k]-t;}return (1);}⎪⎩⎪⎨⎧=---=-+-=+-0232122743321321321x x x x x x x x x结果:x1=2,x2=1,x3=0.5高斯全选主元法:#include<stdio.h>#include<math.h>#include<stdlib.h>main(){int gauss(int n,double a[],double b[]);int i;double a[3][3]={{3,-1,4},{-1,2,-2},{2,-3,-2}}; double b[3]={7,-1,0};if(gauss(3,&a[0][0],b)!=0)for(i=0;i<=2;i++)printf("\nx[%d]=%f\n",i,b[i]);}int gauss(int n,double a[],double b[]){int *js,i,j,L,k,is,p,q;double d,t;js=malloc(n*sizeof(int));L=1;for(k=0;k<=n-2;k++){d=0.0;for(i=k;i<=n-1;i++)for(j=k;j<=n-1;j++){t=fabs(a[i*n+j]);if(t>d){d=t;is=i;js[k]=j;}}if(d+1.0==1.0)L=0;else{if(js[k]!=k)for(i=0;i<=n-1;i++){p=i*n+k;q=i*n+js[k];t=a[p];a[p]=a[q];a[q]=t;}if(is!=k){for(j=k;j<=n-1;j++){p=k*n+j;q=is*n+j;t=a[p];a[p]=a[q];a[q]=t;}t=b[k];b[k]=b[is];b[is]=t;}}if(L==0){free(js);printf("fail\n");return(0);}d=a[k*n+k];for(j=k+1;j<=n-1;j++){p=k*n+j;a[p]=a[p]/d;}b[k]=b[k]/d;for(i=k+1;i<=n-1;i++){for(j=k+1;j<=n-1;j++){p=i*n+j;a[p]=a[p]-a[i*n+k]*a[k*n+j];}b[i]=b[i]-a[i*n+k]*b[k];}}d=a[(n-1)*n+n-1];if(fabs(d)+1.0==1.0){free(js);printf("fail\n");return(0);}b[n-1]=b[n-1]/d;for(i=n-2;i>=0;i--){t=0.0;for(j=i+1;j<=n-1;j++)t=t+a[i*n+j]*b[j];b[i]=b[i]-t;}js[n-1]=n-1;for(k=n-1;k>=0;k--)if(js[k]!=k){t=b[k];b[k]=b[js[k]];b[js[k]]=t;} free(js);return(1);}结果:x1=2,x2=1,x3=0.5。
C语言写高斯消元法

高斯消元法C语言程序及其输出结果杨学玉(33)C语言程序:#include <stdio.h>#include <stdlib.h>#include <math.h>#define N 10double a[N+1][N+1],b[N+1],x[N+1];/* 用在此处以便可以让下面的程序也调用*/main(){ int n,i,j,k;double temp;printf("请输入方程组的维数:\n");scanf("%d",&n);if(n>N){printf("错误:元素超过初设定的值%d\n",N);exit(0);}printf("开始输入各元素的值:");for(i=1;i<=n;i++){for(j=1;j<=n;j++){printf("请输入元素[%d][%d]",i,j);scanf("%lf",&a[i][j]);}printf("请输入常数b[%d]",j);scanf("%lf",&b[i]);}for(j=1;j<=n-1;j++){for(i=j+1;i<=n;i++){temp=a[i][j]/a[j][j];for(k=1;k<=n;k++){a[i][k]=a[i][k]-temp*a[j][k];}b[i]=b[i]-temp*b[j];}}fun(n,n,a,b);x[n]=b[n]/a[n][n];for(j=n-1;j>=1;j--){x[j]=b[j];for(k=n;k>=j+1;k--){x[j]=x[j]-x[k]*a[j][k];}x[j]=x[j]/a[j][j];}for(j=1;j<=n;j++){printf("x[%d]=%f\n",j,x[j]);}}/*列出高斯消元后得到的数组*/fun(int m,int n,double a[N+1][N+1],double b[N+1]) {int i,j;printf("消元后的矩阵是:\n");for(i=1;i<=m;i++){for(j=1;j<=n;j++){printf("%f",a[i][j]);}printf("\n") ;}}C语言输出结果:Mat-lab。
高斯消元法【模板】
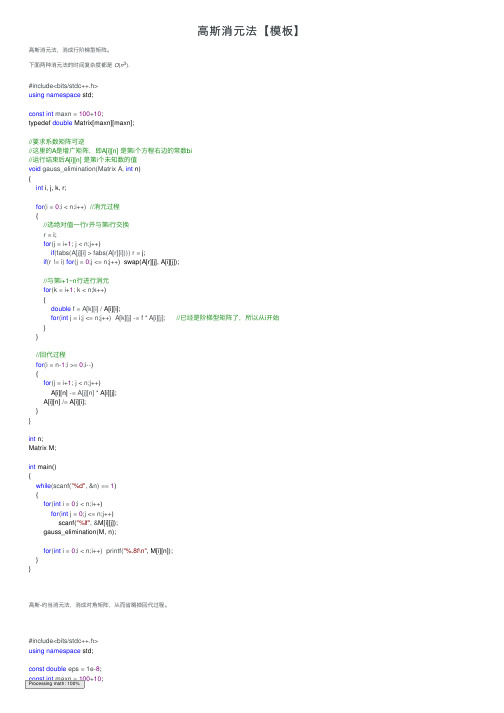
⾼斯消元法【模板】⾼斯消元法,消成⾏阶梯型矩阵。
下⾯两种消元法的时间复杂度都是 O (n 3).⾼斯-约当消元法,消成对⾓矩阵,从⽽省略掉回代过程。
#include<bits/stdc++.h>using namespace std;const int maxn = 100+10;typedef double Matrix[maxn][maxn];//要求系数矩阵可逆//这⾥的A 是增⼴矩阵,即A[i][n] 是第i 个⽅程右边的常数bi//运⾏结束后A[i][n] 是第i 个未知数的值void gauss_elimination(Matrix A, int n){int i, j, k, r;for (i = 0;i < n;i++) //消元过程{//选绝对值⼀⾏r 并与第i ⾏交换r = i;for (j = i+1; j < n;j++)if (fabs(A[j][i] > fabs(A[r][i]))) r = j;if (r != i) for (j = 0;j <= n;j++) swap(A[r][j], A[i][j]);//与第i+1~n ⾏进⾏消元for (k = i+1; k < n;k++){double f = A[k][i] / A[i][i];for (int j = i;j <= n;j++) A[k][j] -= f * A[i][j]; //已经是阶梯型矩阵了,所以从i 开始 }}//回代过程for (i = n-1;i >= 0;i--){for (j = i+1; j < n;j++)A[i][n] -= A[j][n] * A[i][j];A[i][n] /= A[i][i];}}int n;Matrix M;int main(){while (scanf("%d", &n) == 1){for (int i = 0;i < n;i++)for (int j = 0;j <= n;j++)scanf("%lf", &M[i][j]);gauss_elimination(M, n);for (int i = 0;i < n;i++) printf("%.8f\n", M[i][n]);}}#include<bits/stdc++.h>using namespace std;const double eps = 1e-8;const int maxn = 100+10;Processing math: 100%typedef double Matrix[maxn][maxn];//结果为A[i][n]/A[i][i]void gauss_jordan(Matrix A, int n){int i, j, k, r;for(i = 0;i < n;i++){//选绝对值⼀⾏r并与第i⾏交换r = i;for(j = i+1;j < n;j++)if(fabs(A[j][i]) > fabs(A[r][i])) r = j;if(fabs(A[r][i]) < eps) continue; //放弃这⼀⾏,直接处理下⼀⾏if(r != i) for(j = 0;j <= n;j++) swap(A[r][j], A[i][j]);//与除第i⾏外的其他⾏进⾏消元for(k = 0;k < n;k++) if(k != i)for(j = n;j >= i;j--) A[k][j] -= A[k][i] / A[i][i] * A[i][j];}}int n;Matrix M;int main(){while(scanf("%d", &n) == 1){for(int i = 0;i < n;i++)for(int j = 0;j <= n;j++)scanf("%lf", &M[i][j]);gauss_jordan(M, n);for(int i = 0;i < n;i++) printf("%.8f\n", M[i][n] / M[i][i]);}}Code From:《算法竞赛⼊门经典训练指南》——刘汝佳、陈锋编著。
数值分析算法C语言程序

数值分析算法C语言程序数值分析是研究数学问题的近似解法的一门学科,其中包括了各种数值方法和算法。
本文将介绍数值分析中的常见算法,并给出相应的C语言程序。
1.二分法(Bisection Method)二分法是一种求函数零点的简单且常用的方法。
该方法的基本思想是通过不断将区间进行二分,并比较中点处函数值的正负来找到零点所在的区间。
```c#include <stdio.h>double f(double x)return x * x - 2;double bisection(double a, double b, double eps)double c;while ((b - a) > eps)c=(a+b)/2;if (f(c) == 0)break;}else if (f(a) * f(c) < 0)b=c;}elsea=c;}}return c;int maidouble a = 0.0;double b = 2.0;double result = bisection(a, b, eps);printf("The root is: %lf\n", result);return 0;```2.牛顿迭代法(Newton's Method)牛顿迭代法是一种高效的求函数零点的方法。
该方法的基本思想是通过对函数进行线性逼近,不断逼近函数的零点。
```c#include <stdio.h>#include <math.h>double f(double x)return x * x - 2;double df(double x)return 2 * x;double newton(double x0, double eps) double x = x0;double deltaX = f(x) / df(x);while (fabs(deltaX) > eps)deltaX = f(x) / df(x);x = x - deltaX;}return x;int maidouble x0 = 2.0;double result = newton(x0, eps); printf("The root is: %lf\n", result); return 0;```3.高斯消元法(Gaussian Elimination)高斯消元法是一种用于求解线性方程组的方法。
高斯消去法C++代码

cout<<"请输入:"<<endl;
for(i=0;i<n;i++)
{
for(j=0;j<=n;j++)
cin>>a[i][j];
}
*/
/*方法二:
//直接进行赋值
int i,j,n=4;
double a[][5]={{0.4096,0.1234,0.3678,0.2943,0.4043},{0.2246,0.3872,0.4015,0.1129,0.1550},
{0.3645,0.192,0.3781,0.0643,0.424},{0.1784,0.4002,0.2786,0.3927,-0.2557}};
cout<<"增广矩阵为:"<<endl;
for(i=0;i<ห้องสมุดไป่ตู้;i++)
{
for(j=0;j<=n;j++)
cout<<setw(5)<<a[i][j]<<" ";
a[i][k]=a[i][k]/a[k][k];
for(j=k+1;j<n+1;j++)
a[i][j]-=a[i][k]*a[k][j]; //对第i行元素进行一次消元
}
}
//判断Xn是否为有唯一解,否则返回错误
if(a[n-1][n-1]==0)
return false;
//回代求解
for(k=n-1;k>=0;k--)
printf("%8.4f",a[i][j]);
c语言求矩阵的秩算法

c语言求矩阵的秩算法矩阵的秩是矩阵中非零行的最大数量。
在C语言中,可以通过高斯消元法求解矩阵的秩。
具体步骤如下:1. 将矩阵转换为行阶梯矩阵。
2. 统计行阶梯矩阵中非零行的数量。
3. 将行阶梯矩阵中每一行的首个非零元素所在的列标记为“基列”。
4. 检查是否存在重复的基列,若存在则将其合并。
5. 统计合并后的基列的数量,即为矩阵的秩。
C语言代码实现如下:```c#include <stdio.h>#define ROWS 3 // 矩阵的行数#define COLS 4 // 矩阵的列数int matrix[ROWS][COLS] = {{1, 2, 3, 4},{2, 4, 6, 8},{3, 6, 9, 12}}; // 待求矩阵int main() {int rank = 0; // 矩阵的秩int lead = 0; // 当前基列的列号if (lead >= COLS) break;int i = r;while (matrix[i][lead] == 0) { i++;if (i == ROWS) {i = r;lead++;if (lead == COLS) break;}}if (lead < COLS) {int* temp = matrix[r];matrix[r] = matrix[i];matrix[i] = temp;int div = matrix[r][lead];for (int j = 0; j < COLS; j++) { matrix[r][j] /= div;}for (int k = 0; k < ROWS; k++) { if (k != r) {int mult = matrix[k][lead];matrix[k][j] -= mult * matrix[r][j];}}}lead++;rank++;}}printf('The rank of the matrix is %d.', rank); // 输出矩阵的秩return 0;}```以上代码使用了指针和循环来实现高斯消元法求矩阵的秩。
c语言 高斯消元

#include<iostream>#include<iomanip>#include<fstream>#include<cmath>using namespace std;#define Max 50void output(double x[],int n){cout<<"Gauss 消去法得到的原方程组的解为:"<<endl;for(int k=0;k<n;k++)cout<<"x"<<k+1<<"="<<x[k]<<" ";}int main(){ifstream ifile;ifile.open("zhilu.txt");double data[Max][Max+1];double a[Max][Max+1],x[Max],sum,max,t;int n,row,line,i,j,k,l,ad,max_i;cout<<"输入信息矩阵的行数:"<<endl;cin>>row;cout<<"输入信息矩阵的列数:"<<endl;cin>>line;for(i=0;i<row;i++)for(j=0;j<line;j++)ifile>>data[i][j];cout<<"节点电压方程的阶数:"<<endl;cin>>n;for(i=0;i<n;i++)for(j=0;j<(n+1);j++)a[i][j]=0;for(i=0;i<row;i++){if( data[i][3]==1){if(data[i][1]*data[i][2]==0){if(data[i][1]>0)ad=data[i][1];elsead=data[i][2];a[ad-1][ad-1]+=data[i][4];}else{ k=data[i][1]-1;l=data[i][2]-1;ad=data[i][4];a[k][k]=a[k][k]+ad;a[l][l]=a[l][l]+ad;a[k][l]=a[k][l]-ad;a[l][k]=a[l][k]-ad;}}else{if(data[i][1]*data[i][2]!=0){k=data[i][1]-1;l=data[i][2]-1;ad=data[i][4];a[k][n]=a[k][n]-ad;a[l][n]=a[l][n]+ad;}else{if(data[i][1]>0)l=data[i][1]-1;elsel=data[i][2]-1;ad=data[i][4];a[l][n]=a[l][n]+ad;}}}cout<<"计算机建立的节点电压方程为:"<<endl;for(i=0;i<n;i++){for(j=0;j<(n+1);j++)cout<<setw(6)<<a[i][j];cout<<endl;}for(k=0;k<n-1;k++)//选主元素{max=a[k][k];max_i=k;for(i=k+1;i<n;i++)if(fabs(a[i][k])>fabs(max)){max=a[i][k];max_i=i;}if(max==0)break;if(max_i!=k)//交换两行for(j=k;j<n+1;j++){t=a[k][j];a[k][j]=a[max_i][j];a[max_i][j]=t;}for(i=k+1;i<n;i++){a[i][k]=a[i][k]/-a[k][k];for(j=k+1;j<n+1;j++)a[i][j]=a[i][j]+a[i][k]*a[k][j];}//消元}if(max==0)cout<<"原方程组无解!"<<endl; else{for(k=n-1;k>=0;k--){sum=0;for(j=k+1;j<n;j++)sum=sum+a[k][j]*x[j];x[k]=(a[k][n]-sum)/a[k][k];}//回代output(x,n);cout<<endl;}return 0;}。
解方程组的直接法(1) 高斯消去法 cpp源代码 数值计算

数值分析实验报告(三) 一.实验名称:解方程组的直接法(1)二.实验目的:高斯消去法三.题目:(验证用)准确值为x1 = -7;x2 = 3;x3 = 2;x4 = 2四.程序:高斯消去法附件:1-26liaoli_3_Gauss_Elimination.cpp#include<stdio.h>//输出方程组void Printf_Equations(int n, double**_a){for(int i = 0;i<n;i++){for(int j = 0;j < n;j++){if(j != 0 && _a[i][j] >= 0)printf("+");printf("%lfX%d ",_a[i][j],j+1);}printf(" = %lf",_a[i][j]);printf("\n");}}//输出结果void Printf_Result(int n, double *_result){for(int i = 0;i<n;i++){printf("X%d = %8lf",i+1,_result[i]);printf("\n");}}//Gauss消去法bool Elimination(int n, double **_a, double *_result) {int i,j,k;double mid;double *flag = new double[n+1];for(i = 0; i < n-1; i++){for(j = i; j < n; j++){if(_a[j][i] != 0){if( i!=j){flag = _a[i];_a[i] = _a[j];_a[j] = flag;}break;}}if(_a[i][i] != 1){for(j = i + 1; j < n+1; j++){_a[i][j] /= _a[i][i];}_a[i][i] = 1;}for(j = i+1; j < n; j++){for(k = i+1 ; k < n+1;k++){_a[j][k] = _a[j][k] - (_a[j][i] / _a[i][i]) * _a[i][k];}_a[j][i] = 0;}}if(_a[n-1][n-1] == 0){printf("no unique solution exists.");return false;}_result[n-1] = _a[n-1][n] / _a[n-1][n-1];for(i = n-2; i >= 0;i--){mid = 0;for(j = i+1 ; j < n; j++){mid += (_a[i][j] * _result[j]);}_result[i] = (_a[i][n] - mid) / _a[i][i];}return true;}void main(){int n;double **a,*result;//输入数据printf("请输入方程数n\t:");scanf("%d",&n);a = new double*[n];result = new double[n];printf("请输入增广矩阵A\t:\n");for(int i = 0;i<n;i++){a[i] = new double[n+1];for(int j = 0;j <= n;j++){scanf("%lf",&a[i][j]);}}//输出方程组Printf_Equations(n, a);//计算结果并输出Elimination(n, a, result);Printf_Result(n, result);}五.运行结果:六.体会:….信计20100810010126 liaoli。
C++列主元高斯消去法

#include<iostream>2 #include<cstdio>3 #include<iomanip>4using namespace std;5#define e 0.000000016#define maxn 5078int n;//规模nXn9double a[maxn][maxn];//系数矩阵10double b[maxn];//b矩阵11double m[maxn][maxn];//中间变量矩阵12double x[maxn];//最终解13int H=1;//扩大H被结算(优化)14/*15读取数据16*/17void read(){18 cout<<"请输入系数矩阵规模n:= ";19 cin>>n;20 cout<<"|-----------------------------\n";21 cout<<"|请输入系数矩阵,如:\n";22 cout<<"|1.1348 3.8326 1.1651 3.4017\n";23 cout<<"|0.5301 1.7875 2.5330 1.5435\n";24 cout<<"|3.4129 4.9317 8.7643 1.3142\n";25 cout<<"|1.2371 4.9998 10.6721 0.0147\n";26 cout<<"|-----------------------------\n"; 27for(int i=1;i<=n;i++)28for(int j=1;j<=n;j++){29 cin>>a[i][j];30 a[i][j]*=H;31 }32 cout<<"|-----------------------------\n";33 cout<<"|请输入b矩阵,如:\n";34 cout<<"|9.5342 6.3941 18.4231 16.9237\n";35 cout<<"|-----------------------------\n"; 36for(int i=1;i<=n;i++){37 cin>>b[i];38 b[i]*=H;39 }40 }4142/*43中间矩阵输出44参数:消元次数45*/46void PrintProc(int cases){47 printf("--------第%d次消元结果如下:\n",cases); 48for(int i=1;i<=n;i++){49for(int j=1;j<=n;j++){50 cout<<setw(10)<<a[i][j]<<'';51 }52 cout<<setw(10)<<b[i]<<'\n';53 }54 cout<<"END THIS SHOW-------------\n";55 }5657/*58显示结果59*/60void Print(){61 cout<<"|-----------------------------\n";62 cout<<"|结果为:\n";63for(int i=1;i<=n;i++){64 printf("x[%d]= %lf\n",i,x[i]);65 }66 cout<<"|-----------------------------\n\n";67 }6869/*70顺序消元法71*/72void ShunXuXiaoYuan(){73//消元计算74for(int k=1;k<n;k++){75for(int i=k+1;i<=n;i++){76 m[i][k]=a[i][k]/a[k][k];77for(int j=k+1;j<=n;j++){78 a[i][j]-=m[i][k]*a[k][j];79 }80 }81for(int i=k+1;i<=n;i++){82 b[i]-=m[i][k]*b[k];83 }84 PrintProc(k);//输出中间计算过程85 }86//回代求解87 x[n]=b[n]/a[n][n];88for(int i=n-1;i>0;i--){89 x[i]=b[i];90for(int j=i+1;j<=n;j++)91 x[i]-=a[i][j]*x[j];92 x[i]/=a[i][i];93 }94//输出结果95 Print();96 }9798/*99列主消元100*/101void LieZhuXiaoYuan(){102for(int k=1;k<n;k++){103//选主元[这一列的绝对值最大值]104double ab_max=-1;105int max_ik;106for(int i=k;i<=n;i++){107if(abs(a[i][k])>ab_max){108 ab_max=abs(a[i][k]);109 max_ik=i;110 }111 }112//交换行处理[先判断是否为0矩阵]113if(ab_max<e){//0矩阵情况114 cout<<"det A=0\n";115break;116 }else if(max_ik!=k){//是否是当前行,不是交换117double temp;118for(int j=1;j<=n;j++){119 temp=a[max_ik][j];120 a[max_ik][j]=a[k][j];121 a[k][j]=temp;122 }123 temp=b[max_ik];124 b[max_ik]=b[k];125 b[k]=temp;126 }127//消元计算128for(int i=k+1;i<=n;i++){129 a[i][k]/=a[k][k];130for(int j=k+1;j<=n;j++){131 a[i][j]-=a[i][k]*a[k][j];132 }133 b[i]-=a[i][k]*b[k];134 }135 PrintProc(k);//输出中间计算过程136if(k<n-1)continue;137else{138if(abs(a[n][n])<e){139 cout<<"det A=0\n";140break;141 }else{//回代求解142 x[n]=b[n]/a[n][n];143for(int i=n-1;i>0;i--){144 x[i]=b[i];145for(int j=i+1;j<=n;j++) 146 x[i]-=a[i][j]*x[j]; 147 x[i]/=a[i][i];148 }149//输出结果150 Print();151 }152 }153 }154 }155156/*157主函数158*/159int main(){160while(1){161 read();162 LieZhuXiaoYuan();163//ShunXuXiaoYuan();164 }return0;165 }166/*167书上高斯消元的例子:1681 1 11691 3 -21702 -2 11711726 1 1173*/174/*175书上列主消元的例子:176-0.002 2 21771 0.78125 0 1783.996 5.5625 4 1791800.4 1.3816 7.4178 181*/。
c语言求逆矩阵高斯约旦消元法

c语言求逆矩阵高斯约旦消元法一、啥是高斯约旦消元法求逆矩阵呢?嘿呀,咱在学C语言的时候啊,就会碰到求逆矩阵这个事儿。
那高斯约旦消元法呢,就像是一个超厉害的魔法,能帮咱们搞定这个逆矩阵的计算。
简单说呢,就是把一个矩阵和一个单位矩阵放在一起,然后通过一些行变换,把原来的矩阵变成单位矩阵,这个时候啊,原来的单位矩阵就变成了原来矩阵的逆矩阵啦。
这就好比是把两个小伙伴放在一起训练,一个变得超级厉害的时候,另一个也跟着变成了一种很特别的状态,这个特别的状态就是咱们要的逆矩阵呢。
二、C语言里怎么实现这个高斯约旦消元法呢?咱先得在C语言里把矩阵表示出来呀。
可以用二维数组来表示矩阵,这就像是给矩阵在C语言里安了个家。
然后呢,就开始进行那些行变换的操作。
这行变换可有点像玩数字游戏呢。
比如说,我们要把某一行的某个元素变成1,那就得找到合适的数去乘这一行。
这就像是在找一个魔法数字,让这个数字一乘,那个元素就乖乖听话变成1啦。
然后呢,再用这个1去把这一列其他的元素都变成0,就好像是这个1有了超能力,把周围的数字都清理成0啦。
就这样一步一步地对每一行每一列进行操作,最后就能得到逆矩阵啦。
不过呢,这个过程中可千万要小心,一步算错了,那可就像多米诺骨牌一样,后面全错啦。
三、实际操作中的小技巧和注意点在写C语言代码的时候啊,咱得注意循环的使用。
循环就像是一个勤劳的小助手,能帮我们把那些重复的操作快速地完成。
比如说,我们要对每一行进行同样的操作,那就可以用一个for循环来搞定。
还有就是那些中间变量的使用,可不能随便乱用啊,要给它们安排好合适的任务,不然就会搞得一团糟。
而且呢,在进行行变换的时候,要时刻注意矩阵的边界,可不能越界了,就像走路不能走出马路一样,不然程序就会出错啦。
另外呢,在调试的时候,如果结果不对,不要慌,要一步一步地检查,看看是哪一步的行变换出了问题,就像侦探破案一样,仔细地寻找线索,肯定能找到问题所在的。
概括来说呢,高斯约旦消元法求逆矩阵在C语言里虽然有点小复杂,但只要我们耐心地去做,就一定能搞定的啦。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
#ifndef FUNCTION_H
#define FUNCTION_H
#include<iostream>
#include<iomanip>
#include<cmath>
using namespace std;
class juZhen{
private:
double **m_p;
cin>>p[i];
return p;
}
void main(){
int pp(1);
while(pp){
cout<<"**********************************************************"<<endl;
cout<<"* 高斯消元法解方程组 *"<<endl;
}
}
void juZhen::display(){ //显示矩阵
cout.setf(ios::right);
for(int x=0;x<m_sizex;x++){
for(int y=0;y<m_sizey;y++){
cout<<setw(10)<<m_p[x][y]<<setw(10);
cout<<"* ⑤退出当前矩阵运算 *"<<endl;
cout<<"* *"<<endl;
cout<<"* ⑥退出程序 *"<<endl;
p={
cout<<"方程组无确定解!"<<endl;
break;
}
else{
double t;
for(int y=n;y<m_sizey;y++){
t=m_p[n][y];
m_p[n][y]=m_p[p][y];
void columnPrincipalComponentEliminationMethod(); //列主元消去法函数
void principalComponentEliminationMethod(); //全主元消去法
void result(); //输出结果函数
for(int i=0;i<m_sizex;i++)
delete[] m_p[i];
}
void display(); //显示函数
void eliminationGaussian(); //高斯消去法函数
}
cout<<endl;
}
}
void juZhen::eliminationGaussian(){ //高斯直接消去法
for(int n=0;n<m_sizey-2;n++){
for(int x=n;x<m_sizex-1;x++){
double d1=m_p[x+1][n]/m_p[n][n];
}
m=(m_p[k][m_sizey-1]-sum2)/m_p[k][k];
sum1[k]=m;
cout<<"**********************************************************"<<endl;
cout<<"X("<<k+1<<")="<<m<<endl;
}
}
}
}
display();
result();
}
void juZhen::principalComponentEliminationMethod(){ //全主元消去法
for(int n=0;n<m_sizey-2;n++){
}
for(int x=0;x<m_sizex;x++){ //列变换
t=m_p[x][n];
m_p[x][n]=m_p[x][p2];
m_p[x][p2]=t;
}
for(int x=n;x<m_sizex-1;x++){
double d1=m_p[x+1][n]/m_p[n][n];
}
delete[] sum1;
}
}
main.cpp
#include"function.h"
using namespace std;
double* input(){
double *p;
int size;
cout<<"请输入矩阵元素的总和:"<<endl;
for(int y=n;y<m_sizey;y++){
m_p[x+1][y]=m_p[x+1][y]-d1*m_p[n][y];
}
}
}
display();
result();
}
void juZhen::result(){
int m_sizex; //矩阵的行数
int m_sizey; //矩阵的列数
public:
juZhen(double *p=0,int sizex=0,int sizey=0); //构造函数
~juZhen(){ //析构函数
for(int y=n;y<m_sizey;y++){
m_p[x+1][y]=m_p[x+1][y]-d1*m_p[n][y];
}
}
}
display();
result();
}
void juZhen::columnPrincipalComponentEliminationMethod(){ //列主元消去法
cin>>size;
p=new double[size];
cout<<"请输入矩阵元素:"<<endl;
for(int i=0;i<size;i++)
cin>>p[i];
return p;
}
#include"function.h"
using namespace std;
};
#endif
function.cpp
#include"function.h"
juZhen::juZhen(double *p,int sizex,int sizey){ //构造函数
m_sizex=sizex;
m_sizey=sizey;
m_p=new double*[m_sizex];
cout<<"X("<<m_sizey-1<<")="<<m<<endl;
for(int k=m_sizex-2;k>=0;k--){
double sum2(0);
for(int y=k+1;y<m_sizey-1;y++){
sum2+=m_p[k][y]*sum1[y];
if(m_p[m_sizex-1][m_sizey-2]==0)
cout<<"方程组无确定解!"<<endl;
else{
cout<<"**********************************************************"<<endl;
cout<<"该方程组解如下:"<<endl;
cout<<"* *"<<endl;
cout<<"* ①直接消元法 *"<<endl;
cout<<"* *"<<endl;
m_p[p][y]=t;
}
for(int x=n;x<m_sizex-1;x++){
double d1=m_p[x+1][n]/m_p[n][n];
for(int y=n;y<m_sizey;y++){
m_p[x+1][y]=m_p[x+1][y]-d1*m_p[n][y];
for(int i=0;i<sizex;i++)
m_p[i]=new double[m_sizey];
for(int x=0;x<m_sizex;x++){
for(int y=0;y<m_sizey;y++){
m_p[x][y]=p[x*m_sizey+y];
}
p1=x;
p2=y;
}
}
}
double t;
for(int y=n;y<m_sizey;y++){ //行变换
