MATLAB仿真课后习题
MATLAB语言与控制系统仿真-参考答案-第7章
7.3控制系统根轨迹分析MATLAB 仿真实训7.3.1实训目的1. 掌握运用MATLAB 绘制180度、0度根轨迹图的编程方法;2. 学会通过根轨迹图获取相关信息的方法;3. 利用仿真结果对系统根轨迹进行分析;4.学会通过根轨迹图分析和解决一些实际问题。
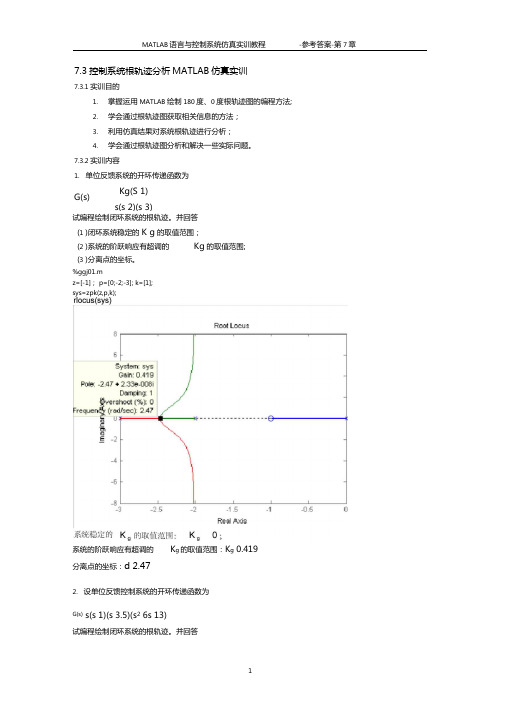
7.3.2实训内容1. 单位反馈系统的开环传递函数为试编程绘制闭环系统的根轨迹。
并回答 (1 )闭环系统稳定的 K g 的取值范围; (2 )系统的阶跃响应有超调的 Kg 的取值范围;(3 )分离点的坐标。
%ggj01.mz=[-1]; p=[0;-2;-3]; k=[1]; sys=zpk(z,p,k);系统的阶跃响应有超调的 K g 的取值范围:K g 0.419分离点的坐标:d 2.472. 设单位反馈控制系统的开环传递函数为G(s) s(s 1)(s 3.5)(s 2 6s 13)试编程绘制闭环系统的根轨迹。
并回答G(s)Kg(S 1) s(s 2)(s 3)(1 )闭环系统稳定的K的取值范围;(2) 根轨迹与虚轴的交点坐标; (3) 分离点的坐标。
ggj02.m%根轨迹仿真实训第 2题 n=1;d=co nv([1,0],co nv([1,1],co nv([1,3.5],[1,6,13]))); rlocus( n,d)10 -s由图上数据可知:闭环系统稳定的 K 的取值范围:0 K 70.9 ; 根轨迹与虚轴的交点坐标:j1.02 ;分离点的坐标:d 0.403。
3. 设单位反馈控制系统的开环传递函数为KG(s)- s(s 4)( s 4s 20)试编程绘制闭环系统的根轨迹。
并回答 (1 )闭环系统稳定的K 的取值范围;(2) 根轨迹与虚轴的交点坐标; (3) 各个分离点的坐标。
%根轨迹仿真实训第 3题Root Locus640 ■2-10-40 2斗6Real AxisDaimninn- -Fl IT10125System 割g j : i go^ainc £4祁怎比〕:3.15Pole : -2 + 7.51e-D06i Damping: 1 Overshoot (%): 0 Frequency (racVsec): 2由图上数据可知:闭环系统稳定的 K 的取值范围:0 K 262 ; 根轨迹与虚轴的交点坐标:j3.18 ;分离点的坐标:d,2,d 2,32 j2.45。
控制系统仿真matlab第六章习题答案汇总
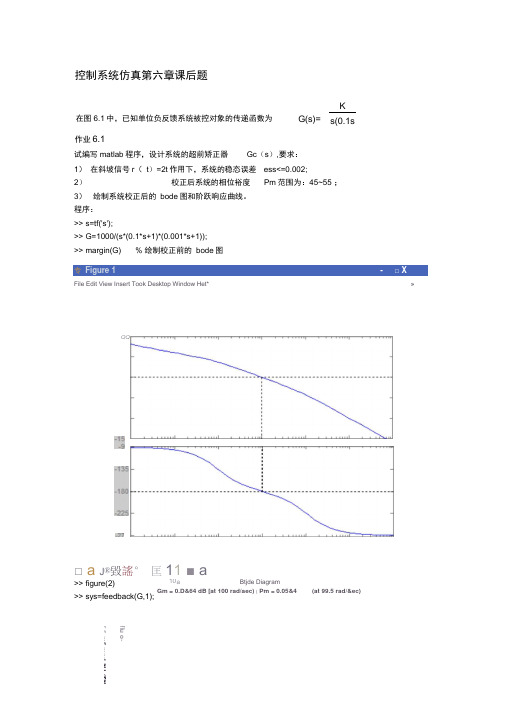
控制系统仿真第六章课后题作业6.1试编写matlab 程序,设计系统的超前矫正器 Gc (s ),要求:1) 在斜坡信号r ( t )=2t 作用下,系统的稳态误差 ess<=0.002;2)校正后系统的相位裕度 Pm 范围为:45~55 ; 3) 绘制系统校正后的 bode 图和阶跃响应曲线。
程序:>> s=tf('s');>> G=1000/(s*(0.1*s+1)*(0.001*s+1));>> margin(G)% 绘制校正前的 bode 图 专 Figure 1 - □ X File Edit View Insert Took Desktop Window Het* »□ a J ®毀謠° 匡11 ■ a >> figure(2)>> sys=feedback(G,1); 在图6.1中,已知单位负反馈系统被控对象的传递函数为G(s)= Ks(0.1s 1)(0.0QQo oBtjde Diagram Gm = 0.D&64 dB [at 100 rad/aec) ( Pm = 0.05&4 (at 99.5 rad/&ec)flu o-5 5 mE mprl 左一6『左 a 10>> step(sys) %绘制校正前的单位阶跃响应曲线Figure 2File Edit 过ew Insert Tools Window Help□已鸟|罠4紗®悬乙| 口目| ■回Step Response1.3>> [Gm,Pm]=margin(G); %该句值计算bode图的增益裕量Gm和相位裕量Pm >> [mag,phase,w]=bode(G); %该句只计算bode图上多个频率点w对应的幅值和相位>> QWPm=50; %取矫正后的相位为50>> Flm=QWPm-Pm+5;>> Flm=Flm*pi/180;>> alfa=(1-si n(FIm))/(1+si n( FIm));>> adb=20*log10(mag);>> am=10*log10(alfa);>> wc=spli ne(adb,w,am);>> T=1/(wc*sqrt(alfa));>> alfat=alfa*T;>> Gc=tf([T 1],[alfat 1]) %校正器的传递函数Tran sfer function:0.01794 s + 1Time 330.00179 s + 1>> figure(3)>> margin(Gc*G) %系统矫正后的bode图Ffgure 3Filt gdit yisw ifisert Hcdt Mfimdcw title】I ■回Bode DiagramGm = 17.6 dB (st 69B rad/sec) s Pm = 4S.2 deg (at 176 rad/sec)"I 0 0 N -- 1 1 I I I ! 1 ! | ! ■' I I ' ' I J I I ........... | I I « i i i | i | i f ■ J !!|!|>> figure(4)>> step(feedback(Gc*G ,1)) % 校正后的单位阶跃响应曲线Figure 4n xl Fie Edit 辺足w Insert Tools Desktop Window HelpO t3 J -S □ S ■ Q1010°ID1 1 孑10Frequency (r&fh'see)作业6.2在图6.1中,已知单位负反馈系统被控对象的传递函数为试编写matlab 程序,设计系统的滞后校正器 Gc ( s ),要求:1) 在斜坡信号r(t)=t 作用下,系统的稳态误差ess 乞0.01 ; 2) 校正后系统的相位裕度 Pm 范围为:40~50 ;3) 绘制系统矫正前后的 bode 图和阶跃响应曲线。
MATLAB课后习题集附标准答案

第2章MATLAB概论1、与其他计算机语言相比较,MA TLAB语言突出的特点是什么?答:起点高、人机界面适合科技人员、强大而简易的作图功能、智能化程度高、功能丰富,可扩展性强.2、MA TLAB系统由那些部分组成?答:开发环境、MATLAB数学函数库、MATLAB语言、图形功能、应用程序接口3、安装MATLAB时,在选择组件窗口中哪些部分必须勾选,没有勾选的部分以后如何补安装?答:在安装MATLAB时,安装内容由选择组件窗口中各复选框是否被勾选来决定,可以根据自己的需要选择安装内容,但基本平台(即MATLAB选项)必须安装.第一次安装没有选择的内容在补安装时只需按照安装的过程进行,只是在选择组件时只勾选要补装的组件或工具箱即可.4、MATLAB操作桌面有几个窗口?如何使某个窗口脱离桌面成为独立窗口?又如何将脱离出去的窗口重新放置到桌面上?答:在MATLAB操作桌面上有五个窗口,在每个窗口的右下角有两个小按钮,一个是关闭窗口的Close 按钮,一个是可以使窗口称为独立的Undock按钮,点击Undock按钮就可以使该窗口脱离桌面称为独立窗口,在独立窗口的view菜单中选择Dock,菜单项就可以将独立的窗口重新防止的桌面上.5、如何启动M文件编辑/调试器?答:在操作桌面上选择“建立新文件”或“打开文件”操作时,M文件编辑/调试器将被启动.在命令窗口中键入edit命令时也可以启动M文件编辑/调试器.6、存储在工作空间中的数组能编辑吗?如何操作?答:存储在工作空间的数组可以通过数组编辑器进行编辑:在工作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输入修改内容即可.7、命令历史窗口除了可以观察前面键入的命令外,还有什么用途?答:命令历史窗口除了用于查询以前键入的命令外,还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中.8、如何设置当前目录和搜索路径,在当前目录上的文件和在搜索路径上的文件有什么区别?答:当前目录可以在当前目录浏览器窗口左上方的输入栏中设置,搜索路径可以通过选择操作桌面的file菜单中的Set Path菜单项来完成.在没有特别说明的情况下,只有当前目录和搜索路径上的函数和文件能够被MATLAB运行和调用,如果在当前目录上有与搜索路径上相同文件名的文件时则优先执行当前目录上的文件,如果没有特别说明,数据文件将存储在当前目录上.9、在MA TLAB中有几种获得帮助的途径?答:(1)帮助浏览器:选择view菜单中的Help菜单项或选择Help菜单中的MATLAB Help菜单项可以打开帮助浏览器.(2)help命令:在命令窗口键入“help”命令可以列出帮助主题,键入“help 函数名”可以得到指定函数的在线帮助信息.(3)lookfor命令:在命令窗口键入“lookfor 关键词”可以搜索出一系列与给定关键词相关的命令和函数.(4)模糊查询:输入命令的前几个字母,然后按Tab键,就可以列出所有以这几个字母开始的命令和函数.注意:lookfor和模糊查询查到的不是详细信息,通常还需要在确定了具体函数名称后用help命令显示详细信息.第3章 MATLAB 数值运算3.1在MA TLAB 中如何建立矩阵⎥⎦⎤⎢⎣⎡194375,并将其赋予变量a ? 答:在Command Window 窗口输入操作:>> a=[5 7 3;4 9 1]3.2有几种建立矩阵的方法?各有什么优点? 答:(1)直接输入法,如a=[1 2 3 4],优点是输入方法方便简捷;(2)通过M 文件建立矩阵,该方法适用于建立尺寸较大的矩阵,并且易于修改; (3)由函数建立,如y=sin(x),可以由MATLAB 的内部函数建立一些特殊矩阵; (4)通过数据文件建立,该方法可以调用由其他软件产生数据.3.3在进行算术运算时,数组运算和矩阵运算各有什么要求?答:进行数组运算的两个数组必须有相同的尺寸.进行矩阵运算的两个矩阵必须满足矩阵运算规则,如矩阵a 与b 相乘(a*b )时必须满足a 的列数等于b 的行数.渗釤呛俨匀谔鱉调硯錦。
matlab课后习题及答案

第一章 5题已知a=4.96,b=8.11,计算)ln(b a eba +-的值。
解:clear clc a=4.96; b=8.11;exp(a-b)/log(a+b) ans =0.0167 6题已知三角形的三边a=9.6,b=13.7, c=19.4,求三角形的面积。
提示:利用海伦公式area =))()((c s b s a s s ---计算,其中S=(A+B+C)/2. 解:clear clc a=9.6; b=13.7; c=19.4; s=(a+b+c)/2area=sqrt(s*(s-a)*(s-b)*(s-c)) s =21.3500 第二章 8题已知S=1+2+2^2+2^3+……+2^63,求S 的值 解:clear clc S=0;for i=0:1:63 S=S+2^i; end S S =1.8447e+019 9题分别用for 和while 循环结构编写程序,计算∑=-1001n 1n 2)(的值。
解:clear clc s=0;for n=1:100 s=s+(2*n-1); end s s =10000 clear clc n=1; s=0;while n<=100 s=s+(2*n-1); n=n+1; end s s =10000 第三章 2题在同一坐标下绘制函数x ,,2x-,2x xsin(x)在()∏∈,0x 的曲线。
解:clear clcx=0:0.2:pi; y1=x; y2=x.^2; y3=-(x.^2); y4=x.*sin(x);plot(x,y1,'-' ,x,y2,'-' ,x,y3,'-' ,x,y4,'-')0.511.522.53-10-8-6-4-202468109题用不同的线型和颜色在同一坐标内绘制曲线y1=2ex5.0 、y2=sin(2∏x )的图形。
matlab课后习题答案(附图)

matlab课后习题答案(附图)习题2.1画出下列常见曲线的图形y (1)⽴⽅抛物线3x命令:syms x y;ezplot('x.^(1/3)')(2)⾼斯曲线y=e^(-X^2);命令:clearsyms x y;ezplot('exp(-x*x)')(3)笛卡尔曲线命令:>> clear>> syms x y;>> a=1;>> ezplot(x^3+y^3-3*a*x*y)(4)蔓叶线命令:>> clear>> syms x y;>> a=1ezplot(y^2-(x^3)/(a-x))(5)摆线:()()tsin-=,=-by1命令:>> clear>> t=0:0.1:2*pi;>> x=t-sin(t);>>y=2*(1-cos(t)); >> plot(x,y)7螺旋线命令:>> clear >> t=0:0.1:2*pi; >> x=cos(t); >> y=sin(t); >> z=t;>>plot3(x,y,z)(8)阿基⽶德螺线命令:clear>> theta=0:0.1:2*pi;>> rho1=(theta);>> subplot(1,2,1),polar(theta,rho1)(9) 对数螺线命令:cleartheta=0:0.1:2*pi;rho1=exp(theta);subplot(1,2,1),polar(theta,rho1)(12)⼼形线命令:>> clear >> theta=0:0.1:2*pi; >> rho1=1+cos(theta); >> subplot(1,2,1),polar(theta,rho1)练习2.21. 求出下列极限值(1)nnn n3→命令:>>syms n>>limit((n^3+3^n)^(1/n)) ans = 3(2))121(lim n n n n ++-+∞→命令:>>syms n>>limit((n+2)^(1/2)-2*(n+1)^(1/2)+n^(1/2),n,inf) ans = 0(3)x x x 2cot lim 0→命令:syms x ;>> limit(x*cot(2*x),x,0) ans = 1/2 (4))(coslimcm xx ∞→命令:syms x m ; limit((cos(m/x))^x,x,inf) ans = 1(5))111(lim 1--→exx x命令:syms x>> limit(1/x-1/(exp(x)-1),x,1) ans =(exp(1)-2)/(exp(1)-1) (6))(2lim x x xx -+∞>> limit((x^2+x)^(1/2)-x,x,inf)ans = 1/2练习2.41. 求下列不定积分,并⽤diff 验证:(1)+x dxcos 1>>Clear >> syms x y >> y=1/(1+cos(x)); >> f=int(y,x) f =tan(1/2*x) >> y=tan(1/2*x); >> yx=diff(y ,x); >> y1=simple(yx) y1 =1/2+1/2*tan(1/2*x)^2 (2)+exdx1clear syms x yy=1/(1+exp(x));f=int(y,x) f =-log(1+exp(x))+log(exp(x)) syms x yy=-log(1+exp(x))+log(exp(x)); yx=diff(y,x); y1=simple(yx) y1 = 1/(1+exp(x)) (3)dx x x ?sin 2syms x yy=x*sin(x)^2; >> f=int(y,x) f =x*(-1/2*cos(x)*sin(x)+1/2*x)-1/4*cos(x)^2-1/4*x^2 clearsyms x y y=x*(-1/2*cos(x)*sin(x)+1/2*x)-1/4*cos(x)^2-1/4*x^2; yx=diff(y,x); >> y1=simple(yx) y1 = x*sin(x)^2 (4)xdx ?sec3syms x y y=sec(x)^3;f=int(y,x) f =1/2/cos(x)^2*sin(x)+1/2*log(sec(x)+tan(x)) clear syms x yy=1/2/cos(x)^2*sin(x)+1/2*log(sec(x)+tan(x)); yx=diff(y,x); y1=simple(yx) y1 =1/cos(x)^32. 求下列积分的数值解 1)dx x-10clearsyms xy=int(x^(-x),x,0,1) y =int(x^(-x),x = 0 .. 1) vpa(y,10) ans =1.291285997 2)xdx e x cos3202?πclearsyms xy=int(exp(2*x)*cos(x)^3,x, clear syms xy=int((1/(2*pi)^(1/2))*exp(-x^2/2),x,0,1) y =7186705221432913/36028797018963968*erf(1/2*2^(1/2))*2^(1/2)*pi^(1/0,2*pi) y =22/65*exp(pi)^4-22/65vpa(ans,10)(3)dx xe21221-π>> clear >> syms x>> y=int(1/(2*pi)^(1/2)*exp(-x^2/2),0,1); >> vpa(y,14) ans =.341344746068552(4)>> clear >> syms x>> y=int(x*log(x^4)*asin(1/x^2),1,3); Warning: Explicit integral could not be found. > In sym.int at 58 >> vpa(y,14) ans = 2.45977212823752(5) >> clear >> syms x1判断下列级数的收敛性,若收敛,求出其收敛值。
Matlab与控制系统仿真部分习题答案

【4.2】程序:num=[5,0];den=conv([1,1],conv([1,2],[1,3])); [numc,denc]=cloop(num,den);[z,p,k]=tf2zp(numc,denc);[A,B,C,D]=tf2ss(numc,denc);g_zp=zpk(z,p,k)g_tf=tf(numc,denc)g_ss=ss(A,B,C,D)运行结果:Zero/pole/gain:5 s----------------------------------(s+0.4432) (s^2 + 5.557s + 13.54)Transfer function:5 s----------------------s^3 + 6 s^2 + 16 s + 6a =x1 x2 x3x1 -6 -16 -6x2 1 0 0x3 0 1 0b =u1x1 1x2 0x3 0c =x1 x2 x3y1 0 5 0d =u1y1 0【4.3】程序:A=[0 0 0 -1;1 0 0 -2;0 1 0 -3;0 0 1 -4]; B=[0;0;0;1];C=[1 0 0 0];g_ss=ss(A,B,C,D)[num,den]=ss2tf(A,B,C,D);g_tf=tf(num,den)[z,p,k]=ss2zp(A,B,C,D);g_zpk=zpk(z,p,k)运行结果:a =x1 x2 x3 x4x1 0 0 0 -1x2 1 0 0 -2x3 0 1 0 -3x4 0 0 1 -4b =u1x1 0x2 0x3 0x4 1c =x1 x2 x3 x4y1 1 0 0 0d =u1y1 0Continuous-time model.Transfer function:-3.109e-015 s^3 - s^2 - 3.331e-015 s - 4.441e-016 -------------------------------------------------s^4 + 4 s^3 + 3 s^2 + 2 s + 1Zero/pole/gain:- s^2----------------------------------------------(s+0.6724) (s+3.234) (s^2 + 0.0936s + 0.4599)【5.1】(1)程序num=[0,10];den=conv([1,0],[1,7,17]); [numc,denc]=cloop(num,den,-1); G=tf(numc,denc)[y,t]=step(G);plot(t,y,'b-')C=dcgain(G);n=1;while y(n)<0.1*Cn=n+1;endm=1;while y(m)<0.9*Cm=m+1;endrisetime=t(m)-t(n)[Y,k]=max(y); percentovershoot=100*(Y-C)/Ci=length(t);while(y(i)>0.98*C)&(y(i)<1.02*C) i=i-1;endsettlingtime=t(i)运行结果:Transfer function:10-----------------------s^3 + 7 s^2 + 17 s + 10risetime =2.7312percentovershoot =-0.4399settlingtime =5.1372图:0123456700.10.20.30.40.50.60.70.80.91(2)程序k=[10,100,1000];t=linspace(1,20,200);num=1;den=conv([1,0],[1,7,17]);for j=1:3;s1=tf(num*k(j),den);sys=feedback(s1,1)y(:,j)=step(sys,t);endplot(t,y(:,1),'r',t,y(:,2),'b',t,y(:,3),'g')gtext('k=10');gtext('k=100');gtext('k=1000') 运行结果:Transfer function:10-----------------------s^3 + 7 s^2 + 17 s + 10Transfer function:100------------------------s^3 + 7 s^2 + 17 s + 100Transfer function:1000-------------------------s^3 + 7 s^2 + 17 s + 1000图:024681012141618200.20.40.60.811.21.41.61.8图:02468101214161820-3-2-1123422【6.1】程序:(1)num1=[1,1];den1=conv([1,0,0],conv([1,2],[1,4]));sys1=tf(num1,den1)rlocus(sys1)运行结果:-12-10-8-6-4-2024-8-6-4-202468Root LocusReal Axis I m a g i n a r y A x i s(2)num2=[1,1];den2=conv([1,0],conv([1,-1],[1,4,16]));sys2=tf(num2,den2)rlocus(sys2)运行结果:-10-8-6-4-2024-8-6-4-202468Root LocusReal Axis I m a g i n a r y A x i s(3)num3=[1,8];den3=conv([1,0,0],conv([1,3],conv([1,5],conv([1,7],[1,15])))); sys3=tf(num3,den3)rlocus(sys3)运行结果:-30-25-20-15-10-5051015-20-15-10-505101520Root LocusReal Axis I m a g i n a r y A x i s【6.3】程序:num=[1,2];den=conv([1,0],conv([1,4],conv([1,8],[1,2,5])));sys=tf(num,den)rlocus(sys)[k,poles]=rlocfind(sys)运行结果:Transfer function:s + 2---------------------------------------s^5 + 14 s^4 + 61 s^3 + 124 s^2 + 160 sSelect a point in the graphics windowselected_point =0.0296 + 2.2826i k =135.8815poles =-7.3248-5.41040.0145 + 2.3021i0.0145 - 2.3021i -1.2939图:-20-15-10-5051015-15-10-551015Root LocusReal Axis I m a g i n a r y A x i s【7.3】程序(1)画波特图num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)bode(sys)grid图(1)-150-100-50050100M a g n i t u d e (d B)10-210-1100101102103-270-225-180-135-90P h a s e (d e g )Bode DiagramFrequency (rad/sec)程序(2)画奈奎斯特图num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)nyquist(sys)grid图(2)-16-14-12-10-8-6-4-20-300-200-100100200300Nyquist DiagramReal Axis I m a g i n a r y A x i s程序(3)画零极点图num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)pzmap(sys1)gird图(3)P ole-Zero MapReal Axis I m a g i n a r y A x i s -12-10-8-6-4-20-1.5-1-0.50.511.5程序(4)计算相角裕量和幅值裕量num=[50];den=conv([1,0],conv([1,10],[3,1]));sys=tf(num,den)sys1=feedback(sys,1)[gm,pm,wcg,wcp]=margin(sys)运行结果Transfer function:50---------------------3 s^3 + 31 s^2 + 10 sTransfer function:50--------------------------3 s^3 + 31 s^2 + 10 s + 50gm =2.0667pm =7.5615wcg =1.8257wcp =1.2645程序(5)绘制阶跃响应曲线num=[50];den=conv([1,0],conv([1,10],[3,1])); sys=tf(num,den)sys1=feedback(sys,1)step(sys1)图(5)00.20.40.60.811.21.41.61.82Step ResponseTime (sec)A m p l i t u d e【7.4】程序如下:num=[300];den=conv([1,0,0],conv([0.2,1],[0.02,1]));sys=tf(num,den)margin(sys)grid波特图如下:-150-100-50050100M a g n i t u d e (d B )10-1100101102103-360-315-270-225-180P h a s e (d e g )Bode DiagramGm = Inf , P m = -78 deg (at 11 rad/sec)Frequency (rad/sec)【9.3】程序:A=[-2 2 -1;0 -2 0;1 -4 0];B=[0;0;1];C=[1,0,0];D=0;M=ctrb(A,B)m=rank(M)if m==3;disp('系统可控')elsedisp('系统不可控')endN=obsv(A,C)n=rank(N)if n==3;disp('系统可观')elsedisp('系统不可观') endsys=ss(A,B,C,D) [num,den]=ss2tf(A,B,C,D) sys1=tf(num,den)[z,p,k]=ss2zp(A,B,C,D)运行结果:M =0 -1 20 0 01 0 -1m =2系统不可控N =1 0 0-2 2 -13 -4 2n =2系统不可观a =x1 x2 x3x1 -2 2 -1x2 0 -2 0x3 1 -4 0b =u1x1 0x2 0x3 1c =x1 x2 x3y1 1 0 0d =u1y1 0 Continuous-time model.0 0 -1 -2den =1 4 5 2Transfer function:-s - 2---------------------s^3 + 4 s^2 + 5 s + 2z =-2p =-1-1-2k = -1【10.1】(1)程序:A=[0,1,0,0;0,5,0,0;0,0,-7,0;0,0,0,-8]; B=[0;1;0;1];C=[1,2,3,4];D=zeros(1,1);G_ss=ss(A,B,C,D)运行结果:a =x1 x2 x3 x4x1 0 1 0 0x2 0 5 0 0x3 0 0 -7 0x4 0 0 0 -8u1x1 0x2 1x3 0x4 1c =x1 x2 x3 x4y1 1 2 3 4d =u1y1 0(2):程序:[num1,den1]=ss2tf(A,B,C,D); p=roots(den1)i=0;for k=1:1:length(p)if real(p(k))>0i=i+1;endendif i>0disp('系统不稳定');elsedisp('系统稳定');end运行结果:p =5.0000-8.0000-7.0000系统不稳定(3)(4)程序:AA=[0,1,0;0,5,0;0,0,-8];BB=[0;1;1];P=[-1,-2,-8];K=acker(AA,BB,P);i=4;K(4)=0;Kpp=eig(A-B*K)sys1=tf(num1,den1);[y1,t]=step(sys1);plot(t,y1)hold onA_feedback=A-B*K;[num2,den2]=ss2tf(A_feedback,B,C,D); sys2=tf(num2,den2);[y2,t]=step(sys2);plot(t,y2,'r')gridgtext('反馈前')gtext('反馈后')运行结果:K =2 8 0 0pp =-8-2-1-7图形:01234560123456【13.1】程序:A=[0,1;0,0];B=[0;1];C=[1,0];D=zeros(1,1);G_ss=ss(A,B,C,D)M=ctrb(A,B);if rank(M)==2disp('系统完全能控'); elsedisp('系统不完全能控'); endS=[1,0];N=obsv(A,S);if rank(N)==2disp('(A,S)可观测'); elsedisp('(A,S)不可观测'); endR=1;Q=[1,0;0,0];[K,P,E]=Lqr(A,B,Q,R)A_new=A-B*K;G_new=ss(A_new,B,C,D);t=linspace(0,5,100)';y1=step(G_ss,t);y2=step(G_new,t);plot(t,y1,'r:',t,y2,'b-')gridgtext('反馈前')gtext('反馈后')运行结果:a =x1 x2x1 0 1x2 0 0b =u1x1 0x2 1c =x1 x2y1 1 0d =u1y1 0Continuous-time model. 系统完全能控(A,S)可观测K =1.0000 1.4142P =1.4142 1.00001.0000 1.4142E =-0.7071 + 0.7071i-0.7071 - 0.7071i图形:00.51 1.52 2.53 3.54 4.5502468101214。
完整word版,Matlab课后习题

习题 11. 执行下列指令,观察其运算结果, 理解其意义: (1) [1 2;3 4]+10-2i(2) [1 2; 3 4].*[0.1 0.2; 0.3 0.4] (3) [1 2; 3 4].\[20 10;9 2] (4) [1 2; 3 4].^2 (5) exp([1 2; 3 4]) (6)log([1 10 100]) (7)prod([1 2;3 4])(8)[a,b]=min([10 20;30 40]) (9)abs([1 2;3 4]-pi)(10) [1 2;3 4]>=[4,3;2 1](11)find([10 20;30 40]>=[40,30;20 10])(12) [a,b]=find([10 20;30 40]>=[40,30;20 10]) (提示:a 为行号,b 为列号) (13) all([1 2;3 4]>1) (14) any([1 2;3 4]>1) (15) linspace(3,4,5) (16) A=[1 2;3 4];A(:,2)2. 执行下列指令,观察其运算结果、变量类型和字节数,理解其意义: (1) clear; a=1,b=num2str(a),c=a>0, a= =b, a= =c, b= =c (2) clear; fun='abs(x)',x=-2,eval(fun),double(fun)3. 本金K 以每年n 次,每次p %的增值率(n 与p 的乘积为每年增值额的百分比)增加,当增加到rK 时所花费的时间为)01.01ln(ln p n rT +=(单位:年)用MA TLAB 表达式写出该公式并用下列数据计算:r =2, p =0.5, n =12.4.已知函数f (x )=x 4-2x 在(-2, 2)内有两个根。
取步长h =0.05, 通过计算函数值求得函数的最小值点和两个根的近似解。
MATLAB语言与控制系统仿真-参考答案-第5章

5.6 控制系统的时域响应MATLAB 仿真实训5.6.1实训目的 1. 学会利用MATLAB 绘制系统的单位阶跃响应曲线,掌握读取系统动态性能指标的方法; 2. 学会利用MATLAB 绘制系统的单位脉冲响应曲线的方法; 3. 掌握利用MATLAB 绘制系统的零输入响应曲线的方法; 4. 掌握利用MATLAB 绘制系统的一般输入响应曲线的方法;5.学会通过仿真曲线读取相关信息,并依据有关信息进行系统的时域分析。
5.6.2实训内容1.编写程序求取下列各系统的单位阶跃响应,完成表5-5并记录相关曲线。
162.316)(21++=s s s G 164.216)(22++=s s s G 166.116)(23++=s s s G 1616)(24++=s s s G 解:>> n1=16;>> d1=[1,3.2,16]; >> sys1=tf(n1,d1); >> step(sys1)>> n2=16;>> d2=[1,2.4,16]; >> sys2=tf(n2,d2); >> step(sys2)>> n3=16;>> d3=[1,1.6,16]; >> sys3=tf(n3,d3); >> step(sys3)>> n4=16;>> d4=[1,1,16]; >> sys4=tf(n4,d4); >> step(sys4)w=4;cmax1=1+exp(-z1*pi/sqrt(1-z1^2)); tp1=pi/(w*sqrt(1-z1^2));ts1=3.5/(z1*w);[cmax1,tp1,ts1]ans =1.2538 0.85692.1875 >> z2=0.3;w=4;cmax2=1+exp(-z2*pi/sqrt(1-z2^2)); tp2=pi/(w*sqrt(1-z2^2));ts2=3.5/(z2*w);[cmax2,tp2,ts2]ans =1.3723 0.82332.9167 >> z3=0.2; w=4;cmax3=1+exp(-z3*pi/sqrt(1-z3^2)); tp3=pi/(w*sqrt(1-z3^2)); ts3=3.5/(z3*w); [cmax3,tp3,ts3]ans =1.5266 0.8016 4.3750 >> z4=0.125; w=4;cmax4=1+exp(-z4*pi/sqrt(1-z4^2)); tp4=pi/(w*sqrt(1-z4^2)); ts4=3.5/(z4*w); [cmax4,tp4,ts4] ans =1.6731 0.7916 7.0000说明:对于二阶欠阻尼系统(10<<ξ),若系统的闭环传递函数为2222)(nn ns s s Φωξωω++= 则系统单位阶跃响应的输出最大值21max 1ξξπ--+=ec峰值时间21ξωπ-=n p t调整时间估算值ns t ξω5.3= (以5%为误差带) ns t ξω4.4=(以2%为误差带)2.已知二阶系统的闭环传递函数如下,编程求取系统的单位阶跃响应并完成表5-6,记录相关曲线。
MATLAB语言与控制系统仿真_参考题答案_第3章

3.5 MATLAB 绘图实训3.5.1 实训目的1.学会MATLAB 绘图的基本知识;2.掌握MATLAB 子图绘制、图形注释、图形编辑等基本方法;3.学会通过MATLAB 绘图解决一些实际问题;4.练习二维、三维绘图的多种绘图方式,了解图形的修饰方法;5.学会制作简单的MATLAB 动画。
图3-46 炮弹发射示意图3.5.2 实训内容1. 炮弹发射问题〔1炮弹发射的基础知识炮弹以角度α射出的行程是时间的函数,可以分解为水平距离)(t x 和垂直距离)(t y 。
)cos()(0αtv t x = %水平方向的行程; 205.0)sin()(gt tv t y -=α %垂直方向的行程;其中,0v 是初速度;g 是重力加速度,为9.82m/s ;t 是时间。
〔2炮弹发射程序举例:分析以下程序以及图3-47各个图形的实际意义。
a=pi/4; v0=300; g=9.8;t=0:0.01:50; x=t*v0*cos<a>;y=t*v0*sin<a>-0.5*g*t.^2;subplot<221>;plot<t,x>;grid;title<‘时间-水平位移曲线'>; subplot<222>;plot<t,y>;grid;title<‘时间-垂直位移曲线'>; subplot<223>;plot<x,y>;grid;title<‘水平位移-垂直位移曲线'>; subplot<224>;plot<y,x>;grid;title<‘垂直位移-水平位移曲线'>; 图3-4745角发射曲线 〔3编程解决炮弹发射问题①假设在水平地面上以垂直于水平面的角度向上发射炮弹,即发射角90=α,假设初速度分别为[310,290,270]m/s,试绘制时间-垂直位移曲线,编程求取最高射程;绘图要求:◆ 标题设为"炮弹垂直发射问题";◆ 在图上通过添加文本的方式表明初速度; ◆ 在x 轴标注"时间";◆ 在y 轴上标注"垂直距离"; ◆ 添加网格线;◆ 将310m/s 的曲线改为线粗为2的红色实线; ◆ 将290m/s 的曲线改为线粗为3的绿色点划线;◆ 将270m/s 的曲线改为线粗为2的蓝色长点划线;a=pi/2; v1=310; g=9.8;t=0:0.01:50; x1=t*v1*cos<a>;y1=t*v1*sin<a>-0.5*g*t.^2;plot<t,y1>;grid; title<'炮弹垂直发射问题'>; xlabel<'时间'>; ylabel<'垂直距离'>; hold on; v2=290;x2=t*v2*cos<a>;y2=t*v2*sin<a>-0.5*g*t.^2; plot<t,y2>; v3=270;x3=t*v3*cos<a>;y3=t*v3*sin<a>-0.5*g*t.^2; plot<t,y3>;zgsc=[max<y1>; max<y2>; max<y3>] %三次发射的最高射程 运行结果如下: zgsc =1.0e+003 * 4.9031 4.29083.7194最高射程分别为:4903.1米,4290.8米,3719.4米。
MATLAB与控制系统仿真练习题(含图)及答案
MATLAB 与控制系统仿真练习题(含图)1、已知函数x x e x f x sin cos )(-=,作出函数的大致图像。
>> syms x>> y=exp(x)*cos(x)-sin(x); >> ezplot(y)2、求下列极限:(1)30sin lim xx x x -→ >> syms x>> y=(x-sin(x))/(x^3);>> limit(y,x,0)ans =1/6(2) xx x ⎪⎭⎫ ⎝⎛+∞→11lim >> y=(1+1/x)^x;>> limit(y,x,inf)ans =exp(1)3、求下列函数的导数:(1)x e y x sin =>> syms x>> y=exp(x)*sin(x);>> diff(y,x)ans =exp(x)*sin(x)+exp(x)*cos(x)(2) x e x x y 22sin +=>> syms x>> y=sin(x)+x^2*exp(2*x);>> diff(y,x)ans =cos(x)+2*x*exp(2*x)+2*x^2*exp(2*x)4、求.)1(532⎰-dx x x 和.sin ⎰xdx e x(1).)1(532⎰-dx x xsyms x>> int(x^2*(1-x^3)^5)ans =-1/18*x^18+1/3*x^15-5/6*x^12+10/9*x^9-5/6*x^6+1/3*x^3(2).sin ⎰xdx e x>> int(exp(x)*sin(x))ans =-1/2*exp(x)*cos(x)+1/2*exp(x)*sin(x)5、求.)(102⎰-dx x x 和.1102⎰-dx x x (1) .)(102⎰-dx x x>> syms x>> int(x-x^2,0,1)ans =1/6(2) .1102⎰-dx x x>> syms x>> int(x*(1-x^2)^0.5,0,1)ans =1/36、已知二元函数),(cos )sin(2xy xy z +=试求y x z x z y z x z ∂∂∂∂∂∂∂∂∂222,,,。
MATlab 仿真部分习题答案
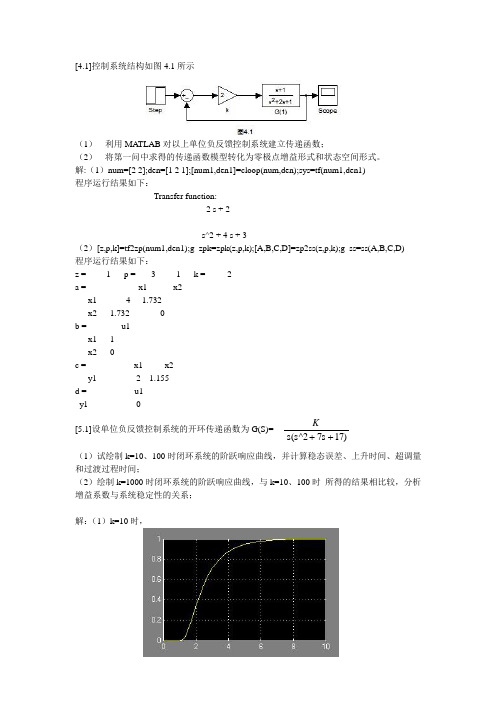
[4.1]控制系统结构如图4.1所示(1)利用MATLAB对以上单位负反馈控制系统建立传递函数;(2)将第一问中求得的传递函数模型转化为零极点增益形式和状态空间形式。
解:(1)num=[2 2];den=[1 2 1];[num1,den1]=cloop(num,den);sys=tf(num1,den1)程序运行结果如下:Transfer function:2 s + 2-------------s^2 + 4 s + 3(2)[z,p,k]=tf2zp(num1,den1);g_zpk=zpk(z,p,k);[A,B,C,D]=zp2ss(z,p,k);g_ss=ss(A,B,C,D)程序运行结果如下:z = -1 p = -3 -1 k = 2a = x1 x2x1 -4 -1.732x2 1.732 0b = u1x1 1x2 0c = x1 x2y1 2 1.155d = u1y1 0K[5.1]设单位负反馈控制系统的开环传递函数为G(S)=+s(s^2+7s17)(1)试绘制k=10、100时闭环系统的阶跃响应曲线,并计算稳态误差、上升时间、超调量和过渡过程时间;(2)绘制k=1000时闭环系统的阶跃响应曲线,与k=10、100时所得的结果相比较,分析增益系数与系统稳定性的关系;解:(1)k=10时,K=100时,K=10时,利用MA TLAB工作区输入程序:num=[10];den=[1,7,17,0];[z,p,k]=tf2zp( num,den);运行得z,p,k的值p= -3.5+2.1794*i -3.5-2.1794*i k=10G=zpk([ ],[-3.5+2.1794*i,-3.5-2.1794*i],10);c=dcgain(G);[y,t]=step(G);plot(t,y)[Y,K]=max(y);timetopeak=t(k);percentovershoot=100*(y-c)/cn=1;while y(n)<c n=n+1;end risetime=t(n) i=length(t);while(y(i)>0.98*c&y(i)<1.02*c) i=i-1;End setllingtime=t(i) 运行程序结果为:稳定值c=0.5882,响应时间setllingtime=1.0096s,上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555% 同理得k=100时,稳定值c=5.882,响应时间setllingtime=1.0096s, 上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555%(3)k=1000时,由其响应曲线可知,增益系数越大,其稳定性越差。
MATLAB语言及控制系统仿真_参考答案解析_第2章

2.12 MATLAB 语言的数值运算-实训2.12.1实训目的1.学会矩阵的建立方法及其矩阵的转置、相乘、求逆等运算;2.识别了解特殊矩阵;3.学会求解方程与方程组;4.学会通过编程解决一些实际问题; 2.12.2实训内容 1.矩阵建立及其运算]4321012345[1-----=A[]0.19.08.07.06.05.04.03.02.01.02=A ]0.19.08.07.06.05.04.03.02.01.0[3=A][40.19.08.07.06.05.04.03.02.01.0e e e e e e e e e e A = ]2222222222[50.19.08.07.06.05.04.03.02.01.0=A求(1)211A A D += (2)232A A D -= (3)4/.13A D = (4)5*.44A A D = (5)5*35A D = (6))2(.^16A D =>> A1=-5:4;>> A2=0.1:0.1:1.0; >> A3=sqrt(A2); >> A4=exp(A2); >> A5=2.^(A2); >> format bank >> D1=A1+A2 D1 =-4.90 -3.80 -2.70 -1.60 -0.50 0.60 1.70 2.80 3.90 5.00 >> D2=A3-A2 D2 =0.22 0.25 0.25 0.23 0.21 0.17 0.14 0.09 0.05 0 >> D3=1./A4 D3 =0.90 0.82 0.74 0.67 0.61 0.55 0.50 0.45 0.41 0.37 >> D4=A4.*A5D4 =1.18 1.40 1.66 1.972.33 2.763.27 3.874.595.44 >> D5=3*A5 D5 =3.22 3.45 3.69 3.964.24 4.55 4.875.22 5.606.00 >> D6=A1.^2 D6 =25.00 16.00 9.00 4.00 1.00 0 1.00 4.00 9.00 16.002.建立矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----=1418712106114231359152345686420B(1)矩阵B 的逆矩阵)(inv B (2)矩阵B 对应的行列式)det(B>> B=[0:2:8;-6:-2;15,9,5,13,3;2,4,11,6,10;12,7,8,1,14]B =0 2.00 4.00 6.00 8.00 -6.00 -5.00 -4.00 -3.00 -2.00 15.00 9.00 5.00 13.00 3.00 2.00 4.00 11.00 6.00 10.00 12.00 7.00 8.00 1.00 14.00 >> inv(B) ans =-0.18 0.29 0.11 0.07 0.07 0.31 -0.72 -0.20 -0.23 -0.07 -0.21 0.11 0.03 0.21 -0.02 0.05 0.11 0.08 0.02 -0.04 0.12 0.04 -0.02 -0.06 0.06 >> det(B) ans =-17568.00(3)利用矩阵元素的提取方法建立以下矩阵 ①矩阵b01:矩阵B 的3~4行元素; ②矩阵b02:矩阵B 的2~5列元素;③矩阵b03:由矩阵B 的1~3行2~4列交叉点所对应的元素组成; >> B=[0:2:8;-6:-2;15,9,5,13,3;2,4,11,6,10;12,7,8,1,14]; >> b01=B(3:4,:) b01 =15.00 9.00 5.00 13.00 3.002.00 4.00 11.00 6.00 10.00 >> b02=B(:,2:5) b02 =2.00 4.00 6.00 8.00 -5.00 -4.00 -3.00 -2.00 9.00 5.00 13.00 3.004.00 11.00 6.00 10.00 7.00 8.00 1.00 14.00 >> b03=B(1:3,2:4) b03 =2.00 4.00 6.00 -5.00 -4.00 -3.00 9.00 5.00 13.00 3.矩阵的转置与翻转已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=151413121110987654321m ,求取以下矩阵观察并记录。
第12章--MATLAB-Simulink系统仿真-习题答案

第12章--M A T L A B-S i m u l i n k系统仿真-习题答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第12章 MATLAB Simulink系统仿真习题12一、选择题1.启动Simulink后,屏幕上出现的窗口是()。
AA.Simulink起始页 B.Simulink Library Browser窗口C.Simulink Block Browser窗口 D.Simulink模型编辑窗口2.模块的操作是在()窗口中进行的。
DA.Library Browser B.Model BrowserC.Block Editer D.模型编辑3.Integrator模块包含在()模块库中。
BA.Sources B.Continuous C.Sinks D.Math Operations 4.要在模型编辑窗口中复制模块,不正确的方法是()。
B A.单击要复制的模块,按住鼠标左键并同时按下Ctrl键,移动鼠标到适当位置放开鼠标B.单击要复制的模块,按住鼠标左键并同时按下Shift键,移动鼠标到适当位置放开鼠标C.在模型编辑窗口选择Edit→Copy命令和Edit→Paste命令D.右键单击要复制的模块,从快捷菜单中选择Copy命令和Paste命令5.已知仿真模型如图12-41(a)所示,示波器的输出结果如图12-41(b)所示。
(a)仿真模型3(b )示波器输出结果图12-41 习题仿真模型及仿真结果则XY Graph 图形记录仪的输出结果是( )。
CA .正弦曲线B .余弦曲线C .单位圆D .椭圆二、填空题1.Simulink (能/不能)脱离MATLAB 环境运行。
2.建立Simulink 仿真模型是在 窗口进行的。
模型编辑窗口3.Simulink 仿真模型通常包括 、系统模块和 三种元素。
信号源(Source ),信宿(Sink )4.由控制信号控制执行的子系统称为 ,它分为 、 和 。
控制系统的MATLAB仿真和设计课后答案

第二章1>>x=[15 22 33 94 85 77 60]>>x(6)>>x([1 3 5])>>x(4:end)>>x(find(x>70))2>>T=[1 -2 3 -4 2 -3] ;>>n=length(T);>>TT=T';>>for k=n-1:-1:0>>B(:,n-k)=TT.^k;>>end>>B>>test=vander(T)3>>A=zeros(2,5);>>A(:)=-4:5>>L=abs(A)>3>>islogical(L)>>X=A(L)4>>A=[4,15,-45,10,6;56,0,17,-45,0] >>find(A>=10&A<=20)5>>p1=conv([1,0,2],conv([1,4],[1,1]));>>p2=[1 0 1 1];>>[q,r]=deconv(p1,p2);>>cq='商多项式为'; cr='余多项式为';>>disp([cq,poly2str(q,'s')]),disp([cr,poly2str(r,'s')]) 6>>A=[11 12 13;14 15 16;17 18 19];>>PA=poly(A)>>PPA=poly2str(PA,'s')第三章1>>n=(-10:10)';>>y=abs(n);>>plot(n,y,'r.','MarkerSize',20)>>axis equal>>grid on>>xlabel('n')2>>x=0:pi/100:2*pi;>>y=2*exp(-0.5*x).*sin(2*pi*x);>>plot(x,y),grid on;3>>t=0:pi/50:2*pi;>>x=8*cos(t);>>y=4*sqrt(2)*sin(t);>>z=-4*sqrt(2)*sin(t);>>plot3(x,y,z,'p');>>title('Line in 3-D Space');>>text(0,0,0,'origin');>>xlabel('X'),ylable('Y'),zlable('Z');grid;4>>theta=0:0.01:2*pi;>>rho=sin(2*theta).*cos(2*theta); >>polar(theta,rho,'k');5>>[x,y,z]=sphere(20);>>z1=z;>>z1(:,1:4)=NaN;>>c1=ones(size(z1));>>surf(3*x,3*y,3*z1,c1);>>hold on>>z2=z;>>c2=2*ones(size(z2));>>c2(:,1:4)=3*ones(size(c2(:,1:4))); >>surf(1.5*x,1.5*y,1.5*z2,c2);>>colormap([0,1,0;0.5,0,0;1,0,0]); >>grid on>>hold off第四章1>>for m=100:999m1=fix(m/100);m2=rem(fix(m/10),10);m3=rem(m,10);if m==m1*m1*m1+m2*m2*m2+m3*m3*m3 disp(m)endend2M文件:function[s,p]=fcircle(r)s=pi*r*r;p=2*pi*r;主程序:[s,p]=fcircle(10)3>>y=0;n=100;for i=1:ny=y+1/i/i;end>>y4 M文件:function f=factor(n)if n<=1elsef=factor(n-1)*n; end主程序:>>s=0;for i=1:5s=s+factor(i); end>>s5>>sum=0;i=1; while sum<2000sum=sum+i;i=i+1;end;>>n=i-26for循环M文件:function k=jcsum(n) k=0;for i=0:nk=k+2^i;end>>jcsum(63)While循环M文件:function k=jcsum1(n)k=0;i=0;while i<=nk=k+2^i;i=i+1;end主程序:>>jcsum1(63)第五章1>>A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4]; >>b=[13,-9,6,0]';>>x=A\b2M文件:function f=fxyz(u)x=u(1);y=u(2);z=u(3);f=x+y.^2./x/4+z.^2./y+2./z;[U,fmin]=fminsearch('fxyz',[0.5,0.5,0.5])3>>X=linspace(0,2*pi,50);>>Y=sin(X);>>P=polyfit(X,Y,3)>>AX=linspace(0,2*pi,50);>>Y=sin(X);>>Y1=polyval(P,X)>>plot(X,Y,':O',X,Y1,'-*')4>>x=0:2.5:10;>>h=[0:30:60]';>>T=[95,14,0,0,0;88,48,32,12,6;67,64,54,48,41]; >>xi=[0:0.5:10];>>hi=[0:10:60]';>>temps=interp2(x,h,T,xi,hi,'cubic');>>mesh(xi,hi,temps);第六章1>>syms x>>y=finverse(1/tan(x))2>>syms x y>>f=1/(1+x^2); g=sin(y);>>fg=compose(f,g)>>g=(exp(x)+x*sin(x))^(1/2);>>dg=diff(g)4>>F=int(int('x*exp(-x*y)','x'),'y')5>>syms x>>F=ztrans(x*exp(-x*10))6>>a=[0 1;-2 -3];>>syms s>>inv(s*eye(2)-a);7>>f=solve('a*x^2+b*x+c')8>>f=solve('x+y+z=1','x-y+z=2','2*x-y-z=1')9>>y=dsolve('D2y+2*Dy+2*y=0','y(0)=1','Dy(0)=0') >>ezplot(y),grid on10>>a=maple('simplify(sin(x)^2+cos(x)^2);')11>>f=maple('laplace(exp(-3*t)*sin(t),t,s);')12>>syms t x>>F=sin(x*t+2*t);>>L=laplace(F)第七章1234567第八章1-1>>h=tf([5,0],[1,2,2])1-2>>s = tf('s');>>H = [5/(s^2+2*s+2) ];>>H.inputdelay =21-3>>h=tf([0.5,0],[1,-0.5,0.5],0.1) 2>>num=2*[1,0.5];den=[1,0.2,1.01];>>sys=tf(num,den)>>[z,p,k]=tf2zp(num,den);>>zpk(z,p,k)>>[A,B,C,D]=tf2ss(num,den);>>ss(A,B,C,D)3 >>num=[1,5]; den=[1,6,5,1]; ts=0.1; >>sysc=tf(num,den);>>sysd=c2d(sysc,ts,'tustin')4>>r1=1;r2=2;c1=3;c2=4;>>[A,B,C,D]=linmod('x84');>>[num,den]=ss2tf(A,B,C,D);>>sys=tf(num,den)5>>A=[1,1,0;0,1,0;0,0,2];B=[0,0;1,0;0,-2]; >>n=size(A)>>Tc=ctrb(A,B);if n==rank(Tc)disp('系统完全能控');elsedisp('系统不完全能控');end第九章1>>num=[2,5,1];den=[1,2,3];>>bode(num,den);grid on ;>>figure;>>nyquist(num,den);2>>num=5*[1,5,6];den=[1,6,10,8];>>step(num,den);grid on ;>>figure;>>impulse(num,den);grid on ;3>>kosi=0.7;wn=6;>>num=wn^2;den=[1,2*kosi*wn,wn^2];>>step(num,den);grid on ;>>figure;>>impulse(num,den);grid on ;4 M文件:function [rtab,info]=routh(den)info=[];vec1=den(1:2:length(den)); nrT=length(vec1); vec2=den(2:2:length(den)-1);rtab=[vec1; vec2, zeros(1,nrT-length(vec2))];for k=1:length(den)-2,alpha(k)=vec1(1)/vec2(1);for i=1:length(vec2),a3(i)=rtab(k,i+1)-alpha(k)*rtab(k+1,i+1);endif sum(abs(a3))==0a3=polyder(vec2);info=[info,'All elements in row ',...int2str(k+2) ' are zeros;'];elseif abs(a3(1))<epsa3(1)=1e-6;info=[info,'Replaced first element;'];endrtab=[rtab; a3, zeros(1,nrT-length(a3))];vec1=vec2; vec2=a3;end主程序:>>den=[1,2,8,12,20,16,16];>>[rtab,info]=routh(den)>>a=rtab(:,1)if all(a>0)disp('系统是稳定的');elsedisp('系统是不稳定的');end5>>num=7*[1,5];den=conv([1,0,0],conv([1,10],[1,1])); >>[gm,pm,wg,wc]=margin(num,den)第十章1 M文件:function varargout=rg_lead(ng0,dg0,s1)if nargout==1ngv=polyval(ng0,s1);dgv=polyval(dg0,s1);g=ngv/dgv;thetal=pi-angle(g);zc=real(s1)-imag(s1)/tan(thetal);t=-1/zc;varargout{1}=[t,1];elseif nargout==2ngv=polyval(ng0,s1); dgv=polyval(dg0,s1);g=ngv/dgv; theta=angle(g); phi=angle(s1);if theta>0phi_c=pi-theta;endif theta<0;phi_c=-thetaendtheta_z=(phi+phi_c)/2; theta_p=(phi-phi_c)/2;z_c=real(s1)-imag(s1)/tan(theta_z);p_c=real(s1)-imag(s1)/tan(theta_p);nk=[1 -z_c]; varargout{2}=[1 -p_c]; kc=abs(p_c/z_c);if theta<0kc=-kcendvarargout{1}=kc*nk;elseerror('输出变量数目不正确!');end主程序:>> ng0=[1]; dg0=10000*[1 0 -1.1772];>>g0=tf(ng0,dg0); %满足开环增益的为校正系统的传递函数>>s=kw2s(0.7,0.5) %期望的闭环主导极点>>ngc=rg_lead(ng0,dg0,s);>>gc=tf(ngc,1)>>g0c=tf(g0*gc);>>rlocus(g0,g0c);>>b1=feedback(g0,1); %未校正系统的闭环传递函数>>b2=feedback(g0c,1); %校正后系统的闭环传递函数>>figure,step(b1,'r--',b2,'b'); grid on%绘2M文件:function [ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a)ngv=polyval(ng0,s1);dgv=polyval(dg0,s1);g=dgv/ngv;k=abs(g); %期望主导极点处的根轨迹增益beta=k/KK;[kosi1,wn1]=s2kw(s1);zc=-wn1*sin(a*pi/180)/sin(pi-atan(sqrt(1-kosi1^2)/kosi1)-(a*pi/180)); %利用正弦定理pc=beta*zc;ngc=beta*[1,-zc];dgc=[1,-pc];主程序:>>KK=20;s1=-2+i*sqrt(6);a=1>>ng0=[10];dg0=conv([1,0],[1,4]);>>g0=tf(ng0,dg0);>>[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a);>>gc=tf(ngc,dgc)>>g0c=tf(KK*g0*gc);>>b1=feedback(k*g0,1);>>step(b1,'r--',b2,'b');grid on3M文件:function [ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a)ngv=polyval(ng0,s1);dgv=polyval(dg0,s1);g=dgv/ngv;k=abs(g); %期望主导极点处的根轨迹增益beta=k/KK;[kosi1,wn1]=s2kw(s1);zc=-wn1*sin(a*pi/180)/sin(pi-atan(sqrt(1-kosi1^2)/kosi1)-(a*pi/180)); %利用正弦定理pc=beta*zc;ngc=beta*[1,-zc];dgc=[1,-pc];主程序:>>KK=128;s1=-2+i*2*sqrt(3);a=2>>ng0=[10];dg0=conv([1,0],conv([1,2],[1,8]));>>g0=tf(ng0,dg0);>>[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a);>>gc=tf(ngc,dgc)>>g0c=tf(KK*g0*gc);>>rlocus(g0,g0c);>>b2=feedback(g0c,1);>>figure,step(b1,'r--',b2,'b');grid on4M文件:function [ngc,dgc]=lead4(ng0,dg0,KK,Pm,w)[mu,pu]=bode(KK*ng0,dg0,w); [gm,pm,wcg,wcp]=margin(mu,pu,w); alf=ceil(Pm-pm+5); phi=(alf)*pi/180;a=(1+sin(phi))/(1-sin(phi)), dbmu=20*log10(mu);mm=-10*log10(a); wgc=spline(dbmu,w,mm), T=1/(wgc*sqrt(a)),ngc=[a*T,1]; dgc=[T,1];主程序:>>ng0=[1];dg0=conv([1,0,0],[1,5]);>>g0=tf(ng0,dg0);>>w=logspace(-3,3);>>KK=1;Pm=50;>>[ngc,dgc]=lead4(ng0,dg0,KK,Pm,w);>>gc=tf(ngc,dgc);g0c=tf(KK*g0*gc);>>bode(KK*g0,w);hold on,bode(g0c,w);grid on,hold off>>[gm,pm,wcg,wcp]=margin(g0c)>>Kg=20*log10(gm)>>g1=feedback(g0c,1);>>bode(g1),grid on,>>[mag,phase,w]=bode(g1);>>a=find(mag<=0.707*mag(1));>>wb=w(a(1))>>max(mag)>>b=find(mag==max(mag))>>wr=w(b)5M文件:function [ngc,dgc]=fg_lead_pm(ng0,dg0,Pm,w)[mu,pu]=bode(ng0,dg0,w); %计算原系统的对数频率响应数据[gm,pm,wcg,wcp]=margin(mu,pu,w); %求取原系统的相角裕度和剪切频率alf=ceil(Pm-pm+5); %计算控制器提供的最大超前角度,phi=(alf)*pi/180; %将最大超前角转换为弧度单位a=(1+sin(phi))/(1-sin(phi)); %计算a值dbmu=20*log10(mu); %系统的对数幅值mm=-10*log10(a); %wm处的控制器对数幅值wgc=spline(dbmu,w,mm); %差值求取wm,认为wm=wc T=1/(wgc*sqrt(a)); %计算Tngc=[a*T,1]; dgc=[T,1];主程序:>>KK=40; Pm=50;>>ng0= KK *[1]; dg0=conv([1,0],conv([1,1],[1,4])); >>g0=tf(ng0,dg0) ;>>w=logspace(-2,4);>>[ngc,dgc]=fg_lead_pm(ng0,dg0,Pm,w)>>gc=tf(ngc,dgc),g0c=tf(g0*gc);>>b1=feedback(g0,1); b2=feedback(g0c,1);>>step(b1,'r--', b2,'b'); grid on>>figure, bode(g0,'r--',g0c,'b',w), grid on,>>[gm,pm,wcg,wcp]=margin(g0c), Km=20*log10(gm)。
matlab仿真实例100题

matlab仿真实例100题Matlab是一种强大的数学软件,广泛应用于科学计算、数据分析和工程仿真等领域。
在学习和使用Matlab的过程中,通过实例的方式进行仿真练习是一种非常有效的学习方法。
下面将给出100个Matlab仿真实例题目,帮助读者更好地掌握Matlab的使用。
1. 编写一个程序,计算并输出1到100之间所有奇数的和。
2. 编写一个程序,计算并输出1到100之间所有偶数的乘积。
3. 编写一个程序,计算并输出1到100之间所有素数的个数。
4. 编写一个程序,计算并输出1到100之间所有整数的平方和。
5. 编写一个程序,计算并输出1到100之间所有整数的立方和。
6. 编写一个程序,计算并输出1到100之间所有整数的阶乘和。
7. 编写一个程序,计算并输出1到100之间所有整数的倒数和。
8. 编写一个程序,计算并输出1到100之间所有整数的平均值。
9. 编写一个程序,计算并输出1到100之间所有整数的中位数。
10. 编写一个程序,计算并输出1到100之间所有整数的标准差。
11. 编写一个程序,计算并输出1到100之间所有整数的方差。
12. 编写一个程序,计算并输出1到100之间所有整数的最大值。
13. 编写一个程序,计算并输出1到100之间所有整数的最小值。
15. 编写一个程序,计算并输出1到100之间所有整数的平方根和。
16. 编写一个程序,计算并输出1到100之间所有整数的立方根和。
17. 编写一个程序,计算并输出1到100之间所有整数的对数和。
18. 编写一个程序,计算并输出1到100之间所有整数的指数和。
19. 编写一个程序,计算并输出1到100之间所有整数的正弦和。
20. 编写一个程序,计算并输出1到100之间所有整数的余弦和。
21. 编写一个程序,计算并输出1到100之间所有整数的正切和。
22. 编写一个程序,计算并输出1到100之间所有整数的双曲正弦和。
23. 编写一个程序,计算并输出1到100之间所有整数的双曲余弦和。
matlab仿真实验答案

实验一(1)单位脉冲序列n=0:10;ns=3;x1n=[(n-ns)==0];subplot(221)stem(n,x1n)(2)单位阶跃序列n=0:10;ns=3;x2n=[(n>=ns)];subplot(222);stem(n,x2n)(3)复指数序列a=-0.2;w=0.5;n=0:10;xn=[n>=0];x3n=xn.*exp((a+j*w).*n); real=real(x3n);imag=imag(x3n);subplot(223);stem(n,real)subplot(224);stem(n,imag)(4)差分方程b=[3,7,1];a=[1,0.1,0.15,-0.225];n=1:20;u=exp(0.1.*n);y=filter(b,a,u);stem(n,y)实验二:1.序列的相加和相乘 ny=-2:8;x1=[0 1 2 3 4 3 2 1 0 0 0]; x2=[0 0 0 0 2 2 0 0 0 -2 -2]; ya=x1+x2;%序列的相加 yp=x1.*x2;%序列的相乘%绘图,画出x1,a2,ya,yp 的离散图 subplot(221); stem(ny,x1) subplot(222); stem(ny,x2) subplot(223); stem(ny,ya) subplot(224); stem(ny,yp)-551001234nyx 1-5510-2-1012nyx 2-5510-20246nyy a-551002468nyy p2.序列的移位和周期延拓运算 N=24; M=8; m=3;n=0:N-1;R8n=[ones(1,8),zeros(1,16)]; %矩形序列,补零拓展至24位 xn=(0.8.^n).*R8n;%原序列 subplot(221) stem(n,xn)R8nn=[zeros(1,3),ones(1,8),zeros(1,13)]; xnm=(0.8.^(n-3)).*R8nn; %右移3位 subplot(222); stem(n,xnm)xn8=xn(mod(n,8)+1); %周期延拓 subplot(223); stem(n,xn8)xm8=xn(mod(n-m,8)+1); %循环移位 subplot(224); stem(n,xm8)10203000.51nx n01020300.51nx n m10203000.51nx n 的周期延拓01020300.51nx n 的循环移位实验四:1.LTI 系统的卷积 dt=0.5;u=ones(1,10);h=exp(-0.1*[1:15]); y=conv(u,h); subplot(311);stem(0:length(u)-1,u) subplot(312);stem(0:length(h)-1,h) subplot(313);stem(dt*([1:length(y)]-1),y)012345678900.51u024********00.51h024681012510c o n v (u ,h )2.离散序列的卷积计算 N=20;n=0:N-1;xn1=[.9.^n,zeros(1,20)];hn1=[ones(1,10),zeros(1,10)]; Xm=zeros(1,34) for i=1:34xn2(i+5)=xn1(i); endhn2=hn1;yn1=conv(xn1,hn1); yn2=conv(xn2,hn2);subplot(3,2,1),stem(0:length(xn1)-1,xn1); subplot(3,2,2),stem(0:length(xn2)-1,xn2); subplot(3,2,3),stem(0:length(hn1)-1,hn1); subplot(3,2,4),stem(0:length(hn2)-1,hn2); subplot(3,2,5),stem(0:length(yn1)-1,yn1); subplot(3,2,6),stem(0:length(yn2)-1,yn2);010********.5101020304000.510510152000.510510152000.51020406005100204060510实验六:有限序列的Z 变换和逆Z 变换 1.有限序列的Z 变换 x1=[1,2,3]; x2=[2,4,3,5]; n=-3:2;x=conv(x1,x2);2.有限序列的逆Z 变换.x=[2,4,3,5,zeros(1,10)]; BW=-3;AW=[2,-2.2,0.5]; y=filter(BW,AW,x); stem(0:length(y)-1,y) x=conv(x1,x2) x =2 8 17 23 19 15024********-25-20-15-10-5有限序列的逆Z 变换实验七 离散傅里叶变换DFT N1=16;n=0:N1-1; R16=[ones(1,16)];x1=exp(j*pi*n/8).*R16;%复正弦序列x1序列的产生 x2=cos(pi*n/8).*R16;%余弦序列x2的产生 x3=sin(pi*n/8).*R16; %正弦序列x3的产生 x1K=fft(x1,N1);%x1的16点DFT x2K=fft(x2,N1); %x2的16点DFT x3K=fft(x3,N1); %x3的16点DFT subplot(331)stem(n,real(x1),'.');title('x1(n)');ylabel('x1(n)'); hold on%使得两个图形画在一起stem(n,imag(x1));title('x1(n)');ylabel('x1(n)'); subplot(332)stem(n,x2,'.');title('x2(n)');ylabel('x2(n)'); subplot(333)stem(n,x3,'.');title('x3(n)');ylabel('x3(n)'); subplot(334)stem(n,abs(x1K),'.');title('16点DTFx1(n)'); subplot(335)stem(n,abs(x2K),'.');title('16点DTFx2(n)'); subplot(336)stem(n,abs(x3K),'.');title('16点DTFx3(n)'); N2=8;n1=0:N2-1; R8=[ones(1,8)];x11=exp(j*pi*n1/8).*R8; %复正弦序列x11序列的产生 x22=cos(pi*n1/8).*R8; %余弦序列x22的产生x33=sin(pi*n1/8).*R8; %正弦序列x33的产生x4K=fft(x11,N2); %x11的8点DFTx5K=fft(x22,N2); %x22的8点DFTx6K=fft(x33,N2); %x33的8点DFTsubplot(337)stem(n1,abs(x4K),'.');title('8点DTFx1(n)'); subplot(338)stem(n1,abs(x5K),'.');title('8点DTFx2(n)'); subplot(339)stem(n1,abs(x6K),'.');title('8点DTFx3(n)');实验九香农公式的分析echo on;pn0_db=[-20:0.1:30];pn0=10.^(pn0_db./10);capacity1=3000*log2(1+pn0/3000);pause;clf;semilogx(pn0,capacity1)title('capacity vs .P/N0 in an AWGN Channel'); xlabel('P/N0');ylabel('Capacity (bits/second)');3.echo on;pn0_db=25;pn0=10.^(pn0_db./10);w=0:10.^5;capacity=w.*log2(1+pn0./w); pause;clf;semilogx(w,capacity)xlabel('w');ylabel('Capacity (bits/second)');实验十双边带(DSB)调制clc;clear all;close all;t0=.15;ts=.001;fc=250;fs=1/ts;t=[0:ts:t0];%message signalm=[ones(1,t0/(3*ts)),-2*ones(1,t0/(3*ts)),zeros(1,t0/(3*ts)+1)]; c=cos(2*pi*fc.*t);u=m.*c;subplot(311)plot(t,m(1:length(t)));xlabel('time');title('the messge signal');subplot(312);plot(t,c(1:length(t)));xlabel('time');title('the carrier');subplot(313);plot(t,u(1:length(t)));xlabel('time');title('the modulated signal');M=fft(m);M=fftshift(M);figure subplot(211); plot(t,abs(M)) U=fft(u);U=fftshift(U); subplot(212); plot(t,abs(U))。
MATLAB仿真课后习题答案

MATLAB仿真课后习题答案MATLAB仿真课后习题答案第一章1.要求在闭区间[0,2Π]上产生具有10个等间距采样点的一维数组。
试用两种不同的指令实现。
解答:方法1:a=0:2*pi/9:2*pi方法2:a1=linspace(0,2*pi,10)4.任意建立矩阵A,然后找出在[10,20]区间的元素的位置。
解答:A=[4,15,-45,10,6;56,0,17,-45,0]A =4 15 -45 10 656 0 17 -45 0>> find(A>=10&A<=20)ans =367第二章M文件的2种形式:命令文件和函数文件。
命令文件没有输入输出参数,执行时只需在命令窗口中键入文件名回车即可;而函数文件是一条以function语句作为引导。
即文件的第一行为function[返回参数1,返回参数2,…]=函数名(输入参数1,输入参数2,…)。
这一行的有无是区分命令文件与函数文件的重要标志。
函数文件可以接受输入变量,还可以返回输出变量,执行时需在命令窗口中以固定格式调用函数方可。
习题22-1.编写程序,建立向量N=[1,2,3,4,5],然后利用向量N产生下列向量:(1) 2,4,6,8,10(2) 1/2, 1, 3/2, 2, 5/2(3) 1, 1/2, 1/3, 1/4, 1/5(4) 1, 1/4, 1/9, 1/16, 1/25解答:>> N1=2*N >> N2=N/2 >> N3=1./N >> N4=1./N.^2 2-2从键盘输入一个3位数的整数,将它反向输出。
如输入639,输出936。
输入一个百分制成绩,要求输出成绩等级A、B、C、D、E。
其中90~100分为A,80~89分为B,70~79分为C,60~69分为D,60分以下为E。
要求:(1)分别用if语句和switch语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
matlab语言与控制系统仿真参考答案第1章
1.6 MATLAB操作基础-实训实训目的1.熟悉MATLAB语言环境,识别MATLAB桌面和命令窗口,命令历史窗口,工作空间窗口等;2.练习设置变量精度或变量显示方式;3.练习通过MATLAB编程解决一些实际问题;4.通过作图总结自变量增量设置对作图结果的影响;5.学会求解方程、方程组的基本方法;6.练习M文件的建立与执行;7.学会进入工具箱的演示系统,以便于进一步了解和学习感兴趣的知识,为以后的自主学习奠定基础。
1.根据表1-2中要求,先使用命令format改变变量的精度或显示方式,然后键入表达式,并将运行结果填入表1-2中,并练习使用clc 清除命令窗口中内容。
>> format bank;>> aa = 3.142.720.611.4164.0081.00>> format short>> aa =3.14162.71830.60651.414264.000081.0000>> format short e>> aa =3.1416e+0002.7183e+0006.0653e-001 1.4142e+000 6.4000e+001 8.1000e+001 >> format rat >> a a =355/113 1457/536 743/1225 1393/985 64 812. 编写MA TLAB 程序计算,根据程序运算结果填空(要求保留两位小数)(1)58.135.0+=-ea =( 4.29 ); 程序为: a=exp(-0.5)+sqrt(13.58)>> format bank;>> a=exp(-0.5)+sqrt(13.58) a =4.29(2)已知两个圆的半径分别为cm 5.31=r , cm 62=r ,则两个圆的周长分别为=1l ( 21.99 )cm, =2l ( 37.70 )cm;面积分别为=1s ( 38.48 )2cm ,=2s ( 113.10 )2cm程序:>> format bank; >> r=[3.5 6]; >> [2*pi*r;pi*r.*r]提示:圆的周长计算公式为:r L π2=,圆的面积2r S π=,其中r 为圆的半径。
MATLAB仿真课后习题

第一章习题3.请指出以下的变量名(函数名、M文件名)中,哪些是合法的?Abc 2004x lil-1 wu_2004 a&b qst.u _xyz 解:合法的变量名有:Abc wu_20044.指令窗操作(1)求[12+2×(7-4)]÷32的运算结果解:>> [12+2*(7-4)]/3^2ans =2(2)输入矩阵A=[1,2,3;4,5,6;7,8,9],观察输出。
解:>> A=[1,2,3;4,5,6;7,8,9]A =1 2 34 5 67 8 9(3)输入以下指令,观察运算结果;clear;x=-8:0.5:8;y=x';X=ones(size(y))*x;Y=y*ones(size(x));R=sqrt(X.^2+Y.^2)+eps;Z=sin(R)./R;mesh(X,Y,Z);colormap(hot)xlabel('x'),ylabel('y'),zlabel('z')解:7.指令行编辑(1)依次键入以下字符并运行:y1=2*sin(0.3*pi)/(1+sqrt(5))解:>>y1=2*sin(0.3*pi)/(1+sqrt(5))y1 =0.5000(2)通过反复按键盘的箭头键,实现指令回调和编辑,进行新的计算;y2=2*cos(0.3*pi)/(1+sqrt(5))解:>>y2=2*cos(0.3*pi)/(1+sqrt(5))y2 =0.363311.编写题4中(3)的M脚本文件,并运行之。
解:第二章习题1.在指令窗中键入x=1:0.2:2和y=2:0.2:1,观察所生成的数组。
解:>> x=1:0.2:2 x =1.0000 1.2000 1.4000 1.6000 1.80002.0000 >> y=2:0.2:1 y =Empty matrix: 1-by-02.要求在[0,2π]上产生50个等距采样数据的一维数组,试用两种不同的指令实现。
MATLAB仿真课后习题答案

MATLAB仿真课后习题答案第一章1.要求在闭区间[0,2Π]上产生具有10个等间距采样点的一维数组。
试用两种不同的指令实现。
解答:方法1:a=0:2*pi/9:2*pi方法2:a1=linspace(0,2*pi,10)4.任意建立矩阵A,然后找出在[10,20]区间的元素的位置。
解答:A=[4,15,-45,10,6;56,0,17,-45,0]A =4 15 -45 10 656 0 17 -45 0>> find(A>=10&A<=20)ans =367第二章M文件的2种形式:命令文件和函数文件。
命令文件没有输入输出参数,执行时只需在命令窗口中键入文件名回车即可;而函数文件是一条以function语句作为引导。
即文件的第一行为function[返回参数1,返回参数2,…]=函数名(输入参数1,输入参数2,…)。
这一行的有无是区分命令文件与函数文件的重要标志。
函数文件可以接受输入变量,还可以返回输出变量,执行时需在命令窗口中以固定格式调用函数方可。
习题22-1.编写程序,建立向量N=[1,2,3,4,5],然后利用向量N产生下列向量:(1) 2,4,6,8,10(2) 1/2, 1, 3/2, 2, 5/2(3) 1, 1/2, 1/3, 1/4, 1/5(4) 1, 1/4, 1/9, 1/16, 1/25解答:>> N1=2*N >> N2=N/2 >> N3=1./N >> N4=1./N.^22-2从键盘输入一个3位数的整数,将它反向输出。
如输入639,输出936。
输入一个百分制成绩,要求输出成绩等级A、B、C、D、E。
其中90~100分为A,80~89分为B,70~79分为C,60~69分为D,60分以下为E。
要求:(1)分别用if语句和switch语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章习题3.请指出以下的变量名(函数名、M文件名)中,哪些是合法的?Abc 2004x lil-1 wu_2004 a&b qst.u _xyz 解:合法的变量名有:Abc wu_20044.指令窗操作(1)求[12+2×(7-4)]÷32的运算结果解:>> [12+2*(7-4)]/3^2ans =2(2)输入矩阵A=[1,2,3;4,5,6;7,8,9],观察输出。
解:>> A=[1,2,3;4,5,6;7,8,9]A =1 2 34 5 67 8 9(3)输入以下指令,观察运算结果;clear;x=-8:0.5:8;y=x';X=ones(size(y))*x;Y=y*ones(size(x));R=sqrt(X.^2+Y.^2)+eps;Z=sin(R)./R;mesh(X,Y,Z);colormap(hot)xlabel('x'),ylabel('y'),zlabel('z')解:7.指令行编辑(1)依次键入以下字符并运行:y1=2*sin(0.3*pi)/(1+sqrt(5))解:>>y1=2*sin(0.3*pi)/(1+sqrt(5))y1 =0.5000(2)通过反复按键盘的箭头键,实现指令回调和编辑,进行新的计算;y2=2*cos(0.3*pi)/(1+sqrt(5))解:>>y2=2*cos(0.3*pi)/(1+sqrt(5))y2 =0.363311.编写题4中(3)的M脚本文件,并运行之。
解:第二章习题1.在指令窗中键入x=1:0.2:2和y=2:0.2:1,观察所生成的数组。
解:>> x=1:0.2:2 x =1.0000 1.2000 1.4000 1.6000 1.80002.0000 >> y=2:0.2:1 y =Empty matrix: 1-by-02.要求在[0,2π]上产生50个等距采样数据的一维数组,试用两种不同的指令实现。
解: y1=0:2*pi/49:2*piy2=linspace(0,2*pi,50)3.计算e -2t sint ,其中t 为[0,2π]上生成的10个等距采样的数组。
解:>> t=linspace(0,2*pi,10); x=exp(-2*t).*sin(t) x =0 0.1591 0.0603 0.0131 0.0013 -0.0003 -0.0002 -0.0001 -0.0000 -0.00004.已知A=⎥⎦⎤⎢⎣⎡4321 , B=⎥⎦⎤⎢⎣⎡8765,计算矩阵A 、B 乘积和点乘. 解:>> A=[1,2;3,4]; B=[5,6;7,8]; x=A*B x =19 22 43 50 >> x=A.*B x =5 1221 325.已知A=⎥⎦⎤⎢⎣⎡05314320,B=⎥⎦⎤⎢⎣⎡05314320,计算A&B, A|B, ~A, A==B, A>B. 解:>> A=[0,2,3,4;1,3,5,0]; B=[1,0,5,3;1,5,0,5]; a1=A&Ba2=A|B a3=~A a4=(A==B) a5=(A>B) a1 =0 0 1 1 1 1 0 0 a2 =1 1 1 1 1 1 1 1 a3 =1 0 0 0 0 0 0 1 a4 =0 0 0 0 1 0 0 0 a5 =0 1 0 1 0 0 1 07.将题5中的A 阵用串转换函数转换为串B ,再size 指令查看A 、B 的结构,有何不同?解:>> A=[0,2,3,4;1,3,5,0] B=num2str(A)size(A)size(B)A =0 2 3 41 3 5 0B =0 2 3 41 3 5 0ans =2 4ans =2 10第三章习题1.已知系统的响应函数为)sin(11)(θββε+-=-t e t y t ,其中⎪⎪⎭⎫⎝⎛-=-=εεθεβ221arctan ,1 ,要求用不同线型或颜色,在同一图上绘制ε取值分别为0.2、0.4、0.6、0.8时,系统在t ∈[0,18] 区间的响应曲线,并要求用ε=0.2和 ε=0.8对他们相应的两条曲线进行文字标志。
解: clcclose all clear all t=0:0.02:18;xi=[0.2,0.4,0.6,0.8]'; sxi=sqrt(1-xi.^2); sita=atan(sxi./xi);y=1-exp(-xi*t).*sin(sxi*t+sita*ones(1,901))./(sxi*ones(1,901))plot(t,y(1), 'r-', t,y(2), ' b*', t,y(3), ' g+', t,y(4), ' k.')text(4.2,1.4,'\xi =0.2') text(3.8,0.9,'\xi=0.8')2.用plot3、mesh 、surf 指令绘制()()2222111yx y x z ++++-=三维图(x,y 围自定)。
解:clc;close all ;clear all ; x=-5:0.1:5;y=-5:0.1:5; [X,Y]=meshgrid(x,y); a=sqrt((1-X).^2+Y.^2); b=sqrt((1+X).^2+Y.^2); Z=1./(a+b);a1=sqrt((1-x).^2+y.^2); b1=sqrt((1+x).^2+y.^2); z=1./(a1+b1);subplot(1,3,1),plot3(x,y,z),xlabel('x'),ylabel('y'),zlabel('z');box on ; subplot(1,3,2),surf(X,Y,Z),xlabel('x'),ylabel('y'),zlabel('z');box on ; subplot(1,3,3),mesh(X,Y,Z),xlabel('x'),ylabel('y'),zlabel('z');box on ;3.对向量t进行以下运算可以构成三个坐标的值向量:x=sin(t),y=cos(t),z=t.利用指令plot3,并选用绿色的实线绘制相应的三维曲线.解:t=(0:0.01:2)*pi;x=sin(t);y=cos(t);z=t;plot3(x,y,z,'b-');box on第四章习题1.请分别用for 和while 循环语句计算K=∑=6302i i的程序,再写出一种避免循环的计算程序。
(提示:可考虑利用MATLAB 的sum(X,n)函数,实现沿数组X 的第n 维求和。
)解:1)K=0;for i=0:63;K=K+2^i;endKK =1.8447e+0192)i=0;K=0;while i<=63;K=K+2^i;i=i+1;end;KK =1.8447e+0193)i=0;X=0:63;for i=0:63;X(i+1)=2^i; endsum(X,2)ans =1.8447e+019第五章习题1.将下列系统的传递函数模型用MATLAB 语言表达出来。
(1))170046842541254289()1700109329135()(23452341+++++++++=s s s s s s s s s s G 解:num=[1,35,291,1093,1700];den=[1,289,254,2541,4684,1700];sys=tf(num,den) (2))15).(5).(1()3(15)(2++++=s s s s s G 解:z=-3;p=[-1,-5,-15];k=15;sys=zpk(z,p,k) (3))252).(1).(1()23.()2.(.100)(23223+++-++++=s s s s s s s s s s G 解:z=[0,-2,-2];p=[-1,1];k=100;sys1=zpk(z,p,k);num=[1,3,2];den=[1,2,5,2];sys2=tf(num,den);sys=series(sys1,sys2)4.求题3中的系统模型的等效传递函数模型和零极点模型。
解:A=[3,2,1;0,4,6;0,-3,-5];B=[1,2,3]' ;C=[1,2,5];D=0;sys=ss(A,B,C,D);systf=tf(sys)syszpk=zpk(sys)Transfer function:20 s^2 - 83 s + 138---------------------s^3 - 2 s^2 - 5 s + 6Zero/pole/gain:20 (s^2 - 4.15s + 6.9)-----------------------(s-3) (s-1) (s+2)5.已知系统的动力学方程如下,试用MATLAB 语言写出它们的传递函数。
(1))(2)()(500)(50)(15)(......)3(t r t r t y t y t y t y +=+++解:num=[1,2,0];den=[1,15,50,500];sys=tf(num,den)Transfer function:s^2 + 2 s-------------------------s^3 + 15 s^2 + 50 s + 500(2) )(4)(4)(6)(3)(...t r dt t y t y t y t y =+++⎰解:num=[4,0];den=[1,3,6,4];sys=tf(num,den)Transfer function:4 s---------------------s^3 + 3 s^2 + 6 s + 46.试用MATLAB 语言表示图5-13所示系统。
当分别以y =x 2和f 为系统输出、输入时的传递函数模型和状态空间模型(图中k=7N/m,c1=0.5N/m.s-1, c2=0.2N/m.s-1,m1=3.5kg, m2=5.6kg)。
f解:)(tk=7;c1=0.5;c2=0.2;m1=3.5;m2=5.6;num=[m1,c1,k];den=[m1*m2,c1*m1+c2*m1+c1*m2,c1*c2+m2*k,c1*k+c2*k,0];sys=tf(num,den)Transfer function:3.5 s^2 + 0.5 s + 7--------------------------------------19.6 s^4 + 5.25 s^3 + 39.3 s^2 + 4.9 s7.试用MATLAB语言分别表示图5-14所示系统质量m1,m2的位移x1,x2对输入f的传递函数X2(s)/F(s)和X1(s)/F(s),其中m1=12kg, m2=38kg,k=1000N/m, c=0.1N/m.s-1。
