电工学课后答案-第2章-电路的瞬态分析习题及答案
《电工学》作业答案第二章
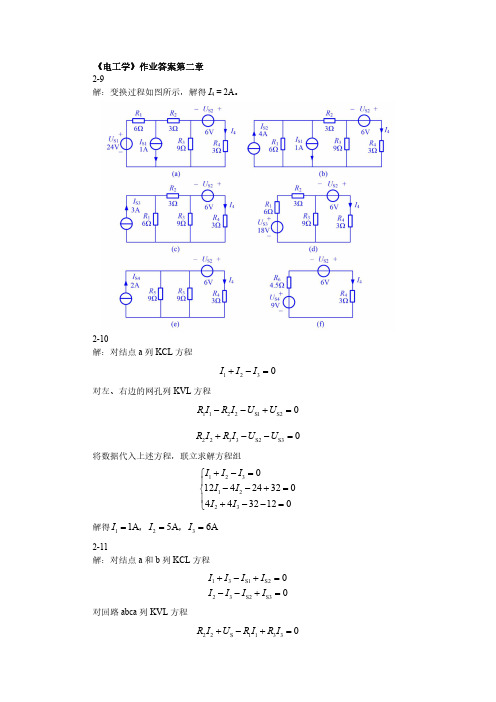
《电工学》作业答案第二章 2-9解:变换过程如图所示,解得I 4 = 2A 。
2-10解:对结点a 列KCL 方程1230I I I对左、右边的网孔列KVL 方程1122S1S20R I R I U U 2233S2S30R I R I U U将数据代入上述方程,联立求解方程组12312230124243204432120I I I I I I I解得1231A 5A 6A I I I ,, 2-11解:对结点a 和b 列KCL 方程13S1S223S2S300I I I I I I I I对回路abca 列KVL 方程22S 11330R I U R I R I将数据代入上述方程,联立求解方程组132321362023022420I I I I I I I解得1232A 1A 2A I I I ,,2-12 解:根据两个结点电路中结点电压方程的一般形式得S1S2S3123a 12312612346V 6V 111111346U U U R R R U R R R 电流I 3可用欧姆定律求得a S333612A 3A 6U U I R2-14解:(a)电路图; (b)电压源U S 单独作用的电路; (c)电流源I S 单独作用的电路电压源U S1单独作用时,将U S2短路,电路如 (b)所示S1123123321232312318A 3.6A 6336333.6A 1.2A 6363.6A 2.4A63U I R R R R R R I I R R R I I R R电压源U S2单独作用时,将U S1短路,电路如图 (c)所示S2213213312131321315A 2A 3362332A 1A3332A 1A33U I R R R R R R I I R R R I I R RU S 和I S 共同作用时111222333 3.61A 2.6A 1.22A 0.8A 2.41A 3.4A I I I I I I I I I 2-16解:(a)I S1单独作用的电路; (b)I S2单独作用的电路; (c)U S 单独作用的电路电流源I S1单独作用时,电路如 (a)所示2S12333A 1.8A 32R I I R R电流源I S2单独作用时,电路如 (b)所示3S22325A 2A 32R I I R R电压源U S2单独作用时,电路如 (c)所示S 2315A 3A 32U I R RI S1、I S1和U S 共同作用时1.823A 6.8A I I I I2-19 解:(a) 求开路电压的电路; (b)求除源电阻的电路; (c) 戴维南等效电路求开路电压的等效电路如 (a)所示。
电工学唐介课后答案第2章思考题

本文由946478976贡献ppt文档可能在WAP端浏览体验不佳。
建议您优先选择TXT,或下载源文件到本机查看。
第 2 章电路的暂态分析分析与思考理想电阻元件与直流电源接通时, 2.1.(1) 理想电阻元件与直流电源接通时,有没有过渡过程?这时电阻中电压和电流的波形是什么样的? 过程?这时电阻中电压和电流的波形是什么样的? 2.1.(2)阶跃电压和直流电压的波形有什么区别? 阶跃电压和直流电压的波形有什么区别? 2.1.(3)含电容或电感的电路在换路时是否一定会产生过渡过程? 过渡过程? 的电容器, 2.2.(1)今需要一只 50 V,10 F 的电容器,但手头 , 只有两只50V,5F 和两只30V,20 F 的电容器,试问只有两只 , , 的电容器, 应该怎样解决? 应该怎样解决? 2.2.(2)可否由换路前的电路求 iC(0) 和 uL(0)?上一页下一页第 2 章电路的暂态分析处于零状态, 2.3.(1)如果换路前电容 C 处于零状态,则 t = 0 时,uC(0) = 0, , 电容相当于短路, →∞而 t→∞时, iC(∞) =0,可否认为 t = 0 时,电容相当于短路, t→∞→∞∞ , 电容相当于开路?如果换路前C不是处于零状态不是处于零状态, 时,电容相当于开路?如果换路前不是处于零状态,上述结论是否成立? 否成立? 电路中,如果串联了电流表, 2.3.(2)在 RC 电路中,如果串联了电流表,换路前最好将电流表短路,这是为什么? 流表短路,这是为什么? 处于零状态, 2.4.(1)如果换路前 L 处于零状态,则 t = 0 时, iL(0) = 0 ,而 t→∞时, uL(∞) =0 ,因此可否认为 t = 0时,电感相当于开路, →∞∞时电感相当于开路, t→∞时,电感相当于短路? 电感相当于短路? →∞不是处于零状态,上述结论是否成立? 2.4.(2)如果换路前 L 不是处于零状态,上述结论是否成立?返回上一页下一页第 2 章电路的暂态分析2.5.(1)任何一阶电路的全响应是否都可以用叠加原理由它的零输入响应和零状态响应求得,请自选一例题试试看. 零输入响应和零状态响应求得,请自选一例题试试看. 一定, 越大, 2.5.(2)在一阶电路中,R一定,而 C 或 L 越大,换路时的过在一阶电路中, 一定渡过程进行得越快还是越慢? 渡过程进行得越快还是越慢?返回上一页下一页第 2 章电路的暂态分析分析与思考解答2.1.(1)理想电阻元件与直流电源接通时,有没有过渡过程? 理想电阻元件与直流电源接通时,有没有过渡过程? 这时电阻中电压和电流的波形是什么样的? 这时电阻中电压和电流的波形是什么样的? 【答】无过渡过程.电阻中电压和电流的波形为阶跃波(设无过渡过程.电阻中电压和电流的波形为阶跃波设接通电源时刻为t=0 ,则电压,电流波形如图 . 则电压,电流波形如图). 接通电源时刻为uiUI(a)返回分析与思考上一页下一页t(b)上一题t下一题第 2 章电路的暂态分析2.1.(2)阶跃电压和直流电压的波形有什么区别? 阶跃电压和直流电压的波形有什么区别? 【答】直流电压的数学表达式为 u(t) =U,波形如图 ;阶 ,波形如图(a);0 跃电压的数学表达式为 u(t ) = { U t <0 t >0,波形如图(b) . 波形如图uuUU(a)t(b)t返回分析与思考上一页下一页上一题下一题第 2 章电路的暂态分析2.1.(3)含电容或电感的电路在换路时是否一定会产生过渡过程? 【答】不一定,若换路并未引起电容的电场能量或电感的磁不一定, 场能量的变化则不会产生过渡过程. 场能量的变化则不会产生过渡过程.返回分析与思考上一页下一页上一题下一题第 2 章电路的暂态分析的电容器, 2.2.(1)今需要一只 50 V,10 F 的电容器,但手头只有两只 , 50V,5F 和两只30V,20 F 的电容器,试问应该怎样解决? 的电容器,试问应该怎样解决? , , 【答】可用二只50V,10 F 的电容并联或用二只 30V,20 , , F 的电容串联.这样,不仅总电容值满足要求,而且每个电容的的电容串联.这样,不仅总电容值满足要求, 实际工作电压亦满足其各自额定工作电压的要求. 实际工作电压亦满足其各自额定工作电压的要求.返回分析与思考上一页下一页上一题下一题第 2 章电路的暂态分析2.2.(2)可否由换路前的电路求 iC(0) 和 uL(0)? 【答】不可以. 不可以.返回分析与思考上一页下一页上一题下一题第 2 章电路的暂态分析处于零状态, 2.3.(1)如果换路前电容 C 处于零状态,则 t = 0 时,uC(0) = 0, , 电容相当于短路, →∞而 t→∞时, iC(∞) =0,可否认为 t = 0 时,电容相当于短路, t→∞→∞∞ , 电容相当于开路?如果换路前C不是处于零状态不是处于零状态, 时,电容相当于开路?如果换路前不是处于零状态,上述结论是否成立? 否成立? 处于零状态, 【答】换路前若电容C处于零状态,则 t = 0 时, uC(0) =0 , 换路前若电容处于零状态时电容相当于短路, →∞又 t→∞时, iC(∞) = 0 ,故可认为 t = 0 时电容相当于短路, t→∞→∞∞时电容相当于开路.而若换路前电容未处于零状态, 时电容相当于开路.而若换路前电容未处于零状态,则 uC(0) ≠ 0 , 电容不可视为短路, 电容仍可相当于开路. 电容不可视为短路,但 t→∞时仍有 C(∞) =0 ,电容仍可相当于开路. →∞时仍有i ∞返回分析与思考上一页下一页上一题下一题第 2 章电路的暂态分析电路中,如果串联了电流表, 2.3.(2)在 RC 电路中,如果串联了电流表,换路前最好将电流表短路,这是为什么? 流表短路,这是为什么? 电路换路瞬间电流发生突变, 【答】由于 RC 电路换路瞬间电流发生突变,产生初始冲击电流,故电路中若串联了电流表,则最好在换路前将电流表短接, 电流,故电路中若串联了电流表,则最好在换路前将电流表短接, 以免初始冲击电流超过电流表的量程而将表损坏. 以免初始冲击电流超过电流表的量程而将表损坏.返回分析与思考上一页下一页上一题下一题第 2 章电路的暂态分析处于零状态, 2.4.(1)如果换路前 L 处于零状态,则 t = 0 时, iL(0) = 0 ,而 t→∞时, uL(∞) =0 ,因此可否认为 t = 0时,电感相当于开路, →∞∞时电感相当于开路, t→∞时,电感相当于短路? 电感相当于短路? →∞【答】可以. 可以.返回分析与思考上一页下一页上一题下一题第 2 章电路的暂态分析不是处于零状态,上述结论是否成立? 2.4.(2)如果换路前 L 不是处于零状态,上述结论是否成立? 未处于零状态, 【答】若换路前L未处于零状态,则 iL(0) ≠ 0 , t=0 时电感若换路前未处于零状态不能视为开路, 仍有u 不能视为开路,而 t→∞时,仍有 L(0) =0 ,即 t→∞时电感相当于→∞→∞短路. 短路.返回分析与思考上一页下一页上一题下一题第 2 章电路的暂态分析2.5.(1)任何一阶电路的全响应是否都可以用叠加原理由它的零输入响应和零状态响应求得,请自选一例题试试看. 零输入响应和零状态响应求得,请自选一例题试试看. 【答】可以. 可以. 例如图(a)所示电路,换路前电路已稳定,t=0 时将开关由 a 端例如图所示电路,换路前电路已稳定, = 所示电路换接到 b 端,已知 US1=3V, US2=15V, R1=1 k , R2= 2k , C=3 F ,求求 uC.a+ b U S1S+ U S1R1+ uCCR2R2 uC ( 0 ) = US 1 = 2V R1 + R 2(a)返回分析与思考上一页下一页上一题下一题第 2 章电路的暂态分析电容有初始储能, 故响应为全响应. 电容有初始储能,且换路后有激励 US2 ,故响应为全响应.可将其分解为零输入响应和零状态响应的叠加,如图(b)和其分解为零输入响应和零状态响应的叠加,如图和(d)a+ b U S1SR1+ ′ uCCR2(b)S+ US2R1+ ′′ uCCR2(d)返回分析与思考上一页下一页上一题下一题第 2 章电路的暂态分析解零输入响应(图(b) ),电容有初始储能,则解零输入响应图 ,电容有初始储能,R2 u′C(0) = U′0 = US1 = 2V R1 + R2换路后,电容向并联电阻放电,电路简化为图(c) 换路后,电容向R1, R2并联电阻放电,电路简化为图 . 2 + R′ = R1 // R 2 = k = 0.667 3 ′ uC C 时间常数 2 ′ = R′C = ×103 × 3 × 106 s = 2 × 103 s τ 3 (c) t 则R′u′C = U ′0eτ′= 2e 500 tV返回分析与思考上一页下一页上一题下一题第 2 章电路的暂态分析解零状态响应(图(d) ),电容无初始储能,换路后利用戴维解零状态响应图 ,电容无初始储能, 宁定理电路可简化为图(e),其中宁定理电路可简化为图其中2 ′′ = R1 // R 2 = k = 0.667 R 3R2 UeS = US 2 = 10V R1 + R2R′′时间常数则u′′C = UeS (1 e2 3 6 τ′′ = R′′C = ×10 × 3×10 s = 2×103 s 3 t+ + ′′ U eS uCCτ′′) = 10(1 e500 t)V(e)根据全响应=零输入响应+零状态响应, 根据全响应=零输入响应+零状态响应,有 uC = u′C + u′′C= ( 2e 500 t + 10 10e 500 t )V = (10 8e 500 t )V返回分析与思考上一页下一页上一题下一题第 2 章电路的暂态分析一定, 越大, 2.5.(2)在一阶电路中,R一定,而 C 或 L 越大,换路时的过在一阶电路中, 一定渡过程进行得越快还是越慢? 渡过程进行得越快还是越慢?L 电路中, 电路中, = 【答】RC电路中,τ=RC ; RL电路中, τ= 电路中 = 电路中 .当 R 一 R定时, 越大则使τ越大过渡过程则进行的越慢. 越大, 定时,C 或L 越大则使越大,过渡过程则进行的越慢.返回分析与思考上一页下一页上一题1。
电工第二章习题及答案

一、选择题1、如图所示,其节点数、支路数、回路数及网孔数分别为(C )。
A、2、5、3、3B、3、6、4、6C、2、4、6、32、如图所示,I=(B )A。
A、2B、7C、5D、63、如图所示,E=(B )V。
A、3B、4C、—4D、—3/4、如图所示电路中,I1和I2的关系为(C )。
A、I1<I2B、I1>I2C、I1=I2D、不确定5、如图所示,求I1和I2的大小。
解:对于左边节点:I1=10+3+5=18A对于右边节点:I2=10+2-5=7A6、基尔霍夫第一定律的依据是(D )A.欧姆定律B.全电流定律C.法拉第定律D.电荷守恒定¥7、理想电压源和理想电流源间(C )A.有等效变换关系B.没有等效变换关系C.有条件下的等效关系D.无法判定8、下列说法错误的是(D )A.在电路节点处,各支路电流参考方向可以任意设定。
B.基尔霍夫电流定律可以扩展应用于任意假定的封闭面。
C.基尔霍夫电压定律应用于任意闭合路径。
D.∑I=0式中各电流的正负号与事先任意假定的各支路电流方向无关9、实际电压源和电流源模型中,其内阻与理想电压源和电流源之间的正确连接关系是(C)A.理想电压源与内阻串联,理想电流源与内阻串联"B.理想电压源与内阻并联,理想电流源与内阻串联C.理想电压源与内阻串联,理想电流源与内阻并联D.理想电压源与内阻并联,理想电流源与内阻并联10、79.下面的叙述正确的是(B )。
A.理想电压源和理想电流源是不能等效变换的B.理想电压源和理想电流源等效变换后内部是不等效的C.理想电压源和理想电流源等效变换后外部是不等效的D.以上说法都不正确二、填空题1、不能用电阻串、并联化简的电路称为__复杂电路_______。
;2、电路中的_____每一分支_______称为支路,____3条或3条以上支路___所汇成的交点称为节点,电路中__________闭合的电路______________都称为回路。
电路分析答案解析第二章

电路分析答案解析第二章第二章习题2.1 如题2.1割集与基本回路。
(a) 树一1T 如图所示。
基本割集为:c1{1,2,4}, c2{1,3,7}, c3{1,3,6,8}, c4{1,3,6,5,4} 基本回路为:l1{5,6,8}, l2{2,4,5}, l3{3,5,8,7}, l4{1,2,5,8,7}(b) 树二2T 如图所示。
基本割集为:c1{4,5,8}, c2{5,7,8}, c3{1,3,7}, c4{4,2,3,7} 基本回路为:l1{2,4,5}, l2{5,6,8}, l3{1,2,3}, l4{1,2,6,7}2.2 题2.2图示电路,求支路电流1I 、2I 、I 解:列两个KVL 回路方程:051)54211=-+++I I I (021)510212=-+++I II (整理为: 45921=+I I 115521=+I I 解得:A I 5.01= A I 1.02-= 而 A I I I 4.0)213-=+-=(2.3 如题2.3图所示电路,已知电流A I 21=解:可列KVL 回路方程: 2I+2+(i-3)R=3已知 i=2A ,代入上式可得:R=3Ω2.4 如题2.4方程求解电流i。
解:10(i-6)+5(0.4i+i)+13i=0解得:i=2A2.5 如题2.5图所示电路,试选一种树,确定基本割集,仅用一个基本割集方程求解电压u程求电压u。
解:①② 选3为参考节点,列方程如下: 52018120124-=-+u u )(已知V u 122-=,代入上式,有: 52012812014-=++u )(解得节点点位: V u 324-=又可知 0124=++u u 得: V u u 201232124=-=--=2.6 如题2.6图所示电路,已知电流A i 21=电压源S u 。
解:列三个网孔方程28)6=-+B A Ri i R (①33)43(-=-+++-C B A i i R Ri ②S C B u i i -=++3)323-(③ 可知: 12==i i B 21==-i i i B A 可得: 32=+=B Ai i由①式可得:283)6=-+R R (解得:Ω=5R 由②式有:33)57(35-=-++?-C i 解得: 0=C i 由③式有: S u -=33- 解得: V u S 6= 根据KVL 有: V i u bc 7432-=--=2.7 如题2.7解该电路的网孔方程。
第二章习题解答.docx

郭木森电工学第二章习题解答2. Ll⅛lU r=IOSinIUo A =IoSin(I∞ΛF∕--) A . (1}钦也曲电擁的州凱图;⑵ 冃• 2Jff憚加法求它们的和•并写出你成电流/的表达式⅛Yι⑴∕l≡ IoSinIoOΛ-/ A e÷ / = ~rc yfl A3.把-h⅛⅛⅛H⅞Λ220V・5OT⅛的交流电閑测得LE耀为0-55A.求⅛⅞ffi.剧用迪容的賊压有效蓮利电流ff效值关系.即节上p73 (2-4-15)式、町得】C=—=一-一 =—————=7 旳FUω(∕^2Λ-/22D 2√Γ-5∪连瓠⑴有效值的符号要大写辛(2)交流电农怖测得的电压和电流为笔j效值=4.把-t½M接于4«V的直流电源时’电流;⅛8A;将它改接J' 50H2. 120V的交蔬电源时•电⅛⅛12A>求线關的电感与电!B∙If IOW:(I)SL⅛时,电⅛⅛⅛t√.ff = —= —= 6Ω/ 8⑵接交流时.和当于电駅和电感串联电路'U 4 iγ = Z= K+ JftX.√÷ -y- = Z∣ = J R' +(Qt)'已如总电压和总电流的彳f效值分别⅛120V.l2ΛIlm FΛ-= √6' ÷(2Λ-'50Λ}2 R f =0τ∪26H12卞as:接交洸时.U = U fi + U i . ^∖U≠l∕f(^U Ii ft总区分相品关泵和有效值关系, I7= IOSin(I(X)JT f - -tΛ ”2÷÷ I = I(X/2 Sin(Io0-T/ - —) A47•在从?串联电路图中•已知输入信号频率为/ =30OH签R=I(XXI•若姜使输出信号伉的村位差(即相移”4)•电容C应取多大?妬比他趙前还是落后?解:方法一:相虽图解法因为是申联电路,所以选电流为聲考相⅛L泉据孑相如的关系作IlHP图如右图所示,已知./和0的相位芳为彳,即这两个郴昴相⅛45β , 故相显图中P Af I =P J = PC I,即U R≈U e => IR=I-A ' ωC从相屋图中也可见• /落后0 45。
第二章习题及答案

电工学第二章习题一、填空题1. 两个均为40F μ的电容串联后总电容为 80 F μ,它们并联后的总电容为 20F μ。
2. 表征正弦交流电振荡幅度的量是它的 最大值 ;表征正弦交流电随时间变化快慢程度的量是 角频率ω ;表征正弦交流电起始位置时的量称为它的 初相 。
三者称为正弦量的 三要素 。
3. 电阻元件上任一瞬间的电压电流关系可表示为 u = iR ;电感元件上任一瞬间的电压电流关系可以表示为dtdiLu =L ;电容元件上任一瞬间的电压电流关系可以表示为dtduCi =C 。
由上述三个关系式可得, 电阻 元件为即时元件; 电感 和 电容 元件为动态元件。
4. 在RLC 串联电路中,已知电流为5A ,电阻为30Ω,感抗为40Ω,容抗为80Ω,那么电路的阻抗为 50Ω ,该电路为 容 性电路。
电路中吸收的有功功率为 750W ,吸收的无功功率又为 1000var 。
二、选择题1. 某正弦电压有效值为380V ,频率为50Hz ,计时始数值等于380V ,其瞬时值表达式为( B )A 、t u 314sin 380=V ;B 、)45314sin(537︒+=t u V ;C 、)90314sin(380︒+=t u V 。
2. 一个电热器,接在10V 的直流电源上,产生的功率为P 。
把它改接在正弦交流电源上,使其产生的功率为P/2,则正弦交流电源电压的最大值为(D ) A 、; B 、5V ; C 、14V ; D 、10V 。
3. 提高供电电路的功率因数,下列说法正确的是( D )A 、减少了用电设备中无用的无功功率;B 、减少了用电设备的有功功率,提高了电源设备的容量;C 、可以节省电能;D 、可提高电源设备的利用率并减小输电线路中的功率损耗。
4. 已知)90314sin(101︒+=t i A ,︒+=30628sin(102t i )A ,则( C )A 、i1超前i260°;B 、i1滞后i260°;C 、相位差无法判断。
电工学电工技术课后答案第二章

电工学电工技术(艾永乐)课后答案第二章(总26页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第二章 电阻电路的分析本章的主要任务是学习电阻电路的分析计算方法,并运用这些方法分析计算各种电阻电路中的电流、电压和功率。
本章基本要求1. 正确理解等效电路的概念,并利用等效变换化简电路。
2. 掌握电阻串、并联等效变换、电源的等效变换。
3. 电阻电路的分压公式和分流公式的应用。
4. 运用支路电流法和结点电压法分析计算电路。
5. 运用叠加定理分析计算电路。
6. 熟练应用戴维宁定理分析计算电路。
7. 应用戴维宁定理求解电路中负载电阻获得的最大功率。
8. 学会含有受控源电路的分析计算。
9. 了解非线性电阻电路的分析方法。
本章习题解析2-1 求习题2-1所示电路的等效电阻,并求电流I 5。
ΩaΩ题解2-1图题2-1图解:电路可等效为题解2-1图 由题解2-1图,应用串并联等效变换得5.1)6//)12(2//2//(3ab =++=R Ω由分流公式3136********=⋅+++⋅+=ab R I A 2-2 题2-2图所示的为变阻器调节分压电路。
50=L R Ω,电源电压220=U V ,中间环节是变阻器。
变阻器的规格是100Ω3A 。
今把它平分为4段,在图上用a 、b 、c 、d 、e 等点标出。
试求滑动触点分别在a 、b 、c 、d 四点是,负载和变阻器所通过的电流及负载电压,并就流过变阻器的电流与其额定电流比较来说明使用时的安全问题。
L解:1)a 点: 0L =U 0L =I 2.2100220ea ea ===R U I A 2) c 点:75eq =R Ω 93.275220eq ec ===R U I A 47.121ec L ==I I A 5.73L =U V3) d 点:55eq =R Ω 455220eq ed ===R U I A 4.2L =I A 6.1da =I A 120L =U V4) e 点: 2.2100220ea ea ===R U I A 4.450220L ==I A 220L =U V 2-3 试求习题2-3ab 之间的输入电阻。
电工学-第二章习题答案
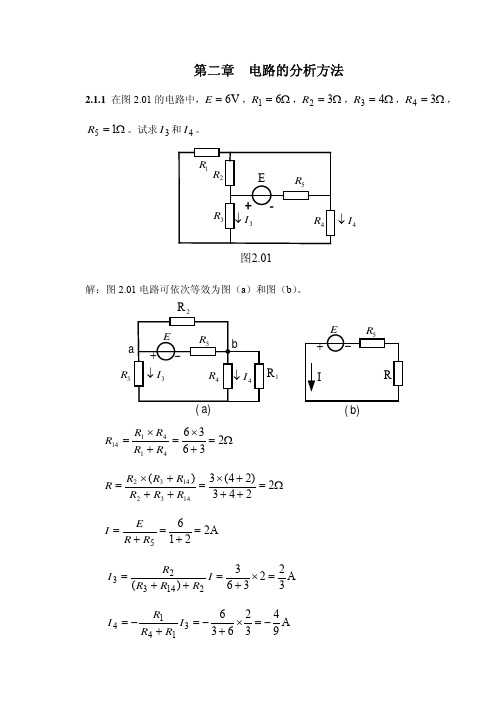
第二章 电路的分析方法2.1.1 在图2.01的电路中,V 6=E ,Ω=61R ,Ω=32R ,Ω=43R ,Ω=34R ,Ω=15R 。
试求3I 和4I 。
4I ↓图2.01解:图2.01电路可依次等效为图(a )和图(b )。
R 3R 1R(b)Ω=+×=+×=23636414114R R R R R Ω=+++×=+++×=2243)24(3)(14321432R R R R R R R A 22165=+=+=R R E IA 322363)(214323=×+=++=I R R R R IA 943263631414−=×+−=+−=I R R R I2.3.3 计算图2.12中的电流3I 。
Ω=1R A2S =图2.12解:根据电压源与电流源的等效变换,图2.12所示电路可依次等效为图(a )和图(b ),由图(b )可求得A 2.15.023=+=I由图(a )可求得:A 6.02.121213=×==I IΩ=1R V22=Ω=14R(b)Ω=12R2.6.1 在图2.19中,(1)当将开关S 合在a 点时,求电流1I ,2I 和3I ;(2)当将开关S 合在b 点时,利用(1)的结果,用叠加定理计算电流321,I I I 和 。
I图2.19I (a)I (b)解:(1)当将开关S 合在a 点时,图2.19所示电路即为图(a ),用支路电流法可得:=+=+=+12042130423231321I I I I I I I 解得:===A 25A 10A 15321I I I(2)开关S 合在b 点时,利用叠加原理图2.19所示电路可等效为图(a )和图(b ),其中图(a )电路中130V 和120V 两个电压源共同作用时所产生的电流已在(1)中求得,即:A 151=,I A 102=,I A 253=,I由图3(b )可求得:A 642422202=+×+=,,I A 464241−=×+−=,,IA26422=×+=则:A 11415111=−=+=,,,I I IA 16610,222=+=+=,,I I IA 27225333=+=+=,,,I I I2.6.2 电路如图2.20(a )所示,V 10ab ,,V 124321=====U R R R R E 。
华东理工大学电工学第二章习题答案

第二章 正弦交流电路2.1 基本要求(1) 深入理解正弦量的特征,特别是有效值、初相位和相位差。
(2) 掌握正弦量的各种表示方法及相互关系。
(3) 掌握正弦交流电路的电压电流关系及复数形式。
(4) 掌握三种单一参数(R ,L ,C )的电压、电流及功率关系。
(5) 能够分析计算一般的单相交流电路,熟练运用相量图和复数法。
(6) 深刻认识提高功率因数的重要性。
(7) 了解交流电路的频率特性和谐振电路。
2.2 基本内容 2.2.1 基本概念 1. 正弦量的三要素(1) 幅值(U m ,E m ,I m )、瞬时值(u, e, i )、有效值(U ,E ,I )。
注:有效值与幅值的关系为:有效值2幅值=。
(2) 频率(f )、角频率(ω)、周期(T )。
注:三者的关系是 Tf ππω22==。
(3) 相位(ϕω+t )、初相角(ϕ)、相位差(21ϕϕ-)。
注:相位差是同频率正弦量的相位之差。
2. 正弦量的表示方法 (1) 函数式表示法:。
)sin();sin();sin(i m e m u m t I i t E e t U u ϕωϕωϕω-=+=+= (2) 波形表示法:例如u 的波形如图2-1-1(a)所示。
(3) 相量(图)表示法:使相量的长度等于正弦量的幅值(或有效值); 使相量和横轴正方向的夹角等于正弦量的初相角; 使相量旋转的角速度等于正弦量的角速度。
注:例。
)60sin(24,)30sin(2621V t u V t u o o +=+=ωω求?21=+u u解:因为同频率同性质的正弦量相加后仍为正弦量,故)sin(221ϕω+==+t U u u u , 只要求出U 及ϕ问题就解决了。
解1:相量图法求解如下:具体步骤为三步法(如图2-1-2所示):第一步:画出正弦量u 1、u 2的相量12U U 、(U 1=6,U 2=4)。
第二步:在相量图上进行相量的加法,得到一个新相量U。
电工学第2章习题答案ppt课件
.
2-2 试求图2-35所示钢杆各段内横截面上的应 力和杆的总变形。钢的弹性模量E=200GPa。
解 1、内力计算 用截面法分别计算左段和右段的内力并作杆 的轴力图(b)
得 F左 =4kN(拉) F右 =4kN(拉).
得 FN2=
F(压)
同理,可以计算横截面3-3上的轴力FN3,
由截面3-3右段图(d)的平衡方程∑Fx=0,
得FN3= 0
.
解b 使用截面法,沿截面1-1将杆分
成两段,取出右段并画出受力图(b)
用FN1表示左段对右段的作用, 由平衡方程∑Fx=0,. 得FN1 =F(拉)
同理,可以计算横截面2-2上的轴力 FN2,由截面2-2右段图(c)的平衡 方程Fx=0 ∑,得FN2= F(压)
螺栓应至少为16个
.
2-5 三角形支架ABC如图2-38所示,在C点受到载荷F 的作用。己知,杆AC由两根10号槽钢所组成, [σ]AC=160MPa;杆BC是20a号工字钢所组成, [σ]BC=100MPa。试求最大许可载荷F。
.
解 选取C为研究对象 1、如图所示,由平衡方程得
∑Fx=0 FAC Cos30o-FBCCos30o=0 ∑Fy=0 FAC Sin30o-F+FBCSin30o =0 解得 FAC =FBC=F
4
4
解得X=1.08m,当F=30KN时,
FA13.8KN FB 16.2KN
正应力
σ AA FA Aπ132.802110036 43.97MPa 4
正应力
σ BA FB Bπ 162.252110036 32.97MPa 4
燕山大学电工技术课后答案第2章

第二章 电路的分析方法三、习题详解2-1 电路如图2-1所示,试利用等效化简法求:(1)电流321,,I I I 和4I ;(2)Ω3电阻消耗的功率Ω3P ;(3)V 4电压源发出的功率V P 4。
解 (1)电路化简过程见图2-2中(a)~(d)。
由图(d)可求得A 6.15.241===R U I 由图(b)可求得A 8.021142===I I I 由图2-1可求得 A 4.02123==I I (2)Ω3电阻消耗的功率W 92.138.032243=⨯=⨯=ΩI P(3)V 4电压源发出的功率W 4.66.1414-=⨯-=-=UI P V2-2 电路如图2-3(a )(b )所示,试用网孔电流法求:(1)网孔电流b a I I ,;(2)图2-1 题2-1图图2-2 图2-1的简化电路19支路电流31,I I 。
(a ) (b )解 图(a ):由网孔电流法列网孔方程如下:⎩⎨⎧-=+-=-332123b a b a I I I I 解得A 53-=a I , A 57-=b I则A 531=-=a I I , A 573-==b I I 图(b ):由网孔电流法列网孔方程如下:⎩⎨⎧+-=+-+-=-13522123b a b a I I I I 解得A 111=a I , A 114-=b I 则A 1111==a I I , A 1143=-=b I I 2-3 电路如图2-4所示,试用网孔电流法求:(1)网孔电流b a I I ,;(2)Ω2电阻消耗的功率Ω2P 。
解 (1)将图2-4电路等效变换成图2-5电路,然后列网孔方程得图2-3 题2-2图20⎩⎨⎧-=++---=-+32)32(2122)21(b a b a I I I I 解得A 1117-=a I , A 119-=b I (2) A 118=-=a b I I I W 1211282118222=⨯⎪⎭⎫⎝⎛==ΩR I P2-4 计算图2-6所示电路中的电流3I 。
电工学课后习题解答

第1章 习题解答(部分)1.5.3 有一直流电源,其额定功率P N =200 W ,额定电压U N =50 V ,内阻只RN =0.5Ω,负载电阻R0可以调节,其电路如图所示。
试求: (1)额定工作状态下的电流及负载电阻, (2)开路状态下的电源端电压,分析 电源的额定值有额定功率P N 。
额定电压U N 和额定电流I N 。
三者间的关系为 P N =U N I N 。
额定电压U N 是指输出额定电流I N 时的端电压,所以额定功率P N 也就是电源额定工作状态下负载所吸收的功率。
解 (1)额定电流 A U P I N N N 450200===负载电阻 5.12450===N N I U R Ω (2)开路状态下端电压U 0 等于 电源电动势E 。
U 0=E =U N +I N R0=50+4×0.5=52 V1.5.6 一只100V ,8W 的指示灯,现在要接在380V 的电源上,问要串多大阻值的电阻?该电阻应选用多大瓦数的?分析 此题是灯泡和电阻器额定值的应用。
白炽灯电阻值随工作时电压和电流大小而变,但可计算出额定电压下的电阻值。
电阻器的额定值包括电阻值和允许消耗功率。
解 据题给的指示灯额定值可求得额定状态下指示灯电流I N 及电阻只R NΩ≈==≈==1510073.0110A 073.01108N N N N N N U U R U P I串入电阻R 降低指示灯电压,使其在380V 电源上仍保持额定电压U N =110V 工作,故有Ω≈-=-=3710073.01103800N N I U U R 该电阻工作电流为I N =0.073 A,故额定功率为W R I P N R 6.193710073.022≈⨯=⋅=可选额定值为3.7k Ω,20 W 的电阻。
1.5.7在图1.03的两个电路中,要在12V 的直流电源上使6V ,50 mA 的电珠正常发光,应该采用哪 一个联接电路? 解 要使电珠正常发光,必须保证电珠 获得6V ,50mA 电压与电流。
《电路》复习提纲+课后习题答案+电路题库及答案(精华版)

复习提纲1.电流的参考方向可以任意指定,分析时:若参考方向与实际方向一致,则i>0,反之i<0。
电压的参考方向也可以任意指定,分析时:若参考方向与实际方向一致,则u>0反之u<0。
2.功率平衡一个实际的电路中,电源发出的功率总是等于负载消耗的功率。
3.全电路欧姆定律:U=E-RI4.负载大小的意义:电路的电流越大,负载越大。
电路的电阻越大,负载越小。
5.电路的断路与短路电路的断路处:I=0,U≠0电路的短路处:U=0,I≠0二.基尔霍夫定律1.几个概念:支路:是电路的一个分支。
结点:三条(或三条以上)支路的联接点称为结点。
回路:由支路构成的闭合路径称为回路。
网孔:电路中无其他支路穿过的回路称为网孔。
2.基尔霍夫电流定律:(1)定义:任一时刻,流入一个结点的电流的代数和为零。
或者说:流入的电流等于流出的电流。
(2)表达式:i进总和=0或:i进=i出(3)可以推广到一个闭合面。
3.基尔霍夫电压定律(1)定义:经过任何一个闭合的路径,电压的升等于电压的降。
或者说:在一个闭合的回路中,电压的代数和为零。
或者说:在一个闭合的回路中,电阻上的电压降之和等于电源的电动势之和。
(2)表达式:1或:2或:3(3)基尔霍夫电压定律可以推广到一个非闭合回路三.电位的概念(1)定义:某点的电位等于该点到电路参考点的电压。
(2)规定参考点的电位为零。
称为接地。
(3)电压用符号U表示,电位用符号V表示(4)两点间的电压等于两点的电位的差。
(5)注意电源的简化画法。
四.理想电压源与理想电流源1.理想电压源(1)不论负载电阻的大小,不论输出电流的大小,理想电压源的输出电压不变。
理想电压源的输出功率可达无穷大。
2.理想电流源(1)不论负载电阻的大小,不论输出电压的大小,理想电流源的输出电流不变。
理想电流源的输出功率可达无穷大。
(2)理想电流源不允许开路。
3.理想电压源与理想电流源的串并联(1)理想电压源与理想电流源串联时,电路中的电流等于电流源的电流,电流源起作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
然后,根据,由换路后 (S 闭合时) 的电路求得
i1 ( 0 ) i2 (0 ) R2 R 1 R2 R1 R1 R 2 iL (0) iL (0) 6 46 4 46 3 A 1 .8 A 3 A 1 .2 A
iL
R2
6Ω
L
1H
返 回
第2章 电路的暂态分析
2.4.2图所示电路原 已处于稳态。试求 S 闭合 后的 i2 、iL 和 uL,并画出 其变化曲线。
i1
IS
S
i2
R3
7Ω
R1
24 A
R2
3Ω
uL
iL
1 .5 Ω
L
0 .4 H
a
S
b
R1
3Ω
2.4.3图所示电路 原已处于稳态。在 t = 0 时将开关 S 从 a 端改合 到 b 端。试求换路后的 iL 和 uL,并说明是什么 响应。
uC U 0 e iC C
30 e U0 R
10
4
C
t
V 3e
10
4
R
t
uC
d uC dt
t
e
A
上一题 下一题
返 回练习题题集
上一页
第2章 电路的暂态分析
2.3.2在图所示电路原已处于稳态,在 t = 0 时,将开 关 S 闭合,试求响应 uC 和 iC,并说明是什么响应?
100 t
)V
e
15 e
mA
返 回练习题题集
上一页
上一题
下一题
第2章 电路的暂态分析
2.3.3图所示电路原已稳定,求开关 S 闭合后的响应 uC 和 i1、 i2 ,并画出其变化曲线。
R3 iC
1 . 6 kΩ
uC
S
i1
R1
4 kΩ
US
20 V
iC
C 2 .5 F
S
2.5.2图所示电路 原已处于稳态。试用三 要素法求 S 闭合后的 uC。
US
18 V
R1
3 kΩ
R3
C
10 F
6 kΩ
R2
6 kΩ
uC
R4
3 kΩ
返 回
第2章 电路的暂态分析
2.5.3图所示电路原已 处于稳态,在 t = 0 时,将开 关 S 断开,试用三要素法求 换路后的 uC 和 iC。
S
US
18 V
R1
8Ω
uC
iC
C
50 F
0 .5 A
R2
12 Ω
IS
S
2.5.4图所示电路原 已处于稳态。试用三要素 法求开关 S 断开后的 iL 和U S uL。
R1
6Ω
12 V
uL
iL L
24 mH
4A
R2
6Ω
IS
返 回
第2章 电路的暂态分析
练习题解答
2.2.1在图所示电路中,开关 S 闭合前电路已处于稳态, 试确定 S 闭合后电压 uC 和电流 iC、i1、i2 的初始值和稳态值。 【解】 (1) 求初始值 由于 S 闭合前,电路已稳定,C 相当于开路,i1 = IS = 1.5 A。因此,根据换路定律,由换路前( S 断开时)的电路,首先 求得 u C ( 0 ) R 1 I S ( 4 1 . 5 ) V 6 V 然后,根据,由换路后 (S 闭合时) 的电路求得
R1
IS
5A
3Ω
iC
R2
8Ω
uC
R2
S
6Ω
iC
C
10 F
返 回练习题题集
上一题
下一题
第2章 电路的暂态分析
【解】 本题目是练习利用电阻的串并联来简化电路,求 出响应。 根据换路定律和电路稳定时电容相当于开路,由换路前 的电路求得
u C ( 0 ) U 0 R 2 I S ( 6 5 ) V 30 V
2.3.2在图所示电 路原已处于稳态,在 t = 0 时,将开关 S 闭合,试 求响应 uC 和 iC,并说明 是什么响应?
S
IS
iC
C 5 F
R1
15 mA 3 kΩ
uC
R2
6 kΩ
2.3.3图所示电路原已 稳定,求开关 S 闭合后的响 应 uC 和 i1、 i2 ,并画出其变 化曲线。
i1 ( ) i L ( ) I Sபைடு நூலகம் 1 A u C ( ) R 2 i L ( ) 12 V
返 回练习题题集 上一题 下一题
第2章 电路的暂态分析
2.3.1在图所示电路原已稳定,在 t = 0 时,将开关 S 闭 合,试求 S 闭合后的 uC 和 iC。
S
R1
R3
i1
U
S
4 kΩ
iC
R2
1 . 6 kΩ
uC
iC
C
2 .5 F
6 kΩ 20 V
返 回
第2章 电路的暂态分析
2.3.4图所示电路中 电容原先未充电。在 t = 0 时将开关 S1 闭合, t = 0.1 s 时将开关 S2 闭合,试求 S2闭合后的响应 uR1,并 说明是什么响应。
R3
3Ω
U S1
6V
U S2
6V
R2
6Ω
uL
iL
L
1H
返 回
第2章 电路的暂态分析
2.5.1图所示电路原已 处于稳态。试用三要素法求 开关 S 闭合后的 uL 和 uR。
R1
US
2 kΩ
C
uC
50 F
40 V
R 2 6 kΩ S R3
12 kΩ
uR
)V
e
3e
mA
返 回练习题题集
第2章 电路的暂态分析
i2
uC R 3 iC R2
12 ( 1 e 100 t ) 3 10 3 e 100 t 1 . 6 10 3 A 3 6 10 ) 10
3 3
( 2 1 .2 e
U eS ( R 1 // R 2 ) I S 30 V R 0 R 1 // R 2 2 kΩ
R0
U eS
100 t
iC
uC
电路的时间常数 则
R 0 C 10
t
2
s
C
u C U eS ( 1 e iC U eS R0
t
) 3 (1 e
eS
R1
R2
S
R0
R 0 ( R 1 // R 2 ) R 3 4 k Ω
U eS
100 t
uC
iC
则 所以
R 0 C 0 . 01 s
C
u C U eS ( 1 e iC U eS R0
t
t
) 12 ( 1 e
100 t
返 回练习题题集
上一页
下一题
第2章 电路的暂态分析
L
2.2.2在图所示电路中, 开关 S 闭合前电路已处于稳态, 试确定 S 闭合后电压 uL 和电流 iL、i1、i2 的初始值和稳态值。
iL
uL
US
12 V
S
i1
R1
4Ω
i2
R2
6Ω
【解】 (1)求初始值 由于 S 闭合前,电路已稳定, L 相当于短路,R2 两端的电压等于 US, R2 中的电流即 iL。 因此,根据换路定律,由换路前( S 断开时)的电路,首先求得
返 回练习题题集
第2章 电路的暂态分析
2.2.3在图所示电路中, 开关 S 闭合前电路已处于稳 态,C 中无储能,试确定 S 闭合后电压 uC、 uL和电流 U S i1 、 iC 、iL 的初始值和稳态 值。 【解】初始值:
uC (0 ) uC (0 ) 0 V iL (0) iL (0 ) i1 ( 0 ) US R1 5A US R1 R 2 R1 R1 R 2
R1
2Ω
US
i1 S
10 V
uC
R2
iC
C
3Ω
uL
iL
5A
IS
L
R1
2.3.1在图所示电路 原已稳定,在 t = 0 时, 将开关 S 闭合,试求 S 闭合后的 uC 和 iC。
IS
5A
3Ω
iC
R2
8Ω
uC
R2
S
6Ω
iC
C
10 F
返 回
上一页
下一页
第2章 电路的暂态分析
R2
6 kΩ
返 回练习题题集
上一题
下一题
第2章 电路的暂态分析
【解】 本题目与上题相同,只是响应为零状态响应。 换路前电容未储能, uC(0) = 0 。 将换路后电路中电容提出,用戴维宁定理将剩下的有源 二端网路化简为等效电压源,则换路后电路可化简为如图所 示。 R2 其中 U U 12 V
S
IS
R1
15 mA 3 kΩ
uC
iC
C 5F
R2
6 kΩ
返 回练习题题集
上一题
下一题
第2章 电路的暂态分析
