惯性系的定义

合集下载

惯性系的名词解释

惯性系的名词解释在物理学中，惯性系是一个基本概念，用以描述观察一个物体运动的参考系。

惯性系的定义其实很简单，就是一个物体在其中自由运动时，其运动状态不会受到非惯性力的影响。

换句话说，一个惯性系是一个相对于物体来说是静止或匀速运动的参考系。

为了更好地理解惯性系，我们需要回顾牛顿运动定律。

牛顿第一定律告诉我们，当一个物体处于平衡状态或者以恒定速度运动时，其所处的参考系就是一个惯性系。

这表明惯性系是可以用于观察物体运动的合适的参考系。

那么，为什么我们需要惯性系呢？想象一下，如果我们处于一个非惯性系中观察一个物体运动，那么我们很可能会受到非惯性力的干扰。

比如，在一辆开始加速的车上观察一个静止的水杯，我们可能会看到水杯向后倾斜，这是由于车辆的加速度导致的惯性力。

但如果我们在一个惯性系中观察相同的情况，我们会发现水杯始终保持竖直状态，因为在惯性系中没有非惯性力的干扰。

惯性系的概念也可以被扩展到更大的尺度上，例如地球的惯性系。

我们通常将地球表面上的参考系视为一个惯性系，因为在这个参考系中物体的运动状态相对稳定。

然而，地球的自转和公转确实会导致一些微弱的非惯性力，在相对精确的测量中有时需要考虑这些影响。

除了地球上的参考系，我们还可以将太阳系内的一些参考系视为惯性系。

比如，太阳系的质心可以被认为是一个近似的惯性系，其中各个行星以不同的速度围绕质心运动。

在这个参考系中，行星的轨道运动可以较好地描述为受到引力定律的影响，而不需要考虑其他非惯性因素。

总结起来，惯性系是一个物体在其中自由运动时不受非惯性力影响的参考系。

惯性系的概念在物理学中起到了至关重要的作用，帮助我们描述和理解物体的运动规律。

无论是地球上的参考系还是更广阔的宇宙中，惯性系的概念都是我们解释自然界中各种物理现象的基础。

通过建立合适的惯性系，我们可以更好地研究和理解各种物质和能量在空间和时间中的运动和相互作用。

惯性系与非惯性系的区分与运动学表述

惯性系与非惯性系的区分与运动学表述惯性系和非惯性系是物理学中常用的两个概念，用于描述物体的运动状态和相对运动关系。

在我们日常生活中，我们常常会遇到各种各样的运动，而了解惯性系和非惯性系的区别以及它们的运动学表述，可以帮助我们更好地理解物体的运动规律。

首先，我们来了解一下惯性系和非惯性系的定义。

惯性系是指一个相对于其他物体或者参考系而言，没有受到任何外力作用的参考系。

在惯性系中，物体的运动状态可以用牛顿运动定律来描述，即物体会保持匀速直线运动或静止状态，除非受到外力的作用。

而非惯性系则是相对于惯性系而言，存在有加速度的参考系。

在惯性系中，物体的运动可以用运动学的方式来描述。

运动学是研究物体运动的学科，主要关注物体的位置、速度和加速度等运动参数。

在惯性系中，物体的运动可以用位置-时间图、速度-时间图和加速度-时间图来表示。

位置-时间图是描述物体位置随时间变化的曲线，速度-时间图是描述物体速度随时间变化的曲线，而加速度-时间图则是描述物体加速度随时间变化的曲线。

然而，在非惯性系中，由于存在加速度，物体的运动规律会有所不同。

在非惯性系中，物体的运动需要引入惯性力来描述。

惯性力是一种虚拟的力，它的作用方向与物体相对于惯性系的加速度相反，大小与物体的质量和加速度成正比。

惯性力的作用是为了使物体在非惯性系中满足牛顿运动定律。

在非惯性系中，物体的运动可以用非惯性系中的运动学方程来描述。

非惯性系中的运动学方程与惯性系中的运动学方程类似，只是需要考虑到惯性力的作用。

例如，对于匀速圆周运动，物体的加速度与向心加速度成正比，而向心加速度则与物体的速度和半径成反比。

因此，在非惯性系中，物体的运动学方程需要考虑到惯性力的作用。

总结起来，惯性系和非惯性系是物理学中用于描述物体运动状态和相对运动关系的重要概念。

在惯性系中，物体的运动可以用运动学的方式来描述，而在非惯性系中，物体的运动需要引入惯性力来描述。

了解惯性系和非惯性系的区别以及它们的运动学表述，可以帮助我们更好地理解物体的运动规律，从而更好地应用于实际问题的解决。

惯性参照系

惯性参考系的认识惯性系的定义对一切运动的描述，都是相对于某个参考系的。

参考系选取的不同，对运动的描述，或者说运动方程的形式，也随之不同。

人类从经验中发现，总可以找到这样的参考系：其时间是均匀流逝的，空间是均匀和各向同性的；在这样的参考系内，描述运动的方程有着最简单的形式。

这样的参考系就是惯性系。

朗道《场论》（主要是相对论电动力学）给出的定义：牛顿第一定律成立的参照系叫做惯性系。

（原文没有用牛顿第一定律，而是直接说在这样的参照系中，一个不受相互作用的粒子将保持静止或匀速直线运动）。

这个定义在牛顿力学和狭义相对论中均适用。

这样①牛顿第一定律定义了惯性系②牛顿力学在惯性系中成立。

（在相对论中，第二条只要修正为麦可斯韦方程组和相对论力学在其中成立即可）这样就不存在逻辑循环的问题，同时也可以说明，牛顿第一定律不是牛顿第二定律在F=0时的特殊情况。

在空间内，相对于任何参考点（静止中或移动中），一个运动中的粒子的位移、速度、和加速度都可以测量计算而求得。

虽然如此，经典力学假定有一组特别的参考系。

在这组特别的参考系内，大自然的力学定律呈现出比较简易的形式。

称这些特别的参考系为惯性参考系。

惯性参考系有个特性：两个惯性参考系之间的相对速度必是常数；相对于一个惯性参考系，任何非惯性参考系必定呈加速度运动。

所以，一个净外力是零的点粒子在任何惯性参考系内测量出的速度必定是常数；只有在净外力非零的状况下，才会有点粒子加速度运动。

问题是，因为万有引力的存在，并无任何方法能够保证找到净外力为零的惯性参考系。

实际而言，相对于遥远星体呈现常速度运动的参考系应是优良的选择。

惯性系判定一个参考系是不是惯性系，只能由试验确定。

最基本的判据就是牛顿运动定律成立与否。

根据伽利略相对性原理，和一个惯性系保持相对静止或相对匀速直线运动状态的参考系也是惯性系。

在实践中，人们总是根据实际需要选取近似的惯性参考系。

比如，在研究地面上物体小范围内的运动时，地球是一个很好的惯性系。

惯性系与非惯性系之间的变换关系

惯性系与非惯性系之间的变换关系引言在物理学中，惯性系和非惯性系是两个重要的概念。

惯性系是指一个不受外力作用的参考系，而非惯性系则是受到外力作用的参考系。

本文将探讨惯性系与非惯性系之间的变换关系，以及这种变换关系在物理学中的应用。

一、惯性系的定义与特点惯性系是指一个不受外力作用的参考系，也就是说，在惯性系中，物体的运动状态将保持不变，即使没有施加任何力。

惯性系的特点是物体在其中运动的速度和方向保持不变。

在日常生活中，我们常常使用地球作为一个近似的惯性系。

在地球上，我们可以观察到物体的运动状态并进行测量。

当我们站在地面上，感受到的力是重力和地面对我们的支持力，而这些力并不会改变我们的运动状态。

二、非惯性系的定义与特点非惯性系是指一个受到外力作用的参考系。

在非惯性系中，物体的运动状态将受到外力的影响而发生改变。

非惯性系的特点是物体在其中运动的速度和方向随时间变化。

例如，在一个以恒定速度旋转的旋转木马上，我们会感受到离心力的作用。

这个离心力会改变我们的运动状态，使我们感觉到向外被拉扯。

在这个旋转木马上，我们处于一个非惯性系中。

三、在物理学中，我们常常需要在惯性系和非惯性系之间进行变换。

这是因为在非惯性系中进行物理实验和观测是非常困难的，而惯性系则提供了一个相对简单的参考系。

为了在惯性系和非惯性系之间建立联系，我们引入了一个叫做惯性力的概念。

惯性力是一种虚拟的力，它的作用是模拟非惯性系中物体的运动状态。

具体而言，当我们从一个非惯性系变换到一个惯性系时，我们需要引入一个与非惯性系中的加速度相等但方向相反的惯性力。

这个惯性力的作用是使物体在惯性系中的运动状态保持不变。

四、惯性系与非惯性系变换的应用惯性系与非惯性系之间的变换关系在物理学中有广泛的应用。

其中一个重要的应用是在运动学和动力学中的问题求解。

例如，在一个以匀速旋转的圆盘上，我们放置一个小球。

在非惯性系中，小球会受到离心力的作用而向外滑动。

然而，如果我们将问题转换到一个惯性系中，我们可以通过引入一个与离心力相等但方向相反的惯性力来解决问题。

大学物理：§2.3 惯性系与非惯性系

P. 13 / 14 .
Chapter 2. 质点作动力者学：杨茂§田2. 3 惯性系与非惯性
P. 14 / 14 .
1. 牛顿定律只适用于惯性参照系；
2. 牛顿第二定律在两种坐标系中的形式：
直角坐标系： Fx max ; Fy may ; Fz maz
自然坐标系：
Fn
man
m
v2
;
F
m
dv dt
出的 v、r 也是相对于非惯性系而言的。
Chapter 2. 质点作动力者学：杨茂§田2. 3 惯性系与非惯性
P. 10 / 14 .
自然现象中的惯性力
☻表观重力： G P引 F惯与纬度值有关。
P引
G
F惯
☻潮汐： F P引 F惯一日两次涨落
回交头叉潮
Chapter 2. 质点作动力者学：杨茂§田2. 3 惯性系与非惯性
Chapter 2. 质点作动力者学：杨茂§田2. 3 惯性系与非惯性
P. 5 / 14 .
地面参照系：地面是近似的惯性系，而不是严格
的惯性系，因为地球有自转角速度
≈7.3×10-5 rad/s ，由于地球的自转，
地球上的物体有法向加速度。
FK4参考系 FK4参考系是以选定的1535颗恒星的平均静止的位形作为基准的参考系，是比以上参考系都严格的惯性系。
Chapter 2. 质点作动力者学：杨茂§田2. 3 惯性系与非惯性
P. 8 / 14 .
地面参照系转台参照系
惯性系: T 0 ，且 an 0 T man
满足牛顿定律！
非惯性系: T 0 ，但 a 0 引入：F惯 man ，则
T F惯 man man 0 ma

初三物理惯性系与非惯性系区分

初三物理惯性系与非惯性系区分初三物理：惯性系与非惯性系区分物理学中，惯性系和非惯性系是两个重要的概念。

它们用来描述物体在运动过程中的参考系特性。

本文将详细介绍初三物理中关于惯性系和非惯性系的区分。

1. 惯性系的定义和特点惯性系是指一个参考系，在其中物体的运动状态不受任何外力作用时，将保持静止或匀速直线运动。

也就是说，如果在惯性系中观察物体，不会感受到加速度或受力的存在。

这是牛顿第一定律的基本原理。

在惯性系中，物体的运动状态可以用矢量来表示。

例如，在一维直线运动中，我们可以使用位置、速度和加速度这三个矢量来描述物体在惯性系中的运动。

2. 非惯性系的定义和特点非惯性系是指一个参考系，在其中物体的运动状态受到了外力的影响，因而具有加速度。

在非惯性系中观察物体，会感受到惯性力的存在。

惯性力是一种虚拟力，它的作用是使物体在非惯性系中仿佛在惯性系中运动，从而保持牛顿第一定律的成立。

非惯性系的一个典型例子是旋转参考系。

在旋转参考系中观察物体，会产生离心力或向心力等惯性力的效果。

比如，我们坐在旋转的摩天轮上，会感受到向外的离心力，这是因为摩天轮以一定的角速度旋转，而我们的身体有惯性继续向前运动。

3. 区分惯性系和非惯性系的方法惯性系和非惯性系可以通过以下方法进行区分：首先，可以观察物体在参考系下的运动状态。

如果物体在参考系中保持静止或匀速直线运动而不受力的作用，那么这个参考系就是惯性系。

反之，如果物体在参考系下运动状态出现加速度，那么这个参考系就是非惯性系。

其次，可以通过观察其他物体在该参考系下的运动情况来判断。

如果其他物体也表现出类似的运动状态，那么这个参考系是惯性系。

如果其他物体的运动表现出与物体自身不一致的加速度或受力情况，那么这个参考系就是非惯性系。

最后，可以通过实验来验证。

在一个参考系中进行实验观测，如果实验结果符合牛顿运动定律，那么这个参考系就是惯性系；如果实验结果出现不符合预期的情况，那么这个参考系就是非惯性系。

大学物理惯性力教材

1. 平移加速参考系中的惯性力
T
y´
a0
F0
x´
mg
惯性力大小：大小等于运动质点的质量 m 与非惯性系加速度 a0 的乘积。
惯性力方向：与非惯性系加速度的方向相反。
F0 ma0
惯性力没有施力者，不具备“力是物体之间的相互作用”这一特性，它和真实力有区别。惯性力的实质是物体的惯性在非惯性系中的表现。
u u 2 u1 r2 r1
沿弧向的加速度：
a u r2 r1 v
t
t
少了个 2 ！
错在哪里？
径向速度转向给力！
v
v
u 2
v
v
u1 v
u r2 r1 v a r v 2v
t t
哦了！
v
力学相对性原理：对于力学规律而言，一切
惯性系都是平权的、等价的。
《关于托勒密和哥白尼两大世界体系的对话》伽利略 1632
y y
s s vt o o z z
伽利略变换
P x x
设初始时刻两坐标原点重合
x x vt y y z z t t
x x vt y y z z t t
在非惯性系中，牛顿运动定律修正为：
F F0 ma
a a a0 F F0 ma ma0
例：电梯中转盘上
2. 匀角速转动速参考系中的惯性力
F0 man
F0 m2r
3. 科里奥利力（Coriolis force）
（1）物体相对转动盘作径向运动
vt
a 2v
F 2mv
fc 2m v
B. 惯性系与非惯性系
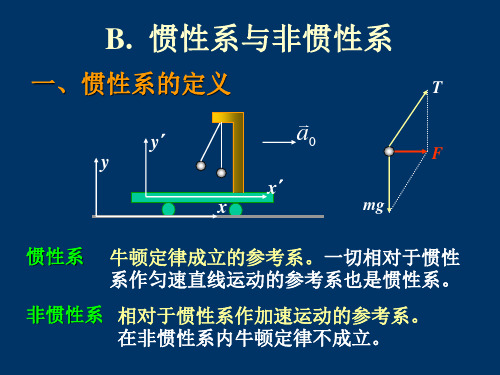
一、惯性系的定义
T
y´ y
a0

惯性与非惯性系

惯性与非惯性系在物理学中，惯性系和非惯性系是研究物体运动和力学定律所必须理解的重要概念。

本文将就惯性系和非惯性系进行较为详细的论述，以便更好地理解这两个概念及其在物理学中的应用。

一、惯性系的定义与特点惯性系是指一个相对于参考物体或观察者保持静止或匀速直线运动的参考系。

在这个参考系中，物体不受外界力的作用时，将保持原来的静止状态或匀速直线运动状态。

简单来说，惯性系是一种相对休息或匀速直线运动的参照系。

在惯性系中，根据牛顿第一定律，物体在无外力作用下将保持匀速直线运动或静止状态。

这意味着物体的速度和加速度在惯性系中是恒定的。

当我们观察某个物体时，如果其速度和加速度保持不变，那么我们可以判断该观察参考系是一个惯性系。

二、非惯性系的定义与特点非惯性系是指一个相对于参考物体或观察者具有加速度的参考系。

在非惯性系中，物体在没有外力作用下却能加速或偏离直线运动。

非惯性系中的物体会受到与其加速度大小和方向相等的惯性力的作用，以使其保持运动状态。

在非惯性系中，由于存在加速度，牛顿第一定律不再适用。

物体的速度和加速度会随着时间的推移而发生变化。

对于在非惯性系中的观察者来说，他们必须考虑到惯性力的存在，以进行力学分析和预测物体的运动状态。

三、惯性与非惯性系的关系惯性系和非惯性系是相对于观察者或参考物体而言的。

同一个物体在不同的参考系下可能是惯性系，也可能是非惯性系。

例如，对于恒速行驶的火车上的乘客来说，火车是一个惯性系，而对于外部观察者来说，火车则是非惯性系。

在分析物体运动和应用力学定律时，我们通常选择一个适当的参考系。

在惯性系中，物体的运动较为简单，力学定律更易于应用。

而在非惯性系中，由于惯性力的存在，力学分析相对较为复杂。

因此，我们通常倾向于选择一个惯性系进行分析。

四、惯性和非惯性系在物理学中的应用惯性系和非惯性系在物理学中有着广泛的应用。

在惯性系中，机械物体的运动状态可以非常直观地描述和分析，力学定律也更为简洁。

惯性系和非惯性系

惯性系和非惯性系引言在物理学中，惯性系和非惯性系是非常重要的概念。

它们对于我们研究物体运动以及描述物理现象有着重要的意义。

本文将介绍惯性系和非惯性系的定义，以及它们在物理学中的应用。

惯性系的定义惯性系是指一个参考系，在该参考系中，一个物体如果不受外力作用，将会保持静止或匀速直线运动。

也就是说，物体在惯性系中的运动状态是恒定的，不受任何力的干扰。

在惯性系中，牛顿第一定律成立。

非惯性系的定义非惯性系是指一个参考系，在该参考系中，有一外力作用在物体上。

由于外力的作用，物体在非惯性系中的运动状态将发生变化，不再是简单的匀速直线运动或静止状态。

惯性力的引入当物体在非惯性系中运动时，由于外力的作用，物体会出现看似无法解释的非惯性现象，在分析这些现象时，我们常常需要引入惯性力的概念。

惯性力是指一个与物体的加速度方向相反的力，它的大小等于物体的质量乘以加速度的大小。

应用举例1.离心力：想象一个绳子上带有小球的旋转木马，当木马转动时，小球会受到一个向外的离心力，这是因为在旋转坐标系中，小球受到了一个向中心的加速度，而离心力则是一个向外的力，使小球始终保持在木马上。

2.地球自转：地球自转产生了一个向外的离心力，这使得我们站在地面上的物体受到向下的压力，也就是我们常说的重力。

在非惯性系中，地球的自转速度会使物体受到一个看似向下的加速度，而这个加速度正好被重力所抵消，所以我们感觉不到地球的自转运动。

3.电梯加速：当乘坐电梯上升或下降时，我们会感受到一个向上或向下的力，这其实是地球引力与电梯的加速度之和，这个力使我们感觉到了重量的变化。

总结惯性系和非惯性系是物理学中非常重要的概念。

惯性系是一个物体在其中保持静止或匀速直线运动的参考系，而非惯性系则是一个物体在其中受到外力作用的参考系。

在非惯性系中，我们常常需要引入惯性力来解释一些看似无法解释的现象。

惯性力是与物体的加速度方向相反的力，它的大小等于物体的质量乘以加速度的大小。

惯性系

牛顿第一定律和惯性参考系基本概念：孤立质点：不受其它物体作用或离其它物体都足够远的质点（理想模型）。

牛顿第一定律：孤立质点静止或作等速直线运动（每个物体继续保持其静止或作等速直线运动的状态，除非有力加于其上迫使它改变这种状态）。

使用范围：质点和惯性参考系。

牛顿第一定律的理解：（1）定性的说明了运动和力的关系：物体的运动并不需要力去维持，只有当物体的运动状态（速度）发生变化即产生加速度时，才需要力的作用。

力的定义：力是一物体对另一物体的作用，是物体产生加速度的原因。

（2）提出了“惯性”的概念：物体保持原来运动状态不变的特性，是物体所固有的。

1．惯性参考系：孤立粒子相对它静止或作等速直线运动的参考系。

简称“惯性系”。

或者：牛顿第一定律能成立的参考系叫惯性系，否则称为非惯性参考系。

一般情况下，由观察和实验的性质来判断，如：在精度不太高时，地球参考系可以看作惯性参考系，又称实验室参考系，或实验室坐标系。

在人造地球卫星时，常选“地心——恒星坐标系”：以地心为原点，坐标轴指向恒星的惯性参考系。

在研究行星等天体的运动时，常选“日心——恒星坐标系”：以太阳中心为原点，坐标轴指向其它恒星的惯性参考系。

相对于惯性参考系作等速直线运动的参考系亦为惯性参考系，这就是惯性参考系的“传递性”：发现一个惯性系，变有无穷多个惯性系。

注：运动只能是相对于参考系而言的，没有参考系的运动描述都是没有任何物理意义的。

练习题：质量为2kg的质点的运动学方程为：(t为时间，单位为秒；长度单位为米）求证：质点受恒力而运动，并求力的大小、方向．惯性质量动量和动量守恒定律一．惯性质量实验：一气桌，包含平台和滑块，将平台调至水平，铺以白纸，通过电打火花可以在纸上形成斑点，由斑点的距离来确定滑块的速率。

斑点排位的方向给出滑块方向，滑块1和滑块2以某初速度运动并碰撞，滑块1和2的速度改变量分别为和，改变滑块初速度反复实验多次，总有：或：(1)其中，为常量，改变滑块质量，(1)式仍成立，仅取值不同，与滑块质量有关。

惯性系与非惯性系

电磁诠释78 惯性系与非惯性系一、经典理论中惯性系与非惯性系的概念经典理论认为凡是牛顿运动定律适用的参照系为惯性系，牛顿运动定律不成立的参照系为非惯性系。

所有相对于惯性系做匀速直线运动的参照系都是惯性系，相对于惯性系做非匀速直线运动的参照系就不是惯性系。

在一般精度范围内，地球或静止在地面上的任一物体都可以近似看作惯性系。

同样，在地面上做匀速直线运动的物体也可以近似地看作惯性系，但在地面上做变速运动的物体就不能看作惯性系。

可以看出，经典理论是把匀速直线运动的参照系作为惯性系，非匀速直线运动的参照系作为非惯性系。

二、匀速直线运动和非匀速直线运动的统一通过以前的论述，我们知道不管是匀速直线运动，还是非匀速直线运动，都存在实际加速度0αA 或αA 。

并且实际加速度的量值不随参照系的改变而改变。

这样，我们就可以用实际加速度把匀速直线运动和非匀速直线运动统一起来。

下面我们用实际加速度曲线说明之。

惯性系与非惯性系79图1 实际加速度曲线（惯性系曲线）物体m 在极地作匀速直线运动，其实际加速度0tan 00ααα⋅=g A0200tan )(α⋅-=rv g 00220tan )sin (αα⋅-=rc g 取极地g 0=9.8322 m/s 2，极地半径r =6.3568×106m ，光速c =3×108m/s 时，根据上式可画出极地实际加速度0αA 与速度斜角0α的关系曲线，如上图所示。

1. 当0α=0或v 0=0时，表现为相对静止。

2. 当0α=1.5215×105-或v 0=4.5644×103 m/s 时，极地、匀速直线运动的实际加速度有最大值m ax 0αA =9.9731×电磁诠释80 105- m/s 2。

3. 当0α=2.6353×105-或v 0=7.9058×103m/s 时，形成稳态运动，这时毗邻阻力f B =m 0αA ⋅=0。

惯性与非惯性系大学物理中参考系变换的分析

惯性与非惯性系大学物理中参考系变换的分析惯性与非惯性系：大学物理中参考系变换的分析在大学物理学中，研究运动的参考系变换是一个基本的课题。

参考系变换指的是在不同的观察参考条件下，描述物体运动的方式和规律可能有所不同。

其中，惯性系和非惯性系是关键概念。

一、惯性系的定义与特征惯性系是指一个自由运动的物体在该参考系中的运动状态保持匀速直线运动或静止状态的参考系。

惯性系的特征包括：在一个惯性系中，物体的速度和加速度仅受到物体自身所受到的力的影响，也就是满足惯性定律。

二、非惯性系的定义与特征相对于惯性系，非惯性系描述物体运动时需要考虑虚拟力的作用。

虚拟力是指在非惯性系中观察到的力，但实际上并不存在于物体上。

非惯性系的特征包括：在非惯性系中，物体会出现惯性力的存在，这是观察者引入的一种力，是为了使物体的运动描述满足牛顿定律。

三、参考系变换的基本原理1. 线性参考系变换在不同的惯性系之间进行参考系变换时，物体的速度和加速度在不同系之间是相等的。

这是基于惯性定律的推论，即物体的运动状态不受观察者选取的参考系的影响。

2. 非惯性系的参考系变换在从一个非惯性系到另一个非惯性系的参考系变换中，需要引入惯性力来使物体的运动描述满足牛顿定律。

惯性力的方向和大小是由参考系变换的加速度和物体的质量决定的。

四、参考系变换的应用参考系变换的应用非常广泛，特别是在解决旋转体和离心力等问题时，常常需要使用非惯性系的概念和方法。

1. 常见的非惯性系（1）转动参考系：某些问题需要将旋转天体、自转地球等情况考虑在内，这时需要使用转动参考系进行运动分析。

（2）加速度参考系：当物体受到加速度的影响时，物体的运动状态依赖于加速度参考系，此时需要考虑虚拟力的作用。

2. 应用举例（1）开车过弯：在汽车行驶过弯道时，车内乘客会感觉到一个向外的力，这是由于非惯性系（车体的向心加速度）引起的惯性力。

（2）旋转木马：在旋转木马上，乘客会感受到一个向外的力，也是由于非惯性系（旋转参考系）引起的惯性力。

惯性与非惯性系

惯性与非惯性系惯性与非惯性系是物理学中的重要概念，在描述物体的运动和相对位置时起到了重要的作用。

本文将介绍惯性系和非惯性系的定义、特点和应用，并探讨其在实际生活中的重要性。

首先，我们来定义什么是惯性系和非惯性系。

惯性系是指一个没有受到外力作用并且保持静止或匀速直线运动的参考系。

在惯性系中，牛顿第一运动定律成立，即一个物体会保持匀速直线运动或保持静止，除非有外力作用。

而非惯性系则是指一个受到外力作用或者产生了加速度的参考系。

在惯性系中，物体的运动状态可以由牛顿运动定律准确描述。

物体的运动是由施加在其上的力决定的，而力本身又是由运动物体和相对于运动物体的惯性参考系之间的相互作用产生的。

因此，在惯性系中，物体的运动可以直观地被描述和理解。

与惯性系相对应的是非惯性系。

非惯性系中，物体所受到的其他力（如摩擦力、旋转力等）会对其运动状态产生影响。

在非惯性系中，物体会出现“惯性力”的概念，这是由于非惯性系的变动所产生的看似存在的力。

为了描述物体在非惯性系中的运动，我们通常需要引入其他的方程和概念，如惯性力和旋转力等，以更准确地描述物体的运动。

那么惯性系和非惯性系到底有什么区别呢？首先，惯性系中的物体可以简单地依据牛顿运动定律进行描述，而非惯性系则需要考虑额外的力和因素。

其次，惯性系是相对于其他参考系而言的，当我们将参考系从一个惯性系转换到另一个惯性系时，物体的运动状态不会发生变化。

而非惯性系则没有这样的特点，当我们从一个非惯性系转换到另一个非惯性系时，物体的运动状态会发生变化。

在实际生活中，惯性系和非惯性系在物体的运动和相对位置描述中起到了重要的作用。

例如，在航天飞行中，我们需要考虑地球的自转、航天器的旋转和受力情况等因素，这就涉及到了非惯性系的概念。

同样地，在地面交通中，车辆的转弯、加速和制动等行为也需要考虑非惯性系的影响。

因此，了解惯性系和非惯性系的概念以及其在实际中的应用是非常重要的。

总而言之，惯性系和非惯性系是描述物体运动和相对位置的两个重要概念。

非惯性系和惯性力

解: 以向上的方向为正.设A, B相对于升降机的加速度为a.
以升降机为参考系.
a A机 aB机
a
A m1g
N
a
T T B m2g
A和B分别受到惯性力为：
FiA m1a, FiB m2 a,
由 F外 Fi ma物机 ma 有
19
对A： T m1a， m1 g m1a 0 N 对B：T m2 g m2 a m2 (a)

惯性离心力
7
洗衣机的甩干机
8
气旋ห้องสมุดไป่ตู้形成
北半球
南半球
水涡的形成
9
10
大气环流的形成
四、科里奥利力
在匀速转动圆盘的A处向B 处以相对圆盘v 抛出一小球, 经过一段时间小球到达何处？
O A B B

11
小球受到另一种惯性力 ——科里奥利力
FC 2mv
产生的原因：
1
内容回顾
牛顿运动定律：
第一定律：惯性定律
dp 第二定律： F ma dt 第三定律： F12 F21
2.6 非惯性系和惯性力
a0 F 0，a球对地 0
2
N
mg
N
a F 0 0
a
球对车
mg
？
0
牛顿定律只适用于惯性参考系
m2 解得 a1 (a g ) g m1 m2
a A地
aB地
5 a1 a g 2
2 2
1 a a1 g 2
A m1g
N
a
T T B m2g

惯性系与非惯性系的运动

惯性系与非惯性系的运动惯性系与非惯性系是物理学中非常重要的概念，用以描述物体运动时的参考系。

在本文中，我们将探讨惯性系与非惯性系的概念以及它们在运动中的应用。

一、惯性系和非惯性系的定义惯性系是指一个参考系，其中任何不受外力作用的物体都保持匀速直线运动或静止状态。

在惯性系中，牛顿定律成立，物体的运动和相对位置都能够准确地描述。

非惯性系则是指一个参考系，其中某些物体将受到额外的惯性力。

这些额外的力可能是由于该系相对于某个惯性系做的加速运动引起的。

在非惯性系中，物体的运动无法分析和描述，不符合牛顿定律。

二、相对运动与绝对运动相对运动是指两个物体之间的相对变化，而绝对运动则是指物体相对于绝对参考系的运动状态。

在惯性系中，物体的相对运动和绝对运动是一致的。

例如，当我们坐在火车上时，我们相对于火车是静止的，但相对于地面变化的速度是火车的速度。

这是因为我们和火车一起处于同一个惯性系中。

然而，在非惯性系中，物体的相对运动和绝对运动是不一致的。

例如，当我们坐在车厢中，车厢突然开始加速向前，我们会感到向后的推力。

这是惯性力作用在我们身上的结果，它是由于我们所在的非惯性系相对于地面的加速度而产生的。

三、旋转参考系和离心力除了直线运动的非惯性系外，还存在旋转参考系。

旋转参考系是指以旋转物体为参考的参考系。

在旋转参考系中，由于旋转的效果，物体将受到离心力的影响。

离心力是指一个物体相对于旋转轴的受力方向离开旋转轴的向心方向，它不是真实存在的力，而是由于旋转参考系的加速度变化而产生的一个惯性力。

离心力的大小由物体的质量、线速度和旋转半径决定。

在旋转参考系中，牛顿定律的形式需要进行修正，以考虑这种额外的力。

四、应用与总结惯性系和非惯性系的概念在物理学中有着广泛的应用。

在解决运动问题时，我们需根据问题的场景判断使用何种参考系。

对于简单的匀速直线运动或静止状态的物体，我们可以选取一个惯性系作为参考系，应用牛顿定律进行分析。

而对于复杂的加速运动或旋转运动，我们则需要考虑物体所处的参考系是否为惯性系，以确定是否存在额外的惯性力。

惯性参照系

惯性参照系
惯性参照系是物理学的基本概念，是衡量物体在宇宙中的运动的重要参照系。

它的基本定义是，“相对于某一个参照系，不受任何外力的作用，而具有
恒定运行速度和方向的物体，就称为惯性系。

”惯性参照系可以用于描述物体
的运动方向和物体运动的速度。

惯性参照系是一个虚拟的概念，它不存在于外
部的物理环境中，而是一个抽象的概念。

惯性参照系也是宇宙中运动的最基本的准则。

它指的是，对于一个坐标系
而言，当它以一个固定的速度运动时，在这一参考系中，它会一直保持这样的
运动，而不会被任何外力所影响。

惯性参照系可以让我们清楚地理解物体运动
以及外力在物体运动中所产生的影响。

此外，在实际应用中，惯性参照系也非常重要。

它可以用来对导航、飞行
和航海中的物体实现定位和运动的控制。

它在其它运动学问题的应用中也能发
挥重要作用，如研究基于惯性参照系的物体运动，从而制定出有效的控制策略。

总之，惯性参照系是一个非常重要的概念，它是许多物理问题的基础，同
时也在实际应用中发挥着重要作用。

惯性系与非惯性系的概念与区别

惯性系与非惯性系的概念与区别惯性系和非惯性系是物理学中的重要概念，用于描述物体运动的参照系。

在本文中，我们将详细介绍惯性系和非惯性系的概念，并探讨它们之间的区别。

一、概念解析1. 惯性系惯性系是指在其中一个物体如果不受到外力作用，其状态将保持不变或恒定运动的参照系。

简单来说，当我们不施加任何力或者力平衡的情况下，物体将保持静止或作匀速直线运动。

经典力学的基本定律牛顿第一定律就是根据惯性系的概念来描述物体运动的。

2. 非惯性系非惯性系是指其中一个物体如果不受到外力作用，其状态将不会保持不变或恒定运动的参照系。

也就是说，在非惯性系中，物体在不受外力作用下会发生加速度或者作曲线运动。

非惯性系可以通过加速度进行描述，而加速度是相对于惯性系而言的。

二、概念的区别惯性系和非惯性系之间存在着明显的区别。

下面将从几个方面进行详细比较。

1. 物体状态保持在惯性系中，物体如果不受外力作用，其状态将保持不变或恒定运动。

而在非惯性系中，物体在不受外力作用下会发生改变，可能会发生加速度或者作曲线运动。

2. 参照系的运动状态惯性系可以看作是一个静止或作匀速直线运动的参照系。

而非惯性系往往与我们所处的参照系有关，例如旋转的车辆、电梯等。

3. 引力的影响在惯性系中，物体受到的引力可以通过等效引力来描述，例如在地球上物体受到的重力就可以等效为一个竖直向下的力。

而在非惯性系中，物体所受的引力可能会导致参照系的运动状态发生变化，例如在旋转的车辆中，物体可能会受到向外的离心力。

4. 牛顿定律的适用性牛顿定律适用于惯性系，可以准确描述物体的运动状态。

但在非惯性系中，由于参照系的加速度，牛顿定律将失效。

在非惯性系中，需要引入惯性力的概念，以修正牛顿定律的适用性。

三、总结惯性系是物理学中用于描述物体静止或作匀速直线运动的参照系，可以准确应用牛顿定律描述物体运动；非惯性系是指在其中物体不受外力作用会发生加速度或曲线运动的参照系，需要引入惯性力来修正牛顿定律的适用性。

强基计划物理试题及解答

强基计划是教育部推出的高水平大学和特色高水平学科建设计划，旨在培养具备创新精神和实践能力的优秀人才。

以下是一道物理试题及其解答，供您参考。

试题：一辆卡车以一定的速度行驶，车上的一个小球以该车上某个固定点为参考点做自由落体运动。

在参考点所在的惯性系中，小球做的是直线运动还是曲线运动？为什么？解答：在参考点所在的惯性系中，小球做的是曲线运动，而不是直线运动。

首先，我们需要明确惯性系的定义：惯性系是指一个静止或做匀速直线运动的参照系。

在惯性系中，物体如果不受力，则会保持静止或匀速直线运动，这就是牛顿第一定律的内容。

然而，在卡车上，小球受到了重力和空气阻力等力的作用，因此不是不受力的状态。

由于小球做的是自由落体运动，它在垂直方向上受到了重力的作用，而在水平方向上则受到了空气阻力的作用，因此在惯性系中，小球做的是曲线运动。

具体来说，如果我们以卡车为参考系，则小球的运动可以分解为两个分量：垂直于卡车运动方向的自由落体运动和平行于卡车运动方向的匀速直线运动。

由于自由落体运动是曲线运动，所以小球在参考点所在的惯性系中也做曲线运动。

如果要进一步分析小球的曲线运动，我们需要考虑小球的运动轨迹和运动状态。

在参考点所在的惯性系中，小球的轨迹可以看作是一个抛物线，这是由于它的垂直运动是自由落体运动，而水平运动则是匀速直线运动。

因此，小球的轨迹呈现出一个向下开口的抛物线形状。

而小球的运动状态则可以用速度和加速度来描述。

在垂直方向上，小球的速度始终在增大，而加速度则是恒定的重力加速度。

在水平方向上，由于小球受到的阻力是与速度成正比的，所以小球的速度会逐渐减小，而加速度则近似为零，因为水平方向上没有明显的力作用。

需要注意的是，上述分析是在参考点所在的惯性系中进行的。

如果我们选择卡车为参考系，则小球在水平方向上的速度是不变的，而在垂直方向上则要考虑相对运动和惯性力等因素。

这再次说明了惯性系的重要性，它可以让我们更准确地描述物体的运动状态和运动轨迹。