可用等效电阻
电阻、电感、电容的等效阻抗计算及应用

--是一单向导电器件(无正向阻断能力);
--为不可控器件,由其两断电压的极性控制通断,无其它外部控制;
--普通二极管的功率容量很大,但频率很低;
--开关二极管有三种,其稳态特性和开关特性不同:
--快恢复二极管;
--超快恢复,软恢复二极管;
--萧特基二极管(反向阻断电压降<<200V,无反向恢复问题);
功率MOSFET的反向导通等效二极管的等效电路,可用一电压降等效,此二极管为MOSFET的体二极管,多数情况下,因其特性很差,要避免使用。
功率MOSFET的反向导通等效电路(2)
(1):等效电路(门极加控制)
(2):说明:功率MOSFET在门级控制下的反向导通,也可用一电阻等效,该电阻与温度有关,温度升高,该电阻变大;它还与门极驱动电压的大小有关,驱动电压升高,该电阻变小。详细的关系曲线可从制造商的手册中获得。此工作状态称为MOSFET的同步整流工作,是低压大电流输出开关电源中非常重要的一种工作状态。
功率MOSFET的正向截止等效电路
(1):等效电路
(2):说明:功率MOSFET正向截止时可用一电容等效,其容量与所加的正向电压、环境温度等有关,大小可从制造商的手册中获得。
功率MOSFET的稳态特性总结
(1):功率MOSFET稳态时的电流/电压曲线
(2):说明:功率MOSFET正向饱和导通时的稳态工作点:
当门极不加控制时,其反向导通的稳态工作点同二极管。
(3):稳态特性总结:
--门极与源极间的电压Vgs控制器件的导通状态;当VgsVth时,器件处于导通状态;器件的通态电阻与Vgs有关,Vgs大,通态电阻小;多数器件的Vgs为12V-15V,额定值为+-30V;
等效串联电阻

ESR、滤波-去耦-旁路电容、上-下拉电阻、ESL、肖特基二极管ESR是“等效串连电阻”。
理论上,电容自身不会产生任何能量损失,但实际上因制造电容的材料有电阻,电容的绝缘介质有损耗,这个损耗在外部,表现为就像一个电阻跟电容串连在一起,所以就起了个名字叫做“等效串连电阻”。
我们认为电容上面电压不能突变,当突然对电容施加一个电流,电容因为自身充电,电压会从0开始上升。
但是有了ESR,电阻自身会产生一个压降,这就导致了电容器两端的电压会产生突变。
无疑的,这会降低电容的滤波效果,所以很多高质量的电源都使用低ESR的电容器。
在振荡电路等场合,ESR也会引起电路在功能上发生变化,引起电路失效甚至损坏等严重后果。
所以在多数场合,低ESR的电容,往往比高ESR的有更好的表现。
比如在稳压电路中,有一定ESR的电容,在负载发生瞬变的时候,会立即产生波动而引发反馈电路动作,这个快速的响应,以牺牲一定的瞬态性能为代价,获取了后续的快速调整能力,尤其是功率管的响应速度比较慢,并且电容器的体积/容量受到严格限制的时候。
这种情况见于一些使用mos管做调整管的三端稳压或者相似的电路中。
这时候,太低的ESR反而会降低整体性能。
ESR是等效“串连”电阻,意味着将两个电容串连,会增大这个数值,而并联则会减少之。
实际上,需要更低ESR的场合更多,而低ESR的大容量电容价格相对昂贵,所以很多开关电源采取的并联的策略,用多个ESR相对高的铝电解并联,形成一个低ESR的大容量电容。
牺牲一定的PCB空间,换来器件成本的减少,很多时候都是划算的。
和ESR类似的另外一个概念是ESL,也就是等效串联电感。
早期的卷制电容经常有很高的ESL,而且容量越大的电容,ESL一般也越大。
ESL经常会成为ESR的一部分,并且ESL也会引发一些电路故障,比如串连谐振等。
但是相对容量来说,ESL的比例太小,出现问题的几率很小,再加上电容制作工艺的进步,现在已经逐渐忽略ESL,而把ESR作为除容量之外的主要参考因素了。
初中物理等效替代法表达式

初中物理等效替代法表达式篇一:在物理实验中常用到等效替代法在物理实验中常用到等效替代法,例如将一个7Ω的电阻替换某支路中2Ω和5Ω串联的电阻,在其他条件不变的情况下,该支路中电流不变,说明一个7Ω的电阻与阻值为2Ω和5Ω串联的电阻对电流的阻碍作用是等效的,所以可用7Ω的电阻替代2Ω和5Ω串联的电阻。
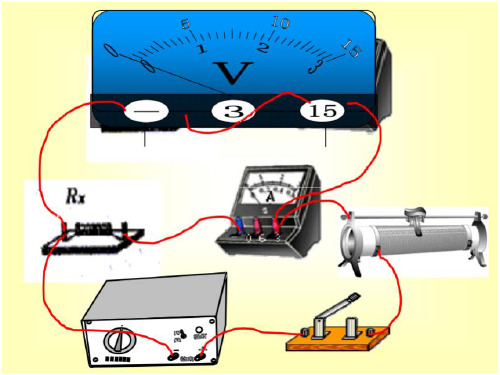
在用如图所示电路测量未知电阻的实验中,用的就是等效替代的方法。
其中Rx是待测电阻(阻值大约为几百欧),R是滑动变阻器,R0是电阻箱(电阻箱的最大阻值大于Rx)。
(1)请根据实验电路图把下列主要实验步骤中的空白填齐;①按电路图连接好电路,并将电阻箱R0的阻值调至最大;②闭合开关S1前,滑片P置于___________端;(选填“a ”或“b”)③闭合开关S1;④闭合开关__________,调节滑片P,使电流表指针指在适当的位置,记下此时电流表的示数I;⑤先断开开关________,再闭合开关__________,保持________的电阻不变,调节_________,使电流表的示数仍为I;⑥计算Rx的值,计算表达式为Rx=_________(2)在此实验中,若将电流表改为电压表,其他器材不变,在虚线框内画出用等效替代法测量Rx电阻的实验电路图。
(要求所设计的电路在连接好后,只能通过开关改变电路连接情况)。
篇二:巧用等效替代法测未知电阻巧用等效替代法测未知电阻例1. 利用电池、开关、一个标准电阻箱、若干导线和一个刻度不准但灵敏性良好的电流表测量待测电阻Rx。
解析:(1)按照图1的方式把实物连成电路,调节电阻箱R0,使电流表指针指向一个适当的位置,记下这时R0的阻值R1。
图1(2)再把Rx从电路中取下,调节R0的电阻,使电流表的指针指向刚才测量的位置,记下这时R0的阻值R2。
(3)由于R1加上Rx在电路中所起的作用与R2相同(电流表指针指示同一位置),则有R1+Rx=R2,故有Rx=R2-R1。
例2. 现有两节电池,三个开关,若干导线,还有电流表、滑动变阻器、电阻箱各一个,请用以上器材设计一个实验方案测出未知电阻Rx的值(电阻箱的最大阻值大于Rx)。
等效电阻的缩写符号

等效电阻的缩写符号全文共四篇示例,供读者参考第一篇示例:等效电阻的缩写符号是R_eq。
在电路中,当多个电阻并联或串联连接时,可以用一个等效电阻来替代这些电阻,从而简化电路分析。
等效电阻的计算方法取决于电路的连接方式。
在并联电路中,多个电阻的等效电阻可以通过以下公式计算:1/R_eq = 1/R1 + 1/R2 + 1/R3 + ...R1、R2、R3等为并联连接的各个电阻值。
将上式两边取倒数并化简即可得到等效电阻R_eq的值。
R1、R2、R3等为串联连接的各个电阻值。
通过计算等效电阻,可以简化复杂的电路分析,帮助工程师更快速地理解电路的特性和性能。
这对于设计和调试电路至关重要。
等效电阻还有一个重要的应用,就是在电路中使用理想电流和电压源模型。
理想电流源的内阻为无限大,可以用一个电阻值很大的等效电阻来模拟。
理想电压源的内阻为零,可以用一个接近于零的等效电阻来模拟。
这样在电路分析时可以简化计算,更容易求解电路参数。
在实际电路应用中,等效电阻的概念也被广泛应用。
在放大器设计中,可以用等效电阻模型来分析放大器的输入输出特性。
在滤波器设计中,可以用等效电阻来简化复杂的网络结构。
在传输线设计中,可以用等效电阻来模拟传输线的特性。
等效电阻在电路分析和设计中起着重要的作用。
通过计算等效电阻,可以简化电路分析,提高工作效率。
掌握等效电阻的计算方法和应用是电子工程师必备的基础知识之一。
希望以上内容对您有所帮助。
第二篇示例:等效电阻是指在电路中表现出相同电阻效果的一个电阻器件或者一个电路,它可以代替原来复杂的电路,简化电路分析,便于计算电路参数。
在电路分析中,等效电阻是一个非常重要的概念,它可以帮助我们更好地理解电路的性质和特性。
等效电阻在电路分析中有着广泛的应用,比如在直流电路中,我们可以通过等效电阻求解电路的电流和电压等参数;在交流电路中,等效电阻可以用来计算电路的阻抗、相位等特性。
掌握等效电阻的概念和计算方法对于理解电路的工作原理和性能至关重要。
戴维宁定理

返回
上一节
下一节
上一页
下一页
第1章 电路分析基础
教学基本要求
1、了解电路的作用和组成。 2、了解电路的通路、开路和短路状态;了解电源的有载、空载和短路 状态。理解额定值、负载大小和电功率的概念。 3、了解电路模型的概念。理解理想电阻元件的耗能特性、理想电压源 的恒压特性和理想电流源的恒流特性。 4、理解电路的基尔霍夫定律并能正确应用。 5、掌握用支路电流法、叠加定理和戴维宁定理分析电路的方法。
:
oc
Uoc
12 6 6 3
3Байду номын сангаас
6
4
12V
(2)ab两端入端电阻 Ri :
Ri
36 36
1
3
(3) 戴维南等效电路如左图 (b)所示。
例2 用戴维宁定理计算下图 (a)所示电路中电流I。
解:
(1)ab两端开路电压Uoc :
选定如上图 (b)所示参考点,用节点电压法求节点①电压:
1 2
返回
上一节
下一节
上一页
下一页
复习题
1、求图4所示电路两电路中的电压 U ab 。
2、计算图5所示电路中各点的电位。
3、求图9电路的等效电源模型。 4、用戴维宁定理计算图10所示电路中的电流I。
5、试用支路电流法求各支路电流。
6、用叠加原理求图示电路中的I,并问当电流源 电流增加4A时,I增加多少?
第四讲 戴维宁定理
1.6 戴维宁定理
基本概念:
所谓二端网络是指具有两个引出端的部分电路。 二端网络有有源二端网络与无源二端网络之分, 不含电源的二端网络称为无源二端网络,如下图左所示的电阻混 联电路。无源二端网络可用一个等效电阻代替。 含有电源的二端网络称为有源二端网络,如下图右所示。有源二 端网络可用电源和电阻组合来等效代替。
电芯等效直流电阻-概述说明以及解释

电芯等效直流电阻-概述说明以及解释1.引言1.1 概述概述电芯等效直流电阻是评估电池性能和稳定性的重要参数之一。
它指的是在直流电流通过电芯时,电芯对电流的阻碍程度。
电芯等效直流电阻的大小直接影响电池的功率输出能力和电池的工作温度。
电芯等效直流电阻是由电芯内部的材料电阻、电解液电阻、电极之间的接触电阻等因素共同决定的。
这些因素会导致电流在电芯内部产生能量损耗,并产生热量。
因此,电芯等效直流电阻的大小与电芯的发热、温升和功率损耗直接相关。
电芯等效直流电阻的准确测量和评估对于电池的设计和应用至关重要。
减小电芯等效直流电阻可以提高电池的功率输出和充放电效率,延长电池的使用寿命。
因此,研究电芯等效直流电阻的影响因素和优化方法具有重要的理论和实践意义。
本文将重点介绍电芯的基本结构和电芯的等效直流电阻。
首先,将对电芯的基本结构进行介绍,包括电芯的正负极材料、电解液及电芯外壳。
然后,将重点讨论电芯等效直流电阻的形成机制和影响因素,包括电芯内部的电阻和接触电阻。
同时,还将介绍目前常用的电芯等效直流电阻测量方法和评估指标。
本文的目的是为读者深入了解电芯等效直流电阻的重要性和影响因素,以及现有的测量方法和评估指标。
同时,也希望能够启发读者对电芯等效直流电阻的未来研究方向进行思考,为电池技术的进一步发展和应用提供参考。
1.2文章结构文章结构部分的内容可以按照以下方式编写:2. 正文2.1 电芯的基本结构2.2 电芯的等效直流电阻在这篇文章中,我们将讨论电芯的等效直流电阻,这是电池性能评估和设计中一个重要的指标。
为了理解电芯等效直流电阻的意义和用途,我们首先将介绍电芯的基本结构。
在2.1小节,我们将概述电芯的基本结构,包括正负极电极、电解液和隔膜等组成部分。
我们将详细讨论每个组成部分的功能和作用,并解释它们在电芯工作中的相互关系。
紧接着,在2.2小节,我们将介绍电芯的等效直流电阻。
等效直流电阻是指在直流工作条件下,电芯对电流的阻碍程度,并且通常用来评估电芯的内阻大小。
【详解各元器件等效电路】电阻、电容、电感、二极管、MOS管!

【详解各元器件等效电路】电阻、电容、电感、二极管、MOS管!2017-08-30EDN电子技术设计电阻电阻等效电路图1 电阻等效电路电阻的等效阻抗同一个电阻元件在通以直流和交流电时测得的电阻值是不相同的。
在高频交流下,须考虑电阻元件的引线电感L0和分布电容C0的影响,其等效电路如图1所示,图中R为理想电阻。
由图可知此元件在频率f下的等效阻抗为式 1上式中ω=2πf, R e和X e分别为等效电阻分量和电抗分量,且式 2从上式可知R e除与f有关外,还与L0、C0有关。
这表明当L0、C0不可忽略时,在交流下测此电阻元件的电阻值,得到的将是R e而非R值电感电感等效电路图2 电感等效电路电感的等效阻抗电感元件除电感L外,也总是有损耗电阻R L和分布电容C L。
一般情况下R L和C L的影响很小。
电感元件接于直流并达到稳态时,可视为电阻;若接于低频交流电路则可视为理想电感L和损耗电阻R L的串联;在高频时其等效电路如图2所示。
比较图1和图 2可知二者实际上是相同的,电感元件的高频等效阻抗可参照式 1来确定式 3式中 R e和L e分别为电感元件的等效电阻和等效电感。
从上式知当C L甚小时或R L、C L和ω都不大时,L e才会等于L或接近等于L。
电容电容等效电路图3 电容等效电路电容的等效阻抗在交流下电容元件总有一定介质损耗,此外其引线也有一定电阻R n和分布电感L n,因此电容元件等效电路如图 3所示。
图中C是元件的固有电容,R c是介质损耗的等效电阻。
等效阻抗为式 4式中 R e和C e分别为电容元件的等效电阻和等效电容, 由于一般介质损耗甚小可忽略(即R c→∞),C e可表示为式 5从上述讨论中可以看出,在交流下测量R、L、C,实际所测的都是等效值R e、L e、C e;由于电阻、电容和电感的实际阻抗随环境以及工作频率的变化而变,因此,在阻抗测量中应尽量按实际工作条件(尤其是工作频率)进行,否则,测得的结果将会有很大的误差,甚至是错误的结果。
高中物理竞赛-电阻等效方法ABC

x
RAB
2 21 21
r
3
田字形电阻丝网络如图所示,每小段电阻丝的电
解: 阻均为R,试求网络中A、B两点间的等效电阻RAB.
I RAB
R
O
I 2
I 24
R
I 8
5I 24
2R
B
I I 5I I 2 24 24 8
A
RAB
29 24
R
O B
R
O
B
2A
R3
5 6
3
r
2 3
125 234
r
递推到分割n次后的图形
Rn
2 3
5 6
n
r
A r
B
r 5r 2 6
5r
5 6
21r2
读题 C
如图所示的平面电阻丝网络中,每一直
线段和每一弧线段电阻丝的电阻均为r.试求A、B两点间
的等效电阻.
解:
B
B
A
B
B就在这个背景下研究按谢尔宾斯基镂垫图形的各边构成的电阻网络的 等如效图2电所阻示问的题图:形设,如其图中1所每示个的 小三 三角 角形形A边B长C边的长电L阻0的是电原阻三均角为形rA;B经C的一边次长分的割电得阻到r 的二分之一;经二次分割得到如图3所示的图形,其中每个小三角形边长的电阻 是原三角形ABC的边长的电阻r的四分之一;三次分割得到如图4所示的图形,其 中每个小三角形边长的电阻是原三角形ABC的边长的电阻r的八分之一.
RAB
452R54c
2022-2023年中考物理复习《“等效替代法”测电阻》
(2)若I1>I2,则I1R0>I1R0
代入上式可得:I1Rx<I2R′
变形得到:
Rx<
I2 I1
R
(3)电阻箱的读数:各旋钮对应的倍数乘以倍数再求和,
所以图乙所示的电阻箱的示数为:
0×1000+3×100+0×10+5×1=305Ω 答为:(1)=;(2)<;(3)305
点评:本题主要考查的是等效替代的研究方法。等效替代 法是指在保证某一方面效果相同的前提下,用理想的、熟 悉的、简单的物理对象、物理过程、物理现象来替代实际 的、陌生的、复杂的物理对象、物理过程、物理现象的思 想方法。
小华在实验中发现,当开关接b后,无论怎样调电阻箱的阻 值,电流表的示数都明显小于I,致使无法测量Rx的阻值,小 明帮助小华分析原因,他认为实验不成功是由于小华第一步
操作中电阻箱R1的阻值Ra选择不当造成的,如果电阻箱R1的 阻值Ra不小于___1_5__Ω实验将保证能成功,或开关S先接b再 接a,其余操作不变,实验也能成功。
解:当开关接a处时,未知电阻与滑动变阻器串联,根据 U=IR和串联电路总电压等于各电阻电压之和, 可得电源电压:U=U0+Ux=I1R0+I1Rx 当开关接b时,电阻箱与滑动变阻器串联,同理可得:
U=U0′+UR=I2R0+I2R′ 因电源电压不变,结合两式可得:
I1R0+I1Rx=I2R0+I2R′ (1)滑动变阻器接入电路的电阻相等,且当I1=I2时, 可得:I1Rx=I2R′,即此时待测电阻值Rx=R′
(2)实验方法:
先合上开关S1,把单刀双掷开关S2打到1,将滑动变阻器滑 片移到适当位置,读出此时电压表的示数U0; 再把单刀双掷开关S2打到2,保持滑动变阻器滑片位置不变, 调节电阻箱的阻值,使电压表的示数仍为U0。
第二章电阻电路的等效变

第二章-电阻电路的等效变第二章 电阻电路的等效变换2.1 学习要点1. 电阻的等效变换:电阻的串并联, Y 与△的等效变换。
2. 电源的串联、并联及等效变换。
3. “实际电源”的等效变换。
4. 输入电阻的求法。
2.2 内容提要 2.2.1 电阻的等效变换1. 电阻的串联:等效电阻: R eq =∑1=k nk R ;分压公式:u k =eqkeq ×R R u ; 2. 电阻的并联:等效电导:G eq =∑1=k nk G ;分流公式:qe G G i i keqk ×=;2.2.2. 电阻的Y 与△的等效变换1. △→Y :一般公式:Y 形电阻=形电阻之和形相邻电阻的乘积∆∆;即31232331*********231231212311++=++=++R R R R R R R R R R R R R R R R R R 2312=2. Y →△:一般公式:形不相邻电阻形电阻两两乘积之和形电阻=Y Y ∆;即:213322131113322123313322112++=++=++=R R R R R R R RR R R R R R R R R R R R R R R R2.2.3 电源的串联、并联等效变换 电源的串联、并联等效变换见表2.1。
表2.1 电源的串联、并联等效变换图2.2.4 “实际电源”的等效变换 1. “实际电压源”→“实际电流源” R i =R u 或 G i =1/R u i s =u s /R u 2. “实际电流源”→“实际电压源”R u =R i =1/G i u s =i s R i =i s /G i两者等效互换的原则是保持其端口的V AR 不变。
2.2.5 输入电阻的求法一端口无源网络输入电阻的定义(见图2.2):R in =u/ i1. 当一端口无源网络由纯电阻构成时,可用电阻的 串并联、Y 形与△形等效变换化简求得。
2. 当一端口无源网络内含有受控源时,可采用外加电压法或外加电流法求得: 即输入电阻R in =u s /i 或 R in =u/ i s方法是:在端口处加一电压源u s (或电流源i s ), 再求比值u s /i 或u/ i s ,该比值即是一端口无源网络的输入电阻。
第二章 电阻电路的等效变换

4
Rab=10
15 10
a b
a b
7
20
15
3
返 回
上 页
下 页
例 2-8 求图 2-5电路 a b 端的等效电阻。
Req (2 // 2 (4 // 4 2) // 4) // 3 (1 4 // 4) // 3 1.5
21
复习
1、电阻的串联 等效电阻、分压
23
例2-4 图2-7所示电路每个电阻都是2Ω, 求a, b两端的等效电阻
解:
c
d
e
根据电路的对称性, 可知 c, d, e三点等电位, 故可用导线短接。
8 2 8 2 16 3 3 2 Req [(2//1) 2]// 2//1 2 // 2 8 2 3 3 15 3 3
26
R12 ( R23 + R31 ) R12 + R23 + R31
i1
i1
i3
i2
i3
i2
R12 R31 R12 + R23 + R31 R23 R12 R12 + R23 + R31 R31 R23 R12 + R23 + R31
27
同理,令i1=0, 可得: R23 ( R12 + R31 ) R2 + R3 = R12 + R23 + R31 同理,令i2=0, 可得:
25
二、 等效变换:保证伏安特性相同
对应端口电压、电流分别相等
i1
u12 = f1 ( i1 , i2 , i3 ) u23 = f 2 ( i1 , i2 , i3 ) u31 = f3 (i1 , i2 , i3 )
等效电阻

物质对电荷流得的阻碍作用的多少,便是电阻。
所以在一个固定的电压上,电路的电流愈强,它的电阻便愈少。所谓并联,即有分支的电路,当电荷流动时 多了一条分支(分路),电荷便更易流动,电流愈大,所以电阻便较小。
用一个比喻。一个运动场挤满了人,若只开一个小门,人的疏散便慢了,这样可看成小门对人的疏散(流动) 产生阻碍作用。但若开多一道门,人的疏散便快了。所以多一道门,疏散时阻碍作用减少,这便等于并联电路, 多一个分支,电阻便减少的性质相似。
所谓“等效”,是指在保持电路的效果不变的情况下,为简化电路分析,将复杂的电路或概念用简单电路或 已知概念来代替或转化,这种物理思想或分析方法称为“等效”变换。需要注意的是,“等效”概念只是应用于 电路的理论分析中,是电工教学中的一个概念,与真实电路中的“替换”概念不同,即“等效”仅是应用于理论 假设中,不是真实电路中的“替换”。“等效”的目的是为了在电路分析时,简化分析过程,易于理解的一种电 路分析手段。
电路理论中涉及到“等效”概念的知识点包括:电阻串并联等效变换、电阻星形联结和三角形联结等效变换, 两种电源模型的等效变换,非正弦周期量(电流和电压)与正弦量的等效等等。
谢谢观看
等效电路
等效电路又称“等值电路”。在同样给定条件下,可代替另一电路且对外性能不变的电路。电机、变压器等 电气设备的电磁过程可用其相应的等效电路来分析研究。
等效电路是将一个复杂的电路,通过电阻等效、电容等效,电源等效等方法,化简成具有与原电路功能相同 的简单电路。这个简单的电路,称作原复杂电路的等效电路。
等效电阻
电工术语
01 概念
目录
02 定理
03 分流和分压定理
04 性质
戴维南定理讲解

教学内容教师活动学生活动时间分配复习提问1、叠加原理的内容、解题布骤和注意事项?2、叠加原理适应的题型有哪些?戴维宁定理一、二端网络的有关概念1、二端网络:具有两个引出端与外电路相联的网络。
又叫做一端口网络。
2、无源二端网络:内部不含有电源的二端网络。
可用一个等效电阻来代替如图13、有源二端网络:内部含有电源的二端网络。
可等效为一个电压源图1二、戴维宁定理1、内容:任何一个线性有源二端电阻网络,对外电路来说,总可以用一个电压源E0与一个电阻r0相串联的模型来替代。
电压源的电动势E0等于该二端网络的开路电压,电阻r0等于该二端网络中所有电源不作用时(即令电压源短路、电流源开路)的等效电阻2、解题步骤:A 分B 求开路电压C 求等效电阻D 求待求量提问引导回答看书例题【例3-5】如图3-10所示电路,已知E 1 = 7 V ,E 2 = 6.2 V ,R 1 = R 2 = 0.2 Ω,R = 3.2 Ω,试应用戴维宁定理求电阻R 中的电流I 。
解:(1) 将R 所在支路开路去掉,如图3-11所示,求开路电压U ab :A 24.08.021211==+-=R R E E I ,U ab = E 2 + R 2I 1 = 6.2 + 0.4 = 6.6 V = E 0(2) 将电压源短路去掉,如图3-12所示,求等效电阻R ab :图3-12 求等效电阻R abR ab = R 1∥R 2 = 0.1 Ω = r 0(3)画出戴维宁等效电路,如图3-13所示,求电阻R 中的电流I : A 23.36.600==+=R r E I【例3-6】如图3-14所示的电路,已知E = 8 V ,R 1=3 Ω,R 2 = 5 Ω,R 3 = R4 = 4 Ω,R5 = 0.125 Ω,试应用戴维宁定理求电阻R 5中的电流I 。
解:(1) 将R 5所在支路开路去掉,如图3-15所示,求开路电压U ab :A 1 A 143432121=+===+==R R EI I R R E I I ,U ab = R 2I 2 -R 4I 4 = 5 - 4 = 1 V = E 0(2) 将电压源短路去掉,如图3-16所示,求等效电阻R ab :R ab = (R 1∥R 2) + (R 3∥R 4) = 1.875 + 2 = 3.875 Ω = r 0 (3) 根据戴维宁定理画出等效电路,如图3-17所示,求电阻R 5中的电流A 25.0415005==+=R r E I课堂练习 总结布置作业 1、2、节练习。
电阻电路等效变换

u31
i2
R1 R2
R1 R2 R3
R3 R1
u23
R1 R2
R3 R2 R3
R3 R1
u12
i3
R1 R2
R2 R2 R3
R3 R1
u31
R1 R2
R1 R2 R3
R3 R1
u23
18
对于电路
i12
u12 R12
i23
u23 R23
i1'
i31
Rsh 1k
14
当K与2相接时分流电阻为R2+R3 ,可测10mA的电流
Ig
I2
( R2
R2 R3 R3 ) (R1
Rg )
I2
R2 R3 Rsh Rg
10A 10m A R2 R3
Ig
RgIg
111.11 1000
R2+R3 =11 .11
R3
R2 R1
R1i1=R2i2 且 R4i4=R3i3
i1=i4 i2=i3
i1 R1 c
R4 i4
a
Ig
b
R2
R3
i2
d +
i3
则: R1 R2 或 R4 R3
根据平衡电桥的特点:
R1R3=R2R4
uS 电桥平衡条件
Ig =0,可将c、d间开路; ucd =0(等电位),可将c、d短路,最后计算的结果相同。
i3'
21
2)形等效为Y形,有:
R1
电阻电路的等效变换

R23
R31
R12 R3 R31 R2 R1 R2 R3
R12 R31 R1
R1
R12
R12 R31 R23
R31
已知电阻,求Y形电阻
R1
R12
R12 R31 R23
R31
R2
R12
R23 R12 R23
R31
R3
R12
R31 R23 R23
R31
请用文字概括以上三个公式
R31 i3/ 3
已知电阻,求Y形电阻
R1
R 12
R12R 31 R 23 R 31
R2
R 12
R 23R12 R 23 R 31
R3
R 12
R 31R 23 R 23 R 31
R1
R2
R3
RY
1 3
R
用电导表示时 已知Y电阻,求形电阻
R12
R1 R2
R2 R3 R3
R3 R1
R23
R1 R2
R2 R3 R1
Y形电阻两两乘积之和 Y形不相邻电阻
Y连接的三个电阻相等R1=R2=R3=RY时 已知Y电阻,求形电阻
R12
R1 R2
R2 R3 R3
R3 R1
R23
R1 R2
R2 R3 R1
R3 R1
R31
R1 R2
R2 R3 R2
R3 R1
R R12 R23 R31 3 RY
连接的三个电阻相等R12=R23=R31=R 时
并联 16 64 12.8
10
16 64
串联12.8 7.2 20
并联 20 30 12 20 30
例: 电路如图,求等效电阻 Rab 和 Rcd。
理想变压器等效电阻

理想变压器等效电阻
理想变压器(IdealTransformer)是一种模拟电路中非常重要的部分,其功能是将较
低电压转换为较高电压或从较高电压转换为较低电压,是一种强有力的电力工具。
另外,
原理上可以把理想变压器理解为一个电磁耦合器,它可以使两个相互使用的电路相互隔离,是电力电子系统中的中介。
由于理想变压器和普通的变压器有很大的不同,因此要建立其
电器特性曲线时,必须使用理想变压器的等效电阻(EquivalentResistance)。
理想变压器的等效电阻是指其在高频和低频的耦合的能量转换中的电流空间(CurrentSpace)交换度的度量,它可以用以下两个方程来定义:
其中,R:是理想变压器等效电阻;K:是理想变压器的耦合转移率;N1、N2:分别表
示理想变压器的原线圈、转换线圈的匝数;Z1、Z2:分别表示理想变压器原线圈和转换线
圈的阻抗。
从理想变压器等效电阻定义式可以知道,理想变压器的变换效率和等效电阻是密切相
关的,也就是说,对于理想变压器的变换效率的改善,必须使用具有较低的等效电阻,从
而获得较好的变压效果。
另外,从理想变压器中交流高频和低频信号可用衡量其等效电阻,而理想变压器等效电阻也可以用来确定理想变压器的耦合系数,从而评估其可靠性。
因此,理想变压器的等效电阻不仅影响变压器的变换效率,也影响其耦合系数以及可
靠性,因此,当选择理想变压器时,应该重视理想变压器的等效电阻,根据不同的应用场景,选择具有较低等效电阻的理想变压器,从而保证变压效果,实现良好的电力工程效果。
天线等效电阻 定义

天线等效电阻定义英文回答:Antenna Effective Resistance Definition.The antenna effective resistance, also known as the radiation resistance, is a measure of the power dissipated by the antenna due to radiation. It is defined as the ratio of the power radiated by the antenna to the square of the current flowing through the antenna terminals. Theeffective resistance is an important parameter for antenna design, as it determines the efficiency of the antenna. A higher effective resistance indicates that the antenna is more efficient at radiating power.The effective resistance of an antenna can be calculated using the following formula:R_e = P_r / I^2。
where:R_e is the effective resistance in ohms.P_r is the power radiated by the antenna in watts.I is the current flowing through the antenna terminals in amperes.The effective resistance of an antenna is affected by a number of factors, including the antenna's geometry, the frequency of the signal being radiated, and the surrounding environment. In general, antennas with larger surface areas have higher effective resistances. Antennas that are resonant at the frequency of the signal being radiated also have higher effective resistances. The presence of nearby objects can also affect the effective resistance of an antenna.中文回答:天线等效电阻定义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
根据欧姆定律:
U
U1
U2
R1
R2
I1
I2
R1=
R2=
R1+R2 =
I
R等效=
R等效
二、串联电路的等效电阻等于 各_串__联_(__分__)_电__阻__之_和__.
公式: R等效=R1+R2
两导体串联
+
=
串联导体相当于增长了导体的_______,所以串 联的等效电阻______任何一个串联导体的电阻。
分析:这是电路变换类型题,这种题的关键就是识别电路的连接方式,而后画出等效 电路图,再根据电路图计算。该题(1)中,S1闭合,S2断开,电路中只是R2和安培 表串联;(3)中S1、S2均闭合,R2和R3并联。在(1)和(3)中都要注意S1闭合时, R1被短路。
解答:(1)S1闭合、S2断开时,R1被短路,R3开路,电路只使用了R2 则U=IR2=0.3安培×20欧=6伏 (2)S1与S2均断开时,电路中R1与R2串联使用。
注:若有n个相同的电阻R0串联: R等效= n R0
小结
求助
例题:如图,电阻R1=3Ω,R2 =6Ω,
电源电压为12V,求R1、R2 两端的电压. 解:
12V
4V
R1=3Ω
8V
R2=6Ω
R1
R2
I
12V
R等效
两导体串联
两导体并联联
串联导体相当于增长了 导体的长度,所以串联 的等效电阻大于各串联 导体的电阻。
并联电路
电
U
I
路
U
I
I1 R1
U1
图
I1 R1 I2 R2
U1
U2
I2 R2 U2
分压电路
分流电路
电流 电压
I = I1 =I2 U =U1+U2
I =I1+I2 U =U1=U2
电阻
R =R1+R2 (R = nR0)
电压与电流 分配关系
U1 R1 分压,
=
与电阻
U2 R2 成正比
1/R =1/R1+1/R2(R=Ro/n)
2.并联导体的个数增多,等效电阻越__小___。
3.若n
个相同的电阻R并联,R等效=
R n
4.若2个电阻R1和R2并联,R等效=
R1 R1
R2 R2
3 等效电路
小结:
等效电阻:几个连接起来的电阻所起的作用, 可以用一个电阻来代替,这个电阻就是那些电 阻的等效电阻
串联电路的等效电阻等于各串联电阻之和 R等效=R1+R2
I1 R2 =
I2 R1
分流, 与电阻 成反比
例5. 如图所示的电路中,当滑动变阻器的滑片P向右滑动时,电流 表的示数将_变__小___;电压表V1的示数将_变_小_____;电压表V2的示 数将__变_大__。
分析:在电路发生变化时,只有电源电压和定值电阻保 持不变,通过电阻的电流和电阻两端的电压均可能发生 变化。推理的一般步骤是:从电路的变化部分开始,找 出总电阻的变化,再应用欧姆定律确定各部分电路的电 流和电压如何变化。
UR=U-UL=4V-2.5V=1.5V
方法2:灯正常发光时的电阻为 根据串联电路电压分配跟电阻成正比的特点,公式
需串联一个5Ω的电阻。
说明:最终结果所求的物理量要用具体数值表示,不能用分数表示。但在运算过 程中可用分数代入,这样一方面可便于计算,另一方面可避免多次舍取而造成的 数值偏差。
串联电路
1 1
R等效
R1
R2
练习:要求写出计算过程
1.求4欧和6欧两个电阻并联后等效电阻
2.求4欧、6欧、 8欧三个电阻并联后的的等效电阻
3.一个15欧的电阻和一个多大的电阻并联后的等效电阻是 3.5欧.
4.求5个20欧的电阻并联后的等效电阻,求10个20欧的电阻 并联后的等效电阻.
四个重要结论:
1.并联导体相当于增加了导体的__横_截__面_积_,所以并联 的等效电阻 小 于各并联导体的电阻。
思路分析:首先画出电路图,并在图中标出已知电路
的电流和电压的特点,利用欧姆定律的变形公式R U
即可求出R2的阻值。整个思路过程是:
I
解答:
例7. 如图所示,R1=10欧姆,R2=20欧姆,R3=30欧姆, 电源电压恒定不变。S1闭合,S2断开时安培表的读数为0.3安
培。问:
(1)电源的电压是多少? (2)当S1与S2均断开时,电流表的读数是多少? R1两端的电压是多少? (3)当S1与S2均闭合时,安培表的读数又是多少? 通过R3的电流强度是多少?
求助?
收音机中一个 10Ω的定值电阻 烧坏了,需要更 换,现身边只有 2Ω、3Ω、5Ω、 7Ω、8Ω、20Ω、 30Ω的电阻若干, 如何解决这一问 题。
小结
教科版初中九年级物理
第六章 欧姆定律
3 等效电路
讨论:
我们根据测量结果所计算的阻大小为15 Ω , 可是实际电路中却是两个电阻,这两个电阻和 15Ω的电阻有什么关系 ?互相讨论一下.
当P向右滑动时R2的取值变大,电路总电阻(R总 =R1+R2)变大,
R2两端的电压U2=U-U1,其中U不变,U1变小,
所以U2变大。
说明:R2两端的电压变化也可用串联分压原理得出,当R2变大时, R2两端分到的电压也变大。
例6. R1=12欧,将它与R2串联后接到8伏的电源上, 已知R2两端的电压 是2伏。求R2的阻值 。
猜想:
并联导体相当于增加了 导体的 横截面积 ,所以 并联的等效电阻 小 于各并联导体的电阻。
理性探究:并联电路的等效电阻
R1
I1
U1
U2
R2
I2
U
分析: 根据欧姆定律
I
根据并联电路的特点:
U U1 U2 I I1 I2
R等效
结论:并联电路的等效电阻的倒数等 于各支路电阻的倒数之和。
公式: 1
被纸覆盖的电路的 等效电路
等效电阻:
几个连接起来的电阻所起的作用,可 以用一个电阻来代替,这个电阻就是那些 电阻的等效电阻
S A
5Ω 15Ω10Ω
R’
R1 R R2
V
理性探究:串联电路的等效电路
猜想: 串联电路中 R等效=R1+R2
证明:
并联电路的等效电阻的倒数等于各支 路电阻的倒数之和
1 1 1 R等效 R 1 R2
例4. 一只小灯泡上标有“2.5V,0.3A”字样,即该灯泡在2.5V的电压下正常发 光时的 电流为0.3A。现在只有一个电压为4V的电源,为了使小灯泡正常发光,要串联一个多大 的电阻?
分析:串联的电阻R必须要分担1.5V的电压, 才能使小灯泡正常发光,其电路如图所示。 解答:方法1:根据串联电路电压关系得到
U1=IR1=0.2安×10欧=2伏 (3)S1与S2均闭合时,电路中R2与R3 并联使用。
