编译原理与实践 第四章 答案
编译原理第4章习题答案

S-> S’ S’->(S)SS’| First( (S)SS’) = { ( } Follow(S)=Follow(S’)= { (, ),$ }
预测分析表
非终结符 S ( S->S’ ) S->S’ $ S->S’
S’
S’->(S)SS’
S’->
S’->
S’->
冲突
仔细分析后,发现该文法 S->S(S)S| 是二义性文法。 二义性文法不可能是LL(1)文法。 例如:( ) ( )
S->aS’ S’->aS’AS’|Ɛ A->+|*
First(S) = First(aS’)={a} First(S’)= First(aS’AS’) ∪ First(Ɛ)= {a} ∪{Ɛ}= {a, Ɛ} First(A) = { +,*}
Follow(S) ={$} 因为 S->aS’,所以把Follow(S)加入到Follow(S’)中。 因为 S’->aS’AS’的第一个S’ ,所以把First(AS’)={+,*}加入到Follow(S’)中。 因为 S’->aS’AS’的第二个S’ ,所以Follow(S)加入到Follow(S’)中。 所以,Follow(S’)= {$, +,*} 对 S’->aS’AS’的A ,当A后面的S’推导出非空时,把First(S’)-{Ɛ}={a}加入到Follow(A)中。 对 S’->aS’AS’的A ,当A后面的S’推导出空时,把Follow(S’)={$,+,*}加入到Follow(A)中。 所以,Follow(A)= {a, +,*,$} 对于S’->aS’AS’|Ɛ,因为First(aS’AS’) ∩Follow(S’)={a} ∩{$,+,*}=空集,所以没有冲突。 对于A->+|*,因为First(+) ∩First(*)={+} ∩{*}=空集,所以没有冲突。 所以该文法是LL(1)文法。
编译原理龙书第四章答案

编译原理龙书第四章答案编译原理是计算机科学中的一门基础课程,是用于教授计算机程序的设计、构建和优化的学科,常常被用于编写编译器和解释器。
在编译原理课程中,龙书(Compilers: Principles, Techniques, and Tools)是一本经典的教材,其中第四章主要讲述了词法分析器的设计和实现。
以下是第四章的答案,按照列表划分:1. 什么是词法分析器?词法分析器(Lexical Analyzer)是编译器的组成部分之一,它用于将程序中的字符序列转换为一系列单词或词法单元(Lexeme),以便后续的语法分析和语义分析使用。
2. 词法分析器的工作流程是什么?词法分析器的工作流程如下:(1)读入字符序列。
(2)将字符序列划分为一个个词法单元,或者检查字符序列是否合法。
(3)生成一个词法单元序列,并将其传递给语法分析器。
3. 词法单元的定义是什么?词法单元是编程语言中的一个基本单元,它是对代码中的一个单一概念进行编码的基本方式。
例如,在C语言中,词法单元包括关键字(如int,if,while等)、标识符(Identifier,即自定义变量名)、运算符和特殊符号等。
4. 有哪些方法可以实现词法分析器?可以使用正则表达式、自动机等方法实现词法分析器。
其中,正则表达式可以表示字符串的集合,因此可以将其用于识别单词类别;自动机是根据输入字符序列转换状态的一种计算模型,因此可以用于实现有限自动机(Deterministic Finite Automaton)和非确定有限自动机(Nondeterministic Finite Automaton)等。
5. DFA和NFA分别是什么?DFA和NFA都是有限自动机的一种,但在转换动作上有所不同。
DFA 是确定的有限自动机,即在状态转换时只有唯一的一个选择;而NFA 是非确定的有限自动机,即在状态转换时可以有多个选择。
6. DFA和NFA之间有什么关系?DFA和NFA虽然在转换动作上不同,但它们可以互相转化。
编译原理第4章答案

第四章 词法分析1.构造下列正规式相应的DFA :(1) 1(0|1)*101(2) 1(1010*| 1(010)*1)*0 (3) a((a|b)*|ab *a)*b (4) b((ab)*| bb)*ab 解:(1)1(0|1)*101对应的NFA 为下表由子集法将NFA 转换为DFA :(2)1(1010*| 1(010)*1)*0对应的NFA 为 10,1下表由子集法将NFA转换为DFA:(3)a((a|b)*|ab *a)*b (略) (4)b((ab)*| bb)*ab (略)2.已知NFA=({x,y,z},{0,1},M,{x},{z})其中:M(x,0)={z},M(y,0)={x,y},M(z,0)={x,z},M(x,1)={x}, M(y,1)=φ,M(z,1)={y},构造相应的DFA 。
解:根据题意有NFA 图如下下表由子集法将NFA 转换为DFA :0,1下面将该DFA最小化:(1)首先将它的状态集分成两个子集:P1={A,D,E},P2={B,C,F}(2)区分P2:由于F(F,1)=F(C,1)=E,F(F,0)=F并且F(C,0)=C,所以F,C等价。
由于F(B,0)=F(C,0)=C,F(B,1)=D,F(C,1)=E,而D,E不等价(见下步),从而B与C,F可以区分。
有P21={C,F},P22={B}。
(3)区分P1:由于A,E输入0到终态,而D输入0不到终态,所以D与A,E可以区分,有P11={A,E},P12={D}。
(4)由于F(A,0)=B,F(E,0)=F,而B,F不等价,所以A,E可以区分。
(5)综上所述,DFA可以区分为P={{A},{B},{D},{E},{C,F}}。
所以最小化的DFA如下:3.将图确定化:1101111解:下表由子集法将NFA 转换为DFA :4.把图的(a)和(b)分别确定化和最小化:(a) (b)解: (a):下表由子集法将NFA 转换为DFA :0,1a可得图(a1),由于F(A,b)=F(B,b)=C,并且F(A,a)=F(B,a)=B,所以A,B 等价,可将DFA 最小化,即:删除B ,将原来引向B 的引线引向与其等价的状态A ,有图(a2)。
编译原理与实践第四章答案

The exercises of Chapter Four4.2Grammar: A → ( A ) A | εAssume we have lookahead of one token as in the example on p. 144 in the text book. Procedure A()if (LookAhead() ∈{‘(‘}) thenCall Expect(‘(‘)Call A()Call Expect (‘)’)Call A()elseif (LookAhead()∈{‘)‘, $}) thenreturn()else/* error */fifiend4.3 Given the grammarstatement→assign-stmt|call-stmt|otherassign-stmt→identifier:=expcall-stmt→identifier(exp-list)[Solution]First, convert the grammar into following forms:statement→identifier:=exp | identifier(exp-list)|otherThen, the pseudocode to parse this grammar:Procedure statementBeginCase token of( identifer : match(identifer);case token of( := : match(:=);exp;( (: match(();exp-list;match());else error;endcase(other: match(other);else error;endcase;end statement4.7 aGrammar: A → ( A ) A | εFirst(A)={(,ε } Follow(A)={$,)}4.7 bSee theorem on P.178 in the text book1.First{(}∩First{ε}=Φ2.ε∈Fist(A), First(A) ∩Follow(A)= Φboth conditions of the theorem are satisfied, hence grammar is LL(1)4.9 Consider the following grammar:lexp→atom|listatom→number|identifierlist→(lexp-seq)lexp-seq→lexp, lexp-seq|lexpa. Left factor this grammar.b. Construct First and Follow sets for the nonterminals of the resulting grammar.c. Show that the resulting grammar is LL(1).d. Construct the LL(1) parsing table for the resulting grammar.e. Show the actions of the corresponding LL(1) parser, given the input string (a,(b,(2)),(c)). [Solution]a.lexp→atom|listatom→number|identifierlist→(lexp-seq)lexp-seq→lexp lexp-seq’lexp-seq’→, lexp-seq|εb.First(lexp)={number, identifier, ( }First(atom)={number, identifier}First(list)={( }First(lexp-seq)={ number, identifier, ( }First(lexp-seq’)={, , ε}Follow(lexp)={, $, } }Follow(atom)= {, $, } }Follow(list)= {, $, } }Follow(lexp-seq)={$, } }Follow(lexp-seq’)={$,} }c. According to the defination of LL(1) grammar (Page 155), the resulting grammar is LL(1) as each table entry has at most one production as shown in (d).4.10 aLeft factored grammar:1. decl → type var-list2. type → int3. type → float4. var-list → identifier B5. B → , var-list6. B→ ε4.10 b4.10 c4.10 e4.12 a. Can an LL(1) grammar be ambigous? Why or Why not?b. Can an ambigous grammar be LL(1)? Why or Why not?c. Must an unambigous grammar be LL(1)? Why or Why not?[Solution]Defination of an ambiguous grammar: A grammar that generates a string with two distinct parse trees. (Page 116)Defination of an LL(1) grammar: A grammar is an LL(1) grammar if the associatied LL(1) parsing table has at most one priduction in each table entry.a.An LL(1) grammar can not be ambiguous, since the defination implies that an unambiguous parse canbe constructed using the LL(1) parsing tableb.An ambiguous grammar can not be LL(1) grammar, but can be convert to be ambiguous by usingdisambiguating rule.c.An unambiguous grammar may be not an LL(1) grammar, since some ambiuous grammar can beparsed using LL(K) table, where K>1.4.13Left recursive grammars can not be LL(1):Consider a grammar with a production A →A βwith symbol t in its first set. IF A is on the top of the stack and the current look-ahead token is t, A will be popped off the stack and then βwill be pushed onto the stack followed by A. A will again be the top of the stack and the look-ahead token will still be t, so it will repeat again, and again, infinitely, or until you get a stack overflow.Note: The first set for the recursive production will have a non-empty intersection with the first set for the terminating production, which will lead to a conflict when creating the LL(1) table.。
编译原理第四章 参考答案

1.1考虑下面文法G1S->a|^|(T)T->T,S|S消去G1的左递归。
然后对每个非终结符,写出不带回溯的递归子程序。
答::(1)消除左递归:S->a|^|(T)T-> ST’T’->,S T’|ε(2)first(S)={ a , ^ , ( } first(T)= { a , ^ , ( } first(T’)={ , ε}First(a)={a},First(^)={^},First( (T) )={ ( }S的所有候选的首符集不相交First(,ST’)={,} ,First(ε)={ε},T’的所有候选的首符集不相交Follow(T’)=Follow(T)={ )}first(T’)∩Follow(T’)={}所以改造后的文法为LL(1)文法。
不带回溯的递归子程序如下:S( ){if (lookahead=’a’) advance;Else if(lookahead=’^’) advance;Else if(lookahead=’(’){advance;T();if(lookahead=’)’) advance;else error();}Else error();}T( ){S( );T’( ):}T’->,S T’|εT’( ){if (lookahead=’,’){advance;T’();}Else if(lookahead=Follow(T’)) advance;Else error;}有文法G(S):S→S+aF|aF|+aFF→*aF|*a(1)改写文法为等价文法G[S’],消除文法的左递归和回溯(2)构造G[S’]相应的FIRST和FOLLOW集合;(3)构造G[S’]的预测分析表,以此说明它是否为LL(1)文法。
(4)如果是LL(1)文法,请给出句子a*a+a*a*a的预测分析过程该文法为LL(1)文法,因为它的预测分析表中无冲突项。
编译原理第四章答案

编译原理第四章答案1. 介绍编译原理是计算机科学中一门重要的课程,它涵盖了编译器设计与实现的基本知识和技术。
本文将针对编译原理第四章的问题进行详细解答。
第四章主要讨论了词法分析的相关内容,包括正则表达式和有限自动机。
2. 正则表达式正则表达式是一种表示字符串模式的方法。
它由一些字符和操作符组成,用于描述一类字符序列的模式。
正则表达式通常用于文本搜索、匹配和替换操作中。
2.1 正则表达式的基本操作符正则表达式的基本操作符包括字符、连接、选择和重复。
•字符:可以是单个字符,例如a、b、c。
•连接:用于连接两个正则表达式,例如ab表示在字符串中同时出现a和b。
•选择:用于在多个正则表达式中选择一个,例如a|b表示字符串中可以是a或者b。
•重复:用于指定某个正则表达式的重复次数,例如a*表示a可以出现任意次数(包括 0 次)。
2.2 正则表达式的语法正则表达式的语法规则如下:•字符:表示一个字符。
•.:表示任意字符。
•[]:表示字符集合,匹配括号内的任意一个字符。
•[^]:表示字符集合的补集,匹配除了括号内的字符之外的任意字符。
•-:表示范围,例如[a-z]匹配任意小写字母。
•*:表示重复零次或多次。
•+:表示重复一次或多次。
•?:表示重复零次或一次。
•():表示分组。
2.3 正则表达式的应用正则表达式在编译原理中的应用非常广泛。
在词法分析中,正则表达式可以用来描述编程语言中的单词(token)和它们的模式。
编译器可以使用正则表达式作为词法分析器的输入,用于将源代码分解为不同的单词。
3. 有限自动机有限自动机(Finite Automaton,FA)是一种用于描述正则语言的理论模型。
它是一种数学模型,包括有限个状态和状态之间的转移。
根据输入的字符,自动机会从一个状态转移到另一个状态。
3.1 有限自动机的组成有限自动机由以下几个部分组成:•有限个状态:每个状态表示自动机在某个时刻的状态。
•输入符号集合:表示自动机接受的输入字符集合。
编译原理第四章作业答案

非终结符
FIRSTVT
LASTVT
E
+ * ↑( i
+ * ↑) i
T
* ↑( i
* ↑) i
F
↑( i
↑)i
P
(i
)i
2).关系 1.由#E#,知 # = # ;由(E)知 ( = ) 2.求 < 关系 考察对象:文法中终结符号在前,非终结符号在后的相邻符号对 由#E # < FIRSTVT(E) 由+T + < FIRSTVT(T) 由*F * < FIRSTVT(F) 由↑F ↑< FIRSTVT(F) 由(E ( < FIRSTVT(E)
T→F
F→-P
F→P
P→(E)
P→i
(1) 构造 G 的算符优先矩阵;
(2) 指出 G 不是算符优先文法,即指出具有多重定义的优先矩阵元素;
(3)将 G 改写为算符优先文法。
解:
(1)求每个非终结符号的 FIRSTVT 集和 LASTVT 集
S→E
E→E-T|T
T→T*F|F
F→-P|P
P→(E)|i
Z 11 Z 12 Z 13
(S
A
B ) = (φ (S ) + () [S ] + [])Z 21
Z 22
Z
23
Z 31 Z 32 Z 33
Z 11 Z 12 Z 13 ε φ φ A B φ Z 11 Z 12 Z 13
Z 21
Z 22
Z
23
=
φ
ε
φ
+
ε
φ
φ
Z
21
Z 22
编译原理第4章习题解答

第4章习题解答:1,2,3,4 解答略!5. 解答:(1)× (2)√ (3)× (4)√ (5)√ (6)√(7)×(8)×6. 解答:(1)A:④ B:③ C:③ D:④ E:②(2)A:④ B:④ C:③ D:③ E:②7.解答:(1) 消除给定文法中的左递归,并提取公因子:bexpr→bterm {or bterm }bterm→bfactor {and bfactor}bfactor→not bfactor | (bexpr) | true |false(2) 用类C语言写出其递归分析程序:void bexpr();{bterm();WHILE(lookahead =='or') { match ('or');bterm();}}void bterm();{bfactor();WHILE(lookahead =='and'){ match ('and');bfactor();}} void bfactor();{if (llokahead=='not') then {match ('not');bfactor();}else if(lookahead=='(') then {match (‘(');bexpr();match(')');}else if(lookahead =='true')then match ('true) else if (lookahead=='false')then match ('false');else error;}8. 解答:消除所给文法的左递归,得G':S →(L)|aL → SL'L'→ ,SL' |实现预测分析器的不含递归调用的一种有效方法是使用一张分析表和一个栈进行联合控制,下面构造预测分析表:根据文法G'有:First(S) = { ( , a ) Follow(S) = { ) , , , #}First(L) = { ( , a ) Follow(L) = { ) }First(L') = { ,} Follow(L') = { ) }按以上结果,构造预测分析表M如下:文法G'是LL(1)的,因为它的LL(1)分析表不含多重定义入口。
编译原理(第三版)第4章课后练习及参考答案中石大版第4章课后练习及参考答案

第4章练习P72作业布置:P723,7,9,11提示1:判断两个正规式是否相等,应判断两个正规式所产生的正规集是否一样。
完成此项任务需要经过四个阶段:第一,画出正规式的NFA;第二,由NFA变换到DFA;第三,将DFA最小化;第四,画出最小化DFA的有限自动机。
如果要判断的正规式的最小化DFA的有限自动机是一样的,则正规式等价;反之,则不等价。
提示2:构造正规表达式的最小化的DFA方法是:首先,按规则将正规表达式用NFA表示;其次,使用ε-closure(Move())将NFA转变为DFA;最后使用子集法将DFA最小化。
对于这类题目要多做练习,熟能生巧。
3.将下图确定化:解:下表由子集法将NFA 转换为DFA :7、给文法G[S]: S →aA|bQ A →aA|bB|bB →bD|aQ0,10,1Q →aQ|bD|b D →bB|aA E →aB|bFF →bD|aE|b构造相应的最小的DFA 。
解:由于从S 出发任何输入串都不能到达状态E 和F ,所以,状态E ,F 为多余的状态,不予考虑。
这样,可以写出文法G[S]对应的NFA M :NFA M={k, Σ, f, S, Z}K={S, A, B, Q, D, Z} S={S} Z={Z} F(S, a)=A f(S, b)=Q F(A, a)=A f(A, b)=B f(A,b)=ZF(B, b)=D f(B, a)=QF(Q, a)=Q f(Q, b)=D f(Q,b)=Z F(D, b)=B f(D, a)=A NFA M 的状态转换图为:下表由子集法将NFA 转换为DFA :a由上表可知:(1)因为C、D是DFA的终态,其他是非终态,可将状态集分成两个子集:P1={S, A, B, E, F},P2={C, D}。
(2)因为{A, B}b={C, D}为终态,{S, E, F}b={B, E, F}为非终态,所以P1可划分为:P11={S, E, F},P12={A, B}。
编译原理第四章典型习题答案
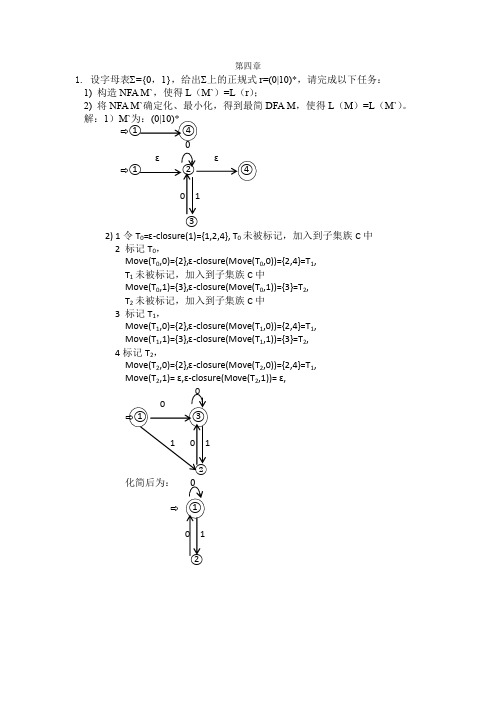
第四章1.设字母表∑={0,1},给出∑上的正规式r=(0|10)*,请完成以下任务:1) 构造NFA M`,使得L(M`)=L(r);2) 将NFA M`确定化、最小化,得到最简DFA M,使得L(M)=L(M`)。
解:1)M`③2) 1令T0=-closure(1)={1,2,4}, T0未被标记,加入到子集族C中2 标记T0,Move(T0,0)={2},-closure(Move(T0,0))={2,4}=T1,T1未被标记,加入到子集族C中Move(T0,1)={3},-closure(Move(T0,1))={3}=T2,T2未被标记,加入到子集族C中3 标记T1,Move(T1,0)={2},-closure(Move(T1,0))={2,4}=T1,Move(T1,1)={3},-closure(Move(T1,1))={3}=T2,4标记T2,Move(T2,0)={2},-closure(Move(T2,0))={2,4}=T1,Move(T2,1)=,-closure(Move(T2,1))=,化简后为:2.已知正规文法G1(S为开始符号)G1: S→0A|1BA→1S|1B→0S|01)该文法产生语言是什么?请用正规式表示;2)构造最简的确定有限自动机DFA,并画出状态转换图。
解:1)S=0A|1BS=(0(1S|1))|(1(0S|0))S=(01(S|))|(10(S|))S=(01|10)(S|)S=(01|10)(01|10)*2)NFA为:②③④ɛɛ①ɛ 1 0 ɛ⑤⑥⑦ɛNFA转化为DFA:1令T0=-closure(1)={1,2,5}, T0未被标记,加入到子集族C中2 标记T0,Move(T0,0)={3},-closure(Move(T0,0))={3}=T1,T1未被标记,加入到子集族C中Move(T0,1)={6},-closure(Move(T0,1))={6}=T2,T2未被标记,加入到子集族C中3 标记T1,Move(T1,0)=,-closure(Move(T1,0))=,Move(T1,1)={4},-closure(Move(T1,1))={4,8,9,10,13,17}=T3,T3未被标记,加入到子集族C中4标记T2,Move(T2,0)={7},-closure(Move(T2,0))={ 4,8,9,10,13,17}=T4,T4未被标记,加入到子集族C中Move(T2,1)=,-closure(Move(T2,1))=,5标记T3,Move(T3,0)={11},-closure(Move(T3,0))={11}=T5,T5未被标记,加入到子集族C中Move(T3,1)={14},-closure(Move(T3,1))={14}=T6,T6未被标记,加入到子集族C中6标记T4,Move(T4,0)={11},-closure(Move(T4,0))={11}=T5,Move(T4,1)={14},-closure(Move(T4,1))={14}=T6,7标记T5,Move(T5,0)=,-closure(Move(T5,0))=,Move(T5,1)={12},-closure(Move(T5,1))={9,10,12,13,16,17}=T7,T7未被标记,加入到子集族C中8标记T6,Move(T6,0)={15},-closure(Move(T6,0))={ 9,10,13,15,16,17}=T8,T8未被标记,加入到子集族C中Move(T6,1)=,-closure(Move(T6,1))=,9标记T7,Move(T7,0)={11},-closure(Move(T7,0))={11}=T5,Move(T7,1)={14},-closure(Move(T7,1))={14}=T6,10标记T8,Move(T8,0)={11},-closure(Move(T8,0))={11}=T5,Move(T8,1)={14},-closure(Move(T8,1))={14}=T6,则DFA为:②①1化简后为:②①13.将R=a(a|d)*转换成相应的正规文法。
编译原理第4章习题及答案(词法分析)

解:
4.8构造以下3型文法相应的最简自动机(“最简自动机”应该是“最简确定自动机”):
G:S → aS|bA|a
A → aS|bA|bB
B →bB | b
解:
a
b
Ia
Ib
-S
SZ
A
-S
SZ
A
A
S
AB
+SZ
SZ
A
B
BZ
A
S
AB
+Z
AB
S
ABZ
+ABZ
S
ABZ
4.9构造以下自动机相应的3型文法G:
(3)由正规式(1|…|9)(0|1|2|…|9)*构造的DFA3为:
(4)依题意构造的DFA4为:
(5)确定有限自动机与3型文法等价。而“a和b的个数相等的所有ab串”属上下文有关,需要1型文法描述,故确定有限自动机不能描述。
4.4构造下列正规式相应的NFA,然后转换为DFA:
(1)(a|b)*a(a|b|ε)
习题 第4章词法分析
4.1编写以下字符串集的正规式(若没有正规式则说明原因):
(1)以a开头和结尾的所有小写字母串;
(2)以a开头或/和结尾的所有小写字母串;
(3)不以0开头的所有数字串;
(4)每个5均在每个1之前的所有数字串;
(5)a和b的个数相等的所有ab串。
4.2简述由下列正规式生成的语言:
(1)(a|b)*a(a|b|ε)
4.5构造自动机A1和A2,使得
L(A1)={ε,an,ban|n≥1}
L(A2)={ε,(ab)n|n≥1}
4.6将下列NFA确定化:
4.7消除下列εDA的ε边:
编译原理 第4章习题解答

第四章习题解答4.1词法分析的主要任务是对源程序进行扫描,从中识别出单词,它是编译过程的第一步,也是编译过程中不可缺少的部分。
4.2单词符号一般分为五类:关键字、标识符、常数、运算符和界限符。
分别用整数1、2、3、4、5表示。
对于这种非一符一个类别码的编码形式,一个单词符号除了给出它的单词类别码之外,还要给出它的自身值。
标识符的自身值被表示成按字节划分的内部码。
常数的自身值是其二进制值。
由于语言中的关键字、运算符和界限符的数量都是确定的,因此,对这些单词符号可采用一符一个单词类别码。
如果采取一符一个单词类别码,那么这些单词符号的自身值就不必给出了。
4.3设计词法分析程序有如下几种方法:①由正规文法设计词法分析程序——程序设计语言的单词一般都可以用正规文法描述,从正规文法可构造一个FA。
再对FA确定化和状态个数最少化,最后得到一个化简了的DFA。
这个DFA正是词法分析程序的设计框图,这样,由DFA编制词法分析程序就容易了。
②由正规表达式设计词法分析程序——正规表达式也是描述单词的一种方便工具。
由正规表达式转换成NDFA,然后再对它确定化和状态个数最少化,可得一个DFA。
再由DFA编制词法分析程序。
4.4符号表在编译程序中具有十分重要的意义,它是编译程序中不可缺少的部分。
在编译程序中,符号表用来存放在程序中出现的各种标识符及其语义属性。
一个标识符包含了它全部的语义属性和特征。
标识符的全部属性不可能在编译程序的某一个阶段获得,而需要在它的各个阶段中去获得。
在编译程序的各个阶段,不仅要用获取的标识符信息去更新符号表中的内容,添加新的标识符及其属性,而且需要去查找符号表,引用符号表中的信息。
因为,符号表是编译程序进行各种语义检查(即语义分析)的依据,是进行地址分配的依据。
标识符处理的基本思想是,当遇到定义性标识符时,先去查符号表(标识符表)。
如果此标识符已在符号表中登记过,那么表明该标识符被多次声明,将作为一个错误,因为一个标识符只能被声明一次;如果标识符在符号表中未登记过,那么将构造此标识符的机内符,并在符号表中进行登记。
编译原理第四章答案

“编译技术”第四章作业4-1 已知文法G[C]:C→iEtS|iEtSeSE→ a|bS→ a+b|a*b(1)提取左公共因子;(2)计算修改后文法的每个非终结符的FIRST集和FOLLOW集;(3)给出递归下降分析程序。
(3)递归下降分析程序void match(token t){if(lookahead=='t')lookahead = nexttoken;else error;}void C(){if(lookahead=='i'){match('i');E();if(lookahead=='t'){match('t');S();Cprime();}else error;}else error;}void Cprime(){if(lookahead=='e'){match('e');S();}}void E(){if(lookahead=='a')match('a');else if(lookahead=='b')match('b');else error;}void S(){if(lookahead=='a'){match('a');Sprime();}}void Sprime(){if (lookahead=='+'){match('+');if(lookahed=='b'){match('b');}else error();}else if(lookahead=='*'){match('*');if(lookahead=='b'){match('b');}else error();}}4-2 已知文法G[Z]:Z→Az|bA→ Za|a(1)删除左递归;(2)计算修改后文法的每个非终结符的FIRST集和FOLLOW集;(3)给出递归下降分析程序。
编译原理课后习题答案-清华大学-第二版

《编译原理》课后习题答案第二章
第 2 章 PL/0 编译程序的实现
第1题
PL/0 语言允许过程嵌套定义和递归调用,试问它的编译程序如何解决运行时的存储管 理。
答案: PL/0 语言允许过程嵌套定义和递归调用,它的编译程序在运行时采用了栈式动态存储
管理。(数组 CODE 存放的只读目标程序,它在运行时不改变。)运行时的数据区 S 是由 解释程序定义的一维整型数组,解释执行时对数据空间 S 的管理遵循后进先出规则,当每 个过程(包括主程序)被调用时,才分配数据空间,退出过程时,则所分配的数据空间被释放。 应用动态链和静态链的方式分别解决递归调用和非局部变量的引用问题。
(2) 扩充 repeat 语句的语法图为:
EBNF 的语法描述为: 〈 重复语句〉::= repeat〈语句〉{;〈语句〉}until〈条件〉
《编译原理》课后习题答案第三章
第 3 章 文法和语言
第1题
文法 G=({A,B,S},{a,b,c},P,S)其中 P 为: S→Ac|aB A→ab B→bc 写出 L(G[S])的全部元素。
注意:如果问编译程序有哪些主要构成成分,只要回答六部分就可以。如果搞不清楚, 就回答八部分。 第3题
何谓翻译程序、编译程序和解释程序?它们三者之间有何种关系? 答案:
翻译程序是指将用某种语言编写的程序转换成另一种语言形式的程序的程序,如编译程 序和汇编程序等。
编译程序是把用高级语言编写的源程序转换(加工)成与之等价的另一种用低级语言编 写的目标程序的翻译程序。
地址,用以过程执行结束后返回调用过程时的下一条指令继续执行。 在每个过程被调用时在栈顶分配 3 个联系单元,用以存放 SL,DL, RA。
第5题
PL/0 编译程序所产生的目标代码是一种假想栈式计算机的汇编语言,请说明该汇编语 言中下列指令各自的功能和所完成的操作。 (1) INT 0 A (2) OPR 0 0 (3) CAL L A
编译原理第四章 习题解答
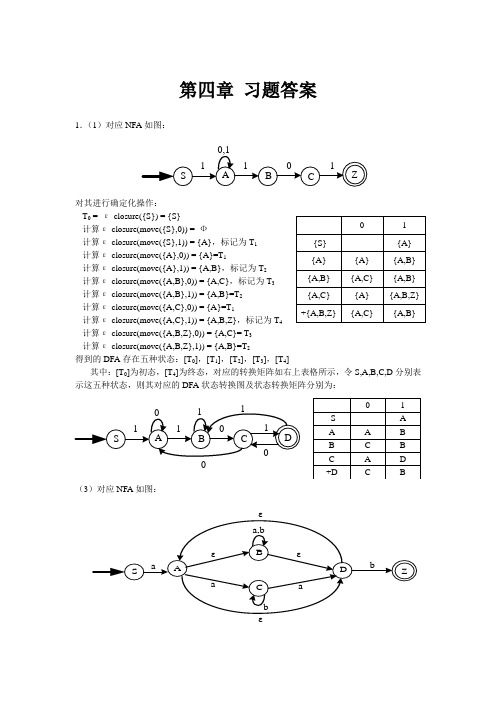
第四章 习题答案1.(1)对应NFA 如图:对其进行确定化操作:T 0 = ε-closure({S}) = {S}计算ε-closure(move({S},0)) = Ф计算ε-closure(move({S},1)) = {A},标记为T 1 计算ε-closure(move({A},0)) = {A}=T 1计算ε-closure(move({A},1)) = {A,B},标记为T 2计算ε-closure(move({A,B},0)) = {A,C},标记为T 3计算ε-closure(move({A,B},1)) = {A,B}=T 2 计算ε-closure(move({A,C},0)) = {A}=T 1计算ε-closure(move({A,C},1)) = {A,B,Z},标记为T 4 计算ε-closure(move({A,B,Z},0)) = {A,C}= T 3 计算ε-closure(move({A,B,Z},1)) = {A,B}=T 2得到的DFA 存在五种状态:[T 0],[T 1],[T 2],[T 3],[T 4]其中:[T 0]为初态,[T 4]为终态,对应的转换矩阵如右上表格所示,令S,A,B,C,D 分别表示这五种状态,则其对应的DFA 状态转换图及状态转换矩阵分别为:(3)对应NFA 如图:εT 0 = ε-closure({S}) = {S}计算ε-closure(move({S},a)) = {A,B,D},标记为T 1 计算ε-closure(move({S},b)) = Ф计算ε-closure(move({A,B,D},a)) = {A,B,C,D},标记为 计算ε-closure(move({A,B,D},b)) = {A,B,D,Z},标记为T 3 计算ε-closure(move({A,B,C,D},a)) = {A,B,C,D}= T 2计算ε-closure(move({A,B,C,D},b)) = {A,B,C,D,Z},标记为T 4 计算ε-closure(move({A,B,D,Z},a)) = {A,B,C,D}= T 2 计算ε-closure(move({A,B,D,Z},b)) = {A,B,D,Z}= T 3 计算ε-closure(move({A,B,C,D,Z},a)) = {A,B,C,D}= T 2 计算ε-closure(move({A,B,C,D,Z},b)) = {A,B,C,D,Z}= T 4 得到的DFA 存在五种状态:[T 0],[T 1],[T 2],[T 3],[T 4]其中:[T 0]为初态,[T 3],[T 4]为终态,对应的转换矩阵如左下表格所示,令S,A,B,C,D 分别2.根据题意,可以得其NFA 状态转换图如下图所示:T 0 = ε-closure({x}) = {x} 计算ε-closure(move({x},0)) = {z},标记为T 1 计算ε-closure(move({x},1)) = {x}=T 0 计算ε-closure(move({z},0)) = {x, z},标记为T 2 计算ε-closure(move({z},1)) = {y},标记为T 3 计算ε-closure(move({x, z},0)) = {x, z}= T 2 计算ε-closure(move({x, z},1)) = {x, y},标记为T 4 计算ε-closure(move({y},0)) = {x, y}= T 4 计算ε-closure(move({y},1)) = Ф计算ε-closure(move({x, y},0)) = {x, y, z},标记为T 5 计算ε-closure(move({x, y},1)) = {x}= T 0计算ε-closure(move({x, y, z},0)) = {x, y, z}= T 5 计算ε-closure(move({x, y, z},1)) = {x, y}= T 4得到的DFA 存在六种状态:[T 0],[T 1],[T 2],[T 3],[T 4],[T 5]其中:[T 0]为初态,[T 1],[T 2],[T 5]为终态,对应的转换矩阵如右上表格所示,令A,B,C,D,E,F 分别表示这六种状态,则其对应的DFA 状态转换图及状态转换矩阵分别为:3.状态转换图如图所示:对其进行确定化操作:T 0 = ε-closure({S}) = {S}计算ε-closure(move({S},0)) = {V ,Q},标记为T 1 计算ε-closure(move({S},1)) = {Q,U},标记为T 2 计算ε-closure(move({V ,Q},0)) = {V,Z},标记为T 3 计算ε-closure(move({V ,Q},1)) = {Q,U}= T 2计算ε-closure(move({Q,U},0)) = {V},标记为T 4计算ε-closure(move({Q,U},1)) = {Q,U,Z},标记为T 5 计算ε-closure(move({V,Z},0)) = {Z}= T 3 计算ε-closure(move({V,Z},1)) = {Z}= T 3计算ε-closure(move({V},0)) = {Z}=T 4 计算ε-closure(move({V},1)) = Ф计算ε-closure(move({Q,U,Z},0)) = {V ,Z},标记为T 6 计算ε-closure(move({Q,U,Z},1)) = {Q,U,Z}= T 5 计算ε-closure(move({Z},0)) = {Z}= T 6 计算ε-closure(move({Z},1)) = {Z}= T 3得到的DFA 存在七种状态:[T 0],[T 1],[T 2],[T 3],[T 4],[T 5],[T 5] 其中:[T 0]为初态,[T 3],[T 5],[T 6]为终态,对应的转换矩阵如右上表格所示,令A,B,C,D,E,F,G 分别表示这七种状态,则其对应的DFA 状态转换图及状态转换矩阵分别为:4.(a )对其进行确定化操作: T 0 = ε-closure({0}) = {0}计算ε-closure(move({0},a)) = {0,1},标记为T 1计算ε-closure(move({0},b)) = {1},标记为T 2计算ε-closure(move({0,1},a)) = {0,1}=T 1计算ε-closure(move({0,1},b)) = {1}= T 2计算ε-closure(move({1},a)) = {0}=T 0 计算ε-closure(move({1},b)) =Ф得到的DFA 存在三种状态:[T 0],[T1],[T 2]其中,[T 0]为初态,[T 0],[T 1]为终态,对应的转换矩阵如右上表格所示,令A,B,C 分别表示这三种状态,则其对应的DFA 状态转换图及状态转换矩阵如下:对其进行最小化操作:该DFA 无多余状态,进行初始划分,得终态组{A,B},非终态组{C}对终态组{A,B}进行审查,输入符号a 后,状态A,B 均转换成状态B ;输入符号b 后,状态A,B 均转换成状态C ,由此可知,状态A,B 等价,不能再分。
清华版编译原理课后答案——第四章参考答案

第四章参考答案 第1题:确定化: S AB CZ重新命名,令{AB}为B 、{AC}为C 、{ABZ}为Z 其中S 为初态,Z 为终态 (3)确定化: 0 1 2 34重新命名,以0、1、2、3、4代替{S},{A}, {AB},{AZ},{ABZ}得DFAa,b其中0为初态,3,4为终态第2题: A B C DE F重新命名,以A 、B、C、D、E、F代替{X},{Z },{XZ },{ Y },{ XY },{XYZ}得DFA 其中A 为初态,B,C,F为终态第3题: 确定化:ABC D E F G重新命名,以A 、B、C、D、E、F代替{S},{VQ },{QU },{ VZ },{ V },{QUZ},{Z}得DFA 其中A 为初态,D ,F ,G 为终态第4题: (1)A BC重新命名,以A、B、C代替{0}、{01}、{1}得DFA 其中A 为初态,A ,B 为终态初始分划得终态组{A,B},非终态组{C} Π0:{A,B},{C}对终态组进行审查,判断A 和B 是等价的,故这是最后的划分 重新命名,以A 、C 代替{A,B}、{C}得DFA(2)这是DFA ,直接最小化初始分划得:终态组{0},非终态组{1,2,3,4,5} Π0:{0},{1,2,3,4,5} 对{1,2,3,4,5}进行审查:∵{4} 输入a 后到达{0},{1,2,3,5}输入a 后到达{1,3,5},故得到新分划 {0,1,3,5},{4} Π1:{0},{4},{1,2,3,5} 对{1,2,3,5}进行审查:∵{1,5} 输入b 后到达{4},{2,3} 输入b 后到达{2,3},故得到新分划 {1, 5},{2,3} Π2:{0},{4},{1, 5},{2,3}对{1, 5},{2,3}进行审查:{1, 5} 输入a 后到达{1, 5}{2} 输入a 后到达{1},{3} 输入a 后到达{3},故得到新分划{2},{3}Π3:{0},{2},{3},{4},{1, 5}这是最后分划了重新命名,以0,2,3,4,1代替{0},{2},{3},{4},{1, 5}得DFA 略 第7题首先判断E ,F 为多余状态根据正则文法转化为NFA 的方法构造确定化: 0 1 2 34 5 6最小化:初始分划得:终态组{3,4},非终态组{0,1,2,5,6}Π0:{3,4},{0,1,2,5,6}对{0,1,2,5,6}进行审查: {1,2}输入b 到达{3,4},而{0,5,6}输入b 到达{2,5,6},故得到新分划{1,2},{0,5,6} Π1:{3,4},{1,2},{0,5,6} 对{0,5,6}进行审查:{0}经过b 到达{2},{5,6}经过b 到达{5,6},故得到新分划{0}{5,6} Π3:{0},{1,2},{3,4},{5,6}这是最后划分了。
编译原理第4章作业答案
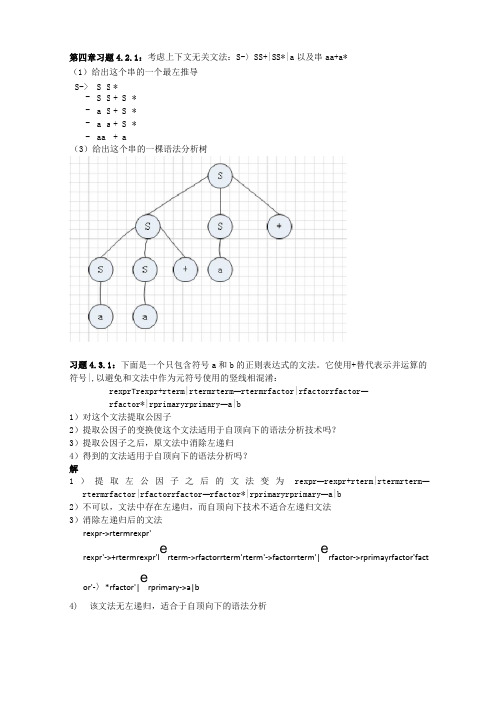
第四章习题4.2.1:考虑上下文无关文法:S-〉SS+|SS*|a 以及串aa+a* (1)给出这个串的一个最左推导 S-> S S *-> S S + S * -> a S + S * -> a a + S * -aa +a(3)给出这个串的一棵语法分析树习题4.3.1:下面是一个只包含符号a 和b 的正则表达式的文法。
它使用+替代表示并运算的符号|,以避免和文法中作为元符号使用的竖线相混淆:rexpr T rexpr+rterm|rtermrterm —rtermrfactor|rfactorrfactor —rfactor*|rprimaryrprimary —a|b1)对这个文法提取公因子2)提取公因子的变换使这个文法适用于自顶向下的语法分析技术吗? 3)提取公因子之后,原文法中消除左递归4)得到的文法适用于自顶向下的语法分析吗? 解1)提取左公因子之后的文法变为rexpr —rexpr+rterm|rtermrterm —rtermrfactor|rfactorrfactor —rfactor*|rprimaryrprimary —a|b 2)不可以,文法中存在左递归,而自顶向下技术不适合左递归文法 3)消除左递归后的文法rexpr->rtermrexpr'rexpr'->+rtermrexpr'l e rterm->rfactorrterm'rterm'->factorrterm'|erfactor->rprimayrfactor'fact or'-〉*rfactor'|erprimary->a|b4) 该文法无左递归,适合于自顶向下的语法分析习题4.4.1:为下面的每一个文法设计一个预测分析器,并给出预测分析表。
可能要先对文法进行提取左公因子或消除左递归 (3)S-〉S(S)S|*(5)S->(L)|aL->L,S|S 解 (3)①消除该文法的左递归后得到文法S-〉S'S'-〉(S)SS'|*②计算FIRST 和FOLLOW 集合FIRST(S)={(,*}FOLLOW(S)={),$} FIRST(S')={(,*}FOLLOW(S')={),$}③构建预测分析表①消除该文法的左递归得到文法S-〉(L)|a L->SL' L'-〉,SL'|£②计算FIRST 与FOLLOW 集合FIRST(S)={(,a}FOLLOW(S)={),,,$}FIRST(L)={(,a}FOLLOW(L)={)} FIRST(L')={,,£}FOLLOW(L')={)}习题4.4.4计算练习4.2.2的文法的FIRST 和FOLLOW 集合3)S T S(S)S|5) S T (L)|a,L T L,S|S 解:3)FIRST(S)={£,(}FOLLOW(S)={(,),$} 5) FIRST(S)={(,a}FOLLOW(S)={),,,$}FIRST (L )={(,a}FOLLOW (L )={),,}习题4.6.2为练习4.2.1中的增广文法构造SLR 项集,计算这些项集的GOTO 函数,给出这个文法的语法分析表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
The exercises of Chapter Four4、2Grammar: A → ( A ) A | εAssume we have lookahead of one token as in the example on p、144 in the text book、Procedure A()if (LookAhead() ∈{‘(‘}) thenCall Expect(‘(‘)Call A()Call Expect (‘)’)Call A()elseif (LookAhead()∈{‘)‘, $}) thenreturn()else/* error */fifiend4、3 Given the grammarstatement→assign-stmt|call-stmt|otherassign-stmt→identifier:=expcall-stmt→identifier(exp-list)[Solution]First, convert the grammar into following forms:statement→identifier:=exp | identifier(exp-list)|otherThen, the pseudocode to parse this grammar:Procedure statementBeginCase token of( identifer : match(identifer);case token of( := : match(:=);exp;( (: match(();exp-list;match());else error;endcase(other: match(other);else error;endcase;end statement4、7 aGrammar: A → ( A ) A | εFirst(A)={(,ε } Follow(A)={$,)}4、7 bSee theorem on P、178 in the text book1.First{(}∩First{ε}=Φ2.ε∈Fist(A), First(A) ∩Follow(A)= Φboth conditions of the theorem are satisfied, hence grammar is LL(1)4、9 Consider the following grammar:lexp→atom|listatom→number|identifierlist→(lexp-seq)lexp-seq→lexp, lexp-seq|lexpa、Left factor this grammar、b、Construct First and Follow sets for the nonterminals of the resulting grammar、c、Show that the resulting grammar is LL(1)、d、Construct the LL(1) parsing table for the resulting grammar、e、Show the actions of the corresponding LL(1) parser, given the input string (a,(b,(2)),(c))、[Solution]a、lexp→atom|listatom→number|identifierlist→(lexp-seq)lexp-seq→lexp lexp-seq’lexp-seq’→, lexp-seq|εb、First(lexp)={number, identifier, ( }First(atom)={number, identifier}First(list)={( }First(lexp-seq)={ number, identifier, ( }First(lexp-seq’)={, , ε}Follow(lexp)={, $, } }Follow(atom)= {, $, } }Follow(list)= {, $, } }Follow(lexp-seq)={$, } }Follow(lexp-seq’)={$,} }c、According to the defination of LL(1) grammar (Page 155), the resulting grammar is LL(1) as each table entry has at most one production as shown in (d)、de4、10 aLeft factored grammar:1、decl → type var-list2、type → int3、type → float4、var-list → identifier B5、B → , var-list6、B→ ε4、10 b4、10 cM[N, T] int float identifier , $decl 1 1type 2 3var-list 4B 5 6Parsing stack Input Action$ decl int x, y, z $ decl →type var-list $ var-list type int x, y, z $ type →int$ var-list int int x, y, z $ match int$ var-list x, y, z $ var-list →identifer B $ B identifier x, y, z $ match identifier w/ x $ B , y, z $ B →, var-list$ var-list , , y, z $ match ,$ var-list y, z $ var-list →identifer B $ B identifier y, z $ match identifier w/ y $ B , z $ B →, var-list$ var-list , , z $ match ,$ var-list z $ var-list →identifer B $ B identifier z $ match identifier w/ z4、12 a、Can an LL(1) grammar be ambigous? Why or Why not?b、Can an ambigous grammar be LL(1)? Why or Why not?c、Must an unambigous grammar be LL(1)? Why or Why not?[Solution]Defination of an ambiguous grammar: A grammar that generates a string with two distinct parse trees、(Page 116)Defination of an LL(1) grammar: A grammar is an LL(1) grammar if the associatied LL(1) parsing table has at most one priduction in each table entry、a.An LL(1) grammar can not be ambiguous, since the defination implies that an unambiguous parse canbe constructed using the LL(1) parsing tableb.An ambiguous grammar can not be LL(1) grammar, but can be convert to be ambiguous by usingdisambiguating rule、c.An unambiguous grammar may be not an LL(1) grammar, since some ambiuous grammar can beparsed using LL(K) table, where K>1、4、13Left recursive grammars can not be LL(1):Consider a grammar with a production A →A βwith symbol t in its first set、IF A is on the top of the stack and the current look-ahead token is t, A will be popped off the stack and then βwill be pushed onto the stack followed by A、A will again be the top of the stack and the look-ahead token will still be t, so it will repeat again, and again, infinitely, or until you get a stack overflow、Note: The first set for the recursive production will have a non-empty intersection with the first set for the terminating production, which will lead to a conflict when creating the LL(1) table、。
