一元二次不等式及其解法
一元二次不等式及其解法
返回目录
返回目录
学点 四
根的分布问题
关于x的方程x2+(m-2)x+5-m=0的两根
都大于2，求实数m的取值范围.
图3-2-1
【解析】
返回目录
返回目录
图3-2-2
【评析】二次方程根的分布问题多借助根的判别式、 韦达定理或者用数形结合法由二次函数图象求解.
返回目录
3.如何研究根的分布问题？ 实数k取何值时，含参数m的二次方程ax2+bx+c=0 （1）有实根、无实根、有两个相等实根. （2）有两正根、两负根，一正一负根. （3）有零根. （4）有两个大于k的根，有两个小于k的根，一根大 于k另一根小于k…的一般讨论方法通常考虑以下几个方 面:①求根公式.②判别式.③对称轴.④开口方向.⑤区间 端点处的函数值. 方法有三类：（一）判别式、韦达定理法；（二） 判别式、对称轴、构造函数法；（三）求根公式法. 以下几类是常见问题：（在a≠0条件下） （1）方程ax2+bx+c=0有实根，有两不等实根，无实 根.主要考虑判别式Δ和二次项系数a的符号. 返回目录
返回目录
m<-5或m>1， ≨ ≨1<m<19. 1<m<19，
综上1≤m<19. 【评析】（1）ax2+bx+c>0(a≠0)恒成立的条件为
a>0,
Δ<0.
（2）ax2+bx+c<0(a≠0)恒成立的条件为 a<0, Δ<0.
返回目录
不等式(a+1)x2+ax+a>m(x2+x+1)对任意x∈R恒成立，求 a与m之间的关系. 解：
一元二次不等式及其解法
一元二次不等式及其解法1. （1）解不等式：(x+4)(x-1)<0，{x|-4<x<1}（2）解不等式：2x 2-3x-2>0，{x|x<21,或x>2}（3）解不等式：-3x 2+6x>2 }331x 331|x {+<<-（4）解不等式：4x 2-4x+1>0 }21x |R x {≠∈解不等式：)x 4(x )1x 2x 2(42->+- 解：32x x 04x 12x 9212==⇒>+-∴原不等式的解集为}32x |R x {≠∈4．分式不等式 3．(1))()(x g x f >0⇔f (x )g(x )>0；(2))()(x g x f <0⇔f (x )g(x )<0；c有两相等实根(3))()(x g x f ≥0⇔⎩⎨⎧≠≥0)(0)()(x g x g x f ；(4))()(x g x f ≤0⇔⎩⎨⎧≠≤0)(0)()(x g x g x f17.（本小题满分6分）已知R U =， 且{}0162<-=x x A ， {}0342≥+-=x x x B ，求（1）A ∪B ； （2）)(A C U ∪)(B C U解：（1）A ∪B=R ；（2）（C U A ）∪（C U B ）={x ∣x ≤-4或1﹤x ﹤3或x ≥4}12. 当0<a 时，关于x 的不等式05422>--a ax x 的解集是BA ．{}a x a x x -<>或5|B ．{}a x a x x -><或5|C ．{}a x a x -<<5|D ．{}a x a x 5|<<-15．不等式2601x x x ---＞的解集为（C ） （A ）{}2,3x x x -＜或＞ （B ）{}213x x x -＜，或＜＜（C ） {}213x x x -＜＜，或＞ （D ）{}2113x x x -＜＜，或＜＜ 21.已知函数20()20x x f x x x +⎧=⎨-+>⎩，≤，，，则不等式2()f x x ≥的解集为（A ）A ．[]11-，B ．[]22-，C ．[]21-，D ．[]12-，10.设集合21{|2},{1}2A x xB x x =-<<=≤，则A B = （A ）（A ）{12}x x -≤< （B ）1{|1}2x x -<≤ （C ）{|2}x x < （D ）{|12}x x ≤<19.已知全集R U =，集合}0)1)(2(|{>-+=x x x A ，}01|{<≤-=x x B ，则)(B C A U 为(C) (A)}12|{>-<x x x 或 (B)}02|{≥-<x x x 或(C)}01|{≥-<x x x 或 (D)}11|{>-<x x x 或 2.若二次不等式ax 2+8ax+21＜0的解集为-7＜x ＜-1，则a 的值为(C)(A) 1 （B ）2 (C)3 (D) 4 5.不等式252(1)x x +-≥的解集是（D ）(A) 132⎡⎤-⎢⎥⎣⎦， (B) 132⎡⎤-⎢⎥⎣⎦， （C ）(]11132⎡⎫⎪⎢⎣⎭ ，， (D) (]11132⎡⎫-⎪⎢⎣⎭，，11.函数2log (2)y x =++的定义域为(D)(A) (,1)(3,)-∞-+∞ (B) (,1][3,)-∞-+∞ (C) (2,1]-- (D) (2,1][3,)--+∞ 2、（广东5月模拟）不等式(1)(2)0x x +->的解集为（C ） （A ）(,1)(2,)-∞-⋃+∞ （B ） (,2)(1,)-∞-⋃+∞ （C ）(1,2)- （D ） (2,1)- 2、（福建质检）不等式203x x ->+的解集是 （D ）（A ）(2,)+∞ （B ） [2,)+∞ （C ）(,3)-∞- （D ）(,3)(2,)-∞-⋃+∞4、已知不等式2364ax x -+>的解集为{|1}x x x b <>或.求,a b ； 答案：1,2a b ==5、若关于x 的不等式01x a x ->+的解集为(,1)(4,)-∞-⋃+∞，则实数4a =.3、（2010全国卷2理数）不等式2601x x x ---＞的解集为（C ）（A ）{}2,3x x x -＜或＞ （B ）{}213x x x -＜，或＜＜ （C ） {}213x x x -＜＜，或＞ （D ）{}2113x x x -＜＜，或＜＜例1 解不等式：3124x x -<-．误：去分母，得324x x -<-，即37x >，得73x >，∴原不等式的解集为7|3x x ⎧⎫>⎨⎬⎩⎭．析：因为分母正负未定，故不等式两边同乘以24x -后不等号方向直接就“定义”不变是不对的．应通过移项、通分解决．正：原不等式变形为3731002424x x x x ---<⇔<--(37)(24)02x x x ⇔-->⇔<或73x >．∴原不等式的解集为7|23x x x ⎧⎫<>⎨⎬⎩⎭，或．第21题. 对任意实数x ，不等式2(2)2(2)40a x a x ----<恒成立，则实数a 的取值范围是（ ） Ａ．(2)-，∞Ｂ．(]2-，∞Ｃ．(22)-，Ｄ．(]22-，答案：Ｄ．例2．已知关于x 的不等式20x mx n -+≤的解集是{|51}x x -≤≤，求实数,m n 之值．例3．已知不等式20ax bx c ++>的解集为{|23}x x <<求不等式20cx bx a -+>的解集．解：由题意 23230b ac a a ⎧+=-⎪⎪⎪⨯=⎨⎪<⎪⎪⎩， 即560b ac a a =-⎧⎪=⎨⎪<⎩．代入不等式20cx bx a -+>得：2650(0)ax ax a a ++=<．即26510x x ++<，∴所求不等式的解集为11{|}32x x -<<-．例4．已知一元二次不等式2(2)2(2)40m x m x -+-+>的解集为R ，求m 的取值范围．解：2(2)2(2)4y m x m x =-+-+为二次函数，2m ∴≠二次函数的值恒大于零，即2(2)2(2)40m x m x -+-+>的解集为R ． 200m ->⎧∴⎨∆<⎩， 即 224(2)16(2)0m m m >⎧⎨---<⎩，解得：226m m >⎧⎨<<⎩ m ∴的取值范围为{|26}m m <<例5．若函数y =中自变量x 的取值范围是一切实数，求k 的取值范围解：y =中自变量x 的取值范围是R ， ∴220x kx k ++≥恒成立．∴2440k k ∆=-≤ ∴01k ≤≤ 故k 的取值范围是{|01}k k ≤≤．例3 (课本第88页)解不等式0322>-+-x x . 解：整理，得0322<+-x x .因为032,02=+-<∆x x 方程无实数解，所以不等式0322<+-x x的解集是∅.从而，原不等式的解集是∅.8.在R 上定义运算⊙：a ⊙b a ab b ++=2，则满足x ⊙0)2(<-x 的实数x 的取值范围为B （A ）)2,0( （B ）)1,2(-（C ）),1()2,(+∞⋃--∞ （D ）)2,1(-【解析】依题意：x ⊙0)2(<-x (2)220x x x x ⇔-++-<，解得21x -<<。
一元二次不等式及解法
(1)a 0 a 4
1 （2）m m 且m 0 4
深化练习
(1)若对于x 1,3, mx mx 1 m 5
2
恒成立，求m的取值范围.
6 (1)m m 7
(2)已知不等式(m2＋4m－5)x2－4(m－1)x＋3＞0
延伸训练
解关于x的不等式 ax (a 1) x 1 0, (a R )
2
综上所述： 1 a＜－1 时，解集为{x|－1＜x＜ }； a a＝－1 时，原不等式无解； 1 －1＜a＜0 时， 解集为{x| ＜x＜－1}； a a＝0 时，解集为{x|x＜－1}； 1 a＞0 时，解集为{x|x＜－1 或 x＞ }． a
1 ， 3
(4)a, b均为负值;
a 3, b 2
考点二
解含参数的一元二次不等式
解关于x的不等式x 2 (a 1) x a 0, (a R)
( x 1)( x a) 0
当a 1时，解集为x a x 1 当a 1时，解集为 当a 1时，解集为x 1 x a 综上所述：
有参变量时，往往需要针对这个系数是否为0进行分类讨论，并且如果对应的一
元二次方程有两个不等的实根且根的表达式中又含有参数时，还要再次针对这 两根的大小进行分类讨论．
3．有关一元二次不等式的恒成立问题 此类问题关键提炼出问题有关于一元二次不等式的本质，对变量进行 分类讨论及借助数形结合等方法进行求解计算.
b 4ac
2
0
y
0
y
x1 x2
0
y
y ax bx c
2
x
x1
x2
一元二次不等式及其解法
2 1 ∴原不等式的解集为{x|－ ≤ x≤ }． 3 2 (2)∵ Δ＝(－ 4)2－ 4× 2× 7＝－ 40<0 ∴原不等式的解集为 Ø.
例2
1 1 已知不等式 ax ＋bx＋2>0 的解为－ <x< ， 2 3
2
求 2x2＋bx＋a<0 的解．
1 1 变式练习 2 已知不等式 ax ＋5x＋c>0 的解集为{x| <x< }， 3 2
2．不等式|x(x－2)|>x(x－2)的解集是(
)
A．(0,2)
C．(2，＋∞)
B．(－∞，0)
D．(－∞，0)∪(0，＋∞)
解析：不等式|x(x－2)|>x(x－2)的解集即x(x－2)<0的 解集，解得0<x<2，故选A. 答案：A
3．不等式－ 6x2－ x＋ 2≤ 0 的解集为( 2 1 A． {x|－ ≤ x≤ } 3 2 1 C． {x|x≥ } 2
2
1 1 故①当 0<a<1 时，(x－1)(x－ )<0⇔1<x< ； a a 1 ②当 a＝1 时，(x－1)(x－ )<0⇔(x－1)2<0⇔x∈Ø； a 1 1 ③当 a>1 时，(x－1)(x－ )<0⇔ <x<1. a a
1 综上所述：当 a<0 时，解集为{x|x< 或 x>1}；当 a a 1 ＝0 时， 解集为{x|x>1}； 当 0<a<1 时， 解集为{x|1<x< }； a 1 当 a＝1 时，解集为 Ø；当 a>1 时，解集为{x| <x<1}． a
)
2 1 B．{x|x≤－ 或 x≥ } 3 2 2 D． {x|x≤－ } 3
一元二次不等式及其解法
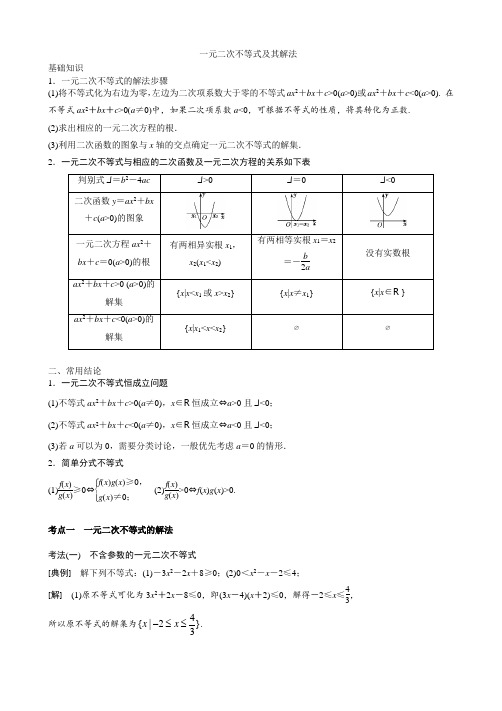
一元二次不等式及其解法基础知识1．一元二次不等式的解法步骤 (1)将不等式化为右边为零，左边为二次项系数大于零的不等式ax 2＋bx ＋c >0(a >0)或ax 2＋bx ＋c <0(a >0). 在不等式ax 2＋bx ＋c >0(a ≠0)中，如果二次项系数a <0，可根据不等式的性质，将其转化为正数. (2)求出相应的一元二次方程的根．(3)利用二次函数的图象与x 轴的交点确定一元二次不等式的解集． 2．一元二次不等式与相应的二次函数及一元二次方程的关系如下表二、常用结论1．一元二次不等式恒成立问题(1)不等式ax 2＋bx ＋c >0(a ≠0)，x ∈R 恒成立⇔a >0且Δ<0； (2)不等式ax 2＋bx ＋c <0(a ≠0)，x ∈R 恒成立⇔a <0且Δ<0； (3)若a 可以为0，需要分类讨论，一般优先考虑a ＝0的情形． 2．简单分式不等式(1)f (x )g (x )≥0⇔⎩⎪⎨⎪⎧f (x )g (x )≥0，g (x )≠0；(2)f (x )g (x )>0⇔f (x )g (x )>0. 考点一 一元二次不等式的解法 考法(一) 不含参数的一元二次不等式[典例] 解下列不等式：(1)－3x 2－2x ＋8≥0；(2)0＜x 2－x －2≤4；[解] (1)原不等式可化为3x 2＋2x －8≤0，即(3x －4)(x ＋2)≤0，解得－2≤x ≤43，所以原不等式的解集为}342|{≤≤-x x .(2)原不等式等价于⎩⎪⎨⎪⎧ x 2－x －2＞0，x 2－x －2≤4⇔⎩⎪⎨⎪⎧ x 2－x －2＞0，x 2－x －6≤0⇔⎩⎪⎨⎪⎧ (x －2)(x ＋1)＞0，(x －3)(x ＋2)≤0⇔⎩⎪⎨⎪⎧x ＞2或x ＜－1，－2≤x ≤3. 借助于数轴，如图所示，原不等式的解集为{}x |－2≤x ＜－1或2＜x ≤3. 考法(二) 含参数的一元二次不等式[典例] 解不等式ax 2－(a ＋1)x ＋1＜0(a ＞0)． [解] 原不等式变为(ax －1)(x －1)＜0， 因为a ＞0，所以a )1(ax -(x －1)＜0. 所以当a ＞1，即1a <1时，解为1a ＜x ＜1；当a ＝1时，解集为∅；当0＜a ＜1，即1a >1时，解为1＜x ＜1a.综上，当0＜a ＜1时，不等式的解集为}11|{ax x <<； 当a ＝1时，不等式的解集为∅； 当a ＞1时，不等式的解集为}11|{<<x ax . [题组训练]1．不等式(x ＋5)(3－2x )≥6的解集是( )A.}291|{≥-≤x x x 或 B.}291|{≤≤-x x C.}129|{≥-≤x x x 或D.}129|{≤≤-x x 解析：选D 不等式(x ＋5)(3－2x )≥6可化为2x 2＋7x －9≤0，所以(2x ＋9)(x －1)≤0，解得－92≤x ≤1.所以不等式(x ＋5)(3－2x )≥6的解集是}129|{≤≤-x x .故选D. 2．已知不等式ax 2－bx －1≥0的解集是]31,21[--，则不等式x 2－bx －a ＜0的解集是( )A ．(2,3)B ．(－∞，2)∪(3，＋∞) C.)21,31( D.)31,(-∞∪),21(+∞ 解析：选A 由题意知－12，－13是方程ax 2－bx －1＝0的两根，所以由根与系数的关系得⎩⎨⎧－12＋⎝⎛⎭⎫－13＝b a，－12×⎝⎛⎭⎫－13＝－1a .解得⎩⎪⎨⎪⎧a ＝－6，b ＝5，不等式x 2－bx －a ＜0即为x 2－5x ＋6＜0，解集为(2,3)．3．求不等式12x 2－ax >a 2(a ∈R )的解集．解：原不等式可化为12x 2－ax －a 2>0，即(4x ＋a )(3x －a )>0， 令(4x ＋a )(3x －a )＝0，解得x 1＝－a 4，x 2＝a3.当a >0时，不等式的解集为)4,(a--∞∪),3(+∞a ； 当a ＝0时，不等式的解集为(－∞，0)∪(0，＋∞)； 当a <0时，不等式的解集为)3,(a --∞∪),4(+∞-a. 考点二 一元二次不等式恒成立问题 考法(一) 在R 上的恒成立问题[典例] 若不等式(a －2)x 2＋2(a －2)x －4<0对一切x ∈R 恒成立，则实数a 的取值范围是( )A ．(－∞，2]B ．[)2,2(-C ．(－2,2]D ．(－∞，－2) [解析] 当a －2＝0，即a ＝2时，不等式为－4<0，对一切x ∈R 恒成立．当a ≠2时，则⎩⎪⎨⎪⎧ a －2<0，Δ＝4(a －2)2＋16(a －2)<0，即⎩⎪⎨⎪⎧a －2<0，a 2<4，解得－2<a <2. ∴实数a 的取值范围是(－2,2]． [答案] C解题技法] 一元二次不等式恒成立的条件(1)ax 2＋bx ＋c >0(a ≠0)恒成立的充要条件是⎩⎪⎨⎪⎧a >0，b 2－4ac <0.(2)ax 2＋bx ＋c <0(a ≠0)恒成立的充要条件是⎩⎪⎨⎪⎧a <0，b 2－4ac <0.考法(二) 在给定区间上的恒成立问题[典例] 若对任意的x ∈[)2,1(-，都有x 2－2x ＋a ≤0(a 为常数)，则a 的取值范围是( ) A ．(－∞，－3] B ．(－∞，0] C ．),1[+∞[ D DD D ．]1,(-∞(解析] 法一：令f (x )＝x 2－2x ＋a ，则由题意，得⎩⎪⎨⎪⎧f (－1)＝(－1)2－2×(－1)＋a ≤0，f (2)＝22－2×2＋a ≤0，解得a ≤－3，故选A.法二：当x ∈[)2,1(-]时，不等式x 2－2x ＋a ≤0恒成立等价于a ≤－x 2＋2x 恒成立，则由题意，得a ≤(－x 2＋2x )min (x ∈[)2,1(-])．而－x 2＋2x ＝－(x －1)2＋1，则当x ＝－1时，(－x 2＋2x )min ＝－3，所以a ≤－3，故选A. 答案] A [解题技法]一元二次不等式在给定区间上的恒成立问题的求解方法(1)若f (x )>0在集合A 中恒成立，即集合A 是不等式f (x )>0的解集的子集，可以先求解集，再由子集的含义求解参数的值(或范围)． (2)转化为函数值域问题，即已知函数f (x )的值域为[m ，n ]，则f (x )≥a 恒成立⇒f (x )min ≥a ，即m ≥a ；f (x )≤a 恒成立⇒f (x )max ≤a ，即n ≤a . 考法(三) 给定参数范围求x 范围的恒成立问题[典例] 求使不等式x 2＋(a －6)x ＋9－3a >0(|a |≤1)恒成立的x 的取值范围． 解] 将原不等式整理为形式上是关于a 的不等式(x －3)a ＋x 2－6x ＋9>0. 令f (a )＝(x －3)a ＋x 2－6x ＋9，因为f (a )>0在|a |≤1时恒成立，所以 (1)若x ＝3，则f (a )＝0，不符合题意，舍去．(2)若x ≠3，则由一次函数的单调性，可得⎩⎪⎨⎪⎧ f (－1)>0，f (1)>0，即⎩⎪⎨⎪⎧x 2－7x ＋12>0，x 2－5x ＋6>0，解得x <2或x >4，综上可知，使原不等式恒成立的x 的取值范围是(－∞，2)∪(4，＋∞)． [解题技法]给定参数范围求x 范围的恒成立问题的解法解决恒成立问题一定要清楚选谁为主元，谁是参数．一般情况下，知道谁的范围，就选谁当主元，求谁的范围，谁就是参数．即把变元与参数交换位置，构造以参数为变量的函数，根据原变量的取值范围列式求解． [题组训练]1．(2018·忻州第一中学模拟)已知关于x 的不等式x 2－4x ≥m 对任意x ∈(0,1]恒成立，则实数m 的取值范围为( )A ．(－∞，－3]B ．[－3，＋∞)C ．[－3,0)D ．[－4，＋∞)解析：选A x 2－4x ≥m 对任意x ∈(0,1]恒成立，令f (x )＝x 2－4x ，∵f (x )图象的对称轴为直线x ＝2，∴f (x )在(0,1]上单调递减，∴当x ＝1时，f (x )取到最小值，为－3，∴实数m 的取值范围是(－∞，－3]，故选A. 2．若不等式x 2＋mx －1<0对于任意x ∈[m ，m ＋1]都成立，则实数m 的取值范围是________．解析：由题意，得函数f (x )＝x 2＋mx －1在[m ，m ＋1]上的最大值小于0，又抛物线f (x )＝x 2＋mx －1开口向上，所以只需⎩⎪⎨⎪⎧ f (m )＝m 2＋m 2－1<0，f (m ＋1)＝(m ＋1)2＋m (m ＋1)－1<0，即⎩⎪⎨⎪⎧2m 2－1<0，2m 2＋3m <0，解得－22<m <0. 答案：)0,22(-3．不等式(a －3)x 2＜(4a －2)x 对a ∈(0,1)恒成立，则x 的取值范围是________．解析：由题意知(a －3)x 2＜(4a －2)x 对a ∈(0,1)恒成立等价于(x 2－4x )a －3x 2＋2x ＜0对a ∈(0,1)恒成立．令g (a )＝(x 2－4x )a －3x 2＋2x ，当x ＝0时，g (a )＝0，不满足题意．当x ≠0时，则⎩⎪⎨⎪⎧g (0)＝－3x 2＋2x ≤0，g (1)＝(x 2－4x )－3x 2＋2x ≤0，得x ≤－1或x ≥23.答案：(－∞，－1]∪),32[+∞ [课时跟踪检测]1．(2019·石家庄模拟)若集合A ＝{x |x 2－2x <0}，B ＝{x ||x |≤1}，则A ∩B ＝( )A ．[－1,0)B ．[－1,2)C ．(0,1]D ．[1,2)解析：选C 由x 2－2x <0得0<x <2，所以A ＝{x |0<x <2}，由|x |≤1得－1≤x ≤1，所以集合B ＝{x |－1≤x ≤1}，所以A ∩B ＝{x |0<x ≤1}，故选C. 2．不等式3x －1x －2≤0的解集为( )A.}231|{≤≤x x B.}312|{≤>x x x 或 C.}231|{<≤x x D ．{x |x <2} 解析：选C 不等式3x －1x －2≤0等价于(3x －1)(x －2)≤0，且x －2≠0，解得13≤x <2.故选C.3．不等式－3<4x －4x 2≤0的解集是( ) A.}231021|{<≤≤<-x x x 或 B ．{x |x ≤0或x ≥1} C.}2321|{<<-x x D.}2321|{≥-≤x x x 或 解析：选A 不等式可化为⎩⎪⎨⎪⎧4x (x －1)≥0，4x 2－4x －3<0，解得⎩⎪⎨⎪⎧x ≤0或x ≥1，－12<x <32，所以－12<x ≤0或1≤x <32.4．(2019·广州模拟)已知不等式ax 2－5x ＋b >0的解集为{x |－3<x <－2}，则不等式bx 2－5x ＋a >0的解集为( ) A.}3121|{-<<-x x B.}2131|{-<->x x x 或 C ．{x |－3<x <2} D ．{x |x <－3或x >2} 解析：选A 由题意得⎩⎨⎧5a＝－3－2，ba ＝－3×(－2)，解得a ＝－1，b ＝－6，所以不等式bx 2－5x ＋a >0为－6x 2－5x－1>0，即(3x ＋1)(2x ＋1)<0，所以解集为}3121|{-<<-x x ，故选A. 5．若关于x 的不等式x 2－ax －a ≤－3的解集不是空集，则实数a 的取值范围是( )A ．[]2,(-∞)B B ． (－∞，－6]]C ． ]2,6[-D ．(－∞，－6]∪[2，＋∞)解析：选D 由关于x 的不等式x 2－ax －a ≤－3的解集不是空集，得对应方程x 2－ax －a ＋3＝0有实数根，即Δ＝a 2＋4(a －3)≥0，解得a ≥2或a ≤－6，所以a 的取值范围是 (－∞，－6]∪[2，＋∞)．故选D.6．某商场若将进货单价为8元的商品按每件10元出售，每天可销售100件，现准备采用提高售价来增加利润．已知这种商品每件销售价提高1元，销售量就要减少10件．那么要保证每天所赚的利润在320元以上，销售价每件应定为( )A ．12元B ．16元C ．12元到16元之间D ．10元到14元之间解析：选C 设销售价定为每件x 元，利润为y ，则y ＝(x －8)[100－10(x －10)]， 依题意有，(x －8)[100－10(x －10)]＞320，即x 2－28x ＋192＜0，解得12＜x ＜16， 所以每件销售价应为12元到16元之间．7．存在x ∈[－1,1]，使得x 2＋mx －3m ≥0，则m 的最大值为( )A ．1 B.14 C.12D ．－1解析：选C 若对于任意x ∈[－1,1]，不等式x 2＋mx －3m <0恒成立，则由函数f (x )＝x 2＋mx －3m 的图象可知⎩⎪⎨⎪⎧f (－1)＝1－m －3m <0，f (1)＝1＋m －3m <0，解得m >12.所以若存在x ∈[－1,1]，使得x 2＋mx －3m ≥0，则m ≤12，所以m的最大值为12.故选C.8．(2018·北京东城区期末)设不等式x 2－2ax ＋a ＋2≤0的解集为A ，若A ⊆]3,1[，则a 的取值范围为( )A.]511,1(- B.)511,1( C.)511,2( D ．[)3,1( 解析：选A 设f (x )＝x 2－2ax ＋a ＋2，因为不等式x 2－2ax ＋a ＋2≤0的解集为A ，且A ⊆[]3,1[]， 所以对于方程x 2－2ax ＋a ＋2＝0，若A ＝∅，则Δ＝4a 2－4(a ＋2)<0，即a 2－a －2<0，解得－1<a <2；若A ≠∅，则⎩⎪⎨⎪⎧Δ＝4a 2－4(a ＋2)≥0，f (1)≥0，f (3)≥0，1≤a ≤3，即⎩⎪⎨⎪⎧a ≥2或a ≤－1，a ≤3，a ≤115，1≤a ≤3，所以2≤a ≤115.综上，a 的取值范围为]511,1(-，故选A. 9．不等式|x (x －2)|>x (x －2)的解集是________．解析：不等式|x (x －2)|>x (x －2)的解集即x (x －2)<0的解集，解得0<x <2，故不等式的解集为{x |0<x <2}． 答案：{x |0<x <2}10．若a <0，则关于x 的不等式组⎩⎪⎨⎪⎧ax －a 2<0，x 2－ax －2a 2<0的解集为________． 解析：因为a <0，所以由ax －a 2＝a (x －a )<0，得x >a ，由x 2－ax －2a 2＝(x －2a )(x ＋a )<0，得2a <x <－a .所以原不等式组的解集为(a ，－a )． 答案：(a ，－a )11．若关于x 的不等式5x 2－a ≤0的正整数解是1,2,3，则实数a 的取值范围是________．解析：关于x 的不等式5x 2－a ≤0的正整数解是1,2,3，所以a >0，解不等式得x 2≤a5，所以－a5≤x ≤ a5，所以3≤ a 5<4，所以9≤a5<16，即45≤a <80， 所以实数a 的取值范围是[45,80)． 答案：[45,80)12．不等式a 2＋8b 2≥λb (a ＋b )对于任意的a ，b ∈R 恒成立，则实数λ的取值范围为________．解析：因为a 2＋8b 2≥λb (a ＋b )对于任意的a ，b ∈R 恒成立，所以a 2＋8b 2－λb (a ＋b )≥0恒成立，即a 2－λba ＋(8－λ)b 2≥0恒成立，由二次不等式的性质可得Δ＝λ2b 2＋4(λ－8)b 2＝b 2(λ2＋4λ－32)≤0，所以(λ＋8)(λ－4)≤0，解得－8≤λ≤4. 答案：[－8,4]13．已知函数f (x )＝ax 2＋2ax ＋1的定义域为R . (1)求a 的取值范围； (2)若函数f (x )的最小值为22，解关于x 的不等式x 2－x －a 2－a <0. 解：(1)因为函数f (x )＝ax 2＋2ax ＋1的定义域为R ，所以ax 2＋2ax ＋1≥0恒成立， 当a ＝0时，1≥0恒成立．当a ≠0时，则有⎩⎪⎨⎪⎧a >0，Δ＝(2a )2－4a ≤0，解得0<a ≤1，综上可知，a 的取值范围是[0,1]． (2)因为f (x )＝ax 2＋2ax ＋1＝a (x ＋1)2＋1－a ，因为a >0，所以当x ＝－1时，f (x )min ＝1－a ，由题意得，1－a ＝22，所以a ＝12， 所以不等式x 2－x －a 2－a <0可化为x 2－x －34<0.解得－12<x <32，所以不等式的解集为)23,21(-。
一元二次不等式及其解法
∵ 32 4 2 2 7 0
∴方程 2x 2 3x 2 0 无实数根 ∴原不等式的解集为 R.
习题 1: 解下列不等式: （1） x 2 5x 6 0 ;
（2） x 2 7x 6 ;
x 2 6x 10 0
（3） 2 xx 3 0 ;
;
当 a 1 ,即 a 1或0 a 1 时,原不等式的解集为 x a x 1 .
原不等式可化为 x 22 0 或 x 22 0 ,所以原不等式的解集为 x x 2或 x x 2;
当 0 ,即 4 a 4 时 方程 x 2 ax 4 0 无实数根,所以原不等式的解集为 R.
例 7. 解不等式 m2 1x 2 4x 1≥0 m R.
第1页
（2）一元二次不等式 ax 2 bx c 0 （≤0）的解集就是二次函数 y ax 2 bx c 0a 0
的图象位于 x 轴下方（包括 x 轴）的部分所对应的自变量的取值范围.
表（1）一元二次方程、二次函数以及一元二次不等式的关系:
判别式 b 2 4ac
解:∵ m 2 ≥0 ∴m2 1 0
42 4m2 1 12 4m2
当 0 ,即
一元二次不等式及其解法
2021年新高考数学总复习第七章《不等式》一元二次不等式及其解法一元二次不等式的解集判别式Δ＝b2－4ac Δ>0Δ＝0Δ<0二次函数y＝ax2＋bx＋c(a>0)的图象方程ax2＋bx＋c＝0 (a>0)的根有两相异实根x1，x2(x1<x2)有两相等实根x1＝x2＝－b2a没有实数根ax2＋bx＋c>0(a>0)的解集{x|x<x1或x>x2}⎩⎨⎧⎭⎬⎫x⎪⎪x≠－b2a{x|x∈R} ax2＋bx＋c<0(a>0)的解集{x|x1< x<x2} ∅∅概念方法微思考1．一元二次不等式ax2＋bx＋c>0(a>0)的解集与其对应的函数y＝ax2＋bx＋c的图象有什么关系？提示ax2＋bx＋c>0(a>0)的解集就是其对应函数y＝ax2＋bx＋c的图象在x轴上方的部分所对应的x的取值范围．2．一元二次不等式ax2＋bx＋c>0(<0)恒成立的条件是什么？提示显然a≠0.ax2＋bx＋c>0恒成立的条件是⎩⎪⎨⎪⎧a>0，Δ<0；ax2＋bx＋c<0恒成立的条件是⎩⎪⎨⎪⎧a<0，Δ<0.题组一思考辨析1．判断下列结论是否正确(请在括号中打“√”或“×”)(1)若不等式ax 2＋bx ＋c <0的解集为(x 1，x 2)，则必有a >0.( √ )(2)若不等式ax 2＋bx ＋c >0的解集是(－∞，x 1)∪(x 2，＋∞)，则方程ax 2＋bx ＋c ＝0的两个根是x 1和x 2.( √ )(3)若方程ax 2＋bx ＋c ＝0(a ≠0)没有实数根，则不等式ax 2＋bx ＋c >0的解集为R .( × ) (4)不等式ax 2＋bx ＋c ≤0在R 上恒成立的条件是a <0且Δ＝b 2－4ac ≤0.( × )(5)若二次函数y ＝ax 2＋bx ＋c 的图象开口向下，则不等式ax 2＋bx ＋c <0的解集一定不是空集．( √ )题组二 教材改编2．已知集合A ＝{x |x 2－x －6>0}，则∁R A 等于( )A ．{x |－2<x <3}B ．{x |－2≤x ≤3}C ．{x |x <－2}∪{x |x >3}D ．{x |x ≤－2}∪{x |x ≥3}答案 B解析 ∵x 2－x －6>0，∴(x ＋2)(x －3)>0，∴x >3或x <－2，即A ＝{x |x >3或x <－2}．在数轴上表示出集合A ，如图所示．由图可得∁R A ＝{x |－2≤x ≤3}．故选B.3． y ＝log 2(3x 2－2x －2)的定义域是________________．答案 ⎝ ⎛⎭⎪⎫－∞，1－73∪⎝ ⎛⎭⎪⎫1＋73，＋∞ 解析 由题意，得3x 2－2x －2>0，令3x 2－2x －2＝0，得x 1＝1－73，x 2＝1＋73， ∴3x 2－2x －2>0的解集为⎝ ⎛⎭⎪⎫－∞，1－73∪⎝ ⎛⎭⎪⎫1＋73，＋∞. 题组三 易错自纠4．不等式－x 2－3x ＋4>0的解集为________．(用区间表示)答案 (－4，1)。
一元二次不等式及其解法
反思与感悟
解析答案
方法二
当x∈[1,3]时，f(x)<－m＋5恒成立，
即当x∈[1,3]时，m(x2－x＋1)－6<0恒成立.
1 3 2 2 ∵x －x＋1＝x－2 ＋4>0，
6 又 m(x －x＋1)－6<0，∴m< 2 . x －x＋1
当 a＞0
1 ； x | － ＜ x ＜ 1 时，原不等式的解集是 a
当a＝－1时，原不等式的解集是{x|x≠1}；
当－1＜a＜0
当 a＜－1
1 时，原不等式的解集是x|x＜1或x＞－a .
1 . x | x ＜－ 或 x ＞ 1 时，原不等式的解集是 a
反思与感悟
跟踪训练2
解关于x的不等式x2－(a＋a2)x＋a3＞0.
解
原不等式可化为
(x－a)(x－a2)＞0
讨论a与a2的大小
(1)当a2＞a即a＞1或a＜0时，
x＞a2或x＜a.
(2)当a2＝a即a＝0或a＝1时，
x≠a.
解析答案
(3)当a2＜a即0＜a＜1时， x＞a或x＜a2. 综上，当a＜0或a＞1时，解集为{x|x＞a2或x＜a}， 当a＝0或1时，解集为{x|x≠a}， 当0＜a＜1时，解集为{x|x＞a或x＜a2}.
当a＝0时，x＜1；
当 a＞0
1 ∴－a＜x＜1；
当a＝－1时，x≠1；
当－1＜a＜0
1 时，x＋a(x－1)＞0，
1 ∴x＞－a或 x＜1；
反思与感悟 解析答案
一元二次不等式及其解法-一元二次不等式解集
一元二次不等式也可以通过因式分解或配方法转换为 (x - x1)(x - x2) ≥ 0 或 (x - x1)(x - x2) ≤ 0 的形式，其中 x1 和 x2 是方程 ax^2 + bx + c = 0 的根。
02 一元二次不等式的解法
配方法
总结词
通过配方将一元二次不等式转化为完全平方形式，从而求解。
05 一元二次不等式的扩展
一元高次不等式
一元高次不等式是指形如 ax^n > b (n ≥ 2) 的不等式，其中 a、b 是常数 且 a ≠ 0。
解一元高次不等式时需要注意不等式 的符号和临界点，确保解集的准确性。
解一元高次不等式需要利用因式分解、 不等式的性质以及数轴等方法，逐步 化简不等式，最终得到解集。
二元一次不等式组的解集可以通过平 面区域来表示，通过确定临界点和约 束条件来确定区域的边界。
一元二次不等式的解集可以通过抛物 线的开口方向和顶点坐标来表示，一 元高次不等式的解集可以通过相应函 数的图像来表示。
利用几何意义可以更加直观地理解不 等式的解集，有助于解决复杂的不等 式问题。
THANKS FOR WATCHING
函数分析
通过一元二次不等式，可以对一元二次函数进行全面的分析，包括函数的单调性、极值点、零点等。
在物理领域的应用
力学问题
在解决物理中的力学问题时，常常需要用到 一元二次不等式。例如，在解决碰撞、落体 等问题时，可以通过一元二次不等式来描述 物理量的变化范围。
波动问题
在研究波动问题时，如声波、电磁波等，一 元二次不等式可以用来描述波的传播范围以 及某些物理量的变化范围。
因式分解法
总结词
通过因式分解将一元二次不等式转化为 两个一次不等式的乘积形式，从而求解 。
一元二次不等式及解法
的图像。 画出函数 y = x − x − 6 的图像。
2
注意画二次函数简图的一般过程 y -2 3 x
当x=-2或x=3时，y x=x=3时
＝ ＞
0，即x2 -x-6 ＝ 0。 0，即x2 -x-6 ＞ 0
当x＜-2或x＞3时，y 当-2＜x＜3时，y
＜
0，即x2 -x-6 ＜ 0
方程ax 方程 2＋bx＋c=0（a≠0）；不等式 ＋ （ ax2＋bx＋c <0或ax2＋bx＋c >0 （a≠0） ；与函 ＋ 或 ＋ ） 数y= ax2＋bx＋c （a≠0）的图象有什么关系？ ＋ ）的图象有什么关系？
一、复习一元 一、复习一元二次方程 一元二次方程
一元二次方程:ax 一元二次方程 2+bx+c=0(a≠0) 二次方程
∆ > 0 方程有两个不等的根
∆ = 0 方程有一个根
∆ < 0 方程没有根
求根的方法： 1）公式法 X= 求根的方法： ） （
b 2 4ac − b =0 （2）配方法，化为顶点式 a( x + ) − ）配方法， 2a 4a
1 方程4x 4x＋ =0的解是 解:因为△ =0,方程4x2－4x＋1 =0的解是 x1 = x2 = , △ =0,方程 2 1 所以, 所以,原不等式的解集是 x | x ≠
2
4x＋ 4x2－4x＋1＜0
无解
四、应用举例
4.解不等式－ 2x－ 4.解不等式－x2 ＋2x－3＞0 解不等式 略解:－ 2x－ 略解 －x2＋2x－3＞0 2x+3＜ x2-2x+3＜0 无解 2x+3＞ x2 -2x+3＞0
四、应用举例
2.解不等式－ 6x＞ 2.解不等式－3x2＋6x＞2 解不等式 略解: 6x＞ 略解 －3x2＋6x＞2 6x＋ 3x2－6x＋2＜0
一元二次不等式及其解法
7．2一元二次不等式及其解法1．解不等式的有关理论(1)若两个不等式的解集相同，则称它们是；(2)一个不等式变形为另一个不等式时，若两个不等式是同解不等式，这种变形称为不等式的；(3)解不等式变形时应进行同解变形；解不等式的结果，一般用集合表示．2．一元一次不等式解法任何一个一元一次不等式经过不等式的同解变形后，都可以化为ax＞b(a≠0)的形式．当a＞0时，解集为；当a＜0时，解集为．若关于x的不等式ax>b的解集是R，则实数a，b满足的条件是．3．一元二次不等式及其解法(1)我们把只含有一个未知数，并且未知数的最高次数是2的不等式，称为__________不等式．(2)使某个一元二次不等式成立的x的值叫做这个一元二次不等式的解，一元二次不等式所有的解组成的集合叫做一元二次不等式的________．(3)若一元二次不等式经过同解变形后，化为一元二次不等式ax2＋bx＋c＞0(或ax2＋bx＋c＜0)(其中a＞0)的形式，其对应的方程ax2＋bx＋c＝0有两个不相等的实根x1，x2，且x1＜x2(此时Δ＝b2－4ac＞0)，则可根据“大于号取__________，小于号取__________”求解集．4.分式不等式解法(1)化分式不等式为标准型．方法：移项，通分，右边化为0，左边化为f （x ）g （x ）的形式．(2)将分式不等式转化为整式不等式求解，如：f （x ）g （x ）＞0 ⇔ f (x )g (x )＞0； f （x ）g （x ）＜0 ⇔ f (x )g (x )＜0； f （x ）g （x ）≥0 ⇔ ⎩⎪⎨⎪⎧f （x ）g （x ）≥0，g （x ）≠0； f （x ）g （x ）≤0 ⇔ ⎩⎪⎨⎪⎧f （x ）g （x ）≤0，g （x ）≠0. 自查自纠1．(1)同解不等式 (2)同解变形2.⎩⎨⎧⎭⎬⎫x |x ＞b a ⎩⎨⎧⎭⎬⎫x |x ＜b a a ＝0，b ＜0 3．(1)一元二次 (2)解集 (3)两边 中间(4)①{}x |x ＜x 1或x ＞x 2 ②⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠－b 2a ③∅(2016·宜昌模拟)设集合A ＝{x |x 2＋x －6≤0}，集合B 为函数y ＝1x －1的定义域，则A ∩B 等于( ) A ．(1，2) B ．[1，2] C ．[1，2) D ．(1，2]解：A ＝{x |x 2＋x －6≤0}＝{x |－3≤x ≤2}，由x －1>0得x >1，即B ＝{x |x >1}，所以A ∩B ＝{x |1<x ≤2}．故选D .(2016·梧州模拟)不等式2x ＋1<1的解集是( )A ．(－∞，－1)∪(1，＋∞)B ．(1，＋∞)C ．(－∞，－1)D ．(－1，1)解：因为2x ＋1<1，所以2x ＋1－1<0，即1－x x ＋1<0，该不等式可化为(x ＋1)(x －1)>0，所以x <－1或x >1.故选A .(2016·青海模拟)不等式(a －2)x 2＋2(a －2)x －4<0，对一切x ∈R 恒成立，则实数a 的取值范围是( ) A ．(－∞，2] B ．(－2，2]C ．(－2，2)D ．(－∞，2)解：当a ≠2时，有⎩⎪⎨⎪⎧a －2＜0，Δ＜0， 所以－2<a <2.当a ＝2时，原式化为－4<0，恒成立．所以－2<a ≤2.故选B .(2015·广东)不等式－x 2－3x ＋4>0的解集为________．(用区间表示) 解：由－x 2－3x ＋4＞0得x 2＋3x －4＜0，解得－4＜x ＜1.故填(－4，1)．(北京市2017届普通高中会考)如果关于x 的不等式x 2<ax ＋b 的解集是{x |1<x <3}，那么b a 等于________． 解：不等式x 2<ax ＋b 的解集是{x |1<x <3}，则1，3是方程x 2－ax －b ＝0的两根，由根与系数的关系，得a ＝1＋3＝4，－b ＝1×3＝3，b ＝－3，所以b a ＝81.故填81.类型一 一元二次不等式的解法(1)解下列不等式： (Ⅰ)x 2－7x ＋12＞0； (Ⅱ)x 2－2x ＋1＜0.解：(Ⅰ)方程x 2－7x ＋12＝0的解为x 1＝3，x 2＝4.而y ＝x 2－7x ＋12的图象开口向上，可得原不等式x 2－7x ＋12＞0的解集是{x |x ＜3或x ＞4}． (Ⅱ)方程x 2－2x ＋1＝0有两个相同的解x 1＝x 2＝1.而y ＝x 2－2x ＋1的图象开口向上，可得原不等式x 2－2x ＋1＜0的解集为∅.(2)解关于 x 的不等式 kx 2－2x ＋k ＜0(k ∈R )． 解：①当 k ＝0 时，不等式的解为 x ＞0.②当 k ＞0 时，若Δ＝4－4k 2＞0，即 0＜k ＜1 时，不等式的解为1－1－k 2k ＜x ＜1＋1－k 2k；若Δ≤0，即 k ≥1 时，不等式无解． ③当 k ＜0 时，若Δ＝4－4k 2＞0，即－1＜k ＜0时，x ＜1＋1－k 2k 或x ＞1－1－k 2k；若Δ＜0，即 k ＜－1 时，不等式的解集为 R ； 若Δ＝0，即 k ＝－1 时，不等式的解为 x ≠－1. 综上所述，当k ≥1 时，不等式的解集为∅；当0＜k ＜1 时，不等式的解集为⎩⎨⎧⎭⎬⎫x |1－1－k 2k ＜x ＜1＋1－k 2k ； 当k ＝0 时，不等式的解集为{x |x ＞0}； 当－1＜k ＜0时，不等式的解集为⎩⎨⎧⎭⎬⎫x |x ＜1＋1－k 2k 或x ＞1－1－k 2k ； 当k ＝－1时，不等式的解集为{x |x ≠－1}； 当k ＜－1时，不等式的解集为R .【点拨】解一元二次不等式的步骤：(1)将二次项系数化为正数；(2)解相应的一元二次方程；(3)根据一元二次方程的根，结合不等号的方向画图；(4)写出不等式的解集．容易出现的错误有：①未将二次项系数化正，对应错标准形式；②解方程出错；③结果未按要求写成集合．解含参数的有理不等式时分以下几种情况讨论：①根据二次项系数讨论(大于 0，小于 0，等于 0)；②根据根的判别式讨论(Δ>0，Δ＝0，Δ<0)；③根据根的大小讨论(x 1>x 2，x 1＝x 2，x 1<x 2)．(1)解下列不等式：(Ⅰ)－x 2－2x ＋3≥0； (Ⅱ)x 2－2x ＋2＞0.解：(Ⅰ)不等式两边同乘以－1，原不等式可化为x 2＋2x －3≤0. 方程x 2＋2x －3＝0的解为x 1＝－3，x 2＝1.而y ＝x 2＋2x －3的图象开口向上，可得原不等式－x 2－2x ＋3≥0的解集是{x |－3≤x ≤1}．(Ⅱ)因为Δ＜0，所以方程x 2－2x ＋2＝0无实数解，而y ＝x 2－2x ＋2的图象开口向上，可得原不等式x 2－2x ＋2＞0的解集为R .(2)(2015·贵州模拟)关于x 的不等式x 2－(a ＋1)x ＋a <0的解集中，恰有3个整数，则实数a 的取值范围是________． 解：原不等式可化为(x －1)(x －a )<0，当a >1时，得1<x <a ，此时解集中的整数为2，3，4，则4<a ≤5；当a <1时，得a <x <1，此时解集中的整数为－2，－1，0.则－3≤a <－2，故a ∈[－3，－2)∪(4，5]．故填[－3，－2)∪(4，5]．类型二 二次不等式、二次函数及二次方程的关系(1)(2015·贵州模拟)已知不等式ax 2＋bx ＋2>0的解集为{x |－1<x <2}，则不等式2x 2＋bx ＋a <0的解集为( )A.⎩⎨⎧⎭⎬⎫x |x <－1或x >12 B.⎩⎨⎧⎭⎬⎫x |－1<x <12C.{x |－2<x <1} D ．{x |x <－2或x >1}解：由题意知x ＝－1，x ＝2是方程ax 2＋bx ＋2＝0的两根，且a ＜0.由韦达定理得⎩⎨⎧－1＋2＝－ba ，（－1）×2＝2a⇒⎩⎪⎨⎪⎧a ＝－1，b ＝1.所以不等式2x 2＋bx ＋a <0，即2x 2＋x －1<0.解得－1＜x ＜12.故选B .【点拨】已知一元二次不等式的解集，就能够得到相应的一元二次方程的两根，由根与系数的关系，可以求出相应的系数．注意结合不等式解集的形式判断二次项系数的正负．(2)若方程2ax 2－x －1＝0在(0，1)内有且仅有一解，则a 的取值范围是( ) A ．(－∞，－1) B ．(1，＋∞) C ．(－1，1) D ．[0，1)解法一：令f (x )＝2ax 2－x －1，则f (0)·f (1)＜0，即－1×(2a －2)＜0，解得a ＞1.解法二：当a ＝0时，x ＝－1，不合题意，故排除C ，D ；当a ＝－2时，方程可化为4x 2＋x ＋1＝0，而Δ＝1－16＜0，无实根，故a ＝－2不适合，排除A.故选B .【点拨】本题考查一元二次方程的根的分布与系数的关系，画出相应函数的图象后“看图说话”，主要从以下四个方面分析：①开口方向；②判别式；③区间端点函数值的正负；④对称轴x ＝－b2a 与区间端点的关系．本书2.4节有较详细的讨论，可参看．(1)已知不等式ax 2－3x ＋6>4的解集为{x |x <1或x >b }．(Ⅰ)求a ，b ；(Ⅱ)解不等式ax 2－(ac ＋b )x ＋bc <0.解：(Ⅰ)因为不等式ax 2－3x ＋6>4的解集为{x |x <1或x >b }，所以x 1＝1与x 2＝b 是方程ax 2－3x ＋2＝0的两个实数根，且b >1.由根与系数的关系，得⎩⎨⎧1＋b ＝3a ，1×b ＝2a.解得⎩⎪⎨⎪⎧a ＝1，b ＝2. (Ⅱ)不等式ax 2－(ac ＋b )x ＋bc <0， 即x 2－(2＋c )x ＋2c <0，即(x －2)(x －c )<0. ①当c >2时，不等式的解集为{x |2<x <c }； ②当c <2时，不等式的解集为{x |c <x <2}； ③当c ＝2时，不等式的解集为∅.(2)(2015·贵州模拟)已知二次函数f (x )＝ax 2－(a ＋2)x ＋1(a ∈Z )，且函数f (x )在(－2，－1)上恰有一个零点，则不等式f (x )>1的解集为________． 解：根据题意有f (－2)f (－1)<0，所以(6a ＋5)(2a ＋3)<0.所以－32<a <－56.又a ∈Z ，所以a ＝－1.检验知合要求． 不等式f (x )>1即为－x 2－x ＋1>1，解得－1<x <0. 故填{x|－1＜x ＜0}．类型三 分式不等式的解法(1)不等式1x<1的解集为________．解：1x <1⇔1x －1<0⇔1－x x <0⇔x －1x >0，解得x <0，或x >1.故填(－∞，0)∪(1，＋∞)．(2)若集合A ＝{x |－1≤2x ＋1≤3}，B ＝⎩⎨⎧⎭⎬⎫x |x －2x ≤0，则A ∩B ＝( )A ．{x |－1≤x ＜0}B ．{x |0＜x ≤1}C ．{x |0≤x ≤2}D ．{x |0≤x ≤1}解：易知A ＝{x |－1≤x ≤1}，B 集合就是不等式组⎩⎪⎨⎪⎧x （x －2）≤0，x ≠0 的解集，求出B ＝{}x |0＜x ≤2，所以A ∩B＝{x |0＜x ≤1}．故选B .【点拨】首先通过“移项、通分”，将不等式右边化为0，左边化为f （x ）g （x ）的形式，将原分式不等式化为标准型，然后将化为标准型的分式不等式等价转化为整式不等式(组)来求解，注意分母不为0.(1)不等式x －12x ＋1≤1的解集为________．解：x －12x ＋1≤1 ⇔ x －12x ＋1－1≤0 ⇔ －x －22x ＋1≤0 ⇔ x ＋22x ＋1≥0.解法一：x ＋22x ＋1≥0 ⇔⎩⎪⎨⎪⎧（x ＋2）（2x ＋1）≥0，2x ＋1≠0.得⎩⎨⎧⎭⎬⎫x |x ＞－12或x ≤－2. 解法二：x ＋22x ＋1≥0 ⇔⎩⎪⎨⎪⎧x ＋2≥0，2x ＋1＞0 或 ⎩⎪⎨⎪⎧x ＋2≤0，2x ＋1＜0.得⎩⎨⎧⎭⎬⎫x |x ＞－12或x ≤－2.故填⎩⎨⎧⎭⎬⎫x|x ＞－12或x ≤－2.(2)(2016·丽水模拟)已知两个集合A ＝{x |y ＝ln(－x 2＋x ＋2)}，B ＝⎩⎨⎧⎭⎬⎫x |2x ＋1e －x ≤0，则A ∩B ＝( ) A.⎣⎡⎭⎫－12，2 B.⎝⎛⎦⎤－1，－12 C ．(－1，e) D ．(2，e)解：由题意得A ＝{x |－x 2＋x ＋2>0}＝{x |－1<x <2}，B ＝⎩⎨⎧⎭⎬⎫x |x >e 或x ≤－12，故A ∩B ＝⎝⎛⎦⎤－1，－12.故选B . 类型四 和一元二次不等式有关的恒成立问题(1)若不等式x 2＋ax ＋1≥0对于一切x ∈⎝⎛⎦⎤0，12成立，则实数a 的最小值为( ) A ．0 B ．－2 C ．－52 D ．－3解法一：不等式可化为ax ≥－x 2－1，由于x ∈⎝⎛⎦⎤0，12， 所以a ≥－⎝⎛⎭⎫x ＋1x .因为f (x )＝x ＋1x 在⎝⎛⎦⎤0，12上是减函数， 所以⎝⎛⎭⎫－x －1x max＝－52.所以a ≥－52.解法二：令f (x )＝x 2＋ax ＋1，对称轴为x ＝－a2.①⎩⎪⎨⎪⎧－a 2≤0，f （0）≥0⇒a ≥0.(如图1) ②⎩⎨⎧0＜－a 2＜12，f ⎝⎛⎭⎫－a 2≥0⇒－1＜a ＜0.(如图2)③⎩⎨⎧－a 2≥12，f ⎝⎛⎭⎫12≥0⇒－52≤a ≤－1.(如图3)图1图2图3综上 ①②③，a ≥－52.故选C .(2)已知对于任意的a ∈[－1，1]，函数f (x )＝x 2＋(a －4)x ＋4－2a 的值总大于0，则x 的取值范围是( ) A ．{x |1＜x ＜3} B ．{x |x ＜1或x ＞3} C ．{x |1＜x ＜2} D ．{x |x ＜1或x ＞2}解：记g (a )＝(x －2)a ＋x 2－4x ＋4，a ∈[－1，1]，依题意，只须⎩⎪⎨⎪⎧g （1）＞0，g （－1）＞0⇒⎩⎪⎨⎪⎧x 2－3x ＋2＞0，x 2－5x ＋6＞0⇒x ＜1或x ＞3，故选B .【点拨】(1)一元二次不等式恒成立问题，对于x 变化的情形，解法一利用参变量分离法，化成a ＞f (x )(a ＜f (x ))型恒成立问题，再利用a ＞f (x )max (a ＜f (x )min )，求出参数范围．解法二化归为二次函数，由于是轴动区间定，结合二次函数对称轴与定义域的位置关系、单调性等相关知识，求出参数范围．(2)对于参数变化的情形，大多利用参变量转换法，即参数转换为变量；变量转换为参数，把关于x 的二次不等式转换为关于a 的一次不等式，化繁为简，然后再利用一次函数的单调性，求出x 的取值范围．(3)解决恒成立问题一定要搞清谁是主元，谁是参数，一般地，知道谁的范围，谁就是主元，求谁的范围，谁就是参数．(1)(2016·南昌模拟)对于任意实数x ，不等式mx 2＋mx －1<0恒成立，则实数m 的取值范围是( )A ．(－∞，－4)B ．(－∞，－4]C ．(－4，0)D ．(－4，0] 解：当m ＝0时，不等式显然成立；当m ≠0时，由⎩⎪⎨⎪⎧m ＜0，Δ＝m 2＋4m <0 得－4<m <0. 综上所述，所求实数m 的取值范围是(－4，0]．故选D .(2)对于满足|a |≤2的所有实数a ，使不等式x 2＋ax ＋1＞2x ＋a 成立的x 的取值范围为________．解：原不等式转化为(x －1)a ＋x 2－2x ＋1＞0，设f (a )＝(x －1)a ＋x 2－2x ＋1，则f (a )在[－2，2]上恒大于0，故有：⎩⎪⎨⎪⎧f （－2）＞0，f （2）＞0 即⎩⎪⎨⎪⎧x 2－4x ＋3＞0，x 2－1＞0 解得⎩⎪⎨⎪⎧x ＞3或x ＜1，x ＞1或x ＜－1. 所以x ＜－1或x ＞3.故填(－∞，－1)∪(3，＋∞)．1．一元二次不等式ax 2＋bx ＋c ＞0(或ax 2＋bx ＋c ＜0)(a ≠0)的解集的确定，受二次项系数a 的符号及判别式Δ＝b 2－4ac 的符号制约，且与相应的二次函数、一元二次方程有密切联系，可结合相应的函数y ＝ax 2＋bx ＋c (a ≠0)的图象，数形结合求得不等式的解集；二次函数y ＝ax 2＋bx ＋c 的值恒大于0的条件是a ＞0且Δ＜0；若恒大于或等于0，则a ＞0且Δ≤0.若二次项系数中含参数且未指明该函数是二次函数时，必须考虑二次项系数为0这一特殊情形．2．解分式不等式要使一边为零；求解非严格分式不等式时，要注意分母不等于0，转化为不等式组.()注：形如f （x ）g （x ）≥0或f （x ）g （x ）≤0的不等式称为非严格分式不等式3．解含参数的不等式的基本途径是分类讨论，能避免讨论的应设法避免讨论．对字母参数的逻辑划分要具体问题具体分析，必须注意分类不重、不漏、完全、准确．4．解不等式的过程，实质上是不等式等价转化的过程．因此保持同解变形是解不等式应遵循的基本原则． 5．各类不等式最后一般都要化为一元一次不等式(组)或一元二次不等式(组)来解，这体现了转化与化归的数学思想．6．对给定的一元二次不等式，求解的程序框图是：1．不等式x 2－x －2≤0的解集是( ) A ．(－∞，－1)∪(－1，2] B ．[－1，2] C ．(－∞，－1)∪[2，＋∞) D ．(－1，2]解：原不等式⇔(x ＋1)(x －2)≤0，即x ∈[－1，2]，故选B .2．设集合A ＝⎩⎨⎧⎭⎬⎫x |x －1x ＋1≤0，B ＝{x ||x |≤1}，则“x ∈A ”是“x ∈B ”的( ) A ．充要条件 B ．必要不充分条件 C ．充分不必要条件 D ．既不充分也不必要条件解：A ＝{x |－1<x ≤1}，B ＝{x |－1≤x ≤1}，则A 是B 的真子集．故选C .3．(四川省广元市2017届适应性统考(三诊))已知集合A ＝{x |x 2－4x ＜0}，B ＝{x |x ＜a }，若A ⊆B ，则实数a 的取值范围是( )A ．(0，4]B ．(－∞，4)C ．[4，＋∞)D ．(4，＋∞)解：集合A ＝{x |x 2－4x ＜0}＝(0，4)，B ＝{x |x ＜a }＝(－∞，a )，若A ⊆B ，则实数a 满足a ≥4.故选C . 4．(2015·湖北模拟)不等式f (x )＝ax 2－x －c >0的解集为{x |－2<x <1}，则函数y ＝f (－x )的图象为( )解：由题意得⎩⎨⎧－2＋1＝1a，－2×1＝－c a ，解得⎩⎪⎨⎪⎧a ＝－1，c ＝－2.则f (x )＝－x 2－x ＋2，所以f (－x )＝－x 2＋x ＋2.故选C .5．(北京朝阳区2017届高三上学期期中)已知函数f (x )＝ax 2－x ，若对任意x 1，x 2∈[2，＋∞)，且x 1≠x 2，不等式f （x 1）－f （x 2）x 1－x 2>0恒成立，则实数a 的取值范围是( )A.⎝⎛⎭⎫12，＋∞B.⎣⎡⎭⎫12，＋∞ C.⎝⎛⎭⎫14，＋∞ D.⎣⎡⎭⎫14，＋∞ 解：任意x 1，x 2∈[2，＋∞)，当x 1<x 2，f （x 1）－f （x 2）x 1－x 2>0有f (x 1)<f (x 2)，函数f (x )＝ax 2－x 在区间[2，＋∞)上是增函数，所以a >0，且函数f (x )＝ax 2－x 对称轴12a ≤2⇒a ≥14.故选D .6．(2016·黄冈模拟)若函数f (x )＝(a 2＋4a －5)x 2－4(a －1)x ＋3的图象恒在x 轴上方，则a 的取值范围是( ) A ．[1，19] B ．(1，19) C ．[1，19) D ．(1，19]解：函数图象恒在x 轴上方，即不等式(a 2＋4a －5)x 2－4(a －1)x ＋3>0对于一切x ∈R 恒成立．当a 2＋4a －5＝0时，有a ＝－5或a ＝1.若a ＝－5，不等式化为24x ＋3>0，不满足题意；若a ＝1，不等式化为3>0，满足题意．当a 2＋4a －5≠0时，应有⎩⎪⎨⎪⎧a 2＋4a －5＞0，16（a －1）2－12（a 2＋4a －5）＜0， 解得1<a <19. 综上1≤a <19.故选C .7．(2015·浙江模拟)不等式log 2⎝⎛⎭⎫x ＋1x ＋6≤3的解集为________． 解：log 2⎝⎛⎭⎫x ＋1x ＋6≤3⇔log 2⎝⎛⎭⎫x ＋1x ＋6≤log 28⇔0＜x ＋1x ＋6≤8⇔－6＜x ＋1x ≤2.当x ＞0时，x ＋1x≥2，此时x ＝1；当x ＜0时，x ＋1x ≤－2，此时x ＋1x ＞－6，解得－3－22＜x ＜－3＋2 2.故填(－3－22，－3＋22)∪{1}．8．(广州市2017届高三第一次模拟)已知a <0，关于x 的不等式ax 2－2(a ＋1)x ＋4>0的解集是________．解：原不等式等价为(x －2)(ax －2)>0，即a (x －2)(x －2a)>0，因为a <0，所以不等式等价为(x －2)⎝⎛⎭⎫x －2a <0，所以2a <x <2，即原不等式的解集为⎝⎛⎭⎫2a ，2.故填⎝⎛⎭⎫2a ，2. 9．若关于x 的不等式x 2－ax －a ≤－3的解集不是空集，求实数a 的取值范围．解法一：设f (x )＝x 2－ax －a .则关于x 的不等式x 2－ax －a ≤－3的解集不是空集⇔f (x )min ≤－3，即f ⎝⎛⎭⎫a 2＝－4a ＋a24≤－3，解得a ≤－6或a ≥2.解法二：x 2－ax －a ≤－3的解集不是空集⇔x 2－ax －a ＋3＝0的判别式Δ≥0，解得a ≤－6或a ≥2.10．若关于x 的方程3x 2－5x ＋a ＝0的一个根大于－2且小于0，另一个根大于1且小于3，求实数a 的取值范围．解：设f (x )＝3x 2－5x ＋a ，则由题意有 ⎩⎪⎨⎪⎧f （－2）＞0，f （0）＜0，f （1）＜0，f （3）＞0.即⎩⎪⎨⎪⎧22＋a ＞0，a ＜0，－2＋a ＜0，12＋a ＞0.解得－12＜a ＜0.故实数a 的取值范围为(－12，0)．(2016·湖北模拟)已知不等式ax 2＋bx ＋c >0的解集为(1，t )，记函数f (x )＝ax 2＋(a －b )x －c . (1)求证：函数y ＝f (x )必有两个不同的零点；(2)若函数y ＝f (x )的两个零点分别为m ，n ，求|m －n |的取值范围．解：(1)证明：由题意知a ＜0，a ＋b ＋c ＝0，且－b2a >1，所以c ＜a ＜0，所以ac >0，所以对于函数f (x )＝ax 2＋(a －b )x －c 有Δ＝(a －b )2＋4ac >0，所以函数y ＝f (x )必有两个不同零点．(2)|m －n |2＝(m ＋n )2－4mn ＝（b －a ）2＋4ac a 2＝（－2a －c ）2＋4ac a 2＝⎝⎛⎭⎫c a 2＋8·c a＋4， 由不等式ax 2＋bx ＋c >0的解集为(1，t )可知，方程ax 2＋bx ＋c ＝0的两个解分别为1和t (t >1)，由根与系数的关系知ca ＝t ，所以|m －n |2＝t 2＋8t ＋4，t ∈(1，＋∞)．所以|m －n |>13，所以|m －n |的取值范围为(13，＋∞)．1．不等式x －12x ＋1≤0的解集为( )A.⎝⎛⎦⎤－12，1 B.⎣⎡⎦⎤－12，1 C.⎝⎛⎭⎫－∞，－12∪[1，＋∞) D.⎝⎛⎦⎤－∞，－12∪[1，＋∞) 解：x －12x ＋1≤0⇔⎩⎪⎨⎪⎧（x －1）（2x ＋1）≤0，2x ＋1≠0得－12<x ≤1.故选A .2．已知－12<1x<2，则x 的取值范围是( )A ．(－2，0)∪⎝⎛⎭⎫0，12 B.⎝⎛⎭⎫－12，2 C.⎝⎛⎭⎫－∞，－12∪(2，＋∞) D ．(－∞，－2)∪⎝⎛⎭⎫12，＋∞ 解：当x >0时，x >12；当x <0时，x <－2.所以x 的取值范围是x <－2或x >12，故选D .3．(2016·山东枣庄一模)关于x 的不等式x 2－ax ＋a >0(a ∈R )在R 上恒成立的充分不必要条件是( ) A ．a <0或a >4 B ．0<a <2 C ．0<a <4 D ．0<a <8解：因为不等式x 2－ax ＋a >0(a ∈R )在R 上恒成立的充要条件是Δ＝a 2－4a <0，即0<a <4，所以不等式x 2－ax ＋a >0(a ∈R )在R 上恒成立的充分不必要条件是0<a <2.故选B .4．一元二次不等式ax 2＋bx ＋2>0的解集是⎝⎛⎭⎫－12，13，则不等式bx 2＋2x －a <0的解集是( ) A ．{x |x <－2或x >3} B ．{x |x <－3或x >2}C ．{x |－2<x <3}D ．{x |－3<x <2}解：由条件得－12，13是方程ax 2＋bx ＋2＝0的两根，由韦达定理，a ＝－12, b ＝－2，所以bx 2＋2x －a <0即为－2x 2＋2x ＋12<0，解得x <－2或x >3.故选A .5．已知一元二次不等式f (x )<0的解集为⎩⎨⎧⎭⎬⎫x|x <－1或x >12，则f (10x )>0的解集为( ) A ．{x |x <－1或x >lg2} B ．{x |－1<x <lg2}C ．{x |x >－lg2}D ．{x |x <－lg2}解：可设f (x )＝a (x ＋1)⎝⎛⎭⎫x －12(a <0)，由f (10x )>0可得(10x ＋1)⎝⎛⎭⎫10x －12<0，从而10x <12，解得x <－lg2，故选D . 6．(2016·云南模拟)若关于x 的不等式x 2－(a ＋1)x ＋a ≤0的解集是[－4，3]的子集，则a 的取值范围是( )A ．[－4，1]B ．[－4，3]C ．[1，3]D ．[－1，3]解：原不等式等价于(x －a )(x －1)≤0，当a <1时，不等式的解集为[a ，1]，此时只要a ≥－4即可，即－4≤a <1；当a ＝1时，不等式的解为x ＝1，此时符合要求；当a >1时，不等式的解集为[1，a ]，此时只要a ≤3即可，即1<a ≤3.综上可得－4≤a ≤3.故选B .7．(2016·广东惠州模拟)不等式9x －7＜－1的解集为________． 解：由9x －7＜－1得x ＋2x －7＜0，可化为(x ＋2)(x －7)＜0，解得－2＜x ＜7.故填(－2，7)． 8．(2016·西安模拟)已知函数f (x )＝x 2＋ax ＋b (a ，b ∈R )的值域为[0，＋∞)，若关于x 的不等式f (x )<c 的解集为(m ，m ＋6)，则实数c 的值为________.解：由题意得a 2－4b ＝0，所以b ＝a 24. 所以f (x )<c 可化为x 2＋ax ＋a 24－c <0， 由题意知m 和m ＋6为关于x 的一元二次方程x 2＋ax ＋a 24－c ＝0的两根，所以⎩⎪⎨⎪⎧m ＋m ＋6＝－a ，m （m ＋6）＝a 24－c ， 所以c ＝a 24－m (m ＋6)＝（2m ＋6）24－m (m ＋6)＝9.故填9. 9．(2016·西安模拟)某商场若将进货单价为8元的商品按每件10元出售，每天可销售100件，现准备提高售价来增加利润．已知这种商品每件售价提高1元，销量就要减少10件．那么要保证该商品每天的利润在320元以上，求其每件售价的取值范围．解：设售价定为每件x 元，利润为y 元，则：y ＝(x －8)[100－10(x －10)]，依题意，有(x －8)[100－10(x －10)]＞320，即x 2－28x ＋192＜0，解得12＜x ＜16，所以每件售价的取值范围为(12，16)(单位：元)．10．解关于x 的不等式ax 2－2≥2x －ax (a ∈R )．解：不等式整理为ax 2＋(a －2)x －2≥0，当a ＝0时，解集为(－∞，－1]．当a ≠0时，ax 2＋(a －2)x －2＝0的两根为－1，2a， 所以当a ＞0时，解集为(－∞，－1]∪⎣⎡⎭⎫2a ，＋∞； 当－2＜a ＜0时，解集为⎣⎡⎦⎤2a ，－1；当a ＝－2时，解集为{x |x ＝－1}；当a ＜－2时，解集为⎣⎡⎦⎤－1，2a .(2016·郑州模拟)设二次函数f (x )＝ax 2＋bx ＋c ，函数F (x )＝f (x )－x 的两个零点为m ，n (m <n )．(1)若m ＝－1，n ＝2，求不等式F (x )>0的解集；(2)若a >0，且0<x <m <n <1a，比较f (x )与m 的大小． 解：(1)由题意知，F (x )＝f (x )－x ＝a (x －m )(x －n )， 当m ＝－1，n ＝2时，不等式F (x )>0，即a (x ＋1)(x －2)>0.那么当a >0时，不等式F (x )>0的解集为{x |x <－1或x >2}； 当a <0时，不等式F (x )>0的解集为{x |－1<x <2}．(2)f (x )－m ＝a (x －m )(x －n )＋x －m＝(x －m )(ax －an ＋1)．因为a >0，且0<x <m <n <1a ，所以x －m <0，1－an ＋ax >0.所以f (x )－m <0，即f (x )<m .。
一元二次不等式及其解法
3.2.1 一元二次不等式及其解法1.一元二次不等式的概念我们把只含有一个未知数，且未知数的最高次数是2的不等式叫做一元二次不等式．破疑点：(1)在一元二次不等式的表达式中，一定有条件a≠0，即二次项的系数不为零．(2)对于ax2＋bx＋c>0(或<0)的形式，如果不指明是二次不等式，那么它也可能是一次不等式，应特别注意分类讨论．练习：判断下列不等式中哪些是一元二次不等式．①x2>0；②－x2－x≤5；③x3＋5x－6>0；④mx2－5y<0(m为常数)；⑤ax2＋bx＋c>0.[解析]①②是．③不是，因为x3的最高次数是3，不符合定义．④不是．当m＝0时，它是一元一次不等式，当m≠0，它含有两个未知数x，y.⑤不一定是．当a＝0时，它不符合一元二次不等式的定义；当a≠0时，是．2．一元二次不等式的解与解集使一元二次不等式成立的x的值，叫做这个一元二次不等式的解，其解的集合，称为这个一元二次不等式的解集．破疑点：(1)解集是解的集合，故一元二次不等式的解集一定要写成集合或区间的形式．(2)一元二次不等式解集的形式是在a>0的条件下给出的，若a<0，应将不等式两边同乘以－1转化为二次项系数为正的形式，再求解．练习：画出函数y＝x2－2x－3的图象，观察图象．回答问题：(1)x∈________时，y＝0，方程x2－2x－3＝0的根为________．(2)x∈________时，y>0，∴不等式x2－2x－3>0的解集为________；(3)x∈________时，y<0，∴不等式x2－2x－3<0的解集为________．[答案](1){－1,3}x1＝－1，x2＝3(2){x|x<－1或x>3}{x|x<－1或x>3} (3){x|－1<x<3}{x|－1<x<3}[解析]方程x2－2x－3＝0的两根分别是x1＝－1，x2＝3，函数y＝x2－2x －3的图象如图所示．由图象可知，当x∈{－1,3}时，y＝0，方程x2－2x－3＝0的根为x1＝－1，x2＝3.当x∈{x|x<－1或x>3}时，y>0，∴不等式x2－2x－3>0的解集为{x|x<－1或x>3}．当x∈{x|－1<x<3}时，y<0，∴不等式x2－2x－3<0的解集为{x|－1<x<3}．3．一元二次不等式的解法．一元二次不等式经过变形，可以化成以下两种标准形式：(1)ax2＋bx＋c＞0(a＞0)；(2)ax2＋bx＋c＜0(a＞0)．上述两种形式的一元二次不等式的解集，可通过方程ax2＋bx＋c＝0的根确定．设△＝b2－4ac，则：①△＞0时，方程ax2＋bx＋c＝0有两个不相等的实数根x1、x2，设x1＜x2，则不等式(1)的解集为{x|x＜x1或x＞x2}，不等式(2)的解集为{x|x1＜x＜x2}；②△＝0时，方程ax2＋bx＋c＝0有两个相等的根，即x1＝x2＝－b2a，此时不等式(1)的解集为{x∈R|x≠－b2a}，不等式(2)的解集为∅；③△＜0时，方程ax2＋bx＋c＝0无实数根，则不等式(1)的解集为R；不等式(2)的解集为∅.对于二次项系数是负数(即a＜0)的不等式，可以先依据不等式的性质把二次项系数化成正数，再参照上述两种形式求解．也可以直接参照a＞0的情形画出图象，对比图象上的正负值区间写出解集．练习：解不等式6x－2－3x2>0.[解析]原不等式可化为3x2－6x＋2<0，∵Δ＝36－4×3×2＝12>0，∴方程3x2－6x＋2＝0的两实根分别为x1＝1－33，x2＝1＋33，∴原不等式的解集为{x|1－33<x<1＋33}．考点一：简单的一元二次不等式的解法例1、解下列不等式：(1)2x2－3x－2>0；(2)x2－3x＋5>0；(3)－6x2－x＋2≥0；(4)－4x2≥1－4x；(5)2x2－4x＋7<0.[解析](1)∵Δ＝(－3)2－4×2×(－2)＝25>0，∴方程2x2－3x－2＝0有两个不同实根，分别是－12，2，∴原不等式的解集为{x|x>2，或x<－1 2}．(2)∵Δ＝(－3)2－4×5＝9－20<0，∴x2－3x＋5>0的解集为R.(3)原不等式可化为6x2＋x－2≤0，∵Δ＝12－4×6×(－2)＝49>0，∴方程6x2＋x－2＝0有两个不同实根，分别是－23，12，∴原不等式的解集为{x|－23≤x≤12}．(4)原不等式可化为4x2－4x＋1≤0，即(2x－1)2≤0.∴原不等式的解集是{x|x＝1 2}．(5)∵Δ＝(－4)2－4×2×7＝－40<0，∴不等式2x2－4x＋7<0的解集为∅.跟踪练习：不等式x2－4x＋5＜0的解集为________．[答案]∅[解析]∵Δ＝16－20＝－4<0，∴方程x2－4x＋5＝0无实根，∴原不等式的解集为∅.考点二：一元二次不等式的实际应用例2、某热带风暴中心B位于海港城市A东偏南30°的方向，与A市相距400 km.该热带风暴中心B以40km/h的速度向正北方向移动，影响范围的半径是350 km.问：从此时起，经多少时间后A市将受热带风暴影响，大约受影响多长时间？[解析]如图，以A市为原点，正东方向为x轴建立直角坐标系．∵AB＝400，∠BAx＝30°，∴台风中心B的坐标为(2003，－200)，x h后台风中心B到达点P(2003，40x－200)处．由已知，A市受台风影响时，有|AP|≤350，即(2003)2＋(40x－200)2≤3502，整理得16x2－160x＋375≤0，解这个不等式得，3.75≤x≤6.25，A市受台风影响的时间为6.25－3.75＝2.5.故在3.75h后，A市会受到台风的影响，时间长达2.5h.跟踪练习：汽车在行驶中，由于惯性作用，刹车后还要向前滑行一段距离才能停住，我们称这段距离为“刹车距离”．刹车距离是分析事故的一个重要因素，在一个限速40km/h以内的弯道上，甲、乙两车相向而行，发现情况不对，同时刹车，但还是相碰了．事后现场测得甲车的刹车略超过12m，乙车的刹车略超过10m，又知甲、乙两种车型的刹车距离s(m)与车速x(km/h)之间有如下关系：s甲＝0.1x＋0.01x2，s乙＝0.05x＋0.005x2.问：超速行驶应负主要责任的是谁？[解析]要分清谁是应付主要责任者，就需分析行车速度，要弄清速度问题，就要利用刹车距离函数与实测数据，构建数学模型，由题意列出不等式甲：0.1x＋0.01x2＞12，乙：0.05x＋0.005x2＞10，∵x＞0，∴解得x甲＞30 km/h，x乙＞40 km/h，经比较知乙车超过限速，应付主要责任.考点三：“三个二次”关系的应用例3、若不等式ax2＋bx＋c≥0的解集是{x|－13≤x≤2}，求不等式cx2＋bx＋a<0的解集．[解析]解法一：由ax2＋bx＋c≥0的解集为{x|－13≤x≤2}，知a<0，又(－13)×2＝ca<0，则c>0.又－13，2为方程ax2＋bx＋c＝0的两个根，∴－ba＝53. ∴ba＝－53.又ca＝－23，∴b＝－53a，c＝－23a.∴不等式cx2＋bx＋a<0化为(－23a)x2＋(－53a)x＋a<0，即2ax2＋5ax－3a>0.又∵a<0，∴2x2＋5x－3<0⇔(2x－1)(x＋3)<0.∴不等式cx2＋bx＋a<0的解集为{x|－3<x<1 2}．跟踪练习：已知方程ax2＋bx＋2＝0的两根为－12和2.(1)求a、b的值；(2)解不等式ax2＋bx－1>0.[解析](1)∵方程ax2＋bx＋2＝0的两根为－12和2，由根与系数的关系，得⎩⎪⎨⎪⎧－12＋2＝－b a ，－12×2＝2a .解得a ＝－2，b ＝3.(2)由(1)知，ax 2＋bx －1>0化为－2x 2＋3x －1>0，即2x 2－3x ＋1<0，解得12<x <1. ∴不等式ax 2＋bx －1>0的解集为{x |12<x <1}．例 4 设f (x )、g (x )都是R 上的奇函数，关于x 的不等式f (x )>0的解集为{x |4<x <10}，g (x )>0的解集为{x |2<x <5}，则关于x 的不等式f (x )·g (x )>0的解集为( )A ．{x |2<x <10}B ．{x |4<x <5}C ．{x |－10<x <－2或2<x <10}D ．{x |－5<x <－4或4<x <5} [错解] 选B.[辨析] f (x )g (x )>0⇔⎩⎨⎧ f (x )>0g (x )>0或⎩⎨⎧f (x )<0g (x )<0.误选B ，是忽视了f (x )<0且g (x )<0的情况．[正解] 选D.∵f (x )、g (x )都是R 上的奇函数， ∴f (x )·g (x )为偶函数，f (x )>0且g (x )>0的解集为{x |4<x <10}∩{x |2<x <5}＝{x |4<x <5}． 由偶函数的对称性知f (x )<0且g (x )<0的解集为{x |－5<x <－4}，故选D.3.2.2 含参数一元二次不等式的解法1.含参数的一元二次不等式的解法解答含参数的不等式时，一般需对参数进行讨论，常见的有以下几种情况： (1)二次项系数含参数时，根据二次不等式化标准形式需要化二次项系数为正，所以要对参数符号进行讨论．(2)解“Δ”的过程中，若“Δ”表达式含有参数且参数的取值影响“Δ”符号，这时根据“Δ”符号确定的需要，要对参数进行讨论．(3)方程的两根表达式中如果有参数，必须对参数讨论才能确定根的大小，这时要对参数进行讨论．总之，参数讨论有三个方面：①二次项系数；②“Δ”；③根．但未必在这三个地方都进行讨论，是否讨论要根据需要而定．练习：解关于x 的不等式56x 2＋ax －a 2＜0.[解析] 原不等式化为(7x ＋a )(8x －a )＜0，方程(7x ＋a )(8x －a )＝0的两根为x 1＝－a 7，x 2＝a 8，∴a ＞0时，解集为{x |－a 7＜x ＜a8}； a ＝0时，解集为∅；a ＜0时，解集为{x |a 8＜x ＜－a7}． 2．分式不等式的解法(1)分式不等式：分母中含有未知数，且分子、分母都是关于x 的多项式的不等式称为分式不等式．(2)等价转化法解分式不等式：解分式不等式的基本方法是将其转化为与之同解的整式 不等式(组)．具体情况见下表：练习：解下列不等式：(1)4－x 2x ＋3≤0； (2)x ＋12－x ≥3. [解析] (1)4－x 2x ＋3≤0⇔x －42x ＋3≥0⇔⎩⎨⎧(x －4)(2x ＋3)≥02x ＋3≠0⇔{x |x ≥4或x <－32}． ∴原不等式的解集为{x |x <－32或x ≥4}．(2)x ＋12－x ≥3⇔x ＋12－x －3≥0 ⇔4x －52－x ≥0 ⇔4x －5x －2≤0，⇔⎩⎨⎧(4x －5)(x －2)≤0x －2≠0， ⇔{x |54≤x <2}．∴原不等式的解集为{x |54≤x <2}． 3．简单的高次不等式的解法 (1)高次不等式不等式最高次项的次数高于2，这样的不等式称为高次不等式． (2)穿根法解高次不等式的步骤 ①将f (x )最高次项系数化为正数；②将f (x )分解为若干个一次因式的积或二次不可分因式的积；③将每一个一次因式的根标在数轴上，自上而下，从右向左依次通过每一点画曲线(注意重根情况，偶次方根穿而不过，奇次方根既穿又过)；④观察曲线显现出的f (x )的值的符号变化规律，写出不等式的解集． 练习：解不等式：(x ＋2)(x ＋1)(x －1)(x －2)≤0. [解析] 设y ＝(x ＋2)(x ＋1)(x －1)(x －2)， 则y ＝0的根分别是－2，－1,1,2，将其分别标在数轴上，并画出如图所示的示意图：所以原不等式的解集是{x |－2≤x ≤－1，或1≤x ≤2}．[点评] (1)大于0的不等式的解，对应着曲线在x 轴上方部分的实数x 的取值集合；反之，对应着x 轴下方部分的实数x 的取值集合．注意端点处值是否取到．(2)穿根法可形象地称为“穿根引线法”，这样的“线”可看成是函数的图象草图，只不过不画y 轴而已．考点一：含参数的一元二次不等式的解法例1、 解关于x 的不等式：x 2－(2m ＋1)x ＋m 2＋m ＜0.[解析] 解法一：∵方程x 2－(2m ＋1)x ＋m 2＋m ＝0的解为x 1＝m ，x 2＝m ＋1，且知m ＜m ＋1.∴二次函数y ＝x 2－(2m ＋1)x ＋m 2＋m 的图象开口向上，且与x 轴有两个交点． ∴不等式的解集为{x |m ＜x ＜m ＋1}．解法二：注意到m 2＋m ＝m (m ＋1)，及m ＋(m ＋1)＝2m ＋1，可先因式分解，化为(x －m )(x －m －1)＜0， ∵m ＜m ＋1，∴m ＜x ＜m ＋1. ∴不等式的解集为{x |m <x <m ＋1}．跟踪练习：当a >0时，解关于x 的不等式ax 2－(a ＋1)x ＋1<0. [解析] 不等式ax 2－(a ＋1)x ＋1<0可化为(ax －1)(x －1)<0， ∵a >0，∴不等式(ax －1)(x －1)<0，可化为(x －1a )(x －1)<0， 当a ＝1时，不等式无解； 当0<a <1时，1<x <1a ； 当a >1时，1a <x <1.综上可知，当0<a <1时，原不等式的解集为{x |1<x <1a }；当a ＝1时，原不等式的解集为空集；当a >1时，原不等式的解集为{x |1a <x <1}.考点二：分式不等式的解法例2、 (1)不等式x －1x ≥2的解集为( ) A ．[－1,0) B ．[－1，＋∞)C ．(－∞，－1]D ．(－∞，－1]∪(0，＋∞)(2)不等式2x －13－4x ＞1的解集为________．[答案] (1)A (2){x |23<x <34}[解析] (1)x －1x －2≥0∴－x －1x ≥0，∴⎩⎨⎧x (x ＋1)≤0x ≠0，∴－1≤x ＜0.(2)原不等式化为：6x －44x －3＜0， ∴(6x －4)(4x －3)＜0，∴23＜x ＜34，∴原不等式的解集为{x |23＜x ＜34}．跟踪练习：不等式3x －12－x≥1的解集是( ) A ．{x |34≤x ≤2} B ．{x |x ≤34或x ＞2}C ．{x |34≤x ＜2}D ．{x |x ＜2}[答案] C[解析] 不等式3x －12－x≥1，化为：4x －32－x≥0，∴34≤x ＜2. 考点三：简单高次不等式解法例3、 不等式x (x ＋2)x －3＜0的解集为( ) A ．{x |x ＜－2，或0＜x ＜3} B ．{x |－2＜x ＜2，或x ＞3}C ．{x |x ＜－2，或x ＞0}D ．{x |x ＜0，或x ＜3}[答案] A[解析] 原不等式等价于x (x ＋2)(x －3)＜0.结合数轴穿根法(如图)可知：x ＜－2或0＜x ＜3.跟踪练习：解不等式：x (x －1)2(x ＋1)3(x －2)>0.[解析] 原不等式可化为⎩⎨⎧ x (x ＋1)(x －2)>0x －1≠0 ⇔⎩⎨⎧－1<x <0，或x >2x ≠1⇔－1<x <0，或x >2.∴原不等式的解集为{x |－1<x <0，或x >2}.考点四：不等式恒成立的问题例4、 关于x 的不等式(1＋m )x 2＋mx ＋m <x 2＋1对x ∈R 恒成立，求实数m 的取值范围．[解析] 原不等式等价于mx 2＋mx ＋m －1<0对x ∈R 恒成立，当m ＝0时，0·x 2＋0·x －1<0对x ∈R 恒成立．当m ≠0时，由题意，得⎩⎨⎧ m <0Δ＝m 2－4m (m －1)<0⇔⎩⎨⎧ m <03m 2－4m >0⇔⎩⎪⎨⎪⎧m <0m <0，或m >43⇔m <0. 综上，m 的取值范围为m ≤0.跟踪练习：已知不等式ax 2＋(a －1)x ＋a －1<0对于所有的实数x 都成立，求a 的取值范围．[解析] 若a ＝0，则原不等式为－x －1<0，即x >－1，不合题意．故a ≠0.令f (x )＝ax 2＋(a －1)x ＋a －1，∵原不等式对任意x ∈R 都成立．∴二次函数f (x )的图象在x 轴的下方．∴a <0且Δ＝(a －1)2－4a (a －1)<0.即⎩⎨⎧a <0(a －1)(3a ＋1)>0，∴a <－13. 故a 的取值范围为(－∞，－13)．例5、 若函数y ＝kx 2－6kx ＋(k ＋8)的定义域为R ，则k 的取值范围是________．[错解] 0<k ≤1由题意知kx 2－6kx ＋(k ＋8)≥0恒成立，∴⎩⎨⎧ k >0Δ＝36k 2－4k (k ＋8)≤0，∴0<k ≤1，即k 的取值范围是0<k ≤1. [辨析] 错解忽视了k ＝0时，kx 2－6kx ＋(k ＋8)≥0也成立，考虑问题不全面导致错[正解] 0≤k ≤1由题意kx 2－6kx ＋(k ＋8)≥0恒成立．当k ＝0时满足，当k ≠0时⎩⎪⎨⎪⎧k ＞0△＝36k 2－4k (k ＋8)≤0 ，∴0＜k ≤1，综上得0≤k ≤1.。
一元二次不等式及其解法
基础自测
1 1 1.不等式 ( x )( x ) 0 的解集为 2 3 1 1 A. ( , ) 3 2 1 1 B. ( , ) ( , ) 3 2 1 1 C. ( , ) 2 3 1 1 D. ( , ) ( , ) 2 3
（ ）
解析
1 1 又∵相应方程 ( x )( x ) 0 的两根为 2 3 1 1 x1 , x2 , 3 2 1 1 1 1 ( x )(x ) 0的解为 x . 2 3 3 2 1 1 故原不等式的解集为 {x | x }. 3 2 答案 A
当a=1时,原不等式的解集为{x|x≠1}.
题型四
一元二次不等式的恒成立问题
【例4】（12分）已知不等式mx2-2x-m+1<0.
（1）若对所有的实数x不等式恒成立，求m的取值范围； （2）设不等式对于满足|m|≤2的一切m的值都成立,
求x的取值范围.
思维启迪 （1）由于二次项系数含有字母，所以首先讨论m=0的 情况，而后结合二次函数图象求解.
一元二次函数
复习一元二次函数:y=ax2+bx+c(a≠0)
当a>0时图像 y
y y
O
x1
x2
x
O
b 2a
x
O
x
0
0
0
一元二次函数
复习一元二次函数:y=ax2+bx+c(a≠0)
当a<0时图像 y 0
x
y
0
y 0
O
x1
x2
O
b 2a
x
O
x
一元二次不等式定义：
定义：含有一个未知数，并且未知数的最高次数
一元二次不等式及其解法
1 2 (5)－2x ＋3x－5>0；
(6)－2x2＋3x－2<0.
解不含参数的一元二次不等式的一般步骤 (1)通过对不等式的变形，使不等式右侧为 0，使二次项 系数为正． (2)对不等式左侧因式分解，若不易分解，则计算对应 方程的判别式． (3)求出相应的一元二次方程的根或根据判别式说明方 程有无实根． (4)根据一元二次方程根的情况画出对应的二次函数的
ax2－bx＋2<0 的解集为{x|1<x<2}，则 a＋b＝_________. (2)已知二次方程 ax2＋bx＋c＝0 的两个根是－2,3， a>0， 那么 ax2－bx＋c>0 的解集是__________________．
[规律小结] 1.对一元二次不等式概念的三点说明 (1)“只含一个未知数”，并不是说在代数式中不能含有 其他字母类的量，只要明确指出这些字母所代表的量，即哪 一个是变量“未知数”，哪一个是“参数”即可． (2)“次数最高是 2”，仅限于“未知数”，若还含有其他 参数，则次数不受此条件限制． (3)必须是整式不等式．
3.2.1一元二次不等式及其解法
1．一元二次不等式的定义 只含有 1 个 未知数，并且未知数的 最高次数为 2 的 不等式，称为一元二次不等式．即形如 ax2＋bx＋c>0(≥0) 或 ax2＋bx＋c<0(≤0)(其中 a≠0)的不等式叫做一元二次不等 式． 2．一元二次不等式的解与解集 使一元二次不等式成立的 式的 解
【跟踪训练 2】
解关于 x 的不等式：x2－ax－2a2<0.
题型三 例3
“三个二次”之间的转化关系
若不等式 ax2， 求
不等式 bx2＋2ax－c－3b<0 的解集．
一元二次不等式及其解法课件
1 2
, 32
)
【活学活用】
1.已知函数f(x)=(ax-1)·(x+b)，如果不
等式f(x)>0的解集是(-1,3)，则不等式
f(-2x)<0的解集是( A)
(A)(-∞,
3 2
)∪( 12
,+∞)
(B)( 3 , 1) 22
(C)(-∞,
12)∪(
3 2
,+∞)
(D)(
1 2
, 32
)
思维拓展：高次不等式穿根法
基础 篇
例1：解下列一元二次不等式
(1)x2 3x 4 0; (2) x2 x 3 1; (3)2x2 3x 2 0; (4)4x2 12x 9 0.
例1：解下列一元二次不等式
(1)x2 3x 4 0;-，-1 U4，+
(2) x2 x 3 1;-1, 2
专题二
一元二次不等式及其解法
学习目标
❖ 学习目标: 通过复习进一步理解“三个二次”的关 系，掌握一元二次不等式的解法并会实际运用。
❖ 学法指导：体会数形结合、分类讨论的思想方法， 加强计算能力的培养。
❖ 学习重点、难点：一元二次不等式的解法及其步骤、 恒成立问题、实际应用问题。
[导入新知] 【概念回顾】 1．一元二次不等式 我们把只含有 一个 未知数，并且未知数的 最高次数是2 的 不等式，称为一元二次不等式，即形如 ax2＋bx＋c＞0(≥0)或 ax2＋ bx＋c＜0(≤0)(其中 a≠0)的不等式叫做一元二次不等式．
[类题通法] 解含参数的一元二次不等式时：
(1)若二次项系数含有参数，则需对二次项系数大于 0 与小 于 0 进行讨论；
(2)若求对应一元二次方程的根需用公式，则应对判别式 Δ 进行讨论；
一元二次不等式及其解法
当 a＝0 时，原不等式的解集为(－∞，－1]；
而g
a
是一次函数，所以
g g
(1) (1)
x
x2 2
5x 3x
2
6
0
0，
解得x 1或x 3.所以x的取值范围是{x | x 1或x 3}．
5.已知函数y＝lg[(a2－4)x2＋2(a＋2)x＋a－1]的定 义域为R，求实数a的取值范围．
a的取值范围是(4，＋∞)．
解关于 x 的不等式 x2－2ax－8a2<0.
【自主解答】 不等式 x2－2ax－8a2<0 可化为(x＋2a)·(x－ 4a)<0，
(1)当－2a＝4a，即 a＝0 时，不等式即为 x2<0，解集为∅； (2)当－2a>4a，即 a<0 时，则 4a<x<－2a； (3)当－2a<4a，即 a>0 时，则－2a<x<4a. 综上所述：当 a＝0 时，原不等式的解集为∅； 当 a<0 时，原不等式解集为{x|4a<x<－2a}； 当 a>0 时，原不等式解集为{x|－2a&式恒成立问题
(1)不等式 ax2＋bx＋c>0 的解集是全体实数(或恒成立)的等价条
件是
a＝0 b＝0 c>0
或a>0 Δ<0
；
(2)不等式 ax2＋bx＋c<0 的解集是全体实数(或恒成立)的等价条
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
提示：交点的横坐标为方程的根．
问题 4：观察二次函数图象，x 满足什么条件，图象在 x 轴上 方？
提示：x＞2 或 x＜0.
问题 5：能否利用问题 4 得出不等式 x2－2x＞0，x2－2x＜0 的解集？
提示：能，不等式的解集为{x|x＞2 或 x＜0}，{x|0＜x＜2}．
[导入新知] 一元二次不等式与相应的二次函数及一元二次方程的关系 如表
[活学活用]
2
1 3．已知方程 ax ＋bx＋2＝0 的两根为－ 和 2.(1)求 a、b 的值； 2 (2)解不等式 ax2＋bx－1＞0.
1 解：(1)∵方程 ax ＋bx＋2＝0 的两根为－ 和 2， 2
2
b 1 － ＋ 2 ＝－ 2 a， 由根与系数的关系，得 －1×2＝2. a 2 解得 a＝－2，b＝3.
高中数学高一年级必修五 第三章 第二节
一元二次不等式及其解法
学习目标
学习目标:理解一元二次不等式的概念及其与二次函 数、一元二次方程的关系。初步树立“数形结合次 函数、一元二次方程的关系。 学法指导：发现、讨论法；数形结合。”的观念。 掌握一元二次不等式的解法及步骤。 学习重点、难点：一元二次不等式、二次函数、一 元二次方程的关系；一元二次不等式的解法及其步 骤。
(2)原不等式可化为 x2－7x＋6<0. 解方程 x2－7x＋6＝0 得，x1＝1，x2＝6. 结合二次函数 y＝x2－7x＋6 的图象知，原不等式的解集为 {x|1<x<6}． (3)原不等式可化为(x－2)(x＋3)>0. 方程(x－2)(x＋3)＝0 两根为 2 和－3. 结合二次函数 y＝(x－2)(x＋3)的图象知，原不等式的解集为 {x|x<－3 或 x>2}．
[随堂即时演练] 1．不等式 x(2－x)＞0 的解集为( A．{x|x＞0} C．{x|x＞2 或 x＜0} ) B．{x|x＜2} D．{x|0＜x＜2}
解析：原不等式化为 x(x－2)＜0，故 0＜x＜2.
答案：D
2．已知集合 M＝{x|x2－3x－28≤0}，N＝{x|x2－x－6＞0}， 则 M∩N 为( )
[活学活用] 2．解关于 x 的不等式：ax2－(a－1)x－1＜0(a∈R)．
解：原不等式可化为： (ax＋1)(x－1)＜0，当 a＝0 时，x＜1，当 a＞0 －1)＜0 1 ∴－a＜x＜1.当 a＝－1 时，x≠1，
1 时x＋a(x
当－1＜a＜0
1 1 时，x＋a(x－1)＞0，∴x＞－a或
92 (3)原不等式可化为 2x－2 ≤0 ，所以原不等式的解集为 9 x|x＝ . 4
(4)原不等式可化为 x2－6x＋10＜0，Δ＝(－6)2－40＝－4 ＜0，所以方程 x2－6x＋10＝0 无实根，又二次函数 y＝x2－6x ＋10 的图象开口向上，所以原不等式的解集为∅.
(5)原不等式可化为 2x2－3x＋2＞0，因为 Δ＝9－4×2×2＝－7 ＜0，所以方程 2x2－3x＋2＝0 无实根，又二次函数 y＝2x2－3x＋2 的图象开口向上，所以原不等式的解集为 R.
[类题通法] 解一元二次不等式的一般步骤 (1)通过对不等式变形，使二次项系数大于零； (2)计算对应方程的判别式； (3)求出相应的一元二次方程的根，或根据判别式说明方程没 有实根； (4)根据函数图象与 x 轴的相关位置写出不等式的解集．
[解]
方程 x2＋(1－a)x－a＝0 的解为 x1＝－1，x2＝a，函数
y＝x2＋(1－a)x－a 的图象开口向上，则当 a＜－1 时，原不等式 解集为{x|a＜x＜－1}； 当 a＝－1 时，原不等式解集为∅； 当 a＞－1 时，原不等式解集为{x|－1＜x＜a}．
[类题通法] 解含参数的一元二次不等式时： (1)若二次项系数含有参数，则需对二次项系数大于 0 与小 于 0 进行讨论； (2)若求对应一元二次方程的根需用公式，则应对判别式 Δ 进行讨论； (3)若求出的根中含有参数，则应对两根的大小进行讨论．
答案：A
3．二次函数 y＝x2－4x＋3 在 y＜0 时 x 的取值范围是________．
解析：由 y＜0 得 x2－4x＋3＜0，∴1＜x＜3
答案：(1,3)
4．若不等式 ax ＋bx＋2＞0
2
1 的解集为x|－2＜x＜2 ，则实数
a＝________，实数 b＝________.
1 1 ＝－ 与 x2＝ 是方程 x2＋px＋q＝0 的两个实数根， 2 3
1 1 3－2＝－p， 由根与系数的关系得 1 1 ×－ ＝q， 3 2
2
1 p＝6， 解得 q＝－1 . 6
1 2 1 所以不等式 qx ＋px＋1＞0 即为－ x ＋ x＋1＞0，整理得 x2 6 6 －x－6＜0，解得－2＜x＜3. 即不等式 qx2＋px＋1＞0 的解集为{x|－2＜x＜3}．
[活学活用] 1．解下列不等式： (1)x2－5x－6>0； (3)(2－x)(x＋3)<0； (2)－x2＋7x>6. (4)4(2x2－2x＋1)>x(4－x)．
解：(1)方程 x2－5x－6＝0 的两根为 x1＝－1， x2＝6. 结合二次函数 y＝x2－5x－6 的图象知，原不等式的解集为 {x|x<－1 或 x>6}．
A．{x|－4≤x＜－2 或 3＜x≤7} B．{x|－4＜x≤－2 或 3≤x＜7} C．{x|x≤－2 或 x＞3} D．{x|x＜－2 或 x≥3}
解析：∵M＝{x|x2－3x－28≤0} ＝{x|－4≤x≤7}，N＝{x|x2－x－6＞0}＝{x|x＜－2 或 x＞3} ∴M∩N＝{x|－4≤x＜－2 或 3＜x≤7}．
[类题通法] 1．一元二次不等式 ax2＋bx＋c＞0(a≠0)的解集的端点值是 一元二次方程 ax2＋bx＋c＝0 的根， 也是函数 y＝ax2＋bx＋c 与 x 轴交点的横坐标． 2．二次函数 y＝ax2＋bx＋c 的图象在 x 轴上方的部分，是由 不等式 ax2＋bx＋c＞0 的 x 的值构成的； 图象在 x 轴下方的部分， 是由不等式 ax2＋bx＋c＜0 的 x 的值构成的， 三者之间相互依存、 相互转化．
判别式 Δ＝b2 －4ac 一元二次方程
2
Δ>0 有两相异
Δ＝ 0 有两相等
Δ<0
实根 x1＝x2 没有实数 ax ＋bx＋c＝ 实根 x1， 根 b 0(a>0)的根 x2， (x1＜x2) ＝－ 2a
判别式 Δ＝b2－ 4ac 二次函数 y＝ax2＋ bx＋c(a>0)的图象 ax ＋bx＋ c>0(a>0) 的解集 ax2＋bx＋ c<0(a>0) 的解集
(2)由(1)知，ax2＋bx－1＞0 可变为－2x2＋3x－1＞0， 1 即 2x －3x＋1＜0，解得 ＜x＜1. 2
2
1 ∴不等式 ax ＋bx－1＞0 的解集为{x| ＜x＜1}． 2
2
5.有关三个“二次”关系的不等式的解法
[ 典例 ] 已知关于 x 的不等式 ax2 ＋ bx ＋ c ＜ 0 的解集是 ax2－bx＋c＞0 的解集．
1 x|x＜－2或x＞－ ，求 2
[活学活用] 已知一元二次不等式 x ＋px＋q＜0 求不等式 qx2＋px＋1＞0 的解集．
2
1 1 的解集为x|－2＜x＜3 ，
解：因为 x ＋px＋q＜0
2
1 1 的解集为x|－2＜x＜3 ，所以 x1
[提出问题] 观察下列不等式： (1)x2>0；(2)－x2－2x≤0；(3)x2－5x＋6>0. 问题 1：以上给出的 3 个不等式，它们含有几个未知数？未 知数的最高次数是多少？
提示：它们只含有一个未知数，未知数的最高次数都是 2. 问题 2：上述三个不等式在表达形式上有何共同特点？
提示：形如 ax2＋bx＋c>0(或≤0)，其中 a，b，c 为常数， 且 a≠0.
合或区间的形式.
[提出问题] 已知：一元二次函数 y＝x2－2x，一元二次方程 x2－2x＝0， 一元二次不等式 x2－2x＞0. 问题 1：试求二次函数与 x 轴交点坐标
提示：(0,0)、(2,0)
问题 2：一元二次方程根是什么？
提示：x1＝0，x2＝2.
问题 3：问题 1 中的坐标与问题 2 中的根有何内在联系？
x＜1.
1 1 当 a＜－1 时，－a＜1，∴x＞1 或 x＜－a， 综上原不等式的解集是： 当 a＝0 时，{x|x＜1}；当 a＞0
1 时， x|－a＜x＜1； 1 时，x|x＜1或x＞－a .
当 a＝－1 时，{x|x≠1}；当－1＜a＜0 当 a＜－1
(4)由原不等式得 8x2－8x＋4>4x－x2. ∴原不等式等价于 9x2－12x＋4>0. 2 解方程 9x －12x＋4＝0，得 x1＝x2＝ . 3
2
结合二次函数 y＝9x2－12x＋4 的图象知， 原不等式的解集为 2 {x|x≠ }. 3
[例 2]
解关于 x 的不等式 x2＋(1－a)x－a＜0.
[例 1]
解下列不等式：
(1)2x2＋7x＋3＞0；(2)x2－4x－5≤0； 81 1 2 (3)－4x ＋18x－ ≥0；(4)－ x ＋3x－5＞0； 4 2
2
(5)－2x2＋3x－2＜0.
[解]
(1)因为 Δ＝72－4×2×3＝25＞0， 所以方程 2x2＋7x
1 ＋3＝0 有两个不等实根 x1＝－3，x2＝－ .又二次函数 y＝2x2 2 1 ＋7x＋3 的图象开口向上，所以原不等式的解集为{x|x＞－ ， 2 或 x＜－3}． (2)原不等式可化为(x－5)(x＋1)≤0， 所以原不等式的解集 为{x|－1≤x≤5}．