高中数学公式总结-默写版
高中数学必背公式大全

高中数学必背公式大全一、代数部分。
1. 二项式定理。
(a+b)ⁿ = Cⁿ₀aⁿb⁰ + Cⁿ₁aⁿ⁻¹b¹ + ... + Cⁿᵢaⁿ⁻ⁱbⁱ + ... + Cⁿₙa⁰bⁿ。
2. 一元二次方程求根公式。
ax²+bx+c=0的解为x= (-b±√(b²-4ac))/2a。
3. 等差数列通项公式。
an = a₁ + (n-1)d。
4. 等比数列通项公式。
an = a₁ q^(n-1)。
5. 两点间距离公式。
两点A(x₁, y₁)和B(x₂, y₂)间的距离为√((x₂-x₁)² + (y₂-y₁)²)。
6. 直线斜率公式。
直线y=kx+b的斜率为k。
7. 二次函数顶点坐标。
二次函数y=ax²+bx+c的顶点坐标为(-b/2a, c-b²/4a)。
二、几何部分。
1. 直角三角形勾股定理。
a² + b² = c²。
2. 直角三角形中正弦、余弦、正切公式。
sinA = a/c, cosA = b/c, tanA = a/b。
3. 三角形面积公式。
三角形面积S=√(p(p-a)(p-b)(p-c)),其中p为半周长。
4. 圆周长和面积公式。
圆周长C=2πr, 圆面积S=πr²。
5. 正多边形内角和公式。
正n边形内角和为(n-2) 180°。
6. 圆锥、圆柱、球体积公式。
圆锥体积V=1/3πr²h, 圆柱体积V=πr²h, 球体积V=4/3πr³。
三、概率与统计部分。
1. 随机事件概率公式。
P(A) = n(A)/n(S)。
2. 期望公式。
E(X) = x₁p₁ + x₂p₂ + ... + xᵢpᵢ。
3. 正态分布概率公式。
P(a < X < b) = ∫(a, b) 1/√(2πσ²) e^(-(x-μ)²/2σ²) dx。
高中数学必修一公式整理精选全文

可编辑修改精选全文完整版高中数学必修一公式整理一、几何公式1、直线:(1) 直线的方程是y=kx+b,其中k为斜率,b为y轴截距;(2) 直线的斜率的计算公式:斜率K=(点1的纵坐标减去点2的纵坐标)除以(点1的横坐标减去点2的横坐标)。
2、平面图形(1) 三角形三边关系:任意一边长加上另外两边长,总长度要大于第三边。
(2) 三角形面积公式:面积 = (底边×高)÷2(3) 矩形的面积公式:面积 = 长×宽(4) 圆的面积公式:面积= π × 半径×半径二、代数公式1、平方差(1) 一元二次方程的解法:ax²+bx+c=0,解法为:x={-b±√(b²-4ac) }/2a(2) 二元二次方程的解法:ax²+bxy+cy²+dx+ey+f=0,解法为:x=(-be+√(b²-4ac)(-de+√(d²-4af))/(2a);y=(2a(-be+√(b²-4ac))/(-de+√(d²-4af))。
2、二次函数(1) 二次函数公式:y=ax²+bx+c,其中a不等于0(2) 二次函数的对称轴:x轴的方程为: x= -b/2a(3) 二次函数的极值的计算:极值的 x 值为: -b/2a , 极值的 y 值为:y=a(-b/2a)²+b(-b/2a)+c三、数列公式1、等差数列公式(1) 求和公式:Sn=n(a1+an)/2,其中n为项数,a1为首项,an为末项;(2) 首项公式:a1=Sn/n-(n-1)d,其中n为项数,Sn为该数列的前n项和,d为公差;(3) 末项公式:an=a1+(n-1)d,其中a1为首项,n为项数,d为公差;(4) 公差公式:d=(an-a1)/(n-1),其中an为末项,a1首项,n为项数;2、等比数列的公式(1) 求和公式:Sn=a1(1-qn)/(1-q),其中a1为首项,q为公比,n为项数;(2) 首项公式:a1=Sn(1-q)/(1-qn),其中Sn为该数列的前n项和,q为公比,n为项数;(3) 末项公式:an=a1q(n-1),其中a1为首项,q为公比,n为项数;(4) 公比公式:q=(an/a1)^(1/(n-1)),其中an为末项,a1首项,n 为项数;。
高中必背的数学公式(完整归纳)

高中必背的数学公式(完整归纳)高中必背的数学公式(一)两角和公式1、sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA2、cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB3、tan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)4、ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)(二)倍角公式1、cos2A=cos2A-sin2A=2cos2A-1=1-2sin2A2、tan2A=2tanA/(1-tan2A)ctg2A=(ctg2A-1)/2ctgA(三)半角公式1、sin(A/2)=√((1-cosA)/2)sin(A/2)=-√((1-cosA)/2)2、cos(A/2)=√((1+cosA)/2)cos(A/2)=-√((1+cosA)/2)3、tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))4、ctg(A/2)=√((1+cosA)/((1-cosA))ctg(A/2)=-√((1+cosA)/((1-cosA))(四)和差化积公式1、2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2、2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)3、sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)4、tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB5、ctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB(五)几何体表面积和体积公式1、圆柱体:表面积:2πRr+2πRh体积:πR2h(R为圆柱体上下底圆半径,h为圆柱体高)2、圆锥体:表面积:πR2+πR[(h2+R2)的平方根]体积:πR2h/3(r为圆锥体低圆半径,h为其高)3、正方体:表面积:S=6a2,体积:V=a3(a-边长)4、长方体:表面积:S=2(ab+ac+bc)体积:V=abc(a-长,b-宽,c-高)5、棱柱:体积:V=Sh(S-底面积,h-高)6、棱锥:体积:V=Sh/3(S-底面积,h-高)7、棱台:V=h[S1+S2+(S1S2)^1/2]/3(S1上底面积,S2下底面积,h-高)8、拟柱体:V=h(S1+S2+4S0)/6(S1-上底面积,S2-下底面积,S0-中截面积,h-高)9、圆柱:S底=πr2,S侧=Ch,S表=Ch+2S底,V=S底h=πr2h(r-底半径,h-高,C—底面周长,S底—底面积,S侧—侧面积,S表—表面积)10、空心圆柱:V=πh(R^2-r^2)(R-外圆半径,r-内圆半径,h-高)11、直圆锥:V=πr^2h/3(r-底半径,h-高)12、圆台:V=πh(R2+Rr+r2)/3(r-上底半径,R-下底半径,h-高)13、球:V=4/3πr^3=πd^3/6(r-半径,d-直径)14、球缺:V=πh(3a2+h2)/6=πh2(3r-h)/3(h-球缺高,r-球半径,a-球缺底半径)15、球台:V=πh[3(r12+r22)+h2]/6(r1球台上底半径,r2-球台下底半径,h-高)16、圆环体:V=2π2Rr2=π2Dd2/4(R-环体半径,D-环体直径,r-环体截面半径,d-环体截面直径)(六)椭圆公式1、椭圆周长公式:l=2πb+4(a-b)2、椭圆周长定理:椭圆的周长等于该椭圆短半轴,长为半径的圆周长(2πb)加上四倍的该椭圆长半轴长(a)与短半轴长(b)的差3、椭圆面积公式:s=πab4、椭圆面积定理:椭圆的面积等于圆周率(π)乘该椭圆长半轴长(a)与短半轴长(b)的乘积如何提高高中数学成绩1、记数学笔记,特别是对概念理解的不同侧面和数学规律,教师在课堂中拓展的课外知识。
高中数学公式默写
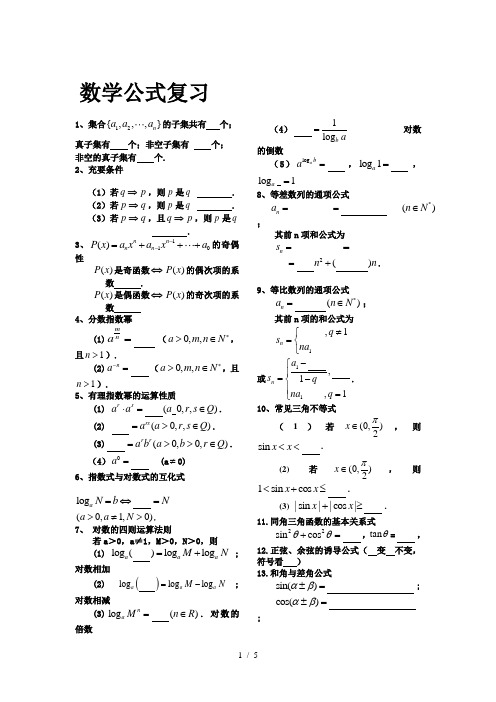
数学公式复习1、集合12{,,,}n a a a 的子集共有 个;真子集有 个;非空子集有 个; 非空的真子集有 个. 2、充要条件(1)若q p ⇒,则p 是q . (2)若p q ⇒,则p 是q . (3)若p q ⇒,且q p ⇒,则p 是q. 3、110()nn n n P x a x a x a --=+++的奇偶性()P x 是奇函数⇔()P x 的偶次项的系数 .()P x 是偶函数⇔()P x 的奇次项的系数4、分数指数幂(1)m na=(0,,a m n N *>∈,且1n >).(2)n a -=(0,,a m n N *>∈,且1n >).5、有理指数幂的运算性质(1) (0,,)r s a a a r s Q ⋅=∈.(2) (0,,)rs a a r s Q =>∈. (3)(0,0,)r r a b a b r Q =>>∈.(4)0a =(a ≠0)6、指数式与对数式的互化式log a N b N=⇔=(0,1,0)a a N >≠>.7、 对数的四则运算法则若a >0,a ≠1,M >0,N >0,则 (1)log ()log log a a a M N =+; 对数相加(2) ()log loglog aaa M N =-;对数相减(3)log ()na M n R =∈. 对数的倍数(4)1log b a=对数的倒数(5)log a b a =,log 1a =,log 1a =8、等差数列的通项公式*________()n a n N ==∈;其前n 项和公式为n s =____________________=2()n n =+.9、等比数列的通项公式*()n a n N =∈;其前n 项的和公式为1_____,1n q s na ≠⎧=⎨⎩ 或11,1,1n a s q na q -⎧⎪=-⎨⎪=⎩.10、常见三角不等式(1)若(0,)2x π∈,则sin x x <<. (2)若(0,)2x π∈,则1sin cos x x <+≤.(3) |sin ||cos |x x +≥.11.同角三角函数的基本关系式22sin cos θθ+=,tan θ=,12.正弦、余弦的诱导公式( 变 不变,符号看 )13.和角与差角公式 sin()αβ±=;cos()αβ±=;tan()αβ±=.sin cos a x b x +=)x ϕ+(辅助角ϕ 所在象限由点(,)a b 的象限决定,tan ϕ= )14.二倍角公式sin 2α=.cos 2α===tan 2α==.15.三角函数部分性质对比16.正弦定理17.余弦定理18.三角形面积19.在△ABC 中,有何特殊关系的三角函数。
高中数学必背公式大全

高中数学必背公式大全【代数基本公式】1. 二次方程的根公式:若二次方程ax²+bx+c=0的判别式Δ=b²-4ac≥0,则它的根公式为:x₁=(-b+√Δ)/2a,x₂=(-b-√Δ)/2a。
2. 四则运算公式:(a+b)²=a²+2ab+b²,(a-b)²=a²-2ab+b²,(a+b)(a-b)=a²-b²。
3. 余弦定理:a²=b²+c²-2bc·cosA,b²=a²+c²-2ac·cosB,c²=a²+b²-2ab·cosC。
4. 正弦定理:a/sinA=b/sinB=c/sinC=2R(R为三角形外接圆半径)。
5.二项式定理:(a+b)ⁿ=Cⁿ₀aⁿb⁰+Cⁿ₁aⁿ⁻¹b+Cⁿ₂aⁿ⁻²b²+……+Cⁿₙa⁰bⁿ。
【平面几何公式】1.两点间距离公式:AB=√[(x₂-x₁)²+(y₂-y₁)²]。
2. 直线斜率公式:k=tgθ=∆y/∆x=(y₂-y₁)/(x₂-x₁)。
3.两条直线垂直公式:k₁k₂=-1,其中k₁和k₂分别为两条直线的斜率。
4.点到直线距离公式:点A(x₀,y₀)到直线Ax+By+C=0的距离为d=,(Ax₀+By₀+C)/√(A²+B²)。
【解析几何公式】1. 点乘公式:a·b=,a,b,cosθ,其中a=(x₁,y₁)和b=(x₂,y₂)。
2.向量模长公式:,a,=√(x²+y²)。
3. 向量夹角公式:cosθ=(a·b)/(,a,b,),其中a和b为向量。
【三角函数公式】1. 正弦函数基本关系:sin²θ+cos²θ=12. 余弦函数基本关系:1+tan²θ=sec²θ,1+cot²θ=csc²θ。
高中数学公式总结-默写版

高中数学公式总结一、集合1、 若集合A 中有n )(N n ∈个元素,则集合A 的所有不同的子集个数为______,所有非空真子集的个数是______。
2、 若AB A A B B =⇔=⇔_________________3、 真值表4、常见结论的否定形式5、充要条件(1)充分条件:____________________ (2)必要条件:____________________ (3)充要条件:____________________. 二、函数1、 二次函数c bx ax y ++=2的图象的对称轴方程是______________,顶点坐标是___________。
用待定系数法求二次函数的解析式时,解析式的设法有3种形式,即____________________,____________________和____________________ .2、0)(2>++=c bx ax x f 恒成立的充要条件是_________________;0)(2<++=c bx ax x f 恒成立的充要条件是_____________________; 0)(2≥++=c bx ax x f 恒成立的充要条件是_________________; 0)(2≤++=c bx ax x f 恒成立的充要条件是_________________;3、单调性单调增:①_________________________________________;②___________________________; 单调减:①_________________________________________;②___________________________; 4、奇偶性 (1)前提:(2)奇函数:______________________________________;其图像_______________________; 偶函数:______________________________________;其图像_______________________; (3)若函数)(x f y =是奇函数,且在0=x 处有定义,则_____________;(4) 多项式函数110()n n n n P x a x a x a --=+++的奇偶性:多项式函数()P x 是奇函数⇔______________________________________;. 多项式函数()P x 是偶函数⇔______________________________________;. 5、定义域:6、相同函数:_________________________,_____________________;7、函数图象: (1)指数函数:(2)对数函数:(3)幂函数: (4)三角函数8、对称性与周期性:(1)若)()(x a f x a f -=+,则_______________;若)()(x b f x a f -=+,则_______________; (2)若)()(a x f a x f -=+,则_______________;若)()(a x f x f += ,则_______________;(3)若)(1)(x f a x f =+, 则_______________;若)()(x f a x f -=+ ,则_______________; 9、计算: (1)=nm a________________;=n n a _____________________(2)=sr a a _______________;=s r a )(_______________;=rab )(_______________.(3)=+N M a a log log _____________;=-N M a a log log _____________;=ma M n log_____________;(4)=oa _____________;=Na a log _____________;0______log =a ;1______log =a .10、导数:(1) ='C __________;(2)=')(n x ____________;(3) =')(sin x _____________;.(4) =')(cos x _____________;(5) =')(ln x _____________;(6)=')(log xa _____________;. (7) =')(xe _____________;(8)=')(xa _____________; 11、图像变化(1))()(a x f x f +→:___________________________________; (2)a x f x f +→)()(:___________________________________;(3)|)(|)(x f x f →:___________________________________; (4)|)(|)(x f x f →:___________________________________; 三、三角函数1、 若点),(y x P ,点P 到原点的距离记为r ,则sin α=_____,cos α=_____,tan α=____。
高中数学必备的289个公式

(2)f(x+a)=-f(x)⇒T=2a;
(3)f(x+a)=±f(x)⇒T=2a
43.对称轴标志:f(x+a)=-f(b-x)⇒对称中心为(a+b,0);
如常见的对称中心有:f(x+a)=-f(a-x)⇒对称中心为(a,0);f(x+1)=-f(1-x)⇒对称 中心为(1,0).
16.不等式相同性:任意x∈D,证明:
f(x)>g(x)⇔h(x)=f(x)-g(x)>0⇔h(x)min>0;
存在x∈D,证明:f(x)≤g(x)⇔h(x)=f(x)-g(x)≤0⇔h(x)min≤0.
17.不等式相异性:任意x1、x2∈D,证明:f(x1)<g(x2)⇔x∈D,f(x)max<g(x)min;存在x1、x2∈D,证明:f(x1)>g(x2)⇔x∈D,f(x)max>g(x)min.
第2章函数
31.几个近似值:2≈1.414,3≈1.732,5≈2.236,
π≈3.142,e≈2.718,e2≈7.389,
ln3≈1.0986,ln2≈0.693.32.指数公式:(1)am=man;(2)nan={|a|,n为偶数.
33.对数公式:
(1)ax=N⇔x=logaN;(2)alogaN=N;
x1+y1x2+y2≥x1x2+y1y2.
(1+x)n≥xn+nx;n≥1(1+x)n≤1+nx;0≤n≤1
86.洛必达法则:limf(x)=limf'(x)(当f(x)→0或∞时使用).
87.恒成立问题:(1)a≥f(x)⇔a≥f(x)max;(2)a<f(x)⇔a<f(x)min.
高中必背88个数学公式

高中必背88个数学公式1. 勾股定理:直角三角形的两条直角边的平方和等于斜边平方。
2. 余弦定理:在任意三角形中,一个角的余弦等于与该角相对的边的平方和减去另外两条边的平方的差再除以两倍的另一条边与该角相对的角的正弦的乘积。
3. 正弦定理:在任意三角形中,一个角的正弦等于与该角相对的边长和另外两条边长的比例的乘积。
4. 长方形面积公式:长方形的面积等于长乘以宽。
5. 平行四边形面积公式:平行四边形面积等于底边长乘以高。
6. 梯形面积公式:梯形的面积等于上底加下底乘以高再除以二。
7. 三角形面积公式:三角形面积等于底边长乘以高再除以二。
8. 圆面积公式:圆的面积等于圆周率乘以半径的平方。
9. 圆周长公式:圆的周长等于直径乘以圆周率。
10. 球体表面积公式:球体的表面积等于四倍的圆面积。
11. 球体体积公式:球体的体积等于四分之三的圆面积乘以半径的立方。
12. 一次函数方程: y = kx + b。
13. 二次函数方程: y = ax² + bx + c。
14. 等差数列通项公式: an = a1 + (n - 1)d,其中a1为首项,d为公差,an为第n项。
15. 等差数列前n项和公式: Sn = n(a1 + an)/2,其中a1为首项,an为第n项,n为项数。
16. 等比数列通项公式:an = a1 × qⁿ⁻¹,其中a1为首项,q为公比,n为项数。
17. 等比数列前n项和公式: Sn = a1(1 - qⁿ)/1 - q,其中a1为首项,q为公比,n为项数。
18. 三角函数正弦的定义:在直角三角形中,任意一锐角的正弦是指这个角的对边与这个角所在的斜边的比值。
19. 三角函数余弦的定义:在直角三角形中,任意一锐角的余弦是指这个角的邻边与这个角所在的斜边的比值。
20. 三角函数正切的定义:在直角三角形中,任意一锐角的正切是指这个角的对边与这个角的邻边的比值。
21. 三角函数余切的定义:在直角三角形中,任意一锐角的余切是指这个角的邻边与这个角的对边的比值。
最新高中数学公式默写

数学公式复习1、集合12{,,,}n a a a 的子集共有 个;真子集有 个;非空子集有 个; 非空的真子集有 个. 2、充要条件(1)若q p ⇒,则p 是q . (2)若p q ⇒,则p 是q . (3)若p q ⇒,且q p ⇒,则p 是q. 3、110()nn n n P x a x a x a --=+++的奇偶性()P x 是奇函数⇔()P x 的偶次项的系数 .()P x 是偶函数⇔()P x 的奇次项的系数4、分数指数幂(1)m na=(0,,a m n N *>∈,且1n >).(2)n a -=(0,,a m nN *>∈,且1n >).5、有理指数幂的运算性质(1) (0,,)r s a a a r s Q ⋅=∈. (2) (0,,)rs a a r s Q =>∈. (3)(0,0,)r r a b a b r Q =>>∈. (4)0a =(a ≠0)6、指数式与对数式的互化式l o g a N b N=⇔=(0,1,0)a a N >≠>. 7、 对数的四则运算法则若a >0,a ≠1,M >0,N >0,则 (1)l o g ()l o g l o g a a a M N =+; 对数相加(2) ()l o g l o g l o g aa a M N =-;对数相减(3)l o g ()na M n R =∈. 对数的倍数 (4)1l o g b a=对数的倒数 (5)l o g a ba=,l o g 1a =,l o g 1a= 8、等差数列的通项公式*________()n a n N ==∈;其前n 项和公式为n s =____________________=2()n n =+.9、等比数列的通项公式*()n a n N =∈;其前n 项的和公式为1_____,1n qs na ≠⎧=⎨⎩ 或11,1,1n a s q na q -⎧⎪=-⎨⎪=⎩.10、常见三角不等式(1)若(0,)2x π∈,则sin x x <<. (2)若(0,)2x π∈,则1sin cos x x <+≤.(3) |sin ||cos |x x +≥.11.同角三角函数的基本关系式22sin cos θθ+=,tan θ=,12.正弦、余弦的诱导公式( 变 不变,符号看 )13.和角与差角公式 sin()αβ±=;cos()αβ±=;tan()αβ±=.sin cos a x b x+=sin()x ϕ+(辅助角ϕ 所在象限由点(,)a b 的象限决定,tan ϕ= )14.二倍角公式sin 2α=.cos 2α===tan 2α==.15.三角函数部分性质对比16.正弦定理17.余弦定理18.三角形面积19.在△ABC 中,有何特殊关系的三角函数。
高数公式(默写)

高数公式默写☐ 麦克劳林公式 0x →x e =sin x =cos x =11x =-11x=+ln(1)x +=(1)ax +=☐ 等价无穷小(除以上,其他重要部分)sin sin x x arc x x -⎧⎪⎨⎪-⎩tan arctan x x x x -⎧⎪⎨⎪-⎩1cos ax-1x a-☐ 其余 ⑴()f x 、()g x 在0x =的邻域内C ,且0()lim1()x f x g x →=则()()xxg t dtf t dt⎰⎰⑵0100lim ln (0)sin lim lim(1)x x x x +∂→→→⎧=∂>⎪⎨⎪=+=⎩ ☐ 间断点第I 类:(0)(0)f x f x +-∃、⎧⎨⎩可去:跳跃:第II 类:☐ 极值点、拐点⑴0'()0f x =,00''()0f x >⎧⎨<⎩ ⇒推(21)000'()''()()0k f x f x f x -===且(2)00()0k f x >⎧⎨<⎩ ⑵''()0f x >''()0f x <凹凸性'()f x ⇒的 性⑶0''()0f x =,0'''()0f x ≠⇒推(2)000''()'''()()0k f x f x f x ===且(21)00()0k fx x +≠⇒是注:若00(,())x f x 为()f x 极值点则or ⎧⎪⎨⎪⎩若00(,())x f x 为()f x 拐点则or ⎧⎪⎨⎪⎩☐无穷大 n →∞log (1)(1)(1)!n k n na a n n k a a n n ><<><><<默一次:<<<<☐重要不等式:【默一遍】 ⑴ 222 ab a b +⑵ln(1) (0)1x x x x x+>+⑶0 arctan sin arcsin tan 2sin tan x x x x x xx x xπ<<⑷2211(1)02!2!xxxx e x x e x e x +=+++⋅⋅⋅⇒-+=+⋅⋅⋅>⑸12na a a n+++≤⑹柯西不等式:222(()())()()bbbaaaf xg x dx f x dx g x dx≤⋅⎰⎰⎰☐ 一些必备公式1n x -=cos2x =2tan 2x=tan2x =22sec csc x x ⎧=⎪⎨=⎪⎩tan() 2cot() 2παπα⎧±=⎪⎪⎨⎪±=⎪⎩☐ 求导工具⑴()'ax =()'c =(sin )'x =(cos )'x =()'x e =()'x a =(log )'a x =(ln )'x =⑵(tan )'x =(cot )'x =(sec )'x =(csc )'x =(sin )'arc x =(cos )'arc x =(arctan )'x =(cot )'arc x =☐ ⑶考前背熟ln('x ⎡⎤+=⎣⎦[]ln(sec tan )'x x +=⑷高阶导数()1()n ax b=+()(sin )n kx =()(cos )n kx =()()n uv =⑸()xa d f t dt dx =⎰21()()()x x d f t dt dx ϕϕ=⎰☐ 渐近线⑴铅直渐近线:找点x a <=>()()lim x a x a x a y +-→→→=∞⑵水平渐近线y A <=>lim x y A →∞=(二条不同的+∞⎧⎨-∞⎩)y A V==±条⑶斜渐近线y ax b <=+>a b =⎧⎨=⎩☐积分公式 ⑴kdx =⎰x dx α=⎰1dx x =⎰xe dx =⎰=x a dx =⎰211dx x =+⎰⑵2sec xdx =⎰2c cs xdx =⎰sec tan x xdx =⎰csc cot x xdx =⎰sin xdx =⎰cos xdx =⎰⑶==22dx a x =+⎰22dx x a =-⎰⇒ 令(4)tan xdx =⎰cot xdx =⎰△sec xdx =⎰△csc xdx =⎰(5)三角函数替换⇒⇒⇒☐定积分重要公式N L -:()baf t dt =⎰对称区间:()aaf x dx -=⎰⎧⎨⎩奇:偶:三角函数:(sin )xf x dx π=⎰22201sin cos n n n n n I xdx xdx I nππ--===⎧=⎨⎩⎰⎰ 奇偶☐ 积分中值定理[]() (,)()() ,b a baf x dx a b f xg x dx a b δδ⎧=∈⎪⎨⎪=∈⎩⎰⎰① ② ☐ Γ函数10()x e x dxαα+∞--Γ=⎰①(1)αΓ+=②(1)n Γ+=③1()2Γ=☐ 面积or 体积()baS f x dx=⎰2()bx aV f x dxπ=⎰2()by aV xf x dxπ=⎰☐多元函数微分学 (,)Z f x y = (,,)0F x y z =zx∂=∂z y∂=∂00(,)x yz x∂=∂00(,)x yz y∂=∂dz =+若22lim0x y x y→→=+⇒则eg 0(,)(0,0)()lim 0()f x y f A x B y Ax By ρρ→--+==+ρ=0(,)(0,0)()lim 0f x y f Ax By ρρ→--+==关系:连续可偏导可微连续可偏导偏导数连续☐ 条件极值与无条件极值无条件极值1step :00zxz y∂⎧=⎪∂⎪⎨∂⎪=∂⎪⎩ 求出驻点00(,)x y 2step : 2,,“”000“”A B C B AC A A ⎧⎧⎪⎪===⎪⎪⎪⎪=-⎨⎪⎨⎪<⎧⎪⎪⇒⎨⎪⎪>⎩⎩⎪⎪⎩若求极值,验证 才为极值点 若求最值,无须验证条件极值 (,)(,)0z f x y x y ϕ==求在条件下的极值拉格朗日乘数法 令(,)(,)Ff x y x y λϕ=+000x y F F F λ'⎧=⎪'=⇒⎨⎪'=⎩ 求出☐ 微分方程 一阶齐次:()0dyP x y dx+= 通解y =一阶非齐:()()dyp x y Q x dx+= 通解y =二阶齐次:'''0y py qy ++=1︒令,24p q=- 2︒ 0 ==0 =>⇒<⇒=⇒齐通齐通齐通, y y , y ⎧⎪⎨⎪⎩二阶非齐次:'''()y py qy f x ++= 1︒求 ,算出1λ、2λ⇒2︒看()f x 的形式:1)()()xn f x p x e α=*y k α=⎧⎪⎧⎪⇒=⎨⎪=⎨⎪⎪⎪⎩⎩2)()()cos ()sin xn m n m f x e p x x Q x x αββ>⎡⎤=+⎣⎦*y ⇒=其中k αβ⇒⎧⎪⎧⎨=⎨⎪⎩⎩、☐ 二重积分性质 1)(,)(,)DDf x y d f x y d σσ⎰⎰⎰⎰2)当(,)m f x y M ≤≤,S 为区域D 的面积则 (,) DmS f x y d MSσ⎰⎰直角坐标系1)先y 后x()()(,)bf x ax dx g x y dyϕ⎰⎰2)先x 后y 11()()(,)cf x dx dy g x y dxϕ⎰⎰可利用性质:对称性:利用x 轴、y 轴对称 利用y x =对称⇒x ,y 可对调 极坐标 r d rd d σθ=泰勒公式:()f x =有理式拆分:1()()ax b cx d =++1()nax b =+21()()ax bx c cx d =+++此无法解级数 ⑴常数项级数 判敛:【方法】①111,(),,n n n n n n n n n n n n nu v u v u v u v u v ∞∞∞===⇒⎧⎪±=±⇒⎨⎪⇒⎩∑∑∑都收敛其中一个发散都发散②必要条件:1lim 0n n n n a a ∞→∞==∑收敛③重要级数:1)11p n n ∞=∑11p p ≤⎧⎨>⎩11n n∞=∑发 2)1nn aq ∞=∑11q q ⎧≤⎪⎨>⎪⎩11a s q=-3)221111(ln )1ln p q n n p p q n n n n∞∞==⎧>⎧⎨⎪=>⎪⎩⎨⎪⎪⎩∑∑ 且 发④针对正项级数:0n a ≥1nn a∞=∑ 有上界⇒收1)比较审敛法:向零跑的速度快,收敛可能性越高lim 0n n n c a b →∞⎧⎪=⎨⎪+∞⎩ 2)比值审敛法:【阶乘】11lim 1n n na a ρρρ+→∞<⎧=⎨>⎩ 3)根值审敛法:【带n次方】1lim1n ρρρ→∞<⎧=⎨>⎩ ⑤交错级数及其审敛法:莱布尼茨审敛法:11(1)(0)n n n n u u ∞-=⎧->⎨⎩∑⇒收敛⑥一些:tips添加| | ⇒ 发散性↑添加( ) ⇒ 收敛性↑(2)幂级数00/()nnn n n n a x a x x ∞∞==-∑∑①求收敛域:1:step 求R1limlim n n nn a a R ρρ+→∞→∞⎧=⎪⎪⇒=⎨⎪=⎪⎩2:step 单独讨论 x R =±的敛散性3:step 收敛域:note 对0n n n a x ∞=∑,在0x 处条件下收敛,则R =②和函数:1)常见公式:()000()()()!n nn f x f x x x n ∞==-∑xe =sin x =cos x =11x =-11x =+ln(1) ln (1)x x '-=-=ln(1)x +=2)分析性质:逐项可导性质:1()'nn n n n n a x a nx ∞∞-===∑∑ 逐项可积性质:1000()1xxnnn n n n n n n a a x dx a x dx x n ∞∞∞+=====+∑∑∑⎰⎰ 注:R 仍是R ,但端点处收敛性须判断数三专项○背差分方程一阶差分:1t t t y y y +-=二阶差分:221()2t t t t ty y y y y ++==-+差分方程☆形如:1() 0t t y ay f t a ++=≠⑴齐次:10t t y ay ++=1aλ=-y =齐 C 为∀常⑵非齐:12()tt t m y ay p t λ++=⋅仍齐+非齐*y =特:1()t t m y ay p t ++=*y =。
高中数学公式大全(最整理新版)

高中数学公式大全(最整理新版)一、代数1. 一元一次方程:ax + b = 0,其中a ≠ 0。
解为 x = b/a。
2. 一元二次方程:ax^2 + bx + c = 0,其中a ≠ 0。
解为 x =[b ± sqrt(b^2 4ac)] / 2a。
3. 一元三次方程:ax^3 + bx^2 + cx + d = 0,其中a ≠ 0。
解为x = [b ± sqrt(b^2 3ac)] / 3a。
4. 一元四次方程:ax^4 + bx^3 + cx^2 + dx + e = 0,其中 a≠ 0。
解为x = [b ± sqrt(b^2 4ac)] / 2a。
5. 分式方程:分子和分母均为多项式。
解法为将方程两边乘以分母的乘积,得到一个等价的整式方程,然后求解。
6. 二元一次方程组:由两个一元一次方程组成的方程组。
解法为消元法或代入法。
7. 二元二次方程组:由两个一元二次方程组成的方程组。
解法为消元法或代入法。
8. 三元一次方程组:由三个一元一次方程组成的方程组。
解法为消元法或代入法。
9. 等差数列:首项为 a1,公差为 d。
第 n 项为 an = a1 + (n 1)d。
前 n 项和为 Sn = n/2(a1 + an)。
10. 等比数列:首项为 a1,公比为 q。
第 n 项为 an = a1q^(n 1)。
前 n 项和为 Sn = a1 (1 q^n) / (1 q),其中q ≠ 1。
二、几何1. 平面几何(1)直线:两点确定一条直线,直线方程为 y = mx + b,其中m 是斜率,b 是截距。
(2)圆:圆心为 (a, b),半径为 r。
圆的方程为 (x a)^2 +(y b)^2 = r^2。
(3)椭圆:中心为 (a, b),长轴为 2a,短轴为 2b。
椭圆的方程为 (x a)^2 / a^2 + (y b)^2 / b^2 = 1。
(4)双曲线:中心为 (a, b),实轴为 2a,虚轴为 2b。
高中数学公式总结-默写版

高中数学公式总结-默写版高中数学公式总结必要条件是指某个条件必须满足,否则结论就不成立。
充要条件是指某个条件既是必要条件,又是充分条件,只要满足这个条件,结论就一定成立。
一、集合如果集合A中有n个元素,那么集合A的所有不同的子集个数为2^n,所有非空真子集的个数是2^n - 1.二、函数1.二次函数y = ax^2 + bx + c的图像的对称轴方程是x = -b/2a,顶点坐标是(-b/2a。
f(-b/2a))。
用待定系数法求二次函数的解析式时,解析式的设法有3种形式,即标准式、顶点式和一般式。
2.若AB = A,则B = A;若AB = B,则A = AUB。
3.真值表p q 非p p或q p且q真真假真真真假真真假假真真真假假假真假假4.常见结论的否定形式原结论反设词原结论反设词是不是至少有一个一个也没有大于不大于至少有n个至多有(n-1)个对所有x,成立存在某x,不成立p或q 非p且非q5.充要条件充分条件是指某个条件成立,则结论一定成立;必要条件是指结论成立,则该条件一定成立。
2.f(x) = ax^2 + bx + c。
恒成立的充要条件是a。
0;f(x) = ax^2 + bx + c < 恒成立的充要条件是a < 0;f(x) = ax^2 + bx + c ≥ 恒成立的充要条件是a ≥ 0,且a = 0时b ≥ 0;f(x) = ax^2 + bx + c ≤ 恒成立的充要条件是a ≤ 0,且a = 0时b ≤ 0.3.单调性单调增:①f'(x)。
0;②f''(x) ≥ 0.单调减:①f'(x) < 0;②f''(x) ≤ 0.4.奇偶性1)前提:函数f(x)在区间(-a。
a)内有定义。
2)奇函数:f(-x) = -f(x);其图像关于原点对称。
偶函数:f(-x) = f(x);其图像关于y轴对称。
3、若函数y=f(x)是奇函数,且在x=0处有定义,则f(0)=0.4、多项式函数P(x)=ax^n+an-1x^(n-1)+。
(完整版)高中数学公式总结-默写版

高中数学公式默写一、集合1、 若集合A 中有n )(N n ∈个元素,则集合A 的所有不同的子集个数为______,所有非空真子集的个数是______。
2、 若AB A A B B =⇔=⇔_________________3、 真值表4、常见结论的否定形式5、充要条件(1)充分条件:____________________ (2)必要条件:____________________ (3)充要条件:____________________. 二、函数1、 二次函数c bx ax y ++=2的图象的对称轴方程是______________,顶点坐标是___________。
用待定系数法求二次函数的解析式时,解析式的设法有3种形式,即____________________,____________________和____________________ .2、0)(2>++=c bx ax x f 恒成立的充要条件是_________________;0)(2<++=c bx ax x f 恒成立的充要条件是_____________________; 0)(2≥++=c bx ax x f 恒成立的充要条件是_________________; 0)(2≤++=c bx ax x f 恒成立的充要条件是_________________;3、单调性单调增:①_________________________________________;②___________________________; 单调减:①_________________________________________;②___________________________; 4、奇偶性 (1)前提:(2)奇函数:______________________________________;其图像_______________________; 偶函数:______________________________________;其图像_______________________; (3)若函数)(x f y =是奇函数,且在0=x 处有定义,则_____________;(4) 多项式函数110()n n n n P x a x a x a --=+++的奇偶性:多项式函数()P x 是奇函数⇔______________________________________;. 多项式函数()P x 是偶函数⇔______________________________________;.5、定义域:6、相同函数:_________________________,_____________________;7、函数图象: (1)指数函数:(2)对数函数:(3)幂函数: (4)三角函数8、对称性与周期性:(1)若)()(x a f x a f -=+,则_______________;若)()(x b f x a f -=+,则_______________; (2)若)()(a x f a x f -=+,则_______________;若)()(a x f x f += ,则_______________;(3)若)(1)(x f a x f =+, 则_______________;若)()(x f a x f -=+ ,则_______________; 9、计算:(1)=nm a________________;=n n a _____________________(2)=sr a a _______________;=s r a )(_______________;=rab )(_______________.(3)=+N M a a log log _____________;=-N M a a log log _____________;=m a M n log _____________;(4)=oa _____________;=Na a log _____________;0______log =a ;1______log =a .10、导数:(1) ='C __________;(2)=')(n x ____________;(3) =')(sin x _____________;.(4) =')(cos x _____________;(5) =')(ln x _____________;(6)=')(log xa _____________;. (7) =')(xe _____________;(8)=')(xa _____________; 11、图像变化(1))()(a x f x f +→:___________________________________; (2)a x f x f +→)()(:___________________________________; (3)|)(|)(x f x f →:___________________________________; (4)|)(|)(x f x f →:___________________________________;三、三角函数1、 若点),(y x P ,点P 到原点的距离记为r ,则sin α=_____,cos α=_____,tan α=____。
高一数学必修一公式默写-打印版

高一数学必修一公式默写-打印版介绍这份文档提供了高一数学必修一的公式默写内容,可以用于打印,以便学生在研究和复过程中使用。
公式列表以下是高一数学必修一的公式列表:1. 一次函数的标准方程:$$y = kx + b$$2. 一次函数的斜率公式:$$k = \frac{{y_2 - y_1}}{{x_2 -x_1}}$$3. 二次函数的标准方程:$$y = ax^2 + bx + c$$4. 二次函数的顶点坐标:$$x_v = -\frac{b}{{2a}}, y_v = -\frac{{\Delta}}{{4a}}$$5. 二次函数的判别式:$$\Delta = b^2 - 4ac$$6. 二次函数的轴对称线方程:$$x = -\frac{b}{{2a}}$$7. 平方差公式:$$(a + b)(a - b) = a^2 - b^2$$8. 二项式定理:$$(a + b)^n = C_n^0 \cdot a^n \cdot b^0 + C_n^1 \cdot a^{n-1} \cdot b^1 + \ldots + C_n^n \cdot a^0 \cdot b^n$$9. 直角三角形勾股定理:$$a^2 + b^2 = c^2$$10. 三角形面积公式:$$S = \frac{1}{2} \cdot a \cdot b \cdot\sin(C)$$使用说明学生可以使用这份打印版文档进行公式默写练。
建议按照顺序逐个默写公式,并在旁边标注出公式的名称。
默写过程中可以对照课本内容,以确保正确记忆和理解公式。
小结这份文档为高一数学必修一的公式默写提供了方便的打印版,能够帮助学生复习和记忆数学公式。
学生可以根据自己的需要,通过不断的练习来提高默写公式的准确性和熟练度。
高考数学必背公式整理(衡水中学高中数学组)

高考数学必背公式整理一、平面几何公式1. 直线方程- 一般式:Ax + By + C = 0- 斜截式:y = kx + b- 截距式:x/a + y/b = 1- 两点式:(y-y₁)/(x-x₁) = (y₂-y₁)/(x₂-x₁)2. 圆的方程- 标准方程:(x-a)² + (y-b)² = r²- 一般方程:x² + y² + Dx + Ey + F = 0 - 中心半径方程:(x-h)² + (y-k)² = r²3. 直角三角形- 勾股定理:a² + b² = c²- 正弦定理:a/sinA = b/sinB = c/sinC - 余弦定理:c² = a² + b² - 2abcosC- 正切定理:tanA = b/a4. 圆锥曲线- 椭圆:x²/a² + y²/b² = 1- 双曲线:x²/a² - y²/b² = 1- 抛物线:y² = 2px二、空间几何公式1. 空间中的直线- 参数方程:x = x₁ + at, y = y₁ + bt, z = z₁ + ct - 对称式:(x-x₁)/l = (y-y₁)/m = (z-z₁)/n2. 空间中的平面- 一般方程:Ax + By + Cz + D = 0- 点法式:A(x-x₁) + B(y-y₁) + C(z-z₁) = 0- 三点式:[ABCD] = 03. 空间中的球面- 标准方程:(x-a)² + (y-b)² + (z-c)² = r²- 一般方程:x² + y² + z² + Dx + Ey + Fz + G = 0 - 中心半径方程:(x-h)² + (y-k)² + (z-l)² = r²4. 空间向量- 点积:a·b = |a| |b| cosθ- 叉积:a×b = |a| |b| sinθn- 混合积:[a,b,c] = a·(b×c)三、解析几何公式1. 直线和平面- 平面方程:Ax + By + Cz + D = 0- 直线方程:(x-x₁)/l = (y-y₁)/m = (z-z₁)/n- 点到直线距离:d = |Ax₀ + By₀ + Cz₀ + D|/√(A² + B² + C²) - 点到平面距离:d = |Ax₀ + By₀ + Cz₀ + D|/√(A² + B² + C²)2. 点、向量和运算- 点积:a·b = |a| |b| cosθ- 叉积:a×b = |a| |b| sinθn3. 曲线和曲面- 曲线斜率:y‘ = f'(x) = dy/dx- 曲面切面:z = f(x, y)- 曲线弧长:L = ∫√(1 + (dy/dx)²)dx四、数列与级数公式1. 数列- 等差数列通项公式:aₙ = a₁ + (n-1)d- 等比数列通项公式:aₙ = a₁qⁿ⁻¹- 通项公式求和:Sₙ = (a₁+aₙ)n/22. 级数- 等差级数求和:Sₙ = n(a₁+aₙ)/2- 等比级数求和:Sₙ = a₁(1-qⁿ)/(1-q)3. 数学归纳法- 数学归纳法证明- 数学归纳法应用五、概率统计公式1. 概率- 事件概率:P(A) = n(A)/n(Ω)- 加法公式:P(A∪B) = P(A) + P(B) - 条件概率:P(A|B) = P(A∩B)/P(B)2. 统计- 样本均值:μ = Σxᵢ/n- 样本方差:σ²= Σ(xᵢ-μ)²/n- 标准差:σ = √σ²3. 随机变量- 期望:E(X) = ΣxᵢP(X=xᵢ)- 方差:Var(X) = E(X²) - [E(X)]²- 协方差:Cov(X,Y) = E((X-E(X))(Y-E(Y)))六、函数与导数公式1. 基本函数- 幂函数:f(x) = xⁿ- 指数函数:f(x) = aⁿ- 对数函数:f(x) = logₐx- 三角函数:f(x) = sinx, cosx, tanx2. 函数性质- 奇函数和偶函数- 单调性和极值- 函数图像和性态3. 导数与微分- 导数定义:f'(x) = lim(h→0)(f(x+h)-f(x))/h - 函数求导:(xⁿ)’ = nxⁿ⁻¹- 链式法则:(f(g(x)))’ = f’(g(x))·g’(x)- 微分运算:dy = f’(x)dx七、积分公式1. 不定积分- 基本积分公式 - 定积分计算 - 变限积分求导2. 定积分- 定积分性质 - 定积分应用 - 变限积分求导3. 微分方程- 微分方程定解 - 微分方程解法 - 微分方程应用八、高等代数公式1. 行列式- 二阶行列式 - 三阶行列式 - 克拉默法则2. 矩阵运算- 矩阵相加- 矩阵相乘- 矩阵转置3. 线性方程组- 高斯消元法- 矩阵法解方程组- 克拉默法则以上是高考数学必背公式的整理,希望同学们能够认真学习并灵活运用这些公式,提高数学应用能力,取得优异的成绩。
高中数学公式大全必背

高中数学公式大全必背一、集合1. 集合的基本运算- 交集:A∩ B = {x|x∈ A且x∈ B}- 并集:A∪ B={x|x∈ A或x∈ B}- 补集:∁_U A={x|x∈ U且x∉ A}(U为全集)2. 集合元素个数关系(容斥原理)- n(A∪ B)=n(A)+n(B)-n(A∩ B)二、函数1. 函数的定义域- 分式函数y = (f(x))/(g(x)),g(x)≠0。
- 偶次根式函数y=sqrt[n]{f(x)}(n为偶数),f(x)≥slant0。
2. 函数的单调性- 设x_1,x_2∈[a,b],x_1≠ x_2- 对于函数y = f(x),若f(x_1)-f(x_2)<0(当x_1 < x_2时),则y = f(x)在[a,b]上单调递增。
- 若f(x_1)-f(x_2)>0(当x_1 < x_2时),则y = f(x)在[a,b]上单调递减。
3. 函数的奇偶性- 对于函数y = f(x)定义域内任意x- 若f(-x)=f(x),则y = f(x)是偶函数。
- 若f(-x)= - f(x),则y = f(x)是奇函数。
4. 一次函数- 表达式y = kx + b(k≠0),斜率k=(y_2 - y_1)/(x_2 - x_1)。
5. 二次函数- 表达式y=ax^2+bx + c(a≠0)- 对称轴x =-(b)/(2a)- 顶点坐标(-(b)/(2a),frac{4ac - b^2}{4a})6. 指数函数- 表达式y = a^x(a>0,a≠1)- 当a > 1时,函数在R上单调递增;当0 < a < 1时,函数在R上单调递减。
7. 对数函数- 表达式y=log_{a}x(a > 0,a≠1,x>0)- 当a > 1时,函数在(0,+∞)上单调递增;当0 < a < 1时,函数在(0,+∞)上单调递减。
高二数列公式默写

高二数列公式默写
1.等差数列的通项公式:$a_n = a_1 + (n-1)d$,其中$a_1$ 是首项,
$d$ 是公差。
2.等差数列的求和公式:$S_n = \frac{n}{2}(a_1 + a_n)$。
3.等比数列的通项公式:$a_n = a_1 \times q^{(n-1)}$,其中$a_1$ 是首
项,$q$ 是公比。
4.等比数列的求和公式:当 $q
5.eq 1$ 时,$S_n = \frac{a_1(1 - q^n)}{1 - q}$。
6.裂项相消法求和:例如,对于形如$\frac{1}{n(n+1)}$ 的数列,其求和结
果为 $\frac{1}{n} - \frac{1}{n+1}$。
7.倒序相加法:当数列是等差数列或等比数列时,可以使用倒序相加法来求
和。
8.阶乘的定义:$n! = 1 \times 2 \times 3 \times \ldots \times n$。
9.二项式定理展开式:$(a+b)^n = \sum_{k=0}^{n} C_n^k a^{n-k} b^k$,
其中 $C_n^k = \frac{n!}{k!(n-k)!}$。
10.线性方程组的解法:包括加减消元法和代入法。
11.韦达定理:对于一元二次方程$ax^2 + bx + c = 0$,其根的和为$-
\frac{b}{a}$,根的积为 $\frac{c}{a}$。
数学必修二公式默写
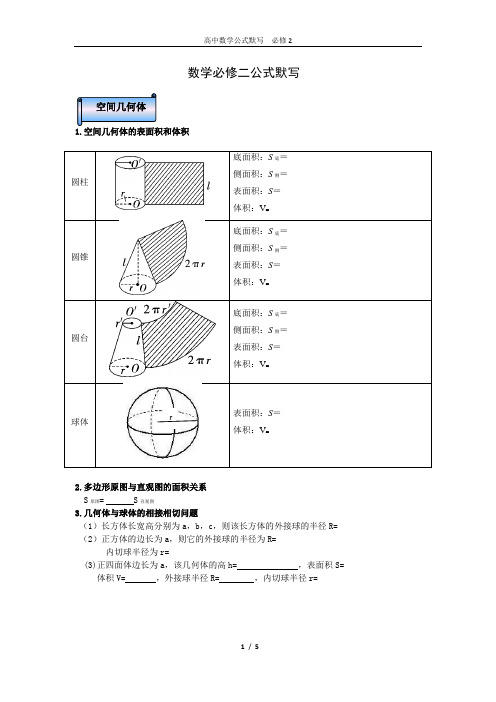
数学必修二公式默写圆柱底面积:侧面积:表面积:体积:圆锥底面积:侧面积:表面积:体积:圆台底面积:侧面积:表面积:体积:球体表面积:体积:2.多边形原图与直观图的面积关系S原图=S直观图3.几何体与球体的相接相切问题(1)长方体长宽高分别为a,b,c,则该长方体的外接球的半径R= (2)正方体的边长为a,则它的外接球的半径为R= 内切球半径为r=(3)正四面体边长为a,该几何体的高h= ,表面积S=体积V= ,外接球半径R= ,内切球半径r=r1.点线面的位置关系(1)空间中直线与直线的位置关系有(2)直线和平面的位置关系有(3)平面和平面的位置关系有2.空间中的平行关系(1)直线和平面平行的判定定理文字语言符号语言(2)平面和平面平行的判定定理文字语言符号语言(3)直线和平面平行的性质定理文字语言符号语言(4)平面和平面平行的性质定理文字语言符号语言3.空间中的垂直关系(1)直线和平面垂直的判定定理文字语言符号语言(2)平面和平面垂直的判定定理文字语言符号语言(3)直线和平面垂直的性质定理文字语言符号语言(4) 平面和平面垂直的性质定理文字语言符号语言4.空间中的角(1)异面直线所成的角(作图说明), 范围为(2)直线和平面所成的角(作图说明),范围为(3)二面角的平面角(作图说明), 范围为异面直线所成角 直线和平面所成角 二面角平面角1.倾斜角和斜率 (1)倾斜角定义: 倾斜角范围 (2)斜率定义:过两点P(11,y x ),Q(22,y x )(21x x )的直线斜率k=2.直线方程(1)点斜式:点P (x 0,y 0)和斜率k 直线方程(2)斜率k 和在y 轴上的截距b 直线方程(3)两点式:P 1(x 1,y 1),P 2(x 2,y 2),其中x 1≠x 2,y 1≠y 2 直线方程(4)截距式:在x ,y 轴上的截距分别为a ,b 且ab ≠0 直线方程3.直线的平行和垂直的判定(1) 111:b x k y l += ,222:b x k y l +=,则两直线平行的条件是垂直的条件是 ,(2)若l 1: A 1x + B 1y + C 1 = 0 , l 2:A 2x + B 2y + C 2 = 0,则两直线平行的条件 垂直的条件是(3) 与直线 Ax + By + C = 0 平行的直线可设为__________________与直线 Ax + By + C = 0 垂直的直线可设为_______________________4.距离(1)已知平面直角坐标系xoy 中,),(211x x p 和),(222y x P ,则21P P =_________________(2)已知),(00y x P 和直线l :0=++C By Ax ,则P 到直线l 的距离d =_______________(3)已知两条平行线直线1l :01=++C By Ax ,直线2l :02=++C By Ax ,则1l 和2l 之间的距离为__________________________________(4)过直线直线1l :0111=++C y B x A ,直线2l :0222=++C y B x A 交点的直线可设为 ____________________________1.圆的定义:____________________________________________2.圆的圆心为),(b a ,半径为r 的圆的标准方程为 ____________________________3.圆的一般方程中022=++++F Ey Dx y x (0422>-+F E D )中,圆心坐标为______半径r =____________________4.直线和圆的位置关系有 , , 。
高中数学必背公式大全高考必考数学公式

高中数学必背公式大全高考必考数学公式1.二次方程的根与系数之间的关系:设二次方程 ax^2 + bx + c = 0(a ≠ 0)的根为 x1 和 x2,那么有以下关系式:x1+x2=-b/ax1*x2=c/a2.一元二次不等式的求解:设二次不等式 ax^2 + bx + c > 0(a ≠ 0)的解集为 S,那么有以下关系式:a>0时,S={x,x<x1或x>x2}a<0时,S={x,x1<x<x2}3.二次函数的顶点坐标:设二次函数 y = ax^2 + bx + c 的顶点坐标为 (h, k)那么有 h = -b/2a,k = f(h) = (4ac - b^2)/4a4.一次函数的斜率与函数图像的关系:设一次函数 y = mx + c 的斜率为 m,那么有以下关系式:m>0时,函数图像上升;m<0时,函数图像下降;m=0时,函数图像水平。
5.三角函数和三角公式:sin(A + B) = sinA * cosB + cosA * sinBcos(A + B) = cosA * cosB - sinA * sinBtan(A + B) = (tanA + tanB) / (1 - tanA * tanB)sin^2A + cos^2A = 1sin²θ + cos²θ = 16.幂函数的性质:若 a > 0 且a ≠ 1,则函数 y = ax^n (n 是整数)的性质如下:n>0时,函数图像单调递增;n<0时,函数图像单调递减;n为偶数时,函数图像关于y轴对称;n为奇数时,函数图像关于原点对称。
7.对数函数的性质:若 a > 0 且a ≠ 1,则函数 y = log_a(x) 的性质如下:a>1时,函数图像单调递增;0<a<1时,函数图像单调递减;函数图像过点(1,0),且以x轴为渐近线;log_a(a^b) = b8.指数函数的性质:若a>0且a≠1,则函数y=a^x的性质如下:a>1时,函数图像单调递增;0<a<1时,函数图像单调递减;函数图像过点(0,1),且a^0=1a^m*a^n=a^(m+n)9.排列组合公式:将n个物体排成一列,有以下公式:排列公式:从n个物体中任选m个物体的排列数为A(n,m)=n!/(n-m)!组合公式:从n个物体中任选m个物体的组合数为C(n,m)=n!/(m!*(n-m)!)10.三角函数的和差化积:sin(A + B) = sinA * cosB + cosA * sinBsin(A - B) = sinA * cosB - cosA * sinBcos(A + B) = cosA * cosB - sinA * sinBcos(A - B) = cosA * cosB + sinA * sinBtan(A + B) = (tanA + tanB) / (1 - tanA * tanB)tan(A - B) = (tanA - tanB) / (1 + tanA * tanB)这些公式是高中数学中的常用公式,掌握并熟练运用它们对于高考数学考试非常重要。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学公式总结一、集合1、若集合A 中有n )(N n个元素,则集合A 的所有不同的子集个数为______,所有非空真子集的个数是______。
2、若A B A A B BI U _________________3、真值表pq非pp或qp且q真真真假假真假假4、常见结论的否定形式原结论反设词原结论反设词是不是至少有一个一个也没有大于不大于至少有n 个至多有(1n )个对所有x ,成立存在某x ,不成立p 或q p 且q5、充要条件(1)充分条件:____________________(2)必要条件:____________________ (3)充要条件:____________________.二、函数1、二次函数c bx ax y2的图象的对称轴方程是______________,顶点坐标是___________。
用待定系数法求二次函数的解析式时,解析式的设法有3种形式,即____________________,____________________和____________________ . 2、0)(2cbx ax x f 恒成立的充要条件是_________________; 0)(2c bx ax x f 恒成立的充要条件是_____________________; 0)(2c bx ax x f 恒成立的充要条件是_________________; 0)(2cbxaxx f 恒成立的充要条件是_________________;3、单调性单调增:①_________________________________________;②___________________________;单调减:①_________________________________________;②___________________________;4、奇偶性(1)前提:(2)奇函数:______________________________________;其图像_______________________;偶函数:______________________________________;其图像_______________________; (3)若函数)(x f y是奇函数,且在0x处有定义,则_____________;(4) 多项式函数110()nn n n P x a xa xa L的奇偶性:多项式函数()P x 是奇函数______________________________________;. 多项式函数()P x 是偶函数______________________________________;.5、定义域:6、相同函数:_________________________,_____________________;7、函数图象:(1)指数函数:(2)对数函数:(3)幂函数:(4)三角函数8、对称性与周期性:(1)若)()(x a f x a f ,则_______________;若)()(x b f x a f ,则_______________;(2)若)()(a x f a xf ,则_______________;若)()(a xf x f ,则_______________;(3)若)(1)(x f a x f ,则_______________;若)()(x f a x f ,则_______________;9、计算:(1)nma________________;nna_____________________(2)sr aa _______________;sr a )(_______________;rab)(_______________. (3)NM a a log log _____________;NM a a log log _____________;ma Mnlog _____________; (4)oa_____________;Na alog _____________;0______log a ;1______log a .10、导数:(1)C__________;(2)')(n x ____________;(3) )(sin x _____________;. (4) )(cos x _____________;(5))(ln x _____________;(6))(log xa _____________;.(7) )(xe _____________;(8))(xa _____________;11、图像变化(1))()(a x f x f :___________________________________; (2)a x f x f )()(:___________________________________;(3)|)(|)(x f x f :___________________________________; (4)|)(|)(x f x f :___________________________________;三、三角函数1、若点),(y x P ,点P 到原点的距离记为r ,则sin=_____,cos =_____,tan =____。
2、同角三角函数的关系中,平方关系是:__________________;倒数关系是:__________________;相除关系是:__________________.3、诱导公式可用十个字概括为:______________________________________;例如计算:4、函数B x A y )sin(),(其中00A 的最大值是_________,最小值是_________,周期是_________,其图象的对称轴是直线_________。
5、三角函数的单调区间:x y sin 的递增区间是____________________)(Z k,递减区间是_________-___________)(Z k;x y cos 的递增区间是____________________)(Z k,递减区间是_________-___________)(Z k,x y tan 的递增区间是____________________)(Z k 6、和角、差角公式:)sin(___________________________;)cos(_____________________________)tan(____________________7、二倍角公式是:sin2=_____________;cos2=______________=_______________=_______________;tan2=______________。
8、降幂公式是:2sin_______________;2cos_______________;cossin _______________.9.特殊角的三角函数值:643223sin cos tan10、正弦定理:______________________________________适用情况:___________________________________11、余弦定理:(边的形式)__________________________________(角的形式)____________________________12、面积公式:______________________________________ 13、△ABC 中:________.B)+cos(A ,________=B)+sin(A 14、辅助角公式:sin cos a b =____________________________四、平面向量1、坐标运算:设2211,,,y x b y x a,则_____________ba设A 、B 两点的坐标分别为(x 1,y 1),(x 2,y 2),则_______________AB .2.实数与向量的积的运算律:___________________________,b a a a设y x a ,,则λ_________,y x a .3.平面向量的数量积:定义:______________________________________ba ,_______0a;_______2a ;_______||a 4.重要定理、公式: (1)平面向量的基本定理如果1e 和2e 是同一平面内的两个不共线向量,那么对该平面内的任一向量a ,有且只有一对实数21, ,使______________a (2)两个向量平行的充要条件______________________________//b a (3)两个非零向量垂直的充要条件______________________________/ba 五、数列等差数列等比数列公式定义__________________________________________作用:这是证明一个数列是等差数列或等比数列的方法通项公式___________________________na ___________________________na 前n 项和____________________________ns _____________n s 性①________________________(等差中项)________________________(等比中项)质②qp n m _____________________qp n m _____________________③_____________________________成等差数列_____________________________成等比数列④六、排列组合、二项式定理②加法原理:_____________________;乘法原理:_____________________。
2、排列数公式:mn A =_____________________=_____________________;排列数与组合数的关系:_____________________;组合数公式:mn C =_____________________=_____________________;组合数性质:(1)m nC =______________,m n C+1m nC=_______________,(2)L_______...210nnr n nnnC CCCC 3、二项式定理:__________________________________)(nb a 二项展开式的通项公式:___________________1rT ),2,1,0(n r七、解析几何③同一坐标轴上两点距离公式:._____________AB ④直角坐标平面内的两点间距离公式:.________________________AB⑤若点),(),(),(222111y x P y x P y x P ,,,点P 分有向线段21P P 成定比λ,则:λ=___________;x =_____________,y =________________.若),(),(),(332211y x C y x B y x A ,,,则△ABC 的重心G 的坐标是____________________.6、直线的斜率为k=_________=____________.7、直线方程的几种形式:点斜式:_______________________,斜截式:_______________________ 截距式:_______________________,一般式:_______________________.8、点),(00y x P 到直线0C By Ax l :的距离:_______________________10、两平行直线002211C ByAxl C ByAxl :,:距离_______________________11、若21//l l ,则_______________________;_______________________. 12、若21l l ,则_______________________;_______________________.13、圆的标准方程:_______________________圆的一般方程:_______________________,成立条件_______________________ 其中,半径是r=_______________________,圆心坐标是_______________________14、点00(,)P x y 与圆222)()(r b y a x 的位置关系:____________________________________;____________________________________;____________________________________;15、直线0CBy Ax与圆222)()(r b y a x的位置关系:_______________________________________________________;_______________________________________________________;_______________________________________________________;16、两圆的位置关系:(位置,判断方法,交点个数)_______________________________________________________;_______________________________________________________;_______________________________________________________;_______________________________________________________;_______________________________________________________;17、抛物线标准方程的四种形式是:_______________________________.定义:________________________________;18、抛物线px y22的焦点坐标是:____________,准线方程是:____________。
