小学五年级奥数 容斥原理(二)
五年级奥数:用例题讲解【容斥问题】的解题方法

五年级奥数:用例题讲解【容斥问题】的解题方法
容斥问题是指在计数时,必须注意没有重复,没有遗漏。
例题
五年级(2)班有45人,其中有35人参加了美术兴趣小组,有21人参加了体育兴趣小组,并且每个人至少参加了一个兴趣小组。
那么,两个兴趣小组都参加的有多少人?
解题方法一
分析
因为:
两个兴趣小组的总人数是:35+21=56(人),五年级(2)班只有45人,就出现了(多出了):56-45=11(人)。
所以:
这个多出的11人就是35和21重叠(重复)的部分。
我们在计算时既不能重复,也不能遗漏。
这个题目里重复的部分(11人)就是两个兴趣小组都参加的人数。
列式
(1)35+21=56(人)
(2)56-45=11(人)
答:两个兴趣小组都参加的有11人
解题方法二
1、我们来看下面的图解法:
2、根据题意以及图解,可以得出:
(1)35+21=56(人)
(2)56-45=11(人)
3、答:两个兴趣小组都参加的人数是11人。
练习题
1、五年级(1)班有46人,参加音乐兴趣小组的有30人,参加舞蹈兴趣小组的有25人,并且每个人至少参加了一个兴趣小组。
你知
道两个小组都参加的有多少人吗?
2、1-500这500个数字中,能被5或7整除的数一共有多少个?
(附练习题答案:第1题9人;第2题157个)。
容斥原理奥数原题

容斥原理在计数时,为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
容斥原理(1)如果被计数的事物有A、B两类,那么,A类或B类元素个数= A类元素个数+B类元素个数—既是A类又是B类的元素个数。
例1一次期末考试,某班有15人数学得满分,有12人语文得满分,并且有4人语、数都是满分,那么这个班至少有一门得满分的同学有多少人?分析:依题意,被计数的事物有语、数得满分两类,“数学得满分”称为“A类元素”,“语文得满分”称为“B类元素”,“语、数都是满分”称为“既是A类又是B类的元素”,“至少有一门得满分的同学”称为“A类或B类元素个数”的总和。
试一试:某班学生每人家里至少有空调和电脑两种电器中的一种,已知家中有空调的有41人,有电脑的有34人,二者都有的有27人,这个班有学生多少人?(并说一说你的想法。
)容斥原理(2)如果被计数的事物有A、B、C三类,那么,A类或B类或C类元素个数= A类元素个数+B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数—既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数1、某艺术团的小演奏家们每人都至少会演奏小提琴和钢琴中的一种。
他们中有32人会拉小提琴,27人会弹钢琴,小提琴和钢琴都能演奏的有11人。
这个团共有多少个小演奏家?2、一个班有学生42人,参加体育队的有30人,参加文艺队的有25人,并且全班每人至少参加一个队。
问:这个班两队都参加的有多少人?3、京华小学五年级学生采集标本。
采集昆虫标本的有25人,采集植物标本的有19人,两种标本都采集的有8人。
全班学生共有40人,没有采集标本的有多少人?4、有100位旅客,其中有10人既不懂英语又不懂日语,有75人懂英语,83人懂日语。
奥数训练专题容斥原理

容斥原理1、某班学生手中分别拿红、黄、蓝三种颜色的小旗,手中有红旗的共有34人,手中有黄旗的共有26人,手中有蓝旗的共有18人.其中手中有红、黄、蓝三种小旗的有6人.而手中只有红、黄两种小旗的有9人,手中只有黄、蓝两种小旗的有4人,手中只有红、蓝两种小旗的有3人,那么这个班共有多少人?2、某班有42人,其中26人爱打篮球,17人爱打排球,19人爱踢足球,9人既爱打篮球又爱踢足球,4人既爱打排球又爱踢足球,没有一个人三种球都爱好,也没有一个人三种球都不爱好.问:既爱打篮球又爱打排球的有几人?3、四年级一班有46名学生参加3项课外活动.其中有24人参加了数学小组,20人参加了语文小组,参加文艺小组的人数是既参加数学小组也参加文艺小组人数的3.5倍,又是3项活动都参加人数的7倍,既参加文艺小组也参加语文小组的人数相当于3项都参加的人数的2倍,既参加数学小组又参加语文小组的有10人.求参加文艺小组的人数.〔6级〕4、五年级三班学生参加课外兴趣小组,每人至少参加一项.其中有25人参加自然兴趣小组,35人参加美术兴趣小组,27人参加语文兴趣小组,参加语文同时又参加美术兴趣小组的有12人,参加自然同时又参加美术兴趣小组的有8人,参加自然同时又参加语文兴趣小组的有9人,语文、美术、自然3科兴趣小组都参加的有4人.求这个班的学生人数.〔6级〕5、光明小学组织棋类比赛,分成围棋、中国象棋和国际象棋三个组进展,参加围棋比赛的有42人,参加中国象棋比赛的有55人,参加国际象棋比赛的有33人,同时参加了围棋和中国象棋比赛的有18人,同时参加了围棋和国际象棋比赛的有10人,同时参加了中国象棋和国际象棋比赛的有9人,其中三种棋赛都参加的有5人,问参加棋类比赛的共有多少人?〔6级〕6、新年联欢会上,共有90人参加了跳舞、合唱、演奏三种节目的演出.如果只参加跳舞的人数三倍于只参加合唱的人数;同时参加三种节目的人比只参加合唱的人少7人;只参加演奏的比同时参加演奏、跳舞但没有参加合唱的人多4人;50人没有参加演奏;10人同时参加了跳舞和合唱但没有参加演奏;40人参加了合唱;那么,同时参加了演奏、合唱但没有参加跳舞的有多少人?7、五年级三班有46名学生参加三项课外活动,其中24人参加了绘画小组,20人参加了合唱小组,参加朗读小组的人数是既参加绘画小组又参加朗读小组人数的倍,又是三项活动都参加人数的7倍,既参加朗读小组又参加合唱小组的人数相当于三项都参加人数的2倍,既参加绘画小组又参加合唱小组的有10人,求参加朗读小组的人数.8、六年级100名同学,每人至少爱好体育、文艺和科学三项中的一项.其中,爱好体育的55人,爱好文艺的56人,爱好科学的51人,三项都爱好的15人,只爱好体育和科学的4人,只爱好体育和文艺的17人.问:有多少人只爱好科学和文艺两项?只爱好体育的有多少人?9、在某个风和日丽的日子,10个同学相约去野餐,每个人都带了吃的,其中6个人带了汉堡,6个人带了鸡腿,4个人带了芝士蛋糕,有3个人既带了汉堡又带了鸡腿,1个人既带了鸡腿又带了芝士蛋糕.2个人既带了汉堡又带了芝土蛋糕.问:三种都带了的有几人?只带了一种的有几个?9、盛夏的一天,有10个同学去冷饮店,向效劳员交了一份需要冷饮的统计表:要可乐、雪碧、橙汁的各有5人;可乐、雪碧都要的有3人;可乐、橙汁都要的有2人;雪碧、橙汁都要的有2人;三样都要的只有1人,证明其中一定有1人这三种饮料都没有要.10、全班有25个学生,其中17人会骑自行车,13人会游泳,8人会滑冰,这三个运动工程没有人全会,至少会这三项运动之一的学生数学成绩都及格了,但又都不是优秀.假设全班有6个人数学不及格,那么,数学成绩优秀的有几个学生?有几个人既会游泳,又会滑冰?11、在一个自助果园里,只摘山莓者两倍于只摘李子者;摘了草莓、山莓和李子的人数比只摘李子的人数多3个;只摘草莓者比摘了山莓和草莓但没有摘李子者多4人;50个人没有摘草莓;11个人摘了山莓和李子但没有摘草莓;总共有60100,你能答复以下问题吗?①有人摘了山莓;②有人同时摘了三种水果;③有人只摘了山莓;④有人摘了李子和草莓,而没有摘山莓;⑤有人只摘了草莓.12、五年级一班共有36人,每人参加一个兴趣小组,共有A、B、C、D、E五个小组,假设参加A组的有15人,参加B组的人数仅次于A组,参加C组、D组的人数一样,参加E组的人数最少,只有4人.那么,参加B组的有多少人?13、五一班有28位同学,每人至少参加数学、语文、自然课外小组中的一个.其中仅参加数学与语文小组的人数等于仅参加数学小组的人数,没有同学仅参加语文或仅参加自然小组,恰有6个同学参加数学与自然小组但不参加语文小组,仅参加语文与自然小组的人数是3个小组全参加的人数的5倍,并且知道3个小组全参加的人数是一个不为0的偶数,那么仅参加数学和语文小组的人有多少人?14、某学校派出假设干名学生参加体育竞技比赛,比赛一共只有三个工程,参加长跑、跳高、标枪三个工程的人数分别为10、15、20人,长跑、跳高、标枪每一项的的参加选手中人中都有五分之一的人还参加了别的比赛工程,求这所学校一共派出多少人参加比赛?图形中的重叠问题1、 把长38厘米和53厘米的两根铁条焊接成一根铁条.焊接局部长4厘米,焊接后这根铁条有多长?2、把长23厘米和37厘米的两根铁条焊接成一根铁条.焊接局部长3厘米,焊接后这根铁条有多长?3、两张长4厘米,宽2厘米的长方形纸摆放成如下图形状.把它放在桌面上,覆盖面积有多少平方厘米?4、 如图,一张长8厘米,宽6厘米,另一个正方形边长为6厘米,它们中间重叠的局部是一个边长为4厘米的正方形,求这个组合图形的面积.5、一个长方形长12厘米,宽8厘米,另一个长方形长10厘米,宽6厘米,它们中间重叠的局部是一个边长4厘米的正方形,求这个组合图形的面积.图32厘米4厘米图36、三个面积均为50平方厘米的圆纸片放在桌面上(如图),三个纸片共同重叠的面积是10平方厘米.三个纸片盖住桌面的总面积是100厘米.问:图中阴影局部面积之和是多少?7、如图,三角形纸板、正方形纸板、圆形纸板的面积相等,都等于60平方厘米.阴影局部的面积总和是40平方厘米,3张板盖住的总面积是100平方厘米,3张纸板重叠局部的面积是多少平方厘米?8、如下图,A 、B 、C 分别是面积为12、28、16的三张不同形状的纸片,它们重叠在一起,露在外面的总面积为38.假设A 与B 、B 与C 的公共局部的面积分别为8、7,A 、B 、C 这三张纸片的公共局部为3.求A 与C 公共局部的面积是多少?容斥原理在数论问题中的应用1、 在1~100的全部自然数中,不是3的倍数也不是5的倍数的数有多少个?2、 在自然数1100~中,能被3或5中任一个整除的数有多少个?3、 在前100个自然数中,能被2或3整除的数有多少个?4、 在从1至1000的自然数中,既不能被5除尽,又不能被7除尽的数有多少个5、求在1至100的自然数中能被3或7整除的数的个数.5、 以105为分母的最简真分数共有多少个?它们的和为多少? CB A107、分母是385的最简真分数有多少个?并求这些真分数的和.8、在1至2021这2021个自然数中,恰好是3、5、7中两个数的倍数的数共有个.9、在从1到1998的自然数中,能被2整除,但不能被3或7整除的数有多少个?10、50名同学面向教师站成一行.教师先让大家从左至右按1,2,3,…,49,50依次报数;再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转.问:现在面向教师的同学还有多少名11、有2000盏亮着的电灯,各有一个拉线开关控制着,现按其顺序编号为1,2,3, (2000)然后将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,三次拉完后,亮着的灯有多少盏?12、写有1到100编号的灯100盏,亮着排成一排,每一次把编号是3的倍数的灯拉一次开关,第二次把编号是5的倍数的灯拉一次开关,那么亮着的灯还有多少盏?13、在游艺会上,有100名同学抽到了标签分别为1至100的奖券.按奖券标签号发放奖品的规那么如下:〔1〕标签号为2的倍数,奖2支铅笔;〔2〕标签号为3的倍数,奖3支铅笔;〔3〕标签号既是2的倍数,又是3的倍数可重复领奖;〔4〕其他标签号均奖1支铅笔.那么游艺会为该项活动准备的奖品铅笔共有多少支14、在一根长木棍上,有三种刻度线,第一种刻度线将木棍分成十等份;第二种将木棍分成十二等份;第三种将木棍分成十五等份;如果沿每条刻度线将木棍锯断,那么木棍总共被锯成________段.15、一根101厘米长的木棒,从同一端开场,第一次每隔2厘米画一个刻度,第二次每隔3厘米画一个刻度,第三次每隔5厘米画一个刻度,如果按刻度把木棒截断,那么可以截出段.16、一根1.8米长的木棍,从左端开场每隔2厘米画一个刻度,涂完后再从左端开场每隔3厘米画一个刻度,再从左端每隔5厘米画一个刻度,再从左端每隔7厘米画一个刻度,涂过按刻度把木棍截断,一共可以截成多少段小木棍?容斥原理中的最值问题1、将1~13这13个数字分别填入如下图的由四个大小一样的圆分割成的13个区域中,然后把每个圆内的7个数相加,最后把四个圆的和相加,问:和最大是多少?2、如图,5条同样长的线段拼成了一个五角星.如果每条线段上恰有1994个点被染成红色,那么在这个五角星上红色点最少有多少个3、某班共有学生48人,其中27人会游泳,33人会骑自行车,40人会打乒乓球.那么,这个班至少有多少学生这三项运动都会?4、某班有50名学生,参加语文竞赛的有28人,参加数学竞赛的有23人,参加英语竞赛的有20人,每人最多参加两科,那么参加两科的最多有人.5、60人中有23的人会打乒乓球,34的人会打羽毛球,45的人会打排球,这三项运动都会的人有22人,问:这三项运动都不会的最多有多少人?6、图书室有100本书,借阅图书者需在图书上签名.这100本书中有甲、乙、丙签名的分别有33,44和55本,其中同时有甲、乙签名的图书为29本,同时有甲、丙签名的图书为25本,同时有乙、丙签名的图书为36本.问这批图书中最少有多少本没有被甲、乙、丙中的任何一人借阅过7、甲、乙、丙都在读同-一本故事书,书中有100个故事.每个人都从某一个故事开场,按顺序往后读.甲读了75个故事,乙读了60个故事,丙读了52个故事.那么甲、乙、丙3人共同读过的故事最少有多少个8、在阳光明媚的一天下午,甲、乙、丙、丁四人给100盆花浇水,甲浇了30盆,乙浇了75盆,丙浇了80盆,丁浇了90盆,请问恰好被3个人浇过的花最少有多少盆?恰好被1个人浇过的花最多有多少盆?9、甲、乙、丙同时给100盆花浇水.甲浇了78盆,乙浇了68盆,丙浇了58盆,那么3人都浇过的花最少有多少盆。
专题22容斥原理(解析)2

20222023学年小学五年级思维拓展举一反三精编讲义专题22 容斥原理专题简析:集合是指具有某种属性的事物的全体,它是数学中的最基本的概念之一。
如某班全体学生可以看作是一个集合,0、1、2、3、4、5、6、7、8、9便组成一个数字集合。
组成集合的每个事物称为这个集合的元素。
如某班全体学生组成一个集合,每一个学生都是这个集合的元素,数字集合中有10个元素。
两个集合中可以做加法运算,把两个集合A 、B 合并在一起,就组成了一个新的集合C 。
计算集合C 的元素的个数的思考方法主要是包含与排除:先把A 、B 的一切元素都“包含”进来加在一起,再“排除”A 、B 两集合的公共元素的个数,减去加了两次的元素,即:C=A +B -AB 。
在解包含与排除问题时,要善于使用形象的图示帮助理解题意,搞清数量关系的逻辑关系。
有些语言不易表达清楚的关系,用了适当的图形就显得很直观、很清楚,因而容易进行计算。
【典例分析01】五年级96名学生都订了报纸,有64人订了少年报,有48人订了小学生报。
两种报纸都订的有多少人?【思路引导】用左边的圆表示订少年报的64人,右边的圆表示订小学报的48人,中间重叠部分表示两种报刊都订的人数。
显然,两种报刊都订的人数被统计了两次:64+48=112人,知识精讲典例分析比总人数多112-96=16人,这16人就是两种报刊都订的人数。
【典例分析02】某校教师至少懂得英语和日语中的一种语言。
已知有35人懂英语,34人懂日语,两种语言都懂的有21人。
这个学校共有多少名教师?【思路引导】把懂英语和懂日语的人数加起来得35+34=69人,但是,两种语言都懂的21人被统计过两次,应该从69里去掉一个21才能得出这个地区外语教师的总人数:69-21=48人。
【典例分析03】学校开展课外活动,共有250人参加。
其中参加象棋组和乒乓球组的同学不同时活动,参加象棋组的有83人,参加乒乓球组的有86人,这两个小组都参加的有25人。
小学奥数总复习第七讲《容斥原理》练习
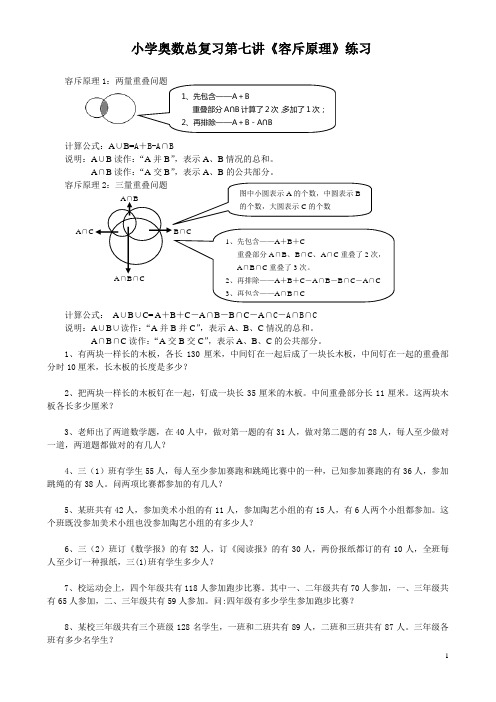
1、先包含——A +B 重叠部分A ∩B 计算了2次,多加了1次;2、再排除——A +B -A ∩B小学奥数总复习第七讲《容斥原理》练习容斥原理1:两量重叠问题计算公式:A ∪B=A +B-A ∩B说明:A ∪B 读作:“A 并B ”,表示A 、B 情况的总和。
A ∩B 读作:“A 交B ”,表示A 、B 的公共部分。
容斥原理2:三量重叠问题计算公式: A ∪B ∪C= A +B +C -A ∩B -B ∩C -A ∩C -A ∩B ∩C说明:A ∪B ∪读作:“A 并B 并C ”,表示A 、B 、C 情况的总和。
A ∩B ∩C 读作:“A 交B 交C ”,表示A 、B 、C 的公共部分。
1、有两块一样长的木板,各长130厘米,中间钉在一起后成了一块长木板,中间钉在一起的重叠部分时10厘米,长木板的长度是多少?2、把两块一样长的木板钉在一起,钉成一块长35厘米的木板。
中间重叠部分长11厘米。
这两块木板各长多少厘米?3、老师出了两道数学题,在40人中,做对第一题的有31人,做对第二题的有28人,每人至少做对一道,两道题都做对的有几人?4、三(1)班有学生55人,每人至少参加赛跑和跳绳比赛中的一种,已知参加赛跑的有36人,参加跳绳的有38人。
问两项比赛都参加的有几人?5、某班共有42人,参加美术小组的有11人,参加陶艺小组的有15人,有6人两个小组都参加。
这个班既没参加美术小组也没参加陶艺小组的有多少人?6、三(2)班订《数学报》的有32人,订《阅读报》的有30人,两份报纸都订的有10人,全班每人至少订一种报纸,三(1)班有学生多少人?7、校运动会上,四个年级共有118人参加跑步比赛。
其中一、二年级共有70人参加,一、三年级共有65人参加,二、三年级共有59人参加。
问:四年级有多少学生参加跑步比赛?8、某校三年级共有三个班级128名学生,一班和二班共有89人,二班和三班共有87人。
三年级各班有多少名学生?A ∩C A ∩B ∩C B ∩C A ∩B 图中小圆表示A 的个数,中圆表示B 的个数,大圆表示C 的个数 1、先包含——A +B +C 重叠部分A ∩B 、 B ∩C 、 A ∩C 重叠了2次, A ∩B ∩C 重叠了3次。
小学数学五年级下册奥数思维 — 容斥原理

小学数学五年级下册奥数思维—容斥原理知识点解析:容斥问题涉及到一个重要原理——包含与排除原理,也叫容斥原理。
即当两个计数部分有重复包含时,为了不重复计数,应从它们的和中排除重复部分。
容斥原理:对n个事物,如果采用不同的分类标准,按性质a分类与性质b分类(如图),那么具有性质a或性质b 的事物的个数=Na+Nb-Nab。
例1:一个班有48人,班主任在班会上问:“谁做完语文作业?请举手!”有37人举手。
又问:“谁做完数学作业?请举手!”有42人举手。
最后问:“谁语文、数学作业都没有做完?”没有人举手。
求这个班语文、数学作业都完成的人数。
例2:某班有36个同学在一项测试中,答对第一题的有25人,答对第二题的有23人,两题都答对的有15人。
问多少个同学两题都答得不对?例3:某班有56人,参加语文竞赛的有28人,参加数学竞赛的有27人,如果两科都没有参加的有25人,那么同时参加语文、数学两科竞赛的有多少人?例4:在1到100的自然数中,既不是5的倍数也不是6的倍数的数有多少个?例5:光明小学举办学生书法展览。
学校的橱窗里展出了每个年级学生的书法作品,其中有24幅不是五年级的,有22幅不是六年级的,五、六年级参展的书法作品共有10幅,其他年级参展的书法作品共有多少幅?1.分析与解答完成语文作业的有37人,完成数学作业的有42人,一共有37+42=79人,多于全班人数。
这是因为语文、数学作业都完成的人数在统计做完语文作业的人数时算过一次,在统计做完数学作业的人数时又算了一次,这样就多算了一次。
所以,这个班语文、数作业都完成的有:79-48=31人。
2.分析与解答:已知答对第一题的有25人,两题都答对的有15人,可以求出只答对第一题的有25-15=10人。
又已知答对第二题的有23人,用只答对第一题的人数,加上答对第二题的人数就得到至少有一题答对的人数:10+23=33人。
所以,两题都答得不对的有36-33=3人。
容斥原理及公式的证明
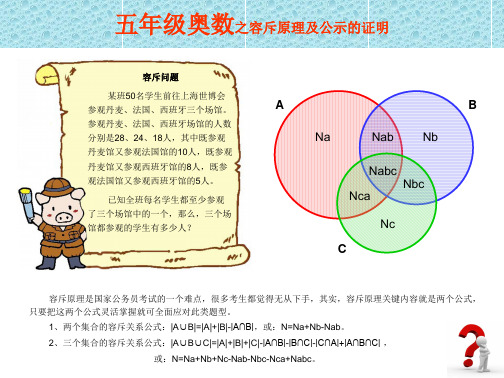
=50-(28+24+18)+(10+8+5) =3(人) 答:三个场馆都参观的有3人。
或:N=Na+Nb+Nc-Nab-Nbc-Nca+Nabc。
四年级奥数之容斥原理及公示的证明
பைடு நூலகம்
A
B
N1 Na
N4
N2
Nab Nb
Nabc
Nca N6
N7
Nbc N5
Nc
N3 C
定理: |A∪B∪C|=|A|+|B|+|C|-|A∩B|-|B∩C|-|C∩A|+|A∩B∩C| 或:N=(Na+Nb+Nc)-(Nab+Nbc+Nca)+Nabc
证明:设Na、Nb、Nc分别表示图A、B、C覆盖的 面积;Nab、Nbc、Nca分别表示图A和B、B和C、C和 A共同覆盖的面积;Nabc表示图A、B、C共同覆盖的面 积。再设N1、N2、N3、N4、N5、N6、N7分别表示7个 互不覆盖区域的面积;N表示7个互不覆盖区域的面积 总和。
则:N1=Na-Nab-Nca+Nabc, N2=Nb-Nab-Nbc+Nabc, N3=Nc-Nbc-Nca+Nabc N4=Nab-Nabc N5=Nbc-Nabc N6=Nca-Nabc N7=Nabc
五年级奥数之容斥原理及公示的证明
容斥问题
某班50名学生前往上海世博会 参观丹麦、法国、西班牙三个场馆。 参观丹麦、法国、西班牙场馆的人数 分别是28、24、18人,其中既参观 丹麦馆又参观法国馆的10人,既参观 丹麦馆又参观西班牙馆的8人,既参 观法国馆又参观西班牙馆的5人。
五年级奥数容斥问题_学科竞赛

1、五一小学举行小学生田径运动会,其中24名运动员不是六年级的,28名运动员不是五年级的,已 知五、六年级运动员共32名,五、六年级和中低年级运动员各有几名?
2、少年乐团学生中有170名不是五年级的,有135名不是六年级的,已知五六年级的共有205人,少 年乐团中五六年级以外的学生共有多少人?
3、六一儿童节同学们做小花,有24朵不是红色的,有20朵不是黄色的,已知红花和黄花一共有18 朵,其他颜色的花一共做了多少朵?
3、老师在统计考试成绩。数学得90分以上的有25人,语文得90分以上的有21人,两科中有一科有 90分以上的有38人,问:两样都得90分以上的有多少人?
例:实验小学各年级都参加的一次书法比赛中,四年级与五年级共有20人获奖,在获奖者中有16人 不是四年级的,有12人不是五年级的。该校书法比赛获奖的总人数是多少人?
0.87-0.49= 17×40=
14-7.4= 5.4×400=
5×1.06=
5.7-3.9= 6.3÷0.7= 3.06÷0.3=
4=
0.125÷0.25= 2.56-0.37=
3.2+1.68= 4.3÷0.5= 18.2+1.8= 1.05×4=
1.5+0.25×4= 3×0.2×0.5= 0.84×1.60.84×0.6= 12.5×18.5×0.8=
83+86-25=169-25=144(人) 250-144=106(人) 答:乒乓球组都不会参加的有106人。
1、100位旅客中,有70人懂英语,有65人懂日语,既懂英语又懂日语的有45 人,则,既不懂英语又 不懂日语的有多少人?
2、五(1)班有学生50人,在一次测试中,语文90分以上的有30人,数学90分以上的35人,语文和 数学都在90分以上的有20人,90分以下的有多少人?
小学奥数教程:容斥原理之重叠问题(二)全国通用(含答案)

1. 了解容斥原理二量重叠和三量重叠的内容;2. 掌握容斥原理的在组合计数等各个方面的应用.一、两量重叠问题在一些计数问题中,经常遇到有关集合元素个数的计算.求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成:A B A B A B =+-(其中符号“”读作“并”,相当于中文“和”或者“或”的意思;符号“”读作“交”,相当于中文“且”的意思.)则称这一公式为包含与排除原理,简称容斥原理.图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A B ,即阴影面积.图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A B ,即阴影面积.包含与排除原理告诉我们,要计算两个集合A B 、的并集A B 的元素的个数,可分以下两步进行:第一步:分别计算集合A B 、的元素个数,然后加起来,即先求A B +(意思是把A B 、的一切元素都“包含”进来,加在一起);第二步:从上面的和中减去交集的元素个数,即减去C A B =(意思是“排除”了重复计算的元素个数).二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数.用符号表示为:A B C A B C A B B C A C A B C =++---+.图示如下:在解答有关包含排除问题时,我们常常利用圆圈图(韦恩图)来帮助分析思考.教学目标例题精讲 知识要点7-7-2.容斥原理之重叠问题(二)1.先包含——A B + 重叠部分A B 计算了2次,多加了1次; 2.再排除——A B A B +- 把多加了1次的重叠部分A B 减去.图中小圆表示A 的元素的个数,中圆表示B 的元素的个数,大圆表示C 的元素的个数.1.先包含:A B C ++重叠部分A B 、B C 、C A 重叠了2次,多加了1次.2.再排除:A B C A B B C A C ++---重叠部分A B C 重叠了3次,但是在进行A B C ++-A B B C A C --计算时都被减掉了. 3.再包含:A B C A B B C A C A B C ++---+.模块一、三量重叠问题【例 1】 一栋居民楼里的住户每户都订了2份不同的报纸。
五年级奥数-容斥原理最新解读

例如:一次期末考试,某班有15人数学得满分,有12 人语文得满分,并且有4人语、数都是满分,那么这个 班至少有一门得满分的同学有多少人? 分析:依题意,被计数的事物有语、数得满分两类, “数学得满分”称为“A类元素”,“语文得满分” 称为“B类元素”,“语、数都是满分”称为“既是A 类又是B类的元素”,“至少有一门得满分的同学” 称为“A类和B类元素个数”的总和。为15+12-4=23。
练1.C班的同学都至少喜欢一项运动,有37人喜欢 乒乓球,26人喜欢篮球,21人两种球都喜欢, 问C班有多少人? 解: 练2.自然数1,2,3…,99,100当中,能被3整除或能被4整除的 数共有几个?
Байду номын сангаас
解: 练3.某校参加数学竞赛的有120名男生、80名女生,语文竞赛的有 120女生,80男生,总共参赛人数有260名,其中75名男生两科都 参加了,问,只参加数学没参加语文的女生有多少?
问题1.十月国庆节,学校门口挂了一行彩 旗。小张从前数起,红旗是第8面;从后数 起,红旗是第10面。这行彩旗共多少面?
问题2.同学们排队做操,每行人数同样多。小明的位 置从左数起是第4个,从右数起是第3个,从前数起是 第5个,从后数起是第6个。做操的同学共有多少个? 问题3.把两块一样长的木板像下图这样钉在一起成 了一块木板。如果这块钉在一起的木板长120厘米, 中间重叠部分是16厘米,这两块木板各长多少厘米?
例1. A班共有40人,同学们都喜欢打篮球或者打羽毛球。 喜欢打篮球的有26人,喜欢打羽毛球的有24人,问两 种球都喜欢的同学有多少人? 解:
原理1:既是A又是B的数量=A的数量+B的数量-A或B的数量。
A或B的数量=A的数量+B的数量-既是A又是B的数量
小学奥数之容斥原理

容斥原理(一)【例题分析】例1. 有长8厘米,宽6厘米的长方形与边长5厘米的正方形。
如图放在桌面上,求这两个图形盖住桌面的面积?分析与解:阴影部分是直角三角形,是两个图形的重叠部分,它的面积是:(平方厘米)方法一:(平方厘米)方法二:(平方厘米)方法三:(平方厘米)答:盖住桌面的面积是67平方厘米。
例2. 六一班参加无线电小组和航模小组的共26人,其中参加无线电小组的有17人,参加航模小组的有14人,两组都参加的有多少人?分析与解:把17人和14人相加,是把两组都参加的人算了两次,所以减去总人数,就是两组都参加的人数(人)。
也可以这样解:(人)或(人)答:两组都参加的有5人。
例3。
六一班有学生46人,其中会骑自行车的有19人,会游泳的有25人,既会骑车又会游泳的有7人,既不会骑自行车又不会游泳的有多少人?分析与解:先求出46人中会骑车或会游泳的有多少人,从中减去会骑车或会游泳的人数,剩下的就是既不会骑车也不会游泳的人数。
(人)(人)答:既不会骑车又不会游泳的有9人。
例4. 某年级的课外小组分为美术、音乐、手工三个小组,参加美术小组有20人,参加音乐小组有24人,参加手工小组有31人,同时参加美术和音乐两个小组有5人,同时参加音乐和手工两个小组有6人,同时参加美术和手工两个小组的有7人,三个小组都参加的有3人,这个年级参加课外小组的同学共有多少人?分析与解:图中的5、6、7人都是两两重叠的部分,图中的3人是三个重叠的部分,要从三个组的总人数中减去重复多余的部分.(人)答:这个年级参加课外小组的有60人。
例5。
某班在短跑、投掷和跳远三项检测中,有4人三项都未达到优秀,其他人至少有一项是优秀,下表是得优秀的情况,请你算出全班人数.短跑投掷跳远跑跳跑投跳投三项19 21 20 9 10 6 3分析与解:根据题意画出如下图要求全班有多少人,先要求出跑、跳、投至少有一项达到优秀的人数,加上三项都未达到优秀的,就是全班人数。
五年级下册奥数较复杂的容斥原理人教版

加语文和英语小组的有12人,同时参加数学和英语小组的有15人,三个学习小组都参加的有5人。
51+48+32-16-11-13+7=98(人)
例2:榆树园小学五(1)班许多同学参加了学习小组,已知参加语文学习小组的有35人,参加数学小组的的有32人,参加英语小组的有45人,同时参加语文和数学小组的有10人,同时参
11+12=23 (人) 答:至少有一门得满分的同学有23人。 答:五年级的学生有98人。 51+48+32-16-11-13+7=98(人)
答:这个班一共有80名学生参加了学习小组。 C:4×4=16﹙cm2﹚
求这个班学生参加了学习小组? A或B或C=A+B+C-AB-AC-BC+ABC 答:五年级的学生有98人。 A+B+C-A又B-A又C-B又C+A又B又C。
100+64+16-25-8-8+4=143﹙cm2﹚
答:它们盖住的面积是143平方厘米。
第十九页,编辑于星期四:十五点 五十一分。
即学即练
在一个边长为90厘米的正方形桌面上,放上两张边长分别为20厘米 和45厘米的正方形纸,如图。桌面上没被纸片盖住的面积是多少?
45×45+20×20-15×10=2275(平方厘米)
54-(23+27+18-7-4-5)=2(人)
答:其中三个小组都参加的有2人。
第十四页,编辑于星期四:十五点 五十一分。
例4:某班的全体学生在进行了短跑、游泳、投掷三个项目的测试后 ,有4名学生在这三个项目上都没有达到优秀,其余每人至少有一项达 到了优秀,达到了优秀的这部分学生情况如下表:
短游 投 跑泳 掷
第六页,编辑于星期四:十五点 五十一分。
五年级奥数学习之容斥原理(彩色版_含解答)

ڈᆐபைடு நூலகம் ڈᆐఅ
28
容斥原理
课本
瓜子的例子相对简单,一斤瓜子里 ̙۟Џԅఆ
̙ׅ۟ԅఆ
一部分是瓜子仁,另一部分就是瓜子壳,
两者各不相关.但本讲要学习的包含与
排除问题要复杂一些,各部分之间会有
重叠.比如一个办公室中每个人都至少 爱喝茶或咖啡中的一种,已知有 7 个人
̙۟ޛЏရ̙ׅ۟ԅఆ
这种问题通常需要画出示意图(如喝茶与喝咖啡的图),这样的示意图又叫做文氏图,下
面我们就用文氏图推导两个对象的容斥原理公式. 如右图所示,如果要计算三个部分的总数,直接计算 A+B A ķ Ĺ ĸ B
就会算多了,而多算的正好是③部分,只要把多算的减掉就可
以了.上述分析总结成公式就是:
这个公式就是两个对象的容斥原理.
29
五年级
上册第 5 讲
进一步明确起见,他还引入了一些数学难题作为实例.虽然在维恩之前,莱布尼茨(Leibniz) 已系统地运用过这类逻辑图,但今天这种逻辑图仍称作“维恩图”(Venn Diagram).
另外,维恩在概率论和逻辑学方面也有很大贡献,他的著作——《机会逻辑》和《符 号逻辑》,在 19 世纪末 20 世纪初曾享有很高的声誉.
五年级
上册第 5 讲
5 容斥原理
这一讲我们主要学习和“包含”与“排除”有关的问题,这样 的问题在生活中就有不少,比如吃瓜子.我们说吃掉了一斤瓜子, 指的是带壳的瓜子,并非真的吃到肚子里一斤,因为这一斤中还“包 含”着瓜子壳.如果要计算到底吃了多少,最简单的方法就是称一 称瓜子壳,用原来的一斤“排除”掉瓜子壳的重量.
练一练
五年级有 122 名学生参加语文、数学考试,每人至少有一门功课的成绩是优秀, 其中语文成绩优秀的有 65 人,数学优秀的有 87 人.语文、数学都优秀的有多少人?
小学五年级奥数 容斥原理(二)

容斥原理(二)【例2】(★★★★)【例1】(★★★)唐僧西天取经共经历了81难,其中单独度过了3难,与孙悟空一起度过了77难,与猪八戒一起度过了65难,与沙和尚一起度过了62难,同时与孙悟空和猪八戒一起度过了64难,同时与孙悟空和沙和尚一起度过了61难,同时与猪八戒和沙和尚一起度过了60难。
请问:师徒四人共同度过的有多少难?某班人数60人,在一次抽考英语、数学、化学的考试中,英语及格的有41人,数学及格的有39人,化学及格的有42人;英语、数学两科不及格的有14人,数学、化学两科不及格的有13人,英语、化学两科不及格的有11人,有两科或两科以上不及格的人数为20人,则:⑴三科都不及格的有几人?⑵至少有一科不及格的有几人?⑶三科都及格的人数有几人?【例3】(★★★★)五年级一班有46名学生参加数学、语文、文艺三项课外小组。
其中有24人参加了数学小组,20人参加了语文小组,既参加数学小组又参加语文小组的有10人.参加文艺小组的人数是既参加数学小组又参加文艺.,,也参加语文小组的人数等于三项小组都参加的人数的2倍,求参加文艺小组的人数。
【例4】(★★★)六年级⑴班有32人参加数学竞赛,有27人参加英语竞赛,有22人参加语文竞赛,其中参加了数学和英语的有12人,参加了英语和语文的有14 人,参加了数学和语文的有10人,那么六年级⑴班全班至少有多少人?【例5】(★★★)甲、乙、丙三人都在读同一本故事书,书中有100个故事。
已知甲读了85个故事,乙读了70个故事,丙读了62个故事。
请问:甲、乙、丙三人共同读过的故事最少有多少个?1【例6】(★★★★★)在阳光明媚的一天下午,甲、乙、丙、丁四人给100盆花浇水,已知甲浇了30盆,乙浇了75盆,丙浇了80盆,丁浇了90盆,请问恰好被3个人浇过的花最少有多少盆?一、本讲重点知识回顾1.基本原理⑴二者容斥⑵三者容斥【例7】(★★★)中国田径队的40名运动员在训练基地进行封闭训练,其中男运动员有20名,训练长跑的运动员有15名,训练竞走的女运动员有8名,那么训练长跑的男运动员有多少名?C A BCA B C A B B C A CA B C2.口诀:奇层加,偶层减3.解题技巧:画图——文氏图,线段图方程列表高斯记号应用——取整运算答案【例1】59难【例3】21人【例2】⑴9人⑵29人⑶31人【例4】47人二、本讲经典例题容斥原理㈠:例1,例2,例5,例6 【例5】17个【例6】15盆容斥原理㈡:例1,例3,例6,例7【例7】3名2。
五年级奥数容斥问

五年级奥数容斥问题:容斥原理(1)如果被计数的事物有a、b两类,那么,a类或b类元素个数= a类元素个数+b类元素个数—既是a类又是b类的元素个数。
容斥原理(2)如果被计数的事物有a、b、c三类,那么,a类或b类或c类元素个数= a类元素个数+b类元素个数+c类元素个数—既是a类又是b类的元素个数—既是a类又是c类的元素个数—既是b类又是c类的元素个数+既是a类又是b类而且是c类的元素个数1、艺术小学举行学生画展,其中18幅画不是六年级的,20幅画不是五年级的,现在知道五、六年级共展出22幅画。
问其他年级展出多少幅?分析:18幅不是六年级,那就是五年级和其他年级的,20幅不是五年级,就是六年级和其他年级,已知五六年级展出22幅,所以其他年级展出就是八幅。
(18+20-22)/2=8(幅)2、某地区100个外语教师中,每人至少懂英语和日语中的一种语言。
已知懂英语的75人,懂日语的有45人。
问只懂英语的有几人?分析;两种语言都懂的人为;懂英语的和懂日语和减外语教师总数。
只懂英语的就是75减两种都懂得了。
75+45-100=20(人)75-20=55(人)3、在1至100的整数中,能被2整除或能被3整除的数共有几个?分析:100中,能被2整除的有100/2=50个,能被3整除的有100/3=33个,同时能被2和3整除的100/6=16个,注意这16个包括在能被2和3整除的,要去掉。
就是100内能被或3整除的。
50+33-16=67个4、全班50人,不会骑自行车的有23人,不会滑旱冰的有35人,两样都会的有4人,两样都不会的有多少人?分析:骑自行车:27人会滑旱冰:15人都会:4人都不会的:50-(27+15-4)=12人画个图就可以看出来了,4个人是多加的,所以要减去。
5、六年级有52人,其中喜欢绘画的36人,喜欢书法的有42人,喜欢唱歌的有48人,喜欢跳舞的有34人,这个班最少有多少学生对这四项活动都喜欢?分析:52-36=16个人不喜欢绘画,52-42=10个人不喜欢书法,52-48=4个人不喜欢唱歌,52-34=18个人不喜欢跳舞。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、本讲重点知识回顾 1.基本原理 ⑴二者容斥
⑵三者容斥 A B
A B A B
CA
A BC
BC A BC A B BC AC A BC
2.口诀:奇层加,偶层减 3.解题技巧:画图——文氏图,线段图
方程 列表 高斯记号应用——取整运算 二、本讲经典例题 容斥原理㈠:例1,例2,例5,例6 容斥原理㈡:例1,例3,例6,例7
1
【例6】(★★★★★) 在阳光明媚的一天下午,甲、乙、丙、丁四人给100盆花浇水,已知甲 浇了30盆,乙浇了75盆,丙浇了80盆,丁浇了90盆,请问恰好被3个人 浇过的花最少有多少盆?
【例7】 (★★★) 中国田径队的40名运动员在训练基地进行封闭训练,其中男运动员有 20名,训练长跑的运动员有15名,训练竞走的女运动员有8名,那么训 练长跑的男运动员有多少名?
【例4】(★★★) 六年级⑴班有32人参加数学竞赛,有27人参加英语竞赛,有22人参加语 文竞赛,其中参加了数学和英语的有12人,参加了英语和语文的有14 人,参加了数学和语文的有10人,那么六年级⑴班全班至少有多少人?
【例5】(★★★) 甲、乙、丙三人都在读同一本故事书,书中有100个故事。已知甲读了 85个故事,乙读了70个故事,丙读了62个故事。请问:甲、乙、丙三人 共同读过的故事最少有多少个?
【例1】59难 【例2】 ⑴9人 【例3】 21人 【例4】 47人 【例5】 17个 【例6】 15盆 【例7】 3名
答案 ⑵29人
⑶31人
2
【例2】(★★★★) 某班人数60人,在一次抽考英语、数学、化学的考试中,英语及格的 有41人,数学及格的有39人,化学及格的有42人;英语、数学两科不及 格的有14人,数学、化学两科不及格的有13人,英语、化学两科不及 格的有11人,有两科或两科以上不及格的人数为20人,则: ⑴三科都不及格的有几人? ⑵至少有一科不及格的有几人? ⑶三科都及格的人数有几人?
容斥原理(二)
【例1】(★★★) 唐僧西天取经共经历了81难,其中单独度过了3难,与孙悟空一起度过 了77难,与猪八戒一起度过了65难,与沙和尚一起度过了62难,同时与 孙悟空和猪八戒一起度过了64难,同时与孙悟空和沙和尚一起度过了 61难,同时与猪八戒和沙和尚一起度过了60难。请问:师徒四人共同 度过的有多少难?
【例3】(★★★★) 五年级一班有46名学生参加数学、语文、文艺三项课外小组。其中有 24人参加了数学小组,20人参加了语文小组,既参加数学小组又参加 语文小组的有10人.参加文艺小组的人数是既参加数学小组又参加文艺 小组人数的3.5倍,还是三项小组都参加的人数的7倍,既参加文艺小组 也参加语文小组的人数等于三项小组都参加的人数的2倍,求参加文艺 小组的人数。
