针梁台车模板受力分析
台车受力分析范文

台车受力分析范文台车通常由车架、轮轴和轮子组成。
在使用中,台车托放货物,然后由人力或马力推动。
在这个过程中,台车受到了多个力的作用。
首先,考虑到货物的重力作用。
货物在台车上会施加一个向下的重力,这个力由于质量不同而有所差异。
重力是指物体被地球吸引而产生的力,它作用在物体的质心上。
台车必须能够承受这个力的作用,以确保货物的安全运输。
其次,考虑到台车本身的重量对其运动的影响。
台车的重量是台车本身及其构件的质量之和。
当人力或马力推动台车时,需要克服台车的重量才能使它移动。
除了重力和台车本身的重量外,还需要考虑到地面对台车的支持力。
地面在台车轮子下产生支持力,以平衡重力和台车重量的作用,使得台车能够稳定地行驶。
对于台车来说,支持力可以通过轮子与地面的接触面积和地面对轮子的反作用力来实现。
而轮轴和轮子之间的摩擦力也很重要。
当台车运行时,轮子与地面之间的摩擦力产生了一个向后的推力,使得台车能够移动。
这种摩擦力是由于轮子与地面的接触而产生的。
在一些情况下,需要通过增加或减少摩擦力来控制台车的行进速度和稳定性。
另外,如果台车在运输过程中需要改变方向或加速,还会产生横向的力。
这些力是由于台车的转向或加速而产生的。
通常情况下,可以通过向台车施加一个水平向内的力或一个水平向外的力来实现方向变化或加速;而改变速度或停止需要施加向前或向后的水平力。
综上所述,台车受力分析涉及到重力、台车本身重量、地面支持力、轮子与地面的摩擦力以及转向和加速时产生的横向力。
了解这些力的分布和作用有助于我们更好地进行台车的设计和使用,并确保台车在运输中的稳定和安全。
浅谈全圆针梁液压钢模衬砌台车工作原理及施工方法
3 施工方案
3 . 1 施工机械 粉喷桩的施工机械主要由粉体搅拌机、 粉体发送器、空气压缩机、搅拌钻头等组成。 根据加固深度及现场地质情况 , 选择使用 DH一 型粉喷桩机。 SA 3 . 1. 1 主机 钻头直径5戊 比m, 单轴并具有正向反转提 升功能, 提升力大, 并能实现匀速变速提升和 钻进。 粉体搅拌机的主机是一台能完成钻进及 搅拌的钻机, 主要有步履底座、传动系统、 加减压系统和液压系统、塔架、钻头等组 成 。 3 . 1. 2 粉体发送器 它是定时定量发送粉喷材料的设备 , 是关
下位移。
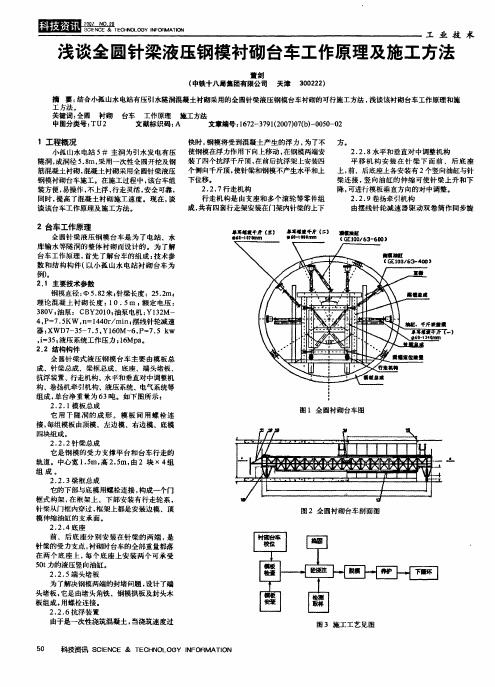
,工程概况 小孤山水电站 5 # 主洞为引水发电有压 隧洞, 成洞径 5. sm , 采用一次性全圆开挖及钢 筋混凝土衬砌, 混凝土衬砌采用全圆针梁液压 钢模衬砌台车施工。在施工过程中, 该台车组 装方便, 易操作, 不上浮, 行走灵活, 安全可靠, 同时, 提高了混凝土衬砌施工速度。现在, 谈 谈该台车工作原理及施工方法。
0 3 0222 )
摘 要: 介绍在黄河冲洪积平原区采用深层搅拌桩加固 软土地基的施工方法, 并详细阐述了 该方法的加固机理, 施工工艺及质t 检侧、 控
关键词:搅拌桩 软土 中圈分类号: T UZ 地基加固 施工 文献标识码: A 文章编号: 1672一 3791(2007)07(b卜0 5l 一 ) ( 02 在 3 . 0 一16 . om 之间。
方。
2 .2 .8 水平和垂直对中 调整机构
平移机构安装在针梁下面前、后底座 上, 前、后底座上各安装有2 个竖向油缸与针 梁连接, 竖向油缸的伸缩可使针梁上升和下 降, 可进行模板垂直方向的对中调整。 2 . 2 . 9 卷扬牵引机构 由摆线针轮减速器驱动双卷筒作同步旋
翻权油位 ‘ 生 6, 6 的 】 GE 00/ 一
针梁式模板台车在全圆隧道施工中抗浮措施的应用

针梁式模板台车在全圆隧道施工中抗浮措施的应用摘要:针梁式全圆模板台车是为全断面一次性混凝土浇筑而设计的一种专用台车。
由于混凝土浇筑过程中对模板产生的径向垂直应力,全圆模板台车在混凝土浇筑时,产生上浮力是不可避免的。
本文以实际施工为例,阐述相关抗浮措施在施工中的应用及效果。
关键词:模板台车施工抗浮Abstract: the needle beam in the template for the shutter is round, whole section one-time concrete pouring and design of a special car. Because concrete casting process for the template of the radial vertical stress produced, all round in concrete casting template car, produce the buoyancy is inevitable. Based on the actual construction as an example, this paper expounds the construction measures related anti-uplift the application and effect.Keywords: template construction anti-uplift car中图分类号:TU74文献标识码:A 文章编号:1工程概况北京市南水北调配套工程南干渠工程施工第二标段,起讫里程为中1+200~中2+612.04,中线导线全长1412.04m,双线长2824.08m。
暗涵主洞为内径3400mm的钢筋混凝土圆涵,二衬为现浇C30W10防水钢筋混凝土,厚度为350mm,采用针梁式全圆模板台车,全断面一次浇筑成型。
发电洞针梁台车施工方案

新疆吉勒布拉克水电站发电厂房建筑及金属机构安装工程发电洞针梁针梁台车施工方案发电洞针梁针梁台车施工方案一、编制依据1、厂家设计图纸《φ8M全圆针梁22M液压针梁台车》总图2、厂家设计图纸《液压原理图》、《电器原理图》3、国标GB50231-98《机械设备安装工程施工及验收通用规范》4、《新疆吉勒布拉克水电站发电厂房建筑及金属结构安装工程》([招标/合同编号:XJXH-JLBLK-TJ03-ZB201009-01-040])。
二、工程概述根据2012年进度计划,为加快施工进度,在上平洞发0+010.000-发0+119.047桩号采用全圆断面液压针梁式钢模针梁台车对隧洞进行整体衬砌。
该针梁针梁台车的底、边、顶一次性成型,立模、拆模用液压油缸执行,定位找正由底座竖向油缸和调平油缸执行。
全圆针梁式液压钢模针梁台车重74t,主要由16块模板、16块模板托架、一片主梁、2片外框架梁、水平和垂直对中调整机构、震动装置机构、抗浮装置等组成。
针梁台车为自行式,安装在针梁台车上的液压系统,使钢模和针梁作相对运动,针梁台车便可前后移动。
针梁台车主要参数:钢模直径:Φ8m;针梁长度: 22m;理论混凝土衬砌长度:10.5m;额定电压: 380V;油泵: CBY2016,Q=16.4ml/r;油泵电机: Y160M-4,P=11KW,n=1460r/min;摆线针轮减速器(一):XWD8-43-11,P=11 kw ,i=43;液压系统工作压力: 16Mpa。
三、施工准备3.1模板受力分析针梁针梁台车模板分顶模、左右边模及底模,由于顶模受到混凝土自重、施工载荷及注浆口封口时的挤压力等载荷的作用,其受力条件显然比其它部位的模板更复杂、受力更大、结构要求更高。
由于边模、底模与顶模的结构构造一样,边模、底模不受砼自重,载荷较小,因此对其强度分析时只考虑顶模。
3.1.1分析部分的混凝土自重P1由于模板的长为3.5米,宽为3.3米,混凝土厚为0.6m,其密度为2.45t/m3,则混凝土自重W=3.5×3.3×0.6×2.45=16.98(t)。
浅谈隧洞二衬针梁台车质量控制

浅谈隧洞二衬针梁台车质量控制前言:北京市南水北调配套工程东干渠工程隧洞二衬施工,是在隧洞一次衬砌基础上采用针梁台车全圆衬砌施工,衬砌为C35W10F150模筑钢筋混凝土,两层衬砌间设置连续防水板。
隧洞二衬属薄壁混凝土结构,壁厚40cm,洞内直径4.6m,外径6m。
隧洞二衬针梁台车在整个二衬施工过程中扮演着非常重要的角色,如针梁台车质量存在问题将直接影响隧洞二衬外观质量,增加施工成本,影响施工进度。
关键词:全圆衬砌针梁台车质量控制设计专家意见一、工程概况北京市南水北调配套工程东干渠工程输水隧洞工程,起点位于团城湖至第九水厂输水工程末端(关西庄泵站北)预留接口,沿北五环向东,至广顺桥向南折向东五环,其后沿东五环向南,至亦庄桥与五环路分离,其后穿越凉水河,沿凉水河南(右)岸至荣京西街向南至亦庄镇工程终点与南干渠工程相接,总长44.7km。
[1]东干渠输水隧洞分两次衬砌施工,隧洞一衬采用盾构法施工,结构采用复合衬砌形式,一次衬砌为C50预制管片衬砌。
是在隧洞一次衬砌基础上进行采用针梁台车全圆衬砌施工,衬砌为C35W10F150模筑钢筋混凝土,两层衬砌间设置连续防水板。
隧洞二衬属薄壁混凝土结构,壁厚40cm,洞内直径4.6m,外径6m。
[1]隧洞最终横断面为一条内径4.6m钢筋砼衬砌圆形暗涵。
隧洞二衬针梁台车在整个二衬施工过程中扮演着非常重要的角色,台车模板的拼装质量如控制不好将直接影响着隧洞二衬外观质量,导致成本增加,影响施工进度。
见图1-1。
图1-1隧洞断面图[2]本文参阅台车设计文件,借鉴专家意见,并结合隧洞二衬实际施工经验对隧洞二衬全圆衬砌针梁台车由生产至使用全过程质量控制措施进行梳理,详见下文。
二针梁台车全过程质量控制2.1 台车设计质量控制(1)评标对有台车生产能力并有相关工程业绩的单位进行邀请招标,对应标单位进行评标,选择适合本工程设计优秀的生产商,并参与厂商组织的专家专项设计论证会,签订合同,下发生产计划。
模板台车受力分析

全液压自行式钢模台车受力分析一、前言:钢模台车(简称台车)沿洞轴线方向看是一个不完整的圆柱壳(模板),和内部门架组成。
模板分两侧边模和顶部模板。
台车在衬砌过程中受力分析很复杂,由于砼是半流体且易凝固, 浇注过程为动态过程,所以受力也为动态程过。
(即在一定时间范围内,砼一边浇注一边凝固,在砼未初凝时有力存在,初凝后力消失)。
两侧边模主要受砼的侧向挤压力,顶部模板主要受砼的正压力,门架部份既受侧向力又受正压力及各种弯矩,受力情况较复杂。
二、边模侧压力的确定(侧压力只与浇注混凝土高度有关,与浇注混凝土厚度无关)。
根据《建筑手册》中“现浇砼结构模板的设计”可知侧压力公式为:F=0.22r c t0β1β2V1/2F—新浇筑砼对模板的最大侧压力(KN/M2)r c—混凝土的重力密度(KN/M3)t0—新浇筑混凝土的初时间(h),可按实测确定,当缺乏试验资料时,可采用t0=200/(T+15)计算(T为混凝土的温度o C)V—混凝土的浇筑速度(m/h)β1—外加剂影响修正参数,不掺外加剂时取1.0,掺具有缓凝作用的外加剂时取1.2β2—混凝土坍落度影响修正参数,当坍落度小于30mm时取0.85,50—90mm 时取1.0, 110—150mm时取1.151、各参数的确定:①r c取24KN/ M3②t0=200/(T+15)=200/(25+15)=5③V的确定: V≤2.0 m/h(根据经验及参考日本歧阜工业公司计算值)④β1取1.0⑤β2取1.152、侧压力计算:F0=0.22x24x5x1.125x1x21/2=42 KN/M2混凝土侧压力设计值:=F0×分项系数×折减系数F1=42×1.2×0.85=42.84KN/m2倾倒混凝土时产生的水平荷载、插入振捣时产生的水平荷载取4 KN/m2,则混凝土的总荷载设计值为:F’=42.84+4=46.84 KN/m2(日本歧阜工业公司侧压力计算值为47KN/m2)三、边模的强度验算1、模板强度验算由于模板的内表面每隔230mm有一根加强角钢,因此,我们可以把它简化成每隔230mm的梁单元来考虑。
内模二衬台车受力计算书

内模二衬台车受力计算书20XX 年 X月目录一、计算依据.................................. .. - 2 -二、设计计算指标采用值....................... .. - 2 -三、侧压力计算............................... .. - 3 -四、台车模板受力计算......................... .. - 5 -1、面板受力分析.............................. .. - 5 -2、模板纵向主肋校核.......................... .. - 9 -五、门架受力计算 .............................. - 13 -1、桁架强度计算(应力云图) ................... - 15 -2、桁架刚度计算 ............................... - 17 -六、支撑丝杆受力计算 .......................... - 18 -七、结论.................................... .. - 19 -一、计算依据1.《钢结构设计规范》(GB 50017-2017);2.《建筑工程大模板技术规程》JGJ/T74-2017;3.《钢结构焊接规范》GB50661-2011;4.《建筑结构静力计算手册(第二版)》;5.《钢结构设计手册(上册)(第三版)》;6.《预应力混凝土用螺纹钢筋》GB/T 20065-2016;7.《钢模板制作规范》8.《混凝土结构工程施工及验收规范》等。
9.建筑施工模板安全技术规范 JGJ162-2016二、设计计算指标采用值1.钢材物理性能指标弹性模量E=2.06×105N/mm2 ;质量密度ρ=7850kg/m3 ;2.钢材强度设计值抗拉、抗压、抗弯 f=215N/mm2;抗剪 fv=125N/mm2;3.容许挠度(见表:JGJ162-2016)表:4.4.2 组合钢模板及构配件的容许变形值(mm )注:L 为计算跨度,B 为柱宽三、侧压力计算(一)荷载计算① 水平荷载统计:新浇混凝土对模板的水平侧压力标准值。
针梁式钢模台车在芦杆桥水电站引水隧洞混凝土施工中的应用

针梁式钢模台车在芦杆桥水电站引水隧洞混凝土施工中的应用针梁式钢模台车对引水隧洞混凝土施工的应用,笔者在此就针梁式钢模台车在芦杆桥水电站工程中的应用简单阐述如下。
总所周知,在施工中不断的总结、优化,使得混凝土施工达到理想状态,是我们一直追求的目标,本文将着重介绍在引水隧洞混凝土施工中的几点施工经验。
标签:施工经验;改变;混凝土;引水隧洞;针梁式钢模台车一、工程情况芦杆桥水电站引水隧洞全长6424m,根据设计修改通知,结合目前实际洞挖状况,K2+950至上游0#主洞方向隧洞主要开挖断面为φ4.8m全圆形衬砌断面,过水断面为φ4.0m全圆形;K2+950至下游3#洞方向主要开挖断面为非衬砌型φ4.16m马蹄形,过水断面为φ4.0m马蹄形,其中,2#洞下游至3#洞上游K5+482~K5+862之间为不良地质段二次扩挖后的全断面衬砌洞段。
本工程上述部位之间约3330m长度需要进行全断面混凝土衬砌。
二、针梁式钢模台车概况2.1 根据引水隧洞的情况、结构长度以及施工的环境等,并参考以往的隧洞工程衬砌混凝土施工资料,引水隧洞采用针梁式钢模台车衬砌、隧洞全圆断面底、边、顶一次成型,针梁式钢模台车设计根据长度和直径进行施工。
2.2 根据不同的地区和施工条件的不同,使用不同的施工方式。
针梁式液压钢模台车主要由模板总成、針梁总成、梁框总成、水平和垂直对中调整机构、抗浮装置、液压系统等组成。
A.模板总成它对于隧洞的形成至关重要,隧洞的形状和尺寸要靠它来制约。
考虑到混凝土对模板的压缩作用,模板半径较理论半径大,模板用螺栓链接,每组模板由顶模、左右模、底部模四个部分组成。
B.针梁总成它是钢模的受力支撑平台和台车行走的轨道,针梁总成是桁架组合结构。
针对梁上、下焊接有四方刚性轨道。
C.底座前后底座分别根据不同的情况安装在针梁的两端,衬砌时台车的全部重量都落在两个底座上,每个底座上安装两个液压竖向油缸。
2.3、工作原理A、钢模工作原理钢模上安装了三组油缸,可完成立模、拆模工作。
全圆针梁式液压钢模台车在水利枢纽供水工程中的应用

全圆针梁式液压钢模台车在水利枢纽供水工程中的应用【内容摘要】通过全圆针梁式液压钢模台车在水利枢纽供水隧洞衬砌施工,介绍了针梁台车的结构,重点叙述了针梁台车的施工工艺;采用科学合理的施工工艺,将“全圆钢模台车”应用于圆型混凝土一次性模注,有效地保证了圆型有压隧洞混凝土的浇筑质量。
【关键词】水利全圆针粱式液压钢模台车施工1 工程概况红花尔基水利枢纽电厂供水工程位于海拉尔河一级支流伊敏河中游,供水工程水源为红花尔基水利枢纽。
供水工程目的地伊敏电厂位于坝址下游约40 km,鲁能电厂位于坝址下游约65 km。
供水工程为线型布设,主要沿伊敏河河谷展线。
起点为红花尔基水利枢纽工业供水洞,即供水工程头部,终点分别为两电厂厂外的接管点。
2.1 模板选择供水隧洞结构是圆形断面,断面直径为D=2.2m的圆形断面,全长1843m。
方案采用了全圆针梁式液压钢模台车进行混凝土衬砌施工。
该针梁台车衬砌隧洞为全圆断面,底、边、顶一次性成型,立模、拆模用液压油缸执行.定位找正由底座竖向油缸和调平油缸执行。
台车为自行式,安装在台车上的卷扬机使钢模和针梁作相对运动。
台车便可前后移动。
2.2 钢模台车参数台车针梁长度25.4m,总重24.6t,水平最大调整量0.5m (单边),台车钢模直径2.2m,侧模油缸行程0.6m,台车每段衬砌长度10.5m,顶模油缸行程0.5m,最小脱模量度0.15m。
2.3 全圆针梁式液压钢模台车主要部件全圆针梁式液压钢模台车主要由模板总成、针梁总成、梁框总成、水平和垂直对中调整机构、卷扬牵引机构、抗浮装置等组成。
2.3.1 模板总成用于隧洞的成形,隧洞的形状和尺寸主要靠它来制约。
模板间用螺栓联接,每组模板由顶模、左边模、右边模、底模四块组成。
各模块与圆心的夹角分别为:顶模114°,左边模103°,右边模103°,底模40°。
底模两边分别用铰耳销轴连接左、右侧模板。
大型混凝土针梁钢模台车抗浮动技术研究

大型混凝土针梁钢模台车抗浮动技术研究作者:汪仁平来源:《广东科技》 2014年第14期汪仁平(中国葛洲坝集团股份有限公司四川分公司,四川成都 610036)摘要:木里河立洲水电站引水隧洞全长16727m,圆形断面,设计采用钢筋混凝土衬砌,衬砌后断面为直径8.2m。
施工中采用12m长针梁钢模台车全断面衬砌。
由于混凝土浮力大,针梁台车自重难以抵消浮力,造成台车整体上浮,造成相邻仓次混凝土错台,上部钢筋局部隐显等质量缺陷。
通过探索成功解决了混凝土上浮难题。
关键词:大型圆形断面引水隧洞;钢筋混凝土衬砌;针梁钢模台车;混凝土浮力1 概述立洲水电站坝址区位于四川省凉山彝族自治州木里藏族自治县境内,电站采用混合式开发,枢纽工程由碾压混凝土双曲拱坝、坝身泄洪系统、右岸地下长引水隧洞及地面厂房组成。
电站装机三台,总装机容量351MW。
引水隧洞全长16727m。
由于引水隧洞地质条件较差,采用圆形断面,全洞采用钢筋混凝土衬砌,衬砌后断面为直径8.2m。
根据围岩类别不同,钢筋混凝土厚度0.4~0.8m。
2 模板浮力分析与计算2.1 浮力计算理论根据阿基米德原理,物体受到浮力的大小等于它排开的液体的重力:F浮=G排=ρgv但是混凝土又不能完全等同于液体,特别是隧洞衬砌混凝土特性:(1)虽然泵送混凝土塌落度大,流动性强,但是混凝土不是全流态,所以混凝土的浮力计算不能完全等同于液体,通常情况下用阿基米德原理计算出来的浮力大于实际的浮力;(2)混凝土具有黏结力,和模板之间产生黏结力,对浮力有影响,通常情况下,可能会减少一些浮力;(3)混凝土浇筑过程中,台车上振捣器工作时对浮力有影响,工作时可能造成局部压力增大,浮力增加。
所以混凝土浮力不能完全按照基米德原理浮力公式计算。
2.2 混凝土侧压力计算理论如果将混凝土视为完全流体,公式为压强p=ρgh,根据其推算出来的浮力与阿基米德应完全一致。
但是混凝土与流体静压力情形又存在较大不同,根据液体内部某点的压强在各个方向大小是相等的原理,根据模板形状,利用各点压力向上分力的合力即为浮力的原理,可用侧压力公式计算混凝土对模板浮力。
钢模台车受力分析

中国水电集团路桥工程有限公司渝广高速公路项目隧道钢模台车受力验算书批准:审核:编制:中国水电集团路桥工程有限公司渝广高速公路总承包部土建第三分部清平隧道、三汇隧道二衬模板受力验算书一、概述清平隧道、三汇隧道台车模板分顶模和左右边模,顶模受到混凝土自重、施工荷载及注浆口封口时的挤压力等荷载作用。
受力条件显然比其他部分的模板更复杂,结构要求更高,受力更大。
由于边模与顶模的结构构造一样,且边模不受砼自重,载荷较小,因此对其强度分析时,只考虑顶模。
二、设计计算主要依据1、《机械设计手册》新版,机械工业出版社,2005:15-9;2、《隧道施工机械简明手册》第一册,铁道部隧道工程局,1984;3、《水利水电工程施工组织设计手册》第五卷,中国水利水电出版社,1997:812;4、《施工结构计算方法与设计手册》,中国建筑工业出版社,1999:233;5、《起重运输机金属结构》,中国铁道出版社,1983;6、《钢结构设计规范》(GB50017-2003)。
三、主要技术参数台车门架结构受力分析按 1.0m/h(考虑最大浇筑速度)浇筑速度进行,顶模按衬砌厚度800mm校核(考虑超挖厚度200mm)。
台车材料主要为Q235B,其σs=235MPa、σb=375~460MPa、[σ]=170MPa,混凝土容重Υn=2.45t/m3。
台车总体性能参数如下:1、一个工作循环的理论衬砌长度:12米;2、台车门架纵向榀数:6榀;3、台车横移量:左、右各100mm4、成拱半径:R1=5500mm(轮廓半径放大50mm);5、台车运行速度:8m/min;6、液压系统工作压力:16Mpa;7、允许混凝土浇注速度:≤1.0m/h;8、混凝土初凝时间:5h。
四、载荷分析与计算1、边模侧压力计算:台车在浇注边墙时,门架主要承受边模引起的侧压力,新浇混凝土对钢模板的最大侧压力F,按以下公式(见《施工结构计算方法与设计手册》)计算:F=0.22rt0β1β2V1/2式中F—混凝土侧压力;r—混凝土的比重,2.45t/m3;t0—新浇混凝土的初凝时间(h),取5小时;β1—外加剂影响系数,不加外加剂时取1.0;掺具有缓凝作用用的外加剂时取1.2;β2—混凝土坍落度影响修正系数,当坍落度小于3cm时取0.85;当坍落度为5-9cm时取1.0;当坍落度为11-15cm时取1.15;V—混凝土的浇筑速度(m/h),取1.0m/h;将上述各值代入,F=0.22×2.45×5×1.2×1.15×1.01/2=3.72(t/m2)。
针梁台车在引水隧洞衬砌中的应用

针梁台车在引水隧洞衬砌中的应用摘要:本文以某水电站引水隧洞混凝土衬砌工程为例,根据实际选用针梁台车浇筑施工方案,介绍了针梁台车的结构形式、工作原理、施工工艺、质量管控及进度管控措施等,通过在本工程的实施,加快了衬砌速度,确保了浇筑质量,提高了机械化程度,希望能为类似工程提供借鉴和参考。
关键词:针梁台车引水隧洞衬砌应用1.工程概况某水电站引水隧洞全长8757m,隧洞开挖为马蹄形断面,底部为梯形,上部为圆形,洞径5.5m,坡度0‰~17.19‰,隧洞岩石主要以泥质粉砂岩为主,局部有断层、岩溶等地质构造,整个隧洞属于浅埋深段,岩石以Ⅳ~Ⅴ为主,其中842m为全断面衬砌,衬砌厚度60cm,洞径φ4.20m,结构为C30钢筋混凝土。
由于隧洞衬砌厚度较小,且布置钢筋较密,施工人员无法进入仓内振捣,混凝土内在、外观质量难以保证,加之本段隧洞地质条件较差,前期开挖过程中多次塌方,造成工期严重滞后,进度问题严峻,亟待解决,需月浇筑长度≥180m,才能按期实现节点目标。
2.针梁台车结构形式本工程设计针梁台车全长28m,圆形模板直径φ4.22m,模板长度12.2m,整机外形尺寸Ф4.22×28m。
主要由钢模、针梁、门架、卷扬牵引机构、液压系统、电器控制系统等组成。
(1)钢模由底模、左边模、右边模、顶模组成全圆,顶模、左右边模均能围绕门架上的绞轴转动,以便脱模;考虑到混凝土衬砌施工时对模板的压缩作用,模板的直径较理论直径大20mm,为4.22m。
(2)针梁为装配式桁架组合结构,宽1.55米,高1.59米,由6米、8米各2节组成。
每节针梁均由H钢和工字钢焊接而成,上下各设有两条50×50mm方钢轨道,可在门架内的滚轮上沿轴线方向水平滑动。
(3)门架宽2.05米,高2.2米,主要由工字钢焊接而成,底端通过螺栓和底模连接,门架升降时可带动底模同时升降。
(4)液压系统由液压操纵台(电机、油泵、滤清器、液压阀等组成)、两组顶升油缸,三组脱模油缸、两组抗浮油缸、油阀及液压管路等组成。
台车模板螺栓连接受力分析

台车模板螺栓连接螺栓连接件分析如图所示为一台车模板螺栓连接的法兰连接件简图:1、模板弧板厚度14mm2、螺栓型号为M18*75(结构用),共68套3、载荷分析载荷:68套螺栓均施加预应力 IOOON根据实际情况,设定接触类型,a模板弧板为摩擦类型接触对,摩擦系数为 0.15b螺栓与模板弧板为全固定类型接触对c螺帽与模板弧板为全固定类型接触对d螺杆与模板弧板为摩擦类型接触对,摩擦系数为 0.154、材料设置为方便设置,模板弧板材料均取钢材Q235B,螺栓为结构钢,求其变形及应力5、边界条件螺栓连接件分析a导入几何筷型,进入 DS 模块b材料设置选择默认的材料:Structural Steelc设置接触鲸校与螺悖的接触类型为 Bonded 螺栓杆与法兰的接触类型为 Frictional ,摩擦系数为 0.15 螺栓杆与垫片内擎的接触类型为 Frictional ,摩擦系数为 0.15 其余接触类型为 No Separationd网格划分e选择分析类型·在“woekbench” 中选择结构静力学分析“Static Structural ”:f施加约束与载街l)施加归定约束·点击“Static Structural”,在“Supports” 中选择固定约束“FixSupport”选择靶向模板弧板为约束面2)施加载街·依次选择载荷:螺栓杆表,添加螺栓预应力“Bol tPretension ,大小为1OOON6、求解a求解变形·点击“solution 气点击“Deformation "选择“Total ’·,求解变形·点击“S位ess”,选择“Equivalent (Von-Mises)气求解等效应力b单击“Solve” 求解7观察求解结果·点击“Total Deformation ” 查看变形·点击“Equivalent Stress” 查辛苦应力分布模板弧板位移云图由图可知,模板弧板在68套螺栓作用下,最大变形量为0.02mm,满足使用要求模板弧板应力云图由图可知,模板弧板在68套螺栓作用下,最大应力为7.2MPa 满足使用要求螺栓位移云图由图可知,螺栓M18*75,最大变形量为0.001mm,满足使用要求螺栓应力云图由图可知,螺栓M18*75,最大应力为6.5MPa,满足使用要求。
针梁式钢模台车在隧洞施工中的运用

机容量 2 W。工程等别为Ⅲ等 , 5 M X7 工程规模为中 型。枢纽 主要 由碾压混 凝土重力 坝 、 电 引水 隧洞 、 发
调压井 、 力管道 、 压 厂房 及升压 站等组 成 。 引水 隧洞开挖 断 面 为直 径 77m 的圆 形 断面 , .
衬砌断面为直径 66m的圆形断面, . 电站引水隧洞 总长 71 , 0m 其中 5 9 8 60m长的 2 个施工标段 , 因洞 线覆盖层较薄 , 地质破碎软弱 , 围岩差 , 地下水丰富 , 开挖 渗 流水 量大 , 开挖 初期 6 %支护 为 架 立 /0工 5 2 字钢拱架和锚喷支护 , %进行整体混凝土衬砌。 8 0 结合引水隧洞实际情况 , 地质差 , 工程量大 , 工 期短, 为了提高衬砌混凝土结构质量和施工进度, 取 消了普通钢模衬砌台车 , 四川广汉金达隧道机械 与
有限公 司联合研 究设计 生产加 工 了引水隧 洞全 圆整
图 1 针梁台车总装图
3 主要部件
全圆针梁式液压钢模 台车主要 由模板总成、 针 梁总成、 梁框总成 、 水平和垂直对中调整机构、 卷扬 牵引机构、 抗浮装置等组成。 3 1 模 板总成 .
模板 总 成用 于 隧洞 的成 形 , 隧洞 的形 状 和尺寸 主要靠 它来 制 约 。考 虑 到混 凝 土 对 模 板 的 压缩 作
4 工作原理
4 1 钢模 工作 原理 .
为装配式桁架组合结构。针梁主要 由槽 钢构成 , 其
长度 为 2 .8 针 梁 上 、 有 四条 4 l×4 888m; 下 0mn 0姗 的方钢 轨道 , 接 在 针梁 上 , 了 运输 和安 装 方 便 , 焊 为
钢模上安装 了 3组油缸 , 可完成立模 、 模工 拆 作。在顶模和边模 的对应位置上安装螺旋千斤顶, 油缸伸出 , 钢模定 位后 , 旋紧螺旋千斤顶 , 这样保证 衬砌尺寸的准确性 , 并减轻油缸载荷 。脱模时 , 先脱 顶模 , 再脱右边模 , 然后脱左边模 , 最后底座竖向油 缸向上顶 , 使整个 台车 向上运动 , 底模便与混凝土脱 离。
【精品文档类】模板台车受力分析报告
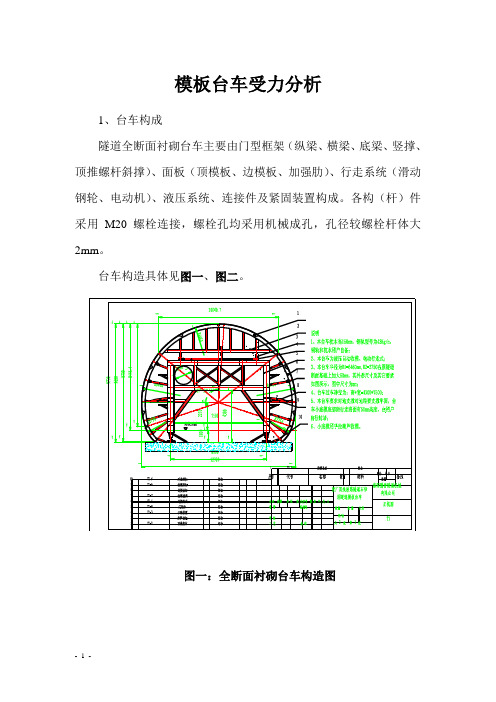
模板台车受力分析1、台车构成隧道全断面衬砌台车主要由门型框架(纵梁、横梁、底梁、竖撑、顶推螺杆斜撑)、面板(顶模板、边模板、加强肋)、行走系统(滑动钢轮、电动机)、液压系统、连接件及紧固装置构成。
各构(杆)件采用M20螺栓连接,螺栓孔均采用机械成孔,孔径较螺栓杆体大2mm。
台车构造具体见图一、图二。
图一:全断面衬砌台车构造图图二:9m长衬砌台车侧视图整体式衬砌台车总体构造如下所示:顶模总成:2组;顶部架体:1组;升降油缸:4件;平移装置:2组;门架体:1组;边模总成:2组;边模丝杠:26件;边模通梁:8件;边模油缸:4件;底部丝杠体:14件。
台车标准长度为9m时,设置12个工作窗口。
二、台车结构受力检算模板支架如图1所示。
计算参照《建筑结构荷载规范》(GB50009-2001)、《混凝土结构工程施工质量验收规范》(GB50204-2002)、《铁路混凝土与砌体工程施工规范》(TB10210-2001)、《钢结构设计规范》(GB50017-2003)、《砼泵送施工技术规程》(JG/T3064-1999)。
1、荷载计算(1)、荷载计算1)、上部垂直荷载永久荷载标准值:上部混凝土自重标准值:1.9×0.6×11.0×24=200.64KN钢筋自重标准值:9.8KN模板自重标准值:1.9×11.0×0.01×78.5=16.4KN弧板自重标准值:(11.0×0.3×0.01×2+11.0×0.3×0.01)×78.5=7.77KN台梁立柱自重:0.0068×(1.15+1.45)×2×78.5=2.78KN上部纵梁自重:(0.0115×8.2+0.015×1.9×2)×78.5=11.88KN 可变荷载标准值:施工人员及设备荷载标准值:2.5振捣混凝土时产生的荷载标准值:2.02)、中部侧向荷载永久荷载标准值:新浇注混凝土对模板侧面的压力标准值:F=0.22rctoβ1β2v 1/2=0.22×25×8×1.2×1.15×10.5=60.6KN/m2F=rc×H=25×3.9=97.5KN/m2取两者中的较小值,故最大压力为60.6KN/m2有效压力高度h=2.42m换算为集中荷载:60.6×1.9×0.6=69.1KN其中:F—新浇混凝土对模板的最大侧压力;rc—混凝土的表观密度;to—新浇混凝土的初凝时间;v—混凝土的浇筑速度;H—混凝土侧压力计算位置处至新浇混凝土顶面的总高度;β1—外加剂影响修正系数;β2—混凝土坍落度影响修正系数;h—有效压力高度。
全园针梁式模板台车

竭诚为您提供优质文档/双击可除全园针梁式模板台车篇一:cb取水隧道二次衬砌模板台车应用技术总结龙源期刊网.cncb取水隧道二次衬砌模板台车应用技术总结作者:陈斌左艳智来源:《建筑工程技术与设计》20xx年第07期【摘要】某核电工程cb隧道1#、3#两条隧道为一心圆,圆形断面隧道开挖直径6.3m,衬砌厚度0.4m,隧道长约1300~1350m。
二次衬砌采用全圆针梁式液压钢模衬砌台车及其技术,并针对本工程的实际情况做了抗浮力计算,满足本工程的实际施工需要,使得本工程取得了圆满的效果,为核电隧道施工总结了经验。
【关键词】液压钢模衬砌台车;二次衬砌;抗浮力1、工程概况cb取水隧道是某核电项目的一子项工程。
它的主体部分有三条隧道组成。
隧道中心线之间的水平距离为15m,它与取水头部及px泵房相连。
该隧道起点中心标高为-21.700m,末端隧道中心标高为-19.900m,自起点隧道中心标高至末端隧道中心逐渐升高,坡度为0.0019,隧道长约1300~1350m。
两侧1#、3#两条隧道为一心圆,圆形断面隧道开挖直径6.3m,衬砌厚度0.4m。
中间2#隧道开挖尺寸为三心圆,隧道开挖宽度3.8m、高2.7m,衬砌浇筑成型为两条内经1.4m的圆形隧道。
cb隧道1#、3#洞二次衬砌采用全圆针梁式液压钢模衬砌台车,台车有效衬砌长度为12米/循环,每循环施工2.5天2、全圆针梁式液压钢模衬砌台车全圆形针梁式液压钢模台车由整圆钢模板、针梁式走行架、全圆形针梁式模板台定位机构、液控传动系统及电气控制五部分组成,台车设计总重量80t。
钢模在纵向长度上分为八节,每节1.5m,模板的整圆环由一块顶模、两块侧模和一块底模构成。
顶模与侧模的连接为铰接,可在油缸控制下收拢和撑开,以达到穿行和立模的目的;两底模之间也为铰接,在起吊油缸和起吊架作用下,以铰轴为圆心向台车纵向中心垂直平面收拢,以便从门架中间穿过。
2.1全圆针梁式液压钢模衬砌台车结构模板由模板、针梁(滑梁)、液压系统、电动系统和防浮支撑系统等组成。
全圆针梁钢模台车组件详解与技术性能介绍

广汉金达隧道机械有限公司
Guanghan Jinda Tunnel Machinery Co.,Ltd.
卷筒
卷扬系统
摆线针轮减速 器 链条
链轮
卷扬基座
轴承座
广汉金达隧道机械有限公司
Guanghan Jinda Tunnel Machinery Co.,Ltd.
导向机构(一)
导向机构(一)是安装在行 走机构前后两端,是对模板在移 动中起导向作用。
广汉金达隧道机械有限公司
Guanghan Jinda Tunnel Machinery Co.,Ltd.
底模总成
12米全圆针梁台车底模总共8件 ,主要由面板、拱板、托架、加强钢 板及角钢组焊而成。
广汉金达隧道机械有限公司
Guanghan Jinda Tunnel Machinery Co.,Ltd.
前、后底座分别安装在针梁的两端,是针梁的
受力支点,衬砌时台车的全部重量都落在两个底座 上,每个底座上安装两个可承受50t力的液压竖向 油缸。
平移机构安装在针梁下面前、后底座上,前、后
底座上各安装有2个竖向油缸与针梁连接,竖向油 缸的伸缩可使针梁上升和下降,以便模板垂直方向 的对中调整,从而完成底模的脱模和立模,最大脱 模行程为390mm;前、后底座上各安装有1个水平油 缸,利用其左、右移动来调整模板中心线与隧洞中 心线相吻合,左右移动行程为200mm。
单耳螺旋千斤
前底座
广汉金达隧道机械有限公司
Guanghan Jinda Tunnel Machinery Co.,Ltd.
侧视图
导向机构(一) 导向机构(二)
竖向油缸
油缸锁定双耳螺旋千斤
广汉金达隧道机械有限公司
中小型断面过车全圆针梁台车的设计与应用

中小型断面过车全圆针梁台车的设计与应用摘要:八十一大板隧洞直径为Φ6.04m,采用全圆针梁台车进行混凝土衬砌。
全圆针梁台车具有全断面一次成型、施工速度快、外观质量好、施工成本低,性价比高等优点。
文章全面介绍了全圆针梁台车的工作原理、结构组成、针梁有限元分析,以及针梁内部过车的现场使用情况。
关键词:针梁台车内部过车有限元分析ANSYS技术1、技术背景八十一大板隧洞是新疆伊犁特克斯河恰甫其海综合利用水利枢纽工程——南岸干渠工程的引水隧洞。
隧洞开挖直径为6.5m,衬砌厚度为25cm,衬砌后过水直径为6.0m。
现如今,国内外对中小型全圆隧道的混凝土施工采用的唯一最佳选择是一次性全圆衬砌。
根据新工局伊犁项目处的要求,该隧道采用全圆针梁台车进行一次性全圆衬砌混凝土施工,同时要求不影响小型工程车通行作业。
如此的全圆断面的衬砌,并要在针梁内部过车在国内尚属首例,也未见到国外有关的报道及技术资料。
该项目的成功实施,为我国中小型断面过车全圆针梁台车的设计及应用提供了借鉴。
2、结构组成全圆针梁台车是为了电站隧洞的整体衬砌而设计。
立模、拆模用液压油缸执行,定位找正由底座竖向油缸和调平油缸执行。
台车为自行式,安装在台车上的卷扬机使钢模和针梁作相对运动,台车便可向前后移动。
全圆针梁台车主要由模板总成、针梁总成、梁框总成、水平和垂直对中调整机构、卷扬牵引机构、抗浮装置等组成,见图1、图2。
由于该全圆针梁台车主要特点是其针梁内部可以过车,给施工提供更好的条件。
因此下面对针梁总成作重点介绍,其他部件在此不作叙述。
针梁总成是钢模的受力支撑平台和台车行走的轨道。
由3组×2块组成,为装配式桁架组合结构。
针梁主要由H型钢构成,其长度为21.029m;针梁上、下焊接有40×40mm的方钢轨道;为了运输和安装方便,针梁分为三节,节与节之间每联接处上下端各用10套高强度螺栓连接。
特别强调的是为便于内部过车,针梁设计成空心框架结构。
针梁台车模板受力分析

针梁台车模板受力分析针梁台车模板分顶模、左右边模及底模,由于顶模受到混凝土自重、施工载荷及注浆口封口时的挤压力等载荷的作用,其受力条件显然比其它部位的模板更复杂、受力更大、结构要求更高。
由于边模、底模与顶模的结构构造一样,边模、底模不受砼自重,载荷较小,因此对其强度分析时只考虑顶模。
由于针梁模板是全园式,在衬砌时的混凝土自重及边墙压力靠模板承受。
模板的每个部分都有托架联接,模板的整体强度既有拱板承受又有托架支承,以保证模板工作时的绝对可靠。
台车模板沿洞轴方向看是一个圆柱壳,只不过它是由多个1.5米高的圆柱形组合而成。
通过计算得知模板下的托架支承及圆弧拱板(300mm宽,12mm 厚)的刚度是足够的,而顶模最危险处应在最顶部(由于灌注时的压力)。
因此,其力学模型可取最顶部2米长度、1.5米宽的这部分模板进行受力分析及强度校核,其受力简图如图1。
图1、分析部分受力简图图2、梁单元结构受力简图该部分载荷由两部分组成,一是砼的自重;二是注浆口封口时产生的较大挤压力,该值的取值是一个不确定的,它与灌注封口时的操作有极大关系。
如果混凝土已经灌满,而操作人员仍然由输送泵输送混凝土,由于输送泵的理论出口压力(36.5kg/cm2)很大,就有可能造成模板的变形破坏。
由于输送管的长度及高度的变化,注浆口接口处压力实际有多大,目前没有理论及实验验证的数据可供参考。
据此情况,操作者就必须及时掌握和控制灌注情况,根据操作经验判定已经灌满,并及时停止输送。
1、分析部分的混凝土自重P1如图1,分析部分的长为2米,宽为1.5米,混凝土厚为0.8m,其密度为2.45t/m3,则混凝土自重W=2×1.5×0.8×2.45=5.88(t)。
折算成单位面载荷P1=5.88/(2×1.5)=1.96t/m2。
2、分析部分的挤压面载荷P2该值取为4.7t/m2,参考自日本歧阜工业公司提供的参数[1]。
单侧墙模板台车力学分析计算书

全钢大模板地铁单侧墙模板台车力学分析计算书(6.0m<层高≤7.25m)北京xx模板有限公司二00六年十一月地铁模板台车力学分析计算书——6.0m<层高≤7.25m一、单侧模板台车技术简介1、单侧支撑简介因砼墙体结构布置要求,只能单侧配设模板,而不能利用穿墙栓控制模板侧压力,只能在单侧模板背侧配设抵抗砼浇筑侧压力的支撑装置,称为单侧支撑。
单侧支撑可分为:刚性三角架,铰接三角架,分段刚性架等。
铰接三角架单侧支撑和台车单侧是xx公司在行业中首创研发并应用的新型单侧模板支撑技术。
2、单侧模板台车结构单侧模板台车包括:混合三角架、万向轮、榀架连接装置、螺旋顶四个部分,并由2榀以上混合三角架连接而成为整体。
其功能:一是施工场地运输模板;二是安装支承单侧墙模。
其辅助相关构造还有地锚和地锚横梁。
混合三角架由梯形桁架和铰接三角架组拼成整体。
二、分析计算内容:1、台车强度分析2、辅件及连接件强度分析三、分析计算依据1、钢结构设计规范:GB50017-20032、建筑工程大模板技术规程:JGJ74-20033、全钢大模板应用技术规程:DBJ01-89-2004四、荷载分析1、基本荷载分析(1)yc=24 KN/m3;V=0.75 m/h(单侧墙模施工侧压力不应过大,控制浇筑速度也不宜过快);β1=1.2;β2=1.1;T=10℃(按地下施工最低温度);t 0=15T200+=1510200+=8(2)砼最大侧压力:q砼侧=0.22 yctβ1β2V=0.22×24×8×1.2×1.1×75.0=48.29 KN/m2h y =c y q 砼侧=2429.48≈2 m (3)浇筑砼水平荷载q 水平=6 KN/m 2 2、荷载组合:(1)系数取值:K 活=1.4 K 恒=1.2 (2)浇砼侧压力计算值:q 侧计=K 恒 q 砼侧+K 活q 水平=1.2×48.29+1.4×6=66.35 2m KN =0.066 2m m N(3)计算单元选取:按台车布置最大间距取1050mm (4)台车背楞处模板线荷载:q 线=1050×0.066=69.3 mm N ,取q 线=70 mm N五、台车结构布置及受力分析 1、台车结构布置如图1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
针梁台车模板受力分析
针梁台车模板分顶模、左右边模及底模,由于顶模受到混凝土自重、施工载荷及注浆口封口时的挤压力等载荷的作用,其受力条件显然比其它部位的模板更复杂、受力更大、结构要求更高。
由于边模、底模与顶模的结构构造一样,边模、底模不受砼自重,载荷较小,因此对其强度分析时只考虑顶模。
由于针梁模板是全园式,在衬砌时的混凝土自重及边墙压力靠模板承受。
模板的每个部分都有托架联接,模板的整体强度既有拱板承受又有托架支承,以保证模板工作时的绝对可靠。
台车模板沿洞轴方向看是一个圆柱壳,只不过它是由多个1.5米高的圆柱形组合而成。
通过计算得知模板下的托架支承及圆弧拱板(300mm宽,12mm 厚)的刚度是足够的,而顶模最危险处应在最顶部(由于灌注时的压力)。
因此,其力学模型可取最顶部2米长度、1.5米宽的这部分模板进行受力分析及强度校核,其受力简图如图1。
图1、分析部分受力简图图2、梁单元结构受力简图
该部分载荷由两部分组成,一是砼的自重;二是注浆口封口时产生的较大挤压力,该值的取值是一个不确定的,它与灌注封口时的操作有极大关系。
如果混凝土已经灌满,而操作人员仍然由输送泵输送混凝土,由于输送泵的理论出口压力(36.5kg/cm2)很大,就有可能造成模板的变形破坏。
由于输送管的长度及高度的变化,注浆口接口处压力实际有多大,目前没有理论及实验验证的数据可供参考。
据此情况,操作者就必须及时掌握和控制灌注情况,根据操作经验判定已经灌满,并及时停止输送。
1、分析部分的混凝土自重P1
如图1,分析部分的长为2米,宽为1.5米,混凝土厚为0.8m,其密度为2.45t/m3,则混凝土自重W=2×1.5×0.8×2.45=5.88(t)。
折算成单位面载荷P1=5.88/(2×1.5)=1.96t/m2。
2、分析部分的挤压面载荷P2
该值取为4.7t/m2,参考自日本歧阜工业公司提供的参数[1]。
那么,这部分模板就受到P1与P2的作用,两部分的合力P=P1+P2=1.96+4.7=6.66t/m2。
3、模板的弯曲应力
由于模板的内表面每隔250mm有一根加强角钢,因此,我们可以把它简化成每隔250mm的梁单元来考虑。
将宽度为250mm的模板所受到的载荷折算成梁上线载荷。
这是在有限元单元处理中常用的方法,其翼缘板的宽度取它与之相邻筋板间距的30%(参考[2]中97页),即250×0.3=75 mm,偏于安全。
根据上述模板所受的面载荷为6.66t/m2,那么在250mm宽,1500 mm长的面积上所受到的载荷为6.66×0.25×1.5=2.5(t),将此载荷作用在1.5米长的梁上,则其线载荷q为2.5/1.5=1.67(t/m)。
如要对整个模板进行受力分析,就必须将整个模板等效成梁单元的空间框架结构,利用有限元理论,通过电算进行有限元分析。
这里,我们只能取一根梁进行分析,简化后的梁单元力学模型按简支梁处理,其受力简图如图2,这是因为两边有250mm高的拱板及立柱支承。
梁的横截面如图3。
图3、梁单元的横截面
为计算梁的弯曲应力,必先计算该梁横截面的形心,该截面是由75×6的角钢及150×8的组合截面,根据图示坐标系,计算组合截面形心O0的X、Y 坐标。
根据[3]中附1-4组合截面形心公式计算形心的X、Y坐标。
x=∑A i x i/∑A i, y=∑A i y i/∑A i
查表可知角钢75×6的横截面积A=879.7 mm2,惯性矩Ix=469500 mm4。
将各值代入,则x=(150×8×75+879.7×95.7)/(1200+879.7)
= 83.76 mm
y=(150×8×79+879.7×20.7)/(1200+879.7)
= 54.34 mm
根据组合截面的平行移轴公式计算组合截面的惯性矩:
Ix =150×83/12+8×150×24.662+469500+879.7×33.642=2201150.87 mm4。
抗弯截面模数W1= Ix/(83-54.34) = 76802 mm3。
抗弯截面模数W2= Ix/54.34 = 40507 mm3。
简支梁受到均布载荷作用下的最大弯矩位于跨中,其值为:Mmax= ql2/8 = 1.67×104×1.52/8 = 4.7×103(N.m)。
梁的最大弯曲应力σ=Mmax/W2
= 4.7×103/4.0507×10-5
= 116.03[Mpa]。
对A3钢,[6s]=160Mpa,所以,梁的强度通过。
4、模板的最大位移
梁单元的最大变形量,即模板的最大位移。
根据公式[4]1-114中对应的受均布载荷简支梁的位移公式:
f max= 5ql4/384EI
式中,E-弹性模量,E=2.1×105 Mpa;
I-截面的惯性矩,I=2.2 ×10-6 m4;
q-梁受到的均布载荷, q=1.67 ×104 N;
l-梁的长度,l=1.5 m;
将各值代入上式:
f max = 5×1.67 ×104×1.54/(384×2.1×1011×2.2 ×10-6)
= 0.0024 m = 2.4 mm。
即模板的最大变形为2.4mm。
通过上述的分析计算可知,整个模板的强度及刚度是足够的。
