初中数学巧用辅助圆解题(可编辑修改word版)
2020年中考数学专题突破6 辅助圆在解题中的应用

图②
微专题 辅助圆在解题中的应用 专题六 辅助圆在解题中的应用
针对训练 10. 如图,已知四边形ABCD. (1)如图①,在矩形ABCD中,请你在矩形ABCD的边上画出使∠APB=30°的所 有点P;
针对训练 7. 如图,已知矩形ABCD,请你在矩形ABCD的边上画出使∠BPC=90°的所有点P.
解:如解图,点P1、P2即为所求点.
第7题图
第7题解图
微专题 辅助圆在解题中的应用 专题六 辅助圆在解题中的应用
8. 如图,已知在Rt△ABC中,AC=5,BC=12,∠ACB=90°,P是边AB上的动
第3题图
微专题 辅助圆在解题中的应用 专题六 辅助圆在解题中的应用
4. 如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB上一 个动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长的最小值
为___7___1__.
第4题图
微专题 辅助圆在解题中的应用 专题六 辅助圆在解题中的应用
第12题图
专题六 辅助圆在解题中的应用
模型分析
模型六 四点共圆
(ⅰ) 如图①、②,Rt△ABC和Rt△ABD共斜边,取AB中点O,根据直角三角形斜边 中线等于斜边一半,可得:OC=OD=OA=OB,∴A、B、C、D四点共圆,共斜边 的两个直角三角形,同侧或异侧,都会得到四点共圆;四点共圆后可以根据圆周角定 理得到角度相等,完成角度等量关系的转化,是证明角度相等重要的途径之一.
辅助圆解题精讲

第二十五讲辅助圆在处理平面几何中的许多问题时,常需要借助于圆的性质,问题才得以解决.而我们需要的圆并不存在(有时题设中没有涉及圆;有时虽然题设涉及圆,但是此圆并不是我们需要用的圆),这就需要我们利用条件,借助图形把需要的实际存在的圆找出来,添补辅助圆的常见方法 1.利用圆的定义添补辅助圆; 2.作三角形的外接圆;3.运用四点共圆的判定方法:(1)假设一个四边形的一组对角互补,则它的四个顶点共圆.(2)同底同侧等角的三角形,各顶点共圆.(3)假设四边形ABCD 的对角线相交于P ,且PA ·PC=PB ·PD ,则它的四个顶点共圆.(4)假设四边形ABCD 的一组对边AB 、DC 的延长线相交于P ,且PA ·PB =PC ·PD ,则它的四个顶点共圆.【例题求解】一·利用圆的定义添加辅助圆【例1】 如图,假设PA=PB ,∠APB=2∠ACB ,AC 与PB 交于点P ,且PB=4,PD=3,则AD ·DC 等于( )A .6B .7C .12D .16思路点拨 作出以P 点为圆心、PA 长为半径的圆,为相交弦定理的应用创设了条件.注:到一个定点等距离的几个点在同一个圆上,这是利用圆的定义添辅助圆的最根本方法. 变式练习:如图,OA=OB=OC ,且∠AOB=k ∠BOC ,则∠ACB 是∠BAC 的( )A .k 21倍 B .是k 倍 C .k 2 D .k1 二·作三角形的外接圆【例2】 如图,在△ABC 中,AB=AC ,任意延长CA 到P ,再延长AB 到Q ,使AP=BQ ,求证:△ABC 的外心O 与A ,P ,Q 四点共圆.思路点拨 先作出△ABC 的外心O ,连PO 、OQ ,将问题转化为证明角相等.变式练习:5.如图,在等腰梯形ABCD 中,AB ∥CD ,AB=998,CD=1001,AD=1999,点P 在线段AD 上,满足条件的∠BPC=90°的点P 的个数为( )A .0B .1C .2 1D .不小于3的整数(全国初中数学联赛题) 三·四点共圆1·假设有一个四边形对角互补,则四边形的四个顶点四点共圆。
巧用辅助圆解决问题

巧用辅助圆解决问题
丰志胜
【期刊名称】《科学大众:科学中考》
【年(卷),期】2022()9
【摘要】圆是初中数学的重要内容之一,与圆相关的证明或计算是中考必考的知识.有些几何问题看似没有圆,却隐藏着圆,要解决问题需要添加“辅助圆”.本文就从具体的实例分析如何发现圆、构造圆、利用圆.
【总页数】2页(P21-22)
【作者】丰志胜
【作者单位】不详
【正文语种】中文
【中图分类】G63
【相关文献】
1.巧用辅助圆,活解直线题
2.巧用辅助圆,活解直线题
3.探究点运动形成的路径问题构造辅助圆解决问题
4.巧用辅助圆,妙解几何题
5.巧用辅助线构造三角形全等解决问题的策略
因版权原因,仅展示原文概要,查看原文内容请购买。
巧解初中几何问题——以构造辅助圆为例

2023年12月下半月㊀解法探究㊀㊀㊀㊀巧解初中几何问题以构造辅助圆为例◉江苏省靖江市外国语龙馨园学校㊀徐㊀乐㊀㊀圆是初中数学平面几何中非常重要的一个知识点,与初中数学中其他几何问题有着紧密的联系.所以在解决几何问题时,一些无法利用常规思路求解的综合问题可以尝试通过构造辅助圆的方式来解决.因此,在初中数学几何问题解题教学中,教会学生如何正确使用辅助圆来巧解几何问题是教师需要重点研究的问题.下面将通过例题对辅助圆的应用进行说明.1角的问题例1㊀在әA B C 中,A B =A C ,øA B C 的平分线交A C 于点D ,已知B C =B D +A D ,求øA 的度数.分析:根据题中所给已知条件,可以判定әA B C为等腰三角形,但是想要根据已知条件通过常规方式求øA 的度数存在一定困难.结合题中所给的角平分线,可以联想圆中共顶点的角的问题,作әA B D 的外图1接圆,与әA B C 的B C 边交于点E ,连接D E ,如图1.根据B D 是øA B C 的角平分线,可以知道A D =D E ,同时还能得到这个辅助圆为四边形A B E D 的外接圆.根据圆内接四边形的对角互补的性质可得øA B C =øE D C ,根据әA B C 为等腰三角形可知øA B C =øE D C =øC ,于是可得øB E D =2øC ,且әE D C 为等腰三角形.所以D E =C E ,则A D =D E =C E ,然后结合B C =B E +A D 得到B D =B E ,所以øB D E =øB E D =2øC .这样就可以在әB D E 中计算øC 的度数,即12øC +2øC +2øC =180ʎ,所以øC =40ʎ,最后计算得出øA =100ʎ.在初中数学几何问题中构造辅助线需要充分结合试题的情况来进行.本题中辅助圆的构造就是结合了本题所给定的角平分线的关系,根据相等的圆周角所对应的弧和弦长相等的性质来实现;然后通过辅助圆及相关线段关系来与相关角取得联系;最后利用三角形的性质求解.教师要对学生进行相应的引导,让学生掌握通过角的关系来构造辅助圆,进而借助辅助圆解决问题.2线段长度的问题图2例2㊀如图2所示,在R t әA B C中,A B ʅB C ,A B =6,B C =4,P 是R t әA B C 内部的一个动点,且满足øP A B =øP B C ,则线段C P 的最小值为(㊀㊀).A.32㊀㊀㊀㊀㊀㊀B .2C .81313D.121313图3分析:根据A B ʅB C 可以知道øA B C =90ʎ,结合øP A B =øP B C 可得到øA P B =90ʎ,所以әA B P 是直角三角形.根据直角三角形中斜边的中线等于斜边的一半以及圆的直径所对的圆周角是90ʎ,可知点P 在以A B 为直径的圆上.以A B 的中点O 为圆心,A B 为直径作圆,如图3所示.这样就可得到当P C 的值最小时,点P 正好在线段O C 上.因为A B =6,所以O B =3.在R t әO B C 中,B C =4,根据勾股定理得到O C =5,于是可求出P C 的最小值为2.所以正确答案是选项B .例2的解题关键是需要判断点P 的轨迹,首先根据试题中所给定的关系得到øA P B =90ʎ,结合直角三角形的性质和圆的性质很容易判断出点P 在以直线A B 为直径的圆上,然后就能够求解最小值.因此,在解题的过程中,只有认真分析题目条件,才能顺利找到解题思路.教师在进行解题教学时需要教会学生如何根据题目中所给定的已知条件来进行分析,从而找到解题思路.很多几何问题都是需要在解题的过程中才能够找到相应的解题思路,并不是通过对试题的观察就能得到解题思路的.因此结合已知条件来对试97解法探究2023年12月下半月㊀㊀㊀题中存在的关系进行分析,在解题的过程中发现解题思路,是解决问题最好的方式.教师需要引导学生先根据已知条件尝试找到解题的思路,进而解决问题.3三角形相似的问题例3㊀әA B C 中,A D 是øB A C 的外角平分线,交B C 的延长线于点D ,求证:B D D C =A BA C.分析:A B ,A C 是әA B C 的两条边,而B D ,D C则是线段B D 上的两条线段,根据所学的知识,要证明B D D C =A BA C ,线段成比例关系可以通过证明三角形相似来解决.因此需要将线段B A 延长至点F ,连接D F ,构建出әB A C ʐәB D F ,得到A B A C =B DD F,然后证明C D =D F 就可以了,从而将证明的关键转化为证明C D =D F .结合题意,øB A C 的外角平分线交B C的图4延长线于点D ,如图4,根据例题1中的方式构造әA C D 的外接圆,B A 的延长线与圆交于点F ,连接D F .根据圆的性质可以得到C D =D F ,通过相似三角形的证明就可以解决问题.几何问题中需要求证的结论存在线段比例关系或者线段等积关系时,都会涉及三角形相似或者全等的证明,通过构造圆为三角形相似或者全等提供条件,实现对问题的求解.在这个过程中,需要充分结合例题1和例题2中辅助圆构造的方式来找到相应的关系.4动点的问题图5例4㊀如图5所示,边长为3的等边三角形A B C ,D ,E 分别是B C ,A C 边上的两个动点,且B D =C E ,A D ,B E 交于点P ,求点P 的运动路径长和C P 的最小值.分析:首先需要对点P 的运动路径进行判定.根据等边三角形的相关性质和B D =C E 可以得到әA B D ɸәB C E ,这样就得到øC B E =øB A D ,然后通过øC B E +øA B P =60ʎ得到øB A P +øA B P =øA P E =60ʎ,于是øA P B =120ʎ.可以发现在点D 和点E 移动的过程中,øA P B =120ʎ是恒成立的,所以可以认为点P 在A B 为弦的圆上.假设弦A B 所在圆的圆心为O ,连接O P ,O A ,O B ,根据圆的性质㊁әA B C 的边长为3可计算出圆O 的半径O A =3,然后计算出点P 的运动路径长度为233π,C P 的最小值为3.解:由A B =B C ,øA B D =øB C E ,B D =C E 得әA B D ɸәB C E .由øC B E +øA B P =60ʎ,得øB A P +øA B P =øA P E =60ʎ.所以øA P B =120ʎ.故点P 的运动轨迹是以A B 为弦的圆上的一段弧.图6如图6所示,作әA B P 的外接圆,圆心为O ,连接O A ,O B ,O P ,O C .由O A =O B ,A C =B C ,得әA O C ɸәB O C .所以øO A C =øO B C ,øA C O =øB C O =12øA C B =30ʎ,øA O C =øB O C =12øA P B =60ʎ.故øO A C =90ʎ.根据勾股定理,可得O A =3,O C =23.所以,弦A B 所对的弧长为3ˑ23π=233π;当O ,P ,C 三点共线时,C P 最小,且最小值为3.在三角形的动点问题中,如果动点与一条线段所构成的角度固定,则说明这个动点的轨迹是以这个线段为弦的圆上的一段弧,通过这个关系可以构造辅助圆,然后利用圆的性质来求解问题.本题给定的是正三角形,当然不同的三角形中所呈现的关系可能会存在差别,但是本质没有变化.例如,在例题2中通过计算所得到的角度为90ʎ的特殊角,这个辅助圆的圆心就在直角三角形的斜边上.例4中这个角度为120ʎ,圆心在三角形的外部,通过辅助圆来充分利用圆的相关性质,能够更好地对问题进行求解,实现问题的解决.本文中对辅助圆在初中数学平面几何中的应用进行了总结,并通过相关例题对其用法进行了说明.在初中数学平面几何问题中巧用辅助圆能够优化试题解法,实现快速求解.因此,教师在解题教学的过程中需要对学生进行有效地引导,让学生掌握辅助圆的应用,从而提升解题能力;提升数学素养.Z08。
(完整版)初三《圆》知识点及定理(可编辑修改word版)
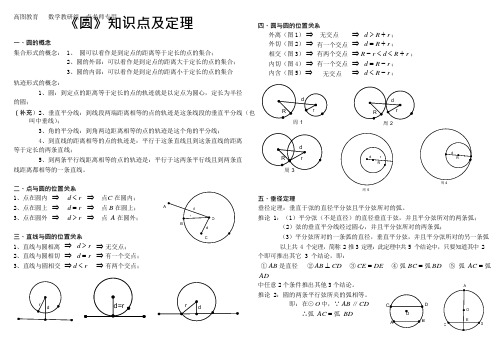
高图教育 数学教研组 卢老师专用《圆》知识点及定理四、圆与圆的位置关系一、圆的概念集合形式的概念: 1、 圆可以看作是到定点的距离等于定长的点的集合;2、圆的外部:可以看作是到定点的距离大于定长的点的集合;3、圆的内部:可以看作是到定点的距离小于定长的点的集合外离(图 1) ⇒ 外切(图 2) ⇒ 相交(图 3) ⇒ 内切(图 4) ⇒ 内含(图 5) ⇒ 无交点有一个交点有两个交点有一个交点无交点⇒ d > R + r ; ⇒ d = R + r ;⇒ R - r < d < R + r ; ⇒ d = R - r ; ⇒ d < R - r ;轨迹形式的概念:1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径 的圆;(补充)2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线);周 1周 23、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线; 4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线;5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直 线距离都相等的一条直线。
周 4二、点与圆的位置关系周 51、点在圆内2、点在圆上3、点在圆外 ⇒ d < r ⇒ ⇒d = r ⇒ ⇒ d > r ⇒ 点C 在圆内; 点 B 在圆上;A 点 A 在圆外;五、垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论 1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;三、直线与圆的位置关系(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧 1、直线与圆相离 2、直线与圆相切 ⇒ d > r ⇒ d = r ⇒ 无交点; ⇒ 有一个交点; 以上共 4 个定理,简称 2 推 3 定理:此定理中共 5 个结论中,只要知道其中 2个即可推出其它 3 个结论,即: 3、直线与圆相交 ⇒ d < r⇒ 有两个交点;① AB 是直径② AB ⊥ CD AD③ CE = DE④ 弧 BC = 弧 BD ⑤ 弧 AC = 弧中任意 2 个条件推出其他 3 个结论。
初中数学竞赛讲解教材第二讲巧添辅助妙解竞赛题

第二讲 巧添辅助 妙解竞赛题在某些数学竞赛问题中 , 巧妙添置辅助圆常可以沟通直线形和圆的内在联系 , 通过圆的有关性质找到解题途径 . 下面举例说明添置辅助圆解初中数学竞赛题的若干思路 .1 挖掘隐含的辅助圆解题有些问题的题设或图形本身隐含着“点共圆” , 此时若能把握问题提供的信息 , 恰当补出辅助圆 , 并合理挖掘图形隐含的性质 , 就会使题设和结论的逻辑关系明朗化 .1.1 作出三角形的外接圆例 1 如图 1, 在△ ABC 中, AB =AC, D 是底边 BC A 上一点 , E 是线段 AD 上一点且∠ BED = 2∠ CED =∠A. 求证: BD =2CD.E分析:关键是寻求∠ BED =2∠CED 与结论的联系 .容易想到作∠ BED 的平分线 , 但因 BE ≠ ED, 故不能 B G D C直接证出 BD =2CD. 若延长 AD 交△ ABC 的外接圆 F图1 于 F, 则可得 EB = EF, 从而获取 .证明: 如图 1, 延长 AD 与△ ABC 的外接圆相交于点 F, 连结 CF 与 BF, 则∠ BFA =∠ BCA =∠ ABC =∠ AFC, 即∠ BFD =∠ CFD. 故 BF: CF =BD: DC.又∠ BEF =∠ BAC, ∠BFE =∠ BCA, 从而∠ FBE =∠ ABC =∠ ACB =∠ BFE.故 EB =EF.作∠ BEF 的平分线交 BF 于 G, 则 BG =GF.因∠ GEF = 1∠ BEF =∠ CEF, ∠ GFE =∠ CFE, 故△ FEG ≌2 △ FEC. 从而 GF = FC. 于是, BF =2CF. 故 BD =2CD.1.2 利用四点共圆例 2 凸四边形 ABCD 中, ∠ABC =60°, ∠ BAD =∠BCD =90°,CB ODAB =2, CD = 1, 对角线 AC 、BD 交于点 O, 如图 2. 则 sin ∠ AOB = ____.分析:由∠ BAD =∠ BCD =90°可知 A 、 B 、 C 、DAP图2四点共圆 , 欲求 sin ∠AOB, 联想到托勒密定理 , 只须求出 BC 、AD 即可 .解:因∠ BAD =∠ BCD =90° , 故 A 、B 、 C 、 D 四点共圆 . 延长BA 、CD 交于 P, 则∠ ADP =∠ ABC =60°.设 AD = x, 有 AP = 3 x, DP = 2x. 由割 线 定理 得 (2 +13 x) 3x =2x(1 + 2x). 解得 AD = x =2 3 - 2, BC = BP =4-3 .由托勒密定理有BD ·CA =(4 - 3 )(2 3-2) +2×1=10 3 -12.又 S ABCD = S △ ABD +S △BCD = 3 3.2故 sin ∠AOB =15 63 .26例 3 已知:如图 3, AB =BC =CA =AD, AH ⊥CD 于 H, CP ⊥BC, CP 交 AH 于 P. 求证: A△ ABC 的面积 S =3BPAP · BD.Q4D3BC 2=3AC ·BC, 只分析:因 S △ABC =C H图34 4须证 AC ·BC =AP ·BD, 转化为证△ APC ∽△ BCD. 这由 A 、B 、C 、Q 四点共圆易证 ( Q 为 BD 与 AH 交点).证明: 记 BD 与 AH 交于点 Q, 则由 AC =AD, AH ⊥ CD 得∠ ACQ =∠ ADQ.又 AB =AD, 故∠ ADQ =∠ ABQ.从而 , ∠ABQ =∠ ACQ. 可知 A 、B 、C 、Q 四点共圆 . ∵∠ APC =90°+∠ PCH =∠ BCD, ∠CBQ =∠ CAQ, ∴△ APC ∽△ BCD. ∴AC ·BC =AP ·BD.于是, S =3AC ·BC =3AP ·BD.442构造相关的辅助圆解题有些问题貌似与圆无关 , 但问题的题设或结论或图形提供了某些与圆的性质相似的信息 , 此时可大胆联想构造出与题目相关的辅助圆 , 将原问题转化为与圆有关的问题加以解决.2.1联想圆的定义构造辅助圆例 4如图 4, 四边形 ABCD 中, AB∥CD, AD=DC B A=DB= p, BC=q. 求对角线 AC 的长 .分析:由“ AD=DC=DB=p”可知 A、B、C 在C E 半径为 p 的⊙ D 上 . 利用圆的性质即可找到AC 与Dp、q 的关系 .解:延长 CD 交半径为 p 的⊙ D 于 E 点, 连结 AE.图4显然 A、B、C 在⊙D 上.∵AB∥CD,∴BC=AE.从而 , BC=AE=q.在△ ACE 中 , ∠ CAE=90°, CE= 2p, AE=q, 故AC= CE 2AE 2= 4 p2q 2.2.2联想直径的性质构造辅助圆例 5 已知抛物线 y=-x2+2x+8 与 x 轴交于 B、C 两点,点 D 平分BC. 若在 x 轴上侧的 A 点为抛物线上的动点 , 且∠ BAC 为锐角 , 则AD 的取值范围是 ____.分析:由“∠BAC 为锐角”可知点A 在以定线段BC 为直径的圆外 , 又点 A 在 x 轴上侧 , 从而可确定动点 A 的范围 , 进而确定 AD 的取值范围 .解:如图 5, 所给抛物线的顶点为 A0(1,9), 对称轴为 x= 1, 与 x 轴交于两点 B( -2,0) 、C(4,0).分别以 BC、DA 为直径作⊙ D、⊙ E, 则两圆与抛物线均交于两点 P(1 -2 2 ,1) 、Q(1 +2 2 ,1).可知 , 点 A 在不含端点的抛物线 PA0Q 内时 , ∠BAC<90°. 且有 3=DP=DQ<AD ≤ DA0=9,即 AD 的取值范围是 3<AD≤9.yA0 (1,9)EP QB DC x (-2,0)(4,0)图52.3联想圆幂定理构造辅助圆例 6 AD 是 Rt△ABC 斜边 BC 上的高 , ∠ B 的平行线交 AD 于 M, 交 AC 于 N. 求证: AB2-AN2=BM·BN.分析:因 AB2- AN2=( AB+ AN)( AB-AN) = BM·BN, 而由题设易知 AM=AN, 联想割线定理 , 构造辅助圆即可证得结论 .证明:如图 6,∵∠ 2+∠ 3=∠ 4+∠ 5=90°,又∠ 3=∠ 4, ∠1=∠ 5,∴∠ 1=∠ 2. 从而 , AM = AN.以 AM 长为半径作⊙ A, 交 AB 于 F, 交 BA 的延长线于 E. 则 AE =AF =AN.由割线定理有 BM ·BN =BF ·BE=( AB + AE)( AB - AF)= ( AB + AN)( AB - AN)= A B 2- AN 2,EA2NF 13 5 M4 B D C图6即 AB 2 -AN 2= BM · BN.例 7 如图 7, ABCD 是⊙ O 的内接四边形 , 延长 AB 和 DC 相交于 E,延长 AB 和 DC 相交于 E,延长 AD 和 BC 相交于 F,EP 和 FQ 分别切⊙ O 于 P 、Q. 求证: EP 2+FQ 2= EF 2.分析:因 EP 和 FQ 是⊙ O 的切线 , 由结论联想到切割线定理 , 构造辅助圆使 EP 、FQ 向 EF 转化 .证明: 如图 7, 作△ BCE 的外接圆交 EF 于 G, 连 A 结 CG.因∠FDC =∠ ABC =∠ CGE, 故 F 、D 、C 、 PQG 四点共圆 .OD 由切割线定理 , 有CB EF 2 =( EG +GF) · EF E GF=EG · EF +GF · EF =EC ·ED +FC ·FB =EC ·ED +FC ·FB =EP 2 +FQ 2,即 EP 2 +FQ 2= EF 2. 2.4 联想托勒密定理构造辅助圆例 8 ' ' AA' 如图 8, △ABC 与△ A BcbC ' 的三边分别为 a 、b 、c 与 a ' 、c' b'b 、c', 且∠B =∠ B, ∠A +∠ACB'a' C'''Ba= 180°. 试证: aa=bb(2) '+cc .(1)' ''分析:因∠ B =∠ B' , ∠A +∠ A'图8= 180°, 由结论联想到托勒密定理 , 构造圆内接四边形加以证明 . 证明: 作△ ABC 的外接圆 , 过 C 作 CD ∥AB 交圆于 D, 连结 AD 和 BD,如图 9 所示.∵∠ A +∠ A ' =180°=∠ A +∠ D,∠BCD =∠ B =∠ B ' ,∴∠A ' =∠ D, ∠B ' =∠ BCD.∴△A ' B ' C ' ∽△ DCB. 有 A'B'= B'C'= A'C',DC CB DB即 c' = a' = b' .DCaDB故 DC =ac', DB =ab'.a'a'Acb CBabD图9又 AB ∥DC, 可知 BD =AC =b, BC =AD =a. 从而 , 由托勒密定理 , 得AD ·BC =AB ·DC +AC ·BD,即a 2=c · ac ' + b · ab' .a'a'故 aa ' =bb ' +cc ' .练 习 题1. 作一个辅助圆证明:△ ABC 中, 若 AD 平分∠ A, 则AB=BD.AC DC( 提示:不妨设 AB ≥AC, 作△ ADC 的外接圆交 AB 于 E, 证△ ABC ∽△ DBE, 从而AB=BD=BD.)ACDE DC2. 已知凸五边形 ABCDE 中, ∠BAE = 3a, BC =CD = DE, ∠BCD =∠ CDE = 180°- 2a. 求证:∠ BAC =∠ CAD =∠ DAE.( 提示:由已知证明∠ BCE =∠ BDE = 180°- 3a, 从而 A 、 B 、C 、D 、E 共圆, 得∠ BAC =∠ CAD =∠ DAE.)3. 在△ ABC 中 AB =BC, ∠ABC =20°, 在 AB 边上取一点 M, 使 BM =AC. 求∠ AMC 的度数 .( 提示:以 BC 为边在△ ABC 外作正△ KBC, 连结 KM, 证 B 、 M 、 C 共圆 , 从而∠ BCM = 1∠BKM =10°, 得∠AMC =30°.)24.如图 10, AC 是 ABCD 较长的对角线 , 过 C 作 F CCF ⊥AF, CE ⊥AE. 求证: AB · AE +AD · AF =AC 2. D( 提示:分别以 BC 和 CD 为直径作圆交 AC 于点G 、 H. 则 CG =AH, 由割线定理可证得结论 .)AB E5. 如图 11. 已知⊙ O 1 和⊙ O 2 相交于 A 、B, 直线 图10CD 过 A 交⊙ O 1 和⊙O 2 于 C 、D, 且 AC =AD, EC 、ED 分别切两圆于 C 、D. 求证: AC 2=AB ·AE.( 提示:作△ BCD 的外接圆⊙ O3, 延长 BA 交⊙ O3E于 F, 证 E 在⊙ O3上, 得△ ACE≌△ ADF, 从而 AE D= AF, 由相交弦定理即得结论 .)AC O1O26.已知 E 是△ ABC 的外接圆之劣弧 BC 的中点 .B求证: AB·AC=AE2-BE2.图11 ( 提示:以 BE 为半径作辅助圆⊙ E, 交 AE 及其延长线于 N、M,由△ ANC∽△ ABM 证 AB· AC= AN· AM.)7.若正五边形ABCDE 的边长为 a, 对角线长为b, 试证:b-a a b= 1.( 提示:证 b2=a2+ab, 联想托勒密定理作出五边形的外接圆即可证得 .)。
中考数学备考课件:辅助圆问题 (共19张PPT)

BM C
∴△ABM≌△BCN(SAS)
∴ BAM CBN
∵ ABP CBN 90o ∴ ABP BAM 90o ∴ APB 90o ∴点 P 在以 AB 为直径的圆上
运动,设圆心为 O,连接 OC 交⊙O 于 P,此时 PC 最小 ∵ AB 4 ∴ OP OB 2
A
D
O
N
P B MC
解:∵ AB AC AD 2
E
∴点 B,C,D 在以点 A 为圆心, 半径为 2 的圆上延长 BA 交 D ⊙A 于 E,连接 DE
∵AB∥CD ∴ EBD BDC
A
B
C
∵ DE DE , BC BC ∴ EAD 2EBD ,
BAC 2BDC
∴ EAD BAC
E
A
B
∴ ED BC 1
小值为 BC sin B 3 3
∴DE 长的最小值为
3 2
PC
3 2
3
3
9 2
.
类型二 定点 定长模型 方法与技巧 常见图形中共顶点的多条线段相等,可考虑利用到 定点的距离等于定长推导共圆,再利用圆有关性质 解决问题.
3.如图,在四边形 ABCD 中, AB AC AD 2 , BC 1,AB∥CD.求 BD 的长.
由勾股定理,得 OC OB2 BC2 2 5
∴ PC OC OP 2 5 2
∴PC 长的最小值为 2 5 2 .
2.如图,在 Rt△ ABC 中, ACB 90o , AB 5,
cos
B
4 5
,⊙A
与边
BC
交于点
C,过
A
作
DE∥BC,
交⊙A 于点 D,E,点 F 在 DC 上,连接 EF,过 A 作
(完整word版)初二数学图形辅助线常见做法

八年级数学培优训练题补形法的应用班级________ 姓名__________ 分数_______一些几何题的证明或求解,由原图形分析探究,有时显得十分繁难,若通过适当的“补形”来进行,即添置适当的辅助线,将原图形填补成一个完整的、特殊的、简单的新图形,则能使原问题的本质得到充分的显示,通过对新图形的分析,使原问题顺利获解。
这种方法,我们称之为补形法,它能培养思维能力和解题技巧。
我们学过的三角形、特殊四边形、圆等都可以作为“补形”的对象。
现就常见的添补的图形举例如下,以供参考。
一、补成三角形1.补成三角形例1.如图1,已知E为梯形ABCD的腰CD的中点;证明:△ABE的面积等于梯形ABCD面积的一半。
分析:过一顶点和一腰中点作直线,交底的延长线于一点,构造等面积的三角形。
这也是梯形中常用的辅助线添法之一。
略证:2.补成等腰三角形例2 如图2.已知∠A=90°,AB=AC,∠1=∠2,CE⊥BD,求证:BD=2CE分析:因为角是轴对称图形,角平分线是对称轴,故根据对称性作出辅助线,不难发现CF=2CE,再证BD=CF即可。
略证:3.补成直角三角形例3.如图3,在梯形ABCD中,AD∥BC,∠B+∠C=90°,F、G分别是AD、BC的中点,若BC=18,AD=8,求FG的长。
分析:从∠B、∠C互余,考虑将它们变为直角三角形的角,故延长BA、CD,要求FG,需求PF、PG。
略解:图34.补成等边三角形例4.图4,△ABC是等边三角形,延长BC至D,延长BA至E,使AE=BD,连结CE、ED。
证明:EC=ED分析:要证明EC=ED,通常要证∠ECD=∠EDC,但难以实现。
这样可采用补形法即延长BD到F,使BF=BE,连结EF。
略证:二、补成特殊的四边形1.补成平行四边形例5.如图5,四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点,并且E、F、G、H 不在同一条直线上,求证:EF和GH互相平分。
最全最新初中数学竞赛专题讲解辅助圆

初中数学竞赛专题讲解辅助圆在处理平面几何中的许多问题时,常需要借助于圆的性质,问题才得以解决.而我们需要的圆并不存在(有时题设中没有涉及圆;有时虽然题设涉及圆,但是此圆并不是我们需要用的圆),这就需要我们利用已知条件,借助图形把需要的实际存在的圆找出来, 添补辅助圆的常见方法有:1.利用圆的定义添补辅助圆;2.作三角形的外接圆;3.运用四点共圆的判定方法: (1)若一个四边形的一组对角互补,则它的四个顶点共圆. (2)同底同侧张等角的三角形,各顶点共圆.(3)若四边形ABCD 的对角线相交于P ,且PA ·PC=PB ·PD ,则它的四个顶点共圆.(4)若四边形ABCD 的一组对边AB 、DC 的延长线相交于P ,且PA ·PB =PC ·PD ,则它的四个 顶点共圆.推论:同斜边的直角三角形顶点共圆(斜边就是圆的直径). 4.画出辅助圆就可以应用圆的有关性质.常用的有:① 同弧所对的圆周角相等.② 圆内接四边形对角互补,外角等于内对角. ③ 圆心角(圆周角)、弧、弦、弦心距的等量关系. ④ 圆中成比例线段定理:相交弦定理 ,切割线定理. 5.证明型如ab+cd=m 2常用切割线定理一、基础过关1.如图1,AB=AC=AD,如果∠DAC 是∠CAB 的K 倍(K 为实数).求:∠DBC 是∠BDC 的多少倍?2.△ABC 中,作BD ⊥AC 于D ,CE ⊥AB 于E ,连DE ,若∠ABC =45°, 求∠EDB 的度数。
A COD EB3.如图,B 是线段AC 的中点,过点C 的直线l 与AC 成60°的角,在直线l 上取一点P ,使得∠APB=30°,则满足条件的点P 的个数是( )(A)3个(B)2个 (C)1个 (D)不存在4.已知:如图,直尺的宽度为2,A 、B 两点在直尺的一条边上,AB=6,C 、D 两点在直尺的另一条边上.若∠ACB=∠ADB=90°,求则C 、D 两点之间的距离 .4.如图,矩形ABCG(AB<BC)与矩形CDEF 全等,点B 、C 、D 在同一条直线上,∠APE 的顶点P 在线段BD 上移动,使∠APE 为直角的点P的个数是 ( ) A.0 B.1 C.2 D.35.如图,点A 与点B 的坐标分别是(1,0),(5,0),点P 是该平面直角坐标系内的一个动点. (1)若点C 平面直角坐标系内的一个点,且△ABC 是等边三角形,则点C 的坐标是 ; (2)若点P 在y 轴上,且∠APB=30°,求满足条件的点P 的坐标;(3)当点P 在y 轴上移动时,∠APB 是否有最大值?若有,求点P 的坐标,并说明此时∠APB 最大的理由;若没有,也请说明理由.二、例题讲解1.根据圆的定义作辅助圆例1:如图,四边形ABCD 中,AB ∥CD ,AB =AC =AD =p ,BC =q ,求BD 的长.解析:以点A 为圆心、AB 为半径作⊙A .因为AB =AC =AD ,所以B 、C 、D 三点在⊙A 上.延长BA 交⊙A 于点E ,连结DE .因为DC ∥EB ,所以弧ED =弧BC ,所以ED =BC =q .在Rt △BDE 中,根据勾股定理,得BD =.例2:如图,PA =PB ,∠APB =2∠ACB ,AC 与PB 交于点D ,且PB =5,PD =3,求AD ·DC 的值.解析:以点P 为圆心、P B为半径的作⊙P .因为PA =PB ,∠APB =2∠ACB ,所以点A、B 、C在⊙P 上.此时⊙P 的直径BE =10,DE =8,DB =2, 由相交弦定理,得AD ·DC =DE ·DB =8216⨯=2.作三角形的外接圆例3:如图,D 、E 为△ABC 边BC 上的两点,且BD=CE ,∠BAD=∠CAE ,求证:AB=AC . 解析:作△ADE 的外接圆,分别交AB 、AC 于点M 、N ,连结MD 、NE .因为∠BAD =∠CAE ,所以∠BAD +∠DAE =∠CAE+∠DAE ,即∠NAD =∠MAE .因为∠BDM =∠MAE ,∠CEN =∠NAD ,所以∠BDM =∠CEN . 又BD =CE ,DM =EN ,所以△BDM ≌△CEN ,所以∠B =∠C ,即AB =AC .例4:如图,△ABC 中,BF 、CE 交于点D ,BD =CD ,∠BDE =∠A ,求证:BE =CF . 解析:作△ABC 的外接⊙O ,延长CE 交⊙O 于G ,连接BG .因为∠G =∠A ,∠BDE =∠A ,所以∠G =∠BDE ,所以BG=BD . 又BD =CD ,所以BG =CD.又因为∠G =∠CDF ,∠GBE =∠DCF ,所以△GBE ≌△DCF . 所以BE =CF .BC例5:如图,在△ABC 中,AB =AC ,∠BAC =100°,∠B 的平分线交AC 于D , 求证:BC =BD +AD .解析:作△ABD 的外接圆交BC 于E ,连结DE .因为BD 是∠ABC 的平分线,所以弧AD =弧DE ,所以AD =DE . 在△BDE 中,∠DBE =20°,∠BED =180°―100°=80°, 所以∠BDE =80°, 所以BE =BD .在△DEC 中,∠EDC =80°―40°=40°,所以EC =DE . 所以BC =BE +EC =BD +AD .3.结论类似于圆幂定理的形式时作辅助圆例6:如图,在△ABC 中,AB =AC =3,D 是边BC 上的一点,且A D=1,求BD ·DC 的值. 解析:以点A 为圆心、AB 为半径作⊙A ,交直线AD 于点E 、F ,则点C 在⊙A 上,DE =13-,DF =13+.由相交弦定理,得BD ·DC =DE ·DF =)13)(13(+-=2.例7:如图,在△ABC 中,∠DAB =∠C ,∠B 的平分线BN 交AD 于M .求证:(1)AM =AN ;(2)AB 2-AN 2=BM ·BN .解析:(1)略;(2)由(1),得AM =AN .以点A 为圆心、AM 为半径作⊙A ,交AB 于E ,交BA 的延长线于F ,则N 在⊙A 上,且AE =AF =AN .由割线定理,得BM ·BN =BE ·BF =(AB -AE)(AB +AF)=(AB ―AN)(AB +AN =AB 2-AN 2,即AB 2-AN 2=BM ·BN .4.探究动点对定线段所张的角时作辅助圆例8:如图,在直角梯形ABCD 中,AB ∥DC ,∠B =90°,设AB =a ,DC =b ,AD =c , 当a 、b 、c 之间满足什么关系时,在直线BC 上存在点P ,使AP ⊥PD ?解析:以AD 为直径作⊙O ,根据直径所对的圆周角是直角,当⊙O 与直线BC 有公共点(相切或相交)时,在直线BC 上存在点P ,使AP ⊥PD .因为⊙O 的半径r =22cAD =,圆心O 到直线BC 的距离d =22b a DC AB +=+. 所以,当d ≤r ,即a +b ≤c 时,在直线BC 上存在点P ,使AP ⊥PD .C例9:如图,在平面直角坐标系xOy 中,给定y 轴正半轴上的两点A (0,2)、B(0,8),试在x 轴正半轴上求一点C ,使∠ACB 取得最大值。
中学考试复习策略梳理——巧构“辅助圆”,全面辅助圆解题技巧

全班玩魔方日记结尾作文
魔方,这小小的玩意儿,可把咱们全班给迷住了!每个人都玩
得不亦乐乎,你瞧!
小红拿着魔方,眼睛亮得跟什么似的,嘴里嘀咕着,“这次我
一定要把它给拼好!”小手翻飞,好像在跟魔方跳舞似的。
小刚就厉害了,魔方在他手里就像变魔术一样,一会儿工夫就
搞定了!同学们纷纷围过去,好奇地问,“你咋这么快啊?是不是
有啥秘诀?”小刚得意地笑了,“哈哈,熟能生巧嘛!”。
角落里的小明,倒是挺沉得住气。
他默默地拧着魔方,虽然速
度不如小刚,但那股认真劲儿,看着就让人佩服。
有时候拧错了,
他也不气馁,重新开始。
这种精神,值得我们学习!
啊!终于放学了!大家收拾书包,准备回家。
但手里还紧紧握
着魔方,好像怕它跑了似的。
魔方,真是个让人着迷的小东西啊!
回想起今天玩魔方的时光,真是又开心又有趣。
这小小的魔方,
不仅让我们玩得开心,还让我们学会了坚持和耐心。
嘿,下次还要一起玩魔方!。
中考数学模型巧构辅圆解难题一题多解
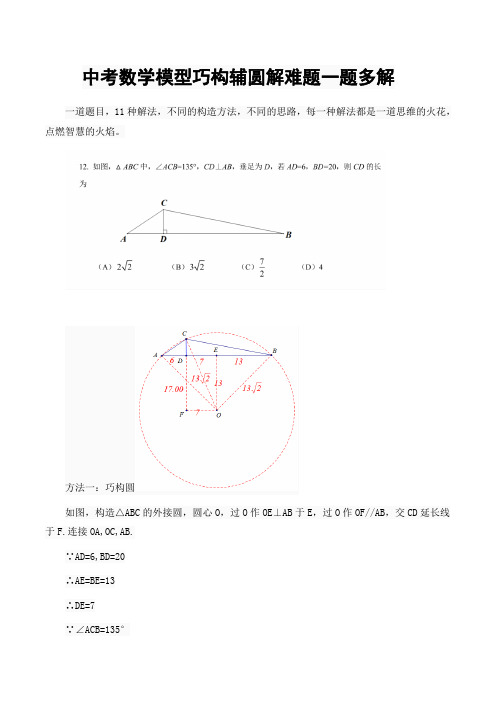
中考数学模型巧构辅圆解难题一题多解一道题目,11种解法,不同的构造方法,不同的思路,每一种解法都是一道思维的火花,点燃智慧的火焰。
方法一:巧构圆如图,构造△ABC的外接圆,圆心O,过O作OE⊥AB于E,过O作OF//AB,交CD延长线于F.连接OA,OC,AB.∵AD=6,BD=20∴AE=BE=13∴DE=7∵∠ACB=135°∴∠AOB=90°∴OE=13,AO=BO=CO=13√2由辅助线易得,四边形OEDF是矩形.∴OF=7由勾股定理可得,CF=17∴CD=4方法二:勾股定理如图,延长AC,过点B作BE⊥AC延长线于E设,BE=x,因为∠ACB=135°,所以∠BCE=45°,则CE=x,BC=√2x,则勾股定理可得其余线段的长度如上图。
由题很容易得到△ADC∽△AEB,则则CD=4或9√10(多出来一个解,有谁知道为什么吗?).备注:上面的方程很难解!所以虽然这个方法可以解出来,但是不推荐。
如果数字小一点,可以使用。
向另外一边作垂线一样可以求出,如下图:评述:第一种方法,根据135度圆周角所对圆心角是90度,巧妙的构造圆,然后巧妙转化,解决问题。
第二种方法,从135度的邻补角是45度入手,构造直角三角形。
通过勾股定理来解决。
第一种方法辅助线多,构思巧妙,不容易想到,第二种方法容易想到,但是数字比较大,方程难解。
从普通的条件入手,开拓思路,张引路老师的方法还是很巧妙的解法三:面积法如上图,过A作AE//BC,BE//AC交于E点.过E作EF⊥BC于F.因为∠ACB=135°,所以∠CBE=45°∴∴∴解得 x=4简评:这个方法同样存在方程难题的问题,如果数字比较小可以用。
解法三变式三角形的面积公式可以表示为直接用三角形面积公式,不过初中没有学过这个公式,还有一个就是sin135°的问题,好的学生可以补充,老师参考一下,拓宽一下思路。
辅助圆在初中数学解题中的运用

辅助圆在初中数学解题中的运用作者:金明明来源:《中学生数理化·教与学》2015年第11期摘要:在初中数学的解题过程中,有很多的几何论证题目是常规思路无法解决的,可以利用圆所具有的特征,结合题目的具体情况,对难以解决的几何题目进行论证.本文简单介绍几种利用圆的特征建造辅助圆,然后对需要论证的问题进行解决的思路.关键词:辅助圆初中数学解题思路一、根据圆的定义构建辅助圆解题某些直线形平面几何竞赛题,用常规方法求解难度很大,技巧性强,且不易奏效.若能针对题目的本质特征,恰当地构造辅助圆,巧妙地运用圆的有关知识,往往可化难为易,化繁为简.在同圆或者等圆中,假如两个圆周角以及两条弧线都相等的话,可以利用这个道理去解决很多难题.二、利用圆的圆周角进行辅助圆的建造在前人对圆进行了很多的研究之后,我们可以知道圆的圆周角存在很多的性质,也就是我们平时所说的圆周角定理:同弧或等弧所对圆周角等于它所对圆心角的一半,半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径,如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做多边形的外接圆.利用圆的圆周角进行辅助圆建造,从而解决初中几何问题.学生遇到用一般的几何方法无法解决的问题时,不妨开阔自己的思路,利用圆周角所特有的一些性质来解题,这样能够达到事半功倍的效果.三、利用圆的内角以及外角和圆周角的关系建造辅助圆在圆上的一个顶点,并且在这个顶点两边都和圆有相交的点存在,这几点形成的角度就是圆周角.因为圆上的每一条弧所对应的圆周角等于形成这个角所对应的圆周角的一半,但是圆周角的度数就是和自身所对应的弧的度数,所以圆周角的度数就等于它所对的弧线的度数的一半.对于圆周角以及圆内角我们可以这样定义:在圆外存在的一顶点,而且两边都和圆具有相交点,这种角度叫做圆外角,而在圆内存在的一个顶点,并且两边也和圆具有相交的点,这种角叫做圆内角.例1在圆O上有一点C,而点P为圆O内部的一点,而且该两点都在弧AB的同一侧,线段AP和BP交于P所形成的∠APB,线段AC和CB交于点C所形成的∠ACB.证明:∠APB>∠ACB.证明:通过延长BP交圆心O为点D,连接AD.因为同一段弧所对应的角度都相等,而∠ACB和∠ADB所对应的都是弧AB,所以∠ACB=∠ADB.又因为∠APB是△ABC的外角,∠APB=∠ADB+∠DAP,所以∠APB=∠ACB+∠DAP.所以∠APB>∠ACB.我们可以得出以下结论:在同一圆中,同一弧线所对应的圆周角都比这一弧线所对应的圆内角小.同理,同一弧线所对应的圆周角都比这一弧线所对应的圆外角大.四、利用圆幂定理构造辅助圆圆幂定理是一个总结性的定理,是对相交弦定理、切割线定理及割线定理(切割线定理推论)以及它们推论的统一与归纳.根据两条与圆有相交关系的线的位置不同,有以下定理:1.相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等.2.切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.3.割线定理:从圆外一点P引两条割线与圆分别交于点A、B和点C、D,则有PA·PB=PC·PD.根据上述介绍我们可以知道,两条线的位置可以在圆的内部也可以在圆的外部,但是最终的结论都是相同的,将这些定理以及过程总结,就是我们所知道的圆幂定理.例2CD为Rt△ABC斜边上的高,O为AC上的一点,其中OA=OB=a.证明:OD2+CD2=a2.证明:由圆幂定理知,CD2=DA·DB,而且DA、DB、DO的位置具有相交弦的特点.又因OA=OB,所以以点O为圆心,OA为圆的半径作圆O交DO的延长线于E、F两点.所以DA·DB=DE·DF=(OE-OD)(OF+OD)=a2-OD2.所以OD2+CD2=OD2+DA·DB=a2.有的几何题目利用常规方法无法解决时,利用圆幂定理,通过建立辅助圆,就可以对问题进行解决.总之,不管怎么样的解决方法,在几何问题的论证过程中,巧妙利用辅助圆,可以解决一些利用常规解题思路难以解决的问题解决.在数学解题过程中,学生应该将自己的思路活跃化,进而掌握更多的解题方法.参考文献谢雅礼. 神奇的辅助圆——构造辅助圆解决平面几何问题的基本类型[J]. 中国数学教育,2010,24.张振继. 构造辅助圆解题探究[J]. 高中数理化,2013,21.袁贤琼.构造辅助圆处理解及问题的若干途径[J].中学教研,2012,09.唐平生. 巧作辅助圆证题[J]. 中学数学教学参考,2013,09.方世超.“辅助圆”——学生不大熟悉的重要辅助线[J]. 中学数学杂志,2008,12.。
中考压轴题专题:辅助圆的应用

第1页,共3页帮助圆的运用 【1 】【进修目的】1.闇练控制运用圆结构等腰三角形和直角三角形;2.学会在适当的时刻运用圆为帮助线解决现实问题.【重点难点】运用圆为帮助线解决现实问题. 【进修进程】一、 运用“两圆一中垂线”结构等腰三角形如图,已知抛物线(a≠0)与轴交于点A(1,0)和点B(-3,0)与y 轴交于点C .(1)抛物线的解析式为;(2) 设抛物线的对称轴与轴交于点M ,问在对称轴上是否消失点P,使△CAP 为等腰三角形?若消失,请直接写出所有相符前提的点P 的坐标.二、 运用“两垂线一圆”结构直角三角形如图,已知抛物线(a≠0)与轴交于点A(1,0)和点B(-3,0),与y 轴交于点C .在抛物线的对称轴上是否消失点Q,使△CBQ 是直角三角形,若消失,请直接写出所有相符前提的点Q 的坐标.三、 运用圆求线段的最值1. 如图①,菱形ABCD 的边长为2,∠ABC=60°,点E 是AD 边的中点,F 是CD 上的动点,将△DEF 沿EF 折叠,点D 落在P 处,则线段BP 最短时的长度为.2. 如图②,在Rt △ABC 中,∠CAB=90°,AC=AB=1,以AC 上动点O 为圆心,以AO 为半径作圆O,交AC 于点D,衔接BD 交圆O 于点E,则的最小值为3.如图③,⊙O 的半径为5,OP=3,经由点P 的最长弦为,最短弦为. 四、 三点及三点以上到统一点距离相等,作帮助圆 如图,四边形ABCD 中,DC ∥AB,BC=2,AB=AC=AD=4.则BD 的长为.B P ECD F A 图① 图③ 图②E DAB O第2页,共3页 五、 四点共圆时作帮助圆1. 如图①,在△ABC 中, BE 和CD 分离是AC 和AB 边上的高,衔接DE,△ADE 与四边形DBCE 的面积比为1:8,则sinA=.2.如图②,在Rt △ABC 中,∠ABC=90°,∠ACB=30°,在Rt △ADC 中,∠ADC=90°,∠ACD=45°,若BD=8,则AB=.思虑:若何断定四点共圆? 六、 运用圆的切线性质作帮助圆 如图,在平面直角坐标系内A (8,0),B (0,6),若直线L 与AB 平行,且在直线L 上有且只有一点P 使∠OPA=90°,求知足前提的直线L 的解析式.七、 运用圆结构相等角(课后拓展)如图,已知抛物线y=ax2+bx+c (a ≠0)与x 轴交于A (1,0).B(4,0)两点,与y 轴交于C (0,2),衔接AC.BC .(1)BC 的垂直等分线交抛物线于D.E 两点,则直线DE 的解析式为;(2)若点P 在抛物线的对称轴上,且∠CPB=∠CAB,求出所有知足前提的P 点坐标.25. 在矩形ABCD 中,点P 在AD 上,AB=2,AP=1,将三角板的直角极点放在点P 处,三角板的两直角边分离能与AB.BC 边订交于点E.F,衔接EF .(1)如图,当点E 与点B 重应时,点F 正好与点C 重合,求此时PC 的长;(2)将三角板从(1)中的地位开端,绕点P 顺时针扭转,当点E 与点A 重应时停滞,在这个进程中,请你不雅察.探讨并解答:①∠PEF 的大小是否产生变更?请解释来由;②在扭转中,当点F 与BC 边中点重应时,求四边形AEFP 的面积;③直接写出从开端到停滞,线段EF 的中点所经由的路线长.备用图ED BC A 图①D A B C图② F D CAB E第3页,共3页 16.如图,在平面直角坐标系中,直线与x 轴交于点A,与y 轴交于点B .点Q 在直线AB 上,点P 在x 轴上,且∠OQP=90°. (1)当点P 与点A 重应时,点Q 的坐标为▲;(2)设点P 的横坐标为a,则a 的取值规模是▲. 1.如图,在Rt △ABC 中,∠C=90°,AC=6,BC=8,D 为AB 边上一点,过点D 作CD 的垂线交直线BC 于点E,则线段CE 长度的最小值是.注解,以CE 为固定值,当作直径作圆与AB 是否有交点.2.如图,⊙O 的直径为4,C 为⊙O 上一个定点,∠ABC=30°,动点P 从A 点动身沿半圆弧向B 点活动(点P 与点C 在直径AB 的异侧),当P 点到达B 点时活动停滞,在活动进程中,过点C 作CP 的垂线CD 交PB 的延伸线于D 点.(1)在点P 的活动进程中,线段CD 长度的取值规模为;(2)在点P 的活动进程中,线段AD 长度的最大值为.OA Byx第16题图。
中考几何专题word讲义——辅助圆问题

中考几何专题word讲义——辅助圆问题
类型一:定点定长作圆
类型二:点圆最值
•①直径是例中最长的弦
•②点圆最值:过该点与圆心作一条直线,直线与圆的交点即为所求的点。
类型三:线圆最值
类型四:定弦定角
类型五:定角定高
类型六:最大张角
解决问题的理论依据:同孤所对圆周角相等,圆外角小于圆周角。
类型七:四点共圆
类型八:阿氏圆
解题思路:
一找:找带有系数k的线段PA
二构:在线段OA上取一点C,构造△PCO∽△APO
•①在线段OA上截取OC,使OC=k·r
•②连接PC、OP,证明△PCO∽△APO
三转化:通过相似三角形的对应边成比例,将k·PA转化为PC:
四求解:使得PB十k·PA=PB十PC,利用“两点之间线段最短”转化为求BC的长。
欢迎留言交流。
利用辅助圆 巧解数学题

利用辅助圆 巧解数学题江苏省姜堰中学 张圣官(225500)圆是最简单的二次曲线,也是学生比较熟悉的基础曲线。
不仅仅在解析几何中,而且在其它数学分支中,圆都有着广泛的应用。
一些数学问题,若能巧妙构造出辅助圆,往往可迅速沟通题设与结论之间的联系,从而使问题得解,起到铺路搭桥的作用。
例1求直线L 的方程,使点A (1,1)、B (5,3)到L 的距离都等于1。
解:如图1,分别以A ,B 为圆心,作半径为1的辅助圆,于是原问题就转化为求两圆的外公切线与内公切线方程。
∵21=AB k ,∴可设外公切线方程为b x y +=21,即x-2y+2b=0 , 由A (1,1)到切线的距离为1,得15|221|=+-b ,∴2521±=b ;∵AB 的中点为(3,2),∴可设内公切线方程为y-2=k(x-3),即kx-y-3k+2=0,由A (1,1)到切线的距离为1,得11|231|2=++--k k k ,∴34,0==k k 。
(图1) 故所求直线L 为:252121±+=x y ,或y=2,或4x-3y-6=0 。
例2(1986年高考题)如图2,平面直角坐标系中,给定y 轴正半轴上两点A (0,a ),B(0,b)(a>b>0),试在x 轴正半轴上求一点C ,使∠ACB 取得最大值。
解:设C 是x 轴正半轴上一点,在⊿ABC 中,由正弦定理,有sin ∠ACB=Rba 2-,其中R是⊿ABC 的外接圆的半径。
可见,当R 取最小值时,∠ACB 取得最大值。
在过A 、B 两定点且与x 轴正向有交点C 的诸圆中,当且仅当点C 是与x 轴的切点时,半径最小。
故切点C 即为所求。
由切割线定理,得OC 2=OA •OB=ab∴OC=x=ab ,即点C 的坐标为(ab ,0)时,∠ACB 取得最大值。
(图2)例3已知θ∈R ,求证:3232cos 22sin 22+≤≤-++θθ。
(word完整版)初中数学中考几何如何巧妙做辅助线大全,推荐文档

人教版北师大初中数学中考几何如何巧妙做辅助线大全人们从来就是用自己的聪明才智创造条件解决问题的,当问题的条件不够时,添加辅助线构成新图形,形成新关系,使分散的条件集中,建立已知与未知的桥梁,把问题转化为自己能解决的问题,这是解决问题常用的策略。
一.添辅助线有二种情况:1按定义添辅助线:如证明二直线垂直可延长使它们,相交后证交角为90°;证线段倍半关系可倍线段取中点或半线段加倍;证角的倍半关系也可类似添辅助线。
2按基本图形添辅助线:每个几何定理都有与它相对应的几何图形,我们把它叫做基本图形,添辅助线往往是具有基本图形的性质而基本图形不完整时补完整基本图形,因此“添线”应该叫做“补图”!这样可防止乱添线,添辅助线也有规律可循。
举例如下:(1)平行线是个基本图形:当几何中出现平行线时添辅助线的关键是添与二条平行线都相交的等第三条直线(2)等腰三角形是个简单的基本图形:当几何问题中出现一点发出的二条相等线段时往往要补完整等腰三角形。
出现角平分线与平行线组合时可延长平行线与角的二边相交得等腰三角形。
(3)等腰三角形中的重要线段是个重要的基本图形:出现等腰三角形底边上的中点添底边上的中线;出现角平分线与垂线组合时可延长垂线与角的二边相交得等腰三角形中的重要线段的基本图形。
(4)直角三角形斜边上中线基本图形出现直角三角形斜边上的中点往往添斜边上的中线。
出现线段倍半关系且倍线段是直角三角形的斜边则要添直角三角形斜边上的中线得直角三角形斜边上中线基本图形。
(5)三角形中位线基本图形几何问题中出现多个中点时往往添加三角形中位线基本图形进行证明当有中点没有中位线时则添中位线,当有中位线三角形不完整时则需补完整三角形;当出现线段倍半关系且与倍线段有公共端点的线段带一个中点则可过这中点添倍线段的平行线得三角形中位线基本图形;当出现线段倍半关系且与半线段的端点是某线段的中点,则可过带中点线段的端点添半线段的平行线得三角形中位线基本图形。
巧用辅助圆,妙解几何题

在一些数学题中,看似与圆毫无关系但是用常规的解题方法却无法解决问题,而通过题中的某些条件构造辅助圆,运用圆的知识进行解答,往往就会使题目简单化,从而使难题迎刃而解.本文结合一些实例,探析如何巧用辅助圆妙解几何题.一、几何问题中的求线段长度求线段的长度是初中数学比较常见的问题.该问题的常规解法是通过做垂直线构建直角三角形从而运用勾股定理或是巧用面积公式.但是在一些问题中,通过直接作出垂线,往往会使图形更加复杂,从而不能成功解题例 1 如图所示,在四边形ABCD 中,//AD BC ,已知BC CD AC ===,AB =.则BD = .解析 通过题干中的条件BC CD AC ==,我们可以想到以C 为圆心,BC 为半径作圆.根据圆的性质:直径对应的圆周角为直角,可以延长BC 交于⊙C 于点E ,连接DE ,如图所示,此时BDE V 为直角三角形.//AD BC Q ,AB DE ∴==,由勾股定理得BD =BD.点拨 根据题干中的线段相等,从而构建辅助圆,接着利用圆的性质进行解题.其中需要注意的是,虽然辅助圆能做出,但是要想解题,就要对圆的性质有一个深刻的理解.二、几何问题中的求角的度数求角的度数问题一般都是以三角形为载体,该问题的常规解法是利用三角函数的知识去解答,但是由于初中数学只学习了一些特殊的三角函数值且在直角三角形的载体中.当遇到一般的三角形,此时学生往往会无计可施例 2 如图所示,在ABC V 中,其中AB AC =,BD 是ABC ∠的平分线,BD AD BC +=,则A ∠= .解析 由题意得,本题要求的是A ∠,由于此题告知任意一个角的大小且ABC V 也不是直角三角形,因此运用三角函数的知识是很难解答该题的.由题干中BD 平分ABC ∠,可得ABD DBC ∠=∠.作ABC V 的外接圆,如图所示.根据圆的性质可得,AD DE =.因为四边形ABED 为内接四边形,所以ABC EDC C ∠=∠=∠,所以2C DEB ∠=∠,DE EC =.因为BD AD BC BE EC +==+且AD DE EC ==,所以BE BD =.因为2DEB BDE C ∠=∠=∠,在BDE V 中,180DEB BDE DBE ∠+∠+∠=︒,即141802C C ∠+∠=︒,得40C ∠=︒.在ABC V 中,180A ABC C ∠+∠+∠=︒,得100A ∠=︒.点拨 此题是根据角平分线从而想到画出三角形的外接圆,然后找出各角之间的关系进行解答的.因此,在求解角的度数时,要充分运用辅助圆,找出相等的角,最后通过运用三角形内角和为180︒列出式子求解.此类题型的难点在于,如何画出辅助圆.三、几何问题中的求最值求最值的问题在中考中是常见问题,其一般的思路就是设未知数,然后寻找关系列出函数表达式,即可解答出.虽然解题思路清晰,但是此类题型的难点就是在如何将条件整合起来,找出其之间的关系,例3 如图所示,在Rt ABC V 中,30BAC ∠=︒,AB =动点P 、Q 分别在AB 、AC 上,90CPQ ∠=︒,则min CQ = .解析 经过审题后,感觉CQ 就是独立的,无法向已知条件上靠,唯一可以用的就是90CPQ ∠=︒,但是无法运用勾股定理,因为三条边都是未知的.但是通过仔细审题,从条件90CPQ ∠=︒出发,可以想到圆的直径对应的圆周角为直角此时可以试一下,看画出辅助圆对解题有无帮助.通过图可以看出,要想CQ 最小,AB 与⊙O 要相切.此时就可以根据OP AB ⊥,OP OC =,可得30APQ ∠=︒,此时设PQ OQ OP OC r ====,3cos303r AC AB ==︒=g ,解得1r =,所以min 2CQ =.点拨 根据题干中条件画出辅助圆,借助圆的性质:圆心到切点之间的线段最短是解答本题关键,可见辅助圆对题目的综合分析起了很大的作用.其中需要特别注意的是,当题中给出直角时不能单单的只想到勾股定理也要联想到圆.综上所述,在解答几何问题时,如若发现运用常规方法不能解决问题或是解决过程比较繁琐,此时可以通过仔细审题,挖掘题干中与圆有联系的条件,从而做出辅助圆进行分析解题.由于做出辅助圆的关键就是善于捕捉题干的细节之处,这对学生的要求比较高,因此学生要在以后的学习中勤总结.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1初中数学巧用辅助圆解题添加辅助圆解平面几何题,虽远不如辅助(直)线那么为人们所熟知,但许多直线形问题,若辅助圆添加得合理,则能收到化难为易,事半功倍的效果.一、根据圆的定义作辅助圆例1 如图,四边形ABCD 中,AB∥CD,AB =AC =AD =p ,BC =q ,求BD 的长.解析:以点A 为圆心、AB 为半径作⊙A.因为AB =AC =AD ,所以B 、C 、D 三点在⊙A 上.延长BA 交⊙A 于点E ,连结DE .因为DC∥EB,所以弧ED =弧BC ,所以ED =BC =q .在Rt△BDE 中,根据勾股定理,得BD =.例2 如图, PA =PB ,∠APB=2∠ACB,AC 与PB 交于点D ,且PB =5,PD =3,求AD·DC 的值.解析:以点P 为圆心、P B为半径的作⊙P.因为PA =PB ,∠APB=2∠ACB,所以点A、B 、C 在⊙P 上.此时⊙P 的直径BE =10,DE =8,DB =2,由相交弦定理,得AD·DC =DE·DB =8×2=16二、作三角形的外接圆例3 如图,D 、E 为△ABC 边BC 上的两点,且BD=CE ,∠BAD=∠CAE,求证:AB=AC .解析:作△A DE 的外接圆,分别交AB 、AC 于点M 、N ,连结MD 、NE .因为∠BAD=∠CAE,所以∠BAD+∠DAE=∠CAE+∠DAE,即∠NAD=∠MAE.因为∠BDM=∠MAE,∠CEN=∠NAD,所以∠BDM=∠CEN.又BD =CE ,DM =EN ,所以△BDM≌△CEN,所以∠B=∠C,即AB =AC .例4 如图,△ABC 中,BF 、CE 交于点D ,BD =CD ,∠BDE=∠A,求证:BE =CF . 解析:作△ABC 的外接⊙O,延长CE 交⊙O 于G ,连接BG .因为∠G=∠A,∠BDE=∠A,所以∠G=∠BDE,所以BG=BD .又BD =CD ,所以BG =CD.又因为∠G=∠CDF,∠GBE=∠DCF,所以△GBE≌△DCF.所以BE =CF .例5 如图,在△ABC 中,AB =AC ,∠BAC=100°,∠B 的平分线交AC 于D ,求证:BC =BD +AD .解析:作△ABD 的外接圆交BC 于E ,连结DE .因为BD 是∠ABC 的平分线,所以弧AD =弧DE ,所以AD =DE .BCC2在△BDE 中,∠DBE=20°,∠BED=180°―100°=80°,所以∠BDE=80°,所以BE =BD .在△DEC 中,∠EDC=80°―40°=40°,所以EC =DE .所以BC =BE +EC =BD +AD .三、结论类似于圆幂定理的形式时作辅助圆例6 如图,在△ABC 中,AB =AC =,D 是边BC 上的一点,且A D=1,求BD·DC 3的值.解析:以点A 为圆心、AB 为半径作⊙A,交直线AD 于点E 、F ,则点C 在⊙A 上,DE =,DF =.13-13+由相交弦定理,得BD·DC =DE·DF ==2.)13)(13(+-例7如图,在△ABC 中,∠DAB=∠C,∠B 的平分线BN 交AD 于M .求证:(1)AM =AN ;(2)AB 2-AN 2=BM·BN .解析:(1)略;(2)由(1),得AM =AN .以点A 为圆心、AM 为半径作⊙A,交AB 于E ,交BA 的延长线于F ,则N 在⊙A 上,且AE =AF =AN .由割线定理,得BM·BN =BE·BF =(AB -AE)(AB +AF)=(AB―AN)(AB+AN)=AB 2-AN 2,即AB 2-AN 2=BM·BN .四、探究动点对定线段所张的角时作辅助圆例8 如图,在直角梯形ABCD 中,AB∥DC,∠B=90°,设AB =a ,DC =b ,AD =c ,当a 、b 、c 之间满足什么关系时,在直线BC 上存在点P ,使AP⊥PD?解析:以AD 为直径作⊙O,根据直径所对的圆周角是直角,当⊙O 与直线BC 有公共点(相切或相交)时,在直线BC 上存在点P ,使AP⊥PD.因为⊙O 的半径r =,圆心O 到直线BC 的距离22cAD =d =.22b a DC AB +=+所以,当d≤r,即a +b≤c 时,在直线BC 上存在点P ,使AP⊥PD.例9 如图,在平面直角坐标系xOy 中,给定y 轴正半轴上的两点A (0,2)、B(0,8),试在x 轴正半轴上求一点C ,使∠ACB 取得最大值。
解析:经过A 、B 、C 三点作⊙M,设⊙M 的半径为R ,由正弦定理,得.RR AB ACB 262sin ==∠3由此可见,当R 取得最小值时,∠ACB 取得最大值.而当点⊙M 与x 轴的相切于点C 时,R 取得最小值.根据切割线定理,得OC 2=OB·OA ,所以OC =4.故当点C 的坐标为 (4,0)时,∠ACB 取得最大值.例10 已知Rt△ABC 中,AC =5,BC =12,∠ACB=90°,P 是边AB 上的动点,Q 是边BC 上的动点,且∠CPQ=90°,求线段CQ 的取值范围.解析:以CQ 为直径作⊙O,根据直径所对的圆周角是直角,若AB 边上的动点P 在圆上,∠CPQ 就为直角.当⊙O 与AB 相切时,直径CQ 最小.由切线长定理,得AP =AC =5,所以BP =13―5=8.再根据切割线定理,得BP 2=BQ·BC ,所以 BQ =,CQ =.当316320点Q 与点B 重合时,直径CQ 最大,此时CQ=12.综上所述,≤CQ≤12. 320五、四点共圆判断四点共圆的常用方法有(1)对角互补的四边形的四个顶点共圆;(2)同底同侧顶角相等的两个三角形的四个顶点共圆.判断四点共圆后,就可以借助过这四点的辅助圆解题.例11 如图,E 是正方形ABCD 的边AB 上的一点,过点E 作DE 的垂线交∠ABC 的外角平分线于点F ,求证:FE =DE .解析:连接DB 、DF .因为∠CBF=45°,∠DBC=45°,所以∠DBF=90°.又∠DEF=90°,所以D 、E 、B 、F 四点共圆,所以∠DFE=∠DBE=45°,所以FE =DE .例12 如图等边△PQR 内接于正方形ABCD ,其中点P 、Q 、R 分别在边AD 、AB 、DC 上,M 是QR 的中点,求证:不论等边△PQR 怎样运动,点M 为不动点.解析:连接PM 、AM 、DM ,因为M 是QR 的中点,所以∠PMQ=90°.又∠PAQ=90°,所以A 、Q 、M 、P 四点共圆,所以∠MAP=∠MQP=60°.同理,∠MDP=60°.所以△MAD 是等边三角形,即点M 为不动点.例13 如图,正方形ABCD 的中心为O ,面积为1989,P 为正方形内的一点,且∠OPB=45°,PA∶PB=5∶14,求PB 的长. 解析:连接OA 、OB .因为∠OPB=∠OAB=45°,所以A 、B 、O 、P 四点共圆,所以∠APB=∠AOB=90°.在Rt△APB 中,设PA =5x ,PB =14x ,根据勾股定理,得(5x)2+(14x)2=1989,解得x =3,所以PB =42.CBFRCB4练习1.在直角坐标系中,过A (-1,0)和B (3,0)的⊙M 上有点P.(1)若cos ∠APB= (∠APB 是锐角),求⊙M 的半径;13(2)在y 轴上,是否存在一点D ,使得∠ADB=45°?若存在,求出点D 的坐标.2.在平面直角坐标系中,抛物线与轴交于两点(点在点的左侧),2y x bx c =++x A B ,A B 与轴交于点,点的坐标为,将直线沿轴向上平移3个单位长度后恰好y C B (30),y kx =y 经过两点.B C ,(1)求直线及抛物线的解析式;BC (2)设抛物线的顶点为,点在抛物线的对称轴上,且,求点的坐标.D P APD ACB ∠=∠P 3. 已知平面直角坐标系中两定点A (-1,0)B (4,0)、,抛物线过点22y ax bx =+-A 、B 顶点为C ,点P (m ,n )n<0为抛物线上一点.(1)求抛物线的解析式和顶点C 的坐标;(2)当为钝角时,求的取值范围.APB ∠m 4. 如图,已知点A (1,0),B (0,3),C (-3,0),动点P (x ,y )在线段AB 上,CP 交y 轴于点D ,设BD 的长为t.(1)求t 关于动点P 的横坐标x 的函数表达式;(2)若S △BCD :S △AOB =2:1,求点P 的坐标,并判断线段CD 与线段AB 的数量5及位置关系,说明理由;(3)在(2)的条件下,若M 为x 轴上的点,且∠BMD 最大,请求出点M 的坐标.5.(2014山东淄博中考)如图,点A 与点B 的坐标分别是(1,0),(5,0),点P 是该平面直角坐标系内的一个动点.(1)若点C 平面直角坐标系内的一个点,且△ABC 是等边三角形,则点C 的坐标是 ;(2)若点P 在y 轴上,且∠APB=30°,求满足条件的点P 的坐标;(3)当点P 在y 轴上移动时,∠APB 是否有最大值?若有,求点P 的坐标,并说明此时∠APB 最大的理由;若没有,也请说明理由.6. (2014泉州中考)如图,直线y=﹣x+3与x ,y 轴分别交于点A ,B ,与反比例函数的图象交于点P (2,1).(1)求该反比例函数的关系式;(2)设PC ⊥y 轴于点C ,点A 关于y 轴的对称点为A′;①求△A′BC 的周长和sin ∠BA′C 的值;②对大于1的常数m ,求x 轴上的点M 的坐标,使得sin ∠BMC=.1m。
