Monte Carlo模拟研究聚合诱导高分子自组装
聚合物链状分子的构象统计——推荐一个高分子实验

大学化学Univ. Chem. 2022,37 (7), 2110015 (1 of 6)•化学实验• doi: 10.3866/PKU.DXHX202110015 聚合物链状分子的构象统计——推荐一个高分子实验陈彦涛1,*,胡惠媛1,杨波1,石玉磊2,*1深圳大学化学与环境工程学院,广东深圳 5180712深圳浦华系统技术有限公司,广东深圳 518129摘要:介绍了利用分子模拟对链状分子进行构象统计的实验设计。
选取常见且结构简单的聚乙烯作为研究对象,利用软件Materials Studio对聚乙烯进行建模,模拟其运动过程,在微观层面重现了链状分子构象,验证了构象尺寸的标度理论,有利于学生对链构象建立形象化认知。
该实验设计便于学生在个人电脑上操作,满足有限的实验课时要求。
关键词:高分子实验;聚合物链;构象统计;分子模拟中图分类号:G64;O6Conformation Statistics of Polymer Chain: A Recommended Polymer ExperimentYantao Chen 1,*, Huiyuan Hu 1, Bo Yang 1, Yulei Shi 2,*1 School of Chemical and Environmental Engineering, Shenzhen University, Shenzhen 518071, Guangdong Province, China.2 Shenzhen Puhua System Tech Co., LTD, Shenzhen 518071, Guangdong Province, China.Abstract:An experimental design on conformation statistics and analysis of polymer chains by means of molecular simulation is introduced in this paper. Polyethylene, which is commonly used and has a simple structure, was selected as the research object, and the “Materials Studio” software was used to construct the polyethylene chain, simulate its thermal relaxation, and verify the scaling theory of conformation size in combination with statistical methods. In this experiment, the latest molecular simulation software was used to reproduce the microscopic images of polymer chains at the microscopic level, which is helpful for students to achieve visual understanding of the concept of “random coils” and deepen their understanding of polymers. In addition, conditions such as vacuum and high temperature were chosen, which considerably accelerate the simulation process and help students quickly obtain reliable experimental results on personal computers and meet the time requirements of the experimental courses.Key Words: Polymer experiment; Polymer chain; Conformation statistics; Molecular simulation高分子拥有数目巨大的构象,这是与小分子的重要区别,也是学习高分子课程过程中的重点与难点。
生物多肽分子的折叠与自组装过程研究

生物多肽分子的折叠与自组装过程研究生物多肽是由氨基酸单元组成的聚合物,是生命体中不可或缺的重要分子。
除了构成蛋白质这种线性的构造体之外,生物多肽还是许多生物学重要过程的执行者和调节器。
因此,探究生物多肽折叠与自组装过程的机制,对于了解生命现象、理解生物体的结构和功能以及研发生物医学材料具有重要的科学意义和应用前景。
一、生物多肽折叠机理生物多肽的折叠机理是指其在生命体内或人工条件下变成具有特定三维结构的过程。
折叠使得生物多肽能够发挥具体的生物学功能,如催化酶反应、携带物质、传递信息等。
而生物多肽的折叠过程也是一种信息转移、能量转换和互作的过程。
其折叠机理的探究可以帮助人们了解蛋白质的三维结构及其对生命过程的影响,进而构建针对蛋白质相关疾病的研究和治疗方法。
当前,关于生物多肽折叠机理的研究主要依托于理论、仿真、实验等方法手段。
在理论方面,物理学、工程学、计算机科学、化学等学科组成的跨学科领域“蛋白质科学”致力于描绘蛋白质的结构和性质。
其主要手段是基于理论计算和分子模拟方法研究蛋白质溶液的物理性质和动力学行为,探究蛋白质折叠和聚集的机制。
常用的方法包括分子力学、量子化学、分子动力学模拟、Monte Carlo模拟、离散化模型等,其中分子动力学模拟被广泛应用于研究生物多肽分子的折叠机理。
二、生物多肽自组装过程生物多肽自组装是基于生物多肽的某些特定性质,通过一定条件的调控和刺激,使生物多肽分子自主组装成为具有特定形态的超分子结构。
生物多肽自组装结构广泛存在于生物体内外,如细胞膜、细胞骨架、DNA包裹、蛋白质酶、激素、免疫球蛋白等。
生物多肽自组装的研究不仅有助于揭示蛋白质分子在生命体内的储能转换、机械传送、信号传导和修复维护等生命过程中的作用机制。
而且可以用于结构材料领域的研究,如用生物多肽纳米纤维作为基底,制作功能性基材和纳米器件等。
在生物多肽自组装的研究方面,通常使用的方法是生物技术、化学合成、纳米技术等多种手段。
双亲3嵌段共聚物刷在选择性溶液中自组装形态的Monte Carlo模拟

, 理 论 的[ 1 0 1 1 ] 和计 算机 模拟 的 l _ 1 。 . 然而, 与 2嵌 段共
聚物刷相 比 , 3 嵌 段共 聚物刷 [ 1 5 1 6 ] , 尤其 是按 照 亲水 , 疏水 再亲水 顺 序合成 的 AB A 型 或 AB C型 3 嵌 段共
聚物刷 , 由于其链 结构更 加接 近生物 薄膜 , 因此越 来越 受到研 究者 的青 睐l _ 】 .
第 3期
徐纪华 : 双 亲 3嵌 段 共 聚 物 刷 在 选 择 性 溶 液 中 自组 装 形 态 的 Mo n t e C a r l o模 拟
・8 5・
装形 态进 行 Mo n t e C a r l o模 拟. 模 型 和方法 的详 细描 述见 参考 文献 E 1 2 —1 4 ]研究 的热点 之一 .
嵌段 共 聚物刷 是指 两种 或多 种均 聚物链 的其 中一端 被接枝 在 表面或 界 面 的嵌 段 共 聚物链 . 相 比于脂
类, 嵌段 共 聚物刷 能够形 成 化学 上更 加稳定 的薄膜 , 并且 根据 不 同的需要 可 以 引入相 应 的功 能 团 , 这一 点
作者简介 : 徐 纪华 ( 1 9 8 2 一) , 男, 山 东 淄 博人 , 博士研究生. 通 讯 作者 :李 宝会 ( 1 9 6 5 一) , 女, 天津人 , 教授 , 主 要从 事 高 分子 物理 研 究 .e ma i l : b a o h u i @n a n k a i . e d u . c n
徐纪华, 尹玉华, 王 铮, 蒋 润, 李宝会
(南 开 大 学 物 理 科 学 学 院 , 天津 3 0 0 0 7 1)
摘要 : 利 用 Mo n t e C a r l o方法 研 究 了对 称 AB A型双亲 3 嵌 段共 聚物 刷 在 选 择 性 溶 液 中 的 自组 装形 态. 针 对 溶 剂 对 A 嵌 段 为 良溶 剂 , 对 B嵌 段 为 不 良溶 剂 的 体 系 , 研 究 了 亲 水 A 嵌 段 长 度 和 疏 水 B嵌 段 的 长 度 对 溶 液 中 3
动力学蒙特卡洛方法(KMC)及相关讨论

动力学蒙特卡洛方法(KMC)及相关讨论动态模拟在目前的计算科学中占据着非常重要的位置。
随着计算能力和第一原理算法的发展,复杂的动态参数(扩散势垒、缺陷相互作用能等)均可利用第一原理计算得出。
因此,部分复杂的体系动态变化,如表面形貌演化或辐射损伤中缺陷集团的聚合-分解演变等,已可以较为精确的予以研究。
KMC——动力学蒙特卡洛方法(kinetic Monte Carlo)原理简单,适应性强,因此在很多情况下都是研究人员的首选。
此外,KMC在复杂体系或复杂过程中的算法发展也非常活跃。
本文试图介绍KMC方法的基础理论和若干进展。
KMC方法基本原理在原子模拟领域内,分子动力学(molecular dynamics, MD)具有突出的优势。
它可以非常精确的描述体系演化的轨迹。
一般情况下MD的时间步长在飞秒(s)量级,因此足以追踪原子振动的具体变化。
但是这一优势同时限制了MD在大时间尺度模拟上的应用。
现有的计算条件足以支持MD到10 ns,运用特殊的算法可以达到10 s的尺度。
即便如此,很多动态过程,如表面生长或材料老化等,时间跨度均在s 以上,大大超出了MD的应用范围。
有什么方法可以克服这种局限呢?当体系处于稳定状态时,我们可以将其描述为处于维势能函数面的一个局域极小值(阱底)处。
有限温度下,虽然体系内的原子不停的进行热运动,但是绝大部分时间内原子都是在势能阱底附近振动。
偶然情况下体系会越过不同势阱间的势垒从而完成一次“演化”,这类小概率事件才是决定体系演化的重点。
因此,如果我们将关注点从“原子”升格到“体系”,同时将“原子运动轨迹”粗化为“体系组态跃迁”,那么模拟的时间跨度就将从原子振动的尺度提高到组态跃迁的尺度。
这是因为这种处理方法摈弃了与体系穿越势垒无关的微小振动,而只着眼于体系的组态变化。
因此,虽然不能描绘原子的运动轨迹,但是作为体系演化,其“组态轨迹”仍然是正确的。
此外,因为组态变化的时间间隔很长,体系完成的连续两次演化是独立的,无记忆的,所以这个过程是一种典型的马尔可夫过程(Markov process),即体系从组态到组态,这一过程只与其跃迁速率有关。
【国家自然科学基金】_动态monte carlo模拟_期刊发文热词逐年推荐_20140731
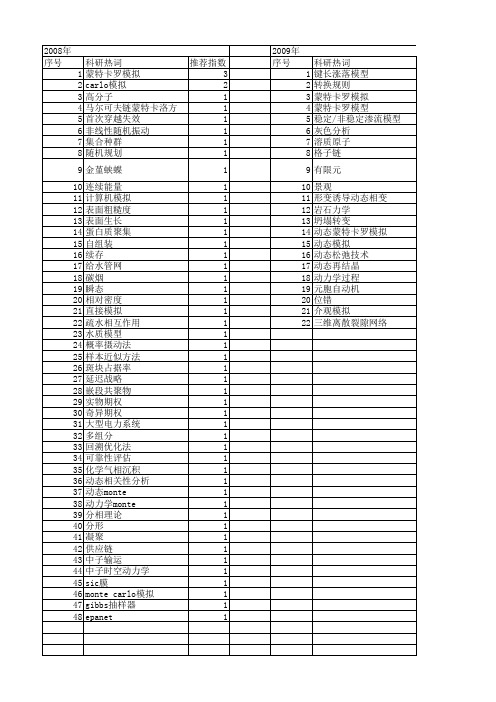
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
高分子构象模拟研究中的Monte Carlo方法

高分子构象模拟研究中的Monte Carlo方法李海普;钟志辉;李星;宋振伟【摘要】Monte Carlo method and its characteristic were introduced,its advantages in the conformation simulation of polymer were further analyzed,and two simulation models were also described.With emphasis on the development of Monte Carlo in conformation simulations,the applications of the method during the research of polymer conformation in confined space and non-confined space were summarized,and the trends and prospects for the Monte Carlo simulations of polymer conformations for future were speculated.%介绍了Monte Carlo方法及其特点,进而分析了Monte Carlo用于高分子模拟的优势,并描述了两类模拟模型。
论文重点综述了近年来Monte Carlo方法在高分子构象模拟中的一些研究与应用,并展望了Monte Carlo方法在高分子构象模拟中的发展趋势和前景。
【期刊名称】《广州化工》【年(卷),期】2012(040)015【总页数】3页(P3-5)【关键词】Monte;Carlo;分子模拟;高分子;构象【作者】李海普;钟志辉;李星;宋振伟【作者单位】中南大学化学化工学院,湖南长沙410083;中南大学化学化工学院,湖南长沙410083;中南大学化学化工学院,湖南长沙410083;中南大学化学化工学院,湖南长沙410083【正文语种】中文【中图分类】O631.1高分子构象是指高分子由于单键的旋转而形成的各原子或基团在空间中的排列。
分子模拟方法及模拟软件MaterialsStudio在高分子材料中的应用

分子模拟方法及模拟软件MaterialsStudio在高分子材料中的应用一、引言高分子材料是当今工业界和科学界中的一种重要材料,广泛应用于各个领域。
为了进一步了解高分子材料的性质和行为,研究人员采用了许多不同的方法进行研究。
其中,分子模拟方法是一种有效的工具,可用于预测高分子材料的结构、动力学和性质。
二、分子模拟方法1. 分子动力学模拟分子动力学模拟是分子模拟方法中最常用的方法之一。
它通过模拟分子系统中原子之间的相互作用,通过求解牛顿方程来研究粒子在给定势场中的运动行为。
这种方法可以模拟高分子材料的力学性质、热力学性质和动态行为。
2. 蒙特卡洛模拟蒙特卡洛模拟是一种基于概率统计方法的模拟方法。
它通过随机生成分子的构象,计算系统的能量,然后根据一定的概率准则来决定是否接受这个构象。
通过大量的随机实验,蒙特卡洛模拟可以得到高分子材料的平衡态性质和相变行为。
三、MaterialsStudio软件介绍MaterialsStudio是由Accelrys公司(现在是Biovia公司的一部分)开发的一款功能强大的分子模拟软件。
它提供了许多用于高分子材料模拟的工具和模块,包括分子动力学模拟、蒙特卡洛模拟、量子力学计算等。
通过MaterialsStudio软件,研究人员可以模拟高分子材料的结构、性质和行为。
四、MaterialsStudio在高分子材料中的应用1. 高分子材料的结构模拟MaterialsStudio软件可以进行高分子材料的结构模拟。
通过分子动力学模拟,研究人员可以了解高分子材料的构象分布、空间排布和相互作用。
通过蒙特卡洛模拟,研究人员可以得到高分子材料的稳定结构和相变行为。
这些模拟结果可以帮助研究人员理解高分子材料的结构特征,指导高分子材料的设计和合成。
2. 高分子材料的热力学性质模拟MaterialsStudio软件可以进行高分子材料的热力学性质模拟。
通过分子动力学模拟,研究人员可以计算高分子材料的力学性质、热胀缩性和热导率等热力学性质。
MonteCarlo模拟对策活性聚合及聚合诱导自组装[4]
![MonteCarlo模拟对策活性聚合及聚合诱导自组装[4]](https://img.taocdn.com/s3/m/3866a662a517866fb84ae45c3b3567ec102ddc32.png)
MonteCarlo模拟研究活性聚合及聚合诱导自组装机理有关,改变反应发生的概率即是改变自组装与聚合增长反应发生的相对几率,聚合概率越低,自组装越占主导,当低至极值0时,就与溶液自装相同。
聚合自组装是边聚合边自组装的过程,聚合反应概率的大小决定着体系是先以较短的分子链主要进行自组装,在自组装基本结束后再以聚合反应为主,链逐渐增长,还是在开始阶段单体就基本增长完毕,接着这些长链大分子再发生自组装。
因为成壳链段A是以大分子引发剂形式加入,所以A链段长度不变,反应概率较小时,主要是成核链段B较短的分子链自组装形成的聚集体,以球状为主,反应概率较高时,主要是由较长的B链段组成的分子链自组装形成聚集体,如第二章所述,成核链段较长时主要形成棒状胶束,成核链段较短时主要形成球状胶束。
(2)退火对胶束形貌的影响从以上的平行试验还可以发现,在退火步长为3×104MCS时,随着反应速率的增加,先出现的是棒状胶束,后转变为球状胶束,这与先出现球状后出现棒状的一般规律不一致,说明退火步长对胶束形貌也有影响。
退火步长溶液自组装结构聚合诱导自组装(尸r=0.01)《一:I≤:一一一:,一.:711:-翻礴蘸函酸≥j一感巍一——匿4×104MCS、_/mIii,。
,/,.,/,§I、、j一一”酲糍‰.、_一——豳融k圈l-5x104MCS矗第四章聚合诱导自组装计算机模拟方法可以观察聚合诱导自组装过程中体系形成的胶束形态。
如图4.13所示,在R=o.0001时,体系中单体转化率随着反应的进行逐渐增加。
其中a到f六个阶段,体系从无序分布状态逐渐演变生成球形胶束。
如图4—13中a到f所示,单体转化率为O.3左右时,绿色的成核单体B已经开始通过活性聚合反应增长到大分子引发剂A链上,此时共聚物和单体B均匀分布在体系内没有出现明显的胶束形态;随着反应的进行,嵌段共聚物链上B单体的比例逐渐增大,嵌段共聚物开始聚集,如b,c所示;单体转化率为0.8时,体系已经基本形成B嵌段为核、A嵌段包裹B嵌段形成壳层的球状胶束,未参加反应的B单体分散在胶束周围,如d,e所示;聚合反应接近完成时,体系最终形成规整的球状胶束,如f所示。
蒙特卡洛方法在高分子科学研究中的应用

蒙特卡洛方法在高分子科学研究中的应用摘要蒙特卡洛方法于上世纪提出,随着现代科技的发展,蒙特卡洛方法的基本思想在愈来愈多的领域得到运用与研究。
蒙特卡洛方法作为一种重要的统计模拟方法,广泛应用于高分子科学、统计物理、生物医药、金融等领域中的模拟计算。
蒙特卡洛方法可以用于模拟高分子的各种微观状态,构建不同概率分布的高分子构象。
本文介绍了蒙特卡洛方法的基本原理和方法以及在高分子科研中的特征与应用。
关键词:蒙特卡洛方法高分子蒙特卡洛,在世界地图上是俯卧在地中海沿岸国度摩纳哥的一个城市,那里也凭借弥漫着随机性的赌场闻名于世。
而将蒙特卡洛作为一种计算方法的命名显然已经赋予了其新的内容。
所以,顾名思义,蒙特卡洛方法与赌博中的随机性,概率性有着天然且密切的联系。
几乎涉及到复杂的、与概率相关的数值计算的领域都有可能会用到,比如计算物理、经济金融等。
在数学上,蒙特卡洛方法被称为随机模拟方法、随机抽样技术或者统计试验方法。
别看它的别称这么多,其实,蒙特卡洛方法并没有什么高深的理论,它只是一种方法或者说是策略,如果一定要说的话那只有概率论或统计学中的大数定律了。
它的最基本思想是:为了求解数学、物理及化学等问题,建立一个概率模型或随机过程,使它的参数等于问题的解;当所解的问题本身属随机性问题时,则可采用直接模拟法;然后通过对模型或过程的观察抽样试验来计算所求参数的统计特征,最后给出所求解的近似值。
在高分子科研中蒙特卡洛主要采用直接模拟法。
蒙特卡洛方法的突出特点是,它的解是由试验得到的,而不是计算出来的。
其程序结构简单,解题时受问题条件限制的影响较小,具有广泛的适应性。
但不能解决精确度要求很高的问题。
其次,蒙特卡洛方法需要大量的随机数,计算量很大,人工计算需耗费大量的时间,而利用计算机可大大减少计算时间,增加试验次数以提高计算精度,因此,蒙特卡洛方法的广泛应用与计算机技术的发展是不可分割的。
(伪)随机数是蒙特卡洛方法的实现基础,一个良好的随机数可以加快模型的收敛。
物理化学中的自组装动力学研究

物理化学中的自组装动力学研究自组装动力学研究是物理化学领域的一个重要研究方向,其研究的是分子之间的相互作用和组装过程。
自组装动力学研究的重要性在于其可以为自组装材料的设计、合成和性能调控提供基础理论。
本文将介绍自组装动力学研究的相关理论和应用,并分析当前研究的进展。
一、自组装动力学的基本理论自组装动力学是一种描述分子组装过程的动力学理论。
其基本原理是分子之间的相互吸引和排斥作用,并通过热力学平衡来实现分子组装。
自组装动力学可以描述分子在不同温度下的组装和相转移行为,如液-液相分离、胶-液相转变等。
自组装动力学的研究需要考虑分子之间的相互作用,主要包括范德华力、电荷相互作用、亲疏水性等。
分子之间的相互作用导致分子间的吸引和排斥,从而影响分子的排列和组装。
自组装动力学理论的推导和模拟需要考虑分子的结构和性质,如分子的大小、形状、极性等。
这些因素都会影响分子的组装方式和构象,从而影响材料的性质和应用。
自组装动力学的研究方法包括实验和理论两种。
实验方法主要包括激光光散射、小角X射线散射、电子显微镜等。
这些技术可以分析材料的结构和性质,如粒径、形态、相互作用等。
理论方法主要包括分子动力学模拟、Monte Carlo方法等。
这些方法可以模拟材料的组装和相转移行为,从而预测材料的动态性质和结构。
二、自组装材料的设计和合成自组装动力学的研究成果可以为自组装材料的设计和合成提供指导。
自组装材料的设计需要考虑分子之间的组装方式和构象,以及材料的性质和应用。
例如,自组装纳米材料可以用于制备超级电容器、纳米晶体等高性能材料,自组装聚集体则可以用于制备高精度光学元件和传感器等。
自组装材料的设计和合成可以通过分子间的相互作用来实现。
例如,亲疏水交替的分子可以形成水性胶体材料;疏水链可以通过疏水效应自组装成囊泡和微胶束等结构;类固醇类分子可以通过相互作用形成超分子结构等。
通过对分子之间的相互作用进行调控,可以实现自组装材料的设计和合成。
计算生物学中的分子模拟方法

计算生物学中的分子模拟方法计算生物学是利用数学、物理学和计算机科学的方法,研究生命科学中的各种现象和问题的学科。
其中,分子模拟方法是计算生物学中的一个重要分支,它通过计算机仿真模拟分子之间在物理层面上的相互作用,研究分子间的结构、功能和动力学行为等问题。
本文将介绍计算生物学中的分子模拟方法及其应用。
1.分子模拟方法的类型(1)分子力学模拟方法分子力学模拟是分子模拟方法中应用最广泛的一种方法之一。
它利用分子力学的原理,即通过描述分子内原子、键和键角等物理量的运动方程,来模拟分子的运动和相互作用。
这种方法可以用于描述分子间热力学、结构、动力学等各种行为。
(2)分子动力学模拟方法分子动力学模拟是分子模拟方法中的另一种方法。
它将分子描述为一系列基本粒子,通过离散化的时间步长对其运动进行数值积分,得到分子的运动轨迹。
分子动力学模拟可以有效地描述分子的运动、结构和功率转换等。
(3)Monte Carlo模拟方法Monte Carlo模拟方法是基于随机事件的一种统计性模拟方法。
在Monte Carlo模拟中,分子的状态不是根据力学定律,而是根据概率分布进行变化。
这种方法可以用于研究分子在复杂环境中的行为。
2.分子模拟方法的应用(1)药物筛选分子模拟方法可以用于药物发现的各个阶段。
在药物筛选的初期阶段,分子模拟可以通过模拟药物与蛋白质的相互作用,筛选出具有潜在活性的分子。
在候选分子确定后,分子模拟可以进一步用于优化分子的化学结构,从而提高分子与蛋白质的亲和力。
(2)酶催化机理分子模拟可以用于探究酶的催化机理。
与实验技术相比,分子模拟可以提供更加详细的信息,比如中间体和过渡态的结构和能量等。
通过对这些信息的分析,可以揭示酶催化机理中的关键步骤和物理原理,有助于设计更加高效的酶催化剂。
(3)膜蛋白结构和功能膜蛋白是细胞膜中的重要成分之一,它们在细胞中发挥着多种重要功能。
由于膜蛋白的结构复杂性和实验技术受限,目前对于膜蛋白的结构和功能还存在很多疑问。
两亲性梳形高分子在油水界面自组装行为的Monte Carlo模拟

Ab t a t S l— s e b y sr c : ef a s m l b h v o s o a e a i r f mp i h l c mb s a e o o y e — t r o l hp ic o i — h p e p l m r wa e — i s s e s we e s m u a e y a t r e d me so a o t ro l t ie mo e . e r s le y tm r i 1td b h e — i n i n l M n eCa l a t d 1 Th e u t d e
C mb S a eCo oy r nteWae / l ne fc o —h p p lmesi h tr Oi I tra e
F NG  ̄n U i—in ,Z O J—u HE Xi— a g E ig ,S IJaxa HA i o ,C N nf n r
( , l g P lme ce c n a ie r g 2 D p rme t0 p i h mi r , n d o I si t o e c l 1 Col e e o y rS in ea d E gn e [ , e at n f a Ap l d C e s y Qig a n t ue f e t t Ch mi a
文章编号 :0 1 46 (0 2 0 — 020 1 0 — 7 4 2 0 ) 1 0 3 6
两亲性梳形 高分子在油水界面 自 组装行为 的 Mo t C r ne al o模拟
冯 莺 ,隋家贤 ,赵季若 ,陈欣方。
3 吉秫大学材料系.吉林 长春 1 0 2 ) . 30 3 ( 岛化工学院 1 高分子科学与工程学院 .2 信息与控 制工程学院 , 青 . . 山东 青岛 2 64 602
固液界面多分散高分子吸附构型的Monte Carlo模拟

固液界面多分散高分子吸附构型的Monte Carlo 模拟*刘梅堂 牟伯中 刘洪来 胡 英 (华东理工大学化学系, 上海 200237)摘 要: 在格子模型基础上用Monte Carlo 方法模拟研究了多分散高分子在固液界面的吸附行为,重点考察了平均分布和正态分布两种不同链长分布形式的高分子在固液界面吸附构型的分布规律。
发现高分子不同的链长分布形式,对高分子吸附构型的性质影响较大。
正态分布的高分子体系中高分子的三种吸附构型(tails ,loops 和 trains )的浓度和数目比相同条件下平均分布的高分子体系内要低的多。
特别是当高分子链节吸附能较低时,两者的差别非常大。
平均分布的高分子体系高分子吸附构型对温度和高分子总链节浓度的变化更加敏感。
tails 构型由于受到高分子链节热运动以及吸附层压缩作用的影响,在高温或高吸附作用能下,其密度分布表现出和其它两种吸附构型完全不同的形式。
温度,高分子链节吸附作用能以及高分子总链节浓度对三种吸附构型的影响和单分散体系趋势一致,但是存在着定量的差别。
关键词:多分散性,高分子,吸附构型,固液界面, Monte Carlo 模拟 中图分类号:O63/4713 文献标识码:Monte Carlo Simulations for Polymer Conformation of Polydisperse Polymersat S/L InterfacesLiu Meitang Mu Bozhong Liu Honglai Hu Ying(Department of Chemistry, East China University of Science and Technology, Shanghai 200237,China )Abstract : The adsorption behavior of polydisperse polymers at solid-liquid interfaces is studied by the method of Monte Carlo simulations based on the lattice model, and effects of the polymer chain length in systems of both average and normal distributions on the polymer conformation (tails, trains and loops distribution) are evaluated. Apparent conformation differences are found between these two polydisperse systems especially when the polymer-interface interaction energy is low enough. The concentration of tails, trains and loops in different layer are much lower in normal distribution systems than that in average ones, whereas the change in polymer conformation is more sensitive to temperature and the concentration of the total polymer segments in average distribution systems than that in normal ones. Results also show that when temperature increases, the concentration of tails in layers far away from the adsorption interface increases accompanied by concentrations of trains and loops decreasing rapidly. This indicate that more stand-up conformation exist near the adsorption interfaces. All data from this work also reveals that quantitative system errors will exist when using monodisperse models to evaluate the real polydisperse polymer systems.Key words : Polydispersity, Polymer, Adsorption conformation, Solid-liquid interfaceMonte Carlo simulation收稿日期: 修订日期:基金项目:国家自然科学基金(No.20025618, 20236010)、油气藏地质与开发工程国家重点实验室开放基金(PLN0137)和上海市教委资助 作者简介:刘梅堂(1975-),男,山东泰安人,华东理工大学博士生。
聚丙烯基结晶行为的计算模拟

聚丙烯基结晶行为的计算模拟聚丙烯(Polypropylene, PP)是一种热塑性合成树脂,具有良好的耐热性、耐化学物质侵蚀性、机械性能和电气绝缘性。
因此,聚丙烯广泛应用于各种领域中,如包装、汽车、医疗器械等。
然而,聚丙烯的结晶过程是一种复杂的物理化学过程,在热塑性聚合物的加工制备、性能改善、表面改性等方面起着至关重要的作用。
随着计算机技术的快速发展,计算模拟在热塑性聚合物领域中获得越来越广泛地应用。
本文探讨了聚丙烯的结晶行为计算模拟方法及其在聚合物领域中的应用。
一、聚丙烯分子的结构特点聚丙烯的分子结构特点决定了其在加工过程中的熔化和结晶过程。
聚丙烯的结构是线性的,由丙烯单体(propylene, C3H6)通过共价键连接而成。
聚丙烯分子的主链上存在着一个独特的CH3侧链,这个侧链的存在使得聚丙烯的结晶性能比其他的热塑性聚合物更容易。
同时,聚丙烯分子中存在着大量的伸展链段,在加工过程中可通过加热从而变得活跃,从而影响其熔融和结晶过程。
二、聚丙烯的结晶过程聚丙烯在加工过程中,先经历熔融过程,然后经历结晶过程,形成晶态结构。
聚丙烯的结晶过程一般可以分为两个阶段,即原始结晶阶段和晶核成熟阶段。
在原始结晶阶段,熔融聚丙烯中出现了一些局部结构的有序区域,称为初期结晶区。
在这个阶段,聚丙烯分子链开始逐渐排列起来,构成有序结构,即结晶。
同时,随着分子链的不断移动,聚丙烯中出现了许多晶核,形成许多小的结晶颗粒,逐渐生长并连接在一起,形成更大的晶体,进入晶核成熟阶段。
三、计算模拟方法随着计算机技术和软件的不断发展,计算模拟方法被越来越广泛地应用于聚合物材料研究领域中。
其中,分子动力学模拟(Molecular dynamics, MD)和蒙特卡罗模拟(Monte Carlo, MC)是两种常用的模拟方法。
1.分子动力学模拟分子动力学模拟是模拟链状分子运动的一种方法,其模拟的物理过程是基于牛顿力学和统计力学理论的。
在分子动力学模拟中,聚合物分子被视为一系列质点,模拟的参数为模拟系统中的粒子位置、速度和能量等。
巨正则蒙特卡罗方法

巨正则蒙特卡罗方法一、前言巨正则蒙特卡罗方法(Grand Canonical Monte Carlo,简称GCMC)是一种重要的计算化学方法,广泛应用于气体吸附、离子吸附、溶剂扩散等领域。
本文将从基本原理、模拟流程和结果分析三个方面详细介绍巨正则蒙特卡罗方法的实现过程。
二、基本原理1.巨正则系综巨正则系综是指在恒定温度、压力和化学势下,系统与外界交换粒子数的系综。
在巨正则系综中,系统中的粒子数不是固定不变的,而是可以随时增加或减少。
系统与外界之间通过化学势μ来交换粒子数。
2.蒙特卡罗模拟蒙特卡罗模拟是一种基于概率统计方法的计算机模拟技术,用于研究复杂系统的性质。
在蒙特卡罗模拟中,通过随机抽样和概率分布函数来模拟系统中各个粒子之间相互作用以及与外界之间的作用,并通过统计平均值来得到系统性质。
3.巨正则蒙特卡罗方法巨正则蒙特卡罗方法是将巨正则系综和蒙特卡罗模拟相结合的一种计算化学方法。
在巨正则蒙特卡罗方法中,通过随机抽样和概率分布函数来模拟系统中各个粒子之间相互作用以及与外界之间的作用,并通过统计平均值来得到系统性质。
三、模拟流程1.确定模拟系统首先,需要确定要模拟的系统。
例如,可以考虑气体吸附过程中的吸附剂表面、溶液中的分子等。
2.设定初始状态在进行模拟前,需要设定初始状态。
对于巨正则蒙特卡罗方法,需要设定温度、压力和化学势等参数,并随机生成一组初始粒子数和位置。
3.选择移动方式在进行模拟时,需要选择不同的移动方式。
常见的移动方式包括平移、旋转、插入和删除等。
4.计算能量变化在进行粒子移动时,需要计算能量变化。
对于气体吸附过程来说,可以采用Lennard-Jones势函数或Mie势函数等来计算相互作用能。
5.接受或拒绝移动在计算能量变化后,需要根据Metropolis准则来决定是否接受粒子移动。
如果能量降低,则接受移动;否则,根据概率分布函数决定是否接受。
6.更新状态如果粒子移动被接受,则需要更新系统状态。
试验十七高分子链构象的计算机模拟试验目的对高分子链构象

实验十七高分子链构象的计算机模拟一、实验目的1.对高分子链构象有直观、形象的了解。
2.了解Monte Carlo方法的原理。
二、实验原理l.高分子的链构象链构象就是分子链在空间中的形状和尺寸,高分子溶液和本体的许多性质,诸如热力学、光学、电学、声学、流体动力学和力学等性质,都与链构象有关。
而链的柔性,使构象具有统计性。
可以说,链构象理论是研究高分子的基础,我们在《高分子物理》课程中曾学到,高分子链构象可以分成两类,即理想链和真实链。
理想链即无干扰状态下的高分子链,它可以用无规行走来描述,故又称无规链,其均方末端距(h2)可以表示为(h2)=NL2–----------------------------------- (1)式中N是链节数;L是链节长度。
又M =M0N -------------------------------------- (2)式中M为高分子链的分子量;M0为链节分子量。
这样,由(1)、(2)两式,我们就可以得到均方末端距同链分子量M的关系。
真实链即有排除体积效应的高分子链。
由于原子之间相互作用的存在。
两个原子不能在空间占据同一位置。
换言之,在分子链中,组成链的原子相互被排除于同一体积。
这种效应即称为排除体积效应。
在链构象的统计理论和数学模拟中又称自回避链。
排除体积效应引起分子链扩张,即分子链有较大的均方末端距,表示为:(h2)= NvL2, v ≈6/5一般来讲,高分子链是真实链,但高分子链若处于θ状态(在θ温度、θ溶剂中)则成为理想链。
这时,从无规行走的角度来看,无规行走的迹线可以前后重叠。
本实验的主要目的就是直观地从计算机上“看到”这两种链、同时,通过观察高分子的链构象,找出高分子线团尺寸与分子链节数的关系,亦即均方末端距与分子量的关系。
2.链构象的模拟从高分子链的二次结构上看。
链分子是由链节依照一定的键角和旋转角,一个一个地连接而成的。
一个具有N个链节数的高分子链,从计算机模拟的角度来看,相当于一步一步走N步而成的。
高分子物理学中的突破——聚合物自组装

高分子物理学中的突破——聚合物自组装聚合物自组装是高分子物理学研究领域中的一个新兴方向,在材料科学、生物医药领域中具有广泛的应用前景。
在聚合物自组装中,将分子自发地聚集在一起,并形成一定的结构和功能。
这种自发的组装方式为高分子材料设计和制备提供了新的思路和方法。
本文将探讨聚合物自组装的研究进展和应用前景。
1.聚合物自组装的基础理论聚合物自组装是指由单体分子自发地形成的有序结构和功能材料。
这种自组装是由分子间的非共价相互作用(如范德华力、静电作用、氢键、水合等)驱动的。
这些相互作用不同程度地影响着聚合物分子间的相互作用和组装方式。
因此,理解相互作用的本质和影响因素对聚合物自组装的控制至关重要。
在聚合物自组装的过程中,通常涉及到三个方面的基本问题:组装模式、组装驱动力和组装得到的结构和性能。
组装模式可以分为两种类型:微相分离和纳米粒子自组装。
微相分离是指在溶液中,由于亲疏水性差异等因素,聚合物分子以不同的相相互分离。
纳米粒子自组装是指聚合物分子通过非共价相互作用形成的纳米级结构,如纳米球、管、棒等形态。
这些形态的产生和具有的功能与聚合物分子结构及其间相互作用密切相关。
聚合物自组装的驱动力是由相互作用导致的,其中范式力是最主要的相互作用。
范式力是由于电荷、磁性、极性和诸如索尔霍夫是斯基效应等成分所引起的各种作用力。
在聚合物自组装过程中,静电作用可以使分子通过相互吸引在一起。
氢键也是非常重要的相互作用,由于氢键受到许多因素的影响,如H原子的性质、原子间距、方向等,因此可以通过改变这些因素来调控聚合物的自组装方式和组装结构。
此外,其他相互作用力如疏水作用、π-π堆栈作用、水合等也在聚合物自组装中发挥了重要作用。
组装得到的结构和性能是聚合物自组装的最终目标之一。
聚合物组装形态的多样性和复杂性往往决定了组装材料的性能和特性。
例如,纳米球可用于生物医学载体、纳米管可用于导电材料、纳米棒可以用于催化剂等等。
2.聚合物自组装的应用前景聚合物自组装在材料科学、生物医药、新能源领域中具有广泛的应用前景。
《高分子自组装》课件

高分子自组装新技术
随着技术的进步,高分子自组装领域 也不断涌现出新的技术手段。例如, 利用先进的纳米技术、生物技术等手 段,可以实现高分子自组装的精准控 制和高效制备。
熔融法
总结词
将高分子加热至熔融状态,然后通过降温或加入其他物质诱导其自组装。
详细描述
熔融法是将高分子加热至熔融状态,然后在特定的温度和条件下,通过降温或加入其他物质诱导高分 子自组装。这种方法可以用来制备各种不同形貌和尺寸的自组装体,如球状、柱状、纤维等。
界面法
总结词
将高分子溶液置于两个不同相的界面上 ,通过调节界面性质诱导高分子自组装 。
高分子自组装在交叉学科中的应用
生物学
高分子自组装在生物学领域有着广泛的应用,如蛋白质、核酸等生 物大分子的自组装,可以模拟生命过程中的复杂结构和功能。
材料科学
高分子自组装在材料科学领域的应用也日益广泛,如利用高分子自 组装制备高性能复合材料、功能材料等。
医学
高分子自组装在医学领域的应用也备受关注,如药物载体、生物支架 、组织工程等领域的应用。
模板法是利用预先制备的模板作为模板,使高分子在模板中自组装,最后去除模板得到 有序结构。这种方法可以用来制备各种不同形貌和尺寸的自组装体,如柱状、纤维、有
序孔洞等。
04
高分子自组装结构与性能的 关系
自组装结构对力学性能的影响
增强韧性
自组装结构能够提高聚合物的韧性,使其在受到外力时不易 脆断。
1
提高强度
耐热性
自组装结构可以提高聚合物的耐热性,使其在高温环境下仍能保持稳定。
溶剂尺寸对ABA两亲性三嵌段共聚物在选择性溶剂中自组装行为影响的Monte Carlo模拟

21 0 1年 7月
高 等 学 校 化 学 学 报
CHEMI AL J C OURNAL OF CHI NES E UNI VERS T E IIS
No 7 .
l 5j — l 5 6 6 5
溶 剂 尺 寸 对 A A 两 亲 性 三 嵌 段 共 聚 物 B 在 选 择 性 溶 剂 中 自组 装 行 为 影 响 的 Mo t a l 拟 neC r o模
目前 , 关溶 剂尺 寸对 嵌段 共 聚物胶 束形 态影 响 的理 论研 究相对 较 少. 等 采用 自洽平均场 方 有
法研究 了小 分子溶 剂 ( 溶剂体 积 与高分 子链 段体 积相 当) 寸对 AB两嵌段 共 聚物在 选择性 溶剂 中 自组 尺 装 胶束形 态 的影 响 , 果 表 明小 分 子溶剂 尺寸 的减 小 有利 于 A 结 B两嵌 段 共 聚 物囊 泡 的形成 .然而 中分 子溶剂尺 寸对 胶束 形态 的影 响 尚不 清 楚.本 文 采 用 Mo t C A n a o模 拟 方法 研 究 中分子 溶 剂尺 寸 对 A A e B 两 亲性 三嵌段 共 聚物在 选择 性溶 剂 中 自组装 行 为 的影 响 .
N . o7
樊 娟 娟 等 : 剂 尺 寸 对 A A 两 亲 性 三 嵌 段 共 聚 物 … … 的 Mot C r 溶 B ne al 拟 o模
性三嵌 段共 聚物 在选 择性 溶剂 中 自组 装所 形成 的胶 束 形 态.灰 色部 分代 表 亲水 链 段 A,黑 色部 分 代表 疏 水链 段 B .随着 中分子 溶剂 尺 寸 的变化 ,自组 装形 态发 生 明显 改变 .当 ( =1时 ( 明体 系 中完 全是 b 表
分 别用小 分子 溶剂 ( 和 中分 子溶剂 ( 来 表示 .定义 参数 咖为溶 剂分 子与 高分子 链段 的体 积 比. S) S) 若 1 则 为小分 子溶 剂 ; , 若 >1 则 为 中分子 溶剂 .在 模拟 过程 中保证 小分 子溶 剂 的体 积 占总溶 剂 的 ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关键词 : M o n t e C a r l o 模拟 ; 活性可控聚合 ; 聚合诱导 自组装 ; 胶 束 中图分类号 : 0 6 3 1 . 5 文献标志码 : A 文章编号 : 1 0 0 0 — 2 1 6 2 ( 2 0 1 3 ) 4— 0 0 0 8 1 — 0 7
Mo nt e Ca r l o s i mu l a t i o n o n p o l y me r i z a t i o n- i n d uc e d c o p o l y me r s s e l f - a s s e m bl y
a 1 .T h e a u t h o r s s t u d i e d t h e p o l y me r i z a t i o n i n d u c e d s e l f —a s s e mb l y a n d o b s e ve r d s p h e i r c a l a n d
E n v i r o n m e n t — f r i e n d l y P o l y me r Ma t e i r a l s o f A n h u i P r o v i n c e , H e f e i 2 3 0 6 0 1 , C h i n a )
2 0 1 3年 7月
安徽大学学报 ( 自然 科 学 版 )
J o u r n a l o f A n h u i U n i v e r s i t y( N a t u r a l S c i e n c e E d i t i o n )
J u l y 2 0 1 3
C HE N P e n g , X U X i n ,S H A O J i n g , X I A R u , Q I A N J i a - s h e n g
( S c h o o l o f C h e m i s t r y a n d C h e m i c a l E n g i n e e i r n g ,A n h u i U n i v e r s i t y , K e y L a b o r a t o y r o f
t h a t h a s b e e n o b s e r v e d i n e x p e i r me n t s ,a n d r e v e a l e d t h e d y n a mi c p r o c e s s o f i t .T h e i r r e s e a r c h i n g
2 3 0 6 0 1 ) ( 安徽大学 化学化工学 院, 安徽省绿色高分子材料重点 实验 室 , 安徽 合肥 摘
要: 学过程 , 在聚 合反应 的 同时, 观察 高分子在 溶
液中的 自组装相行为. 通过统计模拟 聚合反应 过程 中的单体转 化率 、 聚合物分子量 、 分 子量分布等信 息 , 证 明 聚合反应是可控 的活性 聚合 . 在聚合反应 中, 通过调控聚合反 应概率 、 链段 与溶剂之 间的相容性等参数 , 观 察
Ab s t r ac t:A Mo n t e Ca r l o s i mul a t i o n s c he d u l e i s d e v e l o p e d b a s e d o n “s i n g l e — s i t e b o n d lu f c t u a t i o n’ ’ mo d e l t o s t u dy t he k i n e t i c s o f l i v i n g r a d i c a l p o l y me iz r a t i o n a n d o b s e r v e t h e p ha s e b e ha v i o r o f c o p o l y me r s e l f - a s s e mb l y i n s o l ut i o n. T he p o l y me iz r a t i o n k i n e t i c s i s p r o v e d t o b e a l i v i ng p o l y me iz r a t i o n b y i n v e s t i g a t i ng mo n o me r c o n v e r s i o n,mo l e c ul a r we i g h t a nd mo l e c u l a r d i s t ib r u t i o n e t
Vo 1 . 37 No. 4
第3 7卷 第 4期
d o i : 1 0 . 3 9 6 9 / j . i s s n . 1 0 0 0 — 2 1 6 2 . 2 0 1 3 . 0 4 . 0 1 4
Mo n t e C a r l o模拟 研究聚合诱 导高分子 自组装
陈 鹏 , 许 欣, 邵 静, 夏 茹 , 钱 家盛
c y l i nd ic r a l mi c e l l e s i n s o l u t i o n.Th e i r s i mu l a t i o n c o n ir f me d t he p o l y me iz r a t i o n i n d uc e d s e l f - a s s e mb l y
到诱导组装形成 的球状 和柱状胶 束. 模拟研究 验证 了实验 中观察 到 的聚合诱 导 自组装 现象 , 揭示 了聚合诱 导 自组装的动力学过程. 研究结果证 明, 文中所建立 的单格点 Mo n t e C a r l o模拟 方法 , 可 以应 用于研究 聚合诱 导
高 分 子 自组 装 相 行 为 .
