高三文科数学公式
高考文科数学公式汇总

高考文科数学公式汇总在高考文科数学中,掌握各类公式是取得好成绩的关键。
以下为大家汇总了一些重要的公式,希望能对同学们的复习有所帮助。
一、函数相关公式1、一次函数:y = kx + b(k、b 为常数,k ≠ 0)当 k > 0 时,函数单调递增;当 k < 0 时,函数单调递减。
2、二次函数:y = ax²+ bx + c(a ≠ 0)对称轴为 x = b / 2a ,顶点坐标为(b / 2a ,(4ac b²) / 4a )当 a > 0 时,抛物线开口向上,函数在 x = b / 2a 处取得最小值;当 a < 0 时,抛物线开口向下,函数在 x = b / 2a 处取得最大值。
3、反比例函数:y = k / x(k 为常数,k ≠ 0)当 k > 0 时,函数在一、三象限,在每个象限内单调递减;当 k <0 时,函数在二、四象限,在每个象限内单调递增。
4、指数函数:y = a^x(a > 0 且a ≠ 1)当 a > 1 时,函数单调递增;当 0 < a < 1 时,函数单调递减。
5、对数函数:y =logₐ x(a > 0 且a ≠ 1)其与指数函数互为反函数,logₐ a = 1,logₐ 1 = 0 。
二、三角函数公式1、同角三角函数基本关系sin²α +cos²α = 1tanα =sinα /cosα2、诱导公式sin(π +α) =sinαcos(π +α) =cosαsin(α) =sinαcos(α) =cosα3、和差角公式sin(α +β) =sinαcosβ +cosαsinβsin(α β) =sinαcosβ cosαsinβcos(α +β) =cosαcosβ sinαsinβcos(α β) =cosαcosβ +sinαsinβ4、二倍角公式sin2α =2sinαcosαcos2α =cos²α sin²α =2cos²α 1 =1 2sin²αtan2α =2tanα /(1 tan²α)5、辅助角公式a sinα +b cosα =√(a²+b²) sin(α +φ),其中tanφ = b / a三、数列相关公式1、等差数列通项公式:aₙ = a₁+(n 1)d ,前 n 项和公式:Sₙ = n(a₁+ aₙ) / 2 = na₁+ n(n 1)d / 2其中 a₁为首项,d 为公差。
高三必背数学知识点公式

高三必背数学知识点公式一、代数运算1. 加法公式:(a + b)^2 = a^2 + 2ab + b^2(a - b)^2 = a^2 - 2ab + b^22. 幂的性质:a^m * a^n = a^(m + n)(a^m)^n = a^(mn)a^(-m) = 1 / a^m3. 根式的性质:√(a * b) = √a * √b√(a / b) = √a / √b(√a)^2 = a4. 二次根式的展开和收集:√(a + b) ≠ √a + √b(√a + √b)(√a - √b) = a - b5. 平方差公式:a^2 - b^2 = (a + b)(a - b)6. 二次方程求根公式:x = (-b ± √(b^2 - 4ac)) / 2a7. 余弦定理:c^2 = a^2 + b^2 - 2abcosC8. 正弦定理:a / sinA =b / sinB =c / sinC二、几何图形相关公式1. 长方形的面积和周长:面积 S = 长 a * 宽 b周长 P = 2a + 2b2. 正方形的面积和周长:面积 S = a^2周长 P = 4a3. 圆的面积和周长:面积S = πr^2周长C = 2πr4. 圆柱体的体积和表面积:体积V = πr^2h表面积A = 2πrh + 2πr^25. 直角三角形特殊关系:勾股定理:a^2 + b^2 = c^26. 同位角与内错角关系:同位角相等,内错角互补:∠A = ∠B ⇒∠C = ∠D, ∠E = 180° - ∠B7. 圆锥的体积和表面积:体积V = (1/3)πr^2h表面积A = πrl + πr^2三、三角函数和三角恒等式1. 三角函数的基本关系:sinθ = 对边 / 斜边cosθ = 临边 / 斜边tanθ = 对边 / 临边2. 三角函数的正负:第一象限:sinθ > 0, cosθ > 0, tanθ > 0第二象限:sinθ > 0, cosθ < 0, tanθ < 0第三象限:sinθ < 0, cosθ < 0, tanθ > 0第四象限:sinθ < 0, cosθ > 0, tanθ < 03. 三角函数的周期性:sin(θ + 2πn) = sinθcos(θ + 2πn) = cosθtan(θ + πn) = tanθ4. 三角函数的和差化积:sin(A ± B) = sinAcosB ± cosAsinBcos(A ± B) = cosAcosB ∓ sinAsinBtan(A ± B) = (tanA ± tanB) / (1 ∓ tanAtanB)5. 三角函数的倍角公式:sin2θ = 2sinθcosθcos2θ = cos^2θ - sin^2θtan2θ = (2tanθ) / (1 - tan^2θ)四、概率和统计相关公式1. 排列公式:A(n, m) = n! / (n - m)!2. 组合公式:C(n, m) = n! / (m!(n - m)!)3. 互斥事件的概率公式:P(A ∪ B) = P(A) + P(B)4. 独立事件的概率公式:P(A ∩ B) = P(A) * P(B)5. 条件概率公式:P(A | B) = P(A ∩ B) / P(B)总结:以上是高三数学知识点公式的概要,掌握这些公式对于成功备战高考至关重要。
高中文科数学公式总结大全

高中文科数学公式总结大全1500字数学是一门基础性学科,它的理论体系和方法论在科学研究和生产实践中扮演着重要角色。
在高中阶段,学习数学有助于培养学生的逻辑思维、分析问题和解决问题的能力。
而数学公式则是数学知识的核心,它们能够帮助我们快速理解和解决问题。
以下是高中文科数学公式的总结大全:1. 代数- 求根公式:二次方程:$x=\\frac{-b\\pm\\sqrt{b^2-4ac}}{2a}$三次方程:$x=\\sqrt[3]{-d+\\sqrt{d^2-4e^3}}+\\sqrt[3]{-d-\\sqrt{d^2-4e^3}}$四次方程:$x=\\pm\\frac{1}{2a}(b\\pm\\sqrt{b^2-4ac}+2\\sqrt{\\frac{2b^2-4ac}{b\\pm\\sqrt{b^2-4ac}}})$- 平方差公式:$(a-b)^2=a^2-2ab+b^2$$(a+b)^2=a^2+2ab+b^2$- 平方和公式:$a^2+b^2=(a+b)^2-2ab$$a^2-b^2=(a+b)(a-b)$- 二次函数顶点坐标:对于二次函数$y=ax^2+bx+c$,其顶点坐标为$(-\\frac{b}{2a}, -\\frac{D}{4a})$ 其中,$D=b^2-4ac$2. 几何- 勾股定理:$c^2=a^2+b^2$- 正弦定理:$\\frac{a}{\\sin A}=\\frac{b}{\\sin B}=\\frac{c}{\\sin C}$- 余弦定理:$a^2=b^2+c^2-2bc\\cos A$$b^2=a^2+c^2-2ac\\cos B$$c^2=a^2+b^2-2ab\\cos C$- 面积公式:三角形面积:$S=\\frac{1}{2}ab\\sin C$四边形面积:$S=\\frac{1}{2}d_1d_2\\sin\\theta$圆的面积:$S=\\pi r^2$3. 概率与统计- 排列组合:排列:$A_n^m=\\frac{n!}{(n-m)!}$组合:$C_n^m=\\frac{A_n^m}{m!}=\\frac{n!}{m!(n-m)!}$ - 排列公式:重复排列:$P_n=n^n$不重复排列:$P_n^n=n!$- 组合公式:重复组合:$C_{n+m-1}^{m}=\\frac{(n+m-1)!}{m!(n-1)!}$ 不重复组合:$C_n^m=\\frac{n!}{m!(n-m)!}$- 概率公式:概率:$P(A)=\\frac{N(A)}{N(S)}$加法原则:$P(A\\cup B)=P(A)+P(B)-P(A\\cap B)$乘法原则:$P(A\\cap B)=P(A)P(B|A)$4. 三角函数- 弧度与角度的转换:弧度制:$\\theta=\\frac{\\pi}{180}\\times\\text{角度}$角度制:$\\text{角度}=\\frac{180}{\\pi}\\times\\theta$- 三角函数的定义:正弦函数:$\\sin\\theta=\\frac{y}{\\text{半径}}$余弦函数:$\\cos\\theta=\\frac{x}{\\text{半径}}$正切函数:$\\tan\\theta=\\frac{y}{x}$反正弦函数:$\\sin^{-1}(\\frac{y}{\\text{半径}})=\\theta$ 反余弦函数:$\\cos^{-1}(\\frac{x}{\\text{半径}})=\\theta$反正切函数:$\\tan^{-1}(\\frac{y}{x})=\\theta$- 三角函数的平方和与差:$\\sin^2\\theta+\\cos^2\\theta=1$$\\sin(\\theta\\pm\\phi)=\\sin\\theta\\cos\\phi\\pm\\cos\\theta\\sin\\phi$$\\cos(\\theta\\pm\\phi)=\\cos\\theta\\cos\\phi\\mp\\sin\\theta\\sin\\phi$5. 矩阵与行列式- 二阶矩阵的行列式:$\\begin{vmatrix} a & b \\\\ c & d \\end{vmatrix}=ad-bc$- 二元一次方程组的解:设$\\begin{vmatrix} a & b \\\\ c & d \\end{vmatrix}\eq0$,则方程组的解为$x=\\frac{\\begin{vmatrix} e & b \\\\ f & d\\end{vmatrix}}{\\begin{vmatrix} a & b \\\\ c & d \\end{vmatrix}}$,$y=\\frac{\\begin{vmatrix} a & e \\\\ c & f \\end{vmatrix}}{\\begin{vmatrix} a & b \\\\ c & d \\end{vmatrix}}$- 行列式的性质:交换行列式的两行(列):行列式的值不变某行(列)全部乘以常数k:行列式的值乘以k某行(列)的倍加到另一行(列)上去:行列式的值不变以上只是文科数学常见的一些公式总结,各个学校或老师的教学内容可能会有所不同。
高中文科数学知识点全总结

高中文科数学知识点全总结1、常用数学公式表(1)乘法与因式分解a2-b2=(a+b)(a-b);a3+b3=(a+b)(a2-ab+b2);a3-b3=(a-b)(a2+ab+b2)。
(2)三角不等式|a+b|≤|a|+|b|;|a-b|≤|a|+|b|;|a|≤b-b≤a≤b;|a-b|≥|a|-|b|-|a|≤a≤|a|。
(3)一元二次方程的解:-b+√(b2-4ac)/2a-b-b+√(b2-4ac)/2a。
(4)根与系数的关系:x1+x2=-b/ax1*x2=c/a,备注:韦达定理。
(5)判别式1)b2-4a=0,备注:方程存有成正比的两实根。
2)b2-4ac\ue0,注:方程有一个实根。
3)b2-4ac\uc0,备注:方程存有共轭复数根。
2、三角函数公式(1)两角和公式sin(a+b)=sinacosb+cosasinb;sin(a-b)=sinacosb-sinbcosa;cos(a+b)=cosacosb-sinasinb;cos(a-b)=cosacosb+sinasinb;tan(a+b)=(tana+tanb)/(1-tanatanb);tan(a-b)=(tana-tanb)/(1+tanatanb);ctg(a+b)=(ctgactgb-1)/(ctgb+ctga);ctg(a-b)=(ctgactgb+1)/(ctgb-ctga)。
(2)倍角公式tan2a=2tana/(1-tan2a);ctg2a=(ctg2a-1)/2ctga;cos2a=cos2a-sin2a=2cos2a-1=1-2sin2a。
(3)半角公式sin(a/2)=√((1-cosa)/2);sin(a/2)=-√((1-cosa)/2);cos(a/2)=√((1+cosa)/2);cos(a/2)=-√((1+cosa)/2);tan(a/2)=√((1-cosa)/((1+cosa));tan(a/2)=-√((1-cosa)/((1+cosa));ctg(a/2)=√((1+cosa)/((1-cosa));ctg(a/2)=-√((1+cosa)/((1-cosa))。
高三文科数学公式总结

高三文科数学公式总结
高三文科数学公式是高中数学学习中,非常重要的部分。
它们不仅是解决高等数学问题的必要工具,而且也是理解数学的基础。
高三的数学公式总结,将帮助学生更加全面深入地学习数学。
一、几何公式
(1)直角三角形
直角三角形面积公式:S=1/2*a*b
直角三角形内角和公式:a+b+90=180
(2)圆形
圆形面积公式:S=pi*r^2
圆形周长公式:C=2*pi*r
(3)四边形的面积公式:S=a*b*sinC
二、代数公式
(1)一元二次方程
一元二次方程的解公式:
x=(-b±√b^2-4ac)÷2a
(2)二元一次方程的解公式
联立一元二次方程无理解方法:
x=(c2-b2)/(2a2) y=(c1-b1)/(2a1)
(3)有理函数的定义域公式:D = {x | P(x)≠0}
三、概率统计公式
(1)互斥事件概率公式
p(A1∪A2∪A3)=p(A1)+p(A2)+p(A3)
(2)条件概率公式
p(A|B)=p(A∩B)/p(B)
(3)独立事件概率公式
p(A∩B)=p(A)*p(B)
四、时间函数公式
(1)速度公式
v=s/t
(2)加速度公式
a=Δv/Δt
(3)动量公式
p=m*v
以上就是高三文科数学公式总结,它们在高中数学学习中都有着重要的作用,对于学生而言,考前熟练掌握各种公式也会大有裨益,从而更加深入地学习数学。
高中数学公式大全文科

高中数学公式大全文科1.代数运算公式:(1) 二项式公式:(a + b)^2 = a^2 + 2ab + b^2,(a - b)^2 = a^2 - 2ab + b^2,(a + b)(a - b) = a^2 - b^2(2) 平方差公式:(a + b)^2 - (a - b)^2 = 4ab(3) 证明等式:(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3,(a -b)^3 = a^3 - 3a^2b + 3ab^2 - b^3(4)等比数列求和:S_n=a(1-q^n)/(1-q),其中a为首项,q为公比,n为项数(5) 二次根式相加:√a + √b = √(a + b + 2√ab)(6)三次方程和四次方程的求根公式2.几何公式:(1) 三角形面积公式:S = 1/2 * a * b * sinC,其中a,b为两边的长度,C为两边夹角的度数(2) 三角形边长关系:a/sinA = b/sinB = c/sinC = 2R,其中R为外接圆半径(3) 三角函数的和与差的公式:sin(A ± B) = sinAcosB ± cosAsinB,cos(A ± B) = cosAcosB ∓ sinAsinB,tan(A ± B) = (tanA ± tanB)/(1 ∓ tanAtanB)(4) 三角函数的倍角公式:sin2A = 2sinAcosA,cos2A = cos^2A - sin^2A = 2cos^2A - 1 = 1 - 2sin^2A,tan2A = (2tanA)/(1 - tan^2A)(5)圆的面积公式:S=πr^2,其中r为半径(6)圆的周长公式:C=2πr,其中r为半径3.概率与统计公式:(1)加法原理:P(A∪B)=P(A)+P(B)-P(A∩B),其中P(A)为事件A发生的概率,P(B)为事件B发生的概率,P(A∩B)为事件A与事件B同时发生的概率(2)乘法原理:P(A∩B)=P(A)×P(B,A),其中P(A)为事件A发生的概率,P(B,A)为在事件A发生的条件下事件B发生的概率(3)期望:E(X)=μ=∑(xP(x)),其中X为随机变量,x为随机变量X 的取值,P(x)为X取值为x的概率(4) 方差:Var(X) = σ^2 = E((X - μ)^2),其中E为期望,σ^2为方差,(X - μ)^2为随机变量X与其期望之差的平方以上是高中数学文科相关的一些公式,但由于篇幅有限,可能并未包含所有相关的公式。
高中数学公式及知识点总结大全(精华版)

高中文科数学公式及知识点速记一、函数、导数1、函数的单调性(1)设2121],,[x x b a x x <∈、那么],[)(0)()(21b a x f x f x f 在⇔<−上是增函数; ],[)(0)()(21b a x f x f x f 在⇔>−上是减函数.(2)设函数)(x f y =在某个区间内可导,若0)(>'x f ,则)(x f 为增函数;若0)(<'x f ,则)(x f 为减函数.2、函数的奇偶性对于定义域内任意的x ,都有)()(x f x f =−,则)(x f 是偶函数; 对于定义域内任意的x ,都有)()(x f x f −=−,则)(x f 是奇函数。
奇函数的图象关于原点对称,偶函数的图象关于y 轴对称。
3、函数)(x f y =在点0x 处的导数的几何意义函数)(x f y =在点0x 处的导数是曲线)(x f y =在))(,(00x f x P 处的切线的斜率)(0x f ',相应的切线方程是))((000x x x f y y −'=−.*二次函数: (1)顶点坐标为24(,)24b ac b a a −−;(2)焦点的坐标为241(,)24b ac b a a−+− 4、几种常见函数的导数 ①'C 0=;②1')(−=n n nxx ; ③x x cos )(sin '=;④x x sin )(cos '−=;⑤a a a xx ln )('=;⑥xx e e =')(; ⑦a x x a ln 1)(log '=;⑧xx 1)(ln '= 5、导数的运算法则(1)'''()u v u v ±=±. (2)'''()uv u v uv =+. (3)'''2()(0)u u v uv v v v −=≠. 6、会用导数求单调区间、极值、最值7、求函数()y f x =的极值的方法是:解方程()0f x '=.当()00f x '=时: (1) 如果在0x 附近的左侧()0f x '>,右侧()0f x '<,那么()0f x 是极大值; (2) 如果在0x 附近的左侧()0f x '<,右侧()0f x '>,那么()0f x 是极小值. 指数函数、对数函数分数指数幂(1)m na =0,,a m n N *>∈,且1n >).(2)1m nm naa−==(0,,a m n N *>∈,且1n >).根式的性质(1)当na =; 当n,0||,0a a a a a ≥⎧==⎨−<⎩.有理指数幂的运算性质(1) r sa a⋅=(2) ()r s rsa a=(3)()r rab a b=注:若a>0,指数幂都适用..(0,1,0)a a N>≠>..1a≠,0m>,且1m≠,0N>).对数恒等式:).推论logmnab).常见的函数图象822sin cosθθ+9απ±kα看成锐角时该函数的符号;αππ±+2kα看成锐角时该函数的符号。
高中文科数学公式大全(精华版)

高中数学公式及知识点速记1、函数的单调性(1)设1212[,],x x a b x x ∈<、且那么],[)(0)()(21b a x f x f x f 在⇔<-上是增函数; ],[)(0)()(21b a x f x f x f 在⇔>-上是减函数. (2)设函数)(x f y =在某个区间内可导,若0)(>'x f ,则)(x f 为增函数; 若0)(<'x f ,则)(x f 为减函数; 若()=0f x ',则)(x f 有极值。
2、函数的奇偶性若)()(x f x f =-,则)(x f 是偶函数;偶函数的图象关于y 轴对称。
若)()(x f x f -=-,则)(x f 是奇函数;奇函数的图象关于原点对称。
3、函数)(x f y =在点0x 处的导数的几何意义函数)(x f y =在点0x 处的导数)(0x f '是曲线)(x f y =在))(,(00x f x P 处的切线的斜率,相应的切线方程是))((000x x x f y y -'=-.4、几种常见函数的导数①'C 0=; ②1')(-=n n nx x ; ③x x cos )(sin '=; ④x x sin )(cos '-=; ⑤a a a x x ln )('=; ⑥x x e e =')(; ⑦a x x a ln 1)(log '=; ⑧xx 1)(ln '= 5、导数的运算法则(1)'''()u v u v ±=±. (2)'''()uv u v uv =+.(3)'''2()u u v uv v v-=. 6、求函数()y f x =的极值的方法是:解方程()0f x '=得0x .当()00f x '=时:① 如果在0x 附近的左侧()0f x '>,右侧()0f x '<,那么()0f x 是极大值; ② 如果在0x 附近的左侧()0f x '<,右侧()0f x '>,那么()0f x 是极小值. 7、分数指数幂(1)mna =.(2)1m nm naa-==.8、根式的性质 (1)n a =.(2)当na =;当n,0||,0a a a a a ≥⎧==⎨-<⎩.9、有理指数幂的运算性质 (1)rs r s aa a +⋅=;(2)()r srsa a =;(3)()r r rab a b =. 10、对数公式(1)指数式与对数式的互化式: log b a N b a N =⇔=。
高中文科数学公式及知识点总结大全(精华版).doc

高中文科数学公式及知识点速记一、函数、导数1、函数的单调性(1)设2121],,[x x b a x x <∈、那么],[)(0)()(21b a x f x f x f 在⇔<-上是增函数; ],[)(0)()(21b a x f x f x f 在⇔>-上是减函数.(2)设函数)(x f y =在某个区间内可导,若0)(>'x f ,则)(x f 为增函数;若0)(<'x f ,则)(x f 为减函数.2、函数的奇偶性对于定义域内任意的x ,都有)()(x f x f =-,则)(x f 是偶函数; 对于定义域内任意的x ,都有)()(x f x f -=-,则)(x f 是奇函数。
奇函数的图象关于原点对称,偶函数的图象关于y 轴对称。
3、函数)(x f y =在点0x 处的导数的几何意义函数)(x f y =在点0x 处的导数是曲线)(x f y =在))(,(00x f x P 处的切线的斜率)(0x f ',相应的切线方程是))((000x x x f y y -'=-.*二次函数: (1)顶点坐标为24(,)24b ac b a a --;(2)焦点的坐标为241(,)24b ac b a a-+- 4、几种常见函数的导数①'C 0=;②1')(-=n n nx x ; ③x x cos )(sin '=;④x x sin )(cos '-=;⑤a a a x x ln )('=;⑥xx e e =')(; ⑦a x x a ln 1)(log '=;⑧xx 1)(ln '= 5、导数的运算法则(1)'''()u v u v ±=±. (2)'''()uv u v uv =+. (3)'''2()(0)u u v uv v v v -=≠. 6、会用导数求单调区间、极值、最值7、求函数()y f x =的极值的方法是:解方程()0f x '=.当()00f x '=时: (1) 如果在0x 附近的左侧()0f x '>,右侧()0f x '<,那么()0f x 是极大值; (2) 如果在0x 附近的左侧()0f x '<,右侧()0f x '>,那么()0f x 是极小值. 指数函数、对数函数分数指数幂(1)m na =0,,a m n N *>∈,且1n >).(2)1m nm naa-==0,,a m n N *>∈,且1n >).根式的性质(1)当na =; 当n,0||,0a a a a a ≥⎧=⎨-<⎩.有理指数幂的运算性质(1) r sa a⋅=(2) ()r s rsa a=(3)()r rab a b=注:若a>0,指数幂都适用..(0,1,0)a a N>≠>..1a≠,0m>,且1m≠,0N>).对数恒等式:).推论log m nab).常见的函数图象822sin cosθθ+9απ±kα看成锐角时该函数的符号;αππ±+2kα看成锐角时该函数的符号。
高中数学文科公式表重要公式记忆版
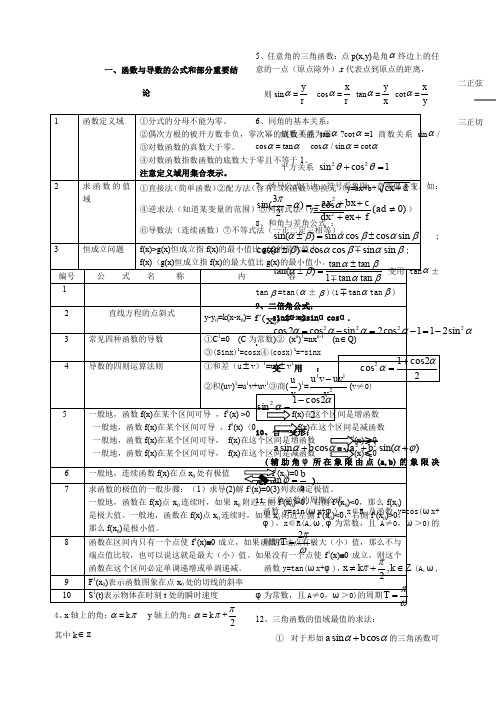
一、函数与导数的公式和部分重要结论1函数定义域①分式的分母不能为零。
②偶次方根的被开方数非负,零次幂的底数不能为零。
③对数函数的真数大于零。
④对数函数指数函数的底数大于零且不等于1。
注意定义域用集合表示。
2求函数的值域①直接法(简单函数)②配方法(含有二次函数)③换元 (y=ax+b+d cx +)④逆求法(知道某变量的范围)⑤判别式法(y=)0(22≠++++ad fex dx c bx ax )⑥导数法(连续函数)⑦不等式法(一正二定三相等)。
3 恒成立问题 f(x)>g(x)恒成立指f(x)的最小值比g(x)的最大值大。
f(x)〈g(x)恒成立指f(x)的最大值比g(x)的最小值小。
编号 公 式 名 称 内 容 1 2 直线方程的点斜式 y-y 0=k(x-x 0)=0()f x ' (x-x 0)3 常见四种函数的导数 ①C 1=0 (C 为常数)② (x n )1=nx n-1(n ∈Q)③(Sinx)1=cosx ④(cosx)1=-sinx4导数的四则运算法则①和差(u ±v )1=u 1±v 1 ②积(uv)1=u 1v+uv 1③商(v u )1=211v uv v u -(v ≠0)5一般地,函数f(x)在某个区间可导 ,f 1(x) >0 f(x)在这个区间是增函数 一般地,函数f(x)在某个区间可导 ,f 1(x)〈0 f(x)在这个区间是减函数一般地,函数f(x)在某个区间可导, f(x)在这个区间是增函数 f 1(x)≥0 一般地,函数f(x)在某个区间可导, f(x)在这个区间是减函数 f 1(x)≤06 一般地,连续函数f(x)在点x 0处有极值 f 1(x 0)=0 7求函数的极值的一般步骤:(1)求导(2)解f 1(x)=0(3)列表确定极值。
一般地,函数在f(x)点x 0连续时,如果x 0附近左侧f 1(x 0)>0,右侧f 1(x 0)<0,那么f(x 0)是极大值。
高中文科数学公式大全(完美版)-高中文科数学公式

高三文科数学公式及知识点一、函数、导数1、函数的单调性(1)设2121],,[x x b a x x <∈、那么],[)(0)()(21b a x f x f x f 在⇔<-上是增函数;],[)(0)()(21b a x f x f x f 在⇔>-上是减函数.(2)设函数)(x f y =在某个区间内可导,若0)(>'x f ,则)(x f 为增函数;若0)(<'x f ,则)(x f 为减函数.2、函数的奇偶性对于定义域内任意的x ,都有)()(x f x f =-,则)(x f 是偶函数;对于定义域内任意的x ,都有)()(x f x f -=-,则)(x f 是奇函数。
奇函数的图象关于原点对称,偶函数的图象关于y 轴对称。
3、函数)(x f y =在点0x 处的导数的几何意义函数)(x f y =在点0x 处的导数是曲线)(x f y =在))(,(00x f x P 处的切线的斜率)(0x f ',相应的切线方程是))((000x x x f y y -'=-.4、几种常见函数的导数①'C 0=;②1')(-=n n nx x ; ③x x cos )(sin '=;④x x sin )(cos '-=;⑤a a a x x ln )('=;⑥x x e e =')(; ⑦ax x a ln 1)(log '=;⑧x x 1)(ln '= 5、导数的运算法则(1)'''()u v u v ±=±. (2)'''()uv u v uv =+. (3)'''2()(0)u u v uv v v v -=≠. 6、会用导数求单调区间、极值、最值7、求函数()y f x =的极值的方法是:解方程()0f x '=.当()00f x '=时:(1) 如果在0x 附近的左侧()0f x '>,右侧()0f x '<,那么()0f x 是极大值;(2) 如果在0x 附近的左侧()0f x '<,右侧()0f x '>,那么()0f x 是极小值.二、三角函数、三角变换、解三角形、平面向量8、同角三角函数的基本关系式22sin cos 1θθ+=,tan θ=θθcos sin . 10、和角与差角公式 sin()sin cos cos sin αβαβαβ±=±;cos()cos cos sin sin αβαβαβ±=;tan tan tan()1tan tan αβαβαβ±±=.11、二倍角公式sin 2sin cos ααα=.2222cos 2cos sin 2cos 112sin ααααα=-=-=-.22tan tan 21tan ααα=-. 公式变形: ;22cos 1sin ,2cos 1sin 2;22cos 1cos ,2cos 1cos 22222αααααααα-=-=+=+= 12、三角函数的周期函数sin()y x ωϕ=+,cos()y x ωϕ=+,x ∈R 的周期2T πω=; 函数tan()y x ωϕ=+,,2x k k Z ππ≠+∈的周期T πω=. 13、 函数sin()y x ωϕ=+的周期、最值、单调区间、图象变换14、辅助角公式)sin(cos sin 22ϕ++=+=x b a x b x a y 其中ab =ϕtan 15、正弦定理 2sin sin sin a b c R A B C===. 16、余弦定理2222cos a b c bc A =+-;2222cos b c a ca B =+-;2222cos c a b ab C =+-.17、三角形面积公式111sin sin sin 222S ab C bc A ca B ===. 18、三角形内角和定理在△ABC 中,有()A B C C A B ππ++=⇔=-+19、与的数量积(或内积)θcos ||||⋅=⋅20、平面向量的坐标运算(1)设A 11(,)x y ,B 22(,)x y ,则2121(,)AB OB OA x x y y =-=--.(2)设a =11(,)x y ,b =22(,)x y ,则b a ⋅=2121y y x x +.(3)设a =),(y x ,则22y x a +=21、两向量的夹角公式 设=11(,)x y ,=22(,)x y ,且≠,则 222221212121cos y x y x y y x x b a ba +⋅++=⋅=θ22、向量的平行与垂直//⇔λ=12210x y x y ⇔-=.)0(≠⊥a b a ⇔0=⋅b a 12120x x y y ⇔+=.三、数列23、数列的通项公式与前n 项的和的关系11,1,2n n n s n a s s n -=⎧=⎨-≥⎩ 24、等差数列的通项公式*11(1)()n a a n d dn a d n N =+-=+-∈;25、等差数列其前n 项和公式为1()2n n n a a s +=1(1)2n n na d -=+ 26、等比数列的通项公式1*11()n n n a a a q q n N q-==⋅∈; 27、等比数列前n 项的和公式为11(1),11,1n n a q q s q na q ⎧-≠⎪=-⎨⎪=⎩ 或 11,11,1n n a a q q q s na q -⎧≠⎪-=⎨⎪=⎩.四、不等式28、已知y x ,都是正数,则有xy y x ≥+2,当y x =时等号成立。
高中文科数学公式大全(完整完全精华版)

高中数学公式及知识点速记1、函数的单调性(1)设1212[,],x x a b x x ∈<、且那么],[)(0)()(21b a x f x f x f 在⇔<-上是增函数; ],[)(0)()(21b a x f x f x f 在⇔>-上是减函数.(2)设函数)(x f y =在某个区间内可导,若0)(>'x f ,则)(x f 为增函数; 若0)(<'x f ,则)(x f 为减函数; 若()=0f x ',则)(x f 有极值。
2、函数的奇偶性若)()(x f x f =-,则)(x f 是偶函数;偶函数的图象关于y 轴对称。
若)()(x f x f -=-,则)(x f 是奇函数;奇函数的图象关于原点对称。
3、函数)(x f y =在点0x 处的导数的几何意义函数)(x f y =在点0x 处的导数)(0x f '是曲线)(x f y =在))(,(00x f x P 处的切线的斜率,相应的切线方程是))((000x x x f y y -'=-. 4、几种常见函数的导数①'C 0=; ②1')(-=n n nx x ; ③x x cos )(sin '=; ④x x sin )(cos '-=; ⑤a a a x x ln )('=; ⑥x x e e =')(; ⑦a x x a ln 1)(log '=; ⑧xx 1)(ln '= 5、导数的运算法则(1)'''()u v u v ±=±. (2)'''()uv u v uv =+.(3)'''2()u u v uv v v-=. 6、求函数()y f x =的极值的方式是:解方程()0f x '=得0x .当()00f x '=时:① 若是在0x 周围的左侧()0f x '>,右边()0f x '<,那么()0f x 是极大值; ② 若是在0x 周围的左侧()0f x '<,右边()0f x '>,那么()0f x 是极小值. 7、分数指数幂(1)mna =.(2)1m nm naa-==.八、根式的性质(1)n a =.(2)当na =;当n,0||,0a a a a a ≥⎧==⎨-<⎩.九、有理指数幂的运算性质 (1)rs r s aa a +⋅=;(2)()r srsa a =;(3)()r r rab a b =. 10、对数公式(1)指数式与对数式的互化式: log b a N b a N =⇔=。
高中文科数学公式

高中文科数学公式
以下是一些常见的高中文科数学公式:
1.一次函数的方程:y = kx + b,其中 k 为斜率,b 为截距。
2.二次函数的方程:y = ax^2 + bx + c,其中 a、b、c 为常数。
3.立方函数的方程:y = ax^3 + bx^2 + cx + d,其中 a、
b、c、d 为常数。
4.指数函数的方程:y = a^x,其中 a 为底数。
5.对数函数的方程:y = loga(x),其中 a 为底数。
6.三角函数的方程:sin(x)、cos(x)、tan(x)、csc(x)、
sec(x)、cot(x)等。
7.平面几何中的勾股定理:a^2 + b^2 = c^2,其中 a、b、
c 分别为直角三角形的两个直角边和斜边的长度。
8.平面几何中的正弦定理:a/sinA = b/sinB = c/sinC,其中 a、b、c 为三角形的边长,A、B、C为对应的角度。
9.平面几何中的余弦定理:c^2 = a^2 + b^2 - 2abcosC,其中 a、b、c 为三角形的边长,C为夹角。
10.概率计算中的排列公式:P(n, r) = n!/(n-r)!,其中 n 为总数,r 为选取的数目。
以上是一些常见的高中文科数学公式,希望能够帮到你。
文科高考数学必背公式

文科高考数学必背公式在文科高考中,数学是一个重要的科目。
虽然数学不是文科生的强项,但是通过对一些必背公式的掌握,可以在考试中取得更好的成绩。
以下是文科高考数学必背公式。
1. 一次函数的表达式:y = kx + b。
其中,k为斜率,b为截距。
2. 二次函数的标准形式:y = ax² + bx + c。
其中,a、b、c为常数,且a≠0。
3. 二次函数的顶点坐标:顶点的横坐标为x = -b/2a,纵坐标为y = -Δ/4a。
其中,Δ为判别式,Δ = b² - 4ac。
4.一元二次方程的解:解为x=(-b±√Δ)/2a。
5.二次函数的对称轴方程:x=-b/2a。
6. 三角函数的定义:sinθ = 对边/斜边,cosθ = 邻边/斜边,tanθ = 对边/邻边。
7. 三角函数的正负关系:sinθ、tanθ在0~π范围内非负,cosθ在π/2时为0,在0~π/2范围内非负,在π/2~π范围内非正。
8. 三角函数的周期性:sin(θ ± 2πn) = sinθ,cos(θ ± 2πn) = cosθ,tan(θ ± πn) = tanθ。
其中,n为整数。
9. 三角函数的和差化积公式:sin(A ± B) = sinAcosB ± cosAsinB,cos(A ± B) = cosAcosB ∓ sinAsinB。
10. 三角函数的倍角公式:sin2θ = 2sinθcosθ,cos2θ =cos²θ - sin²θ,tan2θ = (2tanθ) / (1 - tan²θ)。
11.平面几何中的相似三角形:对应角相等,对应边成比例。
12.平行线的性质:同位角互等、内错角互补、同旁内角互补。
13. 同余式的性质:如果a≡b (mod m),则a±c≡b±c (mo d m),ac≡bc (mod m)。
高三文科数学公式总结

高三文科数学公式总结在高三年级,学生需要参加高考,数学是其中一个重要的课程。
随着数学的进一步学习,学生将接触到更加复杂的内容,有必要对所学的公式做出总结,将重点公式及其应用做出总结,方便查阅和运用。
针对高三文科数学的学习,下面就重点公式做出总结:一、指数函数的几何意义1.物线:指数函数f(x) = a^x (a>0)的图象是一条开口向上的抛物线,当a>1时,抛物线上表示增长,当0<a<1时,抛物线上表示减小。
2.称轴:指数函数f(x) = a^x (a>0)的图象有一个关于y轴对称的对称轴(x = 0)。
3.凸性:指数函数f(x) = a^x (a>0)的图象是凹凸性的,并且当a>1时,凹凸性是“凹”的,当0<a<1时,凹凸性是“凸”的。
二、对数函数的几何意义1.数函数f(x) = lnx,其图象是一条开口向下的抛物线,表示减小。
2.于y轴对称的对称轴(x = 1)。
3.凸性是“凹”的,凹凸性表示减小。
三、三角函数的几何意义1.弦函数、余弦函数和正切函数的图象分别是一个x轴为首部的正弦曲线、余弦曲线和正切曲线。
2.称轴:正弦函数的对称轴是y轴,余弦函数的对称轴是x轴,正切函数的对称轴是x =/2和x = 3π/2。
3.凸性:三角函数的凹凸性是“凹”的,表示减小。
四、几何图像判断1.果一个图象是一条开口向上的抛物线,则该图象可能是指数函数的图象;2.果一个图象是一条开口向下的抛物线,则该图象可能是对数函数的图象;3.果一个图象是一个x轴为首部的正弦曲线、余弦曲线或正切曲线,则该图象是三角函数的图象。
总之,高三文科数学的学习是一个比较复杂的过程,其中涉及到了很多的重要公式及其几何意义。
本文对于高三文科数学的重点公式做出了总结,从而帮助学生更好地理解其几何意义,更好地运用其公式,方便查阅和重新记忆。
公式大全 文科版
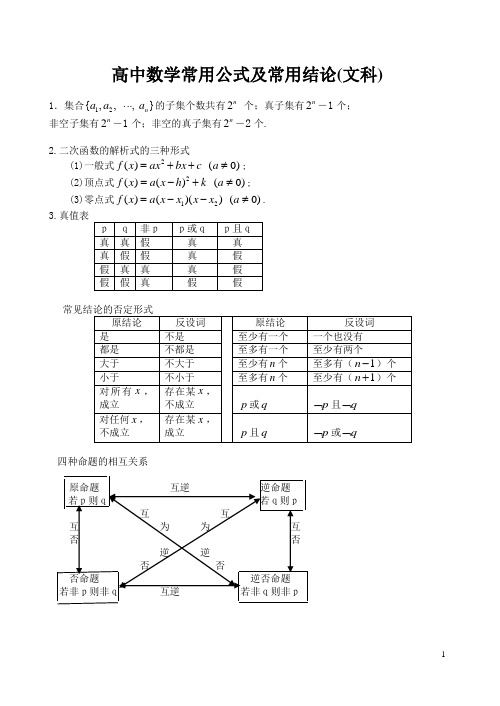
高中数学常用公式及常用结论(文科)1.集合12{,, , }n a a a ⋅⋅⋅的子集个数共有2n 个;真子集有2n -1个; 非空子集有2n -1个;非空的真子集有2n -2个.2.二次函数的解析式的三种形式(1)一般式2() (0)f x ax bx c a =++≠; (2)顶点式2()() (0)f x a x h k a =-+≠; (3)零点式12()()() (0)f x a x x x x a =--≠. 3.真值表四种命题的相互关系充要条件(1)充分条件:若p q ⇒,则p 是q 充分条件.(2)必要条件:若q p ⇒,则p 是q 必要条件.(3)充要条件:若p q ⇒,且q p ⇒,则p 是q 充要条件.注:如果甲是乙的充分条件,则乙是甲的必要条件;反之亦然.4.函数的单调性(1)设[]2121,,x x b a x x ≠∈⋅那么[]1212()()()0x x f x f x -->⇔[]b a x f x x x f x f ,)(0)()(2121在⇔>--上是增函数;[]1212()()()0x x f x f x --<⇔[]b a x f x x x f x f ,)(0)()(2121在⇔<--上是减函数.(2)设函数)(x f y =在某个区间内可导,如果0)(>'x f ,则)(x f 为增函数;如果0)(<'x f ,则)(x f 为减函数.5.如果函数)(x f 和)(x g 都是减函数,则在公共定义域内,和函数)()(x g x f +也是减函数; 如果函数)(u f y =和)(x g u =在其对应的定义域上都是减函数,则复合函数)]([x g f y =是增函数.6.奇偶函数的图象特征奇函数的图象关于原点对称,偶函数的图象关于y 轴对称;反过来,如果一个函数的图象关于原点对称,那么这个函数是奇函数;如果一个函数的图象关于y 轴对称,那么这个函数是偶函数.7.若函数)(x f y =是偶函数,则)()(a x f a x f --=+;若函数)(a x f y +=是偶函数,则)()(a x f a x f +-=+.若函数)(x f y =是奇函数,则()()f x a f x a --=-+;若函数)(a x f y +=是奇函数,则()()f x a f x a -+=-+.8.对于函数)(x f y =(R x ∈),)()(x b f a x f -=+恒成立,则函数)(x f 的对称轴是函数2b a x +=;两个函数)(a x f y +=与)(x b f y -= 的图象关于直线2ba x +=对称.9.若)()(a x f x f +--=,则函数)(x f y =的图象关于点)0,2(a对称; 若)()(a x f x f +-=,则函数)(x f y =为周期为a 2的周期函数.10.多项式函数110()n n n n P x a x a xa --=++⋅⋅⋅+的奇偶性多项式函数()P x 是奇函数⇔()P x 的偶次项(即奇数项)的系数全为零. 多项式函数()P x 是偶函数⇔()P x 的奇次项(即偶数项)的系数全为零.11.函数()y f x =的图象的对称性(1)函数()y f x =的图象关于直线x a =对称()()f a x f a x ⇔+=-(2)()f a x f x ⇔-=.(2)函数()y f x =的图象关于直线2a bx +=对称()()f a mx f b mx ⇔+=- ()()f a b mx f mx ⇔+-=.12.两个函数图象的对称性(1)函数()y f x =与函数()y f x =-的图象关于直线0x =(即y 轴)对称.(2)函数)(x f y =和)(1x fy -=的图象关于直线y=x 对称.13.若将函数)(x f y =的图象右移a 、上移b 个单位,得到函数b a x f y +-=)(的图象;若将曲线0),(=y x f 的图象右移a 、上移b 个单位,得到曲线0),(=--b y a x f 的图象.14.互为反函数的两个函数的关系 a b f b a f =⇔=-)()(1.15.几个常见的函数方程(1)正比例函数()f x cx =,()()(),(1)f x y f x f y f c +=+=.(2)指数函数()xf x a =,()()(),(1)0f x y f x f y f a +==≠.(3)对数函数()log a f x x =,()()(),()1(0,1)f xy f x f y f a a a =+=>≠. (4)幂函数()f x x α=,()()(),(1)f xy f x f y f α==.16.几个函数方程的周期(约定a>0)(1))()(a x f x f +=,则)(x f 的周期T=a ;(2)0)()(=+=a x f x f ,或)0)(()(1)(≠=+x f x f a x f , 或1()()f x a f x +=-(()0)f x ≠,则)(x f 的周期T=2a ;17.分数指数幂(1)m na =0,,a m n N *>∈,且1n >).(2)1m nm naa-==0,,a m n N *>∈,且1n >).18.根式的性质(1)na =.(2)当na =; 当n,0||,0a a a a a ≥⎧==⎨-<⎩.19.指数式与对数式的互化式log b a N b a N =⇔=(0,1,0)a a N >≠>.20.对数的换底公式log log log m a m NN a=(0a >,且1a ≠,0m >,且1m ≠, 0N >).推论 log log m n a a nb b m =(0a >,且1a >,,0m n >,且1m ≠,1n ≠, 0N >).21.对数的四则运算法则若a >0,a ≠1,M >0,N >0,则 (1)log ()log log a a a MN M N =+;(2) log log log aa a MM N N =-; (3)log log ()na a M n M n R =∈.对数恒等式 log a N a N =22.设函数)0)((log )(2≠++=a c bx ax x f m ,记ac b 42-=∆. 若)(x f 的定义域为R ,则0>a ,且0<∆;若)(x f 的值域为R ,则0>a ,且0≥∆.对于0=a 的情形,需要单独检验.23. 平均增长率的问题如果原来产值的基础数为N ,平均增长率为p ,则对于时间x 的总产值y ,有(1)x y N p =+.24.数列的同项公式与前n 项的和的关系11,1,2n n n s n a s s n -=⎧=⎨-≥⎩( 数列{}n a 的前n 项的和为12n n s a a a =++⋅⋅⋅+).25.等差数列的通项公式*11(1)()n a a n d dn a d n N =+-=+-∈;其前n 项和公式为1()2n n n a a s +=1(1)2n n na d -=+ 211()22d n a d n =+-.26.等比数列的通项公式1*11()n nn a a a q q n N q-==⋅∈; 其前n 项的和公式为11(1), 11, 1n n a q q s q na q ⎧-≠⎪=-⎨⎪=⎩ 或11, 11, 1n n a a qq q s na q -⎧≠⎪-=⎨⎪=⎩.27.同角三角函数的基本关系式22sin cos 1θθ+=,tan θ=θθcos sin ,tan 1cot θθ⋅=. 诱导公式可用十个字概括为“奇变偶不变,符号看象限”。
高三文科数学公式大全

高三文科数学公式大全数学公式是人类长期生产劳动的经验总结,包含着历代数学家辛勤汗水和智慧,它揭示了数学知识的基本规律,是学生数学认知发展的重要载体。
学习数学,前提就是对公式和定理有着正确透彻的理解。
牢固掌握并灵活运用公式定理是提高数学能力的关键。
以下是店铺为大家精心准备的:高三文科数学公式大全。
欢迎参考阅读!高三文科数学公式大全如下:一、对数函数log.a(MN)=logaM+logNloga(M/N)=logaM-logaNlogaM^n=nlogaM(n=R)logbN=logaN/logab(a>0,b>0,N>0 a、b均不等于1)二、简单几何体的面积与体积S直棱柱侧=c*h(底面周长乘以高)S正棱椎侧=1/2*c*h′(底面的周长和斜高的一半)设正棱台上、下底面的周长分别为c′,c,斜高为h′,S=1/2*(c+c′)*hS圆柱侧=c*lS圆台侧=1/2*(c+c′)*l=兀*(r+r′)*lS圆锥侧=1/2*c*l=兀*r*lS球=4*兀*R^3V柱体=S*hV锥体=(1/3)*S*hV球=(4/3)*兀*R^3三、两直线的位置关系及距离公式(1)数轴上两点间的距离公式|AB|=|x2-x1|(2) 平面上两点A(x1,y1),(x2,y2)间的距离公式|AB|=sqr[(x2-x1)^2+(y2-y1)^2](3) 点P(x0,y0)到直线l:Ax+By+C=0的距离公式d=|Ax0+By0+C|/sqr(A^2+B^2)(4) 两平行直线l1:=Ax+By+C=0,l2=Ax+By+C2=0之间的距离d=|C1-C2|/sqr(A^2+B^2)同角三角函数的基本关系及诱导公式sin(2*k*兀+a)=sin(a)cos(2*k*兀+a)=cosatan(2*兀+a)=tanasin(-a)=-sina,cos(-a)=cosa,tan(-a)=-tanasin(2*兀-a)=-sina,cos(2*兀-a)=cosa,tan(2*兀-a)=-tanasin(兀+a)=-sinasin(兀-a)=sinacos(兀+a)=-cosacos(兀-a)=-cosatan(兀+a)=tana四、二倍角公式及其变形使用1、二倍角公式sin2a=2*sina*cosacos2a=(cosa)^2-(sina)^2=2*(cosa)^2-1=1-2*(sina)^2tan2a=(2*tana)/[1-(tana)^2]2、二倍角公式的变形(cosa)^2=(1+cos2a)/2(sina)^2=(1-cos2a)/2tan(a/2)=sina/(1+cosa)=(1-cosa)/sina五、正弦定理和余弦定理正弦定理:a/sinA=b/sinB=c/sinC余弦定理:a^2=b^2+c^2-2bccosAb^2=a^2+c^2-2accosBc^2=a^2+b^2-2abcosCcosA=(b^2+c^2-a^2)/2bccosB=(a^2+c^2-b^2)/2accosC=(a^2+b^2-c^2)/2abtan(兀-a)=-tanasin(兀/2+a)=cosasin(兀/2-a)=cosacos(兀/2+a)=-sinacos(兀/2-a)=sinatan(兀/2+a)=-cotatan(兀/2-a)=cota(sina)^2+(cosa)^2=1sina/cosa=tana两角和与差的余弦公式cos(a-b)=cosa*cosb+sina*sinbcos(a-b)=cosa*cosb-sina*sinb两角和与差的正弦公式sin(a+b)=sina*cosb+cosa*sinbsin(a-b)=sina*cosb-cosa*sinb两角和与差的正切公式tan(a+b)=(tana+tanb)/(1-tana*tanb) tan(a-b)=(tana-tanb)/(1+tana*tanb)。
高考文科数学公式总结

高考文科数学公式总结数学作为高考文科考试中的一门重要科目,公式的掌握和运用对考生来说至关重要。
下面将对高考文科数学中常用的公式进行总结,希望能帮助考生们更好地备战高考。
一、代数部分。
1. 二项式定理。
(a+b)^n = C(n,0)a^n + C(n,1)a^(n-1)b + C(n,2)a^(n-2)b^2 + ... + C(n,n-1)a b^(n-1) + C(n,n)b^n。
2. 平方差公式。
(a+b)(a-b) = a^2 b^2。
3. 一元二次方程根的判别式。
Δ = b^2 4ac。
当Δ > 0时,方程有两个不相等的实根;当Δ = 0时,方程有两个相等的实根;当Δ < 0时,方程没有实根。
二、几何部分。
1. 直线的点斜式方程。
y y₁ = k(x x₁)。
2. 三角形面积公式。
S = 1/2 × a × b × sinC。
3. 圆的面积和周长。
圆的面积 S = πr²。
圆的周长 L = 2πr。
三、概率与统计部分。
1. 排列组合公式。
排列,A(n, m) = n!/(n-m)!组合,C(n, m) = n!/(m!(n-m)!)。
2. 期望的计算。
E(X) = Σ(x×P(x))。
3. 正态分布的标准差计算。
P(a < X < b) = Φ(b) Φ(a)。
其中Φ(x)表示标准正态分布曲线下面积为x的部分。
四、导数与微积分部分。
1. 导数的基本公式。
(1) (x^n)' = nx^(n-1)。
(2) (e^x)' = e^x。
(3) (sinx)' = cosx。
(4) (cosx)' = -sinx。
2. 不定积分的基本公式。
(1) ∫x^n dx = x^(n+1)/(n+1) + C。
(2) ∫e^x dx = e^x + C。
(3) ∫sinx dx = -cosx + C。
高中文科数学公式大全(精华版)

高中数学公式及知识点速记1、函数的单调性(1)设1212[,],x x a b x x ∈<、且那么],[)(0)()(21b a x f x f x f 在⇔<-上是增函数; ],[)(0)()(21b a x f x f x f 在⇔>-上是减函数. (2)设函数)(x f y =在某个区间内可导,若0)(>'x f ,则)(x f 为增函数; 若0)(<'x f ,则)(x f 为减函数; 若()=0f x ',则)(x f 有极值。
2、函数的奇偶性若)()(x f x f =-,则)(x f 是偶函数;偶函数的图象关于y 轴对称。
若)()(x f x f -=-,则)(x f 是奇函数;奇函数的图象关于原点对称。
3、函数)(x f y =在点0x 处的导数的几何意义函数)(x f y =在点0x 处的导数)(0x f '是曲线)(x f y =在))(,(00x f x P 处的切线的斜率,相应的切线方程是))((000x x x f y y -'=-.4、几种常见函数的导数①'C 0=; ②1')(-=n n nx x ; ③x x cos )(sin '=; ④x x sin )(cos '-=; ⑤a a a x x ln )('=; ⑥x x e e =')(; ⑦a x x a ln 1)(log '=; ⑧xx 1)(ln '= 5、导数的运算法则(1)'''()u v u v ±=±. (2)'''()uv u v uv =+.(3)'''2()u u v uv v v -=.6、求函数()y f x =的极值的方法是:解方程()0f x '=得0x .当()00f x '=时:① 如果在0x 附近的左侧()0f x '>,右侧()0f x '<,那么()0f x 是极大值; ② 如果在0x 附近的左侧()0f x '<,右侧()0f x '>,那么()0f x 是极小值. 7、分数指数幂(1)m na =.(2)1m nm naa-==.8、根式的性质 (1)n a =.(2)当na =;当n,0||,0a a a a a ≥⎧==⎨-<⎩.9、有理指数幂的运算性质 (1)rs r s aa a +⋅=;(2)()r srsa a =;(3)()r r rab a b =. 10、对数公式(1)指数式与对数式的互化式: log b a N b a N =⇔=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1·集合12{,,,}n a a a 的子集个数共有2n 个;真子集有2n –1个;非空子集有2n –1个;非空的真子集有2n –2个.2.二次函数的解析式的三种形式(1)一般式2()(0)f x ax bx c a =++≠; (2)顶点式2()()(0)f x a x h k a =-+≠; (3)零点式12()()()(0)f x a x x x x a =--≠ 3.真值表4.5 (1)充分条件:若p q ⇒,则p 是q 充分条件.(2)必要条件:若q p ⇒,则p 是q 必要条件.(3)充要条件:若p q ⇒,且q p ⇒,则p 是q 充要条件. 6.函数的单调性(1)设[]2121,,x x b a x x ≠∈⋅那么[]1212()()()0x x f x f x -->⇔[]b a x f x x x f x f ,)(0)()(2121在⇔>--上是增函数;[]1212()()()0x x f x f x --<⇔[]b a x f x x x f x f ,)(0)()(2121在⇔<--上是减函数. (2)设函数)(x f y =在某个区间内可导,如果0)(>'x f ,则)(x f 为增函数;如果0)(<'x f ,则)(x f 为减函数.7·)()(x f x f =-则)(x f 是偶函数;)()(x f x f -=-,则)(x f 是奇函数8·对于函数)(x f y =(R x ∈),)()(x b f a x f -=+恒成立,则函数)(x f 的对称轴是函数2b a x +=9.若)()(a x f x f +--=,则函数)(x f y =的图象关于点)0,2(a对称; 若)()(a x f x f +-=,则函数)(x f y =为周期为a 2的周期函数. 10 .函数()y f x =的图象的对称性(1)函数()y f x =的图象关于直线x a =对称()()f a x f a x ⇔+=- (2)()f a x f x ⇔-=.(2)函数()y f x =的图象关于直线2a bx +=对称()()f a mx f b mx ⇔+=- ()()f a b mx f mx ⇔+-=.11. 函数的导数①'C 0=;②1')(-=n n nxx ; ③x x cos )(sin '=;④x x sin )(cos '-=;⑤a a a xx ln )('=;⑥x x e e =')(; ⑦a x x a ln 1)(log '=;⑧xx 1)(ln '= 导数的运算法则(1)'''()u v u v ±=±. (2)'''()uv u v uv =+. (3)'''2()(0)u u v uv v v v -=≠ 函数()y f x =的极值,()0f x '=.当()00f x '=时:(1) 如果在0x 附近的左侧()0f x '>,右侧()0f x '<,那么()0f x 是极大值; (2) 如果在0x 附近的左侧()0f x '<,右侧()0f x '>,那么()0f x 是极小值.12 .若将函数)(x f y =的图象右移a 、上移b 个单位,得到函数b a x f y +-=)(的图象;若将曲线0),(=y x f 的图象右移a 、上移b 个单位,得到曲线0),(=--b y a x f 的图象. 13.互为反函数的两个函数的关系a b f b a f =⇔=-)()(114.几个常见的函数方程(1)正比例函数()f x cx =,()()(),(1)f x y f x f y f c +=+=.(2)指数函数()xf x a =,()()(),(1)0f x y f x f y f a +==≠.(3)对数函数()log a f x x =,()()(),()1(0,1)f xy f x f y f a a a =+=>≠.(4)幂函数()f x x α=,'()()(),(1)f xy f x f y f α==.(5)余弦函数()cos f x x =,正弦函数()sin g x x =,()()()()()f x y f x f y g x g y -=+,()(0)1,lim1x g x f x→==. 15.分数指数幂(1)m na =(0,,a m n N *>∈,且1n >). (2)1m nm naa-=(0,,a m n N *>∈且1n >).根式的性质(1)na =.(2)当na =;当n,0||,0a a a a a ≥⎧==⎨-<⎩有理指数幂的运算 1) (0,,)rsr sa a aa r s Q +⋅=>∈.(2) ()(0,,)r s rsa a a r s Q =>∈. (3)()(0,0,)rr rab a b a b r Q =>>∈16.指数式与对数式的互化式log b a N b a N =⇔=(0,1,0)a a N >≠>.对数的换底公式log log log m a m NN a=(0a >,且1a ≠,0m >,且1m ≠, 0N >).推论 log log m na a nb b m =(0a >,且1a >,,0m n >,且1m ≠,1n ≠, 0N >).对数的四则运算若a >0,a ≠1,M >0,N >0,则 (1)log ()log log a a a MN M N =+;(2) log log log aa a MM N N =-; (3)log log ()na a M n M n R =∈.对数换底不等式及其推广若0a >,0b >,0x >,1x a ≠,则函数log ()ax y bx = (1)当a b >时,在1(0,)a 和1(,)a +∞上log ()ax y bx =为增函数., (2)当a b <时,在1(0,)a 和1(,)a+∞上log ()ax y bx =为减函数.推论:设1n m >>,0p >,0a >,且1a ≠,则 (1)log ()log m p m n p n ++<. (2)2log log log 2a a am nm n +<.数列的同项公式与前n 项的和的关系11,1,2n n n s n a s s n -=⎧=⎨-≥⎩( 数列{}n a 的前n 项的和为12n n s a a a =+++).17.**等差数列的通项公式*11(1)()n a a n d dn a d n N =+-=+-∈;其前n 项和公式为1()2n n n a a s +=1(1)2n n na d -=+ 211()22d n a d n =+-. **等比数列的通项公式1*11()n nn a a a q q n N q-==⋅∈; 其前n 项的和公式为11(1),11,1n n a q q s q na q ⎧-≠⎪=-⎨⎪=⎩或11,11,1n n a a qq q s na q -⎧≠⎪-=⎨⎪=⎩.***等比差数列{}n a :11,(0)n n a qa d a b q +=+=≠的通项公式为 1(1),1(),11n n n b n d q a bq d b q d q q -+-=⎧⎪=+--⎨≠⎪-⎩;其前n 项和公式为(1),(1)1(),(1)111n n nb n n d q s d q db n q q q q +-=⎧⎪=-⎨-+≠⎪---⎩. 18.常见三角不等式(1)若(0,)2x π∈,则sin tan x x x <<.(2) 若(0,)2x π∈,则1sin cos x x <+≤(3) |sin ||cos |1x x +≥.同角三角函数的基本关系式22sin cos 1θθ+=,tan θ=θθcos sin ,tan 1cot θθ⋅=. 和角与差角公式sin()sin cos cos sin αβαβαβ±=±;cos()cos cos sin sin αβαβαβ±=;tan tan tan()1tan tan αβαβαβ±±=.22sin()sin()sin sin αβαβαβ+-=-(平方正弦公式); 22cos()cos()cos sin αβαβαβ+-=-.sin cos a b αα+=)αϕ+(辅助角ϕ所在象限由点(,)a b 的象限决定,tan baϕ= )..二倍角公式sin 2sin cos ααα=.2222cos 2cos sin 2cos 112sin ααααα=-=-=-.22tan tan 21tan ααα=-.;22cos 1sin ,2cos 1sin 2;22cos 1cos ,2cos 1cos 22222αααααααα-=-=+=+= 三倍角公式3sin 33sin 4sin 4sin sin()sin()33ππθθθθθθ=-=-+.3cos34cos 3cos 4cos cos()cos()33ππθθθθθθ=-=-+.323tan tan tan 3tan tan()tan()13tan 33θθππθθθθθ-==-+-..三角函数的周期公式函数sin()y x ωϕ=+,x ∈R 及函数cos()y x ωϕ=+,x ∈R(A,ω,ϕ为常数,且A ≠0,ω>0)的周期2T πω=;函数tan()y x ωϕ=+,,2x k k Z ππ≠+∈(A,ω,ϕ为常数,且A ≠0,ω>0)的周期T πω=. .正弦定理2sin sin sin a b cR A B C===. 余弦定理2222cos a b c bc A =+-;2222cos b c a ca B =+-;2222cos c a b ab C =+-..面积定理(1)111222a b c S ah bh ch ===(a b c h h h 、、分别表示a 、b 、c 边上的高). (2)111sin sin sin 222S ab C bc A ca B ===..三角形内角和定理在△ABC 中,有()A B C C A B ππ++=⇔=-+222C A Bπ+⇔=-222()C A B π⇔=-+.19.向量平行的坐标表示设a =11(,)x y ,b =22(,)x y ,b a //12210x y x y ⇔-=设a =11(,)x y ,b =22(,)x y ,)0(≠⊥a b a a ·b=12120x x y y ⇔+=cos θ=20.不等式222a b ab +≥2a b +≥3333(0,0,0).a b c abc a b c ++≥>>>已知y x ,都是正数,则有xy yx ≥+2,当y x =时等号成立。
