约束满足与邻域搜索结合的混合算法及应用
约束满足混合算法求解并行机Job-Shop调度问题

中图分类号:T 3 16 P0 .
文献标志码 : A
文章编号:10 —652 1 )822 .3 0 139 (0 1o.820
di1.99jin 10 .65 21.805 o: 3 6/. s.0 139 .0 10 .0 0 s
C n tan ai a t n b s d h b i lo i m o o — h p o sr its t f ci - a e y rd ag rt frJ b- o s o h S
第 2 第8 8卷 期
2 11 8月 01年
计 算 机 应 用 研 究
Ap l a in Re e r h o o u e s p i t s a c fC mp tr c o
Vo _ 8 No 8 l2 . Au ,2 I g 01
约束 满足 混 合 算 法求解 并行 机 J bS o o — h p调度 问题
邻域培植多目标遗传算法ncga简介

邻域培植多目标遗传算法ncga简介邻域培植多目标遗传算法(NCga)是一种用于解决多目标优化问题的进化算法。
与传统的单目标遗传算法不同,多目标遗传算法旨在寻找一组解,这组解中每个解都是最优解的其中之一,而不是一个单一的最优解。
NCga算法是多目标遗传算法的一种改进版本,它主要解决了传统多目标遗传算法在收敛速度和解的多样性方面的不足。
NCga算法的主要特点包括以下几个方面:1. 遗传算法的基本原理:NCga算法是基于遗传算法的基本原理设计的,包括选择、交叉、变异等基本操作。
遗传算法通过模拟生物进化的过程,不断优化种群中的个体,逐步接近最优解。
2. 邻域培植策略:NCga算法引入了邻域培植策略,通过在当前种群中选择最优解的邻域解来更新种群,以提高种群的多样性和全局搜索能力。
3. 多目标优化:NCga算法可以同时优化多个目标函数,找到一组解,这组解中每个解都是最优解的其中之一。
通过多目标优化,NCga算法可以在不同的目标之间找到平衡,得到更加全面的解集。
4. 收敛速度和解的多样性:NCga算法通过邻域培植策略,可以加速算法的收敛速度,同时保持解的多样性,避免陷入局部最优解。
5. 适用范围:NCga算法适用于各种多目标优化问题,包括工程优化、组合优化、调度问题等。
通过调整算法的参数和优化策略,可以灵活应用于不同的问题领域。
总的来说,邻域培植多目标遗传算法(NCga)是一种有效的多目标优化算法,通过结合遗传算法的基本原理和邻域培植策略,可以有效解决多目标优化问题,具有收敛速度快、解的多样性高的优点,适用于各种多目标优化问题的求解。
NCga算法在实际问题中具有广泛的应用前景,可以帮助优化问题的求解,提高问题的解的质量和效率。
广义邻域搜索算法及其统一结构

智能优化计算
7.2 广义邻域搜索算法的要素
搜索方式的选择 决定优化的结构,即每代有多少解参与优化; 并行搜索:以多点同时或交叉优化,计算和储存量 较大,如GA、ACO、PSO等; 串行搜索:始终只有一个当前状态,处理简单,效 率较差,如SA、TS等。
智能优化计算
7.2 广义邻域搜索算法的要素
智能优化计算
7.1 广义邻域搜索算法
7.1.1 传统邻域算法
特点 (1)通用易实现,只要设计好状态发生器(邻域函 数),就能求解组合或函数优化; (2)算法性能对邻域函数和初始值具有依赖性,邻 域函数和初始值选取不同,算法最终的性能将会有 差异; (3)算法的局部优化特性,没有跳出局部极值的能 力。
智能优化计算
7.3 广义邻域搜索算法的一般结构
7.3.2 统一优化结构
整体流程
智能优化计算
7.4 优化算法的性能评价体系
优化性能指标 离线最优性能指标:
Em,off
line
cb c* c*
100 %
其中,cb为算法多次运行所得的最佳优化值,c*为问 题的最优解,若最优解未知,可用已知最佳优化值
7.5.1 理论研究概述 7.5.2 应用研究概述 7.5.3 发展性研究
智能优化计算
7.1 广义邻域搜索算法
7.1.1 传统邻域算法
传统邻域算法的优化流程 从一个初始解 x 出发,利用状态发生器持续地
在解 x 的邻域中搜索比它好的解,若能找到如此的 解,就以之替代解 x 成为新的当前解,然后重复上 述过程;否则结束搜索过程,以当前解作为最终解。
(ACO,1992)
Particle Swarm Optimization (PSO,1995)
【国家自然科学基金】_变邻域搜索算法_基金支持热词逐年推荐_【万方软件创新助手】_20140802
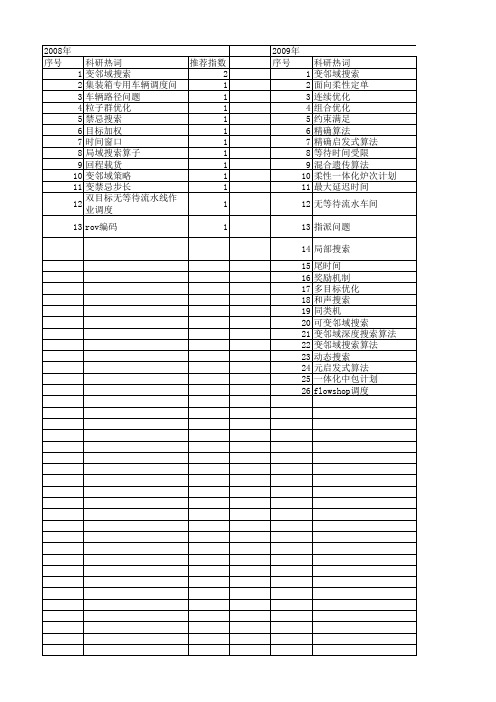
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
科研热词 变邻域搜索 面向柔性定单 连续优化 组合优化 约束满足 精确算法 精确启发式算法 等待时间受限 混合遗传算法 柔性一体化炉次计划 最大延迟时间 无等待流水车间 指派问题 局部搜索 尾时间 奖励机制 多目标优化 和声搜索 同类机 可变邻域搜索 变邻域深度搜索算法 变邻域搜索算法 动态搜索 元启发式算法 一体化中包计划 flowshop调度
推荐指数 4 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44
科研热词 变邻域搜索 变邻域搜索算法 项目调度 需求预测 配送车辆路径模型 邻域搜索 迭代局部搜索 运筹学 车辆路线问题 车辆路径问题 资源受限 调度 设施选址 设施布局问题 装箱 类电磁 禁忌搜索算法 禁忌搜索 生鲜食品 环保 炉次计划 港口集卡 流水车间 油耗 时间窗 时间序列分析 改进遗传算法 推广p-中位问题 批处理机 成像卫星 快速消费品 微粒群算法 库存决策 宽度区间 多元回归模型 变领域策略 变邻域 及时性 单行布局问题 动态调度 共享模式 公平性 优化算法 优化
邻域分析技术及其在计算机科学中的应用

邻域分析技术及其在计算机科学中的应用导言在计算机科学领域,邻域分析技术被广泛应用在图像处理、网络分析、自然语言处理等领域中。
其基本思想是通过寻找和某个对象相邻的其他对象,从而分析对象间的关系和特征。
本文将介绍邻域分析技术的概念、算法和应用,并探讨其未来的发展趋势。
邻域分析技术的概念邻域分析技术,英文名为“Neighborhood Analysis”,是一种基于数据挖掘和机器学习的分析方法。
它主要用于探索数据集中对象与其周围对象的相似性和关系,从而识别对象之间的模式和规律。
其核心思想是通过寻找对象周围的其他对象或者通过距离函数来衡量对象之间的相似性,从而建立对象之间的联系。
邻域分析技术的算法邻域分析技术具体实现有多种不同方法,下面我们分别介绍几种常用的算法。
1. k-Nearest Neighbor算法k-Nearest Neighbor(k-NN)算法是邻域分析技术中的经典算法之一。
它基于“相似的对象靠在一起”的思想,通过计算对象间的距离或相似性度量,将每个对象归为靠近它的k个最邻近的训练样本中的多数类别。
2. DBSCAN算法DBSCAN(Density-Based Spatial Clustering of Applications with Noise)算法是一种需要指定邻域半径的聚类算法,用于将密度相似的对象组成一组。
它的基本思想是集合内部的对象比集合之间的对象更相似,通过寻找密度相似的区域来分组。
3. PCA算法PCA(Principal Component Analysis)算法是一种降维算法,能够将高维空间的数据映射到低维空间中,同时还能保留原始数据的结构特征。
它通过计算数据的协方差矩阵,来找到数据中最主要的成分,并用这些主成分组成一个新的低维空间。
邻域分析技术在计算机科学中的应用邻域分析技术在计算机科学领域中被广泛应用,其中比较常见的领域包括:1. 图像处理在图像处理中,邻域分析可以应用于图像去噪、边缘检测、形态学处理等领域。
基于约束和邻域的炼钢连铸重调度算法

e p rme t h w t a h d la d a g rt m r f cie xe i n s s o h t e mo e n lo h a e ef t . t i e v
Ke r s:se l k n -o tn o a tn y wo d t ema i g c n i u usc si g;r s h d ln e c e u i g;d n mi o sr i ts tsa to y a c c n tan aif ci n;n ih o h o eg b r o d sac e h r
中图分类号 :P 9 T 2 文献标志码 : A 文章编号 :077 7 (0 1 0 —0 40 10 - 5 2 1 )6 0 8 -6 3
Re c e u i g Alo i m o t em a i g a d Co tn o sCa t g Ba e n s h d l g rt n h f r S e l k n n n i u u si s d o n
o h s r b e t ma i z t e q a t y o n i o sc s n n i li ewe n t n t ls h d f rt i p o l m xmi h u n i f o t u u a t g a d t e smi r y b t e e i i a c e - o e t c n i h at h i
ueadteajs o e ae nti moe a db n yigtec aatr t so epo lm, xd l n dut n .B sdo s d l n ya a z hrce sc f h rbe ami h h l n h ii t e
l o ih t a o i e o ta n aifc i e h o o ywi n i h o h o e r h i r p s d.Si lto ag rt m h tc mb n sc nsr i ts tsa t n t c n lg t eg b r o d s a c sp o o e o h mu ain
遗传算法解决多约束优化问题的启发式搜索方法

遗传算法解决多约束优化问题的启发式搜索方法随着科学技术的不断发展,人们对于优化问题的需求也越来越迫切。
在实际生活和工作中,我们常常会遇到多约束优化问题,即在满足一系列约束条件的前提下,寻找最优解。
传统的优化算法往往无法高效地解决这类问题,而遗传算法作为一种启发式搜索方法,具有很好的适应性和鲁棒性,被广泛应用于多约束优化问题的求解。
遗传算法的核心思想是模拟自然界中的进化过程,通过模拟遗传、变异和选择等操作,不断优化解的适应度,最终找到最优解。
在解决多约束优化问题时,遗传算法可以通过设计适应度函数、交叉和变异操作等方式,有效地搜索解空间,并找到满足约束条件的最优解。
在设计适应度函数时,我们需要考虑多个目标函数和约束条件。
一种常用的方法是将目标函数和约束条件进行加权求和,得到一个综合的适应度值。
通过调整不同目标函数和约束条件的权重,可以在搜索过程中平衡不同的优化目标和约束条件。
此外,还可以使用罚函数法,将不满足约束条件的解进行惩罚,以防止这些解被选择和进化。
交叉和变异操作是遗传算法的核心操作,通过模拟自然界中的基因交换和突变,产生新的解,并逐步改进解的适应度。
在解决多约束优化问题时,我们需要设计合适的交叉和变异操作,以保证生成的新解满足约束条件。
一种常用的方法是通过交叉和变异操作生成的解与父代解进行比较,保留满足约束条件且适应度更好的解,丢弃不满足约束条件或适应度较差的解。
除了适应度函数、交叉和变异操作,遗传算法还有其他一些关键的参数需要调整,例如种群大小、迭代次数等。
种群大小的选择会影响搜索过程中的多样性和收敛速度,迭代次数的选择会影响搜索过程的终止条件。
在解决多约束优化问题时,我们需要根据具体问题的特点和要求,合理地选择这些参数,以获得更好的求解效果。
然而,遗传算法也存在一些局限性。
首先,遗传算法是一种启发式搜索方法,其搜索过程是基于概率和随机性的,因此无法保证找到全局最优解。
其次,遗传算法的求解效率受到问题规模和复杂度的限制,对于大规模和高维度的问题,可能需要更多的时间和计算资源。
带有复杂约束的组合优化问题的求解

带有复杂约束的组合优化问题的求解组合优化问题是计算机科学中的一种重要问题,它涉及到在一定的约束条件下对各种不同元素进行组合以达到最优解的目的。
组合优化问题不仅需要考虑计算的效率,也需要考虑解的准确性和实用性,因此在实际应用过程中会遇到许多复杂的约束条件。
本文将围绕带有复杂约束的组合优化问题展开讨论,介绍一些常用算法和方法来应对这些问题。
一、问题定义组合优化问题的定义可以用以下形式表示:给定一个大小为n的元素集合A={a1,a2,…,an},并要求从中选择k个元素的子集S,使得满足若干个约束条件且达到最优解。
其中,约束条件可以是单调性、集合的大小限制、元素互斥关系、概率限制等等多种形式。
例如,假设有n个任务,每个任务需要用一个不同的机器处理,每台机器一次只能处理一个任务。
我们要求出一种分配方案,使得每个任务都被分配给某台机器处理且每台机器都只处理一个任务。
这是一个约束条件为配对和不得重复的组合优化问题。
二、常见算法及其应用1.贪心算法贪心算法是一种很常见的算法,通常用于组合算法的近似求解。
它的核心思想是通过贪心地选择当前最佳的元素来构建解决方案,然后用这个方案来尽可能地满足约束条件。
但是,贪心算法并不能保证找到最优解,因为可能存在某个元素组合的组合方式比刚刚的选择更优。
以任务分配问题为例,如果我们选择的策略是尽可能选取能够完成任务的全部节点,那么可能会造成部分节点没有合适的机器分配,从而无法保证最优解。
如果我们选择其他的贪心策略,是否会得到更好的结果,还需要继续优化。
2.分支定界法分支定界法是解决组合优化问题的常见算法之一,其基本思想是通过对问题的搜索,逐步缩小可行解的集合,而且能够在较少的搜索次数内得到一个最优解。
核心思想是将问题划分为两个或多个独立的子问题,然后对每个子问题进行求解,再将各个子问题的解整合成一个整体解。
除此之外,在处理带有约束条件的组合优化问题时,还可以使用禁忌搜索、模拟退火、遗传算法等进化算法来解决。
多目标中间包计划模型及混合优化算法

多目标中间包计划模型及混合优化算法马天牧;罗小川;柴天佑【摘要】中间包计划是重要的炼钢-连铸批量计划之一,其功能是在给定的炉次计划中,根据炼钢-连铸生产能力及下游工序生产所需材料的数量,挑选出待生产的炉次并制定出合理的中间包使用数量及每个中间包内生产的炉次.在对中间包计划问题描述的基础上及现有文献中未考虑中间包利用率及中间包内炉次宽度差异性,建立了多目标中间包计划数学模型.为了求解模型将模型分解为两个子模型,并针对两个子模型设计了迭代局部搜索算法(iterated local search,ILS)及变邻域搜索算法(variable neighborhood search,VNS)相结合的双层混合算法,考虑到中间包利用率及多目标权重对解的影响,在算法中加入了可调整模型参数的方法,最后用实际生产数据对模型及算法进行验证.【期刊名称】《系统工程学报》【年(卷),期】2015(030)004【总页数】15页(P451-465)【关键词】中间包计划;多目标;迭代局部搜索;变邻域搜索;混合算法【作者】马天牧;罗小川;柴天佑【作者单位】东北大学流程工业综合自动化国家重点实验室,辽宁沈阳110819;东北大学流程工业综合自动化国家重点实验室,辽宁沈阳110819;东北大学流程工业综合自动化国家重点实验室,辽宁沈阳110819;东北大学自动化研究中心,辽宁沈阳110819【正文语种】中文【中图分类】TP273炼钢–连铸工序是整个钢铁生产过程的瓶颈工序,其特点是生产前设备准备时间长,生产过程中要求高温连续,生产的产品必须能够充分供应后续工序生产需求.因此合理有效制定其生产计划可以充分提高设备利用率、减少设备因停机准备的时间,使前后工序协调生产.炼钢–连铸生产计划的管理分为批量计划和调度计划,其中批量计划的功能是确定每日或班组的生产任务,包括炉次计划、中间包计划、浇注计划,调度计划的功能是为生产任务确定设备及生产起止时间.本文主要讨论中间包计划.中间包计划是在炉次计划的基础上,负责考虑在满足本工序生产能力的同时,还要满足其下游生产工序正常生产所需原料的供给,其作用重于炉次计划.炼钢–连铸生产过程涉及的设备种类多、工艺路径复杂,其调度计划一直是国内外学者和工程技术人员研究的热点,对调度计划的研究从静态调度发展到动态调度、重调度和钢包调度[1−5].而对批量计划研究较少[6],目前对中间包计划研究较为深入的有文献[7,8].文献[7]提出了中间包批量计划,并将其归结为车辆路径问题(vehicle routing problem,VRP),以最少中间包数、未组入中间包炉次惩罚、下游工序需求为目标.文献[8]将中间包计划归结为能力受限的调度问题建立了多目标模型,其在目标中考虑了最少中间包数、下游工序需求,开发了新型的变邻域搜索方法.但两者没有考虑中间包利用率变化及炉次宽度区间相似性,且都仅采用一组实例数据验证.在工厂里中间包计划主要是由计划人员采用试凑的方法编制,计划的质量取决于人的经验,并且每次都需耗费大量的时间.基于以上问题,本文以某大型钢铁企业实施制造执行系统(manufacturing execution system,MES)项目为背景,在描述该企业的中间包计划问题基础上,建立多目标的中间包批量计划数学模型.为了求解模型,首先将模型分解为两个子模型,然后设计了迭代局部搜索与变邻域搜索相结合的双层混合优化算法,由于中间包利用率是可变化的且对问题的解有影响,同时考虑到多目标转换为单目标时权重对解也有影响,因此在算法中加入了动态改变中间包利用率及权重的方法,最后采用现场中多组数据进行验证.2.1 问题描述在炼钢–连铸生产中,中间包是连铸机上用来盛钢水的容器.中间包具有一定的使用寿命,根据所盛钢水的成本不同使用寿命不同,一般在4炉~6炉,且不论是否达到使用寿命都需要对其耐高温层维护,每次维护的成本是很可观的[7].使用同一中间包浇铸的钢水成份和相应板坯浇铸宽度必须相同或相近.当出现钢水成份或宽度调整(宽度每次调整幅度最大100 mm,最小50 mm)时,会分别出现叫做交接坯和梯形坯的两类板坯.这两类板坯在实际生产中都是需要减少或避免的。
变邻域搜索算法综述

2009年7月第16卷增刊控制工程Contr o l Eng i n eering o f ChinaJu l.2009Vo l.16,S 1文章编号:1671-7848(2009)S 1-0001-05收稿日期:2009-04-20; 收修定稿日期:2009-06-29基金项目:国家自然科学基金资助项目(70671020,70431003,70721001,60673159);新世纪优秀人才支持计划基金资助项目(NCET-05-0295,NCET-05-0289);高等学校博士学科点专项科研基金资助项目(20070145017,20060145012);国家高技术研究发展计划基金资助项目(2006AA01Z214)作者简介:董红宇(1982-),男,吉林长春人,博士,主要研究方向为M et ah euristics ,流程工业生产计划与调度等;黄敏(1968-),女,教授,博士生导师。
变邻域搜索算法综述董红宇1,2,黄 敏1,2,王兴伟1,郑秉霖2(1.东北大学信息科学与工程学院,辽宁沈阳 110004;2.教育部流程工业综合自动化重点实验室(东北大学),辽宁沈阳 110004)摘 要:变邻域搜索算法(V ar i able N e i ghborhood Search ,VN S)作为一种新的元启发式算法,已初步成功地用于解决优化问题,尤其是对于大规模组合优化问题效果良好。
对VN S 的扩展研究层出不穷,并将其成功地应用到旅行商问题、车辆路径问题、调度、图着色等问题中。
简述了经典的元启发式算法,并依次论述了优化问题,VN S 算法起源,VN S 算法原理,VNS 算法分析,扩展的VNS 分析,VN S 在初始解构造、邻域结构构造、局部搜索和停止准则几个方面的改进方法,针对不同版本的VNS 归纳了其在各种优化问题应用情况。
基于对改进的VNS 的分类,从算法自身研究角度和实际应用角度提出了未来研究方向。
多参数约束组合优化问题

多参数约束组合优化问题是一类复杂的优化问题,涉及到多个参数和约束条件的组合。
这类问题通常出现在实际工程和科研领域中,如生产调度、资源分配、物流规划等。
解决多参数约束组合优化问题的关键在于如何有效地处理多个参数和约束条件,以找到最优解或近似最优解。
解决多参数约束组合优化问题的方法有很多,以下是一些常用的方法:1. 数学规划方法:数学规划方法是一种常用的解决多参数约束组合优化问题的方法。
它通过建立数学模型,将问题转化为数学形式,然后利用数学方法求解。
常见的数学规划方法包括线性规划、整数规划、非线性规划等。
2. 启发式搜索方法:启发式搜索方法是一种基于经验和规则的搜索方法,它通过不断迭代搜索过程,逐步逼近最优解。
常见的启发式搜索方法包括遗传算法、模拟退火算法、蚁群算法等。
3. 智能优化方法:智能优化方法是一种基于人工智能技术的优化方法,它通过模拟人类智能的过程,实现问题的优化求解。
常见的智能优化方法包括神经网络、支持向量机、决策树等。
在解决多参数约束组合优化问题时,需要根据问题的具体情况选择合适的方法。
同时,还需要注意以下几点:1. 确定问题的目标和约束条件:明确问题的目标和约束条件,是解决问题的前提。
只有明确了问题的目标和约束条件,才能有针对性地选择合适的优化方法。
2. 选择合适的优化算法:不同的优化算法适用于不同的问题,需要根据问题的具体情况选择合适的优化算法。
同时,还需要考虑算法的效率、稳定性和可靠性等因素。
3. 处理多参数和约束条件:多参数约束组合优化问题涉及到多个参数和约束条件的组合,需要有效地处理这些参数和约束条件。
可以通过建立数学模型、引入罚函数等方法来处理多参数和约束条件。
4. 验证和优化解的质量:在得到解之后,需要对解进行验证和优化,以确保解的质量和可行性。
可以通过对比不同解之间的优劣、进行灵敏度分析等方法来验证和优化解的质量。
总之,多参数约束组合优化问题是一类复杂的优化问题,需要综合运用数学、计算机科学、人工智能等多个领域的知识来解决。
变邻域搜索算法研究及在组合优化中的应用

致 谢本文是在导师高雷阜教授的悉心指导下完成的。
在两年半的学习和科研活动中,高老师渊博的知识、严谨的治学态度、深厚的学术造诣、勇于开拓的科研精神、对国内外学术动态敏锐的洞察力以及平易近人的处世态度、热爱生活的美好品质深深打动和潜移默化的影响着我,给我留下了深刻的印象,并将使我受益终身。
在本文的完成过程中,高老师给予了耐心的指导,提出了许多宝贵的意见和建议,本文的完成离不开高老师的悉心指导。
在此向高老师致以真挚的感谢和崇高的敬意。
感谢理学院的每一位老师,是他们一丝不苟的工作态度以及严谨的治学态度给了我前进的动力和学习的榜样,这种力量也将继续伴随我走向今后的学习和工作。
感谢数学与系统科学研究所的所有师兄、师姐、师弟、师妹。
在我硕士期间,与他们和睦相处,得到了他们的热情帮助与勉励。
感谢我宿舍的韩建、冯昌利、纪秀浩,他们给了我很多关心和帮助,兄弟般的感情让我终生难忘。
感谢华中科技大学的韩磊同学和上海大学的金峰同学,帮我搜集了大量的相关文献,让我能够顺利完成研究工作。
感谢我的父母,正是多年来他们的辛勤劳动、无私奉献为我的学业提供了莫大的物质保障和精神支持。
我的每一步成长的历程,都倾注着他们的辛劳和汗水。
最后,我特别感谢在百忙中抽出时间来参加我的论文评阅和答辩的各位老师,感谢你们对我的帮助与指导。
摘 要对变邻域搜索算法做出改进,提出了一种解决连续优化问题的变邻域搜索算法和一种结合粒子群算法的变邻域搜索混合算法。
并将改进的算法应用于旅行商问题和0-1非线性混合整数规划问题中。
主要的研究成果和创新点包括:首先,针对因连续优化问题的可行解空间特点而无法直接应用变邻域搜索算法的问题,将SQP算法与变邻域搜索算法结合,用SQP问题求解局部最优解,用变邻域搜索算法跳出局部最优解,进而求得全局最优解。
通过数据仿真,证明变邻域搜索算法比其他启发式算法在全局收敛性等方面更好。
其次,针对一般变邻域搜索算法计算时间长的问题,借鉴粒子群优化算法的思想,提出一种结合粒子群算法的变邻域搜索混合算法。
基于邻域的算法

基于邻域的算法邻域算法,也称为局部邻域算法,是一类以局部信息为基础进行计算的算法。
它们在各种领域中都有广泛的应用,从图像处理到机器学习。
邻域算法的核心思想是基于邻近的数据点之间的关系来进行计算和预测。
邻域算法最常见的应用之一是图像处理。
在图像中,每个像素的值与其周围像素的值有很强的关联。
邻域算法利用这种关联性来进行图像增强、边缘检测和去噪等任务。
例如,高斯模糊算法就是一种基于邻域的图像平滑算法,它将每个像素的值替换为其周围像素的加权平均值,以达到模糊图像的效果。
在机器学习中,邻域算法被广泛应用于分类和回归问题。
其中最著名的算法是K最近邻算法(KNN)。
KNN算法根据样本之间的距离(邻域)来进行分类或回归预测。
它的基本思想是将待分类样本与最近的K个已知类别的样本进行比较,根据它们的标签来预测待分类样本的标签。
邻域算法的另一个重要应用领域是推荐系统。
推荐系统在电子商务和社交媒体等领域中起着重要的作用。
邻域算法可以根据用户之间的相似性来推荐他们可能感兴趣的商品或内容。
例如,协同过滤算法就是一种基于邻域的推荐算法,它根据用户的历史行为和其他用户的行为进行比较,来为用户生成个性化的推荐列表。
邻域算法虽然简单,但却非常有效。
它们通常易于理解和实现,并且能够处理大量数据。
然而,邻域算法也有一些局限性。
首先,它们对数据的局部结构非常敏感,并且容易受到噪声的影响。
其次,邻域算法的计算复杂度随着数据量的增加而增加,因此在处理大规模数据时可能会面临挑战。
为了克服这些局限性,研究人员不断提出改进和扩展邻域算法。
例如,局部敏感哈希算法可以加速邻域搜索,减少计算复杂度。
同时,集成学习和深度学习等技术也可以与邻域算法结合,进一步提升预测性能。
总之,邻域算法是一类基于邻近数据点之间关系的算法,在图像处理、机器学习和推荐系统等领域有广泛应用。
尽管存在一些局限性,但邻域算法的简单性和有效性使其成为许多实际问题的理想选择。
通过不断改进和扩展,邻域算法将继续为我们解决各种挑战提供有力的工具。
基于邻域的算法

基于邻域的算法基于邻域的算法是一种常用的数据挖掘和机器学习方法,它主要是基于某个样本的邻居来推断该样本的特征或标签。
在实际应用中,基于邻域的算法被广泛应用于分类、聚类、推荐系统等领域。
基于邻域的算法有很多种,其中最常见的包括k最近邻算法、均值漂移算法和DBSCAN算法等。
下面将分别介绍这几种算法的原理和应用。
1. k最近邻算法(k-Nearest Neighbor,简称kNN)是最简单、最常用的基于邻域的算法之一。
其基本原理是通过计算待分类样本与训练集中各个样本之间的距离,找出距离最近的k个邻居,然后根据这k个邻居的标签来预测待分类样本的标签。
kNN算法适用于多分类和二分类问题,且对样本的分布情况没有太高要求。
2. 均值漂移算法(Mean Shift)是一种基于邻域密度的密度估计方法。
其原理是通过计算样本点周围邻域内点的密度分布情况,将样本点向密度高的方向移动,直到达到局部最大密度。
均值漂移算法的应用比较广泛,包括图像分割、无监督聚类等。
3. DBSCAN算法(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的聚类算法,可以自动发现具有各种形状的聚类,并能够将孤立点(噪声)排除在外。
该算法的核心是通过计算样本点周围邻域内的密度,并通过设置一定的密度阈值和最小样本数来划分聚类。
DBSCAN算法广泛应用于图像分割、异常检测等领域。
基于邻域的算法有以下几个特点:1. 算法简单易于实现:基于邻域的算法通常基于简单的原理,易于理解和实现,不需要太多的数学基础。
2. 高效处理大规模数据:由于基于邻域的算法主要关注于局部信息,而不需要全局计算,因此适用于处理大规模数据。
3. 对数据分布要求较低:基于邻域的算法对数据的分布情况没有太高要求,可以处理各种形状和密度的数据。
在实际应用中,基于邻域的算法被广泛应用于各个领域。
例如,在推荐系统中,可以利用基于邻域的算法来为用户推荐相似的商品或用户;在文本分类中,可以利用kNN算法来根据文本的内容将其分类至相应的类别;在图像处理中,可以利用均值漂移算法来实现图像分割等。
模拟退火算法的约束条件

模拟退火算法的约束条件模拟退火算法(Simulated Annealing)是一种用于优化问题的随机搜索算法,其灵感来源于固体退火的物理过程。
在模拟退火算法中,系统通过一系列的状态转移来寻找全局最优解或近似最优解。
在搜索过程中,模拟退火算法遵循一定的约束条件,以保证搜索结果的有效性和可靠性。
1. 初始解的生成:模拟退火算法对于初始解的生成没有具体的限制,可以使用随机生成、贪心算法等方法。
初始解的质量和多样性会对算法的性能产生影响,因此在实际应用中需要根据具体问题进行调整。
2. 邻域结构的定义:邻域结构是模拟退火算法中的一个关键概念,它定义了当前解的周围的解空间。
在搜索过程中,模拟退火算法通过在邻域内进行随机搜索来寻找更好的解。
邻域结构的定义需要满足以下条件:能够包含当前解的所有可能的变动方案,能够通过改变一个或多个参数来生成新的解。
3. 目标函数的定义:模拟退火算法的目标是在解空间中寻找最优解或近似最优解。
因此,需要明确定义一个目标函数来评估每个解的质量。
目标函数的设计需要考虑问题的具体性质和约束条件,并且应能够准确地反映解的优劣程度。
4. 温度控制策略:模拟退火算法通过温度参数来控制搜索过程中的随机性。
温度越高,搜索过程中的随机性越大,有利于避免陷入局部最优解;温度越低,搜索过程中的随机性越小,有利于稳定解的质量。
温度控制策略需要满足以下条件:初始温度应足够高以保证全局搜索能力,温度下降的速度应适中以平衡全局搜索和局部搜索的性能。
5. 接受准则的定义:模拟退火算法通过接受准则来决定是否接受新的解。
接受准则的定义需要考虑当前解的质量、新解的质量以及温度参数。
一般情况下,接受准则满足Metropolis准则,即如果新解的质量更好,那么接受新解;否则,以一定的概率接受新解,概率与新解的质量差和温度参数有关。
6. 终止条件的设定:模拟退火算法需要设定一个终止条件来结束搜索过程。
终止条件可以是达到一定的迭代次数、达到一定的时间限制、解的质量达到一定的阈值等。
第五章约束优化方法2惩罚函数法课件

5.3.4.1 内点法
㈠引例 设有一维不等式约束优化问题的数学模型
S.T. :
由图可见,目标函数的可行域为x≥b,在可行域内目标函数 单调上升,它的最优解显然是
x*=b ,F*=ab
对引例的惩罚函数进行分析,以对内点法有初步认识:
⑴本问题是不等式约束优化问题,故只有一项惩罚项
,一个罚因子 ⑵规定罚因子 为某一正数,当迭代点是在可行域内 时,则惩罚项的值必为正值,因此必有
⑹由终止准则,若满足则转步骤⑺,否则转⑸
⑺,
输出最优解(x*,F*)
入口
给定:x(0) ∈D,r(0),C,ε1,ε2
内
点
k←0
法
流 程 图
用无约束优化方法求罚函数
的优化点 xk* F F(xk* )
出口
x* xk* , F* F(xk* )
+
-
K=0?
+
r ( k 1) Cr ( k )
1
u1 gu (x)
关于惩罚因子规定为正,即 。且在优化过程中
是减小的,为确保为递减数列,取常数C
r (k) Cr (k1) ,
0<C<1
称系数C为罚因子降低系数
=0 或
p
关于惩罚项 r (k)
,1由于在可行域内有
u1 gu (x)
g,u (x) 0
且 r(永k) 远取正值,故在可行域内惩罚项永为正。 r ( k )的值越小则惩罚项的值越小。
先讨论解不等式约束优化问题 设有不等式约束优化问题
S.T. :
u=1,2……,p
构造外点法惩罚函数的常见形式
取正递增
引入罚因子递增系数C>1,并令
基于邻居信息聚合的子图同构匹配算法

2021⁃01⁃10计算机应用,Journal of Computer Applications 2021,41(1):43-47ISSN 1001⁃9081CODEN JYIIDU http ://基于邻居信息聚合的子图同构匹配算法徐周波,李珍,刘华东*,李萍(广西可信软件重点实验室(桂林电子科技大学),广西桂林541004)(∗通信作者电子邮箱ldd@ )摘要:图匹配在现实中被广泛运用,而子图同构匹配是其中的研究热点,具有重要的科学意义与实践价值。
现有子图同构匹配算法大多基于邻居关系来构建约束条件,而忽略了节点的局部邻域信息。
对此,提出了一种基于邻居信息聚合的子图同构匹配算法。
首先,将图的属性和结构导入到改进的图卷积神经网络中进行特征向量的表示学习,从而得到聚合后的节点局部邻域信息;然后,根据图的标签、度等特征对匹配顺序进行优化,以提高算法的效率;最后,将得到的特征向量和优化的匹配顺序与搜索算法相结合,建立子图同构的约束满足问题(CSP )模型,并结合CSP 回溯算法对模型进行求解。
实验结果表明,与经典的树搜索算法和约束求解算法相比,该算法可以有效地提高子图同构的求解效率。
关键词:子图同构;约束满足问题;图卷积神经网络;信息聚合;图匹配中图分类号:TP391文献标志码:ASubgraph isomorphism matching algorithm based on neighbor informationaggregationXU Zhoubo ,LI Zhen ,LIU Huadong *,LI Ping(Guangxi Key Laboratory of Trusted Software (Guilin University of Electronic Technology ),Guilin Guangxi 541004,China )Abstract:Graph matching is widely used in reality ,of which subgraph isomorphic matching is a research hotspot and has important scientific significance and practical value.Most existing subgraph isomorphism algorithms build constraints based on neighbor relationships ,ignoring the local neighborhood information of nodes.In order to solve the problem ,a subgraph isomorphism matching algorithm based on neighbor information aggregation was proposed.Firstly ,the aggregated local neighborhood information of the nodes was obtained by importing the graph attributes and structure into the improved graph convolutional neural network to perform the representation learning of feature vector.Then ,the efficiency of the algorithm was improved by optimizing the matching order according to the characteristics such as the label and degree of the graph.Finally ,the Constraint Satisfaction Problem (CSP )model of subgraph isomorphism was established by combining the obtained feature vector and the optimized matching order with the search algorithm ,and the model was solved by using the CSP backtracking algorithm.Experimental results show that the proposed algorithm significantly improves the solving efficiency of subgraph isomorphism compared with the traditional tree search algorithm and constraint solving algorithm.Key words:subgraph isomorphism;Constraint Satisfaction Problem (CSP);graph convolutional neural network;information aggregation;graph matching0引言图匹配技术被广泛地应用于社交网络、网络安全、计算生物学和化学等领域[1]中。
mip启发式算法

mip启发式算法摘要:1.引言2.MIP启发式算法的定义和特点3.MIP启发式算法的基本原理4.MIP启发式算法在解决组合优化问题中的应用5.实例分析6.总结与展望正文:【引言】在当今复杂多样的优化问题中,启发式算法作为一种求解方法,得到了广泛的关注。
其中,MIP(Mixed-Integer Programming,混合整数规划)启发式算法在解决组合优化问题中具有显著优势。
本文将详细介绍MIP启发式算法的基本概念、原理以及在实际问题中的应用,以期为读者提供有益的参考。
【MIP启发式算法的定义和特点】MIP启发式算法是一种求解混合整数优化问题的方法。
它结合了整数规划和连续优化技术的优点,可以有效地解决具有整数约束的优化问题。
MIP启发式算法具有以下特点:1.高效性:相较于传统的整数规划方法,MIP启发式算法在求解过程中可以更快地找到近似最优解。
2.灵活性:MIP启发式算法可以处理多种类型的整数约束,适应性强。
3.易于调整:根据问题特点,可以方便地调整算法参数以提高求解效果。
【MIP启发式算法的基本原理】MIP启发式算法主要基于以下几个步骤:1.构建混合整数规划模型:根据问题特点,建立混合整数规划数学模型。
2.初始解生成:采用启发式方法生成初始解。
3.局部搜索:在初始解的基础上,采用局部搜索策略改进解的质量。
4.邻域搜索:在局部搜索的基础上,进行邻域搜索,扩大解空间,寻找更优解。
5.终止条件:当满足终止条件时,停止搜索,输出当前解。
6.迭代优化:若不满足终止条件,则返回第二步,继续迭代。
【MIP启发式算法在解决组合优化问题中的应用】MIP启发式算法在组合优化问题中具有广泛的应用,如:1.运输问题:通过MIP启发式算法求解货物分配问题,优化运输方案。
2.背包问题:利用MIP启发式算法解决有限资源下物品选择问题,提高效益。
3.车辆路径问题:通过MIP启发式算法优化车辆调度,降低成本。
【实例分析】以运输问题为例,假设有一个制造商和四个销售点,需要将货物从制造商运输到销售点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
约束满足与邻域搜索结合的混合算法及应用[摘要] 总结约束满足求解技术和邻域搜索算法,分析约束满足与邻域搜索
单一算法的优劣,以及两者结合的优势,提出约束满足与邻域搜索相结合的混合算法的一般框架,并以Job Shop 调度优化问题为例对该算法框架进行实例说明。
[关键词] 约束满足;邻域搜索;混合算法
ddoi : 10 . 3969 / j . issn . 1673 - 0194 . 2009 . 21 . 017
1引言
约束满足技术集成了运筹学、人工智能、逻辑编程和图论中的方法和思想,是解决组合优化问题的一门新兴技术。
约束满足建模能力较强,在约束求解中,能够充分利用问题的结构信息和约束关系,采用约束传播、回溯等技术对求解空间快速缩减,提高问题的求解效率。
邻域搜索算法是一种非常有效的解决组合优化问题的方法,在搜索空间内利用局部指导规则探索优良解,搜索效率高,具有可衡量性。
约束满足与邻域搜索法均存在自身的优势和局限性,相互结合可以有效利用算法的互补性。
目前对约束满足与邻域搜索相结合的混合算法的研究成果比较少。
文献[1]将邻域搜索和向前看(Look Ahead)技术结合,在搜索过程中遇到死点时要么回溯,要么应用邻域搜索继续新的空间搜索。
文献[2]中提出的“Decision-Repair”方法集成了禁忌搜索、一致性技术和基于冲突的启发式方法来引导搜索过程。
文献[3]在系统搜索过程中,使用变量排序和值排序法,进行不完全搜索,用N皇后问题进行算法测试。
文献[4]用约束规划算法产生一个可行解,作为禁忌搜索算法的初始解。
文献[5]对NEH算法加以扩展,得到高质量的初始解,提出跳出局部极值方法,改进约束满足修复算法。
本文首先介绍约束满足技术和邻域搜索技术,然后总结两者相结合的混合算法的框架,最后以Job Shop 调度为例,给出混合算法实现步骤。
2约束满足技术和邻域搜索技术
2.1 约束满足技术
约束满足的优势体现在:问题建模和约束求解相对独立,具有开放性,并可通过计算机系统有效实现。
在问题建模中,约束满足技术以接近于现实世界的方式描述领域知识,能够表达各种线性、非线性的复杂约束,并能通过递增约束扩展问题,可以应用松弛约束来处理问题的动态特征,具有较强的建模能力;在约束求解中,约束满足技术能够充分利用问题的结构信息、约束关系,采用约束传播、回溯、搜索等技术对求解空间快速缩减,提高问题的求解效率。
约束满足技术中的系统搜索和回溯方法是一种完备算法,搜索遍历整个问题空间,保证解的全局性,能够找到问题的解或者证明问题无解,对于优化问题,能够找到最优解,并能证明最优性。
缺陷是问题的规模变大时,算法的可衡量性非常差,而且最坏情况下,回溯具有指数复杂度。
约束满足技术[6]主要包括树搜索算法、约束传播技术和启发式修复算法。
(1) 树搜索算法。
树搜索算法又称构造算法,以回溯算法为基础,通过不断扩充一致的部分解,最后得到一致的完整解。
树搜索算法是一种系统搜索算法,搜索遍历整个问题空间,能够完全确定某约束问题有解还是无解。
最坏情况下,树搜索具有指数复杂度。
树搜索基本算法是回溯法(Back Tracking, BT),是一种既带有系统性又带有跳跃性的搜索算法。
(2) 约束传播。
约束传播是修剪搜索空间的主要技术,当一个变量被赋值或其值域发生变化后,可能对其他变量的取值造成影响,这一影响通过变量之间的约束关系进行传播,进而导致其他变量的取值或值域的上界或下界发生改变。
这一过程称为约束传播。
约束传播策略主要分为两种:回顾策略(Look Back)[7]和展望策略。
体现回顾策略的算法有BT算法、智能回溯算法。
常用的展望策略算法是前向检查(Forward Checking, FC)算法。
(3) 启发式修复算法。
启发式修复算法从有约束冲突的不可行初始解开始,通过采用约束传播等技术迭代性地进行修复,以减少冲突数目,最后得到无冲突的可行解。
启发式修复算法是一种不完备算法,不能保证解的全局性。
很多启发式方法能够被引入启发式修复算法,提高搜索效率和克服局部极值。
2.2邻域搜索算法
定义:设t ?缀T是目标函数f的一个可行解,T是所有可行解的集合,tbest ?缀T是f的目前邻域空间的最优解。
初始值tbest = t,邻域N(t)是指对一个可行解t 作部分预先规定的变动, t*是搜索邻域后所得到的另外一个可行解。
如果f(t*) < f(tbest),则tbest = t*,否则tbest = t,然后继续搜索。
总之,邻域搜索方法(Neighborhood Search Method)是一种通过对t的邻域N(t)内的可行目标函数进行再计算(iterative)来获得更好解的方法。
若邻域计算结果好于当前最优解,则保留之,否则抛弃。
邻域搜索算法通用易实现,只要设计好邻域函数,就能求解组合或函数优化问题;在搜索空间内利用局部指导规则探索优良解,搜索效率高;对于组合优化问题,
在限定的时间内,能够找到一个高质量的解。
缺陷是算法性能对邻域函数和初值具有依赖性,以损失解的完备性为代价来提高求解效率,不能够保证在规定的时间内找到解,也不能够判定问题是不可行的,而且最大的问题是容易陷入局部最优。
邻域定义的好坏对算法性能起着举足轻重的作用,如果邻域的范围较小,那么搜索就可能很快陷入局部最优,相反如果邻域的范围很大,则搜索的效率会很低。
因此,邻域搜索算法的关键是定义与具体问题相关的邻域,而对于不同问题来说,其邻域的定义也不尽相同。
3约束满足与邻域搜索结合的混合算法的一般框架
约束满足与邻域搜索单一算法均有各自的优势和劣势,两者的结合可以有效利用这两种算法的互补性,提高求解约束满足问题的能力,优化解的质量。
目前对约束满足与邻域搜索相结合的混合算法的研究内容主要包括以下几方面:
(1) 改进约束满足修复算法:如何提高初始解的质量;在约束满足修复算法中加入启发式方法,克服局部极值。
比如文献[4]列出一种解决动态生产调度问题的混合优化算法:用约束规划算法产生一个可行解,作为禁忌搜索算法的初始解,采用调度规则、变量排序算法变更禁忌表,对关键路径上的一对操作互换,进行邻域变换,但是并没有对这种混合算法进行实验分析。
(2) 约束满足树搜索与邻域搜索的结合,树搜索过程中使用邻域搜索,用约束指导搜索,利用约束传播技术修剪搜索空间;在邻域搜索过程中使用系统搜索,能够遍历当前解的邻域,提高解的全局性;变量排序方法、值排序方法、约束传播策略与搜索方法的结合。
(3) 约束满足与邻域搜索算法相结合的结合策略。
针对不同的问题,设计不同的混合算法。
但这些混合算法都有一个共同点:一种算法作为主搜索过程,另一种算法则作为改进的启发式算法。
本文参考文献[4]和文献[5],总结约束满足技术与邻域搜索算法结合的混合算法的一般框架,如图1所示。
首先针对问题的特征,建立约束满足优化问题(Constraint Satisfaction Optimization Problem, CSOP)模型;可以采用3种方式求解问题。
第一种初始变量集为空,使用约束满足树搜索方法获得初始可行解,利用约束满足求解技术变量排序方法、值排序方法选择变量和值构造树节点;约束传播对搜索空间进行修剪;约束一致性检查进行冲突检测,如果有冲突则进行回溯,再对初始可行解进行邻域搜索。
第二种初始变量集为非空,但小于变量个数,则从一个部分一致解开始进行树搜索构造方法获得初始可行解。
第三种初始变量集为变量个数,则从一个完整的初始解开始,进行邻域搜索。
可以松弛约束条件,求得一个不一致的初始完整解;也可以应用线性规划方法或其他启发式方法得到一个高质量的初始解。
下面以Job Shop调度优化问题为例。
设计混合算法步骤如下:。
