数值分析实验答案
数值分析参考答案

数值分析参考答案数值分析参考答案数值分析是一门研究使用数值方法解决数学问题的学科。
它涉及到数值计算、数值逼近、数值解法等方面的内容。
在实际应用中,数值分析可以帮助我们解决各种各样的问题,如线性方程组的求解、非线性方程的根的求解、插值、数值积分等等。
本文将给出一些数值分析常见问题的参考答案。
1. 线性方程组的求解线性方程组的求解是数值分析中的一个重要问题。
常见的求解方法有直接法和迭代法。
直接法包括高斯消元法、LU分解法等,迭代法包括雅可比迭代法、高斯-赛德尔迭代法等。
2. 非线性方程的根的求解非线性方程的根的求解是数值分析中的另一个重要问题。
常见的求解方法有二分法、牛顿法、割线法等。
其中,牛顿法是一种迭代法,通过不断迭代逼近方程的根。
3. 插值插值是数值分析中的一个常见问题,它可以用于构造函数的近似值。
常见的插值方法有拉格朗日插值法、牛顿插值法等。
这些方法通过已知的数据点来构造一个多项式函数,从而近似原函数。
4. 数值积分数值积分是数值分析中的另一个重要问题,它可以用于计算函数的定积分。
常见的数值积分方法有梯形法则、辛普森法则等。
这些方法通过将定积分转化为求和的形式,从而进行数值计算。
5. 常微分方程的数值解法常微分方程的数值解法是数值分析中的一个重要问题。
常见的数值解法有欧拉法、改进的欧拉法、龙格-库塔法等。
这些方法通过将微分方程转化为递推关系,从而逐步逼近解。
6. 线性规划问题的求解线性规划问题是数值分析中的一个重要问题,它可以用于求解最优化问题。
常见的线性规划求解方法有单纯形法、内点法等。
这些方法通过不断迭代来逼近最优解。
7. 矩阵特征值和特征向量的计算矩阵特征值和特征向量的计算是数值分析中的一个重要问题。
常见的计算方法有幂法、反幂法、QR方法等。
这些方法通过迭代来逼近矩阵的特征值和特征向量。
总结起来,数值分析是一门研究使用数值方法解决数学问题的学科。
它涉及到线性方程组的求解、非线性方程的根的求解、插值、数值积分、常微分方程的数值解法、线性规划问题的求解以及矩阵特征值和特征向量的计算等方面的内容。
(完整版)数值分析答案第三章习题

解:(1)建立假设 H0 : 0.973
n=100, x 2.62 ,s=0.06
(2)在 H0 成立的前提下,构造统计量
u x 0 ~ N (0,1)
s/ n
(3)给定 0.05 ,查得 u 1.96 ,使
2
p u u
2
(4)由样本计算,
x 62.24,s*2 404.77,问这天保险丝融化时间
分散度与通常有无明显差异( 1%)?假定融
化时间是正态母体。
解:(1)建立假设H0: 2 02 400
(2)在H
成立前提下,构造统计量
0
2
(n
1)s*2
02
~
2 (n 1)
(3)给定显著水平 0.01,查得
20.00(5 24) 45.559, 20.99(5 24) 9.886,使
:
2
2 0
1.62
s* 2.296
(2)在 H0 成立的前提下,构造统计量
2 (n 1)s* ~ 2 (n 1) 0
(3)给定 0.05 ,查得
2 (5) 14.49
2
1 2 (5) 1.237 2
(4)由样本计算,
2
6 2.296 2 1.62
12.355
2 (6) 14.49
确,收集到一组使用新安眠药的睡眠时间为
26.7,22.0,24.1,21.0,27.2,25.0,
23.4
试问:从这组数据能否说明新安眠药的睡眠时
间已达到新的疗效(假定睡眠时间服从正态分
布,取 0.05 )?
解:
x1 ~ (20.8,1.62 ) x2 ~ (, 22 )
数值分析题库答案(含详细解题步骤)

第 1 页/共 22 页1. 正方形的边长大约为100cm ,应怎样测量才干使面积误差不超过1cm 22. 已测得某场地长l 的值为110=*l m ,宽d 的值为80=*d m ,已知 2.0≤-*l l m,1.0≤-*d d m, 试求面积ld s =的绝对误差限与相对误差限.3.为使π的相对误差小于0.001%,至少应取几位有效数字?4.设x的相对误差界为δ,求n x的相对误差界.5.设有3个近似数a=2.31,b=1.93,c=2.24,它们都有3位有效数字,试计算p=a+bc的误差界和相对误差界,并问p的计算结果能有几位有效数字?第 3 页/共 22 页6. 已知333487.034.0sin ,314567.032.0sin ==,请用线性插值计算3367.0sin 的值,并预计截断误差.7. 已知sin0.32=0.314567, sin0.34=0.333487, sin0.36= 0.352274,用抛物插值计算sin0.3367的值, 并预计误差.8. 已知16243sin ,sin πππ===请用抛物插值求sin50的值,并预计误差9. . .6,8,7,4,1)(,5,4,3,2,1求四次牛顿插值多项式时设当==i i x f x第 5 页/共 22 页10. 已知4)2(,3)1(,0)1(=-=-=f f f , 求函数)(x f 过这3点的2次牛顿插 值多项式.11. 设x x f =)(,并已知483240.1)2.2(,449138.1)1.2(,414214.1)0.2(===f f f ,试用二次牛顿插值多项式计算(2.15)f 的近似值,并研究其误差12. 设],[)(b a x f 在上有四阶延续导数,试求满意条件)2,1,0()()(==i x f x P i i 及)()(11x f x P '='的插值多项式及其余项表达式.13. 给定3201219(),,1,,44f x x x x x ====试求()f x 在1944⎡⎤⎢⎥⎣⎦,上的三次埃尔米特插值多项式()P x ,使它满意11()()(0,1,2),()(),i i P x f x i P x f x ''===并写出余项第 7 页/共 22 页表达式.14. 设],1,0[,23)(2∈++=x x x x f 试求)(x f 在]1,0[上关于,,1{,1)(x span x =Φ=ρ}2x 的最佳平方逼近多项式15.已知实验数据如下:用最小二乘法求形如y=a+bx2的拟合曲线,并计算均方误差.16.已知数据表如下第 9 页/共 22 页x i 1 2 3 4 5 y iωi4 4.56 8 8.5 2 1 3 1 1试用最小二乘法求多项式曲线与此数据组拟合17. .1)(},1{span ,1]41[)(的最佳平方逼近多项式中的关于上的在在求==Φ=x x x x f ρ18. 决定求积公式⎰++≈10110)1()(32)0()(f A x f f A dx x f 中的待定参数110,,A x A , 使其代数精度尽量高,并指出所决定的求积公式的代数精度.19. 用复化辛普森公式计算积分⎰=10dx e I x , 问区间[0,1]应分多少等分才干使截断误差不超过?10215-⨯第 11 页/共 22 页20. 利用下表中给出的数据,分离用复化梯形公式和复化辛甫生公式计算定积分dx x I ln 21⎰=的近似值(要求结果保留到小数点后六位)21. 用复化梯形公式和复化辛甫生公式计算积分⎰=6.28.1)(dx x f I ,函数)(x f 在某些节点上的值如下图:(本题共14分)22. 决定公式⎰+≈101100)()()(x f A x f A dx x f x 的系数1010,,,x x A A ,使其具有最高代数精度23. 决定求积公式⎰++≈1110)1()(32)0()(f A x f f A dx x f 中的待定参数110,,A x A ,使其代数精度尽量高,并指出所决定的求积公式的代数精度第 13 页/共 22 页24.用LU 分解法求解以下方程组 (10分)123123142521831520x x x ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭25.用LU 分解法求解以下方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛8892121514131615141321x x x26. 用LU 分解法求解以下方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛542631531321321x x x27. 设方程组b Ax =,其中⎪⎪⎪⎭⎫⎝⎛-=220122101A ,Tb ⎪⎭⎫ ⎝⎛-=32,31,21, 已知它有解Tx ⎪⎭⎫⎝⎛-=0,31,21,若右端有小扰动61021-∞⨯=bδ,试预计由此引起的解的相对误差.第 15 页/共 22 页28. 设方程组b Ax =,其中212 1.0001A -⎛⎫= ⎪-⎝⎭,11.0001b -⎛⎫= ⎪⎝⎭,当右端向量b 有误差00.0001δ⎛⎫= ⎪⎝⎭b 时,试预计由此引起的解的相对误差(用∞范数计算)29. 给定b Ax =,其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111a a a a a a A 证实:(1) 当121<<-a 时,A 对称正定,从而GS 法收敛. (2) 惟独当2121<<-a 时,J 法收敛.30. 对于线性方程组⎪⎩⎪⎨⎧-=+-=-+=+1242043 16343232121x x x x x x x ,列出求解此方程组的Jacobi 迭代格式,并判断是否收敛。
(完整版)数值分析第五版答案(全)(最新整理)

第一章 绪论1.设,的相对误差为,求的误差。
0x >x δln x 解:近似值的相对误差为*x *****r e x x e x x δ-===而的误差为ln x ()1ln *ln *ln **e x x x e x =-≈进而有(ln *)x εδ≈2.设的相对误差为2%,求的相对误差。
x n x 解:设,则函数的条件数为()n f x x ='()||()p xf x C f x =又, 1'()n f x nx -= 1||n p x nx C n n-⋅∴==又((*))(*)r p r x n C x εε≈⋅ 且为2(*)r e x ((*))0.02n r x nε∴≈3.下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指出它们是几位有效数字:,, , ,*1 1.1021x =*20.031x =*3385.6x =*456.430x =*57 1.0.x =⨯解:是五位有效数字;*1 1.1021x =是二位有效数字;*20.031x =是四位有效数字;*3385.6x =是五位有效数字;*456.430x =是二位有效数字。
*57 1.0.x =⨯4.利用公式(2.3)求下列各近似值的误差限:(1) ,(2) ,(3) .***124x x x ++***123x x x **24/x x 其中均为第3题所给的数。
****1234,,,x x x x 解:*41*32*13*34*151()1021()1021()1021()1021()102x x x x x εεεεε-----=⨯=⨯=⨯=⨯=⨯***124***1244333(1)()()()()1111010102221.0510x x x x x x εεεε----++=++=⨯+⨯+⨯=⨯***123*********123231132143(2)()()()()1111.10210.031100.031385.610 1.1021385.6102220.215x x x x x x x x x x x x εεεε---=++=⨯⨯⨯+⨯⨯⨯+⨯⨯⨯≈**24****24422*4335(3)(/)()()110.0311056.430102256.43056.43010x x x x x x x εεε---+≈⨯⨯+⨯⨯=⨯=5计算球体积要使相对误差限为1,问度量半径R 时允许的相对误差限是多少?解:球体体积为343V R π=则何种函数的条件数为23'4343p R V R R C V R ππ===A A (*)(*)3(*)r p r r V C R R εεε∴≈=A 又%1(*)1r V ε=故度量半径R 时允许的相对误差限为εr (V ∗)=13∗1%=13006.设,按递推公式 (n=1,2,…)028Y =1n n Y Y -=-计算到(5位有效数字),试问计算将有多大误差?100Y 27.982≈100Y解: 1n n Y Y -=10099Y Y ∴=9998Y Y =9897Y Y =-……10Y Y =-依次代入后,有1000100Y Y =-即,1000Y Y =-, 27.982≈100027.982Y Y ∴=-*310001()()(27.982)102Y Y εεε-∴=+=⨯的误差限为。
数值分析期末实验试题及答案

A =
1 0 0 2
0 1 0 4
0 0 1 3
Jacobi输出结果:
N x1 x2 x3 err
2, 1.656250, 3.875000, 3.175000, 1.250000
3, 1.925000, 3.850000, 2.887500, 0.287500
4, 1.990625, 3.948437, 3.000000, 0.112500
Gauss-Seidel迭代法:
N x1 x2 x3 err
2, 1.875000, 3.937500, 2.962500, 0.437500
3, 1.993750, 3.992188, 2.999063, 0.118750
4, 1.998281, 3.999023, 2.999508, 0.006836
SOR迭代法
N x1 x2 x3 err
2, 1.721568, 3.608925, 2.679907, 0.233925
3, 1.824455, 3.629131, 2.727301, 0.102888
4, 1.812174, 3.627893, 2.720033, 0.012281
5, 1.814371, 3.628155, 2.721265, 0.002197
end
function[y,n]=sor(A,b,x0,ep,w)
D=diag(diag(A));
L=-tril(A,-1);
U=-triu(A,1);
B=(D-w*L)\((1-w)*D+w*U);
f=w*(D-w*L)\b;
y=B*x0+f;
n=1;
whileabs(norm(y-x0,inf))>=ep
《数值分析》所有参考答案

等价三角方程组
, ,
11.设计算机具有4位字长。分别用Gauss消去法和列主元Gauss消去法解下列方程组,并比较所得的结果。
解:Gauss消去法
回代
列主元Gauss消去
15.用列主元三角分解法求解方程组。其中
A= ,
解:
等价三角方程组
回代得
, , ,
16.已知 ,求 , , 。
解:
, ,
17.设 。证明
,(II)
,
当 时
当 时
迭代格式(II)对任意 均收敛
3) ,
构造迭代格式 (III)
,
当 时
当 时
迭代格式(III)对任意 均收敛
4)
取格式(III)
, , ,
4.用简单迭代格式求方程 的所有实根,精确至有3位有效数。
解:
当 时, ,
1 2
当 时
,
,
, ,
1)
迭代格式 ,
,
当 时, ,
任取 迭代格式收敛于
是中的一种向量范数。
解:
当 时存在 使得
,
,
所给 为 上的一个范数
18.设 。证明
(1) ;
(2) ;
(3) 。
解:(1)
(2)
(3)
19.设
A=
求 , , 及 , 。
解: ,
Newton迭代格式
,
20.设 为 上任意两种矩阵(算子)范数,证明存在常数
, 使得
对一切 均成立。
解:由向量范数的等价性知道存在正常数 使得
,
=0.187622
[23.015625 , 23.015625+0.187622]
数值分析书本答案

习题一1、取3.14,3.15,722,113355作为π的近似值,求各自的绝对误差,相对误差和有效数字的位数。
解:14.31=x312110211021--⨯=⨯≤-x π 所以,1x 有三位有效数字绝对误差:14.3-=πe ,相对误差:ππ14.3-=r e 绝对误差限:21021-⨯≤ε,相对误差限:213106110321-+-⨯=⨯⨯=r ε21122105.0105.01084074.000840174.015.315.3---⨯=⨯≤⨯==-=πx所以,2x 有两位有效数字绝对误差:15.3-=πe ,相对误差:ππ15.3-=r e 绝对误差限:11021-⨯=ε,相对误差限:11061-⨯=r ε31222105.0105.01012645.00012645.0722722---⨯=⨯≤⨯==-=πx所以,3x 有三位有效数字绝对误差:722-=πe ,相对误差:ππ722-=r e绝对误差限:21021-⨯=ε,相对误差限:21061-⨯=r ε1133551=x 7166105.0105.01032.000000032.0113355---⨯=⨯≤⨯==-π 所以,4x 有七位有效数字 绝对误差:113355-=πe ,相对误差:ππ113355-=r e绝对误差限:61021-⨯=ε,相对误差限:61061-⨯=r ε3、下列各数都是对准确数四舍五入后得到的近似数,试分别指出它们的绝对误差限和相对误差限,有效数字的位数。
5000,50.31,3015.0,0315.04321====x x x x解:0315.01=x m=-13141*10211021---⨯=⨯≤-x x 所以,n=3,1x 有三位有效数字绝对误差限:41021-⨯=ε,相对误差:2110611021-+-=⨯=n r a ε3015.02=x m=04042*10211021--⨯=⨯≤-x x所以,n=4,1x 有四位有效数字绝对误差限:41021-⨯=ε,相对误差:3110611021-+-=⨯=n r a ε50.313=x m=24223*10211021--⨯=⨯≤-x x所以,n=4,1x 有四位有效数字绝对误差限:21021-⨯=ε,相对误差:3110611021-+-=⨯=n r a ε50004=x m=44404*10211021-⨯=⨯≤-x x所以,n=4,1x 有四位有效数字绝对误差限:5.010210=⨯=ε,相对误差:23110105211021--+-=⨯=⨯=n r a ε 4、计算10的近似值,使其相对误差不超过%1.0。
数值分析实验题答案

数值分析实验报告姓名:院系:能源学院热能工程学号:2014年4月习题一实验3.2编制正交化多项式最小二乘拟合程序,并用于求解3次多项式最小二乘拟合为基的多项式最小问题,作拟合曲线的图形,计算平方误差,并与以函数{}0n k kx=二乘拟合的结果作比较表1x-1.0-0.50.00.5 1.0 1.5 2.0iy-4.447-0.4520.5510.0480.4470.549 4.552 i首先使用以函数{}0n k k为基的多项式最小二乘拟合,代码如下:x=然后使用正交化多项式方法作最小二乘拟合并画图,代码如下:拟合得到的图形如下(图1):从图形来看,二者与数据点都很吻合。
计算结果为:delta1=2.1762e-05delta2=4.4701e-04为基的多项式拟合精度更高。
可以看出对于3次多项式以{}0n k kx=图1习题二 实验4.2分别用复化Simpson 公式与变步长Simpson 公式计算,要求绝对误差限为71=102ε-⨯,输出每种方法所需的节点数和积分近似值并分析比较结果。
(1)6220()10x x x dx -+⎰ (2)10⎰ (3)6220()10x x x dx -+⎰对于复化Simpson 公式,使用事前误差估计法得到所需计算节点数,有以下误差估计公式:4(4)()()()(),(,)1802n b a h R f f a b ηη-=-∈对(1)式有:(4)22max ()36144x f x x ===0.0266h ≤75.2b aN h -≥=取76N =,计算节点数为21153N N =+= 对(2)(3)式由于其4阶导数值分布极不均匀,用最大值来估计所需计算节点数造成很大浪费,尝试多次后分别取153N =和1091N =代码如下:计算结果如下:(1)计算结果用复化Simpson公式计算:节点数:153近似值:1.161904777用变步长Simpson公式计算:节点数:77近似值:1.161904766标准值:1.161904762(2)计算结果用复化Simpson公式计算:节点数:153近似值:0.400000049用变步长Simpson公式计算:节点数:33近似值:0.400000069标准值:0.400000000(3)计算结果用复化Simpson公式计算:节点数:1091近似值:23.812135331用变步长Simpson公式计算:节点数:145近似值:23.812135297标准值:23.812135292从以上计算结果可以看出,变步长simpson公式所需节点数明显减少,因为3个函数的4阶导数在积分区间内分布都部均匀,(2)(3)式更为严重,在先范围区间内导数值远大于其他区间,只需要在这些区间增加节点数就可以达到指定精度,而Simpson公式需要在全体积分限内采用较小间距才满足条件。
清华大学高等数值分析实验设计及答案
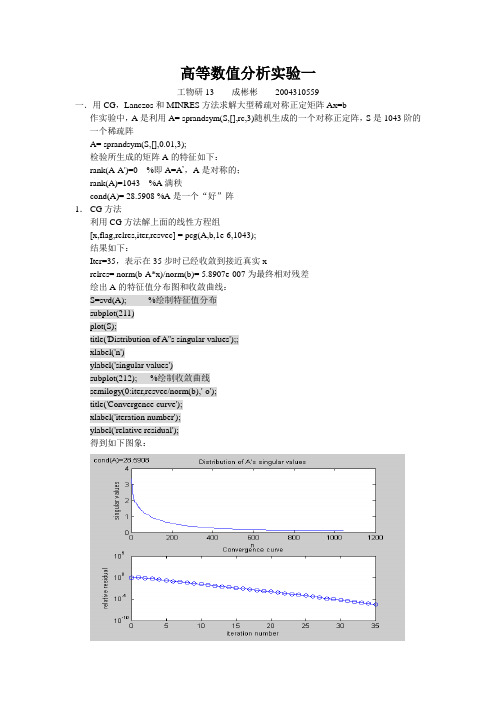
高等数值分析实验一工物研13 成彬彬2004310559一.用CG,Lanczos和MINRES方法求解大型稀疏对称正定矩阵Ax=b作实验中,A是利用A= sprandsym(S,[],rc,3)随机生成的一个对称正定阵,S是1043阶的一个稀疏阵A= sprandsym(S,[],0.01,3);检验所生成的矩阵A的特征如下:rank(A-A')=0 %即A=A’,A是对称的;rank(A)=1043 %A满秩cond(A)= 28.5908 %A是一个“好”阵1.CG方法利用CG方法解上面的线性方程组[x,flag,relres,iter,resvec] = pcg(A,b,1e-6,1043);结果如下:Iter=35,表示在35步时已经收敛到接近真实xrelres= norm(b-A*x)/norm(b)= 5.8907e-007为最终相对残差绘出A的特征值分布图和收敛曲线:S=svd(A); %绘制特征值分布subplot(211)plot(S);title('Distribution of A''s singular values');;xlabel('n')ylabel('singular values')subplot(212); %绘制收敛曲线semilogy(0:iter,resvec/norm(b),'-o');title('Convergence curve');xlabel('iteration number');ylabel('relative residual');得到如下图象:为了观察CG方法的收敛速度和A的特征值分布的关系,需要改变A的特征值:(1).研究A的最大最小特征值的变化对收敛速度的影响在A的构造过程中,通过改变A= sprandsym(S,[],rc,3)中的参数rc(1/rc为A的条件数),可以达到改变A的特征值分布的目的:通过改变rc=0.1,0.0001得到如下两幅图以上三种情况下,由收敛定理2.2.2计算得到的至多叠代次数分别为:48,14和486,由于上实验结果可以看出实际叠代次数都比上限值要小较多。
数值分析计算实习题答案

数值分析计算实习题答案数值分析计算实习题答案数值分析是一门研究如何利用计算机对数学问题进行近似求解的学科。
在数值分析的学习过程中,实习题是一种重要的学习方式,通过实践来巩固理论知识,并培养解决实际问题的能力。
本文将为大家提供一些数值分析计算实习题的答案,希望能够帮助大家更好地理解和掌握数值分析的相关知识。
一、插值与拟合1. 已知一组数据点,要求通过这些数据点构造一个一次插值多项式,并求出在某一特定点的函数值。
答案:首先,我们可以根据给定的数据点构造一个一次插值多项式。
假设给定的数据点为(x0, y0), (x1, y1),我们可以构造一个一次多项式p(x) = a0 + a1x,其中a0和a1为待定系数。
根据插值条件,我们有p(x0) = y0,p(x1) = y1。
将这两个条件代入多项式中,可以得到一个方程组,通过求解这个方程组,我们就可以确定a0和a1的值。
最后,将求得的多项式代入到某一特定点,就可以得到该点的函数值。
2. 已知一组数据点,要求通过这些数据点进行最小二乘拟合,并求出拟合曲线的表达式。
答案:最小二乘拟合是一种通过最小化误差平方和来找到最佳拟合曲线的方法。
假设给定的数据点为(x0, y0), (x1, y1),我们可以构造一个拟合曲线的表达式y =a0 + a1x + a2x^2 + ... + anx^n,其中a0, a1, ..., an为待定系数。
根据最小二乘拟合原理,我们需要最小化误差平方和E = Σ(yi - f(xi))^2,其中yi为实际数据点的y值,f(xi)为拟合曲线在xi处的函数值。
通过求解这个最小化问题,我们就可以确定拟合曲线的表达式。
二、数值积分1. 已知一个函数的表达式,要求通过数值积分的方法计算函数在某一区间上的定积分值。
答案:数值积分是一种通过将定积分转化为数值求和来近似计算的方法。
假设给定的函数表达式为f(x),我们可以将定积分∫[a, b]f(x)dx近似为Σwi * f(xi),其中wi为权重系数,xi为待定节点。
数值分析课后答案

1、解:将)(x V n 按最后一行展开,即知)(x V n 是n 次多项式。
由于ni i inn n n n i n x x x x x x x x x x V ...1...1 (1))(21110200---=,.1,...,1,0-=n i故知0)(=i n x V ,即110,...,,-n x x x 是)(x V n 的根。
又)(x V n 的最高次幂nx 的系数为)(...1...1..................1),...,,(101121112222102001101j n i j i n n n n n n n n n n n x x x x x x x x x x x x x x V -==∏-≤<≤-----------。
故知).)...()()(,...,,()(1101101------=n n n n x x x x x x x x x V x V6、解:(1)设.)(k x x f =当n k ,...,1,0=时,有.0)()1(=+x f n对)(x f 构造Lagrange 插值多项式,),()(0x l x x L j nj k j n ∑==其0)()!1()()()()(1)1(=+=-=++x w n f x L x F x R n n n n ξ,ξ介于j x 之间,.,...,1,0n j =故),()(x L x f n =即.,...,1,0,)(0n k xx l x kjnj k j ==∑=特别地,当0=k 时,10)(=∑=nj x j l。
(2)0)()1(1)()1()()(0000=-=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=--=-===∑∑∑∑k j j i j i k j ki i j ii k j nj ki i j knj j x x x x i k x l x x i k x l x x )利用(。
7、证明:以b a ,为节点进行线性插值,得)()()(1b f ab ax a f b a b x x P --+--=因0)()(==b f a f ,故0)(1=x P 。
数值分析实验报告 课后答案_【khdaw_lxywyl】

包含工大硕士生数值分析课上机试验所有试题及答案 实验一:非线性方程求解 程序1:二分法: syms f x;f=input('请输入f(x)=');A=input('请输入根的估计范围[a,b]='); e=input('请输入根的误差限e='); while (A(2)-A(1))>e c=(A(1)+A(2))/2; x=A(1); f1=eval(f); x=c;f2=eval(f); if (f1*f2)>0 A(1)=c; elseA(2)=c; end endc=(A(1)+A(2))/2;fprintf('c=%.6f\na=%.6f\nb=%.6f\n',c,A)用二分法计算方程:1.请输入f(x)=sin(x)-x^2/2请输入根的估计范围[a,b]=[1,2] 请输入根的误差限e=0.5e-005 c=1.404413 a=1.404411 b=1.4044152.请输入f(x)=x^3-x-1请输入根的估计范围[a,b]=[1,1.5] 请输入根的误差限e=0.5e-005 c=1.324717 a=1.324715 b=1.324718程序2:newton 法: syms f x;f=input('请输入f(x)=');w ww .k hd aw .c o m课后答案网df=diff(f);x0=input('请输入迭代初值x0='); e1=input('请输入奇异判断e1='); e2=input('请输入根的误差限e2='); N=input('请输入迭代次数限N='); k=1;while (k<N) x=x0; if abs(eval(f))<e1fprintf('奇异!\nx=%.6f\n 迭代次数为:%d\n',x0,k) break elsex1=x0-eval(f)/eval(df); if abs(x1-x0)<e2fprintf('x=%.6f\n 迭代次数为:%d\n',x1,k) break elsex0=x1; k=k+1; end end end if k>=Nfprintf('失败\n') end用newton 法计算方程: 1.请输入f(x)=x*exp(x)-1请输入迭代初值x0=0.5请输入奇异判断e1=0.1e-010 请输入根的误差限e2=0.5e-005 请输入迭代次数限N=10 x=0.567143 迭代次数为:42.请输入f(x)=x^3-x-1请输入迭代初值x0=1请输入奇异判断e1=0.1e-010 请输入根的误差限e2=0.5e-005 请输入迭代次数限N=10w ww .k hd aw .c o m课后答案网x=1.324718 迭代次数为:53.1:请输入f(x)=(x-1)^2*(2*x-1)请输入迭代初值x0=0.45 请输入奇异判断e1=0.1e-010 请输入根的误差限e2=0.5e-005 请输入迭代次数限N=10 x=0.500000 迭代次数为:43.2:请输入f(x)=(x-1)^2*(2*x-1)请输入迭代初值x0=0.65 请输入奇异判断e1=0.1e-010 请输入根的误差限e2=0.5e-005 请输入迭代次数限N=10 x=0.500000 迭代次数为:93.3:请输入f(x)=(x-1)^2*(2*x-1)请输入迭代初值x0=0.55 请输入奇异判断e1=0.1e-010 请输入根的误差限e2=0.5e-005 请输入迭代次数限N=10 x=0.500000 迭代次数为:4程序3:改进的newton 法: syms f x;f=input('请输入f(x)='); df=diff(f);x0=input('请输入迭代初值x0='); e1=input('请输入奇异判断e1='); e2=input('请输入根的误差限e2='); N=input('请输入迭代次数限N='); k=1;while (k<N) x=x0; if abs(eval(f))<e1fprintf('奇异!\nx=%.6f\n 迭代次数为:%d\n',x0,k) break elsew ww .k hd aw .c o m课后答案网x1=x0-2*eval(f)/eval(df); if abs(x1-x0)<e2fprintf('x=%.6f\n 迭代次数为:%d\n',x1,k) break elsex0=x1; k=k+1; end end end if k>=Nfprintf('失败\n') end用改进的newton 法计算方程: 1.请输入f(x)=(x-1)^2*(2*x-1)请输入迭代初值x0=0.55 请输入奇异判断e1=0.1e-010 请输入根的误差限e2=0.5e-005 请输入迭代次数限N=10 失败2.请输入f(x)=(x-1)^2*(2*x-1)请输入迭代初值x0=0.55 请输入奇异判断e1=0.1e-010 请输入根的误差限e2=0.5e-005 请输入迭代次数限N=20 失败3.请输入f(x)=(x-1)^2*(2*x-1)请输入迭代初值x0=0.55 请输入奇异判断e1=0.1e-010 请输入根的误差限e2=0.5e-005 请输入迭代次数限N=100 失败实验二:Gauss 列主元消去法 程序1:Gauss 列主元消去法A=input('请输入线性方程组的增广矩阵A='); n=length(A)-1; x=zeros(n,1);w ww .k hd aw .c o m课后答案网aa=zeros(n,1); for j=1:n for i=1:(n+1)AA(j,i)=abs(A(j,i)); end endfor k=1:(n-1) for i=k:naa(i-(k-1))=AA(i,k); end for i=k:nif AA(i,k)==max(aa) break end end if AA(i,k)==0 breakfprintf('方程组系数矩阵奇异\n'); else for j=k:(n+1) jh=A(i,j); A(i,j)=A(k,j); A(k,j)=jh; end endfenzi=A(k,k); for j=k:(n+1)A(k,j)=A(k,j)/fenzi; end for p=(k+1):n jj=A(p,k); for j=k:(n+1)A(p,j)=A(p,j)-jj*A(k,j); end end endif k==(n-1)x(n)=A(n,(n+1))/A(n,n); for i=(n-1):(-1):1w ww .k hd aw .c o m课后答案网he=0; for j=(i+1):nhe=he+A(i,j)*x(j); endx(i)=A(i,(n+1))-he; end end x用Gauss 列主元消去法解方程组:1.请输入线性方程组的增广矩阵A=[1e-008,2,3,1;-1,3.172,4.623,2;-2,1.072,5.643,3]x =-0.4653 -0.0700 0.38002.请输入线性方程组的增广矩阵A=[4,-2,4,10;-2,17,10,3;-4,10,9,-7];x =2.9464 0.6071 -0.14293.请输入线性方程组的增广矩阵A=[0.3e-020,1,0.7;1,1,0.9]x =0.20000.7000程序2:不选主元的高斯消去法A=input('请输入线性方程组的增广矩阵A='); n=length(A)-1; x=zeros(n,1); for k=1:(n-1) if A(k,k)==0 breakfprintf('方程组不能用普通的高斯消去法解\n'); elsefenzi=A(k,k); for j=k:(n+1)A(k,j)=A(k,j)/fenzi; endw ww .k hd aw .c o m课后答案网for p=(k+1):n jj=A(p,k); for j=k:(n+1)A(p,j)=A(p,j)-jj*A(k,j); end endx(n)=A(n,(n+1))/A(n,n); for i=(n-1):(-1):1 he=0;for j=(i+1):nhe=he+A(i,j)*x(j); endx(i)=A(i,(n+1))-he; end end end x用不选主元的Gauss 消去法解方程组:1.请输入线性方程组的增广矩阵A=[4,-2,4,10;-2,17,10,3;-4,10,9,-7];x =2.9464 0.6071 -0.14292.请输入线性方程组的增广矩阵A=[1e-008,2,3,1;-1,3.172,4.623,2;-2,1.072,5.643,3];x =-0.4653 -0.07000.38003.请输入线性方程组的增广矩阵A=[0.3e-020,1,0.7;1,1,0.9]x =0 0.7000实验三:Runge 现象的产生和克服 程序1:lagrange 多项式插值 syms f x p dp lx L; f=1/(1+25*x^2);N=input('请输入插值节点数N=');w ww .k hd aw .c o m课后答案网xx=-1:2/N:1; p=1; L=0;ff=zeros(1,length(xx)); for i=1:(N+1) x=xx(i); ff(i)=eval(f); syms x;p=p*(x-xx(i)); enddp=diff(p); for j=1:(N+1) x=xx(j); k=eval(dp); syms x;lx=p/((x-xx(j))*k); L=L+lx*ff(j); endaa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96]; for i=1:length(aa) x=aa(i);S(i)=eval(L); fff(i)=eval(f); end e=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2; ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e) ezplot(f,[-1,1]) hold onezplot(L,[-1,1]) hold onplot(xx,ff,'*') hold on plot(aa,S,'o') hold off程序2:分段线性插值 syms f x p lx; f=1/(1+25*x^2);N=input('请输入插值节点数N='); xx=-1:2/N:1; p=1; L=0;ff=zeros(1,length(xx)); for i=1:(N+1) x=xx(i); ff(i)=eval(f); end syms xw ww .k hd aw .c o m课后答案网for i=1:N for j=1:(N+1) if j==ilx(i,j)=(x-xx(i+1))/(xx(i)-xx(i+1)); else if j==i+1lx(i,j)=(x-xx(i))/(xx(i+1)-xx(i)); elselx(i,j)=0; end end end end p=lx*ff';aa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96]; for i=1:length(aa) x=aa(i); for j=1:N+1 if x<xx(j) break end endS(i)=eval(p(j-1)); fff(i)=eval(f); end e=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2; ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e) ezplot(f,[-1,1]) hold onxxx=(-1:0.01:1); for i=1:length(xxx) x=xxx(i); for j=1:N+1 if x<xx(j) break end endSS(i)=eval(p(j-1)); endplot(xxx,SS,'r') hold onplot(xx,ff,'*') hold on plot(aa,S,'o') hold off程序3:三转角插值法w ww .k hd aw .c o m课后答案网syms f x df s s1 s2 s3 s4; f=1/(1+25*x^2); df=diff(f);N=input('请输入插值节点数N='); h=2/N;xx=-1:2/N:1; p=1; L=0;ff=zeros(1,length(xx)); for i=1:(N+1) x=xx(i); ff(i)=eval(f); dff(i)=eval(df); end syms x for i=1:Ns1=(x-xx(i+1))^2*(h+2*(x-xx(i)))*ff(i)/h^3; s2=(x-xx(i))^3*(h+2*(xx(i+1)-x))*ff(i+1)/h^3; s3=(x-xx(i+1))^2*(x-xx(i))*dff(i)/h^2; s4=(x-xx(i))^2*(x-xx(i+1))*dff(i+1)/h^2; s(i)=s1+s2+s3+s4; endaa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96]; for i=1:length(aa) x=aa(i); for j=1:N+1 if x<xx(j) break end endS(i)=eval(s(j-1)); fff(i)=eval(f); end e=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2; ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e) ezplot(f,[-1,1]) hold onxxx=(-1:0.01:1); for i=1:length(xxx) x=xxx(i); for j=1:N+1 if x<xx(j) break end endSS(i)=eval(s(j-1)); endw ww .k hd aw .c o m课后答案网plot(xxx,SS,'r') hold onplot(xx,ff,'*') hold on plot(aa,S,'o') hold off程序4:三弯矩插值法: syms f x ddf s; f=1/(1+25*x^2); ddf=diff(diff(f));N=input('请输入插值节点数N='); h=2/N;xx=-1:2/N:1; p=1; L=0;ff=zeros(1,length(xx)); for i=1:(N+1) x=xx(i); ff(i)=eval(f);ddff(i)=eval(ddf); end syms x for i=1:NA=(ff(i+1)-ff(i))/h-h*(ddff(i+1)-ddff(i))/6; B=ff(i)-h^2*ddff(i)/6;s(i)=(xx(i+1)-x)^3*ddff(i)/(6*h)+(x-xx(i))^3*ddff(i+1)/(6*h)+A*(x-xx(i))+B; endaa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96]; for i=1:length(aa) x=aa(i); for j=1:N+1 if x<xx(j) break end endS(i)=eval(s(j-1)); fff(i)=eval(f); end e=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2; ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e) ezplot(f,[-1,1]) hold onxxx=(-1:0.01:1); for i=1:length(xxx) x=xxx(i);w ww .k hd aw .c o m课后答案网for j=1:N+1 if x<xx(j) break end endSS(i)=eval(s(j-1)); endplot(xxx,SS,'r') hold onplot(xx,ff,'*') hold on plot(aa,S,'o') hold off图1:观察Runge 现象图2:分段线性插值w ww .k hd aw .c o m课后答案网图3:三转角插值:w ww .k hd aw .c o m课后答案网图4:三弯矩插值:w ww .k hd aw .c o m课后答案网实验四:多项式最小二乘法程序1:要求给出插值次数的多项式最小二乘法 syms x f;xx=input('请输入插值节点 as [x1,x2...]\n'); ff=input('请输入插值节点处对应的函数值 as [f1,f2...]\n'); m=input('请输入要求的插值次数m='); n=length(xx); for i=1:(m+1) syms fai x; fai=x^(i-1); for j=1:n x=xx(j);H(i,j)=eval(fai); end endA=ff*(H)'*inv(H*(H)'); syms x; f=0; for i=1:(m+1)w ww .k hd aw .c o m课后答案网f=f+A(i)*x^(i-1); endplot(xx,ff,'*') hold onezplot(f,[xx(1),xx(n)])用此程序作出课本上的两道题: 1. 请输入插值节点 as [x1,x2...] [0 0.9 1.9 3 3.9 5.0]请输入插值节点处对应的函数值 as [f1,f2...] [0 10 30 50 80 110]请输入要求的插值次数m=2 图:2.请输入插值节点 as [x1,x2...] [0 0.9 1.9 33.9 5.0]请输入插值节点处对应的函数值 as [f1,f2...] [19.0 32.3 49.0 73.3 97.8] 请输入要求的插值次数m=2 图:w ww .k hd aw .c o m课后答案网程序2:自适应多项式最小二乘法 syms x f nihef nihe;xx=input('请输入插值节点 as [x1,x2...]\n'); ff=input('请输入插值节点处对应的函数值 as [f1,f2...]\n'); n=length(xx); for m=1:(n-1) for i=1:(m+1) syms fai x; fai=x^(i-1); for j=1:nx=xx(j);H(i,j)=eval(fai); end endA=ff*(H)'*inv(H*(H)'); syms x f; f=0; for i=1:(m+1)f=f+A(i)*x^(i-1);w ww .k hd aw .c o m课后答案网endnihef(m)=f; for i=1:n x=xx(i);niheff(i)=eval(f); ee(i)=ff(i)-niheff(i); end e(m)=0; for i=1:(n-1)e(m)=(ee(i))^2+e(m); ende(m)=sqrt(e(m)/(n*(n-1))); eee(m)=1/e(m); endfor k=1:n if eee(k)==max(eee); break end end syms x;nihe=nihef(k); emcino=e(k); plot(xx,ff,'*') hold onezplot(nihe,[xx(1),xx(n)])fprintf('插值误差为e=%.6f',emcino) 用此程序作实验中要求的题目: 3.请输入插值节点 as [x1,x2...] [3 4 5 6 7 8 9]请输入插值节点处对应的函数值 as [f1,f2...] [2.01 2.98 3.50 5.02 5.47 6.02 7.05] 插值误差为e=0.000010 图:w ww .k hd aw .c o m课后答案网实验五:龙贝格积分法 程序:龙贝格积分: syms f x;f=input('请输入积分函数f='); A=input('请输入积分区间[a,b]='); e=input('请输入误差限e='); x=A(1); fa=eval(f); x=A(2); fb=eval(f);T(1)=(A(2)-A(1))*(fa+fb)/2; m=1;x=(A(1)+A(2));t=T(1)/2+(A(2)-A(1))*eval(f)/2; while abs(t-T(1))>e t=T(1); new=0; for i=1:(2^m)x=A(1)+(2*i-1)*(A(2)-A(1))/(2^(m+1));w ww .k hd aw .c o m课后答案网new=new+eval(f); endT(m+1)=T(m)/2+(A(2)-A(1))*new/(2^(m+1)); for i=m:(-1):1 L(m,i)=T(i); end for p=m:(-1):1T(p)=((4^(m+1-p))*T(p+1)-T(p))/(4^(m+1-p)-1); endm=m+1; endfprintf('数值积分结果为T(1)=%.8f\n',T(1)); fprintf('经过了%d 次迭代\n',m);用龙贝格积分法计算积分的近似值: 1.1请输入积分函数f=x^3请输入积分区间[a,b]=[6,100] 请输入误差限e=1000数值积分结果为T(1)=25000289.75465907 经过了15次迭代1.2请输入积分函数f=x^3请输入积分区间[a,b]=[6,100] 请输入误差限e=500数值积分结果为T(1)=24999982.87732918 经过了16次迭代2.1请输入积分函数f=sin(x)/x请输入积分区间[a,b]=[0.1e-010,1] 请输入误差限e=0.1e-004数值积分结果为T(1)=0.94607740 经过了12次迭代2.2请输入积分函数f=sin(x)/x请输入积分区间[a,b]=[0.1e-010,1] 请输入误差限e=0.1e-005数值积分结果为T(1)=0.94608236 经过了15次迭代w ww .k hd aw .c o m课后答案网3.1请输入积分函数f=sin(x^2) 请输入积分区间[a,b]=[0 1] 请输入误差限e=0.0001数值积分结果为T(1)=0.31031986 经过了11次迭代3.2请输入积分函数f=sin(x^2) 请输入积分区间[a,b]=[0,1] 请输入误差限e=0.1e-005数值积分结果为T(1)=0.31026911 经过了17次迭代实验六:常微分方程初值问题的数值解法程序1:R-K 和 修正Adams 预测-校正法的组合 syms f x y;f=input('请输入f(x,y)=');jx=input('请输入计算区间[a,b]='); yy(1)=input('请输入初值y0='); h=0.1;xx=jx(1):0.1:jx(2); for n=1:3x=xx(n); y=yy(n); k1=eval(f); x=xx(n)+h/2; y=yy(n)+k1*h/2; k2=eval(f);y=yy(n)+k2*h/2; k3=eval(f); x=xx(n+1); y=yy(n)+h*k3; k4=eval(f);yy(n+1)=yy(n)+(k1+2*k2+2*k3+k4)*h/6; endc(4)=yy(4); p(4)=yy(4); for i=1:4x=xx(i); y=yy(i); ff(i)=eval(f); endfor n=4:(length(xx)-1)p(n+1)=yy(n)+(55*ff(n)-59*ff(n-1)+37*ff(n-2)-9*ff(n-3))*h/24; m(n+1)=p(n+1)+251*(yy(n)-p(n))/270; x=xx(n+1); y=m(n+1);w ww .k hd aw .c o m课后答案网fff(n+1)=eval(f);c(n+1)=yy(n)+(9*fff(n+1)+19*ff(n)-5*ff(n-1)+ff(n-2))*h/24; yy(n+1)=c(n+1)-19*(c(n+1)-p(n+1))/270; y=yy(n+1); ff(n+1)=eval(f); endplot(xx,yy,'*') hold on程序2:Runge-Kutta 法 syms f x y;f=input('请输入f(x,y)=');jx=input('请输入计算区间[a,b]='); yy(1)=input('请输入初值y0='); h=0.1;xx=jx(1):0.1:jx(2); for n=1:(length(xx)-1) x=xx(n); y=yy(n); k1=eval(f); x=xx(n)+h/2; y=yy(n)+k1*h/2; k2=eval(f);y=yy(n)+k2*h/2; k3=eval(f); x=xx(n+1); y=yy(n)+h*k3; k4=eval(f);yy(n+1)=yy(n)+(k1+2*k2+2*k3+k4)*h/6; endplot(xx,yy,'o')程序3:第一题的求解析解的程序 syms sv x jx=[-1,0];sv=dsolve('Dy=(x^2-y^2)','y(-1)=0','x'); xxx=jx(1):0.01:jx(2); for n=1:length(xxx) x=xxx(n);yyy(n)=eval(sv); endplot(xxx,yyy)w ww .k hd aw .c o m课后答案网程序4:第二题的求解析解的程序 syms sv x jx=[0,1.5];sv=dsolve('Dy=(y-2*x/y)','y(0)=1','x'); xxx=jx(1):0.01:jx(2); for n=1:length(xxx) x=xxx(n);yyy(n)=eval(sv); endplot(xxx,yyy)图1:第一题的计算图形结果图2:第二题的计算图形结果:w ww .k hd aw .c o m课后答案网w ww .k hd aw .c o m课后答案网。
数值分析书本答案

习题一1、取3.14,3.15,722,113355作为π的近似值,求各自的绝对误差,相对误差和有效数字的位数。
解:14.31=x312110211021--⨯=⨯≤-x π 所以,1x 有三位有效数字绝对误差:14.3-=πe ,相对误差:ππ14.3-=r e 绝对误差限:21021-⨯≤ε,相对误差限:213106110321-+-⨯=⨯⨯=r ε21122105.0105.01084074.000840174.015.315.3---⨯=⨯≤⨯==-=πx所以,2x 有两位有效数字绝对误差:15.3-=πe ,相对误差:ππ15.3-=r e 绝对误差限:11021-⨯=ε,相对误差限:11061-⨯=r ε31222105.0105.01012645.00012645.0722722---⨯=⨯≤⨯==-=πx所以,3x 有三位有效数字绝对误差:722-=πe ,相对误差:ππ722-=r e绝对误差限:21021-⨯=ε,相对误差限:21061-⨯=r ε1133551=x 7166105.0105.01032.000000032.0113355---⨯=⨯≤⨯==-π 所以,4x 有七位有效数字 绝对误差:113355-=πe ,相对误差:ππ113355-=r e绝对误差限:61021-⨯=ε,相对误差限:61061-⨯=r ε3、下列各数都是对准确数四舍五入后得到的近似数,试分别指出它们的绝对误差限和相对误差限,有效数字的位数。
5000,50.31,3015.0,0315.04321====x x x x解:0315.01=x m=-13141*10211021---⨯=⨯≤-x x 所以,n=3,1x 有三位有效数字绝对误差限:41021-⨯=ε,相对误差:2110611021-+-=⨯=n r a ε3015.02=x m=04042*10211021--⨯=⨯≤-x x所以,n=4,1x 有四位有效数字绝对误差限:41021-⨯=ε,相对误差:3110611021-+-=⨯=n r a ε50.313=x m=24223*10211021--⨯=⨯≤-x x所以,n=4,1x 有四位有效数字绝对误差限:21021-⨯=ε,相对误差:3110611021-+-=⨯=n r a ε50004=x m=44404*10211021-⨯=⨯≤-x x所以,n=4,1x 有四位有效数字绝对误差限:5.010210=⨯=ε,相对误差:23110105211021--+-=⨯=⨯=n r a ε 4、计算10的近似值,使其相对误差不超过%1.0。
数值分析实验答案

实验0截断误差与舍入误差#include ”stdio.h”#include ”math.h"const double 1112=0.693147190546;const double el=5e-6;void main(){mt sign;double s;long i;s=0.0;sign=l;i=l;wliile(fabs(hi2-s)>=el){s+=(1.0/i)*sign;sign=-sign:i++;}戸山1厅(”11=%1(1皿1);getch();}实验1拉格朗口插值法编写拉格朗口插值法通用子程序,并用以下函数表来上机求/(0.15)丿(0・31)。
#include <stdio.h>main(){static float Lx[10],Ly[10]; mt nj j;float xyp; pnntf(M enter n=M); scanfC%cT,&n); pnntf(M enter xfoT);fbr(i=0;i<n;i-H-) scanf(H%f\&Lx[i]);pnntf(M enter yi\n n); fbr(i=0;i<n;i-H-) scanf(H%f\&Ly[i]);pnntf(M enter x=”);scanf(n%f\&x);n=6;Lx[O]=O;Lx[l]=0.1;Lx[2]=0.195;Lx[3]=0・3;Lx[4]=0.401;Lx[5]=0.5;Ly[0]=0.39894;Ly[l]=0.39695;Ly[2]=0.39142;Ly[3]=0・38138;Ly[4]=0.36812;Ly[5]=0.35206; x=0.15;*/fbr( i=O;i<n;i++){P=l;for(j=Oj<nj++){軟=J)p=p*(x-Lx[j])/(Lx[i]-Lx[j]);}y+=p*Ly[i];}prmtf(” y=%f\n",y);getch();}实验2最小二乘法测得铜导线在温度77(°C)时的电阻Ri0)如下表,求电阻与温度T的近似函数关系。
数值分析参考答案

1、确定参数p 、q 、r ,使得迭代2 丽p+d 耳=73 39爲 2 2qa 5ra p 03 ” 3 276qa 30ra 2 _ ° 9 27,3 题外话:解这样比较复杂的方程组,不太适合手算,最好自己利用 MATLAB 编写一 个小程序:附带自编小程序:syms p q r a;s1= 'sqrt(3)*p+(q*a)/3+(r*a A 2)/(9*sqrt(3))=sqrt(3)' ;s2= 'p-(2*q*a)/(3*sqrt(3))-(5*r*aA2)/27=0' ;s3= '(6*q*a)/9+(30*r*aA2)/(27*sqrt(3))=0' ;[p,q,r]=solve(s1,s2,s3,p,q,r)2、用MATLAE 编程 求著名的Van Der Pol 方程x (x 2-1)x x = 0的数值解并绘制其 时间响应曲线和状态轨迹图(给出源程序)(14分)解:先建立一个函数文件fname.m :fun cti on xdot=f name(t,x)xdot=zeros(2,1);xdot(1)=(1-x(2)A2)*x(1)-x(2);xdot(2)=x(1); 解:2迭代方程 (x) px - 2 - 5 , k =1,2,=: (x)x 2qa 5ra 2,收敛到..3,并使收敛的阶尽可能高。
(16 分)2 力,6qa 30ra (x) 4 7 - x x利用局部收敛性与收敛阶定理4 知要使收敛的阶尽可能高,需满足I * I I * ®(x )= 0® x [今 0 * 又知 (x ) 二X 则可得到以下式子: 由以上三式可解得:q¥ 3a 收敛的阶数为3。
2调用函数文件fname.m 求Van Der Pol 方程的数值解并绘制时间响应曲线和状态轨迹图: ts=[O 30]; %设置仿真时间3O 秒x0=[1;0]; %设置仿真初值[t,x]=ode45( 'fname' ,ts,xO);subplot(1,2,1),plot(t,x)subplot(1,2,2),plot(x(:,1),x(:,2))13、试确定常数A , B , C,使得数值求积公式[f(x)dx 拓Af(O)+Bf(xJ + Cf (1)具有尽可能 高的代数精度。
数值分析实验(参考答案)

数值分析上机实验学生姓名: 学号: 教师:实验1:1. 实验项目的性质和任务通过上机实验,使学生对病态问题、线性方程组求解和函数的数值逼近方法有一个初步理解。
2.教学内容和要求 1)对高阶多多项式201()(1)(2)(20)()k p x x x x x k ==---=-∏编程求下面方程的解 19()0p x x ε+=并绘图演示方程的解与扰动量ε的关系。
Matlab 程序:x=1:20;y=zeros(1,20); ve=zeros(1,21); plot(x,y,'o') hold on ; pause; for x=1:5ve(2)=10^(-x);e=roots(poly(1:20)+ve);plot(e,'*') hold on pause; end0510152025303540-20-15-10-5051015202)对2~20n =,生成对应的Hilbert 矩阵,计算矩阵的条件数;通过先确定解获得常向量b 的方法,确定方程组 n H x b =最后,用矩阵分解方法求解方程组,并分析计算结果。
Matlab 程序:for n=2:20; H=hilb(n); ca=cond(H,2) x=(1:n)'; b=H*x; [L,U]=lu(H); y=L\b;x1=U\yplot(x,x,'o',x1,x1,'*') hold on pause; end-500-400-300-200-100100200300400500-500-400-300-200-10001002003004005003)对函数 21()[1,1]125f x x x=∈-+的Chebyshev 点 (21)cos()1,2,...,12(1)kk x k n n π-==++编程进行Lagrange 插值,并分析插值结果。
Matlab 程序:function y=lagrangen(x0,y0,x) n=length(x0);m=length(x); for i=1:m z=x(i);s=0;for k=1:nL=1;for j=1:nif j~=kL=L*(z-x0(j))/(x0(k)-x0(j));endends=s+L*y0(k);endy(i)=s;endy;for n=5:20x=-1:0.01:1; y=1./(1+25*x.^2);plot(x,y,'r')hold onk=n+1:-1:1;x0=cos((2*k-1)*pi./(2*(n+1))),y0=1./(1+25*x0.^2);x=-1:0.01:1; y1=lagrangen(x0,y0,x);plot(x0,y0,'o',x,y1), pausehold off end-1-0.8-0.6-0.4-0.200.20.40.60.81-0.200.20.40.60.811.2-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.60.81。
清华大学第五版《数值分析》课后答案

第1章绪论内容提要#〜误差度量1数值分析研究两类误差:舍入误差和截断误差,由于计算机字长的有限性,对相关数据进行存储表示时便产生舍入误差,计算机必须在有限的时间内得到运行结果,于是无穷的运算过程必须截断为有限过程,由此产生截断误差,2,误差的度量分式有:绝对误差(限)、相对误差(限〗和有效数字,设?是真值工的一个近似,绝对误差为一:!相对误差为& ,绝对误差限〉和相对误X X差限6^ 〉分别是〉 |和^(:^ ^|的上限,3^对于非零近似值^的如下规格化标准形式X^ ^ 10^ X0#!1X2'&X&,&!' ?X I ^0 〈1. 1〉如果存在尽可能大的&,使得〉| & ^乂10"-",则称?有"位有效数字.进而当&^》时,称X,是有效数.4,有效数字和相对误差的关系定理1. 1 如果形如式〈1. V的有&位有效数字,则定理1.2如果形如式〈1. 0的:^的相对误差满足^|《"二" X化1-"则纟^至少有&位有效数字,二、浮点数系统对于5+ ^ + 2位的浮点数系0表示二进制阶码数值的二进制位数〃表示尾数的二进制位数,其他两位表示阶码和尾数的符号〉,机器数绝对值的范围是2-21〜22'-、实数表示的相对舍入误差限是2-'.当数据的绝对值大于22'-1时,计算机非正常停机,称之为上溢,当非零数据的绝对值小于2-2',用机器零表示,精度损失,称之为下溢,、误差传播如果在运算过程中舍入误差能够得到控制,或者舍入误差的增长不影响产生可靠的结果则纟称该算法是数值稳定的,函数值绝对误差传播公式如下^/(^" 丫) ## /(;:)〉 1 2〉^(/(^" ^-^:》#亡"";二…、^ 〉(丄门)!.^^")〉#| /'(?) |〈1.4〉、数值稳定性不同的教材对数值方法稳定性的定义有所不同,有的要求随计算过程的深入误差不增长,有的则要求误差增长速度不能太快^只要不影响产生具有有效数字的近似值即认为是稳定的,读者应注意教材中的定义.随着学习的深入,会针对各种具体算法给出稳定性的确切定义,^ 2 ^典型例题与解题技巧【例1】求!&的近似值,使其绝对误差限精确到1乂1。
数值分析实验报告答案

一、实验目的1. 理解数值分析的基本概念和常用方法;2. 掌握数值方法的基本原理和实现步骤;3. 提高编程能力和对数值问题的处理能力;4. 培养实验操作和数据分析能力。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3. 数值分析库:NumPy、SciPy三、实验内容及步骤1. 实验一:解线性方程组(1)问题背景线性方程组是数值分析中常见的求解问题,本实验以求解线性方程组为例,验证数值方法的正确性和稳定性。
(2)实验步骤1)导入NumPy库;2)定义系数矩阵A和增广矩阵B;3)调用SciPy库中的线性方程组求解函数;4)输出求解结果。
(3)实验代码```pythonimport numpy as npfrom scipy.linalg import solve# 定义系数矩阵A和增广矩阵BA = np.array([[2, 1, -1], [-3, -1, 2], [-2, 1, 2]])B = np.array([8, -11, -3])# 调用求解函数x = solve(A, B)# 输出求解结果print("解为:", x)```2. 实验二:求多项式系数(1)问题背景多项式系数的求解是数值分析中的一项基本任务,本实验以求解多项式系数为例,验证数值方法的正确性和精度。
(2)实验步骤1)导入NumPy库;2)定义多项式值;3)调用SciPy库中的多项式系数求解函数;4)输出求解结果。
(3)实验代码```pythonimport numpy as npfrom scipy.special import roots_legendre# 定义多项式值x_values = np.linspace(-1, 1, 100)y_values = np.sin(x_values)# 调用求解函数coefficients = np.polyfit(x_values, y_values, 3)# 输出求解结果print("多项式系数为:", coefficients)```3. 实验三:数值积分(1)问题背景数值积分是数值分析中的重要内容,本实验以求解定积分为例,验证数值方法的正确性和精度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验3变步长复合梯形公式
求 的近似值。
(1)编写定步长复合梯形程序求解上式;
(2)编写变步长复合梯形程序求解上式,使误差不超过10-6。
#include"math.h"
double f(double x)
{ double f1;
f1=4/(1+x*x);
return(f1) ;
}
double trapezia2(int k,double h,double a,double tn)
{ double t2n,s=0;
int i;
t2n=tn/2;
for(i=1;i<=pow(2,k);i++)
{
s+=f(a+(2*i-1)*h);
}
t2n=t2n+s*h;
return t2n;
}
void main()
{double a,b,h,Tn,T2n,e;
int n,k;
printf("please input a,b,n,e\n");
scanf("%lf%lf%d%lf",&a,&b,&n,&e);
h=b-a;
Tn=(b-a)*(f(a)+f(b))/2;
}
}
k=k+1;
}
for(k=n+1;k>=1;k--)
{
s=0;
for(l=k+1;l<=n+1;l++)
s=s+a[k][l]*b[l];
b[k]=(b[k]-s)/a[k][k];
}
return 0;
}
main()
{
static float b[20],Lx[20],Ly[20],c[20][20],ct[20][20],a[20][20];
{int i,j,k,l;
float s;
k=1;
while(k!=n+1)
{
if(a[k][k]!=0)
{
for(i=k+1;i<=n+1;i++)
{
a[i][k]=a[i][k]/a[k][k];
b[i]=b[i]-a[i][k]*b[k];
for(j=k+1;j<=n+1;j++)
a[i][j]=a[i][j]-a[i][k]*a[k][j];
i=1;
while(fabs(ln2-s)>=e1)
{s+=(1.0/i)*sign;
sign=-sign;
i++;
}
printf("n=%ld\n",i-1);
getch();
}
实验1拉格朗日插值法
编写拉格朗日插值法通用子程序,并用以下函数表来上机求 , 。
x
0.0
0.1
0.195
0.3
0.401
Lx[0]=0;
Lx[1]=0.1;
Lx[2]=0.195;
Lx[3]=0.3;
Lx[4]=0.401;
Lx[5]=0.5;
Ly[0]=0.39894;
Ly[1]=0.39695;
Ly[2]=0.39142;
Ly[3]=0.38138;
Ly[4]=0.36812;
Ly[5]=0.35206;
x=0.15;
ct[j][i]=c[i][j];
for( i=1;i<=n+1;i++)
for(j=1;j<=n+1;j++)
a[i][j]=0;
for( i=1;i<=n+1;i++)
b[i]=0;
for( i=1;i<=n+1;i++)
for(k=1;k<=n+1;k++)
for(j=1;j<=m;j++)
a[i][k]=a[i][k]+ct[i][j]*c[j][k];
printf("enter xi\n");
for(i=0;i<n;i++)
scanf("%f",&Lx[i]);
printf("enter yi\n");
for(i=0;i<n;i++)
scanf("%f",&Ly[i]);
printf("enter x=");
scanf("%f",&x);
/*
n=6;
int m,n,i,j,k=0,l;
float s,rtn;
printf("enter m=");
scanf("%d",&m);
printf("enter n=");
scanf("%d",&n);
printf("enter xi\n");
for(i=1;i<=m;i++)
scanf("%f",&Lx[i]);
i
0
1
2
3
4
5
6
(℃)
19.1
25.0
30.1
36.0
40.0
45.1
50.0
76.30
77.80
79.25
80.80
82.35
83.90
85.10
#include <stdio.h>
#include <math.h>
float gs(float a[20][20],float b[20],int n )
实验0截断误差与舍入误差
#include "stdio.h"
#include "math.h"
const double ln2=0.693147190546;
const double e1=5e-6;
void main()
{
int sign;
double sprintf("enter yi\n");
for(i=1;i<=m;i++)
scanf("%f",&Ly[i]);
for( i=1;i<=m;i++)
{ c[i][1]=1;
for(j=2;j<=n+1;j++)
c[i][j]=Lx[i]*c[i][j-1];
}
for( i=1;i<=m;i++)
for(j=1;j<=n+1;j++)
0.5
f(x)
0.39894
0.39695
0.39142
0.38138
0.36812
0.35206
#include <stdio.h>
main()
{
static float Lx[10],Ly[10];
int n,i,j;
float x,y,p;
printf("enter n=");
scanf("%d",&n);
for(i=1;i<=n+1;i++)
for(j=1;j<=m;j++)
b[i]+=ct[i][j]*Ly[j];
gs(a,b,n);
printf("\nThe result is:");
for(i=1;i<=n+1;i++)
{ j=i-1;
printf("\na[%d]=%f",j,b[i]);
}
*/
for( i=0;i<n;i++)
{ p=1;
for(j=0;j<n;j++)
{ if(i!=j)
p=p*(x-Lx[j])/(Lx[i]-Lx[j]);
}
y+=p*Ly[i];
}
printf("y=%f\n",y);
getch();
}
实验2最小二乘法
测得铜导线在温度 (℃)时的电阻 如下表,求电阻R与温度T的近似函数关系。
