ERDAS Imagine 2013 转移矩阵计算

Erdas 2013下载及破解

Erdas Imagine2013破解亲测可用，win7和win8均兼容（有图）作者: lelegan(站内联系TA)发布: 2013-03-23Erdas Imagine2013破解亲测可用，含破解文件！！！win7和win8均兼容（两环境均测试过），附件文件最详尽！有图大家自己看，自己对比哈！！！！！尤其注意：由于资源时效性，且安装文件过大，ERDAS Foundation 2013和ERDAS IMAGINE 2013可以直接从网络上下载其他资源。

但是ERDAS2013Crack.rar一定要用本文附件提供的！！！安装步骤：（1）先安装ERDAS Foundation 2013，再安装ERDAS IMAGINE 2013。

复制bin_crack 目录所有文件到安装目录:\Intergraph\ERDAS IMAGINE 2013\bin\Win32Release覆盖原版文件；（2）复制licensing_crack目录所有文件到安装目录:\Program Files (x86)\Intergraph\Lice nsing\11.10.1\Program覆盖原版文件，以管理员身份（下划线处很重要，不然可能出错）运行flexlm.ecc.generic.patcher.exe，点击patch，并选择INGRTS_libFNP.dll文件并破解,修改license.dat中计算机名为你的计算机名；（3）运行lmtools.exe，点击config services，新建service name：Intergraph License S erver，首先在第一栏选择安装目录:\Program Files (x86)\Intergraph\Licensing\11.10.1\Pr ogram下的lmgrd文件；第二栏选择刚改名的许可证文件license.dat；第三栏可以将压缩包中的Erdas.log文件拷到任意目录下，然后选择其所放置路径即可。

马尔科夫转移矩阵

马尔科夫转移矩阵(2012-01-14 18:47:32)分类：工作篇标签：校园马尔科夫转移矩阵法在预测市场占有率上，是运用转移概率矩阵对市场占有率进行市场趋势分析的方法。

马尔科夫是俄国数学家，他在20世纪初发现：一个系统的某些因素在转移中，第n次结果只受第n-1的结果影响，只与当前所处状态有关，与其他无关。

在马尔科夫分析中，引入状态转移这个概念。

所谓状态是指客观事物可能出现或存在的状态；状态转移是指客观事物由一种状态转穆到另一种状态的概率。

一、马尔科夫转移矩阵法的涵义定义单个生产厂家的产品在同类商品总额中所占的比率，称为该厂产品的市场占有率。

在激烈的竞争中，市场占有率随产品的质量、消费者的偏好以及企业的促销作用等因素而发生变化。

企业在对产品种类与经营方向做出决策时，需要预测各种商品之间不断转移的市场占有率。

比如：研究一个商店的累计销售额，如果现在时刻的累计销售额已知，则未来某一时刻的累计销售额与现在时刻以前的任一时刻的累计销售额都无关。

步骤马尔科夫分析法的一般步骤为：①调查目前的市场占有率情况；②调查消费者购买产品时的变动情况；③建立数学模型；④预测未来市场的占有率。

二、马尔科夫分析模型实际分析中，往往需要知道经过一段时间后，市场趋势分析对象可能处于的状态，这就要求建立一个能反映变化规律的数学模型。

马尔科夫市场趋势分析模型是利用概率建立一种随机型的时序模型，并用于进行市场趋势分析的方法。

马尔科夫分析法的基本模型为：X(k+1)=X(k)×P 公式中：X(k)表示趋势分析与预测对象在t=k时刻的状态向量，P表示一步转移概率矩阵，X(k+1)表示趋势分析与预测对象在t=k+1时刻的状态向量。

必须指出的是，上述模型只适用于具有马尔科夫性的时间序列，并且各时刻的状态转移概率保持稳定。

若时间序列的状态转移概率随不同的时刻在变化，不宜用此方法。

由于实际的客观事物很难长期保持同一状态的转移概率，故此法一般适用于短期的趋势分析与预测。

马尔可夫模型转移矩阵怎么算

马尔可夫模型转移矩阵怎么算马尔可夫模型是用来描述离散随机过程的数学模型，常用于解决序列问题。

在马尔可夫模型中，转移矩阵是一个重要的概念，用来描述状态之间的转移概率。

那么，如何计算马尔可夫模型的转移矩阵呢？首先，我们需要明确什么是马尔可夫链。

马尔可夫链是指一个满足马尔可夫性质的随机过程，即在给定当前状态下，未来的状态只依赖于当前状态，而与过去的状态无关。

这一性质使得马尔可夫链能够简洁地描述一系列随机事件的演化过程。

在马尔可夫模型中，转移矩阵用来表示状态之间的转移概率。

假设我们有n个状态，那么转移矩阵的维度就是n×n。

矩阵中的每个元素表示从当前状态转移到下一个状态的概率。

计算转移矩阵的方法有多种，常见的有频率法和极大似然估计法。

频率法是根据观测数据中的频率来计算转移概率。

具体而言，我们需要统计每个状态出现的频率以及每个状态转移对出现的频率，然后将频率归一化得到概率。

这种方法的优点是简单直观，但对于数据量较小的情况下可能存在估计偏差。

极大似然估计法是基于最大似然估计原理来计算转移概率。

在这种方法中，我们假设转移概率服从某个分布，然后通过最大化观测数据的似然函数来选择合适的分布参数。

这种方法的优点是可以更准确地估计转移概率，但需要对分布进行假设，并且对于数据量较大的情况下计算量较大。

除了这两种方法，还有其他一些基于贝叶斯估计等的计算转移概率的方法，具体选择哪种方法可以根据实际问题和数据情况来确定。

总之，计算马尔可夫模型的转移矩阵是描述离散随机过程中状态之间转移概率的重要步骤。

通过统计观测数据或者使用估计方法，我们可以得到转移矩阵，从而进一步分析和预测随机事件的演化过程。

转移矩阵描述

转移矩阵描述
转移矩阵（Transition Matrix），又称跃迁矩阵，是俄国数学家马尔科夫提出的。

他发现，一个系统的某些因素在转移中，第n次结果只受第n-1次结果的影响，即只与当前所处状态有关，而与过去状态无关。

这种性质被称为“无后效性”或“马尔科夫性”。

在具有这种性质的系统中，状态转移的概率可以用转移矩阵来描述。

转移矩阵是一个矩阵，其元素都是非负的，且各行元素之和等于1。

这些元素用概率表示，表示在一定条件下，从一个状态转移到另一个状态的概率。

例如，在市场决策中，转移矩阵的元素可以表示市场或顾客的保留、获得或失去的概率。

转移矩阵有以下特征：
每个元素都是非负的，表示概率不能为负。

每一行元素之和等于1，这是因为一个状态转移到其他所有可能状态的概率之和必须等于1。

转移矩阵在马尔科夫链分析中有着广泛的应用。

马尔科夫链是一种随机过程，其中每个状态的未来变化只依赖于其当前状态，而与过去状态无关。

通过转移矩阵，我们可以计算出在给定初始状态下，经过一定步数后系统处于各个状态的概率分布。

除了马尔科夫链分析外，转移矩阵还广泛应用于其他领域，如物理学中的量子力学、化学中的反应动力学、生态学中的种群
动态等。

在这些领域中，转移矩阵被用来描述系统状态之间的转移概率和动态变化过程。

2-2转移矩阵的求法

3
2.2.3 对角形法与约当形法 1.矩阵的特征值互不相同， 1.矩阵A的特征值 λ1， λ2，… , λn互不相同，其状矩阵态转移矩阵可由下式求得
e
At
e λ1t = P 0
e
λ2 t
0 P −1 O λn t e
其中：是使化成对角线标准形的线性变换矩阵是使A化成对角线标准形的线性变换矩阵。其中：P是使化成对角线标准形的线性变换矩阵。
e At = α 0 (t ) I + α1 (t ) A + L + α n −1 (t ) An −1
3.待定系数 (t)的求法 3.待定系数αi(t)的求法第一种情况：的特征值互异第一种情况：A的特征值互异
e λ1t = α 0 ( t ) + α1 ( t )λ1 + L + α n−1 ( t )λ1n−1 M e λn t = α ( t ) + α ( t )λ + L + α ( t )λ n−1 0 1 n n −1 n
f (λ ) = (λI − A) = λn + a1λn −1 + a2λn − 2 + L + an −1λ + an
f ( A) = An + a1An −1 + a2 An − 2 + L + an −1 A + an I = 0
证明：证明：
adj (λI − A) (λI − A) (λI − A) = (λI − A) = I λI − A)
e λ1t
e
At
Q −1 λ3 t e

转移矩阵及其应用

转移矩阵及其应用矩阵理论是数学中的一个重要分支，而矩阵在科学中的应用非常广泛，例如在物理学、化学、工程学和经济学等领域都有涉及。

其中，转移矩阵是一种在概率理论和马尔可夫过程中常用的数学工具。

一、转移矩阵的定义转移矩阵是指某个概率分布通过一次转换后得到的新概率分布。

在具体的定义中，设有一组由状态 $i$ 转移到状态 $j$ 的概率，用$P_{i,j}$ 表示。

如果一开始某个状态分布为$\boldsymbol{\pi}=(\pi_1,\pi_2,...,\pi_n)$，则经过一次状态转移后，新的状态分布为 $\boldsymbol{\pi}'=(\pi_1',\pi_2',...,\pi_n')$，其中$\pi_i'$ 表示从状态 $i$ 转移过来的概率，即：$$\boldsymbol{\pi}'=\boldsymbol{\pi}P$$其中，$P$ 是一个 $n\times n$ 的矩阵，$P_{i,j}$ 表示从状态$i$ 转移到状态 $j$ 的概率，且这个矩阵的每一行元素之和为1，即$\sum_{j=1}^{n}P_{i,j}=1$。

二、转移矩阵的应用在实际应用中，转移矩阵有着广泛的应用，其中最常见的应用是在马尔可夫过程中。

所谓马尔可夫过程，是指某个系统在几个状态间进行转移，每次转移只和当前状态有关，而与之前的状态无关。

这个过程中涉及了许多概率问题，其中一个关键就是转移矩阵的使用。

1. 马尔可夫过程最常见的马尔可夫过程是随机游走。

假设一个人在一个无限长的一维路线上随机游走，每一步都向左或右移动一个单位长度，那么他下一次停留在哪里就只与他当前所在的位置有关，而与他之前的历史路线无关。

这就是一个典型的马尔可夫过程。

一个马尔可夫过程可以通过一个转移矩阵来描述。

例如，对于上述随机游走过程，其转移矩阵可以表示为：$$P=\begin{pmatrix}0.5 & 0.5 & 0 & 0 & \cdots & 0\\0.5 & 0 & 0.5 & 0 & \cdots & 0\\0 & 0.5 & 0 & 0.5 & \cdots & 0\\0 & 0 & 0.5 & 0 & \cdots & 0\\\vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\0 & 0 & 0 & 0 & \cdots & 1\end{pmatrix}$$其中第 $i$ 行第 $j$ 列的元素表示从第 $i$ 个状态转移到第$j$ 个状态的概率。

马尔可夫转移矩阵法计算

马尔可夫转移矩阵法计算好嘞，今天咱们聊聊马尔可夫转移矩阵法。

听起来是不是有点高深？别担心，咱们用轻松点的方式来聊，让它变得像喝茶一样舒服。

想象一下，你在一个城镇里，镇上有好多地方，比如咖啡馆、公园、电影院。

你今天想去的地方可能是咖啡馆，明天去公园，后天去电影院。

可你知道吗，这些选择其实都是在和概率打交道。

马尔可夫转移矩阵就像是你出门前先打个草稿，把每个地方和它们之间的关系写下来。

举个例子，你今天去了咖啡馆，明天想去公园。

于是，你就得看看从咖啡馆到公园的概率有多大。

这就像是你问朋友“今天我们去哪儿？”他们给你推荐几个地方，你根据这些建议做决定。

要是你每次都是随心所欲，那么你可能永远都不知道自己最爱的是哪个地方，哈哈，是吧？接着说到转移矩阵，它其实是把这些地方和概率关系整理得特别清晰。

就像你把家里的玩具整理成一排一排的，不用再找得头晕眼花。

在这个矩阵里，每一行代表你现在所在的地方，每一列代表你可能去的地方，格子里的数字就是你从当前地方转移到下一个地方的概率。

听起来有点复杂，但其实只要用心，就能把它搞明白。

就像你第一次学骑自行车，开始的时候总是摔倒，但慢慢地，你就能骑得飞起。

好了，再说说这些概率的意义。

假如从咖啡馆到公园的概率是0.6，意味着你有60%的机会选择公园。

听到这个，可能有人会想，“哇，这不是很高吗？”对呀，这就是生活中的选择嘛。

生活就是一系列的选择，有些选择让你开心，有些选择则可能让你后悔。

不过，别担心，反正生活就是这样，总有惊喜在等着你。

再回过头来，如果你把这个过程重复很多次，甚至上千次，就会发现某些地方会被你更频繁地光顾。

这就是所谓的“稳态分布”。

你可能会发现，最终你总是最爱去某个地方。

这个过程就像是你在锻炼，不管多累，久而久之，你就会适应，变得更强。

人生的道理，谁说就不能用数学来解释呢？还有个很有趣的现象。

如果你把这个矩阵再细分，你会发现有些地方是“吸收状态”，也就是说，一旦你到了那里，就不再离开，比如说“家”。

(整理)传输矩阵法.

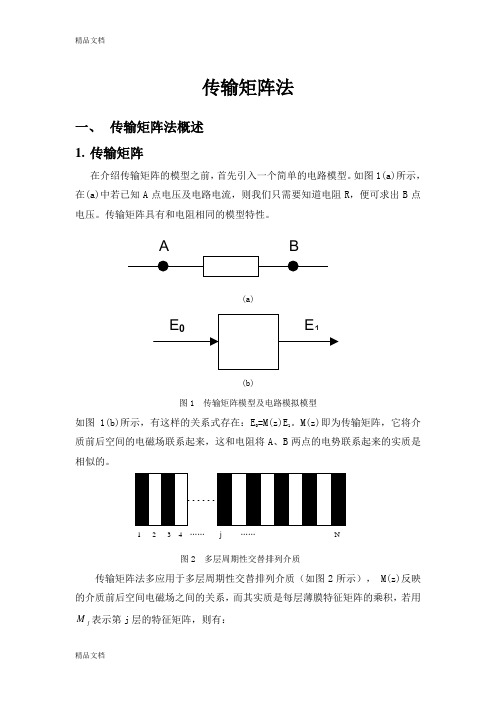
传输矩阵法一、传输矩阵法概述 1. 传输矩阵在介绍传输矩阵的模型之前，首先引入一个简单的电路模型。

如图1(a)所示，在(a)中若已知A 点电压及电路电流，则我们只需要知道电阻R ，便可求出B 点电压。

传输矩阵具有和电阻相同的模型特性。

(a)(b)图1 传输矩阵模型及电路模拟模型如图1(b)所示，有这样的关系式存在：E 0=M(z)E 1。

M(z)即为传输矩阵，它将介质前后空间的电磁场联系起来，这和电阻将A 、B 两点的电势联系起来的实质是相似的。

图2 多层周期性交替排列介质传输矩阵法多应用于多层周期性交替排列介质（如图2所示）， M(z)反映的介质前后空间电磁场之间的关系，而其实质是每层薄膜特征矩阵的乘积，若用j M 表示第j 层的特征矩阵，则有：1 2 3 4 …… j …… N（1）其中，（2）j δ为相位厚度，有（3）如公式（2）所示，j M 的表示为一个2×2的矩阵形式，其中每个矩阵元都没有任何实际物理意义，它只是一个计算结果，其推导过程将在第二部分给出。

2. 传输矩阵法在了解了传输矩阵的基础上，下面将介绍传输矩阵法的定义：传输矩阵法是将磁场在实空间的格点位置展开，将麦克斯韦方程组化成传输矩阵形式，变成本征值求解问题。

从其定义可以看出，传输矩阵法的实质就是将麦克斯韦方程转化为传输矩阵，也就是传输矩阵法的建模过程，具体如下：利用麦克斯韦方程组求解两个紧邻层面上的电场和磁场，从而可以得到传输矩阵，然后将单层结论推广到整个介质空间，由此即可计算出整个多层介质的透射系数和反射系数。

传输矩阵法的特点：矩阵元少（4个），运算量小，速度快；关键：求解矩阵元；适用介质：多层周期性交替排列介质。

二、传输矩阵的基础理论——薄膜光学理论 1.麦克斯韦方程组麦克斯韦方程组由四个场量：D 、E 、B 、H ，两个源量：J 、ρ以及反映它们之间关系的方程组成。

而且由媒质方程中的参数ε、μ、σ反映介质对电磁场的影响。

ERDAS_IMAGINE的基本操作

•
移动视窗中的查询光标，则在Inquire Cursor 窗口显示十字光标当前所在位置像元的纵横坐标（地图坐标Map、文件坐标File、地理坐标 Lat/Lon）、各波段的颜色、灰度值等信息
5 图像剖面工具
• 图像剖面工具提供了自动生成光谱剖面曲线、空间剖面曲线和三维空间剖面三种功能在菜单条单击 Raster | Profile Tools | Select profile Tool 命令，打开Select profile Tool对话框
THE END
2 ERDAS图标面板（基本用户界面）
启动ERDAS后,用户首先看到的就是ERDAS图标面板,包括菜单条和工具条两部分,其中提供了启动ERDAS软件所有模块的菜单和图标.
菜单条
工具条
3 ERDAS的基本模块与功能
1）视窗操作
Viewer：视窗操作，实现栅格图像、矢量图形、 AOI（感兴区域）等数据层的显示与基本操作。
2 数据叠加显示
• 叠加数据准备：在Viewer视窗中可同时打开多个文件，注意在打开第一个文件之后的时，一定要在 Raster Options选项卡或Vector Options选项卡中取消选中Clear Display复选框叠加数据操作：混合显示（Utility | Blend）卷帘显示（Utility | Swipe）闪烁显示（Utility | Flicker）
•
3 文件信息操作
图像信息显示： • 包括文件信息、数据层信息、投影信息、统计信息、像元灰度信息等在菜单条单击Utility | Layer Info ，打开 Layer Info窗口
•
4 光标查询功能
• 在菜单条单击 Utility | Inquire Cursor 命令，打开Inquire Cursor窗口，同时VIEWER视窗中出现十字查询光标。

ERDAS+IMAGINE

ERDAS IMAGINE遥感图像处理软件ERDAS IMAGINE是ERDAS公司开发的面向企业级的遥感图像处理系统。

它以其先进的图像处理技术，友好、灵活的用户界面和操作方式，面向广阔应用领域的产品模块，服务于不同层次用户的模型开发工具以及高度的3S（遥感图像处理，地理信息系统和全球定位系统）集成功能，为遥感及相关应用领域的用户提供了内容丰富而功能强大的图像处理工具，代表了遥感图像处理系统未来的发展趋势。

ERDAS IMAGINE是容易使用的、以遥感影像处理为主要目标的软件系列工具。

不管您处理影像的经验或是专业背景如何，通过它，您能像老练的专家一样从影像中提取重要的信息。

ERDAS IMAGINE提供大量的工具，支持对各种遥感数据源，包括航空、航天；全色、多光谱、高光谱；雷达、激光雷达等影像的处理。

呈现方式从打印地图到3D模型，ERDAS IMAGINE针对遥感影像及影像处理需求，为您提供一个全面的解决方案。

它简化了操作，工作流化您的生产线，在保证精度的前提下，为您节省了大量的时间、金钱和资源。

ERDAS IMAGINE是业界唯一一个3S 集成的企业级遥感图像处理系统，主要应用方向侧重于遥感图像处理，同时与地理信息系统的紧密结合，并且具有与全球定位系统集成的功能。

ERDAS IMAGINE通过将遥感、遥感应用、图象处理、摄影测量、雷达数据处理、地理信息系统和三维可视化等技术结合在一个系统中，实现地学工程一体化结合；无需做任何格式和系统的转换就可以建立和实现整个地学相关工程。

呈现完整的工业流程，为用户提供计算速度更快，精度更高，数据处理量更大，面向工程化的新一代遥感图像处理与摄影测量解决方案。

ERDAS IMAGINE产品架构ERDAS IMAGINE面向不同需求的用户，对于系统的扩展功能采用开放的体系结构以IMAGINE Essentials、IMAGINE Advantage、IMAGINE Professional的形式为用户提供了基本、高级、专业三档产品架构，并有丰富的功能扩展模块供用户选择，使产品模块的组合具有极大的灵活性，遥感研究和应用的用户可以根据自己的要求、资金情况选择不同的软件级别，最大程度上满足需求。

转移矩阵的建立与齐次马尔可夫过程的计算与应用

05
转移矩阵与马尔可夫过程的关系
转移矩阵与马尔可夫过程的关系概述
转移矩阵定义：描述状态转移概率的矩阵
马尔可夫过程的定义：一个随机过程，其中每个状态只与前一状态有关
转移矩阵与马尔可夫过程的关系：转移矩阵是马尔可夫过程的数学表示，用于计算状态转移概率
齐次马尔可夫过程的定义：马尔可夫过程的一种特殊形式，其中所有状态转移概率仅与时间步长有关
齐次马尔可夫过程的转移概率仅依赖于当前状态和时间步长，与其他状态和时间步长无关。
在齐次马尔可夫过程中，每个状态都有唯一的转移概率，且这些转移概率在所有时间步长上都是恒定的。
齐次马尔可夫过程可以用转移矩阵来表示，其中每个元素表示从一个状态转移到另一个状态的概率。
状态转移概率的计算
平均周期时间的计算
定义：平均周期时间是指在马尔可夫过程中，从任意状态出发，经过一定数量的步数后回到该状态所需时间的平均值。
计算方法：通过转移矩阵和状态转移概率计算平均周期时间。
应用场景：在排队论、生产制造、交通规划等领域中，平均周期时间是一个重要的性能指标。
注意事项：在计算平均周期时间时，需要考虑所有可能的状态转移和步数。
转移矩阵的建立与齐次马尔可夫过程的计算与应用
XX,a click to unlimited possibilities
汇报人：XX
目录 /目录
01
转移矩阵的建立
02
齐次马尔可夫过程的计算
03
齐次马尔可夫过程的应用
04
非齐次马尔可夫过程简介
05
转移矩阵与马尔可夫过程的关系
01 转移矩阵的建立
优势与局限：处理连续时间或离散时间的情况

ERDAS_IMAGINE_软件操作

ERDAS IMAGINE 软件培训内容一、软件概述ERDAS IMAGINE 是美国ERDAS公司开发的遥感图像处理软件。

该软件集成了图像处理软件和地理信息系统软件的功能。

广泛应用于土地利用、自然资源管理、城市规划/建设、测绘/制图、林业、设施管理、石油/地质、电力/电信、交通运输及高等教育等领域。

该软件包括的主要功能有：视窗功能、文件管理、数据输入/输出、图像裁切、图像镶嵌、几何纠正、图像解译、分类、空间建模、矢量处理、制图、Virtual GIS及航空相片的数字微分纠正和高分辨率卫星数据的正射纠正等。

二、ERDAS IMAGINE 系统功能简介2.1ERDAS8.7菜单栏由5个菜单项组成，分别为Session管理器、主菜单项（Main）、工具菜单项（Tools）、实用功能菜单项（Utilities）和帮助菜单项（Help）。

见图1：图12.1.1 Session菜单项：见图22.1.2 主菜单项（Main）：与菜单下面各图标按钮的功能一致。

见图32.1.3 工具菜单（Tools）：见图4坐标计算功能（Coordinate Calculator）：用于转换不同投影的地面控制点坐标。

2.1.4 实用功能菜单（Utilities）：见图52.1.5 帮助菜单（Help）图2图3图4图52.2ERDAS8.7图标面板工具条模块按钮功能图6●Viewer：打开视窗●Import：数据输入输出●DataPre：数据预处理●Composer：专题制图●InterPreter：图像解译●Catalog：图像库管理●Classifier：图像分类●Modeler：空间建模●Vector：矢量模块●Radar：雷达模块●Virtual GIS：虚拟GIS模块三、数据的输入输出功能ERDAS8.7 的数据输入输出模块具有强大的功能，接受和输出多种数据格式。

软件中的文件类型包括矢量数据类型和栅格数据类型。

该软件栅格数据的内部文件格式为.img，矢量数据的内部文件格式为coverage。

马尔可夫转移矩阵计算程序

马尔可夫转移矩阵计算程序马尔可夫链是一种随机过程，其中每个状态的未来变化只取决于其当前状态，而与过去状态无关。

转移矩阵是描述马尔可夫链状态之间转移概率的矩阵。

在转移矩阵中，每个元素(P_{ij}) 表示从状态 (i) 转移到状态 (j) 的概率。

以下是一个简单的Python程序，用于计算马尔可夫链的转移矩阵。

假设我们有一个马尔可夫链，其状态集为 {0, 1, 2}，并且我们有一系列的状态转移样本。

pythonimport numpy as npfrom collections import Counterdef calculate_transition_matrix(samples):# 获取所有可能的状态states = set(sample for sample in samples)num_states = len(states)# 初始化转移矩阵transition_matrix = np.zeros((num_states, num_states))# 计算每个状态转移的概率for i in range(len(samples) - 1):current_state = samples[i]next_state = samples[i + 1]# 增加从当前状态到下一个状态的转移计数transition_matrix[states.index(current_state),states.index(next_state)] += 1# 将转移计数转换为转移概率for i in range(num_states):transition_matrix[i, :] /= transition_matrix[i, :].sum()return transition_matrix# 示例数据：一系列状态转移样本samples = [0, 0, 1, 1, 2, 0, 0, 1, 2, 2, 0, 1, 2, 2, 1]# 计算转移矩阵transition_matrix = calculate_transition_matrix(samples)# 打印转移矩阵print(transition_matrix)这个程序首先获取所有可能的状态，并初始化一个转移矩阵，其中所有元素都为零。

ERDAS_IMAGINE核心模块操作手册

ERDAS IMAGINE Professional 操作手册目录第一章 ERDAS Imagine软件概述 (3)1．1 ERDAS IMAAGINE软件概述 (3)1．1．1 IMAGINE Essentials级 (3)1．1．2 IMAGINE Advantage级 (3)1．1．3 IMAGINE Professional级 (3)1．1．4 IMAGINE动态连接库 (3)1．2 启动ERDAS IMAGINE 2011 (4)1．3 ERDAS IMAGINE 功能体系 (5)第二章图像显示 (6)2．1 图像显示视窗 (6)2．2 图像显示 (6)第三章数据输入 (9)3．1 单波段二进制图像数据输入 (9)3．2 组合多波段数据 (10)第四章数据预处理 (12)4．1 图像几何校正 (12)4．2 图像拼接处理 (18)4．3 图像分幅裁剪 (29)4．3．1 规则分幅裁剪 (29)4．3．2 不规则分幅裁剪 (31)第五章图像增强处理 (33)5．1 图像增强处理的基本内容 (33)5．2 图像空间增强 (33)5．2．1 空间增强 (33)5．2．2 卷积增强处理 (33)5．2．3 纹理分析 (34)5．3 辐射增强处理 (36)5．3．1 辐射增强 (36)5．3．2 查找表拉抻处理 (36)5．3．3 直方图均衡化处理 (37)5．4 光谱增强处理 (39)5．4．1 光谱增强处理的功能 (39)5．4．2 主成份变换 (39)5．4．3 缨帽变换 (41)5．4．4 色彩变换 (43)第六章非监督分类 (45)6．1 图像分类简介 (45)6．2 非监督分类 (45)6．2．1 分类过程 (46)6．2．2 分类评价 (48)第七章监督分类 (52)7．1 定义分类模板 (52)7．2 评价分类模板 (58)7．2．1分类预警评价 (58)7．2．2 可能性矩阵 (61)7．2．3 由特征空间模板产生图像掩膜 (62)7．2．4 模板对象图示 (63)7．2．5 直方图方法 (65)7．2．6 类别的分离性 (66)7．3 执行监督分类 (68)7．4 评价分类结果 (71)7．4．1 分类叠加 (71)7．4．2 阈值处理 (71)7．4．3 分类重编码 (74)7．4．4 分类精度评估 (76)7．5 分类后处理 (79)7．5．1 聚类统计 (79)7．5．2 过滤分析 (81)7．5．3 去除分析 (82)7．5．4 分类重编码 (83)第一章ERDAS Imagine软件概述1．1 ERDAS IMAAGINE软件概述ERDAS IMAGINE是美国ERDAS公司开发的专业遥感图像处理与地理信息系统软件。

转移矩阵计算公式

转移矩阵计算公式转移矩阵是在线性代数和概率论等领域中经常会用到的一个重要概念，它有着一系列的计算公式和应用。

咱先来说说转移矩阵到底是啥。

比如说，想象一下有一群小猫咪，它们每天的状态要么是开心，要么是不开心。

假设第一天有 80%的小猫咪开心，20%不开心。

到了第二天，根据它们的心情变化规律，70%原本开心的小猫咪依然开心，30%变得不开心了；而原本不开心的小猫咪中，有 40%变得开心，60%还是不开心。

那这个描述小猫咪心情状态变化的矩阵，就是转移矩阵。

转移矩阵通常用一个方阵来表示，如果状态有 n 种，那矩阵就是n×n 的。

计算公式嘛，就拿刚才小猫咪的例子来说。

设第一天开心的小猫咪比例为 p1，不开心的比例为 p2，第二天开心的比例变成了 q1，不开心的变成了 q2。

转移矩阵 A 就可以写成：\[A =\begin{pmatrix}0.7 & 0.4 \\0.3 & 0.6\end{pmatrix}\]然后通过矩阵乘法，就能算出后续每天小猫咪的心情状态比例。

\[\begin{pmatrix}p1 \\p2\end{pmatrix}\times\begin{pmatrix}0.7 & 0.4 \\0.3 & 0.6\end{pmatrix}=\begin{pmatrix}q1 \\q2\end{pmatrix}\]我记得之前有个学生，死活搞不明白这个转移矩阵咋算。

我就跟他说，你别把它想得太复杂，就当成是小猫咪心情的变化密码。

你看啊，原本开心的小猫咪，有70%保持开心，这就是矩阵第一行第一列的0.7；30%变得不开心，就是第一行第二列的0.3。

原本不开心的小猫咪，40%变开心，那就是第二行第一列的 0.4；60%依旧不开心，就是第二行第二列的 0.6。

这学生听完，恍然大悟，后来做题可顺溜了。

在实际应用中，转移矩阵用处可大了。

比如在市场分析里，可以用它来预测消费者对不同品牌的喜好变化；在生态研究中，能推测物种数量的动态变化；在通信领域，能帮助分析信号的传输和误差校正。

概率转移矩阵计算方式

概率转移矩阵计算方式
概率转移矩阵是在马尔可夫链中使用的一种工具，用于描述系
统在不同状态之间转移的概率。

它通常表示为一个方阵P，其中P(i, j)表示系统从状态i转移到状态j的概率。

概率转移矩阵的计算方式取决于具体的马尔可夫链模型。

一般
来说，计算概率转移矩阵的步骤如下：
1. 确定状态空间，首先需要确定系统可能的状态集合，然后将
这些状态分配给矩阵的行和列。

2. 收集转移概率数据，根据系统的实际观测数据或者根据问题
的设定，收集系统在不同状态之间转移的概率数据。

3. 归一化概率，对于每个状态i，将其到达其他状态的转移概
率进行归一化处理，确保每一行的概率之和为1。

4. 构建矩阵，将归一化后的概率填入概率转移矩阵P中的相应
位置，得到完整的概率转移矩阵。

需要注意的是，概率转移矩阵的计算涉及到对系统状态转移概率的建模和估计，这通常需要依赖于具体问题的背景知识和数据。

在实际应用中，可以使用统计方法、机器学习算法或者基于领域专家的经验知识来计算概率转移矩阵。

总之，计算概率转移矩阵的方式是通过收集系统状态转移的概率数据，并将其归一化填入矩阵中，以描述系统在不同状态之间的转移概率。

转移矩阵计算

写文章的过程中，同样也用到了土地利用/景观转移矩阵。

转移矩阵的制作很多软件可以实现，有Arcview、Arcmap、还有人用matlab。

但是网上都写的都不详细，在这里，本文才用arcmap的叠加操作＋excel的数据统计功能，可以轻松完成这一过程。

相信看完了本文，初学者或者对GIS了解不多的人，也能轻松的制作出转移矩阵。

方法一：1数据准备准备好两期的coverage或shape文件。

（注意：拓扑关系要建好，不然无法计算），采用Arcmap打开上述两期文件。

2叠加操作选择Arcmap里面的“ArcToolbox”按钮下面的“Analysis Tools”工具下面的叠加分析模块（Overlay）下面的交叉分析功能（Intersect）。

选择已经打开的两期数据进行叠加分析。

叠加的结果存在一个可以找到的地方。

同时，把叠加后的结果添加在Arcmap里。

3输出叠加文件的属性数据A、右键打开intersect产生的矢量文件的数据属性表（open attribute table）。

B、点击“options”按钮，选择“add field”，然后给出一个新name“newarea”，数据类型为doubleC、右键点击刚刚产生的“newarea”，并选择“calculate values”D、然后点击“field calculator”对话框里面的“Advanced”后选择“help”将Dim Output as doubleDim pArea as IareaSet pArea = [shape]Output = pArea.area拷入到“field calculator”对话框下面的空白处E、在对话框“field calculator”最下面的空白处填上“output”F、在属性表点击“options”按钮，→export（导出），属性以.dbf格式结果存储。

4 Excel进行转移矩阵制作A、刚才存储的.dbf文件可以使用excel打开，打开的结果重新保存为.xls（excel）文件。

ENVI后处理之转移矩阵计算

ENVI后处理之转移矩阵计算转移矩阵是环境影响评价（Environmental Impact Assessment, EIA）中常用的一种分析工具。

在ENVI（Environment for Visualizing Images）后处理过程中，转移矩阵用于计算影响因素在不同环境媒介之间的转移程度，以评估环境影响的传递和累积情况。

本文将介绍转移矩阵的计算方法及其应用。

转移矩阵描述了环境影响因素在不同环境媒介之间的转移关系。

环境媒介可以是空气、水、土壤等。

转移矩阵中的每一个元素表示从一个媒介到另一个媒介的转移比例或概率。

例如，转移矩阵的第i行第j列元素表示影响因素从第i个媒介转移到第j个媒介的比例或概率。

计算转移矩阵的方法通常包括两个步骤：采样和分析。

在采样阶段，需要对环境媒介和影响因素进行采样，并获取相应的样品数据。

例如，对于水中的重金属污染，可以在不同位置采集水样，然后对水样进行化学分析，得到各个位置的重金属含量。

在分析阶段，需要对采样数据进行处理和分析，以计算转移矩阵。

常用的计算方法包括百分比、平均值、标准差、相关性等。

例如，对于水中的重金属污染情况，可以计算不同位置之间的重金属含量的平均值和标准差，并以此得到转移比例或概率。

计算得到的转移矩阵可以用于评估环境影响的传递和累积情况。

通过分析转移矩阵，可以确定哪些环境媒介对环境影响的传递起到关键作用，进而采取相应的环境保护措施。

例如，如果一些环境媒介之间的转移比例较高，则可以考虑在这些环境媒介之间设置屏障或采取其他措施，以减少环境影响的传递。

转移矩阵的计算在环境影响评价中具有广泛的应用。

例如，在工业废水排放评价中，可以计算废水中各类污染物在水体中的转移比例，以评估废水对水环境的影响程度。

在大气污染源评价中，可以计算排放源中的污染物在大气中的传输比例，以评估排放源对大气污染的贡献程度。

总结而言，转移矩阵是ENVI后处理过程中常用的一种计算方法，用于评估影响因素在不同环境媒介间的转移程度。