(完整版)《计算方法》期末考试试题
计算方法期末考试模拟试题3及参考答案

计算方法期末考试模拟试题3一选择(每题3分,合计42分)1.设A X =3.141是真值T X =π的近似值,则A X 有____位有效数字。
A 、3B 、4C 、5D 、62.用毫米刻度的直尺测量一长度为x*的物体,测得其长度的近似值为x =25mm ,其误差上限为mm 。
A 、20.510-⨯B 、10.510-⨯C 、0.5D 、53.设x =37.134678,取5位有效数字,x ≈____。
A 、37.1347B 、37.13468C 、37.135D 、37.134674.数值x *的近似值为x ,那么按定义x 的绝对误差是___。
**A B *C *D **x x x x x x x x x x ----、、、、5.用列主元高斯消去法解线性方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-20111.0310********x x x ,进行第二次列主元选择时所选取的列主元为。
A 、5B 、4C 、-2.5D 、-36.用选列主元的方法解线性方程组AX =b ,是为了。
A 、提高计算速度B 、简化计算步骤C 、降低舍入误差D 、方便计算7.以下方程求根的数值计算方法中,其迭代格式为111()()()()k k k k k k k f x x x x x f x f x +--=---的是:。
A 、二分法B 、简单迭代法C 、牛顿迭代法D 、割线法8.牛顿迭代法是用曲线f (x )上点的与x 轴的交点的横坐标逐步逼近f (x )=0的解。
A 、弧线B 、折线C 、割线D 、切线9.设b >a ,在区间[],a b 上的插值型求积公式其系数为01,,A A ┅,n A ,则01A A ++┅+n A =____。
A 、3(b-a )B 、4(b-a )C 、b-aD 、b 2-a 210.通过____个点来构造多项式的插值问题称为线性插值。
A 、1B 、2C 、3D 、411.用紧凑格式对矩阵4222222312A -⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦进行LU 三角分解,则22l =。
计算方法期末试题及答案

计算方法期末试题及答案1. 选择题1.1 下面哪种方法不适合求解非线性方程组?A. 牛顿迭代法B. 二分法C. 割线法D. 高斯消元法答案:D1.2 在计算机中,浮点数采用IEEE 754标准表示,64位浮点数的指数部分占用几位?A. 8位B. 11位C. 16位D. 64位答案:B1.3 对于一个矩阵A,转置后再乘以自身得到的是:A. AB. A^2C. A^TD. I答案:B2. 填空题2.1 假设一个函数f(x)有一个根,使用二分法求解,且初始区间为[a,b]。
若在第k次迭代后的区间长度小于等于epsilon,那么迭代次数不超过:log2((b-a)/epsilon) + 1次。
2.2 求解线性方程组Ax=b的高斯消元法的计算复杂度为:O(n^3),其中n表示矩阵A的维度。
2.3 牛顿迭代法是利用函数的局部线性化来求解方程的方法。
3. 解答题3.1 请简要说明二分法的基本原理和步骤。
答案:二分法是一种不断将区间二分的方法,用于求解函数的根。
步骤如下:1) 确定初始区间[a, b],其中f(a)和f(b)异号。
2) 计算区间中点c = (a + b) / 2。
3) 如果f(c)等于0或小于某个给定的误差限,则c为近似的根。
4) 如果f(a)和f(c)异号,则根在[a, c],令b = c;否则根在[c, b],令a = c。
5) 重复步骤2-4,直至找到满足要求的根或区间长度小于误差限。
3.2 简要描述高斯消元法的基本思想和步骤。
答案:高斯消元法是一种求解线性方程组的方法,基本思想是通过行变换将方程组化为上三角形式,然后通过回代求解。
步骤如下:1) 将增广矩阵[A | b]写为增广矩阵[R | d],其中R为系数矩阵,d为常数向量。
2) 从第一行开始,选取一个非零元素作为主元,通过行变换使得主元下方的元素为0。
3) 对剩余的行重复步骤2,直至得到上三角形矩阵。
4) 从最后一行开始,依次回代求解未知量的值。
计算方法测试题及答案
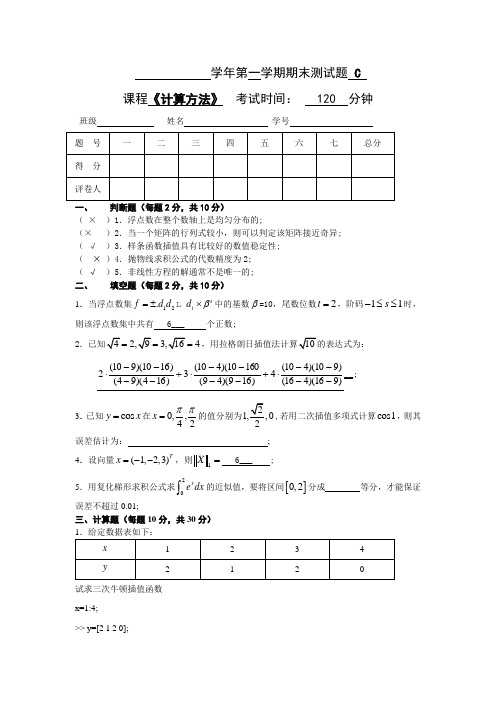
学年第一学期期末测试题 C 课程《计算方法》 考试时间: 120 分钟班级 姓名 学号 题 号 一 二 三 四 五 六 七 总分 得 分 评卷人一、判断题(每题2分,共10分)( × )1.浮点数在整个数轴上是均匀分布的;(× )2.当一个矩阵的行列式较小,则可以判定该矩阵接近奇异; ( √ )3.样条函数插值具有比较好的数值稳定性; ( × )4.抛物线求积公式的代数精度为2; ( √ )5.非线性方程的解通常不是唯一的; 二、 填空题(每题2分,共10分)1.当浮点数集12.st f d d d β=±⨯ 中的基数β=10,尾数位数2t =,阶码11s -≤≤时,则该浮点数集中共有 6___ 个正数;2.已知42,93,164===,用拉格朗日插值法计算10的表达式为:)916)(416()910)(410(4)169)(49(16010)(410(3)164)(94()1610)(910(2----⋅+----⋅+----⋅__;3.已知cos y x =在0,,42x ππ=的值分别为21,,02,若用二次插值多项式计算cos 1,则其误差估计为:________________________________;4.设向量(1,2,3)Tx =--,则=1X6___ ;5.用复化梯形求积公式求2x e dx ⎰的近似值,要将区间[]0,2分成 ___ 等分,才能保证误差不超过0.01;三、计算题(每题10分,共30分) 1.给定数据表如下:x1 2 3 4 y212试求三次牛顿插值函数 x=1:4; >> y=[2 1 2 0];>> n=length(x) D=zeros(n) D(:,1)=y'; >> for j=2:n for i=j:nD(i,j)=(D(i,j-1)-D(i-1,j-1))/(x(i)-x(i-j+1)); end end >> D D =2.0000 0 0 0 1.0000 -1.0000 0 0 2.0000 1.0000 1.0000 0 0 -2.0000 -1.5000 -0.8333 p=2.0000-1(x-1)+1(x-1)(x-2)-08333(x-1)(x-2)(x-3) 2.用最小二乘法求形如1y ax b=+(,a b 为常数)的经验公式,使它与下表数据相拟合:x0 1 2 3 y0.50000.33330.25000.2000x=0:3;>> y=[0.5000 0.3333 0.2500 0.2000]; >> subplot(2,2,1) >> plot(x,y,'+') >> subplot(2,2,2) >> plot(x,1./y ,'+')>> polyfit(x,1/.y,1)ans = 1.0000 2.0001 y=0001.21+x3.已知一组实验数据如下表: x 1 3 5 7 9 11 y 0.6595 1.7927 4.873013.246236.006997.8768试求该数据的拟合曲线。
数值计算方法期末考试题精选版

数值计算方法期末考试题Document serial number【KKGB-LBS98YT-BS8CB-BSUT-BST108】一、单项选择题(每小题3分,共15分)1. 和分别作为π的近似数具有( )和( )位有效数字. A .4和3 B .3和2 C .3和4 D .4和42. 已知求积公式()()211211()(2)636f x dx f Af f ≈++⎰,则A =( )A . 16B .13C .12D .233. 通过点()()0011,,,x y x y 的拉格朗日插值基函数()()01,l x l x 满足( )A .()00l x =0,()110l x =B .()00l x =0,()111l x =C .()00l x =1,()111l x = D .()00l x =1,()111l x =4. 设求方程()0f x =的根的牛顿法收敛,则它具有( )敛速。
A .超线性B .平方C .线性D .三次5. 用列主元消元法解线性方程组1231231220223332x x x x x x x x ++=⎧⎪++=⎨⎪--=⎩作第一次消元后得到的第3个方程( ).A .232x x -+= B .232 1.5 3.5x x -+=C .2323x x -+= D .230.5 1.5x x -=-单项选择题答案二、填空题(每小题3分,共15分)1. 设TX )4,3,2(-=, 则=1||||X ,2||||X = .2. 一阶均差()01,f x x =3. 已知3n =时,科茨系数()()()33301213,88C C C ===,那么()33C = 4. 因为方程()420x f x x =-+=在区间[]1,2上满足 ,所以()0f x =在区间内有根。
5. 取步长0.1h =,用欧拉法解初值问题()211y y yx y ⎧'=+⎪⎨⎪=⎩的计算公式 .填空题答案1. 9和292.()()0101f x f x x x --3. 184.()()120f f <5. ()1200.11.1,0,1,210.11k k y y k k y +⎧⎛⎫⎪ ⎪=+⎪ ⎪=+⎨⎝⎭⎪=⎪⎩三、计算题(每题15分,共60分)1. 已知函数211y x =+的一组数据:求分段线性插值函数,并计算()1.5f 的近似值.计算题1.答案1. 解[]0,1x ∈,()1010.510.50110x x L x x --=⨯+⨯=--- []1,2x ∈,()210.50.20.30.81221x x L x x --=⨯+⨯=-+--所以分段线性插值函数为2. 已知线性方程组1231231231027.21028.35 4.2x x x x x x x x x --=⎧⎪-+-=⎨⎪--+=⎩(1) 写出雅可比迭代公式、高斯-塞德尔迭代公式; (2) 对于初始值()()0,0,0X =,应用雅可比迭代公式、高斯-塞德尔迭代公式分别计算()1X (保留小数点后五位数字).计算题2.答案1.解 原方程组同解变形为 1232133120.10.20.720.10.20.830.20.20.84x x x x x x x x x =++⎧⎪=-+⎨⎪=++⎩ 雅可比迭代公式为()()()()()()()()()1123121313120.10.20.720.10.20.830.20.20.84m m m m m m m m m x x x x x x x x x +++⎧=++⎪⎪=-+⎨⎪=++⎪⎩(0,1...)m = 高斯-塞德尔迭代法公式()()()()()()()()()1123112131113120.10.20.720.10.20.830.20.20.84m m m m m m m m m x x x x x x x x x ++++++⎧=++⎪⎪=-+⎨⎪=++⎪⎩(0,1...)m = 用雅可比迭代公式得()()10.72000,0.83000,0.84000X = 用高斯-塞德尔迭代公式得()()10.72000,0.90200,1.16440X =3. 用牛顿法求方程3310x x --=在[]1,2之间的近似根 (1)请指出为什么初值应取2 (2)请用牛顿法求出近似根,精确到.计算题3.答案4. 写出梯形公式和辛卜生公式,并用来分别计算积分101dx x +⎰.计算题4.答案确定下列求积公式中的待定系数,并证明确定后的求积公式具有3次代数精确度证明题答案1. 设2.3149541...x *=,取5位有效数字,则所得的近似值x= .2.设一阶差商 ()()()21122114,321f x f x f x x x x --===---,()()()322332615,422f x f x f x x x x --===--则二阶差商()123,,______f x x x =3. 设(2,3,1)TX =--, 则2||||X = ,=∞||||X 。
(完整版)计算方法考试试卷及答案

《计算方法》试卷 A 第1页(共2页)《计算方法》试卷(A 卷)一、填空题(每空3分,共27分)1、若15.3=x 是π的的近似值,则误差限是 0.05 ,有 2 位有效数字。
2、方程013=--x x 在区间]2,1[根的牛顿迭代格式为1312131-)()(23231-+=---='-=+k k k k k k k k k k x x x x x x x f x f x x 。
3、对252)(23-+-=x x x f ,差商 =]3,3,3,3[432f -2 ,=]3,3,3,3,3[5432f 0 。
4、数值积分中的梯形公式为)]()([2)(b f a f ab dx x f ba+-≈⎰,Simpson 公式为 )]()2(4)([6)(b f ba f a f ab dx x f ba+++-≈⎰。
5、求解微分方程初值问题⎩⎨⎧==∈=5.01)0(]1,0['h y x xy y 用欧拉公式计算得到=1y 1 ,用改进的欧拉公式计算得到=1y 1.125 。
二、已知方程14-=x x 在区间]2,0[内有根 (1)用二分法求该方程的根,要求误差不超过0.5。
(2)写出求解方程的一种收敛的简单迭代格式,并说明收敛原因。
解:(1)由题意,令分。
3....,.........013)2(,01)0(,1)(4<-=>=+-=f f x x x f 列表如下:所以取1满足误差不超过0.5。
...........................................7 分 (2) 原方程等价变形为41+=x x ,迭代函数41)(+=x x ϕ,……………………….2分则43)1(41)(+='x x ϕ且在区间]2,0[上141)1(41)(043<<+='<x x ϕ,即1)(<'x ϕ…......5分 所以41)(+=x x ϕ单调递增且在区间]2,0[上23)2(1)()0(1044<=≤+=≤=<ϕϕϕx x ,.7分符合简单收敛的全局收敛条件,所以收敛的简单迭代格式可构造为:315+=+k k x x .............................................8 分三、利用x x f sin )(=在点2,6,0ππ的函数值:(1)建立其拉格朗日插值多项式,并进行误差分析;(2)构造差商表,建立牛顿插值多项式。
《计算方法》期末考试试题

《计算方法》期末考试试题1. 已知x*=1.xxxxxxxx8,取x=1.7320,则x具有几位有效数字?A、3B、4C、52. 取3≈1.73(三位有效数字),则3 1.73≤__。
A、0.510 3B、0.510 2C、0.510 13. 下面哪个不是数值计算应注意的问题?A、注意简化计算步骤,减少运算次数B、要避免相近两数相减C、要防止大数吃掉小数4. 对任意初始向量x()及常向量g,迭代过程x(k1)=Bx(k)g收敛的充分必要条件是__。
A、B1<1B、B<1C、(B)<15. 用列主元消去法解线性方程组,消元的第k步,选列主元arkA、maxaik(k1)<i≤n,使得ark=__。
B、maxaik(k1)<i≤nC、maxakj(k1)<j≤n6. 用选列主元的方法解线性方程组AX=b,是为了__。
A、提高计算速度B、简化计算步骤C、降低舍入误差7. 用简单迭代法求方程f(x)=0的实根,把方程f(x)=0转化为x=(x),则f(x)=0的根是__。
B、y=x与y=(x)交点的横坐标C、y=x与x轴的交点的横坐标8. 已知x=2,f(x)=46,x1=4,f(x1)=88,则一阶差商f[x,x1]为__。
9. 已知等距节点的插值型求积公式f x dx≈Akf(xk),那么A3kk=___。
10. 用高斯消去法解线性方程组,消元过程中要求aik0(k1)<i≤n。
下面哪个选项是正确的?A、a110B、a110C、akk011. 如果对不超过m次的多项式,求积公式bf(x)dx≈Akf(xk)精确成立,则该求积公式具有m次代数精度。
A、至少mB、mC、不足m12. 计算积分21dx/x,用梯形公式计算求得的值为__。
计算方法期末考试试卷(7)及解答

计算方法期末考试试卷(7)及解答一.(20分)给定代数方程01.21.12=--x x(1) 证明该方程只有唯一正根,并取步长1h = 搜索含有该正根的区间。
(2) 适当选定初值,用Newton 迭代法求该正根(精度要求210ε-= )二.(20分)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡8117152362205321x x x(1) 用全主元约当消去法求上述方程组。
(2) 建立收敛的Gauss-Seidel 迭代格式,并用此迭代格式求解上述方程组,取初值T x )0,0,0()0(=,计算到)3(x ,(保留小数点后三位数)。
三.(20分)(1(2)求解矛盾方程组 ⎪⎪⎩⎪⎪⎨⎧=+-=-=+-=-4332222121212121x x x x x x x x四.(20分)试利用函数x xe x f -=)(在节点kh x x k +=0,其中00=x ,h =1/8,k =0,1,2,3,4,5,6,7,8上的值,分别用复化Simpson 公式和复化梯形公式计算定积分⎰-10dx xe x ,(保留小数点后三位数).五.(20分)(1)取步长0.1h =,用改进的Euler 公式求解常微分方程初值问题⎩⎨⎧=='+-0)0()(y e y y x在0.3x =处的近似值。
(计算结果保留三位小数) (10分)(2)试分析改进欧拉法的局部截断误差。
参考答案及评分标准一.(20分)(1)证明:由1200x x ∆>⎧⎨<⎩ ⇒该方程只有唯一正根 (5分)由 f(0)=-2.1 f(1)<0 f(2)<0 f(3)<0可知 f(2)f(3)<0 推得 正根区间为 (2,3) (5分)(2)计算公式为)()(1k k k k x f x f x x '-=+ (4分) (3)建立计算结果表格,判断达到计算精度要求的迭代结果21010.2-± (6分)。
《计算方法》期末考试试题

《计算方法》期末考试试题一 选 择(每题3分,合计42分)1. x* = 1.732050808,取x =1.7320,则x 具有 位有效数字。
A 、3 B 、4 C 、5 D 、62. 取73.13≈(三位有效数字),则≤-73.13 。
A 、30.510-⨯B 、20.510-⨯C 、10.510-⨯D 、0.5 3. 下面_ _不是数值计算应注意的问题。
A 、注意简化计算步骤,减少运算次数B 、要避免相近两数相减C 、要防止大数吃掉小数D 、要尽量消灭误差 4. 对任意初始向量)0(x ϖ及常向量g ϖ,迭代过程g x B x k k ϖϖϖ+=+)()1(收敛的充分必要条件是__。
A 、11<B B 、1<∞BC 、1)(<B ρD 、21B <5. 用列主元消去法解线性方程组,消元的第k 步,选列主元)1(-k rka ,使得)1(-k rk a = 。
A 、 )1(1max -≤≤k ikni a B 、 )1(max -≤≤k ikni k a C 、 )1(max -≤≤k kj nj k a D 、 )1(1max -≤≤k kj nj a6. 用选列主元的方法解线性方程组AX =b ,是为了A 、提高计算速度B 、简化计算步骤C 、降低舍入误差D 、方便计算7. 用简单迭代法求方程f (x )=0的实根,把方程f (x )=0转化为x =(x ),则f (x )=0的根是: 。
A 、y =x 与y =(x )的交点B 、 y =x 与y =(x )交点的横坐标C 、y =x 与x 轴的交点的横坐标D 、 y =(x )与x 轴交点的横坐标 8. 已知x 0=2,f (x 0)=46,x 1=4,f (x 1)=88,则一阶差商f [x 0, x 1]为 。
A 、7 B 、20 C 、21 D 、42 9. 已知等距节点的插值型求积公式()()463kkk f x dx A f x =≈∑⎰,那么4kk A==∑_____。
最新国家开放大学电大本科《计算方法》期末试题标准题库及答案(试卷号:1084)

最新国家开放大学电大本科《计算方法》期末试题标准题库及答案(试卷号:1084)
考试说明:本人汇总了历年来该科的试题及答案,形成了一个完整的标准考试题库,对考生的复习和考试起着非常重要的作用,会给您节省大量的时间。
内容包含:单选题、填空题、计算题、证明题。
做考题时,利用本文档中的查找工具(Ctrl+F),把考题中的关键字输到查找工具的查找内容框内,就可迅速查找到该题答案。
本文库还有其他网核、机考及教学考一体化试题答案,敬请查看。
《计算方法》题库一
试题答案及评分标准(仅供参考)
《计算方法》题库二
试题答案及评分标准(仅供参考)
《计算方法》题库三
试题答案及评分标准(仅供参考)
《计算方法》题库四
试题答案及评分标准(仅供参考)
《计算方法》题库五一、单项选择题(每小题5分,共15分)
二、填空题(每小题5分,共15分)
三、计算题(每小题15分,共60分)
四、证明题(本题10分)
试题答案及评分标准
(仅供参考)
《计算方法》题库六
试题答案及评分标准(仅供参考)。
数值分析计算方法期末考试(一) +答案

4. 计算积分 1 x dx , 取 4 位有效数字, 用梯形公式计算求得的值为_______,用辛普森 0.5 公式计算求得的值为_____________.
5. 设 f (x) 可微, 求方程 x f (x) 根的牛顿迭代格式是______________________.
=
2
x
3 k
+1 ,
(k
3xk2 − 3
= 0,
1,
2,) ,
计算得
x0 = 2, x1 = 1.8889, x2 = 1.8795, 由 | x2 − x* |≈ 1.148 ×10−4 < 5 ×10−5 ,
所以 x ≈ 1.8795
(2) 用弦截法:
xk +1
= xk
−
f
(
xk
f )
(xk −f
1 x2 式,并用它分别计算 x 1 处的值.
3 2. 求三个不同的节点 x0 , x1, x2 和常数 c ,使求积公式
1
1 f (x) dx c[ f (x0 ) f (x1) f (x2 ) ]
具有尽可能高的代数精确度.
3. 用最小二乘法求下列数据的线性拟合函数 y ax b
xi -2
Lagrange 插值多项式为
f (−1) = 1 , f (0) = 1, f (1) = 1 . 由 此 确 定 的 二 次
2
2
L2 (x)
=
x(x −1) (−1)(−1 −1)
f
(−1) +
(x + 1)(x −1) (0 + 1)(0 −1)
数值计算方法期末考试题

一、单项选择题〔每题3分,共15分〕1. 3.142和3.141分别作为π的近似数具有〔〕和〔〕位有效数字. A .4和3 B .3和2C .3和4D .4和42. 求积公式()()211211()(2)636f x dx f Af f ≈++⎰,那么A =〔〕A .16B .13C .12D .233. 通过点()()0011,,,x y x y 的拉格朗日插值基函数()()01,l x l x 满足〔 〕A .()00l x =0,()110l x = B .()00l x =0,()111l x =C .()00l x =1,()111l x = D .()00l x =1,()111l x =4. 设求方程()0f x =的根的牛顿法收敛,那么它具有〔 〕敛速。
A .超线性B .平方C .线性D .三次5. 用列主元消元法解线性方程组1231231220223332x x x x x x x x ++=⎧⎪++=⎨⎪--=⎩ 作第一次消元后得到的第3个方程〔 〕.A .232x x -+= B .232 1.5 3.5x x -+=C .2323x x -+= D .230.5 1.5x x -=-单项选择题答案1.A2.D3.D4.C5.B二、填空题〔每题3分,共15分〕1. 设TX )4,3,2(-=, 那么=1||||X ,2||||X = .2. 一阶均差()01,f x x =3. 3n =时,科茨系数()()()33301213,88C C C ===,那么()33C = 4. 因为方程()420x f x x =-+=在区间[]1,2上满足 ,所以()0f x =在区间有根。
5. 取步长0.1h =,用欧拉法解初值问题()211yy yx y ⎧'=+⎪⎨⎪=⎩的计算公式 .填空题答案5. ()1200.11.1,0,1,210.11k k y y k k y +⎧⎛⎫⎪ ⎪=+⎪ ⎪=+⎨⎝⎭⎪=⎪⎩三、计算题〔每题15分,共60分〕1. 函数211y x =+的一组数据:求分段线性插值函数,并计算()1.5f 的近似值.计算题1.答案1. 解[]0,1x ∈,()1010.510.50110x x L x x --=⨯+⨯=---[]1,2x ∈,()210.50.20.30.81221x x L x x --=⨯+⨯=-+--所以分段线性插值函数为()[][]10.50,10.80.31,2x x L x x x ⎧-∈⎪=⎨-∈⎪⎩()1.50.80.3 1.50.35L =-⨯=2. 线性方程组1231231231027.21028.35 4.2x x x x x x x x x --=⎧⎪-+-=⎨⎪--+=⎩〔1〕 写出雅可比迭代公式、高斯-塞德尔迭代公式;〔2〕 对于初始值()()0,0,0X =,应用雅可比迭代公式、高斯-塞德尔迭代公式分别计算()1X〔保存小数点后五位数字〕.计算题2.答案1.解 原方程组同解变形为 1232133120.10.20.720.10.20.830.20.20.84x x x x x x x x x =++⎧⎪=-+⎨⎪=++⎩雅可比迭代公式为()()()()()()()()()1123121313120.10.20.720.10.20.830.20.20.84m m m m m m m m m x x x x x x x x x +++⎧=++⎪⎪=-+⎨⎪=++⎪⎩(0,1...)m =高斯-塞德尔迭代法公式()()()()()()()()()1123112131113120.10.20.720.10.20.830.20.20.84m m m m m m m m m x x x x x x x x x ++++++⎧=++⎪⎪=-+⎨⎪=++⎪⎩ (0,1...)m =用雅可比迭代公式得()()10.72000,0.83000,0.84000X =用高斯-塞德尔迭代公式得()()10.72000,0.90200,1.16440X =3. 用牛顿法求方程3310x x --=在[]1,2之间的近似根 〔1〕请指出为什么初值应取2?〔2〕请用牛顿法求出近似根,准确到0.0001.计算题3.答案3. 解()331f x x x =--,()130f =-<,()210f =>()233f x x '=-,()12f x x''=,()2240f =>,故取2x =作初始值4. 写出梯形公式和辛卜生公式,并用来分别计算积分111dxx+⎰.计算题4.答案四、证明题〔此题10分〕确定以下求积公式中的待定系数,并证明确定后的求积公式具有3次代数准确度()()()()1010hhf x dx A f h A f A f h --=-++⎰证明题答案1. 设2.3149541...x *=,取5位有效数字,那么所得的近似值x= .2.设一阶差商()()()21122114,321f x f x f x x x x --===---,()()()322332615,422f x f x f x x x x --===--那么二阶差商()123,,______f x x x =3. 设(2,3,1)TX =--, 那么2||||X = ,=∞||||X 。
江理数值分析(计算方法)期末试卷3及参考答案

5 2
2xk3 5 3xk2 2
将 x0 1.5 代入上式,得
x1 1.34286 , x2 1.37012 , x3 1.32920 , x4 1.32827 , x5 1.32826
x5 x4 0.00001 104
所以,方程的近似根
x5 1.32826
5.解,Jacobi 迭代公式是:
(2) 求出用 Jacobi 迭代法和 Gauss-Seidel 迭代法求解该方程组的迭代
序列,同时证明该迭代法是收敛的。
矩阵.并判断用 Gauss-Seidel 迭代法求解该方程组的收敛性。(15 分)
第 3 页 ︵ 共 3 页 ︶
姓名
江 西 理 工 大 学 教 务 处
专业、班级
2007-2008-2 数值分析 A 参考答案
一. 填空(每空 3 分,共 30 分)
1. 截断误差
2. x(x 2) , x(x 1) ,
10
3. 1
2
4. xk1
xk
xk2 2xk
f (xk ) f (xk )
5. 6,5, 26 ,9
二. 计算
1. 构造重节点的差商表:
n
x
y
一阶 二阶 三阶
0
1
0
1
2
-5
-5
2
3
-6
-1
2
3
4
3
9
5
72
3.解:改进的 Euler 公式是:
具体到本题中,求解的公式是:
代入求解得: y1 1.4 , y1 1.54
y2 2.276, y2 2.4832
yn1 yn hf (xn , yn )
yn1
计算方法期末试题

楚雄师范学院2010-2011学年第一学期期末测试题 B课程《计算方法》考试时间: 120 分钟班级姓名学号判断题(每题2分, 共10分)(√)1. 浮点数构成有限集合;(√)2.当一个矩阵的条件数较大, 则该矩阵为病态矩阵;( X )3. 高次的Lagrange插值多项式很常用;( X )4. 梯形求积公式的代数精度为2;一、(√)5. Newton法有可能不收敛;填空题(每题2分, 共10分)1. 当浮点数集中的基数=2, 尾数位数, 阶码时, 则该浮点数集中共有28 个正数;2. 已知, 用拉格朗日插值法计算的表达式为: ;3. 已知在的值分别为,若用二次插值多项式计算, 则其误差估计为: ;4. 设向量, 则;5. 用复化梯形求积公式求的近似值, 要将区间分成 3 等分, 才能保证误差不超过0.01;三、计算题(每题10分, 共30分)试求三次牛顿插值函数。
解: 先构造牛顿插值差分表,>> x=1:4;y=[1 0 1 2];>> n=length(x);>> D=zeros(n);>> D(:,1)=y';>> for j=2:nfor i=j:nD(i,j)=(D(i,j-1)-D(i-1,j-1))/(x(i)-x(i-j+1));endend>> DD =1.0000 0 0 00 -1.0000 0 01.0000 1.0000 1.0000 02.0000 1.0000 0 -0.3333 故所求三次牛顿插值函数为:3()1(1)(1)(2)0.3333(1)(2)(3)P x x x x x x x =--+------解: 为求出待定系数 将函数 变形为:令 , 则所求函数变形为线性函数: (3分) 由最小二乘法原理, 可得正规方程组:444211144114i i i i i i i i i i i a x b x x Y a x b Y =====⎧+=⎪⎪⎨⎪+=⎪⎩∑∑∑∑∑ (2分)利用MA TLAB 的polyfit(x,1./y,1)命令可得:故所求拟合函数为: (5分)试求该数据的拟合曲线。
2019-2020学年第一学期期末考试《计算方法》大作业答案

吉林大学网络教育学院2019-2020学年第一学期期末考试《计算方法》大作业答案学生姓名专业层次年级学号学习中心成绩年月日作业完成要求:大作业要求学生手写,提供手写文档的清晰扫描图片,并将图片添加到word文档内,最终wod文档上传平台,不允许学生提交其他格式文件(如JPG,RAR等非word文档格式),如有雷同、抄袭成绩按不及格处理。
一、解线性方程(每小题8分,共80分)1、用矩阵的LU分解算法求解线性方程组X1+2X2+3X3= 02X1+2X2+8X3= -4-3X1-10X2-2X3= -11答:2、用矩阵的Doolittle分解算法求解线性方程组X1+2X2+3X3= 12X1– X2+9X3= 0-3X1+ 4X2+9X3= 1答:3、用矩阵的Doolittle分解算法求解线性方程组2X1+X2+X3= 46X1+4X2+5X3=154X1+3X2+6X3= 13答:4、用高斯消去法求解线性方程组2X1- X2+3X3= 24X1+2X2+5X3= 4-3X1+4X2-3X3= -3答:5、用无回代过程消元法求解线性方程组2X1- X2+3X3= 24X1+2X2+5X3= 4-3X1+4X2-3X3= -3答:6、用主元素消元法求解线性方程组2X1- X2+3X3= 24X1+2X2+5X3= 4-3X1+4X2-3X3= -3答:7、用高斯消去法求解线性方程组1231231232344272266x x x x x x x x x -+=++=-++=答:8、利用Doolittle 分解法解方程组Ax=b ,即解方程组12341231521917334319174262113x x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦ 答:9、利用Doolittle 分解法解方程组Ax=b ,即解方程组123421111443306776081011112x x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦ 答:10、用高斯消元法解方程组1237811351341231x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦答案:二、计算(每小题10分,共20分)1、已知节点x1,x2及节点处函数值f(x1),f(x2),构造线性插值多项式p1(x). 答:2、设f(xi)=i(i=0,1,2),构造二次式p2(x),使满足: p2(xi)=f(xi)(i=0,1,2)答:。
计算方法试题集及答案(新)

11、已知f(1)=2,f(2)=3,f(4)=5.9,则二次Newton插值多项式中x2系数为( 0.15 );
12、设 ,则 , 的二次牛顿插值多项式为 。
13、 是以整数点 为节点的Lagrange插值基函数,则 =1, = ,,当 时 ( )。
14、设一阶差商 , 则二阶差商
A. 5 B. 6 C. 7 D. 8
6、( D )的3位有效数字是0.236×102。
(A) 0.0023549×103 (B) 2354.82×10-2 (C) 235.418(D)235.54×10-1
7、取 计算 ,下列方法中哪种最好?( C )
(A) ; (B) ; (C) ; (D) 。
2、3.141580是π的有( B )位有效数字的近似值。
A. 6 B. 5 C. 4 D. 7
3、用 1+x近似表示ex所产生的误差是( C )误差。
A. 模型 B. 观测 C. 截断 D. 舍入
4、用1+ 近似表示 所产生的误差是( D )误差。
A. 舍入 B. 观测 C. 模型 D. 截断
5、-324.7500是舍入得到的近似值,它有( C )位有效数字。
8、若用复化梯形公式计算 ,要求误差不超过 ,利用余项公式估计,至少用477个求积节点。
9、数值积分公式 的代数精度为2。
10、已知 ,则用辛普生(辛卜生)公式计算求得 ,用三点式求得 。
答案:2.367,0.25
10、数值微分中,已知等距节点的函数值 , 则由三点的求导公式,有
11、对于n+1个节点的插值求积公式 至少具有n次代数精度.
(A) f(x,x0,x1,x2,…,xn)(x-x1)(x-x2)…(x-xn-1)(x-xn),
成人教育《计算方法 提纲》期末考试复习题及参考答案

一、单项选择题1、Jacobi迭代法解方程组Ax = b的必要条件是( C ).A.A的各阶顺序主子式不为零 B.ρ(A)<1C. D.|A|≤12、设,均差( B )A.3B. -3C. 5D.03、设,则ρ(A)为( C ).A. 2B. 5C. 7D. 34、三点的高斯求积公式的代数精度为( B ).A. 2B.5C. 3D. 45、幂法的收敛速度与特征值的分布( A )。
A. 有关B. 不一定C. 无关6、求解线性方程组Ax=b的分解法中,A须满足的条件是( B )。
A. 对称阵B. 正定矩阵C. 任意阵D. 各阶顺序主子式均不为零7、舍入误差是( A )产生的误差。
A.只取有限位数B.模型准确值与用数值方法求得的准确值C. 观察与测量D.数学模型准确值与实际值8、3.141580是π的有( B )位有效数字的近似值。
A.6B.5C. 4D. 79、幂法是用来求矩阵( A )特征值及特征向量的迭代法。
A. 按模最大B. 按模最小C. 所有的D. 任意一个10、用1+x近似表示所产生的误差是( C )误差。
A. 模型B. 观测C.截断D. 舍入11、解线性方程组的主元素消去法中选择主元的目的是( A )。
A.控制舍入误差B. 减小方法误差C.防止计算时溢出D. 简化计算12、解线性方程组Ax=b的迭代格式收敛的充要条件是( D )。
A. |M|<1B. ρ(A)<1C. |ρ(M)|<1D. ρ(M)<113、用近似表示所产生的误差是( D )误差。
A. 舍入B. 观测C.模型D. 截断14、-324.7500是舍入得到的近似值,它有( C )位有效数字。
A. 5B. 6C.7D. 815、反幂法是用来求矩阵( B )特征值及相应特征向量的一种向量迭代法。
A. 按模最大B. 按模最小C.全部D. 任意一个16、用表示自由落体运动距离与时间的关系式( g为重力加速度),是在时间t内的实际距离,则是( C )误差。
2018-2019学年第二学期期末考试《计算方法》大作业参考答案

吉林大学网络教育学院2018-2019学年第二学期期末考试《计算方法》大作业学生姓名专业层次年级学号学习中心成绩年月日一、构造次数不超过三次的多项式P3(X),使满足:(10分)P3(0)= 1;P3(1)=0;P3′(0)=P3′(1)=0。
二、设f(x i)=i(i=0,1,2),构造二次式p2(x),使满足:(10分) p2(x i)=f(x i)(i=0,1,2)三、设节点x i=i(i=0,1,2,3),f(0)=1,f(1)=0,f(2)=-7,f(3)=26,构造次数不超过3次的多项式p3(x),满足p3(x i)=f(x i),i=0,1,2,3 (10分)四、对于上题的问题,构造Newton插值多项式。
(10分)五、构造三次多项式P 3(X )满足:P 3(0)= P 3(1)=0,P 3′(0)=P 3′(1)=1。
(10分)六、利用Doolittle 分解法解方程组Ax=b 即解方程组 (15分) 12341231521917334319174262113x x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦解:用公式七、基于迭代原理证明(10分)+++=22 (22)八、构造二次多项式2()x p 满足: (10分)'010222()1;()0;()1p p p x x x ===九、构造一个收敛的迭代法求解方程3210x x --=在[1.3,1.6]内的实根。
合理选择一个初值,迭代一步,求出1x 。
(15分)作业完成要求:大作业要求学生手写,提供手写文档的清晰扫描图片,并将图片添加到word 文档内,最终word文档上传平台,不允许学生提交其他格式文件(如JPG,RAR等非word 文档格式),如有雷同、抄袭成绩按不及格处理。
计算方法及答案.docx

A. det A = 0B.detA k = 0(1 乞 k n)c. detA 0D. det A :: 0《计算方法》练习题一一、填空题1.理=3.14159…的近似值3.1428 ,准确数位是()。
2 .满足 f(a) = C, f(b) = d 的插值余项 R(X)=()。
3 .设{P k (x)}为勒让德多项式,则(F 2(χ), P 2(x)) - ( )o4 •乘幕法是求实方阵()特征值与特征向量的迭代法。
5 .欧拉法的绝对稳定实区间是()o6. e =2.71828…具有3位有效数字的近似值是( )。
7 .用辛卜生公式计算积分[fc ( ) oVHx8 .设A (kJ0 =(a (Z )第k 列主兀为a Pk J),则a (Pk A) =()10 •已知迭代法:X n 1 =(X n ), (n=0,1,…)收敛,则:(x)满足条件()。
、单选题1•已知近似数a,b,的误差限;(a), ;(b),则;(ab)=()。
A. E(a)E(b)B. E(a)+^(b)c. ag(a)+∣bw(b) D . a E (b)+'b w(a)2 .设 f(x) =X 2 X ,则 f[1,2,3]=()。
A.lB. 2C. 3D .4 3 . 设A =们 ,则化A 为对角阵的平面旋转 Q =().:1 3一ππππ A.—B .—C .—D .—23 464 . 若双点弦法收敛, 则双点弦法具有()敛速.A.线性B.超线性C.平方D .三次5 .改进欧拉法的局部截断误差阶是().A. o(h)Bo(h 2)C.o(h 3)D.o(h 4)6 .近似数 a = 20.47820 "0的误差限是()o1 一 c -51 _ -4 1__3 1 _ _2A. ×10B.×10 C.×10D . × 1022229 .已知贝TtJ 1 25 4_-7 .矩阵A满足(),则存在三角分解A=LR)&已知 X =(—1,3,-5)T ,则 X 1 =()。
计算方法考试试题及答案

2006级《计算方法》试题B 卷答案一、填空,每题4分,共34分1)a 的绝对误差界为21102-⨯,a 的相对误差界为41104-⨯;2)法方程组为:2221281824a b ππππ⎛⎫⎪⎛⎫⎛⎫⎪= ⎪ ⎪ ⎪⎝⎭⎝⎭⎪⎝⎭; ()00,,2πϕϕ=()201,,8πϕϕ=()2111,,32πϕϕ⎛⎫= ⎪⎝⎭()0,sin 1,x ϕ=()210,sin sin 1,x x xdx πϕ==⎰3)设∞=A17 ,()cond ∞=A 17×17=289;117107105757⎛⎫-⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭4)应改写为()()()()()()()1608116171814131x x x x x x x x x +++--+---5)均差[0,1,2]f = 0 ,()()()0212x x l x --=;6)此数值求积公式的代数精度为: 3 ; 7)求解1u u t e -'=-+-的隐式Euler :()1111n n n u t ehu h-+++-=+;8)用二分法进行一步后根所在区间为: [ 1, 2]。
9)TLL 分解为:10122101⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭; 10) [0,1]上以1()lnx xρ=权函数的正交多项式()0x φ= 1 ,()1x φ=14x -。
11);11,0,1,2,1kkx k k k x x e x x k e+--=-=+12) 正交矩阵22112123122⎛⎫⎪=⨯-- ⎪⎪-⎝⎭H :二、计算题1.(15分)解:已知,21,α=10,α=01,α=-20,β=11,2β=032β=。
0110,c =-=11320,22c =--=211320222c ⎛⎫=⨯-=≠ ⎪⎝⎭,故此为二步一阶方法。
局部误差主项为:()()2332n h u t O h''-+。
又()21ρλλ=-,满足根条件,故此差分格式收敛。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
14 0 1 x2
dx
的近似值,要求总共选取
9
个节点。(10 分) 4. 用高斯消去法解下列方程组:
xx
x x x x
x x x
(8 分)
5. 给定线性方程组
2
x1 x1
2x2 5x2
3x3 2x3
14, 18,
(1) (2)
3x1 x2 5x3 20, (3)
第 2 页 (共 2 页)
写出雅可比迭代公式与高斯-赛德尔迭代公式。(8 分)
6. 已知函数 y=f(x)的观察数据为
xk
-2
0
4
5
yk
5
1
-3
1
试构造三次拉格朗日插值多项式 Pn (x)(8 分)
7.
dy
dx
y
2x y
y(0) 1
在区间[0, 0.8]上,取 h = 0.1,用改进欧拉法求解初值问题。要求计算过程至少保留小 数点后 4 位数字。(8 分)
n
11.
如果对不超过 m 次的多项式,求积公式
a
f (x)dx Ak f (xk ) 精确成立,则该求积
k 0
公式具有 次代数精度。
A、至少 m B、 m C、不足 m D、多于 m
12.
2 1
计算积分 dx ,用梯形公式计算求得的值为 1x
。
A、0.75 B、1 C、1.5 D、2.5
第 1 页 (共 2 页)
3. 下面_ _不是数值计算应注意的问题。
A、注意简化计算步骤,减少运算次数 B、要避免相近两数相减
C、防止大数吃掉小数
D、要尽量消灭误差
4.
对任意初始向量
x
(0)
及常向量
g
,迭代过程
x
(
k
1)
Bx
(
k
)
g
收敛的充分必要条件是_
_。
A、 B 1 1
B、 B 1
C、 (B) 1 D、 B 1 2
《计算方法》期末考试试题
一 选 择(每题 3 分,合计 42 分) 1. x* = 1.732050808,取 x=1.7320,则 x 具有
A、3 B、4 C、5 D、6
位有效数字。
2. 取 3 1.73 (三位有效数字),则 3 1.73
。
A、 0.5103 B、 0.5102 C、 0.5101 D、0.5
① x 1 1 ;② x 1
x2
x 1
试在区间[1.40,1.55]上判断以上两种格式迭代函数的收敛性。(8 分)
2. 设方程 f(x)=0 在区间[0,1]上有惟一实根,如果用二分法求该方程的近似根,试分析至 少需要二分几次才能使绝对误差限为 0.001。(8 分)
3.
用复化梯形公式、复化辛卜生公式分别计算积分
13. 设函数 f(x)在区间[a,b]上连续,若满足
,则方程 f(x)=0 在区间[a,b]内一定有实根。
A、f(a)+f(b)<0 B、f(a)+f(b)>0 C、f(a)f(b)<0 D、f(a)f(b)>0 14. 由 4 个互异的数据点所构造的插值多项式的次数至多是____。
A、 2 次 B、3 次 C、4 次 D、5 次 二、计 算(共 58 分) 1. 将方程 x3 x2 1 0 写成以下两种不同的等价形式:
5. 用列主元消去法解线性方程组,消元的第
k
步,选列主元
a (k 1) rk
,使得
a (k 1) rk
=
。
A、
max
1in
a(k ik
1)
B、
max
k in
a(k ik
1)
C、
max
k jn
a (k 1) kj
D、
max
1 jn
a(k kj
1)
6. 用选列主元的方法解线性方程组 AX=b,是为了
A、提高计算速度 B、简化计算步骤 C、降低舍入误差 D、方便计算
7. 用简单迭代法求方程 f(x)=0 的实根,把方程 f(x)=0 转化为 x=(x),则 f(x)=0 的根
是: 。
A、y=x 与 y=(x)的交点
B、 y=x 与 y=(x)交点的横坐标
C、y=x 与 x 轴的交点的横坐标
D、 y=(x)与 x 轴交点的横坐标
8. 已知 x0=2,f(x0)=46,x1=4,f(x1)=88,则一阶差商 f [x0, x1]为 。 A、7 B、20 C、21 D、42
6
4
4
9. 已知等距节点的插值型求积公式 f 3
x dx Ak f
k 0
xk
,那么 Ak _____。
k 0
A、0 B、2 C、3 D、9 10. 用高斯消去法解线性方程组,消元过程中要求____。
A、 aij 0
B、
a (0) 11
0
C、
a
(k kk
)
0
D、
a
(k kk
1)
0
b
