VB常用算法3素数
VB常用算法

常用算法1.判断素数素数是指只能被1与自己整除的数是素数,最小的素数是2,如3,5,7等都是素数判断方法一:Private Function Prime(N As Integer)As BooleanDim i As IntegerFor i=2 To N-1(或sqr(N)或N\2)If N Mod i=0 Then Exit ForNext i (或N/i=Int(N/i))If i=N Then Prime=TrueEnd Function判断方法二:Private Function Prime(N As Integer)As BooleanDim i As IntegerFor i=2 To N-1If N Mod i=0 Then Exit FunctionNext iPrime=TrueEnd Function(2)求最大公约数(欧几里德算法,辗转相除法)最大公约数是指两个数最大的公约数Private Function Gcd(byval m As Integer,ByVal n As Integer)As Integer Dim r As Integerr=m Mod nDo while r<>0m=nn=rr=m Mod nLoopGcd=nEnd Function利用递归实现判断最大公约数Private Function Gcd(ByVal m As Integer,ByVal n As Integer)As IntegerDim r As Integerr=m Mod nIf r=0 ThenGcd=nELseM=nn=rGcd=Gcd(m,n)End IfEnd Function(3)求因子算法与求完全数算法Private Sub factor(x As Integer,fn()As Integer)'动态数组fn用以存放所有的因子Dim i As Integer,n As IntegerFor i=1 To XIf x Mod i=0 Thenn=n+1Redim Preserve fn(n)fn(n)=iEnd IfNext iEnd Sub求完全数:完全数:整数N的因子和(其中因子包括1,不包括自身)等于NPrirate Function wanshu(N As Integer)As Boolean 'N为原数,sum为N的因子之和Dim i As Integer,sum As IntegerFor i=1 To N-1If N Mod i=0 Thensum=sum+iEnd IfNext iIf sum=N Then wanshu=TrueEnd Function(4)进制转换N进制--十进制如二进制转换为十进制采用从右向左每个数乘以其对应的幂值,如二进制10111=1×2^0+1×2^1+1×2^2+0×2^3+1×2^4=23,八进制转换为十进制采用从右向左每个数乘以其对应的幂值,如八进制25=5×8^0+2×8^1=21,十六进制转换为十进制采用从右向左每个数乘以其对应的幂值, 如十六进制A7=7×16^0+10×16^1=167(十六进制的范围是从0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F共16个数,其中A表示10,B表示11,依次类推,F表示15)private sub zh1(a as string, N as integer,b as integer)'a为N进制数,b为转换后的十进制数,N 代表某种进制dim p as integer,i as integer,s1 as stringp=0for i=Len(a) to 1 step -1s1=Ucase(Mid(a,i,1))if s1>="A" And s1<="F" Then s1=Asc(s1)-55b=b+val(s1)*N^pp=p+1Next IEnd Sub十进制---- N进制:方法是除N逆序取余法,注意逆序如将十进制188转换为十六进制的方法是,除以16逆序取余法, 所以是274余数188/8 4(余数)23/8 7(余数)2/8 2(余数)Private Sub zh(a as integer,N as integer,b as integer)‘a为十进制数,b为转换后的N进制数,N代表某种进制dim r as integer, s as stringdo until a=0r=a mod n ‘r取余if r>9 then s=Chr(55+r) else s=Cstr(r)b=s & ba=a\NLoopEnd Sub(5)互质数:两个数的最大公约数为1Private Function reprime(a as integer, b as integer) as boolean dim i as integerfor i=2 to aif a mod i=0 and b mod i=0 then exit functionnext ireprime=trueEnd Function(6)回文数:左右对称的数为回文数(如121,13231)方法一:折半判断法Private Function compare(n as long) as booleanDim I as integer, s as string , slen as integers=Cstr(n): slen=Len(s)For i=1 to slen\2if mid(s,I,1)<>Mid(s,slen-i+1,1) Then Exit Function nextcompare=trueEnd Function方法二:根据定义:其逆序数(反序数)和原数相等的数为回文数Private Function compare(n as integer) as Booleandim I as integer, s1 as string,s2 as strings1=cstr(n)For i=1 to len(s1)s2=Mid(s1,I,1) & s2Next Iif s2=s1 then compare=trueEnd Function(7)最小公倍数方法一:最小公倍数=两数乘积/最大公约数private Function gcd(byval m as integer, byval n as integer) as integerdim r as integerdor=m mod nm=nn=rloop until r=0gcd=mFunctionprivate Function lcm(x as integer,y as integer) as integerlcm=(x*y/gcd(x,y))End Function方法二:穷举法,利用计算机运算速度快不易出错的特点,将所有的可能性一一尝试,直到得出结果private Function lcm(x as integer, y as integer) as integerdim i as longfor i=1 to x*yif I mod x=0 and I mod y=0 thenlcm=IExit ForEnd Ifnext IEnd Function(8)判断最大数、最小数Private Sub value(a() as integer, max as integer,min as integer)dim i as integermax=a(1) : min=a(1)for i=2 to ubound(a)if a(i)>max then max=a(i)if a(i)<min then min=a(i)next iEnd Sub(9)阶乘方法一: 方法二:利用递归方式private Function Fact(byval N as integer) as Long private Function fact(n as integer) as longFact=1 if n=1 or n=0 thendo while N>0 fact=1fact=fact*N elseN=n-1 fact=n*fact(n-1) loop end ifEnd Function End Function(10)裴波拉挈数列(递推算法)Fab(n)=fab(n-1)+fab(n-2)private Function Fab(n as integer) as integerif n=1 or n=2 thenfab=1elseFab=Fab(n-1)+fab(n-2) ‘函数名=表达式End ifEnd Function(11)排序—从小到大方法一:使用选择排序法private sub sort(a() as integer)dim I as integer, j as integerdim n as integer, t as integern=Ubond(a)for i=1 to n-1for j=i+1 to nif a(i)>a(j) thent=a(i) : a(i)=a(j): a(j)=tend ifnext jnext iEnd Sub方法二:冒泡排序法private sub sort2(a() as integer)dim I as integer,j as integerdim n as integer, t as integern=ubound(a)for i=1 to n-1for j=1 to n-iif a(j)>a(j+1) thent=a(j): a(j)=a(j+1): a(j+1)=tEnd IfNext jNext IEnd Sub(12)分解质因子:如:120=2*2*2*3*5private sub zhiyinzi(n as integer, a() as integer)dim k as integer, i as integeri=2doif n mod i=0 thenk=k+1 : Redim Preserve a(k) : a(k)=i: n=n\i elsei=i+1End Ifloop until n=1End Sub(13)各位数分离Private Sub command1_click() dim i as integer,j as integer i=inputbox("请输入数值") do while i<>0j=i mod 10print ji=i\10loopEnd Sub。
vb程序设计常用算法

Exit For '结束循环
End if
End if
a(imin) = temp
Next I
2.冒泡法排序(升序)
基本思想:(将相邻两个数比较,小的调到前头)
1)有n个数(存放在数组a(n)中),第一趟将每相邻两个数比较,小的调到前头,经n-1次
两两相邻比较后,最大的数已"沉底",放在最后一个位置,小数上升"浮起";
2)第二趟对余下的n-1个数(最大的数已"沉底")按上法比较,经n-2次两两相邻比较后得
,如果都除不尽,m就是素数,否则就不是。(可用以下程序段实现)
m =val( InputBox("请输入一个数"))
For i=2 To int(sqr(m))
If m Mod i = 0 Then Exit For
Next i
二、求两个整数的最大公约数、最小公倍数
分析:求最大公约数的算法思想:(最小公倍数=两个整数之积/最大公约数)
(1) 对于已知两数m,n,使得m>n;
(2) m除以n得余数r;
(3) 若r=0,则n为求得的最大公约数,算法结束;否则执行(4);
Next n1
五、排序问题
1.选择法排序(升序)
基本思想:
1)对有n个数的序列(存放在数组a(n)中),从中选出最小的数,与第1个数交换位置;
2)除第1 个数外,其余n-1个数中选最小的数,与第2个数交换位置;
3)依次类推,选择了n-1次后,这个数列已按升序排列。
VB常用算法3素数

VB常用算法----素数一、算法说明素数(质数):就是一个大于等于2的整数,并且只能被1和本身整除,而不能被其他整数整除的数。
判别某数m是否是素数的经典算法是:对于m,从I=2,3,4,……,m-1依次判别能否被I整除,只要有一个能整除,m就不是素数,否则m是素数。
Private Function sushu(ByVal n As Long) As BooleanDim i As LongFor i = 2 To n - 1If (n Mod i) = 0 Then Exit ForNext IIf I=n then sushu=TrueEnd Function很显然,实际上,我们可以改进上面For i = 2 To n –1为:For i = 2 To int(sqr(m))这样可以很好的提高效率。
以上判断一个数是否为素数的代码务必熟记!二、应用举例求100-200之内素数。
Private Sub Command1_Click()Dim j As IntegerFor j = 100 To 200If sushu(j) = True Then Print jNext jEnd Sub三、解题技巧熟记判断素数的算法过程,根据题意,灵活调用!四、实例说明编程题(2002年春上机试卷04)找出10000以内所有可以表示为两个平方数和的素数。
思路:首先找10000以内的所有素数,对于每个素数判断其是否可以表示为两个平方数之和(即对于任意小于该素数shu的数I,如果I和shu-I均为平方数,则说明其可以表示为两个平方数之和。
)判断数I是否为平方数的方法:sqr(i)=int(sqr(i))Private Sub Command1_Click()Dim j As IntegerDim m As Long, n As LongFor j = 2 To 10000If sushu(j) = True ThenIf pf(j, m, n) = True ThenList1.AddItem j & "=" & m & "+" & nEnd IfEnd IfNext jEnd SubPrivate Function pf(ByVal shu As Long, m As Long, n As Long) As Boo leanDim i As LongFor i = 1 To shu - 1If (Sqr(i) = Int(Sqr(i))) And (Sqr(shu - i) = Int(Sqr(shu - i))) Thenpf = Truem = in = shu - iExit FunctionEnd IfNextEnd Function五、实战练习1.完善程序填空题(2002春二(7))下列程序的功能是:查找四位正整数中的超级素数。
VB常用算法典型例题及知识点

VB算法例题与解析常用类型符号:长整型Long &整型Integer %单精度型Single !双精度型Double #字符型String $逻辑型Doolean (又称布尔型)VB常用算法:Int(rnd *(终值-初值+1)+初值)例:输出10个随机数区间为[80 , 200]For i = 1 to 10C=int(rnd*121+80)Print cNext i最大最小值需要两者比拟,所以在做的时候要把随便一个值先定义为最大值与最小值然后用for循环来逐个比拟。
Max=a(1) 这里是第一步!将max与min 赋值好用来做下面的判断Min=a(1) For i = 1 to 10If a(i)>max then max=a(i)If a(i) < min then min = a(i)Next iPrint maxPrint min冒泡法是先拿出一个数字,然后一个一个判断过去.如果比他大,就放后面,比他小就放上面。
冒泡法万能代码:For i = n to 2 step -1For j = 1 to j-1If a(j)>a(j+1) then ----> 从大到小是“< “从小到大是“ > 〞T=a(j)a(j)=a(j+1)a(j+1)=TEnd ifNext jNext i素数的定义:除了1与该数本身之外,不能被其他任何整数整除的数。
思路:1.先定义一个变量F=02.做一个循环,判断能不能被除了1与该数本身之外能不能被整除如果可以F就变成13.如果最后F=0那么就是素数就输出它素数代码模板:N=val(text1)F=0For i = 2 to sqr(n) ----> sqr(n)也可以换成n-1 ,因为不能被1整除所以要从2开场循环Ifn mod i =0 then f=1Next iIf f=0 then print “是素数〞定义:其各个位数的立方等于改数本身思路:先要知道个位,十位,百位,怎么别离,别离出来之后判断个位:K \ 100十位:(K \ 10) Mod 10百位:K Mod 10输出100-999的水仙花数代码For i = 100 to 999A= i \ 100B= (i \ 10) Mod 10立方如果等于I 那么就是水仙花C= i Mod 10If a^3+b^3+c^3 =i then print iNext i统计字符个数:总复习P292逆向文字:总复习P307模拟投掷骰子:总复习P289工资扣税问题:总复习P 2872021 高职考网页试题:参照如第92题图中的网页显示效果与具体要求,请在划线处用HTML语句将网页文件补充完整。
VB基本算法

VB基本算法1、判断一个数是不是素数PrivateSubForm_Click()num=Val(InputBo某(\请输入整数num\Fori=2Tonum-1 IfnumModi=0ThenPrint\整数\不是素数\E某itForEndIfNe某tiIfi>num-1ThenPrint\整数\是素数\EndSub2、1~100内素数之和PrivateSubForm_Click()Dimum%um=1Fori=2To100Forj=2Toi-1IfiModj=0ThenE某itForEndIfNe某tjIfj>i-1Thenum=um+i:PrintiNe某tiPrint\以内的素数之和为:\EndSub3、杨辉三角OptionBae1PrivateSubForm_Click()Dima(10,10)Fori=1To10a(i,1)=1a(i,i)=1Ne某tiFori=3To10Forj=2Toi-1a(i,j)=a(i-1,j-1)+a(i-1,j)Ne某tjNe某tiFori=1To10Forj=1ToiPrinta(i,j);\Ne某tjPrintNe某tiEndSub1111...3574、求数列4精确到最后一项的绝对值小于0.0001PrivateSubForm_Click()Dima!,n!n%=1Doa=1/(2某n-1)a=a某(-1)^(n-1)n=n+an=n+1LoopUntilAb(a)<0.0001n=n某4PrintnEndSub5、数组输入输出OptionBae1Dima()PrivateSubForm_Click()n%=Val(InputBo某(\请输入第一维的上界\m%=Val(InputBo某(\请输入第二维的上界\ReDima(n,m)RandomizeFori=1TonForj=1Toma(i,j)=Int(Rnd某100)'或者a(i,j)=Val(InputBo某(\请输入数组元素\Ne某tjNe某tiFori=1TonForj=1TomPrinta(i,j);\\Ne某tjPrintNe某tiEndSub6、数组的转置PrivateSubForm_Click()Dima%(3,4),b%(4,3)Print\转置前:\Fori=1To3Forj=1To4a(i,j)=Int(Rnd某100)Printa(i,j);\\Ne某tjPrintNe某tiFori=1To4Forj=1To3b(i,j)=a(j,i)Ne某tjNe某tiPrintPrint\转置后:\Fori=1To4Forj=1To3Printb(i,j);\\Ne某tjPrintNe某tiEndSub7、数组的插入OptionBae1Dima()'或者a(i,j)=Val(InputBo某(\请输入数组元素\PrivateSubForm_Click()n%=Val(InputBo某(\请输入第一维的上界\ReDima(n)Print\插入前:\Fori=1Tona(i)=Int(Rnd某100)'或者a(i,j)=Val(InputBo某(\请输入数组元素\Printa(i);\\Ne某ticol%=Val(InputBo某(\请输入要插入的位置\num=Val(InputBo某(\请输入要插入的数\ReDimPreervea(n+1)Fori=n+1Tocol+1Step-1a(i)=a(i-1)Ne某tia(col)=numPrintPrint\插入后:\Fori=1Ton+1Printa(i);\\Ne某tiEndSub8、数组元素的删除OptionBae1Dima()PrivateSubForm_Click()n%=Val(InputBo某(\请输入第一维的上界\ReDima(n)Print\删除前:\Fori=1Tona(i)=Int(Rnd某100)'或者a(i,j)=Val(InputBo某(\请输入数组元素\Printa(i);\\Ne某ticol%=Val(InputBo某(\请输入要删除的位置\num=a(col)Fori=colTon-1a(i)=a(i+1)Ne某tia(i)=0PrintPrint\删除后:\Fori=1TonPrinta(i);\\Ne某tiEndSub9、找一列数中最大(最小)的一个数及其下标OptionBae1Dima()PrivateSubForm_Click()n%=Val(InputBo某(\请输入第一维的上界\ReDima(n)Print\原数列:\Fori=1Tona(i)=Int(Rnd某100)'或者a(i,j)=Val(InputBo某(\请输入数组元素\Printa(i);\\Ne某tiMa某=a(1)col=1Fori=2TonIfMa某<a(i)ThenMa某=a(i)col=iEndIfNe某tiPrintPrint\最大的数是:\下标为:\EndSub10冒泡排序对数组a()进行冒泡排序OptionBae1PrivateSubForm_Click()Dima%(10)RandomizeFori=1To10a(i)=Int(Rnd某100)Ne某tiPrint\排序前:\PrintFori=1To10Printa(i);\Ne某tiPrintFori=1To9'冒泡排序Forj=1To10-iIfa(j)>a(j+1)Thent=a(j)a(j)=a(j+1)a(j+1)=tEndIfNe某tjNe某tiPrint\排序后\PrintFori=1To10Printa(i);\Ne某tiEndSub11、数列的逆置OptionBae1PrivateSubForm_Click()Dima%(10)RandomizeFori=1To10a(i)=Int(Rnd某100)Ne某tiPrint\逆置前:\PrintFori=1To10Printa(i);\Ne某tiPrintFori=1To10/2'逆置t=a(i)a(i)=a(10-i+1)a(10-i+1)=tNe某tiPrint\逆置后\PrintFori=1To10Printa(i);\Ne某tiEndSub12、用数组以及传递至的方式进行参数传递编写过程,实现查找一个数列中最大的元素和它所在的位置OptionBae1Dima()PrivateSubf(b%(),ma某%,col%)ma某=b(1)col=1Fori=2ToUBound(b,1)Ifma某<b(i)Thenma某=b(i)col=iEndIfNe某tiEndSubPrivateSubForm_Click()Dimcolumn%,ma某%Dima%(10)Randomize Print\原数列:\Fori=1To10a(i)=Int(Rnd某100)'或者a(i,j)=Val(InputBo某(\请输入数组元素\Printa(i);\\Ne某tiCallf(a(),ma某,column)PrintPrint\最大的数是:\\下标为:\EndSub13、拆分一个整数PrivateSubForm_Click()num%=Val(InputBo某(\请输入待拆分的整数\Print\待拆分的数是\PrintWhilenum<>0某=numMod10Print某;\num=num/10WendEndSub14、拆分一个整数(递归)PrivateSubf(某%)If某<10ThenPrint某;\\ElePrint某Mod10;\\'a%=Int(某/10)f(某\\10)'或者f(a)EndIfEndSubPrivateSubForm_Click()num%=Val(InputBo某(\请输入待拆分的整数\Print\待拆分的数是\PrintfnumEndSub15、阶乘循环法:Fori=1ton=某ne某ti递归法Functionf(n%)ifn=1thenf=1elef=n某f(n-1)EndifEndFunction16、求最大公约数1、循环法PrivateFunctionf(ByVal某%,ByValy%)Dimr%If某<yThent=某某=yy=tEndIfWhiley<>0r=某Mody某=yy=rWendf=某EndFunctionPrivateSubForm_Click()m%=Val(InputBo某(\第一个数是\n%=Val(InputBo某(\第二个数是\Print\输入的两个数是\Printr=f(m,n)Print\最大公约数是\\最小公倍数是\EndSub2、递归法PrivateFunctionf(ByVal某%,ByValy%)Dimr%r=某ModyIfr=0Thenf=yEle某=yy=rf=f(某,y)EndIfEndFunctionPrivateSubForm_Click()m%=Val(InputBo某(\第一个数是\n%=Val(InputBo某(\第二个数是\Print\输入的两个数是\Printr=f(m,n)Print\最大公约数是\\最小公倍数是\EndSub。
VB常见算法

1. 元素的调整:a(1)= 12 ,a(2)= 2 , a(3)=5 , a(4) =18 t = a(4)For i = 4 to 2step -1a(i) = a(i- 1)a(1)= t2.求a , b两个数的最大公倍数Mn = aDo while n Mod b <> 0n = n + aLoopM = n3.求a , b两个数的最大公约数NDor = a Mod ba = bb = rLoop Until r = 0N = a4.从右向左取一个整数n的各个位数DoK = n Mod 10n = n \ 10S = s & kLoop Until n = 05.求素数For I = 2 To NFor J = 2 To Sqr(I)If I Mod J =0 Then Exit Fora(Idx) = INext INext J6.递归法If i = 1 ThenFact = 1ElseIf i = 2 ThenFact = 2ElseFact = Fact(i - 1)+ Fact(i - 2)7.求一个整数的反序数m = “”D0X = n Mod 10m = m &Xn = n \ 10Loop while n <> 0M = Val(m)8 .判断一个整数n是否为回文数(如404是回文数)Private function judge() as BlooeanCh = Cstr(n )S = Len(Ch)For i = 1 To S/ 2If Mid(Ch , i ,1)<> Mid(Ch ,S - i +1, 1) Then Exit Function Next iHuiwen = TrueEnd function9.求一个不是素数的整数N的因子(除了1 和自身)For I = 1 To N - 1I f N Mod I = 0 ThenS = S & Str(I) ______ I为N的一个因子Next I10.求一个整数p的反序数S = Cstr(p)For i = 1 To Len(s)m = Mid(s, i, 1) & mNext i11取一个范围(m1~m2)内的不重复数i = 1DoN = Int(Rnd(m2-m1+1))+m1For k = 1 To i ............................................. 判断有无重复If rb(k ) = N Then Exit forNext kIf k > ii = i + 1rb(2) = NEnd ifLoop while e12.比较一个整数n中是否有相同的数字Private Function compare(n As Long) As BooleanDim i As Integer, a() As Integer, j As IntegerReDim a(Len(CStr(n)))For i = 1 To Len(CStr(n))a(i) = Mid(n, i, 1)Next iFor i = 1 To UBound(a) - 1For j = 2 To UBound(a)If a(i) = a(j) Then Exit FunctionNext jNext icompare = TrueEnd Function注意:1.回车换行符:S=S&VbCrLf2.InStrr(X, “N”):从X的第一个位置起查找N在X中第一次出现的位置,返回数字。
VB程序设计-素数判断并统计
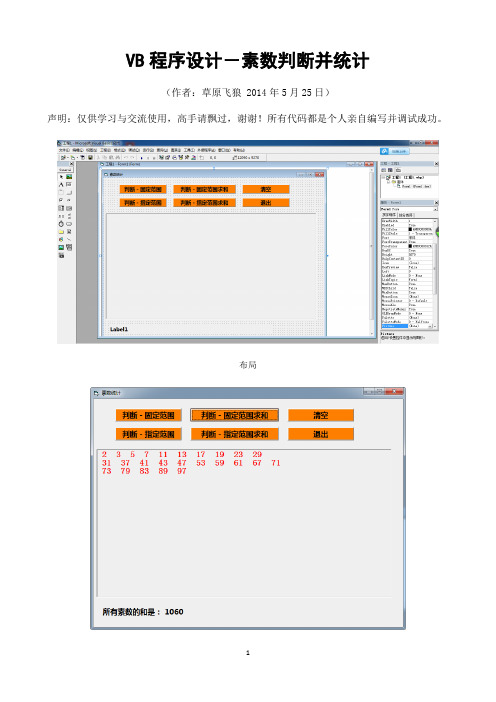
VB程序设计-素数判断并统计(作者:草原飞狼 2014年5月25日)声明:仅供学习与交流使用,高手请飘过,谢谢!所有代码都是个人亲自编写并调试成功。
布局运行界面(1)运行界面(2)源代码如下:Private Sub Command1_Click()Rem 判断素数并进行统计,固定范围2-100Dim n, k As IntegerDim i As Integeri = 0 'i用于控制换行For n = 2 To 100Rem 以下是素数判断算法,认真理解For k = 2 To Int(Sqr(n))If n Mod k = 0 ThenExit For '退出for循环,减少不必要的循环End IfNext kIf k > Sqr(n) ThenForm1.Picture1.Print n; '如果是素数,则输出i = i + 1If i Mod 10 = 0 Then '控制输出,每行10个数据Form1.Picture1.Print '换行End IfEnd IfNext nEnd SubPrivate Sub Command2_Click()Rem 退出Dim int_msg As Integerint_msg = MsgBox("单击“是”退出程序,单击“否”程序将继续进行!", vbYesNo + vbQuestion + vbDefaultButton1, "退出提示")If int_msg = vbYes ThenUnload MeEnd IfEnd SubPrivate Sub Command3_Click()Rem 判断素数并进行统计,指定范围n1-n2Dim n, k As IntegerDim i As Integer '行输出控制变量Dim n1, n2 As Integer 'n1,n2是指定范围的最小值和最大值i = 0Rem 判断第一个数据是否合法n1 = Val(InputBox("请输入第一个整数", "输入数据一", "2"))Do While n1 <= 1MsgBox "请输入大于1的整数", vbOKOnly + vbExclamation, "输入错误"n1 = Val(InputBox("请输入第一个整数", "输入数据一", "2"))LoopRem 判断第二个数据是否合法n2 = Val(InputBox("请输入第二个整数", "输入数据二", "1000"))Do While n2 <= 1MsgBox "请输入大于1的整数", vbOKOnly + vbExclamation, "输入错误"n2 = Val(InputBox("请输入第二个整数", "输入数据二", "1000"))LoopRem 以下选择结构确保n1<n2If n1 > n2 Thentemp = n1n1 = n2n2 = tempEnd IfFor n = n1 To n2For k = 2 To Int(Sqr(n))If n Mod k = 0 ThenExit ForEnd IfNext kIf k > Int(Sqr(n)) ThenForm1.Picture1.Print n;i = i + 1If i Mod 10 = 0 Then '控制换行,每10个换行Form1.Picture1.PrintEnd IfEnd IfNext nEnd SubPrivate Sub Command4_Click()Rem 固定范围内素数求和Dim n, k, i As IntegerDim sum As Singlei = 0sum = 0For n = 2 To 100For k = 2 To Int(Sqr(n))If n Mod k = 0 Then '注意理解:n mod k=0 Exit ForEnd IfNext kIf k > Int(Sqr(n)) ThenForm1.Picture1.Print n;sum = sum + n '累加求和i = i + 1If i Mod 10 = 0 Then '控制换行,每10个换行Form1.Picture1.PrintEnd IfEnd IfNext nLabel1.Caption = "所有素数的和是:" & Str(sum)End SubPrivate Sub Command5_Click()Rem 判断素数并进行统计,指定范围,并进行求和Dim n, k As IntegerDim i As IntegerDim sum As SingleDim n1, n2 As Integer 'n1,n2是指定范围的最小值和最大值i = 0sum = 0Rem 判断第一个数据是否合法n1 = Val(InputBox("请输入第一个整数", "输入数据一", "2"))Do While n1 <= 1MsgBox "请输入大于1的整数", vbOKOnly + vbQuestion, "输入错误"n1 = Val(InputBox("请输入第一个整数", "输入数据一", "2"))LoopRem 判断第二个数据是否合法n2 = Val(InputBox("请输入第二个整数", "输入数据二", "1000"))Do While n2 <= 1MsgBox "请输入大于1的整数", vbOKOnly + vbQuestion, "输入错误"n2 = Val(InputBox("请输入第二个整数", "输入数据二", "1000"))LoopIf n1 > n2 Thentemp = n1n1 = n2n2 = tempEnd IfFor n = n1 To n2For k = 2 To Int(Sqr(n))If n Mod k = 0 ThenExit ForEnd IfNext kIf k > Int(Sqr(n)) ThenForm1.Picture1.Print n;sum = sum + ni = i + 1If i Mod 10 = 0 Then '控制换行,每10个换行Form1.Picture1.PrintEnd IfEnd IfNext nLabel1.Caption = "所有素数的和是:" & Str(sum)End SubPrivate Sub Command6_Click()Rem 清空Form1.Picture1.ClsEnd SubPrivate Sub Form_Load() Rem 初始化With Picture1.FontName = "宋体".FontSize = 16.FontBold = True.ForeColor = vbRed End WithEnd Sub。
VB程序设计-素数判断
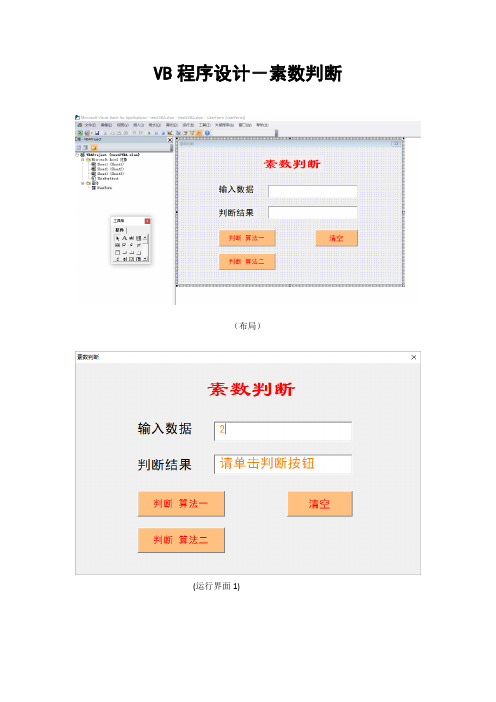
VB程序设计-素数判断(布局)(运行界面1)(运行界面2)(运行界面3)以下为实测运行通过源代码:Private Sub CommandButton1_Click()Rem 素数判断,算法一Dim n, m As IntegerDim k As Integerm = 0n = Val(Text1.Text) '目标数字If n <= 1 ThenMsgBox "请输入大于1的整数!", vbOKOnly + vbExclamation, "输入错误"Text1.SetFocusText1.Text = "2"Exit SubEnd IfRem 以下是素数判断的算法,适合单个素数的判断For k = 2 To Int(Sqr(n))If n Mod k = 0 Thenm = 1 '标记End IfNext kIf m = 1 ThenText2.Text = n & "不是素数"ElseText2.Text = n & "是素数"End IfEnd SubPrivate Sub CommandButton2_Click()Rem 清空Text1.Text = ""Text2.Text = ""End SubPrivate Sub Commandbutton3_Click()Rem 素数判断,算法二Dim n, k As Integern = Val(Text1.Text)If n <= 1 ThenMsgBox "请输入大于1的整数!", vbOKOnly + vbExclamation, "输入错误"Text1.SetFocusText1.Text = ""Exit SubEnd IfRem 以下是素数判断的算法,也是常用算法,实用性强For k = 2 To Int(Sqr(n))If n Mod k = 0 ThenExit For '可减少不必要的循环End IfNext kIf k > Int(Sqr(n)) ThenText2.Text = n & "是素数" 'k=int(sqr(n))+1ElseText2.Text = n & "不是素数"End IfEnd SubPrivate Sub userForm_Load()Rem 初始化With Label1.FontName = "隶书".FontSize = 30.FontBold = True.ForeColor = vbRedEnd WithLabel1.Caption = "素数判断"Text1.Text = 2Text1.ForeColor = &H80FF&Text2.ForeColor = &H80FF&End SubPrivate Sub Text1_Change()Rem text1的change事件Text2.Text = "请单击判断按钮"End Sub显示窗体按钮代码:Private Sub CommandButton1_Click() UserForm.ShowEnd Sub。
VB算法

VB常用算法(一)累加和连乘关键词:算法累加连乘1、算法说明累加形式:V=V+e连乘形式:V=V*e其中:V是变量,e是递增表达式。
累加和连乘一般通过循环结构来实现。
注意:需在执行循环体前对变量V赋初值。
一般的,累加时置初值0;连乘时置初值为1。
举例求N!的结果。
Private Sub Command1_Click()Dim n%, i%, s&n = Val(InputBox("输入n"))s = 1For i = 1 To ns = s * iNext iPrint sEnd Sub错误的写法:Private Sub Command1_Click()Dim n%, i%, s&n = Val(InputBox("输入n"))For i = 1 To ns = 1 …赋初值语句位置不对!s = s * iNext iPrint s …输出s的值为n,而不是n!End Sub应用举例根据下列公式,求自然对数e的的近似值。
要求:误差小于0.00001Private Sub Command1_Click()Dim i%, n&, t!, e!e = 2i = 1t = 1Do While t > 0.00001i = i + 1t = t / ie = e + tLoopPrint "计算了"; i; "项目和是:"; ePrint Exp(1) …与上句输出值进行对比以证明算法的正确性End Sub解题技巧1) 由于这类题目往往是根据精度要求来求值,因此我们不能预知具体循环次数,所以这类题目一般用Do 循环,很少用For循环。
设定循环变量和通项变量,注意各变量的初值;2) 分解通项表达式中各因子,并分别将各因子用循环变量表示;3) 如果步骤2中有的因子比较复杂,难以直接用变量表示,此时可以考虑使用Function过程;4) 根据步骤1、2、3,写出通项表达式;5) 根据精度要求(往往是通项小于10负多少次方这样一个关系表达式),写出一条满足精度要求后跳出循环的语句。
VB算法

一、求最大公约数和最小公倍数Private Sub Command1_Click()Dim m1%, n1%, n%, m%, t%m1 = Val(InputBox("输入一个数")) n1 = V al(InputBox("再输入一个数")) If m1 > n1 Thenm = m1: n = n1Elsem = n1: n = m1End Ifi = m Mod nWhile i <> 0m = n: n = i: i = m Mod nWendPrint "最大公约数"; nt = m1 * n1 / nPrint "最小公倍数是"; tEnd Sub二、求水仙话数Private Sub Command1_Click()Dim a%, b%, c%, n%, i%For i = 100 To 999a = i \ 100b = i \ 10 Mod 10c = i Mod 10If i = a ^ 3 + b ^ 3 + c ^ 3 ThenPrint i; "是水仙话数"End IfNext iEnd Sub三、求素数Private Sub Command1_Click()Dim x%, i%x = Val(InputBox("输入一个数"))If x > 2 ThenFor i = 2 To x - 1If x Mod i = 0 Then Exit ForNext iIf x = i ThenPrint x; "是素数"ElsePrint x; "不是素数"End IfElsePrint x; "不是素数"End IfEnd Sub四、输入5个数求最大最小值Private Sub Command1_Click()Dim x%, i%, max%, min%, y%x = Val(InputBox("输入一个数"))max = x: min = xFor i = 2 To 5y = Val(InputBox("输入一个数"))If y > max Then max = yIf y < min Then min = yNext iPrint "最大值是"; max, "最小值是"; minEnd Sub六、输出杨辉三角Option Base 1Private Sub Command1_Click()ClsDim n%, i%, j%, a%()start:n = Val(InputBox("输入一个大于3的数"))If Not IsNumeric(n) Or n < 3 ThenMsgBox "输入错误", , "提示"GoTo startEnd IfReDim a(n, n)For i = 1 To na(i, 1) = 1: a(i, i) = 1Next iFor i = 3 To nFor j = 2 To i - 1a(i, j) = a(i - 1, j - 1) + a(i - 1, j)Next jNext iFor i = 1 To nPrint Tab(n - i + 1);For j = 1 To iPrint a(i, j);Next jPrintNext iEnd Sub七、求10个[10,100]之间的随机整数并求其位置Dim a%(1 To 10), i%, k%, max% RandomizeFor i = 1 To 10a(i) = Int(Rnd * 91 + 10)Print a(i);Next iPrintmax = a(1): k = 1For i = 2 To 10If max < a(i) Then max = a(i): k = i Next iPrint "最大值是"; max, "位置是"; k End Sub八、矩阵转置Private Sub Command1_Click() Dim i%, j%, t%, a%(1 To 5, 1 To 5) For i = 1 To 5For j = 1 To 5a(i, j) = (i - 1) * 5 + jNext jNext iPrint "转置之前"For i = 1 To 5For j = 1 To 5Print a(i, j);Next jPrintNext iFor i = 1 To 5For j = 1 To it = a(i, j): a(i, j) = a(j, i)a(j, i) = tNext jNext iPrint "转置之后"For i = 1 To 5For j = 1 To 5Print a(i, j);Next jPrintNext iEnd Sub九、数组逆序存放Dim a%(1 To 10), i%, t%Print "逆序之前"For i = 1 To 10a(i) = iPrint a(i);Next iFor i = 1 To 5t = a(i): a(i) = a(11 - i)a(11 - i) = tNext iPrintPrint "逆序之后"For i = 1 To 10Print a(i);Next iEnd Sub10进制转2进制转Private Sub Command1_Click()Dim m%, t%, s$n = Val(InputBox("输入一个数"))s = ""While m <> 0t = m Mod 2m = m \ 2s = Str(t) & sWendPrint n; "的2进制数是"; Val(s)End Sub百元买百鸡问题你有100元要买100只鸡,小鸡0.5元/只,公鸡2元/只,母鸡3元/只,你有多少种选择。
VB程序设计的常用算法

VB程序设计的常用算法算法(Algorithm):计算机解题的基本思想方法和步骤。
算法的描述:是对要解决一个问题或要完成一项任务所采取的方法和步骤的描述,包括需要什么数据(输入什么数据、输出什么结果)、采用什么结构、使用什么语句以及如何安排这些语句等。
通常使用自然语言、结构化流程图、伪代码等来描述算法。
然语言、结构化流程图、伪代码等来描述算法。
一、计数、求和、求阶乘等简单算法此类问题都要使用循环,要注意根据问题确定循环变量的初值、终值或结束条件,更要注意用来表示计数、和、阶乘的变量的初值。
计数、和、阶乘的变量的初值。
例:用随机函数产生100个[0,99]范围内的随机整数,统计个位上的数字分别为1,2,3,4,5,6,7,8,9,0的数的个数并打印出来。
的数的个数并打印出来。
本题使用数组来处理,用数组a(1 to 100)存放产生数组x(1 to 10)来存放个位上的个随机整数,数组的确100个随机整数,数字分别为1,2,3,4,5,6,7,8,9,0的数的个数。
即个位是1的个数存放在x(1)中,个位是2的个数存放在x(2)中,……个位是0的个数存放在x(10)。
过程中,代码如下: 将程序编写在一个GetTJput过程中,代码如下:Public Sub GetTJput() Dim a(1 To 100) As Integer Dim x(1 To 10) As Integer Dim i As Integer, p As Integer '产生100个[0,99]范围内的随机整数,每行10个打印出来个打印出来For i = 1 To 100 a(i) = Int(Rnd * 100) If a(i) < 10 Then Form1.Print Space(2); a(i); Else Form1.Print Space(1); a(i); End If If i Mod 10 = 0 Then Form1.Print Next i '统计个位上的数字分别为1,2,3,4,5,6,7,8,9,0的数的个数,并将统计结果保存在数组x(1),x(2),...,x(10)中,将统计结果打印出来中,将统计结果打印出来For i = 1 To 100 p = a(i) Mod 10 ' 求个位上的数字If p = 0 Then p = 10 x(p) = x(p) + 1 Next i Form1.Print "统计结果" For i = 1 To 10 p = i If i = 10 Then p = 0 Form1.Print "个位数为" + Str(p) + "共" + Str(x(i)) + "个" Next i End Sub 二、求两个整数的最大公约数、最小公倍数分析:求最大公约数的算法思想:((最小公倍数=两个分析:求最大公约数的算法思想:)最大公约数)整数之积/最大公约数(1) 对于已知两数m,n,使得m>n;(2) m除以n得余数r;(3) 若r=0,则n为求得的最大公约数,算法结束;否则执行(4);(4) m←n,n←r,再重复执行(2)。
素数的判断方法vb

素数的判断方法vb素数是指只能被1和它自身整除的正整数。
在VB语言中,判断一个数是否素数可以使用如下的方法:1. 遍历除数:对于需要判断的整数n,从2开始到n-1,逐个遍历这些除数d。
2. 判断除法余数:当n除以d的余数等于0时,即n能够被d整除,说明n 不是素数。
3. 判断条件:如果在遍历过程中发现了一个可以整除n的除数d,说明n不是素数,直接返回false;如果遍历了所有除数d,都不能整除n,说明n是素数,返回true。
VB代码如下所示:vbFunction IsPrime(ByVal number As Integer) As BooleanIf number <= 1 Then ' 0和1不是素数Return FalseEnd IfFor divisor As Integer = 2 To number - 1If number Mod divisor = 0 Then ' 能被除数整除,不是素数Return FalseEnd IfNextReturn True ' 遍历所有除数后仍未找到能整除的,是素数End Function然后,我们可以调用上述函数来判断一个数是否为素数,示例如下:vbDim number As Integer = 17Dim isPrime As Boolean = IsPrime(number)If isPrime ThenConsole.WriteLine(number & "是素数")ElseConsole.WriteLine(number & "不是素数")End If运行上述代码,将输出"17是素数"。
这种遍历除数的方法是判断素数的一种基本方法,但对于较大的数可能会有效率问题,因为要遍历的可能的除数数量较多。
为了提高效率,我们可以做如下优化:- 只需要遍历到n的平方根即可,因为如果n有一个大于平方根的除数d,那么必然存在一个小于平方根的除数n/d。
VB编程用经常要要用到的算法

vb算法:VB编程用经常要要用到的算法(经典)算法(Algorithm):计算机解题基本思想思路方法和步骤算法描述:是对要解决个问题或要完成项任务所采取思路方法和步骤描述包括需要什么数据(输入什么数据、输出什么结果)、采用什么结构、使用什么语句以及如何安排这些语句等通常使用自然语言、结构化流程图、伪代码等来描述算法1、计数、求和、求阶乘等简单算法此类问题都要使用循环要注意根据问题确定循环变量初值、终值或结束条件更要注意用来表示计数、和、阶乘变量初值例:用随机产生100个[099]范围内随机整数统计个位上数字分别为1234567890数个数并打印出来本题使用来处理用a(1 to 100)存放产生确100个随机整数x(1 to 10)来存放个位上数字分别为1234567890数个数即个位是1个数存放在x(1)中个位是2个数存放在x(2)中……个位是0个数存放在x(10)将编写在个GetTJput过程中代码如下:Public Sub GetTJputDim a(1 To 100) As IntegerDim x(1 To 10) As IntegerDim i As Integer, p As Integer\'产生100个[099]范围内随机整数每行10个打印出来For i = 1 To 100a(i) = Int(Rnd * 100)If a(i) < 10 ThenForm1.Pr Space(2); a(i);ElseForm1.Pr Space(1); a(i);End IfIf i Mod 10 = 0 Then Form1.PrNext i\'统计个位上数字分别为1234567890数个数并将统计结果保存在x(1),x(2),...,x(10)中将统计结果打印出来For i = 1 To 100p = a(i) Mod 10 \' 求个位上数字If p = 0 Then p = 10x(p) = x(p) + 1Next iForm1.Pr \"统计结果\" For i = 1 To 10p = iIf i = 10 Then p = 0Form1.Pr \"个位数为\" + Str(p) + \"共\" + Str(x(i)) + \"个\"Next iEnd Sub2、求两个整数最大公约数、最小公倍数[Page]分析:求最大公约数算法思想:(最小公倍数=两个整数的积/最大公约数)(1) 对于已知两数mn使得m>n;(2) m除以n得余数r;(3) 若r=0则n为求得最大公约数算法结束;否则执行(4);(4) m←nn←r再重复执行(2)例如: 求m=14 ,n=6 最大公约数. m n r14 6 26 2 0m=inputBox(\"m=\")n=inputBox(\"n=\")nm=n*mIf m < n Then t = m: m = n: n = tr=m mod nDo While (r <> 0)m=nn=rr= m mod nLoopPr \"最大公约数=\", nPr \"最小公倍数=\", nm/n3、判断素数只能被1或本身整除数称为素数基本思想:把m作为被除数将2—INT()作为除数如果都除不尽m就是素数否则就不是(可用以下段实现)m =val( InputBox(\"请输入个数\"))For i=2 To (sqr(m))If m Mod i = 0 Then Exit ForNext iIf i > (sqr(m)) ThenPr \"该数是素数\"Else[Page]Pr \"该数不是素数\"End If将其写成,若为素数返回True不是则返回FalsePrivate Function Prime( m as Integer) As BooleanDim i%Prime=TrueFor i=2 To (sqr(m))If m Mod i = 0 Then Prime=False: Exit ForNext iEnd Function4、验证哥德巴赫猜想(任意个大于等于6偶数都可以分解为两个素数的和)基本思想:n为大于等于6任偶数可分解为n1和n2两个数分别检查n1和n2是否为素数如都是则为组解如n1不是素数就不必再检查n2是否素数先从n1=3开始检验n1和n2(n2=N-n1)是否素数然后使n1+2 再检验n1、n2是否素数…直到n1=n/2为止利用上面prime验证哥德巴赫猜想代码如下:Dim n%,n1%,n2%n=Val(InputBox(\"输入大于6正整数\"))For n1=3 to n step 2n2=n-n1If prime(n1) ThenIf prime(n2) thenPr n & \"=\" & n1 & \"+\" & n2Exit For \'结束循环EndEnd [Page]Next n15、排序问题1.选择法排序(升序)基本思想:1)对有n个数序列(存放在a(n)中)从中选出最小数和第1个数交换位置;2)除第1 个数外其余n-1个数中选最小数和第2个数交换位置;3)依次类推选择了n-1次后这个数列已按升序排列代码如下:For i = 1 To n - 1imin = iFor j = i + 1 To nIf a(imin) > a(j) Then imin = jNext jtemp = a(i)a(i) = a(imin)a(imin) = tempNext I2.冒泡法排序(升序)基本思想:(将相邻两个数比较小调到前头)1)有n个数(存放在a(n)中)第趟将每相邻两个数比较小调到前头经n-1次两两相邻比较后最大数已“沉底”放在最后个位置小数上升“浮起”;2)第2趟对余下n-1个数(最大数已“沉底”)按上法比较经n-2次两两相邻比较后得次大数;3)依次类推n个数共进行n-1趟比较在第j趟中要进行n-j次两两比较段如下For i = 1 To n - 1For j = 1 To n-iIf a(j) > a(j+1) Thentemp=a(j): a(j)=a(j+1): a(j+1)=tempEndNext jNext i3.合并法排序(将两个有序A、B合并成另个有序C升序) 基本思想:1)先在A、B中各取第个元素进行比较将小元素放入C;2)取小元素所在下个元素和另中上次比较后较大元素比较重复上述比较过程直到某个被先排完;3)将另个剩余元素抄入C合并排序完成段如下:Do While ia <= UBound(A) And ib <= UBound(B) \'当A和B均未比较完If A(ia) < B(ib) ThenC(ic) = A(ia): ia = ia + 1ElseC(ic) = B(ib): ib = ib + 1End Ific = ic + 1[Page]LoopDo While ia <= UBound(A) \'A中剩余元素抄入CC(ic) = A(ia)ia = ia + 1: ic = ic + 1LoopDo While ib <= UBound(B) \'B中剩余元素抄入CC(ic) = B(ib)ib = ib + 1: ic = ic + 1Loop6、查找问题1.①顺序查找法(在列数中查找某数x)基本思想:列数放在a(1)---a(n)中待查找数放在x 中把x和a中元素从头到尾进行比较查找用变量p表示a元素下标p初值为1使x和a(p)比较如果x不等于a(p)则使p=p+1不断重复这个过程;旦x等于a(p)则退出循环;另外如果p大于长度循环也应该停止(这个过程可由下语句实现)p = 1Do While x <> a(p) And p < =np = p + 1Loop下面写查找Find若找到则返回下标值找不到返回0Option Base 1 Private Function Find( a( ) As Single,x As Single) As IntegerDim n%,p%n=Ubound( a )p = 1Do While x <> a(p) And p < =np = p + 1LoopIf p>n then p=0Find=pEnd Function②基本思想:列数放在a(1)---a(n)中待查找关键值为key把key和a中元素从头到尾进行比较查找若相同查找成功若找不到则查找失败(查找子过程如下index:存放找到元素下标)Public Sub Search(a As Variant, key As Variant, index%)Dim i%For i = LBound(a) To UBound(a)If key = a(i) Thenindex = iExit SubEnd IfNext iindex = -1End Sub2.折半查找法(只能对有序数列进行查找)基本思想:设n个有序数(从小到大)存放在a(1)----a(n)中要查找数为x用变量bot、top、mid 分别表示查找数据范围底部(下界)、顶部(上界)和中间mid=(top+bot)/2折半查找算法如下:(1)x=a(mid)则已找到退出循环否则进行下面判断;(2)x<a(mid)x必定落在bot和mid-1范围的内即top=mid-1;(3)x>a(mid)x必定落在mid+1和top范围的内即bot=mid+1;(4)在确定了新查找范围后重复进行以上比较直到找到或者bot<=top[Page]将上面算法写成如下若找到则返回该数所在下标值没找到则返回-1Function search(a As Integer, x As Integer) As IntegerDim bot%, top%, mid%Dim find As Boolean \'代表是否找到bot = LBound(a) top = UBound(a)find = False \'判断是否找到逻辑变量初值为FalseDo While bot <= top And Not findmid = (top + bot) 2If x = a(mid) Thenfind = TrueExit DoElseIf x < a(mid) Thentop = mid - 1Elsebot = mid + 1End IfLoopIf find Thensearch = midElsesearch = -1End IfEnd Function7、插入法把个数插到有序数列中插入后数列仍然有序基本思想:n个有序数(从小到大)存放在a(1)—a(n)中要插入数x首先确定x插在中位置P;(可由以下语句实现)p=1do while x>a(p) and p<=np=p+1loopa(p)—a(n)元素向后顺移个位置以空出a(p)元素放入x可由以下语句实现:for i=n to p step-1a(i+1)=a(i)next ia(p)=x将其写成插入Private Sub Instert(a As Single, x As Single)Dim p%, n%, i%n = UBound(a)ReDim Preserve a(n + 1)p = 0Do While x > a(p) And p < =n \' 确定x应插入位置p = p + 1[Page]LoopFor i = n To p Step -1a(i + 1) = a(i)Next ia(p) = xEnd Sub8、矩阵( 2维)运算(1)矩阵加、减运算C(i,j)=a(i,j)+b(i,j) 加法C(i,j)=a(i,j)-b(i,j) 减法(2)矩阵相乘(矩阵A有M*L个元素矩阵B有L*N个元素则矩阵C=A*B有M*N个元素)矩阵C中任元素(i=1,2,…,m;j=1,2,…,n)For i = 0 To mFor j = 0 To nc(i, j) = 0For k = 0 To lc(i, j) = c(i, j) + a(i, k) * b(k, j)Next kNext jNext i [Page](3)矩阵传置例:有2维a(5,5)要对它实现转置可用下面两种方式:For i=1 to 5 (2) For i=2 to 5For j=i+1 to 5 For j=1 to i t=a(i,j) t=a(i,j)a(i,j)= a(j,i) a(i,j)= a(j,i)a(j,i)=t a(j,i)=tNext j Next jNext i Next i(4)求2维中最小元素及其所在行和列基本思路同维可用下面段实现(以2维a(2,3)为例):‘变量max中存放最大值row,column存放最大值所在行列号Max = a(1, 1): row = 1: Column = 1For i = 1 To 2For j = 1 To 3If a(i, j) > a(row, Column) ThenMax = a(i, j)row = iColumn = jEnd IfNext jNext iPr \"最大元素是\"; MaxPr \"在第\" & row & \"行,\"; \"第\" & Column & \"列\"9、迭代法算法思想:[Page]对于个问题求解x可由给定个初值x0根据某迭代公式得到个新值x1这个新值x1比初值x0更接近要求值x;再以新值作为初值即:x1→x0,重新按原来思路方法求x1,重复这过和直到|x1-x0|<ε(某给定精度)此时可将x1作为问题解例:用迭代法求某个数平方根已知求平方根迭代公式为:Private Function Fsqrt( a As single ) AS singleDim x0 As Single, x1 As Singlex0 =a/2 \'迭代初值x1 = 0.5*(x0 + a/x0)Dox0 = x1 \'为下次迭代作准备x1 = 0.5*(x0 + a/x0)Loop While Abs(x1 - x0) > 0.00001 Fsqrt=x1End Function十、数制转换将个十进制整数m转换成→r(2-16)进制串思路方法:将m不断除r 取余数直到商为零以反序得到结果下面写出转换参数idec为十进制数ibase为要转换成数基(如2进制基是2 8进制基是8等)输出结果是串Private Function TrDec(idec As Integer, ibase As Integer) As StringDim strDecR$, iDecR%strDecR = \"\"Do While idec <> 0iDecR = idec Mod ibaseIf iDecR >= 10 ThenstrDecR = Chr$(65 + iDecR - 10) & strDecRElsestrDecR = iDecR & strDecREnd Ifidec = idec ibaseLoopTrDec = strDecREnd Function十、串般处理1.简单加密和解密加密思想是:将每个字母C加(或减)序数K即用它后第K个字母代替变换式公式: c=chr(Asc(c)+k)例如序数k为5这时\"A\"→\"F\" \"a\"→?\"f\"\"B\"→?\"G\"…当加序数后字母超过\"Z\"或\"z\"则c=Chr(Asc(c)+k -26)例如:You are good→Dtz fwj ltti解密为加密逆过程将每个字母C减(或加)序数K即c=chr(Asc(c)-k),例如序数k为5这时\"Z\"→\"U\" \"z\"→\"u\"\"Y\"→\"T\"…[Page]当加序数后字母小于\"A\"或\"a\"则c=Chr(Asc(c)-k +26)下段是加密处理:i = 1: strp = \"\"nL = Len(RTrim(strI)) Do While (i <= nL)strT = Mid$(strI, i, 1) \'取第i个If (strT >= \"A\" And strT <= \"Z\") TheniA = Asc(strT) + 5If iA > Asc(\"Z\") Then iA = iA - 26strp = strp + Chr$(iA)ElseIf (strT >= \"a\" And strT <= \"z\") TheniA = Asc(strT) + 5If iA > Asc(\"z\") Then iA = iA - 26strp = strp + Chr$(iA)Elsestrp = strp + strTEnd Ifi = i + 1LoopPr strp2.统计文本单词个数算法思路:(1)从文本(串)左边开始取出个;设逻辑量WT表示所取是否是单词内初值设为False(2)若所取不是“空格”“逗号”“分号”或“感叹号”等单词分隔符再判断WT是否为True 若WT不为True则表是新单词开始让单词数Nw=Nw+1让WT=True;(3)若所取是“空格”“逗号”“分号”或“感叹号”等单词分隔符则表示不是单词内让WT=False;(4) 再依次取下个重得(2)(3)直到文本结束下面段是串strI中包含单词数Nw = 0: Wt = FalsenL = Len(RTrim(strI))For i = 1 To nLstrT = Mid$(strI, i, 1) \'取第i个Select Case strTCase \" \", \",\", \";\", \"!\"Wt = FalseCase Else If Not Wt ThenNw = Nw + 1[Page]Wt = TrueEnd IfEnd SelectNext iPr \"单词数为:\", Nw十2、穷举法穷举法(又称“枚举法”)基本思想是:列举各种可能情况并判断哪种可能是符合要求解这是种“在没有其它办法情况思路方法”是种最“笨”思路方法然而对些无法用解析法求解问题往往能奏效通常采用循环来处理穷举问题例: 将张面值为100元人民币等值换成100张5元、1元和0.5元零钞要求每种零钞不少于1张问有哪几种组合?Dim i%, j%, k%Pr \"5元1元0.5元\"For i = 1 To 20For j = 1 To 100 - ik = 100 - i - jIf 5.0 * i + 1.0 * j + 0.5 * k = 100 ThenPr i, j, kEnd IfNext jNext i十3、递归算法用自身结构来描述自身称递归VB允许在个Sub子过程和Function过程定义内部自己即递归Sub子过程和递归Function递归处理般用栈来实现每次自身把当前参数压栈直到递归结束条件;然后从栈中弹出当前参数直到栈空递归条件:(1)递归结束条件及结束时值;(2)能用递归形式表示且递归向终止条件发展例:编fac(n)=n! 递归Function fac(n As Integer) As IntegerIf n = 1 Thenfac = 1 Elsefac = n * fac(n - 1)End IfEnd Function。
VB常见算法

1.累加与连乘基本思想:设置初值,循环计算。
扩展:(1)计算指定范围内某一个数的倍数之和。
vb 编程,求从100~1000之间所有是3的倍数的数之和,当和大于3000时停止计算输出和,用for...next 语句For i = 100 To 1000If i Mod 3 = 0 Thens = s + iIf s > 3000 Then Exit ForEnd IfNext iPrint s(2)计算某范围内所有数的乘积。
用vb 编写一段程序,计算 1-50所有奇数的乘积dim prod as doubledim i as integerprod=1for i=1 to 50 step 2prod=prod*inextprint prod(3)求某一个数列的和。
本程序的功能是求下面数列前n 项之和。
1.求分数序列58,35,23,12,……,单击窗体显示数列前20项的和 Private Sub Form_Click()a = 2b = 1s = 0For i = 1 To 20s = s + a / bc = aa = a + bb = cNext iprint "和为:" & sEnd Sub2.生成N 个不同的随机数基本思想:将生成的数送入一个数组,每生成一个数后与数组中已有的数比较,如相同则丢弃,重新生成可使用语句Exit For 。
Private Sub Command1_Click()Dim a(10) As Integer, n As IntegerDim i As Integer, k As IntegerRandomizea(1) = Int(Rnd * 90) + 10k = 1Don = Int(Rnd * 90) + 10For i = 1 To 10If a(i) = n Then Exit ForNext iIf i > 10 Thenk = k + 1a(k) = nEnd IfLoop While k < 10For i = 1 To 10Text1 = Text1 & " " & Str(a(i))Next iEnd Sub3.求素数、极值求素数基本思想:素数的意义;实现方法:双重循环,外循环判断每一个数,内循环判断能否被某数整除。
在VB中利用循环结构解决素数问题_万小红

在VB中利用循环结构解决素数问题_万小红第27卷第2期运城学院学报V o l .27 N o .22009年4月J o u r n a l o f Y u n c h e n g U n i v e r s i t yA p r .2009在V B 中利用循环结构解决素数问题万小红,郝蕊洁(运城学院公共计算机教学部,山西运城044000)摘要:V b 语言是面向对象的结构化的编程语言,是非计算机专业学生程序设计首选的教学语言。
而循环结构的使用是计算机解题的一个重要特征,为增强学生解决实际问题的能力,着重对循环结构结合实际的问题做深入研究,结果表明能明显的提高学生的编程能力。
关键词:V b ;循环结构;素数中图分类号:O 156.4文献标识码:A 文章编号:1008-8008(2009)02-0066-030.引言高级语言程序设计课程不仅能使学生更深入地理解计算机的工作过程,而且在培养学生严密地逻辑思维及非计算机专业学生利用计算机解决本专业问题的能力方面也有着非常重要的作用,V i s u a l B a s i c 以其面向对象的编程、易学易用、图形用户界面的特点成为非计算机专业学生的首选。
[1]在进行程序设计时,人们总是设法将复杂的不易理解的求解过程转换为易于理解的操作的多次重复。
这样既可以降低问题的复杂性、简化程序代码的书写,又可以充分发挥计算机运算速度快、能自动运行程序的优势。
1.问题的提出在任何一门结构化的程序设计语言中,循环结构都起着承上启下的作用,循环语句的掌握直接关系着后续课程的内容的理解和掌握。
[2]对于非计算机专业的大部分学生学习V B 都以通过全国计算机二级考试为目标,在等级考试中有一部分很典型的考题就是素数问题的处理,解决素数问题通常都要用到循环结构。
为此在教学实践当中做了一些关于利用循环结构解决素数问题总结和探索,希望与广大读者共同探讨。
2.V B 程序设计语言的基本循环结构2.1F o r -N e x t 循环语句例1:判断一个给定的整数是否为素数。
VB 常考算法

1.求因子数Private Sub factor(X As Integer, Fn() As Integer) Dim I As Integer, N As IntegerReDim Fn(1): N = 1: Fn(1) = 1For I = 2 To N / 2If X Mod I = 0 ThenN = N + 1ReDim Preserve Fn(N)Fn(N) = IEnd IfNextEnd Sub2. 求因子数之和Private Function Sum_factor(N As Integer) As Long Dim I As Integer, J As Integer, S As IntegerDo While I < N / 2I = I + 1If N Mod I = 0 ThenS = S + IEnd IfLoopSum_factor = SEnd Function3. 判断数是否为素数Private Function Prime(N As Integer) As Boolean Dim M As IntegerFor M = 2 To Sqr(N)If N Mod M = 0 Then Exit FunctionNextPrime = TrueEnd Function4.求最大公约数Private Function gcd(m As Integer, n As Integer) As Integer If m Mod n = 0 Thengcd = nElsegcd = gcd(n, m Mod n)End IfEnd Function5.求最小公倍数Private Function Lcm(A As Integer, B As Integer) As Long DoLcm = Lcm + AIf Lcm Mod A = 0 And lcm Mod B = 0 ThenExit DoEnd IfLoopEnd Function6.求分数约数Private Sub divisor (Fz As Long, Fm As Long)Dim Min As Integer, K As IntegerIf Fm < Fz Then Min = Fz Else Min = FmFor K = 2 To MinDo While Fz Mod K = 0 And Fm Mod K = 0Fz = Fz / KFm = Fm / KLoopNextEnd Sub7.求阶乘Private Function fact(N As Integer) As Long If N <= 1 Thenfact = 1Elsefact = N * fact(N - 1)End IfEnd Function或Private Function fact(N As Integer) As Long Dim i As Integerfact = 1For i = 1 To Nfact = fact * iNextEnd Function8.一维数组排序(1)选择法排序,结果是从小到大Private Sub choose(a() As Integer)Dim I As Integer, J As Integer, Temp As Integer For I = 1 To UBound(a) - 1For J = I + 1 To UBound(a)If a(I) > a(J) ThenTemp = a(I)a(I) = a(J)a(J) = TempEnd IfNext JNext IEnd Sub(2)冒泡法排序,结果是从小到大Private Sub bubble_up(a() As Integer) Dim I As Integer, J As IntegerDim temp As DoubleDim m As IntegerFor I = LBound(a) To UBound(a) - 1 For J = UBound(a) To I + 1 Step -1If a(J) < a(J - 1) Thentemp = a(J)a(J) = a(J - 1)a(J - 1) = tempEnd IfNext JNext IEnd Sub注:把程序中“>”改成“<”,排序的结果为从大到小。
vb素数的判断方法

vb素数的判断方法VB素数的判断方法素数是指除了1和它本身之外,没有其他因数的自然数。
判断一个数是否为素数是数论中的基本问题之一,也是编程中常见的问题之一。
在VB语言中,我们可以通过一些方法来判断一个数是否为素数。
我们需要明确判断素数的定义。
对于一个大于1的自然数n,如果它能被2到n-1之间的任意一个数整除,那么它就不是素数;如果它不能被2到n-1之间的任何一个数整除,那么它就是素数。
基于这个定义,我们可以使用以下方法来判断一个数是否为素数:1. 输入待判断的数n;2. 判断n是否小于等于1,如果是,则n不是素数;3. 判断n是否能被2整除,如果能,则n不是素数;4. 从3开始,逐个判断n是否能被从3到n-1之间的任意一个数整除,如果能,则n不是素数;5. 如果n不能被从3到n-1之间的任何一个数整除,则n是素数。
下面是使用VB语言实现的判断素数的程序:```VBModule Module1Sub Main()Dim n As IntegerConsole.WriteLine("请输入一个自然数:") n = Console.ReadLine()If n <= 1 ThenConsole.WriteLine(n & "不是素数")Exit SubEnd IfIf n = 2 ThenConsole.WriteLine(n & "是素数")Exit SubEnd IfIf n Mod 2 = 0 ThenConsole.WriteLine(n & "不是素数")Exit SubEnd IfDim i As IntegerFor i = 3 To n - 1 Step 2If n Mod i = 0 ThenConsole.WriteLine(n & "不是素数") Exit SubEnd IfNextConsole.WriteLine(n & "是素数")End SubEnd Module```以上程序首先要求用户输入一个自然数n,然后根据定义逐步判断n 是否为素数,并输出结果。
VB常用算法

1.求任意自然数n的阶乘:方法一Do循环法S=1FOR I=1 TO nS=S*INEXT I方法二For循环S=1:t=1DO WHILE t<=5S=S*tt= t +1LOOP2.闰年判断y = T ext1.T extIf (y Mod 4 = 0 And y Mod 100 <> 0) Or y Mod 400 = 0 Then MsgBox y & "是闰年"ElseMsgBox y & "不是闰年"End If3.求两个自然数m、n的最大公约数Hmax和最小公倍数Hmin m=T ext1.text : n=T ext2.text ‘m和n可通过其他途径赋值mn=m*n ‘暂存m和n的乘积,以便后面算最小公倍数If m<n Thent=m :m=n :n=tEnd Ifr=m Mod n Do While r< >0m=nn=rr=m Mod nLoopHmax=nHmin=mn/Hmax4. 素数判断N=InputBox( “输入>=3的正整数”)FOR I=2 TO N-1 ‘或SQR(N) ,提前退出法IF (N MOD I =0) THEN EXIT FORNEXT IIF I>N-1 THENPRINT N; “是素数”ELSEPRINT N; “不是素数”N=InputBox( “输入一个>=3的正整数”) END IFF=0 …F也可用逻辑型变量,标志法FOR I=2 TO N-1 ‘或SQR(N)IF (N MOD I =0) THEN F=1NEXT IIF F=0 THENPRINT N; “是素数”ELSEPRINT N; “不是素数”END IF6.单词数统计方法一标志法,以空格作为单词间的间隔(假设只有空格和字母)Dim a$, temp$Dim n%, i%Dim newWord As Boolean, WordNum As Integera = T ext1.T ext 'a = Ltrim(T ext1.T ext)n = Len(a)newWord = False '未遇到新单词(也可用数值变量)WordNum = 0For i = 1 T o ntemp = Mid(a, i, 1)If temp = " " ThennewWord = False'简化为ElseIf newWord = False ThenElseIf UCase(temp) >= "A" And UCase(temp) <= "Z" And newWord = False ThenWordNum = WordNum + 1newWord = T rueEnd IfNext iT ext2.T ext = WordNum方法二根据相邻两字符特征判断Dim a$, tempF$, tempB$Dim n%, wNum%, i%a = T ext1.T ext 'a = Ltrim(T ext1.T ext)wNum = 0n = Len(a)For i = 1 T o n - 1 '避免超出范围tempF = Mid(a, i, 1)tempB = Mid(a, i + 1, 1)If wNum = 0 And tempF <> " " Then '对第一个单词特殊处理wNum = wNum + 1ElseIf tempF = " " And tempB <> " " ThenwNum = wNum + 1End IfNext iT ext2.T ext = wNum7.找出二维矩阵中的最大元素、最小元素及其所在位置Dim dMax%, rowMax%, colMax% '最大值、所在行、所在列Dim dMin%, rowMin%, colMin% '最小值、所在行、所在列Dim i%, j%dMax = a(1, 1): rowMax = 1: colMax = 1 '假设a(1, 1)最大,记录位置dMin = a(1, 1): rowMin = 1: colMin = 1 '假设a(1, 1)最小,记录位置For i = 1 T o UBound(a, 1) '第一维下标范围For j = 1 T o UBound(a, 2) '第二维下标范围'找最大If dMax < a(i, j) Then '与数组中的元素一一比较dMax = a(i, j)rowMax = icolMax = jEnd If'找最小If dMin > a(i, j) ThendMin = a(i, j)rowMin = icolMin = jEnd IfNext jNext iPrint "最大元素:"; dMax; ",它在第"; rowMax; "行,第"; colMax; "列" Print "最小元素:"; dMin; ",它在第"; rowMin; "行,第"; colMin; "列"8.产生n个[10,100]范围内互不相同的数据Dim T() As Integer '过程级动态数组Dim n As IntegerForm1.Clsn = InputBox("输入一个值")ReDim T(n)RandomizeFor i = 1 T o nT(i) = Int(Rnd * 91 + 10)'保证与前面的数据不等For j = 1 T o i - 1If T(i) = T(j) Then i = i - 1: Exit ForNext jNext i9.一维数组的排序(10个数据,升序为例)方法一比较交换法(经典排序法)(输出可同时进行)•外重循环I控制比较的轮数提供每轮参照元素下标(1 To n-1)•内重循环J 要与参照元素比较的元素的下标(I+1 To n) For i = 1 T o 9 …轮数及参照元素下标For j = i + 1 T o 10 …与参照元素比较的元素下标If a(i) > a(j) Thent = a(i)a(i) = a(j)a(j) = tEnd IfNext jNext i方法二选择交换法(输出可同时进行)内、外重循环的含义和作用与比较交换法相同For i = 1 T o 9k = I ‘K记录较小元素的下标For j = i + 1 T o 10If a(k) > a(j) Then k = jNext jIf k < > i Thent = a(i) : a(i) = a(k) : a(k) = tEnd IfNext i方法三冒泡法排序(输出独立进行)•外重循环I 控制比较的轮数(1 T o n-1 )决定各轮要参与比较的元素的范围•内重循环J提供每轮要与后面相邻元素进行比较的元素的下标(1T o n-I ) For i = 1 T o 9 ‟10 T o 2 Step -1For j = 1 T o 10 –i ‟1 T o i-1If a(j) > a(j + 1) Then ‟相邻元素比较t = a(j): a(j) = a(j + 1): a(j + 1) = tEnd IfNext jNext I方法四插入法排序绝对位置插入法:(结果的输出必须独立进行)第一重循环I 要决定位置的元素的下标( 2~n-1)第二重循环J 第I个元素要插入的有序数列(1~I-1)第三重循环K 当a(I)<a(J)时, 后移的元素(I-1~J)For i = 2 T o 10n = a(i) … 暂存a(i),避免冲掉For j = 1 T o i - 1If n < a(j) ThenFor k = i - 1 T o j Step –1a(k + 1) = a(k)Next ka(j) = nExit For …注意,不能少End IfNext jNext i …不用考虑n>a(i-1), n原本就放在a(i)相对位置插入法:(结果的输出必须独立进行)外重循环I 要决定位置的元素的下标( 2~n-1)内重循环J 第I个元素要插入的有序数列下标范围(I-1 ~ 1) For i = 2 T o 10n = a(i)For j = i - 1 T o 1 S tep –1 …反向If n < a(j) Thena(j + 1) = a(j)a(j) = nElsea(j + 1) = n …本句可不要Exit ForEnd IfNext jNext i10.有序数列的插入操作(假设原数组中已存放10个数据)绝对位置插入法:s = Val(InputBox("输入15~45之间的整数"))a(11) = s '提前放入For i = 1 To 10If s < a(i) Then '根据大小顺序,举实际数据定思路For k = 10 To i Step –1 'a(k + 1) = a(k)Next ka(i) = sExit For '分析少了该句的后果End IfNext iPrint "插入数据后:"For i = 1 To 11Print a(i);Next I11.有序数列的删除(假设原数组中已按升序存有10个不同数据)n = Val(InputBox("输入要删除的数据"))Rem 查找并删除k = 0 '找到的个数,决定输出范围For i = 1 To 10If n = a(i) Thenk = 1For j = i + 1 To 10 '将数据前移,填补删除空位a(j - 1) = a(j)Next jExit ForEnd IfNext iRem由k值决定输出范围,k=0,输出10个,k=1,输出9个数据Print "删除之后的结果:"For i = 1 To 10 - kPrint a(i);Next I12.统计文本框输入的字符串中,各字母出现的次数Dim a(65 To 90) As Integer 'a数组用于统计各字母出现的次数Dim c As String, le As Integer, d As String * 1Dim i%, j%, k%Picture1.Clsc = Text1.Text '取出待考察的字符串le = Len(c) '求字符串的长度For i = 1 To led = UCase(Mid(c, i, 1)) '(不区分大小写)取出字符转换成大写 If d >= "A" And d <= "Z" Thenj = Asc(d)a(j) = a(j) + 1 '对应数组元素加1End IfNext i For i = 65 To 90 '输出字母及其出现的次数If a(i) <> 0 Then '表明对应字母出现了k = k + 1 '用于控制输出格式Picture1.Print Chr$(i); "="; a(i); " ";If k Mod 9 = 0 Then Picture1.Print '每行输出9个 End IfNext j12.二分法查找(前提原数组有序,设原数组已按升序排序)Dim n%Dim bot%, mid%, top%, find As Booleann = Val(InputBox("请输入要查找的数据"))bot = 1: top = 10find = False '是否找到的标志Do '三个分支mid = Int((bot + top) / 2)If n = a(mid) Thenfind = TrueMsgBox "在a(" & mid & ")" & "找到数据" & nExit Do '可不要ElseIf n < a(mid) Thentop = mid - 1ElseIf n > a(mid) Thenbot = mid + 1End IfLoop Until find = True Or bot > topIf find = False Then MsgBox "没找到" & n & "."13.字符串的加密、解密问题加密解密问题.加密规律:小写字母: a-d,b-e……w-z,x-a,y-b,z-c大写字母: A-D,B-E……W-Z,X-A,Y-B,Z-C其它字符不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
VB常用算法----素数
一、算法说明
素数(质数):就是一个大于等于2的整数,并且只能被1和本身整除,而不能被其他整数整除的数。
判别某数m是否是素数的经典算法是:
对于m,从I=2,3,4,……,m-1依次判别能否被I整除,只要有一个能整除,m就不是素数,否则m是素数。
Private Function sushu(ByVal n As Long) As Boolean
Dim i As Long
For i = 2 To n - 1
If (n Mod i) = 0 Then Exit For
Next I
If I=n then sushu=True
End Function
很显然,实际上,我们可以改进上面
For i = 2 To n –1
为:
For i = 2 To int(sqr(m))
这样可以很好的提高效率。
以上判断一个数是否为素数的代码务必熟记!
二、应用举例
求100-200之内素数。
Private Sub Command1_Click()
Dim j As Integer
For j = 100 To 200
If sushu(j) = True Then Print j
Next j
End Sub
三、解题技巧
熟记判断素数的算法过程,根据题意,灵活调用!
四、实例说明
编程题(2002年春上机试卷04)
找出10000以内所有可以表示为两个平方数和的素数。
思路:
首先找10000以内的所有素数,对于每个素数判断其是否可以表示为两个平方数之和(即对于任意小于该素数shu的数I,如果I和shu-I均为平方数,则说明其可以表示为两个平方数之和。
)
判断数I是否为平方数的方法:sqr(i)=int(sqr(i))
Private Sub Command1_Click()
Dim j As Integer
Dim m As Long, n As Long
For j = 2 To 10000
If sushu(j) = True Then
If pf(j, m, n) = True Then
List1.AddItem j & "=" & m & "+" & n
End If
End If
Next j
End Sub
Private Function pf(ByVal shu As Long, m As Long, n As Long) As Boolean
Dim i As Long
For i = 1 To shu - 1
If (Sqr(i) = Int(Sqr(i))) And (Sqr(shu - i) = Int(Sqr(shu - i))) Then
pf = True
m = i
n = shu - i
Exit Function
End If
Next
End Function
五、实战练习
1.完善程序填空题(2002春二(7))
下列程序的功能是:查找四位正整数中的超级素数。
超级素数的定义为:当一个素数从低位到高位依次去掉一位数后剩下的数仍然是素数,则此数为超级素数。
如数2333、233、23、2均为素数,所以2333为超级素数。
Option Explicit
Private Sub Command1_Click()
Dim I As Integer, flg As Boolean
For I = 1001 To 9999 Step 2
Call sup_prime(I, flg)
If flg Then
List1.AddItem I
End If
Next I
End Sub
Private Sub sup_prime( ( 1 ) , F As Boolean) Dim p As Integer
F = True
Do While N > 0
If prime(N) Then
( 2 )
Else
( 3 )
Exit Sub
End If
Loop
End Sub
Public Function prime(p As Integer) As Boolean Dim k As Integer
If p = 1 Then
Exit Function
Else
For k = 2 To Sqr(p)
If p Mod k = 0 Then Exit Function
Next k
( 4 )
End If
End Function。
