VB程序设计的常用算法
VB常用算法介绍
VB常用算法介绍在VB程序开发中，常常需要使用各种算法来处理数据和解决问题。
下面将介绍几种常用的VB算法，包括排序算法、算法和图算法等。
1.排序算法排序算法用来将一组数据按照一定的规则进行排列。
常见的排序算法包括冒泡排序、选择排序、插入排序、归并排序和快速排序等。
冒泡排序（Bubble Sort）是一种交换排序算法，通过不断地相邻元素比较和交换，将较大的元素逐渐交换到末尾，从而实现排序。
冒泡排序的时间复杂度为O(n^2)。
选择排序（Selection Sort）是一种排序算法，每次从待排序的数据元素中选择最小（或最大）的一个元素，放到已排序的序列的末尾。
选择排序的时间复杂度为O(n^2)。
插入排序（Insertion Sort）是一种排序算法，将数组元素分为已排序和未排序两部分，每次从未排序的部分中取出一个元素，插入到已排序的部分的适当位置。
插入排序的时间复杂度为O(n^2)。
归并排序（Merge Sort）是一种分治排序算法，将待排序的数据分为两个子序列，然后递归地对子序列进行排序，并将两个已排序的子序列合并成一个有序序列。
归并排序的时间复杂度为O(nlogn)。
快速排序（Quick Sort）是一种分治排序算法，通过一次划分将待排数据分成左右两个子序列，然后递归地对子序列进行排序。
快速排序的时间复杂度为O(nlogn)。
2.算法算法用来在一个数据集合中查找一些元素或满足特定条件的元素。
常见的算法包括线性、二分和深度优先。
线性（Linear Search）是一种简单的算法，从数据集合的第一个元素开始逐个比较，直到找到目标元素或遍历完整个集合。
线性的时间复杂度为O(n)。
二分（Binary Search）是一种在有序数据集合中查找目标元素的算法，通过每次将范围缩小一半来快速定位目标元素。
二分的时间复杂度为O(logn)。
深度优先（Depth-First Search，DFS）是一种用来在图或树结构中遍历所有节点的算法，从一个起始节点开始，先遍历一个邻接节点，然后再递归地遍历该邻接节点的邻接节点。
VB常用算法总结大全
VB常用算法总结大全VB（Visual Basic）是一种对初学者友好的编程语言，因其简单易学的特点而受到很多人的喜爱。
在VB中，算法是编程过程中非常重要的一部分，它们用来解决各种问题，从简单的数学计算到复杂的数据处理。
本文将总结一些常用的算法，帮助VB程序员更好地应用于实际项目中。
一、排序算法1.冒泡排序冒泡排序是一种简单的排序算法，它通过不断地交换相邻的元素来对数据进行排序。
它的基本思想是从列表的第一个元素开始，依次比较相邻的两个元素，如果顺序不正确，则交换它们的位置。
重复这个过程，直到整个列表都已经排序。
2.快速排序快速排序是一种高效的排序算法，它通过选择一个基准元素，将列表分为两部分，一部分小于基准元素，一部分大于基准元素。
然后对这两部分分别进行快速排序，最后将它们合并在一起。
3.插入排序插入排序是一种简单直观的排序算法，它将列表分为已排序和未排序两部分，每次选择未排序部分的第一个元素，并插入到已排序部分的适当位置。
重复这个过程，直到整个列表都已经排序。
二、查找算法1.顺序查找顺序查找是一种简单的查找算法，它从列表的第一个元素开始，依次比较每个元素，直到找到目标元素或者遍历完整个列表。
2.二分查找二分查找是一种高效的查找算法，它要求列表已经排序。
它通过比较目标元素与列表中间元素的大小关系来确定要的部分，并缩小范围。
重复这个过程，直到找到目标元素或者确定列表中没有目标元素。
三、图算法1.深度优先（DFS）深度优先是一种用于图遍历的算法，它从一个起始点开始，沿着一个路径尽可能深地访问节点，直到遇到一个没有未访问过的相邻节点为止。
然后回溯到前一个节点，寻找其他路径。
2.广度优先（BFS）广度优先也是一种用于图遍历的算法，它从一个起始点开始，依次访问所有与起始点相邻的节点，然后再依次访问这些节点的相邻节点，直到遍历完图中的所有节点。
四、动态规划动态规划是一种解决多阶段决策问题的方法，它将问题分解为若干个阶段，并定义状态和决策。
vb常用算法介绍
vb常用算法介绍编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（vb常用算法介绍）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为vb常用算法介绍的全部内容。
一、累加算法如果在设计过程中遇到求1+2+3+……+100等连加问题时，就可以用累加算法来解决.累加算法的一般做法是设一个变量 s，作为累加器使用，初值为0,设一个变量用来保存加数.一般在累加算法中的加数都是有规律可循，可结合循环程序来实现。
一个循环程序的设计,如果以下三方面确定下来：变量的赋初值、循环体的内容、循环结束条件，那么根据循环语句的格式，就很容易写出相应的循环程序。
例：求1+2+3++100的累加和，并打印输出分析：设累加器S,初值为0，加数用变量I表示当I=1时,累加器S= S+I = 0+1=1当I=2时，累加器S= S+I =1+2= 3当I=3时，累加器S=S+I =3+3 =6当I=4时，累加器S=S+I =6+4 =10……当I=100时，累加器S=S+100=1+2+3+……+99+100=5050不难看出，I的值从1变化到100的过程中，累加器均执行同一个操作：S=S+I，S=S+I的操作执行了100次,所以该程序段可写成：Dim I As Integer, S As IntegerS = 0 ‘给累加器s赋初值For S = 1 To 100S= S + I ‘I既作为循环变量，又作为加数Next IPrint "1+2+……100="； S考虑一下:语句Print ”1+2+……100="; S可以放在循环体中吗?延伸一下：上述算法对数值型数据,执行的是累加操作，如果对字符串型数据，完成的是字符串的连接。
VB常用算法总结
VB常用算法总结在VB（Visual Basic）编程中，常用的算法有很多。
下面将对其中一些常见和重要的算法进行总结。
请注意，由于篇幅限制，这只是一个简要总结，无法涵盖所有算法的细节。
1.排序算法：排序算法是计算机科学中最基本和常见的算法之一、在VB中，常用的排序算法包括冒泡排序、插入排序、选择排序、快速排序和归并排序等。
排序算法通过比较和交换来对一组数据进行重新排列，使其按照指定的顺序排列。
2.查找算法：查找算法用于在一个数据集中寻找特定的值或元素。
在VB中，常用的查找算法有二分查找和线性查找等。
二分查找是一种高效的算法，可以在有序数组中快速地找到目标元素。
3.图算法：图算法是用于解决与图相关的问题的算法。
在VB中，常用的图算法包括广度优先（BFS）和深度优先（DFS）等。
这些算法可以用于寻找图中的路径、检测环和遍历图等操作。
4.动态规划：动态规划是一种用于解决最优化问题的算法。
在VB中，常用的动态规划算法有背包问题、最长公共子序列和最短路径等。
动态规划算法通过拆解问题为子问题，并保存子问题的解来避免重复计算，从而提高算法的效率。
5.字符串匹配：字符串匹配算法用于在一个字符串中查找另一个字符串。
在VB中，常用的字符串匹配算法有暴力匹配算法、KMP算法和Boyer-Moore算法等。
这些算法通过比较字符来确定字符串的匹配位置。
6.线性代数：线性代数是数学的一个分支，用于解决线性方程组和向量空间等问题。
在VB中，常用的线性代数算法有矩阵运算、向量运算和线性方程求解等。
这些算法可以应用于计算机图形学、数据分析和机器学习等领域。
7.数学运算：数学运算在VB编程中非常常见。
常用的数学运算算法包括求和、平均值、最大值、最小值和中值等。
这些算法可以通过循环和条件判断来实现。
8.加密与解密：加密和解密算法用于保护数据的安全性。
在VB中，常用的加密算法有对称加密算法（如DES和AES）和非对称加密算法（如RSA和ECC）等。
VB程序设计理论课提纲-排序,分治法,哈希函数,算法时间复杂性分析
②重复①过程，直至i=n+1 且j=m+1
合并排序法算法分析
在内循环的执行次数：
每执行一次循环，完成一个元素的合并 完成合并需执行循环m+n次
算法时间复杂性O(n) 算法空间复杂度O(2n)
冒泡排序+合并排序会提高算法效率 吗？
考虑对n个数的冒泡排序
时间复杂性n2/2 空间复杂性n （需要一个数组a[1..n]）
算法的计算次数最坏情况为10001次
解方程方案二
使用二分法进行动态步长试探求算
根据题意则在区间[0,1]中有10001个可用于试探 的x值是有序排列的，可用二分法求解 算法过程见教材P.79，例4.33
算法时间复杂度最坏情况为log2n，即 15次
解方程方案三
使用牛顿切线法进行动态步长试探求算
对算法效率的认识
一．算法复杂度基本概念 二．三种控制结构的算法时间复杂度 三．降低算法复杂度的基本策略 四．排序算法复杂度的认识
一、算法复杂度基本概念
算法复杂度是指程序执行过程所占用的机 器时间和空间。 一般采用大O标记法来描述复杂度的数量级 常见的复杂度的数量级有
O(n0) ：常量级 O(n) ：线性级 O(n2) ：平方级 O(2n) ：指数级 O(log2n) ：对数级
根据题意则在区间[0,1]中的x值和y值存在函数 关系，利用函数的导数求切线与x轴的焦点作为 步长进行求解 算法过程见教材P.79，例4.32
可以证明其算法时间复杂度比二分法 还要小。
四、对排序算法复杂度的认识
数组中元素的查找策略 选择排序算法复杂 冒泡排序算法复杂 归并排序算法复杂 二路归并排序算法复杂 分治思想下的冒泡排序(快速排序）算法复 杂
VB常用简单算法
VB常用简单算法VB是一种过程式编程语言，被广泛用于Windows平台的软件开发。
它提供了一系列的算法和数据结构可以用于解决复杂的问题。
下面是一些VB常用的简单算法：1. 顺序（Sequential Search）：顺序是一种简单的算法，它检查数组中的每个元素，直到找到目标元素或完整个数组。
该算法的时间复杂度为O(n)。
```vbFunction SequentialSearch(arr( As Integer, target As Integer) As IntegerDim i As IntegerFor i = 0 To UBound(arr)If arr(i) = target ThenReturn iEnd IfNextReturn -1 '表示未找到End Function```2. 二分（Binary Search）：二分是一种高效的算法，它将目标元素与数组的中间元素比较，根据比较结果确定目标元素在数组的左半部分还是右半部分，并重复这个过程，直到找到目标元素或范围缩小到空集。
该算法要求数组必须是有序的，并且时间复杂度为O(log n)。
```vbFunction BinarySearch(arr( As Integer, target As Integer) As IntegerDim low As Integer = 0Dim high As Integer = UBound(arr)While low <= highDim mid As Integer = (low + high) \ 2If arr(mid) = target ThenReturn midElseIf arr(mid) < target Thenlow = mid + 1Elsehigh = mid - 1End IfEnd WhileReturn -1 '表示未找到End Function```3. 冒泡排序（Bubble Sort）：冒泡排序是一种简单的排序算法，它重复地比较相邻的元素并交换顺序，直到整个数组按照升序或降序排列。
VB常用算法总结大全
精选ppt
3.穷举法
“穷举法”也称为“枚举法”或“试凑法”， 即将可能出现 的各种情况一一测试，判断是否满足条件，一般采用循环来实 现。
例百元买百鸡问题。假定小鸡每只5角,公鸡每只2元，母鸡每 只3元。现在有100元钱要求买100只鸡，编程列出所有可能的 购鸡方案。
设母鸡、公鸡、小鸡各为x、y、z只，根据题目要求，列出方 程为： x+y+y=100
3x+2y+0.5z=100 三个未知数，两个方程，此题有若干个解。
解决此类问题采用“试凑法”，把每一种情况都考虑到。
方法一：最简单三个未知数利用三重循环来实现。
方4 法二：从三个未知数的关精系选pp，t 利用两重循环来实现。
方法一：
方法二：
For X= 0 To 33
Private Sub Form_click() For Y= 0 To 50
Else Do
‘求最大公约数
判断数据是否合法
r = m Mod n
m=n
n=r
Loop Until r = 0 Text3.Text = CStr(m) ‘输出最大公约数
End If
End Sub
7、关于循环嵌套(一个循环体内又包含了一个完
8
精选ppt
6、求最大公约数
9
精选ppt
Private Sub Command1_Click()
Dim m, n, r As Long m = Val(Text1.Text) n = Val(Text2.Text)
‘取数据M ‘取数据N
If m <> Int(m) or m < 1 or n <> Int(n) or n < 1 Then Text3.Text = "数据错误！"
(完整版)VB常用算法——排序
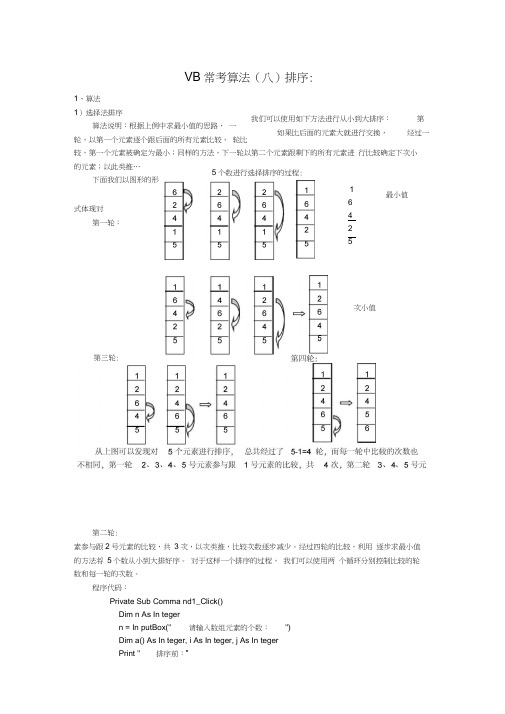
VB 常考算法（八）排序:1、算法 1）选择法排序算法说明：根据上例中求最小值的思路， 一轮，以第一个元素逐个跟后面的所有元素比较， 轮比较，第一个元素被确定为最小；同样的方法，下一轮以第二个元素跟剩下的所有元素进 行比较确定下次小的元素；以此类推…下面我们以图形的形式体现对第一轮：第二轮:素参与跟2号元素的比较，共 3次，以次类推，比较次数逐步减少。
经过四轮的比较，利用 逐步求最小值的方法将 5个数从小到大排好序。
对于这样一个排序的过程， 我们可以使用两 个循环分别控制比较的轮数和每一轮的次数。
程序代码：Private Sub Comma nd1_Click() Dim n As In teger n = In putBox(" 请输入数组元素的个数：")Dim a() As In teger, i As In teger, j As In tegerPrint "排序前：”我们可以使用如下方法进行从小到大排序：第 如果比后面的元素大就进行交换，经过一16 4 2 5最小值次小值5个数进行选择排序的过程:第三轮:ReDim a(n)For i = 1 To na(i) = In t(R nd * (99 -10 + 1) + 10) Print a(i);Next iFor i = 1 To n - 1 For j = i To nIf a(i) > a(j) Then temp = a(i)' a(i) = a(j) a(j) = temp End If Next j Next i PrintPrint " 排序后：" For i = 1 To n Print a(i); Next i End Sub2)冒泡法排序算法说明：相邻的元素进行比较，如果前面的元素比后面的元素大，则将它们进行交换,具体思路：设在数组 a 中存放n 个元素，第一轮，将 a(1)和a(2)进行比较，若a(1)>a(2), 则交换这两个元素的值，然后继续用a(2)和a(3)比较，若a(1)>a(2)，则交换这两个元素的值，以此类推，直到a(n-1)和a(n)进行比较处理后，a(n)中就存放了 n 个数中最大的值; 第二轮，用a(1)与a(2),a(2) 与a(3),…,a(n-2)与a(n-1)进行比较，处理方法相同，这一 轮下来，a(n-1)中存放n 个数中第二大的值；…；第 n-1轮，a(1)与a(2)进行比较处理，确保最小值在a(1)中。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
VB程序设计的常用算法算法（Algorithm）：计算机解题的基本思想方法和步骤。
算法的描述：是对要解决一个问题或要完成一项任务所采取的方法和步骤的描述，包括需要什么数据（输入什么数据、输出什么结果）、采用什么结构、使用什么语句以及如何安排这些语句等。
通常使用自然语言、结构化流程图、伪代码等来描述算法。
一、计数、求和、求阶乘等简单算法此类问题都要使用循环，要注意根据问题确定循环变量的初值、终值或结束条件，更要注意用来表示计数、和、阶乘的变量的初值。
例：用随机函数产生100个[0，99]范围内的随机整数，统计个位上的数字分别为1，2，3，4，5，6，7，8，9，0的数的个数并打印出来。
本题使用数组来处理，用数组a(1 to 100)存放产生的确100个随机整数，数组x(1 to 10)来存放个位上的数字分别为1，2，3，4，5，6，7，8，9，0的数的个数。
即个位是1的个数存放在x(1)中，个位是2的个数存放在x(2)中，……个位是0的个数存放在x(10)。
将程序编写在一个GetTJput过程中，代码如下：Public Sub GetTJput()Dim a(1 To 100) As IntegerDim x(1 To 10) As IntegerDim i As Integer, p As Integer'产生100个[0，99]范围内的随机整数，每行10个打印出来For i = 1 To 100a(i) = Int(Rnd * 100)If a(i) < 10 ThenForm1.Print Space(2); a(i);ElseForm1.Print Space(1); a(i);End IfIf i Mod 10 = 0 Then Form1.PrintNext i'统计个位上的数字分别为1，2，3，4，5，6，7，8，9，0的数的个数，并将统计结果保存在数组x(1),x(2),...,x(10)中，将统计结果打印出来For i = 1 To 100p = a(i) Mod 10 ' 求个位上的数字If p = 0 Then p = 10x(p) = x(p) + 1Next iForm1.Print "统计结果"For i = 1 To 10p = iIf i = 10 Then p = 0Form1.Print "个位数为" + Str(p) + "共" + Str(x(i)) + "个"Next iEnd Sub二、求两个整数的最大公约数、最小公倍数分析：求最大公约数的算法思想：(最小公倍数=两个整数之积/最大公约数)(1) 对于已知两数m，n，使得m>n；(2) m除以n得余数r；(3) 若r=0，则n为求得的最大公约数，算法结束；否则执行(4)；(4) m←n，n←r，再重复执行(2)。
例如:求m=14 ,n=6的最大公约数. m n r6 26 0m=inputBox("m=")n=inputBox("n=")nm=n*mIf m < n Then t = m: m = n: n = tr=m mod nDo While (r <> 0)m=nn=rr= m mod nLoopPrint "最大公约数=", nPrint "最小公倍数=", nm/n三、判断素数只能被1或本身整除的数称为素数基本思想：把m作为被除数，将2—INT（m）作为除数，如果都除不尽，m就是素数，否则就不是。
（可用以下程序段实现）m =val( InputBox("请输入一个数"))For i=2 To int(sqr(m))If m Mod i = 0 Then Exit ForNext iIf i > int(sqr(m)) ThenPrint "该数是素数"ElsePrint "该数不是素数"End If将其写成一函数,若为素数返回True，不是则返回FalsePrivate Function Prime( m as Integer) As BooleanDim i%Prime=TrueFor i=2 To int(sqr(m))If m Mod i = 0 Then Prime=False: Exit ForNext iEnd Function四、验证哥德巴赫猜想（任意一个大于等于6的偶数都可以分解为两个素数之和）基本思想：n为大于等于6的任一偶数，可分解为n1和n2两个数，分别检查n1和n2是否为素数，如都是，则为一组解。
如n1不是素数，就不必再检查n2是否素数。
先从n1=3开始，检验n1和n2（n2=N-n1）是否素数。
然后使n1+2 再检验n1、n2是否素数，… 直到n1=n/2为止。
利用上面的prime函数，验证哥德巴赫猜想的程序代码如下：Dim n%,n1%,n2%n=Val(InputBox("输入大于6的正整数"))For n1=3 to n\2 step 2n2=n-n1If prime(n1) ThenIf prime(n2) thenPrint n & "=" & n1 & "+" & n2Exit For '结束循环End ifEnd ifNext n1五、排序问题1．选择法排序（升序）基本思想：1）对有n个数的序列（存放在数组a(n)中），从中选出最小的数，与第1个数交换位置；2）除第1 个数外，其余n-1个数中选最小的数，与第2个数交换位置；3）依次类推，选择了n-1次后，这个数列已按升序排列。
程序代码如下：For i = 1 To n - 1imin = iFor j = i + 1 To nIf a(imin) > a(j) Then imin = jNext jtemp = a(i)a(i) = a(imin)a(imin) = tempNext I2．冒泡法排序（升序）基本思想：(将相邻两个数比较，小的调到前头)1）有n个数（存放在数组a(n)中），第一趟将每相邻两个数比较，小的调到前头，经n-1次两两相邻比较后，最大的数已“沉底”，放在最后一个位置，小数上升“浮起”；2）第二趟对余下的n-1个数（最大的数已“沉底”）按上法比较，经n-2次两两相邻比较后得次大的数；3）依次类推，n个数共进行n-1趟比较，在第j趟中要进行n-j次两两比较。
程序段如下For i = 1 To n - 1For j = 1 To n-iIf a(j) > a(j+1) Thentemp=a(j)： a(j)=a(j+1)： a(j+1)=tempEnd ifNext jNext i3．合并法排序（将两个有序数组A、B合并成另一个有序的数组C，升序）基本思想：1）先在A、B数组中各取第一个元素进行比较，将小的元素放入C数组；2）取小的元素所在数组的下一个元素与另一数组中上次比较后较大的元素比较，重复上述比较过程，直到某个数组被先排完；3）将另一个数组剩余元素抄入C数组，合并排序完成。
程序段如下：Do While ia <= UBound(A) And ib <= UBound(B) '当A和B数组均未比较完If A(ia) < B(ib) ThenC(ic) = A(ia)：ia = ia + 1ElseC(ic) = B(ib)：ib = ib + 1End Ific = ic + 1LoopDo While ia <= UBound(A) 'A数组中的剩余元素抄入C数组C(ic) = A(ia)ia = ia + 1：ic = ic + 1LoopDo While ib <= UBound(B) 'B数组中的剩余元素抄入C数组C(ic) = B(ib)ib = ib + 1：ic = ic + 1Loop六、查找问题1．①顺序查找法（在一列数中查找某数x）基本思想：一列数放在数组a(1)---a(n)中，待查找的数放在x 中，把x与a数组中的元素从头到尾一一进行比较查找。
用变量p表示a数组元素下标，p初值为1，使x与a(p)比较，如果x不等于a(p)，则使p=p+1，不断重复这个过程；一旦x等于a(p)则退出循环；另外，如果p 大于数组长度，循环也应该停止。
（这个过程可由下语句实现）p = 1Do While x <> a(p) And p < =np = p + 1Loop下面写一查找函数Find，若找到则返回下标值，找不到返回0Option Base 1Private Function Find( a( ) As Single,x As Single) As IntegerDim n%,p%n=Ubound( a )p = 1Do While x <> a(p) And p < =np = p + 1LoopIf p>n then p=0Find=pEnd Function②基本思想：一列数放在数组a(1)---a(n)中，待查找的关键值为key，把key与a数组中的元素从头到尾一一进行比较查找，若相同，查找成功，若找不到，则查找失败。
(查找子过程如下。
index：存放找到元素的下标。
)Public Sub Search(a() As Variant, key As Variant, index%)Dim i%For i = LBound(a) To UBound(a)If key = a(i) Thenindex = iExit SubEnd IfNext iindex = -1End Sub2．折半查找法（只能对有序数列进行查找）基本思想：设n个有序数（从小到大）存放在数组a(1)----a(n)中，要查找的数为x。
用变量bot、top、mid 分别表示查找数据范围的底部（数组下界）、顶部（数组的上界）和中间，mid=(top+bot)/2，折半查找的算法如下：（1）x=a(mid)，则已找到退出循环，否则进行下面的判断；（2）x<a(mid)，x必定落在bot和mid-1的范围之内，即top=mid-1；（3）x>a(mid)，x必定落在mid+1和top的范围之内，即bot=mid+1；（4）在确定了新的查找范围后，重复进行以上比较，直到找到或者bot<=top。