《聚类分析法》PPT课件
合集下载
聚类分析及其应用实例ppt课件

在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
Outlines
聚类的思想 常用的聚类方法 实例分析:层次聚类
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
3. 实例分析:层次聚类算法
定义:对给定的数据进行层次的分解
第4 步
➢
凝聚的方法(自底向上)『常用』
思想:一开始将每个对象作为单独的
第3 步
一组,然后根据同类相近,异类相异 第2步 的原则,合并对象,直到所有的组合
并成一个,或达到一个终止条件。 第1步
a, b, c, d, e c, d, e d, e
X3 Human(人) X4 Gorilla(大猩猩) X5 Chimpanzee(黑猩猩) X2 Symphalangus(合趾猿) X1 Gibbon(长臂猿)
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
离差平方和法( ward method ):
各元素到类中心的欧式距离之和。
Gp
Cluster P
Cluster M
Cluster Q
D2 WM Wp Wq
G q
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
凝聚的层次聚类法举例
Gp G q
Dpq max{ dij | i Gp , j Gq}
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
Outlines
聚类的思想 常用的聚类方法 实例分析:层次聚类
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
3. 实例分析:层次聚类算法
定义:对给定的数据进行层次的分解
第4 步
➢
凝聚的方法(自底向上)『常用』
思想:一开始将每个对象作为单独的
第3 步
一组,然后根据同类相近,异类相异 第2步 的原则,合并对象,直到所有的组合
并成一个,或达到一个终止条件。 第1步
a, b, c, d, e c, d, e d, e
X3 Human(人) X4 Gorilla(大猩猩) X5 Chimpanzee(黑猩猩) X2 Symphalangus(合趾猿) X1 Gibbon(长臂猿)
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
离差平方和法( ward method ):
各元素到类中心的欧式距离之和。
Gp
Cluster P
Cluster M
Cluster Q
D2 WM Wp Wq
G q
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
凝聚的层次聚类法举例
Gp G q
Dpq max{ dij | i Gp , j Gq}
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
聚类分析 ppt课件
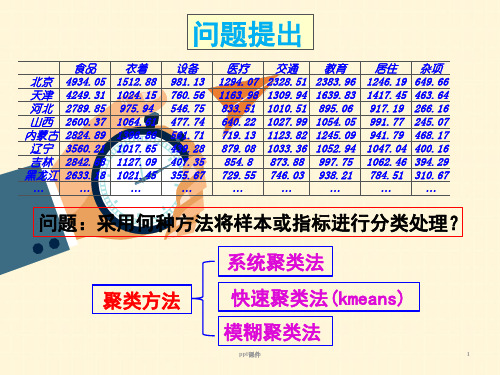
(2)相关系数
(3)距离和相关系数转换
di2j 1Ci2j
ppt课件
9
7.3 系统聚类法
1.基本思想 n个样本分成n类 计算任何两类距离 最小距离归为1类
整个过程画成聚类图
最短距离
最长距离 取
距 类平均法
离
方
重心法
法
中心距离法
离差平方和法 (Ward法)
ppt课件
10
2.系统聚类法计算公式
(1)最短距离法
…
教育 2383.96 1639.83 895.06 1054.05 1245.09 1052.94 997.75 938.21
…
居住 杂项
1246.19 649.66
1417.45 463.64
917.19 266.16
991.77 245.07
941.79 468.17
1047.04 400.16
0 0 0
0
结论:六种系统聚类法的并类原则和过程完全相同, 不同之处在于类与类之间的距离定义不同。
ppt课件
15
(7)程序实现
hc<-hclust(dist(X),method="single") #最短距离法 cbind(hc$merge,hc$height) #分类过程 plot(hc) #聚类图
[,1] [,2] [,3] [1,] -4 -5 1 [2,] -1 1 1.414 [3,] -2 2 4.123 [4,] -3 3 4.123
…
设备 981.13 760.56 546.75 477.74 561.71 439.28 407.35 355.67
…
医疗 1294.07 1163.98 833.51 640.22 719.13 879.08 854.8 729.55
(3)距离和相关系数转换
di2j 1Ci2j
ppt课件
9
7.3 系统聚类法
1.基本思想 n个样本分成n类 计算任何两类距离 最小距离归为1类
整个过程画成聚类图
最短距离
最长距离 取
距 类平均法
离
方
重心法
法
中心距离法
离差平方和法 (Ward法)
ppt课件
10
2.系统聚类法计算公式
(1)最短距离法
…
教育 2383.96 1639.83 895.06 1054.05 1245.09 1052.94 997.75 938.21
…
居住 杂项
1246.19 649.66
1417.45 463.64
917.19 266.16
991.77 245.07
941.79 468.17
1047.04 400.16
0 0 0
0
结论:六种系统聚类法的并类原则和过程完全相同, 不同之处在于类与类之间的距离定义不同。
ppt课件
15
(7)程序实现
hc<-hclust(dist(X),method="single") #最短距离法 cbind(hc$merge,hc$height) #分类过程 plot(hc) #聚类图
[,1] [,2] [,3] [1,] -4 -5 1 [2,] -1 1 1.414 [3,] -2 2 4.123 [4,] -3 3 4.123
…
设备 981.13 760.56 546.75 477.74 561.71 439.28 407.35 355.67
…
医疗 1294.07 1163.98 833.51 640.22 719.13 879.08 854.8 729.55
聚类分析 PPT课件
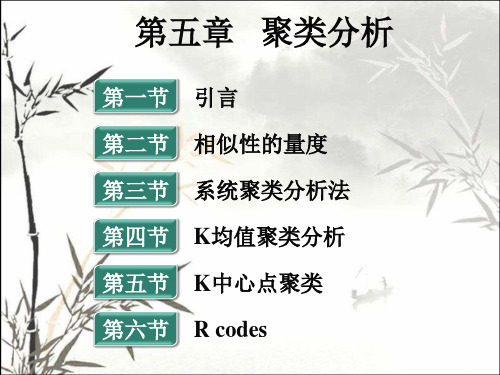
(f) (f) p dij f 1 ij d (i, j) (f) p f 1 ij
f is binary or nominal: dij(f) = 0 if xif = xjf , or dij(f) = 1 otherwise f is ordinal Compute ranks rif and Treat zif as interval-scaled
x1 x2 x3 x4
x1 0 3.61 5.1 4.24
x2 0 5.1 1
x3
x4
5
0 5.39
0
第二节 相似性的量度
一 样品相似性的度量
二 变量相似性的度量
含名义变量样本相似性度量
例: 学员资料包含六个属性:性别(男或女);外语语种
(英、日或俄);专业(统计、会计或金融);职业(教师 或非教师);居住处(校内或校外);学历(本科或本科以 下) 现有两名学员: X1=(男,英,统计,非教师,校外,本科)′ X2=(女,英,金融,教师,校外,本科以下)′ 对应变量取值相同称为配合的,否则称为不配合的 记配合的变量数为m1,不配合的变量数为m2,则样本之间 的距离可定义为
第五章 聚类分析
第一节 第二节 第三节 第四节 第五节 引言 相似性的量度 系统聚类分析法 K均值聚类分析 K中心点聚类
第六节
R codes
第一节 引言
“物以类聚,人以群分” 无监督分类聚类分析 分析如何对样品(或变量)进行量化分类的 问题 Q型聚类—对样品进行分类 R型聚类—对变量进行分类
用他们的序代替xif
zif
rif 1 M f 1
10
混合型属性
A database may contain all attribute types Nominal, symmetric binary, asymmetric binary, numeric, ordinal 可以用加权法计算合并的影响
f is binary or nominal: dij(f) = 0 if xif = xjf , or dij(f) = 1 otherwise f is ordinal Compute ranks rif and Treat zif as interval-scaled
x1 x2 x3 x4
x1 0 3.61 5.1 4.24
x2 0 5.1 1
x3
x4
5
0 5.39
0
第二节 相似性的量度
一 样品相似性的度量
二 变量相似性的度量
含名义变量样本相似性度量
例: 学员资料包含六个属性:性别(男或女);外语语种
(英、日或俄);专业(统计、会计或金融);职业(教师 或非教师);居住处(校内或校外);学历(本科或本科以 下) 现有两名学员: X1=(男,英,统计,非教师,校外,本科)′ X2=(女,英,金融,教师,校外,本科以下)′ 对应变量取值相同称为配合的,否则称为不配合的 记配合的变量数为m1,不配合的变量数为m2,则样本之间 的距离可定义为
第五章 聚类分析
第一节 第二节 第三节 第四节 第五节 引言 相似性的量度 系统聚类分析法 K均值聚类分析 K中心点聚类
第六节
R codes
第一节 引言
“物以类聚,人以群分” 无监督分类聚类分析 分析如何对样品(或变量)进行量化分类的 问题 Q型聚类—对样品进行分类 R型聚类—对变量进行分类
用他们的序代替xif
zif
rif 1 M f 1
10
混合型属性
A database may contain all attribute types Nominal, symmetric binary, asymmetric binary, numeric, ordinal 可以用加权法计算合并的影响
聚类分析(共8张PPT)
第4页,共8页。
聚类分析
三、聚类分析中的测度与标准化
在聚类分析技术的发展过程中,形成了很多种测度相似性的方法。每一种方法 都从不同的角度测度了研究对象的相似性。
在数据采集过程中,一般可以用三种方式采集数据:二分类型数据、等级类型 数据和连续类型数据。在进行聚类分析时可以根据不同的数据特点采用相应的测度 方法。
尽量避免绝对数据。
研究个案 A B C
受教育年限 10 16 6
年收入(万元) 2
1.5 1
年收入(元) 20000 15000 10000
A、B、C在不同距离单位时的距离图
A
B
B
10.01
C
A
10000
C
单位:万元
第6页,共8页。
单位:元
聚类分析
四、常用两种聚类分析方法
1.快速聚类法
快速聚类过程是初始分类的有效方法。适用于大容量样本的情形,由用户指定须聚类的 类数之后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。
m维空间中点与点之间的某种距离就可用来描述样品之间的亲疏程度。 而聚类分析则较常使用于将变量属性相似程度较高的观察值,加以分类,使类与类间的异质性达到最大,而同一类的几个观察值同质性很高。 ③对数据进行变换处理,(如标准化或规格化);
mm维维空 空间间中中点点与与点点实之之际间间的的应某某用种种距距时离离,就就可可两用用者来来描描的述述主样样品品要之之差间间的的别亲亲在疏疏程程于度度因。。子分析是针对“变量”予以分组,而聚类分析 按照这种方则法是不断将进“行合观并察,直值到个把所体有”的样予品以合为分一组个,大类亦为即止。因子分析时,根据因变量(题项)间关系密切与 四⑦、最常 后用绘两制否种系,聚统类聚将分类变析谱方系量法图予,按以不分同的类分(类标分准为或不几同个的层分类面原因则,子得)出不;同而的分聚类类结果分。析则较常使用于将变量属性相似 从数据结构程和度统计较形高式上的看观,因察子值分析,是加一种以“横分向类合并,”的使方类法,与聚类类分间析的则是异一质种“性纵向达合到并”最的方大法,。 而同一类的几个观察值 适每用一于 种大方容法同量都质样从本不性的同很情的形角高,度。由测用度户了指研定究须对聚象类的的相类似数性之。后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。 研究学生学业差异、因教师素教分学水析平:等等横,向都需简要化对研,究聚对象类进分行分析类:。纵向分组
聚类分析
三、聚类分析中的测度与标准化
在聚类分析技术的发展过程中,形成了很多种测度相似性的方法。每一种方法 都从不同的角度测度了研究对象的相似性。
在数据采集过程中,一般可以用三种方式采集数据:二分类型数据、等级类型 数据和连续类型数据。在进行聚类分析时可以根据不同的数据特点采用相应的测度 方法。
尽量避免绝对数据。
研究个案 A B C
受教育年限 10 16 6
年收入(万元) 2
1.5 1
年收入(元) 20000 15000 10000
A、B、C在不同距离单位时的距离图
A
B
B
10.01
C
A
10000
C
单位:万元
第6页,共8页。
单位:元
聚类分析
四、常用两种聚类分析方法
1.快速聚类法
快速聚类过程是初始分类的有效方法。适用于大容量样本的情形,由用户指定须聚类的 类数之后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。
m维空间中点与点之间的某种距离就可用来描述样品之间的亲疏程度。 而聚类分析则较常使用于将变量属性相似程度较高的观察值,加以分类,使类与类间的异质性达到最大,而同一类的几个观察值同质性很高。 ③对数据进行变换处理,(如标准化或规格化);
mm维维空 空间间中中点点与与点点实之之际间间的的应某某用种种距距时离离,就就可可两用用者来来描描的述述主样样品品要之之差间间的的别亲亲在疏疏程程于度度因。。子分析是针对“变量”予以分组,而聚类分析 按照这种方则法是不断将进“行合观并察,直值到个把所体有”的样予品以合为分一组个,大类亦为即止。因子分析时,根据因变量(题项)间关系密切与 四⑦、最常 后用绘两制否种系,聚统类聚将分类变析谱方系量法图予,按以不分同的类分(类标分准为或不几同个的层分类面原因则,子得)出不;同而的分聚类类结果分。析则较常使用于将变量属性相似 从数据结构程和度统计较形高式上的看观,因察子值分析,是加一种以“横分向类合并,”的使方类法,与聚类类分间析的则是异一质种“性纵向达合到并”最的方大法,。 而同一类的几个观察值 适每用一于 种大方容法同量都质样从本不性的同很情的形角高,度。由测用度户了指研定究须对聚象类的的相类似数性之。后,系统采用标准迭代算法进行运算,把所有的个案归并在不同的类中。 研究学生学业差异、因教师素教分学水析平:等等横,向都需简要化对研,究聚对象类进分行分析类:。纵向分组
聚类分析法ppt课件全

8/21/2024
25
1.2.2 动态聚类分析法
1.2 聚类分析的种类
(3)分类函数
按照修改原则不同,动态聚类方法有按批修改法、逐个修改法、混合法等。 这里主要介绍逐步聚类法中按批修改法。按批修改法分类的原则是,每一步修 改都将使对应的分类函数缩小,趋于合理,并且分类函数最终趋于定值,即计 算过程是收敛的。
8/21/2024
23
1.2.2 动态聚类分析法
1.2 聚类分析的种类
(2)初始分类 有了凝聚点以后接下来就要进行初始分类,同样获得初始分类也有不同的
方法。需要说明的是,初始分类不一定非通过凝聚点确定不可,也可以依据其 他原则分类。
以下是其他几种初始分类方法: ①人为分类,凭经验进行初始分类。 ②选择一批凝聚点后,每个样品按与其距离最近的凝聚点归类。 ③选择一批凝聚点后,每个凝聚点自成一类,将样品依次归入与其距离
8/21/2024
14
1.2 聚类分析的种类
(2)系统聚类分析的一般步骤 ①对数据进行变换处理; ②计算各样品之间的距离,并将距离最近的两个样品合并成一类; ③选择并计算类与类之间的距离,并将距离最ቤተ መጻሕፍቲ ባይዱ的两类合并,如果累的个
数大于1,则继续并类,直至所有样品归为一类为止; ④最后绘制系统聚类谱系图,按不同的分类标准,得出不同的分类结果。
8/21/2024
18
1.2 聚类分析的种类
(7)可变法
1 2 D kr
2 (8)离差平方和法
(D k 2 pD k 2 q)D p 2q
D k 2 rn n ir n n p i D i2 pn n ir n n q iD i2 qn rn in iD p 2 q
8/21/2024
聚类分析解析课件

类间距的度量
类:一个不严格的定义
定义9.1:距离小于给定阀值的点的集合 类的特征
◦ 重心:均值 ◦ 样本散布阵和协差阵 ◦ 直径
类间距的定义
最短距离法 最长距离法 重心法 类平均法 离差平方和法 等等
最小距离法(single linkage method)
极小异常值在实际中不多出现,避免极 大值的影响
类的重心之间的距离
对异常值不敏感,结果更稳定
离差平方和法(sum of squares
method或ward method)
W代表直径,D2=WM-WK-WL
即
DK2L
nL nk nM
XK XL XK XL
Cluster K
Cluster M
Cluster L
◦ 对异常值很敏感;对较大的类倾向产生较大的距 离,从而不易合并,较符合实际需要。
如表9.2所示,每个样品有p个指标,共 有n个样品
每个样品就构成p维空间中的一个点
:第i个样品的第k个指标对应的取值
◦ i=1……n; k=1……p
:第i个样品和第j个样品之间的距离
◦ i=1……n; j=1……n
点间距离测量问题
样品间距离与指标间距离 间隔尺度、有序尺度与名义尺度 数学距离与统计距离 相似性与距离:一个硬币的两面
类图上发现相同的类
饮料数据
16种饮料的热量、咖啡因、钠及价格四种变量
SPSS实现
选择Analyze-Classify-Hierarchical Cluster, 然 后 把 calorie ( 热 量 ) 、 caffeine ( 咖 啡
因)、sodium(钠)、price(价格)选入 Variables, 在Cluster选Cases(这是Q型聚类:对观测 值聚类),如果要对变量聚类(R型聚类) 则选Variables, 为 了 画 出 树 状 图 , 选 Plots , 再 点 Dendrogram等。 可以在Method中定义点间距离和类间距 离
聚类分析法ppt课件

7
(2)计算样品的距离。
d ij xi x j yi y j
8
G1
D(0)
G2 G3
G4
G5
G1 G2 G3 G4 G5
0 0.34 1.37 1.34 1.33
0 1.03 1 1.67
0 0.63 1.3
0 0.67
0
9
(3)找出D(0)非对角线上的最小元素, 将其对应的两个类合并为一个新类。
0 0.63 1.30 0 0.67
0
19
0
D(2)
1.37 0
1.67 1.30
0
20
0 1.67
D(3)
0
21
G1 G2 G3 G4 G5
0.4
0.8 1.2 1.6 2.0
聚类距离
பைடு நூலகம்22
G1 G2 G3 G4 G5
0.2 0.4 0.6 0.8 1.0
G1 G2 G3 G4 G5
0.4
0.8
1.2
1.6
2.0
聚类距离
聚类距离
23
某村对5个地块就其土壤质地和土壤有机 质含量进行了评估,结果如下。请分别 使用最长距离法和最短距离法对这5个地 块进行聚类分析,要求分为两类。
地块 A
B
C
D
E
质地 8
3
6
6
4
有机质 5
7
4
9
7
含量
24
聚类分析法
Cluster Analysis
1
聚类分析
将具有相似(similarity)性质(或距离)的 个体(样本)聚为一类,具有不同性质 的个体聚为不同的类。
聚类分析PPT课件
S1 S2
S3
S4 S5
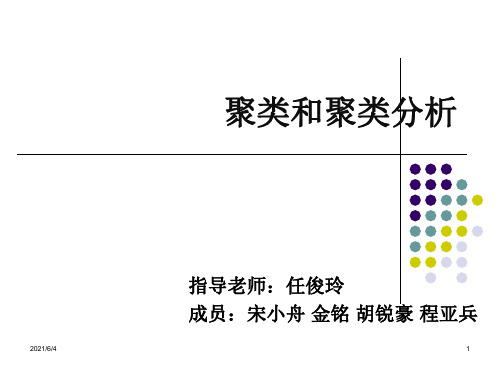
平均距离(average)
D 1 2 21 6(d 1 2 4d 1 2 5d 2 2 4d 2 2 5d 3 2 4d 3 2)5
2021/6/4
19
类间距离
S1 S2
S3
最短距离
2021/6/4
S4 S5
20
例 6个不同民族的标化死亡率与出生时的期望寿命
2021/6/4
5
聚类分析法的分类
Q型聚类分析是对样本进行分类处理的 R 型聚类分析是对变量(指标)进行分类处理的。
R型聚类分析的特点 (1) R型聚类分析不但可以了解个别
变量之间的亲疏程度,而且可以了解
各个变量组合之间的亲疏程度。
(2)根据变量的分类结果以及它们之
间的关系,可以选择主要变量进行回
归分析。
2021/6/4
2021/6/4
12
把不同的类型一一划分出来,形成一个由小到 大的分类系统,最后在把所有的样品(或指标 )间的亲把疏关系表示出来,这种方法称为系统 聚类分析法
2021/6/4
13
系统聚类的基本步骤
1. 构造n个类,每个类包含且只包含一个样品。 2. 计算n个样品两两间的距离,构成距离矩阵,记作D0。 3. 合并距离最近的两类为一新类。
聚类和聚类分析
指导老师:任俊玲 成员:宋小舟 金铭 胡锐豪 程亚兵
2021/6/4
1
目录
1.聚类的概念 2.聚类分析的原理 3.聚类分析的分类 4.距离和相似系数 5.系统聚类分析 6.快速聚类 7.致谢
2021/6/4
2
什么是聚类
早在孩提时代,人就通过不断改进下意识 中的聚类模式来学会如何区分猫和狗,动物和 植物
S3
S4 S5
平均距离(average)
D 1 2 21 6(d 1 2 4d 1 2 5d 2 2 4d 2 2 5d 3 2 4d 3 2)5
2021/6/4
19
类间距离
S1 S2
S3
最短距离
2021/6/4
S4 S5
20
例 6个不同民族的标化死亡率与出生时的期望寿命
2021/6/4
5
聚类分析法的分类
Q型聚类分析是对样本进行分类处理的 R 型聚类分析是对变量(指标)进行分类处理的。
R型聚类分析的特点 (1) R型聚类分析不但可以了解个别
变量之间的亲疏程度,而且可以了解
各个变量组合之间的亲疏程度。
(2)根据变量的分类结果以及它们之
间的关系,可以选择主要变量进行回
归分析。
2021/6/4
2021/6/4
12
把不同的类型一一划分出来,形成一个由小到 大的分类系统,最后在把所有的样品(或指标 )间的亲把疏关系表示出来,这种方法称为系统 聚类分析法
2021/6/4
13
系统聚类的基本步骤
1. 构造n个类,每个类包含且只包含一个样品。 2. 计算n个样品两两间的距离,构成距离矩阵,记作D0。 3. 合并距离最近的两类为一新类。
聚类和聚类分析
指导老师:任俊玲 成员:宋小舟 金铭 胡锐豪 程亚兵
2021/6/4
1
目录
1.聚类的概念 2.聚类分析的原理 3.聚类分析的分类 4.距离和相似系数 5.系统聚类分析 6.快速聚类 7.致谢
2021/6/4
2
什么是聚类
早在孩提时代,人就通过不断改进下意识 中的聚类模式来学会如何区分猫和狗,动物和 植物
聚类分析-基因芯片ppt课件

样品之间的距离和类与类之间的距离,然后将距离 最近的两类合并成一个新类,计算新类与其他类的 距离;重复进行两个最近类的合并,每次减少一类, 直至所有的样品合并为一类。
常用的系统聚类方法
❖ 一、最短距离法 ❖ 二、最长距离法 ❖ 三、中间距离法 ❖ 四、类平均法 ❖ 五、重心法 ❖ 六、离差平方和法(Ward方法)
❖ 最短距离法、最长距离法、可变法、类平均法、可 变类平均法和离差平方和法都具有单调性,但中间 距离法和重心法不具有单调性。
类的个数
❖ 如果能够分成若干个很分开的类,则类的个数就比 较容易确定;反之,如果无论怎样分都很难分成明 显分开的若干类,则类个数的确定就比较困难了。
❖ 确定类个数的常用方法有: 1.给定一个阈值T。 2.观测样品的散点图。 3.使用统计量。包括R:2 统计量,半偏R2 统计量, 伪F 统计量和伪t2 统计量。
一、最短距离法
❖ 定义类与类之间的距离为两类最近样品间的距离, 即
DKL
min
iGK , jGL
dij
最短距离法的聚类步骤
❖ (1) 规定样品之间的距离,计算 n 个样品的距离矩
阵 D0 ,它是一个对称矩阵。
❖ ❖
(合 (23))并选计成择算一新D个类0新中G类的M 与,最任记小一为元类G素MG,,J 设之即为间G距MDK离L ,G的K则递将G推LG公K 和式为GL
❖ (3)重复步骤(2),直至所有的样品都不能再分配为止。
❖ 最终的聚类结果在一定程度上依赖于初始凝聚点或 初始分类的选择。经验表明,聚类过程中的绝大多 数重要变化均发生在第一次再分配中。
例6.4.2
❖ 对例6.3.3使用k均值法进行聚类,聚类前对各变量作 标准化变换,聚类结果如下:
常用的系统聚类方法
❖ 一、最短距离法 ❖ 二、最长距离法 ❖ 三、中间距离法 ❖ 四、类平均法 ❖ 五、重心法 ❖ 六、离差平方和法(Ward方法)
❖ 最短距离法、最长距离法、可变法、类平均法、可 变类平均法和离差平方和法都具有单调性,但中间 距离法和重心法不具有单调性。
类的个数
❖ 如果能够分成若干个很分开的类,则类的个数就比 较容易确定;反之,如果无论怎样分都很难分成明 显分开的若干类,则类个数的确定就比较困难了。
❖ 确定类个数的常用方法有: 1.给定一个阈值T。 2.观测样品的散点图。 3.使用统计量。包括R:2 统计量,半偏R2 统计量, 伪F 统计量和伪t2 统计量。
一、最短距离法
❖ 定义类与类之间的距离为两类最近样品间的距离, 即
DKL
min
iGK , jGL
dij
最短距离法的聚类步骤
❖ (1) 规定样品之间的距离,计算 n 个样品的距离矩
阵 D0 ,它是一个对称矩阵。
❖ ❖
(合 (23))并选计成择算一新D个类0新中G类的M 与,最任记小一为元类G素MG,,J 设之即为间G距MDK离L ,G的K则递将G推LG公K 和式为GL
❖ (3)重复步骤(2),直至所有的样品都不能再分配为止。
❖ 最终的聚类结果在一定程度上依赖于初始凝聚点或 初始分类的选择。经验表明,聚类过程中的绝大多 数重要变化均发生在第一次再分配中。
例6.4.2
❖ 对例6.3.3使用k均值法进行聚类,聚类前对各变量作 标准化变换,聚类结果如下:
聚类分析ppt课件

第七章 聚类分析
第一节 引言 第二节 相似性的量度 第三节 系统聚类分析法 第四节 K均值聚类分析 第五节 两步聚类分析
1
第一节 引言
什么是聚类分析? ❖ 聚类分析是根据“物以类聚”的道理,对样本或指
标进行分类的一种多元统计分析方法,它们讨论的 对象是大量的样本,要求能合理地按各自的特性进 行合理的分类,没有任何模式可供参考或依循,即 在没有先验知识的情况下进行的。
1.明考夫斯基距离
p
dij (q) (
X ik X jk )q 1/ q
k 1
明考夫斯基距离简称明氏距离。
(7.1)
13
按q的取值不同又可分成下面的几个式子
(1)绝对距离( q 1)
p
dij (1) X ik X jk k 1
பைடு நூலகம்
(7.2)
(2)欧氏距离( q 2)
p
dij (2) (
X ik X jk )2 1/ 2
22
第三节 系统聚类分析法
一 系统聚类的基本思想 二 类间距离与系统聚类法
23
一、系统聚类的基本思想
❖ 系统聚类的基本思想是:距离相近的样品(或变量)先聚成 类,距离相远的后聚成类,过程一直进行下去,每个样品( 或变量)总能聚到合适的类中。系统聚类过程是:假设总共 有n个样品(或变量),第一步将每个样品(或变量)独自 聚成一类,共有n类;第二步根据所确定的样品(或变量) “距离”公式,把距离较近的两个样品(或变量)聚合为一 类,其它的样品(或变量)仍各自聚为一类,共聚成n 1类 ;第三步将“距离”最近的两个类进一步聚成一类,共聚成 n 2类;……,以上步骤一直进行下去,最后将所有的样品 (或变量)全聚成一类。为了直观地反映以上的系统聚类过 程,可以把整个分类系统画成一张谱系图。所以有时系统聚 类也称为谱系分析。除系统聚类法外,还有有序聚类法、动 态聚类法、图论聚类法、模糊聚类法等。
第一节 引言 第二节 相似性的量度 第三节 系统聚类分析法 第四节 K均值聚类分析 第五节 两步聚类分析
1
第一节 引言
什么是聚类分析? ❖ 聚类分析是根据“物以类聚”的道理,对样本或指
标进行分类的一种多元统计分析方法,它们讨论的 对象是大量的样本,要求能合理地按各自的特性进 行合理的分类,没有任何模式可供参考或依循,即 在没有先验知识的情况下进行的。
1.明考夫斯基距离
p
dij (q) (
X ik X jk )q 1/ q
k 1
明考夫斯基距离简称明氏距离。
(7.1)
13
按q的取值不同又可分成下面的几个式子
(1)绝对距离( q 1)
p
dij (1) X ik X jk k 1
பைடு நூலகம்
(7.2)
(2)欧氏距离( q 2)
p
dij (2) (
X ik X jk )2 1/ 2
22
第三节 系统聚类分析法
一 系统聚类的基本思想 二 类间距离与系统聚类法
23
一、系统聚类的基本思想
❖ 系统聚类的基本思想是:距离相近的样品(或变量)先聚成 类,距离相远的后聚成类,过程一直进行下去,每个样品( 或变量)总能聚到合适的类中。系统聚类过程是:假设总共 有n个样品(或变量),第一步将每个样品(或变量)独自 聚成一类,共有n类;第二步根据所确定的样品(或变量) “距离”公式,把距离较近的两个样品(或变量)聚合为一 类,其它的样品(或变量)仍各自聚为一类,共聚成n 1类 ;第三步将“距离”最近的两个类进一步聚成一类,共聚成 n 2类;……,以上步骤一直进行下去,最后将所有的样品 (或变量)全聚成一类。为了直观地反映以上的系统聚类过 程,可以把整个分类系统画成一张谱系图。所以有时系统聚 类也称为谱系分析。除系统聚类法外,还有有序聚类法、动 态聚类法、图论聚类法、模糊聚类法等。
