第3章 复合材料力学性能的复合规律(全)
合集下载
第3章复合材料的原材料
3.2 增强材料（第六讲）
3.2.1 纤维增强体 纤维：几至几十微米的多晶材料或非晶材料 晶须：约1微米的近单晶或单晶材料）
3.2.2 颗粒增强体
第3章复合材料的原材料
3.2.1 纤维增强体
一、长纤维（玻璃、高熔点金属、碳、硼纤维、 SiC 纤维 、 Al2O3纤维、 Si3N4系纤维、BN系、AlN系纤 维、芳伦纤维、陶瓷纤维） 二、晶须（SiCw、Si3N4w、钛酸钾晶须（KTw）、 硼酸铝晶须（AlBw）、氧化锌晶须（ZnOw）、石 墨晶须（Grw））
美国生产，用于碳-碳复合材料。但是由于其碳化收得 率较低（约25%），且性能与其它碳纤维相比较低，现 在已逐渐被PAN原料的碳纤维所取代。
第3章复合材料的原材料
2） 以沥青作为原材料
沥青 （相对分子质量500）
加热350℃ 脱水缩合反应
平面缩合芳香环分子 （分子质量大于1000）
液晶连续相
数量超过40%
225 392
第3章复合材料的原材料
延伸率（%）
1.8
0.6
2.0 0.5～0.7
1.5 0.6
碳纤维
第3章复合材料的原材料
镀镍碳纤维
第3章复合材料的原材料
碳短纤维
第3章复合材料的原材料
碳纤维织物
第3章复合材料的原材料
碳 纤 维 不 织 布
第3章复合材料的原材料
碳纤维小结
➢ 纤维素纤维：复杂应力，石墨化，收得率低 ➢ 沥青纤维：原料便宜，收得率高；杂质影响性能 ➢ PAN纤维：基础研究全面，工艺成熟
第3章复合材料的原材料
4）各种碳纤维的力学性能
原料
抗拉强度（MPa）
人造丝（低弹性模量丝）
686
3.2.1 纤维增强体 纤维：几至几十微米的多晶材料或非晶材料 晶须：约1微米的近单晶或单晶材料）
3.2.2 颗粒增强体
第3章复合材料的原材料
3.2.1 纤维增强体
一、长纤维（玻璃、高熔点金属、碳、硼纤维、 SiC 纤维 、 Al2O3纤维、 Si3N4系纤维、BN系、AlN系纤 维、芳伦纤维、陶瓷纤维） 二、晶须（SiCw、Si3N4w、钛酸钾晶须（KTw）、 硼酸铝晶须（AlBw）、氧化锌晶须（ZnOw）、石 墨晶须（Grw））
美国生产，用于碳-碳复合材料。但是由于其碳化收得 率较低（约25%），且性能与其它碳纤维相比较低，现 在已逐渐被PAN原料的碳纤维所取代。
第3章复合材料的原材料
2） 以沥青作为原材料
沥青 （相对分子质量500）
加热350℃ 脱水缩合反应
平面缩合芳香环分子 （分子质量大于1000）
液晶连续相
数量超过40%
225 392
第3章复合材料的原材料
延伸率（%）
1.8
0.6
2.0 0.5～0.7
1.5 0.6
碳纤维
第3章复合材料的原材料
镀镍碳纤维
第3章复合材料的原材料
碳短纤维
第3章复合材料的原材料
碳纤维织物
第3章复合材料的原材料
碳 纤 维 不 织 布
第3章复合材料的原材料
碳纤维小结
➢ 纤维素纤维：复杂应力，石墨化，收得率低 ➢ 沥青纤维：原料便宜，收得率高；杂质影响性能 ➢ PAN纤维：基础研究全面，工艺成熟
第3章复合材料的原材料
4）各种碳纤维的力学性能
原料
抗拉强度（MPa）
人造丝（低弹性模量丝）
686
复合材料原理3.PPT
增强体表面的结晶特性包括表面的结晶程度及晶体 分布状态，都会影响到界面作用和整体性能。
晶体越小，比表面积越大，对与基体结合有利的的 晶棱数目就越多；同时，也增大了粘接面积。
以上特性同时会影响到增强体的表面能，高表面能 的增强体与基体形成较强的界面结合。但应注意， 对于超微细粉末填料，超过某一细度时，可能会有 相反表现。
最简单的传递方式有串联和并联两种,复杂的可能有 多种组合方式.
2.3.2.3 强度性质
是材料承受外作用场极限能力的表征.如机械强度等.
对于非匀质的复合材料,材料的承载能力不是各组分 承载能力的叠加,而与外场的分布,组分间作用,相含 量,几何状态等因素有关.
2.3.2.4 转换性质
是指材料在一种外场的作用下,转换产生另一种新场 量.如电-热,热-光等.
对于增强体与基体界面结合很弱的复合材料,可以出 现平行效应.
三、相补效应:基体和增强体性能互补,整体性能提 高.
对于脆性的高强度纤维与韧性基体复合,结合适宜时 可以产生相补效应.
四、相抵效应:基体与增强体性能相互制约, 限制了整体性能的提高.
如脆性的纤维与韧性基体复合当结合很强时, 则材料整体容易脆性断裂.
增强体表面的物理特性主要是指其比表面积及表面 形态结构及表面能，通常涉及比表面积、多孔性、 表面极性、表面结构的均一性，表面的结晶特性和 表面能。 3.5.1.1 比表面积及多孔性
增强体的巨大的比表面积是导致复合材料中巨大的 界面存在并引起界面效应的根本所在。
增强体表面存在部分孔隙，孔隙中存在气体，复合 时部分孔隙被基体填充，呈机械镶嵌的结合状态。
五、相乘效应:两种具有转换效应的材料复合 即可产生相乘效应.
如把具有电磁效应的材料与具有磁光效应的 材料复合,即可产生电光效应.
晶体越小，比表面积越大，对与基体结合有利的的 晶棱数目就越多；同时，也增大了粘接面积。
以上特性同时会影响到增强体的表面能，高表面能 的增强体与基体形成较强的界面结合。但应注意， 对于超微细粉末填料，超过某一细度时，可能会有 相反表现。
最简单的传递方式有串联和并联两种,复杂的可能有 多种组合方式.
2.3.2.3 强度性质
是材料承受外作用场极限能力的表征.如机械强度等.
对于非匀质的复合材料,材料的承载能力不是各组分 承载能力的叠加,而与外场的分布,组分间作用,相含 量,几何状态等因素有关.
2.3.2.4 转换性质
是指材料在一种外场的作用下,转换产生另一种新场 量.如电-热,热-光等.
对于增强体与基体界面结合很弱的复合材料,可以出 现平行效应.
三、相补效应:基体和增强体性能互补,整体性能提 高.
对于脆性的高强度纤维与韧性基体复合,结合适宜时 可以产生相补效应.
四、相抵效应:基体与增强体性能相互制约, 限制了整体性能的提高.
如脆性的纤维与韧性基体复合当结合很强时, 则材料整体容易脆性断裂.
增强体表面的物理特性主要是指其比表面积及表面 形态结构及表面能，通常涉及比表面积、多孔性、 表面极性、表面结构的均一性，表面的结晶特性和 表面能。 3.5.1.1 比表面积及多孔性
增强体的巨大的比表面积是导致复合材料中巨大的 界面存在并引起界面效应的根本所在。
增强体表面存在部分孔隙，孔隙中存在气体，复合 时部分孔隙被基体填充，呈机械镶嵌的结合状态。
五、相乘效应:两种具有转换效应的材料复合 即可产生相乘效应.
如把具有电磁效应的材料与具有磁光效应的 材料复合,即可产生电光效应.
复合材料力学性能ppt课件
低分子是瞬变过程
（10-9 ～ 10-10 秒）
各种运动单元的运动需要 克服内摩擦阻力，不可能
瞬时完成。
高分子是松弛过程
运动单元多重性：
键长、键角、侧基、支链、 链节、链段、分子链
需要时间
（ 10-1 ～ 10+4 秒）
.
8
Tg 粘流态
Tf
Td
Tf ～ Td
分解温 度
（1）分子运动机制：整链分子产生相对位移
应变硬化
E D A
D A
O A
B
y
图2.4 非晶态聚合物的应力. -应变曲线（玻璃态）
20
2.2 高分子材料的力学性能
.
21
2.2 高分子材料的力学性能
序号 类型
1
2
硬而脆 硬而强
3 强而韧
4 软而韧
5 软而弱
曲线
模量
高
高
高
低
低
拉伸强度
中
高
高
中
低
断裂伸长率 小
中
大
很大
中
断裂能
小
中
大
大
小
F
F
A0
一点弯曲
三点弯曲
均匀压缩 体积形变 压缩应变
F
扭转
F
.
17
2.2 高分子材料的力学性能
应力-应变曲线 Stress-strain curve
标准哑 铃型试
样
实验条件：一定拉伸速率和温度
.
电子万能材料试验机
18
2.2 高分子材料的力学性能
图2.3 高分子材料三种典型的应力-应变曲线
.
19
第3章复合原理good
当θ>π/2时，不浸润； 当θ<π/2时，浸润；
当θ=π时，完全不浸润。
或者：增强体表面能大时
易浸润。
1964年Zisman提出能产生良好结合的两个条件： (1)液体粘度要尽量低； (2)γSG略大于γLG。
与θ有关的度的关系
—— 温度↑，θ↓
1. 机械结合：机械咬合，再加上热膨胀系数不同，基
体收缩抱住纤维。
说明：此时粗糙度起决定作用。(要求润湿 )
钨丝/Al
Vf=12%
界面状况
结合类型 性能（拉伸）
1.φ0.2mm
光滑
化学反应 95%
2.φ0.2mm
表面有C形成光滑表面 没有反应 35%
3.腐蚀，改变粗 粗糙 糙度φ0. 165mm
通过基体改性和改进复合条件能有效地改变界面结合状 态和断裂破坏的特征。
纤维表面处理和涂层可改善纤维表面的性能，增加基体 的浸润性，防止界面不良的反应改善界面结合。例如碳 纤维增强铝基复合材料中，由于纤维表面能很低，一般 不能被铝浸润，但用化学气相沉积(CVD)法在纤维表面 上形成TiB2并含有氯化物，则铝对其浸润能力不仅大大 改善，而且遏制了碳-铝界面的不良反应（Al4C3）。
➢ 低分子物质(水)的应力浸蚀使界面化学键断裂， 而在应力作用下处理剂能沿增强纤维表面滑移， 使已断裂的键重新结合。与此同时，应力得以松 弛，减缓了界面处的应力集中。
界面类 型
要形成复合材料、必须在界面上建立一定的结 合力。界面结合力大致可分为物理结合力和化学结 合力。物理结合力一般指范德华力，包括偶极定向 力，诱导偶极定向力和色散力，也可将氢键作用力 归人物理结合力范畴，该结合力大大高于前三种结 合力；化学结合力是在界面上产生共价键和金属键。 实际上又根据界面形成中物理和化学形式进行分类。 陶瓷基和金局基复合材料分类情况类似，树脂基复 合材料与前者有一定差别。
当θ=π时，完全不浸润。
或者：增强体表面能大时
易浸润。
1964年Zisman提出能产生良好结合的两个条件： (1)液体粘度要尽量低； (2)γSG略大于γLG。
与θ有关的度的关系
—— 温度↑，θ↓
1. 机械结合：机械咬合，再加上热膨胀系数不同，基
体收缩抱住纤维。
说明：此时粗糙度起决定作用。(要求润湿 )
钨丝/Al
Vf=12%
界面状况
结合类型 性能（拉伸）
1.φ0.2mm
光滑
化学反应 95%
2.φ0.2mm
表面有C形成光滑表面 没有反应 35%
3.腐蚀，改变粗 粗糙 糙度φ0. 165mm
通过基体改性和改进复合条件能有效地改变界面结合状 态和断裂破坏的特征。
纤维表面处理和涂层可改善纤维表面的性能，增加基体 的浸润性，防止界面不良的反应改善界面结合。例如碳 纤维增强铝基复合材料中，由于纤维表面能很低，一般 不能被铝浸润，但用化学气相沉积(CVD)法在纤维表面 上形成TiB2并含有氯化物，则铝对其浸润能力不仅大大 改善，而且遏制了碳-铝界面的不良反应（Al4C3）。
➢ 低分子物质(水)的应力浸蚀使界面化学键断裂， 而在应力作用下处理剂能沿增强纤维表面滑移， 使已断裂的键重新结合。与此同时，应力得以松 弛，减缓了界面处的应力集中。
界面类 型
要形成复合材料、必须在界面上建立一定的结 合力。界面结合力大致可分为物理结合力和化学结 合力。物理结合力一般指范德华力，包括偶极定向 力，诱导偶极定向力和色散力，也可将氢键作用力 归人物理结合力范畴，该结合力大大高于前三种结 合力；化学结合力是在界面上产生共价键和金属键。 实际上又根据界面形成中物理和化学形式进行分类。 陶瓷基和金局基复合材料分类情况类似，树脂基复 合材料与前者有一定差别。
复合材料力学性能的复合规律
D W
D W
若D
和
f
Dm分别为纤维和基体的变形量，则有
D D f Dm
f
D WV f
m
D WV m
W f WV f mWV m
f V f mVm
而
G12
f
Gf
m
Gm
G12
Gf
Vf
Gm Vm
1 V f Vm G12 G f Gm
或
G12
G f Gm G f Vm GmV f
Em Ef
2r x
x
s 2 r
树脂应变放大
x s 2 Em （含纤维部分）
r
Ef
● x x
与V f
的关系：
2R s 2r R 1 s 1
r 2r
s 2( R 1) rr
Vf
r 2
( r )2
2R 2R 4 R
s 2( 4V f 1)
r
将上式代入 x x
的表达式中,即得
x x
W
12
W
1
W f
f
VfW
1
Wm
m
VmW
1
121W V f f 1W Vm m1W
12 V f f Vm m
⑷单层板的面内剪切模量G12
假定纤维和基体所承受的剪切应力相等，并假 定复合材料的剪切特性是线性的，总剪切变量为D。
试样的剪切特性： f m
若试样宽度为W，则有剪切应变：
纤维对横向强度有负的增强作用（即复合材料横向 强度小于基体强度）
横向拉伸时，单层板的破坏应变与基体的破坏应变 关系不大。
纤维与基体间没有结合强度时：
对于简单的正方形排列模型有：
第3章复合材料的界面状态解析
吸附按作用力的性质，分为物理吸附和化学吸附。
3.3.2.1 物理吸附 当固体表面的原子的原子价被相邻的原子所饱和， 表面分子与吸附物之间的作用力是分子间引力（范德华 力）。 特点： 1）、无选择性，吸附量相差较大； 2）、吸附可呈单分子层或多分子层；
3）、物理吸附、解吸速度较快，易平衡。
一般在低温下进行的吸附是物理吸附。
注意： 对于复合材料来说，界面并非是一个理想的几何面。 实验证明： 复合材料中相与相之间的两相交接区是一个具有相当 厚度的界面层，两相的接触会引起多种界面效应，使界面层 的结构和性能不同于它两侧邻近的结构和性质。
图3.1 聚合物复合材料界面示意 （a）含界面物质； （b）不含界面物质
复合材料的界面层，除了在性能和结构上不同 于相邻两组分相外，还具有如下特点： (1)具有一定的厚度； (2)性能在厚度方向上有一定的梯度变化； (3)随环境条件变化而改变 。
3．2 复合材料界面的研究对象 表面处理物质 I
增强体
F
表面处理技术
增强体 表面处理物质层
F 表面 F/I 界面 I 表面 I 结构
增强体 表面处理物质层 基体
F/I 界面
复合技术
基体
M
增强体
I/M 界面 基体 F/M 界面
复合材料界面的研究对象： （1）增强体表面有关的问题： ①、增强体表面的化学、物理结构与性能； ②、增强体与表面处理物质界面层的结构与性质及对增强 体表面特性的影响； ③、增强体表面特性与基体之间的相互关系及两者间的相 互作用（增强体未处理时）； ④、增强体与表面处理物质的界面作用； ⑤、增强体表面特性与复合材料特性的相互关系。 （2）表面处理物质的有关问题： ①、最外层的化学、物理结构及内层的化学、物理结构； ②、表面处理物质与基体之间的相互作用； ③、表面处理物质对基体的影响； ④、处理条件及处理剂层的特性； ⑤、处理剂层随时间的变化； ⑥、处理剂层与复合材料性能的相互关系。
南京工业大学 复合材料原理 第3章 复合材料力学性能的复合规律(全)
V E
f f
f
V f E m (1 V f )
Vm E
m
高性能纤维复合材料，由于Ef>Em
E1 E f V f E2 Em /Vm
第3章 复合材料力学性能的复合规律
3.1.1 单向板的力学性能
3、单向板的主泊松比
主泊松比定义为:
12 2 / 1
W W
f
f
(1 V f )
在外力作用下，复合材料的强度取决于基体以及纤维的性能， 主要是材料的应变情况 ,
u f u m
u f
; m
u
u f
; m
u
u f
u m
第3章 复合材料力学性能的复合规律
3.1.3 材料力学法分析单向板的强度性能
1、均匀强度的纤维单向板的纵向拉伸强度
结构简化模型
承受的应力：
2
2 f
2m
（2.1）
2
复合料应变：
E
2
;
E2
2 f
产生的应变：
增强体应变：
f
;
（2.2）
基体的应变：
m
2
Em
第3章 复合材料力学性能的复合规律
3.1.1 单向板的力学性能 2、纵向弹性模量E2
材料宽度W上变形是由增强体和基体共同产生的：
3.1.1 单向板的力学性能 1、纵向弹性模量E1
单向板 模型
产生的应变（外力作用下长度变化量）
对于复合材料有： 1 E 1 1
（1.1） （1.2） （1.3）
f f
f
V f E m (1 V f )
Vm E
m
高性能纤维复合材料，由于Ef>Em
E1 E f V f E2 Em /Vm
第3章 复合材料力学性能的复合规律
3.1.1 单向板的力学性能
3、单向板的主泊松比
主泊松比定义为:
12 2 / 1
W W
f
f
(1 V f )
在外力作用下，复合材料的强度取决于基体以及纤维的性能， 主要是材料的应变情况 ,
u f u m
u f
; m
u
u f
; m
u
u f
u m
第3章 复合材料力学性能的复合规律
3.1.3 材料力学法分析单向板的强度性能
1、均匀强度的纤维单向板的纵向拉伸强度
结构简化模型
承受的应力：
2
2 f
2m
（2.1）
2
复合料应变：
E
2
;
E2
2 f
产生的应变：
增强体应变：
f
;
（2.2）
基体的应变：
m
2
Em
第3章 复合材料力学性能的复合规律
3.1.1 单向板的力学性能 2、纵向弹性模量E2
材料宽度W上变形是由增强体和基体共同产生的：
3.1.1 单向板的力学性能 1、纵向弹性模量E1
单向板 模型
产生的应变（外力作用下长度变化量）
对于复合材料有： 1 E 1 1
（1.1） （1.2） （1.3）
复合材料力学讲义
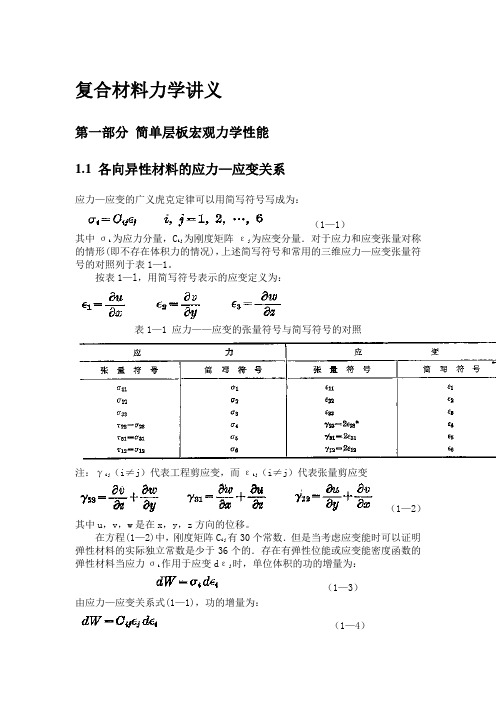
复合材料力学讲义第一部分简单层板宏观力学性能1.1各向异性材料的应力—应变关系应力—应变的广义虎克定律可以用简写符号写成为：（1—1）其中σi 为应力分量，Cij为刚度矩阵εj为应变分量．对于应力和应变张量对称的情形(即不存在体积力的情况)，上述简写符号和常用的三维应力—应变张量符号的对照列于表1—1。
按表1—l，用简写符号表示的应变定义为：表1—1 应力——应变的张量符号与简写符号的对照注：γij （i≠j）代表工程剪应变，而εij（i≠j）代表张量剪应变（1—2）其中u，v，w是在x，y，z方向的位移。
在方程(1—2)中，刚度矩阵Cij有30个常数．但是当考虑应变能时可以证明弹性材料的实际独立常数是少于36个的．存在有弹性位能或应变能密度函数的弹性材料当应力σi 作用于应变dεj时，单位体积的功的增量为：（1—3）由应力—应变关系式(1—1)，功的增量为：（1—4）沿整个应变积分，单位体积的功为：（1—5）虎克定律关系式(1—1)可由方程(1—5)导出：（1—6）于是（1—7）同样（1—8）因W的微分与次序无，所以：（1—9）这样刚度矩阵是对称的且只有21个常数是独立的。
用同样的方法我们可以证明：（1—10）其中S是柔度矩阵，可由反演应力—变关系式来确定应变应力关系式为ij（1—11）同理（1—12）即柔度矩阵是对称的，也只有21个独立常数．刚度和柔度分量可认为是弹性常数。
在线性弹性范围内，应力—应变关系的一般表达式为：（1—13）实际上，关系式(1—13)是表征各向异性材料的，因为材料性能没有对称平面．这种各向异性材料的别名是全不对称材料．比各向异性材料有更多的性能对称性的材料将在下面几段中叙述．各种材料性能对称的应力—应变关系式的证明由蔡（Tais）等给出。
如果材料有一个性能对称平面应力—应变关系式可简化为（1—14）对称平是z＝0．这种材料称为单对称材料．单对称材料有13个独立的弹性常数。
复合材料的力学性能ppt课件
外表改性剂对植物纤维/ 聚丙烯复 合资料力学性能的影响
采用不同的外表改性剂(苯甲酸、硬脂酸、 有机硅烷) 对植物纤维/ 聚丙烯复合体系进 展了处置,研讨了外表改性剂对体系力学性 能的影响规律,讨论了复合资料界面粘接机 理,分析了力学性能的变化规律。研讨结果 阐明,苯甲酸的参与可以使复合资料的拉伸 强度有较大提高,但冲击强度下降;经硬脂 酸处置的复合资料,其冲击强度有明显提高; 经有机硅烷处置的复合资料,拉伸强度及冲 击强度均有所提高。
由以下图可知,随着有机硅烷用量的加,复合资料的 拉伸强度会明显添加, 当有机烷含量达115 %时,拉 伸强度达最大值。以上结果阐明,硅烷偶联剂水溶 液的浸透性极强,可浸透植物纤维颗粒的一切间隙, 从而进一步浸润植物纤维颗粒的全部外表,使得偶 联剂与植物纤维外表坚持良好的接触;而有机硅烷 中的烷氧基团水解后构成硅醇,这样,硅醇就可以跟 植物纤维中的羟基作用,使纤维的吸水性减少,降低 了纤维的极性[3 ] 。
复合资料的特点
以天然植物纤维与热塑性树脂混合制备的复合资料 具有质量轻,加工性能好的特点,在许多领域有着广 泛的运用前景。植物纤维价廉易得,具有较大的强 度,刚度和耐热性。作为天然资料,植物纤维还可被 生物降解,植物纤维/ 热塑性树脂复合资料也因此具 备一定的环境相容性,是一条减轻目前“白色污染 〞的可行途径。因此,对植物纤维/ 聚丙烯复合资料 的研讨有着很重要的实际意义和适用价值。由于植 物纤维分子构造中含有大量的羟基,极性较强,与非 极性的聚丙烯混合时相互作用力很小,界面结合力 差,会影响复合资料的力学性能。故必需运用外表 改性剂对资料进展改性,以提高两种资料的界面结
苯甲酸含量对复合资料拉伸性能和冲击性能的影响
硬脂酸含量对复合资料力学性能的影响
以下图分别表示了在复合资料中参与了硬脂酸之 后,其拉伸性能和冲击性能的变化。从图 中可知, 复合资料的拉伸性能随硬脂酸含量的添加变化不
采用不同的外表改性剂(苯甲酸、硬脂酸、 有机硅烷) 对植物纤维/ 聚丙烯复合体系进 展了处置,研讨了外表改性剂对体系力学性 能的影响规律,讨论了复合资料界面粘接机 理,分析了力学性能的变化规律。研讨结果 阐明,苯甲酸的参与可以使复合资料的拉伸 强度有较大提高,但冲击强度下降;经硬脂 酸处置的复合资料,其冲击强度有明显提高; 经有机硅烷处置的复合资料,拉伸强度及冲 击强度均有所提高。
由以下图可知,随着有机硅烷用量的加,复合资料的 拉伸强度会明显添加, 当有机烷含量达115 %时,拉 伸强度达最大值。以上结果阐明,硅烷偶联剂水溶 液的浸透性极强,可浸透植物纤维颗粒的一切间隙, 从而进一步浸润植物纤维颗粒的全部外表,使得偶 联剂与植物纤维外表坚持良好的接触;而有机硅烷 中的烷氧基团水解后构成硅醇,这样,硅醇就可以跟 植物纤维中的羟基作用,使纤维的吸水性减少,降低 了纤维的极性[3 ] 。
复合资料的特点
以天然植物纤维与热塑性树脂混合制备的复合资料 具有质量轻,加工性能好的特点,在许多领域有着广 泛的运用前景。植物纤维价廉易得,具有较大的强 度,刚度和耐热性。作为天然资料,植物纤维还可被 生物降解,植物纤维/ 热塑性树脂复合资料也因此具 备一定的环境相容性,是一条减轻目前“白色污染 〞的可行途径。因此,对植物纤维/ 聚丙烯复合资料 的研讨有着很重要的实际意义和适用价值。由于植 物纤维分子构造中含有大量的羟基,极性较强,与非 极性的聚丙烯混合时相互作用力很小,界面结合力 差,会影响复合资料的力学性能。故必需运用外表 改性剂对资料进展改性,以提高两种资料的界面结
苯甲酸含量对复合资料拉伸性能和冲击性能的影响
硬脂酸含量对复合资料力学性能的影响
以下图分别表示了在复合资料中参与了硬脂酸之 后,其拉伸性能和冲击性能的变化。从图 中可知, 复合资料的拉伸性能随硬脂酸含量的添加变化不
3(2).复合材料的复合效应解析
10
表3．3 单向复合材料模型的基本假设
名称
基本假设
单元体 宏观均匀、无缺陷、增强体与基体性能恒定、线弹性
增强体 匀质、各向同性、线弹性、定向排列、连续
基 体 匀质、各向同性、线弹性
界 面 粘结完好(无孔隙、滑移、脱粘等)、变形协调
11
3.3.1 复合材料的模型
根据复合材料组分之增强体（或功能体）和基体的几何形 态，常见的几何结构模型有以下几种。
Vm＝1－V f －Vi
注：对于非球形体微粒增强体，可以采用粒子的当
量半径rd=(0.75Vf/π)1/3代替rf。球形模型的特点是各 向同性材料。
13
作业２
假设2 wt%二氧化钍（ThO2）加入到镍 （Ni）中， ThO2颗粒直径为100 nm， 已知ThO2和Ni的密度分别为9.69和8.9 g/cm3，请计算每立方厘米的复合材料中 有多少个ThO2颗粒。（假设界面上没有反 应产物）
y
3GmGpbVp1 2 2d (1Vp )c
作用
响应 4
材料模型化的方法
连续介质理 论
待确定复合 模型化 材料的微观
体系性能
结构模型
相微观作用
O
（O）
1 V
OdV
场Ii,响应场Oi
给定宏观作 用场I
有效性能ε
O= ε(I)
宏观响应场 O
O表示宏观响应场，V表示单元体积
5
3.3.1 复合材料的模型
在研究材料复合的有关理论时，建立一个能包含主要 影响因素、显示材料真实性能、易得确切结果的材料模型 是十分重要的。
（Angew. Chem. Int. Ed. 2009, 48, 7035 –7039）
表3．3 单向复合材料模型的基本假设
名称
基本假设
单元体 宏观均匀、无缺陷、增强体与基体性能恒定、线弹性
增强体 匀质、各向同性、线弹性、定向排列、连续
基 体 匀质、各向同性、线弹性
界 面 粘结完好(无孔隙、滑移、脱粘等)、变形协调
11
3.3.1 复合材料的模型
根据复合材料组分之增强体（或功能体）和基体的几何形 态，常见的几何结构模型有以下几种。
Vm＝1－V f －Vi
注：对于非球形体微粒增强体，可以采用粒子的当
量半径rd=(0.75Vf/π)1/3代替rf。球形模型的特点是各 向同性材料。
13
作业２
假设2 wt%二氧化钍（ThO2）加入到镍 （Ni）中， ThO2颗粒直径为100 nm， 已知ThO2和Ni的密度分别为9.69和8.9 g/cm3，请计算每立方厘米的复合材料中 有多少个ThO2颗粒。（假设界面上没有反 应产物）
y
3GmGpbVp1 2 2d (1Vp )c
作用
响应 4
材料模型化的方法
连续介质理 论
待确定复合 模型化 材料的微观
体系性能
结构模型
相微观作用
O
（O）
1 V
OdV
场Ii,响应场Oi
给定宏观作 用场I
有效性能ε
O= ε(I)
宏观响应场 O
O表示宏观响应场，V表示单元体积
5
3.3.1 复合材料的模型
在研究材料复合的有关理论时，建立一个能包含主要 影响因素、显示材料真实性能、易得确切结果的材料模型 是十分重要的。
（Angew. Chem. Int. Ed. 2009, 48, 7035 –7039）
高中化学复合材料知识点总结
高中化学复合材料知识点总结复合材料的结构通常是一个相为连续相，称为基体；基体的作用是将增强体粘合成整体并使复合材料具有一定的形状，传递外界作用力、保护增强体免受外界的各种侵蚀破坏作用。
当然也决定复合材料的某些性能和加工工艺。
高中学习网小编为您带来高中化学复合材料知识点，希望对大家有所帮助！高中化学复合材料知识点（一）1、复合材科的定义、组分功能和作用：定义：由两种或两种以上物理和化学性质不同的物质组合而成的一种多相固体材料。
复合后的产物为固体时才称为复合材料，为气体或液体不能称为复合材料。
组分：其组分相对独立，通常有一相连续相，称为基体，另一相分散相，称为增强相（增强体）。
功能和作用：复合材料既可以保持原材料的特点，又能发挥组合后的新特征，可以根据需要进行设计，从而最合理地达到使用所要求的性能。
2、复合材料的命名强调基体，以基体材料的名称为主，如树脂基复合材料，金属基复合材料，陶瓷基复合材料等；强调增强体，以增强体材料的名称为主，如玻璃纤维增强复合材料，碳纤维增强复合材料，陶瓷颗粒增强复合材料；基体材料与增强体材料名称并用，如玻璃纤维增强环氧树脂复合材料（玻璃钢）。
3、复合材料的分类方式按基体材料类型分：聚合物基复合材料，金属基复合材料，无机非金属基复合材料；按增强材料种类分：玻璃纤维复合材料，碳纤维复合材料，有机纤维复合材料，金属纤维复合材料，陶瓷纤维复合材料；按增强材料形态分：连续纤维复合材料，短纤维复合材料，粒状填料复合材料，编制复合材料；按用途分：结构复合材料，功能复合材料；4、常用的基体材料及各自的适用范围轻金属基体（主要包括铝基和镁基），用于450℃左右；钛合金及钛铝金属间化合物作基体的复合材料，适用温度650℃左右，镍、钴基复合材料可在1200℃使用。
5、常用热固性基体复合材料：环氧树脂，热固性聚酰亚胺树脂。
常用热塑性基体复合材料：聚醚醚酮，聚苯硫醚，聚醚砜，热塑性聚酰亚胺。
常用陶瓷基体复合材料：玻璃，氧化物陶瓷，非氧化物陶瓷，无机胶凝材料；6、玻璃和玻璃陶瓷的定义及不同玻璃是无机材料经高温熔融、冷却硬化而得到的一种非晶态固体；玻璃陶瓷是将特定组成的玻璃进行晶化热处理，在玻璃内部均匀析出大量微小晶体并进一步长大，形成致密的微晶相；玻璃相充填于晶界，得到的像陶瓷一样的多晶固体材料。
复合材料的力学性能
第四节 单向复合材料的破坏模式
• 依据纤维与基体之间的界面状态和载荷由基 体向纤维传递的机理，纤维间基体的剪切破 坏和部分脱胶可能同时发生，也有可能分别 独立发生。在脆性或短纤维与韧性基体构成 的复合材料中会出现纤维拔出的现象，因而 阻止了基体裂纹的扩展，这一裂纹可能参与 邻近其它纤维的断裂。
第四节 单向复合材料的破坏模式
• 通常发生横向拉伸破坏的模式有两种： ①基体拉伸破坏；②脱胶或纤维横向 断裂。如图（ a）为单向复合材料横 向拉伸破坏模式示意图。
第四节 单向复合材料的破坏模式
四、横向压缩破坏
• 单向复合材料横向受压时，因基体发生 剪切而破坏如图（b）。同时还可能发生 部分脱胶及纤维破断现象，所以其破坏 模式可以分成两种：基体剪切破坏和基 体剪切破坏的同时伴随脱胶或纤维横向 破碎。
第三节 纤维复合材料的疲劳行为
• 在实际使用过程中，构件或制品常常在比 屈服强度低得多的应力下发生失效，这种 现象多与材料在加工过程中存在的某些缺 陷，如气泡、裂纹、杂质和局部应力集中 等有关。对纤维复合材料在交变载荷作用 下的损伤与破坏行为作出正确的评价，是 复合材料结构设计与应用中必须要考虑的 问题。
第四节 单向复合材料的破坏模式
一、纵向拉伸破坏
• 单向复合材料的破坏起源于材料中固有的缺 陷。这些缺陷可以是破损的纤维、基体中的 裂纹以及界面脱胶等。如图，单向复合材料 在纤维方向受到拉伸载荷作用时，至少有三 种破坏模式，即①脆性断裂；②伴有纤维拔 出的脆性断裂；③伴有纤维拔出、界面基体 剪切或脱胶破坏的脆性断裂。
第四节 单向复合材料的破坏模式
• 沿纤维方向的拉伸和压缩试验、垂直于 纤维方向的拉伸和压缩试验以及面内剪 切试验是单向复合材料的5个基本力学 试验。一般而言，在纤维方向拉压及垂 直于纤维方向拉伸试验中，应力-应变 关系多呈线性，而在垂直于纤维方向压 缩及纵横方向剪切试验中应力-应变关 系则表现出非线性特征。
复合材料的复合原则及界面
第七章
复合材料的复合原则及界面
整理课件
1
第一节 复合原则
要想制备一种好的复合材料，首先应 根据所要求的性能进行设计，这样才能成 功地制备出性能理想的复合材料。
复合材料的设计应遵循的原则如下：
整理课件
2
一、材料组元的选择
挑选最合适的材料组元尤为重要。
在选择材料组元时，首先应明确各组 元在使用中所应承担的功能，也就是说， 必须明确对材料性能的要求。
表面层的力学特性，润湿速度等。
整理课件
37
由于界面区相对于整体材料所占比重甚 微，欲单独对某一性能进行度量有很大困难。
因此常借于整体材料的力学性能来表征 界面性能，如层间剪切强度(ILSS)就是研究 界面粘结的良好办法；
如再能配合断裂形貌分析等即可对界面
的其他性能作较深入的研究。
整理课件
38
由于复合材料的破坏形式随作 用力的类型、原材料结构组成不同 而异，故破坏可开始在树脂基体或 增强剂，也可开始在界面。
(2)阻断效应 结合适当的界面有阻止裂纹
扩展、中断材料破坏、减缓应力集中的作用。
整理课件
27
(3)不连续效应 在界面上产生物理性能 的不连续性和界面摩擦出现的现象，如抗电性、 电感应性、磁性、耐热性、尺寸稳定性等。
(4)散射和吸收效应 光波、声波、热弹
性波、冲击波等在界面产生散射和吸收，如透
光性、隔热性、隔音性、耐机械冲击及耐热冲
20
如金属基复合材料中，采用纤维与颗粒、 晶须增强时，同样采用固态法，但用纤维增 强时，一般采用扩散结合；而用颗粒或晶须 增强时，往往采用粉末冶金法结合。
因为颗粒或晶须增强时若采用扩散结合，
势必使制造工艺十分复杂，且无法保证颗粒
复合材料的复合原则及界面
整理课件
1
第一节 复合原则
要想制备一种好的复合材料，首先应 根据所要求的性能进行设计，这样才能成 功地制备出性能理想的复合材料。
复合材料的设计应遵循的原则如下：
整理课件
2
一、材料组元的选择
挑选最合适的材料组元尤为重要。
在选择材料组元时，首先应明确各组 元在使用中所应承担的功能，也就是说， 必须明确对材料性能的要求。
表面层的力学特性，润湿速度等。
整理课件
37
由于界面区相对于整体材料所占比重甚 微，欲单独对某一性能进行度量有很大困难。
因此常借于整体材料的力学性能来表征 界面性能，如层间剪切强度(ILSS)就是研究 界面粘结的良好办法；
如再能配合断裂形貌分析等即可对界面
的其他性能作较深入的研究。
整理课件
38
由于复合材料的破坏形式随作 用力的类型、原材料结构组成不同 而异，故破坏可开始在树脂基体或 增强剂，也可开始在界面。
(2)阻断效应 结合适当的界面有阻止裂纹
扩展、中断材料破坏、减缓应力集中的作用。
整理课件
27
(3)不连续效应 在界面上产生物理性能 的不连续性和界面摩擦出现的现象，如抗电性、 电感应性、磁性、耐热性、尺寸稳定性等。
(4)散射和吸收效应 光波、声波、热弹
性波、冲击波等在界面产生散射和吸收，如透
光性、隔热性、隔音性、耐机械冲击及耐热冲
20
如金属基复合材料中，采用纤维与颗粒、 晶须增强时，同样采用固态法，但用纤维增 强时，一般采用扩散结合；而用颗粒或晶须 增强时，往往采用粉末冶金法结合。
因为颗粒或晶须增强时若采用扩散结合，
势必使制造工艺十分复杂，且无法保证颗粒
复合材料讲稿2
第二章复合材料的复合效应第一节复合效应概述复合材料的复合原理是研究复合材料的结构特性、开拓新材料领域的基础。
耦合：不同性质材料之间的相互作用。
→复合材料性能与结构的协同相长特性（即复合后的材料性能优于每个单独组分的性能）。
从力学、物理学上理解复合材料多样性的基础。
拟解决的问题：寻找材料复合的一般规律。
研究增强机理。
一、材料的复合效应线性效应：平均效应、平行效应、相补效应、相抵效应。
非线性效应：相乘效应、诱导效应、共振效应、系统效应。
复合效应是复合材料的研究对象和重要内容，也是开拓新型复合材料、特别是功能型复合材料的基础理论问题。
非线性效应尚未被充分认识和利用，有待于研究和开发。
1、平均效应：P c=P m V m+P f V f（P：材料性能；V：材料体积含量；c：复合材料；m：基体；f：增强体或功能体）应用：力学性能中的弹性模量、线膨胀率等结构不敏感特性；热传导、电导等物理常数。
例：复合材料的弹性模量：E c=E m V m+E f V f（混合定律）2、相补效应：性能互补→提高综合性能。
例：脆性高强度纤维与韧性基体复合，适宜的结合形成复合材料。
→性能显示为增强体与基体互补。
3、相乘效应：X/Y·Y/Z=X/Z（X、Y、Z：物理性能）两种具有转换效应的材料复合→发生相乘效应→设计功能复合材料。
例：磁电效应（对材料施加磁场产生电流）——传感器，电子回路元件中应用。
压电体BaTiO3与磁滞伸缩铁氧体NiFe2O4烧结而成的复合材料。
对该材料施加磁场时会在铁氧体中产生压力，此压力传递到BaTiO3，就会在复合材料中产生电场。
最大输出已达103V·A。
单一成分的Cr2O3也有磁电效应，但最大输出只有约170V·A。
4、共振效应：两个相邻的材料在一定条件下，产生机械的、电的、磁的共振。
应用：改变复合材料某一部位的结构→复合材料固有频率的改变→避免材料工作时引起的破坏。
吸波材料：调整复合材料的固有频率，吸收外来波。
复合材料力学ppt课件
最新编辑ppt
7
（3）复合材料结构力学 它借助现有均匀各向同性材料结构力学的分 析方法，对各种形状的结构元件如板、壳等 进行力学分析，其中有层合板和壳结构的弯 曲、屈曲与振动问题以及疲劳、断裂、损伤 、开孔强度等问题。
最新编辑ppt
8
4复合材料的优点和缺点
复合材料的优点
(1)比强度高。
(2)比模量高。
示对称，“±”号表示两层正负角交错。
40/5 90/0 0 0/0 0/90/0 405 还可表示为 405 /900 /0 0s ，s表示
铺层上下对称。
最新编辑ppt
5
3复合材料的力学分析方法 （1）细观力学 它以纤维和基体作为基本单元，把纤维和基 体分别看成是各向同性的均匀材料(有的纤维 属横观各向同性材料)，根据材料纤维的几何 形状和布置形式、纤维和基体的力学性能、 纤维和基体之间的相互作用(有时应考虑纤维 和基体之间界面的作用)等条件来分析复合材 料的宏观物理力学性能。
21
四 单层复合材料的宏观力学分析 1 平面应力下单层复合材料的应力一应变关系 可近似认为 3 0 ， ，这就定义 23 431 50 了平面 应力状态，对正交各向异性材料，平面应力状态下 应力应变关系为
(3.1)
其中，
S 11
1 E1
S 22
1 E2
S 66
1 G12
S12E121E212
主方向应变分量间关系为
反过来有
最新编辑ppt
26
（3）任意方向上的应力一应变关系 在正交各向异性材料巾，平面应力状态主方向有下 列应力应变关系式
(3.4)
现应用式(3.3)和式(3.4)可得出偏轴向应力-应变 关系：
现用 Q 表示 T1Q(T1) ，则在x-y坐标中应力应变关系 可表示为
复合材料力学性能的复合规律-3.
影响单向板的纵向压缩强度的因素：纤维和 基体的性质，界面粘结强度和空隙含量
复合材料的Vf和树脂性能对压缩破坏的模式影 响很大
可简化模型为：纤维薄片和基体的构件，纤 维受压而基体只承受横向支持，当纵向压缩载 荷达到某一值时，纤维发生屈曲(buckling)
剪切模式：纤维发生 同相屈曲，同时基体 受剪切，发生变形；
由于基体存在如图所示的应变集中和应力 集中，导致横向强度减小，减小的程度与 应力或应变集中的程度有关
Tu
u m
s
,
其中s叫应力集中因子:
s
1Vf
(1
EmT E fT
)
1 4Vf (1 EmT
)
E fT
注：脆性树脂的拉伸强度取决于微裂纹效应， 不适于用应力集中效应来解释。
剪切破坏发生在平面ＡＢＣＤ内
小结
纵向拉伸强度 纤维拔出强度 横向拉伸强度 纵向压缩强度 横向压缩强度
（6）单向板的偏轴拉伸强度 单向板承受偏轴拉伸时，其破坏大致有三种模式： 垂直于纤维的破坏－纤维方向拉伸造成的；
平行于纤维的破坏－基体破坏或纤维－基体的界面的 拉伸引起的； 基体或纤维－基体的界面的剪切引起的破坏。
拉伸模式：基体以 异相方式受横向拉 伸和压缩，纤维薄 片的屈曲互为反向
压缩模式是导致层板的层间损失或缺陷产生 的最严重的加载条件，由于内部的屈曲 （buckling）的存在，使得材料极易破坏。
压缩破坏机理分析较复杂，目前未完全搞清 楚，较成熟的屈曲分析基于能量方法。能量方 法假设当复合材料从受压但未屈曲的状态转入 到屈曲状态时所引起的纤维和基体的应变能变 化Δ Uf和 Δ Um等于外载荷所做的功Δ W：
若树脂对切口不敏感，横向强度为：
复合材料的Vf和树脂性能对压缩破坏的模式影 响很大
可简化模型为：纤维薄片和基体的构件，纤 维受压而基体只承受横向支持，当纵向压缩载 荷达到某一值时，纤维发生屈曲(buckling)
剪切模式：纤维发生 同相屈曲，同时基体 受剪切，发生变形；
由于基体存在如图所示的应变集中和应力 集中，导致横向强度减小，减小的程度与 应力或应变集中的程度有关
Tu
u m
s
,
其中s叫应力集中因子:
s
1Vf
(1
EmT E fT
)
1 4Vf (1 EmT
)
E fT
注：脆性树脂的拉伸强度取决于微裂纹效应， 不适于用应力集中效应来解释。
剪切破坏发生在平面ＡＢＣＤ内
小结
纵向拉伸强度 纤维拔出强度 横向拉伸强度 纵向压缩强度 横向压缩强度
（6）单向板的偏轴拉伸强度 单向板承受偏轴拉伸时，其破坏大致有三种模式： 垂直于纤维的破坏－纤维方向拉伸造成的；
平行于纤维的破坏－基体破坏或纤维－基体的界面的 拉伸引起的； 基体或纤维－基体的界面的剪切引起的破坏。
拉伸模式：基体以 异相方式受横向拉 伸和压缩，纤维薄 片的屈曲互为反向
压缩模式是导致层板的层间损失或缺陷产生 的最严重的加载条件，由于内部的屈曲 （buckling）的存在，使得材料极易破坏。
压缩破坏机理分析较复杂，目前未完全搞清 楚，较成熟的屈曲分析基于能量方法。能量方 法假设当复合材料从受压但未屈曲的状态转入 到屈曲状态时所引起的纤维和基体的应变能变 化Δ Uf和 Δ Um等于外载荷所做的功Δ W：
若树脂对切口不敏感，横向强度为：
复合材料力学ppt
yx
y
yz
zx zy z
变形分析
物质坐标和空间坐标 应变张量的定义 微小应变张量的几何解释 主应变和应变主轴 应变协调方程
几何方程
x
u , x
yz
y
v , y
zx
z
w z
,
xy
w y
v z
;
u z
w ; x
v x
u y
.
x
yx
zx
xy y zy
x z
– 美国国防部委托国家科学研究院发表的面向21世纪国 防需求的材料研究报告指出
• 复合材料包括三要素：
• 基体材料 • 增强相 • 复合方式界面结合形式
• 复合材料的分类
– 按增强剂形状不同;可分为颗粒 连续纤维 短纤维 弥散晶须 层状 骨架或网状 编织体增强复合材料 等
– 按照基体材料的不同;复合材料包括聚合物基复合 材料 金属基复合材料 陶瓷基复合材料 碳/碳复合 材料等
y z
z
变形协调方程
2 x y 2
2 y x 2
2 xy xy
2 y z 2
2 z y 2
2 yz yz
2 z x 2
2 x z 2
2 xz zx
x
xz y
xy z
yz x
2 2x yz
y
xy z
yz x
zx y
2 2y zx
z
yz x
zx y
xy z
2 2z xy
物理方程— 本构关系 Hooke 定理
on S :
s
u u*
v v*
w w*
• 第三类基本问题
– 在弹性体的一部分表面上都给定了外力;在 其余的表面上给定了位移;要求确定弹性体 内部及表面任意一点的应力和位移
7[1].1 复合材料力学性能的复合规律-2
![7[1].1 复合材料力学性能的复合规律-2](https://img.taocdn.com/s3/m/38d8641633687e21af45a9ec.png)
尺度参数
形状参数
纤维强度的分布函数 F(σ)
F( ) f ( )d 1 exp( L ) 1 exp[L( ) ], 0
0
0
F( )是长为L的纤维在应力不超过时的破坏概率,
1
0 ( )仍叫尺度参数
Daniels提出的这种Weibull分布的长度为 L的N束纤维的强度可用正态分布描述, 其平均强度为：
σBL=(Lαβe)-1/ β
其中： σBL标准差与N-1/2成正比，所以当 N足够大时，所有纤维束趋于同一强度 平均值σBL
复合材料断裂的两个特性： •每根纤维的强度有变化； •纤维/基体在断裂纤维附近的相互作用。
过程：在基体中产生高剪切应力，从断裂处 开始在短距离内衰减，同时，纤维承受的拉 应力从断裂端的零增加到未断裂纤维所承受 的全部应力。
提示：对n个样品排序号，最低的为1号，断 裂几率为序号除以（n+1），并采用weibull分 布函数确定参数。
Weibull统计分布: (强度与纤维长度关系）
式中 f(σ)——机率密度函数，即纤维在σ和σ+d σ之 间破坏的机率；
L——纤维长度； α、β——材料常数 α：决定Weibull分布的位置，尺度参数， β：决定其形状，形状参数 α、β可通过实验获得
m称为形状参数。该表达式定义了概率分布函 数（pdf）
而累积分布函数（cdf），即z发生的可能性：
p(z;m) 1 exp (zm ) z,m 0
脆性材料强度非常敏感于裂纹尺寸及其分布， 对于体积为V的材料来说，假设其包含N个微 元V0，每个微元有相同的裂纹特征
则该脆性材料在应力σ下发生破坏的几率为：
7.1.1 单向板的力学性能
7.1.1.1 材料力学法分析单向板的弹性性能 7.1.1.2 材料力学法预测E1、E2的修正 7.1.1.3 弹性理论法分析单向板的弹性性能 7.1.1.4 材料力学法分析单向板的强度性能 7.1.1.5 单向板断裂韧性的一般概念
工程材料的基本力学性能
材料的屈服和强化都是材料微观组织发生变化，主要是晶体滑移产生的结 果。 由于这种滑移，经过抛光的试样表面在屈服阶段会出现许多与试样轴线约 成 ４５°的条纹，称为滑移线（ Ｌüｄｅｒ 线） ，如图 ３ －６ 所示。 大批晶体滑移的结果改 变了材料的微观组织，使产生进一步的晶体滑移更为困难，这就是强化现象。 由 于晶体滑移是不可逆的，所以在屈服 和 强 化 阶 段 由 晶 体 滑 移 而 产 生 的 宏 观 变 形 即使在载荷完全卸去以后也不会消失，这种变形称为塑性变形。
在屈服阶段以后试样出现明显的变形变形量较大用试样的原始横截面面积a和标距长度l表示的名义应力和工程应变已经不能代表真实的应力和应变的大小应该用瞬时截面面积at和标距瞬时长度lt来表示这样得到的应力和应变称为真应力和真应变
第三章 工程材料的基本力学性能
§ 3 －1 工程材料在常温静载下的拉压力学性能
一、 常温静载拉压试验
了解材料基本力学性能的主要手段是在常温静载下对细长杆进行轴向拉伸
试验，或对短粗试样进行轴向压缩试验。 常温即室温，静载则指加载速度极其平
稳缓慢。 试验所用的试样的制备和形状尺寸，试验方法和测试要求，各国都制定
了相应的标准，我国的国家标准①中也作了详细规定。
拉压试验得到的是拉伸（ 压缩） 图，即轴向载荷 F 与伸长（ 压缩） 量 Δl 的关
（４） 局部变形阶段：de 段。 强 度极限 σｂ 是整个应力应 变曲线的最高点的 应力值。 应力达到 σｂ 以后，试样某一小段内的变形突然迅速增加，使该段横截 面的尺寸急剧缩小，出现“ 缩颈” 现象，如图 ３ －６ 所示。 这一阶段试样的变形集 中发生在缩颈区，故称为局部变形阶段。 在该阶段由于截面减小，试样承载能力 降低，F 随之减小，相应的名义应力 σ＝F ／A 也随之减小，σ－ε 曲线急剧下降。 最后试样在缩颈区中部断裂。 低碳钢断裂时的应变可达最大弹性应变的 ３００ 倍 左右。
在屈服阶段以后试样出现明显的变形变形量较大用试样的原始横截面面积a和标距长度l表示的名义应力和工程应变已经不能代表真实的应力和应变的大小应该用瞬时截面面积at和标距瞬时长度lt来表示这样得到的应力和应变称为真应力和真应变
第三章 工程材料的基本力学性能
§ 3 －1 工程材料在常温静载下的拉压力学性能
一、 常温静载拉压试验
了解材料基本力学性能的主要手段是在常温静载下对细长杆进行轴向拉伸
试验，或对短粗试样进行轴向压缩试验。 常温即室温，静载则指加载速度极其平
稳缓慢。 试验所用的试样的制备和形状尺寸，试验方法和测试要求，各国都制定
了相应的标准，我国的国家标准①中也作了详细规定。
拉压试验得到的是拉伸（ 压缩） 图，即轴向载荷 F 与伸长（ 压缩） 量 Δl 的关
（４） 局部变形阶段：de 段。 强 度极限 σｂ 是整个应力应 变曲线的最高点的 应力值。 应力达到 σｂ 以后，试样某一小段内的变形突然迅速增加，使该段横截 面的尺寸急剧缩小，出现“ 缩颈” 现象，如图 ３ －６ 所示。 这一阶段试样的变形集 中发生在缩颈区，故称为局部变形阶段。 在该阶段由于截面减小，试样承载能力 降低，F 随之减小，相应的名义应力 σ＝F ／A 也随之减小，σ－ε 曲线急剧下降。 最后试样在缩颈区中部断裂。 低碳钢断裂时的应变可达最大弹性应变的 ３００ 倍 左右。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
界面效应弱时，由基体决定材料的横向拉伸强度。此时，材料的强度， 可简单计算为：
ζ2u=ζmu [1-2（Vf/π）1/2]
根据应变放大理论，可以证明：Vf 增加，ζ2u 降低
提高强度方法： ① 弹性微粒改性体增强 ② 增强体一基体界面采用过渡层，消除应力集中效应
第3章 复合材料力学性能的复合规律
作用对材料的“平均性能”进行预测，而非准确的设计数据
研究模型及方法：
细观力学结构模型
一种理想的情况：增强体均匀、细弹性、各向同性、间隔相、排 列整齐等等；基体均匀、细弹性、各向同性等等。在处理的方法上则 采用“材料力学”方法和“弹性理论”
宏观模型结构模型
材料中存在孔隙、脱粘以及残余应力等诸多缺陷
3.1.3 材料力学法分析单向板的强度性能
2、单向板纵向拉伸中纤维的拔出
假设：基体纤维长度为le 、纤维直径为2r、强度σfu 、 界面剪切度η、破坏拉力ζ
πr2σ=2πr leτ lc=σfu• r/2τ
第3章 复合材料力学性能的复合规律
3.1.3 材料力学法分析单向板的强度性能
3、单向板的横向拉伸强度 特点：无法直接计算，横向强度小于基本强度，纤维具有负增强作用。
u ' 1 uV f mVm f
临界体积分数
b) Vf 低，基体承受载荷，不被破坏，复合 材料强度为：
u u u 1 mVm m (1 V f )
u ' m m V u u ' f m m ' f
第3章 复合材料力学性能的复合规律
V f Vm 1
（1.5）
1 f V f m Vm f V f m (1 V f )
（1.6）
E1 1 E f f V f Em m Vm E f f V f Em m (1 V f )
基本条件：基体及增强体所承剪切应力相等，满足线性关系
材料总剪切变形： D W D f Dm f (V f W ) m (VmW )
其中：γ为复合材料的剪切应变；W为试样的宽度
复合材料、基体及增强体所受剪切应力相等：
mGm f G f G12
2
Ef
2 f V f mVm f V f m (1 V f )
2 2 f 2m
变： m
2
Em
Vf Vm 1 E2 Ef Em
（2.5）
第3章 复合材料力学性能的复合规律
3.1.1 单向板的力学性能 2、纵向弹性模量E2
第3章 复合材料力学性能的复合规律
3.1.3 材料力学法分析单向板的强度性能
4、单向板的纵向压缩强度
u 1 Gm /(1 V f )
第3章 复合材料力学性能的复合规律
3.1.3 材料力学法分析单向板的强度性能
4、单向板的纵向压缩强度
u 1 2V f [
V f Em E f 3(1 V f )
]1/ 2
第3章 复合材料力学性能的复合规律
3.1.3 材料力学法分析单向板的强度性能 5、单向板的横向压缩强度ζ2u
取决于作用力与纤维的方向
6、单向板的偏轴拉伸强度
对于大多数复合材料 ζ1u》ζ2 ζ＝〔cos4θ/ζ1u2＋（1/ηu2－1/ζ1u2）sin2Φcos2Φ＋sin4Φ/ζ2u2〕-1/2
在θ介于8～12º 上式可表达为：ηu＝0.5ζusin2θ
第3章 复合材料力学性能的复合规律
3.1.1 单向板的力学性能 2、横向弹性模量E2
结构简化模型
承受的应力：
2 2 f 2m
复合料应变： 2
（2.1）
2
E2
; ;
（2.2）
产生的应变：
增强体应变： f 基体的应变： m
2
Ef
2
Em
第3章 复合材料力学性能的复合规律
第3章 复合材料力学性能的复合规律
本章主要是从细观力学的角度，采用“材料力学”方法和 “弹性理论”的方法，根据材料的组分、结构来确定纤维 增强、粒子增强复合材料的弹性模量以及强度等力学性质。
基本参数含义：
作为单向纤维复合材料，其主弹性常数为：
E1 ----------- 纵向弹性模量
12 ----------- 主泊比
第3章 复合材料力学性能的复合规律
3.1.3 材料力学法分析单向板的强度性能
由于复合材料在横向的拉伸、剪切刚度和强度要比纵向的小得多，因此 单向的复合材料应用得很少。前者取决于基体，后者取决于纤维的性质。
一、单向板的纵向拉伸强度
符号及其意义：
1
f
1u
1 f m 1u u f
u m
第3章 复合材料力学性、断裂表面能（γ）
衡量材料断裂韧性或抗裂纹护层 阻力的度量。 定义为：产生单位自由表面所需求 的最小能量， 单位：千焦/米2
▼
▲
R＝2γ断裂阻力 Gc 称为断裂能量
对于复合材料 R1>> VfRf＋VmRm
第3章 复合材料力学性能的复合规律
超细粒子对复合材料力学性能的影响
重 点:
• 连续纤维增强复合材料的力学复合
• 短纤维增强复合材料的力学复合 • 粒子复合材料的力学性能 • 复合材料力学复合的其他问题
难 点:
纤维增强复合材料的力学复合，复合材料物理和 化学性能的复合规律
第3章 复合材料力学性能的复合规律
研究层次：
★ 宏观侧重于对材料实际物理化学等性能的测试研究 ★ 微 观根据材料微观结构以及组成结构的各组份间的相互
3.1.1 单向板的力学性能 2、纵向弹性模量E2
材料宽度W上变形是由增强体和基体共同产生的：
W W f Wm
2W f (V f W ) m (VmW ) f (V f W ) m (1 V f )W
2
E2 ; ;
（2.3）
变： 2
变： f
第三章 复合材料力学性能 的复合规律
课件及作业下载： 邮箱：fuhecailiao2012@ 密码：20122012
简要回顾:
1、复合材料的复合效应 2、复合材料的结构与复合效果
3、模型与性能的一般规律
第3章 复合材料力学性能的复合规律
基本要求:
了 解：
复合材料物理和化学性能的复合规律
在纤维断裂前，先发生基体的断裂，此时 所有载荷转移到纤维上。材料最终的状态取 决于材料中纤维的体积含量 V f
临界体积分数
a) Vf 低，纤维不能承受载荷，被破坏， 复合材料强度为：
u 1 'f V f m (1 V f )
b) Vf 高，纤维承受载荷不被破坏，此时 复合材料的强度为：
3.1.1 单向板的力学性能 1、纵向弹性模量E1
单向板 模型
产生的应变（外力作用下长度变化量）
1 f m
各部分承受的应力： 1 , f , m 各部分的弹性模量：E1 , E f , Em
对于复合材料有： 1 E1 1
对于基体材料有： m Em m
E1 E f V f Em Vm E f V f Em (1 V f ) 符合加合规律
第3章 复合材料力学性能的复合规律
；
3.1.1 单向板的力学性能
1、纵向弹性模量E1
这种影响基本上小于 1~2%，可以忽略不计
复合材料的横向收缩产生的附加应力对材料纵向模量的影响的没有考虑在内
2W 121W f f Wf m mWm） f f (WVf ) m m (WVm )） （ （
1 f m
12 f V f mVm
第3章 复合材料力学性能的复合规律
3.1.1 单向板的力学性能
4、单向板的剪切模量 G12
3.1.4 单向板断裂韧性的一般概念 2、断裂力学
裂纹扩展的能量条件：能量释效率 Gs ≥ 断裂表面能R 临界条件: G=Gc=R 应力强度因子：KI
3.1.3 材料力学法分析单向板的强度性能
1、均匀强度的纤维单向板的纵向拉伸强度 复合材料、纤维及基体的应变、强度以及模量满足以下关系：
1 f m
m Em m
f E f f
1 f V f m Vm Em m V f E f f (1 V f )
E2 ----------- 横向弹性模量
G12 ----------- 面内剪切模量
材料的主强度值为：
1u ----------u 2 -----------
纵向强度（拉、压）
横向强度（拉、压） 剪切强度
12 -----------
第3章 复合材料力学性能的复合规律
3.1 连续纤维增强复合材料的力学复合
对于 增强体 有： f E f f
（1.1） （1.2） （1.3）
第3章 复合材料力学性能的复合规律
；
3.1.1 单向板的力学性能
1、纵向弹性模量E1
根据力的合成原理:
1 A f Af m Am
定义： V f Af / A
（1.4）
Vm Am / A
m 1u u f
u m
f
m
材料 破坏前 单向板承受的应力 纤维 破坏前 纤维 承受的应力 基体 破坏前 基体 承受的应力 单向板平行轴向纤维的拉伸破坏应力 平行于纤维轴向的拉伸破坏应力 平行于基体轴向的拉伸破坏应力 基体破坏时纤维承受的拉伸应力 纤维破坏时纤维承受的拉伸应力