粒子滤波MATLAB代码
matlab滤波器设计(源代码)

某合成信号,表达式如下:f=10cos(2pi*30t)+cos(2pi*150t)+5cos(2pi*600t),请设计三个滤波器,分别提取出信号中各频率分量,并分别绘制出通过这三个滤波器后信号的时域波形和频谱这个信号的频率分量分别为30、150和600Hz,因此可分别设计一个低通、带通和高通的滤波器来提取。
以FIR滤波器为例,程序如下:clear;fs=2000;t=(1:1000)/fs;x=10*cos(2*pi*30*t)+cos(2*pi*150*t)+5*cos(2*pi*600*t);L=length(x);N=2^(nextpow2(L));Hw=fft(x,N);figure(1);subplot(2,1,1);plot(t,x);grid on;title('滤波前信号x');xlabel('时间/s');% 原始信号subplot(2,1,2);plot((0:N-1)*fs/L,abs(Hw));% 查看信号频谱grid on;title('滤波前信号频谱图');xlabel('频率/Hz');ylabel('振幅|H(e^jw)|');%% x_1=10*cos(2*pi*30*t)Ap=1;As=60;% 定义通带及阻带衰减dev=[(10^(Ap/20)-1)/(10^(Ap/20)+1),10^(-As/20)];% 计算偏移量mags=[1,0];% 低通fcuts=[60,100];% 边界频率[N,Wn,beta,ftype]=kaiserord(fcuts,mags,dev,fs);% 估算FIR滤波器阶数hh1=fir1(N,Wn,ftype,kaiser(N+1,beta));% FIR滤波器设计x_1=filter(hh1,1,x);% 滤波x_1(1:ceil(N/2))=[];% 群延时N/2,删除无用信号部分L=length(x_1);N=2^(nextpow2(L));Hw_1=fft(x_1,N);figure(2);subplot(2,1,1);plot(t(1:L),x_1);grid on;title('x_1=10*cos(2*pi*30*t)');xlabel('时间/s');subplot(2,1,2);plot((0:N-1)*fs/L,abs(Hw_1));% 查看信号频谱grid on;title('滤波后信号x_1频谱图');xlabel('频率/Hz');ylabel('振幅|H(e^jw)|');%% x_2=cos(2*pi*150*t)Ap=1;As=60;% 定义通带及阻带衰减dev=[10^(-As/20),(10^(Ap/20)-1)/(10^(Ap/20)+1),10^(-As/20)];% 计算偏移量mags=[0,1,0];% 带通fcuts=[80,120,180,220];% 边界频率[N,Wn,beta,ftype]=kaiserord(fcuts,mags,dev,fs);% 估算FIR滤波器阶数hh2=fir1(N,Wn,ftype,kaiser(N+1,beta));% FIR滤波器设计x_2=filter(hh2,1,x);% 滤波x_2(1:ceil(N/2))=[];% 群延时N/2,删除无用信号部分L=length(x_2);N=2^(nextpow2(L));Hw_2=fft(x_2,N);figure(3);subplot(2,1,1);plot(t(1:L),x_2);grid on;title('x_2=cos(2*pi*150*t)');xlabel('时间/s');subplot(2,1,2);plot((0:N-1)*fs/L,abs(Hw_2));% 查看信号频谱grid on;title('滤波后信号x_2频谱图');xlabel('频率/Hz');ylabel('振幅|H(e^jw)|');%% x_3=5*cos(2*pi*600*t)Ap=1;As=60;% 定义通带及阻带衰减dev=[10^(-As/20),(10^(Ap/20)-1)/(10^(Ap/20)+1)];% 计算偏移量mags=[0,1];% 高通fcuts=[500,550];% 边界频率[N,Wn,beta,ftype]=kaiserord(fcuts,mags,dev,fs);% 估算FIR滤波器阶数hh2=fir1(N,Wn,ftype,kaiser(N+1,beta));% FIR滤波器设计x_3=filter(hh2,1,x);% 滤波x_3(1:ceil(N/2))=[];% 群延时N/2,删除无用信号部分L=length(x_3);N=2^(nextpow2(L));Hw_3=fft(x_3,N);figure(4);subplot(2,1,1);plot(t(1:L),x_3);grid on;title('x_3=5*cos(2*pi*600*t)');xlabel('时间/s');subplot(2,1,2);plot((0:N-1)*fs/L,abs(Hw_3));% 查看信号频谱grid on;title('滤波后信号x_3频谱图');xlabel('频率/Hz');ylabel('振幅|H(e^jw)|');。
matlab滤波器代码

数字信号处理:已知通带截止频率fp=5kHz,通带最大衰减ap=2dB,阻带截止频率fs=2kHz,阻带最小衰减as=30dB,按照以上技术指标设计巴特沃斯低通滤波器:wp=2*pi*5000;ws=2*pi*12000;Rp=2;As=30;[N,wc]=buttord(wp,ws,Rp,As,'s');[B,A]=butter(N,wc,'s');k=0:511;fk=0:14000/512:14000;wk=2*pi*fk;Hk=freqs(B,A,wk);subplot(2,2,1);plot(fk/1000,20*log10(abs(Hk)));grid onxlabel('频率(kHz)');ylabel('幅度(dB)')axis([0,14,-40,5])切比雪夫1型低通滤波器:wp=2*pi*3000;ws=2*pi*12000;Rp=0.1;As=60;[N1,wpl]=cheb1ord(wp,ws,Rp,As,'s');%cheb1ord,里面的是1,不是L[B1,A1]=cheby1(N1,Rp,wpl,'s');subplot(2,2,1);fk=0:12000/512:12000;wk=2*pi*fk;Hk=freqs(B1,A1,wk);plot(fk/1000,20*log10(abs(Hk)));grid onxlabel('频率(kHz)');ylabel('幅度(dB)')axis([0,12,-70,5])椭圆模拟低通滤波器:wp=2*pi*3000;ws=2*pi*12000;Rp=0.1;As=60;[N,wpo]=ellipord(wp,ws,Rp,As,'s');[B,A]=ellip(N,Rp,As,wpo,'s');subplot(2,2,1);fk=0:12000/512:12000;wk=2*pi*fk;Hk=freqs(B1,A1,wk);plot(fk/1000,20*log10(abs(Hk)));grid onxlabel('频率(kHz)');ylabel('幅度(dB)')axis([0,12,-70,5])p195-14wp=2*4/80;ws=2*20/80;rp=0.5;rs=45;[N,wc]=buttord(wp,ws,rp,rs);[B,A]=butter(N,wc);[hk,wk]=freqz(B,A);fk=wk/pi*40;plot(fk,20*log10(abs(hk)));axis([0,30,-100,0])xlabel('频率(kHZ)');ylabel('幅度(db)');grid on P195-16wp=2*325/2500;ws=2*225/2500;rp=1;rs=40;[N,wc]=ellipord(wp,ws,rp,rs);[B,A]=ellip(N,rp,rs,wc);[hk,wk]=freqz(B,A);fk=wk/pi*40;plot(fk,20*log10(abs(hk)));axis([0,30,-100,0])xlabel('频率(kHZ)');ylabel('幅度(db)');grid onP195-15wp=2*4/80;ws=2*20/80;rp=0.5;rs=45;[N,wc]=cheb1ord(wp,ws,rp,rs);[B,A]=cheby1(N,rp,wc);[hk,wk]=freqz(B,A);fk=wk/pi*40;plot(fk,20*log10(abs(hk)));axis([0,30,-100,0])xlabel('频率(kHZ)');ylabel('幅度(db)');grid on 切比雪夫低通滤波器wp=2*pi*3000;ws=2*pi*12000;rp=0.1;as=60;[N1,wp1]=cheb1ord(wp,ws,rp,as,'s');[B1,A1]=cheby1(N1,rp,wp1,'s');subplot(2,2,1);fk=0:12000/512:12000;wk=2*pi*fk;hk=freqs(B1,A1,wk);plot(fk/1000,20*log10(abs(hk)));grid onxlabel('频率(kHZ)');ylabel('幅度(db)');axis([0,12,-70,5])双音频检测audiofile='test.wav'[in_audio,fs,bits]=wavread(audiofile); [b,a]=cheby1(5,0.1,0.3);out_audio=filter(b,a,in_audio);sound(out_audio,fs,bits);wavwrite(out_audio,fs,bits,'test_out'); xk1=fft(in_audio,512);xk2=fft(out_audio,512);subplot(2,1,1);stem(abs(xk1));subplot(2,1,2);stem(abs(xk2));巴特沃斯模拟高通滤波器。
matlab 粒子滤波代码

以下是一个简单的 MATLAB 粒子滤波器的代码示例:```matlab% 初始化参数N = 100; % 粒子数量dt = 0.1; % 时间步长x = [0 0]; % 初始位置P = eye(2); % 初始协方差矩阵Q = eye(2); % 过程噪声协方差矩阵R = eye(2); % 观测噪声协方差矩阵G = [0.9 0.1; 0.1 0.9]; % 转换矩阵N_particles = size(Q,1); % 粒子数量particles = zeros(N_particles,2); % 初始化粒子particles(:,1) = x(1); % 设置粒子的 x 分量particles(:,2) = x(2); % 设置粒子的 y 分量weights = ones(N_particles,1) / N_particles; % 初始化权重% 模拟观测数据z = [1.2 0.5]; % 观测位置R_inv = inv(R); % 观测噪声协方差矩阵的逆H = [z(1) -z(2); z(2) z(1)]; % 观测矩阵y = H * x; % 预测的观测值% 粒子滤波步骤for t = 1:100% 重采样步骤weights = weights / sum(weights);index = randsample(1:N_particles, N, true, weights); particles = particles(index,:);% 预测步骤x_pred = particles;P_pred = Q;x_pred = G * x_pred;P_pred = P_pred + dt * G * P_pred;P_pred = P_pred + P_pred * G' + R;% 更新步骤y_pred = H * x_pred;S = H * P_pred * H' + R_inv;K = P_pred * H' * inv(S);x = x_pred + K * (z - y_pred);P = P_pred - P_pred * K * H';end```在这个代码示例中,我们使用了两个步骤:重采样步骤和预测/更新步骤。
粒子滤波算法matlab实例

一、介绍粒子滤波算法粒子滤波算法是一种基于蒙特卡洛方法的非线性、非高斯滤波算法,它通过一组随机产生的粒子来近似表示系统的后验概率分布,从而实现对非线性、非高斯系统的状态估计。
在实际应用中,粒子滤波算法被广泛应用于目标跟踪、导航、机器人定位等领域。
本文将以matlab 实例的形式介绍粒子滤波算法的基本原理和应用。
二、粒子滤波算法的原理及步骤粒子滤波算法的主要原理是基于贝叶斯滤波理论,通过一组随机产生的粒子来近似表示系统的后验概率分布。
其具体步骤如下:1. 初始化:随机生成一组粒子,对于状态变量的初始值和方差的估计,通过随机抽样得到一组粒子。
2. 预测:根据系统模型,对每个粒子进行状态预测,得到预测状态。
3. 更新:根据测量信息,对每个预测状态进行权重更新,得到更新后的状态。
4. 重采样:根据更新后的权重,对粒子进行重采样,以满足后验概率分布的表示。
5. 输出:根据重采样后的粒子,得到对系统状态的估计。
三、粒子滤波算法的matlab实例下面以一个简单的目标跟踪问题为例,介绍粒子滤波算法在matlab中的实现。
假设存在一个目标在二维空间中运动,我们需要通过一系列测量得到目标的状态。
我们初始化一组粒子来近似表示目标的状态分布。
我们根据目标的运动模型,预测每个粒子的状态。
根据测量信息,对每个预测状态进行权重更新。
根据更新后的权重,对粒子进行重采样,并输出对目标状态的估计。
在matlab中,我们可以通过编写一段简单的代码来实现粒子滤波算法。
我们需要定义目标的运动模型和测量模型,然后初始化一组粒子。
我们通过循环来进行预测、更新、重采样的步骤,最终得到目标状态的估计。
四、总结粒子滤波算法是一种非线性、非高斯滤波算法,通过一组随机产生的粒子来近似表示系统的后验概率分布。
在实际应用中,粒子滤波算法被广泛应用于目标跟踪、导航、机器人定位等领域。
本文以matlab实例的形式介绍了粒子滤波算法的基本原理和应用,并通过一个简单的目标跟踪问题,展示了粒子滤波算法在matlab中的实现过程。
matlab小波滤波器代码 -回复

matlab小波滤波器代码-回复MATLAB是一种强大的数学计算工具和编程语言,广泛应用于科学研究、工程设计、数据分析和算法开发等领域。
在信号处理中,MATLAB提供了许多函数和工具箱,其中包括用于小波滤波的函数和工具。
本文将介绍MATLAB中小波滤波器的基本原理及其代码实现。
在信号处理中,小波滤波器是一种能够将信号分解成不同频率带的滤波器。
小波分析通过对信号进行连续或离散的小波变换,将信号分解为多个不同频率的小波子带。
小波滤波器是一种能够在不同频率范围内改变信号幅度的滤波器,可以用于信号去噪、信号压缩、边缘检测等应用。
MATLAB中提供了许多小波滤波的函数,其中最常用的是`wavedec`函数。
`wavedec`函数可以将信号进行小波变换,将信号分解成多个频带的小波系数。
该函数的基本语法如下:[c,l] = wavedec(x,n,wname)其中,`x`是输入信号,`n`是小波分解的级别,`wname`是小波函数的名称。
函数的输出结果包括小波系数`c`和分解层数`l`。
小波函数是小波变换中的一个重要组成部分,它决定了小波分解的性质。
MATLAB中有许多内置的小波函数,如`haar`、`db`、`coif`、`sym`等。
可以通过`wfilters`函数查看所有可用的小波函数及其参数。
下面是一个示例:[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters(wname)其中,`Lo_D`是分解低通滤波器的系数,`Hi_D`是分解高通滤波器的系数,`Lo_R`是重构低通滤波器的系数,`Hi_R`是重构高通滤波器的系数。
这些滤波器用于将信号分解为不同频率的小波子带,并通过小波逆变换将其重构。
除了小波分解外,MATLAB还提供了小波重构函数`waverec`,用于将小波系数重构为原始信号。
该函数的基本语法如下:xrec = waverec(c,l,wname)其中,`c`是小波系数,`l`是分解层数,`wname`是小波函数的名称。
pf算法举例及其matlab实现-概述说明以及解释

pf算法举例及其matlab实现-概述说明以及解释1.引言1.1 概述PF算法(Particle Filter Algorithm),又称为粒子滤波算法,是一种基于蒙特卡洛方法的非线性滤波算法。
与传统的滤波算法相比,PF算法具有更大的灵活性和鲁棒性,在估计复杂非线性系统状态的过程中表现出良好的性能。
PF算法基于一种随机采样的思想,通过对系统状态进行一系列粒子的采样,再通过对这些粒子的权重进行重要性重采样,最终获得对状态估计的准确性更高的结果。
在PF算法中,粒子的数量决定了滤波算法的精度,粒子越多,估计结果越准确,但也会增加计算复杂度。
因此,在实际应用中需要根据实际情况灵活选择粒子数量。
作为一种高效的滤波算法,PF算法在众多领域都有广泛的应用。
例如,粒子滤波算法在目标跟踪、传感器网络定位、机器人定位与导航等领域都有着重要的作用。
其在目标跟踪领域的应用尤为突出,由于PF算法可以处理非线性和非高斯分布的情况,使得目标跟踪更加准确和稳定。
在Matlab中,PF算法也得到了广泛的应用和实现。
Matlab提供了丰富的函数和工具箱,可以便捷地实现PF算法。
借助Matlab的强大数据处理和可视化功能,我们可以更加便捷地进行粒子滤波算法的实现和结果分析。
本文将从PF算法的基本概念出发,介绍其应用举例和在Matlab中的具体实现。
通过对PF算法的研究和实践,我们可以更好地理解和应用这一强大的滤波算法,为实际问题的解决提供有效的手段。
通过对Matlab 的使用,我们还可以更加高效地实现和验证粒子滤波算法的性能,为进一步的研究和应用奠定基础。
在接下来的章节中,我们将详细介绍PF算法的原理及其在现实应用中的具体案例。
随后,我们将展示如何使用Matlab实现PF算法,并通过实验结果对其性能进行评估和分析。
最后,我们将总结PF算法和Matlab 实现的主要特点,并对未来的发展进行展望。
文章结构的设定在撰写一篇长文时非常重要,它能够为读者提供一个整体的概览,帮助他们更好地理解文章的内容安排。
【三维路径规划】基于matlab改进的粒子滤波无人机三维航迹规划【含Matlab源码1527期】

【三维路径规划】基于matlab改进的粒⼦滤波⽆⼈机三维航迹规划【含Matlab源码1527期】⼀、⽆⼈机简介0 引⾔随着现代技术的发展,飞⾏器种类不断变多,应⽤也⽇趋专⼀化、完善化,如专门⽤作植保的⼤疆PS-X625⽆⼈机,⽤作街景拍摄与监控巡察的宝鸡⾏翼航空科技的X8⽆⼈机,以及⽤作⽔下救援的⽩鲨MIX⽔下⽆⼈机等,决定飞⾏器性能主要是内部的飞控系统和外部的路径规划问题。
就路径问题⽽⾔,在具体实施任务时仅靠操作员⼿中的遥控器控制⽆⼈飞⾏器执⾏相应的⼯作,可能会对操作员⼼理以及技术提出极⾼的要求,为了避免个⼈操作失误,进⽽造成飞⾏器损坏的危险,⼀种解决问题的⽅法就是对飞⾏器进⾏航迹规划。
飞⾏器的测量精度,航迹路径的合理规划,飞⾏器⼯作时的稳定性、安全性等这些变化对飞⾏器的综合控制系统要求越来越⾼。
⽆⼈机航路规划是为了保证⽆⼈机完成特定的飞⾏任务,并且能够在完成任务的过程中躲避各种障碍、威胁区域⽽设计出最优航迹路线的问题。
1 常见的航迹规划算法图1 常见路径规划算法⽂中主要对⽆⼈机巡航阶段的航迹规划进⾏研究,假设⽆⼈机在飞⾏中维持⾼度与速度不变,那么航迹规划成为⼀个⼆维平⾯的规划问题。
在航迹规划算法中,A算法计算简单,容易实现。
在改进A算法基础上,提出⼀种新的、易于理解的改进A算法的⽆⼈机航迹规划⽅法。
传统A算法将规划区域栅格化,节点扩展只限于栅格线的交叉点,在栅格线的交叉点与交叉点之间往往存在⼀定⾓度的两个运动⽅向。
将存在⾓度的两段路径⽆限放⼤、细化,然后分别⽤两段上的相应路径规划点作为切点,找到相对应的组成内切圆的圆⼼,然后作弧,并求出相对应的两切点之间的弧所对应的圆⼼⾓,根据下式计算出弧线的长度式中:R———内切圆的半径;α———切点之间弧线对应的圆⼼⾓。
⼆、粒⼦群算法简介1 引⾔⾃然界中的鸟群和鱼群的群体⾏为⼀直是科学家的研究兴趣所在。
⽣物学家Craig Reynolds在1987年提出了⼀个⾮常有影响的鸟群聚集模型,在他的仿真中,每⼀个个体都遵循:避免与邻域个体相撞:匹配邻域个体的速度;飞向鸟群中⼼,且整个群体飞向⽬标。
粒子滤波PF算法在无线传感器网络定位跟踪的matlab源码

% 二维直线运动模型:%X=FX+V 状态模型%Z=[z1;z2] 观测模型clc;clear all;%%N1=300; %粒子数time=60;x_state(1)=1;vx(1)=5;y_state(1)=1;vy(1)=7;%%Process Noise Covariance%%%%%%%% 都是标准差xstate_noise=10; %没有用的参数Vx_noise=1;%%Measurement Noise Covariance%%%% 都是标准差theta_noise=0.1; %3/180*pidistance1_noise=3;xobs = [];yobs = [];theta1(1)=0;%%Ture State%%%%%%%%for i=2:time%% State model%%%%%%%%%%%accx = normrnd(0,Vx_noise,1,1);x_state(i)=x_state(i-1)+vx(i-1)+0.5*accx;vx(i)=vx(i-1)+accx;accy = normrnd(0,Vx_noise,1,1);y_state(i)=y_state(i-1)+vy(i-1)+0.5*accy;vy(i)=vy(i-1)+accy;end%%Measurement Value%%%%%for i=1:time%%Measure model%%%%%%%%%distance1(i)=sqrt(x_state(i)^2+y_state(i)^2)+distance1_noise*randn(1);%theta1(i)=atan(y_state(i)/x_state(i))+theta_noise*randn(1);%使用下面增加了象限判断的角度计算方式[-pi,pi]if x_state(i)>0 && y_state(i)>=0theta1(i) = atan(y_state(i)/x_state(i))+theta_noise*randn(1) ; %观测方程endif x_state(i)<0 && y_state(i)>=0theta1(i) = (atan(y_state(i)/x_state(i))+pi) +theta_noise*randn(1); %观测方程endif x_state(i)<0 && y_state(i)<=0theta1(i) = (atan(y_state(i)/x_state(i))-pi) +theta_noise*randn(1); %观测方程endif x_state(i)>0 && y_state(i)<=0theta1(i) = atan(y_state(i)/x_state(i)) +theta_noise*randn(1); %观测方程endxobs = [xobs distance1(i)*cos(theta1(i))];yobs = [yobs distance1(i)*sin(theta1(i))];end%%%Particle Filtering%%%%%%%%%%%%%%x_pf(1)=x_state(1);vx_pf(1)=vx(1);y_pf(1)=y_state(1);vy_pf(1)=vy(1);xp1=zeros(1,N1);xp2=zeros(1,N1);xp3=zeros(1,N1);xp4=zeros(1,N1); %%%%%Initial particles 得到初始化的粒子群%%%%%%%%for n=1:N1;%M1=[delta1*randn(1),delta2*randn(1),delta3*randn(1),delta4*randn(1)];%M1=diag(M1);xp1(n)=x_pf(1)+normrnd(0,Vx_noise,1,1);xp2(n)=vx_pf(1)+normrnd(0,Vx_noise,1,1);xp3(n)=y_pf(1)+normrnd(0,Vx_noise,1,1);xp4(n)=vy_pf(1)+normrnd(0,Vx_noise,1,1);end%**filter process*** angel and distance**************** for t=2:time%%%Prediction Process%%%%for n=1:N1accx = normrnd(0,Vx_noise,1,1);xpre_pf(n)=xp1(n)+xp2(n)+0.5*accx;vxpre_pf(n)=xp2(n)+accx;accy = normrnd(0,Vx_noise,1,1);ypre_pf(n)=xp3(n)+xp4(n)+0.5*accy;vypre_pf(n)=xp4(n)+accy;end%%%Calculate Weight Particles%%%%for n=1:N1vhat1=sqrt(xpre_pf(n)^2+ypre_pf(n)^2)-distance1(t);%vhat2=atan(ypre_pf(n)/xpre_pf(n))-theta1(t);%使用下面增加了象限判断的角度计算方式if xpre_pf(n)>0 && ypre_pf(n)>=0ag = atan(ypre_pf(n)/xpre_pf(n)) ; %观测方程endif xpre_pf(n)<0 && ypre_pf(n)>=0ag = (atan(ypre_pf(n)/xpre_pf(n))+pi); %观测方程endif xpre_pf(n)<0 && ypre_pf(n)<=0ag = (atan(ypre_pf(n)/xpre_pf(n))-pi) ; %观测方程endif xpre_pf(n)>0 && ypre_pf(n)<=0ag = atan(ypre_pf(n)/xpre_pf(n)); %观测方程endvhat2=ag-theta1(t);q1=(1/distance1_noise/sqrt(2*pi))*exp(-vhat1^2/2/distance1_noise^2);q2=(1/theta_noise/sqrt(2*pi))*exp(-vhat2^2/2/theta_noise^2);q(n)=q1*q2+1e-99;endq = q./sum(q);P_pf = cumsum(q);%%Resampling Process 这是一种均匀的重采样方法,随机数的产生不再是从[0,1]上任意产生,而是使这个随机数渐进式的增大,与权重累加和一样,都是交替上升,这样的比较更有规律性,更周到%%%%%%%%%%%%%%ut(1)=rand(1)/N1;k = 1;hp = zeros(1,N1);for j = 1:N1ut(j)=ut(1)+(j-1)/N1;while(P_pf(k)<ut(j));k = k + 1;end;hp(j) = k;q(j)=1/N1;end;xp1 = xpre_pf(hp); xp2 = vxpre_pf(hp); % The new particles xp3 = ypre_pf(hp); xp4 = vypre_pf(hp);%% Compute the estimate%%%%%%%%%%%%%x_pf(t)=mean(xp1);y_pf(t)=mean(xp3);end%%%%Result of Tracking%%%%%%%%%%%%% figure;plot(x_state,y_state,'r-*',x_pf,y_pf,'b-o',xobs,yobs,'g-d') xlabel('x state'); ylabel('y state');legend('实际轨迹','滤波轨迹','观测轨迹');set(gcf,'Color','White');%figure;%plot(1:time,distance_error,'r');%legend('distance error');。
粒子滤波MATLAB代码

function ParticleEx1% Particle filter example, adapted from Gordon, Salmond, and Smith paper.x = 0.1; % initial stateQ = 1; % process noise covarianceR = 1; % measurement noise covariancetf = 50; % simulation lengthN = 100; % number of particles in the particle filterxhat = x;P = 2;xhatPart = x;% Initialize the particle filter.for i = 1 : Nxpart(i) = x + sqrt(P) * randn;endjArr = [0];xArr = [x];yArr = [x^2 / 20 + sqrt(R) * randn];xhatArr = [x];PArr = [P];xhatPartArr = [xhatPart];close all;for k = 1 : tf% System simulationx = 0.5 * x + 25 * x / (1 + x^2) + 8 * cos(1.2*(k-1)) + sqrt(Q) * randn;%状态方程y = x^2 / 20 + sqrt(R) * randn;%观测方程% Extended Kalman filterF = 0.5 + 25 * (1 - xhat^2) / (1 + xhat^2)^2;P = F * P * F' + Q;H = xhat / 10;K = P * H' * (H * P * H' + R)^(-1);xhat = 0.5 * xhat + 25 * xhat / (1 + xhat^2) + 8 * cos(1.2*(k-1));%预测xhat = xhat + K * (y - xhat^2 / 20);%更新P = (1 - K * H) * P;% Particle filterfor i = 1 : Nxpartminus(i) = 0.5 * xpart(i) + 25 * xpart(i) / (1 + xpart(i)^2) + 8 * cos(1.2*(k-1)) + sqrt(Q) * randn;ypart = xpartminus(i)^2 / 20;vhat = y - ypart;%观测和预测的差q(i) = (1 / sqrt(R) / sqrt(2*pi)) * exp(-vhat^2 / 2 / R);end% Normalize the likelihood of each a priori estimate.qsum = sum(q);for i = 1 : Nq(i) = q(i) / qsum;%归一化权重end% Resample.重采样for i = 1 : Nu = rand; % uniform random number between 0 and 1qtempsum = 0;for j = 1 : Nqtempsum = qtempsum + q(j);if qtempsum >= uxpart(i) = xpartminus(j);if k == 20qArr=q;jArr = [jArr j];endbreak;endendend% The particle filter estimate is the mean of the particles.xhatPart = mean(xpart);% Plot the estimated pdf's at a specific time.if k == 20% Particle filter pdfpdf = zeros(81,1);for m = -40 : 40for i = 1 : Nif (m <= xpart(i)) && (xpart(i) < m+1)pdf(m+41) = pdf(m+41) + 1;endendendfigure;m = -40 : 40;plot(m, pdf / N, 'r');hold;title('Estimated pdf at k=20');disp(['min, max xpart(i) at k = 20: ', num2str(min(xpart)), ', ', num2str(max(xpart))]);% Kalman filter pdfpdf = (1 / sqrt(P) / sqrt(2*pi)) .* exp(-(m - xhat).^2 / 2 / P);plot(m, pdf, 'b');legend('Particle filter', 'Kalman filter');grid on;end% Save data in arrays for later plottingxArr = [xArr x];yArr = [yArr y];xhatArr = [xhatArr xhat];PArr = [PArr P];xhatPartArr = [xhatPartArr xhatPart];endt = 0 : tf;%figure;%plot(t, xArr);%ylabel('true state');figure;plot(t, xArr, 'b.', t, xhatArr, 'g-.', t, xhatArr-2*sqrt(PArr), 'r:', t, xhatArr+2*sqrt(PArr), 'r:'); axis([0 tf -40 40]);set(gca,'FontSize',12); set(gcf,'Color','White');xlabel('time step'); ylabel('state');legend('True state', 'EKF estimate', '95% confidence region');grid on;figure;plot(t, xArr, 'b.', t, xhatPartArr, 'k-');set(gca,'FontSize',12); set(gcf,'Color','White');xlabel('time step'); ylabel('state');legend('True state', 'Particle filter estimate');grid on;xhatRMS = sqrt((norm(xArr - xhatArr))^2 / tf);xhatPartRMS = sqrt((norm(xArr - xhatPartArr))^2 / tf);disp(['Kalman filter RMS error = ', num2str(xhatRMS)]);disp(['Particle filter RMS error = ', num2str(xhatPartRMS)]);/*qArrtt=max(qArr)t=jArr[m,n]=hist(jArr,100)mnsum(m)。
matlab filter函数源代码

matlab filter函数源代码MATLAB中的filter函数是一种数字滤波器设计和信号处理的工具。
它可以用于对数字信号进行滤波处理,滤除信号中的噪声或干扰,使得信号更加平滑和清晰。
filter函数的源代码如下:```matlabfunction y = filter(b, a, x)% 设置输入和输出数组的长度nx = length(x);ny = nx + max(length(a), length(b)) - 1;% 初始化输出数组y = zeros(ny, 1);% 进行滤波处理for n = 1:nyfor k = 1:length(b)if n-k+1 > 0 && n-k+1 <= nxy(n) = y(n) + b(k) * x(n-k+1);endendfor k = 2:length(a)if n-k+1 > 0 && n-k+1 <= nyy(n) = y(n) - a(k) * y(n-k+1);endendy(n) = y(n) / a(1);endend```该函数的输入参数包括滤波器的系数b和a,以及待滤波的输入信号x。
输出结果为滤波后的信号y。
在filter函数的实现中,首先根据输入信号的长度确定输出信号的长度。
然后,根据滤波器的系数和输入信号的延迟,对输入信号进行滤波处理。
具体而言,通过两个嵌套的for循环,分别计算输出信号的每个样本值。
第一个for循环用于计算输出信号的每个样本值的前向部分,即滤波器的前向传递。
第二个for循环用于计算输出信号的每个样本值的反向部分,即滤波器的反向传递。
最后,将每个样本值除以a(1)进行归一化,得到最终的输出信号。
使用filter函数可以实现多种滤波器设计和信号处理的应用。
例如,可以使用滤波器系数设计一个低通滤波器,将高频噪声从输入信号中滤除,得到一个平滑的信号。
也可以使用滤波器系数设计一个高通滤波器,将低频噪声从输入信号中滤除,得到一个突出高频成分的信号。
matlab频率滤波代码

matlab频率滤波代码以下是一个简单的MATLAB频率滤波代码示例: matlab.% 读取图像。
img = imread('example.jpg');% 将图像转换为灰度图像。
gray_img = rgb2gray(img);% 计算图像的傅里叶变换。
fft_img = fft2(double(gray_img));% 将零频率分量移到频谱的中心。
fft_img_shifted = fftshift(fft_img);% 设定滤波器。
[M, N] = size(fft_img);R = 10; % 设定滤波器半径。
X = 0:N-1;Y = 0:M-1;[X, Y] = meshgrid(X, Y);Cx = 0.5 N;Cy = 0.5 M;low_pass_filter = double((X-Cx).^2 + (Y-Cy).^2 < R^2); % 应用滤波器。
fft_img_filtered = fft_img_shifted . low_pass_filter;% 将频谱移回原来的位置。
fft_img_filtered_shifted = ifftshift(fft_img_filtered); % 计算逆傅里叶变换。
filtered_img = ifft2(fft_img_filtered_shifted);% 显示原始图像和滤波后的图像。
subplot(1,2,1), imshow(gray_img, []);title('原始图像');subplot(1,2,2), imshow(abs(filtered_img), []);title('滤波后的图像');这段代码首先读取一张图像,然后将其转换为灰度图像。
接着计算图像的傅里叶变换,并将零频率分量移到频谱的中心。
然后设定一个低通滤波器,将其应用于图像的傅里叶变换。
最后计算出滤波后的图像并显示原始图像和滤波后的图像。
粒子滤波及matlab实现
粒子滤波及matlab 实现粒子滤波就是指:通过寻找一组在状态空间中传播的随机样本来近似的表示概率密度函数,用样本均值代替积分运算,进而获得系统状态的最小方差估计的过程,这些样本被形象的称为“粒子” ,故而叫粒子滤波。
粒子滤波通过非参数化的蒙特卡洛 (Monte Carlo) 模拟方法来实现递推贝叶斯滤波,适用于任何能用状态空间模型描述的非线性系统,精度可以逼近最优估计。
粒子滤波器具有简单、易于实现等特点,它为分析非线性动态系统提供了一种有效的解决方法,从而引起目标跟踪、信号处理以及自动控制等领域的广泛关注。
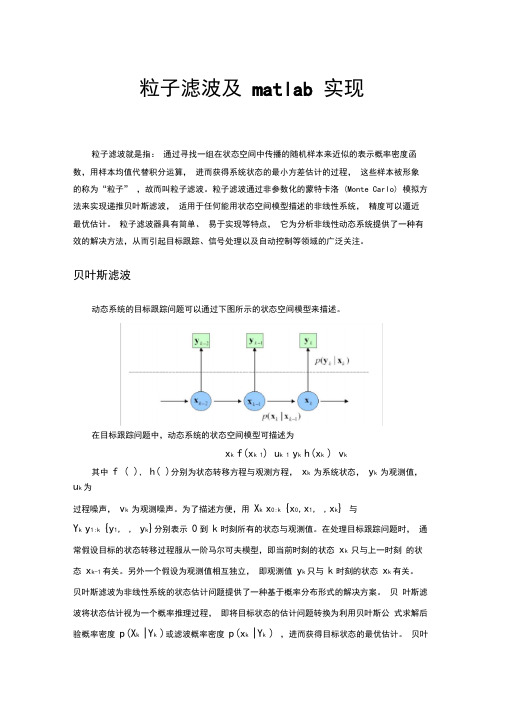
贝叶斯滤波动态系统的目标跟踪问题可以通过下图所示的状态空间模型来描述。
在目标跟踪问题中,动态系统的状态空间模型可描述为x k f(x k 1) u k 1 y k h(x k ) v k其中f ( ), h( )分别为状态转移方程与观测方程,x k 为系统状态,y k 为观测值,u k为过程噪声,v k 为观测噪声。
为了描述方便,用X k x0:k {x0,x1, ,x k} 与Y k y1:k {y1, , y k}分别表示0到k时刻所有的状态与观测值。
在处理目标跟踪问题时,通常假设目标的状态转移过程服从一阶马尔可夫模型,即当前时刻的状态x k 只与上一时刻的状态x k-1有关。
另外一个假设为观测值相互独立,即观测值y k只与k时刻的状态x k有关。
贝叶斯滤波为非线性系统的状态估计问题提供了一种基于概率分布形式的解决方案。
贝叶斯滤波将状态估计视为一个概率推理过程,即将目标状态的估计问题转换为利用贝叶斯公式求解后验概率密度p(X k |Y k )或滤波概率密度p(x k |Y k ) ,进而获得目标状态的最优估计。
贝叶斯滤波包含预测和更新两个阶段, 预测过程利用系统模型预测状态的先验概率密度, 新过程则利用最新的测量值对先验概率密度进行修正,得到后验概率密度。
假设已知 k 1时刻的概率密度函数为 p(x k 1|Y k 1 ) ,贝叶斯滤波的具体过程如下:(1)预测过程,由 p(x k 1|Y k 1) 得到 p(x k |Y k 1):p( x k , x k 1|Y k 1) p(x k | x k 1,Y k 1)p(x k 1|Y k 1)当给定 x k 1时,状态 x k 与 Y k 1相互独立,因此p(x k ,x k 1|Y k 1) p(x k |x k 1)p(x k1|Y k 1)上式两端对 x k 1 积分,可得 Chapman-Komolgorov 方程p(x k |Y k 1) p(x k |x k 1)p(x k 1|Y k 1)dx k 1(2)更新过程,由 p(x k |Y k 1)得到 p(x k |Y k ):获取 k 时刻的测量 y k 后,利用贝叶斯公式对先验概率密度进行更新,得到后验概率p(y k |x k ,Y k 1)p(x k |Y k 1) p( y k |Y k 1) 假设 y k 只由 x k 决定,即p(y k |x k ,Y k 1) p(y k |x k )因此p(y k |x k )p(x k |Y k 1) p(y k |Y k 1)其中, p(y k |Y k 1) 为归一化常数 p(y k |Y k 1) p(y k |x k )p(x k |Y k 1)dx k贝叶斯滤波以递推的形式给出后验 (或滤波 ) 概率密度函数的最优解。
matlab11种数字信号滤波去噪算法

matlab11种数字信号滤波去噪算法Matlab是一种强大的数学软件,广泛应用于信号处理领域。
在数字信号处理中,滤波去噪是一个重要的任务,可以提高信号的质量和准确性。
本文将介绍Matlab中的11种数字信号滤波去噪算法。
1. 均值滤波:该算法通过计算信号中一定窗口内的像素平均值来去除噪声。
它适用于高斯噪声和椒盐噪声的去除。
2. 中值滤波:该算法通过计算信号中一定窗口内的像素中值来去除噪声。
它适用于椒盐噪声的去除。
3. 高斯滤波:该算法通过对信号进行高斯模糊来去除噪声。
它适用于高斯噪声的去除。
4. 维纳滤波:该算法通过最小均方误差准则来估计信号的真实值,并去除噪声。
它适用于高斯噪声的去除。
5. 自适应滤波:该算法通过根据信号的局部特性来调整滤波器的参数,从而去除噪声。
它适用于非线性噪声的去除。
6. 小波去噪:该算法通过将信号分解为不同频率的小波系数,并对系数进行阈值处理来去除噪声。
它适用于各种类型的噪声的去除。
7. Kalman滤波:该算法通过对信号进行状态估计和观测更新来去除噪声。
它适用于线性系统的去噪。
8. 粒子滤波:该算法通过使用一组粒子来估计信号的状态,并通过重采样来去除噪声。
它适用于非线性系统的去噪。
9. 线性预测滤波:该算法通过使用线性预测模型来估计信号的未来值,并去除噪声。
它适用于平稳信号的去噪。
10. 自适应线性组合滤波:该算法通过对信号进行线性组合来估计信号的真实值,并去除噪声。
它适用于各种类型的噪声的去除。
11. 稀疏表示滤波:该算法通过使用稀疏表示模型来估计信号的真实值,并去除噪声。
它适用于各种类型的噪声的去除。
以上是Matlab中的11种数字信号滤波去噪算法。
每种算法都有其适用的场景和优缺点,根据具体的信号和噪声类型选择合适的算法进行去噪处理。
Matlab提供了丰富的函数和工具箱,可以方便地实现这些算法,并对信号进行滤波去噪。
通过合理选择和组合这些算法,可以有效提高信号的质量和准确性,为后续的信号处理任务提供更好的基础。
粒子滤波算法简介与matlab程序

粒子滤波作者-niewei120——nuaaBayes法则:贝叶斯定理由英国数学家贝叶斯( Thomas Bayes 1702-1763 ) 发展,用来描述两个条件概率之间的关系,比如P(A|B) 和P(B|A)。
按照乘法法则:P(A∩B)=P(A)*P(B|A)=P(B)*P(A|B),可以立刻导出贝叶斯定理公式:P(A|B)=P(B|A)*P(A)/P(B)。
通常,事件A在事件B(发生)的条件下的概率,与事件B在事件A的条件下的概率是不一样的;然而,这两者是有确定的关系,贝叶斯法则就是这种关系的陈述。
Pr(A)是A的先验概率或边缘概率。
之所以称为"先验"是因为它不考虑任何B方面的因素。
Pr(A|B)是已知B发生后A的条件概率,也由于得自B的取值而被称作A的后验概率。
Pr(B|A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
Pr(B)是B的先验概率或边缘概率,也作标准化常量(normalized constant)。
先验概率的计算比较简单,没有使用贝叶斯公式;而后验概率的计算,要使用贝叶斯公式。
若用Pr(B|A)/Pr(B)表示标准似然度,则后验概率= 标准似然度* 先验概率。
例子:一座别墅在过去的20 年里一共发生过 2 次被盗,别墅的主人有一条狗,狗平均每周晚上叫 3 次,在盗贼入侵时狗叫的概率被估计为0.9,问题是:在狗叫的时候发生入侵的概率是多少?我们假设A 事件为狗在晚上叫,B 为盗贼入侵,则P(A) = 3 / 7,P(B)=2/(20·365)=2/7300,P(A | B) = 0.9,按照公式很容易得出结果:P(B|A)=0.9*(2/7300)/(3/7)=0.00058贝叶斯决策理论方法基本思想是:1、已知类条件概率密度参数表达式和先验概率。
2、利用贝叶斯公式转换成后验概率。
3、根据后验概率大小进行决策分类。
贝叶斯滤波的核心思想就是利用已知的信息来判断状态变量的后验概率,在目标跟踪中也就是对所有观测值Z1:Zk={Z1,Z2…Zk}已知的情况下,计算出后验概率P(Xk|Z1:k),其计算的方法具体分为预测和更新。
二维粒子滤波纯代码

⼆维粒⼦滤波纯代码% 参数设置N = 100; %粒⼦总数Q = 5; %过程噪声R = 5; %测量噪声T = 20; %测量时间theta = pi/T; %旋转⾓度distance = 80/T; %每次⾛的距离WorldSize = 100; %世界⼤⼩X = zeros(2, T); %存储系统状态Z = zeros(2, T); %存储系统的观测状态P = zeros(2, N); %建⽴粒⼦群PCenter = zeros(2, T); %所有粒⼦的中⼼位置w = zeros(N, 1); %每个粒⼦的权重err = zeros(1,T); %误差X(:, 1) = [50; 20]; %初始系统状态%wgn(m,n,p)产⽣⼀个m⾏n列的⾼斯⽩噪声的矩阵,p以dBW为单位指定输出噪声的强度。
Z(:, 1) = [50; 20] + wgn(2, 1, 10*log10(R)); %初始系统的观测状态%初始化粒⼦群for i = 1 : NP(:, i) = [WorldSize*rand; WorldSize*rand];%在worldSize区域内随机⽣成N个粒⼦dist = norm(P(:, i)-Z(:, 1)); %与测量位置相差的距离,⽤于估算该粒⼦的权重%由于上⾯已经随机⽣成了N个粒⼦,现在将其与真实的测量值z进⾏⽐较,越接近则权重越⼤,或者说差值越⼩权重越⼤%这⾥的权重计算是关于p(z/x)的分布,即观测⽅程的分布,假设观测噪声满⾜⾼斯分布,那么w(i)=p(z/x)w(i) = (1 / sqrt(R) / sqrt(2 * pi)) * exp(-(dist)^2 / 2 / R); %求权重endPCenter(:, 1) = sum(P, 2) / N; %所有粒⼦的⼏何中⼼位置%%err(1) = norm(X(:, 1) - PCenter(:, 1)); %粒⼦⼏何中⼼与系统真实状态的误差figure(1);%利⽤set(gca,'propertyname','propertyvalue'......)命令可以调整图形的坐标属性。
粒子滤波算法原理及Matlab程序(专题)

更新粒子权重
03
根据权重调整因子和似然函数更新粒子的权重。
03 Matlab实现粒子滤波算 法
Matlab编程环境介绍
01
MATLAB是一种高级编程语言和交互式环境,广泛应用于算法 开发、数据可视化、数据分析以及数值计算。
02
MATLAB提供了大量的内置函数和工具箱,使得用户可以方便
地实现各种算法和计算任务。
新应用领域探索
拓展粒子滤波算法在人工智能、机器学习等 领域的应用。
Байду номын сангаас
与其他算法结合
结合深度学习、强化学习等先进算法,提高 粒子滤波的性能和适应性。
实时性研究
优化算法实现,提高粒子滤波在实时系统中 的应用效果。
THANKS FOR WATCHING
感谢您的观看
end
02
% 可视化结果
03
plot(z);
04
```
Matlab实现代码的解读与理解
在上述代码中,我们首先定义了一些参数,包括粒子数量N、初始状态x和初始状态误差协方差矩阵P 。我们还定义了模拟动态系统的参数,包括状态转移矩阵A、控制输入矩阵B、过程噪声协方差矩阵Q 和测量噪声协方差矩阵R。我们还定义了真实状态x_true和控制输入u。
实验方法
采用对比实验、重复实验等方法,对算法性能进行客 观评估。
粒子滤波算法的性能优化
参数调整
根据实际应用需求和实验结果,调整算法参 数以优化性能。
算法改进
针对算法的不足之处进行改进,以提高性能 和鲁棒性。
并行计算
采用并行计算技术,提高算法的计算效率。
05 粒子滤波算法的改进与拓 展
粒子滤波算法的改进方向
一维粒子滤波纯代码

⼀维粒⼦滤波纯代码%⼀维粒⼦滤波代码%状态⽅程:x(k)=x(k-1)/2+25*x(k-1)/(1+x(k-1)^2)+8cos(1.2(k-1))+vk;vk为噪声%测量⽅程:y(k)=x(k)^2/20+nk;nk为噪声%初始化时的状态x0=0.1;%过程噪声的协⽅差,且其均值为0Q=1;%测量噪声的协⽅差,且其均值为0R=1;%仿真步数simu_steps=70;%粒⼦滤波中的粒⼦数N=100;%初始化分布的⽅差V=2;%初始化粒⼦滤波的估计值与初始状态⼀致x_estimate=x0;%⽤⼀个⾼斯分布随机的产⽣初始的粒⼦%randn产⽣标准正太分布的随机数,其实它就是在x状态附近做⼀个随机样本抽样的过程,在这⾥x为均值,P为⽅差for i=1 : N%⽤于存储当前采样到的粒⼦集的数组current_particle(i)=x0+sqrt(V)*randn;end%⽤于存储系统状态⽅程计算得到的每⼀步的状态值,此为数组x_state=[x0];%⽤于存储量测⽅程计算得到的每⼀步的状态值,也为数组y_measure=[x0^2/20+sqrt(R)*randn];%⽤于记录粒⼦滤波每⼀步估计的粒⼦均值(该均值即为对对应步状态的估计值),此为⼀个数组x_estimate_Arr=[x_estimate];%close all 是关闭所有窗⼝(程序运⾏产⽣的,不包括命令窗,editor窗和帮助窗)close all;%为⽅便下⾯进⾏for循环,⽽不⽤使⽤变量x0x=x0;for k=1:simu_steps%从状态⽅程当中获取下⼀时刻的状态值(称为预测)x=0.5*x+25*x/(1+x^2)+8*cos(1.2*(k-1))+sqrt(Q)*randn;%在当前状态下,通过观测⽅程获取的观测量的值y=x^2/20+sqrt(R)*randn;for i=1 : N%从先验分布(在这⾥当做粒⼦滤波中的重要性分布)p(x(k)|x(k-1))中采样,利⽤之前⽣成的粒⼦样本集current_particle(i)带⼊状态⽅程中,记做数组next_particle(i) next_particle(i) = 0.5 * current_particle(i)+25 * current_particle(i) / (1+(current_particle(i))^2)+8 * cos(1.2 * (k-1)) + sqrt(Q) * randn;%已经采样到了新的粒⼦,那么如何来计算每个粒⼦的权重呢,那么肯定要与观测量有关系,则将新的样本粒⼦中的粒⼦分别带⼊观测⽅程当中%计算出通过该粒⼦⽽预测出该粒⼦的量测值y_measure_particle=next_particle(i)^2/20;%由于上⾯已经计算出第i个粒⼦,带⼊观测⽅程后的预测值,现在与真实的测量值y进⾏⽐较,越接近则权重越⼤,或者说差值越⼩权重越⼤%这⾥的权重计算是关于p(y/x)的分布,即观测⽅程的分布,假设观测噪声满⾜⾼斯分布,那么particle_w=p(y/x)particle_w(i)=(1/sqrt(2*pi*R))*exp(-(y-y_measure_particle)^2/(2*R));end%将权值归⼀化,符号./是指两个矩阵对应元素相除,现在权值particle_w已经归⼀化了particle_w=particle_w./sum(particle_w);%下⾯进⾏重采样for i=1:N%⽤rand函数来产⽣在0到1之间服从均匀分布的随机数,⽤于找出归⼀化后权值较⼤的粒⼦u=rand;%在这⾥归⼀化后的权值太⼩了,很难单个粒⼦的权值会⼤于u=rand产⽣的随机数,这⾥⽤累加的⽅式来获得具有较⼤权值的粒⼦%临时权值求和变量particle_w_sumparticle_w_sum=0;for j=1:Nparticle_w_sum=particle_w_sum+q(j);%如果particle_w_sum⼤于等于u,则将该权值的粒⼦保留下来if particle_w_sum>=ucurrent_particle(i)=next_particle(i);%如果找到这样的⼤权值粒⼦,则退出,寻找下⼀个粒⼦,别忘了,在每⼀次寻找粒⼦的时候,都是从头到尾的%故可能会保留到重复的粒⼦,所以在这⾥容易造成粒⼦样本枯竭,即粒⼦的多样性失去,只剩下⼀个⼤的粒⼦,在不断的复制⾃⼰break;endendend%粒⼦滤波的状态估计,利⽤重采样以后的粒⼦计算其均值,那么得到的这个均值就是当前步粒⼦滤波对状态的估计值%x_estimate=mean(current_particle);怀疑取均值是错的,应该各粒⼦的权值乘以对应粒⼦值相加,才是粒⼦滤波的估计值x_estimate=sum(current_particle .* particle_w);%将上⾯的数据保存下来,以便之后的绘图%这是记录状态每⼀步值的数组,始终将新产⽣的x值插⼊数组x_state=[x_state x];%记录测量值的数组,始终将新产⽣的y值插⼊数组y_measure=[y_measure y];%⽤于记录粒⼦滤波每⼀步估计的粒⼦均值(该均值即为对对应步状态的估计值),此为⼀个数组x_estimate_Arr=[x_estimate_Arr x_estimate]; end%下⾯画图t=0:simu_steps;%figurefigure(1);clfplot(t,x_state,'b.', t, x_estimate_Arr, 'k-');set(gca,'FontSize',12);set(gcf,'Color','White');xlabel('time step');ylabel('state');legend('True state','Particle filter estimate');。
正则化粒子滤波代码

正则化粒子滤波代码import numpy as npclass ParticleFilter:"""设置默认粒子数量为1000,默认正态分布精度为1e-5"""def __init__(self, n_p=1000, delta=1e-5):self.N_p = n_p # 粒子个数self.delta = delta # 正态分布精度def init_particles(self, init_x, init_y, std: tuple, seed=None): """生成初始粒子:param std: 正态分布参数(均值,标准差):return:"""np.random.seed(seed)# (x维度, y维度, 粒子个数)self.particles = np.random.randn(2, self.N_p)self.particles[0] *= std[0] * self.deltaself.particles[1] *= std[1] * self.deltaself.particles[0] += init_xself.particles[1] += init_ydef motion_update(self, x, y, std: tuple, f=[1, 1], seed=None): """运动更新:param x: 传感器测量位置的x坐标:param y: 传感器测量位置的y坐标:param std: 正态分布参数:param f: 运动模型参数(默认为[1, 1]):return: None"""np.random.seed(seed)self.particles[0] = self.particles[0]*f[0] +np.random.randn(self.N_p)*std[0]*self.deltaself.particles[1] = self.particles[1]*f[1] +np.random.randn(self.N_p)*std[1]*self.deltaself.particles[0] += xself.particles[1] += ydef calculate_weight(self, obs_x, obs_y, std: tuple):"""计算粒子权重:param obs_x: 传感器测量位置的x坐标:param obs_y: 传感器测量位置的y坐标:param std: 正态分布参数:return: None"""dist = (self.particles[0] - obs_x) ** 2 + (self.particles[1] - obs_y) ** 2self.weight =np.exp(-dist/(2*std[0]**2))+np.exp(-dist/(2*std[1]**2))self.weight /= sum(self.weight)def resampling(self, seed=None):"""重采样:return: None"""np.random.seed(seed)index = np.random.choice(self.N_p, size=self.N_p, replace=True, p=self.weight)self.particles = self.particles[:, index]。
粒子滤波原理及应用matlab仿真

粒子滤波原理及应用matlab仿真一、引言粒子滤波(Particle Filter)是贝叶斯滤波(Bayesian Filter)的一种扩展,用于解决非线性和非高斯问题。
它是一种基于蒙特卡罗方法的状态估计算法,可以用于目标跟踪、机器人定位、信号处理等领域。
本文将详细介绍粒子滤波的原理及其在matlab中的应用。
二、贝叶斯滤波贝叶斯滤波是一种基于贝叶斯定理的概率推断方法,用于估计状态变量在给定观测值下的后验概率分布。
其核心思想是将先验概率分布和观测数据结合起来,得到后验概率分布。
具体地,在时间步k时刻,假设状态变量为x(k),观测变量为y(k),则根据贝叶斯定理:P(x(k)|y(1:k)) = P(y(k)|x(k)) * P(x(k)|y(1:k-1)) / P(y(k)|y(1:k-1))其中,P(x(k)|y(1:k))表示在已知前k个观测值下x(k)的后验概率分布;P(y(k)|x(k))表示在已知x(k)时y(k)的条件概率分布,也称为似然函数;P(x(k)|y(1:k-1))表示在已知前k-1个观测值下x(k)的先验概率分布;P(y(k)|y(1:k-1))表示前k-1个观测值的边缘概率分布。
三、粒子滤波基本原理粒子滤波是一种基于贝叶斯滤波的蒙特卡罗方法,它通过在状态空间中随机采样一组粒子来近似表示后验概率分布。
每个粒子都代表一个可能的状态变量,其权重反映了该状态变量与观测值之间的匹配程度。
具体地,在时间步k时刻,假设有N个粒子{ x(1), x(2), ..., x(N) },则每个粒子都有一个对应的权重w(i),且满足:∑ w(i) = 1根据贝叶斯定理可得:P(x(k)|y(1:k)) = P(y(k)|x(k)) * P(x(k)|y(1:k-1)) / P(y(k)|y(1:k-1))其中,P(y(k)|x(k))和P(x(k)|y(1:k-1))可以通过系统模型和观测模型计算得到。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
function ParticleEx1
% Particle filter example, adapted from Gordon, Salmond, and Smith paper.
x = 0.1; % initial state
Q = 1; % process noise covariance
R = 1; % measurement noise covariance
tf = 50; % simulation length
N = 100; % number of particles in the particle filter
xhat = x;
P = 2;
xhatPart = x;
% Initialize the particle filter.
for i = 1 : N
xpart(i) = x + sqrt(P) * randn;
end
jArr = [0];
xArr = [x];
yArr = [x^2 / 20 + sqrt(R) * randn];
xhatArr = [x];
PArr = [P];
xhatPartArr = [xhatPart];
close all;
for k = 1 : tf
% System simulation
x = 0.5 * x + 25 * x / (1 + x^2) + 8 * cos(1.2*(k-1)) + sqrt(Q) * randn;%状态方程
y = x^2 / 20 + sqrt(R) * randn;%观测方程
% Extended Kalman filter
F = 0.5 + 25 * (1 - xhat^2) / (1 + xhat^2)^2;
P = F * P * F' + Q;
H = xhat / 10;
K = P * H' * (H * P * H' + R)^(-1);
xhat = 0.5 * xhat + 25 * xhat / (1 + xhat^2) + 8 * cos(1.2*(k-1));%预测
xhat = xhat + K * (y - xhat^2 / 20);%更新
P = (1 - K * H) * P;
% Particle filter
for i = 1 : N
xpartminus(i) = 0.5 * xpart(i) + 25 * xpart(i) / (1 + xpart(i)^2) + 8 * cos(1.2*(k-1)) + sqrt(Q) * randn;
ypart = xpartminus(i)^2 / 20;
vhat = y - ypart;%观测和预测的差
q(i) = (1 / sqrt(R) / sqrt(2*pi)) * exp(-vhat^2 / 2 / R);
end
% Normalize the likelihood of each a priori estimate.
qsum = sum(q);
for i = 1 : N
q(i) = q(i) / qsum;%归一化权重
end
% Resample.重采样
for i = 1 : N
u = rand; % uniform random number between 0 and 1
qtempsum = 0;
for j = 1 : N
qtempsum = qtempsum + q(j);
if qtempsum >= u
xpart(i) = xpartminus(j);
if k == 20
qArr=q;
jArr = [jArr j];
end
break;
end
end
end
% The particle filter estimate is the mean of the particles.
xhatPart = mean(xpart);
% Plot the estimated pdf's at a specific time.
if k == 20
% Particle filter pdf
pdf = zeros(81,1);
for m = -40 : 40
for i = 1 : N
if (m <= xpart(i)) && (xpart(i) < m+1)
pdf(m+41) = pdf(m+41) + 1;
end
end
end
figure;
m = -40 : 40;
plot(m, pdf / N, 'r');
hold;
title('Estimated pdf at k=20');
disp(['min, max xpart(i) at k = 20: ', num2str(min(xpart)), ', ', num2str(max(xpart))]);
% Kalman filter pdf
pdf = (1 / sqrt(P) / sqrt(2*pi)) .* exp(-(m - xhat).^2 / 2 / P);
plot(m, pdf, 'b');
legend('Particle filter', 'Kalman filter');
grid on;
end
% Save data in arrays for later plotting
xArr = [xArr x];
yArr = [yArr y];
xhatArr = [xhatArr xhat];
PArr = [PArr P];
xhatPartArr = [xhatPartArr xhatPart];
end
t = 0 : tf;
%figure;
%plot(t, xArr);
%ylabel('true state');
figure;
plot(t, xArr, 'b.', t, xhatArr, 'g-.', t, xhatArr-2*sqrt(PArr), 'r:', t, xhatArr+2*sqrt(PArr), 'r:'); axis([0 tf -40 40]);
set(gca,'FontSize',12); set(gcf,'Color','White');
xlabel('time step'); ylabel('state');
legend('True state', 'EKF estimate', '95% confidence region');
grid on;
figure;
plot(t, xArr, 'b.', t, xhatPartArr, 'k-');
set(gca,'FontSize',12); set(gcf,'Color','White');
xlabel('time step'); ylabel('state');
legend('True state', 'Particle filter estimate');
grid on;
xhatRMS = sqrt((norm(xArr - xhatArr))^2 / tf);
xhatPartRMS = sqrt((norm(xArr - xhatPartArr))^2 / tf);
disp(['Kalman filter RMS error = ', num2str(xhatRMS)]);
disp(['Particle filter RMS error = ', num2str(xhatPartRMS)]);
/*qArr
tt=max(qArr)
t=jArr
[m,n]=hist(jArr,100)
m
n
sum(m) 完。
