粒子滤波算法原理及Matlab程序
matlab 粒子滤波重采样

MATLAB粒子滤波重采样1. 简介粒子滤波(Particle Filter)是一种基于蒙特卡洛方法的滤波算法,用于在非线性和非高斯系统中进行状态估计。
粒子滤波通过使用一组粒子来近似系统的后验概率分布,从而实现对系统状态的估计。
重采样是粒子滤波算法中的一个重要步骤,用于根据粒子的权重对粒子进行重新采样,以提高估计的准确性。
在本文中,我们将使用MATLAB编写粒子滤波算法,并实现重采样步骤。
2. 粒子滤波算法步骤粒子滤波算法通常包括以下步骤:1.初始化粒子集合:根据先验分布或已知信息,生成一组随机粒子,表示系统的可能状态。
2.预测步骤:根据系统的动力学模型,对粒子进行状态预测。
3.更新步骤:使用测量模型和观测值对粒子进行权重更新。
4.规范化权重:对粒子的权重进行规范化,使其总和等于1。
5.重采样步骤:根据粒子的权重,对粒子进行重新采样,以提高估计的准确性。
6.重复步骤2-5,直到达到停止条件。
在本文中,我们将重点关注重采样步骤的实现。
3. 粒子滤波重采样算法重采样步骤的目标是根据粒子的权重,从当前粒子集合中生成新的粒子集合,以便更好地表示后验概率分布。
常用的重采样方法包括多项式重采样和系统性重采样。
下面是系统性重采样算法的伪代码:1. 初始化:给定粒子集合P和对应的权重W。
2. 计算累积权重:计算累积权重C,其中C(i) = sum(W(1:i)),i为粒子的索引。
3. 生成随机数:生成一个均匀分布的随机数r,取值范围为[0, 1]。
4. 重采样:对于每个粒子i,找到满足C(j) > r且C(j-1) <= r的最小索引j,将粒子j 添加到新的粒子集合中。
5. 返回新的粒子集合。
下面是MATLAB代码实现粒子滤波重采样的函数:numParticles = size(particles, 2);newParticles = zeros(size(particles));cumulativeWeights = cumsum(weights);r = rand(1) / numParticles;index = 1;for i = 1:numParticlesu = r + (i - 1) / numParticles;while cumulativeWeights(index) < uindex = index + 1;endnewParticles(:, i) = particles(:, index);endend4. 示例应用为了演示粒子滤波重采样算法的应用,我们将使用一个简单的二维机器人定位问题。
matlab 粒子滤波重采样

matlab 粒子滤波重采样粒子滤波(Particle Filter)是一种非线性滤波方法,用于估计一些隐含的状态变量。
重采样(Resampling)是粒子滤波中的一个步骤,用于更新粒子权重,并确保粒子数保持不变。
在MATLAB中,可以使用以下步骤来实现粒子滤波的重采样:1. 定义初始粒子集合,包括粒子的状态向量和权重。
可以使用normal分布或均匀分布生成初始粒子。
2. 根据系统模型,对每个粒子进行状态更新。
可以使用动态模型描述状态的变化。
3. 通过与观测值比较,计算每个粒子的权重。
可以使用测量模型来计算粒子的权重。
4. 对粒子权重进行归一化,以便于下一步的重采样。
可以使用normalize函数来实现归一化。
5. 根据粒子的权重,进行重采样。
可以使用resample函数来进行重采样。
下面是一个简单的示例代码,演示了如何在MATLAB中实现粒子滤波的重采样:```matlab% 设置初始粒子数和重采样阈值N = 100;resamplingThreshold = N/2;% 生成初始粒子particles = randn(N, 1); % 从标准正态分布中生成初始粒子weights = ones(N, 1)/N; % 初始化粒子权重for t = 1:T% 根据系统模型更新粒子particles = motionModel(particles); % 假设motionModel是一个状态更新函数% 根据观测值计算粒子权重weights = measurementModel(particles, observation(t)); % 假设measurementModel是一个计算粒子权重的函数% 归一化粒子权重weights = normalize(weights); % 使用normalize函数归一化粒子权重% 判断是否需要重采样if 1/sum(weights.^2) < resamplingThresholdparticles = resample(particles, weights); % 使用resample函数进行重采样weights = ones(N, 1)/N; % 重采样后,将粒子权重初始化为均匀分布endend```需要根据具体的系统模型和测量模型来编写对应的函数。
matlab 粒子滤波代码

以下是一个简单的 MATLAB 粒子滤波器的代码示例:```matlab% 初始化参数N = 100; % 粒子数量dt = 0.1; % 时间步长x = [0 0]; % 初始位置P = eye(2); % 初始协方差矩阵Q = eye(2); % 过程噪声协方差矩阵R = eye(2); % 观测噪声协方差矩阵G = [0.9 0.1; 0.1 0.9]; % 转换矩阵N_particles = size(Q,1); % 粒子数量particles = zeros(N_particles,2); % 初始化粒子particles(:,1) = x(1); % 设置粒子的 x 分量particles(:,2) = x(2); % 设置粒子的 y 分量weights = ones(N_particles,1) / N_particles; % 初始化权重% 模拟观测数据z = [1.2 0.5]; % 观测位置R_inv = inv(R); % 观测噪声协方差矩阵的逆H = [z(1) -z(2); z(2) z(1)]; % 观测矩阵y = H * x; % 预测的观测值% 粒子滤波步骤for t = 1:100% 重采样步骤weights = weights / sum(weights);index = randsample(1:N_particles, N, true, weights); particles = particles(index,:);% 预测步骤x_pred = particles;P_pred = Q;x_pred = G * x_pred;P_pred = P_pred + dt * G * P_pred;P_pred = P_pred + P_pred * G' + R;% 更新步骤y_pred = H * x_pred;S = H * P_pred * H' + R_inv;K = P_pred * H' * inv(S);x = x_pred + K * (z - y_pred);P = P_pred - P_pred * K * H';end```在这个代码示例中,我们使用了两个步骤:重采样步骤和预测/更新步骤。
粒子滤波算法综述

粒子滤波算法综述作者:李孟敏来源:《中国新通信》2015年第10期【摘要】对粒子滤波算法的原理、发展历史以及应用领域进行综述,首先针对非线性非高斯系统的状态滤波问题阐述粒子滤波的原理,而后讨论粒子滤波算法存在的主要问题和改进手段,最后阐明其在多个研究领域中的应用现状。
【关键字】非线性滤波概率密度重采样粒子退化一、引言粒子滤波(PF)是一种在处理非线性非高斯系统状态估计问题时具有较好估计效果的方法,其原理是通过非参数蒙特卡洛方法实现贝叶斯滤波。
其最早起源于Hammersley等人在20实际50年代末提出的顺序重要性采样(SIS)滤波思想。
但由于上述方法存在严重的样本权值退化从而导致的粒子数匮乏现象,直到1993年Gordon等人将重采样技术引入蒙特卡洛重要性采样过程,提出一种Bootstrap滤波方法,从而奠定了粒子滤波算法的基础。
二、基本粒子滤波算法三、粒子滤波算法存在的主要问题及改进对于SIS算法来说,容易出现粒子的退化问题,目前存在的诸多对SIS算法的改进中,能够降低该现象影响的有效方法是选择合适的重要性函数和采用重采样方法。
针对状态空间模型的改进算法,如辅助变量粒子滤波算法(APF),局部线性化方法,代表的算法主要有EKF,UKF等。
针对重采样改进方法,文献通过将遗传算法和进化算法引入粒子滤波算法中,增加重采样过程中粒子的多样性。
然APF算法在过程噪声较小时,可获得比标准粒子滤波更高的滤波精度,在过程噪声较大时,其效果则大大降低。
采用局部线性化的方法EKF,UKF都是针对非线性系统的线性卡尔曼滤波方法的变形和改进,因此受到线性卡尔曼滤波算法的条件制约,而对于非高斯分布的状态模型,其滤波性能变差。
将遗传算法和进化算法与粒子滤波结合的改进粒子滤波算法,虽取得了较好的滤波效果,然而是以消耗过多计算资源为代价的。
四、粒子滤波的应用4.1 目标跟踪对目标进行定位和跟踪是典型的动态系统状态估计问题,在诸如纯角度跟踪的运动模型中,采用粒子滤波方法进行实现目标跟踪已获得了较好的跟踪精度,文献研究了多目标跟踪与数据融合问题,文献给出了基于粒子滤波的群目标跟踪算法。
粒子滤波算法matlab实例

一、介绍粒子滤波算法粒子滤波算法是一种基于蒙特卡洛方法的非线性、非高斯滤波算法,它通过一组随机产生的粒子来近似表示系统的后验概率分布,从而实现对非线性、非高斯系统的状态估计。
在实际应用中,粒子滤波算法被广泛应用于目标跟踪、导航、机器人定位等领域。
本文将以matlab 实例的形式介绍粒子滤波算法的基本原理和应用。
二、粒子滤波算法的原理及步骤粒子滤波算法的主要原理是基于贝叶斯滤波理论,通过一组随机产生的粒子来近似表示系统的后验概率分布。
其具体步骤如下:1. 初始化:随机生成一组粒子,对于状态变量的初始值和方差的估计,通过随机抽样得到一组粒子。
2. 预测:根据系统模型,对每个粒子进行状态预测,得到预测状态。
3. 更新:根据测量信息,对每个预测状态进行权重更新,得到更新后的状态。
4. 重采样:根据更新后的权重,对粒子进行重采样,以满足后验概率分布的表示。
5. 输出:根据重采样后的粒子,得到对系统状态的估计。
三、粒子滤波算法的matlab实例下面以一个简单的目标跟踪问题为例,介绍粒子滤波算法在matlab中的实现。
假设存在一个目标在二维空间中运动,我们需要通过一系列测量得到目标的状态。
我们初始化一组粒子来近似表示目标的状态分布。
我们根据目标的运动模型,预测每个粒子的状态。
根据测量信息,对每个预测状态进行权重更新。
根据更新后的权重,对粒子进行重采样,并输出对目标状态的估计。
在matlab中,我们可以通过编写一段简单的代码来实现粒子滤波算法。
我们需要定义目标的运动模型和测量模型,然后初始化一组粒子。
我们通过循环来进行预测、更新、重采样的步骤,最终得到目标状态的估计。
四、总结粒子滤波算法是一种非线性、非高斯滤波算法,通过一组随机产生的粒子来近似表示系统的后验概率分布。
在实际应用中,粒子滤波算法被广泛应用于目标跟踪、导航、机器人定位等领域。
本文以matlab实例的形式介绍了粒子滤波算法的基本原理和应用,并通过一个简单的目标跟踪问题,展示了粒子滤波算法在matlab中的实现过程。
粒子滤波算法的应用研究及优化

粒子滤波算法的应用研究及优化近年来,随着计算机技术的不断发展,人工智能等领域的应用不断扩展,各种算法也不断被提出和应用。
粒子滤波算法是一种常见的非参数滤波算法,其主要应用于状态估计和目标跟踪等领域。
在实际应用中,粒子滤波算法也存在许多问题,需要进行优化和改进。
一、粒子滤波算法的基本原理粒子滤波算法基于蒙特卡罗方法,根据现有的状态量,通过不断地提出指定数量的粒子,不断逼近滤波目标的状态。
具体算法流程如下:1. 初始化。
在搜寻状态量的范围内,随机生成一定数量的粒子(通常为1000个左右),并按照一定的分布方式进行粒子的分配。
2. 预测。
根据系统的动态模型预测每个粒子的下一个状态。
3. 权值更新。
根据每个粒子的当前状态和实际观测值,计算每个粒子的权值,并进行归一化处理。
4. 重采样。
根据每个粒子的权值,进行筛选和抽样,让具有更高权值的粒子具有更高的概率被采样。
5. 状态估计。
根据采样到的粒子状态计算滤波后的目标状态。
二、粒子滤波算法的应用研究1. 目标跟踪。
在目标跟踪中,粒子滤波算法被广泛应用。
通过将目标的位置作为特征,将粒子在搜索范围内分布,并根据目标的位置和速度对每个粒子进行预测和权值更新,从而得到目标的实时跟踪结果。
2. 机器人定位。
在机器人定位领域,粒子滤波算法也有着广泛的应用。
通过机器人的传感器,计算机器人位置的先验概率,并根据传感器获得的信息对每个粒子进行预测和更新,从而得到机器人位置的后验概率估计。
3. 海洋探索。
在海洋探索中,粒子滤波算法也有着广泛的应用。
通过探测器获取海洋中目标的信息,并将其传入计算机进行处理。
在搜寻范围内随机产生一定数量的粒子,并根据海洋环境的不同,在粒子的状态估计过程中添加不同的判据和约束条件,以得到更精确的目标跟踪结果。
三、粒子滤波算法的优化粒子滤波算法的性能受到多个因素的影响,例如粒子数、粒子初始分布、重采样方法等。
为了提高粒子滤波算法的估计精度,以下几个方面可以进行优化:1. 优化初始分布。
Gabor滤波原理和matlab实现

Gabor滤波原理和matlab实现1. 傅⾥叶变换的缺点傅⾥叶变换的公式为从公式中可以看出,傅⾥叶变换对信号在整个时域做了积分处理,因此其结果对时域信号在整个时间轴上进⾏了信息平均。
这对于平稳信号来说是可⾏的,然⽽对于在时间上具有显著变化的⾮平稳信号来说,这样的做法显然不能满⾜我们对信号进⾏精确分析的要求。
我们希望将信号分解到不同频率成分上来研究组成该信号的各频率成分的含量的同时,也能看到在信号的时变过程中,到底在哪⼀个时间段某⼀频率成分含量较多。
(摘⾃)2. Gabor变换Gabor变换是D.Gabor 1946年提出的。
为了由信号的傅⾥叶变换提取局部信息,引⼊了时间局部化的窗函数,得到了窗⼝傅⾥叶变换。
由于窗⼝傅⾥叶变换只依赖于部分时间的信号,所以,现在窗⼝傅⾥叶变换⼜称为短时傅⾥叶变换。
Gabor变换的基本思想:把信号划分成许多⼩的时间间隔,⽤傅⾥叶变换分析每⼀个时间间隔,以便确定信号在该时间间隔存在的频率。
其处理⽅法是对 f(t)加⼀个滑动窗,再作傅⾥叶变换。
Gabor变换所⽤的窗⼝函数是⾼斯函数,⼆维Gabor变换公式为(摘⾃)参数含义:λ:正弦函数波长,它的值以像素为单位指定,通常⼤于等于2,但不能⼤于输⼊图像尺⼨的1/5.θ:Gabor核函数(滤波器)的⽅向,这个参数指定了Gabor函数并⾏条纹的⽅向,他的取值为0到360度ψ:相位偏移,调谐函数的相位偏移,取值-180到180。
σ:带宽,⾼斯函数的标准差,通常取2πγ:空间的宽⾼⽐,决定了Gabor函数形状的椭圆率,当γ=1时,形状是圆的,当γ<1时,形状随着平⾏条纹⽅向⽽拉长。
通常该值为0.5在特征提取⽅⾯,Gabor⼩波变换与其它⽅法相⽐:⼀⽅⾯其处理的数据量较少,能满⾜系统的实时性要求;另⼀⽅⾯,⼩波变换对光照变化不敏感,且能容忍⼀定程度的图像旋转和变形,当采⽤基于欧⽒距离进⾏识别时,特征模式与待测特征不需要严格的对应,故能提⾼系统的鲁棒性。
pf算法举例及其matlab实现-概述说明以及解释

pf算法举例及其matlab实现-概述说明以及解释1.引言1.1 概述PF算法(Particle Filter Algorithm),又称为粒子滤波算法,是一种基于蒙特卡洛方法的非线性滤波算法。
与传统的滤波算法相比,PF算法具有更大的灵活性和鲁棒性,在估计复杂非线性系统状态的过程中表现出良好的性能。
PF算法基于一种随机采样的思想,通过对系统状态进行一系列粒子的采样,再通过对这些粒子的权重进行重要性重采样,最终获得对状态估计的准确性更高的结果。
在PF算法中,粒子的数量决定了滤波算法的精度,粒子越多,估计结果越准确,但也会增加计算复杂度。
因此,在实际应用中需要根据实际情况灵活选择粒子数量。
作为一种高效的滤波算法,PF算法在众多领域都有广泛的应用。
例如,粒子滤波算法在目标跟踪、传感器网络定位、机器人定位与导航等领域都有着重要的作用。
其在目标跟踪领域的应用尤为突出,由于PF算法可以处理非线性和非高斯分布的情况,使得目标跟踪更加准确和稳定。
在Matlab中,PF算法也得到了广泛的应用和实现。
Matlab提供了丰富的函数和工具箱,可以便捷地实现PF算法。
借助Matlab的强大数据处理和可视化功能,我们可以更加便捷地进行粒子滤波算法的实现和结果分析。
本文将从PF算法的基本概念出发,介绍其应用举例和在Matlab中的具体实现。
通过对PF算法的研究和实践,我们可以更好地理解和应用这一强大的滤波算法,为实际问题的解决提供有效的手段。
通过对Matlab 的使用,我们还可以更加高效地实现和验证粒子滤波算法的性能,为进一步的研究和应用奠定基础。
在接下来的章节中,我们将详细介绍PF算法的原理及其在现实应用中的具体案例。
随后,我们将展示如何使用Matlab实现PF算法,并通过实验结果对其性能进行评估和分析。
最后,我们将总结PF算法和Matlab 实现的主要特点,并对未来的发展进行展望。
文章结构的设定在撰写一篇长文时非常重要,它能够为读者提供一个整体的概览,帮助他们更好地理解文章的内容安排。
粒子滤波算法综述

5 与其他非线性滤波方法的比较
随着粒子滤波方法在许多领域中的成功应用,研究人员认为在解决所 有状态估计的滤波问题时,获得滤波性能最好的方法就是粒子滤波算法 ,它甚至优于卡尔曼滤波方法。实际上,粒子滤波作为处理非线性系统 状态估计问题的方法之一,也存在着算法适应性和估计精度问题。
5 与其他非线性滤波方法的比较
m 记录样本 xk ,并将其作为新样本集中的采样,将区间[ 0, 1] i 按 i w j (i 1, 2, , n) 分成 n个小区间,当随机数 ul 落在第m个区 j 0 m 间 I m m1 时,对应样本 xk 进行复制。 在采样总数仍保持为n的情况下,权值较大的样本被多次复制,从 而实现重采样过程。显然,重采样过程是以牺牲计算量和鲁棒性来降 低粒子数匮乏现象。
(5)
蒙特卡罗方法的核心是将式( 2) 中的积分问题转化为有限样本点的概 率转移累加过程,但在实际中由于 p xk z1:k 可能是多变量、非指概率分布与 p xk z1:k 相同, 概率密度分布 q x0:k z1:k 已知且容易从中采样的分布函数,重要性 采样需要得到k 时刻以前所有的观测数据。因此实际中多采用可实现递 推估计的SIS算法。
5 与其他非线性滤波方法的比较
5.3 EKF,UKF,PF3种算法的比较 EKF和UKF都是针对非线性系统的线性卡尔曼滤波方法的变形和改 进形式,因此受到线性卡尔曼滤波算法的条件制约, 即系统状态应满足高 斯分布。表1给出了不同状态方程和观测方程的概率分布特性时的不同滤 波方法 表1 各种滤波算法的适应性范围
i i ˆ p ( xk , z1:k ) wk K h ( xk xk ) i 1 n
(15)
其中K()和h分别是满足 ˆ ˆ)= E[ [ p ( xk , z1:k ) p ( xk , z1:k )]2 dxk ] (16) p MISE( 的核密度函数和核带宽系数。
粒子滤波 matlab

粒子滤波matlab粒子滤波(Particle Filter)是一种基于蒙特卡洛方法的非线性贝叶斯滤波算法,广泛应用于目标跟踪、定位和状态估计等领域。
它在一些特定的问题中,如非线性、非高斯、非线性动态模型和非线性观测模型的情况下,表现出了良好的适应性和准确性。
本文将以MATLAB为例,一步一步介绍粒子滤波(Particle Filter)的原理和实现。
1. 粒子滤波的基本原理:粒子滤波是通过随机样本(粒子)来对目标状态进行估计的一种方法。
它通过构建一个粒子集合来代表目标状态空间上的概率密度函数,并按照贝叶斯滤波的理论进行权重更新和重采样,从而实现对目标状态的估计。
2. 粒子滤波的实现步骤:a) 初始化:根据已知的先验知识,初始化粒子集合。
粒子的初始状态可以根据先验分布随机生成,通常可以使用高斯分布进行初始化。
b) 预测/更新:根据系统的动态模型进行粒子的状态预测,然后根据观测模型,计算每个粒子与观测数据的相似度/权重。
c) 权重归一化:计算出所有粒子的权重之后,对权重进行归一化,使得所有权重之和等于1。
d) 重采样:根据权重对粒子进行重采样,即以一定的概率选取粒子,从而减少粒子集合中的多样性,提高粒子集合的估计准确性。
e) 重复以上步骤:重复预测/更新、权重归一化和重采样的步骤,直到满足终止条件(如达到最大迭代次数)或目标状态已被准确估计。
3. MATLAB中的粒子滤波实现:在MATLAB中,可以使用`particlefilter`函数来实现粒子滤波。
以下是一个简单的例子,演示如何使用MATLAB实现粒子滤波。
MATLAB% 设置粒子滤波参数numParticles = 1000; % 粒子数量maxIterations = 100; % 最大迭代次数% 初始化粒子集合initialParticles = initializeParticles(numParticles);% 初始化权重initialWeights = ones(numParticles, 1) / numParticles;% 创建粒子滤波对象pf = particlefilter(@predictionFcn, @observationFcn, initialParticles, initialWeights);pf.ResamplingMethod = 'systematic'; % 设置重采样方法% 遍历迭代for iteration = 1:maxIterations% 提取当前迭代的观测数据observation = getObservation(iteration);% 预测粒子的状态predictedParticles = predict(pf);% 更新粒子权重updatedWeights = update(pf, observation);% 完成一次迭代的粒子滤波estimate = estimate(pf);% 显示估计结果displayEstimate(estimate);end4. 粒子滤波的应用:粒子滤波广泛应用于目标跟踪、定位和状态估计等领域。
粒子滤波原理

粒子滤波原理粒子滤波(Particle Filter)是一种非参数实时滤波方法,用于估计目标的状态。
它适用于非线性和非高斯问题,并被广泛应用于机器人感知、目标跟踪、信号处理等领域。
本文将介绍粒子滤波的基本原理、流程和应用。
1. 基本原理粒子滤波的基本原理是根据贝叶斯定理,通过推断目标状态的后验分布来预测目标状态。
具体来说,粒子滤波将目标状态表示为一组粒子,每个粒子代表一种可能的状态。
粒子的数量越多,则对目标后验分布的估计就越准确。
粒子滤波算法的流程如下:(1)初始化粒子集合,即根据先验信息生成一组随机的粒子,并赋予它们相应的权重;(2)接收观测数据,并对每个粒子进行状态转移和权重更新。
状态转移是根据系统模型进行的,对于机器人定位问题,状态转移可以使用运动学方程描述机器人在环境中的运动;权重更新是根据观测模型计算得到的,对于机器人定位问题,权重可以用激光传感器的测量值和地图进行匹配计算;(3)根据粒子的权重进行重采样,生成新的粒子集合。
重采样的目的是为了减小样本的方差,并确保样本的代表性。
(4)重复步骤(2)、(3),直到目标状态的后验分布收敛,或达到设定的迭代次数。
2. 算法改进粒子滤波算法在实际应用中存在一些问题,例如样本退化和计算复杂度高等。
为了解决这些问题,学者们提出了一系列改进算法,主要包括以下几种:串行粒子滤波(Sequential Monte Carlo, SMC)、粒子群优化算法(Particle Swarm Optimization, PSO)、希尔伯特-黄变换粒子滤波(Hilbert-Huang Transform Particle Filter, HHTPF)和变分粒子群优化算法(Variational Particle Swarm Optimization, VPSO)等。
串行粒子滤波算法是一种常用的改进算法,它将原始粒子集合分为若干个子集,在每个子集上执行滤波过程。
通过这种方式,可以减少不必要的计算,提高算法的效率。
粒子滤波算法在目标跟踪中的应用

粒子滤波算法在目标跟踪中的应用目标跟踪是计算机视觉领域中的一个重要问题,它的应用涉及到很多方面,包括军事、安防、交通、医疗等。
在目标跟踪的过程中,需要对目标进行检测、跟踪和预测,并且要能够应对各种复杂的环境条件和场景变化。
目前,粒子滤波算法被广泛应用于目标跟踪中,其优良的性能和实用性备受赞誉。
一、粒子滤波算法的基本原理粒子滤波算法是一种基于蒙特卡罗方法的估计算法,该算法通过随机粒子的集合来模拟概率密度函数的形状,进而实现对目标运动状态的预测和跟踪。
在粒子滤波算法中,随机粒子的个数通常会比较大,每个粒子都代表了目标在当前时刻的状态,包括位置、速度、加速度等信息。
当目标状态变化时,粒子的位置和权重也会随之更新,这样就能够实现对目标的精确跟踪和状态预测。
在粒子滤波算法中,每个粒子都有一个重要的权重值,它代表了该粒子代表目标状态的置信度。
在每一次迭代过程中,粒子的权重会根据观测数据进行更新,使得权重较高的粒子更有可能被保留下来,从而更准确地反映目标状态的概率分布。
二、粒子滤波算法在目标跟踪中的应用粒子滤波算法在目标跟踪中的应用非常广泛,包括运动目标追踪、人脸跟踪、行人检测等方面。
下面以运动目标追踪为例,介绍粒子滤波算法在目标跟踪中的具体实现和优势。
在运动目标追踪中,粒子滤波算法通常采用状态空间模型进行建模,将目标状态表示为一个随机向量,其中包括位置、速度、加速度等信息。
在每一时刻,根据观测数据更新粒子的状态和权重,从而实现对目标的跟踪和预测。
通过优化粒子个数、重新采样的策略等参数,可以进一步提高算法的性能和鲁棒性。
相比于其他目标跟踪算法,粒子滤波算法具有很多优点。
首先,它可以非常灵活地应对目标在运动、变形、遮挡等方面的复杂情况,从而实现更加准确和稳定的跟踪效果。
其次,粒子滤波算法可以自适应地调整参数和模型,以适应不同的环境和场景,使算法更加鲁棒和实用。
三、粒子滤波算法的未来发展方向随着计算机视觉领域的飞速发展,粒子滤波算法在目标跟踪中的应用也将持续拓展和深化。
粒子滤波MATLAB代码

function ParticleEx1% Particle filter example, adapted from Gordon, Salmond, and Smith paper.x = 0.1; % initial stateQ = 1; % process noise covarianceR = 1; % measurement noise covariancetf = 50; % simulation lengthN = 100; % number of particles in the particle filterxhat = x;P = 2;xhatPart = x;% Initialize the particle filter.for i = 1 : Nxpart(i) = x + sqrt(P) * randn;endjArr = [0];xArr = [x];yArr = [x^2 / 20 + sqrt(R) * randn];xhatArr = [x];PArr = [P];xhatPartArr = [xhatPart];close all;for k = 1 : tf% System simulationx = 0.5 * x + 25 * x / (1 + x^2) + 8 * cos(1.2*(k-1)) + sqrt(Q) * randn;%状态方程y = x^2 / 20 + sqrt(R) * randn;%观测方程% Extended Kalman filterF = 0.5 + 25 * (1 - xhat^2) / (1 + xhat^2)^2;P = F * P * F' + Q;H = xhat / 10;K = P * H' * (H * P * H' + R)^(-1);xhat = 0.5 * xhat + 25 * xhat / (1 + xhat^2) + 8 * cos(1.2*(k-1));%预测xhat = xhat + K * (y - xhat^2 / 20);%更新P = (1 - K * H) * P;% Particle filterfor i = 1 : Nxpartminus(i) = 0.5 * xpart(i) + 25 * xpart(i) / (1 + xpart(i)^2) + 8 * cos(1.2*(k-1)) + sqrt(Q) * randn;ypart = xpartminus(i)^2 / 20;vhat = y - ypart;%观测和预测的差q(i) = (1 / sqrt(R) / sqrt(2*pi)) * exp(-vhat^2 / 2 / R);end% Normalize the likelihood of each a priori estimate.qsum = sum(q);for i = 1 : Nq(i) = q(i) / qsum;%归一化权重end% Resample.重采样for i = 1 : Nu = rand; % uniform random number between 0 and 1qtempsum = 0;for j = 1 : Nqtempsum = qtempsum + q(j);if qtempsum >= uxpart(i) = xpartminus(j);if k == 20qArr=q;jArr = [jArr j];endbreak;endendend% The particle filter estimate is the mean of the particles.xhatPart = mean(xpart);% Plot the estimated pdf's at a specific time.if k == 20% Particle filter pdfpdf = zeros(81,1);for m = -40 : 40for i = 1 : Nif (m <= xpart(i)) && (xpart(i) < m+1)pdf(m+41) = pdf(m+41) + 1;endendendfigure;m = -40 : 40;plot(m, pdf / N, 'r');hold;title('Estimated pdf at k=20');disp(['min, max xpart(i) at k = 20: ', num2str(min(xpart)), ', ', num2str(max(xpart))]);% Kalman filter pdfpdf = (1 / sqrt(P) / sqrt(2*pi)) .* exp(-(m - xhat).^2 / 2 / P);plot(m, pdf, 'b');legend('Particle filter', 'Kalman filter');grid on;end% Save data in arrays for later plottingxArr = [xArr x];yArr = [yArr y];xhatArr = [xhatArr xhat];PArr = [PArr P];xhatPartArr = [xhatPartArr xhatPart];endt = 0 : tf;%figure;%plot(t, xArr);%ylabel('true state');figure;plot(t, xArr, 'b.', t, xhatArr, 'g-.', t, xhatArr-2*sqrt(PArr), 'r:', t, xhatArr+2*sqrt(PArr), 'r:'); axis([0 tf -40 40]);set(gca,'FontSize',12); set(gcf,'Color','White');xlabel('time step'); ylabel('state');legend('True state', 'EKF estimate', '95% confidence region');grid on;figure;plot(t, xArr, 'b.', t, xhatPartArr, 'k-');set(gca,'FontSize',12); set(gcf,'Color','White');xlabel('time step'); ylabel('state');legend('True state', 'Particle filter estimate');grid on;xhatRMS = sqrt((norm(xArr - xhatArr))^2 / tf);xhatPartRMS = sqrt((norm(xArr - xhatPartArr))^2 / tf);disp(['Kalman filter RMS error = ', num2str(xhatRMS)]);disp(['Particle filter RMS error = ', num2str(xhatPartRMS)]);/*qArrtt=max(qArr)t=jArr[m,n]=hist(jArr,100)mnsum(m)。
matlab11种数字信号滤波去噪算法

matlab11种数字信号滤波去噪算法Matlab是一种强大的数学软件,广泛应用于信号处理领域。
在数字信号处理中,滤波去噪是一个重要的任务,可以提高信号的质量和准确性。
本文将介绍Matlab中的11种数字信号滤波去噪算法。
1. 均值滤波:该算法通过计算信号中一定窗口内的像素平均值来去除噪声。
它适用于高斯噪声和椒盐噪声的去除。
2. 中值滤波:该算法通过计算信号中一定窗口内的像素中值来去除噪声。
它适用于椒盐噪声的去除。
3. 高斯滤波:该算法通过对信号进行高斯模糊来去除噪声。
它适用于高斯噪声的去除。
4. 维纳滤波:该算法通过最小均方误差准则来估计信号的真实值,并去除噪声。
它适用于高斯噪声的去除。
5. 自适应滤波:该算法通过根据信号的局部特性来调整滤波器的参数,从而去除噪声。
它适用于非线性噪声的去除。
6. 小波去噪:该算法通过将信号分解为不同频率的小波系数,并对系数进行阈值处理来去除噪声。
它适用于各种类型的噪声的去除。
7. Kalman滤波:该算法通过对信号进行状态估计和观测更新来去除噪声。
它适用于线性系统的去噪。
8. 粒子滤波:该算法通过使用一组粒子来估计信号的状态,并通过重采样来去除噪声。
它适用于非线性系统的去噪。
9. 线性预测滤波:该算法通过使用线性预测模型来估计信号的未来值,并去除噪声。
它适用于平稳信号的去噪。
10. 自适应线性组合滤波:该算法通过对信号进行线性组合来估计信号的真实值,并去除噪声。
它适用于各种类型的噪声的去除。
11. 稀疏表示滤波:该算法通过使用稀疏表示模型来估计信号的真实值,并去除噪声。
它适用于各种类型的噪声的去除。
以上是Matlab中的11种数字信号滤波去噪算法。
每种算法都有其适用的场景和优缺点,根据具体的信号和噪声类型选择合适的算法进行去噪处理。
Matlab提供了丰富的函数和工具箱,可以方便地实现这些算法,并对信号进行滤波去噪。
通过合理选择和组合这些算法,可以有效提高信号的质量和准确性,为后续的信号处理任务提供更好的基础。
粒子滤波算法原理及Matlab程序(专题)

更新粒子权重
03
根据权重调整因子和似然函数更新粒子的权重。
03 Matlab实现粒子滤波算 法
Matlab编程环境介绍
01
MATLAB是一种高级编程语言和交互式环境,广泛应用于算法 开发、数据可视化、数据分析以及数值计算。
02
MATLAB提供了大量的内置函数和工具箱,使得用户可以方便
地实现各种算法和计算任务。
新应用领域探索
拓展粒子滤波算法在人工智能、机器学习等 领域的应用。
Байду номын сангаас
与其他算法结合
结合深度学习、强化学习等先进算法,提高 粒子滤波的性能和适应性。
实时性研究
优化算法实现,提高粒子滤波在实时系统中 的应用效果。
THANKS FOR WATCHING
感谢您的观看
end
02
% 可视化结果
03
plot(z);
04
```
Matlab实现代码的解读与理解
在上述代码中,我们首先定义了一些参数,包括粒子数量N、初始状态x和初始状态误差协方差矩阵P 。我们还定义了模拟动态系统的参数,包括状态转移矩阵A、控制输入矩阵B、过程噪声协方差矩阵Q 和测量噪声协方差矩阵R。我们还定义了真实状态x_true和控制输入u。
实验方法
采用对比实验、重复实验等方法,对算法性能进行客 观评估。
粒子滤波算法的性能优化
参数调整
根据实际应用需求和实验结果,调整算法参 数以优化性能。
算法改进
针对算法的不足之处进行改进,以提高性能 和鲁棒性。
并行计算
采用并行计算技术,提高算法的计算效率。
05 粒子滤波算法的改进与拓 展
粒子滤波算法的改进方向
粒子滤波原理及Matlab应用

粒子滤波原理及Matlab应用粒子滤波(Particle Filter)是一种基于蒙特卡洛方法的滤波算法,用于解决非线性非高斯系统的状态估计问题。
相比于传统的卡尔曼滤波和扩展卡尔曼滤波,粒子滤波更适用于非线性系统和非高斯噪声。
粒子滤波的原理是通过一组粒子来近似表示系统的状态概率分布。
每个粒子都代表了系统的一个可能的状态。
粒子的数量越多,越能准确地表示系统的状态分布。
粒子在每个时刻根据系统动态模型进行状态的演化,并根据观测数据和测量模型进行状态的更新。
最后,根据粒子的权重对状态进行估计。
粒子滤波的步骤如下:1. 初始化粒子:根据先验的状态分布,生成一组初始的粒子,每个粒子的状态服从先验分布。
2. 粒子演化:根据动态模型,对每个粒子的状态进行预测计算。
通常使用随机扰动模型来考虑系统的不确定性。
3. 更新权重:根据观测数据和测量模型,计算每个粒子的权重。
权重反映了粒子与观测数据的吻合程度。
观测数据越能解释粒子的状态,权重越高。
4. 重采样:根据粒子的权重,进行重采样,选择得分高的粒子,代表系统的更可能状态。
重采样操作消除了粒子之间的权重差异,保持粒子的多样性。
5. 估计状态:根据重采样得到的粒子集合,计算估计的状态值。
可以是粒子的平均值、加权平均值、最大权重对应的状态等。
粒子滤波在Matlab中的应用可以通过以下步骤实现:1. 初始化粒子:根据先验的状态分布,生成一组初始的粒子。
可以使用rand函数生成符合先验分布的随机数,然后根据状态的取值范围进行线性变换得到初始粒子集合。
2. 粒子演化:根据系统的动态方程,对每个粒子的状态进行演化计算。
可以使用for循环对每个粒子进行状态更新,并添加一定的随机扰动来模拟系统的不确定性。
3. 更新权重:根据观测数据和测量模型,计算每个粒子的权重。
可以使用权重的计算公式根据观测数据和测量模型计算后验概率,并对权重进行归一化处理。
4. 重采样:根据粒子的权重,进行重采样操作。
粒子群算法详解-附matlab代码说明
位置更新公式
该算法在文献中讨论了系数 n 取各种不同情况的情况,并且运行来了 20000 次来分析各种系数的结果。
(2)粒子群算法的混合
这个分支主要是将粒子群算法与各种算法相混合,有人将它与模拟退火算法相混合,有些人将它与单纯形方法相
混合。但是最多的是将它与遗传算法的混合。根据遗传算法的三种不同算子可以生成 3 中不同的混合算法。
这两个点就是粒子群算法中的粒子。 该函数的最大值就是鸟群中的食物 计算两个点函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。 更新自己位置的一定公式就是粒子群算法中的位置速度更新公式。 下面演示一下这个算法运行一次的大概过程: 第一次初始化
第一次更新位置
第二次更新位置
第 21 次更新 最后的结果(30 次迭代) 最后所有的点都集中在最大值的地方。
粒子群算法与选择算子的结合,这里相混合的思想是:在原来的粒子群算法中,我们选择粒子群群体的最优值
作为 pg,但是相结合的版本是根据所有粒子的适应度的大小给每个粒子赋予一个被选中的概率,然后依据概率对这些 粒子进行选择,被选中的粒子作为 pg,其它的情况都不变。这样的算法可以在算法运行过程中保持粒子群的多样性, 但是致命的缺点是收敛速度缓慢。
上面罗嗦了半天,那些都是科研工作者写论文的语气,不过,PSO 的历史就像上面说的那样。下面通俗的解释 PSO 算法。
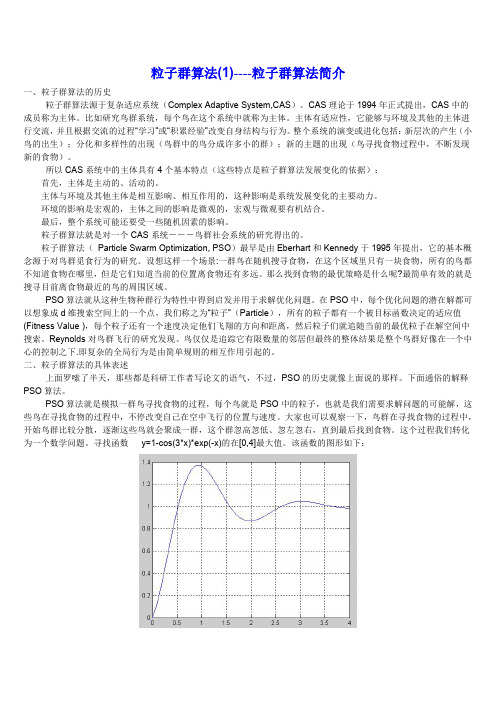
PSO 算法就是模拟一群鸟寻找食物的过程,每个鸟就是 PSO 中的粒子,也就是我们需要求解问题的可能解,这 些鸟在寻找食物的过程中,不停改变自己在空中飞行的位置与速度。大家也可以观察一下,鸟群在寻找食物的过程中, 开始鸟群比较分散,逐渐这些鸟就会聚成一群,这个群忽高忽低、忽左忽右,直到最后找到食物。这个过程我们转化 为一个数学问题。寻找函数 y=1-cos(3*x)*exp(-x)的在[0,4]最大值。该函数的图形如下:
基于粒子滤波的导航与定位研究

基于粒子滤波的导航与定位研究目录:一、引言二、粒子滤波算法介绍三、基于粒子滤波的导航与定位四、实验结果与分析五、结论和展望一、引言粒子滤波是一种基于蒙特卡罗方法的非线性滤波算法,适用于处理非高斯状态不定的问题。
在实际应用中,粒子滤波被广泛应用于导航与定位,机器人控制,雷达跟踪等领域。
本文将围绕基于粒子滤波的导航与定位展开研究,介绍粒子滤波算法原理、基于粒子滤波的导航定位模型、实验结果及结论等内容。
二、粒子滤波算法介绍1. 粒子滤波算法原理粒子滤波(Particle Filter)即蒙特卡罗滤波(Monte Carlo Filter),它是利用粒子(Particle)来描述非高斯分布的一种滤波方式。
粒子滤波的思想是通过在状态空间中对目标进行随机取样,并通过计算每个取样点的权重来精确描述目标的分布状态。
其基本原理如下:1) 粒子集合:将状态分布映射到粒子集合中,即通过抽样的方式在状态空间中生成一系列随机样本(粒子),使用粒子集合来近似真实状态概率分布;2) 状态转移:对粒子进行状态转移,即在当前时刻通过状态转移模型计算下一时刻的状态;3) 观测模型:计算每个粒子与观测结果的匹配度,即通过观测模型计算每个粒子对应的权重;4) 重新采样:对高权重的粒子进行保留,对低权重的粒子进行替换,采用重采样技术保留高权重粒子,使其在下一时刻得到更多的样本,从而提高精度。
2. 粒子滤波算法特点相对于其他滤波算法,粒子滤波的主要特点如下:1) 适用范围广:可用于处理非高斯分布状态和非线性系统中的滤波问题,适用范围广泛;2) 精度高:通过粒子集合的方法能够更准确的描述状态分布情况,从而提高滤波精度;3) 无需状态/观测模型线性化:相较于卡尔曼滤波,粒子滤波不需要对状态/观测模型进行线性化拟合,因此对于非线性问题可以更好的处理;4) 计算量大:由于需要进行随机重采样,因此对计算量的要求较高,计算量较大。
三、基于粒子滤波的导航与定位1. 导航定位模型基于粒子滤波的导航定位模型主要由状态转移模型和观测模型构成。
粒子滤波原理及应用matlab仿真

粒子滤波原理及应用matlab仿真一、引言粒子滤波(Particle Filter)是贝叶斯滤波(Bayesian Filter)的一种扩展,用于解决非线性和非高斯问题。
它是一种基于蒙特卡罗方法的状态估计算法,可以用于目标跟踪、机器人定位、信号处理等领域。
本文将详细介绍粒子滤波的原理及其在matlab中的应用。
二、贝叶斯滤波贝叶斯滤波是一种基于贝叶斯定理的概率推断方法,用于估计状态变量在给定观测值下的后验概率分布。
其核心思想是将先验概率分布和观测数据结合起来,得到后验概率分布。
具体地,在时间步k时刻,假设状态变量为x(k),观测变量为y(k),则根据贝叶斯定理:P(x(k)|y(1:k)) = P(y(k)|x(k)) * P(x(k)|y(1:k-1)) / P(y(k)|y(1:k-1))其中,P(x(k)|y(1:k))表示在已知前k个观测值下x(k)的后验概率分布;P(y(k)|x(k))表示在已知x(k)时y(k)的条件概率分布,也称为似然函数;P(x(k)|y(1:k-1))表示在已知前k-1个观测值下x(k)的先验概率分布;P(y(k)|y(1:k-1))表示前k-1个观测值的边缘概率分布。
三、粒子滤波基本原理粒子滤波是一种基于贝叶斯滤波的蒙特卡罗方法,它通过在状态空间中随机采样一组粒子来近似表示后验概率分布。
每个粒子都代表一个可能的状态变量,其权重反映了该状态变量与观测值之间的匹配程度。
具体地,在时间步k时刻,假设有N个粒子{ x(1), x(2), ..., x(N) },则每个粒子都有一个对应的权重w(i),且满足:∑ w(i) = 1根据贝叶斯定理可得:P(x(k)|y(1:k)) = P(y(k)|x(k)) * P(x(k)|y(1:k-1)) / P(y(k)|y(1:k-1))其中,P(y(k)|x(k))和P(x(k)|y(1:k-1))可以通过系统模型和观测模型计算得到。
粒子滤波 matlab

粒子滤波matlab摘要:1.粒子滤波的概述2.MATLAB 在粒子滤波中的应用3.粒子滤波的优缺点4.粒子滤波的实例应用正文:一、粒子滤波的概述粒子滤波(Particle Filtering)是一种基于蒙特卡洛方法(Monte Carlo Method)的贝叶斯滤波算法,主要用于非线性非高斯系统的状态估计。
粒子滤波方法通过抽取大量样本(粒子)来近似系统的后验分布,然后通过这些样本的加权平均值来估计系统的状态。
与传统的卡尔曼滤波(Kalman Filtering)相比,粒子滤波具有更好的鲁棒性和适应性,可以处理更复杂的非线性非高斯系统。
二、MATLAB 在粒子滤波中的应用MATLAB(Matrix Laboratory)是一款强大的数学软件,可以方便地实现粒子滤波算法。
在MATLAB 中,可以利用现有的函数库(如统计与机器学习工具箱)或自定义函数来实现粒子滤波。
以下是一个简单的MATLAB 粒子滤波示例:1.导入所需的工具箱和函数库2.初始化系统参数和状态变量3.创建一个函数来生成系统观测数据4.创建一个函数来计算观测数据的似然函数5.创建一个函数来计算系统的后验分布6.使用粒子滤波算法来估计系统状态7.输出估计结果并进行分析三、粒子滤波的优缺点粒子滤波具有以下优点:1.适应性强:粒子滤波可以处理非线性非高斯系统,而卡尔曼滤波只能处理线性高斯系统。
2.鲁棒性好:粒子滤波对系统的初始条件和观测数据的噪声具有较好的容差性。
3.计算复杂度较低:粒子滤波的计算复杂度主要与粒子数量有关,相对于卡尔曼滤波,其计算复杂度较低。
粒子滤波也存在以下缺点:1.粒子数量的选择:粒子数量的选择会影响滤波器的性能,不同的粒子数量可能导致不同的估计结果。
2.计算效率:相比于卡尔曼滤波,粒子滤波的计算效率较低,特别是在处理大规模问题时。
四、粒子滤波的实例应用粒子滤波在许多领域都有广泛的应用,如导航定位、信号处理、机器人控制等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X l sin 2
2、蒙特卡洛
❖ %%%%%%%%%%%%%%%%%%%%%%%%%
❖ % 说明:利用蒙特卡洛模拟计算圆周率
❖ Length=100; % 目标运动的场地空间
❖ Width=100; ❖ % 观测站的位置随即部署
❖ Node.x=Width*rand;
❖ Node.y=Length*rand;
Y/ m
error/m
80
60
40
观测站位置
目标真实轨迹
PF算 法 轨 迹
20
0
20
40
60
80
100 120
X/m
5、粒子滤波在多目标跟踪中的应用
❖ 近邻法分类程序
❖ %%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%
❖ % 函数功能:近邻法分类程序
❖ %%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%
❖ function Neighbour_Classify_exam2
RMSE,q=0.0001 2.5
RMS跟 踪 误 差
2
1.5
1
0.5
0
0
5
10
15
20
25
30
time/s
5、粒子滤波在多目标跟踪中的应用
❖ 多目标跟踪系统
❖ 状态方程 ❖ 观测方程
250
200
150
100
50
0
-50
-50
0
50
100
150
200
250
5、粒子滤波在多目标跟踪中的应用
❖ 近邻法分类
❖ % 状态方程 X(k+1)=F*X(k)+Lw(k) ❖ % 观测方程 Z(k)=h(X)+v(k)
❖ function main
❖ %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%
❖ % 初始化参数
❖ clear; ❖ T=1; % 采样周期 ❖ M=30; % 采样点数 ❖ delta_w=1e-4; % 过程噪声调整参数,设得越大,目标运行的机
❖ %llength 是针的长度
❖ %mm 是随机实验次数
❖ frq=0;
❖ xrandnum = unifrnd(0,0.5,1,mm);
❖ phi= unifrnd(0,pi,1,mm);
❖ for ii=1:mm
❖
if (xrandnum(1,ii)<=(llength*sin(phi(1,ii))/2))
4、粒子滤波在单目标跟踪中的应用
❖ 状态方程:
❖ 观测方程: ❖ 噪声模型:Q、R
4、纯方位角单目标跟踪
❖ 纯方位跟踪系统仿真程序
❖ %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%
❖ % 程序说明: 单站单目标基于角度的跟踪系统,采用粒子滤波 算法
1、粒子滤波的发展历史
❖ 90年代初,Gordon、Salmond、和Smith所提出的重采样 (Resampling)技术 。
❖ 90年中期,计算机的计算能力的提高
❖ 近年来的新技术,EPF、UPF、RBPF等
❖ 新的应用领域:目标定位和跟踪、图像处理、语音处理、 故障检测、经济数据处理
2、蒙特卡洛原理
❖ %%%%%%%%%%%%%%%%%%%%%%%%%
❖ function buffon_test
❖ l=0.6;
❖ m=10000; % 实验次数
❖ buffon(l,m);
❖ %%%%%%%%%%%%%%%%%%%%%%%%%
❖ function piguji=buffon(llength,mm)
❖
frq=frq+1;
❖
end
❖ end
❖ piguji=2*llength/(frq/mm)
❖ 实验结果如下:
3、粒子滤波原理
❖ 粒子滤波目前有四大基本 的重采样方法,分别是残 差重采样(Residual resampling),多项式重 采样(Multinomial resampling),系统重采 样(Systematic resampling),随机重采 样(random resampling),关于他们 的原理,读者可以到网上 检索相关的论文。
0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1
0Leabharlann 200400600
800
1000
a=0;
2、蒙特卡洛原理
v 蒙特卡洛的应用
应用说明:利用蒙特卡洛模拟 计算圆周率 方法解决:
从而针线相交的概率为:
p
ˆ
P
X
l 2
sin
0
l sin
2
0
2 dxdw
2l
假设平面上有无数条距离为1的等距平行线, 现向该平面随机投掷一根长度为l的针(l1), 则我们可计算该针与任一平行线相交的概率。
3、粒子滤波原理
❖ 随机重采样
执行仿真程序,得到以下仿真 结果,图中上部就是程序中给 定的W随机样本,而下部分是 由随机采样得到的V样本集合。 从连线关系可以看出,W样本 集中的第2个样本被复制一次, 第3个样本被复制2次,第7个 样本被复制2次,第8个样本被 复制1次,第9个样本被复制2 次,……,W中除了被复制的 样本外,其他样本被舍弃,这 就是“优胜劣汰”的思想。
❖ 粒子滤波技术是以蒙特卡洛为基础的
❖ 蒙特卡洛:用实验模拟的方法解决复杂的积分计算问题
❖ 硬币投掷实验(1)
✓ 掷一枚均匀硬币,正面朝上的次数X服从参数为1,p的二项分 布,X~B(1,p)
✓ 在Matlab中编辑.m文件输入以下命令:
1
0.9
function cion_throw_test1 p=0.3; % 正面朝上的概率 m=1000; % 实验次数 fun(p,m); % 修改不同的p,m值 function fun(p,mm) pro=zeros(1,mm); randnum = binornd(1,p,1,mm); % 服从二项分布
动性越大,轨迹越随机(乱)
❖ Q=delta_w*diag([0.5,1,0.5,1]) ; % 过程噪声均方差
❖ R=pi/180*0.1; 小
% 观测角度均方差,可将0.1设置的更
❖ F=[1,T,0,0;0,1,0,0;0,0,1,T;0,0,0,1];
❖ %%%%%%%%%%%%%%% 系统初始化 %%%%%%%%%%%%%%%%%%
