基于自抗扰控制器的永磁同步电机矢量控制仿真
基于自抗扰控制技术的永磁同步电机矢量控制策略

第5期2011年9月电源学报Journal of Power SupplyNo.5Sep.2011基于自抗扰控制技术的永磁同步电机矢量控制策略顾问,王久和,徐升升,慕小斌(北京信息科技大学自动化学院,北京市100192)摘要:论文研究了一种基于自抗扰控制(Active Disturbance Rejection control,ADRC )技术的永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)矢量控制策略。
即根据矢量控制方法,分别为永磁同步电机的转速环、电流环设计了自抗扰控制器。
同时,考虑到设计的简化性的实时性,对自抗扰控制器的典型结构做了一定的简化,并将得到的简化型自抗扰控制器应用于永磁同步电机矢量控制系统中,以改善永磁同步电机的调速性能。
计算机仿真结果表明:上述控制策略是可行的。
关键词:永磁同步电机;自抗扰控制;矢量控制方法;调速中图分类号:TM 351文献标志码:A文章编号:CN12-1420(2011)05-0065-05收稿日期:2011-05-26基金项目:国家自然科学基金项目(51077005);北京市人才强教深化计划“学术创新团队计划”项目(PHR201007130)作者简介:顾问(1986-),女,硕士研究生,研究方向为永磁同步电机的非线性控制策略研究。
王久和(1959-),男,博士,教授,研究方向为电力电子与电力传动,非线性控制理论与应用。
徐升升(1986-),女,硕士研究生,研究方向为三电平电压型PWM 整流器非线性控制策略研究。
慕小斌(1986-),男,硕士研究生,研究方向为光伏逆变器非线性控制策略研究。
1引言永磁同步电机由于谐波少、转矩的精度高,常用于伺服系统和高性能的调速系统[1],它是典型的非线性多变量强耦合系统,线性控制难以满足其高性能的要求。
为了提高PMSM 的控制性能,国内外学者提出了很多非线性控制策略,如反馈线性化控制[2]、自适应控制[3]、神经网络控制[4]、无源控制[5]等。
基于自抗扰控制器的永磁同步电机矢量控制仿真

基于自抗扰控制技术的永磁同步电机矢量控制仿真摘要:文章针对经典的PID控制器应用于永磁同步电机矢量控制的缺点。
依据永磁同步在两相同步旋转坐标系下的数学模型,设计了转速控制环的ADRC控制器,结合按转子磁场定向的矢量控制在simulink 中建立了永磁同步电机调速系统仿真模型,对一台隐极式永磁同步电机进行仿真。
仿真发现,发现ADRC作为速度环的控制器能够避免使用PI控制器时出现超调的问题,而且在转矩突变干扰下转速能迅速回到原稳定平衡点。
仿真说明使用ADRC控制器代替PI控制器控制永磁同步电机使得系统具有更好的抵抗负载转矩扰动的能力。
关键词:矢量控制;ADRC;抵抗转矩扰动0引言交流永磁伺服电机驱动控制策略研究现状电机控制技术是高性能交流永磁伺服电机驱动器的核心,PMSM作为一个典型的非线性复杂控制对象,具有多变量、强耦合、非线性、变参数等特性,在目前来看,常规的电机调速控制方法主要有矢量控制和直接转矩控制策略。
矢量控制(Vector Control,VC)也称为磁场定向控制(Held Oriented Control,FOC),其基本思路是:通过坐标变换实现模拟直流电机的控制方法来对永磁同步电机进行控制,实现了电机定子电流转矩分量与励磁分量的解耦。
VC的目的是为了改善转矩控制性能,从而使驱动系统具有转矩平滑、调速范围宽等特点,是高性能交流伺服驱动系统的主要控制方式。
和VC不同,直接转矩控(Direct Torque Control,DTC)制摒弃了解耦的思想,取消了旋转坐标变换,简单的通过电机定子电压和电流,借助瞬时空间矢量理论计算电机的磁链和转矩,并根据与给定值比较所得差值,实现磁链和转矩的直接控制。
直接转矩控制可以获得比VC更快的动态响应,在对于动态响应要求高的场合具有独特的优势。
但DTC要保证实际力矩与给定一致就需根据误差选择驱动器件的开关状态,同时保证电机磁链能够按预定轨迹运行,在转矩和磁链的滞环比较器进行控制时会产生转矩脉动,这样将大大的影响电机的低速性能和系统的稳定性,使得电机的宽调速范围受到严重影响,同时导致位置控制精度降低。
基于自抗扰控制器的交流直线永磁同步伺服电机速度控制系统_刘德君

基于自抗扰控制器的交流直线永磁同步伺服电机速度控制系统*刘德君1,2 郭庆鼎1 翁秀华11.沈阳工业大学 2.北华大学 摘要:根据三相交流直线永磁同步伺服电机的非线性动态模型,采用自抗扰控制器的方法,对系统的内部扰动和外部扰动进行观测,并加以补偿。
仿真结果表明,采用自抗扰控制器具有较好的动态性能以及对负载扰动、电动机参数变化都具有较好的鲁棒性。
关键词:交流直线永磁同步伺服电机 自抗扰控制器 扩张状态观测器Speed Control System of AC Linear Permanent Magnet SynchronousServo Motor Based on Auto -disturbance Rejection ControllerLiu Dejun Guo Qing ding Weng XiuhuaAbstract :Accordin g to the nonlinear dynamic math ematical model of the th ree -phase AC linear perman ent magnet synchronous s ervo motor(AC-LPM SM ),the inn er disturbance and outside dis tu rban ce can be ob served w ith the auto-dis tu rban ce rejection controller(ADRC),and us e it to offs et the sys tem.T he res ults of s imulation tes t indicate that the ADRC h as good dynamic perfor mance and th e strong robus tnes s to both load disturbance an d the p arametric variation of m otor. Keywords :AC linear perm anent magnet s yn chronou s servo motor (AC -LPM S M ) auto -dis tu rban ce r ejec-tion con tr oller(ADRC) extended s tate ober cer (ESO) * 国家自然科学基金资助项目(50075057)1 引言在高性能的位置、速度系统,目前主要依据精确的数学模型加上其它一些控制方法,它们在实际应用中有较好的应用。
基于PSIM永磁同步电机矢量控制系统的仿真建模

U q 子模块的底层结构如图 6 所示。 的底层结构如图 5 所示,
将式(2)和式(3)代入式(1),得到电压方程为
0 ua r 0 0 ia L − M u = 0 r 0 ⋅ i + 0 L−M b b uc 0 0 r ic 0 0 i a ea p i + e b b ic ec L − M 0 0
ω m_ ref 速度控 I q_ref + 制器 -I d_ ref q 相电流控制器 d 相电流控制器 - Uq dq 2abc Ud Ua Ub Uc SPWM SPWM SPWM Ia Ib Ic 实际转速w m 逆变 器 PMSM
wm
+
Id abc 2dq Iq
图1
PMSM 控制系统仿真建模组成框图
Abstract: In this paper, based on the mathematical model of the permanent-magnet synchronous–motor (PMSM), a PMSM vector control system model has been established in PSIM6.0.In PSIM/SIMCAD, the isolated functional blocks, such as Vector controller block, Phase voltage block, Coordinate transform block, SPWM block, Speed controller block, etc., have been modeled. By the organic combination of these blocks, the control system model of PMSM can be established easily. In the double loop of control system, a PI controller is adopted in the speed loop and a vector controller is adopted in the current loop. The validity has been testified by the simulation results and other control strategies can be applied to the system to testify their rationality. This novel method offers a new thoughtway for designing and debugging actual motors. Keywords: permanent-magnet synchronous-motor (PMSM); PSIM; modeling and simulation; vector control
基于改进自抗扰和遗传算法的永磁同步电机速度控制

基于改进自抗扰和遗传算法的永磁同步电机速度控制摘要永磁同步电机(PMSM)具有高效、速度响应快和扭矩密度大等优点,已广泛应用于各种工业领域。
然而,在实际应用中,PMSM常常受到干扰和非线性因素的影响,导致其速度控制性能下降。
因此,本文提出了一种基于改进自抗扰(PID)控制器和遗传算法优化的PMSM 速度控制方法。
首先,根据PMSM的数学模型,设计了改进PID控制器,该控制器能够有效地抵抗干扰和非线性因素的影响。
接着,使用遗传算法对PID参数进行优化,以进一步提高控制精度和稳定性。
最后,通过对Simulink仿真模型的测试和分析,证明了本文方法的有效性和优越性。
AbstractPermanent magnet synchronous motor (PMSM) has the advantages of high efficiency, fast speed response and high torque density, and has been widely used in various industrial fields. However, in practical applications, PMSM is often affected by interference and non-linear factors, which can lead to a decline in its speed control performance. Therefore, this paper proposes a speed control method for PMSM based on an improved self-adaptive (PID) controller and genetic algorithm optimization. Firstly, according to the mathematical model of PMSM, an improved PID controller is designed, which can effectively resist the influence of disturbance andnon-linear factors. Then, genetic algorithm is used to optimize the PID parameters to further improve the control accuracy and stability. Finally, the effectiveness and superiority of this proposed method are proved by testing and analysis of Simulink simulation model.Keywords: Permanent magnet synchronous motor; Improved PID controller; Genetic algorithm; Speed control1. 引言永磁同步电机(PMSM)是一种高效、速度响应快和扭矩密度大的电机,已广泛应用于各种工业领域,如机器人、风力发电和电动汽车等。
永磁同步电机矢量控制系统仿真研究

永磁同步电机矢量控制系统仿真研究摘要:随着电力电子、电机制造技术以及新型材料的飞速发展,交流调速理论以及新型控制理论研究的不断深入,永磁交流调速系统在机电一体化、机器人、柔性制造系统等高科技领域中占据了日益重要的地位。
永磁同步电动机具有能量转换效率高、体积小,运行可靠性高、调速范围广,动、静特性好等优点,这使得永磁同步电动机技术得到了迅速发展。
PWM控制技术从最早追求电压波形正弦,到电流波形正弦,再到磁通正弦,得到了不断创新和完善。
本文是在此基础上,参照了众多学者的研究,对永磁同步电机进行了矢量控制的研究,并通过建立仿真模型,对矢量控制下永磁同步电机进行仿真,并对结果进行分析。
关键词:永磁交流调速,PWM控制技术,永磁同步电动机1 PMSM数学模型介绍精确的电机数学模型是电机控制理论得以研究与实现的基础,因此首先给出三相永磁同步电动机数学模型。
推导前作如下假设:1)定子三相绕组对称,Y型连接;2)反电动势正弦;3)铁磁部分磁路线性,即不计饱和、剩磁、涡流、磁滞损耗等影响;4)转子无阻尼绕组,永磁体没有阻尼作用;PMSM在a-b-c坐标系统中电压方程用矩阵形式表示为:(1)其中定子电枢相电阻;、、定子绕组端电压瞬时值;、、定子绕组相电流瞬时值;、、磁链瞬时值;微分算子,。
PMSM定子绕组电感系数是转子位置角的函数,其电压方程、磁链方程都是含有时变系数的微分方程组,在分析PMSM工作过程时用解析法求解时变系数方程组是比较困难的,需要采取数值法求解,不便于工业控制应用。
因此采用park变换矩阵,将PMSM数学模型变换到固定在其转子上的两相旋转坐标系d-q坐标系中,将上述含时变系数的微分方程组变换为易于求解的常系数微分方程组,这对于分析PMSM动态过程和稳态过程都是十分有意义的。
从而得到建立在dq旋转坐标中和三相静止坐标中电机模型之间具有如下关系:(2)(3)PMSM中定子绕组一般为无中线的Y型连接,固。
永磁同步电机矢量控制系统仿真的设计

永磁同步电机矢量控制系统仿真的设计作者:李帅男来源:《数字技术与应用》2018年第10期摘要:本文以下的仿真工作都是直接选取SIMULINK内部提供的PMSM模型,整个矢量控制调速系统需要的模块还有:PARK、CLARK变换与逆变换模块;三相变流器模块;SVPWM 调制模块;控制器模块。
三相变流器直接选取SIMULINK内部提供的模型,SVPWM调制与坐标变换用分立模块搭建;控制器用S函数编写。
关键词:永磁同步电机;SVPWM;模型中图分类号:TP23; ; 文献标识码:A ; ; ;文章编号:1007-9416(2018)10-0000-001 绪论永磁同步电机是一种优良的控制元件。
由于当今电力电子技术,微机控制技术,控制理论的不断发展。
永磁同步电机控制系统展现出越来越卓越的性能以及十足的潜能,被广泛应用于工业控制中。
因此对于其仿真技术的研究也显得格外重要,对其广泛应用起着至关重要的作用[1]。
2 系统仿真模型的搭建2.1 坐标变换模块矢量控制系统中常用的有CLARK、PARK变换与逆变换。
它们是几个数学表达式,直接用Bus Creator模块与Fcn模块搭建即可,在Fcn模块中输入正确的数学表达式[2]。
2.2 SVPWM调制模块SVPWM模块要达到的要求是根据给定的电压矢量信号,用逆变器能够输出的6个基本电压空间矢量以及零矢量作用不同的时间来等效当前交流电机所需要的电压矢量[3]。
(1)扇区判断模块,由于,可以依照的值分析需要合成的Uref处在具体的哪一扇区。
现定义变量ABC:如果名口,则A=1,否则A=0。
如果,则B=1,否则B=0。
如果,则C=1,否则C=0。
N=A+2B+4C,可以根据N的值得到扇区号,扇区号在确定基本电压矢量与电压矢量时间分配时都能用到。
搭建的模块如图1。
(2)为了求出基本电压矢量的作用时间T1与T2。
在仿真与实际编程时,可以先求出三个作用时间量X、Y、Z,最后根据扇区号确定具体的电压矢量作用时间,搭建的模块如图2。
基于自抗扰控制永磁同步电机伺服系统研究

皴 粕
MI CR OM O T O RS
Vo 1 . 4 6 .No .1 2
De c . 2 01 3
基 于 自抗 扰 控 制 永 磁 同步 电机 伺 服 系 统 研 究
陈茂 胜
( 中国科学 院 长 春光学精密机械与物理研究 所 小卫星技 术国家地方联合工程研究 中心 ,长春 1 3 0 0 3 3 ) 摘 要 :为抑制干扰力矩对永磁 同步 电机 ( P MS M) 伺 服系统性 能 的影 响 ,提 出采用 自抗 扰控制 器 ( A D R C) 以提 高伺
t h e s p e e d l o o p r e s p e c t i v e l y we r e d o n e. Fi na l l y,t h e h a r d wa r e e x p e ime r n t o f ADRC wa s c a r ie r d o u t .S i mu l a —
服系统的性能 。首先 ,采用 i = 0的矢 量控制策略建立 了永 磁 同步 电机伺服 系统模 型 ;然后 ,分 析干扰 力矩对伺 服
系统性能的影响 ,并在 M a t l a b中仿真分析速度环分别采用 P I 、A D R C控制器伺服系统 的性能 ;最后 , 对P M S M伺 服
系统的速度采用 A D R C控制算法进行实验验证 。实验结果表 明 :采用 A D R C算法能够有效抑 制系统 中干扰力矩 的影
Ab s t r a c t :To i n h i b i t t h e i n l f ue n c e o f d i s t u r b i n g t o r q u e o n t h e P e r ma n e n t Ma g n e t S y n c h r o n o us Mo t o r
基于自抗扰控制器的永磁同步电机矢量控制
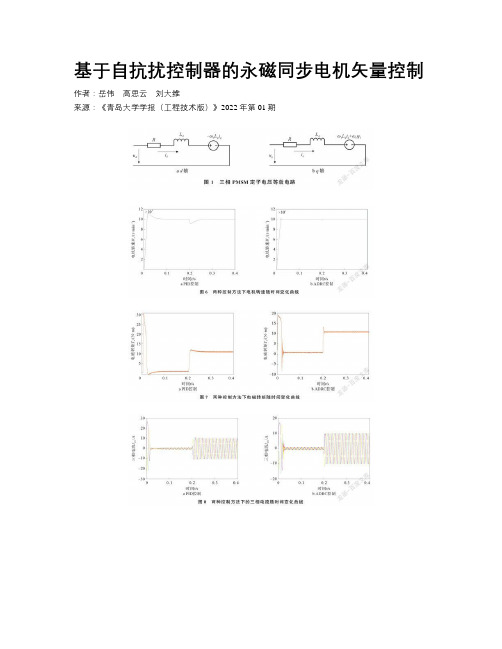
基于自抗扰控制器的永磁同步电机矢量控制作者:岳伟高思云刘大维来源:《青岛大学学报(工程技术版)》2022年第01期文章編号: 10069798(2022)01009706; DOI: 10.13306/j.10069798.2022.01.015摘要:针对传统的三相永磁同步电机存在的矢量控制方式启动电流和超调量过大及抗干扰性不强等问题,本文设计了一种基于自抗扰控制器的三相永磁同步电机矢量控制系统。
在传统双闭环PI控制系统结构的基础上,在Matlab/Simulink软件中,分别采用PI控制器和自抗扰控制器搭建转速环三相永磁同步电机矢量控制系统模型,为了对比控制效果,将两种控制器置于相同电机参数和相同仿真条件下,通过仿真得到两种控制方法下的电机转速、电磁转矩和电流响应。
仿真结果表明,基于自抗扰控制器的三相永磁同步电机矢量控制系统,控制性能更优,具有更小的超调量、更好的动态性和更强的鲁棒性。
该研究为永磁同步电机的矢量控制提供了理论参考。
关键词:永磁同步电机; 矢量控制; PI控制;自抗扰控制器; Simulink仿真中图分类号: TM351文献标识码: A近年来,永磁同步电机(permanent magnet synchronous machine,PMSM)由于体积小、低损耗、响应速度快、能量密度高等性能优势,广泛应用于电动车、冰箱、空调压缩机以及其它高精尖产业[1]。
PMSM是非线性控制系统,其参数多具时变性,多变量之间耦合性强[27]。
为了实现对PMSM的控制,需要采用磁场定向的矢量控制方法对PMSM进行解耦。
在工业应用中,PMSM矢量控制的转速环和电流环广泛采用PI控制器。
传统PI控制器模型简单,可靠性高,鲁棒性好,能抵抗一定程度上的微量扰动,但其参数固定不变,因此基于PI控制器对环境变化的自适应性能较差,且控制参数往往整定不良,难以对突加扰动迅速做出动态响应,对微小的超调具有更强的抗干扰性 [8]。
基于自抗扰控制器的PMSM矢量控制系统设计与实现

觶 1 = V2 V 觶 2 = fh V 觶 1 = Z2 - β1 ( Z1 - Y )+ b0U Z
(9)
(2) 扩 张 状 态 观 测 器 (10) 觶 2 =- β2 fal ( Z1 - Y , α1 , δ ) Z (3) 非 线 性 误 差 反 馈 U0 = β3 fal ( V1 - Z1 , α2 , δ ) (11) (4) 扰 动 补 偿 过 程 U = U0 - Z2 (12) b0 式 (9) ~ 式 (12) 中 V1 是 电 流 给 定 的 跟 踪 值 , Z1 是 电 流 观 测 的 跟 踪 值 。 使 用 ESO 实 时 观 测 出 系 统 “ 内 外 扰 动 ”
* 基 金 项 目 : 国 家 自 然 科 学 基 金 项 目 ( 50975193 ) ; 国 家 科 技 重 大 专 项 ( 2009ZX04014 - 101 - 05 ) ; 天 津 市 科 技 计 划 项 目 ( 08ZCKFGX02300 )
1 ADRC 数 学 模 型
自抗扰控制器是一种基于误差反馈的新型控制器, 主 要 由 非 线 性 跟 踪 微 分 器 (NTD) 、 扩 张 状 态 观 测 器 (ESO) 、
测控技术与仪器仪表
Measurement Control Technology and Instruments
基于自抗扰控制器的 PMSM 矢量控制 系统设计与实现 *
刘 清, 王太勇, 董靖川, 刘清建, 李 勃 ( 天 津 大 学 机 械 学 院 , 天 津 300072 )
摘 要: 针 对永磁 同步电 机存在 的非 线性、强 耦合、参 数 摄 动 等 问 题 ,设 计 并 实 现 了 基 于 自 抗 扰 控 制 器 (ADRC) 的 矢 量 控 制 系 统 。 首 先 提 出 基 于 ADRC 的 控 制 策 略 , 实 时 观 测 出 由 系 统 内 部 非 线 性 因 素 以 及 外 部 扰 动 引 起 的 “ 内 外 扰 动 ” 并 进 行 补 偿 , 从 而 实 现 精 确 控 制 ; 其 次 研 制 基 于 DSP 的 多 轴 运 动 控 制 卡 , 并 在 此 基 础 上 实 现 了 基 于 ADRC 的 PMSM 矢 量 控 制 系 统 。 仿 真 及 实 验 结 果 表 明 , 系 统 具 有 良 好 的动态 性能及 鲁棒性 ,能够快 速加 工出符 合要求 的模型 。 关键词 :永磁同 步电机 ;矢量控 制;自 抗扰控 制器;非 线性;
基于自抗扰控制的永磁同步电机调速系统的研究

基于自抗扰控制的永磁同步电机调速系统的研究郑陆洋;傅惠南;余雷;李增【摘要】永磁同步电机(Permanent Magnetic Synchronous Motor,PMSM)因结构简单、尺寸灵活多样、效率高、可靠性强、易于控制等优点,已在航空航天、武器随动系统、船舶动力定位等领域广泛应用.自抗扰控制作为一种新型的非线性控制技术,可以有效克服PID控制在复杂、高效控制领域的缺点.设计一种自抗扰控制器取代速度、电流环的PI控制器,在MATLAB/Simulink中搭建系统模型.仿真结果表明,运用自抗扰控制可以有效解决超调与抗扰问题,提高控制性能.【期刊名称】《科技视界》【年(卷),期】2019(000)009【总页数】3页(P9-11)【关键词】永磁同步电机;PI控制器;自抗扰控制器;双闭环控制【作者】郑陆洋;傅惠南;余雷;李增【作者单位】广东工业大学机电工程学院,广东广州 510006;广东工业大学机电工程学院,广东广州 510006;广东工业大学机电工程学院,广东广州 510006;广东工业大学机电工程学院,广东广州 510006【正文语种】中文【中图分类】TM3410 引言永磁同步电机因结构简单、运行可靠、效率高、体积小等特点,在国防军工、工业伺服、电动汽车等诸多领域得到广泛应用。
但永磁同步电机是一个强耦合、参数时变、复杂的非线性系统[1],且在运行过程中易受环境、外部负载干扰和其他未知因素的影响,因此传统的PID 控制策略存在着不足和缺点。
自抗扰控制技术是中科院研究员韩京清提出的一种非线性控制理论,是在PID 控制基础上,引入了“安排过渡过程”和同时合理“提取微分信号”的方法,并加入扩张状态观测器对系统的未知模型和外部扰动总和作用量进行实时估计与补偿,来改善控制器的性能,在电机控制领域应用前景比较宽广[2]。
永磁同步电机的调速控制系统一般采用速度环、电流环闭环的串联结构。
电流环作为控制系统内环,其作用是对定子电流的准确与快速跟踪,其控制效果好坏直接决定速度环的控制性能,对整个控制系统而言作用重大;转速环作为控制系统的外环,其主要作用是对速度指令进行跟踪,并输出电流作为电流环的输入,它能够保证系统的抗干扰能力和快速响应性。
基于自抗扰控制器的永磁同步电机位置伺服系统

基于自抗扰控制器的永磁同步电机位置伺服系统一、本文概述随着工业自动化的快速发展,永磁同步电机(PMSM)作为高性能伺服系统的核心部件,在精密制造、航空航天、机器人等领域得到了广泛应用。
然而,PMSM的位置伺服控制面临诸多挑战,如参数不确定性、外部干扰以及系统内部非线性等,这些问题往往导致控制精度和动态性能不足。
为此,本文提出了一种基于自抗扰控制器(ADRC)的永磁同步电机位置伺服系统,旨在通过先进的控制策略提高系统的鲁棒性和精度。
自抗扰控制器是一种源自中国的先进控制技术,它通过扩张状态观测器(ESO)估计并补偿系统总扰动,实现了对不确定性和干扰的有效抑制。
本文首先介绍了PMSM的数学模型和传统控制方法存在的问题,然后详细阐述了自抗扰控制器的设计原理及其在PMSM位置伺服系统中的应用。
通过仿真和实验验证,本文展示了自抗扰控制器在提高系统稳定性、动态响应和定位精度方面的优越性能。
本文的主要内容包括:PMSM的数学模型分析、自抗扰控制器的设计原理、PMSM位置伺服系统的实现方法、仿真和实验结果分析以及结论与展望。
通过本文的研究,旨在为PMSM位置伺服系统的控制策略设计提供新的思路和方法,推动高性能伺服系统在实际应用中的进一步发展。
二、永磁同步电机及位置伺服系统基础永磁同步电机(PMSM)是一种利用永磁体产生磁场的同步电机,具有高效率、高功率密度和良好调速性能等优点,因此在位置伺服系统中得到广泛应用。
PMSM的位置伺服系统是一种典型的闭环控制系统,其目的是通过精确控制电机的转速和转角,实现对目标位置的快速、准确跟踪。
在PMSM位置伺服系统中,电机转子的位置信息通过位置传感器(如编码器)进行实时检测,并与目标位置进行比较,形成位置误差信号。
该误差信号经过控制器处理后,生成相应的控制信号,驱动电机进行运动,以减小位置误差。
因此,控制器的性能对位置伺服系统的精度和动态性能具有重要影响。
自抗扰控制器(ADRC)是一种新型的非线性控制方法,具有强鲁棒性和良好的跟踪性能。
基于自抗扰控制技术的永磁同步电机矢量控制策略

电
源
学
报
No5 .
2 1 午 9月 01
J u n lofPo r S pp y o r a we u l
S p2 e .01 1
基 于 自抗 扰控制技 术 的永 磁 同步 电机矢 量控制 策略
顾 问 , 久和 大学 自动 化 学 院 , 京 市 1 0 9 ) 北 北 0 12
收稿 日期 :0 1 0 - 6 2 1—52 基金 项 目 : 家 自然 科 学 基 金 项 目( 17 0 5 ; 京 市 人 才 强 教 深 化 国 5 0 7 0 )北 计 划 “ 术 创 新 团 队 计 划 ” 目 ( H 2 10 10 学 项 P R 0 073 ) 作 者 简 介 : 问 (9 6 )女 , 士 研 究 生 , 究 方 向 为 永 磁 同 步 电 顾 18一, 硕 研 机 的非 线性 控 制 策 略 研 究 。
基 于磁 场 定 向 理论 ,忽 略 P M 的磁 滞 损 耗 , MS
予 补偿 , 的结 构 简单 且参 数 适应 性 广 。但 是 , 实 它 在
际应用 中 , 自抗 扰控 制 器 参数 较 多 , 不易 调 整 。同时 计 算量 大 , 导致 控 制 周 期 变 长 , 时 性 差 , 响 了 电 实 影 动 机 的控 制 性 能 : 这是 A R D C的 缺点 和不 足 。针 对
非线性控制策略研究 。
上 的分量 ; , 定子 绕 组 由 轴 电感 , 于 隐极 永 £为 对
环 、 流 环 设 计 了 自抗 扰 控 制 器 。 同时 , 虑 到 设 计 的 简 化 性 的 实 时 性 , 自抗 扰 控 制 器 的典 型 结 构 做 了一 定 的 简 电 考 对 化, 并将 得 到 的 简 化 型 自抗 扰 控 制 器应 用 于 永磁 同步 电机 矢量 控 制 系统 中 , 改 善 永 磁 同 步 电机 的 调 速 性 能 。 计 算 以
永磁同步电机矢量控制MATLAB仿真
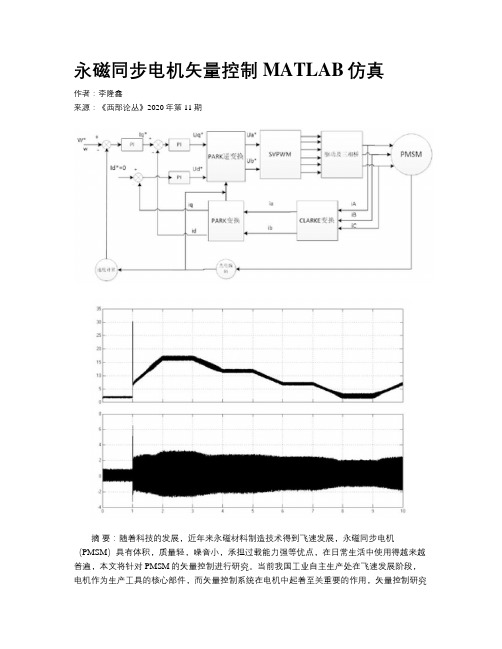
永磁同步电机矢量控制MATLAB仿真作者:李隆鑫来源:《西部论丛》2020年第11期摘要:随着科技的发展,近年来永磁材料制造技术得到飞速发展,永磁同步电机(PMSM)具有体积,质量轻,噪音小,承担过载能力强等优点,在日常生活中使用得越来越普遍,本文将针对PMSM的矢量控制进行研究。
当前我国工业自主生产处在飞速发展阶段,电机作为生产工具的核心部件,而矢量控制系统在电机中起着至关重要的作用,矢量控制研究技术含量高,在实际环境中不易操作,本文通过使用MATLAB/Simulink仿真技术搭建控制系统,研究矢量控制原理特性,针对所选空间矢量控制方法进行仿真模拟,对仿真结果进行研究分析。
关键词:永磁同步电机; Matlab; Simulink; 空间矢量控制; 仿真1永磁同步电机的发展人类历史上第一台电机就是永磁电机,但由于开采能力低下,磁体制作材料使用的是天然磁铁矿石,导致其初来乍到,问题繁多,性能并没有达到预期效果,迅速被电励磁电机取代[1]。
21世纪,随着人类生产与生活水平不断提高,对永磁同步电机的要求也越来越高,为达到这些要求,国内外自动控制技术也相应进行了飞速发展,对永磁材料的制作技术不断提升,生产出越来越高性能的永磁材料,得使永磁同步电机的生产成本随之也大大降低,适用性得到显著提高,逐渐被应用于生活的各个领域[2]。
2永磁同步电机数学模型的建立永磁同步电动机(英文名称为permanent mag⁃net synchronous motor,简称PMSM),主要由定子、转子、脉冲编码器、定子绕组、机壳等部分组成[3]。
由于本文使用电脑仿真分析,一般建立理想化数学模型,从而更加利于分析。
做出如下假设:(1)三相绕组呈Y形对称分布;(2)忽略磁路饱和,磁路涡流对电机的影响;(3)不考虑电机转动阻尼影响。
基于理想环境下,分别给出三相静止坐标系与两相旋转坐标系的数学模型。
建立了三相静止坐标系下的永磁同步电机数学模型后,要进行对电机矢量控制,还要先后经过Clarke变换(三相静止 A-B-C 坐标系变换到两相静止α-β坐标系)和Park变换(两相静止α-β坐标系变换到两相旋转d-q坐标系),得到d-q 坐标系下的电机模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于自抗扰控制技术的永磁同步电机矢量控制仿真摘要:文章针对经典的PID控制器应用于永磁同步电机矢量控制的缺点。
依据永磁同步在两相同步旋转坐标系下的数学模型,设计了转速控制环的ADRC控制器,结合按转子磁场定向的矢量控制在simulink 中建立了永磁同步电机调速系统仿真模型,对一台隐极式永磁同步电机进行仿真。
仿真发现,发现ADRC 作为速度环的控制器能够避免使用PI控制器时出现超调的问题,而且在转矩突变干扰下转速能迅速回到原稳定平衡点。
仿真说明使用ADRC控制器代替PI控制器控制永磁同步电机使得系统具有更好的抵抗负载转矩扰动的能力。
关键词:矢量控制;ADRC;抵抗转矩扰动0引言交流永磁伺服电机驱动控制策略研究现状电机控制技术是高性能交流永磁伺服电机驱动器的核心,PMSM作为一个典型的非线性复杂控制对象,具有多变量、强耦合、非线性、变参数等特性,在目前来看,常规的电机调速控制方法主要有矢量控制和直接转矩控制策略。
矢量控制(Vector Control,VC)也称为磁场定向控制(Held Oriented Control,FOC),其基本思路是:通过坐标变换实现模拟直流电机的控制方法来对永磁同步电机进行控制,实现了电机定子电流转矩分量与励磁分量的解耦。
VC的目的是为了改善转矩控制性能,从而使驱动系统具有转矩平滑、调速围宽等特点,是高性能交流伺服驱动系统的主要控制方式。
和VC不同,直接转矩控(Direct Torque Control,DTC)制摒弃了解耦的思想,取消了旋转坐标变换,简单的通过电机定子电压和电流,借助瞬时空间矢量理论计算电机的磁链和转矩,并根据与给定值比较所得差值,实现磁链和转矩的直接控制。
直接转矩控制可以获得比VC更快的动态响应,在对于动态响应要求高的场合具有独特的优势。
但DTC要保证实际力矩与给定一致就需根据误差选择驱动器件的开关状态,同时保证电机磁链能够按预定轨迹运行,在转矩和磁链的滞环比较器进行控制时会产生转矩脉动,这样将大大的影响电机的低速性能和系统的稳定性,使得电机的宽调速围受到严重影响,同时导致位置控制精度降低。
相比之下,VC的电流环能够保证力矩电流迅速跟随实际给定,保证了实际电机力矩需求,同时使得电机的电磁力矩稳定,实际的调速围更宽,甚至能超低速运行;同时电机所有的电磁转矩都由电枢电流产生,通过对位置环的实时控制,可最终使得电机电流构造的电枢磁场与直轴垂直,同时电机交轴电流与系统控制中的交轴给定量一致,能够实现更优的过载性能,使得电机的启动和制动性能更好,动态响应更快,保证了控制系统的稳定性[1]。
VC 这种常规的控制方法主要是针对集中参数的连续时间动态系统,要求控制对象可以量化,对各种量化参数之间的关系能够用微分方程来描述。
但是,常规的控制方法对具有高度非线性、不确定性因素,且具有高性能要求的复杂系统时,就难以实现满意的控制品质。
将各种控制策略应用于VC 中,可获得比标量控制要理想得多的动态控制性能,因此,高性能的伺服电机驱动系统一般都是基于VC 技术来进行分析和设计的。
经典的VC 技术一般使用PID 控制器,而PID 控制器由于积分环节的存在而容易出现超调问题,且限制了其动态响应速度,而加入微分后虽然能够使系统不出现超调,但是微分环节对外界未知干扰有放大作用,使得系统的抗干扰能力变差。
ADRC[2]。
因此,为了满足高性能交流永磁伺服系统的控制要求, 进一步提高交流永磁伺服驱动系统的动、静态性能,增强系统的鲁棒性和抗扰动能力,本文是在矢量控制策略的基础上采用先进的自抗扰控制算法,充分考虑驱动控制系统与电机性能的匹配性,进一步提高系统控制性能和控制效率。
1永磁同步电机矢量控制1.1永磁同步电机数学模型基于磁场定向理论, 忽略PMSM 的磁滞损耗,则同步旋转坐标系中PMSM 的动态数学模型[3]为: ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-+=---+=---=+-=q d q d q r p r L q d q d q f p r f r d d r p q s q q d q q r p d s d d d i i L L i n B T i i L L i n J t i L n i R u L t i i L n i R u L t i )((T ))(((1d d )(1d d )(1d d eψωψωψωωω) (1)式中d u ,q u ,d i ,q i 分别为定子相电压电流的交直轴分量;d L 为永磁磁同步电机直轴电感;q L 为交轴电感;对于面装式永磁同步电机q d L L =;s R 为定子电阻;f ψ为转子磁链;J 为转动惯量;B 为粘滞摩擦系数;r ω为转子转速;p n 为极对数;L T 为负载转矩;e T 为电磁转矩。
1.2按转子磁场定向矢量控制策略图1 按转子磁场定向的矢量控制结构框图电磁转矩的生成可看成是两个磁场相互作用的结果,可认为是由转子磁场与电枢磁场相互作用生成的。
电磁转矩可以表达为转子磁链与定子电流矢量乘积:s f i ψ⨯==p Sin i p T S f e βψ (2)转子磁链矢量f ψ的幅值不变 ,通过控制定子电流矢量的幅值及与转子磁链矢量的夹角,就可以控制电磁转矩的大小,这就是永磁同步电动机以转子磁场定向的矢量控制的原理。
在转子磁场定向的矢量控制中,将两相旋转坐标系 d 轴放置在转子磁链方向上,通过坐标变换,分别控制定子电流矢量的幅值与相位,如图2所示。
图2 按转子磁场定向矢量图1.3永磁同步电机矢量控制策略根据速度调节围和性能要求的不同,永磁同步电机矢量控制策略主要有0=d i 控制、最大电磁转矩/电流控制、弱磁控制和最大输出功率控制等几种[10]。
其中,0=d i 的矢量控制方法可简化永磁同步电机的数学模型, 使定子电流与电磁转矩输出成正比,且无弱磁电流分量,控制简单。
本文即采用0=d i 的矢量控制策略,通过控制q i 来控制e T ,从而达到控制转速的目的。
2自抗扰控制技术自抗扰控制技术是一种只需要受控对象阶次、控制量作用围、输入输出通道个数和联结方式的一种不依赖对象具体模型参数的新型实用控制技术。
其不再区分线性、非线性,时变、时不变,单变量、多变量,而“时间尺度”才是区别被控对象的新的标准,即具有相同“时间尺度”的被控对象可以利用相同的自抗扰控制器进行控制。
其最本质的控制思想就是将作用于被控对象的所有不确定因素都视为未知扰动,并利用受控对象的输入输出量对其进行估计并给予补偿。
控制器主要包括三部分:微分跟踪器(TD )、非线性PID (NLPID )、扩状态观测器(ESO )[2]。
2.1跟踪微分器跟踪微分器是为了克服经典微分器的噪声放大效应而提出的最速跟踪器。
其作用是:(1)对给定信号安排过度过程,能够无超调、快速跟踪给定信号。
利用其与反馈量的误差对系统进行控制,从而避免直接利用给定信号与反馈量的误差所带来的初始控制力过大而导致的系统超调。
(2)提供给定信号的微分量。
通过TD 获得较为准确的微分信号,使PID 真正发挥作用,而非只是传统的PI 调节。
TD 的离散表达式如下:01001110(,,,)(1)()()(1)()fh fhan v v v r h v k v k hv k v k v k hfh y v =-⎧⎪+=+⎪⎨+=+⎪⎪=⎩(3) 式中,v 是给定信号;0v ,1v 分别是v 的跟踪信号和微分跟踪信号;r 是快速因子,其值越大,0v 就能越快的跟踪给定;h 是仿真步长;y 是输出信号。
其中fhan 是最速控制综合函数,具体表达式如下:202101201022,()()/2(()())/2()(()())/2(/())()y y a a d rh a hx y x a a a a sign y a d s sign y d sign y d a a y a s a s sign a d sign a d fhan r a d sign a s rsign a ⎧==⎪=+⎪⎪=⎪⎪=+-⎪⎨=+--⎪⎪=+-+⎪⎪=+--⎪=---⎪⎩(4)2.2扩状态观测器(ESO )扩状态观测器实现根据输出反馈观测出总体扰动的功能,一阶的离散化ESO 具体形式如下:111121111222122()(1)()(()(,,))(1)()(,,)e z k y z k z k h z k fal e bu z k z k h fal e βαδβαδ=-⎧⎪+=+-+⎨⎪+=-⎩ (5) 上式中1()(,,)/e sign e e fal e e e ααδαδδδ-⎧>⎪=⎨<⎪⎩(6)2.3 非线性组合(NLSEF )非线性组合包含了误差反馈率和扰动补偿部分,实现计算得出控制量的功能,一阶形式的典型非线性组合离散化形式如下:0002(,,)()/e v y u k fal e u u z k b αδ=-⎧⎪=⨯⎨⎪=-⎩完整的一阶自抗扰控制其的结构图如下图所示:图3 一阶自抗扰控制器框图3 PMSM 的ADRC 设计在设PMSM 基于ADRC 的速度控制器时把包括电流环在的逆变器和PMSM 看作一个广义的控制对象的整体。
从式(1)的第3个表达式可以看出,永磁同步电机的转速受到交轴电流、直轴电流、负载转矩和辟擦系数的影响。
根据ADRC 的基本原理将q i 看作转速的控制量,即ADRC 的输出,将负载转矩和摩擦系数的影响看作系统的扰动,即r L B T Jt a ω--=1)(因此,式(1)的第3 式可以看作: q f p r i Jn t a t ψω+=)(d d (7) 将永磁同步电机的速度环看作一阶模型,据此设计一阶的ADRC 速度控制器。
01001110111121111222122002(*,,,)(1)()()(1)()*'()(1)()(()(,,)*)(1)()(,,)*'(,,)*()/r r r q r q fh fhan v v r h v k v k hv k v k v k hfh v e z k z k z k h z k fal e bi z k z k h fal e e y u k fal e i u z k bωωωβαδβαδωαδ=-⎧⎪+=+⎪⎪+=+⎪=⎪⎪=-⎪⎨+=+-+⎪⎪+=-⎪=-=⨯=-⎩⎪⎪⎪⎪ (8) 其中,*r ω为转速给定;r ω为转速反馈;*q i 为转速控制器输出的q 轴电流给定值。
4 ADRC 和PI 作为速度环控制器的仿真对比以simulink 工具箱中的为所控制的电机模型,设置参数如下表[4]:表一、电机模型主要参数转动惯量J 0.0018kg.m^2极对数p 4额定转速wr 100rad/s阻尼系数F 0静摩擦力Tf 0并且设定转子初始角为0°时,转子位置和A相轴线对齐。
