主成分分析实例及含义讲解
主成分分析法精华讲义及实例

主成分分析类型:一种处理高维数据的方法。
降维思想:在实际问题的研究中,往往会涉及众多有关的变量。
但是,变量太多不但会增加计算的复杂性,而且也会给合理地分析问题和解释问题带来困难。
一般说来,虽然每个变量都提供了一定的信息,但其重要性有所不同,而在很多情况下,变量间有一定的相关性,从而使得这些变量所提供的信息在一定程度上有所重叠。
因而人们希望对这些变量加以“改造”,用为数极少的互补相关的新变量来反映原变量所提供的绝大部分信息,通过对新变量的分析达到解决问题的目的。
一、总体主成分1.1 定义设 X 1,X 2,…,X p 为某实际问题所涉及的 p 个随机变量。
记 X=(X 1,X 2,…,Xp)T ,其协方差矩阵为()[(())(())],T ij p p E X E X X E X σ⨯∑==--它是一个 p 阶非负定矩阵。
设1111112212221122221122Tp p Tp pT pp p p pp p Y l X l X l X l X Y l X l X l X l X Y l X l X l X l X⎧==+++⎪==+++⎪⎨⎪⎪==+++⎩(1) 则有()(),1,2,...,,(,)(,),1,2,...,.T T i i i i TT T i j ijij Var Y Var l X l l i p Cov Y Y Cov l X l X l l j p ==∑===∑= (2)第 i 个主成分: 一般地,在约束条件1T i i l l =及(,)0,1,2,..., 1.T i k i k Cov Y Y l l k i =∑==-下,求 l i 使 Var(Y i )达到最大,由此 l i 所确定的T i i Y l X =称为 X 1,X 2,…,X p 的第 i 个主成分。
1.2 总体主成分的计算设 ∑是12(,,...,)T p X X X X =的协方差矩阵,∑的特征值及相应的正交单位化特征向量分别为120p λλλ≥≥≥≥及12,,...,,p e e e则 X 的第 i 个主成分为1122,1,2,...,,T i i i i ip p Y e X e X e X e X i p ==+++= (3)此时(),1,2,...,,(,)0,.Ti i i i Ti k i k Var Y e e i p Cov Y Y e e i k λ⎧=∑==⎪⎨=∑=≠⎪⎩ 1.3 总体主成分的性质1.3.1 主成分的协方差矩阵及总方差记 12(,,...,)T p Y Y Y Y = 为主成分向量,则 Y=P T X ,其中12(,,...,)p P e e e =,且12()()(,,...,),T T p Cov Y Cov P X P P Diag λλλ==∑=Λ=由此得主成分的总方差为111()()()()(),p ppTTiii i i i Var Y tr P P tr PP tr Var X λ=====∑=∑=∑=∑∑∑即主成分分析是把 p 个原始变量 X 1,X 2,…,X p 的总方差1()pii Var X =∑分解成 p 个互不相关变量 Y 1,Y 2,…,Y p 的方差之和,即1()pii Var Y =∑而 ()k k Var Y λ=。
主成分分析法例子剖析-PPT

从以上的分析可以看出,主成分分析的 实质就是确定原来变量xj(j=1,2 ,…, p) 在诸主成分zi(i=1,2,…,m)上的载荷 lij ( i=1,2,…,m; j=1,2 ,…,p)。
分z2代表了人均资源量。
③第三主成分z3,与x8呈显出的正相关程度 最高,其次是x6,而与x7呈负相关,因此可 以认为第三主成分在一定程度上代表了农业 经济结构。
显然,用三个主成分z1、z2、z3代替原来9个变量(x1, x2,…,x9),描述农业生态经济系统,可以使问题更进
一步简化、明了。
rij
n
(xki xi )(xkj x j )
k 1
n
n
(xki xi )2 (xkj x j )2
k 1
k 1
(4)
(二)计算特征值与特征向量:
① 解特征方程 I R 0 ,求出特征值,并 使其按大小顺序排列 ;
1 2 , p 0
② 分别求出对应于特征值 i的特征向量
大家好
1
一、主成分分析的基本原理
❖ 假定有n个样本,每个样本共有p个变量, 构成一个n×p阶的数据矩阵
x11 x12 x1 p
X
x21
x22
x2
p
xn1
xn 2
xnp
(1)
❖降维处理!!!
当p较大时,在p维空间中考察问题比较麻烦。 降维是用较少的几个综合指标代替原来较多 的变量指标,而且使这些较少的综合指标既 能尽量多地反映原来较多变量指标所反映的 信息,同时它们之间又是彼此独立的。
主成分分析实例及含义讲解 优质课件

这里,第一个因子主要和语文、历史、英语三科有很强的正相关; 而第二个因子主要和数学、物理、化学三科有很强的正相关。因 此可以给第一个因子起名为“文科因子”,而给第二个因子起名 为“理科因子”。从这个例子可以看出,因子分析的结果比主成 分分析解释性更强。
25
• 这些系数所形成的散点图(在SPSS中也称载荷图)为
例)。比如第一主成分为数学、物理、化学、语文、历史、英
语这六个变量的线性组合,系数(比例)为-0.806, -0.674, -
0.675, 0.893, 0.825, 0.836。
15
• 如y成1,分用y2为x,1y,3x,2y,4x,3y,5x,4y,6x表5,示x6新分的别主表成示分原,先那的么六,个第变一量和,第而二主用
3
.457
7.619
88.761
4
.323
5.376
94.137
5
.199
3.320
97.457
6
.153
2.543
100.000
Extraction Method: Principal Component Analysis.
Extraction Sums of Squared Loadings
Total
• 当然不能。 • 你必须要把各个方面作出高度概括,用一两个指标简单明了地
把情况说清楚。
2
主成分分析
• 每个人都会遇到有很多变量的数据。 • 比如全国或各个地区的带有许多经济和社会变量的数据;各个
学校的研究、教学等各种变量的数据等等。 • 这些数据的共同特点是变量很多,在如此多的变量之中,有很
多是相关的。人们希望能够找出它们的少数“代表”来对它们 进行描述。 • 本章就介绍两种把变量维数降低以便于描述、理解和分析的方 法:主成分分析(principal component analysis)和因子分 析(factor analysis)。实际上主成分分析可以说是因子分析 的一个特例。在引进主成分分析之前,先看下面的例子。
主成分分析法例子.ppt

表3
主成分 z1 z2 z3 z4 z5 z6 z7 z8 z9
特征值及主成分贡献率
贡献率(%) 51.791 23.216 11.589 5.638 3.502 2.14 1.271 0.504 0.35 累积贡献率(%) 51.791 75.007 86.596 92.234 95.736 97.876 99.147 99.65 100
特征值 4.661 2.089 1.043 0.507 0.315 0.193 0.114 0.0453 0.0315
(3)对于特征值=4.6610,=2.0890, =1.0430分别求出其特征向量l1,l2,l3。
表4
主成分载荷
占方差的百分数 (%) 82.918 80.191 92.948 75.346 85.811 71.843 95.118 98.971 92.939
j 1 p
=1,即 l ij j个分量。 的第 li
li
,
③ 计算主成分贡献率及累计贡献率
▲贡献率:
i
k 1
p
(i 1 ,2, , p)
k
▲累计贡献率:
k 1 k 1 p i k
(i 1,2, , p )
k
, , , 一般取累计贡献率达85—95%的特征值 1 2 m 所对应的第一、第二、…、第m(m≤p)个主成分。
假定有n个样本,每个样本共有p个变量, 构成一个n×p阶的数据矩阵
x11 x 21 X xn 1 x12 x22 xn 2 x1 p x2 p xnp
(1)
降维处理!!!
当p较大时,在p维空间中考察问题比较麻烦。 降维是用较少的几个综合指标代替原来较多 的变量指标,而且使这些较少的综合指标既 能尽量多地反映原来较多变量指标所反映的 信息,同时它们之间又是彼此独立的。
主成分分析法实例

【转】主成分分析法概述、案例实例分析主成分分析法主成分分析也称主分量分析,旨在利用降维的思想,把多指标转化为少数几个综合指标。
在实证问题研究中,为了全面、系统地分析问题,我们必须考虑众多影响因素。
这些涉及的因素一般称为指标,在多元统计分析中也称为变量。
因为每个变量都在不同程度上反映了所研究问题的某些信息,并且指标之间彼此有一定的相关性,因而所得的统计数据反映的信息在一定程度上有重叠。
在用统计方法研究多变量问题时,变量太多会增加计算量和增加分析问题的复杂性,人们希望在进行定量分析的过程中,涉及的变量较少,得到的信息量较多。
主成分分析正是适应这一要求产生的,是解决这类题的理想工具。
主成分分析法是一种数学变换的方法, 它把给定的一组相关变量通过线性变换转成另一组不相关的变量,这些新的变量按照方差依次递减的顺序排列。
在数学变换中保持变量的总方差不变,使第一变量具有最大的方差,称为第一主成分,第二变量的方差次大,并且和第一变量不相关,称为第二主成分。
依次类推,I 个变量就有I个主成分。
这种方法避免了在综合评分等方法中权重确定的主观性和随意性,评价结果比较符合实际情况;同时,主成份分量表现为原变量的线性组合,如果最后综合指标包括所有分量,则可以得到精确的结果,百分之百地保留原变量提供的变差信息,即使舍弃若干分量,也可以保证将85%以上的变差信息体现在综合评分中,使评价结果真实可靠。
是在实际中应用得比较广的一种方法。
由于其第一主成份(因子)在所有的主成分中包含信息量最大,很多学者在研究综合评价问题时常采用第一主成分来比较不同实体间的差别。
综上所述,该方法的优点主要体现在两个方面:1.权重确定的客观性;2.评价结果真实可靠。
1.主成分分析的基本原理主成分分析:把原来多个变量划为少数几个综合指标的一种统计分析方法,是一种降维处理技术。
)记原来的变量指标为x1,x2,…,xP,它们的综合指标——新变量指标为z1,z2,…,zm(m≤p),则z1,z2,…,zm分别称为原变量指标x1,x2,…,xP的第一,第二,…,第m 主成分,在实际问题的分析中,常挑选前几个最大的主成分。
spss主成分分析案例

spss主成分分析案例SPSS主成分分析案例。
主成分分析(Principal Component Analysis, PCA)是一种常用的数据降维方法,它可以将原始变量转换成一组新的互相无关的变量,这些新变量被称为主成分。
主成分分析可以帮助我们发现数据中的模式和结构,从而更好地理解数据的特性。
本文将以一个实际案例来介绍如何在SPSS软件中进行主成分分析,并解释如何解读分析结果。
案例背景:某公司想要了解员工的工作满意度,为了更全面地了解员工对工作的感受,公司设计了一份包含多个问题的调查问卷,涉及到工作内容、工作环境、薪酬福利等方面。
为了简化分析,公司希望利用主成分分析来提取出最能代表员工工作满意度的几个维度。
数据收集:公司对全体员工进行了调查,共有300份有效问卷。
每份问卷包含了20个问题,涉及到不同方面的工作满意度评价。
这些问题涵盖了工作内容、同事关系、上级领导、薪酬福利等多个方面。
数据分析:首先,我们需要将数据导入SPSS软件中,然后依次点击“分析”-“数据降维”-“主成分”命令。
在弹出的对话框中,我们选择需要进行主成分分析的变量,即员工对不同问题的评分。
在选择了变量后,我们可以点击“选项”按钮,对分析进行进一步设置,比如选择旋转方法、提取条件等。
在进行了上述设置后,我们点击“确定”按钮,SPSS将会为我们生成主成分分析的结果。
在结果中,我们可以看到提取的主成分个数、每个主成分的方差解释比例、成分矩阵等信息。
通过这些信息,我们可以判断提取的主成分是否符合要求,以及每个主成分的解释能力如何。
解读结果:在这个案例中,我们提取了3个主成分,这3个主成分分别解释了总方差的60%、25%和15%。
成分矩阵显示了每个问题对应的主成分载荷,通过分析载荷大小,我们可以判断每个主成分所代表的具体内容。
比如,第一个主成分可能代表工作内容满意度,第二个主成分可能代表同事关系满意度,第三个主成分可能代表薪酬福利满意度。
主成分分析例题

主成分分析例题主成分分析(PrincipalComponentAnalysis,简称PCA)是一种常用的数据分析方法,它可以有效分析数据中的多元特征,将多维特征空间映射到低维空间,使得数据的特征可以更加清晰和深入地分析。
主成分分析方法经常用于多元数据的特征提取、因素分析以及因子结构研究,是多元数据分析中常用的统计分析方法之一。
下面介绍一个典型的主成分分析例题,其中涉及因子分析、因子结构分析以及多元统计分析方法等:一个某大学的护士教学实践中心,设有4个实验室,每实验室有自己的实验内容和服务对象,实验室类型主要有医学实验室、护理实验室、外科实验室以及诊断室。
某护士教学实践中心向500名护士学生收集了有关这4类实验室实验内容和服务对象的信息,以下为收集到的具体信息:(1)医学实验室:主要是负责护士学生的临床实习和医学教育,针对的对象为护理学生。
(2)护理实验室:主要的护理实验内容有护理实践、护理研究和护理技能培训,服务对象是护理学生、护理人员和护理专业的其他相关人群。
(3)外科实验室:主要的外科实验内容包括外科实践、外科技能培训及新型外科手术训练,服务对象是护理学生、护理人员和护理专业的其他相关人群。
(4)诊断实验室:主要是负责护士学生的护理诊断和护理诊断教学,服务对象是护理学生。
为了更加清楚地分析护士教学实践中心的护士学生对这4类实验室的实验内容和服务对象的看法,因此将采用主成分分析方法对这500名护士学生收集到的信息进行分析。
首先,通过SPSS对500名护士学生收集到的信息,进行因子分析,提取4个实验室相关的因子,并得出以下结果:表1.子质量统计|子 |差贡献率 |积方差贡献率 ||-----|-----------|--------------|| 1 | 0.717 | 0.717 || 2 | 0.122 | 0.839 || 3 | 0.056 | 0.895 || 4 | 0.004 | 0.899 |从表1中可以看出,前3个因子共计可以解释89.5%的方差,因此可以将前3个因子作为主成分进行处理。
主成分分析法案例

主成分分析法案例主成分分析(Principal Component Analysis,PCA)是一种常用的降维技术,可以将高维数据映射到低维空间,同时保持数据信息最大化。
本文将介绍一个应用主成分分析法的案例,以展示其在实际问题中的应用价值。
假设我们有一个销售数据集,包含100个样本和10个特征。
我们希望通过主成分分析法来降低数据的维度,以便更好地理解和解释数据。
第一步是标准化数据。
由于每个特征的单位和范围可能不同,我们需要将其缩放到相同的尺度。
这样可以避免某些特征对主成分分析结果的影响过大。
通过减去特征均值并除以标准差,我们可以将数据的均值调整为0,方差调整为1。
第二步是计算特征的协方差矩阵。
协方差矩阵可以衡量不同特征之间的关系。
通过计算特征之间的协方差,我们可以得到一个10×10的协方差矩阵。
第三步是计算协方差矩阵的特征值和特征向量。
特征值可以衡量每个特征的重要性,特征向量则表示数据在这些特征方向上的投影。
第四步是选择主成分。
我们可以通过特征值的大小来选择主成分的数量。
特征值越大,说明对应特征向量的信息量越大。
在这个案例中,我们选择前三个特征值最大的特征向量作为主成分。
第五步是计算主成分得分。
我们可以将原始数据映射到选定的主成分上,从而得到主成分得分。
主成分得分是原始数据在主成分上的投影。
最后,我们可以通过对主成分进行可视化和解释来理解数据。
在这个案例中,我们可以绘制主成分之间的散点图,观察样本之间的分布情况。
同时,我们还可以计算主成分与原始特征的相关系数,以评估特征在主成分中的重要性。
总之,主成分分析法是一种强大的降维技术,可以帮助我们更好地理解和解释数据。
通过选择主成分,计算主成分得分以及解释主成分,我们可以在高维数据中寻找关键的信息。
主成分分析案例数据

主成分分析案例数据主成分分析案例数据,这可是个挺有趣的话题呢!咱先来说说啥是主成分分析。
简单来讲,主成分分析就是把一堆乱七八糟的数据,通过一些巧妙的办法,找出其中最关键、最重要的几个成分。
就好比你走进一个乱糟糟的房间,然后想办法找出最显眼、最有用的那几件东西。
给您举个例子吧。
我之前教过一个学生,叫小明。
他特别喜欢收集各种石头,什么形状、颜色、大小的都有。
有一天,他拿着他的宝贝石头来找我,说他想弄清楚这些石头有没有什么规律。
这可把我难住了,那么多石头,怎么找规律呀?这时候我就想到了主成分分析。
我先让小明把石头的一些特征记录下来,比如石头的长度、宽度、高度、重量、颜色的深浅等等。
这就像是我们收集了一堆关于石头的数据。
然后呢,通过主成分分析,我们发现石头的大小(长度、宽度、高度、重量综合起来)和颜色的深浅这两个方面,是最能区分这些石头的关键因素。
比如说,大而颜色深的石头往往是他在河边捡到的;小而颜色浅的石头多数是在公园里找到的。
您看,这就是主成分分析的作用。
它能帮我们从复杂的数据中找出关键的信息,就像在一堆乱麻中理出了几根主要的线头。
再比如说,在学校的成绩分析中也能用到主成分分析。
咱们不只是看学生的语文、数学、英语成绩,还会考虑他们的课堂表现、作业完成情况、参加活动的积极性等等。
这么多的数据,如果一股脑儿地去看,那简直要让人头晕眼花。
但通过主成分分析,我们可能会发现,课堂表现和作业完成情况这两个因素,对学生的综合成绩影响最大。
那咱们就可以重点关注这两个方面,想办法帮助学生提高。
还有在市场调研中,假如一家公司想了解消费者对他们产品的看法。
他们可能会收集消费者的年龄、性别、收入水平、购买频率、对产品的满意度等等数据。
经过主成分分析,也许会发现年龄和购买频率是影响消费者满意度的主要成分。
总之,主成分分析就像是一个神奇的工具,能让我们在纷繁复杂的数据海洋中找到方向,抓住重点。
您想想,如果没有主成分分析,我们面对那么多的数据,不就像没头的苍蝇一样乱撞吗?所以说呀,学会主成分分析,能让我们更聪明地处理数据,做出更准确的判断和决策。
主成分分析原理及详解
第14章主成分分析1 概述1.1 基本概念1.1.1 定义主成分分析是根据原始变量之间的相互关系,寻找一组由原变量组成、而彼此不相关的综合变量,从而浓缩原始数据信息、简化数据结构、压缩数据规模的一种统计方法。
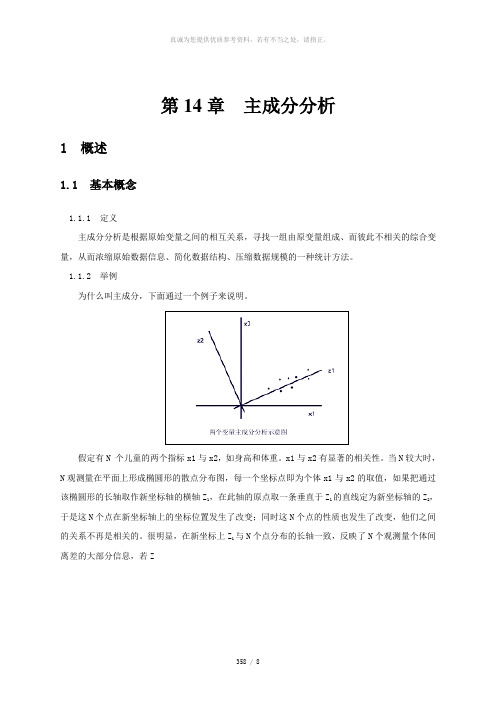
1.1.2 举例为什么叫主成分,下面通过一个例子来说明。
假定有N 个儿童的两个指标x1与x2,如身高和体重。
x1与x2有显著的相关性。
当N较大时,N观测量在平面上形成椭圆形的散点分布图,每一个坐标点即为个体x1与x2的取值,如果把通过该椭圆形的长轴取作新坐标轴的横轴Z1,在此轴的原点取一条垂直于Z1的直线定为新坐标轴的Z2,于是这N个点在新坐标轴上的坐标位置发生了改变;同时这N个点的性质也发生了改变,他们之间的关系不再是相关的。
很明显,在新坐标上Z1与N个点分布的长轴一致,反映了N个观测量个体间离差的大部分信息,若Z1反映了原始数据信息的80%,则Z2只反映总信息的20%。
这样新指标Z1称为原指标的第一主成分,Z2称为原指标的第二主成分。
所以如果要研究N个对象的变异,可以只考虑Z1这一个指标代替原来的两个指标(x1与x2),这种做法符合PCA提出的基本要求,即减少指标的个数,又不损失或少损失原来指标提供的信息。
1.1.3 函数公式通过数学的方法可以求出Z1和Z2与x1与x2之间的关系。
Z1=l11x1+ l12x2Z2=l21x1+ l22x2即新指标Z1和Z2是原指标x1与x2的线性函数。
在统计学上称为第一主成分和第二主成分。
若原变量有3个,且彼此相关,则N个对象在3维空间成椭圆球分布,见图14-1。
通过旋转和改变原点(坐标0点),就可以得到第一主成分、第二主成分和第三主成分。
如果第二主成分和第三主成分与第一主成高度相关,或者说第二主成分和第三主成分相对于第一主成分来说变异很小,即N个对象在新坐标的三维空间分布成一长杆状时,则只需用一个综合指标便能反映原始数据中3个变量的基本特征。
1.2 PCA满足条件1.2.1 一般条件一般来说,N个对象观察p个指标,可以得到N*p个数据(矩阵)。
主成分分析法实例

【转】主成分分析法概述、案例实例分析主成分分析法主成分分析也称主分量分析,旨在利用降维的思想,把多指标转化为少数几个综合指标。
在实证问题研究中,为了全面、系统地分析问题,我们必须考虑众多影响因素。
这些涉及的因素一般称为指标,在多元统计分析中也称为变量。
因为每个变量都在不同程度上反映了所研究问题的某些信息,并且指标之间彼此有一定的相关性,因而所得的统计数据反映的信息在一定程度上有重叠。
在用统计方法研究多变量问题时,变量太多会增加计算量和增加分析问题的复杂性,人们希望在进行定量分析的过程中,涉及的变量较少,得到的信息量较多。
主成分分析正是适应这一要求产生的,是解决这类题的理想工具。
主成分分析法是一种数学变换的方法, 它把给定的一组相关变量通过线性变换转成另一组不相关的变量,这些新的变量按照方差依次递减的顺序排列。
在数学变换中保持变量的总方差不变,使第一变量具有最大的方差,称为第一主成分,第二变量的方差次大,并且和第一变量不相关,称为第二主成分。
依次类推,I 个变量就有I个主成分。
这种方法避免了在综合评分等方法中权重确定的主观性和随意性,评价结果比较符合实际情况;同时,主成份分量表现为原变量的线性组合,如果最后综合指标包括所有分量,则可以得到精确的结果,百分之百地保留原变量提供的变差信息,即使舍弃若干分量,也可以保证将85%以上的变差信息体现在综合评分中,使评价结果真实可靠。
是在实际中应用得比较广的一种方法。
由于其第一主成份(因子)在所有的主成分中包含信息量最大,很多学者在研究综合评价问题时常采用第一主成分来比较不同实体间的差别。
综上所述,该方法的优点主要体现在两个方面:1.权重确定的客观性;2.评价结果真实可靠。
1.主成分分析的基本原理主成分分析:把原来多个变量划为少数几个综合指标的一种统计分析方法,是一种降维处理技术。
)记原来的变量指标为x1,x2,…,xP,它们的综合指标——新变量指标为z1,z2,…,zm(m≤p),则z1,z2,…,zm分别称为原变量指标x1,x2,…,xP的第一,第二,…,第m 主成分,在实际问题的分析中,常挑选前几个最大的主成分。
主成分分析案例

Y2得分
-2.06481 2.32993 -1.47145 0.66326 -0.87181 1.25757 -1.40987 -0.36439 0.04577 -2.04139 -0.42078 0.33126 0.07660 0.86909 0.45974 -0.83575
主成分分析在 市场研究中的应用
1——5 组表示男性,6——10 组表示女性 1——5, 6——10 年龄从小到大排序
假若你是该食品加工业决策部 门的高级顾问,为了对食品生 产作出合理决策,请你对以上 的调查资料进行分析,为决策 者提供建议。
特征向量
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10
特征根 i
方差贡献率
女性喜欢
一般喜欢
孩子 咖喱饭
炸肉饼、火腿面包
成人 鸡蛋烩饭、炸猪排 酸汤、大头鱼
一般不喜欢 特别不喜欢
孩子 干咖喱、浓汤 成人 煮牛肉、生蛋
菜粥、清汤
饼干、带馅面包 酱面条、烧鱼
服装的定型分类问题
为了较好地满足市场的需要,服装生产厂 要了解所生产的一种服装究竟设计几种型号合 适?这些型号的服装应按怎样的比例分配生产 计划才能达到较好的经济效益?
4、取每一组的中心 ( y1*k , y2*k ) (k=1,2,…,g) 作为该组的 代表点。
相应原16个指标的尺寸:
x1' r11 y1*k r12 y2*k x2' r21 y1*k r22 y2*k
x1' 6 r16,1 y1*k r16,2 y2*k
5、各种型号的比例按 该组样品数/128 确定。
Y2
0.513225 0.203116 -0.182858 0.193618 0.217290 0.113642 -0.164527 -0.114637 -0.509240 -0.025832 0.083471 0.132592 0.105402 0.199407 -0.181330 -0.261367 -0.295756
主成分分析实例和含义讲解

a. Rotation converged in 3 iterations.
22
• 这x文6来个)表表,示说hism明toa六rtyh(个(历变数史量学)和),因,e子pnhg的ylis关s(h(系物英。理语为))简,等单ch变记em量,(。我化这们学样用)因x1,,子xli2ft,1e和xr3a,ft2x(与4,语这x5, 些原变量之间的关系是(注意,和主成分分析不同,这里把成分(因 子)写在方程的右边,把原变量写在左边;但相应的系数还是主成分 和各个变量的线性相关系数,也称为因子载荷):
• 那么这个椭圆有一个长轴和一个短轴。在短轴方向上,数据变化很少;在 极端的情况,短轴如果退化成一点,那只有在长轴的方向才能够解释这些 点的变化了;这样,由二维到一维的降维就自然完成了。
6
4
2
0
-2
-4
-4
-2
0
2
4
7
椭球的长短轴
• 当坐标轴和椭圆的长短轴平行,那么代表长轴的变量就描述了数据的主 要变化,而代表短轴的变量就描述了数据的次要变化。
11
主成分分析的数学
• 要寻找方差最大的方向。即使得向量X的线性组合a’X的方差
最大的方向a. • 而Var(a’X)=a’Cov(X)a;由于Cov(X)未知;于是用X的样本相
关阵R来近似.因此,要寻找向量a使得a’Ra最大(注意相关阵 和协方差阵差一个常数 • 记得相关阵和特征值问题吗?回顾一下吧! • 选择几个主成分呢?要看“贡献率.”
16
•可以把第一和第二主成分的载荷点出一个二维图以直 观地显示它们如何解释原来的变量的。这个图叫做载荷 图。
17
Component Plot
1.0
cphheyms
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5
空间的点
• 例中的的数据点是六维的;也就是说,每个观测值是6维空间中的一个点。 我们希望把6维空间用低维空间表示。 • 先假定只有二维,即只有两个变量,它们由横坐标和纵坐标所代表;因此 每个观测值都有相应于这两个坐标轴的两个坐标值;如果这些数据形成一 个椭圆形状的点阵(这在变量的二维正态的假定下是可能的) • 那么这个椭圆有一个长轴和一个短轴。在短轴方向上,数据变化很少;在 极端的情况,短轴如果退化成一点,那只有在长轴的方向才能够解释这些 点的变化了;这样,由二维到一维的降维就自然完成了。
• 这里每一列代表一个主成分作为原来变量线性组合的系数(比例)。比如第一主成分为 数学、物理、化学、语文、历史、英语这六个变量的线性组合,系数(比例)为-0.806, 0.674, -0.675, 0.893, 0.825, 0.836。
15
• 如用 x1,x2,x3,x4,x5,x6 分别表示原先的六个变量,而用 y1,y2,y3,y4,y5,y6 表示新的主成分,那么,第一和第二主成分为
19
• 主成分分析与因子分析的公式上的区别
y1 a11 x1 + a12 x2 + + a1 p x p y2 a21 x1 + a22 x2 + + a2 p x p y p a p1 x1 + a p 2 x2 + + a pp x p
主成分分析
x1 - a11 f1 + a12 f 2 + + a1m f m + 1 x2 - a21 f1 + a22 f 2 + + a2 m f m + 2 x p - a p1 f1 + a p 2 f 2 + + a pm f m + p
-1.0 -1.0 -.5 0.0 .5 1.0
Component 1
18
因子分析
• 主成分分析从原理上是寻找椭球的所有主轴。因此,原先有几个变量,就 有几个主成分。 • 而因子分析是事先确定要找几个成分,这里叫因子( factor )(比如两 个),那就找两个。 • 这使得在数学模型上,因子分析和主成分分析有不少区别。而且因子分析 的计算也复杂得多。根据因子分析模型的特点,它还多一道工序:因子旋 转(factor rotation);这个步骤可以使结果更好。 • 当然,对于计算机来说,因子分析并不比主成分分析多费多少时间。 • 从输出的结果来看,因子分析也有因子载荷(factor loading)的概念,代 表了因子和原先变量的相关系数。但是在因子分析公式中的因子载荷和主 成分分析中的因子载荷位置不同。因子分析也给出了二维图;但解释和主 成分分析的载荷图类似。
Component Number
14
•
怎么解释这两个主成分。前面说过主成分是原始六个变量的线性组合。是怎么样的组合呢?SPSS可 以输出下面的表。
Com ponent
a Matr ix
Component 1 2 3 4 MATH -.806 .353 -.040 .468 PHYS -.674 .531 -.454 -.240 CHEM -.675 .513 .499 -.181 LITERAT .893 .306 -.004 -.037 HISTORY .825 .435 .002 .079 ENGLISH .836 .425 .000 .074 Extraction Method: Principal Component Analysis. a. 6 components extracted. 5 .021 -.001 .002 .077 -.342 .276 6 .068 -.006 .003 .320 -.083 -.197
10
主成分之选取
• 正如二维椭圆有两个主轴,三维椭球有三个主轴一样,有几个变 量,就有几个主成分。 • 选择越少的主成分,降维就越好。什么是标准呢?那就是这些被 选的主成分所代表的主轴的长度之和占了主轴长度总和的大部分。 有些文献建议,所选的主轴总长度占所有主轴长度之和的大约 85%即可,其实,这只是一个大体的说法;具体选几个,要看实 际情况而定。
24
这里,第一个因子主要和语文、历史、英语三科有很强的正相关; 而第二个因子主要和数学、物理、化学三科有很强的正相关。因 此可以给第一个因子起名为“文科因子”,而给第二个因子起名 为“理科因子”。从这个例子可以看出,因子分析的结果比主成 分分析解释性更强。
6
-4
-2
0
2
4
-4
-2
0
2
4
7
椭球的长短轴
• 当坐标轴和椭圆的长短轴平行,那么代表长轴的变量就描述了数据的主 要变化,而代表短轴的变量就描述了数据的次要变化。 • 但是,坐标轴通常并不和椭圆的长短轴平行。因此,需要寻找椭圆的长 短轴,并进行变换,使得新变量和椭圆的长短轴平行。 • 如果长轴变量代表了数据包含的大部分信息,就用该变量代替原先的两 个变量(舍去次要的一维),降维就完成了。 • 椭圆(球)的长短轴相差得越大,降维也越有道理。
2
主成分分析
• 每个人都会遇到有很多变量的数据。 • 比如全国或各个地区的带有许多经济和社会变量的数据;各个学校的 研究、教学等各种变量的数据等等。 • 这些数据的共同特点是变量很多,在如此多的变量之中,有很多是相 关的。人们希望能够找出它们的少数“代表”来对它们进行描述。 • 本章就介绍两种把变量维数降低以便于描述、理解和分析的方法:主 成 分 分 析 ( principal component analysis ) 和 因 子 分 析 ( factor analysis)。实际上主成分分析可以说是因子分析的一个特例。在引 进主成分分析之前,先看下面的例子。
• 这里的Initial Eigenvalues就是这里的六个主轴长度,又称特征值(数 据相关阵的特征值)。头两个成分特征值累积占了总方差的 81.142% 。 后面的特征值的贡献越来越少。
13
• 特征值的贡献还可以从SPSS的所谓碎石图看出
Scree Plot
4
3
2
Eigenvalue
1
0 1 2 3 4 5 6
23
x1 -0.387 f1 + 0.790 f 2 ; x2 -0.172 f1 + 0.841 f 2 ; x3 -0.184 f1 + 0.827 f 2 x4 0.879 f1 - 0.343 f 2 ; x5 0.911 f1 - 0.201 f 2 ; x6 0.913 f1 - 0.216 f 2
3
成绩数据(student.sav)
• 100个学生的数学、物理、化学、语文、历史、英语的成绩如下表(部分)。
4
从本例可能提出的问题
• 目前的问题是,能不能把这个数据的 6个变量用一两个综 合变量来表示呢? • 这一两个综合变量包含有多少原来的信息呢? • 能不能利用找到的综合变量来对学生排序呢?这一类数据 所涉及的问题可以推广到对企业,对学校进行分析、排序、 判别和分类等问题。
12
• 对于我们的数据,SPSS输出为
Tot al Va rianc e Exp laine d Initial Eigenvalues Component Total % of Variance Cumulative % 1 3.735 62.254 62.254 2 1.133 18.887 81.142 3 .457 7.619 88.761 4 .323 5.376 94.137 5 .199 3.320 97.457 6 .153 2.543 100.000 Extraction Method: Principal Component Analysis. Extraction Sums of Squared Loadings Total % of Variance Cumulative % 3.735 62.254 62.254 1.133 18.887 81.142
y1 -0.806 x1 - 0.674 x2 - 0.675 x3 + 0.893x4 + 0.825 x5 + 0.836 x6 y2 0.353x1 + 0.531x2 + 0.513x3 + 0.306 x4 + 0.435 x5 + 0.425 x6
• 这些系数称为主成分载荷( loading),它表示主成分和相应的原先变量的相关 系数。 • 比如y1表示式中x1的系数为-0.806,这就是说第一主成分和数学变量的相关系数 为-0.806。 • 相关系数(绝对值)越大,主成分对该变量的代表性也越大。可以看得出,第一 主成分对各个变量解释得都很充分。而最后的几个主成分和原先的变量就不那 么相关了。
22
• 这个表说明六个变量和因子的关系。为简单记,我们用x1, x2, x3, x4, x5, x6来表示math(数学), phys(物理),chem(化学),literat(语 文),history(历史),english(英语)等变量。这样因子f1和f2与这 些原变量之间的关系是(注意,和主成分分析不同,这里把成分(因 子)写在方程的右边,把原变量写在左边;但相应的系数还是主成分 和各个变量的线性相关系数,也称为因子载荷):
主成分分析和因子分析
吴喜之
1
汇报什么?
• 假定你是一个公司的财务经理,掌握了公司的所有数据,比如固定资产、 流动资金、每一笔借贷的数额和期限、各种税费、工资支出、原料消耗、 产值、利润、折旧、职工人数、职工的分工和教育程度等等。 • 如果让你向上面介绍公司状况,你能够把这些指标和数字都原封不动地 摆出去吗? • 当然不能。 • 你必须要把各个方面作出高度概括,用一两个指标简单明了地把情况说 清楚。
