利用MATLAB进行验证性实验1.划艇比赛的成绩2.机动车刹车距离生猪的出售时机模型求解
Matlab实验指导书含答案

实验一:M a t l a b操作环境熟悉一、实验目的1.初步了解Matlab操作环境。
2.学习使用图形函数计算器命令funtool及其环境。
二、实验内容熟悉Matlab操作环境,认识命令窗口、内存工作区窗口、历史命令窗口;学会使用format命令调整命令窗口的数据显示格式;学会使用变量和矩阵的输入,并进行简单的计算;学会使用who和whos命令查看内存变量信息;学会使用图形函数计算器funtool,并进行下列计算:1.单函数运算操作。
➢求下列函数的符号导数(1) y=sin(x);(2) y=(1+x)^3*(2-x);➢求下列函数的符号积分(1) y=cos(x);(2) y=1/(1+x^2);(3) y=1/sqrt(1-x^2);(4) y=(x-1)/(x+1)/(x+2);➢求反函数(1) y=(x-1)/(2*x+3);(2) y=exp(x);(3) y=log(x+sqrt(1+x^2));➢代数式的化简(1) (x+1)*(x-1)*(x-2)/(x-3)/(x-4);(2) sin(x)^2+cos(x)^2;(3) x+sin(x)+2*x-3*cos(x)+4*x*sin(x);2.函数与参数的运算操作。
➢从y=x^2通过参数的选择去观察下列函数的图形变化(1) y1=(x+1)^2(2) y2=(x+2)^2(3) y3=2*x^2(4) y4=x^2+2(5) y5=x^4(6) y6=x^2/23.两个函数之间的操作➢求和(1) sin(x)+cos(x)(2) 1+x+x^2+x^3+x^4+x^5➢乘积(1) exp(-x)*sin(x)(2) sin(x)*x➢商(1) sin(x)/cos(x);(2) x/(1+x^2);(3) 1/(x-1)/(x-2);➢求复合函数(1) y=exp(u) u=sin(x)(2) y=sqrt(u) u=1+exp(x^2)(3) y=sin(u) u=asin(x)(4) y=sinh(u) u=-x三、设计提示1.初次接触Matlab应该注意函数表达式的文本式描述。
机动车刹车问题(插值拟合回归三种方法解决)

clc
v=[20,25,30,35,40,45,50,55,60,65,70,75,80];
d=[42,56,73.5,91.5,116,142.5,173,209.5,248,292.5,343,401,4);b=a(:,2);
X=[v2',v',ones(b,1)];
数学与计算科学学院
实验报告
实验项目名称机动车刹车问题
所属课程名称数学实验
实验类型综合
实验日期
班级
学号
姓名
成绩
一、实验概述:
【实验目的】
利用插值、拟合及回归模型的方法解决机动车刹车的问题
【实验原理】
利用matlab内置插值函数,采取三次样条插值的方法,并绘制曲线插值的图形;利用polyfit函数进行二次曲线拟合,用polyval函数计算相应的拟合值,并绘制图形;利用回归的方法,调用rgress函数进行回归计算并得出对应的回归系数
三、指导教师评语及成绩:
评语
评语等级
优
良
中
及格
不及格
1.实验报告按时完成,字迹清楚,文字叙述流畅,逻辑性强
2.实验方案设计合理
3.实验过程(实验步骤详细,记录完整,数据合理,分析透彻)
4实验结论正确.
成绩:
指导教师签名:
批阅日期:
附录1:源程序
1.插值:
clc,clear,figure;
v=[20,25,30,35,40,45,50,55,60,65,70,75,80];
0.0825 0.0947
-2.5886 -1.3517
35.8730 64.2459
r =
-4.0934
-0.1758
MATLAB实验指导书(附答案)

MATLAB基础实验指导书漳州师范学院物电系2010年10月目录实验一MATLAB环境的熟悉与基本运算 (2)实验二MATLAB数值运算 (8)实验三MATLAB语言的程序设计 (12)实验四MATLAB的图形绘制 (16)实验五采用SIMULINK的系统仿真 (20)实验六MATLAB在电路中的应用 (25)实验七MATLAB在信号与系统中的应用 (27)实验八MATLAB在控制理论中的应用 (29)实验一 MATLAB环境的熟悉与基本运算一、实验目的:1.熟悉MATLAB开发环境2.掌握矩阵、变量、表达式的各种基本运算二、实验基本知识:1.熟悉MATLAB环境:MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器文件和搜索路径浏览器。
2.掌握MATLAB常用命令3.MATLAB变量与运算符变量命名规则如下:(1)变量名可以由英语字母、数字和下划线组成(2)变量名应以英文字母开头(3)长度不大于31个(4)区分大小写MATLAB中设置了一些特殊的变量与常量,列于下表。
MATLAB运算符,通过下面几个表来说明MATLAB的各种常用运算符表2 MATLAB算术运算符表3 MATLAB关系运算符表4 MATLAB逻辑运算符表5 MATLAB特殊运算4.MATLAB的一维、二维数组的寻访表6 子数组访问与赋值常用的相关指令格式5.MATLAB的基本运算表7 两种运算指令形式和实质内涵的异同表6.MATLAB的常用函数表8 标准数组生成函数表9 数组操作函数三、实验内容1、学习使用help命令,例如在命令窗口输入help eye,然后根据帮助说明,学习使用指令eye(其它不会用的指令,依照此方法类推)2、学习使用clc、clear,观察command window、command history和workspace等窗口的变化结果。
3、初步程序的编写练习,新建M-file,保存(自己设定文件名,例如exerc1、exerc2、exerc3……),学习使用MATLAB的基本运算符、数组寻访指令、标准数组生成函数和数组操作函数。
matlab实验报告

MATLAB数学实验报告指导老师:班级:小组成员:时间:201_/_/_Matlab第二次实验报告小组成员:1题目:实验四,MATLAB选择结构与应用实验目的:掌握if选择结构与程序流程控制,重点掌握break,return,pause语句的应用。
问题:问题1:验证“哥德巴赫猜想”,即:任何一个正偶数(n>=6)均可表示为两个质数的和。
要求编制一个函数程序,输入一个正偶数,返回两个质数的和。
问题分析:由用户输入一个大于6的偶数,由input语句实现。
由if判断语句判断是否输入的数据符合条件。
再引用质数判断函数来找出两个质数,再向屏幕输出两个质数即可。
编程:function [z1,z2]=gede(n);n=input('please input n')if n<6disp('data error');returnendif mod(n,2)==0for i=2:n/2k=0;for j=2:sqrt(i)if mod(i,j)==0k=k+1;endendfor j=2:sqrt(n-i)if mod(n-i,j)==0k=k+1;endendif k==0fprintf('two numbers are') fprintf('%.0f,%.0f',i,n-i) breakendendend结果分析:如上图,用户输入了大于6的偶数返回两个质数5和31,通过不断试验,即可验证哥德巴赫猜想。
纪录:if判断语句与for循环语句联合嵌套使用可使程序结构更加明晰,更快的解决问题。
2题目:实验四,MATLAB选择结构与应用实验目的:用matlab联系生活实际,解决一些生活中常见的实际问题。
问题:问题四:在一边长为1的四个顶点上各站有一个人,他们同时开始以等速顺时针沿跑道追逐下一人,在追击过程中,每个人时刻对准目标,试模拟追击路线,并讨论。
数学建模实验答案_简单优化模型

实验03 简单的优化模型(2学时)(第3章简单的优化模型)1. 生猪的出售时机p63~65目标函数(生猪出售纯利润,元):Q(t) = ( 8 – g t )( 80 + rt ) – 4t – 640其中,t≥ 0为第几天出售,g为每天价格降低值(常数,元/公斤),r为每天生猪体重增加值(常数,公斤)。
求t使Q(t)最大。
1.1(求解)模型求解p63(1) 图解法绘制目标函数Q(t) = ( 8 – g t )( 80 + rt ) – 4t – 640的图形(0 ≤t≤ 20)。
其中,g=0.1, r=2。
从图形上可看出曲线Q(t)的最大值。
(2) 代数法对目标函数Q(t) = ( 8 – g t )( 80 + rt ) – 4t – 640用MATLAB求t使Q(t)最大。
其中,r, g是待定参数。
(先对Q(t)进行符号函数求导,对导函数进行符号代数方程求解)然后将代入g=0.1, r=2,计算最大值时的t和Q(t)。
要求:①编写程序绘制题(1)图形。
②编程求解题(2).③对照教材p63相关内容。
相关的MATLAB函数见提示。
★要求①的程序和运行结果:★要求②的程序和运行结果:1.2(编程)模型解的的敏感性分析p63~64对1.1中(2)所求得的符号表达式t(r,g),分别对g和r进行敏感性分析。
(1) 取g=0.1,对t(r)在r=1.5:0.1:3上求r与t的关系数据,绘制r与t 的关系图形(见教材p65)。
(2) 取r=2,对t(g)在g=0.06:0.01:0.15上求g与t的关系数据,绘制g 与t的关系图形(见教材p65)。
要求:分别编写(1)和(2)的程序,调试运行。
★给出(1)的程序及运行结果:★给出(2)的程序及运行结果:2.(编程)冰山运输模型求解p77~81按函数调用顺序。
(1) 每立方米水所需费用),(),(),(000V u W V u S V u Y =u 为船速,V 0为冰山的初始体积。
数学建模实验二初等模型实验

数学建模实验⼆初等模型实验集美⼤学计算机⼯程学院实验报告课程名称:数学模型班级:计算12 实验成绩:指导教师:付永钢姓名:实验项⽬名称:初等模型试验学号:上机实践⽇期:实验项⽬编号:实验⼆上机实践时间:2014.11⼀、实验⽬的掌握初等模型的建⽴的基本思路和⽅法,并了解其求解过程。
对给定的初等模型问题能够借助Matlab ⼯具进⾏求解。
⼆、实验内容实验 1 ⽤Matlab 验证划艇⽐赛成绩模型的结果,通过数值结果来检验你所得到的模型正确性。
(⾸先要阅读本⽬录中的Matlab 数据拟合和matlab 数据处理的相关材料)实验2 求解汽车刹车距离的模型,⽤Matlab 给出你的求解结果。
验证应该遵循的t 秒准则的标准。
实验3 从教材P56中的第7,13,14题,任选⼀题,建⽴相应的初等模型,并借助matlab 进⾏求解,并给出合理的模型解释。
三、实验使⽤环境WindowsXP 、Matlab6.1四、实验步骤1、划艇⽐赛成绩的模型检验根据推导出的模型公式和数据,对参数βα,进⾏求解βαn t =。
⾸先转换成对数形式:,log 'log n t βα+=其中ααlog '=然后对给定数据进⾏拟合。
代码:n=[1 2 4 8]t=[7.21 6.88 6.32 5.84]lgn=log(n);lgt=log(t);p=polyfit(lgn,lgt,1);alpha=exp(p(2));belta=p(1);x=1:20;y=alpha*x.^belta ;plot(x,y,’c*-‘) ;xlabel(‘Number of Athlete ’);ylabel(‘Time Cost ’);Matlab 拟合函数图像:结果分析:划艇⽐赛模型的结果为t∞n-(1/9).。
在matlab中检验得belta =-0.1035与-(1/9)接近。
因此,模型正确。
2、汽车刹车距离验证代码:function E=fun1(a,x,y)Y=a(1)*x.*x+0.75*x;E=y-Y;%M⽂件结束%⽤lsqnonlin调⽤解决:x=[29.3 44 58.7 73.3 88 102.7 117.3];y=[44 78 124 186 268 372 506];a0=[0.5];options=optimset('lsqnonlin');a=lsqnonlin(@fun1,a0,[],[],options,x,y)%绘图plot(x,y,'o');hold on;x=[0:200];y=a(1)*x.*x+0.75*x;plot(x,y,'-');hold off结果分析:汽车刹车距离求解结果在Matlab的模型如上所⽰。
车辆速度与安全距离的MATLAB模拟毕业论文

本科生毕业论文(设计)题目车辆速度与安全距离的MATLAB模拟姓名专业年级、班级系、部(院)指导教师姓名专业技术职务2017年6月10日目录摘要 (1)英文摘要 (2)引言 (3)正文 (4)1 实验平台概述 (4)1.1MATLAB概述 (4)1.1.1特点 (4)1.1.2常用基本数学函数 (4)1.1.3常用运算符号 (4)1.2刹车距离 (4)1.2.1国家刹车距离标准 (5)1.2.2刹车距离的影响因素 (5)1.3几种测距方法对比 (5)1.3.1激光测量距离(laser distance measuring) (5)1.3.2超声波测量距离(Ultrasonic measurement distance) (5)1.3.3毫米波雷达测量距离(Millimeter wave radar ranging) (5)1.3.4视觉测量距离(Vision measurement) (6)1.3.5红外线测量距离(Infrared ray range) (6)2 实验设计 (7)2.1激光测距图 (7)2.2生活中处处存在的超载现象 (8)2.2.1货车超载标准及相关处罚 (8)2.3MATLAB模拟 (9)3 实验结果与分析 (14)结论 (16)参考文献 (17)综述 (18)致谢 (21)摘要因为公路上行驶的车辆的在不断增多,交通拥挤等问题随之也出现,交通事故也在增加,其中由于天气等周围环境影响,驾驶员由于刹车不及时造成的汽车追尾,侧面擦碰等事情在交通事故中所占比率增加,汽车防撞技术成为了全国性的热点研究话题。
可以看出保持距离,及时报警来进行刹车很重要,而两车间的距离和刹车距离在发展防撞技术中是不容忽视的考虑因素,所以本实验对两者进行了研究。
在其他人研究基础上,对比了一些测量距离的传感器的优缺点,并且考虑了多种因素,本论文决定采用激光来求出车辆间的距离,在其小于刹车距离时进行及时报警。
对乘用车、铰链客车、其他车辆,针对它们在空载、满载、、超载条件下的刹车距离不同研究,用MATLAB软件模拟刹车距离和速度的关系,通过本次的研究工作,可以让我们进一步了解刹车距离,得知保持车辆间距离并及时刹车的重要性,在发展防撞系统时对于刹车距离也是重要的考虑因素,可以尽量避免驾驶员因不及时刹车造成事故的发生。
数学实验(MATLAB版韩明版)5.1,5.3,5.5,5.6部分答案

数学实验(M A T L A B版韩明版)5.1,5.3,5.5,5.6部分答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN练习5.1B的分布规律和分布函数的图形,通过观1、仿照本节的例子,分别画出二项分布()7.0,20察图形,进一步理解二项分布的性质。
解:分布规律编程作图:>> x=0:1:20;y=binopdf(x,20,0.7);>> plot(x,y,'*')图像:yx分布函数编程作图:>> x=0:0.01:20;>>y=binocdf(x,20,0.7)>> plot(x,y)图像:1x观察图像可知二项分布规律图像像一条抛物线,其分布函数图像呈阶梯状。
2、仿照本节的例子,分别画出正态分布()25,2N的概率密度函数和分布函数的图形,通过观察图形,进一步理解正态分布的性质。
解:概率密度函数编程作图:>> x=-10:0.01:10;>> y=normpdf(x,2,5);>> plot(x,y)图像:00.010.020.030.040.050.060.070.08x y分布函数编程作图:>> x=-10:0.01:10;>> y=normcdf(x,2,5);>> plot(x,y)图像:01x y观察图像可知正态分布概率密度函数图像像抛物线,起分布函数图像呈递增趋势。
3、设()1,0~N X ,通过分布函数的调用计算{}11<<-X P ,{}22<<-X P , {}33<<-X P .解:编程求解:>> x1=normcdf(1)-normcdf(-1),x2=normcdf(2)-normcdf(-2),x3=normcdf(3)-normcdf(-3) x1 = 0.6827x2 = 0.9545x3 = 0.9973即:{}6827.011=<<-X P ,{}9545.022=<<-X P ,{}9973.033=<<-X P .4、设()7.0,20~B X ,通过分布函数的调用计算{}10=X P 与{}10<X P .解:编程求解:>> x1=binopdf(10,20,0.7),x2=binocdf(10,20,0.7)-binopdf(10,20,0.7) x1 = 0.0308x2 = 0.0171即:{}0308.010==X P ,{}0171.010=<X P5、设()8~P X ,求:(1){}4≤X P ;(2){}52≤<X P .解:(1)编程求解:>> p=poisscdf(4,8)p = 0.0996即:{}0996.04=≤X P(2)编程求解:>> p=poisscdf(5,8)-poisscdf(2,8)p = 0.1775即:{}1775.052=≤<X P6、(1)设()1,0~N X ,求01.0z ;(2)对2χ分布,求()8205.0χ;(3)对()1305.0t ;(4)对F 分布,求()10,1505.0F 。
武汉理工matlab实验报告

学生实验报告书实验课程名称数学软件与数学实验开课学院指导教师姓名学生姓名学生专业班级2012-- 2013学年第二学期实验教学管理基本规范实验是培养学生动手能力、分析解决问题能力的重要环节;实验报告是反映实验教学水平与质量的重要依据。
为加强实验过程管理,改革实验成绩考核方法,改善实验教学效果,提高学生质量,特制定实验教学管理基本规范。
1、本规范适用于理工科类专业实验课程,文、经、管、计算机类实验课程可根据具体情况参照执行或暂不执行。
2、每门实验课程一般会包括许多实验项目,除非常简单的验证演示性实验项目可以不写实验报告外,其他实验项目均应按本格式完成实验报告。
3、实验报告应由实验预习、实验过程、结果分析三大部分组成。
每部分均在实验成绩中占一定比例。
各部分成绩的观测点、考核目标、所占比例可参考附表执行。
各专业也可以根据具体情况,调整考核内容和评分标准。
4、学生必须在完成实验预习内容的前提下进行实验。
教师要在实验过程中抽查学生预习情况,在学生离开实验室前,检查学生实验操作和记录情况,并在实验报告第二部分教师签字栏签名,以确保实验记录的真实性。
5、教师应及时评阅学生的实验报告并给出各实验项目成绩,完整保存实验报告。
在完成所有实验项目后,教师应按学生姓名将批改好的各实验项目实验报告装订成册,构成该实验课程总报告,按班级交课程承担单位(实验中心或实验室)保管存档。
6、实验课程成绩按其类型采取百分制或优、良、中、及格和不及格五级评定。
实验课程名称:《数学软件与数学实验》4.根据网址为/military/html/784/index.html。
《MATLAB及应用》实验指导书

《MATLAB及应⽤》实验指导书《MATLAB及应⽤》实验指导书班级:姓名:学号:总评成绩:汽车⼯程系电测与汽车数字应⽤中⼼⽬录实验04051001 MATLAB语⾔基础 (1)实验04051002 MATLAB科学计算及绘图 (4)实验04051003 MATLAB综合实例编程 (6)实验04051001 MATLAB语⾔基础1实验⽬的1)熟悉MA TLAB的运⾏环境2)掌握MA TLAB的矩阵和数组的运算3)掌握MA TLAB符号表达式的创建4)熟悉符号⽅程的求解2实验内容(任选6题)1.利⽤rand等函数产⽣下列矩阵:产⽣⼀个均匀分布在(-5,5)之间的随机阵(50×2),要求显⽰精度为精确到⼩数点后⼀位(精度控制指令为format)。
2.在⼀个已知的测量矩阵T(100×100)中,删除整⾏全为0的⾏,删除整列内容全为0的整列(判断某列元素是否为0⽅法:检查T(: , i) .* (T(: , j))是否为0)。
3.假设汽车系在下列各年度的⼈⼝统计如表所⽰试⽤⼀个⼆维矩阵STU表⽰上述数据,并请计算出下列各数值:(1)汽车系在2002~2006年之间的每年平均新⽣、毕业⽣⼈数。
(2)5年来汽车系共有多少毕业⽣?(3)在哪⼏年,新⽣数⽬⽐毕业⽣多?(4) 5年来每年的毕业⽣对新⽣的⽐例平均值为何? 4. 完成下列矩阵运算:(1)使⽤randn 产⽣⼀个(10×10)的矩阵A(2)计算B=(A+A ’)/2。
请注意,B ⼀定是⼀个对称矩阵(3)计算矩阵B 的特征向量e 1 e 2 … e 10(使⽤函数eig )(4)验证在i 不等于j 的情况下,e i 和e j 的内积必定为05. 下列 MA TLAB 语句⽤于画出函数 x 0.2e 2)-=y(x 在 [0, 10] 的值。
x = 0:0.1:10; y = 2*exp(-0.2*x); plot(x, y);利⽤ MA TLAB 的M-⽂件编辑器创建⼀个新的 M-⽂件,输⼊上述代码,保存为⽂件test1.m 。
刹车距离matlab制图
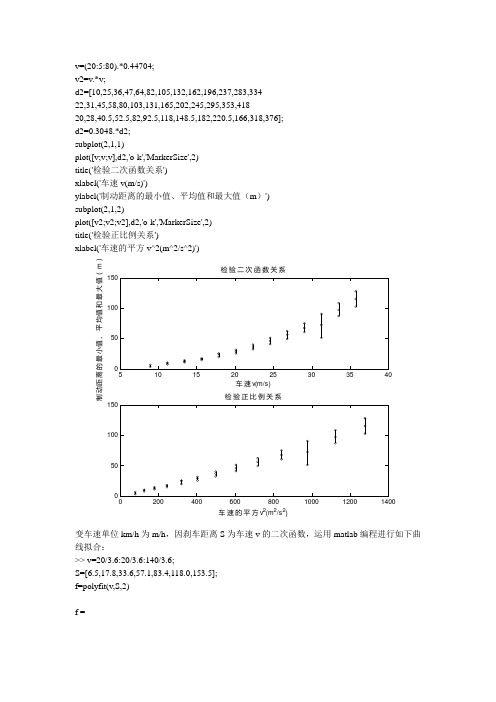
v=(20:5:80).*0.44704;v2=v.*v;d2=[10,25,36,47,64,82,105,132,162,196,237,283,33422,31,45,58,80,103,131,165,202,245,295,353,41820,28,40.5,52.5,82,92.5,118,148.5,182,220.5,166,318,376];d2=0.3048.*d2;subplot(2,1,1)plot([v;v;v],d2,'o-k','MarkerSize',2)title('检验二次函数关系')xlabel('车速v(m/s)')ylabel('制动距离的最小值、平均值和最大值(m )')subplot(2,1,2)plot([v2;v2;v2],d2,'o-k','MarkerSize',2)title('检验正比例关系')xlabel('车速的平方v^2(m^2/s^2)')050100150检验二次函数关系车速v(m/s)制动距离的最小值、平均值和最大值(m )050100150检验正比例关系车速的平方v 2(m 2/s 2)变车速单位km/h 为m/h ,因刹车距离S 为车速v 的二次函数,运用matlab 编程进行如下曲线拟合:>> v=20/3.6:20/3.6:140/3.6;S=[6.5,17.8,33.6,57.1,83.4,118.0,153.5];f=polyfit(v,S,2)f =0.0851 0.6617 -0.1000绘制图形程序如下:>> v=20/3.6:0.1:140/3.6;S=0.0851*v.^2+0.6617*v-0.1000;plot(v,S)xlabel('车速m/s');ylabel('刹车距离/m');title('车速与刹车距离关系图');510152025303540020406080100120140160车速m/s 刹车距离/m 车速与刹车距离关系图matlab 拟合,汽车刹车距离x=[29.3,44,58.7,73.3,88,102.7,117.3];y=[42,73.5,116,173,248,343,464];y=0.75x+k v*2拟合k2030405060708090100110120050100150200250300350400450500x y%%安全距离%%前车静止clc;clear all;t1=1; % t1:驾驶员反应时间 0.4-1.5s ;t2=0.45; %t2:从踩下制动踏板到获得最大制动力经历时间,0.2—0.9s ;k=1.03; % k :汽车质量和转动件当量惯量系数,空挡制动时 k=1.03,非空挡制动 % k=1.09;g=9.8; %g :重力加速度,g=9.8;m:本车质量phi=[0.07,0.15,0.45,0.65,0.7]; % phi :车轮与路面的附着系数,随路况变化,该数值参考《汽车行驶纵向安全距离具体数值的研究》colors = ['r' 'g' 'b' 'c' 'm'];for j=1:5v0=5:25:80; %制动时刻汽车的速度,单位km/h;s1=(v0/3.6)*t1; %驾驶员反应时间内汽车行驶距离v1=(v0/3.6)-(0.5*phi(j)*g*t2)/k; %制动力逐渐增长到最大值时汽车的速度s2=k*((v0/3.6).^2-v1.^2)/(phi(j)*g); %制动力逐渐增长过程中汽车行驶的距离s3=0.5*k*v1.^2/(phi(j)*g); %以最大的制动力完成制动所行驶的距离ds=s1+s2+s3; %安全距离plot(v0,ds,v0,ds,'color',colors(j),'LineWidth',3);hold on;end01020304050607080050100150200250300350400x y 不同的phi 值对应的曲线。
数学建模计算实验1

《数学建模》实验一:matlab函数拟合学时:4学时实验目的:掌握用matlab进行函数拟合的方法。
实验内容:实例1.(汽车刹车距离问题)某汽车司机培训课程中有这样的规则:正常驾驶条件下,车速每增16公里/小时,后面与前车的距离应增一个车身的长度。
实现这个规则的渐变办法是“2秒准则”:后车司机从前车经过某一标志开始默数2秒钟后到达同一标志,而不管车速如何。
这个规则的合理性如何是否有更合理的规则。
下表是测得的车速和刹车距离的一组数据。
车速(km/h)20 40 60 80 100 120 140刹车距离(m) 6.5 17.8 33.6 57.1 83.4 118.0 153.5解:模型假设:(1)刹车距离y等于反映距离y1与制动距离y2之和。
即y=y1+y2.(2)反应距离y1与车速v成正比,比例系数为反应时间k1。
即y1=k1*v(3)刹车时使用最大制动力F,F作的功等于汽车动能的改变,且F与车的质量m成正比.即模型建立由假设2,y1=k1v,由假设3,在F作用下行驶距离y2作的功F*y2使车速从v→0,动能的变化为mv^2/2,又由牛顿第二定律可知F=am,,其中刹车时的减速度a为常数,于是y2=k2*v^2,其中k2为比例系数,实际k2=1/2a,由假设1,刹车距离为 y=k1v +k2v^2模型求解:用最小二乘法拟合,则程式运行过程有:>> v=[20,40,60,80,100,120,140]./3.6;>> s=[6.5,17.8,33.6,57.1,83.4,118.0,153.5];>> fun=inline('k(1).*v+k(2).*v.*v','k','v');>> k=lsqcurvefit(fun,[20,140],v,s)Optimization terminated: relative function valuechanging by less than OPTIONS.TolFun.k =0.6522 0.0853于是s=0.6522v+0.0853v^2;模型应用:因为在实际中k2=1/2a 则a=5.86166 v=at1 且k1为反应时间,即最终时间:t=k1+t1 ,t1为刹车时间。
实验三 MATLAB的符号运算(答案)

MATLAB实验报告
专业班级
姓名
学号
成绩评定
电气与信息学院
和谐勤奋求是创新
实验教学考核和成绩评定办法
1.课内实验考核成绩,严格按照该课程教学大纲中明确规定的比重执行。
实验成绩不合格者,不能参加课程考试,待补做合格后方能参加考试。
2.单独设立的实验课考核按百分制评分,考核内容应包括基本理论、实验原理和实验。
3.实验考核内容包括:1)实验预习;2)实验过程(包括实验操作、实验记录和实验态度、表现);3)实验报告;权重分别为0.2 、0.4 、0.4;原则上根据上述三个方面进行综合评定。
学生未取得1)和2)项成绩时,第3)项成绩无效。
4.实验指导教师应严格按照考核内容分项给出评定成绩,并及时批改实验报告,给出综合成绩,反馈实验中出现的问题。
实验成绩在教师手册中有记载。
实验报告主要内容
一.实验目的
二.实验仪器及设备
三.实验原理
四.实验步骤
五.实验记录及原始记录
六.数据处理及结论
七. 思考题
八.实验体会(可选项)
注:1. 为了节省纸张,保护环境,便于保管实验报告,统一采用A4纸,实验报告建议双面打印(正文采用宋体五号字)或手写,右侧装订。
2. 实验类别指验证、演示、综合、设计、创新(研究)、操作六种类型实验。
3. 验证性实验:是指为了使学生巩固课程基本理论知识而开设的强调演示和证明,注重实验结果(事实、
概念或理论)的实验。
4. 综合性实验:是指实验内容涉及本课程的综合知识或本课程相关的课程知识的实验。
5. 设计性实验:是指给定实验目的、要求和实验条件,由学生自行设计实验方案并加以实现的实验。
数学建模计算实验2
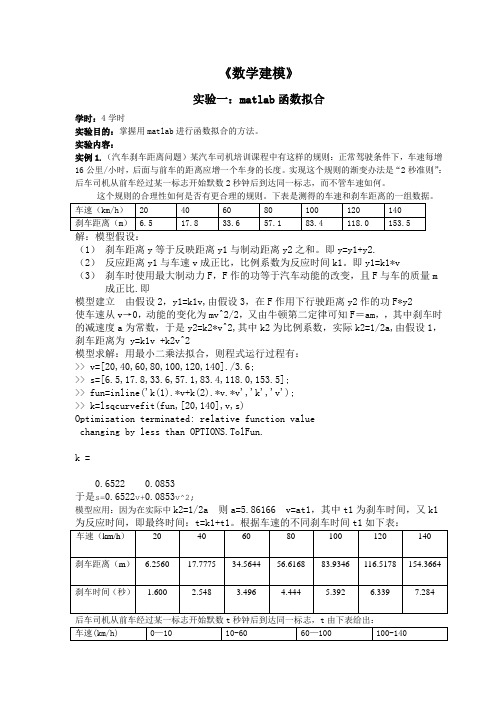
《数学建模》实验一:matlab函数拟合学时:4学时实验目的:掌握用matlab进行函数拟合的方法。
实验内容:实例1.(汽车刹车距离问题)某汽车司机培训课程中有这样的规则:正常驾驶条件下,车速每增16公里/小时,后面与前车的距离应增一个车身的长度。
实现这个规则的渐变办法是“2秒准则”:后车司机从前车经过某一标志开始默数2秒钟后到达同一标志,而不管车速如何。
这个规则的合理性如何是否有更合理的规则。
下表是测得的车速和刹车距离的一组数据。
车速(km/h)20 40 60 80 100 120 140刹车距离(m) 6.5 17.8 33.6 57.1 83.4 118.0 153.5解:模型假设:(1)刹车距离y等于反映距离y1与制动距离y2之和。
即y=y1+y2.(2)反应距离y1与车速v成正比,比例系数为反应时间k1。
即y1=k1*v(3)刹车时使用最大制动力F,F作的功等于汽车动能的改变,且F与车的质量m 成正比.即模型建立由假设2,y1=k1v,由假设3,在F作用下行驶距离y2作的功F*y2使车速从v→0,动能的变化为mv^2/2,又由牛顿第二定律可知F=am,,其中刹车时的减速度a为常数,于是y2=k2*v^2,其中k2为比例系数,实际k2=1/2a,由假设1,刹车距离为 y=k1v +k2v^2模型求解:用最小二乘法拟合,则程式运行过程有:>> v=[20,40,60,80,100,120,140]./3.6;>> s=[6.5,17.8,33.6,57.1,83.4,118.0,153.5];>> fun=inline('k(1).*v+k(2).*v.*v','k','v');>> k=lsqcurvefit(fun,[20,140],v,s)Optimization terminated: relative function valuechanging by less than OPTIONS.TolFun.k =0.6522 0.0853于是s=0.6522v+0.0853v^2;模型应用:因为在实际中k2=1/2a 则a=5.86166 v=at1,其中t1为刹车时间,又k1为反应时间,即最终时间:t=k1+t1。
MATLAB缉私艇追击走私船 数学建模

y
o始位置在点(0,0), 走私船初始位置在点(0,0), (0,0) 行驶方向为y轴正方向, 行驶方向为y轴正方向, 缉私艇的初始位置在点( ,0), 缉私艇的初始位置在点(c,0), 缉私艇行驶的路程为s 。 在时刻t 在时刻t: 走私船的位置到达点 R(0, at ) 缉私艇到达点 D ( x, y )
dy 1 x r c r = − dx 2 c x y (c ) = 0
3) r
=1
1 x2 − c2 x , y = 2 2c − c ln c
y → +∞ ,缉私艇不可能追赶上走私船。 缉私艇不可能追赶上走私船。
MATLAB软件仿真法 软件仿真法 缉私艇的初始位在点( ,0), 缉私艇的初始位在点(c,0), (0 t = t k : 走私船的位置: , at k ) 走私船的位置: 缉私艇的位置: 缉私艇的位置 ( xk , yk )
y
走私船初始位在点(0,0),方向为y轴正方向, 走私船初始位在点(0,0),方向为y轴正方向, (0,0)
11.2 缉私艇追击走私船
1 实验目的 (1)学会用MATLAB软件求解微分方程的初值问题; (2)了解微分方程数值解的思想,掌握微分方程数值解的方法; (3)学会根据实际问题建立简单微分方程数学模型,提高解决问题能力; (4)了解简单的计算机仿真和数据模拟的基本方法.
2 实验问题 海上边防缉私艇发现距c公里处有一走私船正以匀速a沿直线行驶,缉私艇 立即以最大速度b追赶,在雷达的引导下,缉私艇的方向始终指向走私船。问 缉私艇何时追赶上走私船?并求出缉私艇追赶的路线。
k +1
~ = a ( t + ∆t ) yk +1 k
利用MATLAB进行验证性实验1.划艇比赛的成绩2.机动车刹车距离生猪的出售时机模型求解

利⽤MATLAB进⾏验证性实验1.划艇⽐赛的成绩2.机动车刹车距离⽣猪的出售时机模型求解河北⼤学《数学模型》实验实验报告班级专业15计科2班姓名张宇轩学号20151101006实验地点C1-229指导⽼师司建辉成绩实验项⽬利⽤MATLAB进⾏验证性实验1.划艇⽐赛的成绩2.汽车刹车距离3.⽣猪的出售时机模型求解⼀、实验⽬的学会利⽤MATLAB进⾏验证性实验,熟练掌握⽤数据拟合求解模型和参数。
了解并使⽤最⼩⼆乘多项式拟合函数polyfit,仿照案例今后能够⾃⼰解决图形问题。
⼆、实验要求1.划艇⽐赛的成绩的模型:t=αnβ其中,t为⽐赛成绩(时间),n为桨⼿⼈数,α和β为参数。
为适合数据拟合,将模型改为:log t=log α+βlog桨⼿⼈数n ⽐赛平均成绩t1 7.172 6.884 6.328 5.841>. 参数α和β估计程序如下:clear;clc;n=[1 2 4 8];t=[ 7.21 6.88 6.32 5.84];logt=log(t);logn=log(n);p=polyfit(logn,logt,1);beta=p(1)alfa=exp(p(2))2>. 实际值与计算值⽐较(数据⽐较和和拟合图形)参考数据结果:ans =1 7.21 7.28422 6.88 6.77994 6.32 6.31068 5.84 5.8737参考图形结果:图1:题给拟合图形结果要求:1)运⾏以上程序。
2)编程:实际值与计算值⽐较(数据⽐较和和拟合图形)。
3)⽤help查询函数polyfit的⽤法。
2.汽车刹车距离的模型:d=t1v+kv2其中,d为刹车距离,变量v为车速,参数t1为反应时间,参数k为⽐例系数。
取经验值t1=0.75秒。
实际数据表车速实际刹车距离(英⾥/⼩时)(英尺/秒)(英尺)20 29.3 4430 44.0 7840 58.7 12450 73.3 18660 88.0 26870 102.7 37280 117.3 506①⽤数据拟合求参数k为适合数据拟合,将模型改为:y=k其中y=(d-0.75v)/v2程序如下:clear;clc;v=[29.3 44.0 58.7 73.3 88.0 102.7 117.3]; %英尺/秒d=[44 78 124 186 268 372 506]; %最⼤实际刹车距离(英尺)y=(d-0.75*v)./v.^2;k=polyfit(v,y,0)②⽤所得模型计算刹车距离和刹车时间(数据⽐较)程序如下:clear;clc;k= ; %输⼊上题所求得的结果v=[29.3 44.0 58.7 73.3 88.0 102.7 117.3]; %英尺/秒d=[44 78 124 186 268 372 506]; %最⼤实际刹车距离(英尺)dd=0.75*v+k*v.^2; %计算刹车距离t=d./v; %计算刹车时间format short g;[v',d',round(10*[dd',t'])/10]③实际和计算刹车距离的⽐较(拟合图形)程序如下:clear;clc;k= ; %输⼊题1所求得的结果vh=[20 30 40 50 60 70 80]; %英⾥/⼩时v=[29.3 44.0 58.7 73.3 88.0 102.7 117.3];% 英尺/秒d=[44 78 124 186 268 372 506];% 最⼤实际刹车距离(英尺)dd=0.75*v+k*v.^2; %计算刹车距离plot(vh,d,'r+',vh,dd,'b-');title('实际和计算刹车距离的⽐较');axis([20,80,0,510]);xlabel('v 英⾥/⼩时');ylabel('d 英尺');要求:1)运⾏以上程序,结果与教材相应内容⽐较。
浙教版 2021-2022学年度八年级数学上册模拟测试卷 (14688)

(浙教版)2021-2022学年度八年级数学上册模拟测试卷学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.要了解一批电视机的使用寿命,从中任意抽取30台电视机进行试验,在这个问题中,30是( )A .个体B .总体C .样本容量D .总体的一个样本2.如图所示,下列判断正确的是( )A .若∠1 =∠2,则1l ∥2lB .若∠1 =∠4,则3l ∥4lC .若∠2=∠3,则1l ∥2lD .若∠2=∠4,则1l ∥2l3. 如图,不能判定 a ∥b 是( )A .∠1=∠4B .∠1=∠3C .∠2=∠3D .∠3=∠44.如图,能判定EB ∥AC 的条件是( )A .∠C =∠ABEB .∠A =∠EBDC .∠C =∠ABCD .∠A =∠ABE5.如图所示,已知直角三角形ABC 中,∠ABC=90°,BD 平分∠ABC ,CE 平分∠ACB ,CE 、BD 相交于点F ,∠EFB=65°,则∠A=( )A .30°B .40°C .45°D .50°6.已知一个三角形的周长为l5 cm,且其中两边长都等于第三边的2倍,那么这个三角形的最短边为()A.1cm B.2cm C.3 cm D.4 cm7.由若干个相同的小正方体搭成的几何体的俯视图如图,各小方体内的数字表示叠在该层位置的小正方体个数,则这个几何体的左视图是()A.B.C.D.8.某物体的三视图是如图所示的三个图形,那么该物体的形状是()A.长方体B.圆锥体C.正方体D.圆柱体9.如图,由∠2=∠3,可以得出的结论是()A .FG∥BC B.FG∥CE C.AD∥CE D.AD∥BC10.下面四个图形中,经过折叠能围成如图所示的立方体纸盒的是()A. B. C.D.11.如图,直线l与直线a,b相交,且a∥b,∠1=800,则∠2的度数是()A.600 B.800 C.1000 D.120012.下列调查方式中,不合适的是( )A .了解2008年5月18日晚中央也视台“爱的奉献”抗震救灾文艺晚会的收视率,采用抽查的方式B .了解某渔场中青鱼的平均重量,采用抽查的方式C .了解某型号联想电脑的使用寿命,采用普查的方式D .了解一批汽车的刹车性能,采用普查的方式13.在数轴上表示不等式2x ≥-的解集,正确的是( ) .A .B .C .D . 14.如果关于x 的不等式(1)1a x a +>+的解集为1x <,那么 a 的取值范围是( )A .0a >B .0a <C .1a >-D .1a <-15.下列不等式变形正确的是( )A 由412x ->得41x >B .由24x -<得2x <-C .由02y >得2y >D .由53x >得35x > 16.小明将若干个苹果向若干只篮子里分放,若每只篮子分 4个苹果,还剩 20个未分完;若每只篮子里分放 8个苹果,则还有一只篮子没有放,那么小明共有苹果的个数为( )A .44个B . 42个C . 40个D . 38个17.在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形相比( )A .向右平移了3个单位B .向左平移了3个单位C .向上平移了3个单位D .向下平移了3个单位18.点(0,1),(12,0),(-1,-2),(-1,0)中,在x 轴上的点有( )A .1个B .2个C .3个D .4个 19.在海上,灯塔位于一艘船的北偏东40°方向,那么这艘船位于这个灯塔的 ( )A .南偏西50°方向B .南偏西40°方向C .北偏东50°方向D .北偏东40°方向20.直三棱柱、多面体和棱柱之间的包含关系,可以用图形表示为( )A .B .C .D . 二、填空题21.已知一个正比例函数的图象经过点(-4,12),则这个正比例函数的解析式是 . 22.如图是我市2月份某天24小时内的气温变化图,则该天的最大温差是 ℃.23.若关于x 的方程组321431x y p x y p +=+⎧⎨+=-⎩的解满足i x y <,则p 的取值范围是 . 24.一射击运动员连续射靶10次,其中2次命中10环,3次命中9环,5次命中8环,则他 平均每次命中 环.25.一个几何体的三视图如图所示,则该几何体是 .26.在△ABC 中,∠A = 60°,若要使它为等边三角形,则需补充条件: (只需写出一个条件).27.在△ABC 中,到AB ,AC 距离相等的点在 上.28.如图,在Rt △ABC 中,∠C=Rt ∠,AC=6,AB=BC+2,则斜边AB 长为 .29.如图,已知AB ∥CD ,AD ∥BC ,∠B=60°,∠EDA=50°则∠CDO= .30.如图,1l ⊥2l , 3l ⊥2l ,则1l 3l ,理由是 .31.如图,∠1 = 120°,∠2= 60°,则直线 a 与b 的位置关系是 .三、解答题32.甲、乙两人打靶,前三枪甲的成绩分别为9环、8环和7环,乙的成绩为l0环、9环和6环,第四枪甲打了8环.问:(1)乙第四枪要打多少环才能与甲的平均环数相同?(2)在(1)中,如果乙打了这个环数,那么谁发挥得较稳定?33.如图 ,当∠1 = 50°,∠2 = 130°时,直线1l ,2l 平行吗?为什么?34.如图 ,已知 AB ∥DE ,∠B =∠E ,试说明 BC ∥EF.35.如图,在△ABC 中,AB=AC,若AD∥BC,则 AD 平分∠C,请说明理由.36.如果将直角三角形的三条边长同时扩大一倍,得到三角形还是直角三角形吗?扩大n倍呢(n为正整数)?37.如图,已知∠ABC、∠ADC都是直角,BC=DC.说明:DE=BE.38.已知,如图,点B,F,C,E在同一直线上,AC,DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE.试说明:(1)△ABC≌△DEF;(2)GF=GC.39.如图,∠ABC的平分线BF 与△ABC 中∠ACB的相邻外角的平分线CF相交于点F,过F 作DF ∥BC ,交AB 于D ,交AC 于E ,则:(1)图中有哪几个等腰三角形?并说明理由.(2)BD ,CE ,DE 之间存在着什么关系?请证明.40.如图,已知∠α=∠β=60°,求:(1)∠α的同位角∠1的度数;(2) ∠α的同旁内角∠2的度数.41.一位美术老师在课堂上进行立体模型素描教学时,把由圆锥与圆柱组成的几何体(如图 所示,圆锥放置在圆柱上底面的正中间)摆在讲桌上,请画出这个几何体的三视图.42.已知y 是z 的一次函数,z 是x 的正比例函数,问:(1)y 是x 的一次函数吗?(2)若当5x =时,2y =-;当3x =-时,6y =;当=1x 时,求y 的值.43.小玲家的鱼塘里养了2000条鲢鱼,现准备打捞出售,为了估计鱼塘中鲢鱼的总量,从鱼塘中捕捞了3次进行统计,得到数据如下表:试求出鱼塘中鲢鱼的总质量约是多少?44.某校八年级(1)班的一个研究性学习小组的研究课题是“杭州市某高速公路入口的汽车流量问题”.某天上午,他们在该入口处每隔相等的时间,对3分钟内通过的汽车的数量作一次统计,得到如下数据:(1)求平均每3分钟通过汽车多少辆?(2)试估计这天上午(按4小时计)该入口处平均每小时通过多少辆汽车?45.(1)你能找出几个使不等式2 2.515x-≥⋅成立的x的值吗?(2)x=3,5,7 能使不等式225 1.5x-⋅≥成立吗?46.小华家距离学校 2.4 km,某一天小华从家中出发去上学,恰好行走到一半的路程时,发现离到校时间只有 12 min 了.如果小华要按时赶到学校,那么他行走剩下的一半路程的平均速度至少要达到多少?47.张师傅投资 2 万元购买一台机器生产某种产品.己知这种产品的每个成本是 3 元,每个销售价为 5 元,应缴税款和其他费用是销售收入的 12%,问至少要生产、销售多少个产品才能使利润(利润=毛利润一税款和其他费用)超过购买机器的投资款?48.如图,若用A(2,1)表示放置2个胡萝卜,1棵青菜;点B(4,2)表示放置4个胡萝卜, 2棵青菜.(1)请写出其他各点C、D、E、F所表示的意义;(2)若一只小兔子从A到达B(顺着方格走),有以下几条路径可选择:①A→C→D→B;②A→E→D→B;③A→E→F→B.问:走哪条路径吃到的胡萝卜最多?走哪条路径吃到的青菜最多?49.如图所示,在直角坐标系xOy中,A(一l,5),B(一3,0),0(一4,3).(1)在右图中作出△ABC关于y轴的轴对称图形△A′B′C′;(2)写出点C关于,轴的对称点C′的坐标(_____,_______).50.画出如图所示立体图形的三视图.【参考答案】一、选择题1.C2.C3.D4.D5.D6.C7.A8.D9.B10.B11.B12.C14.D 15.D 16.A 17.D 18.B 19.B 20.A二、填空题21.无22.无23.无24.无25.无26.无27.无28.无30.无31.无三、解答题32.无33.无34.无35.无36.无37.无38.无39.无40.无41.无42.无43.无44.无46.无47.无48.无49.无50.无。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北大学《数学模型》实验实验报告班级专业15计科2班姓名张宇轩学号20151101006实验地点C1-229指导老师司建辉成绩实验项目利用MATLAB进行验证性实验1.划艇比赛的成绩2.汽车刹车距离3.生猪的出售时机模型求解一、实验目的学会利用MATLAB进行验证性实验,熟练掌握用数据拟合求解模型和参数。
了解并使用最小二乘多项式拟合函数polyfit,仿照案例今后能够自己解决图形问题。
二、实验要求1.划艇比赛的成绩的模型:t=αnβ其中,t为比赛成绩(时间),n为桨手人数,α和β为参数。
为适合数据拟合,将模型改为:log t=log α+βlog桨手人数n 比赛平均成绩t1 7.172 6.884 6.328 5.841>. 参数α和β估计程序如下:clear;clc;n=[1 2 4 8];t=[ 7.21 6.88 6.32 5.84];logt=log(t);logn=log(n);p=polyfit(logn,logt,1);beta=p(1)alfa=exp(p(2))2>. 实际值与计算值比较(数据比较和和拟合图形)参考数据结果:ans =1 7.21 7.28422 6.88 6.77994 6.32 6.31068 5.84 5.8737参考图形结果:图1:题给拟合图形结果要求:1)运行以上程序。
2)编程:实际值与计算值比较(数据比较和和拟合图形)。
3)用help查询函数polyfit的用法。
2.汽车刹车距离的模型:d=t1v+kv2其中,d为刹车距离,变量v为车速,参数t1为反应时间,参数k为比例系数。
取经验值t1=0.75秒。
实际数据表车速实际刹车距离(英里/小时)(英尺/秒)(英尺)20 29.3 4430 44.0 7840 58.7 12450 73.3 18660 88.0 26870 102.7 37280 117.3 506①用数据拟合求参数k为适合数据拟合,将模型改为:y=k其中y=(d-0.75v)/v2程序如下:clear;clc;v=[29.3 44.0 58.7 73.3 88.0 102.7 117.3]; %英尺/秒d=[44 78 124 186 268 372 506]; %最大实际刹车距离(英尺)y=(d-0.75*v)./v.^2;k=polyfit(v,y,0)②用所得模型计算刹车距离和刹车时间(数据比较)程序如下:clear;clc;k= ; %输入上题所求得的结果v=[29.3 44.0 58.7 73.3 88.0 102.7 117.3]; %英尺/秒d=[44 78 124 186 268 372 506]; %最大实际刹车距离(英尺)dd=0.75*v+k*v.^2; %计算刹车距离t=d./v; %计算刹车时间format short g;[v',d',round(10*[dd',t'])/10]③实际和计算刹车距离的比较(拟合图形)程序如下:clear;clc;k= ; %输入题1所求得的结果vh=[20 30 40 50 60 70 80]; %英里/小时v=[29.3 44.0 58.7 73.3 88.0 102.7 117.3];% 英尺/秒d=[44 78 124 186 268 372 506];% 最大实际刹车距离(英尺)dd=0.75*v+k*v.^2; %计算刹车距离plot(vh,d,'r+',vh,dd,'b-');title('实际和计算刹车距离的比较');axis([20,80,0,510]);xlabel('v 英里/小时');ylabel('d 英尺');要求:1)运行以上程序,结果与教材相应内容比较。
2)题2和题3中要求输入题1所求得的k值。
3)理解程序。
3.生猪的出售时机模型求解目标函数(生猪出售纯利润,元):Q(t)=(8-gt)(80+rt)-4t-640其中,t≥0为第几天出售,g为每天价格降低值(常数,元/公斤),r为每天生猪体重增加值(常数,公斤)。
求t使Q(t)最大。
①图解法绘制目标函数Q(t)=(8-gt)(80+rt)-4t-640的图形(0≤t≤20)。
其中,g=0.1, r=2。
程序如下:clear;clc;g=0.1;r=2;fplot(@(t)(8-g*t)*(80+r*t)-4*t-640,[0,20]);grid;xlabel('t'); ylabel('Q');②代数法对目标函数Q(t)=(8-gt)(80+rt)-4t-640用MATLAB求t使Q(t)最大。
其中,r,g是待定参数。
程序如下:clear;clc;syms t;%定义符号变量tQ=sym('(8-g*t)*(80+r*t)-4*t-640') %建立符号表达式dQ=diff(Q,'t') %求微分dQ/dtt=solve(dQ,t) %求dQ=0的解tr=2;g=0.1;t=eval(t) %求r=2,g=0.1时的t值Q=eval(Q) %求r=2,g=0.1,t=10时的Q值(最大值)要求:1)运行以上程序。
2)理解程序,对照教材相关内容。
三、实验内容划艇比赛的成绩1.用数据拟合求参数α和β。
给出α和β值和模型:alfa =7.2842bata =-0.1035模型:log t=log α+βlog n或t=αnβ2.实际值与计算值比较(数据比较和和拟合图形),程序和运行结果。
数据比较:>> [n',t',(alfa*n.^bata)']ans =1.0000 7.2100 7.28422.0000 6.8800 6.78014.0000 6.3200 6.31098.0000 5.8400 5.8742拟合图形:图2:拟合图形结果源程序如下:>> n=[1 2 4 8];>> t=[7.21 6.88 6.32 5.84];>> logt=log(t);>> logn=log(n);>> p=polyfit(logn,logt,1);>> bata=p(1);>> alfa=exp(p(2));>> x=0:0.01:10;>> y=alfa*x.^bata;>> plot(n,t,'r+',x,y);>> axis[0,10,5,11]>> [n',t',(alfa*n.^bata)']汽车的刹车距离1.用数据拟合求参数k。
给出k值和模型。
k =0.0258模型:k=(d-0.75v)/v22.用所得模型计算刹车距离和刹车时间(数据比较),运行结果。
>> k=0.0258;>> v=[29.3 44.0 58.7 73.3 88.0 102.7 117.3];>> d=[44 78 124 186 268 372 506];>> dd=0.75*v+k*v.^2;>> t=d./v;>> format short g;>> [v',d',round(10*[dd',t'])/10]ans =29.3 44 44.1 1.544 78 82.9 1.858.7 124 132.9 2.173.3 186 193.6 2.588 268 265.8 3102.7 372 349.1 3.6117.3 506 443 4.33.实际和计算刹车距离的比较(拟合图形),运行结果。
>> k=0.0258;>> vh=[20 30 40 50 60 70 80];>> v=[29.3 44.0 58.7 73.3 88.0 102.7 117.3];>> d=[44 78 124 186 268 372 506];>> dd=0.75*v+k*v.^2;>> plot(vh,d,'r+',vh,dd,'b-');>> title('实际和计算刹车距离的比较');>> axis([20,80,0,510]);>> xlabel('v 英里/小时');>> ylabel('d 英尺');图3:拟合图形结果生猪的出售时机模型求解1.题1程序运行结果,从函数图估计t为何值时函数取得最大值。
>> g=0.1;r=2;>> fplot(@(t)(8-g*t)*(80+r*t)-4*t-640,[0,20]);>> grid;>> xlabel('t'); ylabel('Q');图4:拟合图形结果当t=10时函数取得最大值2. 题2程序运行结果。
>> syms t;>> Q=sym('(8-g*t)*(80+r*t)-4*t-640')Q =(8-g*t)*(80+r*t)-4*t-640>> dQ=diff(Q,'t')dQ = -g*(80+r*t)+(8-g*t)*r-4>> t=solve(dQ,t)t =2*(-20*g+2*r-1)/g/r>> r=2;g=0.1;>> t=eval(t)t =10>> Q=eval(Q)Q =20四、实验结果及其分析1.polyfit函数用法:polyfit函数是matlab中用于进行曲线拟合的一个函数。
曲线拟合:已知离散点上的数据集,即已知在点集上的函数值,构造一个解析函数(其图形为一曲线)使在原离散点上尽可能接近给定的值。
调用方法:polyfit(x,y,n)。
用多项式求过已知点的表达式,其中x为源数据点对应的横坐标,可为行向量、矩阵,y为源数据点对应的纵坐标,可为行向量、矩阵,n为你要拟合的阶数,一阶直线拟合,二阶抛物线拟合,并非阶次越高越好,看拟合情况而定。
2关于实验:划艇比赛的成绩.将浆手人数和比赛平均成绩作为两个向量,根据模型,将两向量分别取对数后进行一次拟合,并求出参数alfa =7.2842和bata =-0.1035。
