坡度概念解释
勾选定义坡度的含义

勾选定义坡度的含义好嘞,咱们今天聊聊坡度这个事儿,听起来挺无聊的,但其实它可是个很有趣的话题呢。
想象一下,走在一条山路上,周围绿树成荫,鸟儿在枝头叽叽喳喳。
突然你发现,路面开始变得斜斜的,嘿,这就是坡度在跟你打招呼啦!坡度啊,简单来说,就是地面的倾斜程度。
你走得累不累,能不能一口气爬上去,都是这坡度说了算。
坡度小,平坦,简直像在散步;坡度大,那可真是攀登珠穆朗玛峰的感觉,腿都要给你累断了。
再说这坡度的计算,听上去复杂,实际上跟咱们的日常生活有着千丝万缕的联系。
比如说,骑车上坡和下坡的感觉就完全不同了。
上坡的时候,那真是“哎呀妈呀,心累腿累”,下坡就像飞起来了一样,风在耳边呼啸,感觉自己成了赛车手。
想想看,坡度如果大,骑上去简直就是“蜗牛爬山”,但是下来的时候就有种“飞流直下三千尺”的快感,简直就是人生巅峰!这坡度还有很多不同的表现形式呢,比如说建筑工地上的斜坡,这可是工人们的好帮手。
你要是光靠人力推东西,上下搬运可真是麻烦透顶。
有了斜坡,直接就能把重物轻松推上去,真是太方便了!这坡度设计得合适的话,能让每个人都轻松上下,简直就像为每个人开了一扇方便之门。
说到坡度,很多人可能第一反应就是数学公式。
坡度的公式在生活中也有趣得很。
就像咱们吃饭的时候,盘子放得不平,东西总是往一边滑。
这就是坡度在作祟啊,弄得一桌子狼藉。
坡度合适,菜就能稳稳当当地待在盘子里,不然你可就得一边吃一边捡了,尴尬得不行。
还有一种坡度叫做“地理坡度”,这可是给自然景观打分的,山有多高,坡有多陡,都是一目了然的。
那些壮丽的山川河流,都是因为这坡度的存在。
想想看,去旅游的时候,那些高高的山顶,登顶的瞬间,简直就是“会当凌绝顶,一览众山小”的感觉,真的是回忆满满,心里美滋滋的。
然后,咱们再说说坡度对生活的影响。
你想啊,坡度大了,交通就得受影响,汽车上坡开得慢,下来又快,司机得小心翼翼。
这就让我想起了一个老话,叫“趁热打铁”,其实在坡度的世界里,也可以说是“趁坡行路”,掌握好坡度的变化,生活也能轻松一些。
汽车出土马道的坡度-概述说明以及解释

汽车出土马道的坡度-概述说明以及解释1.引言1.1 概述在概述部分,我们将介绍关于汽车出土马道坡度的背景和基本概念。
汽车出土马道是指在农田、山区或者其他特殊环境下,车辆通行时需要通过的一种特殊道路类型,其路面通常由土壤或泥土构成。
在这些地区,由于地势的限制,道路往往需要经过开挖或填土来达到适宜车辆通行的要求。
在这个过程中,坡度是一个非常重要的因素。
坡度是指路面或道路在水平方向上的倾斜程度,通常以百分比或度数来表示。
它可以影响到车辆的行驶稳定性、牵引力以及制动性能。
在汽车出土马道中,坡度对车辆行驶具有重要的影响。
首先,陡峭的坡度会增加车辆上下坡时的惯性,导致制动距离增加,降低行驶的安全性。
其次,过大的坡度会影响车辆的牵引力,使得车辆在上坡时缺乏足够的动力,或者在下坡时容易失去控制。
此外,坡度还会对车辆的悬挂系统和底盘造成额外的负荷,增加了车辆的磨损和维护成本。
为了确保汽车在出土马道上安全通行,准确测量坡度是至关重要的。
目前,有多种测量方法可供选择,包括使用测斜仪、全站仪、地面测量工具等。
这些方法可以提供准确的坡度数据,帮助工程师们进行合理的设计和施工,以提高车辆的行驶性能和安全性。
综上所述,汽车出土马道的坡度是一个很重要的因素,它对车辆行驶具有直接的影响。
在接下来的正文部分,我们将深入探讨坡度对车辆行驶的影响以及测量方法。
通过对这些内容的了解,读者将能够更好地理解和应用坡度在汽车出土马道设计中的重要性。
1.2 文章结构本文将以以下几个部分展开对汽车出土马道的坡度进行深入探究。
首先,在引言部分,将对文章的背景和目的进行简要介绍。
接着,在正文部分,将分别讨论汽车出土马道的定义、坡度对汽车行驶的影响以及汽车行驶过程中坡度的测量方法。
最后,在结论部分,将总结坡度对汽车出土马道的重要性,探讨坡度设计对汽车行驶的影响,并提出对汽车出土马道坡度的建议。
通过这些内容的阐述,旨在加深对汽车出土马道坡度问题的理解,并为今后的研究和实践提供有益的参考。
28.2 应用举例 方位角、坡度、坡角

因为在 Rt△EBD 中,i=DB∶EB=1∶1, 所以 BD=EB,所以 CD+BC=AE+AB, 即 2+x=4+ 5 x,解得 x=12,所以 BC=12 米.
上,则船C到海岸线l的距离是
km. 3
4.(2017海南)为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供 的方案是水坝加高2米(即CD=2米),背水坡DE的坡度i=1∶1(即DB∶EB=1∶1),如图所示,已 知AE=4米,∠EAC=130°,求水坝原来的高度BC.(参考数据:sin 50°≈0.77, cos 50°≈0.64,tan 50°≈1.20)
探究点二:坡度与坡角问题 【例2】 如图,水坝的横断面为梯形ABCD,已知上底长CB=5米,迎水面坡度为1∶ 面坡度为1∶1,坝高为4米,求:坝底AD和迎水面CD的长及坡角α 和β .
,背3 水
【导学探究】 1.作CE⊥AD,BF⊥AD,由坡度可得,CE∶ DE =1∶ 2.由坡度是坡角的 正切 值可得坡角.
第2课时 方位角、坡度、坡角
一、方位角 1.平面测量时,经常以正北、正南方向为基准描述物体运动的方向,这种表示方向的角叫 做方位角. 2.如图,射线OA,OB,OC,OD分别表示北偏东30°,南偏东70°,南偏西50°,北偏西35°.
二、坡度、坡角 1.坡度:坡面的铅直高度(h)与水平宽度(l)的比叫做坡面的坡度(或坡比),记作 i,即 i= h .
在 Rt△BCD 中,∠CBD=30°,tan 30°= CD = 3 ,所以 CD= 3 BD≈115(km),
坡度

自行车最考体力和耐力是什么路况?毋庸置疑,多数人结论都是——爬坡。
经常也碰到一些骑友谈论骑行道路的坡度问题。
但也发现有些车友对坡度的描述和表达跟实际坡度有出入,有时也有夸大的地方。
为此专门查阅了一些资料,以期对自行车骑行坡度能有一个正确的、直观的判断,至少不会出现误差太大的错误结论。
在道路工程上,坡度都用正切百分比来表示。
知道了坡度的表示方法,再标上大家比较容易理解的角度值,能使大家更方便对照理解感受XX%的坡度(正切百分比)和多少角度(就是圆周为360度,直角为90度)的坡度。
下面请大家看俺搜集整理出来的示意图及文字说明:1、高速公路的坡度最大为3度,坡度再大的话,估计就高速不起来了。
不排除有超过这个坡度的路段,但不可能差很多,5度已经非常惊人了。
2、车库的坡道最大为8度。
肯定不能排除大于这个度数的车库坡道,因为现在不少建筑由于受到各种条件限制,不得不违反设计规范。
但是能大到多少呢?15度应该很过分了吧?3、轿车因为不越野爬山,所以设计和生产都不强求轿车的爬坡性能,一般认为,轿车的最大爬坡能力为20度就已经足够,再大的坡就不该开轿车去爬了。
设想如果有一段路为20度坡,用轿车的极限能力开上去(不是远远的开足马力冲上去,而是慢慢开上去),这样有多危险!所以我们不会遇到正常修建的机动车道路有20度以上的坡。
4、一些品牌的越野车可以达到爬30度坡的能力,请记住这是指极限能力,就算有这样的能力,想开上去也是不容易的。
经查阅,一般正规建筑内的楼梯,大量采用30度的坡度来修建,你可以随便找一处大楼内的楼梯看看,估摸一下这个坡度是否能把凯越开上去。
5、35度坡是悍马H2爬坡的极限,当今世界还没有哪种越野车能突破这个极限,要是谁遇到了35度坡,开的还不是悍马车,赶快掉头回去。
6、45度坡用百分比来表示是100%,也就是百分之一百的坡度。
用这种坡度来修建楼梯都怪吓人的,大概只有风景名胜区才有这样的梯道。
没有人会修建这样的机动车道,也不会有人看见这样的车道,因为能开上这种坡的车不存在(山地运动车、履带车、月球车、火星车除外,因为它们不需要修建道路)。
解直角三角形的应用3-坡度课件

02
坡度在生活中的应用
道路修建中的坡度
道路的坡度决定了车辆行驶的 稳定性和安全性。
适当的坡度可以减少车辆的摩 擦阻力,提高道路的通行效率。
在山区或丘陵地带,道路修建 需要合理规划坡度,以确保车 辆能够安全、顺畅地行驶。
桥梁设计中的坡度
桥梁的坡度设计关乎到桥面排水和行车安全。
在河流、峡谷等跨越障碍物的地方,桥梁的坡度设计需要充分考虑地形、水文等因 素。
应用
通过测量斜边和其中一条直角 边的长度,利用三角比计算锐 角的度数,进而求得坡度。
04
坡度计算的实例分析
实例一:道路修建中的坡度计算
确定道路起点和终点的坐标
根据道路规划图,确定道路起点的坐 标(x1, y1)和终点的坐标(x2, y2)。
计算斜边长度
利用勾股定理计算斜边长度c。
计算坡度
根据斜边长度和垂直距离h,利用坡 度公式计算坡度i。
坡度i。
根据计算得到的坡度i,结合屋 面材料和设计规范,确定屋面
的坡度和排水方式。
05
总结与展望
解直角三角形在坡度计算中的应用总结
坡度概念
坡度是描述斜坡倾斜度的一种方式,通常用角度或比例来 表示。在解直角三角形中,坡度可以通过对边和邻边的比 值计算得出。
实际应用
解直角三角形在坡度计算中有广泛的应用,例如在道路建 设、水利工程、土地测量等领域中,需要利用解直角三角 形的方法来计算斜坡的角度和倾斜度。
在几何学中,斜率是直线或曲 线的倾斜度的量度,通常用比 值或比例来表示。
对于直线,斜率等于直线上任 意两点的纵坐标之差与横坐标 之差的比值,即 $text{斜率} = frac{Delta y}{Delta x}$。
边坡坡度的概念

边坡坡度的概念
边坡坡度是公路工程设计中必须考虑的一项参数。
边坡是指公路边沿路基上的侧面,其坡度是指边坡侧面和水平面交角的大小。
边坡坡度的大小直接影响公路的安全性和稳定性,因此在公路设计和施工中必须高度重视。
边坡坡度的计算一般取决于公路路基的类型和地形地貌的特征。
在平原区域,边坡坡度的设定一般不超过1:2; 在山区,边坡坡度一般设置在1:1.5-1:2的范围内。
边坡坡度过陡,容易导致路基的滑坡、坍塌等现象;而边坡坡度过缓,则会导致边坡的可塑性增加,导致边坡下滑或模型不稳定。
在边坡坡度的设计和施工中,还需要考虑到地质条件和气候条件等因素,以保证公路的安全和稳定。
例如,在地质条件相对复杂的山区区域,需要进行地质勘测和分析,以确定边坡的自然坡度和裸露岩体的稳定性;在高寒区、雨季区等气候条件恶劣的地区,需要制定相应的加固措施,如设置截水沟、加强排水系统等,以防止边坡的冻融作用和水分侵入。
总之,边坡坡度是公路工程设计中必不可少的因素,其大小和设置需
要充分考虑地貌地形、地质条件、气候条件等因素,并制定相应的加固措施,以确保公路的安全和稳定。
倾角度与坡度计算公式

倾角度与坡度计算公式在工程和建筑领域中,倾角度与坡度是非常重要的概念。
倾角度是指某一物体与水平面之间的夹角,而坡度则是指斜面上升或下降的程度。
在实际工程中,我们经常需要计算倾角度和坡度,以便确定斜面的稳定性和适用性。
本文将介绍倾角度与坡度的计算公式,并且讨论它们在工程实践中的应用。
倾角度的计算公式如下:倾角度(θ)= arctan(斜面上升或下降的高度/斜面的水平距离)。
其中,arctan是反正切函数,斜面上升或下降的高度是指斜面的垂直距离,斜面的水平距离是指斜面的水平长度。
倾角度的单位通常是度或弧度,具体取决于所采用的计量单位。
坡度的计算公式如下:坡度(S)= 斜面上升或下降的高度/斜面的水平距离。
与倾角度的计算公式相比,坡度的计算公式更为简单,它直接给出了斜面上升或下降的高度与水平距离的比值。
坡度通常用百分比表示,例如,一个斜坡的坡度为10%意味着斜面上升或下降的高度是水平距离的10%。
在实际工程中,倾角度与坡度的计算常常涉及到地形测量、道路设计、建筑施工等方面。
例如,在道路设计中,需要确定道路的坡度,以便确保车辆能够顺利行驶而不会出现滑坡或者车辆翻车的危险。
在建筑施工中,需要计算建筑物的倾角度,以便确定墙体的倾斜程度和结构的稳定性。
因此,倾角度与坡度的计算对于工程设计和施工具有重要意义。
除了上述的基本计算公式之外,倾角度与坡度的计算还涉及到一些特殊情况和复杂情形。
例如,在地形测量中,如果地形较为复杂,需要考虑多个点的高程和位置信息,然后通过数学模型来计算整个区域的倾角度和坡度分布。
在建筑设计中,还需要考虑到建筑物的结构特点和建筑材料的性质,以便确定合适的倾角度和坡度范围。
因此,倾角度与坡度的计算不仅仅是简单的数学计算,还需要考虑到具体的工程背景和要求。
总之,倾角度与坡度是工程和建筑领域中的重要概念,它们与斜面的稳定性和适用性密切相关。
倾角度与坡度的计算公式可以帮助工程师和设计师确定斜面的倾斜程度和坡度范围,从而确保工程设计和施工的安全性和可行性。
坡度的计算方法

坡度的计算方法
坡度是地形图中表示地物面升降程度的重要概念,它也是道路、河流、山脉和其他陆地物体在自然环境中形状表现的一个重要组成部分。
那么,坡度的计算方法又有哪些呢?
首先,计算坡度时需要考虑横截面图中各点相对于水平面的空间高度差和横向距离,一般来说,坡度就是横向距离与高度差之比。
具体来说,计算坡度的步骤如下:
(1)确定坡度的起点和终点,以及中间所经过的点;
(2)测量相应的横向距离,收集所有点之间的横向距离;
(3)计算相邻的两点之间的高度差,这些点可以是起点,终点
和中间所经过的点;
(4)计算坡度。
坡度的公式为:
坡度=Σ(高度差/横向距离)/点个数
经过上述步骤之后即可得出坡度的计算结果,坡度以“度”表示,一般在0.5°~90°之间,无高度差的表面的坡度等于0°,相对于水平面升高而非下降的水平面的坡度加上90度,这是求取坡度的基本
方法。
除了以上基本方法外,坡度还可以通过各种新技术和仪器来计算。
如此计算机辅助系统(Computer-Aided System),可以测量坡度并将其表示为平面图。
另外,还有一种叫做“激光测量仪”的精密仪器,它可以测量准确而快速地测量地形特性,比如坡度,它能够测量每一米的高度差,从而更加准确地计算坡度。
总之,坡度的计算方法有基本的计算方法和精密的仪器方法,它们都可以帮助我们更准确地计算出坡度。
在计算坡度时,是否使用基本的计算方法还是精密的仪器方法,取决于实际的调查任务,如果要做到精确,还需要考虑调查范围、探测距离等多种因素。
坡度和坡度角

道路设计:坡度 角是道路设计中 重要的参数,用 于确定道路的倾 斜度和排水系统 的布置。
排水系统:坡度 决定了排水系统 的水流速度和流 向,坡度角的大 小影响排水沟的 设计和施工难度。
防洪排涝:在城 市排水设计中, 合理利用坡度和 坡度角,可以有 效地防止洪水、 内涝等自然灾害 的发生。
景观设计:在景 观设计中,可以 利用坡度和坡度 角的变化,创造 出优美的景观效 果,提高城市的 环境品质。
人为因素的影响
道路设计:道路的坡度与坡度角受到设计者的理念和习惯影响 施工方法:施工方法的选择会影响到坡度和坡度角的实现 维护管理:道路的维护和保养也会影响坡度和坡度角的变化 交通流量:交通流量的大小对坡度和坡度角的要求不同
感谢您的观看
汇报人:XX
坡度和坡度角的影响因素
第五章
地形地貌的影响
地形起伏:坡度的变化影响水流、土壤侵蚀等自然现象
坡度角大小:影响土壤的发育和植物生长,进而影响生态系统的结构和功能
地貌类型:不同的地貌类型对坡度和坡度角有不同的影响,如山地、平原、河流等 地形地貌的演变:地形地貌的长期变化会对坡度和坡度角产生影响,如河流的冲刷、 山地的抬升等
土木工程中的应用
道路设计:坡度角是道路设计中重要的参数,用于确定道路的排水和行车安全。
斜坡稳定性分析:坡度角的大小影响斜坡的稳定性,土木工程师需要根据坡度角的大 小进行斜坡稳定性分析。
土压力计算:在挡土墙设计中,坡度角是计算土压力的重要参数。
边坡防护:根据坡度角的大小,采取相应的边坡防护措施,如植草防护、挡土墙等。
土壤和地质的影响
土壤类型:不同类型的土壤对坡度和坡度角的影响不同,例如沙土和粘土的稳定性不同
土壤湿度:土壤湿度对土壤的承载能力和稳定性有影响,进而影响坡度和坡度角
关于数学坡度的知识点总结

关于数学坡度的知识点总结关于数学坡度的知识点总结坡度是数学中一个重要的概念,在几何学、物理学、工程学等领域中都有广泛的应用。
在数学中,我们通常用坡度来描述两点之间的斜率变化,可以帮助我们分析图形的变化趋势,解决各种实际问题。
本文将对数学中与坡度相关的概念和知识点进行总结和探讨,希望能为读者提供一个全面的了解。
一、坡度的定义和表示方式在数学中,两点之间的坡度是指这两点之间的斜率的变化率。
具体来说,对于两个不同的点(A, B),其坐标分别为(x1, y1)和(x2, y2),那么这两点之间的坡度可以表示为:m = (y2 - y1)/(x2 - x1)。
这里的m即为这两点之间的坡度。
二、坡度与直线的关系在解析几何学中,我们知道两点之间的坡度可以帮助我们确定一条直线的特征。
具体来说,当两点的坡度相同时,可以确定它们在同一条直线上。
而当两点的坡度不同时,说明它们不在同一条直线上。
这对我们研究直线和曲线的性质有着重要的意义。
三、坡度的意义和应用1. 判断图形的变化趋势坡度在数学中有一个重要的应用是用来判断图形的变化趋势。
例如,在二维平面上,我们可以计算一条曲线的不同点之间的坡度,根据坡度的正负可以判断这个曲线是递增还是递减的。
通过分析坡度的变化,我们可以得出曲线的最大值、最小值以及拐点等重要信息。
2. 确定最速下降线在物理学和工程学中,坡度也具有重要的意义。
例如,在滑雪场景中,我们可以利用坡度的概念来确定滑雪者在某一时间点上的最速下降线。
通常情况下,最速下降线是指在给定的时间范围内,滑雪者下降距离最短的路径。
通过计算不同点之间的坡度,我们可以找到这条最速下降线,从而提高滑雪者的速度和安全性。
3. 求解斜率和速度在物理学和工程学中,坡度也可以帮助我们求解斜率和速度相关的问题。
例如,在运动学中,我们可以根据物体的坡度和运动速度来计算物体的加速度。
另外,在工程学领域中,坡度还可以用于计算水流、气流等的速度和流速。
坡度的名词解释

坡度的名词解释坡度,是地理和工程学领域常用的术语,用于描述地面或道路的倾斜程度。
它是人们衡量地面或道路倾斜度的指标,也是设计和建造工程项目时的重要考量因素之一。
一、坡度的定义与分类坡度是指地面或道路两点之间的高度差与水平距离之比,通常用百分比或角度表示。
坡度的正负取决于高度差的方向,即从始点到终点是升高还是下降。
从坡度的角度来看,可以将其分为以下几类:1. 平坡:两点之间的高度差几乎为零,即不存在升降。
平坡通常是指相对于建筑物或其他结构物而言的相对平直的地面。
2. 缓坡:两点之间的高度差相对较小,坡度较为平缓。
缓坡常见于山丘、丘陵地带,也是城市规划和道路建设中常用的坡度范围。
3. 陡坡:两点之间的高度差较大,坡度较为陡峭。
陡坡通常出现在山脉、悬崖等地形陡峭的区域。
4. 急坡:两点之间的高度差非常大,坡度极为陡峭。
急坡在自然地理中相对较少见,但在峡谷、断崖等地形特殊的区域可能会出现。
二、坡度在工程中的应用1. 道路建设:坡度是设计和建造道路时必须考虑的要素之一。
不同类型的道路需要不同的坡度,并且应根据道路用途和交通量进行合理设置。
在山区和丘陵地带,合理的坡度设计可以提供良好的排水和减轻车辆行驶负荷,确保道路的安全性和可靠性。
2. 水利工程:在水利工程中,坡度是水流方向和速度的重要影响因素。
合理的坡度设计可以促进水流顺畅,减少水流堆积和水土流失的风险。
例如,农田灌溉系统的坡度应根据需水量和土壤类型进行设计,以确保水流均匀分布。
3. 建筑工程:在建筑设计中,坡度是设计屋顶、地板和台阶等结构物时必须考虑的重要参数。
合理的坡度设计可以防止雨水滞留、减少风险和提高使用寿命。
例如,屋顶坡度应根据降雨量和排水需求设置,以确保雨水迅速排出,避免屋顶渗漏和结构损坏。
4. 地质灾害防治:坡度是评估地质灾害风险的重要指标。
在山区和丘陵地带,地表的坡度对于滑坡、泥石流等自然灾害的发生和发展起着重要作用。
通过准确测量地表坡度,并结合地质条件进行分析,可以及时采取相应的防灾措施,保护人民生命财产安全。
倾角和坡度计算公式

倾角和坡度计算公式在工程和建筑领域中,倾角和坡度是两个重要的概念,它们用于描述物体或地形的倾斜程度。
倾角是指物体或地形与水平面之间的夹角,而坡度则是指物体或地形与水平面之间的斜率。
在实际应用中,我们经常需要根据已知的数据来计算倾角和坡度,因此了解倾角和坡度的计算公式是非常重要的。
倾角的计算公式。
倾角通常用度(°)来表示,它是物体或地形与水平面之间的夹角。
倾角的计算公式如下:倾角 = arctan(坡度)。
其中,arctan是反正切函数,坡度是指物体或地形与水平面之间的斜率。
在实际计算中,我们可以先计算出坡度,然后通过反正切函数来求得倾角。
坡度的计算公式。
坡度是指物体或地形与水平面之间的斜率,它通常用百分比或度数来表示。
坡度的计算公式如下:坡度 = tan(倾角)。
其中,tan是正切函数,倾角是物体或地形与水平面之间的夹角。
通过这个公式,我们可以根据已知的倾角来计算出坡度。
倾角和坡度的实际应用。
倾角和坡度的计算公式在工程和建筑领域中有着广泛的应用。
例如,在道路建设中,我们需要根据地形的倾斜程度来设计路面的坡度,以确保车辆能够顺利通行。
此外,在建筑设计中,我们也需要根据建筑物的倾角来确定其结构和支撑方式。
除此之外,倾角和坡度的计算公式还可以应用于地质勘探、水利工程、航空航天等领域。
通过计算倾角和坡度,我们可以更好地了解地形的特征,从而为工程和建筑设计提供重要的参考信息。
总结。
倾角和坡度是描述物体或地形倾斜程度的重要概念,在工程和建筑领域中有着广泛的应用。
了解倾角和坡度的计算公式对于工程师和设计师来说是非常重要的,它可以帮助他们更好地理解和分析地形的特征,从而为工程和建筑设计提供重要的参考信息。
希望通过本文的介绍,读者们能够更加深入地理解倾角和坡度的计算公式,从而为实际工程和建筑项目的设计和施工提供帮助。
坡度ppt课件

2.07米
17
(2013•眉山)如图,某防洪指挥部发现长江边一处长500米, 高10米,背水坡的坡角为45°的防洪大堤(横断面为梯形 ABCD)急需加固.经调查论证,防洪指挥部专家组制定的 加固方案是:背水坡面用土石进行加固,并使上底加宽3米, 加固后背水坡EF的坡比i=1: 3 (1)求加固后坝底增加的宽度AF; (2)求完成这项工程需要土石多少立方米?(结果保留根 号)
解:在Rt△PBC中, PC=PB•sin∠PBA=4×sin30°=2m, 在Rt△APC中, PA=PC÷sin∠PAB=2÷sin15°≈9.5m. 答:无障碍通道的长度约是9.5m.
21
用字母 表示。
(2)坡度(坡比):坡面
的铅直高度h和水平距离l h
的比叫做坡度,用字母 i
表示. i h tan
l
l
坡度通常写成1:m的形式
4
h α
l
1、斜坡的坡比是1:1 ,则坡角α=______度。
2、斜坡的坡角是600 ,则坡比是 _______。
3、斜坡长是12米,坡高6米,则坡比是_______。
例2、某校教学楼后面紧邻着一个土坡,坡上面是一块平地,
如图所示,BC∥AD,斜坡AB长22m,坡角∠BAD=68°,为了防 止山体滑坡,保障安全, 学校决定对该土坡进行改造.经地质人 员勘测,当坡角不超过50°时, 可确保山体不滑坡.(1)求改造 前坡顶与地面的距离BE的长(精确到0.1m);(2)为确保安全, 学校计划改造时保持坡脚A不动,坡顶B沿BC削进到F点处, 问BF 至少是多少米(精确到0.1m)?
1
1、理解坡角、坡度的概念; 2、会运用解直角三角形有关知识解决
坡度与加速度对照表

坡度与加速度对照表
在我们生活和工作中,坡度和加速度是两个常见的物理概念。
它们在很多领域有着密切的联系,为了更好地理解和应用这两个概念,我们整理了一份坡度与加速度对照表。
本文将详细介绍坡度与加速度的关系,以及如何使用这份对照表。
首先,我们来了解一下坡度与加速度的关系。
在物理学中,坡度指的是物体在垂直于运动方向的平面上的倾斜程度,用角度来表示。
而加速度则是物体在单位时间内速度的变化量,与坡度有一定的关联。
在物体沿斜面滑动的过程中,加速度与坡度成正比,可以通过公式a = gsinθ来计算,其中a为加速度,g为重力加速度,θ为斜面的倾角。
接下来,我们来看看坡度与加速度对照表的实用性。
这份对照表将坡度与加速度之间的关系以直观的形式展示出来,用户只需查找相应坡度对应的加速度值,便可迅速得到所需数据。
这对于工程师、研究人员以及物理爱好者来说,无疑提供了极大的便利。
那么,如何使用这份坡度与加速度对照表呢?很简单,只需根据所需查询的坡度值,在表中找到对应的加速度值即可。
例如,假设我们想要知道30度斜面的加速度,只需在表中找到30度对应的加速度数值,便可得到结果。
坡度与加速度对照表在工程、物理等领域有着广泛的应用。
例如,在建筑领域,工程师可以根据这份表来计算斜坡、屋顶等建筑结构的安全性;在航空航天领域,科学家可以利用对照表来分析飞行器的运动状态。
此外,对照表还可以用于教育、科研等多个方面。
总之,坡度与加速度对照表为我们提供了一个便捷的工具,可以帮助我们更好地理解和应用坡度与加速度之间的关系。
通过本文的介绍,相信大家对这份对照表已经有了更深入的了解。
坡度知识点总结

坡度知识点总结坡度是指地面或者道路在水平方向上的倾斜程度,通常用百分比或者角度来表示。
在建筑、工程、交通等领域中,了解和掌握坡度知识点是非常重要的。
本文将从基本概念、计算方法以及应用领域等方面,对坡度的知识点进行总结。
一、基本概念1.坡度定义:坡度是指地面或者道路在水平方向上的倾斜程度。
它是通过比较垂直距离和水平距离的比例来表示的,可以用百分比、角度或者斜率来表示。
2.百分比坡度:百分比坡度是指在水平距离上垂直变化的百分比。
计算方法为:(垂直距离 / 水平距离) × 100%。
例如,一个坡度为10%的斜坡意味着在水平方向上每移动10米,高度上升1米。
3.角度坡度:角度坡度是指地面或者道路与水平面之间的夹角。
常用的角度单位有度、弧度和百分度。
其中,1度等于0.0175弧度,1度等于100百分度。
4.斜率:斜率是指一条线的倾斜程度,它是用垂直高度变化除以水平位移得到的比值。
斜率的计算方法为:(垂直高度变化 / 水平位移)。
二、计算方法1.百分比坡度的计算:假设有一个斜坡,垂直高度为H,水平距离为D。
百分比坡度的计算公式为:(H / D) × 100%。
2.角度坡度的计算:假设有一个斜坡,垂直高度为H,水平距离为D。
角度坡度的计算公式为:arctan(H / D)。
3.斜率的计算:假设有一条线,垂直高度变化为H,水平位移为D。
斜率的计算公式为:H / D。
三、应用领域1.建筑工程:在建筑设计和施工中,坡度的控制非常重要。
例如,在地基工程中,需要保证坡度合适,以确保建筑物的稳定性。
此外,在室内设计中,也需要考虑坡度,以便排水和地面平整。
2.交通工程:在道路、铁路和桥梁等交通工程中,坡度的控制对于车辆和行人的行驶安全至关重要。
合理的坡度能够减少车辆的制动压力和行驶阻力,提高交通效率。
3.农业工程:在农田的设计和灌溉系统中,坡度的控制对于水分利用和土壤保持具有重要影响。
合理的坡度能够提高土壤排水能力和水分利用效率,减少水土流失。
坡度计算公式坡度高程公式

坡度计算公式-坡度-高程-公式坡度计算在高程测量和土地工程等领域有着重要的应用。
要计算坡度,需要先确定一些基本概念。
坡度是指倾斜面的陡峭程度,通常用角度或坡度比来表示。
高程则是指某一点相对于某一基准面的高度。
在计算坡度时,需要知道高程和距离之间的关系。
一般情况下,坡度的计算公式可以根据实际情况进行不同的表示。
常见的坡度计算公式包括:1.正弦坡度公式:tanθ=h/L其中,θ表示坡度角,h表示垂直距离,L表示水平距离。
2.正切坡度公式:tanθ=h/L这个公式与正弦坡度公式相似,只是将正弦函数换成了正切函数。
3.余弦坡度公式:cosθ=(H^2+L^2)/(2HL)其中,H表示垂直距离,L表示水平距离,θ表示斜面倾角。
该公式也可以用来计算斜率。
4.正切坡率公式:tan(θ)=H/L=(√3)h/L=(√3)dgz/L其中,H表示垂直距离,L表示水平距离,dgz表示最大动摩擦阻力。
该公式也被称为摩擦力公式或正压力公式。
5.道路纵断面坡度公式:tanθ=(P+2B)(V^2-v^2)^(3/2)/gπDR其中,P表示正压力,B表示重力加速度,V表示行车速度,v表示爬坡速度,g表示重力加速度,D表示轮胎与地面之间的摩擦系数,R表示轮胎半径。
该公式也被称为道路纵断面设计公式。
除了以上常见的坡度计算公式之外,还有其他一些特殊情况下的坡度计算公式。
例如,在水利工程中,有一种叫做比流量法的计算方法可以用来计算水流的坡度;在土力学中,土坡的稳定性分析也需要用到坡度计算公式;在测量学中,还有一种叫做高程异常角的计算方法可以用来计算高程异常值;在地理学中,也有一种叫做水文地理学的方法可以用来推算流域的坡度等。
总之,坡度计算公式的具体形式取决于所涉及的领域和实际应用情况。
在实际应用中,需要根据具体情况选择合适的计算方法并掌握相应的计算公式。
这些公式的基本原理是将高程与距离之间的关系转化为数学比例关系来进行计算。
在特殊情况下,还可以根据具体情况采用其他更复杂或特定的公式进行计算。
坡度与坡角

学习目标
1 理解坡度、坡角的概念
2
会运用解直角三角形有关知识解决与坡度坡角有
关的实际问题 (重点)
3 注意数形结合的数学思想和方法 (难点)
1、坡角
坡面
i= h : l
h
α 水平面
l
坡面与水平面的夹角叫做坡角,记作α 。
2、坡度(或坡比)
如图所示,坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面的坡度(或坡比),记作i, 即 i=—h—
C.80sin 20m
D.80cos 20m
5、如图是一个拦水大坝的横断面图,AD∥BC, (1)如果斜坡AB=10m,大坝高为8m,则斜坡AB的 坡度 iAB ____ . (2)如果坡度 iAB 1: 3,则坡角B ____ .
(3)如果坡度 iAB 1: 2, AB 8m,则大坝高度为___.
C
i=1:)垂线BE、CF将梯形分割成Rt△ABE,Rt△CFD和 矩形BEFC,则AD=AE+EF+FD, EF=BC=6m,AE、DF可结 合坡度,通过解Rt△ABE和Rt△CDF求出。
(3)斜坡AB的长度以及斜坡CD的坡角的问题实质上 就是解Rt△ ABE和Rt△ CDF。
A BE
D C
一段路基的横断面是梯形,高为4米,上底的 宽是12米,路基的坡面与地面的倾角分别是 45°和30°,求路基下底的宽.(精确到0.1 米 2 1.414 3 1.732 )
D 12米
4米
45°
A
E
C
30°
F
B
效果检测
1、斜坡的坡度是 1 : 3,则坡角α=______度。 2、斜坡的坡角是450 ,则坡度是 _______。
斜度、锥度与坡度
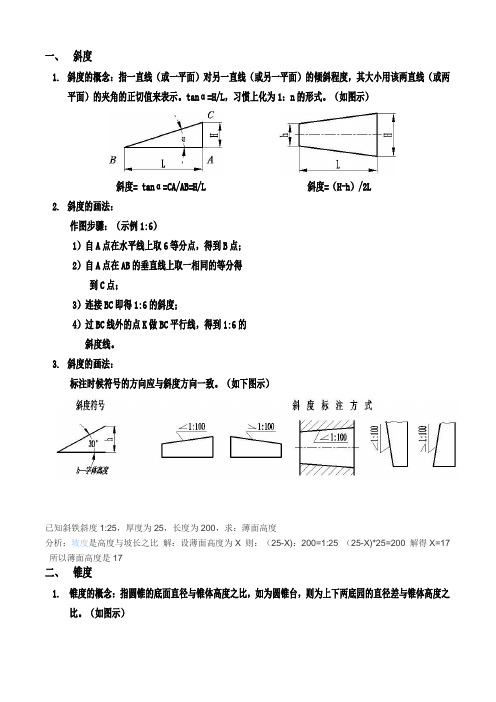
一、斜度1.斜度的概念:指一直线(或一平面)对另一直线(或另一平面)的倾斜程度,其大小用该两直线(或两平面)的夹角的正切值来表示。
tanα=H/L,习惯上化为1:n的形式。
(如图示)斜度= tanα=CA/AB=H/L 斜度=(H-h)/2L2.斜度的画法:作图步骤:(示例1:6)1)自A点在水平线上取6等分点,得到B点;2)自A点在AB的垂直线上取一相同的等分得到C点;3)连接BC即得1:6的斜度;4)过BC线外的点K做BC平行线,得到1:6的斜度线。
3.斜度的画法:标注时候符号的方向应与斜度方向一致。
(如下图示)已知斜铁斜度1:25,厚度为25,长度为200,求:薄面高度分析:坡度是高度与坡长之比解:设薄面高度为X 则:(25-X):200=1:25 (25-X)*25=200 解得X=17所以薄面高度是17二、锥度1. 锥度的概念:指圆锥的底面直径与锥体高度之比,如为圆锥台,则为上下两底园的直径差与锥体高度之比。
(如图示)锥度= D/L 锥度=(D-d)/L2. 锥度的画法:作图步骤:(示例1:3)1)自A点在水平线上取3等分点,得到B点;2)自A点在AB的垂直线上上下各取一相同的等分得到C点和C1点;3)连接BC、BC1即得1:3的锥度;4)过点E、F做BC、BC1的平行线,即得所求圆锥台的锥度线。
3. 锥度的标注:在图样中应采用下图(a)中的图形符号表示锥度,该符号应配置在基准线上。
表示圆锥的图形符号和锥度应靠近圆锥轮廓标注,基准线应与圆锥的轴线平行,图形符号的方向应与圆锥的方向一致(如图b 示)图 a 图 b三、坡度1. 坡度的概念:通常把坡面的铅直高度h与坡面的水平距离l的比叫做坡度(或坡比)。
坡度的表示方法有百分比法、度数法、密位法和分数法。
其中以百分比法和度数法较为常用。
(1) 百分比法表示坡度最为常用的方法,即两点的高程差与其水平距离的百分比,其计算公式如:坡度= (高程差/水平距离)x100% ,即:i=h/l×100%例:1%是指水平距离每100米,垂直方向上升(下降)1米;以次类推!(2) 度数法用度数来表示坡度,利用反三角函数计算而得,其公式如:tanα(坡度)=高程差/水平距离(注意tanα的比值不能作为坡度)▶部分角度的坡度、正切及正弦的关系(如右示)。
离去角 坡度

离去角坡度
离去角和坡度是汽车工程中常用的两个概念,用于描述车辆在不同路面条件下的通过能力。
离去角是指车辆后端底部离开地面的角度,通常用于衡量车辆在爬坡或通过障碍物时后端是否会与地面发生接触。
离去角越大,车辆通过障碍物时后端越不容易与地面接触,从而提高了车辆的通过能力。
坡度则是指路面的倾斜程度,通常用角度或百分比表示。
坡度越大,车辆在爬坡时需要克服的阻力就越大,从而需要更大的动力输出。
在汽车工程中,坡度是一个重要的设计参数,它会影响车辆的动力性能、燃油经济性和行驶稳定性等方面。
离去角和坡度是相互关联的两个概念。
当车辆通过坡度较大的路面时,后端的离去角会减小,从而增加了后端与地面接触的可能性。
因此,在设计车辆时需要考虑离去角和坡度之间的关系,以确保车辆在不同路面条件下具有良好的通过能力和行驶稳定性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
概念:坡度是坡的高度和坡的水平距离之比。
表示坡度最为常用的方法,1.两点的高程差与其水平距离的百分比,坡度=(高程差/水平距离)x100%。
2. 用度数来表示坡度,利用反三角函数计算,公式:α(坡度)=tan-1 (高程差/水平距离)
不同角度的正切坡度对照5°≈9% 10°≈18% 30°≈58% 45°= 100%
汽车的最大爬坡度,是指汽车满载时在良好路面上用第一档克服的最大坡度,它表征汽车的爬坡能力。
爬坡度用坡度的角度值(以度数表示)或以坡度起止点的高度差与其水平距离的比值(正切值)的百分数来表示。
坡度20%,表示坡道直线长度距离(L)为100米,坡高(H)为20米的坡度。
或用斜坡角度theta的tg(theta)的百分数表示。
例如“汽车爬坡度”是30%,根据上述公式得:tgθ×100%=30%,即tgθ=30/100=0.3,查三角函数表得θ≈16°42' ,即此车可爬越的最陡坡度是16°42' 。
如果汽车技术说明书上“汽车爬坡度”直接标注了角度,就是指此车可爬越的最陡坡度。
根据汽车行业规定,只有百分比坡度标注方式才是符合标准的。
如果仅标注数字,实际上也是百分比数字。
国家没有对汽车最大爬坡度强制要求,所以按通常惯例一般越野车最大爬坡度达到30°、小轿车达到20°。
有人也许会问,我的轿车30°、40°的坡都可上去,怎么说只有20多度的爬坡能?其实是我们的车原来已有了行驶速度(动能,即就是死火车也会走)的作用。
假如这个坡足够长时,这个动能就耗尽,车子就会住后退了。
这叫冲坡,和爬坡不是一回事。
这是在襄樊好像,国内最大的试车场。
东风猛士在爬坡。
坡度是60%,约31度。
这可是正经的军用越野车
轿车最高车速大,加速时间短,经常在较好的道路上行驶,一般不强调它的爬坡能力;它的1挡加速能力大,故爬坡能力也强。
货车在各种地区的各种道路上行驶,所以必须具有足够的爬坡能力,一般Imax在30%即16.7°左右。
要进一步说明的是;Imax代表了汽车的极限爬坡能力,它应比实际行驶中遇到的道路最大坡度超出很多,这是因为应考虑到在实际坡道行驶时,在坡道上停车后顺利起步加速、克服松软坡道的大阻力、克服坡道上崎岖不平路面的局部大阻力等要求的缘故。
越野汽车要在坏路或无路条件下行驶,因而爬坡能力是一个很重要的指标,它的最大爬坡度可达60%即31°左右。
车辆的最大爬坡度有两个因素构成:
1.扭矩,保证在爬坡中不致于熄火,与发动机功率和空载重载有关。
2.摩擦力,保证上坡途中不打滑。
在这方面后驱动远远优于前驱动,四轮驱动远远优于二轮驱动,新胎优于旧胎,轮胎的越野花纹优于横花纹,横花纹优于纵花纹轮,干粗路面优于湿平路面。
由于因素较多,以下是在不冲坡(坡前起步)的前提下,爬坡能力一般的近似数据,仅供参考:前驱动轿车,雨雪湿滑路面,<10%,干粗路面15%;4×2货车,25%,6×4货车,32%;4×4吉普车,50%;东风6×6军用越野车,60%,高水平驾驶甚至可以在中途停车起步。
汽车一般能轻松爬上15%的坡度;坦克和装甲车以及军用越野车可爬60%的坡。
有TX会问,再大的坡咋办?那就是工兵的任务了。
上两张豹2爬坡的照片哈,德制豹2的最大爬坡度是60%
%
一般情况下寒冷,积雪地区道路坡度不应大于8%,二级城市道路纵坡不超过5%,高速公路平原<3%,山区<5%,最差的山区道路约为10%。
看似最陡的地下停车场坡道也小于20%。
顺便说一下:铁路轨道坡度超过1%就算陡坡,城市道路要求坡度不超过6%。
早年由于资金和技术的原因,铁路纵向坡度有超过20‰的路段,如宝成线、京原线,但必须减少列车总重和多机车牵引才能运行。
目前新建铁路正线采用长隧道长桥梁等技术,不会再有这样的陡坡了。
列车运行坡度在4‰以下,可不考虑坡度,6‰~8‰为正常的运行坡度,超过13‰的坡度为陡坡,不能停车。
看这个坡有多大?4%而已,这是拍摄角度和镜头透视夸大的。
一般公路坡度标志设在纵坡度在7%和市区纵坡度在大于4%的陡坡道路前适当位置。
综上所述,汽车的爬坡能力远小于我们的想象,人眼对坡度的判断的误差远大于对距离的判断。
